Abstract
Long-distance dispersal (LDD) events, although rare for most plant species, can strongly influence population and community dynamics. Animals function as a key biotic vector of seeds and thus, a mechanistic and quantitative understanding of how individual animal behaviors scale to dispersal patterns at different spatial scales is a question of critical importance from both basic and applied perspectives. Using a diffusion-theory based analytical approach for a wide range of animal movement and seed transportation patterns, we show that the scale (a measure of local dispersal) of the seed dispersal kernel increases with the organisms' rate of movement and mean seed retention time. We reveal that variations in seed retention time is a key determinant of various measures of LDD such as kurtosis (or shape) of the kernel, thinkness of tails and the absolute number of seeds falling beyond a threshold distance. Using empirical data sets of frugivores, we illustrate the importance of variability in retention times for predicting the key disperser species that influence LDD. Our study makes testable predictions linking animal movement behaviors and gut retention times to dispersal patterns and, more generally, highlights the potential importance of animal behavioral variability for the LDD of seeds.
Introduction
Dispersal is the unidirectional movement of an organism, or its reproductive unit (e.g., seeds), away from the place of its origin [1]. In many plant species, a major portion of dispersal events happen close to the parent plant and this short ranged dispersal is an important process that influences both local and larger scale dynamics of the population. It has been suggested that the relatively infrequent but long-distance dispersal (LDD) can also significantly impact larger spatial scale processes such as population abundance, spread, and coexistence with other species [1]–[3]. Due to the role played in determining ecological patterns at higher levels of organization, understanding factors which drive both short-distance and LDD events can provide useful insights into biodiversity management and conservation biology in the context of exotic species invasion, spread of diseases and landscape fragmentation in an increasingly changing world due to anthropogenic influences [4]–[6].
While short-distance dispersal has been well studied for a long time, it is only relatively recently that the significance of the basic as well as applied aspects of LDD in ecology [1] and epidemiology [7] have been well recognized. This has led to a surge in empirical and theoretical studies to device quantitative measures of LDD events. Dispersal patterns are often quantified using dispersal distance kernels/curves, which are functions that describe the probability density of a dispersal unit being deposited at a certain distance from the parent source. Local or short-distance dispersal, i.e., the typical distance within which most of the seeds fall, is often determined by the scale, or standard deviation, of the curve together with its mean [8]. Long-distance dispersal has been quantified by a number of measures such as kurtosis [8]–[10], thickness (or fatness) of tails of dispersal kernels [2] and/or absolute measures such as number of seeds falling beyond a threshold distance [11]. The kurtosis, or the shape, of the kernel measures the distribution of the probability density at both the peak and tails of the kernel [12].
Despite certain limitations involved in using kurtosis as an unambiguous measure of LDD [3], it is widely employed in theoretical [14], simulational [8] as well as empirical studies ([9], [10]). We further note that different definitions of fat-tails are employed in the literature. For example, one approach requires that the tail of the kernel decay at a rate slower than the negative exponential curve [11]. Alternatively, some authors have employed a less restrictive definition that in a fat-tailed kernel, the tail may decay at a rate slower than a Gaussian tail [15]. Theoretical results show that if the tail of the dispersal curve decays like a Gaussian or negative exponential, then the population advances at a constant speed [2], [16], [17]. In contrast, curves with fatter tails can lead to an accelerating rate of invasion of the habitat thus having a large scale and disproportionate impact on population structure [2], [4].
Quantifying LDD in the field, however, is a challenging task owing to its infrequent nature which results in lack of data and reliable statistics [18]–[20]. Therefore it is critical to reveal processes which are key to the formation of a kernel with given statistical properties. More specifically, to gain predictive power on dispersal patterns, one must identify not only the LDD events but also dispersal agents and mechanisms driving these rare events [1], [11]. Wind is a major disperser of seeds and a number of studies based on analytical models, numerical simulations and field data analysis have shown that correlated wind structures, incidence upward drift and seed release during gusts can all drive LDD [21]–[23]. Besides wind, animals form a major vector of dispersal units. Field studies and detailed simulation models have shown that the behavior of dispersers [24]–[32], together with the habitat characteristics and landscape heterogeneity [8] significantly affect dispersal patterns and, in particular, different measures of LDD. With growing interest in animal mediated dispersal there is an increasing need to develop simple and broadly applicable analytical models that can present clear links between measurable aspects of animal behavioral ecology and dispersal events, including LDD. Such a theoretical model can not only provide a better comprehension of the underlying processes influencing dispersal patterns but may also offer useful insights into conservation strategies by identifying key dispersal vectors.
Here, we employ an analytical approach based on a diffusion-theory to link animal movement behavior and seed transportation dynamics to dispersal patterns at different spatial scales (i.e., local and long range dispersal) in one and two spatial dimensions. In particular, we show how the scale (a measure of local dispersal), the kurtosis, the thickness of tail of dispersal kernels (measures of LDD) are determined by animal movement and gut retention time patterns. We also determine how an absolute measure of LDD, defined as the number of seeds falling beyond a threshold distance, is influenced by seed retention time patterns. We show the generality of our results by considering a variety of movement patterns (e.g., diffusive, drift, correlated random walks and home-ranges) and retention time patterns (e.g., passage through the gut, adhesion to the body) likely to be exhibited by animals. We analyze gut-passage time data from the published literature and bird species of a Mediterranean ecosystem and make predictions on the key long-distance dispersers. Finally, we discuss ecological implications of our results, limitations of our study and possible future work.
Methods and Results
During the process of animal mediated dispersal the combined effects of two basic processes, the movement pattern of foraging animals and the method of seed transportation, determine when and where seeds will be released. In this section we describe a simple model to determine how these processes contribute to the construction of a seed dispersal kernel. Since the mathematical framework is general, it can be applied to the dispersal of other units as well (such as pathogens and other micro-organisms).
We assume that seed dispersal processes occur in a spatial domain 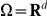 (where
(where 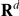 represents
represents 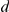 spatial dimensions) and that all seeds originate from a single source,
spatial dimensions) and that all seeds originate from a single source, 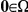 . In calculating the eventual seed dispersal pattern, we assume that animals vary probabilistically in both their movement pattern and seed retention time. Let
. In calculating the eventual seed dispersal pattern, we assume that animals vary probabilistically in both their movement pattern and seed retention time. Let 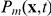 be the probability density that an animal will be at position
be the probability density that an animal will be at position  after
after  units of time since collecting a seed, and let
units of time since collecting a seed, and let 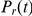 be the probability density that an animal retains the seed for
be the probability density that an animal retains the seed for  units of time. Then the probability density that an animal will release a seed at location
units of time. Then the probability density that an animal will release a seed at location  is obtained by adding the contributions of different dispersal events generated by all probable combinations of animal displacement and seed retention time [8], [26], [33], [34], i.e.,
is obtained by adding the contributions of different dispersal events generated by all probable combinations of animal displacement and seed retention time [8], [26], [33], [34], i.e.,
| (1) |
We refer to 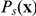 as the seed dispersal kernel (see Table 1 for a summary of model parameters).
as the seed dispersal kernel (see Table 1 for a summary of model parameters).
Table 1. Summary of model parameters.
| Quantity | Description | Dimensions |
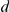
|
number of spatial dimensions | - |
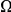
|
spatial domain |
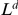
|

|
location in 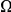
|
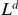
|
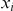
|
 th coordinate of th coordinate of 
|
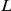
|

|
location in 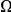 (when (when 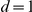 ) ) |
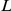
|
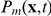
|
animal movement pattern |
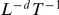
|
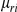
|
mean animal displacement |
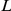
|
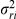
|
variance of animal displacement |
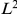
|
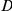
|
diffusion constant |
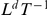
|
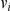
|
velocity |
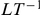
|

|
correlation time |
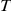
|

|
speed |
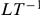
|
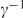
|
average return-time to nesting site in the home-range model |
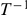
|
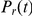
|
seed retention time |
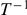
|
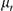
|
mean seed retention time |
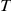
|
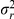
|
variance of seed retention time |
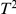
|

|
shape parameter of Gamma distribution | - |
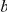
|
scale parameter of Gamma distribution |
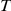
|
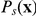
|
seed dispersal kernel |
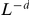
|
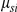
|
mean seed displacement |
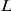
|
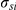
|
standard deviation of seed displacement |
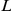
|
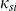
|
excess kurtosis of seed dispersal kernel | - |
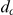
|
threshold dispersal distance |
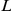
|
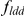
|
proportion of seeds falling beyond a threshold dispersal distance | - |
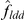
|
normalized 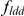 such that, for each fixed such that, for each fixed 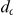 , , 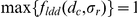
|
- |
Note that 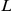 = length,
= length, 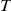 = time. A subscript of
= time. A subscript of  indicates “in the
indicates “in the 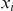 -direction” (when
-direction” (when 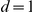 it is omitted).
it is omitted).
Retention time variability can lead to leptokurtic dispersal
Although most animals can move in complex ways within their habitats [35], we will begin our analysis by assuming that animals move randomly in a one-dimensional environment 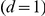 that is both homogeneous and isotropic so that their movement pattern is independent of position and direction. In addition, we assume that individuals do not interact with each other in ways that can alter their movement pattern between the time of seed collection and release. Under these simplistic assumptions, which have been widely employed in the literature to obtain generic principles of movement ecology [17], [35], we recover a familiar form of movement pattern, diffusion. Here, the probability density that an animal will be at location
that is both homogeneous and isotropic so that their movement pattern is independent of position and direction. In addition, we assume that individuals do not interact with each other in ways that can alter their movement pattern between the time of seed collection and release. Under these simplistic assumptions, which have been widely employed in the literature to obtain generic principles of movement ecology [17], [35], we recover a familiar form of movement pattern, diffusion. Here, the probability density that an animal will be at location  after
after  units of time is [17]:
units of time is [17]:
| (2) |
Here, the diffusion constant 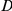 is a measure of an organism's rate of movement or the population's spreading rate.
is a measure of an organism's rate of movement or the population's spreading rate.
Let 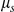 ,
, 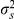 , and
, and 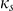 denote the mean, variance, and (excess) kurtosis, respectively, of the seed dispersal kernel
denote the mean, variance, and (excess) kurtosis, respectively, of the seed dispersal kernel 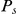 (formal definitions appear in Text S1). Based on Eqs (1) and (2), we show that (see Text S2)
(formal definitions appear in Text S1). Based on Eqs (1) and (2), we show that (see Text S2)
| (3) |
The standard deviation or scale (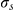 ) is a commonly-used measure of relatively short, or local, dispersal distance. Here, it is seen to increase with spreading rate
) is a commonly-used measure of relatively short, or local, dispersal distance. Here, it is seen to increase with spreading rate 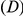 and mean seed retention time
and mean seed retention time 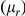 . The kurtosis or shape
. The kurtosis or shape
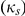 is a frequently used measure of long-distance dispersal [8], [10], [14]. A positive (or negative) kurtosis or shape indicates that events at the peak and tail together occur more (or less) frequently than a Gaussian model would predict. As can be seen in Eq (3), the kurtosis of the seed dispersal kernel is non-negative, positively related to variation in seed retention time
is a frequently used measure of long-distance dispersal [8], [10], [14]. A positive (or negative) kurtosis or shape indicates that events at the peak and tail together occur more (or less) frequently than a Gaussian model would predict. As can be seen in Eq (3), the kurtosis of the seed dispersal kernel is non-negative, positively related to variation in seed retention time 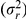 , and inversely related to mean seed retention time
, and inversely related to mean seed retention time 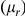 . In contrast, it is unaffected by the spreading rate
. In contrast, it is unaffected by the spreading rate 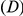 . In other words, variations in the seed retention time is a key generator of leptokurtic seed dispersal kernels. We also emphasize the generality of these results by noting that the expressions in Eq (3) do not depend on the explicit form of the retention time distribution (
. In other words, variations in the seed retention time is a key generator of leptokurtic seed dispersal kernels. We also emphasize the generality of these results by noting that the expressions in Eq (3) do not depend on the explicit form of the retention time distribution (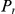 ), but only on the summary statistics (mean and variance) of
), but only on the summary statistics (mean and variance) of 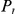 .
.
Retention time variability can lead to power-law seed dispersal kernel
Here, we obtain a sample seed dispersal kernel generated by a diffusively moving population of organisms. To do so, we need to assume a form for the seed retention time distribution (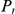 ; see Eq (1)).
; see Eq (1)).
Seed retention time distributions for endozoochory and epizoochory
Endozoochory (passage through the gut) is a widespread form of seed transportation [36], [37], and among animals which disperse seeds in this manner, perhaps the most commonly studied are avian and mammalian frugivores (i.e., consumers of fleshy fruits). Hence, as a starting point, we assume that animals disperse seeds via endozoochory, and following the empirical work of [26], we assume that seed retention times obey a Gamma distribution:
| (4) |
where 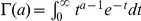 . We remind the reader that a Gamma distribution can reproduce many different kinds of one-sided probability distributions, and moreover that its parameters
. We remind the reader that a Gamma distribution can reproduce many different kinds of one-sided probability distributions, and moreover that its parameters  and
and 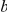 can be written in terms of its mean (
can be written in terms of its mean (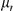 ) and variance (
) and variance (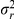 ) as follows
) as follows
| (5) |
Observe that  and
and 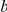 are both non-negative, and they respond in opposite ways to increases in
are both non-negative, and they respond in opposite ways to increases in 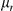 and
and 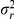 .
.
It is worth remarking that for epizoochory, in which the transportation of seeds is determined by the purely physical process of adhesion, a seed may be released when the adhesive forces become relatively weak, as occurs when an animal's fur slides past an object. If the rate of occurrence of such an event is constant in time, then the probability that an animal will carry a seed for  units of time will follow an exponential distribution, which is itself a Gamma distribution with
units of time will follow an exponential distribution, which is itself a Gamma distribution with 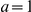 . Furthermore, we note that gamma distribution is often considered a realistic choice for representing survival/waiting times that could be overdispersed or having large coefficients of variation [38].
. Furthermore, we note that gamma distribution is often considered a realistic choice for representing survival/waiting times that could be overdispersed or having large coefficients of variation [38].
Power-law seed dispersal kernel
We now substitute Eqs (2) and (4) into (1) and then integrate to obtain an expression for the seed dispersal kernel
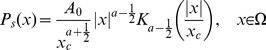 |
(6) |
Here, 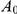 is a positive constant (depending only on
is a positive constant (depending only on  ),
), 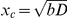 , and
, and 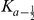 is a modified Bessel function of the second kind [39]. The asymptotic formula
is a modified Bessel function of the second kind [39]. The asymptotic formula 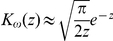 for
for 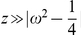 [39] allows us to approximate the seed dispersal kernel at large distances by
[39] allows us to approximate the seed dispersal kernel at large distances by
| (7) |
where 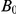 is a positive constant (depending only on
is a positive constant (depending only on  ). In view of this approximation, we see that
). In view of this approximation, we see that 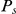 (which decays with distance
(which decays with distance 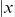 as
as 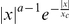 ) has a fatter tail than a Gaussian kernel (which decays as
) has a fatter tail than a Gaussian kernel (which decays as 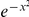 ). It is also important to note that
). It is also important to note that 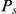 has a power-law behavior for shorter dispersal distances (from Eq (6)). For these reasons, we say that
has a power-law behavior for shorter dispersal distances (from Eq (6)). For these reasons, we say that 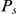 is a power-law kernel with an exponential cut-off. We note similar redistribution kernels have also been derived in the context of heterogeneous population structures and animal movement [15], [33].
is a power-law kernel with an exponential cut-off. We note similar redistribution kernels have also been derived in the context of heterogeneous population structures and animal movement [15], [33].
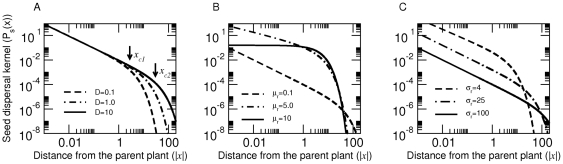
In Fig. 1 we explicitly demonstrate the power-law nature of 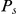 on spatial scales where the log-log plot exhibits a linear relationship. It is useful to refer to
on spatial scales where the log-log plot exhibits a linear relationship. It is useful to refer to  (in
(in 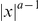 ) as the scaling exponent which can be estimated by the slope of the linear portion of the log-log
) as the scaling exponent which can be estimated by the slope of the linear portion of the log-log 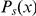 plot. A larger scaling exponent (
plot. A larger scaling exponent ( ) leads to slower decay of the dispersal kernel with distance; when
) leads to slower decay of the dispersal kernel with distance; when 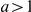 , the power-law part grows with distance but is eventually overtaken by the exponential decay. Next, we define the cut-off distance (
, the power-law part grows with distance but is eventually overtaken by the exponential decay. Next, we define the cut-off distance (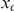 ) as a measure of the spatial scale at which the kernel begins to deviate from the power-law towards exponential decay; the larger the
) as a measure of the spatial scale at which the kernel begins to deviate from the power-law towards exponential decay; the larger the 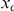 the farther the distance at which this deviation occurs.
the farther the distance at which this deviation occurs.
Figure 1. The seed dispersal kernel 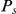 of Eq(6) as a function of movement and retention times.
of Eq(6) as a function of movement and retention times.
For different values of (A) Organism's spreading rate (or diffusion constant 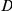 ), (B) mean seed retention time (
), (B) mean seed retention time (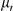 ) and (C) variation in seed retention time (
) and (C) variation in seed retention time (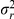 ). In (A),
). In (A), 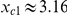 and
and 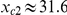 denote the cut-off distance of the power-law behavior for
denote the cut-off distance of the power-law behavior for  and
and 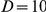 units. Parameters for (A)
units. Parameters for (A) 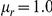 and
and 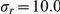 ; (B)
; (B)  and
and 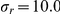 ; (C)
; (C)  and
and 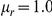 .
.
We now establish links between parameters of the seed dispersal kernel and the two key behaviors (i.e., movement and gut retention times) of the dispersing agent. An increase in the spreading rate of the disperser 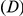 will increase the cut-off distance
will increase the cut-off distance 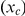 , but the exponent of the power-law (
, but the exponent of the power-law ( ) remains unaffected. In Fig. 1 A we explicitly illustrate that when
) remains unaffected. In Fig. 1 A we explicitly illustrate that when 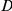 increases from
increases from 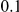 to
to 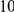 units, the deviation from power-law shifts from
units, the deviation from power-law shifts from 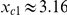 to
to 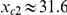 ; and the slope of the linear portion of the log-log plot (and hence the scaling exponent
; and the slope of the linear portion of the log-log plot (and hence the scaling exponent  ) remains the same for different
) remains the same for different 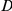 . Furthermore, observe that an increase in the mean seed retention time
. Furthermore, observe that an increase in the mean seed retention time 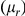 results in an increased power-law exponent (
results in an increased power-law exponent ( ); however, it reduces
); however, it reduces 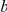 and hence
and hence 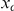 leading to a deviation from power-law at relatively shorter distances (Fig. 1 B). In contrast, an increase in seed retention time variability
leading to a deviation from power-law at relatively shorter distances (Fig. 1 B). In contrast, an increase in seed retention time variability 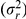 increases the cut-off distance (Fig. 1 C).
increases the cut-off distance (Fig. 1 C).
Kurtosis and thickness of tail of the kernel
We remind the reader that widely used quantities of scale and kurtosis of the seed shadow continue to obey Eq (3). In particular, the measure of kurtosis suggests that the larger the variation in seed retention time, the higher will be long-distance dispersal events in comparison to a Gaussian-like tail. However, the effectiveness of kurtosis as a measure of long-distance dispersal is sometimes questioned [13] because it measures both peakedness and heaviness in tails of a probability distribution [12]. Therefore, it is theoretically possible to construct dispersal kernels where an increased kurtosis may occur only due to peakedness but having no long range dispersal.
To investigate how an increased kurtosis affects the strength of probability distribution at the tail for animal mediated dispersal kernel (Eq (7)), we perform the following analysis. We begin by considering zero variation in retention times (i.e., 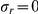 ) that results in a kurtosis of seed dispersal kernel to be
) that results in a kurtosis of seed dispersal kernel to be 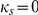 (from Eq (3)). In this special case every animal retains a seed for exactly
(from Eq (3)). In this special case every animal retains a seed for exactly 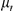 units of time before releasing it. Substituting
units of time before releasing it. Substituting 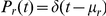 (where
(where 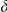 is the Dirac-delta function) and Eq (2) into Eq (1), we obtain
is the Dirac-delta function) and Eq (2) into Eq (1), we obtain
which indeed is a Gaussian kernel. This, in conjunction with the power-law dispersal with an exponential decay of Eqs (6–7), shows that a non-zero retention time variability, and consequently a non-zero kurtosis, does indeed lead to LDD events, as measured by thickness of kernels.
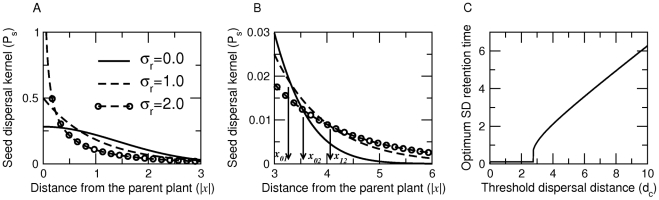
We determine the implications of increasing variations in retention time (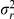 ) on the tail of seed dispersal kernel in more detail. We find that, (i) as
) on the tail of seed dispersal kernel in more detail. We find that, (i) as 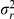 increases, the probability of seed deposition is higher than the Gaussian kernel but only beyond a critical distance, denoted by
increases, the probability of seed deposition is higher than the Gaussian kernel but only beyond a critical distance, denoted by 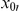 (Fig. 2 A–B). Note that the symbol
(Fig. 2 A–B). Note that the symbol 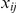 (e.g.,
(e.g., 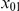 ) indicates the distance at which a seed dispersal kernel with
) indicates the distance at which a seed dispersal kernel with 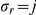 (e.g.,
(e.g., 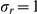 ) begins to have more frequent LDD events than a seed dispersal kernel with
) begins to have more frequent LDD events than a seed dispersal kernel with 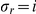 (e.g.,
(e.g., 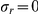 ). Our computations further reveal that this distance (
). Our computations further reveal that this distance (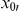 ) increases with an increase in
) increases with an increase in 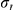 (see Fig. 2 A–B), and consequently with the kurtosis of the seed dispersal kernel (Eq (3)). To give a simple numerical example, when
(see Fig. 2 A–B), and consequently with the kurtosis of the seed dispersal kernel (Eq (3)). To give a simple numerical example, when 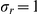 the seed dispersal kernel will have more dispersal events than a Gaussian kernel (generated by
the seed dispersal kernel will have more dispersal events than a Gaussian kernel (generated by 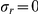 ) would suggest beyond 3.3 units of distance
) would suggest beyond 3.3 units of distance 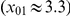 . For a higher value of
. For a higher value of 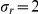 (and hence higher kurtosis in the seed dispersal kernel) we have
(and hence higher kurtosis in the seed dispersal kernel) we have 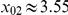 units. In other words, larger variations in seed retention time does indeed lead to higher frequency of dispersal events, than a Gaussian kernel would predict, beyond a threshold distance.
units. In other words, larger variations in seed retention time does indeed lead to higher frequency of dispersal events, than a Gaussian kernel would predict, beyond a threshold distance.
Figure 2. Variation in seed retention time (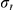 ) that maximizes LDD events.
) that maximizes LDD events.
(A) 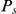 for different values of
for different values of 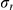 . (B)
. (B) 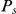 at large distances. The symbol
at large distances. The symbol 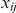 (e.g.,
(e.g., 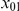 ) indicates the distance at which a seed dispersal kernel with
) indicates the distance at which a seed dispersal kernel with 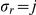 (e.g.,
(e.g., 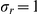 ) begins to have more frequent long-distance dispersal events than a seed dispersal kernel with
) begins to have more frequent long-distance dispersal events than a seed dispersal kernel with 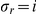 (e.g.,
(e.g., 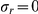 ). As
). As 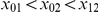 , a larger variability in retention time (
, a larger variability in retention time (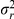 ), thus a larger kurtosis of seed dispersal kernel, leads to fatter seed dispersal tails beyond a threshold distance that increases with
), thus a larger kurtosis of seed dispersal kernel, leads to fatter seed dispersal tails beyond a threshold distance that increases with 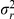 . (C) Optimum value of seed retention time that maximizes absolute LDD (
. (C) Optimum value of seed retention time that maximizes absolute LDD (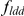 ) (defined as the proportion of seeds falling beyond a threshold dispersal distance
) (defined as the proportion of seeds falling beyond a threshold dispersal distance 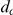 ; also see Text S9). Here we employed two dimensional diffusion with
; also see Text S9). Here we employed two dimensional diffusion with  and
and 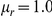 .
.
Retention time variability and an absolute measure of LDD
LDD has also been quantified based on absolute measures ([11]; see Text S9) such as the number of seeds falling beyond a certain threshold distance (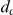 ). It has been shown that larger the organismal rate of movement and mean seed retention times, the larger will be this absolute LDD [11]. Here, we consider how this is influenced by retention time variability.
). It has been shown that larger the organismal rate of movement and mean seed retention times, the larger will be this absolute LDD [11]. Here, we consider how this is influenced by retention time variability.
We compute this absolute measure of LDD for a range of 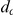 and
and 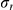 . For each threshold distance (
. For each threshold distance (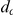 ), we find that there is an optimum variation in seed retention time
), we find that there is an optimum variation in seed retention time 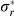 at which the absolute LDD is maximum (Text S9). We then plot
at which the absolute LDD is maximum (Text S9). We then plot 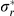 as a function of the threshold distance (
as a function of the threshold distance (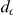 ), which forms a pitchfork-like pattern as shown in Fig. 2 C. When the threshold distance is small, i.e., long-distance dispersal events are not important, there is no need for variation in the retention time. As the threshold dispersal distance increases, the optimal variation in seed retention time also increases.
), which forms a pitchfork-like pattern as shown in Fig. 2 C. When the threshold distance is small, i.e., long-distance dispersal events are not important, there is no need for variation in the retention time. As the threshold dispersal distance increases, the optimal variation in seed retention time also increases.
Generality of results
In this section we test the generality of our results by relaxing various model assumptions. We begin by examining different animal movement patterns 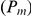 .
.
Animal movement patterns (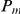 )
)
Animal movement patterns can exhibit a variety of macroscopic properties. Depending on how directional correlations build up, movement patterns can exhibit diffusive, super/sub-diffusive, and/or advective properties over a wide range of spatio-temporal scales [40]. By means of different random walk models, we can explore the generality of our main results.
To begin, consider diffusive movement in a two-dimensional environment 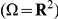 and let
and let 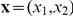 . As shown in Text S3, the mean, scale, and shape of the seed dispersal kernel (
. As shown in Text S3, the mean, scale, and shape of the seed dispersal kernel (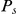 ) along each of the two dimensions (say for the
) along each of the two dimensions (say for the 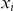 -axis, we denote them by
-axis, we denote them by 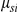 ,
, 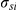 , and
, and 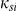 ) all obey the same formulas as their counterparts in Eq (3) (see Fig. 3). In addition, the full kernel
) all obey the same formulas as their counterparts in Eq (3) (see Fig. 3). In addition, the full kernel 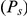 continues to possess a power-law decay with an exponential cut-off.
continues to possess a power-law decay with an exponential cut-off.
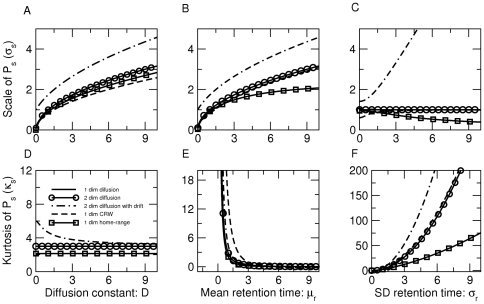
Figure 3. Scale and kurtosis of 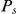 for four different patterns of animal movement.
for four different patterns of animal movement.
Top row of the panel shows scale as a function of the diffusion constant in (A), mean seed retention time in (B), and standard deviation (SD) in seed retention time in (C). In (C) we also demonstrate that in the model with drift, scale increases with SD in retention time and thus differs notably from other movement models. Bottom row (D)–(F) shows kurtosis as a function of the same parameters. Although the qualitative features of kurtosis remain the same across different movement models, it is always larger for the model with drift. For 2 dimensional models, we have plotted scale and kurtosis along one dimension. Parameters for (A) and (D): 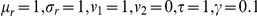 ; for (B) and (E):
; for (B) and (E): 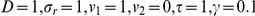 ; for (C) and (F):
; for (C) and (F): 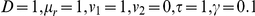 . See Table 1 for a description of parameters.
. See Table 1 for a description of parameters.
Next, suppose that the diffusive motion of animals in two spatial dimensions possesses a drift component in some particular direction. A drift can result for a variety of reasons, including the presence of wind or water, an animal's migratory behavior, or the influence of an elevational gradient [17]. Using the theory of drift-diffusion (also known as advection-diffusion) equations [17], we show in Text S4 that the summary statistics of the seed dispersal kernel (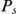 ) are now given by
) are now given by
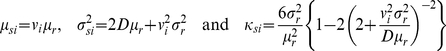 |
The mean seed displacement 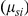 is proportional to the velocity
is proportional to the velocity 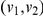 of the advective motion, and the scale
of the advective motion, and the scale 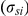 increases with both the mean and variation in seed retention time
increases with both the mean and variation in seed retention time 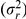 . Both of these results differ qualitatively from the pure diffusion models. Since the kurtosis or shape is larger than the corresponding value in Eq (3), the likelihood of long-distance dispersal is increased when animals have a drift component to their movement (Fig. 3). We also show that the full seed dispersal kernel
. Both of these results differ qualitatively from the pure diffusion models. Since the kurtosis or shape is larger than the corresponding value in Eq (3), the likelihood of long-distance dispersal is increased when animals have a drift component to their movement (Fig. 3). We also show that the full seed dispersal kernel 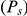 still possesses a power-law structure with an exponential cut-off (Text S4).
still possesses a power-law structure with an exponential cut-off (Text S4).
Suppose now that animals follow correlated random walks (CRW; [35]). A CRW incorporates directional persistence into diffusive motion, reflecting the tendency of randomly moving animals to keep moving in the same direction over a short time scale 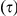 ; this is in contrast to drift-diffusion movement where a constant directional bias exists at all timescales (e.g., downstream of a river). Due to these directional correlations, the wave-front of the animal movement pattern moves at a finite speed, eliminating a dubious feature of diffusive motion in which the wave-front moves infinitely fast [17]. For this movement pattern, a closed form for the seed dispersal kernel
; this is in contrast to drift-diffusion movement where a constant directional bias exists at all timescales (e.g., downstream of a river). Due to these directional correlations, the wave-front of the animal movement pattern moves at a finite speed, eliminating a dubious feature of diffusive motion in which the wave-front moves infinitely fast [17]. For this movement pattern, a closed form for the seed dispersal kernel 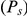 cannot be obtained. Yet, for larger time scales (
cannot be obtained. Yet, for larger time scales (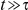 ) the directional correlations decay, resulting in what is effectively diffusive motion [35], [40]. Therefore we expect the qualitative features of the seed dispersal kernel obtained for diffusive motion (i.e., LDD generated through variations in seed retention time), to continue to hold for this movement pattern as well. To support our claim, we show in Text S5 how the scale
) the directional correlations decay, resulting in what is effectively diffusive motion [35], [40]. Therefore we expect the qualitative features of the seed dispersal kernel obtained for diffusive motion (i.e., LDD generated through variations in seed retention time), to continue to hold for this movement pattern as well. To support our claim, we show in Text S5 how the scale 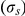 and shape
and shape 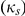 of
of 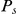 are determined by the effective spreading rate
are determined by the effective spreading rate 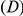 , the mean seed retention time
, the mean seed retention time 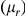 , and seed retention time variability
, and seed retention time variability 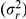 (also see Fig. 3). We find that as the correlations reduce (
(also see Fig. 3). We find that as the correlations reduce (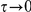 ), the summary statistics of
), the summary statistics of 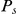 reduce to their counterparts in Eq (3) for diffusive motion.
reduce to their counterparts in Eq (3) for diffusive motion.
In order to avoid competition for resources and/or to reduce predation risks, many animal species possess home-ranges leading to a bounded movement pattern [41]. To model this we assume that, in addition to randomness in motion, animals have a preference to return to a fixed point in space. In Text S6 we show that the features of short-distance dispersal of seeds (i.e., scale) differs qualitatively in comparison to the results of the previous random walk models: it saturates asymptotically to a non-zero constant as mean seed retention time 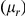 increases and declines to zero as seed retention time variability
increases and declines to zero as seed retention time variability 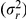 increases. However, the qualitative features of kurtosis remain unaffected (see Fig. 3).
increases. However, the qualitative features of kurtosis remain unaffected (see Fig. 3).
Finally, we consider another extreme in which the animal movement pattern possesses super-diffusive properties over a wide range of scales, e.g., Lévy flights [40]. In Text S7 we utilize a recent model of animal movement in which a power-law animal displacement kernel originates in a statistically structured population [15]. We show that a power-law movement pattern alone can generate LDD of seeds, as one would expect intuitively, even when there is no variability in seed retention time (Text S8).
Seed retention times (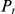 )
)
We now consider the role of the seed retention time distribution (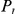 ). Observe from Eq (3) (and its derivation in Text S2) that the scale
). Observe from Eq (3) (and its derivation in Text S2) that the scale 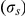 and shape
and shape 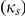 of
of 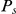 depend only on the mean
depend only on the mean 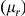 and variance
and variance 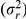 of
of 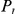 , and not on its particular form. This could imply that details associated with specific mechanisms of seed retention times such as endozoochory, epizoochory, and regurgitation of seeds [42] may be less important in driving LDD, as measured by kurtosis of
, and not on its particular form. This could imply that details associated with specific mechanisms of seed retention times such as endozoochory, epizoochory, and regurgitation of seeds [42] may be less important in driving LDD, as measured by kurtosis of 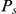 , than the mean
, than the mean 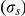 and variations
and variations 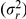 in seed retention times generated by these processes. We note that the Gamma distribution has specific features that can potentially make our results less general; it has a power-law with an exponential cut-off (see the term
in seed retention times generated by these processes. We note that the Gamma distribution has specific features that can potentially make our results less general; it has a power-law with an exponential cut-off (see the term 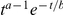 in Eq (4)) and it allows for the occurrence of arbitrarily large values of retention times. In Text S9, based on techniques of ref [15], we argue that a power-law in the seed dispersal kernel (
in Eq (4)) and it allows for the occurrence of arbitrarily large values of retention times. In Text S9, based on techniques of ref [15], we argue that a power-law in the seed dispersal kernel (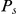 ) appears, albeit for a reduced range of spatial scales, even for seed retention time distributions that do not have these characteristics.
) appears, albeit for a reduced range of spatial scales, even for seed retention time distributions that do not have these characteristics.
Predicting key LDD vectors from empirical data
We consider two empirical data sets for endozoochorial seed retention times (or gut-passage times) in frugivores and use them to predict key vectors responsible for LDD, as measured by kurtosis [10]. Our predictions based on gut-passage time variability (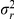 ) identify some vectors as being potentially responsible for LDD, despite the fact that their mean seed retention times
) identify some vectors as being potentially responsible for LDD, despite the fact that their mean seed retention times 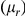 are not among the highest.
are not among the highest.
Our first data set (Table 2) contains mean 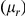 and standard deviation
and standard deviation 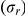 gut-passage times for a variety of plant-frugivorous interactions appearing in the published literature [29], [43], [44]. To compute seed dispersal kernel kurtosis values for each plant-animal interaction, we assume that birds move diffusively in two dimensions while foraging fruits, apply Eq (3) to predict the kurtosis
gut-passage times for a variety of plant-frugivorous interactions appearing in the published literature [29], [43], [44]. To compute seed dispersal kernel kurtosis values for each plant-animal interaction, we assume that birds move diffusively in two dimensions while foraging fruits, apply Eq (3) to predict the kurtosis 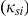 of the seed dispersal kernel along each of the two spatial dimensions, and then obtain the total kurtosis
of the seed dispersal kernel along each of the two spatial dimensions, and then obtain the total kurtosis 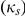 by summing
by summing 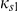 and
and 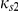 . Note that, in the absence of movement data for the birds considered in this study, we make a simplistic assumption that they move diffusively; however, based on our analysis in the section Generality of results, we expect that the qualitative features of the following analysis will continue to hold.
. Note that, in the absence of movement data for the birds considered in this study, we make a simplistic assumption that they move diffusively; however, based on our analysis in the section Generality of results, we expect that the qualitative features of the following analysis will continue to hold.
Table 2. Seed retention time data from the published literature.
| Bird species | Plant species | # of seeds fed | Gut passage time | Kurtosis (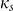 ) ) |
Rank 
|
Reference |
| Casuarius casuarius | Aceratium sericoleopsis | 405 |
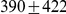
|
7.025 | 1 | [29] |
| Casuarius casuarius | Cryptocarya pleurosperma | 55 |
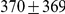
|
5.967 | 2 | [29] |
| Casuarius casuarius | Davidsonia pruriens | 79 |
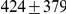
|
4.793 | 3 | [29] |
| Casuarius casuarius | Elaeocarpus grandis | 238 |
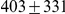
|
4.047 | 4 | [29] |
| Casuarius casuarius | Ficus crassipes | 5730 |
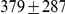
|
3.440 | 5 | [29] |
| Casuarius casuarius | Normanbya normanbyi | 100 |
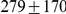
|
2.227 | 6 | [29] |
| Casuarius casuarius | Acmena divaricata | 4 |
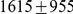
|
2.098 | 7 | [29] |
| Casuarius casuarius | Endiandra longipedicillata | 127 |
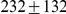
|
1.942 | 8 | [29] |
| Casuarius casuarius | Elaeocarpus largiflorens | 341 |
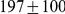
|
1.546 | 9 | [29] |
| Casuarius casuarius | Peripentadenia mearsii | 333 |
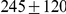
|
1.439 | 10 | [29] |
| Musophaga johnstoni | Syzygium parvifolium | 46 |
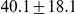
|
1.222 | 11 | [43] |
| Casuarius casuarius | Endiandra impressicosta | 125 |
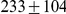
|
1.195 | 12 | [29] |
| Musophaga johnstoni | Psychotria mahonii | 4 |
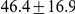
|
0.795 | 13 | [43] |
| Musophaga johnstoni | Maesa lanceolata | 6 |
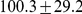
|
0.508 | 14 | [43] |
| Musophaga johnstoni | Ekebergia capensis | 9 |
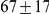
|
0.386 | 15 | [43] |
| Ceratogymna cylindricus | Enantia chlorantha | 6 |
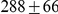
|
0.315 | 16 | [44] |
| Musophaga johnstoni | Balthasarea schliebeni | 3 |
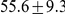
|
0.167 | 17 | [43] |
| Ceratogymna cylindricus | Maesopsis eminii | 3 |
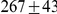
|
0.156 | 18 | [44] |
| Musophaga johnstoni | Ilex mitis | 4 |
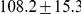
|
0.119 | 19 | [43] |
| Ceratogymna atrata | Cleistopholis patens | 27 |
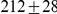
|
0.104 | 20 | [44] |
| Ceratogymna cylindricus | Strombosia scheffleri | 19 |
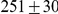
|
0.086 | 21 | [44] |
| Ceratogymna atrata | Xylopia hypolampra | 26 |
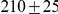
|
0.085 | 22 | [44] |
| Ceratogymna cylindricus | Ficus sp. | 23 |
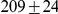
|
0.079 | 23 | [44] |
| Ceratogymna atrata | Staudtia stipitata | 30 |
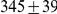
|
0.076 | 24 | [44] |
| Ceratogymna atrata | Rauwolfia macrophylla | 19 |
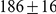
|
0.044 | 25 | [44] |
| Ceratogymna cylindricus | Lannea sp. | 20 |
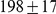
|
0.044 | 26 | [44] |
| Ceratogymna atrata | Maesopsis eminii | 17 |
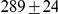
|
0.041 | 27 | [44] |
| Ceratogymna cylindricus | Xylopia hypolampra | 38 |
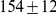
|
0.036 | 28 | [44] |
| Ceratogymna cylindricus | Staudtia stipitata | 22 |
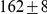
|
0.015 | 29 | [44] |
All plant-animal interactions are ranked according to their predicted kurtosis, with a higher kurtosis indicating that the interaction is more likely to result in the long-distance dispersal of seeds belonging to the plant species. Gut passage times are expressed as mean (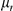 )
) 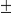 SD (
SD (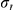 ) (in minutes). Kurtoses are predicted values based on assumed two-dimensional random movement (
) (in minutes). Kurtoses are predicted values based on assumed two-dimensional random movement (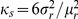 ).
).
First, we find that the same bird species (e.g., Casuarius casuarius) can exhibit large differences in its seed dispersal characteristics (as measured by kurtosis) depending on the type of the seed it consumes and the associated fruit and seed digestive processing. Second, for several plant species there exist multiple frugivores that consume their seeds and are responsible for its dispersal. Based on our kurtosis calculations we predict the relative importance of vectors responsible for LDD. For example, bird species C. cylindricus is likely to fair better as a long-distance disperser of plant species Maesopsis eminii than C. atrata (ranked 18 and 27, respectively); a prediction based on mean seed retention times alone could not have made such a distinction.
Our second empirical gut-passage time data is obtained from P. Jordano (Estación Biológica de Doñana, CSIC), and includes species representative of the avian frugivore fauna of Mediterranean ecosystems. The bird species listed in Table 3 are primarily frugivorous except M. striata (ranked 8), S. torquata (10), F. hipoleuca (12), and S. undata (13) all of which are primarily insectivorous but do disperse seeds occasionally. In dietary experiments, a solution of barium sulphate (an inert tracer that is not digested by birds) was administered, the time of first appearance of the marker in faeces and/or regurgitated seed(s) was noted, and the bird released (Jordano et al, unpublished). The inert tracer technique produces mean and standard deviation gut-passage time data without the influence of seed size, texture, laxative effects of pulp, etc. Therefore the kurtosis can be directly compared across different disperser species to predict the most effective LDD vectors for plants in this ecosystem.
Table 3. Retention time of an inert tracer (barium sulphate) in various Mediterranean bird species.
| Bird species | # of trials | Gut passage time | Kurtosis (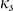 ) ) |
Rank 
|
| Sylvia borin | 37 | 79.0 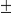 49.0 49.0 |
2.310 | 1 |
| Sylvia melanocephala | 59 | 33.0 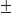 19.8 19.8 |
2.164 | 2 |
| Erithacus rubecula | 38 | 40.7 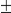 22.7 22.7 |
1.876 | 3 |
| Turdus merula | 7 | 59.1 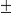 31.2 31.2 |
1.674 | 4 |
| Sylvia atricapilla | 37 | 36.51 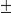 16.5 16.5 |
1.228 | 5 |
| Sylvia communis | 6 | 40.8 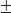 17.8 17.8 |
1.143 | 6 |
| Sylvia cantillans | 10 | 29.9 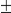 12.9 12.9 |
1.126 | 7 |
| Muscicapa striata | 4 | 48.0 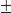 16.5 16.5 |
0.715 | 8 |
| Phoenicurus phoenicurus | 17 | 40.0 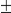 7.9 7.9 |
0.234 | 9 |
| Saxicola torquata | 3 | 52.0 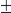 8.5 8.5 |
0.161 | 10 |
| Turdus philomelos | 4 | 60.5 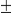 7.7 7.7 |
0.097 | 11 |
| Ficedula hypoleuca | 3 | 58.3 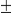 6.0 6.0 |
0.064 | 12 |
| Sylvia undata | 2 | 41.5 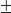 0.7 0.7 |
0.001 | 13 |
Gut passage times are expressed as mean (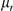 )
) 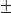 SD (
SD (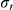 ) (in minutes). Kurtoses are predicted values based on assumed two-dimensional random movement (
) (in minutes). Kurtoses are predicted values based on assumed two-dimensional random movement (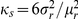 ).
).
As an example, we note large differences between two Turdus species (ranked 4 and 11) as potential long-distance dispersers although their mean retention times are nearly the same (see Table 3 and Figure S1). We add an important note of caution; we have ignored details such as relative abundance of disperser species, frequency of visits to the plant species and quantity of seeds consumed all of which will influence LDD. Our main purpose here is to illustrate predictive power of our simple model and it is possible to extend this formalism to normalize the effects of such detailed mechanisms for a fairer comparison.
Next, we ask whether the spatial range over which power-law dispersal may occur is significant in real systems. This may be obtained, under the assumptions of diffusive movement and gamma distributed retention times, by computing the cut-off distance (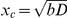 ). For birds of Table 2 and 3, we determine the range of the parameter
). For birds of Table 2 and 3, we determine the range of the parameter 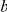 to be in
to be in 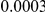 and
and 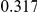 day. We predict that a cut-off distance of
day. We predict that a cut-off distance of 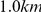 (or more), which is often considered a very large dispersal distance [11], can be achieved when diffusivity of birds is larger than
(or more), which is often considered a very large dispersal distance [11], can be achieved when diffusivity of birds is larger than 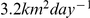 . Since we lack the data for daily foraging movement of birds, we consider natal spreading rates of birds which are more commonly computed [35]; for example, natal diffusivity of obligate frugivores such as white-crowned pigeons in deciduous forests of Florida which has been estimated to be around
. Since we lack the data for daily foraging movement of birds, we consider natal spreading rates of birds which are more commonly computed [35]; for example, natal diffusivity of obligate frugivores such as white-crowned pigeons in deciduous forests of Florida which has been estimated to be around 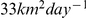 [45]. We emphasize that this is being used as a rough guide to estimate, but not as a substitute for, foraging patterns. Even if the diffusivity of daily foraging movement is smaller by an order of magnitude, it will be large enough to contribute to a substantial (i.e., extending over
[45]. We emphasize that this is being used as a rough guide to estimate, but not as a substitute for, foraging patterns. Even if the diffusivity of daily foraging movement is smaller by an order of magnitude, it will be large enough to contribute to a substantial (i.e., extending over 
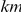 or more) power-law based seed dispersal. We, therefore, suggest that the spatial range over which animal mediated seed dispersal kernel exhibits power-law may indeed be realistically large for certain frugivorous species.
or more) power-law based seed dispersal. We, therefore, suggest that the spatial range over which animal mediated seed dispersal kernel exhibits power-law may indeed be realistically large for certain frugivorous species.
Discussion
We present an analytical model that makes testable predictions relating animal movement behavior and seed retention time characteristics to seed dispersal patterns. We reveal that the scale, which is often employed as a measure of local dispersal, is determined by organisms' rate of movement and mean seed retention time. We then relate patterns of animal movement and gut retention times to different measures of LDD. First, we show that kurtosis or shape of the kernel can be driven by retention time variability of the dispersal units (seeds, pathogens, micro-organisms). Second, we determine that retention time variability can lead to a power-law dispersal with an exponential decay, thus having a tail that decays much slower than a Gaussian kernel. We also compute an absolute measure of LDD, defined as the number of seeds falling beyond a threshold distance, and show that larger the threshold distance, the larger the retention time variance at which LDD is maximized. We demonstrate the potential utility of our results in predicting key drivers of LDD by analyzing real data of frugivores from a Mediterranean forest.
Regardless of the specific mechanism of animal mediated dispersal, we expect that animals that cover larger distances and/or possesses larger seed retention times to more likely to facilitate the long-range transportation of dispersal units. However, it is not obvious how such factors translate into quantitative measures of a seed dispersal curve, such as its mean, scale, and kurtosis (or shape). Our analytical results on how animal behaviors such as rate of movement, and mean seed retention time influence the mean and scale of dispersal kernels are consistent with well established results in the literature on seed dispersal [8], [11], [28]. However, to the best of our knowledge, the variability in the seed retention time has not been identified in previous theoretical and/or empirical studies as an important driver of LDD. Even when such variation has been measured, the focus typically has been on movement patterns and/or large mean seed retention times [26], [28], [29]. We emphasize that it is not our claim that seed retention time variability is the only driver of LDD; instead, we argue that it is sufficient by itself to produce LDD.
We establish the generality and robustness of our results by showing that their qualitative features are largely independent of the details associated with different movement (diffusive, drift with diffusion, correlated random walk and home ranges) and seed transportation mechanisms (endozoochory and epizoochory); i.e., although quantitative differences will occur, these do not affect the main conclusions of our paper. We note that, mathematically, movement and retention times both play an equivalent role in produce dispersal patterns (see Eq(1)). Therefore, we expect that variations in movement, as occurs when populations exhibit multiple modes/scales of movement characteristics ([14]; also see Text S7), will also drive LDD; this is consistent with other works which show that heterogeneous populations may exhibit leptokurtic and fat-tailed dispersal [14], [15], [33]. In addition to our analysis of seed retention times in frugivorous birds of Mediterranean forests, we draw attention to a recent study on an Amazonean frugivore that exhibits huge variations in both movement patterns and gut retention times, and can disperse seeds to extremely large distances [32]. Variability in individual retention times is an inescapable feature of the natural world and together with variations occurring from heterogeneity in movement and population structures, the chances of animal mediated LDD will only enhance.
In this work our aim was to identify minimal features of two key animal behaviors that can explain the large scale phenomenon of LDD. Details such as quantity of seed consumed, relative density of different vectors, habitat quality as well as post dispersal processes such as differential survival rates, germination, etc will all influence the spread and spatial structure of populations in important ways [8], [24]–[31], [46]. Future work can focus on an elaborate testing of our predictions, extend our analytical model to include more complex individual behaviors, heterogeneity in population structure and landscape characteristics as well as how these may affect eventual population and community dynamics.
In summary, we presented a simple analytical study providing clear and empirically testable links between animal movement, seed retention times, and the long-distance dispersal of seeds. A novel prediction of our study is that naturally occurring variations in the retention times of dispersal units by dispersal vectors can lead to long-distance dispersal, as measured through kurtosis, power-law dispersal and/or absolute number of long dispersal events. Such variations may arise, depending on the system and scales studied, at the individual or the population level, or at the community level (i.e., across different species of dispersers). Using empirical data sets we illustrated the importance of variability in seed retention time for predicting the vectors that may potentially drive LDD of seeds. The model framework is general enough to be applicable to other important areas of vector mediated dispersal in ecology such as the spread of diseases. Being able to identify dispersal agents having highly variable retention times of their dispersal units may aid in the design of conservation strategies or the prevention of disease spread.
Supporting Information
Summary statistics of the seed dispersal kernel.
(PDF)
Diffusive movement in one dimension.
(PDF)
Diffusive movement in two dimensions.
(PDF)
Diffusive movement in two dimensions with drift.
(PDF)
Correlated random walks in one dimension.
(PDF)
Random movement in a home-range.
(PDF)
Power-law movement.
(PDF)
Seed retention time distribution.
(PDF)
Absolute measure of long-distance dispersal.
(PDF)
Predicted kurtosis from empirical data sets.
(PDF)
Acknowledgments
The authors V.G., G.H. and A.N. thank Mathematical Biosciences Institute at The Ohio State University where the project was initiated. We are grateful to Pedro Jordano for providing us with the gut-passage data set for a Mediterranean forest; we thank him, Simon Levin and Miguel A Fortuna for comments that improved the manuscript.
Footnotes
Competing Interests: The authors have declared that no competing interests exist.
Funding: The authors thank Mathematical Biosciences Institute (supported by National Science Foundation under Agreement No. 0112050) at the Ohio State University where the project was initiated. FB was supported by a Juan de la Cierva contract from the Spanish Ministry of Science and Innovation. The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
References
- 1.Levin SA, Muller-Landau HC, Nathan R, Chave J. The ecology and evolution of seed dispersal: A theoretical perspective. Annu Rev Ecol Evol Syst. 2003;34:575–604. [Google Scholar]
- 2.Kot M, Lewis MA, van den Driessche P. Dispersal data and the spread of invading organisms. Ecology. 1996;77:2027–2042. [Google Scholar]
- 3.Nathan R, Muller-Landau HC. Spatial patterns of seed dispersal, their determinants and consequences for recruitment. Trends Ecol Evol. 2000;15:278–285. doi: 10.1016/s0169-5347(00)01874-7. [DOI] [PubMed] [Google Scholar]
- 4.Clark JS, Fastie C, Hurtt G, Jackson ST, Johnson C, et al. Reids paradox of rapid plant migration: dispersal theory and interpretation of paleoecological records. Bioscience. 1998;48:13–24. [Google Scholar]
- 5.Higgins SI, Richardson DM. Predicting plant migration rates in a changing world: the role of long-distance dispersal. Am Nat. 1999;153:464–475. doi: 10.1086/303193. [DOI] [PubMed] [Google Scholar]
- 6.Pearson RG, Dawson TP. Long-distance plant dispersal and habitat fragmentation: identifying conservation targets for spatial landscape planning under climate change. Biol Conserv. 2005;123:389–401. [Google Scholar]
- 7.Keeling MJ, Rohani P. Modeling infectious diseases. Princeton: Princeton University Press; 2008. [Google Scholar]
- 8.Morales JM, Carlo TA. The effects of plant distribution and frugivore density on the scale and shape of dispersal kernels. Ecology. 2006;87:1489–1496. doi: 10.1890/0012-9658(2006)87[1489:teopda]2.0.co;2. [DOI] [PubMed] [Google Scholar]
- 9.Clark J, Silman M, Kern R, Macklin E, HilleRisLambers J. Seed dispersal near and far: patterns across temperate and tropical forests. Ecology. 1999;80:1475–1494. [Google Scholar]
- 10.Lowe W. What drives long-distance dispersal? A test of theoretical predictions. Ecology. 2009;90:1456–1462. doi: 10.1890/08-1903.1. [DOI] [PubMed] [Google Scholar]
- 11.Nathan R, Schurr FM, Spiegel O, Steinitz O, Trakhtenbrot A, et al. Mechanisms of longdistance seed dispersal. Trends Ecol Evol. 2008;23:638–647. doi: 10.1016/j.tree.2008.08.003. [DOI] [PubMed] [Google Scholar]
- 12.DeCarlo LT. On the meaning and use of kurtosis. Psychol Methods. 1997;2:292–307. [Google Scholar]
- 13.Lindstrom T, Hakansson N, Westerberg L, Wennergren U. Splitting the tail of the displacement kernel shows the unimportance of kurtosis. Ecology. 2008;89:1784–1790. doi: 10.1890/07-1363.1. [DOI] [PubMed] [Google Scholar]
- 14.Skalski GT, Gilliam JF. A Diffusion-based theory of organism dispersal in heterogeneous populations. Am Nat. 2003;161:441–458. doi: 10.1086/367592. [DOI] [PubMed] [Google Scholar]
- 15.Petrovskii S, Morozov A. Dispersal in a statistically structured population: Fat tails revisited. Am Nat. 2009;173:278–289. doi: 10.1086/595755. [DOI] [PubMed] [Google Scholar]
- 16.Mollison D. Spatial contact models for ecological and epidemic spread. J Roy Stat Soc B (Met) 1977;39:283–326. [Google Scholar]
- 17.Okubo A, Levin SA. Diffusion and ecological problems: modern perspectives. New York: Springer-Verlag; 2001. [Google Scholar]
- 18.Portnoy S, Willson MF. Seed dispersal curves: behavior of the tail of the distribution. Evol Ecol. 1993;7:25–44. [Google Scholar]
- 19.Bullock JM, Clarke RT. Long distance seed dispersal by wind: measuring and modelling the tail of the curve. Oecologia. 2000;124:506–521. doi: 10.1007/PL00008876. [DOI] [PubMed] [Google Scholar]
- 20.Nathan R, Perry G, Cronin JT, Strand AE, Cain ML. Methods for estimating long-distance dispersal. Oikos. 2003;103:261–273. [Google Scholar]
- 21.Nathan R, Katul GG, Horn HS, Thomas SM, Oren R, et al. Mechanisms of long-distance dispersal of seeds by wind. Nature. 2002;418:409–413. doi: 10.1038/nature00844. [DOI] [PubMed] [Google Scholar]
- 22.Katul GG, Porporato A, Nathan R, Siqueira M, Soons MB, et al. Mechanistic analytical models for long-distance seed dispersal by wind. Am Nat. 2005;166:368–381. doi: 10.1086/432589. [DOI] [PubMed] [Google Scholar]
- 23.Soons MB, Bullock JM. Non-random seed abscission, long-distance wind dispersal and plant migration rates. J Ecol. 2008;96:581–590. [Google Scholar]
- 24.Fragoso JMV, Silvius KM, Correa JA. Long-distance seed dispersal by tapirs increases seed survival and aggregates tropical trees. Ecology. 2003;84:1998–2006. [Google Scholar]
- 25.Jordano P, Garcia C, Godoy JA, Garcia-Castano JL. Differential contribution of frugivores to complex seed dispersal patterns. Proc Nat Acad Sci. 2007;104:3278–3282. doi: 10.1073/pnas.0606793104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Murray K. Avian seed dispersal of three neotropical gap-dependent plants. Ecol Monogr. 1988;58:271–298. [Google Scholar]
- 27.Schupp E. Quantity, quality and the effectiveness of seed dispersal by animals. Plant Ecol. 1993;107:15–29. [Google Scholar]
- 28.Westcott DA, Graham DL. Patterns of movement and seed dispersal of a tropical frugivore. Oecologia. 2000;122:249–257. doi: 10.1007/PL00008853. [DOI] [PubMed] [Google Scholar]
- 29.Westcott DA, Bentrupperba'umer J, Bradford MG, McKeown A. Incorporating patterns of disperser behavior into models of seed dispersal and its effects on estimated dispersal curves. Oecologia. 2005;146:57–67. doi: 10.1007/s00442-005-0178-1. [DOI] [PubMed] [Google Scholar]
- 30.Russo SE, Portnoy S, Augspurger CK. Incorporating animal behavior into seed dispersal models: Implications for seed shadows. Ecology. 2006;87:3160–3174. doi: 10.1890/0012-9658(2006)87[3160:iabisd]2.0.co;2. [DOI] [PubMed] [Google Scholar]
- 31.Hawkes C. Linking movement behaviour, dispersal, and population processes: is individual variation key? J Anim Ecol. 2009;78:894–906. doi: 10.1111/j.1365-2656.2009.01534.x. [DOI] [PubMed] [Google Scholar]
- 32.Anderson JT, Nuttle T, Rojas JSS, Pendergast TH, Flecker AS. Extremely long-distance seed dispersal by an overfished amazonian frugivore. Proc Roy Soc B. 2011;278:3329–3335. doi: 10.1098/rspb.2011.0155. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Neubert MG, Kot M, Lewis MA. Dispersal and pattern formation in a discrete-time predatorprey model. Theor Popul Biol. 1995;48:7–43. [Google Scholar]
- 34.Williams EJ. The distribution of larvae of randomly moving insects. Austral J Biol Sci. 1971;14:598–604. [Google Scholar]
- 35.Turchin P. Quantitative Analysis of Movement: Measuring and Modeling Population Redis- tribution in Animals and Plants. Sunderland: Sinauer Associates; 1998. [Google Scholar]
- 36.Janzen DH. Dispersal of seeds by vertebrate guts. In: Futuyma DJ, Slatkin M, editors. Coevolution. Sunderland: Sinauer Associates; 1983. pp. 232–262. [Google Scholar]
- 37.Herrera C. Determinants of plant-animal coevolution: the case of mutualistic dispersal of seeds by vertebrates. Oikos. 1985;44:132–141. [Google Scholar]
- 38.Bolker BM. Ecological models and data in R. Princeton: Princeton University Press; 2008. [Google Scholar]
- 39.Abramowitz M, Stegun IA. Handbook of mathematical functions. New York: Courier Dover Publications; 1965. [Google Scholar]
- 40.Bartumeus F, da Luz MGE, Viswanathan GM, Catalan J. Animal search strategies: a quantitative random-walk analysis. Ecology. 2005;86:3078–3087. [Google Scholar]
- 41.Moorcroft PR, Lewis MA. Mechanistic home range analysis. Princeton: Princeton University Press; 2006. [Google Scholar]
- 42.Levey DJ. Seed size and fruit-handling techniques of avian frugivores. Am Nat. 1987;129:471–485. [Google Scholar]
- 43.Sun C, Ives AR, Kraeuter HJ, Moermond TC. Effectiveness of three turacos as seed dispersers in a tropical montane forest. Oecologia. 1997;112:94–103. doi: 10.1007/s004420050288. [DOI] [PubMed] [Google Scholar]
- 44.Holbrook KM, Smith TB. Seed dispersal and movement patterns in two species of Ceratogymna hornbills in a West African tropical lowland forest. Oecologia. 2000;125:249–257. doi: 10.1007/s004420000445. [DOI] [PubMed] [Google Scholar]
- 45.Strong AM, Bancroft GT. Postedging dispersal of white-crowned pigeons: implications for conservation of deciduous seasonal forests in the Florida Keys. Conservation Biology. 1994;8:770–779. [Google Scholar]
- 46.Dennis AJ, Westcott DA. Estimating dispersal kernels produced by a diverse community of vertebrates. In: Dennis, et al., editors. Seed Dispersal. CAB Internatioal; 2007. pp. 201–208. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Summary statistics of the seed dispersal kernel.
(PDF)
Diffusive movement in one dimension.
(PDF)
Diffusive movement in two dimensions.
(PDF)
Diffusive movement in two dimensions with drift.
(PDF)
Correlated random walks in one dimension.
(PDF)
Random movement in a home-range.
(PDF)
Power-law movement.
(PDF)
Seed retention time distribution.
(PDF)
Absolute measure of long-distance dispersal.
(PDF)
Predicted kurtosis from empirical data sets.
(PDF)