Calculation of Rate Spectra from Noisy Time Series Data

Abstract

As the resolution of experiments to measure folding kinetics continues to improve, it has become imperative to avoid bias that may come with fitting data to a predetermined mechanistic model. Towards this end, we present a rate spectrum approach to analyze timescales present in kinetic data. Computing rate spectra of noisy time series data via numerical discrete inverse Laplace transform is an ill-conditioned inverse problem, so a regularization procedure must be used to perform the calculation. Here, we show the results of different regularization procedures applied to noisy multi-exponential and stretched exponential time series, as well as data from time-resolved folding kinetics experiments. In each case, the rate spectrum method recapitulates the relevant distribution of timescales present in the data, with different priors on the rate amplitudes naturally corresponding to common biases toward simple phenomenological models. These results suggest an attractive alternative to the “Occam’s razor” philosophy of simply choosing models with the fewest number of relaxation rates.

Introduction

Complex kinetics often arises in systems with large of numbers of chemical states. Because of this, one might expect protein folding kinetics to be complex, but remarkably, many proteins appear to fold in a two-state manner (U ⇌ N), with barrier-limited kinetics predicted by a simple Arrhenius model. As the time resolution accessible by folding kinetics experiments continues to improve, however, evidence of more complex folding kinetics can now be observed [1, 2].

Traditionally, the interpretation of experimental kinetics have required fitting to some predetermined mechanistic model. A common procedure is to describe the kinetics with the fewest number of number of relaxation rates, thus producing the “simplest” possible network of barrier-limited states. Herein lies a problem, because the simplest model that explains the data may not necessarily be the model with the fewest number of rates. For example, the kinetics may not be in the barrier-limited regime to begin with. Another problem is that kinetics experiments usually measure a single reaction coordinate, and it is very difficult (especially in folding studies) to design experimental probes that can unambiguously report on specific conformational states. In this case, fitting kinetic data to a simple phenomenological model may not capture important details of the underlying dynamics.

With these issues in mind, we present a rate spectrum approach to analyze timescales present in kinetic data, without imposing any pre-existing mechanistic model. Instead of fitting to a model with a predetermined number of rates, the rate spectrum approach can be thought of as fitting to a distribution of rate amplitudes, in a way that is informed by some simple prior knowledge about the shape of this distribution. In some ways, this approach is in the same spirit of model-free approaches in interpreting NMR experiments [3].

The rate spectrum approach

The rate spectrum approach is akin to calculating a inverse Laplace transform for discrete time series: we assume the signal can be described as a sum of exponential-decay basis functions, and our main task is to estimate the amplitude of each. A somewhat analogous experimental method is modulation fluorometry, in which distributions of relaxation rates can be extracted from fluorescence decays [4]. For a time series (t_i, y_i), i = 1, …, N, the rate spectrum approach can be posed as the problem of finding the coefficients β_j, j = 1, …, K corresponding to a set of rates k_j, (of our choosing), to find the best-fit model:

$${{\displaystyle \widehat{y}}}_i={\displaystyle \sum _{j=1}^K{{\displaystyle \beta }}_j\text{exp}(-k_j{t}_i)}$$ (1)

Computing rate spectra is an example of an ill-conditioned inverse problem, so a regularization scheme is needed to make the solution of this inverse problem well-behaved, especially in the presence of noise. Once a rate spectrum (i.e. set of β_j) is obtained, however, one can identify all the timescales present in the data, and use this information as a starting point for inferring mechanistic models.

The regularized rate spectrum can be obtained as the set of β_j that minimize the quantity

$$\frac{1}{2}{{\displaystyle (\mathbf{y}-\mathbf{X}\beta )}}^T(\mathbf{y}-\mathbf{X}\beta )-\lambda f(\beta )$$ (2)

where X_ij = e^−k_jt_i. The left-hand term is simply the residual sum of squared errors, while the right-hand term is a penalty for large (positive or negative) values of β_j. The strength of this penalty is controlled by λ, the regularization parameter, and f(β) defines the type of regularization. We look at three different types of regularization, each of which impose different penalties on the magnitude of the rate amplitudes: ridge regression $(f=\frac{1}{2}{\sum }_j{\beta }_j^2)$, lasso regression (f = ∑_j|β_j|), and elastic net regression ($f=\frac{\mathrm{\rho }}{2}{\sum }_j{\beta }_j^2+(1-\mathrm{\rho }){\sum }_j|{\beta }_j|$, for mixing parameter 0 ≤ ρ ≤ 1). It can be shown (see Methods) that these different regularization penalties correspond to different prior distributions on the set of rate amplitudes, and (as we show below) are useful in different situations. (For an excellent in-depth discussion of these and other regularization schemes, see Elements of Statistical Learning by Hastie, Tibshirani and Friedman [5].)

What do regularized spectra look like? Without regularization, we obtain the least-squares solution, which usually results in a spiky, irregular spectrum, with ŷ overfit to the noise. As λ increases, the sensitivity to noise decreases, and the spectra broaden (Supplementary Figure S1). When the regularization parameter is very large, or the data very noisy, spectra can become broadened considerably, however, in most cases peaks in the spectra can be recovered that correspond to the most important timescales present in the data (Figure 2).

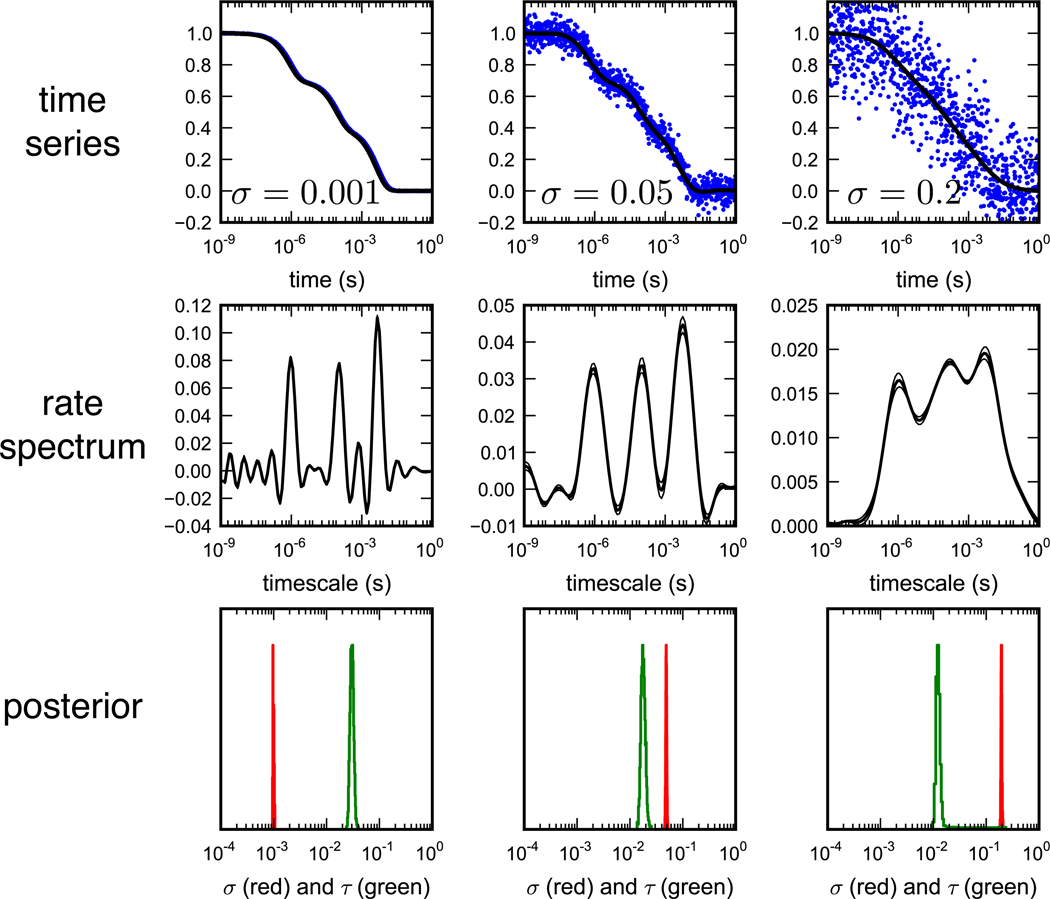
Figure 2.

Noise broadens regularized rate spectra. (top) Regularized rate spectra (using ridge regression) for the tri-exponential data with increasing amounts of noise N(0, s²), for s = 0.001, 0.05 and 0.2. (middle) Rate spectra shown are expectation values from posterior sampling, shown with a 95% confidence interval (in all cases very small). Despite this spectral broadening, regularized rate spectra show three peaks corresponding to each timescale, even for very noisy data. (bottom) The posterior distributions sampled for σ and τ give additional information about the nature of the data being fit. While the posterior distribution of τ remains robust for different values of synthetic noise (reflecting the regularization penalty), the posterior distributions of σ are very narrow and predict extremely well the variance of the artificial noise used to product the time series.

One of the crucial questions in regularization problems is how to choose the regularization parameter λ. Our method treats this as a Bayesian inference problem, in which the posterior likelihood of possible models (i.e. sets of rate amplitudes) can be sampled, along with nuisance parameters σ and τ, which are width parameters for the noise and rate amplitude priors, respectively (see Methods). In this scheme, it can easily be shown that λ = σ²/τ² (see Supplementary Information). We use a Monte Carlo algorithm to sample over σ, τ (and ρ) to obtain estimates of the posterior P(λ|y) (Supplementary Figure S2).

Below, we apply regularization to several examples of synthetic and actual experimental data. Our results show that the rate spectra approach can robustly discern multiple timescales from very noisy data. Moreover, the form of the solutions obtained by these methods sheds light on typical biases in fitting simple models to data.

Methods

Calculation of rate spectra from a time series (t_i, y_i), i = 1, …, N, can be posed as the problem of finding the coefficients β_j, j = 1, …, K corresponding to a set of rates k_j, (of our choosing) such that

$${{\displaystyle \widehat{y}}}_i={\displaystyle \sum _{j=1}^K{{\displaystyle \beta }}_j\text{exp}(-k_j{t}_i)}$$ (3)

The problem can be cast as a linear regression model, if we transform the times t_i into a series of “regressors” x_i = (e^−k₁t_i, e^−k₂t_i, …, e^−k_Kt_i), such that

$$\mathbf{ŷ}=\mathbf{X}\beta$$ (4)

where X_ij = e^−k_jt_i.

In simple least-squares regression, the best-fit β̂ are the values that minimize the residual sum of squared error (RSS):

$$RSS={(\mathbf{y}-\mathbf{ŷ})}^T(\mathbf{y}-\mathbf{ŷ})={(\mathbf{y}-\mathbf{X}\beta )}^T(\mathbf{y}-\mathbf{X}\beta )$$

As long as N ≥ K, and X has full column rank, y = Xβ is an over-constrained system of linear equations, and the β that minimizes the RSS is given by β̂ = X⁺y, where X⁺ is the Moore-Penrose pseudo-inverse X⁺ = (X^TX)⁻¹X^T.

The regression problem, however, is ill-conditioned because the transformation of the time series into x_i is highly nonlinear, so solutions of fitted values β_j may be very sensitive to small changes in the inputs y_i. Additionally, for large values of K, over-fitting becomes a problem, with large positive values of β_j balancing out large negative values in such a way as to tightly fit the y_i training data, regardless of noise.

To deal with these problems, a method of regularization is required. A typical procedure is a method called Tikhonov regularization, also known as ridge regression. In ridge regression, a constrained optimization is used to find the solution for β̂

$$\begin{array}{cc}\widehat{\beta }=& {\text{argmin}}_{\beta }\{{{\displaystyle (y-\mathbf{X}\beta )}}^T(y-\mathbf{X}\beta )\}\\ & \text{subject to}{{\displaystyle \beta }}^T\beta \le t\end{array}$$ (5)

The Lagrangian form of this optimization problem gives a quantity that can be explicitly minimized in order to find β̂, using the Lagrange multiplier λ.

$$\widehat{\beta }={\text{argmin}}_{\beta }\{{{\displaystyle (\mathbf{y}-\mathbf{X}\beta )}}^T(\mathbf{y}-\mathbf{X}\beta )-\lambda {\beta }^T\beta \}$$ (6)

Here, λ is a regularization parameter, and its role is to penalize large (positive or negative) values of β_j. The optimal β can be obtained from $\widehat{\beta }={{\displaystyle \mathbf{X}}}_{\lambda }^{+}y$, where ${{\displaystyle \mathbf{X}}}_{\lambda }^{+}$ is the pseudo-inverse of an (N + K) × K matrix X_λ

$${{\displaystyle \mathbf{X}}}_{\lambda }=\left(\begin{array}{c}\mathbf{X}\\ \sqrt{\lambda }I\end{array}\right)$$

Two related schemes for regularization are lasso regression, in which a penalty is imposed on the sum of the absolute values of β_j,

$$\widehat{\beta }={\text{argmin}}_{\beta }\{\frac{1}{2}{{\displaystyle (\mathbf{y}-\mathbf{X}\beta )}}^T(\mathbf{y}-\mathbf{X}\beta )-\lambda {\displaystyle \sum _{j=1}^K|{{\displaystyle \beta }}_j|}\}$$ (7)

and elastic net regression, in which a combination of penalties is used, with the mixture controlled by an additional parameter ρ:

$$\widehat{\beta }={\text{argmin}}_{\beta }\{\frac{1}{2}{{\displaystyle (\mathbf{y}-\mathbf{X}\beta )}}^T(\mathbf{y}-\mathbf{X}\beta )-\lambda [\frac{\rho }{2}{{\displaystyle \beta }}^T\beta +(1-\rho ){\displaystyle \sum _{j=1}^K|{{\displaystyle \beta }}_j|}]\}$$ (8)

As we will see below, each of these schemes has a particular probabilistic interpretation.

We also note that, unlike ridge regression, solving for β within these other regularization schemes does not come straightforwardly from application of the pseudoinverse. Instead, more general convex optimization schemes must be employed. In the case of lasso regression, for instance, the problem can be reduced to a least-squares problem with additional inequality constraints [6]. In practice, we use a coordinate-descent algorithm to perform minimizations for lasso and elastic net regression.

A Bayesian regularization scheme

An all-important question in regularization problems is: to what extent should our solutions for β be regularized? Ideally, best estimates for λ could be made using the training data itself, with various in-data schemes to avoid overfitting, for example, using generalized cross-validation [5, 7]. Alternatively, a Bayesian approach can be used to obtain the posterior likelihood P(λ|y) of a given regularization parameter λ given the training data y. According to Bayes’ rule, the posterior probability P(λ|y) is proportional to the likelihood of observing the data y given a model parameterized by λ, multiplied by some prior probability P(λ).

$$P(\lambda |\mathbf{y})\propto P(\mathbf{y}|\lambda )P(\lambda )$$

A probabilistic interpretation of λ comes from the following model (see Supplementary Information): If we assume that (1) the coefficients β_j are normally distributed with variance τ², i.e. β ~ N(0, τ²I), and (2) that the training data y_i are contaminated with Gaussian noise of variance σ², i.e. y ~ N (Xβ, σ²I), it can be shown that the λ parameter in ridge regression corresponds to:

$$\lambda =\frac{{\sigma }^2}{{\tau }^2}$$

This provides an intuitive interpretation of the meaning of λ: it is the Lagrange multiplier used to simultaneously enforce the variance (τ²) of the amplitudes β_j, as well as the variance (σ²) in the resulting fit ŷ.

Similarly, lasso regression has the interpretation λ = σ²/τ², but with the amplitudes β_j drawn from the prior distribution

$${{\displaystyle \beta }}_j~\frac{1}{{{\displaystyle 2\tau }}^2}\text{exp}(-\frac{|{{\displaystyle \beta }}_2|}{{{\displaystyle \tau }}^2})$$

Elastic net regression has the interpretation that the prior for each β_j is

$${{\displaystyle \beta }}_j~A(\tau ,\rho )\text{exp}(-\rho \frac{{{\displaystyle \beta }}_j^2}{{{\displaystyle 2\tau }}^2}-(1-\rho )\frac{|{{\displaystyle \beta }}_j|}{{{\displaystyle \tau }}^2})$$

where ρ is a mixing parameter and A(τ, ρ) is a normalization constant (see Supplementary Information).

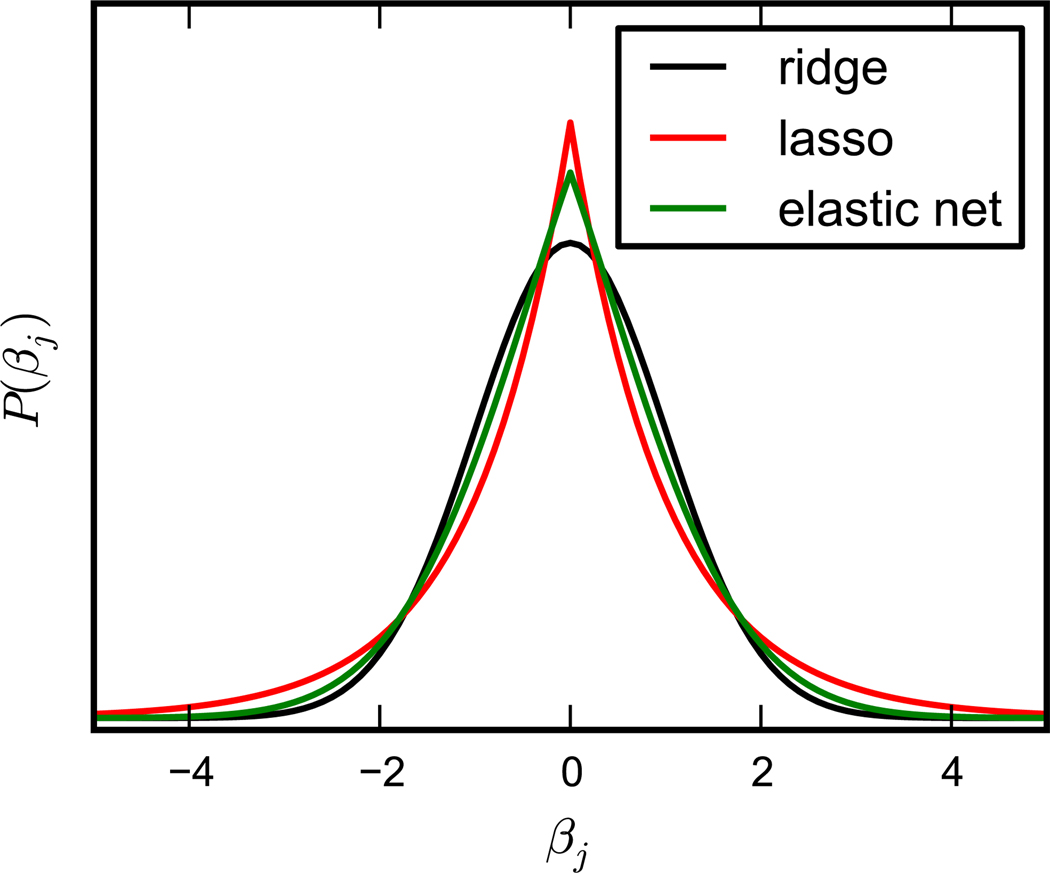
A visual inspection of these prior distributions (Figure 1) shows that the lasso regression should produce more exaggerated peaks in rate spectrum: as compared to ridge regression, it favors β_j either close to zero, or with large amplitude. The prior for elastic net lies somewhere between these two limiting cases.

Figure 1.

Prior distributions of rate amplitudes β_j according to ridge regression (black), lasso regression (red), and elastic net regression (green; shown for ρ = 0.5).

Although we don’t know the values of σ and τ a priori, we can make estimates from the training data, by considering the posterior likelihood of σ and τ given the data y. From Bayes’ rule, this can be computed as:

$$P(\sigma ,\tau |\mathbf{y})\propto P(\mathbf{y}|\sigma ,\tau )P(\sigma )P(\tau )$$

Here P(σ) and P(τ) are prior distributions for σ and τ, respectively, assuming σ and τ are independent. Conjugate priors are often chosen for the sake of obtaining analytical solutions. We can avoid unnecessary assumptions regarding the prior distributions by sampling numerically from the posterior. We use the non-informative (scale-invariant) Jeffrey’s priors P(σ) ~ 1/σ and P(τ) ~ 1/τ to obtain a complete expression for the (unnormalized) posterior likelihood [8]:

$$P(\beta ,\sigma ,\tau |\mathbf{y})\infty \{{\displaystyle \prod _{i=1}^N\frac{1}{\sqrt{{{\displaystyle 2\pi \sigma }}^2}}\text{exp}(\frac{{{\displaystyle -({{\displaystyle y}}_i-{{\displaystyle \sum }}_j{{\displaystyle \mathbf{X}}}_{ij}{{\displaystyle \beta }}_j)}}^2}{{{\displaystyle 2\sigma }}^2})}\}\{{\displaystyle \prod _{j=1}^K\frac{1}{\sqrt{{{\displaystyle 2\pi \tau }}^2}}\text{exp}(\frac{-{{\displaystyle \beta }}_j^2}{{{\displaystyle 2\tau }}^2})}\}(\frac{1}{\sigma })(\frac{1}{\tau })$$

We assume that the distribution P(β) is very sharply peaked at $\widehat{\beta }={\mathbf{X}}_{\lambda }^{+}\mathbf{y}$, so that β is determined completely from λ and the training data y

$${\displaystyle \int P(\beta ,\sigma ,\tau |\mathbf{y})}d\beta \approx P(\sigma ,\tau |\mathbf{y}){|}_{\widehat{\beta }}$$

The posterior can then be written

$$P(\sigma ,\tau |\mathbf{y})\propto \{{\displaystyle \prod _{i=1}^N\frac{1}{\sqrt{{{\displaystyle 2\pi \sigma }}^2}}\text{exp}(\frac{{{\displaystyle -({{\displaystyle y}}_i-{{\displaystyle \sum }}_j{{\displaystyle X}}_{ij}{{\displaystyle \widehat{\beta }}}_j)}}^2}{{{\displaystyle 2\sigma }}^2})}\}\{{\displaystyle \prod _{j=1}^K\frac{1}{\sqrt{{{\displaystyle 2\pi \tau }}^2}}\text{exp}(\frac{-{{\displaystyle \beta }}_j^2}{{{\displaystyle 2\tau }}^2})}\}(\frac{1}{\sigma })(\frac{1}{\tau })$$

We use this expression to obtain posterior estimates of P(λ|y) by simulation-based methods. With enough samples, λ can be treated as a nuisance parameter to obtain an expectation estimate for the set of relaxation amplitudes β_j.

$$\langle \beta (\mathbf{y})\rangle ={\displaystyle \int \widehat{\beta }(\lambda |\mathbf{y})}P(\lambda |\mathbf{y})d\lambda$$

To sample from the posterior distribution, we use a Monte Carlo algorithm using −log P(σ, τ|y) as an effective energy function, which (up to a constant) is easily shown for ridge regression to be:

$$-\text{log}P(\sigma ,\tau |\mathbf{y})=(N+1)\text{log}\sigma +(K+1)\text{log}\tau +{\displaystyle \sum _i\frac{{{\displaystyle ({{\displaystyle y}}_i-{\displaystyle {\sum }_j{{\displaystyle \mathbf{X}}}_{ij}{\widehat{\beta }}_j})}}^2}{{{\displaystyle 2\sigma }}^2}+{\displaystyle \sum _j\frac{{{\displaystyle \widehat{\beta }}}_j^2}{{{\displaystyle 2\tau }}^2}}}$$

The first two terms in this expression favor small values of σ and τ, while the last two terms favor large values of σ and τ, so the posterior has a maximum at some intermediate value of λ = σ²/τ².

For lasso regression, the expression for −log P(σ, τ|y) is the nearly same, but with the terms involving τ slightly modified:

$$-\text{log}P(\sigma ,\tau |\mathbf{y})=(N+1)\text{log}\sigma +(2K+1)\text{log}\tau +{\displaystyle \sum _i\frac{{{\displaystyle ({{\displaystyle y}}_i-{\displaystyle {\sum }_j{{\displaystyle X}}_{ij}{\widehat{\beta }}_j})}}^2}{{{\displaystyle 2\sigma }}^2}+{\displaystyle \sum _j\frac{|{{\displaystyle \widehat{\beta }}}_j|}{{{\displaystyle \tau }}^2}}}$$

For elastic net regression, −log P(σ, τ|y) is found to be (see Supplementary Information):

$$-\text{log}P(\sigma ,\tau |\mathbf{y})=(N+1)\text{log}\sigma +(K+1)\text{log}\tau +K\xi (\tau ,\rho )+{\displaystyle \sum _i\frac{{{\displaystyle ({{\displaystyle y}}_i-{\displaystyle {\sum }_j{{\displaystyle X}}_{ij}{\widehat{\beta }}_j})}}^2}{{{\displaystyle 2\sigma }}^2}}+\rho {\displaystyle \sum _j\frac{{{\displaystyle \widehat{\beta }}}_j^2}{{{\displaystyle 2\tau }}^2}}+(1-\rho ){\displaystyle \sum _j\frac{|{{\displaystyle \widehat{\beta }}}_j|}{{{\displaystyle \tau }}^2}}$$

where $\xi (\tau ,\rho )=-\frac{1}{2}\text{log }\rho +{{\displaystyle \gamma }}^2+\text{log}(1+\text{Erf}(\gamma ))$. This expression comes from the normalization of P(σ, τ|y).

As discussed in [8], sampling from the posterior in this way has a number of advantages compared to cross-validation. For example, the Bayesian approach is completely determined by the data, avoids the need to define any particular partition of the data, and is robust to sparse data. More importantly, a key advantage of Bayesian regression, as opposed to ridge regression (which requires some in-data estimate of optimal λ = σ²/τ², typically by cross-validation), is that the posterior provides some interpretable evaluation of how ill-posed the problem is – i.e. the posterior will be broad if the problem is ill-posed. Performing ridge regression for an ill-conditioned problem using a single λ value, even after optimizing to find the best value of λ, could still result in either a very shrunk estimate with a poor fit, or wildly different estimates that all fit the data. While this too is akin to having a wide posterior, it is much harder to interpret.

Also note that the posterior likelihood function depends on the number of rates K used in computing the spectrum. Thus, when K is large (comparable to N) the regularization penalty in the posterior likelihood becomes much larger, and may result in a broadened spectrum. This reflects the amount of statistical evidence available for the calculation; i.e. if one attempts to find K = 1000 rate coefficients β_j to explain only N = 1000 samples in a time series, the posterior will be more heavily weighted by the prior distribution of β_j. With more evidence (say, using only K = 100 rates), the calculation is more heavily weighted towards the data.

Sampling from the posterior

In practice, to sample from the posterior, we use the following procedure, starting with an initial guess of (σ, τ):

1. propose new candidate (σ′,τ′) as a small perturbation from (σ, τ)

2. calculate $\widehat{\beta }={{\displaystyle \mathbf{X}}}_{\lambda }^{+}\mathbf{y}$, and use it to compute −log P(σ, τ|y)

3. accept or reject the move according the Metropolis criterion (i.e. (σ′,τ′) → (σ, τ) with probability min(1, P(σ′, τ′|y)/P(σ, τ|y))

4. repeat

(For posterior sampling using the elastic net prior, the algorithm is the same, but includes sampling over an additional parameter, ρ. )

For each accepted sample (σ, τ)_m obtained via the Monte Carlo sampling algorithm, we keep track of the predicted β̂_m, and corresponding weight w_m = P(σ, τ|β̂_m), so that we can compute the expectation 〈β〉 using the entire collection of posterior samples:

$$\langle \beta \rangle =\frac{{\displaystyle {\sum }_m{{\displaystyle w}}_m{\widehat{\beta }}_m}}{{\displaystyle {\sum }_m{{\displaystyle w}}_m}}$$

Uncertainty in 〈β〉 can be computed as

$${{\displaystyle \sigma }}_{\beta }^2=\frac{{\displaystyle {\sum }_m{{\displaystyle w}}_m{{\displaystyle ({{\displaystyle \widehat{\beta }}}_m-\langle \beta \rangle )}}^2}}{{\displaystyle {\sum }_m{{\displaystyle w}}_m}}$$

For all the results shown here, twenty thousand steps of Gibbs sampling in (σ, τ) was performed, with moves in σ and τ generated by random perturbations by ε ~ N (0,α²) where a typical value of α was 0.005. (ρ was sampled similarly for elastic net regression.)

Results

Rate spectra of noisy multi-exponential time series

To test the rate spectra approach, we considered the following noisy tri-exponential time series:

$$y(t)={{\displaystyle \alpha }}_1\text{exp}(-t/{{\displaystyle \tau }}_1)+{{\displaystyle \alpha }}_2\text{exp}(-t/{{\displaystyle \tau }}_2)+{{\displaystyle \alpha }}_3\text{exp}(-t/{{\displaystyle \tau }}_3)+N({{\displaystyle 0,s}}^2)$$

where (τ₁, τ₂, τ₃) = (10⁻⁶s, 10⁻⁴s, 5×10⁻³s), (α₁,α₂,α₃) = (0.3, 0.3, 0.4), and N(0, s²) denotes normally-distributed noise of variance s². One thousand samples y_i were generated at time points t_i exponentially-spaced between 10⁻⁹ second and 1 second (i.e. log t_i is linearly-spaced). Rate spectra were calculated using 100 rates, exponentially-spaced (i.e. linear on a log-scale) over a range of 1 s⁻¹ and 10⁹ s⁻¹. Note that if we wish to compare these results to a continuous inverse Laplace transform, each coefficient β_j can be thought of as carrying an additional factor d(log t_i) to account for the change of integration variable.

When we compare the results of ridge, lasso and elastic net regression for the s = 0.05 test data (Figure 3), we see that the lasso regression predicts a much more peaked rate spectrum, more closely approximating the “true” rate spectrum we would expect for a pure tri-exponential decay with no noise. This agreement is because the corresponding prior for the β_j more closely matches our preconceived expectations (that the time series contains a small number of high-amplitude timescales.) The elastic net regression produces rate spectra somewhere in between those of the ridge and lasso. Posterior sampling of ρ shows a range of likely mixing parameters, between 0.2 and 0.5. One attractive feature of both the lasso and elastic net is the prediction of rate coefficients that are exactly zero, due to the presence of terms |β_j| in the regularization constraint.

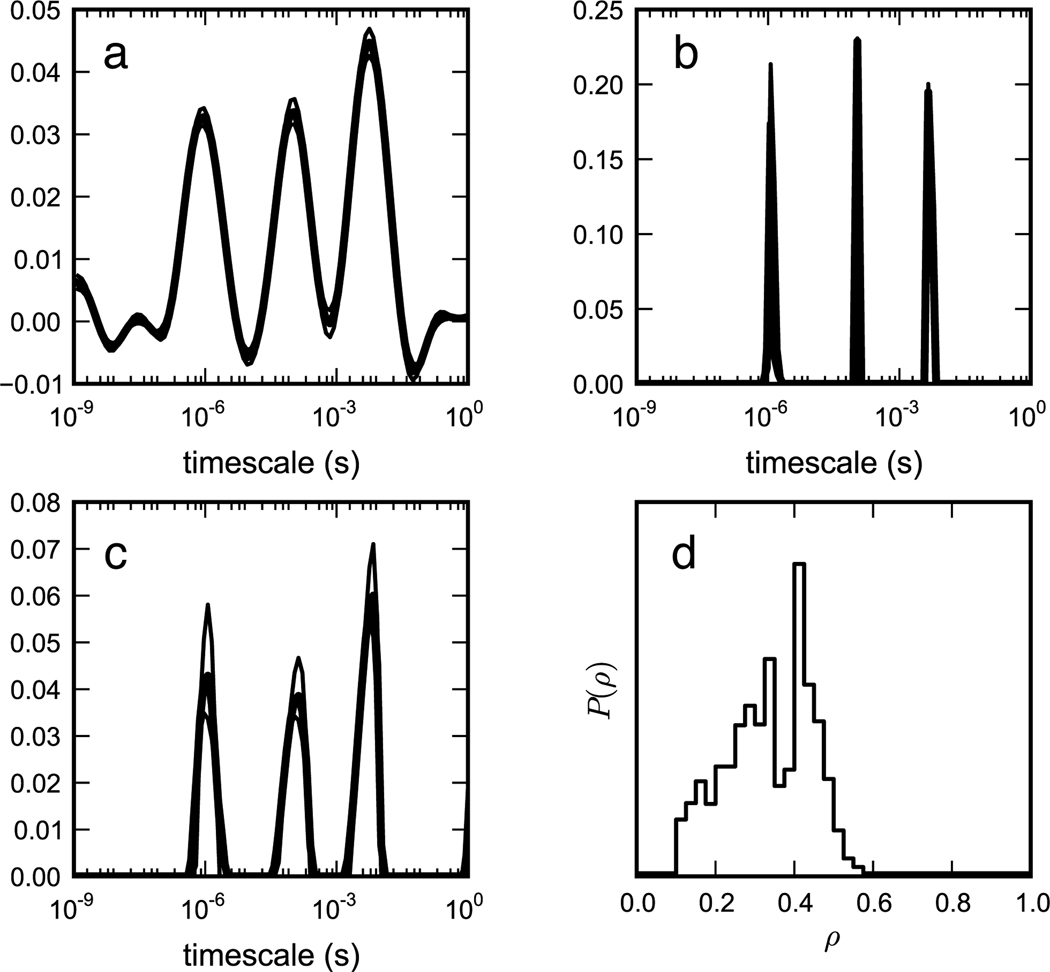
Figure 3.

Rate spectra for the tri-exponential data with artificial noise N(0, s²), s = 0.05, using (a) ridge regression, (b) lasso regression and (c) elastic net regression. Rate spectra shown are expectation values from posterior sampling, shown with a 95% confidence interval. (d) The sampled posterior distribution of mixing parameter ρ in the elastic net regression.

Rate spectra of noisy stretched-exponential time series

For non-exponential kinetics, a common procedure is to fit data with a so-called “stretched exponential” function.

$$y(t)=A\text{ exp }\left[-{{\displaystyle \left(\frac{t}{{{\displaystyle \tau }}_0}\right)}}^{\gamma }\right]$$

where γ is a stretching parameter, 0 < γ ≤ 1. The stretched exponential can be thought of as arising from kinetic phenomena on a broad range of timescales, as in the relaxation of glassy materials [9]. An analytical solution for the (continuous) rate spectrum H_γ(k) exists [10] (see Supplementary Information), which we compare to calculated rate spectra of stretched exponentials in the presence of noise.

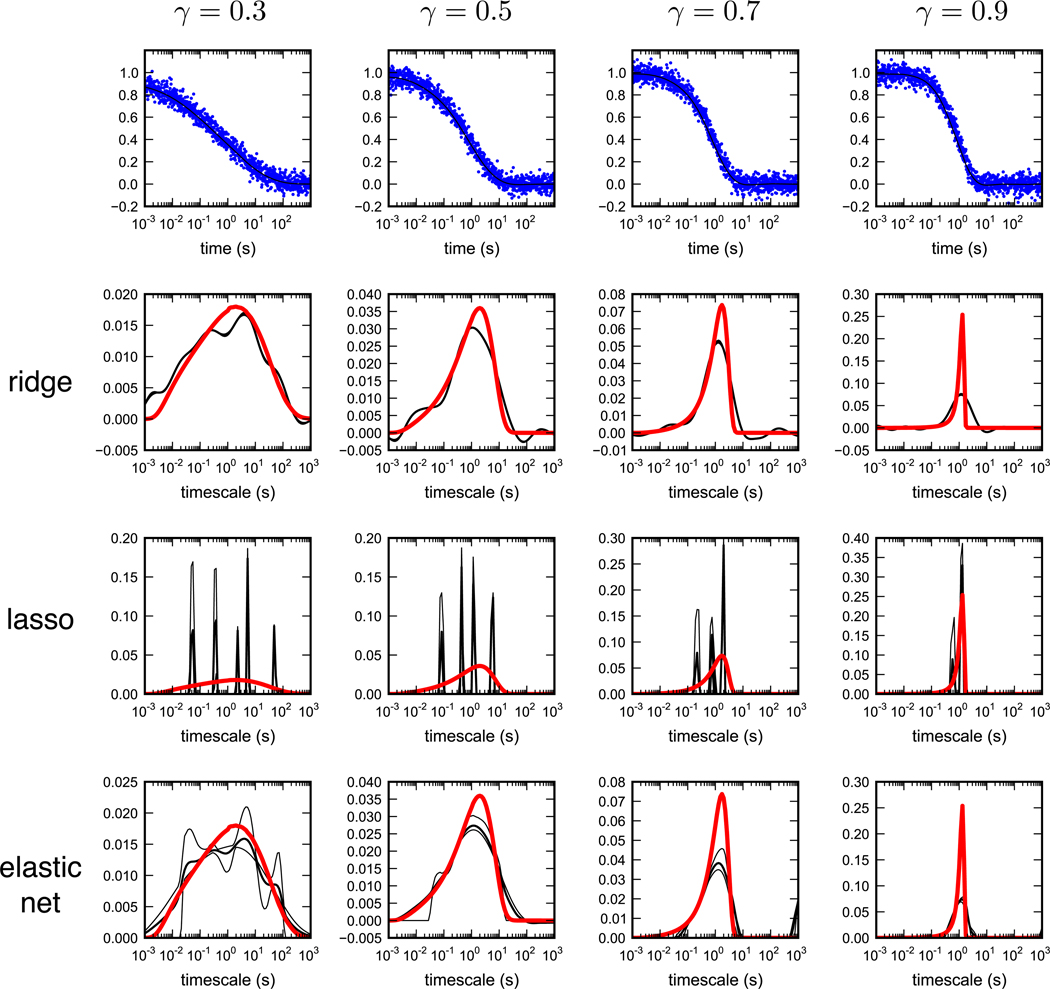
We computed rate spectra using ridge, lasso and elastic net regression for various stretching parameters (Figure 4). For these tests, 1000 samples were generated from a stretched exponential time course (with τ₀ set to 1 second), with synthetic noise added (s = 0.05), over timescales between 10⁻³ and 10³ seconds, for various stretching parameters. As in the tri-exponential tests, 100 rates were used to compute spectra, and posterior sampling of P(λ|y) was used to determine the extent of regularization. Our results confirm that that regularized rate spectra for ridge and elastic net regression can indeed recapitulate rate spectra very similar to the analytic result Hγ(k). Lasso regression, however, consistently predicts spectra dominated by a limited number of timescales. As the stretching parameter decreases, lasso regression essentially predicts the minimum number of timescales needed to explain the data: two timescales for γ = 0.9, three for γ = 0.7, four for γ = 0.5, and five for γ = 0.3.

Figure 4.

Recapitulation of stretched-exponential rate spectra from noisy time series. (top) Noisy data sets (s = 0.05, blue) with best-fit time traces ŷ (shown are the results from ridge regression; best-fits from lasso and elastic net are nearly indistinguighable) for various stretching parameters γ = 0.3, 0.5, 0.7 and 0.9. (bottom) Regularized rate spectra (shown here as the expectation over all posterior samples of λ) for ridge, lasso and elastic net regression. The ridge and elastic net rate spectra correspond well to the analytical results (red line), while lasso regression consistently describes the data with the smallest possible number of timescales. Note that the elastic net posterior takes longer to converge, as can be seen in by the larger error estimates from posterior sampling.

Like the tri-exponential case, the rate spectrum that best approximates the analytic result comes using the prior distribution of rate amplitudes most closely approximating our expectations–in this case, ridge regression, which generates broad, continuous spectra. The lasso regression results, however, show that a small number of exponential relaxations may fit the data equally well. This highlights why stretched-exponential fits must be performed with caution: such models are predicated upon the existence of a broad, continuous spectrum of relaxation rates; this assumption must be justified for reasons other than simply a good fit to the data (for example, by physical argument).

Application to analysis of folding kinetics

While describing folding kinetics using a stretched exponential is common, it is usually an acknowledgement that the kinetic data are sufficiently complex to warrant more than one timescale, yet lack statistical power to make more definite claims about the nature of such timescales. The stretching parameter γ in this case provides a convenient single-parameter model to describe the complex kinetics.

Liu et al. (2008) published temperature-jump (T-jump) fluorescence traces of WW domain folding kinetics at different temperatures, for several sequences having a range of thermal stabilities. Figure 3 of Li et al. shows examples of contrasting traces: a mutant whose kinetics is well-described by a single-exponential (an “apparent two-state folder” [11]), versus a trace that can be fit more accurately to a single-exponential plus a stretched-exponential component. The purpose of this fitting was (mainly) to identify the faster of two relaxation timescales (the so-called molecular timescale, fit by a stretched-exponential) that the authors consistently observed across many experiments.

We were interested to see if our rate spectra method could identify these fast timescales, and perhaps extract more information about them. Ten thousand steps of posterior sampling (using 100 rates between 1 and 10⁸ s⁻¹) were performed for the time traces in Figures 3a and 3b of Li et al., each of which consist of 357 samples between 0 and 100 µs. For clarity, we will refer to these data as traces A and B.

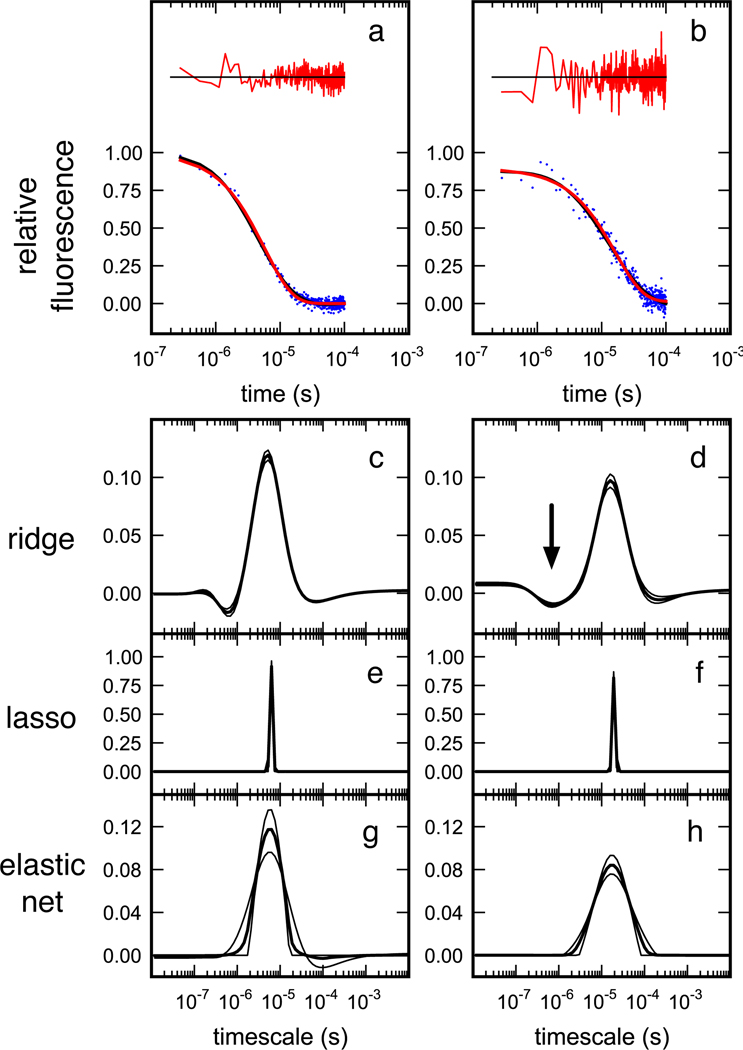
While it is very difficult to discern deviations from single-exponential kinetics by visual inspection (Figure 5), ridge regression is indeed able to reveal a broadened (negative amplitude) peak near a timescale of ~ 1 µs for trace B, corresponding well to the molecular timescale of ~ 1.2 ± 0.5 µs originally found by curve-fitting. The width of this peak also is consistent with the stretching parameter originally found by fitting, γ ~ 0.4.

Figure 5.

Relative fluorescence time traces reprinted from Liu et al. (2008): Relaxation kinetics of a WW domain (variant 20) after T-jump to (a) the melting temperature, and (b) 19° C below the melting temperature. Single-exponential fits to the time traces and their residuals are shown in red; ridge regression fits are shown in black. Rate spectra for these two traces are shown for (c,d) ridge regression, (e,f) lasso regression, and (g,h) elastic net regression. Ridge regression identifies a broadened (negative amplitude) peak near the 1 µs timescale (marked with arrow).

Neither lasso nor elastic net regression supports more than a single timescale given the available data, although we note that the elastic net method predicts a broadened rate distribution for the low-temperature T-jump. This situation could, of course, change with more data at early timescales, as there are many more points sampled in the trace after 10⁻⁵ s than before this time. (Obtaining such experimental data, of course, is very challenging, and a motivation for this analysis in the first place.)

Discussion

In this paper, we have presented a new approach for calculating rate spectra from noisy time series data. We have shown that when rate spectra are calculated with a suitable Bayesian regularization scheme, relaxation timescales can be robustly recovered from noisy time traces. As is clear from the examples we present, the statistical power of such spectral analysis depends on the extent of available data, and our prior assumptions about the distribution of rate amplitudes.

What regulation scheme should be used in a given situation? This depends on how much information is known a priori about the distribution of rates. For situations in which little is known about the underlying rate processes contributing to the observed data, ridge regression works well. While the rate spectra obtained from ridge regression are more broad, our results show how this regularization procedure recapitulates the relevant timescales as maxima in the rate spectra.

In situations where we are much more confident in expecting a limited number of timescales, lasso regression does an excellent job of reproducing the true theoretical rate spectra (a combination of three delta functions) from noisy tri-exponential test data. In a traditional curve-fitting scenario, fitting the fewest number of exponential relaxations would be deemed the “simplest” model, but in the context of rate spectra calculation, lasso regression achieves this by enforcing our prior assumptions that distribution of timescales should be dominated by only a few relevant timescales. The elastic net method, using a mixture of ridge and lasso priors, produces rate spectra that lie between these two extremes.

Our results calculating rate spectra for noisy stretched-exponential time courses suggest that, although such time courses can be fit with curves having very few free parameters (namely τ₀ and γ), this does not imply that a stretched-exponential is the most parsimonious model that explains the data. Rather, the stretched-exponential is a phenomenological law that serves as a proxy to describe complicated distributions of timescales. The analytical rate distributions corresponding to a perfect stretched-exponential are not extracted very efficiently with lasso and elastic net regularization methods, because these methods impose strict penalties on broad distributions of relaxation timescales. Despite this, lasso regression for a noisy stretched-exponential curve (γ = 0.3) shows that a narrow rate spectrum consisting of five main timescales can explain the time course equally well. If our prior expectation is that only a few well-defined relaxation rates exist, lasso regression may be preferred.

This work highlights the importance of model-independent analysis of time series data, and the dangers of conflating two very different questions. One question is: which model best describes my data? This can be answered using any number of hypothesis testing schemes. A very different question, addressed by our work here, is: what timescales are present in my data? The rate spectrum method provides a framework illuminating these timescales from the available data. Unbiased by any preconceived model, rate spectra can thus serve as a very useful starting point for guide more thorough studies of folding kinetics and other dynamic systems.

A growing number of studies have reported that Markov State Models (MSMs) of protein folding, despite having a large number of metastable states and relaxation time scales, predict simple apparent kinetics for experimental observables. These studies have found that projections of the MSM folding dynamics onto experimental observables may be sensitive to only a small number of timescales, masking the underlying complexity [12, 13, 14]. For this and other reasons, we think it is very likely that as the temporal and structural resolution of experiments and simulations continue to increase, using rate spectra to analyze folding kinetics will be increasingly useful.

A python package is available for computing rate spectra using the methods described in this paper. Code and examples are freely downloadable at https://simtk.org/home/ratespec.