Abstract
Cell surface receptors have been extensively studied because they initiate and regulate signal transduction cascades leading to a variety of functional cellular outcomes. An important class of immune receptors (e.g., T-cell antigen receptors) whose ligands are anchored to the surfaces of other cells remain poorly understood. The mechanism by which ligand binding initiates receptor phosphorylation, a process termed “receptor triggering”, remains controversial. Recently, direct measurements of the (two-dimensional) receptor-ligand complex lifetimes at cell-cell interface were found to be smaller than (three-dimensional) lifetimes in solution but the underlying mechanism is unknown. At the cell-cell interface, the receptor-ligand complex spans a short intermembrane distance (15 nm) compared to long surface molecules (LSMs) whose ectodomains span >40 nm and these LSMs include phosphatases (e.g., CD45) that dephosphorylate the receptor. It has been proposed that size-based segregation of LSMs from a receptor-ligand complex is a mechanism of receptor triggering but it is unclear whether the mechanochemistry supports such small-scale segregation. Here we present a nanometer-scale mathematical model that couples membrane elasticity with the compressional stiffness and lateral mobility of LSMs. We find robust supradiffusive segregation of LSMs from a single receptor-ligand complex. The model predicts that LSM redistribution will result in a time-dependent tension on the complex leading to a decreased two-dimensional lifetime. Interestingly, the model predicts a nonlinear relationship between the three- and two-dimensional lifetimes, which can enhance the ability of receptors to discriminate between similar ligands.
Introduction
The binding of ligands to specific cell surface receptors initiates intracellular signaling cascades that lead to various cellular responses (e.g., proliferation, differentiation, survival, etc.). Given their importance in initiating and regulating cellular responses, cell surface receptors have been intensively studied. The process by which ligand binding produces intracellular signaling, termed “receptor triggering”, is well understood for some classes of receptors but remains poorly understood for others. We briefly discuss three classes of receptor: 1), heterotrimeric guanine nucleotide-binding protein G-protein-coupled receptors (GPCRs); 2), receptor tyrosine kinases (RTKs); and 3), noncatalytic tyrosine-phosphorylated receptors (NTRs) (the least understood, and the focus of this article). NTRs include an important class of immune cell receptors that are directly responsible for fundamental immunological decisions and, crucially, the discrimination of foreign antigenic ligands from self (1,2). These immune receptors contain conserved tyrosine-containing motifs (e.g., ITAMs, ITIMs, ITSMs; see Davis and van der Merwe (1) for a review) in their cytoplasmic tails. In contrast to RTKs, these receptors do not contain intrinsic catalytic activity and are instead regulated by extrinsic kinases and phosphatases. In contrast to GPCRs, NTRs do not have multiple transmembrane domains and binding-induced conformational changes in their cytoplasmic tails have not been conclusively demonstrated.
The vast majority of NTR ligands are either surface-anchored molecules or soluble molecules that only trigger NTRs when bound to surfaces (e.g., IgG). This stands in contrast to GPCRs and RTKs, whose ligands are typically soluble. The best-characterized example of an NTR is the T-cell antigen receptor (TCR) (2). This surface receptor binds antigen, in the form of short peptides bound to major-histocompatibility complexes (pMHC), anchored to the surface of antigen-presenting cells. At the cell-cell interface, pMHC binding to TCRs triggers intracellular signaling that may lead to T cell activation.
A key observation made >20 years ago is that the TCR-pMHC complex spans a short intermembrane distance (≈13 nm) compared to other T-cell surface molecules that have ectodomains spanning 50 nm (3) (Fig. 1). Interestingly, one of the most abundant of these long surface molecules (LSMs) on T cells is a transmembrane phosphatase (CD45) that constitutively dephosphorylates the TCR. Based on this observation, it was predicted that the TCR-pMHC complex would be spatially segregated from CD45 allowing the constitutively active kinase, Lck (4), to phosphorylate the receptor (Fig. 1). Evidence for this “kinetic-segregation” model of receptor triggering (1) has come from studies that show abolished receptor triggering when the TCR-pMHC complex is elongated or the ectodomain of CD45 is truncated, impeding size-based segregation (5,6). Other NTRs (e.g., Dectin-1 (7), NKG2D and KIR2DL1 (8,9)) may share similar mechanisms of activation. A schematic of the kinetics of size-based segregation is shown in Fig. 2 and detailed by Davis and van der Merwe (1).
Figure 1.
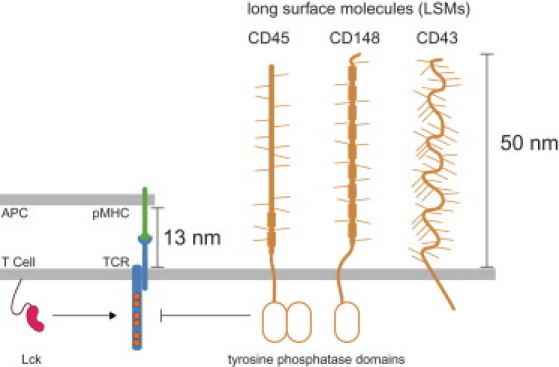
Schematic of the T-cell surface comparing long surface molecules (LSMs), such as the tyrosine phosphatases CD45 and CD148, to the short complex formed by the T-cell receptor (TCR) binding to peptide major-histocompatibility complexes (pMHCs) on the antigen-presenting cell (APC) surface. In the absence of an APC surface, the TCR is unphosphorylated because the constitutive activity of the tyrosine kinase Lck is countered by the constitutive activity of CD45/CD148 (not shown). Upon binding cognate pMHC on an APC surface, LSMs are predicted to spatially segregate from the TCR-pMHC complex because of their long ectodomains and this segregation promotes phosphorylation of the TCR signaling chains (shown). For clarity, only a single TCR signaling chain is shown.
Figure 2.
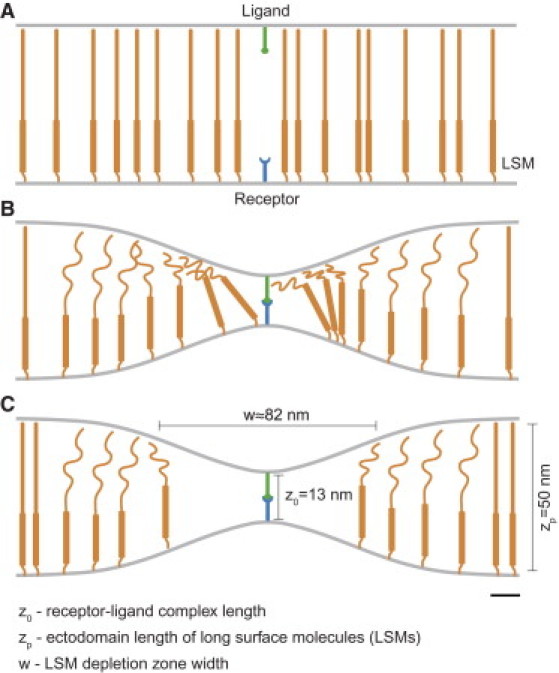
Schematic of binding-induced reorganization of long surface molecules (LSMs). (A) In the absence of a receptor-ligand interaction, the membranes are not deformed and uncompressed LSMs are uniformly distributed. (B) Initial receptor-ligand binding requires the membranes to deform and therefore, nearby LSMs undergo compression in their ectodomains. (C) At equilibrium, a balance between the entropic energy of LSM redistribution and ectodomain compression produces a nonuniform LSM distribution. Relevant length scales are indicated and the scale bar indicates 10 nm.
Although kinetic segregation is a plausible mechanism of receptor triggering, a detailed mechanistic understanding of the process is missing. In particular, given the extremely high sensitivity of T cells to small numbers of agonist pMHC ligands (10), it is natural to ask whether the mechanics of the cell membrane and LSMs support segregation at the scale of a single receptor-ligand complex. Theoretical considerations (11–16) have thus far focused on large-scale spatial patterns (approximately micrometers) that form over large temporal scales (approximately minutes) after initial receptor triggering.
The reaction off-rate constant (koff), the reciprocal of which determines the lifetime of a receptor-ligand complex in solution, is known to modulate the cellular response. Measurements of koff have been widely reported for GPCRs and RTKs binding their natural ligands and engineered variants (17). Typically, in assays to measure koff, one of the binding partners is confined to a surface while the other is in solution (e.g., surface plasmon resonance and radiolabeled ligand binding). Similar studies have reported solution off-rates between NTRs and their ligands (18) and in the case of the TCR, experiments have highlighted the importance of the off-rate in determining the cellular response (19,20). Given that NTRs and their ligands are confined to the two-dimensional plasma membrane, efforts have been made in recent years to directly measure the two-dimensional receptor-ligand reaction rates (21,22) rather than the three-dimensional solution rates. The measured two-dimensional koff was found to be much larger than the three-dimensional koff. However, the reasons for this remain unclear.
Here we formulate a nanometer-scale mechanical model that couples membrane bending and LSM compression, induced by a short receptor-ligand binding event, to the lateral mobility of LSMs. We find robust supradiffusive segregation of LSMs from a single receptor-ligand complex, supporting LSM segregation as a plausible model of receptor triggering. Our dynamic model, which focuses on receptor-ligand unbinding, predicts that LSM reorganization will produce a time-dependent tension on the receptor-ligand complex that increases the unbinding rate. The consequence of this time-dependent tension is that, in addition to increasing the two-dimensional membrane off-rate, the model predicts a nonlinear relationship between three- and two-dimensional off-rates, providing what appears to be a novel mechanical source of ligand sensitivity, which, for example, can contribute to antigen discrimination by immune cells.
Methods
Coupling membrane mechanics to surface molecule dynamics
We model the lateral motion of LSMs on the plasma membrane with a drift-diffusion equation,
| (1) |
where P(r,t) is the concentration of LSMs at distance r from the ligand-receptor complex, D is the diffusion coefficient, μ is the mobility (related to D by the Einstein relation D = μkBT), and Ep is the positional energy of a single LSM. We take the simplest Hookean model for the LSM elasticity, written as
| (2) |
where kp is the effective compressional stiffness of an LSM, z(r,t) is the intermembrane distance at position r and time t, and zp is the ectodomain length of LSMs. A schematic of these length-scales is shown in Fig. 2. The second term on the right-hand side of Eq. 1 describes the flow of LSMs away from regions of small intermembrane separation. We have not included any steric effects due to crowding because the initial uniform concentration of LSMs (P0) is much smaller than 1/A ≈ 10,000 μm−2, where A is the area of a typical LSM. We do not find LSM concentrations near this crowding limit in the calculations presented here.
To determine z(r,t), we minimize the total mechanical energy E of the system. We discuss the assumption of fast mechanical equilibration in the Supporting Material. We use the standard Canham-Helfrich form for the membrane energy (23) assuming membrane bending is small and that changes in surface tension are negligible, which is expected at small length-scales (11). The mechanical energy of the system is thus written as a sum of membrane bending (first term) and LSM compression (second term),
| (3) |
where κM is the membrane-bending stiffness. To describe the situation when both membranes deform we multiply κM by 2 (i.e., κM → 2κM).
Using scaling arguments (see the Supporting Material), we predict that a receptor-ligand bond will influence membrane bending on the scale of w ∼ (κM/kpP0)1/4, which we confirm using numerical calculations. Therefore, all computations are performed on an annular patch of membrane, r0 < r < rmax, where r0 is the receptor radius and rmax ≫ (κM/kp)1/4. We assume that LSMs are sterically occluded from the receptor-ligand bond site (inner boundary conditions) and, given that results are independent of outer boundary conditions, we use no-flux for these. We assume that far away from the receptor-ligand complex, the membranes are held at a distance z(rmax) = zp (e.g., by nonspecific adhesion). At r0, the membrane is held at z(r0) = z0, the length of a receptor-ligand complex. The tension on the receptor-ligand complex is given by f(t) = ∂E/∂z(r,t)|r=r0 by the principle of virtual work. Details of the numerical method we use to solve Eqs. 1 and 3 are presented in the Supporting Material.
Receptor-ligand kinetics
The unbinding rate of a receptor-ligand complex is no longer time-independent when the bond is subjected to a time-dependent tension, f(t). In this case, the effective unbinding rate (koff(t)) can be related to the tension as
| (4) |
where k0off is the unstressed off-rate constant, which we henceforth call the “intrinsic” off-rate, and fb is the force scale constant. This relation is variously known as Bell's model (24) or Kramer's model (25) and has experimental support in a variety of protein-protein interactions (26–28). We note that a time-varying bond tension means that the distribution of unbinding times will no longer be exponential and in fact, Eq. 4 defines a nonhomogeneous Poisson process whose cumulative probability distribution of unbinding times is
This allows us to compute the mean time before unbinding,
| (5) |
We define the effective or apparent off-rate constant as k∗off = 1/ t∗off.
Assumptions about the receptor-ligand attachment process
We assume that, at t = 0, a receptor-ligand bond has formed and that the LSM concentration is initially uniform. For a receptor-ligand bond to form, the membranes must come into proximity. This can occur by LSMs being preevacuated; or LSMs becoming compressed; or a combination of both. In the Supporting Material we show that the spontaneous formation of a preevacuated region of LSM through diffusion is an exceedingly rare event. This suggests that attachment depends on an active process, likely driven by the cytoskeleton (21). An alternative possibility is that attachment occurs when LSM is transiently compressed by random fluctuations of the membrane and LSM itself, which we also show is unlikely in the Supporting Material. In either case, these mechanisms lead to an LSM distribution unperturbed from its equilibrium distribution at the moment of receptor-ligand attachment. Estimate would be different if LSM were collected in protein islands, for example in lipid rafts (29).
Results
Long surface molecules readily segregate from short receptor-ligand complexes
Receptor-ligand binding requires that molecules be laterally aligned on opposing membrane patches that are in close proximity. The mechanical model allows the time-evolution of the system to be followed in detail after receptor-ligand binding. In Fig. 3 A we show the LSM concentration profile for several time points after receptor-ligand binding and in Fig. 3 B we show the LSM depletion zone width as a function of time. We readily observe segregation of LSMs on a spatial scale of 100 nm and a temporal scale of ∼1 ms. Using scaling arguments (see the Supporting Material), we find that the depletion timescale is
where w is the lateral length scale (w = κM/kpP0)1/4), kBT is the thermal energy scale, and all other quantities are defined in Table 1. We observe that when kp(zp−z0)2 ≈ kBT, depletion is diffusion-limited, whereas when kp(zp−z0)2 ≫ kBT, which is the case here (because, for our parameters, kBT/kp(zp−z0)2 = 0.03), we have supradiffusive LSM depletion.
Figure 3.
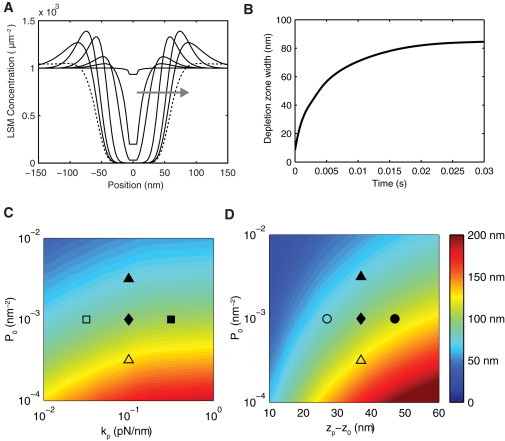
Robust segregation of long surface molecules from a receptor-ligand complex. (A) The concentration profile of LSMs as a function of the distance from the receptor-ligand complex (at 0 nm) at seven time points after a receptor-ligand binding event (t = 0.000, 0.001, 0.002, 0.007, 0.025, 0.075, and 1.5 s; arrow indicates direction of increasing time). (B) The LSM depletion zone width in panel A as a function of time. The depletion zone is the distance between the LSM concentration that is halfway between the maximum and minimum concentration. (C and D) Contours showing the asymptotic (steady-state) LSM depletion zone width as a function of the initial LSM concentration (P0) versus the compressional stiffness of LSMs (kp) in panel C and the difference in length between LSMs and the receptor-ligand complex (zp−z0) in panel D. Segregation is observed over a wide range of parameter values. (Solid diamond) Default parameters used in panels A and B (see Table 1) and additional symbols indicate parameter regimes shown in Fig. 5.
Table 1.
Parameter definitions and estimates
| Parameter | Description | Value | Ref. |
|---|---|---|---|
| D | Diffusion coefficient of LSMs | 0.01 μm2/s | (37) |
| kp | Compressional stiffness of LSMs | 0.1 pN/nm | (38) |
| zp | Height of LSMs | 50 nm | (3,39) |
| κM | Membrane bending stiffness | 50 pN/nm | (40) |
| z0 | Receptor-ligand complex height | 13 nm | (3,39) |
| P0 | Initial LSM concentration | 1000 μm2 | (39) |
| fB | Receptor-ligand force scale | 10 pN | (21) |
| k0off | Receptor-ligand intrinsic off-rate | 0.01–10 s−1 | (14,39) |
See the Supporting Material for a detailed discussion of parameter values.
To determine how the model parameters alter LSM segregation, we recorded the asymptotic (steady-state) LSM depletion zone width, which was reached in <1 s in our model for parameters other than the default set (Table 1). Heat maps showing the LSM depletion zone width as a function of , kp, and z0−zp are shown in Fig. 3, C and D. We find LSM segregation of >50 nm for the majority of parameter space. LSM segregation of <50 nm requires an increase in P0 of an order of magnitude, a decrease in kp by more than an order of magnitude, or a decrease in z0−zp from 37 nm to <18 nm.
In summary, the model predicts robust segregation of LSMs from a newly formed short receptor-ligand complex for a wide range of parameter values. This supradiffusive segregation occurs on a millisecond timescale. Therefore, LSM segregation is a plausible model of NTR triggering when the phosphatase responsible for NTR dephosphorylation has a long ectodomain (i.e., the phosphatase can be identified as an LSM) and when the kinase is constitutively active.
LSM compression and spatial reorganization leads to a time-varying bond tension
The difference in intermembrane distance between ligand-bound NTRs and ectodomains of LSMs has led to the prediction that receptor-ligand complexes are under tension. We use the mathematical model to determine the receptor-ligand bond tension after a binding event (Fig. 4 A). Initially, the proximity of LSMs to the complex produces a large bond tension (f0 = 55 pN) but this tension quickly decays to the steady-state value (fss = 18 pN) as LSMs are rapidly depleted near the complex. The half-life of this tension decay, tf, is on the same scale as the supradiffusive LSM depletion, which for the default parameters occurs at 10 ms. Interestingly, this large change in tension, which is the result of LSMs pushing on the membrane and hence on the receptor-ligand complex, occurs despite only small changes in the intermembrane separation (see Fig. S1 in the Supporting Material). In other words, small membrane bending (∼1%) lead to large changes in receptor-ligand bond tension (∼65%). This sensitivity occurs because tension is proportional to the third spatial derivative of membrane shape (30).
Figure 4.
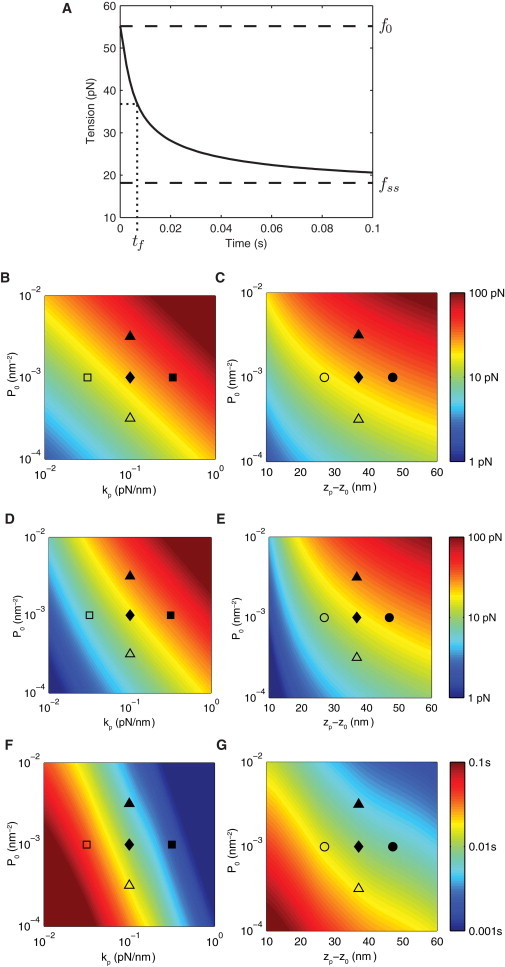
LSM compression and spatial reorganization leads to a time-varying bond tension. (A) Tension on the receptor-ligand complex as a function of time. The initial (f0) and steady-state (fss) tension are indicated in addition to the half-life of tension decay (tf). (B–G) Heat maps showing f0 (B and C), f0–fss (D and E), and tf (F and G) as a function of the initial LSM concentration (P0), the LSM compressional stiffness (kp), and the difference in length between LSMs and the receptor-ligand complex (zp−z0). Parameter regimes that produce large initial tensions and consequently, large changes in tension, lead to small tension decay half-times. Default parameters are listed in Table 1.
As before, we calculate the initial tension (f0), change in tension (f0 − fss), and the half-time of tension decay (tf) as a function of the model parameters (Fig. 4, B–G). We find that large changes in the parameters are required for large changes in model outputs with the exception of the LSM compressional stiffness constant (kp), which sensitively determines the half-time of tension decay (Fig. 4 F). We find rapid tension decay, as exhibited by small decay half-time (tf), occurs in parameter regimes that produce large changes in tension relative to the bond force scale (i.e., (f0–fss)/fB ≫ 1).
Time-varying bond tension leads to sensitivity in bond lifetimes
The unbinding rate of bonds under tension is modified from their unstressed intrinsic unbinding rate constant (k0off). To illustrate this, consider the probability that a receptor-ligand complex remains bound as a function of time (Fig. 5 A). In the absence of tension, we obtain the expected exponentially decreasing probability, which appears linear on a semilog plot (dashed line). In the presence of a constant time-independent tension we also obtain a linear decrease, with a larger negative slope that depends on the magnitude of the applied tension (dotted line). However, when the tension is time-dependent, as predicted by the mathematical model (Fig. 4 A), we observe a highly nonlinear decrease in the probability (solid curve). In all cases, we can use this probability to define the mean unbinding time whose reciprocal defines an effective or apparent off-rate, k∗off. In this way, k∗off can be identified as the stressed two-dimensional membrane off-rate and k0off as the unstressed three-dimensional solution off-rate.
Figure 5.
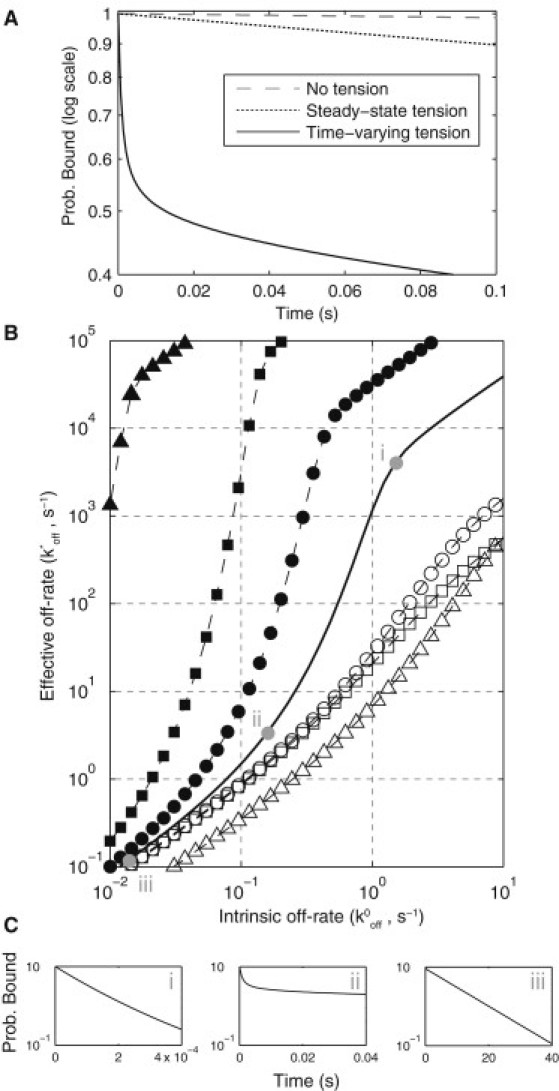
Time-dependent bond tension leads to sensitivity in bond lifetimes. (A) Probability of bond survival as a function of time on a semilog plot. In the absence of tension or in the presence of a constant time-independent tension, bond survival is an exponential process. In the presence of a time-dependent tension, bond survival is a nonhomogeneous Poisson process. In each case, the mean bond survival time (t∗off) can be calculated from the probability distribution (see the Supporting Material). (B) The reciprocal of t∗off defines an effective off-rate (k∗off = 1/ t∗off) that is plotted against the intrinsic off-rate (k0off) for the default parameters (solid black curve). Bonds with large k0off experience only the initial tension (i), bonds with an intermediate k0off experience a time-dependent tension (ii), and bonds with small k0off experience only the steady-state tension (iii). (C) Bond survival curves (log plot) for the three cases show nonexponential decay at intermediate k0off (ii). In addition to the default parameters, the relationship between k0off and k∗off is shown when P0 is multiplied by a factor of (solid triangles) or (open triangles), when kp is multiplied by a factor of (solid squares) or (open squares), and when zp–z0 = 47 nm (solid circles) or zp–z0 = 27 nm (open circles). These symbols correspond to parameter regimes indicated in Fig. 5, C and D, and Fig. 4, B–G. We find that k∗off is sensitive to small changes in k0off.
In Fig. 5 B we use the mathematical model to relate k0off to k∗off and hence predict the relationship between the three-dimensional and two-dimensional off-rates (solid curve for default parameter values). There are several features of this curve that we discuss in turn. We observe that when k∗off ≫ 1/tf (recall that 1/tf = 1/(0.01 s) = 100 s−1 for the default parameters), the complex rapidly dissociates and only experiences the initial tension whereas, when k∗off ≪ 1/tf, the complex remains bound long past the tension decay and therefore experiences only the final steady-state tension. In these extremes, the relation between k0off and k∗off is linear and is given by Eq. 4 with f(t) equal to f0 and fss, respectively. The probability of remaining bound as a function of time in these cases is exponential (Fig. 5 C, i and iii). However, when k∗off ∼ 1/tf, we observe a highly nonlinear relationship between k0off and k∗off, which is a direct result of a nonexponential unbinding process that occurs when the complex experiences a time-dependent tension (Fig. 5 C, ii). The implication of this result is that small changes in k0off can result in large changes in k∗off. Put another way, a time-dependent bond tension means that the two-dimensional membrane off-rate, k∗off, is sensitive to small changes in the intrinsic off-rate, k0off.
As discussed above, the initial and final tensions determine the asymptotic values relating k0off to k∗off, and tf determines the effective off-rate where this transition occurs. However, f0, fss, and tf are not independently controlled by individual model parameters (see Fig. 4, B–G), and therefore it is difficult to predict by intuition alone how the system parameters will alter the relationship between k0off and k∗off. Therefore, in Fig. 5 B we show the predicted relationship between k0off and k∗off for six different parameter regimes that are indicated in Fig. 3, C and D, and Fig. 4, B–G, by various symbols. For parameter regimes where the tension reduction is small (f0 ≈ fss), the nonlinear relationship between k0off and k∗off is lost (open symbols). On the other hand, for parameter regimes where the change in tension is large, we observe a much larger nonlinear regime that occurs at small values of k0off.
In summary, the mathematical model predicts that the conversion between three-dimensional and apparent two-dimensional off-rates may require more than a simple multiplicative constant and that such a conversion may depend on the value of the three-dimensional off-rate. The consequence of this is that small changes in the three-dimensional off-rate may give rise to large changes in the apparent two-dimensional off-rate and therefore, the process of LSM segregation may provide a signaling-independent source of mechanical sensitivity to bond lifetimes.
Discussion
We present a mathematical model that couples the mechanics of membrane deformations and LSM ectodomain compression to the lateral motion of LSMs to investigate the initial dynamics following receptor-ligand binding. The mathematical model has several implications for triggering models of NTRs and for predicting the effective two-dimensional membrane off-rate from three-dimensional solution measurements.
Relation to previous work
Pioneering experiments revealed size-based segregation at membrane interfaces (31–33), which motivated mathematical studies focused on interface dynamics (11–16). These models describe populations of receptors, ligands, and LSM, which interact via membrane mechanics and exhibit patterns on large spatial (∼1 μm) and temporal (∼1 min) scales. Following recent experiments reporting information at the scale of single receptor-ligand bonds (21,22), we analyzed membrane-mediated mechanics of a single receptor-ligand in a population of LSM, considering dynamics on small spatial (∼10 nm) and temporal (<1 s) scales. At larger scales, receptor-ligand kinetics has been modeled using energetic considerations where koff is not explicit (11,15,16), or koff has been assumed to be independent of mechanical forces (12,14). These assumptions conceal the nonlinear relationship between two- and three-dimensional kinetics we report here. In Burroughs and Wülfing (13), detachment was time-dependent; however, local membrane deformation in the vicinity of a bond was treated as a constant model parameter and the (dynamic) effective detachment rate was not reported. Our work is also related to recent models of membrane mechanics in response to forces exerted on membrane-bound protein complexed (34,35). In contrast to several above-mentioned models, our membrane dynamics are considerably simplified, allowing model analysis and derivation of scaling relations while still capturing the observed differences between two- and three-dimensional unbinding rates (see the Supporting Material).
Implications for the kinetic segregation model
The process by which ligand binding to NTRs at cell-cell interfaces initiates intracellular signaling remains controversial (2). The kinetic-segregation model (1) posits that in the absence of ligand, NTRs remain unphosphorylated because phosphatase activity is higher than the kinase activity. Binding of a ligand to an NTR forces LSMs, many of which are phosphatases, to be depleted near the receptor-ligand complex tilting the local balance in favor of NTR phosphorylation. We have shown that this qualitative description is a quantitatively plausible model of NTR triggering on the scale of a single NTR, and is robust to parameter variations.
A key concern in the kinetic-segregation model is the speed at which triggering can take place. We have shown that such segregation is supradiffusive on the millisecond timescale because of the mechanical exclusion of phosphatases from the receptor-ligand complex. In contrast, triggering mechanisms based on receptor aggregation are diffusion-limited.
Implications for TCR ligand discrimination
The discrimination of antigens by T cells is a well-documented phenomenon. It has been shown that a robust T cell response to cognate pMHC is abolished when a peptide mutation increases the solution off-rate by a factor of 3 (36) and it is also known that T cells show no response when encountering antigen-presenting cells (APCs) with a high concentration of endogenous pMHC thought to have three-dimensional off-rates not much larger than agonist pMHC. The nonlinearity between the effective two-dimensional off-rate, which is the relevant rate for antigen discrimination, and the intrinsic three-dimensional off-rate, predicted by our model, means that small changes in the three-dimensional off-rate can give rise to large changes in the effective two-dimensional off-rate. It follows that size-based segregation is a mechanical mechanism for antigen discrimination.
Passive and active mechanisms modulating membrane reactions
Recently, the first direct measurements of koff between TCRs and pMHC at membrane interfaces were reported (21,22). These two-dimensional membrane off-rates were found to be larger than the corresponding three-dimensional solution measurements. The mechanism(s) underlying these differences likely involve both active and passive processes. In this study, we have focused on a passive process that can modulate receptor-ligand bond lifetimes based on differential size of LSMs and receptor-ligand complexes. Size-based segregation has been experimentally observed in multiple systems (5,8,9). The predicted relationship between three-dimensional and two-dimensional off-rates (Fig. 5) can be experimentally determined using a panel of ligands with a large variation in the three-dimensional off-rates. It would be useful to perform these experiments in the absence of binding-induced signaling to decouple active and passive processes. Furthermore, this system can be used to explore whether decreasing the relative size of the receptor-ligand complex, the LSM ectodomain length, or reducing the concentration of LSMs, will modify the relationship between three- and two-dimensional off-rates as predicted by the model (Fig. 5). These experiments will inform on the underlying mechanisms mediating the increase in the membrane off-rate compared to solution.
Experiments have provided evidence that active processes modulate receptor-ligand bond lifetimes at membrane interfaces. Inhibitors of the actin cytoskeleton were found to increase the TCR/pMHC membrane lifetime (21,22), suggesting that the cytoskeleton acts to destabilize TCR/pMHC complexes. Huppa et al. (22) found that the TCR/pMHC membrane off-rate was similar to solution measurements when using cytoskeletal inhibitors, whereas Huang et al. (21) found that the TCR/pMHC membrane off-rate, although smaller in the presence of cytoskeletal inhibitors, remained substantially larger compared to solution measurements. A key difference between these studies is that Huang et al. (21) performed experiments during initial binding whereas Huppa et al. (22) performed experiments after the formation of microclusters. It is plausible that the tension on the receptor-ligand bond induced by passive size-based segregation is distributed among multiple TCR-pMHC complexes in microclusters. Importantly, Huang et al. (21) have shown that the cytoskeleton is insufficient to explain the difference between three- and two-dimensional off-rates. The mathematical model we have constructed is based on passive processes and is valid for initial binding, before active signaling-induced processes take place that may further modulate receptor-ligand interactions. As our understanding of the cytoskeleton, and other processes that determine the distribution of membrane receptors (e.g., protein islands, rafts), improves, it will be important to develop mechanistic models that can explain their effects on receptor-ligand binding.
Acknowledgments
This work has been supported by the National Research and Engineering Council of Canada and by the Royal Society through a Newton Fellowship (to O.D.).
Supporting Material
References
- 1.Davis S.J., van der Merwe P.A. The kinetic-segregation model: TCR triggering and beyond. Nat. Immunol. 2006;7:803–809. doi: 10.1038/ni1369. [DOI] [PubMed] [Google Scholar]
- 2.van der Merwe P.A., Dushek O. Mechanisms for T cell receptor triggering. Nat. Rev. Immunol. 2011;11:47–55. doi: 10.1038/nri2887. [DOI] [PubMed] [Google Scholar]
- 3.Springer T.A. Adhesion receptors of the immune system. Nature. 1990;346:425–434. doi: 10.1038/346425a0. [DOI] [PubMed] [Google Scholar]
- 4.Nika K., Soldani C., Acuto O. Constitutively active Lck kinase in T cells drives antigen receptor signal transduction. Immunity. 2010;32:766–777. doi: 10.1016/j.immuni.2010.05.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Choudhuri K., Wiseman D., van der Merwe P.A. T-cell receptor triggering is critically dependent on the dimensions of its peptide-MHC ligand. Nature. 2005;436:578–582. doi: 10.1038/nature03843. [DOI] [PubMed] [Google Scholar]
- 6.Irles C., Symons A., Acuto O. CD45 ectodomain controls interaction with GEMs and Lck activity for optimal TCR signaling. Nat. Immunol. 2003;4:189–197. doi: 10.1038/ni877. [DOI] [PubMed] [Google Scholar]
- 7.Goodridge H.S., Reyes C.N., Underhill D.M. Activation of the innate immune receptor Dectin-1 upon formation of a ‘phagocytic synapse’. Nature. 2011;472:471–475. doi: 10.1038/nature10071. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Köhler K., Xiong S., Davis D.M. Matched sizes of activating and inhibitory receptor/ligand pairs are required for optimal signal integration by human natural killer cells. PLoS ONE. 2010;5:e15374. doi: 10.1371/journal.pone.0015374. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Brzostek J., Chai J.-G., Gould K.G. Ligand dimensions are important in controlling NK-cell responses. Eur. J. Immunol. 2010;40:2050–2059. doi: 10.1002/eji.201040335. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Irvine D.J., Purbhoo M.A., Davis M.M. Direct observation of ligand recognition by T cells. Nature. 2002;419:845–849. doi: 10.1038/nature01076. [DOI] [PubMed] [Google Scholar]
- 11.Rozycki B., Lipowsky R., Weikl T. Segregation of receptor-ligand complexes in cell adhesion zones: phase diagrams and role of thermal membrane roughness. N. J. Phys. 2010;12:095003. [Google Scholar]
- 12.Qi S.Y., Groves J.T., Chakraborty A.K. Synaptic pattern formation during cellular recognition. Proc. Natl. Acad. Sci. USA. 2001;98:6548–6553. doi: 10.1073/pnas.111536798. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Burroughs N.J., Wülfing C. Differential segregation in a cell-cell contact interface: the dynamics of the immunological synapse. Biophys. J. 2002;83:1784–1796. doi: 10.1016/S0006-3495(02)73944-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Burroughs N.J., Lazic Z., van der Merwe P.A. Ligand detection and discrimination by spatial relocalization: a kinase-phosphatase segregation model of TCR activation. Biophys. J. 2006;91:1619–1629. doi: 10.1529/biophysj.105.080044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Coombs D., Dembo M., Goldstein B. Equilibrium thermodynamics of cell-cell adhesion mediated by multiple ligand-receptor pairs. Biophys. J. 2004;86:1408–1423. doi: 10.1016/S0006-3495(04)74211-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Weikl T.R., Lipowsky R. Pattern formation during T-cell adhesion. Biophys. J. 2004;87:3665–3678. doi: 10.1529/biophysj.104.045609. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Copeland R.A., Pompliano D.L., Meek T.D. Drug-target residence time and its implications for lead optimization. Nat. Rev. Drug Discov. 2006;5:730–739. doi: 10.1038/nrd2082. [DOI] [PubMed] [Google Scholar]
- 18.Davis M.M., Krogsgaard M., Ehrlich L. Dynamics of cell surface molecules during T cell recognition. Annu. Rev. Biochem. 2003;72:717–742. doi: 10.1146/annurev.biochem.72.121801.161625. [DOI] [PubMed] [Google Scholar]
- 19.Kalergis A.M., Boucheron N., Nathenson S.G. Efficient T cell activation requires an optimal dwell-time of interaction between the TCR and the pMHC complex. Nat. Immunol. 2001;2:229–234. doi: 10.1038/85286. [DOI] [PubMed] [Google Scholar]
- 20.Dushek O., Aleksic M., van der Merwe P.A. Antigen potency and maximal efficacy reveal a mechanism of efficient T cell activation. Sci. Signal. 2011;4:ra39. doi: 10.1126/scisignal.2001430. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Huang J., Zarnitsyna V.I., Zhu C. The kinetics of two-dimensional TCR and pMHC interactions determine T-cell responsiveness. Nature. 2010;464:932–936. doi: 10.1038/nature08944. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Huppa J.B., Axmann M., Davis M.M. TCR-peptide-MHC interactions in situ show accelerated kinetics and increased affinity. Nature. 2010;463:963–967. doi: 10.1038/nature08746. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Canham P.B. The minimum energy of bending as a possible explanation of the biconcave shape of the human red blood cell. J. Theor. Biol. 1970;26:61–81. doi: 10.1016/s0022-5193(70)80032-7. [DOI] [PubMed] [Google Scholar]
- 24.Bell G.I. Models for the specific adhesion of cells to cells. Science. 1978;200:618–627. doi: 10.1126/science.347575. [DOI] [PubMed] [Google Scholar]
- 25.Hänggi P., Talkner P., Borkovec M. Reaction-rate theory: fifty years after Kramers. Rev. Mod. Phys. 1990;62:251–341. [Google Scholar]
- 26.Schwesinger F., Ros R., Pluckthun A. Unbinding forces of single antibody-antigen complexes correlate with their thermal dissociation rates. Proc. Natl. Acad. Sci. USA. 2000;97:9972–9977. doi: 10.1073/pnas.97.18.9972. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Evans E. Probing the relation between force—lifetime—and chemistry in single molecular bonds. Annu. Rev. Biophys. Biomol. Struct. 2001;30:105–128. doi: 10.1146/annurev.biophys.30.1.105. [DOI] [PubMed] [Google Scholar]
- 28.Howard J. Mechanical signaling in networks of motor and cytoskeletal proteins. Annu. Rev. Biophys. 2009;38:217–234. doi: 10.1146/annurev.biophys.050708.133732. [DOI] [PubMed] [Google Scholar]
- 29.Leslie M. Mysteries of the cell. Do lipid rafts exist? Science. 2011;334:1046–1047. doi: 10.1126/science.334.6059.1046-b. [DOI] [PubMed] [Google Scholar]
- 30.Landau L., Lifshitz E. 3rd ed. Butterworth-Heinemann, Elsevier; Oxford, UK: 1976. Theory of Elasticity. [Google Scholar]
- 31.Monks C.R., Freiberg B.A., Kupfer A. Three-dimensional segregation of supramolecular activation clusters in T cells. Nature. 1998;395:82–86. doi: 10.1038/25764. [DOI] [PubMed] [Google Scholar]
- 32.Grakoui A., Bromley S.K., Dustin M.L. The immunological synapse: a molecular machine controlling T cell activation. Science. 1999;285:221–227. doi: 10.1126/science.285.5425.221. [DOI] [PubMed] [Google Scholar]
- 33.Johnson K.G., Bromley S.K., Thomas M.L. A supramolecular basis for CD45 tyrosine phosphatase regulation in sustained T cell activation. Proc. Natl. Acad. Sci. USA. 2000;97:10138–10143. doi: 10.1073/pnas.97.18.10138. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Gov N.S., Gopinathan A. Dynamics of membranes driven by actin polymerization. Biophys. J. 2006;90:454–469. doi: 10.1529/biophysj.105.062224. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Dobrowsky T.M., Daniels B.R., Wirtz D. Organization of cellular receptors into a nanoscale junction during HIV-1 adhesion. PLOS Comput. Biol. 2010;6:e1000855. doi: 10.1371/journal.pcbi.1000855. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Altan-Bonnet G., Germain R.N. Modeling T cell antigen discrimination based on feedback control of digital ERK responses. PLoS Biol. 2005;3:e356. doi: 10.1371/journal.pbio.0030356. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.van der Merwe P.A., Davis S.J. Molecular interactions mediating T cell antigen recognition. Annu. Rev. Immunol. 2003;21:659–684. doi: 10.1146/annurev.immunol.21.120601.141036. [DOI] [PubMed] [Google Scholar]
- 38.Yeung A., Evans E. Unexpected dynamics in shape fluctuations of bilayer vesicles. J. Phys. II. 1995;5:1501–1523. [Google Scholar]
- 39.Seifert U., Langer S. Hydrodynamics of membranes: the bilayer aspect and adhesion. Biophys. Chem. 1994;49:13–22. [Google Scholar]
- 40.Krobath H., Schutz G.J., Weikl T.R. Lateral diffusion of receptor-ligand bonds in membrane adhesion zones: effect of thermal membrane roughness. Europhys. Lett. 2007;78:38003. [Google Scholar]
- 41.Veksler A., Gov N.S. Phase transitions of the coupled membrane-cytoskeleton modify cellular shape. Biophys. J. 2007;93:3798–3810. doi: 10.1529/biophysj.107.113282. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Reichl L. Wiley-Interscience; New York: 1998. A Modern Course in Statistical Physics. [Google Scholar]
- 43.Schepartz B. Charles C. Thomas; Springfield, IL: 1980. Dimensional Analysis in the Biomedical Sciences. [Google Scholar]
- 44.LeVeque R. Birkhäuser Verlag; Basel, Switzerland: 1994. Numerical Methods for Conservation Laws. [Google Scholar]
- 45.Bongrand P. Ligand-receptor interactions. Rep. Prog. Phys. 1999;62:921–968. [Google Scholar]
- 46.Cairo C.W., Das R., Golan D.E. Dynamic regulation of CD45 lateral mobility by the spectrin-ankyrin cytoskeleton of T cells. J. Biol. Chem. 2010;285:11392–11401. doi: 10.1074/jbc.M109.075648. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Burroughs N.J., Köhler K., Davis D.M. Boltzmann energy-based image analysis demonstrates that extracellular domain size differences explain protein segregation at immune synapses. PLOS Comput. Biol. 2011;7:e1002076. doi: 10.1371/journal.pcbi.1002076. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Barclay A.N., Brown M.H., van der Merwe P.A. Academic Press; Waltham, MA: 1997. The Leukocyte Antigen Facts Book. [Google Scholar]
- 49.Raucher D., Stauffer T., Meyer T. Phosphatidylinositol 4,5-bisphosphate functions as a second messenger that regulates cytoskeleton-plasma membrane adhesion. Cell. 2000;100:221–228. doi: 10.1016/s0092-8674(00)81560-3. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


