Musical rhythm spectra from Bach to Joplin obey a 1/f power law

Abstract

Much of our enjoyment of music comes from its balance of predictability and surprise. Musical pitch fluctuations follow a 1/f power law that precisely achieves this balance. Musical rhythms, especially those of Western classical music, are considered highly regular and predictable, and this predictability has been hypothesized to underlie rhythm's contribution to our enjoyment of music. Are musical rhythms indeed entirely predictable and how do they vary with genre and composer? To answer this question, we analyzed the rhythm spectra of 1,788 movements from 558 compositions of Western classical music. We found that an overwhelming majority of rhythms obeyed a 1/f^β power law across 16 subgenres and 40 composers, with β ranging from ∼0.5–1. Notably, classical composers, whose compositions are known to exhibit nearly identical 1/f pitch spectra, demonstrated distinctive 1/f rhythm spectra: Beethoven's rhythms were among the most predictable, and Mozart's among the least. Our finding of the ubiquity of 1/f rhythm spectra in compositions spanning nearly four centuries demonstrates that, as with musical pitch, musical rhythms also exhibit a balance of predictability and surprise that could contribute in a fundamental way to our aesthetic experience of music. Although music compositions are intended to be performed, the fact that the notated rhythms follow a 1/f spectrum indicates that such structure is no mere artifact of performance or perception, but rather, exists within the written composition before the music is performed. Furthermore, composers systematically manipulate (consciously or otherwise) the predictability in 1/f rhythms to give their compositions unique identities.

Musical behaviors—singing, dancing, and playing instruments—date back to Neanderthals (1), and have been a part of every human culture as far back as we know (2, 3). People experience great enjoyment and pleasure from music (4–6), and music theorists have argued that this enjoyment stems in part from the structural features of music, such as the generation and violation of expectations (5, 7–11). Mathematics has often been used to characterize, model, and understand music, from Schenkerian analysis (12, 13) to neural topography (14) and geometric models of tonality (15, 16). One particular mathematical relation that has received attention in music is the 1/f distribution, which Mandelbrot (17) termed “fractal.”

1/f distributions have been found to be a key feature of a number of natural and sensory phenomena. In analyzing the frequency of several natural disasters, including earthquakes, landslides, floods, and terrestrial meteor impacts, Hsü (18) found an inverse log-log linear (fractal) relation between the frequency and the intensity of the events:

where f is the temporal frequency, M is a parameter indexing the intensity of the events, c is a constant of proportionality, and D is the fractal dimension. The well-known Richardson Effect (19, 20), which began the modern study of fractals, states that measurements of natural phenomena are characterized by 1/f noise. 1/f fluctuations are also a prominent feature of human cognition. Neurons in primary visual cortex were found to exhibit higher gain, and the spike responses exhibit higher coding efficiency and information transmission rates for 1/f signals (21), and the fluctuations of voltage across the resting membrane of myelinated nerve fibers show a 1/f spectrum (22); these findings suggest that human sensory and neural systems evolved to encode certain regularities in the physical world (23, 24), in this case, those that manifest self-similarity.

The spectral power of such signals decays exponentially with frequency (f) as [1/f]^β (where β is the spectral exponent). Although large values of β (>2) indicate greater long-range correlations, and hence, highly predictable signals, very small βs (<0.5) indicate highly unpredictable signals: An extreme example is white noise (β = 0), the structure of which is entirely unpredictable (25). On the other hand, musical pitch and loudness fluctuations are known to have an intermediate range of β values (1 < β < 2), and this range has been suggested to indicate a level of predictability that is optimal to our musical experience (26, 27).

In contrast, musical rhythms, note onsets, and durations in Western classical music are considered highly regular and predictable, so much so that the term “rhythmic” has come to be synonymous with “recurring,” “regular,” or “periodic.” Because music has a beat and is based on repetition, it has been said that “what” the next musical event will be is not always easy to guess, but “when” it is likely to happen can be easily predicted (11). In fact, this comforting predictability has been suggested to underlie rhythm's fundamental contribution to the aesthetic experience of music (7, 28, 29).

It has been previously suggested that music can be characterized by a fractal geometry (30–32), obeying a 1/f power law. This suggestion was demonstrated for the amplitude (26, 27) and pitch structure (33, 34) of music. Here we show that the temporal/rhythmic properties of music across a wide range of compositions also obey the 1/f law, or fractal relation.

We analyzed the spectral structure of musical rhythms (indexed by note onsets, and using a multitaper spectral analysis) to investigate whether these are indeed as regular and predictable as commonly claimed. Whereas previous researchers have studied only a handful of compositions by Bach, Mozart, and European folk songs (26, 27, 33, 34), we sought to increase the generalizability and importance of such findings by leveraging the power of a large database of notated musical compositions, spanning three centuries and dozens of composers and styles. To that end, we analyzed the scores of 1,788 musical movements from 558 compositions (independent sections of larger compositions of Western classical music). Here, we demonstrate that just like musical pitch and loudness, musical rhythms also obey a 1/f power law with β ranging from ∼0.5–1. Furthermore, we show that composers, even from the same musical era, exhibit systematically different slopes (βs) in their 1/f rhythm spectra: the resulting differences in rhythmic predictability would permit them to uniquely identify their compositions, and to distinguish their works from those of their contemporaries.

Results

To create a representation for musical rhythms in time, we used a raster representation: note onsets were represented as pulses (“spikes”) of a point process, and durations as the intervals between successive pulses. The power spectrum S(f) of the rhythm rasters was then computed for each piece using the multitaper method for point processes (35), commonly used for spectral estimation of spike trains in neurobiology datasets (Materials and Methods).

Previous observations on the relationship between the correlation structure of signals and the slopes of their 1/f spectra have been limited to continuous-time signals (such as pitch and loudness fluctuations) (25–27, 36). Hence, we first verified the validity of these observations for rasterized rhythms with 1/f spectra. We generated simulated 1/f rhythm sequences with different values of the spectral exponent, β (see Materials and Methods for details). Simulated rhythm sequences with small values of β (~0, characteristic of white noise) lacked both short and long range correlations, and hence, were essentially unpredictable (Fig. 1 A and B). Sequences with intermediate values of β (~1) showed an interesting balance of short and long range correlations, and a level of predictability that was intermediate between the two more extreme cases described here (Fig. 1 C and D). Sequences with large values of β (~2) varied gradually over time, showed correlations over long timescales, and hence, were highly predictable over these timescales (Fig. 1 E and F).

Fig. 1.

The 1/f power law in simulated rhythm spectra. (A) (Upper) Representative rhythm sequence the spectra of which obey a power law of the form [1/f]^β for β = 0.0 generated from Eq. 1. (Scale bar, 10 samples.) (Lower) Rhythm rasters (n = 50 realizations, vertical axis) for β = 0.0 (horizontal axis is time). (Scale bar, 1 s). The complete lack of correlations at all timescales is characteristic of white noise. (B) Spectrum of the rhythm rasters from A. Logarithm of spectral power is plotted against logarithm of frequency. Light gray lines represent rhythm spectrum for the individual rasters (n = 100). Dark gray points represent the average spectrum. Black line represents the linear fit to the spectrum in the frequency range of 0.01 to 1 Hz (delineated by dotted vertical gray lines). Dashed black line represents extrapolation of the linear fit to other frequencies. (C) Rhythm sequence and rasters as in A, but for β = 1.0. Variations in the rhythm and range of correlations are intermediate between that of A and E. (D) Spectrum of rasters from C. Other conventions are as in B. (E) Rhythm sequence and rasters as in A, but for β = 2.0. Both sequence and rasters show slow variations (horizontal axis) and long-range correlations. (F) Spectrum of rasters from E. Other conventions are as in B. Scale bars from A also apply to panels C and E. Spectra in panels B, D, and F are displaced arbitrarily along the y axis for clarity of presentation.

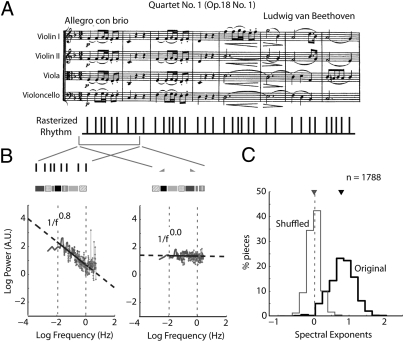
Next, we analyzed the spectral structure of musical rhythms of 1,788 movements from 558 Western classical music compositions. Selections spanned 16 genres and 44 composers (Table S1). Discarding pitch information, we extracted from each voice in each selection their rhythmic content (onsets and durations of notes and rests) that was encoded with the raster representation described above (Fig. 2A). The rhythm spectrum for an example piece (Beethoven's Quartet No. 1) (Fig. 2A) illustrates our central finding: Rhythm spectral power decreased exponentially with frequency as 1/f. In the log-domain, this meant that power decayed linearly with frequency (β = 0.85) (Fig. 2B). One might argue that any sequence of musical rhythms displays 1/f structure and that our experiment lacks a control condition. To address this argument, we conducted additional analyses in which each stimulus served as its own control, disrupting the temporal structure of the rhythm at all frequencies (Materials and Methods) by shuffling the note onsets globally, across the piece, but keeping note durations intact (37, 38). The spectrum of the resulting “shuffled” piece was flat and resembled white noise (β = 0.02) (Fig. 2C), indicating that the 1/f rhythm spectrum reflects the global structure of correlations across the entire piece, and that this structure is a consequence of the specific ordering of the rhythms, not their mere presence in the piece at random locations. The population of all 1,788 selections analyzed showed similar trends: The pooled distribution of βs was significantly different from its null (shuffled) distribution (Fig. 2C), and the median β (0.78, SD = 0.35) was not significantly different from 1. This finding demonstrates that, across compositions analyzed, 1/f spectra ubiquitously characterized the structure of musical rhythms. Converging results were obtained by two independent analysis approaches, Hurst analysis, and detrended fluctuation analysis (SI Materials and Methods).

Fig. 2.

Musical rhythm spectra obey a 1/f power law. (A) Rasterized rhythm representation (Lower) showing note onsets extracted from Beethoven's Quartet Op. 18. No. 1 (score, Upper). The representation shown is schematic: actual durations were extracted from the Humdrum kern format (Materials and Methods). (B) (Left) The spectrum of the rhythm raster from A has power that decays linearly (in a log-scale) with frequency as 1/f (gray dots). The slope of the spectrum (spectral exponent or β) is 0.8. Colored segments show the sequence of durations (internote intervals). Black line represents the linear fit to the spectrum in the frequency range of 0.01 to 1 Hz (delineated by dotted vertical gray lines). Dashed line represents extrapolation of the linear fit to other frequencies. (Right) The spectrum of a sequence with the note onsets shuffled randomly, keeping durations intact. The shuffled spectrum is flat (β = 0.0). Other conventions are as shown (Left). (C) Distribution of rhythm spectral exponents pooled across genres (black) obtained by linear fits to individual pieces across the population of 1,788 pieces analyzed. Gray: spectral exponent distribution for the corresponding shuffled rhythms. Inverted triangles represent the distribution median. Dashed vertical line: β = 0.

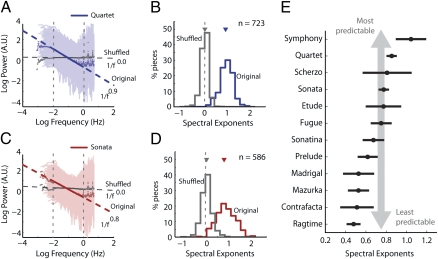
Classical instrumental genres, such as quartets and sonatas (Fig. 3 A and B), and a variety of other folk, dance, and sung music spanning nearly four centuries of compositions all demonstrated 1/f spectra (Figs. S1 and S2 and Table S1). β-Distributions for these genres were significantly different from their respective null (shuffled) counterparts (P < 0.01, Wilcoxon signed rank test, Holm-Bonferroni correction for multiple comparisons) (Fig. 3 C and D and Table S1). We then analyzed how β-distributions varied across different genres of music (Materials and Methods). Symphonies and quartets had the largest β-values, indicating the most predictable rhythms (Fig. 3E and Fig. S1). On the other hand, folk and modern styles, such as mazurka and ragtime, had among the smallest β-values, indicating the least-predictable rhythms (Fig. 3E and Fig. S1).

Fig. 3.

The 1/f rhythm spectra are ubiquitous across genres. (A) Rhythm spectra for quartets. Average spectra (dark blue points) and linear fit (dark blue) to average spectrum in the frequency range of 0.01 to 1 Hz. Faded blue lines represent spectra of individual pieces. Gray data represent spectra of shuffled rhythms. Other conventions are as in Fig. 2B. (B) Distribution of rhythm spectral exponents obtained by linear fits to individual pieces (blue), and for the corresponding shuffled rhythms (gray). Inverted triangle represents median exponents. Dashed vertical line: β = 0. (C) Rhythm spectra for sonatas (red) and corresponding shuffled rhythms (gray). Other conventions are as in A. (D) Distribution of rhythm spectral exponents for sonatas (red) and corresponding shuffled rhythms (gray). Other conventions are as in B. (E) Distribution of rhythm spectral exponents for musical genres ordered from largest mean exponent to smallest. Larger exponents indicate correlations over longer timescales, and hence more predictable rhythms (vertical gray arrow). Circles are mean exponents, and error bars are 95% CI. Disjoint intervals indicate significantly different mean exponents (Tukey–Kramer HSD).

The β-values for compositions grouped by composer revealed a surprising trend: β-distributions varied widely across composers regardless of period or style (Fig. 4 and Table S2). Beethoven, Haydn, and Mozart demonstrated different 1/f rhythm spectra. Beethoven's rhythms exhibited the largest βs (and thus the most predictability), Mozart's βs were among the smallest (with the least predictability), whereas those of Haydn were intermediate between those of Mozart and Beethoven, and significantly different from either (Fig. 4 A, B, and E) [Tukey–Kramer honestly significantly different (HSD), P < 0.05; see Materials and Methods]. Monteverdi and Joplin (Table S2) exhibited nearly identical, overlapping rhythm β-distributions (Tukey–Kramer HSD, P > 0.05) (Fig. 4 C–E). Figs. 3E and 4E display 95% confidence intervals (CI); nonoverlapping CIs are significant at P < 0.05.

Fig. 4.

Composers exhibit distinct 1/f rhythm spectra. (A) Average rhythm spectra for Beethoven (dark green), Haydn (violet), and Mozart (olive green): contemporary composers belonging to the Classical era (1750–1820). Other conventions are as in Fig. 3A. (B) Distribution of rhythm spectral exponents for compositions of Beethoven, Haydn, and Mozart. Color conventions are as in A. Other conventions are as in Fig. 3B. (C) Average rhythm spectra for Monteverdi (blue) and Joplin (green): composers separated by nearly three centuries of compositions. Other conventions are as in Fig. 3A. (D) Distribution of spectral exponents for compositions of Monteverdi and Joplin. Color conventions are as in C. Other conventions are as in Fig. 3B. (E) Distribution of spectral exponents for composers ordered from largest mean exponent to smallest. Spectral exponents of Haydn, for example (dotted vertical lines, 95% CI), are significantly different from those of Beethoven and Mozart (P < 0.05, Tukey–Kramer HSD). Other conventions are as in Fig. 3E.

Discussion

Most listeners find music pleasing when it creates an optimal balance of predictability and surprise (7–9, 28, 29). Whereas such a balance was previously attributed exclusively to 1/f structure in musical pitch and amplitude (26, 27, 33, 34), the present results demonstrate that musical rhythms also exhibit 1/f spectral structure. The 1/f structure allows us to quantify the range of predictability, self-similarity, or fractal-like structure within which listeners find aesthetic pleasure. Critically, compositions across four centuries and several subgenres of Western classical music all demonstrated 1/f structure in their rhythm spectra.

A previous study analyzing classical compositions from the 18th to 20th centuries reported nearly identical 1/f pitch structure among composers, with a very narrow range of spectral exponents (1.79 ≤ β ≤ 1.97) (8). The 1/f pitch structure could not systematically delineate one composer's work from another. In contrast, our findings demonstrate that 1/f rhythm spectral exponents varied widely and systematically among composers (0.48 ≤ β ≤ 1.05). Even composers belonging to the same musical era (1750–1820, the Classical era), such as Beethoven, Haydn, and Mozart, demonstrated distinctive 1/f rhythm spectra. Conversely, Monteverdi and Joplin, composers of entirely different musical eras and composing nearly three centuries apart, exhibited similar rhythm spectra. These results suggest a heretofore underappreciated importance of rhythm and hint at its even greater role than pitch in conveying the distinctive style of composers.

Human perception is known to be sensitive to 1/f structure in the environment (21, 22, 25, 36, 39, 40), and electrophysiological studies have suggested a preference of sensory neural coding for 1/f signals (21, 39, 41). How does this relate to music? The balance of expectations both realized and violated in pleasurable music requires a certain amount of instability in the temporal structure, and such dynamical instability may best be modeled by a power law for temporal fluctuation (42).

Cognitive psychologists (43) have noted that human performance in a variety of tasks, including the production of rhythmic sequences by finger tapping (44), fluctuates over time according to 1/f. Here, we reveal that this same structure characterizes the stage of human cognition before action: the written composition of temporal intervals that will become action plans only at a later date when performed by musicians. Thus, 1/f is not merely an artifact of performance, but exists in the written scores themselves. Perhaps composers can't help but produce 1/f rhythm spectra, perhaps musical conventions require this. From a psychological standpoint, the finding suggests that composers have internalized some of the regularities of the physical world as it interacts with biological systems (including the mind) to recreate self-similarity in works of musical art (cf. 24).

Our finding of 1/f rhythm structure in nearly four centuries of musical compositions may therefore be rooted in a fundamental propensity of our sensory and motor systems to both perceive and produce 1/f structure (44, 45).

Finally, an important methodological contribution of our study is the development of raster representations borrowed from the neuroscience literature, combined with a multitaper spectral analysis (SI Materials and Methods) to rigorously examine rhythm structure in music. Although pitch and loudness are musical attributes that can be represented as a continuous signal having a specific value at each instant of time (36), musical rhythms are essentially sequences of note durations (intervals of time) that, by definition, cannot be represented as a continuous signal with a specific value at each point in time. Representation of rhythmic structure as point processes allows us to examine spectral and temporal dynamics with unprecedented mathematical precision and rigor. The methods developed in our study are likely to useful for addressing many other important questions involving rhythmicity in music and speech across cultures.

Materials and Methods

Analysis of Musical Scores.

All musical scores were drawn from the Humdrum Kern database (46). Voices (instruments) and durations were extracted with custom scripts using the Humdrum Toolkit (47). Musical movements, which are self-contained sections of larger compositions, were treated as independent units (pieces). Onsets for each voice of each piece were converted into a time-aligned raster representation, providing a marker of interonset intervals (interevent durations). Onsets from different voices were merged (as shown in Fig. 2A). Rhythm spectra were then computed with the multitaper approach using the Chronux toolbox (35, 48). The multitaper approach (35) minimizes the variance (and spectral leakage) of the spectral estimate by premultiplying the data with spectrally concentrated orthogonal (Slepian) tapers (35, 49, 50): here, for estimating rhythm spectra, we used three tapers and a sampling rate of 10 Hz (which is well above the Nyquist rate for our temporal frequencies of interest; see next section) (51, 52). Only movements with more than 200 notes were included in the analysis to permit robust spectral estimation (36). We fit straight lines to model the variation in rhythm spectral power over two orders of magnitude of frequency (between 0.01 and 1 Hz) (36) using robust regression. (There are obvious limits of the 1/f linear fit: at one end it is limited by note durations, and at the other end it is limited by the length of the pieces/scores we analyzed.) To generate an empirical null distribution for statistical comparison, and as a control to verify and validate our spectral estimation on rhythm rasters, note onsets were shuffled randomly and rasterized: as expected, shuffled onset rasters showed flat spectra (characteristic of white noise) (Fig. 2 B and C). (If the mere inclusion of notes of specific durations in a musical piece, but not their order, were responsible for 1/f, the random arrangements of notes would still yield this power distribution; thus the shuffled version of the pieces forms a suitable null hypothesis.)

Spectral exponents for pieces were compared with their shuffled counterparts using the Wilcoxon signed rank test (last column, Table S1). To compare exponent distributions across genres and composers, we performed a one-way ANOVA and tested for significant differences between exponent means based on the Tukey–Kramer HSD criterion. Statistical analyses were performed in Matlab. We repeated the spectral analysis for each voice extracted separately, normalizing all pieces to the same total duration, as well as including pieces of all lengths (< 200 notes), and observed results similar to those reported here. Plots of the power spectra for individual composers and genres, as well as additional details on the compositions used in this study, can be found in SI Appendix 1 and SI Appendix 2.

Generation of Simulated 1/f Rhythms.

To generate duration sequences that obey a power law of the form [1/f]^β we modeled the internote intervals, or durations, (τ) as a multiplicative stochastic point process (53):

In this formula, γ is a relaxation factor, ε represents a normally distributed, zero-mean, unit-variance, white-noise process, and σ represents a scaling factor for the SD of the white noise. The relaxation factor (γ) was varied to generate duration sequences with different spectral exponents (β). Other parameters were set to fixed values (μ = 0.0, σ = 0.05). Larger values of the relaxation factor led to sequences with longer (persistent) history effects: such sequences showed correlations over longer time windows (Fig. 1A), and exhibited 1/f spectra with larger βs (Fig. 1B). Duration sequences with β = 2.0 were generated with γ = 0.025, whereas sequences with β = 1.0 were generated with γ = 0.0. Sequences with β = 0.0 (white noise) were generated with γ = 0.0, but without the first term on the right hand side of Eq. 1, thus eliminating all history effects. Rhythm rasters were then derived from the duration sequences by placing “ticks” on the time axis such that successive ticks in time were separated by successive values in the duration sequence. All simulations were performed in Matlab.