Role of sensory input distribution and intrinsic connectivity in lateral amygdala during auditory fear conditioning – A computational study

Abstract

We propose a novel reduced order neuronal network modeling framework that includes an enhanced firing rate model and a corresponding synaptic calcium-based synaptic learning rule. Specifically, we propose enhancements to the Wilson-Cowan firing rate neuron model that permits full spike frequency adaptation seen in biological LA neurons, while being sufficiently general to accommodate other spike frequency patterns. We also report a technique to incorporate calcium-dependent plasticity in the synapses of the network using a regression scheme to link firing rate to postsynaptic calcium. Together, the single cell model and the synaptic learning scheme constitute a general framework to develop computationally efficient neuronal networks that employ biologically-realistic synaptic learning. The reduced order modeling framework was validated using a previously reported biophysical conductance-based neuronal network model of a rodent lateral amygdala (LA) that modeled features of Pavlovian conditioning and extinction of auditory fear (Li et al., 2009). The framework was then used to develop a larger LA network model to investigate the roles of tone and shock distributions and of intrinsic connectivity in auditory fear learning. The model suggested combinations of tone and shock densities that would provide experimental estimates of tone responsive and conditioned cell proportions. Furthermore, it provided several insights including how intrinsic connectivity might help distribute sensory inputs to produce conditioned responses in cells that do not directly receive both tone and shock inputs, and how a balance between potentiation of excitation and inhibition prevents stimulus generalization during fear learning.

INTRODUCTION

Biophysical or conductance-based neuron models with voltage-gated currents have been shown to successfully reproduce membrane potential fluctuations in single neurons (Koch and Segev, 1998, Gerstner and Kistler, 2002, Dayan and Abbott, 2005, Sterratt et al., 2011). However, such models present two distinct challenges: First, they invariably require long simulation times, especially with multiple compartments and high levels of network connectivity, and this can frustrate the process of model development. Second, the complexity and large degrees of freedom in these models can hinder the interpretation of and confidence in the model outputs.

Various reduced-order single cell models have been used to investigate the behavior and properties of neuronal networks. This is because fewer parameters in such models facilitate the process of analysis and design, and provide deeper insights into the underlying mechanisms (Fourcaud and Brunel, 2002, Destexhe and Sejnowski, 2009, Kellems et al., 2010, Yan and Li, 2011). Such methods have been used in neuronal networks with a variety of adaptations (Wilson and Cowan, 1972, Benda and Herz, 2003, Chizhov et al., 2007, Vlachos et al., 2011). The Wilson-Cowan model (Wilson and Cowan, 1972, Wilson, 1999, Destexhe and Sejnowski, 2009) is one such two-variable single neuron model that has been used effectively in networks such as short-term memory networks and adaptation-dependent forgetting, mutually inhibitory winner-take-all networks, half-center oscillators for locomotion, and cortical networks that perform visual pattern recognition. The Wilson-Cowan model, however, does not support full frequency adaptation, i.e., the firing rate cannot adapt to zero for a constant input.

Here we propose a novel firing rate model that implements spike frequency adaptation in response to constant input by modifying the adaptation dynamics of the Wilson-Cowan model. Furthermore, we propose an implementation of a calcium-dependent synaptic learning rule (Shouval et al., 2002a, Shouval et al., 2002b, Li et al., 2009) for firing-rate networks. Since firing-rate models do not possess the features required to explicitly post-synaptic calcium concentration (denoted henceforth as [Ca²⁺]), we propose two regression techniques to link pre- and post-synaptic firing rates to synaptic [Ca²⁺].

We first developed a firing rate network model to investigate if it could replicate the findings of the detailed biophysical LA model of Li et al. (2009). The LA model of Li et al. (2009) “learns” conditioned fear responses, much as a rodent does, when trained by the coincident presentation of a conditioned stimulus (CS; e.g., an audible tone) and a noxious unconditioned stimulus (US; e.g., a foot shock). An increase in pyramidal cell activity to tone (tone response) during conditioning signifies the acquisition of this fear memory (Romanski et al., 1993, Quirk et al., 1995, Quirk et al., 1997, Kim and Jung, 2006, Li et al., 2009). Repeated subsequent presentation of the tone in the absence of the shock causes a gradual decrease in the potentiated pyramidal tone responses (extinction), via formation of a new extinction memory (Quirk, 2002, Barad et al., 2006, Quirk and Mueller, 2007, Likhtik et al., 2008). The reduced order firing-rate network model presented here was able to capture all the salient features of fear conditioning and extinction training, suggesting that the essential dynamics of the detailed LA model were replicated by using the proposed reduced order model framework. The equivalent firing rate framework was then used to develop a larger model to obtain insights into one specific aspect of fear learning in LA that is poorly understood presently and is difficult to investigate experimentally: the role of different tone and shock distributions and of intrinsic network connectivity in the formation of fear and extinction memories.

METHODS

Single cell model

The Wilson-Cowan model equations (Eq. 1; Wilson and Cowan, 1972, Wilson, 1999, Destexhe and Sejnowski, 2009) model the steady state firing rate E of a cell in response to an input P using a Hill function S(P), and has been used extensively by researchers to model network behaviors, e.g., it was used to describe the contrast-response function of striate neurons to visual stimuli in monkeys and cats (Albrecht and Hamilton, 1982). In Equation 1, a neuron’s spike rate (E)

$$\begin{array}{c}\hfill {\tau }_E\frac{\mathit{\text{dE}}}{\mathit{\text{dt}}}=-E+S(P);S(P)=\frac{{\mathit{\text{MP}}}_{+}^N}{{(\sigma +A)}^N+P_{+}^N}\hfill \\ \hfill {\tau }_A\frac{\mathit{\text{dA}}}{\mathit{\text{dt}}}=-A+\mathit{\text{kE}}\hfill \end{array}$$ (1)

converges with a time constant τ_E to a steady-state rate S(P) which is a function of the cell’s synaptic input P (current in pA in our model). In S(P), M is the maximum possible firing rate (Hz), σ is the value of the synaptic input for which the firing rate is half the maximum, A is an adaptation variable, and the dimensionless exponent N describes the steepness of the rise of the firing rate with increasing input. The subscript + indicates that negative arguments are forced to zero. The model produces spike-frequency adaptation by considering a second dynamic equation controlling the adaptation variable A. This adaptation variable A increases with a time constant (τ_A>τ_E) in response to an increase in the firing rate E of the cell. which decreases the instantaneous value of S(P) by effectively increasing the half-maximal input value (Wilson, 1999).

This model has some limitations. First, even with the adaptation modeled in eq. 1, the instantaneous value of E can never be zero if a constant input is present. For a significant class of spiking neurons, including 61% of pyramidal cells in the rodent LA, the spike rate adapts to zero within 400 ms of constant current injection (Faber et al., 2001). Second, the model does not have the capability to incorporate subthreshold stimulation, i.e., it will “spike” for all P > 0.

Enhancements to the firing rate model

To accommodate full spike-frequency adaptation, we propose the following modifications to Eq.1. First, to accommodate subthreshold stimulation, we propose the substitution P=P’–δ, where δ is the rheobase (minimum stimulation required to elicit firing in the biological neuron) and P’ is the sum of the synaptic and injected input to the cell. Because of the subscript +, S(P) = 0 for P’ < δ. Second, instead of producing adaptation via the divisive feedback of A, the steady-state value of E is set to [S(P)–A]₊, and the steady-state value of A is set to S(P)–A(P) (see Eq. 2). Thus, with τ_A>τ_E, in response to input, the value of E increases initially to a quasi steady-state value of S(P), but then decreases to A(P) as A converges to S(P)–A(P). The + subscript in dE/dt was used to ensure that the firing rate did not adapt to negative values. In Eq. 2, the expression τ_A (P) = τ_A0 + k(P−P₁)₊ − k(P − P₂)₊ allowed the adaptation rate to vary as a function of input amplitude. By using different rheobase parameters (δ_S and δ_A) for S(P) and A(P), a firing-rate model cell response can include a large overshoot and then adapt to E = 0 for δ_S < P < δ_A.

$$\begin{array}{cc}\hfill {\tau }_E\frac{\mathit{\text{dE}}}{\mathit{\text{dt}}}=-E+{[S(P)-A]}_{+}\hfill & \hfill S(P)=\frac{M_S{P}_{+}^{\mathit{\text{NS}}}}{{\sigma }_S^{\mathit{\text{NS}}}+P_{+}^{\mathit{\text{NS}}}}\\ \hfill {\tau }_A(P)\frac{\mathit{\text{dA}}}{\mathit{\text{dt}}}=-A+S(P)-A(P)\hfill & \hfill A(P)=\frac{M_A{P}_{+}^{\mathit{\text{NA}}}}{{\sigma }_A^{\mathit{\text{NA}}}+P_{+}^{\mathit{\text{NA}}}}\end{array}$$ (2)

We next discuss how such a model can be integrated into networks with synaptic learning rules.

Network connections and synaptic learning

Synaptic inputs in the firing rate model can be modeled in several ways (Gerstner and Kistler, 2002). One such strategy is to assume the synaptic input P from a presynaptic cell to be a function of its firing rate (Wilson, 1999), and using such an approach, the combined synaptic input to cell j was computed as P_j′ = Σ w_i,jE_i, where w_i,j is the connection weight from cell i to cell j and E_i is the firing rate of cell i. It is noted that other complex functions of the firing rate can also be used in the methodology outlined.

Synaptic plasticity

Synaptic calcium concentration, primarily due to NMDA receptor currents, is critical for synaptic plasticity (Bliss and Collingridge, 1993, Castellani et al., 2001, Shouval et al., 2002a, Shouval et al., 2002b). Connection weights in the model were controlled by a calcium-based plasticity rule (Shouval et al., 2002a) used in the biophysical LA model (Li et al., 2009). According to this rule, conductance of AMPA synapses is modulated by post-synaptic calcium concentration [Ca²⁺], with the change in synaptic weight controlled by eq. 3. Calcium enters from a variety of sources, most notably synaptic NMDA receptor channels activated by presynaptic action potentials. Ω([Ca²⁺]) is a piecewise continuous function that determines how the synaptic weight changes depending on the depression and potentiation thresholds θ_d and θ_p: it is zero for [Ca²⁺] < θ_d, becomes negative and reaches a minimum of −0.15 at [Ca²⁺] = (θ_d + θ_p)/2, and saturates at +1 for [Ca²⁺] > θ_p.

$$\begin{array}{c}\frac{\mathit{\text{dw}}}{\mathit{\text{dt}}}=\eta ([{\mathit{\text{Ca}}}^{2+}])({\lambda }_1\mathrm{\Omega }([{\mathit{\text{Ca}}}^{2+}])-{\lambda }_{2}w)\hfill \\ \eta ([{\mathit{\text{Ca}}}^{2+}])=\frac{0.001}{1+0.1/({10}^{-5}+{[{\mathit{\text{Ca}}}^{2+}]}^3)}\hfill \\ \mathrm{\Omega }([{\mathit{\text{Ca}}}^{2+}])=\{\begin{array}{cc}\hfill 0,\hfill & \hfill [{\mathit{\text{Ca}}}^{2+}]<{\theta }_d\hfill \\ \hfill -\sqrt{{\left(\frac{{\theta }_p-{\theta }_d}{2}\right)}^2-{\left(\frac{[{\mathit{\text{Ca}}}^{2+}]-({\theta }_p+{\theta }_d)}{2}\right)}^2},\hfill & \hfill {\theta }_d<[{\mathit{\text{Ca}}}^{2+}]<{\theta }_p\hfill \\ \hfill \frac{1}{1+50\text{ exp}(-50([{\mathit{\text{Ca}}}^{2+}]-{\theta }_p))},\hfill & \hfill {\theta }_p<[{\mathit{\text{Ca}}}^{2+}].\hfill \end{array}\hfill \end{array}$$ (3)

The term η([Ca²⁺]) (in msec⁻¹) is the learning rate, which ensures that weights do not decay to zero in the absence of significant [Ca²⁺] elevations, and λ₁ and λ₂ are parameters that control the ratio of active plasticity to weight decay. In a series of studies (Castellani et al., 2001, Shouval et al., 2002a, Shouval et al., 2002b, Castellani et al., 2005, Castellani et al., 2009, Shouval et al., 2010) that proposed this specific model of calcium-dependent learning, λ₂ (just λ in those studies) was taken as a linear decay constant that would help stabilize and limit unfettered growth or decay of synaptic weights. In the original biophysical LA model (Li et al. 2009), this was extended to two independent constants (λ₁ and λ₂) to allow a greater degree of control over the rates of growth and decay of the weights, and that strategy was likewise adopted for this study. Intrinsic synapses in LA have been shown to support plasticity, although the experimental data are not conclusive (Pape and Pare, 2010). As in Li et al. (2009), our network model assumes plasticity at all the intrinsic synapses.

Synaptic calcium pools

Calcium concentration in excitatory post-synaptic terminals depends on the opening of synaptic NMDA channels after release of glutamate following presynaptic spikes. However, NMDA currents can flow only after the voltage-dependent magnesium block is removed by post-synaptic depolarization. To model this process in a firing-rate framework, [Ca²⁺] for each connection was controlled by a first-order differential equation with an influx function F dependent upon pre- (E_pre) and post-synaptic (E_post) firing rates, and linear decay to a baseline [Ca²⁺]₀ of 50 nM (eq. 4). This resting [Ca²⁺] is similar to that used for other neuronal models that consider calcium concentrations (Traub et al., 1994, Migliore et al., 1995, Fransén et al., 2004, Hemond et al., 2008, Li et al., 2009).

$${\tau }_{\mathit{\text{Ca}}}\frac{d[{\mathit{\text{Ca}}}^{2+}]}{\mathit{\text{dt}}}=F(E_{\mathit{\text{pre}}},E_{\mathit{\text{post}}})\times f(w)-([{\mathit{\text{Ca}}}^{2+}]-{[{\mathit{\text{Ca}}}^{2+}]}_0)$$ (4)

According to this equation, for a given combination of E_pre and E_post,, [Ca²⁺] approaches F + [Ca²⁺]₀. The time constant of [Ca²⁺] equilibration was 50 msec. AMPA receptors located on interneurons in the LA are calcium-permeable (Mahanty and Sah, 1998), creating the unique possibility that synaptic plasticity might directly lead to adjustments to [Ca²⁺] influx at glutamate synapses. To consider these effects in the biophysical LA model, [Ca²⁺] influx through AMPA receptors channels at interneurons was allowed to increase or decrease with changing synaptic weight (Li et al., 2009). Here, such an effect was implemented by by multiplication of F in Eq. 4 with the linear term f(w) = (w(t) + w’)/(w₀ + w’) for such connections. In f(w), w₀ is the initial weight of the synapse, w(t) is its instantaneous weight, and w’ was a tunable factor set as 12 for pyr-int synapses and 15 for tone-int synapses.

Calcium-dependent plasticity of inhibitory connections has been reported in the LA (Bauer and LeDoux, 2004). The previous biophysical LA model noted that this calcium was known to be dependent upon presynaptic firing frequency, and so modeled it as calcium release from internal stores as a function of GABA_A receptor activation (Li et al., 2009). Influx of calcium through VGCCs in the soma of the interneuron also contributed to this calcium elevation. Since this mechanism assumes dependence of inhibitory plasticity upon both presynaptic and postsynaptic firing, the plasticity of inhibitory synapses in this firing-rate model was controlled again with eq. 4, but using parameters specific to inhibitory connections.

Network model of LA

We used the LA model developed using biological data (Li et al., 2009) as a reference point to illustrate the development of the proposed firing rate model and its use in a network involving [Ca²⁺]-dependent learning.

Single cell firing rate models

We tuned the parameters of the pyramidal cell types A, B, and C, and the interneuron in the firing rate model so that their single cell current injection responses matched in vitro biological data (Li et al., 2009) for 600 msec current steps of magnitudes ranging from 0 to 800 pA in steps of 50 pA.

Network architectures

To validate the firing rate network model, we first selected the same structure for the network model as in the biophysical LA network model (Li et al., 2009). It consisted of eight pyramidal cells and two interneurons (Fig.1). Pyramidal cells 1–5 were of type A, cells 6–7 of type B, and cell 8 of type C. All pyramidal cells were reciprocally connected via excitatory synapses (green arrows in Fig.1), and were inhibited (Black circles in Fig.1) by the two interneurons, which also inhibited each other. Tone inputs were provided to pyramidal cells 3, 5, 7, and 8 (purple arrows), while shock inputs were connected to cells 1, 4, 5, 7, and 8 (red arrows). Both interneurons received tone and shock inputs. Table 1 shows the initial weights for these connections and the corresponding parameters of Eq. 3.

Figure 1.

The preliminary firing-rate network model of the lateral amygdala for comparison with outputs from Li et al. (2009). Green triangles 1–8 are pyramidal cells (5 type A cells [1–5], 2 type B cells [6–7], and 1 type C cell [8]); Black circles are interneurons 1–2; Purple circle is tone input (T); Red circle is shock input (S). Pyramidal cells excited all other pyramidal cells and interneurons, but not themselves. Interneurons inhibited one another and each pyramidal cell. Pyramidal cells 3, 5, 7, and 8, received direct tone, while pyramidal cells 1, 4, 5, 7, and 8 received direct shock input. Both interneurons received direct tone and shock inputs.

Table 1.

Network parameters for calcium pools and synaptic weights.

Synapse type	w0	λ1	λ2	θd	θp
Tone-pyr	5.0	15.0	0.01	0.55	0.7
Tone-int	2.5	0.5	0.02	0.55	0.7
Pyr-pyr	1.5	1.5	0.01	0.5	0.6
Pyr-int	1.0	0.5	0.01	0.55	0.6
Int-pyr	−2.0	0.6	0.02	0.5	0.7

We used a larger network of 75 neurons, with biological ranges of connectivity, for obtaining the biological insights reported in the paper. Neurons were segregated into clusters of four pyramidal cells and one interneuron. Within each cluster, pyramidal-interneuron (pyr-int) and int-pyr connections were made with 100% probability, but no connections to or from interneurons were made between clusters. The connectivity between pyramidal cells was varied from 5–10% to conform to the reported sparse connectivity in biology, as described later. Another slightly modified version of the network configuration was used to accommodate additional tone inputs for a subsequent study related to stimulus generalization.

Calcium-based learning rule

We propose two strategies for determing F in the calcium based learning rule (eqs. 3 and 4), a general one described later, and a specific one that can be obtained using biophysical cell models. We consider the latter first since biophysical models of the specific cells were available to us (Li et al., 2009). The biophysical LA cell models were used to obtain F of eq. 4 as a function of E_pre and E_post. To this end, we connected pairs of biophysical LA cell models, excited both cells at specified firing rates, and measured the resulting steady-state [Ca²⁺]. The resulting data were first fitted as functions of E_post, which produced one polynomial in E_post for each value of E_pre. Then, the coefficients of these polynomials were fitted as functions of E_pre. This procedure was performed for each synapse type, i.e., pyramidal-to-pyramidal (pyr-pyr), pyramidal-to-interneuron (pyr-int), interneuron-to-pyramidal (int-pyr), tone-to-pyramidal (tone-pyr), and tone-to-interneuron (tone-int). For tone-pyr and pyr-pyr connections, F was multiplied by 1–exp(−4E_pre) to ensure that F = 0 for E_pre = 0. For tone-int and pyr-int connections, for which AMPA receptors are Ca²⁺-permeable, w’ in the function f(w) was set to 12 and 15, respectively.

Modeling experiments

The fear training protocol used for the firing-rate LA model was identical to that used for the biophysical LA model (Li et al., 2009). Briefly, the model was exposed to sensitization (40 sec), conditioning (40 sec), first wait (40 sec), early extinction (120 sec), second wait (840 sec), and late extinction (120 sec) training periods (total time = 1200 sec). Tone inputs were presented for 500 msec at 4 second intervals during sensitization, conditioning, and both extinction periods. Shock inputs (100 msec) were presented at random times during the period between tone inputs in the sensitization phase. During conditioning, shock inputs were co-presented during the final 100 msec of each tone input. Tone and shock inputs were represented by constant increases to P’ of 200 Hz (see table 2) and non-plastic shock weights of 40. The tone and shock durations in the model were shorter than those used in experiments (Quirk et al., 1995), and the gaps between tones and between the various phases of the training were shortened in the model to reduce computational times. However, the ratios of tone to shock durations and training periods were similar. In the present model, as in the biophysical LA model (Li et al., 2009), synaptic plasticity occurred either during short, discrete time windows during conditioning and extinction, or gradually during waiting periods (spontaneous synaptic decay). This compression of time thus impacts only the rates at which synaptic weights change, but not their qualitative behavior. Hence the learning and decay rates in the model (eq. 3) represent scaled estimates of such biological rates for synaptic weights.

Table 2.

Parameter values for firing rate model cells.

	Pyr A	Pyr B	Pyr C	Intr
MS	150	160	150	321
NS	1	1	1	1
σS	250	200	200	650
δS	150	100	100	50
MA	113	130	115	--
NA	1	1	1	--
σA	125	200	200	--
δA	500	450	300	--
τA0	5	5	5	--
k	0.6	0.48	0.58	--
P1	350	200	250	--
P2	550	500	300	--

Noisy background inputs

In the biophysical model, random synaptic potentials were provided to each cell via non-specific synaptic connections to simulate the effects of background firing, producing low spontaneous firing rates in each cell. This background activity was previously determined to be critical in the observed spontaneous recovery of fear in behavioral experiments (Quirk et al., 1995, Quirk et al., 1997, Quirk, 2002) due to the resulting low amplitude increases to [Ca²⁺] (Quirk et al., 1997, Quirk, 2002, Quirk and Mueller, 2007, Li et al., 2009). It was not feasible to impose a low, constant firing rate (e.g., E = 1–2 Hz) in single cells, because as shown below in Results, the strong, transient impact of individual spikes on postsynaptic [Ca²⁺] was not captured with such a constant low firing rate. Instead, in the firing-rate LA model brief (10 msec), random additions of synaptic “input” (increases to P in eq. 2) were issued to each cell to produce periodic, spontaneous firing rate increases. These events were able to produce periodic postsynaptic [Ca²⁺] fluctuations that influenced synaptic weight change. Spontaneous inputs to each cell were modeled with a poisson process using the randomizing feature of the “NetStim” object in NEURON with average rates of 1 Hz for pyramidal cells and 8 Hz for interneurons to reproduce the higher rates of LA interneurons (Quirk et al., 1995, Quirk et al., 1997). Additionally, such events were also added to tone inputs at an average rate of 1 Hz.

Quantification of tone responses

Estimates of individual cell spiking in response to tone input were obtained by integrating the time-varying firing rate over the first 400 msec of tone presentation (to exclude shock responses) using the sum Σ E(t)Δt (Wilson, 1999).

Simulation hardware and software

All simulations were performed using serial NEURON (Carnevale and Hines, 2006) on the University of Missouri Beowulf supercluster LEWIS. Simulations were run on single cores in batch mode. Analysis of simulation results in the 75 cell LA networks was performed on LEWIS using MATLAB 7.10 (R2010a). Further data analysis was performed on a Windows XP SP 3 Home workstation using MATLAB 7.0 (R14) (The Mathworks, 2004).

RESULTS

Single cell output

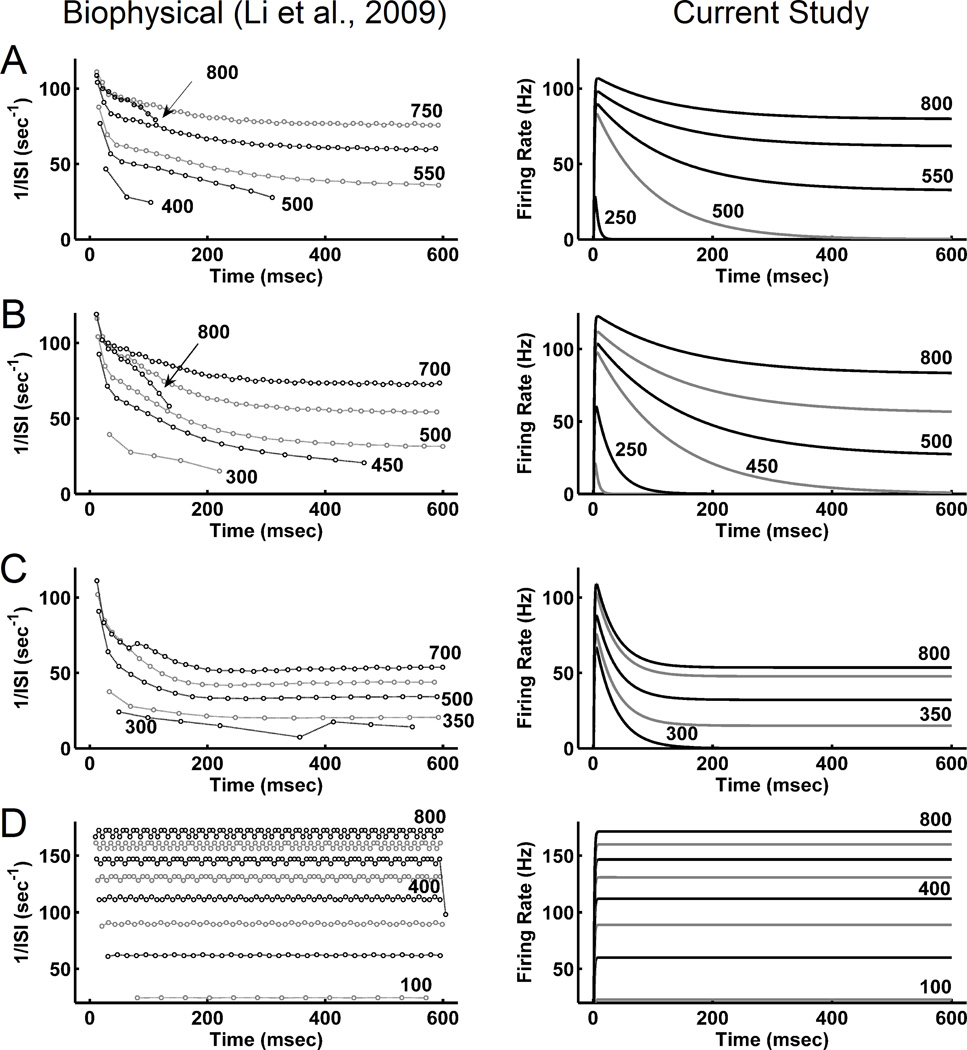
Figure 2 shows the firing rates of the four biophysical LA model cell types and the corresponding reduced order models in response to the various current amplitudes, as described in methods. The responses of these cells can be divided into three categories: i) subthreshold responses with small currents, i.e., no spike case or ‘silent’ case; ii) transient responses for moderate currents, i.e., firing was elicited at the onset but not sustained; and iii) sustained responses for high currents, i.e., spikes were ‘sustained’ throughout the duration of the current injection. In pyramidal cell type A, responses were silent below 200 pA, transient from 200 – 500 pA, and sustained above 500 pA. In pyramidal cell type B, responses were silent below 150 pA, transient from 150 – 450 pA, and sustained above 450 pA. In pyramidal cell type C, responses were silent below 150 pA, transient from 150 – 300 pA, and sustained above 300 pA. The interneuron produced sustained firing for all current injections above 50 pA. Table 2 shows the parameters used in eq. 2 to reproduce the resulting firing rates for each cell type, computed as the reciprocal of inter-spike interval (ISI).

Figure 2.

Comparison of single cell firing-rate output in the biophysical (left) and firing-rate (right) LA model networks. Firing rates for detailed biophysical LA cell models in Li et al. (2009) were computed as 1/ISI. Each trace corresponds to the firing rate calculated for a spike train elicited with a 600 msec current injection (pA). Circles represent spike times at which the ISI was calculated. At current injections below those shown, some cells fired only a single spike, and so ISIs were not calculated. A) type A pyramidal cell, B) type B pyramidal cell, C) type C pyramidal cell, and D) Interneuron.

Post-synaptic [Ca²⁺]

To incorporate [Ca²⁺]-dependent learning in the firing-rate model, we first stimulated pairs of biophysical models at fixed firing rates and recorded the resulting synaptic [Ca²⁺]. These data were then fit as functions of presynaptic (E_pre) and postsynaptic (E_post) firing rates of the connected cells for use in the firing-rate model.

Excitatory synapses

For excitatory connections, themaximum steady-state [Ca²⁺] was approximately 1.0 µM, which was reached with higher firing rates, and the minimal value was the resting value of 50 nM (as cited in Methods) for E_pre = 0. This maximal calcium concentration was necessarily determined by the NMDA receptor channel conductance used in the original biophysical LA model (Li et al. 2009), but this value was inspired by a theoretical model of NMDA receptor dependent plasticity (Shouval et al., 2002a), for which a threshold concentration for LTP production was suggested to be in the sub-1.0 µM range. For E_pre > 0 (because non-zero presynaptic firing is required to trigger synaptic current), steady-state [Ca²⁺] consistently increased for elevated E_pre or E_post. However, increases in E_pre typically caused a smaller increase in calcium when E_post was already high (data not shown). This effect was most prominent for the tone-pyr connection, for which the [Ca²⁺] was nearly independent of presynaptic firing rates above 25 Hz. In contrast, this effect was least prominent for the pyr-pyr connections, for which steady-state [Ca²⁺] increased from 0.25 to 0.75 µM with E_ost = 0 Hz over the range of E_pre values tested, and it saturated to 1.05 µM for E_pre = 125 Hz.

Inhibitory Synapses

Calcium-dependent plasticity at inhibitory synapses differs from that at excitatory synapses (see Methods), and the biophysical LA model captured such differences (Li et al., 2009). In the biophysical LA model, calcium current through voltage gated calcium channels (VGCCs) contributes to the calcium pool of inhibitory synapses. Thus, in contrast to excitatory synapses, [Ca²⁺] elevations can occur in the absence of presynaptic firing (E_pre = 0). In the biophysical LA inhibitory synapse model, [Ca²⁺] at inhibitory synapses reached 0.5 µM for E_pre=0 for high E_post. The maximum observed [Ca2⁺] for inhibitory synapses was also significantly higher than for excitatory synapses (nearly 2.0 µM), owing to the contribution of influx through postsynaptic VGCCs. However, despite these differences, the steady-state calcium concentration for inhibitory synapses showed the same characteristic upward trend as excitatory synapses in which both increases in pre- and postsynaptic firing rates contributed to elevated concentrations.

Synaptic calcium fits

As described in Methods, steady-state [Ca²⁺] for each synapse type was fit as a function of E_pre and E_post. Accordingly, for each tested value of E_pre, a different [Ca²⁺] curve was fit as a function of E_post, typically by polynomials of order 3 or less. Because this procedure resulted in a unique polynomial for each value of E_pre, the coefficients of these polynomials were in turn fit as polynomials of E_pre, yielding [Ca²⁺] for each synapse as a two-dimensional function of E_pre and E_post. In matrix form, this equation is $F_{\mathit{\text{Ca}}}={\stackrel{⃑}{E}}_{\mathit{\text{post}}}^T\mathbf{K}{\stackrel{⃑}{E}}_{\mathit{\text{pre}}}$, where K is the matrix of fitted coefficients, and E⃑_pre and E⃑_post are vectors of the pre- and post-synaptic firing rates raised to descending powers. As an example, for the pyr-int synapse, K is a 3×2 matrix, ${\stackrel{⃑}{E}}_{\mathit{\text{pre}}}={[E_{\mathit{\text{pre}}}^1{E}_{\mathit{\text{pre}}}^0]}^T,\text{and }{\stackrel{⃑}{E}}_{\mathit{\text{post}}}={[E_{\mathit{\text{post}}}^2{E}_{\mathit{\text{post}}}^1{E}_{\mathit{\text{post}}}^0]}^T$. An exception was the excitatory tone-pyr synapse, in which the coefficients of the polynomial F_Ca = K₁E_post + K₀ were better fit by rational functions of E_pre. These equations, as well as the coefficients of the matrix K for each type of synapse, are listed in Table 3.

Table 3.

Coefficients for synaptic calcium dynamics. For the tone-pyr synapse, coefficients of E_post were fractional functions of E_pre.

Synapse type	K
Tone-pyr	$K_1=\frac{1.27}{250}\frac{E_{\mathit{\text{pre}}}}{E_{\mathit{\text{pre}}}+0.5},K_2=\frac{1.27}{2}\frac{E_{\mathit{\text{pre}}}+10}{E_{\mathit{\text{pre}}}+30}$
Tone-int	0 0 0 3.5×10−7	0 0 0 −1.3×10−4	1.1×10−9 −4.1×10−7 4.9×10−5 0.014	4.3×10−8 −1.4×10−5 2.3×10−3 0.088
Pyr-pyr		−6.3×10−6 3.3×10−3	4.4×10−3 0.15
Pyr-int		3.3×10−7 −4.95×10−5 5.11×10−3	−3.75×10−5 7.87×10−3 0.1257
Int-pyr		−2.1×10−5 0.01	3.6×10−3 0.034

Alternative general model

In practice, calcium concentration might not always be easily obtained from either in vitro cells or biophysical cell models. However, it is not uncommon for synaptic plasticity to be quantified in real synapses as a function of spike frequencies of both input stimulation and in the post-synaptic cell (Ishida et al., 1997, Sjöström et al., 2001). Using the biophysical single-cell model, we discovered certain features of [Ca²⁺] that were consistent across all synapse types, and we suggest a fundamental rule for synaptic calcium that uses these findings to more directly relate synaptic plasticity to pre- and post-synaptic firing rates. These features are summarized as follows: i) [Ca²⁺] was zero for E_pre=0 and non-zero for E_post=0; ii) [Ca²⁺] saturated near 1 µM for large values of E_pre and E_post; iii) For E_pre > 0 and E_post > 0, further increases to E_post cause larger increases to [Ca²⁺] than do increases to E_pre. Given these observations, in the absence of biological values for [Ca²⁺], we propose an alternative and more general strategy to incorporate [Ca²⁺]-dependent learning by modeling calcium influx F (of eq.4) using the structure in eq. 5.

$$F(E_{\mathit{\text{pre}}},E_{\mathit{\text{post}}})={[{\mathit{\text{Ca}}}^{2+}]}_P(1-e^{-E_{\mathit{\text{pre}}}/k_{\mathit{\text{pre}}}})(1-(1-K)e^{-E_{\mathit{\text{post}}}/k_{\mathit{\text{post}}}})$$ (5)

In eq. 5, [Ca²⁺]_P is the peak calcium concentration, with a suggested range from θ_p to 2×θ_p (here, θ_p was 0.6–0.7 µM, and a reasonable [Ca²⁺]_P value would be 1.0 µM); K is the desired ratio of the peak value of F with E_post set to 0 to the absolute peak of F, with a suggested range of 0.1 to 0.5 (here, a value of 0.33 would be appropriate); and k_pre and k_post are constants that set the slope of F in the E_pre and E_post dimensions, with suggested ranges of 1–5 sec⁻¹ and 10–30 sec⁻¹, respectively. By using the more general eqs. 4 and 5, networks could be developed with synaptic learning based directly on spike frequency, without the need for information about [Ca²⁺].

Conditioned tone responses

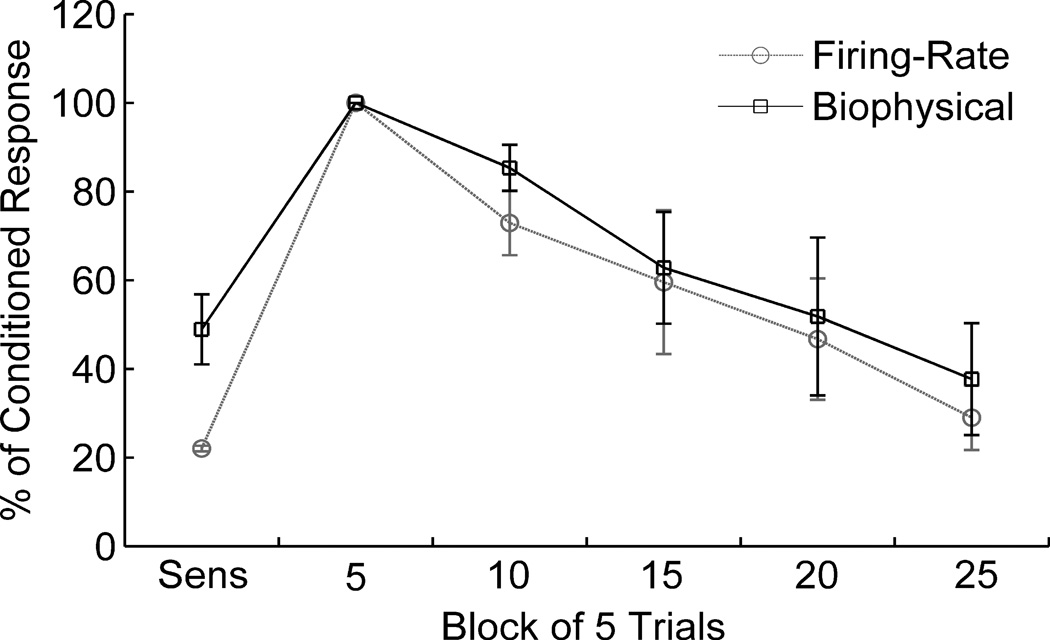
Figure 3 shows the changes in tone responses of the network during the training protocol. These results were averaged for the five cells (cells 1, 4, 5, 7 and 8) whose responses increased (‘conditioned’) during conditioning. The responses of both interneurons decreased during sensitization, but increased during conditioning and during both phases of extinction, contributing to the decrease of pyramidal cell activity (‘extinction’). These results are consistent with those observed in the biophysical LA model (Li et al., 2009), which in turn are consistent with biological observations of individual LA cells (Quirk et al., 1995, Quirk et al., 1997).

Figure 3.

Tone responses of conditioned pyramidal cells in the network model during the phases of fear conditioning. Responses are shown as % of conditioned responses. Sensitization response was measured for final five trials of the sensitization phase, and remaining responses were measured for successive blocks of five trials during extinction. Results reported as mean +/− SE for the four cells that displayed significantly conditioned tone responses. Variations are seen in biological experiments, and so the aim is to match the trends. Very good match was obtained with the results of the detailed biophysical LA model (Li et al., 2009) which itself was previously validated with biological data (Quirk et al., 1997).

Synaptic potentiation and depression

Synaptic inputs and weight changes occur continuously during network activity in the firing-rate model, while such events are organized into discrete events in the biophysical model. Hence, the weights will have to be suitably adjusted for use in a firing rate model. We found that the initial tone-pyr weights had to be decreased from 10.0 to 5.0, and tone-int weights reduced from 3.0 to 2.5 (compared to that in the biophysical model of Li et al., 2009). Initial inhibitory weights had to be reduced from 5.0 to 2.0 for int-pyr connections and from 3 to 1 for int-int connections. Initial excitatory pyr-pyr and pyr-int weights were left unchanged at 1.5 and 1.0, respectively. Additionally, the active learning factor (λ₁) had to be reduced from 2.5 to 1.5 for pyr-pyr synapses, from 2.0 to 0.6 for int-pyr synapses, from 2.0 to 0.5 for pyr-int synapses, and from 1.0 to 0.5 for tone-int synapses. The active learning factor for tone-pyr synapses (15.0) could be left unchanged.

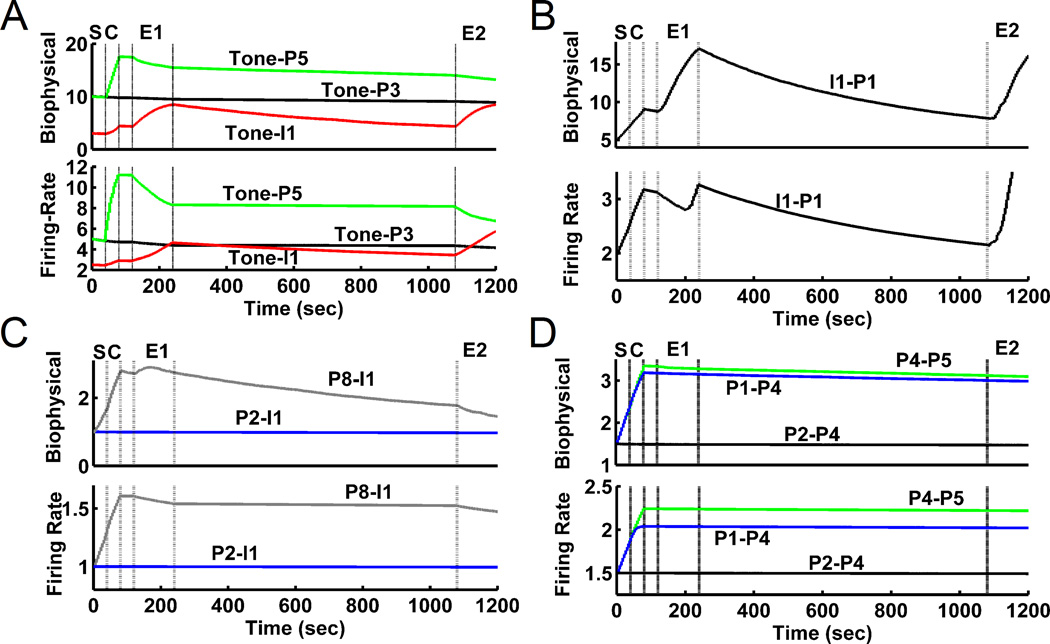
Figure 4 shows that the trends and values of the firing-rate model synaptic weights matched those obtained from the biophysical model very well. Tone-pyr connections to those pyramidal cells that received both tone and shock potentiated during conditioning and depressed during extinction in both models. Tone-int connections potentiated during sensitization, conditioning, and extinction periods. Int-pyr connections in both the biophysical and firing-rate LA models also potentiated during sensitization, conditioning, and extinction, contributing to the reduced pyramidal cell activity at the end of extinction. Plasticity of pyr-int and pyr-pyr connections depended upon the input connections to the pre- and postsynaptic cells. Pyr-int weights potentiated if the presynaptic cell received shock inputs and depressed otherwise (fig. 4C). Pyr-pyr weights potentiated and depressed in a complex manner that was dependent both upon the combination of direct inputs to the pre- and postsynaptic cells as well as secondary inputs from network connections (fig. 4D). In general, weights between cells that received both tone and shock inputs potentiated the most, while weights between cells that received no inputs, especially weights to postsynaptic cells that received no shock input, only depressed. As in the biophysical LA model, the higher spontaneous activity of interneurons caused a higher rate of decay for intpyr and tone-int than for the tone-pyr and pyr-pyr weights, permitting the spontaneous recovery of fear seen in behavioral experiments (Quirk, 2002).

Figure 4.

Comparisons of representative time courses of synaptic weights for the detailed biophysical and firing-rate models during the training protocol showed very good match in all cases: A: Tone synapses (tone-pyr and tone-int). B: int-pyr. C: pyr-int. D: pyr-pyr. Training phases: S, sensitization; C, conditioning ; E1, 1^st (early) extinction; E2, 2^nd (late) extinction.

These observations are consistent with the putative behavior of LA neurons in which coincident and convergent neutral and noxious stimuli are associated (fear conditioning), eventually causing the neutral stimulus to elicit similar neural reaction as the noxious stimulus. Repeated presentation of the neutral stimulus without the noxious stimulus (extinction) reinforces inhibition of the fear response, creating a new memory, rather than erasing the original fear memory (Quirk, 2002). During the interval between extinction trials, spontaneous recovery of fear occurred by the weakening of the extinction memory, which decays faster than the fear memory (Li et al., 2009).

Performance

Using serial NEURON software (Carnevale and Hines, 2006) on the University of Missouri beowulf supercluster, the biophysical LA network model simulation took 4.5 hours to run the full conditioning and extinction protocol with recovery. To run the same protocol using the proposed firing rate model took only 2.5 minutes. Since brain circuits involve numerous neurons, e.g., the rat LA contains approximately 58,000 cells (Tuunanen and Pitkänen, 2000), the savings in computational time using the proposed firing rate model would be considerable if realistic neuron densities are used in future models.

Application of the model to gain insights into encoding of fear memories in LA

Biological data showed that 45–55% of LA pyramidal neurons were responsive to the CS (tone), and 25–35% exhibit potentiated responses following a typical experimental fear conditioning protocol (Quirk et al., 1995, Quirk et al., 1997). These biological observations suggest two possibilities: i) LA pyramidal neurons receive extensive tone and shock inputs, or, ii) they receive sparse tone and shock inputs which are then amplified by intrinsic connections to indirectly provide sufficient activation to a large proportion of principal cells in the network. However, the ‘density’ of tone and shock inputs in LA is not presently known. Similarly, data are only beginning to emerge about intrinsic excitatory connectivity within LA. As a demonstration of the utility of the firing-rate modeling framework, we tested a range of tone and shock densities using a larger LA network under conditions. We first scaled up the network size from 8 pyramidal cells and 2 interneurons to 60 pyramidal cells and 15 interneurons with the neurons segregated into groups of five (four pyramidal cells and one interneuron each, to represent the ratio seen in biology; McDonald, 1984), within which pyr-int and int-pyr connections were made with 100% probability. No connections to or from interneurons were made between such groups. Intrinsic excitatory interconnectivity is estimated to be much less than 10% (D. Paré, personal communications; Samson and Paré, 2006). Also, a large-scale cortical model was developed and validated using 9% short-range connectivity (Izhikevich et al., 2004). Since our model is a scaled down version of the biological LA, the connectivity had to be correspondingly increased (Dyhrfjeld-Johnsen et al., 2007), and so we selected 5–10% as the range for intrinsic connectivity. As cited, biological details about tone and shock densities are not available presently and so we varied those from 0–100%.

In summary, we sought to study the role of intrinsic connectivity in transmitting and amplifying sensory inputs, when the tone and shock densities varied. Towards this end, we ran several model experiments by varying excitatory connections linking pyramidal cells in the range of 5–10%, and with input-pyr (both tone-pyr and shock-pyr), and input-int (both tone-int and shock-int) connectivities varying from 0 to 100%. In each experiment, the model was exposed to the fear conditioning protocol (see methods) through the end of the first extinction phase (240 sec), and we analyzed the effect of intrinsic connectivity and tone and shock densities on two characteristics of individual cells: (i) tone responsiveness, and (ii) conditioning, as described below.

Model experiments were performed using 120 different 75-cell LA networks and this permitted us to study a total of 7200 pyramidal cell and 1800 interneuron motifs with varying numbers of afferent tone and shock inputs, and intrinsic inputs. The tone responses of these cells through fear conditioning and the end of first extinction were assessed, and the cells were classified according to their tone responses. Simulations of each network through the end of first extinction took about 5 minutes on serial NEURON, and we estimated the run time for the comparative conductance-based model as 9 hours.

Neuron classification based on tone responses and learning

Several distinct categories of cell types could be identified based on their responses:

Tone-responsive pyramidal cells were those cells whose firing-rate output was equivalent to the production of a total of at least 5 spikes during either sensitization, conditioning, or first extinction phases. Thus, a cell not considered tone-responsive during sensitization could be considered tone-responsive on the basis of its tone responses after conditioning. Of the total pyramidal cells classified, 61% were tone responsive. Interneurons were similarly classified as tone-responsive using a threshold activity of 25 because of the significantly higher firing rates of interneurons.

Conditioned pyramidal cells were those tone-responsive cells whose summed tone responses during the last 5 trials (tone presentations) of conditioning and first 5 trials of extinction were at least 50% higher than the value during the first 10 trials of sensitization. Based on this criterion, 52% of pyramidal cells conditioned, constituting 78% of tone responsive pyramidal cells.

Extinguished pyramidal cells were those conditioned cells whose summed tone responses during the last 10 trials of first extinction were at least 25% lower than the responses during the last 5 trials of conditioning and first 5 trials of extinction. Only 6% of pyramidal cells extinguished, constituting 13% of all conditioned cells.

Non-learning pyramidal cells were those tone-responsive, but non-conditioned cells whose summed tone responses during the last 10 trials of first extinction were between 75% and 125% of the summed tone responses during the first 10 trials of sensitization. About 9% of pyramidal cells were non-learning, constituting 14% of tone-responsive cells.

Additionally, two other cell types were identified based on their tone responses. These cells were observed in low proportions (<3%), and so they are mentioned solely for completeness.

Fast-extinguished pyramidal cells were those extinguished cells whose summed tone responses during the first 5 trials of extinction were at least 50% lower than those during the last 5 trials of conditioning. These cells exhibited conditioned tone responses, and extinction was established almost immediately during the beginning of the extinction training phase. Only a small portion of extinguished cells (2.5%) exhibited this behavior.

Desensitized pyramidal cells were those tone-responsive, non-conditioned cells whose summed tone responses during the last 10 trials of first extinction were at least 50% lower than those recorded during the first 10 trials of sensitization. Only 1% of tone-responsive pyramidal cells desensitized.

Of the 7200 pyramidal cells analyzed, 180 were discarded due to seizure-like activity in 3 of 120 networks (see below). Of the remaining 7020 cells, 3652 conditioned (52%) and 3368 did not condition (48%). Of the conditioned cells, 1785 received both tone and shock inputs (25.4% of the total); 886 received only shock (12.6%); 661 received only tone (9.4%); and 320 received neither tone nor shock (4.5%). Of the non-conditioned cells, 679 received only shock (9.7%); 1185 received only tone (16.9%); and 1463 received neither tone nor shock inputs (21.4%).

We analyze below how direct sensory inputs into a pyramidal cell interacted with those conveyed indirectly via intrinsic connectivity to shape the tone responsiveness of the cell. It is noted that changes in synaptic weights continue to occur throughout the training protocol (see figure 4 for representative plots). These synaptic weight changes will be influenced by the numbers of intrinsic and direct tone- and shock-information carrying afferents to the cell. So, both the synaptic weight changes and the numbers of afferents considered contribute to the tone responsiveness and conditioning of the cell, although we separate out only the numbers of afferents for analysis here.

Tone responsiveness of pyramidal cells depends upon both input and intrinsic connectivity

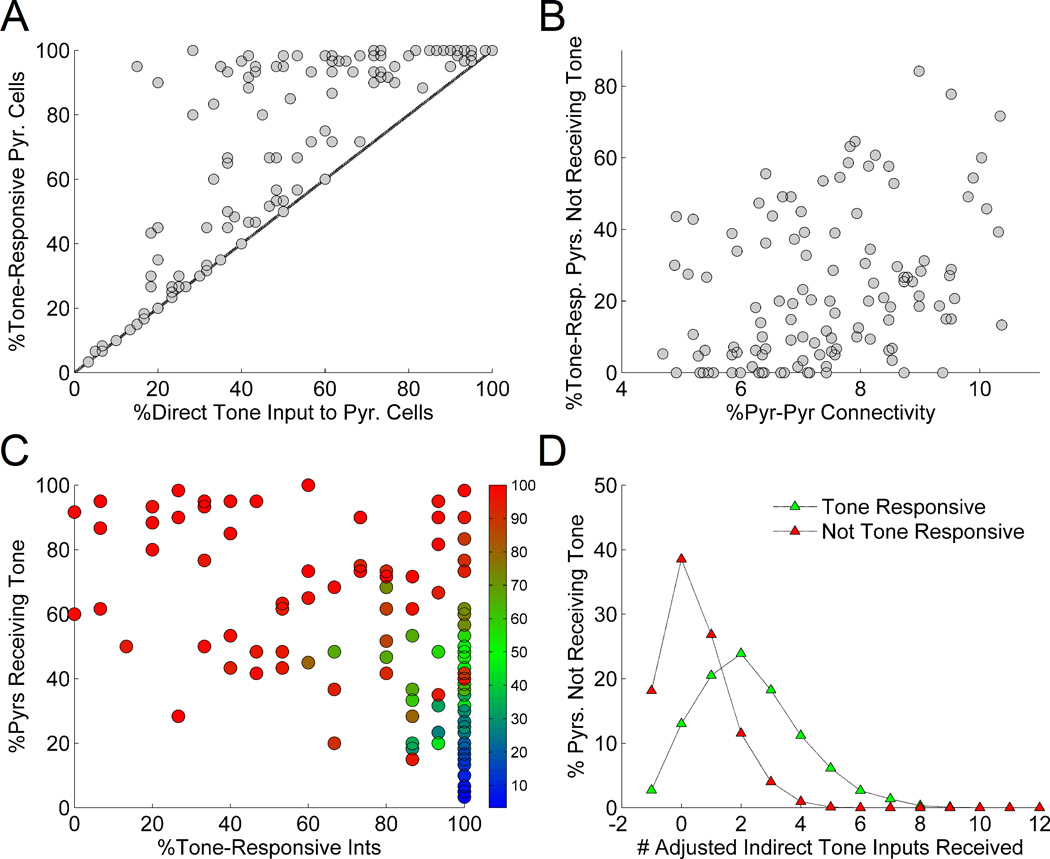
The density of tone or shock inputs in LA is not presently known, i.e., it is not clear what fraction of LA cells receive tone inputs and what fraction receive shock inputs. To shed light on what might be possible densities, we first investigated whether the proportion of tone-responsive cells observed in LA networks was closely tied to the proportion of cells receiving direct tone input. Figure 5A shows the proportions of tone-responsive cells compared to the proportions of tone-receiving cells in the 120 simulated LA networks. Without exception, every pyramidal cell receiving tone was also found to be tone responsive. With tone-pyramidal cell input connectivity below 20%, very few cells that did not receive tone became tone responsive. However, for tone input above 20%, many cells were found that did not receive tone, but were tone responsive. For tone input above 75%, nearly all cells were tone responsive. This non-linear relationship clearly suggests that tone responsiveness in these LA networks was a function not only of direct tone input, but also intrinsic connections within the network.

Figure 5.

Proportions of tone-receiving and tone-responsive pyramidal cells in 120 independent runs of the 75-cell LA network. A: The proportion of tone-responsive cells closely tracked the proportion of tone-receiving cells for tone-pyr input density below 20%. Above this value, many tone-responsive pyramidal cells were generated that did not directly receive tone. Above 75% tone-pyr input density, nearly every pyramidal cell was tone responsive. The line represents the theoretical case in which cells were tone responsive if and only if they received direct tone input. B: The level of intrinsic pyr-pyr connectivity in LA networks was moderately correlated with the proportions of tone-responsive, non-tone-receiving pyramidal cells (r = 0.32). C: Pyramidal cell tone responsiveness (% tone-responsive pyramidal cells encoded by color; note that green points represent networks for which tone-responsiveness were within biological ranges, approximately 35–65%) was most often within biological ranges (approximately within the blue dotted line) for high levels of interneuron tone-responsiveness and low-to-moderate levels of tone input to pyramidal cells. D: Tone-responsive pyramidal cells that did not receive tone input were more likely to receive multiple connections from other tone-receiving pyramidal cells than were non-tone-responsive pyramidal cells that did not receive tone. Adjusted numbers of indirect tone inputs are shown on the x-axis, where the total is the number of connections received from pyramidal cells receiving direct tone minus the number of connections received from interneurons receiving direct tone.

In order to identify differences between tone-responsive and non-tone-responsive cells that do not receive tone, we first looked for potential relationships between excitatory intrinsic connectivity and tone responsiveness of pyramidal cells within the 120 LA network models. Figure 5B shows the proportion of tone-responsive pyramidal cells that did not receive tone in each LA network compared to the pyr-pyr connectivity in that particular network. Over the range of intrinsic connectivities studied (5–10%), a moderate positive correlation was observed (r = 0.32). This result suggests that the overall pyramidal cell connectivity does affect tone-responsiveness of pyramidal cells; however, such connectivity is unlikely to be the sole determining factor for such amplification of the tone responses in the LA network.

Because overall levels of excitatory interconnections did not adequately explain the generation of tone-responsive pyramidal cells that did not receive direct tone, we next assessed the inhibitory impact of tone-responsive interneurons on pyramidal cell tone responsiveness. For each network model, figure 5C shows the proportion of tone responsive pyramidal cells (coded by color) as a function of both tone-responsiveness among interneurons and the level of direct tone input to pyramidal cells. For interneuron tone responsiveness below 60%, tone responsiveness among pyramidal cells was typically high (75% or higher). In contrast, high interneuron tone-responsiveness (e.g., above 75%) produced networks with pyramidal cell tone responsiveness varying between 0–100%. In particular, for tone input to pyramidal cells between 20–60% and interneuron tone responsiveness above 60%, LA networks were most often produced with pyramidal cell tone responsiveness within biological ranges of 45–55%. Higher tone responsiveness among interneurons might allow greater flexibility of tone responsiveness among pyramidal cells in the network, i.e., for LA networks with low interneuron tone responsiveness, nearly all pyramidal cells were tone responsive. In contrast, for LA networks with very high interneuron tone responsiveness, the level of pyramidal cell tone responsiveness varied considerably. This feature likely results from the limited reach of interneurons, but not pyramidal cells; pyramidal cells connect to the entirety of the network, allowing tone responsive pyramidal cells to excite other pyramidal cells. However, interneurons only inhibit local pyramidal cells, and so tone-responsive interneurons affected far fewer pyramidal cells in comparison.

Finally, to explore the role of cell-specific connections, rather than network-wide connectivity, on individual cell behavior, we investigated the properties of the connections received by pyramidal cells that did not receive tone and were or were not tone-responsive. To explore this, we computed the number of ‘adjusted’ indirect tone inputs received by each pyramidal cell that did not receive tone, from among the cells in the 120 LA network models. The number of adjusted indirect tone inputs was computed as the number of pyr-pyr connections received from tone-receiving pyramidal cells minus the number of connections received from tone-receiving interneurons. Consequently, inhibitory connections from tone-receiving interneurons were subtracted from the total indirect excitatory tone input. Thus, a cell receiving −1 indirect tone inputs received no excitatory connections from tone-receiving cells, but one inhibitory connection from a tone-receiving interneuron. Figure 5D shows the number of adjusted indirect tone inputs received by non-tone-receiving pyramidal cells that were tone-responsive versus those that were not. On average, pyramidal cells that received more than one indirect tone input were much more likely to be tone responsive than were those that received one or fewer indirect tone inputs. On a cell-by-cell basis, intrinsic pyr-pyr connections as a whole correlated modestly with the generation of tone-responsive pyramidal cells that did not receive direct tone input. The analysis also suggests that tone-receiving pyramidal cells are indeed able to generate more tone-responsive pyramidal cells by projections to cells that do not receive tone.

Indirect tone and shock inputs supplement direct inputs in conditioning pyramidal cells

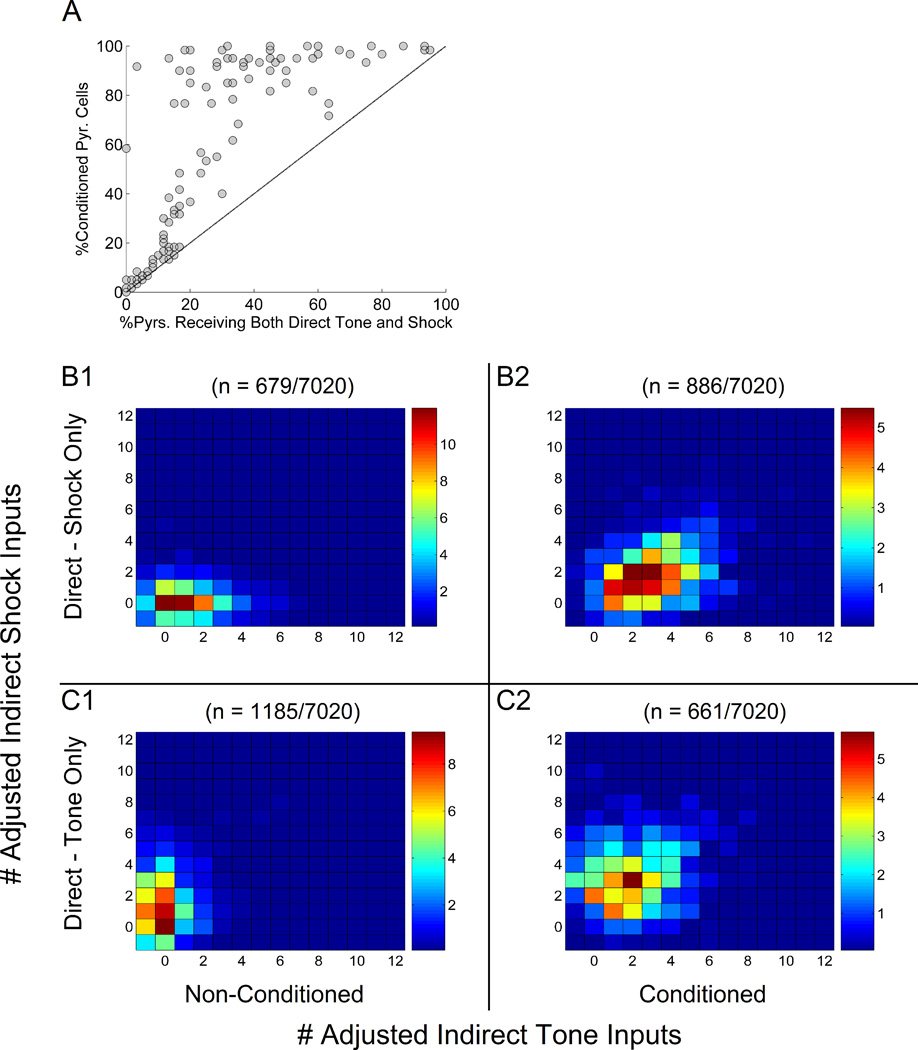
Next, we investigated the combinations of inputs that caused pyramidal cells to exhibit tone responses that were also conditioned, i.e., had tone responses after conditioning that were 50% higher than tone responses during sensitization. Expectedly, all pyramidal cells that received both tone and shock inputs conditioned. However, only 49% of conditioned cells received both tone and shock inputs; 18% received only tone input, 24% received only shock, and 9% received neither. Figure 6A shows the relationship between the proportion of pyramidal cells receiving both tone and shock in a network and the proportion of conditioned cells. For a few networks (fewer than 3%) the proportion of conditioned cells was smaller than the proportion of cells receiving both tone and shock (data not shown). Inspection of the behavior of cells in these networks revealed that recurrent excitation was sufficiently high (and feedback inhibition sufficiently low) to produce seizure-like activity, and all cells activated strongly throughout all phases of the conditioning protocol. These cells were flagged as “non-conditioned” because their tone responses during late conditioning and early extinction were not at least 50% higher than tone responses during sensitization; indeed, near-maximal firing-rates were encountered in all cells of these networks even during sensitization, before conditioning had taken place. Because networks exhibiting such behavior were few in number (< 3%), these seizure-producing LA network models were omitted from further consideration. Figure 6A shows that among the remaining LA networks, if more than 15% of the pyramidal cells received tone and shock, then considerably more pyramidal cells conditioned. This trend mirrored that of tone responsiveness among pyramidal cells (fig. 5A), i.e., intrinsic connectivity amplified the transmission of tone throughout the network. Similarly, fear conditioning was also amplified through the network.

Figure 6.

Intrinsic connectivity produced conditioned tone responses in cells that did not receive direct converging tone and shock inputs. A: The number of conditioned cells in each simulated LA network typically exceeded the number of cells that received direct converging tone and shock. The dashed line represents the hypothetical case in which only those cells that receive both direct tone and direct shock can condition.

B–D: How did indirect transmission of tone or shock input through intermediate pyramidal cells contribute to conditioned tone responses among cells that received only direct shock or only direct tone? Adjusted numbers of indirect tone inputs are shown on the X-axis, and adjusted indirect shock inputs are shown on the Y-axis. Adjusted indirect inputs were computed as the total number of connections received from pyramidal cells receiving direct tone (or shock) minus the number of connections received from interneurons receiving direct tone (or shock). Colorcoding represents the percentages of the indicated subpopulations of pyramidal cells across the 120 model runs that received the numbers of adjusted indirect inputs shown on the X and Y axes. Data can be interpreted as three-dimensional histograms where bar height is instead encoded by color. By way of example, grid box (3,2) in panel B1 shows that approximately 11% of non-conditioned cells that received direct shock, but not direct tone (n=679), received 1 adjusted indirect tone input (X-axis) and 0 adjusted indirect shock inputs (Y-axis). Similarly, grid box (6,5) in panel B2 shows that approximately 3% of conditioned cells that received direct shock, but not direct tone (n=886), received 4 adjusted indirect tone inputs and 3 adjusted indirect shock inputs. The same interpretation holds for data in panels C1 and C2.

Panel B shows the levels of indirect input received by non-conditioned (B1) and conditioned (B2) pyramidal cells that received direct shock, but not direct tone. Non-conditioned cells in this category (n=679) typically received fewer than one indirect shock input and between 0–3 indirect tone inputs, while conditioned cells (n=886) instead received between 0–4 indirect shock inputs and 1–5 indirect tone inputs. Generally, a comparison of B1 to B2 shows that in these simulations, a cell receiving only direct shock and more than zero adjusted indirect tone inputs was unlikely to condition (B1) unless it also received more than zero adjusted indirect shock inputs (B2).

Panel C instead quantifies the levels of adjusted indirect input received by non-conditioned (C1) and conditioned (C2) pyramidal cells that received direct tone, but not shock. Non-conditioned cells in this category (n=1185) typically received fewer than one indirect tone input and between 0–3 indirect shock inputs, while conditioned cells (n=661) instead received between 1–4 indirect shock inputs and 0–4 indirect tone inputs. In panel C, similar to that in panel B, a cell receiving only direct tone input and more than zero indirect shock inputs was unlikely to condition (C1) unless it also received more than zero adjusted indirect tone inputs (C2).

If amplification of tone responsiveness by intrinsic excitatory connectivity assists in the generation of pyramidal cells that learn conditioned fear, then it may be that conditioned cells that do not receive direct tone input do receive strong indirect tone, and conditioned cells that do not receive direct shock receive strong indirect shock. To test this possibility, we investigated the number of indirect tone and shock inputs (i.e., the number of excitatory connections received from cells receiving direct tone or shock inputs, respectively) by conditioned and non-conditioned cells that themselves lacked direct tone or direct shock. Adjusted indirect tone inputs were again computed as described previously: the number of pyr-pyr connections received from tone-receiving pyramidal cells minus the number of int-pyr connections received from tone-receiving interneurons. Adjusted indirect shock inputs were computed in the same manner. After training, the pyramidal cells were divided into conditioned and non-conditioned cells, and we investigated the distributions of inputs to each of these populations to explain why some conditioned while others did not. Figure 6B shows a comparison of the adjusted indirect inputs received by non-conditioned (6B1) and conditioned (6B2) pyramidal cells that received only direct shock. The comparison shows an obvious trend in which conditioned cells received higher numbers of indirect shock inputs and somewhat higher numbers of indirect tone inputs than did non-conditioned cells. Interestingly, cells receiving only shock were more often converted from non-conditioned to conditioned cells by indirect shock than by indirect tone. However, the majority of conditioned cells receiving only shock also received one or more adjusted indirect tone input and zero or more adjusted indirect shock inputs. In the previous biophysical LA model (Li et al., 2009), it was observed that LTP of pyr-pyr synapses occurred only for connections between pyramidal cells that were strongly activated by shock. This provides the insight that that while a non-zero level of indirect tone input was necessary to produce conditioned responses in pyramidal cells that did not receive direct tone, strong indirect shock input caused pyr-pyr connections targeting such cells to more readily potentiate.

Figure 6C shows a similar comparison of adjusted indirect inputs received by conditioned and non-conditioned cells that instead received direct tone, but not shock. Again, conditioned cells in this sub-population (fig. 6C2) generally received more indirect tone and shock inputs than did non-conditioned cells (fig. 6C1). Similar to the trend seen for non-conditioned cells receiving only shock (fig. 6B1), the majority of non-conditioned cells receiving only direct tone (fig. 6C1) received fewer than one adjusted indirect tone input and between 0–3 adjusted indirect shock inputs. However, a majority of conditioned cells in this category (fig. 6C2) received between 0–3 indirect tone inputs and between 1–5 indirect shock inputs. This difference suggests that for these cells, shock input, either direct or indirect, was required for conditioning, but the presence of strong indirect tone input supported direct tone to more often convert non-conditioned to conditioned cells. For completeness, we also separately analyzed the set of networks (N = 20 LA networks) whose pyramidal cell tone-responsiveness was within biologically ranges (35–65%), and the results (data not shown) were qualitatively identical to those described above.

To summarize, the results of these model experiments show that pyramidal cells that receive both direct tone and shock inputs are almost assured to exhibit conditioned tone responses as a result of fear conditioning. These data also suggest that indirect inputs can supplement direct input to allow cells that do not receive convergent tone and shock to nevertheless condition. However, the results show that in addition to indirect pairing of tone and shock, conditioned cells were most often produced by the further addition of indirect inputs of the same type (e.g. indirect tone inputs received by a cell receiving direct tone, but not shock). Panels B1 and B2 of Figure 6 B do indicate a clear correlation between conditioned and non-conditioned cells and the absolute numbers and types of direct and indirect inputs they receive. However, there is some overlap. Panels B1 and B2 show cells that received direct shock and no direct tone. Of these, consider cells that received 1 adjusted indirect tone input and 1 adjusted indirect shock input in both the panels. Grid block (3,3) of panel B1 shows that about 6% did not condition. However, grid block (3,3) of panel B2 indicates that 5% of conditioned cells did receive the same distribution of indirect inputs. As cited earlier, the reason for this is possibly the difference in synaptic weights (due to training) of the afferents to these cells in the two cases. Although not performed here, this illustrates how the effects of synaptic changes on tone responsiveness and conditioning could be analyzed.

Intrinsic connectivity selectively supports stimulus generalization

The results above show that conditioning to a particular tone caused some of the pyr-pyr synapses to potentiate in addition to the tone-pyr synapses. Would potentiation of the pyr-pyr synapses interfere with tone specificity for auditory fear, i.e., would this cause tone of a different pitch to elicit potentiated fear responses resulting in stimulus generalization? Experiments have shown the existence of a stimulus generalization gradient in which the fear response is highest for the original CS but decreases with increasingly dissimilar novel stimuli (for review, see Honig and Urcuioli, 1981). Furthermore, using lesion studies involving the auditory cortex, Armony et al. (1997) showed that stimulus generalization can be supported by plastic changes in LA alone.

We investigated specificity to tones and stimulus generalization and the underlying intrinsic plasticity in such cases using the firing rate model. For this we considered typical configuration motifs found in the network. For example, consider a pair of cells, cell A (receiving tone and shock) and cell B (receiving only shock). It would be expected that the synapse from cell A to cell B would potentiate. As described above, this potentiated connection may subsequently cause higher tone response in cell B despite the lack of direct tone input. However, this could be offset by potentiation of both feedback and feedforward inhibition on cell B that might occur in parallel. As another example, consider a different cell pair motif with cell C (receiving shock as well as an unconditioned tone input, i.e. an auditory input of different pitch) and cell D (receiving only shock). As with cells A and B, the synapse from cell C to cell D would be expected to potentiate due to both cells receiving direct shock input. Similar to the previous case, presentation of the unconditioned tone would be expected to produce a conditioned response in cell D because of the potentiated synapse linking them. Potentiation of the inhibitory sub-circuits converging onto cell D could again modulate the increase in cell D tone responses. Both of these situations constitute varying degrees of stimulus specificity and generalization that could arise due to synaptic plasticity in the LA.

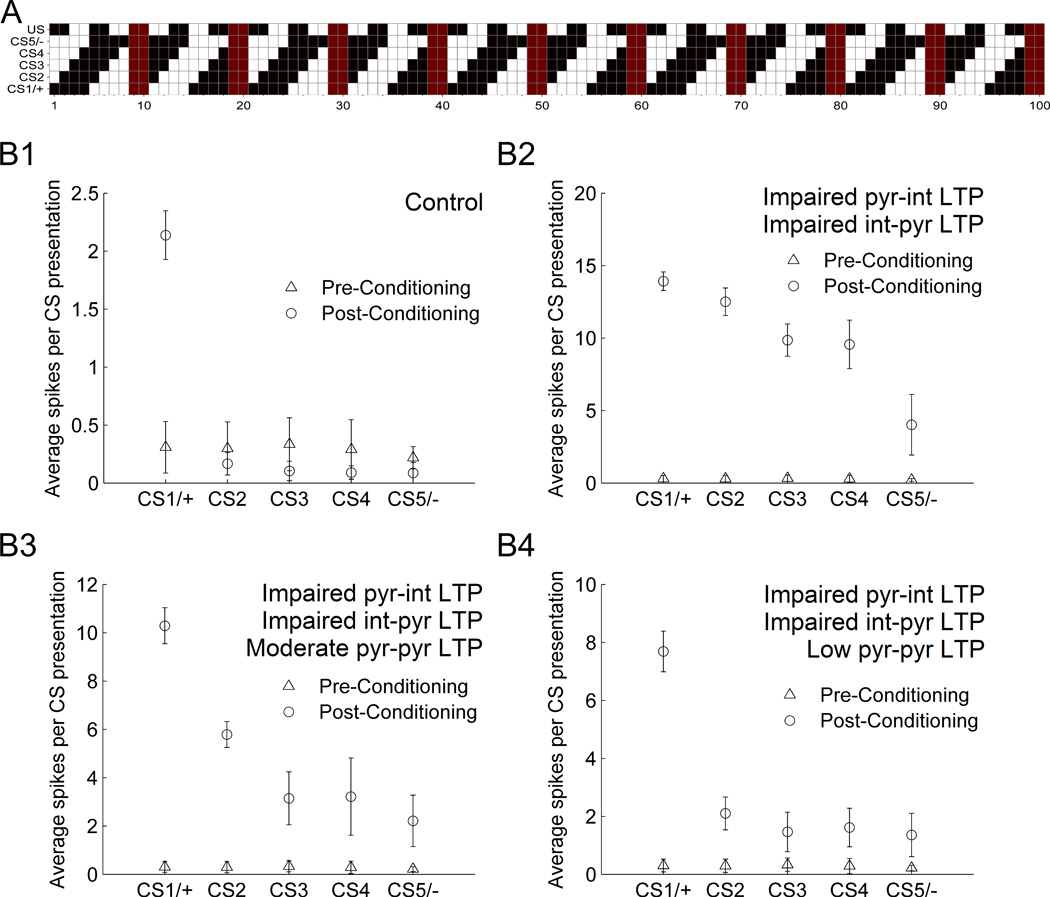
To study these issues, we used five different tone inputs (CSs 1–5) and one shock. To evenly accommodate the larger number of CSs, we used a 100-cell network with 80 pyramidal cells and 20 interneurons. The same clustering configuration was used, but each cluster consisted of 8 pyramidal cells and 2 interneurons as in the original 10-cell LA network (fig. 7a). Pyramidal cells were connected to one another within and across cell clusters with 10% probability. All five CSs and the US targeted 50% of the pyramidal cells and all of the interneurons. CS1 was co-presented with the US, and so is termed CS1/+ or just CS+. For this experimental design, the CSs and US were connected in a pattern that satisfied two criteria: First, the cells targeted by CS2–CS5 overlapped in a graded manner with those targeted by CS1/+. Specifically, CS2 targeted 75% of the cells targeted by CS1; CS3 targeted 50%; CS4 targeted 25%; and CS5 targeted 0% (fig. 7a). Because of the complete lack of overlap between CS1 and CS5, CS5 is also termed CS5/− or just CS−. Second, each CS targeted an identical number of cells of each type (pyramidal cells of types A, B, C). This choice ensured that no CS preferentially targeted a disproportionate number of highly excitable cells. The overall design ensured the best balance among the naïve responses to each CS. To produce baseline fear conditioning that resembled that observed in the 75-cell network, we had to reduce plasticity scaling factors (λ₁) for pyr-pyr and pyr-int synapses to 0.3 and 0.15, respectively. This change was needed because each pyramidal cell received two inhibitory connections rather than only one as in the 75-cell network. Each simulation of this network required 30 minutes.

Figure 7.

Intrinsic plasticity in LA modulates stimulus generalization in a 100-cell network model. A: Schematic of the input connectivity in the network. CS1-5 were identical tone inputs that targeted cells indicated on the X-axis in black (red for interneurons). CS1/+ was paired with the US (shock) during conditioning. CS5/− was also presented during conditioning, but was never paired with the US, and targeted precisely the 50% of pyramidal cells not targeted by CS1/+. Thus, CS2-5 exhibit a graded decline in similarity with CS1. B: Average responses of all pyramidal cells in response to the indicated CS before conditioning (triangle) and after conditioning (circle). B1: At base levels of intrinsic plasticity, no stimulus generalization was observed. With impaired plasticity of int-pyr and pyr-int synapses, high generalization was observed with normal plasticity of pyr-pyr synapses (B2), but moderate (B3) and low (B4) levels of plasticity in pyr-pyr synapses reduced generalization and sharpened the observed gradient.

We followed the protocol in Lissek et al. (2008) and conditioned the network to CS+ (coinciding with the US) and to CS− (unreinforced). This protocol consisted of a test phase to assess response amplitudes to each CS, followed by a habituation phase similar to that used above, but during which CS+ and CS− were alternated, and the total habituation time was doubled to account for the extra CS. After habituation, conditioning continued as before, but again with alternating CS+ and CS− (the latter not co-presented with US). Another test phase followed conditioning. During both test phases, synaptic plasticity was disabled, and the five CSs were presented 10× each in alternating fashion, and the average response to each CS was recorded. Since the focus was on fear generalization, the extinction phase was not considered in this study. Figure 7b1 shows the average pyramidal cell responses to each CS before habituation and after conditioning (the number of spikes was calculated from firing rate as described in Methods). As expected, a significant increase in fear response was observed after conditioning upon presentation of CS+. However, no significant stimulus generalization was observed, i.e., responses to all other CSs were at or below pre-conditioning levels. In other words, while LTP of pyr-pyr connections seems to support conditioning to a specific CS+ by linking direct tone-receiving cells with direct-shock receiving cells (and vice versa), appropriate inhibitory LTP ensured that responses to non-conditioned CSs were not enhanced, and thus preserved specificity to the original CS+.

To further explore the role of intrinsic plasticity in stimulus generalization, we investigated the question of how differing levels of intrinsic plasticity might affect stimulus generalization. This was motivated by behavioral experiments that reported differences in stimulus generalization gradients between healthy subjects and those exhibiting anxiety disorders (Lissek et al., 2010). That is, fearful responses to CSs that are similar, but not identical to the CS+ are more strongly suppressed in healthy subjects compared to patients with anxiety disorders. Impairment of intrinsic plasticity within the LA is a possible mechanism by which such a phenomenon could be generated. To investigate this, we varied the scaling factors of LTP induction in the pyr-pyr, pyr-int and int-pyr connections. Figure 7b2 shows the responses to each CS in this network when plasticity of the int-pyr and pyr-int synapses was impaired. Specifically, the scaling factor for learning in these synapses was reduced to 0.05, a factor that was 4-fold and 6-fold smaller than their respective nominal values. In contrast to the results in Figure 7b1, significant stimulus generalization was observed in this case; CS2–CS5 produced responses that potentiated compared to pre-conditioning levels in proportion to their overlap with CS+. Specifically, the response to CS2 showed the most potentiation and responses to CS5 potentiated the least. Thus, the stimulus generalization gradient expanded to include stimuli that were more similar to the CS+.

Finally, we hypothesized that if a reduction of plasticity in int-pyr and pyr-int synapses can reveal the stimulus generalization gradient, changes to LTP of pyr-pyr synapses should then modulate the shape of that gradient. Figures 7b3–b4 show the stimulus generalization gradient associated with reducing the scaling factor of pyr-pyr plasticity by different amounts (fig 7b3: 1.1; fig 7b4: 0.7; the nominal value in fig. 7b1–b2 was 1.5). The results revealed tight control over the generalization gradient by differing strengths of pyr-pyr LTP induction. Lowering pyr-pyr LTP sharpened the gradient, limiting potentiation to primarily the response to CS+. Note that the conditioned spiking responses are considerably higher in figures 7b2–b4 because of the absence of the inhibitory LTP seen in the control case. For the control case, a balance exists between excitatory and inhibitory learning during conditioning. Blocking LTP in the feedback inhibitory circuit offsets that balance in the direction of excitation. This point is emphasized by the fact that the pre-conditioning values are the same across control and impaired cases in fig. 7b. In general, with a network configuration that produced the desired amount of conditioning-related response potentiation to CS+, modest changes to the strength of the synaptic plasticity in the LA itself was able to considerably modulate stimulus generalization.

To investigate the underlying intrinsic plasticity that might implement tone specificity and generalization, we investigated the two typical cell pair motifs described earlier. These were representative of the typical configurations found within the network.

The synapse linking cell 42 (receiving CS1 and US) to cell 45 (receiving US, but not CS1) is representative of the case in which impairment of inhibitory LTP facilitated potentiation of conditioned responses to CS1/+ in cells that did not receive direct CS1 input. The response of cell 45 to CS1/+ was unchanged by conditioning in the control case (producing < 1 spike both before and after conditioning). However, with only impaired inhibitory LTP (fig 7b2), its response to CS1/+ potentiated considerably as a result of conditioning (from < 1 spike to 11 spikes). Two pathways connect these two cells: A direct excitatory synapse, and feed-forward inhibition through local interneurons 49 and 50. In both the control and impaired inhibitory LTP cases, the excitatory connection potentiated strongly (77% control; 82% impaired case). However, in the control condition, the feed-forward inhibitory pathway potentiated much more than in the impaired inhibitory LTP case. This effect was seen both in the pyr-int synapses from cell 42 to cells 49/50 (62% LTP in the control, 8% in the impaired case), as well as the int-pyr synapses from cells 49/50 to cell 45 (35% LTP in the control, −15% in the impaired case). Cell 45 did not receive direct CS1 input, and the synapse from CS1 to cell 42 potentiated similarly in both cases (121% control, 111% impaired case). Thus, biasing local synaptic plasticity toward excitation contributed to the spread of conditioned responses to CS1/+.

As the second example case, the synapse linking cell 86 (receiving CS3 and US) to cell 81 (receiving CS1 and US, but not CS3) is representative of the case in which impairment of inhibitory LTP facilitated generalization of conditioning by CS1+/US pairing to other CSs. As expected, the response of cell 81 to CS1/+ potentiated in both cases. In contrast, the response of cell 81 to CS3 potentiated only in the impaired inhibitory LTP case (pre-conditioning: < 1 spike; post-conditioning: < 1 spike in control, 19 spikes with impaired inhibitory LTP). Again, the excitatory connection from cell 86 to cell 81 potentiated strongly in both cases (91% control; 98% impaired case); but the feed-forward inhibitory pathway through local interneurons (cells 89 and 90) potentiated much more in control (pyr-int: 74% LTP control, 9% impaired case; int-pyr: 35% LTP control, −12% impaired case). The input synapse from CS3 to cell 86 did not potentiate in either case (< 1% change), indicating that these generalization mechanisms operated independently of tone inputs to the LA. Thus, impairment of inhibitory LTP also contributed to the generalization of conditioned responses to unconditioned stimuli.

It is important to note that the synapses described for the above examples were not the only connections involved in learning, and the aggregate activity of the network would also play a role and needs to be studied. However, many such pairs selected at random revealed similar results. Additionally, the trends of LTP in other synapses targeting cells in such pairs were consistent with the idea that biasing intrinsic plasticity toward excitation can impair specificity and reveal stimulus generalization.

In summary, potentiation of both feedback and feed-forward inhibition in the nominal LA network precluded non-specific conditioning effects and stimulus generalization. However, impairment of LTP in the intrinsic connections supporting inhibition, but not their base strengths (which preserve the fear conditioning properties of the network), revealed stimulus generalization similar to that observed experimentally (Lissek et al., 2008, Lissek et al., 2010). Changes to the efficacy of LTP in excitatory synapses linking LA pyramidal cells were able to further modulate the stimulation generalization features.

DISCUSSION

This study contributes to two different areas. First, a novel computational methodology was proposed by extending the Wilson-Cowan firing-rate model (1999) to incorporate full spike frequency adaptation and a non-zero rheobase. In addition to these enhancements to single-cell dynamics, a methodology is also proposed to incorporate a form of biologically realistic synaptic learning for network models using such cells. This modeling framework required only a fraction of the biological complexity and simulation time (<1%) that was needed for the biophysical LA model (Li et al. 2009). Second, the utility of the modeling framework was illustrated by obtaining biological insights related to encoding of fear in the rodent LA during Pavlovian fear conditioning. Model experiments showed how afferent and intrinsic connectivity in LA contributed to auditory fear conditioning.

Novel method for designing firing model networks with [Ca²⁺]-dependent synaptic learning

Firing rate model

Our work improves upon the Wilson-Cowan firing-rate model (Wilson and Cowan, 1972, Wilson, 1999, Destexhe and Sejnowski, 2009) by accommodating full spike frequency adaptation and a non-zero rheobase. Benda and Herz (2003) propose a universal model of spike frequency adaptation based on the specific dynamics of ion currents that typically produce adaptation. The equations presented here constitute a similar adaptation of a firing rate model. The proposed model is sufficiently versatile for learning networks containing cells with a variety of firing characteristics such as bursting, resonance, or anti-accommodation. Development of a firing rate model using the proposed reduced order modeling framework can summarized as follows:

1. As a first step, obtain initial and steady-state firing rates for the cell in response to a series of input current steps. Inter-spike interval plots are commonly reported in single-cell electrophysiological studies, and so these data exist for many cell types.

2. The data obtained in (i) are then fit to Hill equations as functions of the magnitude of the input current, shown in eq. 2 as S(P) and A(P) for two datasets. Forms other than the Hill equation can be used to provide a better fit in other scenarios. The data from (i) will have a rheobase that should be appropriately incorporated into the chosen form of the function.

3. The approximate time constant τ_A with which the firing rate transitions from one dataset to the next is then measured. This time constant might vary for different input current magnitudes and even between datasets, and the function can be easily selected to take care of this variation. For instance, the fear learning example case used a piece-wise continuous function for τ_A(P) that increased linearly between the two inflection points P₁ and P₂.

Finally, the nonlinear differential equations for the single cell model (eq. 2) can be simulated using any differential equation solver such as MATLAB (The Mathworks, 2004) or using customized software written in a programming language such as C/C++.

Calcium-dependent synaptic learning

We further propose a method to incorporate a form of calcium dependent learning (eqs. 3 and 4) and propose two different implementation schemes:

1. A general implementation applicable for a large class of synapses is to model F of eq. 4 as a function of E_pre and E_post as shown in eq.5. We propose specific ranges for the parameters in the equations in Results. Eqs. 3 and 4, with F(.) substituted for eq. 5, thus provides a general implementation that can be easily modeled.

2. Another implementation of the learning rule would be to obtain synaptic [Ca²⁺] from an existing biophysical model (e.g., LA model in (Li et al., 2009), and use such data to determine parameter values for the learning rule.

Under these assumptions, networks with [Ca²⁺]-dependent plasticity can be constructed and investigated with a variety of properties and structures. Furthermore, synaptic plasticity is often examined in biological systems by stimulating neurons at fixed firing rates (Ishida et al., 1997, Sjöström et al., 2001); a more straight-forward learning rule could be employed to relate synaptic plasticity (dW/dt) directly to pre- and post-synaptic firing rates (see eq. 3).

Network models

The firing rate model can be used to develop network models as illustrated using the fear conditioning experiment. It is noted that synaptic rules that are not dependent on calcium can also be used, so long as they can be modeled as functions of the firing rates.

Insights into [Ca²⁺]-dependent synaptic learning

The NMDA receptor, via the mechanism of transmitter-driven synaptic currents and voltage-dependent magnesium block, has been proposed as a mechanism for Hebbian learning by coincidence detection (Bliss and Collingridge, 1993). Calcium influx through such NMDA receptors engages a postsynaptic cascade that increases or decreases synaptic efficacy by acting at AMPA receptor channels. By investigating NMDA-dependent calcium dynamics in LA cell models, it was discovered here that the long-lived NMDA currents in the LA allow the opening of “windows” of learning opportunity at synaptic terminals in response to even a single presynaptic spike. This assertion is supported by the steady-state [Ca²⁺] measured for varying E_pre and E_post. For a given value of E_post, E_pre > 0 allowed calcium influx (and therefore, synaptic learning), but further increases to E_pre did not significantly increase steady-state [Ca²⁺] compared to increases in E_post. Therefore, the specific presynaptic firing rate was not as important as the post-synaptic firing rate for synaptic learning, as long as E_pre > 0. This phenomenon has important implications for NMDA-dependent learning. It suggests that a relatively weak neural representation of a stimulus may be easily incorporated into an existing activity pattern and “learned” by exploiting a window of opportunity that even a single spike might create.

Amplification of sensory input by intrinsic network might be relevant for learning conditioned fear

Using reduced connectivity akin to those seen biologically, the 75-cell LA model corroborates the principles of LA learning observed in the biophysical 10-cell model

The acceleration of simulation throughput provided by the firing-rate framework allowed exploration of questions using a larger LA network structure that would be prohibitive using biophysical models. Experiments were performed that incorporated biologically realistic connectivity in which connection densities among pyramidal cells were between 5–10% (D. Paré, personal communications), and the tone and shock densities were varied from 0 to 100%. Despite considerable changes to the structure of the network, these randomly generated LA networks consistently learned conditioned fear and extinction memories by using the same NMDA receptor-dependent synaptic plasticity as in the biophysical model network (Li et al., 2009).

Intrinsic excitatory connections conditionally amplify sensory input in the LA network

The model predicts that intrinsic excitation among pyramidal cells can serve to “amplify” sensory inputs to the LA. Such amplification can occur despite relatively low connectivity among pyramidal cells (5–10%). For low tone input density to pyramidal cells, only those cells directly receiving tone were tone responsive, but higher tone input density produced many tone responsive cells that did not receive direct tone (fig. 5). Investigating the intrinsic connections to these cells revealed that such cells typically received at least two “indirect” tone inputs. Higher tone input density also increases the chances of pyramidal cells receiving indirect tone input; thus, intrinsic excitatory synapses “amplify” sensory input. Specifically, we found that LA networks possessing biological ranges of tone-responsive pyramidal cells (between 45–55%, e.g., Quirk et al., 1995, 1997) were most often generated when tone input to pyramidal cells was moderate (20–60%) and interneuron tone responsiveness was above 60% (fig. 5C). Thus, we predict that in order for the LA to “control” tone responsiveness in the network, a majority of interneurons must respond to sensory input; specifically, at least 60% of interneurons must respond to the conditioned stimulus (tone), either through direct tone stimulation, or through indirect tone stimulation due to excitation by pyramidal cells receiving direct tone. For our network, this prediction depends on the assumption that at least two connections from cells receiving tone are required to activate a cell that does not receive tone. If excitatory connections among pyramidal cells are strong enough for a single intrinsic connection to fire its postsynaptic target, then the tone input density that would be required to produce tone amplification would be significantly lower, i.e., amplification could conceivably occur for any tone input density greater than 0%. Conversely, weak connections among pyramidal cells would instead increase the level of tone input density that would be required to produce such amplification. For survival purposes, it might be advantageous for thalamic sensory inputs to be able to activate a larger portion of the LA neurons even with low input density, because high tone responsiveness increases the probability that conditioned (tone) and unconditioned (shock) stimuli will converge on a single cell, either directly or indirectly, and this is critical for fear learning (survival).

Mixed indirect inputs to principal cells supplement direct input to produce conditioned responses

The model predicts that the amplification of tone responsiveness by excitatory interconnections among pyramidal cells in the LA can serve to maximize the number of LA pyramidal cells that respond to CS (tone) or US (shock) stimuli. We found that the number of cells that exhibited conditioned responses was greatly increased if the tone and shock input densities were above 15% (fig. 6A). Furthermore, cells that did not receive both tone and shock input could display conditioned tone responses if sufficient indirect tone and/or shock inputs were received through the intrinsic circuitry. Interestingly, this pattern of connectivity did not simply favor indirect inputs of the absent type, i.e., indirect tone (or shock) to cells receiving only direct tone (or shock) was sufficient to condition them (fig. 6B,C).

For the connection strengths used, our results suggest that robust fear conditioning can be achieved if two activated intrinsic excitatory synaptic connections are sufficient to fire a third cell. Such strong intrinsic excitation within the network, while potentially useful for sensory amplification, might be detrimental to normal function if recurrent excitation, without adequate feedback inhibition, causes seizure-like activity. Note however, that the majority of pyramidal cells in the LA are strongly adaptive, meaning that depolarization of these cells typically produces a few spikes in a short time frame (e.g., less than 100 msec) followed by quiescence (Faber et al., 2001). It is plausible that such spike-frequency adaptation is a resilient trait that protects the LA from runaway neural excitation.

Stimulus generalization in LA is controlled by differential plasticity of inhibitory and excitatory connections

Experimental investigation of the underpinnings of stimulus generalization to tones after auditory fear learning led to the conclusion that neither the auditory cortex (Armony et al., 1997), nor the thalamic inputs (Antunes and Moita, 2010) are necessary for such generalization. This implies that the amygdala is sufficient to control stimulus generalization and discrimination in this case. An extension of our modeling study of intrinsic plasticity within LA led to the finding that rates of plasticity in specific LA synapses were important in determining the level of stimulus generalization. Specifically, the model predicts that impairment of plasticity in synapses supporting feedback and feed-forward inhibition in the LA, i.e., lowered inhibitory transmission, results in significant generalization even when the naïve efficacy of those synapses is normal. In support of this finding, Shaban et al. (2006) showed that mice with a genetic ablation of GABA_B(1a) generalize fear conditioning to previously unconditioned tones. Their in vitro study also showed that addition of a GABA_B antagonist results in homosynaptic LTP at the cortical afferents that is independent of the activity of thalamic afferents or of the postsynaptic cell. However, as the authors note, in light of evidence suggesting that the auditory cortex is not necessary for stimulus discrimination, a relationship between the observed in vitro findings of enhanced cortico-amygdala plasticity and the behavioral finding of increased stimulus generalization becomes less likely. Considering that GABA_B receptor activation is necessary for LTP at inhibitory synapses (Komatsu, 1996), and these experimental results provide support for our finding that impaired inhibitory plasticity increases stimulus generalization. Furthermore, our model suggests a more local relationship between inhibitory transmission and stimulus generalization, independent of potentiation at thalamic or cortical afferents to the LA. Although the role of inhibition within the LA after conditioning is not well understood (reviewed in Pape and Pare, 2010), it is believed that plasticity of inhibition may be very heterogeneous and dependent on the exact sub-circuits recruited by the conditioning protocol (D. Paré, personal communications).

Another finding from the model was that the efficacy of LTP in recurrent excitatory connections among principal cells significantly affected the sharpness of the associated stimulus generalization gradient (fig. 7b2–b4). Notably, they suggest that because fear memory for a single tone is primarily stored in synapses connecting tone-pyr connections, plasticity of intrinsic connections modulates stimulus generalization without significantly affecting the response potentiation associated with CS-US pairing.

Our model highlighted a potential role for plasticity in recurrent LA synapses in controlling the opposing tendencies of specificity to a tone and generalization to novel stimuli in auditory fear learning. Generalization of fear learning to similar novel stimuli is one of the features of Post-Traumatic Stress Disorder (DSM-IV-TR, 2000) and is proposed to underlie the development of panic disorder (Lissek et al., 2010). The model suggests that differences between individuals in rates of plasticity of the intrinsic LA connections could explain some of the increased tendency to generalize fear learning in subjects with such disorders.

The insights reported in this section related to network connectivity were for a specific network size, but the trends should generalize to other network sizes. In summary, these insights are as follows. First, to produce tone responsive cells in biological ranges of 40% in LA (Quirk et al., 1995) the model provides a testable prediction that the tone to interneuron connectivity in LA be more than 60%, and that the range for tone to pyramidal cell connectivity be within 20–75% (fig. 5). Specifically, transmission of input responsiveness (e.g., tone responsiveness) among LA pyramidal cells is strongly influenced by interneuron responses to the same input. Excitatory intrinsic connections amplify input responsiveness. If interneurons form only short-range inhibitory connections with LA pyramidal cells, then it is advantageous for a high percentage of interneurons (> 65% in the network simulations presented here) to respond to that input. Secondly, the number of cells that exhibited conditioned responses was greatly increased if the tone and shock input densities were above 15%, suggesting a lower bound for densities of these sensory inputs. Thirdly, cells receiving only direct tone or only direct shock input typically cannot exhibit conditioned fear responses unless they receive at least one other excitatory connection. In such cases, we also found that the cell is more likely to condition if it receives the excitatory connection from other cells that receive the same direct input (e.g. shock in the case of direct shock; fig. 6B,C). Finally, stimulus generalization of fear conditioning depends strongly on the rates of plasticity of the intrinsic connections within LA. Lower rates of plasticity at pyr-int and int-pyr synapses enhance generalization of fear to novel stimuli, and varying the rates of plasticity of excitatory intrinsic connections determines the steepness of the stimulus generalization gradient. The numbers in these insights may vary upon connection strengths which are not well understood presently, but the trends would be similar. For instance, weaker intrinsic excitatory connections will reduce the probability of signal propagation, and so input responsiveness may not spread significantly beyond those cells directly receiving that input. However, such signal propagation seems advantageous for fear learning and signal propagation in the LA would be an effective mechanism to encourage the coincidence of conditioned and unconditioned stimuli in the absence of dense direct sensory inputs.

Conclusions

We propose an enhanced time-varying firing rate neuronal model, and a form of synaptic learning, which together can capture the essential dynamics of adaptive network interactions. Lack of detailed biological data and excessive computing time requirements presently limit the incorporation of biological realism into network models of brain regions. In that sense, the proposed enhancements to the firing rate model reported here will help add more realism to both single cell membrane potential dynamics and to the particular form of synaptic learning, facilitating the modeling of large networks. A network developed along these lines provided insights into the role of sensory afferents and of intrinsic network connectivity in amplifying and distributing sensory inputs through the LA. The model also helped quantify the input connectivity needed for the formation of cells with varying tone responsive and conditioning features, e.g., amplification of tone responses had a nonlinear relationship with tone-pyramidal input connectivity. Finally, the model predicts that the plasticity rates of intrinsic connections within LA have a strong impact on stimulus generalization. Some of these findings constitute testable predictions that await further investigation.

Highlights.

• New firing rate model with full spike frequency adaptation and non-zero rheobase

• Calcium-based learning rule implementation for networks of firing rate neurons

• Framework to study possible tone-shock distributions in LA for learning fear

• Tone-interneuron connectivity should be > 60% to match experimental data

• Model shows how impairment in inhibitory LTP might cause fear generalization