Marginal additive hazards model for case-cohort studies with multiple disease outcomes: an application to the Atherosclerosis Risk in Communities (ARIC) study

Abstract

In the case-cohort studies conducted within the Atherosclerosis Risk in Communities (ARIC) study, it is of interest to assess and compare the effect of high-sensitivity C-reactive protein (hs-CRP) on the increased risks of incident coronary heart disease and incident ischemic stroke. Empirical cumulative hazards functions for different levels of hs-CRP reveal an additive structure for the risks for each disease outcome. Additionally, we are interested in estimating the difference in the risk for the different hs-CRP groups. Motivated by this, we consider fitting marginal additive hazards regression models for case-cohort studies with multiple disease outcomes. We consider a weighted estimating equations approach for the estimation of model parameters. The asymptotic properties of the proposed estimators are derived and their finite-sample properties are assessed via simulation studies. The proposed method is applied to analyze the ARIC Study.

1. Introduction

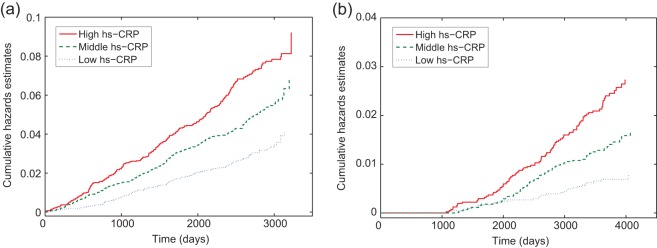
Modern analyses of survival data focus on multiplicative models for relative risk using proportional hazards models (Cox, 1972), mostly due to desirable theoretical properties along with a simple interpretation of the results and the wide availability of computer programs. However, epidemiologists often are interested in the risk difference attributed to the exposure, and the risk difference is known to be more relevant to public health because it translates directly into the number of disease cases that would be avoided by eliminating a particular exposure (Kulich and Lin, 2000). Also, the proportional hazards assumption, which is critical for proportional hazards models , is often violated in practice. Consequently, the additive hazards model, which model risk differences, has often been suggested as an alternative to the proportional hazards model. An interesting example is a study conducted for the Atherosclerosis Risk in Communities (ARIC) study participants (Ballantyne and others, 2004, 2005). It is of interest to: (1) examine the association of high-sensitivity C-reactive protein (hs-CRP) with an increased risk for incident coronary heart disease (CHD) and incident ischemic stroke for the ARIC study subjects, and (2) compare the effect of hs-CRP on the risks of incident CHD and stroke. Hs-CRP is a well-known biomarker for inflammation and has been associated with the increased risks for CHD and stroke (Ridker and others, 1998; Rost and others, 2001). Figure 1 shows that, as time (measured in days) increases, the differences in the cumulative hazards function estimates for three different levels of hs-CRP increase approximately in a linear fashion. Therefore, it is reasonable to assume the additive effect of hs-CRP on the hazards functions both for CHD and stroke.

Fig. 1.

Plots of Nelson–Aalen type cumulative hazards function estimates versus time for three different levels of hs-CRP by event type. (a) For CHD as the event. (b) For stroke as the event.

For full cohort data assuming random samples, Lin and Ying (1994) proposed a semiparametric estimating procedure and derived the large-sample theory of the proposed estimators. This was extended to multivariate failure times (Pipper and Martinussen, 2004; Yin and Cai, 2004), to current status data (Lin and others, 1998), and to the variable selection problem (Martinussen and Scheike, 2009). However, conducting epidemiologic cohort studies often involve follow-up of a large number of subjects for a long period of time, which makes them potentially tremendously expensive. The case-cohort study design (Prentice, 1986) is one of several study designs that have been proposed to achieve the goals of cohort studies in a more efficient way. The key idea of this study design is to obtain the covariate measurements only on a subset of the entire cohort (subcohort) and all the subjects who experience the disease of interest (cases) in the cohort. Thus, the case-cohort study designs are particularly useful for large-scale cohort studies with a low disease rate or for cohort studies with covariates expensive to measure. The ARIC study in the aforementioned example is a large cohort study that involves 15 792 participants. Considering its size, measuring hs-CRP for all the participants in the ARIC study would have been too expensive. Therefore, to reduce costs as well as preserve stored plasma samples, a case-cohort study was carried out: hs-CRP levels were obtained only for the CHD or stroke cases or a random subcohort. Since a subject could experience both the incident CHD and ischemic stroke, times to these two types of events observed from the same subject might be correlated. In order to compare the effect of hs-CRP on the risks of incident CHD and stroke, one needs to consider a possible correlation induced by this clustering of the times to these two types of events within a subject.

Motivated by this, we consider fitting failure time data for more than one disease outcome from case-cohort studies under additive hazards models. Despite the progress in the methods for analyzing case-cohort data, methodologies to address the analysis of case-cohort data with multiple disease outcomes have been limited. For a single disease outcome, Kulich and Lin (2000) developed the semiparametric inference procedure for failure time data from case-cohort studies. Sun and others (2004) extended this approach to competing risks analysis. Since more than one failure time from a subject could induce correlations, statistical methods assuming independence among failure times can no longer be applied. Recently, Kang and Cai (2009) proposed methods for fitting failure time data from case-cohort studies with multiple disease outcomes under marginal proportional hazards models. However, to the best of our knowledge, additive hazard models have not yet been explored for failure time data from case-cohort studies with multiple disease outcomes.

In this article, we propose a weighted estimating equations approach for estimating the parameters in the marginal additive hazards regression models for the multivariate failure time data from case-cohort studies with multiple disease outcomes. We consider the generalized case-cohort study design, which is more appropriate for multiple disease outcomes.

2. Modeling and estimation

Suppose a cohort is composed of n subjects with K different disease outcomes being of interest. Let T_ik and C_ik denote, respectively, the potential failure time and the potential censoring time for disease outcome k(k=1,…,K) of subject i(i=1,…,n). The observed time is 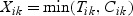. Let N_ik(t) denote the counting process for outcome k of subject i, Y _ik(t)=I(X_ik≥t) denote an “at risk” indicator process, and Δ_ik=I(T_ik≤C_ik) denote an indicator for failure, where I(⋅) is an indicator function. Let Z_ik(t) be a possibly time-dependent p×1 covariate vector for outcome k of subject i at time t. We restrict our attention to the “external” time-dependent covariates Z_ik(t) (Kalbfleisch and Prentice, 2002). We assume that C_ik is independent of T_ik given Z_ik(⋅).

We assume that the marginal hazard function λ_ik(t) is associated with Z_ik(t) as the following:

(2.1)

where λ_0k(t) is a baseline hazard function for outcome k and β₀ is a p×1 vector of regression parameters. Note that disease-specific effects of can be accommodated in (2.1) by defining β₀ and Z_ik(t) in the following manner: and 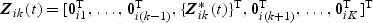where 0_ik are zero vectors. Let 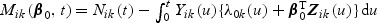denote a martingale with respect to the marginal filtration 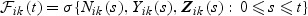and τ denote the study end time.

2.1. Generalized case-cohort study design

The generalized case-cohort design described in this subsection follows the framework of Kang and Cai (2009). In the generalized case-cohort studies with multiple disease outcomes, a subcohort of size 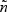is selected from the full cohort via simple random sampling without replacement. Let ξ_i and π_i denote the subcohort sampling indicator and the subcohort sampling probability for the ith subject in the cohort, respectively. Due to the sampling scheme, each subject has equal probability of being sampled into the subcohort, i.e. 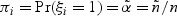, and ξ₁,…,ξ_n are correlated. After the sampling of a subcohort, subsequent samplings of cases outside the subcohort follow. Specifically, for the kth disease, we sample a fixed number of m^(k) cases who are outside the subcohort by simple random sampling. Let η_ik denote the indicator for the ith subject outside the subcohort with the kth disease being selected into the sample and 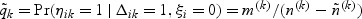denote the sampling probability of the kth disease outcome of the ith subject outside the subcohort where n^(k) and 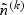denote the number of the kth disease cases in the cohort and in the subcohort, respectively. Note that (η_1k,…,η_nk) are correlated, however, (η_1k,…,η_nk) and (η_1k′,…,η_nk′) are independent for k≠k′. Covariate measurements are taken only on the subcohort members and the sampled cases outside the subcohort. Thus, the observable information for the kth disease outcome of the ith subject is {X_ik,Δ_ik,ξ_i,η_ik,Z_ik(t),0≤t≤X_ik} when ξ_i=1 or η_ik=1 and is {X_ik,Δ_ik,ξ_i,η_ik} when ξ_i=0 and η_ik=0. Note that the case-cohort design, which samples all the cases outside the subcohort, is a special case of the generalized case-cohort design and can be obtained by setting 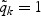for all k. This special case will be referred to as the “original” case-cohort design to distinguish it from the “generalized” case-cohort design.

2.2. Estimation

If the full cohort data were available, the estimate of the true regression parameter β₀ in (2.1) could be obtained by solving the following estimating function (Yin and Cai, 2004)

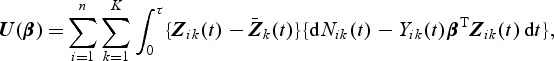(2.2)

where 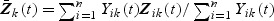. Unlike the Cox model, there exists an explicit solution to the estimating equations U(β)=0_p×1 taking the following form:

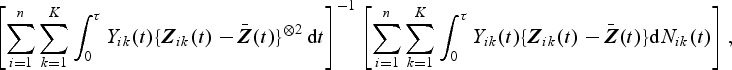where a^⊗2=aa^T.

For data from case-cohort studies, since Z_ik(⋅)'s are not available for cohort members outside the case-cohort samples, (2.2) cannot be calculated. Motivated by inversely weighting the incomplete observations (Horvitz and Thompson, 1951), we propose the weighted estimating function

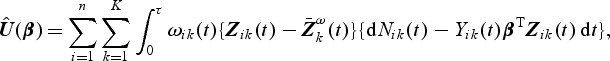(2.3)

where 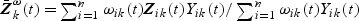and 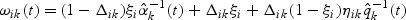is a possibly time-varying weight function, 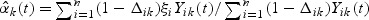, and .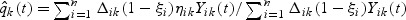

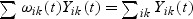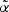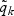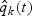Note that for any t≥0; the risk set size is exact with time-varying weights. With fixed weights, i.e. with and in place of and , respectively, equality only holds at t=0.

The estimator of the hazards regression parameter β₀ is defined as the solution to 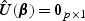. We shall denote this estimator by 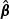and it has the following explicit form:

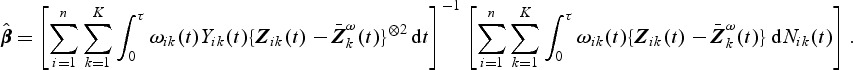The proposed weight function was motivated by the sampling scheme for the study design we have considered in this paper. Under this study design, the subcohort is sampled first and then the cases outside of the subcohort are sampled. Our weight function reflects this two-phased sampling scheme. Specifically, at time t, individuals censored for disease k in the subcohort are weighted by 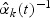, the inverse of their estimated sampling probabilities, while subcohort cases are weighted by 1 as they represent themselves in the cohort. Likewise, the sampled non-subcohort cases are weighted by the inverse of their estimated sampling probabilities, 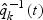, where 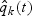denotes the number of sampled non-subcohort cases with the kth disease outcome divided by the number of non-subcohort cases with the kth disease outcome remaining in the risk set at time t.

Let 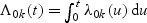. A Breslow–Aalen-type estimator of the cumulative baseline hazard function is given by

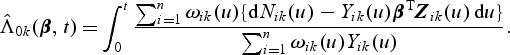Remark 1 —

For the original case-cohort study, the weight function reduces to .

Remark 2 —

Simpler versions of the weight function can be obtained by replacing and with and , true sampling probabilities, respectively. Note that the resulting weight function no longer depends on time. For example, . Throughout this article, whenever it is necessary, we shall use subscript or superscript I and II to denote the estimators with the time-invariant weight function ( and ) and with the time-varying weight function ( and , respectively.

3. Asymptotic properties

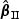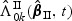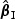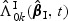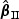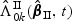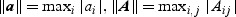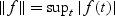In this section, we study the asymptotic properties of the proposed estimates for β₀ and Λ_0k(t) with time-varying weight functions ( and ). Asymptotic properties for and are special cases of and and will be briefly described at the end of this section. Here and hereafter the norms for the vector a, matrix A, and function f are defined as , and , respectively.

We summarize the asymptotic behavior of the regression parameter estimator 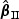in the following theorem.

Theorem 1 —

Under the regularity conditions listed in Section A of the supplementary material (available at Biostatistics online), solving (2.3) is a consistent estimator of β₀. In addition, converges to a zero-mean normal random variable with variance matrix Σ_II(β₀).

To study the asymptotic properties of 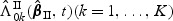, we define the following metric space. Let D[0,τ]^K be a metric space consisting of right-continuous functions f(t) with left-hand limits where 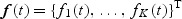and 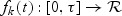. The metric for this space is defined as 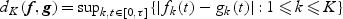for f,g∈D[0,τ]^K. We summarize the asymptotic properties of 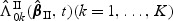in the following theorem.

Theorem 2 —

Under the regularity conditions listed in Section A of the supplementary material (available at Biostatistics online), for each k=1,…,K, converges in probability to Λ_0k(t) uniformly in t∈[0,τ]. In addition, converges weakly to a zero-mean Gaussian process in D[0,τ]^K where .

The proofs of the theorems are outlined in Section A of the supplementary material (available at Biostatistics online). Explicit forms of the asymptotic variance functions in Theorems 1 and 2 as well as their consistent estimators are provided in Section B of the supplementary material (available at Biostatistics online).

Remark 3 —

Asymptotic properties of and are similar to those of and , respectively, with simpler forms of the asymptotic variances. The simplified version is also provided in Section B of the supplementary material (available at Biostatistics online).

Remark 4 —

Asymptotic properties of the estimates for β₀ and Λ_0k(β₀,t) under the original case-cohort study can also be easily derived from Theorems 1 and 2. Since all q_k's are equal to 1 for all k=1,…,K, terms involving q_k's in the asymptotic variances will simply vanish.

4. Simulations

We conducted simulation studies to investigate the finite-sample properties of the proposed estimates. Correlated failure times were generated from the Clayton and Cuzick model (Clayton and Cuzick, 1985) where the joint survival function for (T₁,…,T_K) given (Z₁,…,Z_K) is

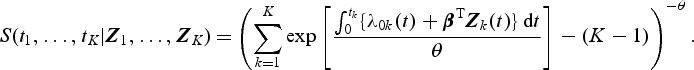Here, θ(>0) is a parameter that controls the degree of dependence between T_k and T_k′(k,k′=1,⋯,K). A smaller θ represents a larger correlation. We considered two types of events (K=2). Here λ_0k was set to be equal to 2 for k=1 and 4 for k=2. Two types of covariates were considered: Bernoulli with probability 0.3 and Uniform (0,3). We examined regression parameters at β₀=0 and 0.2 for both Bernoulli and uniform covariates. Four different values for θ (0.1,0.8,1.25, or 4) were considered to account for strong to weak correlations. The corresponding values of Kendall's tau's are 0.83,0.43,0.29, and 0.09. The censoring time distribution were generated from uniform distribution (0,u) with u chosen to depend on the desired percentage of censoring. We considered event proportion of P_D=[2%,4%] and P_D=[7%,13%] for rare diseases, and P_D=[18%,32%] and P_D=[30%,40%] for non-rare diseases. For rare diseases, we sample all the cases outside the subcohort (q=[1,1]). For non-rare diseases, we sample all as well as a fraction of cases outside the subcohort. The sampling proportions for the cases outside the subcohort are q=[0.5,0.5] and q=[0.37,0.37] for P_D=[18%,32%] and P_D=[30%,40%], respectively. For each configuration, we simulated full cohort samples of size n=1000 and then selected case-cohort samples from each full cohort dataset. The sampling of the subcohort was conducted via simple random sampling. For rare diseases, two different fixed sample sizes (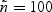 and 200) were considered. For non-rare events, with P_D=[18%,32%], the subcohort size was set to 333. This would result in approximately the same number of cases and controls when all the cases are sampled. With P_D=[30%,40%], the subcohort size was set to 300, which would give us roughly the same number of cases and controls when sampling a fraction of cases outside the subcohort (q=[0.37,0.37]). For each data configuration, we ran R=2000 simulations.

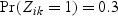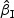We first considered rare events and sampled all the cases. Table 1 shows simulation summary statistics with Bernoulli covariate Z_ik with for and 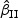, respectively. The notation “mean (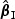)” or “mean (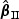)” denotes the average of the estimates of β₀, “SE” denotes the average of standard error estimates based on the proposed method, “SD(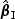)” or “SD(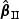)” denotes the sample standard deviation of the 2000 estimates, and “CR” denotes the coverage rate of the nominal 95% confidence interval. The simulation results suggest that the coefficient estimates were approximately unbiased across the setups considered for β₀=0 and β₀=0.2 with both event proportion situations. The proposed estimated standard errors appeared to closely approximate the true variabilities of 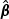s in most of the cases. Increasing subcohort sizes (100–200) resulted in smaller standard errors as expected. Smaller values of Kendall's tau that correspond to a weaker correlation among failure times led to a smaller standard deviation in general. The coverage rate of the nominal 95% confidence intervals using the proposed method were in the 94.0 –96.1% range. Overall, 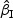and 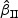performed reasonably well and showed similar results. For all data configuration, the true variabilities of the regression parameter estimates for 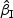and 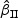were similar.

Table 1.

Summary of simulation results with rare events for 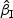and 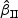: Z_ik∼Bern(0.3)

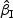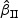β0	Event proportion		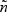τθ	Mean (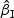)	SE	SD ()	CR	Mean (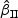)	SE	SD (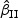)	CR
0	[2%, 4%]	100	0.83	0.002	0.064	0.064	0.946	0.002	0.063	0.064	0.945
			0.43	−0.001	0.061	0.061	0.946	−0.001	0.061	0.062	0.948
			0.29	−0.001	0.061	0.059	0.954	−0.001	0.060	0.059	0.954
			0.09	−0.002	0.061	0.062	0.948	−0.002	0.061	0.062	0.946
		200	0.83	0.002	0.056	0.057	0.940	0.002	0.056	0.057	0.940
			0.43	−0.001	0.053	0.052	0.949	−0.001	0.053	0.052	0.945
			0.29	−0.001	0.052	0.052	0.948	−0.001	0.052	0.052	0.948
			0.09	−0.001	0.052	0.051	0.948	−0.000	0.052	0.051	0.948
	[7%, 13%]	100	0.83	−0.000	0.089	0.091	0.953	−0.000	0.088	0.091	0.951
			0.43	0.002	0.085	0.088	0.953	0.003	0.085	0.088	0.949
			0.29	0.002	0.085	0.085	0.954	0.002	0.085	0.085	0.955
			0.09	0.001	0.084	0.086	0.949	0.001	0.084	0.086	0.944
		200	0.83	0.003	0.070	0.071	0.951	0.003	0.070	0.071	0.951
			0.43	0.003	0.066	0.066	0.957	0.003	0.066	0.066	0.952
			0.29	0.001	0.066	0.066	0.949	0.001	0.066	0.066	0.949
			0.09	−0.001	0.065	0.065	0.957	−0.001	0.065	0.065	0.957
0.2	[2%, 4%]	100	0.83	0.201	0.088	0.084	0.950	0.201	0.087	0.083	0.951
			0.43	0.203	0.084	0.080	0.954	0.203	0.083	0.080	0.955
			0.29	0.203	0.083	0.079	0.952	0.203	0.082	0.078	0.952
			0.09	0.202	0.083	0.082	0.948	0.202	0.082	0.082	0.951
		200	0.83	0.206	0.077	0.074	0.952	0.205	0.076	0.074	0.953
			0.43	0.200	0.072	0.069	0.947	0.200	0.071	0.069	0.950
			0.29	0.199	0.071	0.070	0.943	0.199	0.070	0.070	0.940
			0.09	0.201	0.071	0.069	0.952	0.201	0.070	0.069	0.949
	[7%, 13%]	100	0.83	0.202	0.105	0.105	0.961	0.201	0.105	0.104	0.959
			0.43	0.205	0.101	0.100	0.960	0.205	0.100	0.100	0.961
			0.29	0.204	0.100	0.102	0.954	0.204	0.099	0.102	0.951
			0.09	0.203	0.099	0.101	0.958	0.203	0.098	0.101	0.958
		200	0.83	0.202	0.084	0.085	0.951	0.201	0.083	0.085	0.950
			0.43	0.202	0.078	0.080	0.943	0.202	0.078	0.080	0.942
			0.29	0.203	0.078	0.077	0.953	0.203	0.077	0.077	0.952
			0.09	0.202	0.077	0.078	0.952	0.202	0.076	0.078	0.951

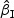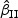Table 2 provides simulation summary statistics for and with the Bernoulli and the Uniform covariates for non-rare events with a non-zero regression coefficient (β₀=0.2) and both sampling all and a portion of the cases, respectively. Overall, the findings were similar to those in Table 1: small biases in the coefficient estimates (<4%) and in the estimated standard errors (<5%), and good coverage rates for most of the cases considered (93–96% ). While sampling half of the cases led to larger sample standard deviations compared with those from sampling all the cases, the magnitude of increase was relatively small. There are only about 7–8% increases in the SEs for the P_D=[18%,32%] situation. When β₀=0, simulation results were similar but slightly better in terms of the accuracy of the estimates in general (results not shown).

Table 2.

Summary of simulation results with non-rare events: β₀=0.2

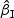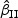Event proportion	q		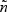τθ	Mean (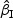)	SE	SD (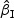)	CR	Mean (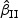)	SE	SD (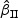)	CR
Zik∼Bern(0.3)
[18%,32%]	[1,1]	333	0.83	0.207	0.094	0.093	0.949	0.207	0.094	0.093	0.951
			0.43	0.204	0.088	0.087	0.955	0.204	0.088	0.087	0.954
			0.29	0.204	0.086	0.086	0.949	0.204	0.086	0.086	0.948
			0.09	0.206	0.083	0.086	0.935	0.206	0.083	0.087	0.935
	[0.5, 0.5]	333	0.83	0.207	0.100	0.100	0.947	0.207	0.100	0.100	0.944
			0.43	0.204	0.094	0.094	0.955	0.204	0.094	0.094	0.954
			0.29	0.205	0.093	0.092	0.955	0.204	0.093	0.093	0.952
			0.09	0.206	0.090	0.093	0.937	0.206	0.091	0.093	0.938
[30%,40%]	[1,1]	300	0.83	0.207	0.099	0.101	0.948	0.207	0.100	0.102	0.946
			0.43	0.204	0.094	0.097	0.944	0.204	0.094	0.097	0.945
			0.29	0.198	0.092	0.091	0.945	0.198	0.092	0.091	0.941
			0.09	0.204	0.088	0.089	0.945	0.204	0.088	0.090	0.946
	[0.37, 0.37]	300	0.83	0.206	0.108	0.108	0.951	0.206	0.109	0.109	0.951
			0.43	0.203	0.103	0.106	0.955	0.203	0.104	0.107	0.959
			0.29	0.203	0.104	0.107	0.959	0.196	0.101	0.100	0.947
			0.09	0.204	0.098	0.101	0.942	0.204	0.099	0.102	0.948
Zik∼U[0,3]
[18%,32%]	[1,1]	333	0.83	0.200	0.058	0.057	0.954	0.200	0.057	0.057	0.957
			0.43	0.202	0.053	0.051	0.959	0.202	0.053	0.051	0.960
			0.29	0.201	0.052	0.053	0.944	0.201	0.052	0.052	0.944
			0.09	0.201	0.051	0.051	0.949	0.201	0.051	0.051	0.949
	[0.5, 0.5]	333	0.83	0.200	0.064	0.064	0.946	0.200	0.063	0.064	0.941
			0.43	0.202	0.059	0.058	0.959	0.202	0.059	0.059	0.957
			0.29	0.201	0.059	0.059	0.938	0.200	0.059	0.059	0.937
			0.09	0.202	0.057	0.058	0.946	0.201	0.057	0.059	0.942
[30%,40%]	[1,1]	300	0.83	0.202	0.061	0.062	0.942	0.202	0.061	0.062	0.944
			0.43	0.202	0.057	0.058	0.946	0.202	0.057	0.058	0.939
			0.29	0.205	0.057	0.056	0.944	0.205	0.056	0.056	0.942
			0.09	0.200	0.054	0.055	0.953	0.200	0.054	0.055	0.947
	[0.37, 0.37]	300	0.83	0.202	0.066	0.067	0.941	0.202	0.067	0.067	0.943
			0.43	0.201	0.063	0.067	0.943	0.202	0.063	0.064	0.945
			0.29	0.205	0.062	0.062	0.947	0.204	0.062	0.063	0.946
			0.09	0.199	0.060	0.060	0.954	0.199	0.061	0.061	0.954

5. Stratified case-cohort design

Suppose that a cohort of size n can be partitioned into L mutually exclusive strata based on some covariates available for the entire cohort. We then extend the method to stratified case-cohort studies, whereby sampling is conducted within each stratum with possibly different sampling probabilities. Specifically, let n_l denote the number of subjects in the lth stratum in the cohort (l=1,…,L) and n=n₁+⋯+n_L. Then, within the lth stratum, we sample 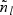subcohort members via simple random sampling with the sampling probability being equal to 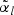where 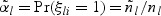. The total subcohort size is 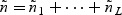. Subsequently, for the kth disease outcome within the lth stratum, we sample 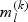cases outside the subcohort via simple random sampling with the sampling probability being equal to 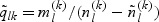, where 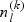and 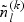are the numbers of subjects with the kth disease outcome in the lth stratum in the cohort and in the subcohort, respectively.

Now, for T_lik given Z_lik(t), we consider the following marginal additive hazards model, 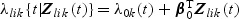where λ_lik(⋅),T_lik and Z_lik(⋅) denote the marginal hazard function, failure time, and a vector-valued covariate for the ith subject with the kth disease outcome in the lth stratum, respectively. Note that subscript l(l=1,…,L) denotes quantities for the lth stratum. Estimation procedures for β₀ and Λ_0k(⋅) described in Section 2.2 can be extended to accommodate the stratified sampling design. Specifically, 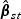, the estimator of β₀, can be obtained by solving 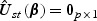where

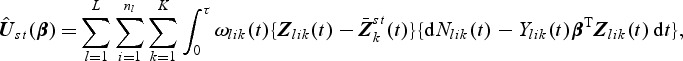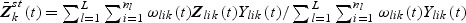and 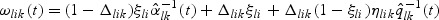. The estimator also has an explicit form where 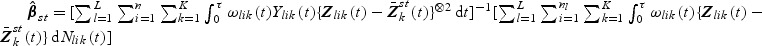. A Breslow–Aalen-type estimator of Λ_0k(t) is given by

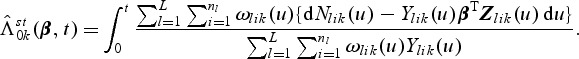By arguments similar to those in the supplementary material (available at Biostatistics online), the consistency and the asymptotic normality of 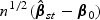can be proved. Likewise, 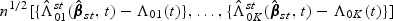can be shown to converge weakly to a zero mean Gaussian process 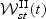based on the arguments similar to those in the supplementary material (available at Biostatistics online). Explicit forms of the components in the asymptotic variance functions are provided in Section C of the supplementary material (available at Biostatistics online).

6. Analysis of the ARIC study data

We applied the proposed inference procedures to a dataset from the ARIC study (Ballantyne and others, 2004, 2005). This study is a large-cohort study involving 15 792 individuals aged 45–64 years old who were sampled from four U.S. communities. After a baseline examination during 1987–1989, subjects in this study were prospectively followed for the development of an incident CHD, including CHD-related death, and for an incident ischemic stroke, a first definite or probable hospitalized stroke through to 1998. Subjects who missed their second visit in 1990–1992, did not have information on CHD or stroke history, had transient ischemic attack or stroke, were under-represented minorities other than blacks, or had no valid follow-up time were excluded from the study. A total of 12 363 subjects comprised the potential full cohort. Those who were alive or free of disease by the end of 1998 or lost to follow-up in the middle of the study periods were treated as censored.

Our primary interest in this analysis was to examine whether levels of hs-CRP were associated with an increased risk for incident CHD and incident ischemic stroke for the ARIC subjects. It is claimed that inflammation plays an important role in cerebrovascular disease as well as CHD and hs-CRP is one of several biomarkers of inflammation that have been associated with an increased risk for CHD and stroke (Ballantyne and others, 2004, 2005).

In order to preserve stored plasma samples and reduce costs, a case-cohort design was implemented. The levels of hs-CRP were measured only on a subset of the ARIC study: individuals who subsequently developed an incident CHD or ischemic stroke and a random subcohort. The subcohort in this study was selected via a stratified random sampling design where the strata were based on sex, race (black versus white), and age at baseline (≤55 versus >55). After excluding the subjects with missing values, 604 incident CHD cases, 183 incident ischemic stroke cases, and 777 subcohort members were used for the analysis. Due to the overlap between CHD/stroke cases and the random subcohort, the total number of assayed sera samples was 1470. To control for confounding factors, the following covariates including several traditional cardiovascular risk factors were considered in the model: age at baseline, sex, race, smoking status, diabetes, systolic blood pressure, LDL cholesterol (LDL-C), and HDL cholesterol (HDL-C). Table 3 shows the baseline characteristics of the subjects in the case-cohort sample and the full cohort. The weighted means and proportions from the subcohort members were similar to those from the full cohort members, which means the subcohort is a well represented subset of the full cohort.

Table 3.

Baseline characteristics of the case-cohort and the full cohort samples

	CHD (n=604)	Stroke (n=183)	Subcohort (n=777)	Full (n=12 108)
Age (SD), years	58.6 (5.44)	59.7 (5.54)	56.9 (5.57)	56.8 (5.70)
Female, %	32.3	44.3	57.3	57.8
African American, %	22.9	43.2	24.8	24.4
Current smoker, %	29.1	34.4	20.1	22.0
Diabetes, %	28.5	37.7	16.4	13.3
Systolic blood pressure (SD), mmHg	129.3 (20.78)	133.5 (21.14)	121.7 (18.89)	121.1 (18.52)
LDL-C (SD), mm/dL	147.1 (38.37)	140.9 (42.53)	132.0 (36.37)	132.8 (36.71)
HDL-C (SD), mm/dL	42.2 (12.28)	45.6 (13.59)	50.8 (17.21)	50.5 (16.69)
hs-CRP (SD), mm/dL	3.9 (3.45)	4.1 (3.44)	3.1 (3.37)	N/A

Table 4 presents hazards regression parameters estimates (Estimate) for hs-CRP, the associated estimated standard errors (SE), and the associated p-values from fitting a marginal additive hazards model for CHD and stroke, which is adjusted for age, sex, race, smoking status, systolic blood pressure, LDL-C, HDL-C, and diabetes. While elevated LDL-C is a well-known risk factor for CHD and a major component of national guidelines for the prevention of CHD, many people still experience CHD events without elevated LDL-C (Ballantyne and others, 2004). The effect of hs-CRP might be different for those with and without an elevated LDL-C level. To allow for this, we added an interaction term between hs-CRP level and a dichotomized LDL-C level (LDL-C<130 mg/dL or LDL-C≥130 mg/dL).

Table 4.

Analysis results for the effect (risk difference) of hs-CRP from the ARIC study. The model is adjusted for age, sex, race, smoking status, systolic blood pressure, LDL-C, HDL-C, and diabetes

	Time-invariant weight			Time-varying weight
Variable	Estimate (×105)	SE (×105)	p-value	Estimate (×105)	SE (×105)	p-value
For the CHD event
CRP2	0.991	0.360	0.006	0.974	0.373	0.009
CRP3	1.770	0.464	<0.001	1.693	0.460	<0.001
CRP2*(LDL-C <130)	−1.021	0.427	0.017	−1.038	0.443	0.019
CRP3*(LDL-C <130)	−1.204	0.511	0.019	−1.147	0.504	0.023
For the stroke event
CRP2	−0.327	0.150	0.029	−0.274	0.153	0.073
CRP3	−0.409	0.159	0.010	−0.331	0.159	0.040
CRP2*(LDL-C <130)	0.243	0.249	0.329	0.216	0.259	0.405
CRP3*(LDL-C <130)	0.170	0.252	0.501	0.141	0.254	0.578
CRP2*(t>1069)	0.255	0.121	0.035	0.247	0.118	0.035
CRP3*(t>1069)	0.603	0.120	<0.001	0.576	0.110	<0.001

Tertiles of hs-CRP were used to define the low (<1.0 mg/L), middle (1.0–3.0 mg/L), and high (>3.0 mg/L) hs-CRP groups. Since, as can be seen in Figure 1, the empirical cumulative hazards functions for the different hs-CRP groups increase approximately in a linear fashion, the additive hazards model is a reasonable choice. For the stroke event, however, the empirical cumulative hazard functions for the different hs-CRP groups are 0 until the first event occurs at 1069 days. To capture this, we added an interaction term between the hs-CRP level and I(t>1069), a time-dependent indicator variable, for the stroke event, to allow the effect of hs-CRP to be different before and after day 1069. We fit model (2.1) to study the effect of hs-CRP and the results are presented in Table 4. “CRP2” and “CRP3” in the “Variable” column in Table 4 denote the indicator variables for the middle hs-CRP and the high hs-CRP levels, respectively. The low hs-CRP group was used as the reference group. We fit the models with type-specific effects of hs-CRP on CHD and stroke.

The results using time-invariant weight show that, after adjusting for age, sex, race, smoking status, systolic blood pressure, LDL-C, HDL-C, and diabetes, subjects in both the middle and high hs-CRP groups with the elevated LDL-C level were significantly associated with increased risks of CHD compared with those in the low hs-CRP group (p-values<0.01). Without the elevated LDL-C level, the effect of the high hs-CRP group was marginal (p-value=0.053). The difference in the risk of CHD comparing the high with the low hs-CRP group was estimated to be 5.66×10⁻⁶ per person-day or 2.07 per 1000 person-years. The middle hs-CRP level was not associated with an elevated CHD risk (p-value=0.919). For those without the elevated LDL-C level, neither the high nor middle hs-CRP level showed a statistically significant effect on the risk of stroke.

We further conducted Wald-type tests to check whether a common effect of hs-CRP on the risks of CHD and stroke could be assumed. The test results show that the effects of high hs-CRP group were significantly different for CHD and stroke with the elevated LDL-C level (χ²=25.952, p-value<0.001) and without the elevated LDL-C level (χ²=10.503, p-value=0.001). Similarly, the effects of middle hs-CRP group were significantly different for CHD and stroke with the elevated LDL-C level (χ²=16.293, p-value<0.001) and without the elevated LDL-C level (χ²=12.742, p-value<0.001). Therefore, we conclude that the hs-CRP level has a different effect for the risks of CHD and of stroke. The results based on time-varying weights were similar.

To check the marginal additive hazards assumption under model (2.1), we adapted the methods in Spiekerman and Lin (1996) to case-cohort data with multiple disease outcomes by incorporating weights in the score-type process, a cumulative sum of martingale residuals with the following form: 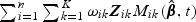. Figure S1 in the supplementary material (available at Biostatistics online) provides graphical representations of the observed score-type processes versus 20 simulated score-type processes for the hs-CRP variables. From the plots, the marginal additive hazards assumption seems reasonable.

7. Concluding remarks

We have proposed methods of fitting marginal additive hazard regression models for case-cohort studies with multiple disease outcomes. Risk differences can provide information valuable to public health intervention. Specifically, risk differences can provide information regarding the reduction in the number of cases developing a certain disease due to a decrease in a particular exposure. One advantage of the additive hazards model is that risk differences between different exposure groups can be readily derived from the coefficients in the additive hazards models. For the ARIC study, our results indicate that for individuals without an elevated LDL-C and with the same age, gender, and race, a reduction of 3.0 CHD cases per 1000 person-years is expected if the hs-CRP level reduces from high to low. This information cannot be easily obtained from the Cox model.

One advantage for the case-cohort design is that the same random subcohort can be used for studying different diseases. By joint modeling different diseases, we are able to compare the effect of exposure on the different diseases. For the ARIC study, without the elevated LDL-C, our results indicate that the effect of high hs-CRP on CHD is significantly larger than that on stroke (p-value=0.001). This information cannot be obtained if we follow the usual practice that analyzes the two case-cohort studies separately.

We considered two types of weight functions: time-invariant and time-varying. In general, the latter requires more time and effort than the former since the form of the asymptotic variance for the former is more complicated than that for the latter, and weight functions for the latter need to be enumerated at each failure time. More importantly, time-varying weight function requires additional information on failure and censoring times of the entire cohort members, which are not always available. For Cox proportional hazards models, the time-varying weighted estimator is known to be more efficient when failure times are independent (Barlow, 1994; Borgan and others, 2000). However, based on our simulation results, no obvious gain in efficiency is guaranteed for multivariate failure times. For these reasons, we recommend using the time-invariant weighted estimator.

Extensions of the proposed weight function ω_ik(t) in several directions would be worthwhile to consider. One such extension, as pointed out by the Associate Editor, is to modify ω_ik(t) so that it can utilize some available information which are not incorporated in the current form of ω_ik(t), such as sampled cases for other diseases. Another extension of the proposed weight function is to incorporate some always observed auxiliary covariates when estimating the sampling probability in the weight function. For univariate failure time data from case-cohort studies, this type of inverse probability-weighted (IPW) estimators using available auxiliary covariates was considered by several authors (Kulich and Lin, 2004; Breslow and Wellner, 2007; Breslow and others, 2009). Similar ideas could be adapted to analyzing case-cohort data with multiple disease outcomes. For example, the doubly weighted estimator proposed by Kulich and Lin (2004) includes the time-varying weighted estimator we considered in this paper as a special case. Specifically, the doubly weighted estimator considers p-dimensional arbitrary random processes in place of at-risk indicator processes. Thus, the implementation of this type of IPW estimator involves the choice and estimation of the p-dimensional random processes in the weight. Following the arguments employed by Kulich and Lin (2004, Section 4) or Breslow and others (2009, p. 40) with some modifications to multiple disease outcomes, and to additive hazards models, one could possibly implement the IPW estimator, which is expected to improve efficiency further.

Supplementary material

Supplementary material is available online at http://biostatistics.oxfordjournals.org.

Funding

This work was partially supported by National Institutes of Health grants (R01-HL57444, P01CA142538) and National Center for Research Resources grant (UL1 RR025747). The ARIC Study is carried out as a collaborative study supported by National Heart, Lung, and Blood Institute contracts (N01-HC-55015, N01-HC-55016, N01-HC-55018, N01-HC-55019, N01-HC-55020, N01-HC-55021, N01-HC-55022).