Geometry of Miura-folded metamaterials

Abstract

This paper describes two folded metamaterials based on the Miura-ori fold pattern. The structural mechanics of these metamaterials are dominated by the kinematics of the folding, which only depends on the geometry and therefore is scale-independent. First, a folded shell structure is introduced, where the fold pattern provides a negative Poisson’s ratio for in-plane deformations and a positive Poisson’s ratio for out-of-plane bending. Second, a cellular metamaterial is described based on a stacking of individual folded layers, where the folding kinematics are compatible between layers. Additional freedom in the design of the metamaterial can be achieved by varying the fold pattern within each layer.

In this paper, we describe the use of origami for mechanical metamaterials, where the fold patterns introduce kinematic deformation modes that dominate the overall structural response. The geometry and kinematics of two types of folded metamaterial are described: a folded shell structure and a folded cellular metamaterial. The examples presented here are both based on a particular fold geometry: the classic Miura-ori pattern. This pattern has previously been considered for applications, such as deployable solar panels (1), and was observed in the biaxial compression of stiff thin membranes on a soft elastic substrate (2, 3).

In recent years, origami has seen a surge in research interest from engineers and physicists. Developments include folded sandwich panel cores (4, 5), origami-inspired stents (6), self-folding membranes (7), and cellular materials made from folded cylinders (8). An important concept is rigid origami, where the fold pattern is modeled as rigid panels connected through frictionless hinges. These assumptions make the study of origami folding a matter of kinematics. Of particular interest here are fold patterns where four fold lines meet at each vertex (so-called degree-4 vertices). Each such vertex has one degree of freedom, a tessellated fold pattern is overconstrained, and folding is only possible under strict geometric conditions. In a landmark paper, Huffman (9) studied rigid folding using spherical geometry; recent work includes the modeling of crease patterns using quaternions (10) and an increased understanding of the foldability conditions for partly folded quadrilateral surfaces (11, 12).

In describing the properties of the folded metamaterials, we are here primarily concerned with the deformation kinematics. If required, these models can straightforwardly be extended to include simple constitutive behavior at the fold lines [for instance, elastic (13) or plastic (14) behavior].

The paper is structured as follows. First, the Miura-ori unit cell is introduced, because its geometry plays a key role in the mechanical properties of the folded metamaterials. The first such metamaterial is based on a single planar Miura-ori sheet: a folded shell structure. Of particular interest are the shell’s out-of-plane kinematics. Second, a bulk metamaterial is proposed based on the stacking of individual Miura-ori layers, and its folding kinematics are explored. A brief discussion concludes the paper.

Unit Cell Geometry

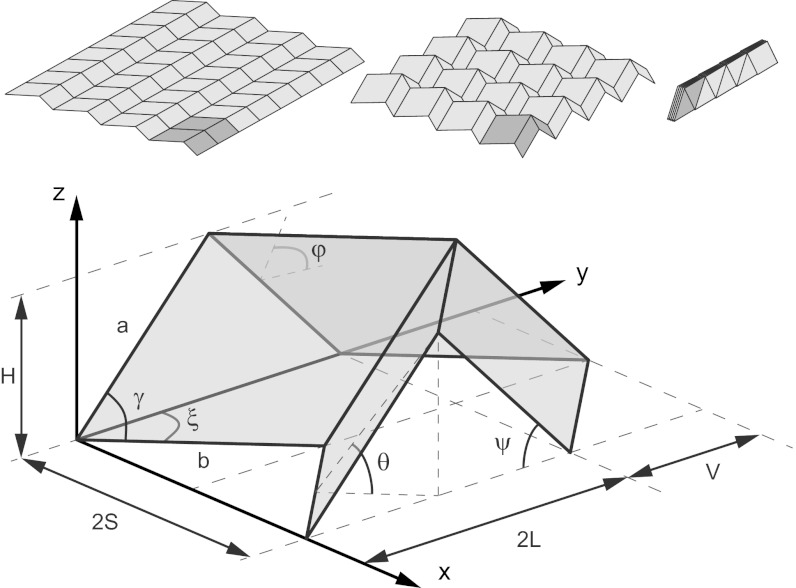
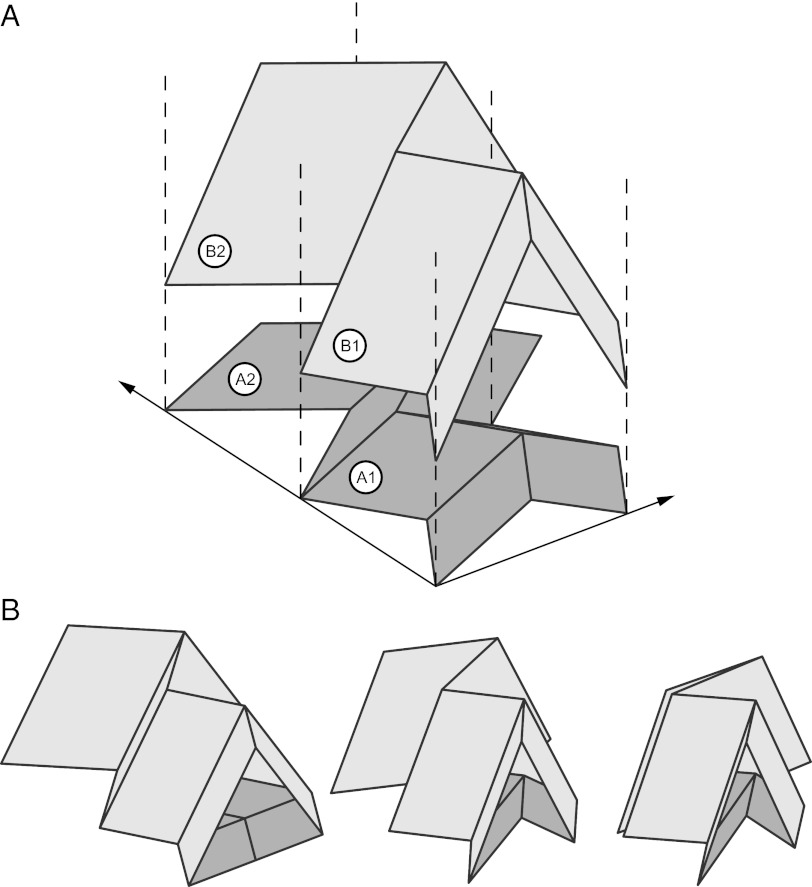
A Miura unit cell is shown in Fig. 1. Its geometry can be parameterized in a number of ways. We here define the unit cell by the dimensions of its smallest constituent component, a parallelogram with sides a and b and acute angle γ, and the dihedral fold angle θ ∈ [0, π/2] between the facets and the xy plane. The outer dimensions are then given by

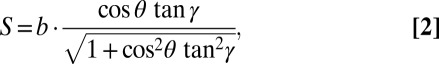and

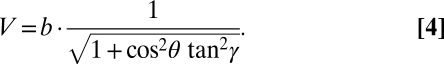When designing metamaterials, the mechanical properties are often characterized in a partly folded state. For a selected set of outer dimensions H, S, V, L, the fold pattern parameters can then be back-calculated (4, 15). Additional useful relationships are

and

with ξ ∈ [0, γ], ψ ∈ [0, γ], and φ ∈ [0, π/2]. Note that a Miura-ori sheet can be folded from a flat sheet with only bending along the fold lines and, therefore, is a developable surface.

Fig. 1.

A folded Miura-ori sheet consists of tessellations of a unit cell. The unit cell geometry can be described using parameters defining a parallelogram facet, a, b, γ, and fold angle θ ∈ [0, π/2]. An alternative parameterization is given by dimensions H, S, V, L. Other useful angles are shown, where ξ and ψ are angles between fold lines and the y axis and θ and φ are dihedral angles between facets and the xy and yz planes, respectively. Three configurations with θ = {0, π/4, π/2} are shown.

Folded Shell Structures

The first metamaterial here described is a folded shell structure. A partly folded Miura-ori sheet is considered as a shell structure, where the local fold pattern alters the shell’s global mechanical properties. It is an example of a compliant shell mechanism (16), where the overall kinematics are a function of the articulation along the fold lines as well as the deformation of the interlaying thin-walled facets. This hierarchical interaction of deformation kinematics can produce unexpected and fascinating mechanical properties.

In describing the kinematics of a Miura-ori sheet, a distinction must be made between the in-plane and out-of-plane deformations of the shell structure.

In-Plane Kinematics.

When modeled as rigid origami, the Miura-ori sheet has a single in-plane expansion mode, with kinematics that can be characterized by an expansion coefficient or Poisson’s ratio:

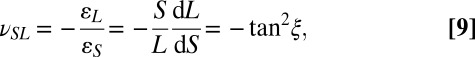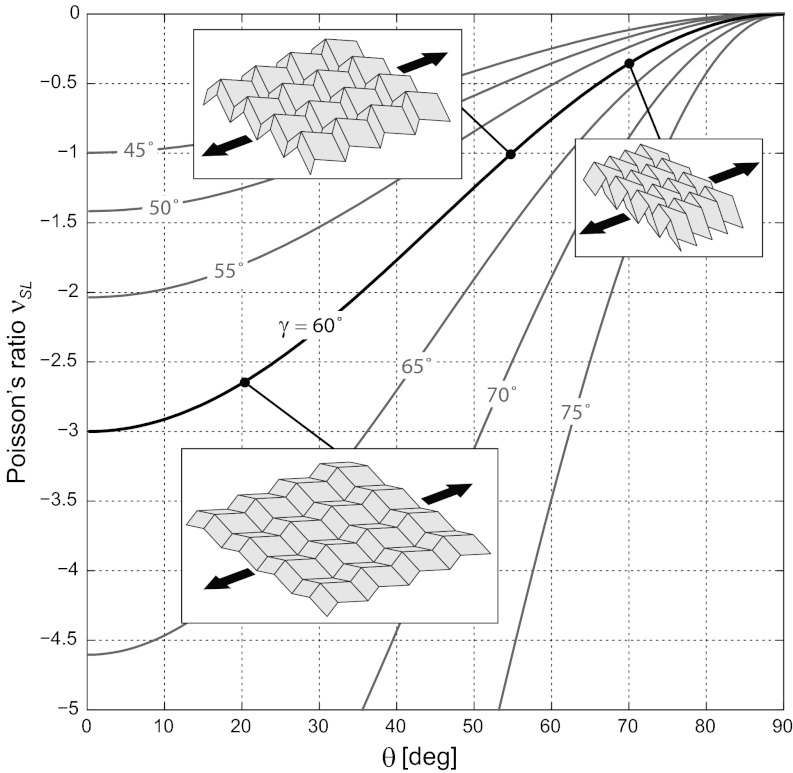
where the strains ɛ_L and ɛ_S are instantaneous true strains. As illustrated in Fig. 2, the Poisson’s ratio is always negative; this unusual material property can be found in microstructured materials referred to as auxetics (17) as well as fluctuating membranes and crumpled papers (18). The negative in-plane Poisson’s ratio of the Miura-ori sheet is well-known (1, 3). However, previous formulations obscured an important insight: the Poisson’s ratio is only a function of the angle ξ in the xy plane or, equivalently, the ratio S/V. This insight will lead on to the folded cellular metamaterial described in the next section.

Fig. 2.

The in-plane expansion coefficient of a Miura-ori sheet, ν_SL = −cos²θ tan²γ, for different geometries γ. The arrows indicate the primary strain direction δS; pictured are configurations with γ = 60° and a/b = 1.

Out-of-Plane Kinematics.

Of particular interest are the out-of-plane kinematics of the Miura-ori folded shell structure (Fig. 3). Simple experiments revealed two out-of-plane deformation modes: saddle and twisting modes (15). A saddle-shaped bending mode is conventionally expected in a material with a positive Poisson’s ratio. For the Miura-ori sheet, therefore, the Poisson’s ratios for in-plane and out-of-plane deformations are of opposite sign.

Fig. 3.

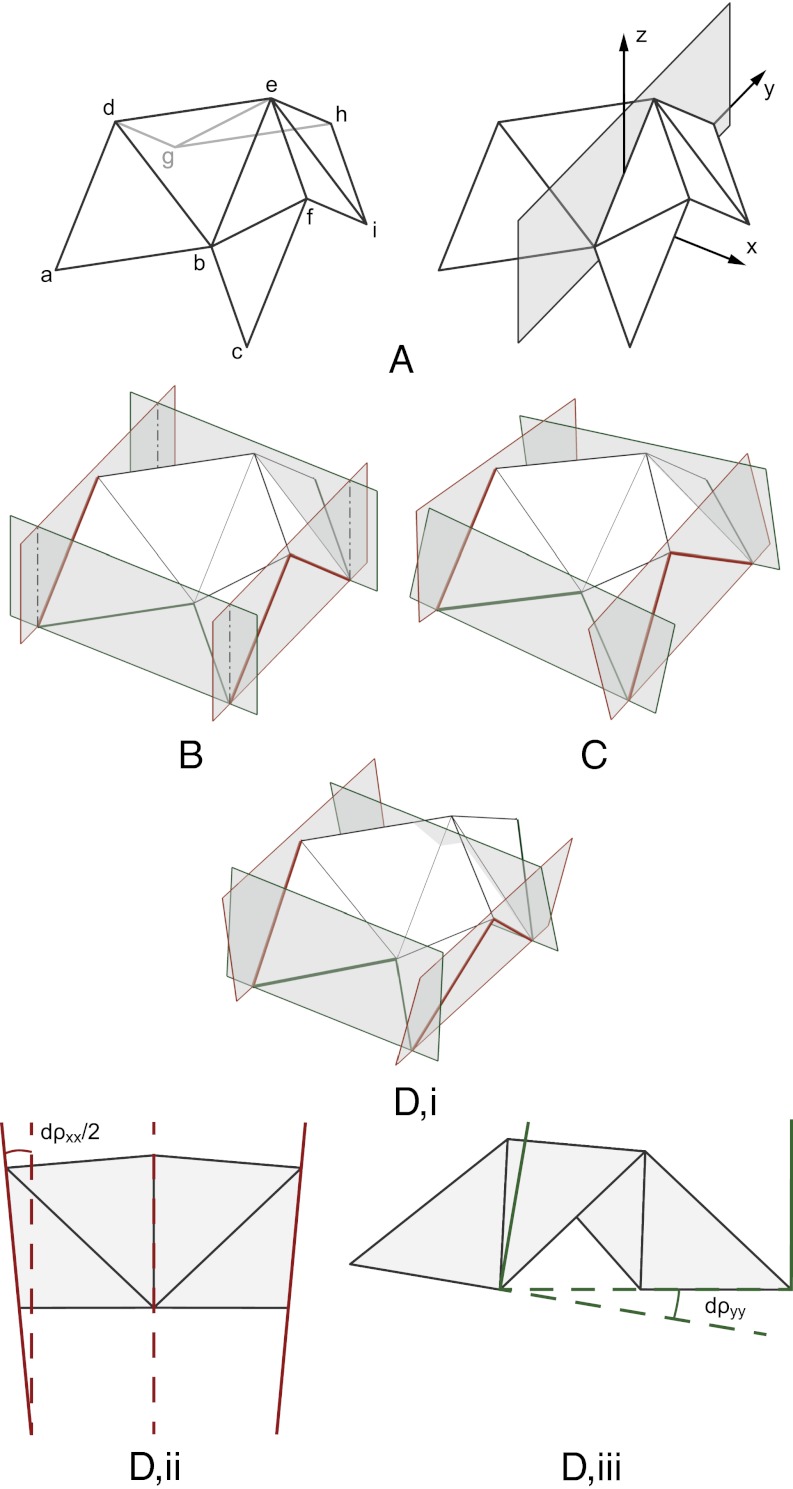
(A) The undeformed configuration and the (B) twisting and (C) saddle-shaped deformation modes of a Miura sheet with 9 × 9-unit cells (a/b = 1, γ = π/3). It is shown in ref. 13 that, over a wide range of geometries and material parameters, these deformation modes are the most flexible. Only for configurations where the bending stiffness of the facets is much greater than the bending stiffness of the fold lines is the planar mechanism (Fig. 1) the most flexible deformation mode.

A key observation is that, for out-of-plane deformations, the facets of the Miura unit cell must bend. These modes can, therefore, not be captured in a rigid origami model without introducing additional fold lines. For the mechanical analysis, the facet bending is modeled by introducing a diagonal fold line to the parallelogram facets. The additional fold lines can be considered as a convenient construct to simplify modeling. However, such spontaneous fold lines can, in fact, be observed in paper models, and indeed, mathematical models of origami folding show that developable deformations of facets bounded by straight lines must remain piecewise planar (19). Their formation is also motivated by the physics of stress concentration in thin-walled shells (20, 21). To first-order approximation, the choice of diagonal for the additional fold line does not matter (SI Appendix, section S1). We here select the shorter diagonal, motivated by observation of physical models as well as energetic considerations.

Schenk and Guest (13) described a simple mechanical model to study the dominant kinematics of the sheets, whereby the folded sheet was modeled as a pin-jointed truss (SI Appendix, section S2). By introducing a bending stiffness along the fold lines, K_fold, and across the facets, K_facet, the modal response of the folded shell was studied. An important nondimensional material parameter is the ratio of the fold and facet stiffness. The modal analysis confirmed the bending and twisting modes as dominant deformation modes over a wide range of unit cell geometries and stiffness ratios.

In previous studies, the coupling coefficient between the opposing curvatures in the saddle-shaped deformation mode was not quantified, because the Gaussian curvature varies across the deformed sheet. The unit cell deformations must necessarily vary across the surface, because the doubly curved geometry cannot be attained through a tessellation of a single deformed unit cell. To first order, however, the doubly curved deformation of the folded sheet can be described by considering a single unit cell with tessellation boundary conditions (Fig. 4). The tessellation boundary conditions reduce the degrees of freedom of the unit cell. As detailed in SI Appendix, section S3, the remaining deformation modes can then be separated into three orthogonal modes: a planar mode, a symmetric out-of-plane mode (i.e., saddle), and an antisymmetric out-of-plane mode (i.e., twisting).

Fig. 4.

To capture out-of-plane deformations, (A) additional fold lines (bd, bf, eg, and ei) are introduced diagonally across the facets. (B) The deformations of the unit cells can be visualized by means of bounding planes, which represent the tessellation boundary conditions ∠adg = ∠cfi and ∠abc = ∠ghi. The resulting out-of-plane deformation modes are (C) twisting and (D) saddle-shaped bending, which are, respectively, antisymmetric and symmetric in the yz plane (15). (D, i) For the bending mode, the tilt angles of the bounding planes, dρ_xx and dρ_yy, can be converted to a corresponding change in curvature of the folded sheets: (D, ii) κ_xx = dρ_xx/2S; (D, iii) κ_yy = dρ_yy/2L. Additional details are in SI Appendix.

For the saddle mode, the out-of-plane coupling coefficient between the curvatures, ν_κ = −κ_yy/κ_xx, is of interest. The first-order deformation modes provide the necessary information to numerically calculate the change in curvature. Remarkably, the out-of-plane coupling coefficient is found to be equal and opposite to the in-plane Poisson’s ratio:

Within the assumed kinematics for the folded sheets (i.e., only developable deformations of the unit cell facets), the attainable geometries are strictly limited. Although a large range of deformed sheet configurations can be attained using combinations of stretching, bending, and twisting, deformations such as in-plane and out-of-plane shear are not compatible with this kinematic model. Physical sheets must, therefore, undergo nondevelopable deformations (i.e., in-plane strains of the facets) to attain those modes (5). Nonetheless, it is worth emphasizing that the initially planar Miura folded shell can attain doubly curved configurations and thus, changes its global Gaussian curvature, with only developable deformations of the unit cell facets.

Another folded shell structure, the eggbox sheet, was studied in the work in ref. 13. It is shown to exhibit a material behavior exactly opposite to the behavior described here for the Miura-ori: it has a positive in-plane Poisson’s ratio but a negative Poisson’s ratio in certain out-of-plane deformation modes. A differentiating feature is that the eggbox sheet is nondevelopable and therefore, cannot be folded from a flat sheet.

Folded Cellular Metamaterial

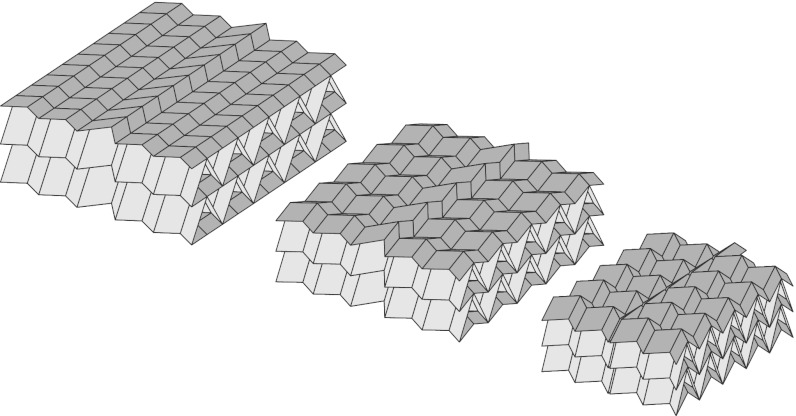
We can build on the results of the in-plane kinematics described previously to show that different Miura sheets can be stacked to form a 3D foldable metamaterial. Eq. 9 shows that the coupling between expansion in the x and y directions shown in Fig. 1 depends only on the in-plane angle ξ. In particular, it does not depend on height H. Hence, Miura sheets with different heights H can be stacked together, bonded along fold lines, and still fold freely (Fig. 5). The result of the stacking is a cellular metamaterial that expands/contracts omnidirectionally and is highly anisotropic. Examples of folded models are shown in SI Appendix, section S4.

Fig. 5.

Individual Miura-ori sheets can be stacked together and bonded along joining fold lines to form a folded cellular metamaterial. Although the Miura-ori unit cell geometry varies between successive layers, the stacked configuration preserves the folding kinematics, and the 3D metamaterial expands/contracts uniformly. Here, a stack with alternating layers ABABABA is shown. An animation of the folding motion is provided by Movie S1.

Stacked Geometry.

In the stacked configuration, the fold pattern may vary from layer to layer, but it is here assumed that the unit cell geometry alternates between successive layers: ABABA etc. The unit cells in successive layers A and B must share at least three geometric parameters, leaving a single free parameter. This constraint can be recognized when considering the extrinsic unit cell geometry: S_A = S_B, V_A = V_B, and L_A = L_B, where the unit cell heights H_A and H_B can be selected independently. This paper assumes, without loss of generality, that H_B ≥ H_A. In terms of the intrinsic geometric parameters, if γ_B ≥ γ_A is taken as the independent variable for layer B, the corresponding unit cell parameters can be calculated by

and

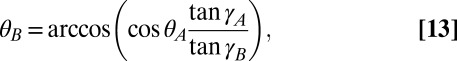where Eq. 13 provides a transfer function between the fold angles of the successive layers A and B. In this paper, we only consider θ_A ∈ [0, π/2]. Extending the range to include θ_A ∈ [−π/2, 0] will result in a metamaterial where the layers are no longer nested but connected along their ridges.

Expansion Coefficient.

As a result of the stacking process, the in-plane expansion coefficient of both the cellular metamaterial and a single Miura sheet are identical. For the 3D metamaterial, the through-thickness expansion coefficient is now relevant. For a single layer, the coefficients can be written as

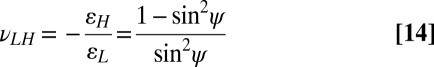and

with ν_SL being the in-plane expansion coefficient from Eq. 9. The single-layer expansion coefficient will, thus, always be positive, and its height will reduce as the sheet expands in plane.

For a stacked metamaterial, the total stack height H_s = n(H_B − H_A) + H_A, with n the number of repeating layer pairs AB. For large values of n, the through-thickness expansion coefficient can be written as

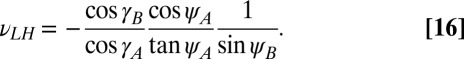Within the given bounds on fold angle θ_A, ν_LH will always be negative. In other words, the expansion coefficient for the 3D metamaterial, consisting of a layering of Miura sheets, is opposite to that of its constituent layers.

For small numbers of n, the expansion coefficient of the metamaterial will transition from a positive to negative Poisson’s ratio behavior, respectively governed by Eqs. 14 and 16, as the number of stacked layers increases.

Relative Density.

An important property of a cellular material is its relative density. For a single-layered Miura-sheet, this quantity is given by

with t is the sheet thickness. The density is minimal when the denominator (i.e., the outer volume of the unit cell) reaches its maximum:

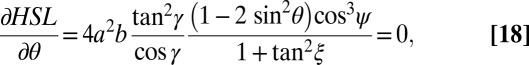which will always be satisfied at θ = π/4. In other words, regardless of its geometry, a single-folded Miura-ori layer will always reach maximal volume at the same fold angle. A similar expression for the stacked configuration is less obviously derived, because the height H_B of the stacking layer can be freely specified. We here state the material density as a function of the partly folded configuration,

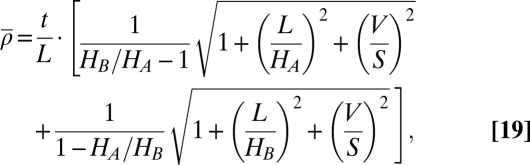expressed in terms of the dimensionless groups ρ_c/ρ, t/L, H_B/H_A, L/H_A, and V/S.

Self-Locking.

An interesting feature of the Miura-ori pattern is the ability to automatically control the maximum fold depth of a sheet, which can be achieved by varying the unit cell geometry within a layer: when a unit cell reaches its maximum fold angle θ = π/2, it locks up, and the folding motion of the entire sheet is halted. It will be shown that, in the stacked configuration, the folding motion is preserved when varying the unit cell geometry within the layers, and the metamaterial can, therefore, be designed to lock in a predetermined configuration (Fig. 6).

Fig. 6.

A self-locking folded cellular metamaterial. As the Miura sheets contract, the unit cells in the central column reach their maximum fold angle before the rest of the layer, thereby halting the folding motion and locking the metamaterial in a predetermined configuration. This behavior can be achieved by varying the unit cell geometry within each layer. An animation of the folding motion is provided by Movie S2.

First consider two adjoining unit cells A1 and A2 with different geometries (Fig. 7). Taking A1 as reference configuration, the relationships ψ_A1 = ψ_A2 and a_A1 = a_A2, thus, leave γ_A2 and b_A2 to be chosen freely for unit cell A2. By selecting γ_A2 < γ_A1, unit cell A2 will lock at θ_A2 = π/2, when ψ_A = γ_A2. The corresponding θ_A1 can be calculated from

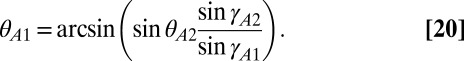Fig. 7.

The unit cell geometry of the Miura pattern can be varied within each layer. A shows layer A with unit cells A1 and A2, on which are stacked unit cells B1 and B2 in layer B. The relationship between the unit cell geometries is given by Eq. 21. The geometry γ_A2 < γ_A1 is selected such that unit cells A2 and B2 will lock in a predetermined configuration, which is shown in B.

Next, consider the stacking of layers A and B, with unit cells B1 and B2 stacked onto A1 and A2, respectively (Fig. 7). Using Eq. 11, with the knowledge that a_A1 = a_A2 and a_B1 = a_B2, the geometric condition

must be satisfied to enable stacking. With the four unit cells in place, their combined kinematics can be studied. The in-plane expansion coefficient of unit cell A2, as transferred from A1 to A2, is given by

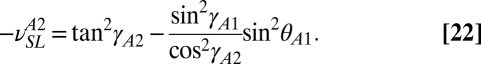Similarly for unit cell B2, as transferred through A1 and B1, the expansion coefficient can be expressed as

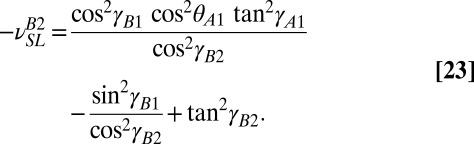To preserve the compatibility between layers A and B during folding, Eqs. 22 and 23 must be equal for any value of θ_A1. It can be shown that this equality is satisfied under the same geometric condition as given in Eq. 21. In other words, when a configuration is found where four unit cells fit together, they will remain compatible in any folded configuration. Therefore, a stacked metamaterial where the unit cell geometry is varied within the layers will still fold freely.

Discussion

In this paper, we have described the geometry of two folded metamaterials, both based on the Miura-ori fold pattern, that display intriguing mechanical properties.

The folded shell structure, consisting of a single Miura sheet, has opposite Poisson’s ratios for in-plane and out-of-plane deformations. For planar deformations, it has a negative Poisson’s ratio, whereas under bending, it deforms into a saddle-shaped configuration characteristic of a positive Poisson’s ratio. Remarkably, these Poisson’s ratios are found to be equal and opposite.

By stacking folded Miura layers into a 3D structure, a cellular folded metamaterial is obtained. Although the unit cell geometry varies between successive layers, the folding motion is preserved for the stack. The result is a metamaterial that can fold and unfold uniformly. What is more, because the folding motion has a single degree of freedom, the folded metamaterial can be machined into any desired shape and still preserve its folding motion. Applications can be found in impact absorption as well as deployable structures. A key difference with the folding metamaterial described in ref. 8 is the potential simplicity of manufacture. The individual folded sheets can be manufactured using established manufacturing methods (14) before being stacked and joined along fold lines.

The geometric richness of the stacked metamaterial can be further exploited by varying the fold pattern within a layer. For instance, the folding motion can be halted at a desired fold angle, enabling the design of metamaterials that can lock into a specific configuration. This ability can be put to effective use in self-assembly techniques. Using established micromanufacturing techniques, a sheet can be folded using strain differentials across the fold lines; the final configuration can then be ensured by using a self-locking geometry. Alternatively, the self-locking can provide a tailored stiffening response of the metamaterial under an impact load.

The geometric approach taken in this paper clearly provides a highly idealized analysis of the structural mechanics of the folded metamaterials. Future work may characterize the mechanical properties that do not follow from the described kinematics, such as shear deformations.