Microsecond folding experiments and simulations: a match is made

Abstract

For the past two decades, protein folding experiments have been speeding up from the second or millisecond time scale to the microsecond time scale, and full-atom simulations have been extended from the nanosecond to the microsecond and even millisecond time scale. Where the two meet, it is now possible to compare results directly, allowing force fields to be validated and refined, and allowing experimental data to be interpreted in atomistic detail. In this perspective we compare recent experiments and simulations on the microsecond time scale, pointing out the progress that has been made in determining native structures from physics-based simulations, refining experiments and simulations to provide more quantitative underlying mechanisms, and tackling the problems of multiple reaction coordinates, downhill folding, and complex underlying structure of unfolded or misfolded states.

I. Introduction

Folding science is a vast field, drawing upon its tools from chemistry, physics, computational science, molecular biology, bioengineering and many other areas. It covers proteins, but also other biomolecules with varied structures such as nucleic acids. This perspective specifically takes a look at how microsecond protein folding experiments and microsecond simulations (either single- or multi-trajectory) have come together sharpen our understanding of how small globular proteins fold.

The era of folding science was ushered in with the structures and thermodynamic principles that began to be revealed by experiments in the 1960s.^{1, 2} Computational protein folding began to develop soon thereafter,^{3, 4} progressing from model systems^{5, 6} to explicit solvent simulations of multiple complete folding/unfolding events.⁷ The era of direct comparison between protein folding experiment and simulation began in the late 1990s when both converged on the microsecond time scale.^8–16 This was made possible by advances in computing power and force fields to push simulation towards microseconds from the bottom up^17–20 and by the development of fast folders and new initiation/detection techniques to push experiments towards microseconds from the top down.^21–23

Experiments

Fast protein folding is often studied by subjecting the sample to a rapid perturbation of a state variable (e.g. temperature, pressure, pH, concentration of denaturant) and monitoring the evolution of the system to a new thermodynamically stable state. The perturbation must be much faster than the rate at which the system is able to respond. A common example is the temperature jump (T-jump). In this method the temperature of protein solution is suddenly (ns time scale) increased by ~5–15 K and the subsequent unfolding of the proteins is probed by fluorescence of the amino acid tryptophan. The resulting signal is representative of the behavior of an ensemble of molecules.²³

In the simplest “two state” case, often assumed as a default for small, fast-folding proteins, the detected response would be a single exponential decay, due to the interconversion of protein populations between the initial and final thermodynamic state. The observed time constant τ_a is the inverse of the activated rate coefficient k_a, which is the sum of the folding and unfolding rates because both reactions are monitored simultaneously at the ensemble level.²⁴

A similar result can be obtained at the single-molecule level.²² If the system is ergodic, monitoring a single protein molecule jumping from one state to the other will yield histograms of dwell times in each of the two states. For two states connected by a large activation barrier, the histograms will follow exponential distributions, yielding time constants for folding and unfolding. In relation to fast protein folding, single-molecule experiments retain their advantages in terms of the ability to differentiate between multiple states and their connectivities more easily. Ensemble experiments have the advantage that better (< 1 µs) time resolution already can be achieved, naturally important for fast protein folding studies.

Both types of experiments can detect more complex mechanisms, revealing additional states occupied during the folding process. When the barriers connecting these are >> RT, we label them as “intermediates.” When the barriers connecting the states approach RT, we label them as “landscape roughness” and speak of a protein folding downhill. This is not an either-or distinction, but a gray scale of more-or-less separable time scales (larger barriers = longer time scales of interconversion). Very recently, fast folding experiments and simulations are making forays into this area,^{25, 26} which was already studied extensively by observing slowly interconverting “intermediates” as long ago as the 70s.²⁷

Simulations

Protein folding can be simulated in full detail using powerful computers.²⁸ In these simulations each atom of a protein is subjected to a potential, i.e. force field, which is determined by the bonds that the atom participates in, the angles that these bonds make with the neighboring atoms and the nonbonding pair interactions with every other atom in the simulation.¹⁸ Three major approaches have emerged to extract long timescale information: long single trajectories with recurring folding/unfolding events observed for a single protein,⁷ multiple shorter trajectories that can be stitched together into an overall picture of folding,^{29, 30} and replica or sequential sampling methods that provide thermodynamic information from multiple ‘copies’ of a protein.^{31, 32} The simulation methods thus span a similar range of philosophies as the experiments.

In the near future, we will undoubtedly see the success of integrating experiment, simulation and theory spread from the current microsecond folders to millisecond and slower folders, and to other complex molecular systems that are currently too expensive to model, such as membrane proteins. These advances will be driven by further improvement of force fields and computational speed, and by new experimental techniques that provide time-resolved yet structurally rich information about folding, both in vitro and in more realistic solvation environments such as live cells. Structurally detailed comparison of computation and experiment in different folding environments brings about its own challenges. First, tying together multiple reaction coordinates from experiment and modeling into a coherent whole at an unprecedented level of structural detail is the next-level unresolved problem in vitro and in silico. Second, comparing results in vitro and in vivo will reveal how cells and organisms modulate the energy landscape to control the action of biomolecules and utilize both frequent (high population) and rare (high energy) dynamic phenomena optimally.

Energy landscapes and pathways

Simulation and experiment are connected by statistical mechanical models, often referred to as the ‘energy landscape picture’.^33–38 This energy landscape involves reducing most of the solvent degrees of freedom and most of the protein degrees of freedom (e.g. dihedral angles of the amino acids) to a small number of coordinates or ‘order parameters.’ There has been a lot of debate in the literature whether proteins fold down ‘one path’ vs. ‘on the landscape.’ Fast folding experiments and simulations show that both pictures are useful, depending on whether population or energy is considered to be the most important variable.

From a biological perspective, population is the most important variable. Proteins are classified into coarse-grained populations, such as ‘folded’ or ‘unfolded.’ Systems biology deals with such populations at the level of “A interacts with B.” This view is indispensable when the complexity at the molecular level is too great to treat in full detail. For example, there is much experimental and computational evidence that fast-folding globular proteins tend to populate a predominant path en route to the folded state.^{39, 40}

From a physics perspective, energy is the most important variable. Protein folding is characterized by an energy landscape. The folded ensemble lies low on this landscape, the unfolded ensemble high-lying in energy. There is much experimental and computational evidence from fast-folding globular proteins that many distinct low-energy states and paths for folding exist on such landscapes, and that different paths can be selected by protein engineering or by choice of solvent conditions.^41–43 Some paths temporarily ‘park’ proteins in traps,⁴⁴ while others make the folding process more robust by providing alternate routes.⁴⁵

Both views have their place in folding science. They are mutually consistent because population P is very sensitive to energy E. The two are related by the exponential Boltzmann factor, P~exp(-E/RT) (Fig. 1). For example, an alternative path just 3 RT above the minimum energy path contributes less than 5% to the observed population. That is not to say the 3 RT path is unimportant. First, in another mutant of the protein, it actually can be the lowest-lying path taken to the native state.⁴¹ Second, evolution is partly based on phenotypic selection of mutants, and low-lying paths are thus input for evolutionary variation of proteins.⁴⁶ Third, higher energy conformations visited by the protein during folding or unfolding may be important for signaling, catalysis or other functions by facilitating conformational rearrangement. The protein may access such conformations only rarely, but they are key to biological function.^{47, 48}

Figure 1.

Relation between populations and free energies of states. (A) The example free energy landscape has three wells. N is the compact helical native state, U is the expanded unfolded state containing residual helix, and B is the compact misfolded state rich in β-sheet. The sequence of states N-B-U or B-U-N depends on the choice of reaction coordinate. If the N-B barrier is high, there is a preferred path B-U-N. Therefore if only one reaction coordinate is chosen to describe the system, helix content would be better than radius of gyration. (B) The population in U is very small compared to B or N because U lies several RT above B and N. Clearly, this does not mean that U is not involved in the interconversion from B to N. By tuning the solvent condition or mutating the protein sequence in (C), it is possible to bring U to lower free energy so its population will be larger than B.²⁶ The nature of the populated non-native states preceding folding, and the actual paths taken, are sensitive to initial conditions.⁴¹ A dominant pathway is observed because population is exponentially sensitive to small changes of the free energy (Boltzmann factor). Two pathways are rarely going to lie at exactly the same free energy, although it has been observed.^{44, 45}

Fast folding proteins make it easier to see non-native conformations experimentally because speed implies smaller energy barriers and gaps, and therefore larger Boltzmann factors. Low-lying paths also make it easier for simulations to sample rare but important folding events (e.g. transition state passage⁴⁹) for direct comparison with experiments. Hence there has been a strong interest in studying small, fast-folding proteins in vitro and in silico. Experiment and simulation have now converged on the microsecond time scale, making fully quantitative comparisons possible for the first time. This quantitative convergence on the microsecond folding time scale is the focus of this perspective. The following sections are organized by a ‘Key concept,’ followed by conceptual ‘Elaboration,’ and finally ‘Support’ from the fast folding experimental and computational literature.

II. Approaching the speed limit from above and below

Key concept

The ‘speed limit’ of protein folding is the fastest time it would take a protein of certain size to fold on an energy landscape with the lowest possible activation barrier(s). The speed limit of folding for single-domain proteins of ~1 µs was established by T-jump and single-molecule fluorescence experiments as well as molecular dynamics simulations.

Elaboration

The chemical reactions of small organic molecules occur in picoseconds or faster, about the time required to make or break a chemical bond.⁵⁰ Although the solvent is intimately involved in these reactions through polarization, viscosity and other properties, we can think of small molecule reactions by using the gas phase formalism of transition state theory because the solvent is not altered in a fundamental way during a reaction. While the crossing of the free energy barrier by an individual molecule takes only picoseconds, the activated rate coefficient k_a=τ_a⁻¹ can be very small at room temperature: barriers often exceed E_a=100 kJ/mol, so the probability of reaching the activation energy, proportional to the Boltzmann factor exp[-E_a/RT], is very small.

Usually the fast barrier crossing dynamics and the slow activated reaction kinetics occur on well-separated time scales, the molecular time scale τ_m and the activated time scale τ_a: ^†51

$$t_a=t_m{e}^{+E_a/RT}>>t_m.$$ [1]

Not so for protein folding. Multiple weak interactions such as hydrogen bond formation, hydrophobic exclusion of water molecules from the protein core, or salt bridge formation occur during folding. The polypeptide chain moves through a solvent that fully participates in these interactions and contributes a large fraction of the folding free energy through its own reorganization. Thus it is almost surprising that folding can be treated as a series of ordinary chemical reaction steps, using a one-dimensional picture analogous to eq. [1], such as Kramers’ theory, simply by substituting “G_a” instead of “E_a” in equation [1].

The separation of time scales between molecular time and activated time is certainly not as large for folding as it is for most small molecule reactions, nor is coarse-graining to one reaction coordinate as accurate. Nonetheless this picture is useful as a starting point. When G_a → 0 and the two time scales meet at the ‘speed limit,’²¹ the Kramers analog of eq. [1] no longer provides a satisfactory description of the folding process. There are many reasons why τ_m in eq. [1] should be picked much slower for proteins than for small molecules. For example, folding requires large-amplitude polypeptide chain motions through a viscous solvent. Also, polypeptides have many coordinates, so numerous unproductive motions orthogonal to the chosen reaction coordinate decrease the apparent diffusion coefficient of the protein along that reaction coordinate.

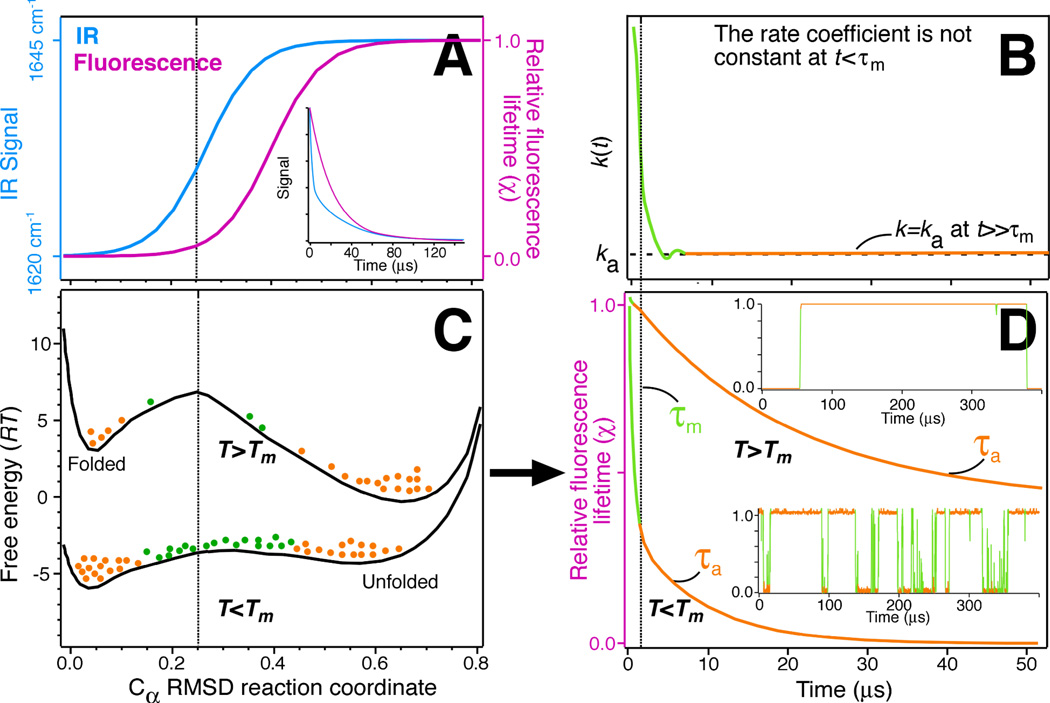
τ_m is the minimum time that must elapse before an activated reaction can be described by eq. [1] with a constant rate coefficient k_a=τ_a⁻¹. To visualize this statement, consider Fig. 2C. The barrier of the upper free energy profile is large, so a negligibly small population (green) of protein is pre-activated. When the reaction is started by jumping the temperature and tipping the free energy profile a little, the tiny green population does not contribute much to the kinetics. Rather, the observed kinetic trace results from slow interconversion of the large orange populations (folded and unfolded) over the barrier, yielding an exponential decay signal with time constant τ_a in Fig. 2D. Now consider the lower free energy profile in Fig. 2C. Its low barrier supports a large pre-activated population of protein (green). The moment the temperature is jumped and the profile is tipped, these proteins react promptly in time t<τ_m, giving rise to a very fast decay of the kinetic trace in Fig. 2D. The orange population has to be activated and kicks in much later, again folding with rate coefficient k_a. Thus the ‘low barrier’ kinetic trace in Fig. 2D has two phases, a fast one below t=τ_m (green), and a slow one (orange). It is as though the rate coefficient k is really large when t<_m, and then drops to a constant value of k_a. This is illustrated in Fig. 2B.

Figure 2.

Folding from activated to downhill, using WW domain experiments and simulations as an example. (A and C) The bottom shows schematic free energy profiles⁷,⁴⁹ along the C_α-RMSD reaction coordinate at temperatures below and above the melting temperature T_m. Protein populations in folded/unfolded minima (orange) and near the barrier (green) are shown as dots. The top (A) shows two probe signal profiles. They increase monotonically with reaction coordinate, and can therefore serve as experimental reaction coordinates. Different probes progress differently as the protein folds,⁴⁹ yielding probe-dependent kinetics particularly when the barrier is low and the protein population samples the transition region (vertical dashed line). (B). On the molecular time scale τ_m (vertical dashed line) the rate coefficient is not a ‘rate constant,’ but depends on time:⁵¹ pre-activated population (green in C) reacts promptly, much faster than population that needs to be activated (orange in C). Only later does the rate coefficient ‘settle down.’ (D) In the example, at T>T_m the pre-activated population is negligible, and exponential-decay kinetics with a ‘slow’ time constant τ_a is observed. At T<T_m, the pre-activated population is large, and a prompt phase precedes the ‘slow’ exponential-decay kinetics. The insets in (D) show corresponding single molecule traces: For a high barrier (T>T_m in the example), the activated protein (green), is sampled rarely. For a low barrier (T<T_m), the activated protein is sampled frequently. In essence, there are always pre-activated proteins that fold promptly downhill at the ‘speed limit.’ If the barrier is large, this population is unobservably small due to the Boltzmann factor. If the barrier is small, the population becomes easy to observe.⁸⁵ The terms ‘molecular time,’ ‘speed limit’, ‘transition state transit time,’ ‘downhill folding time’ refer to the same time scale, but are not identical. Also, the decay in (D) at t<τ_m is not necessarily an exponential with time constant τ_m,⁸⁷ although frequently fitted as such.^{49, 85, 100}

Another way of thinking about it is as follows: there are always some proteins (green) that fold downhill when a folding reaction is initiated. When the barrier is large, those proteins are an invisibly small fraction of the total ensemble. However when the barrier is small, they make an easily detectable contribution to the signal. In terms of single molecule traces (Fig. 2D), this is also evident: a fast-folding protein spends a much larger fraction of the time making transitions (related to τ_m), whereas a slow-folding protein spends most of its time waiting between transitions (related to τ_a).

The ‘molecular time,’ the ‘transit time’ to diffuse across the transition region, and the ‘speed limit’ are related concepts, although defined differently. The ‘speed limit’ of protein folding is the fastest time it would take a protein of certain size to fold on a free energy landscape with the smallest possible barrier. For most of the fast-folding proteins the speed limit is estimated to be on the order of 1 µs. The ‘transit time’ would be about twice τ_m because a successful diffusion to the barrier takes about as long as the diffusion away from the barrier. Exactly how long it takes a protein to transit across the activated region of the free energy depends on the computational or experimental observable (reaction coordinate) chosen to monitor the crossing process (Fig. 2A). For this reason we will not distinguish τ_m, transit time and ‘speed limit’ here. A variety of scalings have been proposed for the ‘speed limit:’ a logarithmic scaling with absolute contact order (which increases with protein size and complexity by measuring the length scale of non-local contacts between amino acids),⁵² and an inverse scaling with sequence length.²¹

Since a protein cannot fold faster than the elementary steps that are required for structural assembly, much effort has been directed at identifying the speed of such elementary steps: loop formation in the unfolded state^53–55, nucleation and growth of secondary structure,^{13, 56–61} and internal friction that controls the dynamics of a collapsed polypeptide chain^62–64. We consider an example of each in turn in the Support section.

Support

Loop formation in the unfolded state was one of the first folding events to bridge the gap between experiments and simulation. For example experiments on Cys-(Ala-Gly-Gln)_k-Trp peptides, where k ranged from 1 to 6, yielded the time constants for loop formation probed by Trp quenching by Cys ranging from 40 to 140 ns.⁶⁵ These experiments were simulated for k=1,2⁶⁶ and the time constant for contact formation between Cys and Trp of ~10 ns was found, faster than determined experimentally. Based on the simulations it was concluded that the rate of loop formation is reaction-controlled, not diffusion-limited.

Several recent studies of α-helix formation are especially noteworthy because of the remarkable time resolution that has been achieved experimentally and because of increased reliability of the modern force fields. To study secondary structure formation, Ma et al. developed an ultrafast temperature jump instrument.⁶⁷ They used this setup to measure ultrafast dynamics of α-helix formation of a 5-residue peptide called W₁H₅, which consisted of a tryptophan and a histidine connected by three alanines, Ac-W(A)₃H⁺NH₂.⁶⁸ They found that the dynamics of α-helix folding after a temperature jump involved two time scales: a fast time scale with a time constant of ~450–850 ps and a slower process with a time constant of ~3.6–5.3 ns with faster kinetics corresponding to the higher temperature for both time scales. The authors attributed the fast time scale to the annealing of the folded structure, while the slow time scale was assigned to the diffusion to a collapsed state. These results were later investigated computationally by De Sancho et al.⁶⁹ using replica exchange molecular dynamics simulations with AMBER ff03w force field. They found that their results were in good agreement with experiment because even though multiple phases could be extracted from the computational model, the dynamics could be approximated well with a double-exponential function. However, the authors came to a conclusion that the slow time scale observed in experiments was most likely due to the shrinking of the helical peptide at the C-terminus and interconversion within the collapsed ensemble was responsible for the fast time scale. Helix nucleation, which is defined in this work as the organization of three consecutive amino acids into a helical geometry, was still proposed to occur on the order of 20–70 ns. A similar time constant for helix nucleation is also supported by several other studies but it is important to note that helix formation time scales reported in the literature vary from tens of nanoseconds to several microseconds because of indirect probes and different model systems used.^{57, 70, 71}

Although β-hairpins are generally thought to fold more slowly, very recent work has shown that they can also zip up from both ends on a sub-microsecond time scale.⁷² Even β-hairpin peptides with more complex kinetics, such as the tryptophan-rich 12-mer called trpzip, have fastest experimental time scales on the order of a microsecond.⁷³ Snow et al.⁷⁴ did a comparison between simulations and temperature jump measurements of trpzip variants. They found reasonable agreement between experiment and simulation for 2 out of 3 variants that they studied. The third variant had a propensity for kinetic trapping, which indicated the need for more accurate potential energy functions.⁷⁵

After a protein reaches a compact state, its motions become limited not only by diffusion through the solvent, but also by the internal interactions of different parts of the polypeptide chain. These interactions slow down the folding process by constraining the torsional angles of the protein chain and preventing it from reaching the native state efficiently. The internal friction concept originates from polymer physics.⁷⁶ Schuler and colleagues have used single-molecule FRET and correlation analysis to quantify unfolded state dynamics and internal friction in unfolded proteins.^{77, 78} They studied a small cold shock protein from Thermotoga maritima called Csp and found that the effects of internal friction are less significant at high denaturant concentration when the protein is expanded but become more pronounced at lower denaturant concentrations when the protein is collapsed. Additionally, they investigated internal friction in two intrinsically disordered proteins (IDP) and discovered that internal friction depends on the sequence of amino acids that constitute the protein and also on the charge repulsion between amino acids, which is an important consideration for IDPs. The small protein trp-cage also illustrates the application of internal friction ideas to experiment and simulation. Qiu et al. ^{79, 80} found a linear dependence of the observed rate constant after the temperature jump on solvent viscosity η_s in correspondence with Kramer's theory, k_obs⁻¹= a + bη_s. A linear fit to the data does not extrapolate to zero but rather a~700 ns. They concluded that solvent viscosity controls protein folding when ·_s > 100 P⁻¹ (viscosity of water at 293 K is 1 cP = 100 P⁻¹ = 1 mPa•s), but below that value the process of folding is governed by other factors including intra-chain diffusion. They argued that the fact that it is the time scales and not the rates that are additive means that the two reaction control mechanisms are sequential. Zagrovic et al. did Trp-cage simulation in generalized Born/surface area (GB/SA) implicit solvent at different solvent viscosities (from as high as that of water to as low as 10⁻⁴ times that of water).⁸¹ They found a k_obs⁻¹ ~ η_s relationship at viscosities 10 P⁻¹ < η_s < 100 P⁻¹ and k_obs⁻¹ ~ η_s^1/5 power law for smaller viscosities. They concluded that low viscosity MD cannot be used to extrapolate the rates of protein folding using the normal Kramer’s scaling of k_obs⁻¹ ~ η_s. The approaches in this example agree that viscosity must be corrected to account for the protein acting as its own solvent. They differ in what description is best; as discussed in section IV, such differences can arise from the ambiguities inherent in coarse-graining folding from a high dimensional process to just one reaction coordinate.⁸²

Chain rearrangement times and relaxation of unfolded states provided the first indirect estimates of the ‘speed limit’ value of τ_m.^{83, 84} The first direct measurement of τ_m was an ensemble T-jump experiment on lambda repressor fragment.⁸⁵ These experiments directly observed the theoretically predicted settling of the rate coefficient into a constant value at t>τ_m, after which two-state folding could be described by a constant rate coefficient k_a and a single-exponential decay. It was shown by T-jump experiments for lambda repressor (α-helix bundle) and WW domain (a three-stranded β-sheet) that the 1 µs molecular phase accounts for more and more of the kinetic amplitude when the protein is stabilized. Simulations of Fip35 WW dynamics on a one-dimensional potential surface⁴⁹ derived from single-trajectory MD simulations⁸⁶ that observed many folding/unfolding events were fully consistent with the experimental results. It was also shown that the transit process is heterogeneous because a stretched exponential is required to fit the short time relaxation dynamics of proteins when high signal-to-noise is achieved in experiments.⁸⁷

Initial single-molecule experiments were not successful at obtaining a firm value, but were able to show that τ_m < 250 µs,⁸⁸,⁸⁹ an upper bound consistent with ensemble measurements.^{49, 85} Single-molecule detection of the transit time for folding is an important but challenging task: important because single-molecule experiments can examine heterogeneity of the transition state ensemble in great detail, and challenging because a statistically significant sample of photons emitted from FRET probes must be collected while the protein is diffusing across the barrier. For RNA folding, Neupane et al.⁹⁰ used an optical trap do determine the upper limit of the transition path time for several structures. They arrived at the instrument-limited value of ≤50 µs. However, when they analyzed one-dimensional free energy landscapes that resulted from their experiments, they estimated the transition path times of ~2–6 µs for most of their samples. In a very recent paper, Chung et al.⁹¹ report measurements of the transition path times of two proteins, which differ in their folding rate coefficients by 4 orders of magnitude. The transition path times only differ by a factor of 5 for these proteins: 2 µs for FBP28 WW domain and an upper bound of 10 µs for GB1. The result for FBP28 WW domain is consistent with ensemble measurements.⁴⁹ as well as simulations⁸⁶ of τ_m for the much faster-folding Fip35 WW domain.

III. Lowering the barrier to go downhill

Key concept

‘Downhill’ protein folding refers to scenarios where the protein folds without a significant free energy barrier (less than several RT) due to quasi-perfect cancellation between the enthalpy and entropy contributions to free energy along the whole reaction coordinate. Many examples of downhill protein folding have been seen experimentally and by molecular dynamics simulation.

Elaboration

One of the major confusions in the folding literature is between energy landscapes and free energy landscapes. The folding enthalpy ΔH(S,P) of globular proteins is generally negative above room temperature: folding becomes increasingly exothermic at higher temperature.⁹² The folding entropy ΔS(E,V) is also negative at sufficiently high temperature: the polypeptide chain organizes during folding. For this reason, a plot of contact enthalpy vs. chain entropy slopes like a funnel as the protein folds (Fig. 3C). The protein goes ‘downhill’ in the funnel-shaped enthalpy surface. Due to non-native contacts or ‘traps’, the funnel is rough and does not go ‘downhill’ completely smoothly. In that way the population picture (traps, native states, etc.) and the energy picture nicely connect.

Figure 3.

Experimental signatures of downhill folding upon protein stabilization: only the fastest-folding, most stable mutants of lambda repressor fragment have a significant population undergoing prompt reaction (the molecular phase shown in Fig. 2D). (A) The measured molecular phase amplitude increases smoothly when the activated rate k_a increases towards the molecular rate k_m ≈ 1 µs⁻¹ (Yang & Gruebele; ⁵² Liu & Gruebele (1) and (2); ^{52, 168} Ma & Gruebele⁸⁷), as predicted when the free energy barrier approaches RT (downhill folding).¹³⁷ (B) The kinetics of mutants that are relatively unstable can be fitted by slow single-exponential kinetics upon temperature jumps (orange area); their activation barrier is too high to carry a measurable pre-activated population. Mutants that have T_m > 60 °C show an additional fast molecular phase (triangles) because their barrier is low enough so there is a promptly reacting (downhill folding) protein population (C) On the left: The normalized enthalpy of the polypeptide chain generally decreases when the configurational entropy s_c decreases: as favorable contacts are made, the polypeptide chain moves less freely. Folding is ‘downhill’ in enthalpy (folding is an exothermic reaction), resulting in an ‘enthalpy funnel,’ but this is not what is meant by downhill folding. On the right: The free energy G can be computed from the enthalpy and entropy as a function of an arbitrarily chosen reaction coordinate x by evaluating H and S at x and averaging over all other orthogonal coordinates. ‘x’ could be the radius of gyration, distance between two FRET labels, etc., and is normalized from -1 (unfolded) to 1 (native) here. Of course, a carefully chosen set of coordinates x,y,^… provides a more complete description of a reaction as complicated as folding than just a single coordinate x. The free energy has a barrier (orange) when the enthalpy does not funnel the protein towards the native state efficiently enough to offset the decreasing entropy (orange funnel on the left). The free energy is downhill (green) when the exothermicity of the reaction is sufficient to offset the loss of entropy everywhere along the reaction coordinate (green funnel on the left). The protein then folds with the molecular rate k_m instead of the slower rate k_a (black circle in (B)). In intermediate cases both rates can be measured simultaneously (triangles+circles in (B) connected by a dot, or T<T_m trace in Fig. 2D), allowing an absolute determination of the free energy barrier height.^{49, 52, 85, 87, 100, 168}

‘Downhill’ in the enthalpy funnel is not at all the same as the downhill folding discussed in the literature, which relates to free energy landscapes, not energy landscapes. In the laboratory, measurements are usually made at constant temperature and pressure, so the Gibbs free energy of folding ΔG (P,T)=ΔH-TΔS is the natural thermodynamic potential obtained from the enthalpy by Legendre transform.⁹³ The negative ΔH and positive –TΔS tend to cancel, leading to very small free energies for folding, on the order of 0.5 kJ/mole per residue (Fig. 3). Entropy favors unfolded polypeptide conformations, enthalpy favors folded ones, leading to free energy minima for the unfolded and folded states. In-between, cancellation is imperfect, producing free energy barriers and intermediate states such as for example traps stabilized by non-native contacts. However, the enthalpy-entropy cancellation is quite good, which is why protein folding reactions are so fast at room temperature compared to many other chemical reactions.

When the cancellation of ΔH and ΔS is further optimized (by protein engineering or natural evolution), even the free energy goes downhill. That is downhill folding (Fig. 3C). We define reactions with barriers < 3 RT (about 7.5 kJ/mol) as downhill or incipient downhill folding reactions. The choice of “3” is somewhat arbitrary, and corresponds to a P≈5% Boltzmann population at the barrier top, detectable by an experiment with a signal to noise of about 20:1. In other words, the fundamental assumption of transition state theory that the barrier-top population is negligible, has been violated by 5%. At 1 RT, the violation is over 25%. (P = exp(-ΔG/RT)/Δ, where Δ is the partition function.)

The discovery of natural and engineered microsecond folders is half of the equation that allows a direct comparison of experiment with simulations on the microsecond time scale. The other half is the improved force fields^94–96 and faster computing that allow not just the barrier crossing itself, but the slower kinetics (the waiting for the barrier to be crossed) to be simulated. Improved force fields are of key importance here: computational power is useless if a protein folds into the wrong state, or even unfolds from its native state, as was the case with early force fields.

Support

We begin our comparison with a ‘long single-trajectory study.’ Lindorff-Larsen et al.⁷ simulated 11 small proteins (and the hairpin chignolin) previously studied by fast protein folding experiments. The largest of these proteins, the 80-residue lambda repressor fragment, approaches the average size of globular protein domains (~120 residues). They observed at least 10 folding and unfolding events for each protein. For these 11 proteins much secondary structure formed before the longer-range native contacts. They found that across the protein set, the unfolded state contained residual secondary structure (16% α-helices and 5% β-sheets). Residual unfolded structure is an important feature that promotes fast folding (section V).

For 9 out of 11 simulated proteins, folding events could be clustered into 2 to 3 folding pathways. These pathways shared 60% of native contacts on average, so to that level of accuracy, each protein folded on ‘a pathway’. For the two remaining proteins (NTL9 and G), several distinct folding pathways were identified based on the order of β-sheet formation. Even proteins that preferentially formed one β-turn first (WW domain)^{86, 97} still have minority populations (10–20%) forming the other turn initially. These results again highlight the importance of energy vs. population (Boltzmann factor). The ensemble of low-energy folding pathways was heterogeneous, but with sufficient coarse-graining most of the population preferred one or two paths. As another example, the lambda repressor fragment simulated by Lindorff-Larsen et al. has been shown experimentally to fold with or without highly helical intermediates, and with or without rapid collapse to a small radius of gyration, depending on mutations and solvent condition.^{41, 42} The same final fold formed in rather different ways, but each specific mutant or solvent condition had a preferred path. As discussed earlier, the presence of multiple paths on the energy landscape may have evolved to confer robustness to the folding process, even if a specific path carries most of the population under specific circumstances.

All 11 proteins simulated by Lindorff-Larsen et al. had a compact and native-like transition state ensemble with a folding barrier < 4.5 RT. BBL, protein B, and homeodomain even folded without an identifiable barrier. This result highlights the near-perfect cancellation of enthalpy and entropy that leads to low-lying paths on the free energy landscape (but see the caveats below). For two of the computed proteins, absolute barrier heights have been determined from experiment by comparing the molecular time τ_m required to equilibrate barrier-top population with the time τ_a required for the activated reaction to occur: ΔG_a/RT=ln(τ_a/τ_m).⁸⁵ For lambda repressor, experiments showed that the amplitude of the molecular phase increases when the protein is stabilized,⁸⁵ in accord with kinetic theory.⁵¹ For the D14A/Y22W/G46,48A mutant, a barrier of ΔG^†=1.5 RT was determined, exactly the value later extracted from molecular dynamics⁷ using the method developed by Hummer.⁹⁸ Microfluidic mixer experiments by DeCamp et al.,⁹⁹ where the bias towards the native state was stronger than in T-jump experiments, observed complete downhill folding of a lambda repressor fragment. For the WW domain variant FiP35, experiments by Liu et al. measured an absolute barrier height of 3.3 RT,¹⁰⁰ whereas the folding/unfolding trajectories simulated an unfolding free energy of ΔG^†= 3.5 RT.⁸⁶ Reasonable to excellent agreement is also obtained in other cases. Thermodynamic studies of a protein BBL mutant found no barrier,¹⁰¹ in perfect agreement with the coarse-grained free energy surface computed by Lindorf-Larssen et al.. Qiu et al. used laser temperature jump to determine that the folding time constant of trp-cage is 4.1 µs, which corresponds to ~4 RT barrier.¹⁰² The folding time constant observed for trp-cage in simulations was 14 ± 4 µs.⁷ Zhu et al.¹⁰³ reported microsecond folding of α₃D, a de novo designed protein with folding time of 3.2 ± 1.2 µs at ~323 K. The folding time reported by Lindorff-Larsen et al.⁷ was 27 ± 8 µs.

Although the discrepancies between molecular dynamics simulations and experiments could arise due to imperfections of force fields or differences in conditions (solvent, temperature), these discrepancies could also result from the inability to describe experiment and modeling with a common reaction coordinate (Fig. 2A). Hence an important caveat: the time scale τ_m depends on the probe signal (reaction coordinate) used. A one-dimensional picture does not capture the full complexity of the folding process at the experimental and computational level of resolution now possible (section V). It should also be noted that much progress is still required to make simulations more accurate. For example, the computed melting temperatures of proteins are generally too high. Nonetheless, it is quite remarkable that a single force field could fold 11 proteins in quantitative agreement with some experimental results, indicating significant progress in MD force field development.

Designed peptides have been important testing grounds for simulations, and recently simulations have made predictions for re-designing fast folders. The first direct comparison between experimental and computed folding rates and equilibrium constants was for the peptide BBAW,²⁹ a design based on BBA5 by Imperiali and coworkers¹⁰⁴ that added a tryptophan probe. Here the simulations were of the ‘multiple shorter trajectories’ type. 700 µs of total simulation time²⁹ yielded a small number of folding events, in agreement with an experimental T-jump folding time of ca. 1.7 µs. More recently, Bunagan et al.¹⁰⁵ used biased Monte Carlo replica exchange methods (BMCREM) to design a mutant of the 20-residue trp-cage (P12W) called Trp²-cage, which folded in 1 µs and was ~15 K more stable than the parent protein. Piana et al.⁹⁷ used a single multiple folding/unfolding trajectory to design the GTT mutant of Fip35 WW domain, which folded about three times faster than the original FiP35, itself a designed construct:^{100, 106–108} τ_obs = 3.7 ± 0.4 µs vs. τ_obs= 13 ± 4 µs. The increase in folding speed was attributed to the preorganization of the unfolded state, again highlighting the importance of residual unfolded structure (section V).

We have proposed that replacing charged functional residues by more hydrophobic residues, and longer functional loops by shorter loops, will re-design a protein towards downhill folding.^{52, 100, 106–110} This design principle of function frustrating efficient folding has been used to design faster-folding WW domains^{106, 111} and lambda repressors.⁵² The same idea has also been put forward by Gai and coworkers: five mutations of an albumin binding domain were predicted to increase the hydrophobicity of the protein in a favorable way to increase the folding speed.¹¹² They found a linear relationship between the log of maximal folding rate and mean hydrophobicity. Wang et al. show that a K5I/K39V mutant of this protein has a folding time constant of only 1.2 µs.¹¹³ They argue that this protein approaches the speed limit is because of its highly optimized hydrophobicity.

There is now a rich interplay between experiments and simulations.^{97, 114–116} We consider just one more model system: the C-terminal domain of chicken villin headpiece. Depending on the variant, this protein contains 35 (HP-35) or 36 (HP-36) amino acids, which arrange into a three-helix bundle in the native state. HP-36 holds the distinction that Duan et al.⁸ ran the first all-atom ≥1 µs single-trajectory explicit solvent 300 K simulation ever. Freddolino et al.¹¹⁷ did explicit solvent MD and identified a trapped state. On the experimental side, Kubelka et al.¹¹⁸ introduced a F35A mutation to test Pande's prediction¹¹⁹ that mutating out F35 would increase the folding rate by eliminating the off-pathway intermediate in which F35 docks into the hydrophobic core. Buscaglia et al.⁵³ used quenching of the triplet state of tryptophan to study the dynamics of C-HP-35. “C” stands for cystein that was introduced into the protein as a quenching probe. The results showed two phases, consistent with previously reported T-jump data. Piana et al.¹²⁰ very recently did an autocorrelation analysis of folding of HP mutants and found – in good correspondence with experiments – two phases with time constants of ~100 ns and ~5 µs. They also estimated the pre-exponential factor to be τ_m ~ 0.5 µs to 1.5 µs, in good agreement with ‘speed limits’ measured for lambda repressor and WW domain.^{49, 85}

As computing power has improved to reach experimental downhill folding timescales, so force fields have improved to reach experimental accuracy. Villin headpiece subdomain has recently been used to compare four molecular dynamics force fields.⁹⁶ The experimental folding rate was reproduced well by all four force fields, and all force fields folded villin into a native-like state. However, the flux through different folding pathways depended on the force field, indicating that the unfolded state and the pathway are not as robust as the folded state (Fig. 4). Thus force fields are good at describing the lowest energy state, but higher lying states, important for protein functions and for denatured protein structure, are not as well described. This is at least partly so because the current goal is for force fields to produce native-like states; higher energy states will become the next grand goal, opening the door for better quality simulation of function (as opposed to just the native structure).

Figure 4.

Systematic benchmark studies of empirical force fields to improve their performance in folding simulations are now more frequently appearing in the literature.^{94, 169–174} (A) Various force fields were tested by Lindorff-Larsen et al.⁹⁵ and a score based on the performance of the force field against the chosen model systems was devised such that the lower score indicates better agreement with experimental data. The plot shows the improvement of force fields over time. (B) Piana et al.⁹⁶ used four different force fields to fold villin headpiece. Although all simulations arrived at the correct native state, the folding mechanism depended on the force field used. The panel shows that the flux through different reaction pathways (123 etc. is the order in which the three helices of villin headpiece form) is a function of the force field that was used.

The other main challenge in molecular dynamics simulations has been the insufficient sampling time. The problem of sampling has been overcome to some extent, as nowadays resources exist to simulate a protein for up to milliseconds in atomistic solvent. Long simulations allow researchers to identify inaccuracies in force field parameterization and sometimes even fix these issues. For example, Freddolino et al.⁹⁴ simulated Pin1 WW domain, a three-stranded β-sheet, using the CHARMM22 force field with CMAP corrections. In their simulation the protein formed α-helical structures instead of the crystallographic native state. They used the deactivated morphing methodology to determine whether these structures were kinetic traps or thermodynamic inaccuracies in the force field.¹²¹ They came to the conclusion that the force field parameterization of linear vs. bent hydrogen bonds was imperfect and favored α-helices over β-sheets by 15–30 kJ/mol.

Mittal et al.¹²² also used a force field that was biased towards α-helices, AMBER ff03, to fold villin headpiece HP-35, a 3-helix bundle. Then they introduced a correction to the backbone potential within the force field (making it AMBER ff03*) and managed to fold Pin WW domain with it, an all- β-sheet protein, which was the first time for a β-sheet protein to be folded with a version of AMBER ff03 force field. Lindorff-Larsen et al.⁹⁵ used extensive single-trajectory simulations to systematically analyze the force field quality. They did simulations on folded proteins, peptides with certain secondary structure propensities and two proteins that have α-helical and β-sheet native states, villin and GTT Fip35 WW domain. They concluded that force fields are getting better with time and that at present AMBER ff99SB-ILDN and CHARMM22* force fields reproduce experimental results better than others (Fig. 4).

Although currently the results of molecular dynamics simulations still depend on force fields and no one perfect force field that the community has agreed on exists, these discrepancies also highlight that energy differences between competing folding pathways are small: while one force field or another may put the wrong path lowest in free energy, it in fact is one of the lowest free energy paths in reality. Certainly examples are known where one protein sequence can fold into a more β-rich or α-rich functional state.¹²³ Thus even nature flips pathway energies as a function of solvent conditions or temperature.

IV. How many reaction coordinates do we need?

Key concept

The number of reaction coordinates that will be sufficient to understand the folding of a protein depends on the level of coarse-graining that one is willing to tolerate. Better reconciliation of experimentally and computationally accessible reaction coordinates is an important goal for the near future.

Elaboration

A question that dogs the field of protein folding in general, and the direct comparison of microsecond experiments and simulations in particular, is the nature and number of reaction coordinates best suited to describe the folding process. Early simulations showed that one coordinate cannot provide a full description even for small peptides:¹²⁴ there may be a predominant pathway, but it is only that – predominant. Likewise even some millisecond or slower experiments demonstrated parallel paths,⁴⁴ a clear sign of multiple reaction coordinates.

How many coordinates? This has been a contentious question, but the answer for a complex process like folding is clear: the number depends on the level of coarse-graining at which we want to understand the process. At one extreme, every backbone and side-chain torsion angle (we can safely ignore stretching and bending motions to a first approximation) is a coordinate. At the other extreme, one predominant coordinate is singled out, leading to eq. [1]. For example an experiment may show with 20:1 signal to noise ratio that some secondary structure forms first, followed by collapse to a small radius of gyration, followed by burial of tryptophan, in that order. We can draw a single coordinate axis, and even put quantitative numbers on it.⁸⁶ The one-dimensional view of protein folding is currently very common in the literature. The coarse-grained picture is very useful because Kramer’s theory does apply reasonably well to many proteins at a low level of resolution (see section II). Nonetheless, both single^{7, 86, 125, 126} and multi-trajectory^{29, 119, 127, 128} simulations have shown that the overall folding process is built up from many faster interconversions on a multidimensional energy landscape.

What coordinates? This difficult question is currently the greatest divide between experiment and simulation. “Fraction of native contacts” is a perfectly acceptable reaction coordinate that can be computed easily. However, no experiment will ever measure it by its literal definition (residue pairs with direct side chain contact in the native state that approached within an arbitrarily chosen cutoff distance, and are assigned a weight of 0 or 1 based thereon). “Circular dichroism at 222 nm” is a perfectly acceptable reaction coordinate for average helix content in an all-α-helical protein that can be measured easily. However, not even quantum-based models are likely to accurately compute it any time soon. Some progress has been made to cross-validate coordinates between fast folding experiments and simulations, including fluorescence vs. fluorophore solvent-exposed area,^{25, 97} or two-dimensional infrared spectra and β-sheet content.^{129, 130} This process needs to continue so we can: 1) quantitatively compare computed and measured reaction coordinates to provide a satisfactory description of folding; 2) determine how linearly independent different coordinates are from one another, so the most informative sets are computed or measured; 3) understand functional excursions of the folded state towards less/differently folded states in terms of rigorous coordinate sets to better describe higher energy functional states.

What about topology? It has been clear for some time that it would be desirable to describe folded structure in general terms rather than via atom-by-atom numerical coordinates.^131–133 Many folds are intuitively related, even if they differ in quantitative detail, and structural classes and families have been identified.¹³⁴ In folding science, the term topology has been used in different ways, not necessarily making a rigorous connection with its mathematical meaning. A useful set of criteria for distinguishing and identifying topologies has been proposed in terms of Gauss integrals,¹³⁵ and has been applied to fast folding simulations.⁷ Gauss integrals are ideally suited to describing how a worm-like chain intertwines with itself. Other parameters such as absolute contact order have also been useful in merging protein size and fold complexity into a single number.¹³⁶

Microsecond folding experiments and simulations have shed light on the aforementioned issues. The use of multiple probes in experiments,^{43, 73, 87, 137} as well as hidden Markov analysis of multiple trajectories,^{32, 138–142} or single long trajectories⁷ all have shown that multiple low energy paths exist, although many of them are not highly populated due to their exponentially decreasing Boltzmann weight. (see the Support section for more information)

An arsenal of new experimental methods, including two-dimensional infrared spectroscopy^{129, 143–146} and resonance Raman^147–150 is now coming online. At the same time, molecular dynamics simulation provides a rich set of coordinate information at various levels of coarse-graining.^{138, 139, 142} The problem is that atomic coordinates are not sufficient to compute accurately experimental reaction coordinates such as circular dichroism at 222 nanometers (a stand-in for α-helix content). Other experimental reaction coordinates fare better, such as the radius of gyration, which can be computed accurately from simulations, including even a solvent correction.¹⁵¹ Yet others are in-between, such as a pairwise distance between FRET labels. The actual FRET-labeled construct is not usually simulated, but distance between the residues where labels are connected, coupled with assumptions about random rotational orientation, yield a proxy to experimental FRET. Only when multiple measured and simulated coordinates can be compared quantitatively, will folding science be able to take the next step towards a multi-dimensional description of folding. An important goal will be to establish fully quantitative correlations between measured coordinates and their computed stand-ins. For example, tryptophan wavelength shift (experimental) and tryptophan solvent exposed area (computed) will have to be compared over a wide range of different folded and unfolded proteins. Much experimental data is already available. Doing the many needed simulations is no longer outlandish with increased computational power and better force fields. Likewise, better stand-ins can be computed thanks to vastly greater computational power. For example, when many microseconds of trajectory for multiple fast folders are becoming practical, one could simulate the actual FRET construct and do orientational averaging over the dipole-dipole coupling. Another possibility would be to simulate many different protein mutants for rigorous comparison with mutation experiments. Such simulations are already coming out, for example for different WW domains,⁹⁷ different lambda repressor mutants,^{25, 126} and different versions of villin headpiece¹¹⁷. These results will settle many of the debates about the appropriateness of the Kramers' equation, or how well coordinate-dependent diffusion coefficients complement one-dimensional models to maximize their descriptive power of the folding process.

Support

Ma et al.⁸⁷ used two simultaneous probes, tryptophan fluorescence lifetime and the infrared amide I’ band to measure the relaxation of a lambda repressor mutant after a temperature jump. Fluorescence (λ~350 nm, τ_fl~ 3 ns) probes protein collapse around a single tryptophan residue, IR (λ~1650 cm⁻¹), probes overall helix vs. random coil content, providing two very different reaction coordinates. IR and fluorescence yielded different kinetics 9 K below the unfolding temperature T_m, but converged to identical kinetics at T_m. Ma et al. concluded that near T_m, lambda repressor fragment folded over a barrier: although IR and fluorescence are different experimental reaction coordinates, both switch from ‘native’ to ‘denatured’ on top of the barrier where population is small, and so both appear to change together. They concluded that 9 K below T_m, the free energy landscape switched to a downhill surface: without a barrier, the protein population passes at different times through the region where the IR and fluorescence probe switch. Ma et al. simulated these observations quantitatively with two-dimensional Langevin dynamics along the two experimental reaction coordinates. Working on the same protein, Dumont et al.⁴¹ measured the radius of gyration (R_g) or ‘compactness’ of lambda repressor using small-angle X-ray scattering, and secondary structure using circular dichroism in stabilizing solvent (45% ethylene glycol in water) at T = 245 K. They observed excessive formation of helical secondary structure before collapse for some mutants, concomitant collapse and secondary structure formation for others. Long trajectory simulations have indeed revealed a variety of folding mechanisms for different lambda repressor fragment mutants.^{7, 125} Again these results highlight that a predominant path usually exists for a mutant/solvent combination, but not for a specific fold topology.

Liu et al.⁴³ investigated folding kinetics of the designed protein α₃D¹⁰³ also by IR and fluorescence T-jump experiments (Fig. 5). The observed rate was nearly temperature-independent by IR, but increased with temperature when probed by fluorescence. They could not reproduce the experimental results with a reasonable diffusion coefficient by Langevin dynamics along just one reaction coordinate. A two-dimensional description yielded a much more reasonable diffusion coefficient. The result of Langevin dynamics simulations depends on the reaction coordinate used: different probes switch at different times during the folding process, and the diffusion coefficient D(x) is a function of position along the reaction coordinate x in coarse-grained pictures.^{52, 152} For the latter case, Best et al.¹⁵² found that D(x) varies significantly along a reaction coordinate that represents fluctuations, but is mostly invariant when a reaction coordinate like fraction of native contacts is used. Full MD simulations show that the folding barrier of α₃D below the melting temperature T_m is less than 2 RT along a C_α-RMSD reaction coordinate, but the simulations have not yet been analyzed in terms of reaction coordinates closely related to the experimentally measured ones (helical content by IR, tryptophan quenching by fluorescence lifetime).

Figure 5.

α₃D is a designed protein¹⁰³ for which a one-dimensional reaction coordinate cannot explain the probe-dependent kinetics using a reasonable diffusion coefficient.⁴³ (A) Structure of α₃D from PDB (2A3D). (B) A contour plot of the optimal two-dimensional free energy surface for α ₃D calculated using Langevin dynamics as described by Scott et al.¹⁷⁵ (C) Kinetic rates measured with infrared absorption spectroscopy are shown as black dots, fluorescence spectroscopy as red dots. The dashed (one-dimensional model) and solid (two-dimensional model) lines represent the fits of the data using Langevin dynamics, but the one-dimensional fit requires an unrealistic diffusion coefficient; diffusion coefficients of incorrect magnitude or with unusual coordinate dependence are a warning sign that the model underestimates the dimensionality of the dynamics. (D) Time traces of Q and C_α-RMSD for α₃D from Lindorff-Larsen et al. show strong correlation, but are not equivalent⁷. Q is the fraction of long-range native contacts. For the quantitative definition of Q see page 3 of Supplemental Materials in reference ⁷.

V. Unfolded, trapped, misfolded

Key concept

Proteins did not evolve for stability or folding speed. They evolved to execute particular biological functions. Therefore, intermediates, partially unfolded proteins, and trapped non-native conformations that slow down the folding process should come as no surprise.

Elaboration

Proteins are evolved biological objects. They are not perfect at folding, but comprise a series of compromises: Many proteins have to fold to function, so their polypeptide chain must be tightly packed to confer stability. Yet with only a 20 amino acid alphabet, positioning of functional amino acids is not perfect,¹⁵³ so the polypeptide chain must be flexible to reach different functional states. Some proteins are disordered so they can bind/fold better.¹⁵⁴ Examples of proteins that exhibit functionality in the disordered state also exist.¹⁵⁵ It remains to be seen how disordered structures behave in the interior of living cells, where some of these proteins could be folded. For example, α-synuclein, a poster child for partly disordered proteins, is debated to be a well-folded tetramer in vivo.¹⁵⁶

Folding stability and speed can be at odds with protein function, and microsecond experiments as well as fast simulation studies have quantitatively illustrated this.¹¹¹ So it is natural for proteins to park ‘needlessly’ in traps from which they have to unfold before they can attempt folding again,¹⁵⁷ or to park in intermediates that slow down folding. ‘Needless’ refers to the folding process only, not to the function. In some cases, the states that are structurally intermediate between an extensively unfolded coil and the native state can be populated as part of protein function, or at least facilitate progress along a functional reaction coordinate. In other cases, difficult-to-fold parts of a protein could be the functional part.¹¹¹ In yet other cases, the trap may be a consequence of physical chemistry: for example, local β-sheet structure forms rather easily in denatured proteins,¹⁵⁸ and may simply be unavoidable even in the best evolved or engineered monomeric protein, as indicated by very recent studies.^{25, 26}

Another important conundrum of protein folding is particularly well illustrated by fast folders and simulations on them: residual unfolded state structure. It is no secret that denatured proteins are not random coils, but contain residual short range order (e.g. α-carbon dihedral angle distributions with native-like averages¹⁵⁹) and long range order.¹⁶⁰ Such residual structure can profoundly affect a protein’s propensity to misfold, or influence its folding speed. For example, many downhill folders probably have relatively compact denatured states with native-like residual secondary structure; mutants with denatured states closer to random coils may fold much more slowly. Experimentally, it is very hard to characterize denatured states or intrinsically disordered proteins because a wide distribution of structures needs to be quantified. Computationally these states are equally problematic because of sampling issues. Since it is much more difficult to characterize the unfolded state structurally, most of the molecular dynamics simulations that are intended to fold proteins assume the absence of residual secondary structure as the initial condition. In the absence of structural information about the unfolded state this assumption is not totally unreasonable: proteins are synthesized vectorially on the ribosome and at least the N-terminus of proteins tends to be disordered some of the time. On the other hand, many proteins unfold and then refold many times over during their life cycle in the cytoplasm, but these unfolded states are likely to contain much residual structure.

Support

In some cases, a simulation has been able to suggest an initial structural ensemble for fast folding experiments. For example, Ensign et al.¹²⁷ did simulations on the double-norleucine mutant of villin HP-35 in which the relaxation rate and the number of observed kinetic time scales depended on the starting structure. The simulations that corresponded most closely to the experimental results¹⁶¹ were initiated from a partially folded state (Fig. 6), which the authors suggested to be a good approximation of an experimentally relevant unfolded state.

Figure 6.

Various conformations of villin headpiece drawn from a simulation by Beauchamp et al.¹⁷⁶ The left-most conformation is the native state. Three structures in the middle broadly represent the unfolded state ranging from the partially disordered conformations that still resemble the native state to the significantly extended conformations with low residual secondary content. The right-most structure is a misfolded trap. Such traps lie off the predominant folding pathway.¹⁵⁷

Some experiments and simulations indicate that non-native states can have rather slow dynamics, as opposed to the homogeneous nature of a random coil. For example, Waldauer et al.¹⁶² used a microfluidic mixer to measure the intramolecular contact formation in the unfolded protein L and discovered that the diffusion coefficient in the absence of denaturant was very low. For this protein they proposed an upper bound for the folding speed limit of 20 µs, a much longer time scale than had been suggested previously²¹. Voelz et al.¹⁶³ made use of state-of-the-art computing methodologies by integrating the Folding@Home distributed computing system and calculations using graphical processing units to study the dynamics of the unfolded state of protein L (Fig. 7). They also compared the results of their simulations with Trp-Cys quenching experiments and applied polymer theory to rationalize their findings. These results agreed with experiment that intramolecular diffusion in the unfolded state of protein L is much slower than expected for a random coil and that point mutations had a significant impact on the unfolded state ensemble. These and other such findings¹⁶⁴ suggest structural complexity of the unfolded state and the importance of non-native structure in the folding process.

Figure 7.

At the top: Contact map of protein L.¹⁶³ The blue squares indicate residues that are in contact in the native state. The structure of the native state (PDB: 2PTL) is shown at the bottom-left of the figure. Data for the contact map were generated using the CMA server at http://ligin.weizmann.ac.il/cma/). The grey scale contour map shows the average distances (0–2 nm) between all pairs of residues at 300 K as simulated by Voelz et al.¹⁶³ The red dots indicate the contact map for one of the conformations of the unfolded state from the simulation. The structure of this state is shown at the bottom-right of the figure. Clearly this unfolded state is not a random coil but a partially structured non-native conformation.

Non-native traps may need some time to escape to more extensively unfolded states, which then fold rapidly to the native state. A specific example of such non-native traps was provided by Bowman et al.²⁵ They discovered a slow (10 millisecond) time scale in the folding of a mutant of lambda repressor fragment, in addition to the known fast kinetics. In the simulations, this slow time scale originated from non-native β-sheet-rich traps. Prigozhin et al.²⁶ observed a slow kinetic phase experimentally not with this mutant, but with a mutant differing only in one residue. It still remains to be discovered whether the experimental slow phase is due to β-sheet rich traps, as suggested by the simulations. But sequence-specific non-native structure clearly plays a role in this case also. If the slow phase in lambda repressor fragment does originate from compact β-sheet-rich structures, then the most likely explanation will be that the actual folding process (the interconversion between the native state and an extensively unfolded state) is fast, but getting out of compact off-pathway ‘intramolecular amyloid’ traps is a slow process.

Returning one last time to the importance of pre-organized structure for folding, Piana et al. recently were able to predict an interaction in FiP35 WW domain that slows down the folding process.⁹⁷ They analyzed long single trajectories with multiple folding/unfolding events and hypothesized that strand 3 of hairpin 2 of Fip35 WW domain, which does not make significant contacts with strand 2 of hairpin 1 in the transition state ensemble, could be engineered to form a more extended structure and dock against hairpin 1 early in the folding process thus stabilizing the transition state and accelerating the folding process. They proposed three mutations within strand 3 based on the Ramachandran angles of the amino acids in Fip35 WW domain. The new protein was called GTT by the names of three amino acids that were mutated into the Fip35 variant. Simulations of the mutant showed that it folded approximately two times faster than Fip35 WW domain. These results were validated by temperature jump experiments⁹⁷ showing that the observed relaxation time for the GTT mutant was ~3 times faster than that of Fip35. The lessons we will learn from protein engineering and design driven by simulations will likely be instrumental in further improvement of force fields and will yield new model systems to continue the dialog between fast protein folding experiments and simulations.

VI. Challenges met and challenges to come

Experiments and simulations of protein folding have come together on the microsecond time scale, helping protein scientists to understand folding in increasing detail. Even fast-folding proteins can visit a complex network of low free energy states,¹²⁷ but a predominant path often exists for a specific sequence in a specific solvation environment.⁷ Populations always look less heterogeneous than the underlying free energy landscape, thanks to the exponential Boltzmann factor relating population and energy.

As the next step, even more important than extending simulations to larger proteins and longer time scales, the time is ripe for a more rigorous comparison of simulation with experiments using consistent sets of reaction coordinates. Such comparisons will have to focus on more than one coordinate, so experiments can provide strong mechanistic constraints on simulations. Current force fields are approaching a level of quality where native states of small proteins can be obtained by direct physical modeling of the folding process, but not the specific mechanism by which they are reached. Correct mechanism involves the proper sorting of low-lying paths and states, highlighting again their important presence on the free energy landscape.

Although low lying states may be a nuisance in simulations, they are likely to play important roles. They may pre-pattern the functional dynamics of a protein as it explores higher energy states during function. Conformational selection or induced fit of enzymes would be a good example. Alternatively, such states may provide routes for protein evolution, which could switch alternate conformations or active sites into the lowest free energy position, creating whole new predominant folding pathways or function.

It will not be easy to achieve a quantitative comparison of folding simulation and experiment beyond rates or other highly averaged quantities because many experimental probes are simply too difficult to compute from classical trajectories. Downhill folding is a good example: the complex fast interconversions among multiple states seen in simulations of WW domain ‘underneath the surface’ of folding kinetics^{165, 166} are lumped into one ‘molecular time’ experimentally. One way to make progress is to find easily computed proxies for experimental reaction coordinates. For example, the tryptophan fluorescence wavelength of a large number of native and denatured proteins with variously exposed single tryptophans could be correlated with tryptophan side chain solvent exposure, local solvent electrostatics and other parameters easily extracted from simulation, to come up with reliable multi-parameter correlations between experiment and simulation. Pioneering attempts in this direction have been made already,¹⁶⁷ but were not fully successful in the past because of the enormous computational requirements, now at hand. Conversely, it behooves experimentalists to develop faster ways to probe radius of gyration, FRET distance, and other variables that are easily and reliably computed. We are entering an era where simulations can run in a reasonable time frame the same protein with different labels attached or in different solvent conditions, so apples can be directly compared to apples. From the perspective of connecting simulation with experiment, protein science is entering an exciting time.

Biographies

Maxim B. Prigozhin received his H. B. Sc. in Chemistry and Physics from the University of Toronto in 2009. He is currently a Ph. D. student in the Chemical Physics program at the University of Illinois at Urbana-Champaign under the supervision of Prof. Martin Gruebele. At Illinois, Maxim is developing state-of-the-art in vitro and ex vivo methodologies to investigate fast protein folding, protein misfolding and protein aggregation. In 2012, he was awarded a Howard Hughes Medical Institute International Student Research Fellowship.

Martin Gruebele obtained his B.S. and Ph.D. at the University of California. Since 1992 he is on the faculty of the University of Illinois in 1992, currently as Professor of Chemistry, Physics, and Biophysics and Computational Biology. He is a Fellow of the American Physical and Biophysical Societies, a member of the German National Academy of Sciences and of the American Academy of Arts and Sciences, as well as a recipient of the Coblentz, Wilhelm Bessel, and Sackler International Prizes among others. His research focuses on protein and RNA dynamics, vibrational energy flow in molecules, as well as single molecule dynamics spectroscopy detected by scanning tunneling microscopy.