Brownian Dynamics of Subunit Addition-Loss Kinetics and Thermodynamics in Linear Polymer Self-Assembly

Abstract

The structure and free energy of multistranded linear polymer ends evolves as individual subunits are added and lost. Thus, the energetic state of the polymer end is not constant, as assembly theory has assumed. Here we utilize a Brownian dynamics approach to simulate the addition and loss of individual subunits at the polymer tip. Using the microtubule as a primary example, we examined how the structure of the polymer tip dictates the rate at which units are added to and lost from individual protofilaments. We find that freely diffusing subunits arrive less frequently to lagging protofilaments but bind more efficiently, such that there is no kinetic difference between leading and lagging protofilaments within a tapered tip. However, local structure at the nanoscale has up to an order-of-magnitude effect on the rate of addition. Thus, the kinetic on-rate constant, integrated across the microtubule tip (k_on,MT), is an ensemble average of the varying individual protofilament on-rate constants (k_on,PF). Our findings have implications for both catastrophe and rescue of the dynamic microtubule end, and provide a subnanoscale framework for understanding the mechanism of action of microtubule-associated proteins and microtubule-directed drugs. Although we utilize the specific example of the microtubule here, the findings are applicable to multistranded polymers generally.

Introduction

Linear biological polymers typically consist of homogenous globular protein subunits that interact noncovalently to form the functional structure. Examples of linear polymers are diverse and include members of the cytoskeleton, such as microtubules and actin filaments, as well as viruses, sickle-hemoglobin, and paired helical filaments. Because most interactions are noncovalent, both assembly and disassembly are reversible reactions that can be readily controlled and adapted. The adaptability of linear polymers such as microtubules and F-actin enables the congression and subsequent separation of chromosomes during mitosis as well as allows migratory cells to rapidly reorganize cellular protrusions in response to extracellular signals. Because of the importance of the linear polymer assembly dynamics in various cellular processes, they have been studied extensively for several decades both experimentally and theoretically.

Assembly theory for linear polymers assumes that the subunit association and dissociation rates are constant and equal for each strand (1). This theory has been corroborated experimentally, fitting with the observed concentration-dependent net-assembly rates for multistranded polymers such as F-actin (2), GTP-tubulin (3,4), and GMPCPP-tubulin (5,6), enabling estimates of the underlying kinetic rate constants. This model for assembly inherently assumes that the dynamic end of the polymer is energetically constant. However, the structure and free energy of the end evolves because of the formation and loss of lateral interactions as individual subunits are gained and lost from the end (7). In the simplest form, single-stranded linear polymers have a single longitudinal interaction; however, the increasing complexity of multistranded polymers introduces lateral interactions between neighboring subunits (Fig. 1 A). Thus, despite fitting with experimental results, the assumptions of basic assembly theory break down for more complex multistranded polymers. This was recently shown in microtubule self-assembly where the off-rate (k_off,MT) increases as the majority of protofilament ends shift from more stable configurations to less stable configurations at higher free tubulin concentrations (8). Not only did these results have significant consequences for how we view microtubule self-assembly, but also demonstrate that kinetics vary as the structure of the microtubule tip evolves. Thus, the dissociation rate of tubulin subunits is not constant, as theory has assumed.

Figure 1.

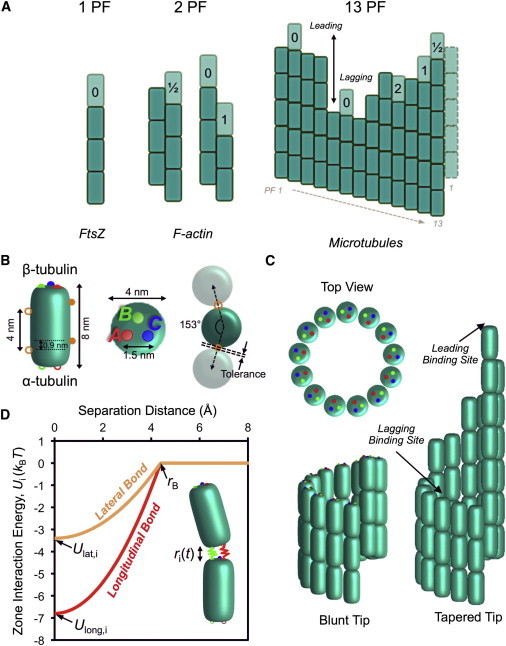
Simulated structures and interactions in linear polymer self-assembly. (A) Examples of single and multistranded linear polymers are shown. The number of possible configurations increases with complexity. Darker subunits are bound, whereas lighter subunits represent potential binding sites for incoming subunits. The number of laterally interacting subunits is indicated for each binding site. (B) Diagram of an αβ-tubulin subunit assumed within the model. Zones constituting the longitudinal bond are A (red), B (green), and C (blue). Lateral zones (solid and open circles in orange) β- and α-tubulin, respectively, with colored symbols indicating the paired binding partners on separate subunits (i.e., open green associates with solid green on a separate subunit). (C) Diagram of the microtubule lattice as constructed within the simulation. Tapered example (right) is four dimer layers. (D) Interaction energy as a function of separation distance is shown for a single longitudinal (red, one of three zones) and lateral bond (orange, one of two zones) zone. Interaction energy increases as a Hookean spring within the binding radius (r_B).

Hill (7) indicated that both the on- and off-rates will depend on the number of lateral interactions, but concluded that the full effect would be on the off-rate for a diffusion-limited process. In agreement, the majority of theoretical models for microtubule self-assembly have assumed a single on-rate constant (k_on,MT) for the microtubule end (9–13). However, Gardner et al. (8) found that an on-rate penalty (k_on,PF2 = k_on,PF/δ, where δ = 15) to protofilaments with two neighboring protofilaments of greater length, although not necessary to qualitatively match tip taper trends with free tubulin concentration, was necessary to quantitatively match the model-predicted protofilament length variance to that estimated experimentally. Without this penalty, the model predicted a protofilament length variance that is smaller than experimentally observed, meaning all protofilaments are of approximately equal length. This suggests that the evolving tip structure and free energy may affect the on-rate constant in addition to the off-rate and that kinetic or thermodynamic inequality at the microtubule end may be necessary to produce the experimentally observed structures (14,15). More generally, multistranded self-assembled polymers, in principle, could have different on-rate constants for each protofilament; however, we currently lack the theoretical underpinnings for on-rate heterogeneity, or whether it is even expected to exist.

To explain the specific case of microtubule tip structure and self-assembly, Gardner et al. (8) imposed an on-rate penalty only to protofilaments with two neighboring protofilaments of greater length and ignored any penalty imposed by a single neighboring protofilament. Even so, a single neighbor may be sufficient to hinder subunit incorporation into the lattice. As the microtubule grows, the tip becomes increasingly tapered (14,16), in which the one-neighbor case will be the most frequent. Thus, a one-neighbor penalty could significantly influence net assembly and the resulting structure of the microtubule tip, as well as influence assembly in multistranded linear polymers generally. Gardner et al. (8) assumed the presence of neighboring protofilaments is unfavorable due to the steric hindrance of aligning incoming units with the orientation of adjacent protofilaments, although the presence of neighboring protofilaments could also be favorable due to the additional free energy of forming lateral bonds. Thus, the net-effect of laterally interacting protofilaments at the end of linear polymers is not clear.

In addition to local effects of neighboring protofilaments, the global structure or the distribution of protofilament lengths at the end of the microtubule could influence the kinetics of individual protofilaments, independent of the local conditions. Individual protofilaments vary in length within a microtubule (often referred to as tip taper or raggedness), and often range up to several hundred nanometers both in vitro (14) and in vivo (15). The tip structures in many cases appear much like the tip of a syringe needle (i.e., like a cylinder cut obliquely; see e.g., Chrétien et al. (14)). The extended leading protofilaments potentially block freely diffusing subunits from reaching shorter lagging protofilaments, thus the rate by which free subunits arrive to a potential binding site could depend upon its global position within the microtubule tip structure.

To investigate the impact of polymer-end structure on kinetics and thermodynamics of linear polymer self-assembly generally, we created a Brownian dynamics computational model for the noncovalent interactions of subunits with the polymer tip. This allowed us to simulate the association and dissociation of individual subunits, using microtubule assembly as a central focus. We found that due to counteracting effects, global structure of the extending tip does not affect the association rate to lagging protofilaments compared to leading protofilaments, assuming there are no lateral neighbors. However, local presence of either one or two neighboring protofilaments inhibits the association despite the presence of short-range favorable interactions. These results demonstrate that the association rate constant for the microtubule (k_on,MT) should be considered an ensemble average of the individual nanoscale rate constants of individual protofilaments (k_on,PF), which are dependent on the number of lateral interactions at the polymer end and evolve with the gain and loss of individual subunits. Additionally, our model serves as a framework to study the specific mechanisms by which microtubule-associated proteins and microtubule-targeting drugs affect the microscale microtubule dynamics through alteration of the underlying kinetics and thermodynamics. To our knowledge, this is the first intermediate-scale simulation of subunit association and dissociation in linear filament self-assembly where the translational and rotational dynamics of subunits are explicitly simulated along with the interaction potentials between subunits. This modeling approach, based on the method articulated by Northrup and Erickson (17), provides a bridge from the atomistic method (18–22) and simple addition-loss methods (9–12,23,24).

Methods

Our model was based on the Brownian dynamics approach described by Northrup and Erickson (17) for estimating kinetic association rate constants, with the following modifications:

• 1.Nonspherical subunit structure;
• 2.Interaction with a self-assembled polymer lattice; and
• 3.Separate near- and far-field simulations to isolate effects on either diffusion-limited arrivals or binding.

Additionally, we implement a modified Metropolis Monte Carlo (25) algorithm for Brownian dynamics in the presence of an external force. All simulations were carried out with custom code written in the software MATLAB (The MathWorks, Natick MA). To test the model predictions, we implemented two specific linear self-assembled polymer structures: microtubules and actin filaments. Simulated structures and interactions are described below. For a detailed description of the simulation procedure, see the Supporting Material.

Microtubule simulation structures

The microtubule structure was modeled as a B-lattice, consisting of 13 protofilaments and a helical pitch of 1 1/2 dimers per turn (Fig. 1). Individual tubulin subunits were modeled as superellipsoids, obtained by rotating the Lamé curve

$${\left|\frac{x}{a}\right|}^n+{\left|\frac{y}{b}\right|}^n=1,$$ (1)

with a = 2 nm, b = 4 nm, and n = 5, about the vertical axis (Fig. 1 B). For a blunt tip, each protofilament consisted of 100 dimers to capture any potential long-range effects and to create variable tip structures through the removal of dimers from the lattice. To create a tapered tip, the first protofilament was 100 dimers in length and the dimer number decreased linearly between protofilaments 1 and 10, which was of equal length to protofilaments 11–13 (Fig. 1 C). Protofilament 11 was then used as the protofilament of interest for simulations of lagging protofilaments to insure that immediately adjacent protofilaments were of equal length. Lag distance was defined as the center-to-center distance between the subunit of interest and either the most distal subunit (when lagging, positive-lag distance) or the closest subunit on a separate protofilament (when leading, negative-lag distance). In simulations where the protofilaments adjacent to the protofilament of interest were of greater length (lateral neighbors), protofilament 7 of a blunt end was used and subunits were then added to one or both of protofilaments 6 and 8 to create the one- and two-neighbor cases, respectively. We define the tolerance of lateral neighbors as the minimum distance (surface-to-surface) between adjacent subunits within the microtubule lattice (Fig. 1 B). Tolerance was adjusted by modifying the radius of the microtubule and keeping the dimensions of individual subunits constant.

Longitudinal and lateral interactions between subunits

To represent the longitudinal bonds between freely diffusing subunits and the protofilament of interest, we used three zones based on the high-resolution description of tubulin subunits within the microtubule lattice (26) (Fig. 1 B). Three zones would be the minimum number necessary for correct rotational orientation to allow for lateral interactions, and is the number of contacts that best matched experimental estimates of kinetic association rates according to Northrup and Erickson (17). The three zones (A, B, and C) were placed noncollinearly in a plane (i.e., in a triangle), tangential to the end of the subunit, normal to and centered on the subunit long axis on both the α- and β-tubulin ends of the dimer (Fig. 1 B). Zones were paired, and mutually exclusive, such that zone A of α-tubulin could only bind with zone A of β-tubulin on the subunit of interest. Zones were rotated about the vertical (long) axis so that their position relative to the inside or outside of the microtubule lattice was independent of protofilament number (e.g., Zone A, red, is always located near the inside face of the microtubule, as in Fig. 1 C).

Two zones, one α and one β, were used to model the lateral bonds between subunits (Fig. 1 B), which was sufficient to ensure that subunits were aligned vertically with neighboring protofilaments. Similar to longitudinal bonds, lateral zones were paired and mutually exclusive. Because of the helical and cylindrical shape of the microtubule lattice, lateral zones were offset from center on either side of the tubulin subunit and rotated inward toward the microtubule lumen (Fig. 1 B). Accounting for both the helical pitch and cylindrical shape of the microtubule lattice minimized the distance between lateral zones when a subunit was bound within the lattice.

Bonds were modeled as Hookean springs of zero rest length with a well-depth equal to the total bond energy for an individual zone (Fig. 1 D). Thus, the energy at each time point was the difference between the total potential energy and the displacement of stretching the spring, given by the harmonic potential

$$U_i\left(t_j\right)=\frac{1}{2}{k}_{\text{bond},i}{\left(r_i\left(t_j\right)\right)}^2+U_{\text{bond},i},$$ (2)

where r_i is the distance between paired zones and k_bond,i is the spring constant of an individual interaction zone. Individual zones were modeled as springs in parallel and the total bond potential energy was evenly distributed across all zones, such that k_bond,i = k_bond/q and U_bond,i = U_bond/q (where q = 3 for the longitudinal bond and q = 2 for lateral bond). We assumed k_long was equal to that previously estimated for the longitudinal bond modeled as a harmonic potential (k_long ≈ 900 pN/nm) (12). We initially established bounds for the total longitudinal bond potential energy (U_long) (see the Supporting Material), but later found that U_long = −20.4 k_BT resulted in ΔG⁰_long = −6.8 k_BT (see Results and Discussion), consistent with that previously estimated for the longitudinal bond free energy (11). Therefore, this value of U_long was used for the longitudinal bond in all simulations unless otherwise noted.

Several studies have noted that the intrinsic bond energy of the lateral bond is weaker (more positive) than the longitudinal bond by ∼12–16 k_BT (11,20,27). To account for this difference, we assumed that the total bond energy for the lateral bond was one-third that of the longitudinal bond (U_lat = −20.4/3 k_BT = −6.8 k_BT), thus weakening the lateral bond by ∼14 k_BT. Additionally, the spring constant of the lateral bond was three-times softer than the longitudinal bond (k_lat = k_long/3) to account for the flexible M-loop involved in the lateral contact between tubulin subunits (26). Softening the lateral bond also made the binding radius (r_B) equal for both the longitudinal and lateral bond. A bond was considered broken when the strain of stretching was greater than the total bond energy. This separation distance (where U_i(t_j) = 0) was defined as the binding radius (r_B) and given by

$$r_B={\left(\frac{-2U_{\text{bond},i}}{k_{\text{bond},i}}\right)}^{1/2}.$$ (3)

Based on the bond strengths and stiffness values indicated above, r_B = 0.43 nm. Individual zones were considered bound when their separation distance was less than the binding radius (Fig. 1 D), and only those zones that were bound contributed to the total energy at a given time point according to

$$U\left(t_j\right)=\sum _{i=1}^N{U}_i\left(t_j\right),$$ (4)

where N is the number of zones within r_B (the longitudinal and lateral zones both contribute to the value of N, such that max(N) = 3, 5, or 7 with zero, one, or two lateral bonds). A subunit was considered completely bound when all three zones constituting the longitudinal bond were within r_B (N = 3 for longitudinal bond).

Actin filaments

To simulate actin (instead of tubulin), we assumed G-actin monomers were superellipsoids with dimensions of 4 × 4 × 6.7 nm (a = 2 nm and b = 3.35 nm in Eq. 1), comparable to de la Cruz et al. (28), and that the protofilaments of F-actin were offset by 2.8 nm (29). Protofilaments were 100 subunits in length, and then subunits were added to the leading protofilament to increase the lag distance of the lagging protofilament. We found a total bond energy of U_long = −19.2 k_BT best fit estimates of the standard Gibbs free energy for the longitudinal bond (30). Additionally, we adjusted the stiffness of the longitudinal bond based on previous estimates for ATP-actin (k_long = 165 k_BT/nm² ≈ 700 pN/nm) (28). Modifying the total bond energy and bond stiffness only slightly changed the binding radius (r_B = 0.46 nm) compared to tubulin. To include the diagonal bonds between actin monomers, we used a single interaction zone per diagonal bond with U_diag = −6.4 k_BT and k_diag = k_long.

Results and Discussion

Global position has no net effect on kinetics

We anticipated two potential effects of global and local tip conditions, either 1), reducing the rate at which freely diffusing tubulin subunits arrive (through diffusion) to a surface some short distance away from the protofilament of interest or 2), inhibiting the subsequent binding. To isolate these two potential effects, we split our simulation into two parts (see the Supporting Material), initially simulating the diffusion-limited arrival rate to a surface a short distance from the bound subunit of interest (k_D(R), where R = 10 nm center-to-center; Fig. 2 A), and then simulating the subsequent binding of units that arrived at this surface. As shown in Fig. 2 B, freely diffusing subunits approach lagging protofilaments at a slower rate compared to leading protofilaments. The arrival rate to leading protofilaments rapidly approaches the predicted Smoluchowski rate (see Eq. S8 in the Supporting Material), whereas the arrival rate to lagging protofilaments is approximately twofold slower. Interestingly, once a protofilament is leading or lagging by a certain distance (on the order of a single subunit layer), there is relatively little change in the rate (Fig. 2 B). The greatest change in rate occurs around zero lag, indicating that only small differences in the relative length of individual protofilaments are necessary to reduce the arrival frequency of freely diffusing subunits. This suggests that global structure would have similar implications in other multistranded polymers that exhibit less variation in protofilament lengths, such as F-actin.

Figure 2.

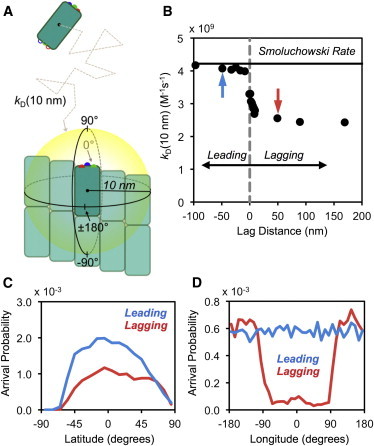
Diffusion-limited arrivals to leading and lagging protofilaments. (A) Freely diffusing subunits arrive to a spherical surface (R = 10 nm, yellow) centered on the leading subunit of the protofilament of interest. Darker subunits identify potential binding partners (subunits of interest), whereas lighter subunits show the immediately surrounding microtubule lattice. (B) Diffusion-limited arrivals to protofilaments at varying global positions within the microtubule tip. (Solid black line) Theoretical Smoluchowski limit to the yellow sphere shown in panel A (4πD_avgR). (Gray vertical line) Zero lag. (Blue and red arrows) Leading (blue) and lagging (red) cases shown in panels C and D. (C and D) Probability that a freely diffusing subunit (starting from R = 400 nm) reaches the 10-nm surface at a given position relative to the subunit of interest within the microtubule lattice.

To more specifically examine the cause of reduced arrivals to lagging protofilaments, we looked at the positions of arriving units (that reach the 10-nm center-to-center distance) relative to the subunit of interest within the microtubule lattice (Fig. 2, C and D). Although there was no apparent spatial bias in the reduction of arrivals above or below the subunit of interest, we found that fewer subunits arrive to lagging protofilaments from the direction of the inside (lumen) of the microtubule compared to leading protofilaments (Fig. 2 D). This supports our original hypothesis that longer protofilaments shield lagging protofilaments, but the fact that the observed effect starts at ∼±90° longitude further suggests that the observed effect is in part due to the neighboring protofilaments of nearly equal length. If adjacent protofilaments were the only effect on diffusion-limited arrivals, we expect there would be no difference among protofilaments 2—11 in a blunt tip, as the local conditions are equivalent for each. As seen in Fig. 2 B, however, protofilaments 2–11 (lag distance ∼0–8 nm) exhibit the greatest absolute rate of change in arrival rate. These results together indicate that the global structure mainly reduces arrivals to lagging protofilaments by blocking the angles from which freely diffusing subunits can approach the binding site.

If the efficiency of binding is independent of the global tip structure, then our estimated on-rate constant for lagging protofilaments should be lower than that for leading protofilaments. As shown in Fig. 3 A, however, binding efficiency is not independent of the global position and exhibits the opposite trend compared to arrivals. This means that freely diffusing dimers, once they have gotten to within a few nanometers of the binding site, are more likely to bind to lagging protofilaments than leading protofilaments. The observed trend in binding efficiency effectively cancels out the trend in diffusion-limited arrivals, such that the on-rate constant is independent of the global position of the binding site within the microtubule tip (Fig. 3 B). The same trend in binding efficiency was observed when starting positions were artificially randomized along the 10-nm surface rather than sampled from the diffusive arrivals (see Fig. S2 in the Supporting Material). Therefore, the observed trend in binding efficiency was not due to bias in the starting positions but due, instead, to an inherent property of lagging versus leading protofilaments.

Figure 3.

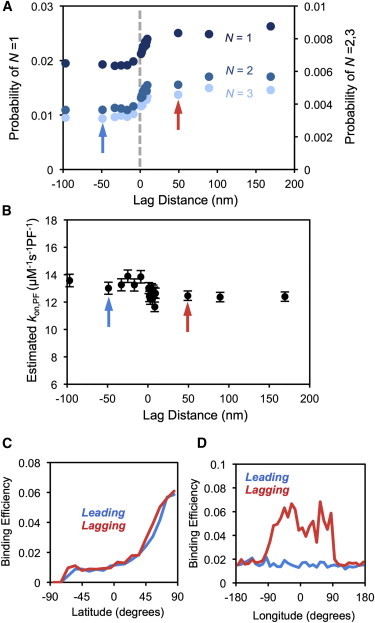
Binding efficiencies and estimated on-rate constants for varying global positions. (A) The probability that subunits satisfy N = 1 (dark blue dots), N = 2 (blue dots), or N = 3 (light blue dots) longitudinal zones within r_B before diffusing to 400-nm center-to-center distance. (Gray line) Zero lag. (B) Estimated on-rate constants of completely bound subunits (N = 3) for a variety of global positions. In panels A and B, the arrows indicate the leading (blue) and lagging (red) cases analyzed in panels C and D. Error bars are mean ± SE. (C and D) Binding efficiencies of all arrival positions are shown. Efficiency is the number of subunits per position that eventually bind before diffusing to 400-nm center-to-center distance divided by the total number of simulations initiated at that position.

The fact that the trend is observed for each degree of contact specificity (N = 1, 2, and 3) indicates that the global structure does not promote the transition to a higher degree of binding, but instead increases the chance that a single contact is established in the first place (Fig. 3 A). Note that the percentage of freely diffusing subunits that reach the N = 1 state is very small (2–3%), thus even though they arrive at a very short distance (10-nm surface) relative to the binding site, the vast majority of subunits diffuse away without ever interacting with the protofilament of interest. Subunits arriving above the binding site are more efficient for both leading and lagging protofilaments; however, those arriving from the direction of the microtubule lumen are approximately three times more efficient when binding to lagging versus leading (Fig. 3, C and D). Thus, even though fewer freely diffusing subunits reach lagging protofilaments from the direction of the inner part of the microtubule (Fig. 2 D), those units are more likely to interact with the protofilament of interest and eventually incorporate into the lattice. These results together suggest that the surrounding longer protofilaments in the lagging case keep free units from escaping, in the same manner that they blocked units from arriving in the first place, thus increasing the probability that the free unit establishes at least one interaction contact. Thus, the extending global tip structure is like a double-edged sword that simultaneously blocks subunit arrivals to and departures from the vicinity of lagging protofilaments, such that leading and lagging protofilaments end up with essentially the same on-rate constant.

Local structure sterically inhibits subunit association

Although global structure did not affect subunit addition, we were interested to see whether local structure might—an effect invoked to quantitatively explain microtubule tip structure in a previous study (8). In a multistranded self-assembled polymer, lateral interactions are formed and lost as a consequence of the gain and loss of individual subunits at the dynamic end of the microtubule, and thus the local conditions for a given protofilament will vary over time. For a multistranded polymer with at least three protofilaments, there are three conditions that an incoming subunit could encounter (7). The protofilament of interest could have zero, one, or two neighboring protofilaments that are longer by at least one subunit. In contrast to global structures, the potential effects of local structures are more immediately apparent. For example, in the case with two adjacent longer protofilaments, an incoming unit would have less freedom of orientation due to the steric hindrance of the neighboring protofilaments. Based on these arguments, Gardner et al. (8) implemented an on-rate penalty (15-fold decrease of the association rate constant, k_on,PF) to protofilaments with two neighboring protofilaments of greater length to replicate the experimentally observed protofilament length variance. Here we sought to use our Brownian dynamics model to investigate whether a single neighboring protofilament of greater length could induce a similar penalty and to obtain a more rigorous estimate of what the two-neighbor penalty should be, if any.

We defined local tip structure as the relative lengths of an individual protofilament to its immediately adjacent neighboring protofilaments (Fig. 1 A). In our simulation, a blunt tip (zero lateral neighbors) assumes both neighboring protofilaments are the same length as the protofilament of interest. The one- and two-lateral-neighbor cases are where one or two adjacent protofilaments, respectively, are longer by at least a single dimer. As seen in Fig. 4 A, our estimated on-rate constant decreases progressively with the addition of one and two lateral neighbors. Thus, the on-rate constant for a protofilament in each condition will be penalized relative to the zero neighbor case. This observation was robust with respect to the details of the shape of the potential as well as the bond stiffness (see Fig. S6). Although we assume that all protofilaments are oriented parallel to the microtubule axis, the gentle outward curling of leading protofilaments in growing ends (14) is not likely to reduce the steric penalty because a single dimer layer is sufficient to impose the penalty. In contrast to global structures, these local structures have little effect (<20% between zero and two neighbors) on the arrival of freely diffusing subunits. Instead, the main effect of local structure is through inhibition of the eventual binding of subunits after they have approached the protofilament of interest (Fig. 4 B and see Movie S1 and Movie S2 in the Supporting Material). This is consistent with a steric penalty, due to the constraint of orientation, imposed by the adjacent protofilaments.

Figure 4.

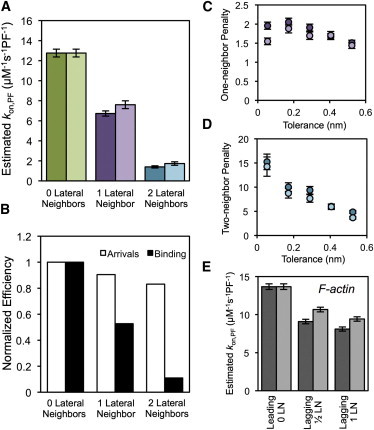
Dependence of on-rate constants on local tip structure. (A) Estimated on-rate constants of freely diffusing subunits for all possible local configurations are shown. Rates for simulations with (lighter) and without (darker) the lateral bond result in equivalent estimates of the on-rate constant. (B) Efficiency of diffusive arrivals to 10-nm center-to-center distance and subsequent binding are shown. Each is normalized to the respective zero neighbor case. (C and D) On-rate penalties (fold decrease from the zero neighbor case) for the single- (C) and two- (D) neighbor cases with (lighter) and without (darker) lateral bonds. Penalties were estimated across a range of tolerances, where tolerance is defined as the minimum distance between adjacent protofilaments within the microtubule lattice. (E) Estimated on-rate constants of G-actin binding to the leading and lagging protofilament are shown (lateral neighbor numbers are illustrated in Fig. 1A) for simulations with (lighter) and without (darker) the diagonal bonds. All error bars are mean ± SE.

If the penalty to the one- and two-neighbor case is indeed due to steric hindrance, then the more severe the orientation constraint, the greater the penalty should be. Therefore, we estimated the one and two-neighbor penalties for a range of tolerances to examine the constraint sensitivity of each penalty (Fig. 4, C and D). Not surprisingly, the two-neighbor case is penalized to a greater extent compared to the one-neighbor case for all tolerances within the range we examined. The one-neighbor penalty is relatively independent of tolerance whereas the two-neighbor penalty becomes more severe at lower tolerances. If we assume that the tolerance range for a microtubule is within the lateral interaction distance defined by Nogales et al. (26) (<4 Å), then protofilaments with one or two lateral neighbors will have ∼2 or ∼10 times, respectively, slower on-rate constants than those without neighbors. While our estimated on-rate constant for the blunt case is greater than previous estimates, the one-neighbor case is within error of previous estimates (see Gardner et al. (8) for summary). It is interesting to note that a binding site with a single lateral neighbor will be common within a tapered tip, thus the average association constant (k_on,MT) estimated from our model is within the range of previous estimates by both experimental and computational approaches (8).

As subunits get close to the binding position, it is possible that the lateral bond will reduce the steric penalty by providing additional favorable free energy, particularly in the presence of two lateral protofilaments. To examine whether this is expected to be a significant effect, we added the lateral bond consisting of two zones (one for α- and β-tubulin each) on both sides of the αβ-tubulin subunit (Fig. 1 B). We decreased both the total bond energy and the spring constant of the lateral bond threefold compared to the longitudinal bond (see Methods). Doing so resulted in the lateral bond being ∼14 k_BT weaker than the longitudinal (consistent with published estimates (11,20,27)) and made the binding radius (r_B) equal for both the longitudinal and lateral bond, giving the lateral bond the best chance to reduce the on-rate penalty. Even so, the lateral bond did not significantly reduce the severity of the one- and two-neighbor penalties for the majority of tolerances examined (Fig. 4, C and D). Because the lateral bond is so weak compared to the longitudinal, the interaction is not sufficient to facilitate the establishment of a longitudinal interaction. This suggests that the longitudinal bond is necessary for a subunit to incorporate into the microtubule lattice (the relative strengths of the lateral and longitudinal bond are discussed further below).

The fact that even one neighbor is sufficient to inhibit the association of incoming subunits suggests that a similar effect will occur in all multistranded polymers. Even in a two-stranded polymer, such as F-actin, one protofilament will be longer than the other, resulting in multiple local structure conditions for incoming subunits (Fig. 1 A). To assess the generality of structurally induced kinetic penalties in linear polymer assembly, we simulated G-actin monomer subunit binding to the leading and lagging protofilament of a two-protofilament polymer. In simulating actin instead of tubulin, we shortened the long axis of the superellipsoid used to define a subunit and adjusted the total bond interaction energies (U_bond) and bond stiffness (k_bond) to better match previous estimates for actin (see Methods). As seen in Fig. 4 E, the estimated on-rate constant is reduced by ∼1.5-fold for the lagging protofilament compared to the leading protofilament. Similar to tubulin, the addition of diagonal bonds did not reduce the steric penalty imposed by the leading protofilament. The effect of one neighbor is not as strong for F-actin compared to the microtubule; however, our results show that neighboring protofilaments sterically hinder addition to lagging protofilaments even in the simple case of a two-stranded polymer.

Kinetic penalties influence polymer tip structures

Despite the one-neighbor on-rate constant being only a factor-of-two slower compared to zero neighbors, it can potentially have a significant effect on net assembly if it occurs frequently. To investigate the consequence of our predicted on-rate penalties, we examined the resulting microtubule tip structure from simulations of individual microtubule net assembly according to VanBuren et al. (11): without penalties; with only a two-neighbor penalty (8); and with our model-predicted penalties for both one and two lateral neighbors (from Fig. 4, C and D). Without penalties, individual protofilaments remain of approximately equal length and tip structures do not achieve the same extension compared to simulations with penalties (Fig. 5, A and B). A two-neighbor penalty is sufficient to achieve experimentally observed tapers (14), but it typically results in a single protofilament that lags many dimer layers behind the others, which remain of approximately equal length (Fig. 5, A and C). It is unlikely that this single trailing protofilament would be resolved by experimental methods and thus would appear as a relatively blunt tip because the fraction of zero- and one-neighbor cases is comparable to the nonpenalized case (Fig. 5 C). Our estimate of the two-neighbor penalty is comparable to that required for quantitative agreement with the protofilament standard deviation in GMPCCP microtubules (8). Addition of the one-neighbor penalty, however, resulted in a gradual loss of protofilaments out to the microtubule end, more closely resembling those structures observed by electron microscopy (14,16,31) (Fig. 5 A). Additionally, the one-neighbor penalty shifted the majority of protofilaments from zero neighbors to one and two neighbors in tapered tips compared to blunt (Fig. 5 D). Because the microtubule on-rate constant is determined by the fraction of protofilaments in each condition, tapered tips will have a slower on-rate constant than blunt tips in this case. In fact, we found the average on-rate constant (k_on,MT) for the microtubule-end decreased ∼22% in tapered tips compared to blunt in the case with one- and two-neighbor penalties; however, the on-rate constant decreased only ∼7% in the case of a two-neighbor penalty only. Thus, on-rate penalties dictate the resulting tip structure, which will feed-back to influence association and promote further tapering of the tip.

Figure 5.

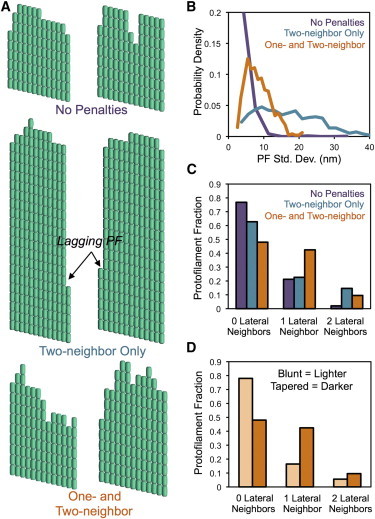
On-rate penalties influence the resulting microtubule tip structure. (A) Examples of tapered microtubule end structures (displayed as two-dimensional sheets) from each of the three simulation conditions: no on-rate penalties (top); a single penalty to protofilaments with two lateral neighbors (middle); and model predicted penalties to protofilaments with both one and two lateral neighbors (bottom). (B) Probability density values of protofilament length standard deviations for tips in each simulation condition are shown. (C and D) The fraction of protofilaments with zero, one, or two lateral neighbors in (C) tapered tips from all three cases and (D) blunt (lighter) or tapered (darker) tips from simulations with one- and two-neighbor penalties.

The observed kinetic inequality between protofilaments due to the local structure provides a potential explanation for the observed history dependence of both catastrophe (16,32,33) and rescue (34). Although it has been shown that gradual tapering of the microtubule tip leads to a higher probability of catastrophe with microtubule age (16), it is not clear how tip taper promotes catastrophe. A potential explanation is that increased taper will correspondingly increase the off-rate (k_off,MT) due to the loss of stabilizing lateral bonds (8), thus reducing the net assembly rate. If tip taper only increases k_off,MT, however, it would be difficult to lose a large GTP-cap at higher tubulin concentrations and as estimated in vivo (35). Our results here suggest that, in addition to affecting the off-rate, increasing tip taper will result in a decrease of the average on-rate constant for the microtubule (k_on,MT). Thus, the net addition of subunits will potentially decrease to a greater extent and be more variable in time. Because the net assembly rate is the small difference between a large on- and off-rate (8), changes in both k_on,MT and k_off,MT could switch the microtubule from a state of net assembly to net disassembly. Thus, a tapered tip will have a net assembly rate that is lower than a blunt tip. We suggest that, rather than there being a series of specific events leading to catastrophe (as indicated by the literature (32,33,36)), gradual tapering of the microtubule tip (16), on average, transitions it to a state of net disassembly, resulting in the loss of the GTP-cap and catastrophe. It may be challenging to experimentally detect this transition, however, because individual tips are highly dynamic (8,16) and variable (14). In contrast to growth, as a microtubule shortens, the tip will evolve toward a blunt structure because of the stability of subunits with two lateral bonds within the microtubule lattice compared to those with one or zero. The transition toward a blunt tip will result in an increase in the net assembly rate, allowing the microtubule to reestablish its GTP-cap and rescue as a result. Thus, the feedback relationship of k_on,MT, k_off,MT, and tip structure can explain history-dependent catastrophe and rescue through the gradual transition between microtubule tip states biased toward net assembly or disassembly.

Simulating subunit dissociation closes the thermodynamic loop

Because the local tip structure affected the association rate constant, we were interested to assess whether it also affects the dissociation rate constant. For a bimolecular reaction, the standard Gibbs free energy of association (ΔG⁰) is related to the ratio of the association and dissociation rate constants by

$$\Delta G^0=-k_{\mathrm{B}}T\text{ln}\left(k_{\text{on}}/k_{\text{off}}\right),$$ (5)

where k_on is defined to have units of M⁻¹ s⁻¹ and k_off to have units of s⁻¹. Due to the nature of our simulation, we separated the standard Gibbs free energy into two contributions: the intrinsic bond energy, ΔG⁰_B (a large negative value assumed here to mainly be the hydrophobic interactions between tubulin subunits in the specific case of the microtubule), and an entropic penalty of binding, ΔG⁰_S (a positive value due to the loss of translational and rotational freedom upon binding) (27,30,37,38), such that

$$\Delta G^0=\Delta G_B^0+\Delta G_S^0.$$ (6)

Because we have already simulated the association of freely diffusing subunits, we can obtain a complete thermodynamic picture of αβ-tubulin subunits at the dynamic end of microtubules by simulating their subsequent unbinding. We defined the time to unbind as the amount of time that passed between when a subunit is completely bound to when it returns to a center-to-center separation distance where the probability of rebinding is <0.01 (R_U = 11 nm, see the Supporting Material for further discussion and Movie S3).

As noted above (see Methods), U_bond is not equivalent to ΔG⁰_B, because for ΔG⁰_B = U_bond, all interacting zones have to be perfectly aligned (r_i = 0 for all i). This is rarely the case, because one zone’s energy decreases at the cost of another zone as the subunit rotates about its center. Instead, we consider U_bond to be an adjustable parameter that will set the intrinsic bond energy, but is not necessarily equal to it. To estimate ΔG⁰_B from the simulation, we calculated the time-averaged interaction energy while a subunit was within R_U, according to

$$\Delta G_B^0=\frac{\sum _{i=1}^m\sum _{j=0}^{n-1}U\left(t_j\right)\cdot \left(t_{j+1}-t_j\right)}{\sum _{i=1}^m{t}_n\left(i\right)},$$ (7)

where m is the total number of unbinding events simulated and n is the number of steps taken before unbinding for a given unbinding event.

To check that our simulations agreed with theoretical thermodynamic expectations, we estimated k_on,PF, k_off, and ΔG⁰_B for values of U_long within the range estimated for the longitudinal bond (see the Supporting Material). From these estimates, we could then estimate ΔG⁰ by Eq. 5 and ΔG⁰_S from Eq. 6. As shown in Fig. 6, both k_on,PF and k_off are dependent on the value of the total bond energy (U_long). From this we found that U_long = −20.4 k_BT resulted in ΔG⁰_long ≈ −6.8 k_BT, as estimated previously for the longitudinal bond (11) (Fig. 6 C). The intrinsic bond energy (ΔG⁰_B) becomes more favorable with decreasing values of U_long, approaching its value but never equal to it. Our estimated values for ΔG⁰_B within this range of U_long are comparable to previous estimates for the intrinsic energy of the longitudinal bond (11,27). Interestingly, ΔG⁰_long >ΔG⁰_B for all values of U_bond (Fig. 6 C). This is due to the loss of translational and rotational freedom introduced by the implementation of Boltzmann’s law while the subunit is bound (see the Supporting Material). Thus, the entropic penalty of binding comes out naturally from the simulation. In the range of values for U_long used here, our estimate of the entropic penalty of binding, ΔG⁰_S ≈ 10 k_BT, is comparable to previous estimates based on tubulin polymerization (27), actin fragmentation (30), and experimentally observed filament lengths (39), and is independent of the total bond energy. Thus, all three components of Eq. 6 can be extracted from the simulation for a given parameter set and, using our estimate of U_long = −20.4 k_BT, are in agreement with previous estimates for tubulin-tubulin interactions.

Figure 6.

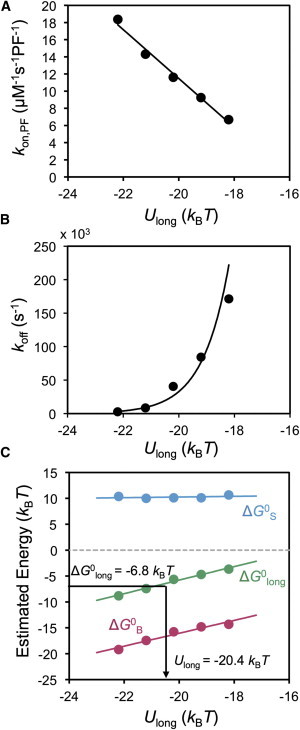
Extracting kinetics and thermodynamics from the model. The estimated on-rate (A) and off-rate (B) constants are dependent on the total bond energy (U_long) used to define the longitudinal bond and are calculated from the simulation. Trend line for k_off is best-fit exponential. (C) The standard Gibbs free energy (ΔG⁰_long, green), intrinsic bond strength (ΔG⁰_B, magenta), and entropic penalty of binding (ΔG⁰_S, blue) are shown as a function of the total bond energy for the longitudinal bond. From the results in panel A and B, and an estimate of the average ΔG⁰_B within the simulation, ΔG⁰_long and ΔG⁰_S can be obtained. The total bond energy that best matched previous estimates of the longitudinal bond free energy (ΔG⁰_long) was extracted from the resulting trend line. All trend lines are linear best fit, unless otherwise noted.

A summary of complete kinetic and thermodynamic results (estimated using Eqs. 5–7) for varying local conditions is shown in Table 1 (see Table S1 in the Supporting Material for F-actin). Interestingly, the estimated entropic penalty of binding is nearly equal between the zero- and one-neighbor conditions (∼1 k_BT difference, which can mostly be attributed to the approximately twofold steric penalty to the on-rate, ln(2) = 0.7 k_BT). This indicates that once a subunit is bound longitudinally it does not pay an additional entropic penalty by forming the lateral bond (consistent with the assumption in VanBuren et al. (11) that the entropic penalty is absorbed entirely by the longitudinal bond). Thus, lateral bonds have a significant stabilizing effect (∼60-fold to >300-fold longer subunit lifetime with one and two lateral bonds, respectively) by contributing favorably to the free energy of association (see Movie S3). Although we only set an upper limit for the off-rate for subunits with two lateral bonds (see the Supporting Material), this upper limit is still fivefold lower than with one lateral bond, thus we expect the addition of the second lateral bond to further contribute favorably to the free energy.

Table 1.

Summary of simulation results with zero, one, and two lateral bonds in addition to the longitudinal bond

Model-estimated parameters	Longitudinal bond only	Longitudinal and lateral bond
	Lateral neighbors = 0	Lateral neighbors = 1	Lateral neighbors = 2
kon,PF (μM−1 s−1 PF−1)	12.7	7.4	1.7
koff (s−1)	15 × 103	250	<50
ΔG0B (kBT)	−17.7	−22.6	−28.5
ΔG0 (kBT)	−6.7	−10.3	<−10.4
ΔG0S (kBT)	+11.0	+12.3	<+18.0

The observed stabilizing effect of the lateral bond is dependent upon the longitudinal bond being established first. Lateral bonds, by themselves, are unfavorable because the entropic penalty of binding is greater than the intrinsic bond strength of the lateral bond, resulting in a very short-lived interaction (see Table S2). The exceptionally short duration of lateral bonds in the absence of a longitudinal bond (∼0.1 μs) explains why they were not able to overcome the steric penalty imposed on association by lateral neighbors (Fig. 4). The reduction in free energy by one lateral bond (−3.6 k_BT) is less than previously estimated for the lateral bond (11); however, it would become more negative for decreasing total bond energies (U_lat). Therefore, we do not consider this to be an estimate of ΔG⁰_lat, but rather a value determined by the total interaction energy used in the simulation, i.e., U_lat could be adjusted downward to obtain previously estimated values of ΔG⁰_lat. Even so, the total bond energy would still be on the order of the entropic penalty. Thus, we conclude that subunits adding to the microtubule lattice require the stronger longitudinal bond to incorporate into the lattice.

The necessity of the longitudinal bond is in qualitative agreement with the suggestion that cracks between protofilaments may be present within the lattice due to a delay in lateral bond formation after a subunit binds (24). However, we argue that quantitatively they would be extremely short-lived, because we find lateral bonds form rapidly after the longitudinal bond (7.0 ± 0.7 ns for one and 9.0 ± 0.8 ns for two lateral bonds, mean ± SE) in our model. The necessity of the longitudinal bond further suggests that additions with either a single or two lateral bonds but no longitudinal bond, resulting in a lattice defect, would be very rare due to their extremely short duration. Thus, the strength difference between the longitudinal and lateral bonds may be an evolutionary advantage to reduce the frequency of lattice defects and resulting structural weakness.

A model to investigate the actions of microtubule-associated proteins and drugs

To our knowledge, the model described here is the first to bridge the gap between molecular dynamics models (18–22) and dimer-level stochastic microtubule models (9–12,23,24). Thus, the Brownian dynamics modeling approach we employed here provides a method to analyze the effects of microtubule-associated proteins (MAPs) and microtubule-directed drugs for which the relative structure and interaction with the microtubule lattice is known. The simplest cases are interactions that modify one of the parameters included in our model, such as longitudinal or lateral bond energy or bond stiffness. For example, the majority of studies have found that paclitaxel decreases the rigidity of microtubules (40–44), except one that saw the opposite effect (45). Because of its binding position close to the M-loop of the β-monomer, it has been suggested that paclitaxel may function to increase the strength of the lateral bond to overcome nucleotide-based structural changes of the tubulin dimer (26,46). Further, drug binding to the taxane-pocket of β-tubulin structures the M-loop closer to that of the bound state before incorporation into the lattice (47). Structuring of the M-loop implies an increase in stiffness in the presence of paclitaxel, which agrees with molecular dynamics simulations that found the M-loop shows reduced root-mean-squared fluctuations in stable forms of tubulin (18,19). In addition to locally altering the lateral interactions, paclitaxel has long-range allosteric effects on the residues that establish the longitudinal bond interface (T1–T5 and H11 loops) in β-tubulin, increasing the root-mean-squared fluctuations (18).

Though it may not be clear which effect (lateral or longitudinal) of paclitaxel is more important for stabilization, it can be assumed that paclitaxel modifies the intrinsic rigidity of regions within the tubulin dimer involved in establishing interdimer interactions. Our model predicts that increased bond stiffness decreases the on-rate constant and increases the off-rate, meaning that softer bonds lead to a more favorable interaction (more negative ΔG⁰_long; see Fig. S4 and Fig. S5). Despite influencing the on-rate constant, the bond stiffness had no effect on the steric penalties imposed by laterally neighboring protofilaments (see Fig. S6). Interestingly, the intrinsic bond strength estimated from the simulation (ΔG⁰_B) is not sensitive to the bond stiffness. Therefore, the change in ΔG⁰_long is due to the entropic penalty of binding (ΔG⁰_S) (see Fig. S4). Because softer bonds do not constrain the translational and rotational freedom to the extent that stiffer bonds do, the entropic penalty of binding is reduced for softer longitudinal bonds.

These results indicate that the stabilizing modifications of paclitaxel are likely through the longitudinal rather than the lateral bond, because structuring of the M-loop itself will be unfavorable due to an increased entropic penalty. To combat this, however, rearrangement of the M-loop favorably positions several additional residues to form lateral contacts with the neighboring β-tubulin (47). These counteracting effects of paclitaxel could potentially explain experimental results suggesting that paclitaxel has no net effect on the lateral interaction between protofilaments when deformed by osmotic stress (48). Our model predicts that softening of the longitudinal bond should increase the association rate constant in the presence of paclitaxel (see Fig. S4 A), and therefore should increase the polymerization rate. While this increase has not been observed experimentally, it may be difficult to detect because paclitaxel increases the amount of tubulin in polymer form at the expense of free tubulin in solution (49,50). A drop in the free concentration would counteract any increase of the association rate constant such that the on-rate (k_on^∗ = k_on,MT [Tub]) might change only weakly in the presence of paclitaxel.

Our Brownian dynamics simulations emphasize the inefficiency of subunit addition, despite the presence of a favorable interaction potential (17). Of those that reach R = 10 nm, only 0.5% ultimately bind (Fig. 3 A). Additionally, although a high percentage of free subunits get close to binding (N = 1), the vast majority ultimately diffuse away from the microtubule lattice before forming a more specific bond and incorporating into the lattice (∼80%, Fig. 3 A). By increasing the probability that these nearly-bound units ultimately bind, a MAP or microtubule-targeting drug could significantly affect the rate at which subunits incorporate into the lattice (k_on,PF). In fact, it was suggested that XMAP215 functions in this manner to increase the on-rate constant, by stabilizing an intermediate, diffusion-limited collision complex (6). Any molecule that binds at the microtubule end will impose an unfavorable steric penalty, similar to that which we have shown here for one- and two-neighbor protofilaments. Thus, for a MAP to function as proposed for XMAP215, an additional favorable effect will have to overcome this steric effect. Additionally, the free subunit would have to associate very favorably with the MAP, because a relatively weak bond, such as the interdimer lateral bond, does not affect the on-rate constant (Fig. 4). Incorporating an interaction similar to that described for XMAP215 into our model could give estimates for the minimum bond strength necessary to increase the on-rate. Alternatively, if a MAP strengthens (makes more negative) the intrinsic bond free energy or decreases the longitudinal bond rigidity, according to our model it then would be predicted to increase the on-rate constant (Fig. 6, and see Fig. S4 and Fig. S5).

Conclusions

To our knowledge, we have developed the most detailed kinetic and thermodynamic computational model to-date for the association and dissociation of individual tubulin subunits at the microtubule plus-end, and find that it is consistent with both experimental observations and theoretical predictions for tubulin-tubulin interactions. This model demonstrates that the on-rates for individual strands in multistranded polymers are independent of the global position, but that local structure imposes a steric penalty on association. Thus, the microscopic on-rate constant will be an average of the individual nanoscale protofilament on-rate constants and will vary in time as subunits are gained and lost at the dynamic end. These findings are robust with regard to molecular structure and the precise shape of interparticle potential. Therefore, we believe similar effects will arise not only in other linear polymers but in any system where local steric constraints are placed on binding. The simulation results suggest a feedback mechanism that slows subunit net addition as the microtubule tip tapers, which would promote history-dependent catastrophe and the possibility of more efficient search-and-capture by microtubule plus-ends in vivo (51). Additionally, the approach that we employ here provides a model with which to theoretically investigate, at a subnanometer length scale and picosecond-to-millisecond timescale, the actions of microtubule-associated proteins and microtubule-targeting drugs on tubulin kinetics and thermodynamics.