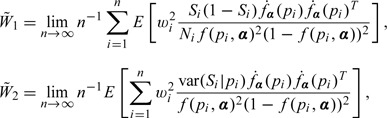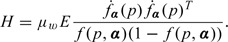Assessing the dependence of sensitivity and specificity on prevalence in meta-analysis

Abstract

We consider modeling the dependence of sensitivity and specificity on the disease prevalence in diagnostic accuracy studies. Many meta-analyses compare test accuracy across studies and fail to incorporate the possible connection between the accuracy measures and the prevalence. We propose a Pearson type correlation coefficient and an estimating equation–based regression framework to help understand such a practical dependence. The results we derive may then be used to better interpret the results from meta-analyses. In the biomedical examples analyzed in this paper, the diagnostic accuracy of biomarkers are shown to be associated with prevalence, providing insights into the utility of these biomarkers in low- and high-prevalence populations.

1. INTRODUCTION

Sensitivity is the probability for a diagnostic test to correctly identify diseased subjects, while specificity is the probability to correctly identify healthy subjects (Zhou and others, 2002, Pepe 2003, Kranowski and Hand, 2009). These two components have long been regarded as the intrinsic accuracy measures of a test independent of the prevalence of the disease (p). That is, the accuracy remains constant across different populations with different disease prevalence. However, in practice such a belief may not be correct. It is sometimes useful to consider the dependence of these accuracy measures on p. In the following, for ease of presentation, we focus on sensitivity, although the results given in this paper are equally applicable to specificity.

The independence of the sensitivity and prevalence has been scrutinized, with many empirical studies suggesting that the disease prevalence may impact the sensitivity. See Brenner and Gefeller (1997) for a comprehensive historical review. Prevalence could influence analyses of accuracy at three levels. First, low prevalence of disease might lead to small number of diseased subjects (denoted by N) included in a study sample. Thus, the estimator $\widehat{\text{se}}$ might have a low precision relative to an estimator obtained from a population with high disease prevalence. Second, as argued in Brenner and Gefeller (1997), the disease prevalence might potentially affect the number of correctly identified diseased subjects (denoted by X). One might assume that the occurrence of the disease is linked to the event that some underlying continuous variable crosses a threshold and that such a latent variable might also determine the binary classification of the diagnostic test. Such dependence might be explained by the disease spectrum being linked to prevalence, for example higher percentages of severe cases in populations with higher prevalences. Third, a human factor might play a role. If prevalence is high, as in a clinical setting, the medical staff who is judging an image might be more aware that the patient might be diseased than in a screening setting with few diseased, but thousands of disease-free individuals. This would result in a positive correlation between prevalence and sensitivity and a negative correlation between prevalence and specificity.

In a given population from a particular study, the distribution of X given N is binomial with probability of success equal to a fixed se. The estimator of sensitivity is naturally $\widehat{\text{se}}=X/N$. However, as we examine sensitivity across multiple studies corresponding to multiple populations, we may view both sensitivity and p as random variables which may be associated. In this paper, we propose methods for understanding how prevalence influences sensitivity. We exclude consideration of case–control studies since they cannot provide the estimation of prevalence.

Meta-analysis provides a convenient avenue for this objective since it synthesizes the results of many studies pertaining to the performance of a diagnostic test. There is a rich literature on statistical methodology for meta-analysis of diagnostic accuracy measures. Moses and others (1993) introduced a useful summary measure to combine multiple studies by plotting the sensitivity against specificity in a single graph. Rutter and Gatsonis (1995, 2001) proposed the regression modeling approach for the meta-analysis. Lijmer and others (2002) further extended the regression method to control confounding factors. Dukic and Gatsonis (2003) examined the role of different thresholds used by different studies. Reitsma and others (2005) analyzed bivariate distribution of sensitivity and specificity across populations via a parametric random-effects approach. Harbord and others (2007) provide a recent review of progress of meta-analysis methodology. However, none of these earlier authors considered modeling the sensitivity as a function of the prevalence. Chu and others (2009) considered joint models for sensitivity and prevalence using a special random-effects structure. Such analyses permit an indirect assessment of associations between sensitivity and prevalence, but do not address these issues using standard tools like correlation and regression analysis. Our goal is to directly apply standard association methods to analyze the bivariate relationships and to develop a rigorous framework for how such methods perform in different scenarios.

The methods developed in this paper are motivated by data commonly encountered in biomedical meta-analyses. We consider two recent examples that are typical of such research. The first, Kang and others (2010), evaluates biomarkers for ovarian cancer, while the second, Kwee and Kwee (2009), assesses the use of imaging for cancer detection. In these publications, it was noted that sensitivities and specificities varied across studies, but the influence of prevalence on such heterogeneity was not explored. Since these systematic reviews involved studies from populations with very different disease spectra, it seems likely that the prevalence of the disease may help explain these observed differences in diagnostic accuracies. The methods we propose will be used to directly evaluate the impact of prevalence in these meta-analyses.

To assess the dependence of diagnostic accuracy measures on the prevalence, we have to resolve several obstacles. First, the true sensitivity (se), a fixed parameter for any given population, is usually unknown and has to be estimated by $\widehat{\text{se}}$. Replacing se with $\widehat{\text{se}}$ could influence the study of its dependence on the prevalence due to the estimation uncertainty. The other difficulty is regarding the unknown prevalence value. In many cross-sectional or cohort studies, it may be possible to estimate p using the observed data and an assessment of the effect of p on se may be carried out using $\widehat{p}$ in place of the true unknown p. Using such an estimated prevalence introduces another source of variability for the analysis. We develop results that demonstrate how the estimation uncertainty of these population-specific parameters influences the inferential procedures.

2. SETTINGS AND KNOWN RESULTS

Suppose se∈Θ⊂[0,1] is the sensitivity for the test, on average, across all different populations. The quantity se may take random value S_i in the ith study population, whereas the prevalence of the disease for that population is p_i∈𝒫⊂(0,1),i = 1,⋯,n. One may regard se as the expectation of the n i.i.d. S_i's. The prevalence p_i might vary across studies and thus are random variables across populations. For the n studies, we assume p_i's are i.i.d. with a probability distribution Π, with μ_p = ∫pdΠ(p) denoting the mean of p_i.

When S_i and p_i are not known a priori we have to estimate them from the observed samples. Denote N_i and M_i as the number of observations used for estimation in study i, respectively. In the simplest design, M_i is the sample size of the ith study and N_i is number of diseased individuals included in this study. We notice that usually a case–control study selects subjects according to their disease status and thus does not provide a valid estimate for the prevalence. Since our primary goal is to show the relationship between the two important population-specific parameters across different studies, we exclude any such kind of studies where the estimates for either S_i or p_i is not available.

We denote ${\widehat{\text{se}}}_i$ to be the estimated sensitivity of the ith study, usually computed as the fraction of positive test recipients among all cases. We use the estimated sensitivity to replace S_i as needed. We assume that such an estimator is conditionally unbiased in that $E({{\widehat{\text{se}}}_i|S}_i,p_i)=S_i$ for the ith study. Such a property can be verified easily for the proportion estimator ${\widehat{\text{se}}}_i=X_i/N_i$ introduced in Section 1. For such estimator, we also have $\text{var}({\widehat{\text{se}}}_i|S_i,p_i)=S_i(1-S_i)/N_i$.

If the ith study is a cross-sectional or cohort study with total sample size M_i, ${\widehat{p}}_i$ can be obtained easily as N_i/M_i, which is the fraction of total number of diseased subjects among the total number of subjects examined. Sometimes one may acquire more complicated estimates ${\widehat{p}}_i$ via statistical modeling (Walter and Irwig, 1988) or combining information from similar observational studies for the particular study population. We assume that ${\widehat{p}}_i$'s are independent and that each ${\widehat{p}}_i$ converges in probability to the true p_i as the sample size M_i based on which ${\widehat{p}}_i$ is constructed tends to infinity. Denote the variance of this estimator as $\text{var}({\widehat{p}}_i|p_i)={\mathrm{\lambda }}_i/M_i$. For a cohort or nested case–control study, λ_i = p_i(1 − p_i).

We argue that ${\widehat{\text{se}}}_i$ and ${\widehat{p}}_i$ are conditionally uncorrelated. This property will be proven by the following equations. Assuming that they are based on the same sample, as with cohort or nested case–control studies, we notice for the ith study (thus S_i and p_i fixed)

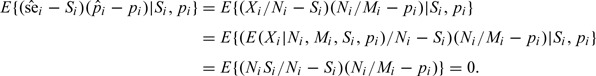Such a fact often leads people to ignore any further examination of the relationship between S_i and p_i. It only claims the conditional uncorrelatedness of two estimators and this conditional uncorrelatedness does not imply their independence. That is, it says nothing about the dependence between S_i and p_i since these two quantities are treated as fixed parameters in the above equations.

Inference for individual p_i and S_i can be made by considering the conditional asymptotical distributions of their estimators. Conditional on p_i, as M_i→∞, we have

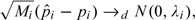(2.1)

and conditional on S_i, as N_i→∞

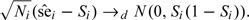(2.2)

In this paper, we assume that asymptotically M_i ^{− 1} = O_p(N_i ^{− 1}), where X = O_p(Y) means X = RY and R is bounded in probability (chapter 2, van der Vaart, 1998). Such a requirement is usually satisfied when the estimations of disease prevalence and sensitivity are based on the same sample.

Of course, it is well known that unconditionally

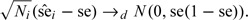Depending on the choice of estimation methods, the unconditional asymptotic distribution of ${\widehat{p}}_i$ may assume a complicated structure, being a mixture of normal distributions with an overall mean equal to μ_p (chapter 17, van der Vaart, 1998).

The purpose of this paper was to explore the relationship between p_i and S_i across different studies. In Section 3, we study a simple correlation measure, while in Section 4, we consider linear/nonlinear regression for predicting sensitivity using disease prevalence.

3. CORRELATION ANALYSIS

A measure of correlation between the random S_i and p_i across populations is

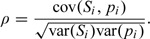(3.1)

Such a Pearson type correlation coefficient is easy to understand and capable of assessing the linear dependence between S_i and p_i. It is important to recognize that the correlation of S_i and p_i is defined with respect to their unconditional joint distribution, with means se and μ_p. In practice, we estimate (3.3) by

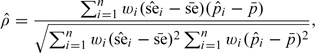(3.2)

where the weights w_i > 0 are chosen to represent the fraction of each specific study population in the overall population, $\stackrel{-}{\text{se}}$ and $\stackrel{-}{p}$ are the sample means of ${\widehat{\text{se}}}_i$ and ${\widehat{p}}_i$, respectively. The weights may be chosen to be the inverses of the study variances and can be normed such that ∑_{i = 1}ⁿw_i = 1. A good choice of weights may reduce the estimation variability of the correlation coefficient. In cases where S_i's or p_i's are known, we plug-in their exact values in (3.4) instead of estimates.

When all study populations are treated with equal emphasis, we may put w_i = 1 uniformly across i. In general, we assume w_i's to be i.i.d. bounded positive variables with a finite expectation μ_w and independent of ${\widehat{\text{se}}}_i,{\widehat{p}}_i,S_i$ and p_i. However, we realize that there are some situations that this assumption is violated when the investigators tend to place higher emphasis on studies with larger estimated prevalence values. The consistency of the estimate (3.4) is unaffected but the asymptotic distribution might be more complicated than what we report below.

The exact mean of $\widehat{\mathrm{\rho }}$ is not equal to ρ. Even in the most ideal case where p_i and S_i are known, it is shown in Meng (2005) that for a finite sample size n ≥ 4 and equal weights,

The absolute relative bias is bounded by n ^{− 1} and therefore usually of no practical concern for a relatively large sample. An unbiased estimator can be constructed by following Olkin and Pratt (1958). The strong consistency of (3.4) is given in the following theorem.

THEOREM 3.1

Suppose E(S_i²) > 0 and E(p_i²) > 0. If n→∞, M_i→∞, and N_i→∞, then the estimate (3.4) converges to (3.3) with probability 1.

The proof of this theorem is provided in the supplementary materials (available at Biostatistics online). Next, by using multivariate central limit theorem on n pairs of independent observations $({\widehat{\text{se}}}_i,{\widehat{p}}_i)$, we can show that under the same conditions in Theorem 3.3,

where

(3.3)

We note that μ_p is the mean prevalence across populations, not the mean prevalence in the combined population, which may differ, depending on the relative contributions of each population to the combined population. The quantity S is a generic notation for a random sensitivity. The standard deviation terms involved in the expression above are defined according to σ_se = {E(S − se)²}^1/2 and σ_p = {E(p − μ_p)²}^1/2.

One should recognize that the variance v² is not influenced by uncertainty in estimation of p_i and S_i. That is, replacing these quantities with their estimators does not influence the variance (3.5). The only quantities influencing this variance are moments from the underlying joint distribution of p_i and S_i. Additional details regarding these results are given in the supplementary materials (available at Biostatistics online). This differs from results in Section 4 when fitting regression models relating p_i to S_i.

The variance can be estimated by plugging in sample versions of various moments. The empirical estimator of v² is

(3.4)

where

The estimator is consistent to the true variance by applying the law of large number.

4. REGRESSION ANALYSIS

We note that the correlation coefficient can only measure the linear dependence and therefore may be rather limited. A finer analysis for the relationship between S_i and p_i can be carried out with a formal regression. We consider the following mean model

(4.1)

where α∈𝒜⊂ℝ^k is an unknown parameter and f is a known link function. We are interested in finding the regression parameter α to determine the relationship between population-specific sensitivity and the prevalence of the population. We assume that variance var(S_i|p_i) exists for all i in this paper.

We seek to estimate the regression parameter by solving the following quasi-likelihood type estimating equations:

(4.2)

where ${\stackrel{.}{f}}_{\mathbf{\alpha }}$ is the derivative of f(p_i,α) with respect to α. Since p_i and S_i are generally unknown in practice, their estimators are substituted in the estimating equations. Denote the solution of the estimating equations (4.8) to be $\widehat{\mathbf{\alpha }}$.

Depending on the form of f, we may choose either linear or nonlinear optimization programs to find the numerical solution $\widehat{\mathbf{\alpha }}$. Provided with the first- and second-order gradient information, most solvers in common statistical computing packages such as R or Matlab can converge quickly to the optimum.

In order to show that the estimator $\widehat{\mathbf{\alpha }}$ is consistent, we have to show that (4.8) is asymptotically unbiased. The proof for the following theorem is contained in the Appendix.

THEOREM 4.1

Suppose the parameter space 𝒜 is compact and ${\stackrel{.}{f}}_{\mathbf{\alpha }}$ is continuous and bounded. If n→∞ and M_i→∞, we have that the solution $\widehat{\mathbf{\alpha }}$ exists and converges to the true parameters α with probability 1.

When p_i and S_i are known, we only need n to go to infinity in the above theorem. The additional requirement for M_i→∞ is necessary when p_i are estimated by ${\widehat{p}}_i$. Basically we need ${\widehat{p}}_i$ to be close enough to the real p_i in the estimation equation so that the regression parameters can be estimated consistently. Otherwise there will be nonignorable biases in the estimates. We do not necessarily need N_i→∞ in practice even though ${\widehat{\text{se}}}_i$ are used to replace S_i. This occurs because of the finitesample unbiasedness property of ${\widehat{\text{se}}}_i$, as shown in the proof in the supplementary materials (available at Biostatistics online).

The following theorem provides the asymptotic distribution property of the estimates.

THEOREM 4.2

Assume the same condition as Theorem 4.1, further assume that ${\stackrel{..}{f}}_{\mathbf{\alpha }}$, the second derivative of f with respect to α, is continuous and bounded. Suppose in probability that ${lim}_{n\to \infty }{n}^{-1}\sum _{i=1}^n{w}_i^2=\check{w}\in (0,\infty )$. If the matrix $E{\stackrel{.}{f}}_{\mathbf{\alpha }}\left(p\right){\stackrel{.}{f}}_{\mathbf{\alpha }}{\left(p\right)}^T$ is nonsingular, then the sequence is asymptotically normal with mean zero and covariance matrix $H^{-1}({\stackrel{\sim }{W}}_1+{\stackrel{\sim }{W}}_2)H^{-1}$. where

and

When p_i and S_i are known, the covariance matrix reduces to $H^{-1}{\stackrel{\sim }{W}}_2{H}^{-1}$. In the above results, $H^{-1}{\stackrel{\sim }{W}}_2{H}^{-1}$ reflects the estimation variation for the conditional analysis of S_i on p_i. $H^{-1}{\stackrel{\sim }{W}}_1{H}^{-1}$ corresponds to the additional variation due to replacing S_i with its estimator ${\widehat{\text{se}}}_i$. If at least one N_i is considered far from being infinity, ${\stackrel{\sim }{W}}_1$ does not vanish and affects the overall variance even if n tends to infinity. The covariance matrix can be approximated by the empirical estimator in practice.

5. SIMULATION STUDIES

To evaluate the performance of the proposed methods, we conduct simulation studies in this section. We set the number of studies n = 15 and 30 and generated p_i from a uniform distribution on [0.1,0.9]. For each study, we fix the total sample size M_i = 200 and simulated the number of cases N_i from a binomial distribution with parameters M_i and p_i. We then considered the following three models for sensitivity:

They represent three typical regression models: linear regression, logit link binary regression and complementary log–log link binary regression. The sensitivity S_i is generated from a Beta distribution (Gupta and Nadarajah, 2004) with two parameters given by

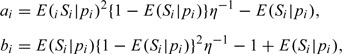where the variance parameter η is chosen so that the Monte Carlo signal-to-noise ratio is roughly 4:1. One can easily verify that the mean of this beta distribution is E(S_i|p_i). For each study, we simulated the number of true-positive X_i from a binomial distribution with parameters N_i and S_i. A total number of 1000 simulations were conducted.

We summarized in Table 1 the results regarding estimation of the correlation coefficient and α in the correctly specified regression model. These results include biases and empirical and model-based variances. Only results for the practically relevant case of unknown S_i and p_i are provided, in which ${\widehat{p}}_i$ and ${\widehat{\text{se}}}_i$ are utilized in the estimation. The correlation estimates have a slight downward bias. In fact, linear correlation is not a sensible measure for Models 2 and 3 since the underlying relationship is not linear. The biases decrease as we enlarge the sample size n. One can see that all the regression parameters and standard errors can be consistently estimated with the proposed methods. Therefore for a study with a small or moderate sample size the regression model approach seems to outperform the simple correlation coefficient since the regression parameters can be estimated more accurately, when the model is correctly specified.

Table 1.

Estimation of correlation and regression parameters under three models over 1000 simulations

Model	Parameter	True	n	Est.	SD	SE
1	ρ	0.85	15	0.78	0.108	0.114
			30	0.82	0.082	0.086
	α0	0.5	15	0.49	0.004	0.003
			30	0.50	0.002	0.002
	α1	0.5	15	0.50	0.014	0.013
			30	0.50	0.010	0.009
2	ρ	0.88	15	0.77	0.13	0.15
			30	0.83	0.11	0.12
	α0	1	15	0.89	0.69	0.75
			30	0.95	0.55	0.60
	α1	3	15	3.09	3.20	3.54
			30	2.98	2.15	2.26
3	ρ	0.94	15	0.85	0.12	0.10
			30	0.90	0.095	0.093
	α0	− 0.5	15	− 0.54	0.035	0.038
			30	− 0.48	0.022	0.026
	α1	− 1.5	15	− 1.46	0.12	0.12
			30	− 1.51	0.092	0.097

True, fixed true parameter values; n, sample size; Est., sample means of the estimated parameters; SD, empirical standard deviations of the parameter estimates; SE, means of the estimated standard errors.

To understand the impact of model misspecification, we next consider fitting a model in which f may be misspecified. That is, the sensitivity is simulated from Model i, while we use Model j to estimate parameters (i,j = 1,2,3;i¬j). We investigate how the predicted sensitivity ${\widehat{S}}^{\text{pred}}$ based on the wrong model might differ from the true sensitivity. The results for the prediction error

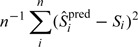are summarized in Table 2. It is noted that when linear model (Model 1) was mistakenly chosen for nonlinearly generated data (Models 2 and 3), the prediction errors were somewhat smaller. Nonetheless, in all settings, the prediction errors for misspecified models are close to the prediction errors for correctly specified models. The procedures are thus to some degree insensitive to the model choices. A similar phenomenon has been witnessed in the analysis of experimental design (chapter 12, Wu and Hamada, 2000) that for a small sample size n usually there may be little qualitative difference between the use of various models or parameterizations. In practice, since we cannot evaluate the true prediction errors due to the lack of knowledge of S_i, we choose to use a leave-one-out cross-validation (CV) procedure to estimate the prediction error and select among candidate models. We may replace ${\widehat{S}}_i^{\text{pred}}$ with the predicted sensitivity for the ith study based on a model built with data excluding the ith study and replace S_i with ${\widehat{\text{se}}}_i$.

Table 2.

Prediction errors for three model specifications and the percentages of the model being selected by CV (in parentheses)

Actual model	n	Specified model
		1	2	3
1	15	0.0062	0.0068	0.0069
		(65.0)	(16.5)	(18.5)
	30	0.0059	0.0065	0.0067
		(72.8)	(15.3)	(11.9)
2	15	0.0029	0.0029	0.0032
		(15.7)	(61.1)	(23.2)
	30	0.0026	0.0025	0.0026
		(8.3)	(72.5)	(19.2)
3	15	0.0033	0.0033	0.0032
		(29.4)	(19.3)	(51.3)
	30	0.0028	0.0028	0.0027
		(19.1)	(12.6)	(69.3)

We thus also report the frequency that CV correctly selects the true model that generates the data in the simulations. The results are reported in the brackets in Table 2, suggesting that CV indeed pinpoints the correct model with high probability. The performance of CV improves as sample size increases.

6. EXAMPLES

Example 1: We consider a meta-analysis for evaluating the diagnostic performance of preoperative CA-125 levels in the assessment of suboptimal cytoreduction in ovarian cancer. Kang and others (2010) reviewed 15 prospective studies that reported sensitivities, specificities, and prevalences. These data are included in Table 1 of the supplementary materials (available at Biostatistics online). The scatter plots of sensitivity and specificity versus prevalence are given in Figure 1. One observes that the specificities of the test are generally quite high regardless of prevalence, while the sensitivities show a decreasing trend.

Fig. 1.

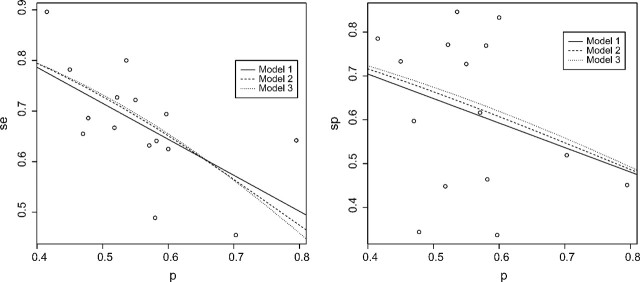
Fitted models for sensitivity (left panel) and specificity (right panel) for Example 1.

The Pearson correlation coefficient between the estimated sensitivity and prevalence is − 0.62 (95% confidence interval [ − 0.86 to − 0.16]), while that between the estimated specificity and prevalence is − 0.30 (95% confidence interval [ − 0.70 to 0.24]). There is no significant linear correlation between specificity and prevalence but a rather strong negative correlation between sensitivity and prevalence, which is statistically significant. To better understand the dependence of accuracy measures on prevalence, we conducted a regression analysis.

For both sensitivity and specificity, we explored using the identity, logit, and complementary log–log link functions (Models 1–3 given in Section 5) to model the association with the prevalence. The estimated parameters and variance estimates are given in Table 3. The fitted response curves were superimposed in the scatter plots of the observed sensitivity–specificity versus the prevalence in Figure 1. For sensitivity, for all three models, the coefficients α₁ are significant in Table 3. These results indicate a strong decreasing relationship between se and prevalence. The CVs for predicting the sensitivity are 0.0125, 0.0145, and 0.0171 for the three models, respectively. The simple linear model may be the most appropriate choice over the observed range of prevalences, although the CV values are fairly small for all models. For specificity, we found no dependence on prevalence since in Table 3 none of the coefficients α₁ was significant. The CVs for predicting the specificity are 0.0325, 0.0329, and 0.0330 for the three models, respectively. These values are quite large in comparison with those for specificity and indicate that the three models perform similarly, as one would expect if prevalence and specificity are not strongly associated.

Table 3.

Fitted results for two examples

	Model 1			Model 2			Model 3
	Est.	SE	P value	Est.	SE	P value	Est.	SE	P value
Example 1
se
α0	1.07	0.14	< 0.0001	2.80	0.70	0.0016	− 2.69	0.59	0.005
α1	− 0.71	0.24	0.0131	− 3.63	1.25	0.0121	3.05	1.05	0.0125
sp
α0	0.92	0.27	0.0048	1.90	1.24	0.1500	− 1.90	0.98	0.0739
α1	− 0.55	0.48	0.2698	− 2.44	2.20	0.286	1.95	1.73	0.2804
Example 2
se
α0	0.68	0.10	< .0001	0.81	1.22	0.5290	− 1.01	1.18	0.4110
α1	0.45	0.24	0.0846	4.03	2.32	0.0830	− 3.72	2.38	0.0970
sp
α0	0.65	0.05	< .0001	− 0.79	0.63	0.2309	0.59	0.60	0.3446
α1	0.48	0.12	0.0024	7.13	1.42	0.0005	− 6.84	1.37	0.0005

Est., estimated regression coefficient; SE, standard error for the estimated parameter; P value, corresponding p value for testing whether the parameter is different from zero.

In summary, by aggregating evidence from multiple studies, we can conclude that sensitivity and specificity have different relationships with disease prevalence. The sensitivity is clearly decreasing as prevalence increases, with a simple linear model providing a reasonable approximation to this relationship, as evidenced in Figure 1. Results for specificity are consistent with the linear correlation analysis—the relationship between specificity and prevalence is weak, even when considering nonlinear association models.

Example 2: We consider another meta-analysis for the accuracy of combined 18F-fluoro-2-deoxyglucose positron emission tomography/computed tomography (FDF-PET/CT) in the detection of primary tumors where 11 prospective studies were investigated (Kwee and Kwee, 2009). The data for sensitivities, specificities, and prevalences from this study are included in Table 2 of the supplementary materials (available at Biostatistics online). The scatter plots of sensitivity and specificity versus prevalence are given in Figure 2 along with the fitted superimposed regression curves from the three models.

Fig. 2.

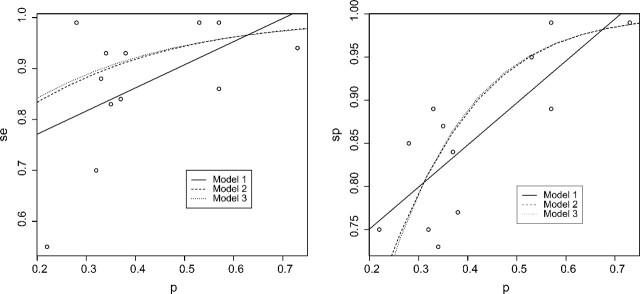
Fitted models for sensitivity (left panel) and specificity (right panel) for Example 2.

The Pearson correlation coefficient between the estimated sensitivity and prevalence is 0.52 (95% confidence interval [ − 0.08 to 0.84]), while that between the estimated specificity and prevalence is 0.79 (95% confidence interval [0.39–0.94]). The correlation between sensitivity and prevalence is moderately strong but not statistically significant, while that between specificity and prevalence is quite strong and statistically significant.

The estimated regression coefficients under three different models are also given in Table 3. For sensitivity, the coefficients α₁ are significant at level 0.10 but not significant at level 0.05. There is only a moderate dependence between sensitivity and prevalence. The CVs for predicting the sensitivity are 0.0183, 0.0180, and 0.0182 for the three models. For specificity, we found the slope coefficients α₁ are significant under three models. The p values are much more significant for logistic and complementary log–log link models than the simple linear model. The models with these more complicated links are thus more likely to detect the association between the specificity and the prevalence. The CVs for predicting the specificity are 0.0038, 0.0032, and 0.0033 for the three models, respectively. The logistic model seems superior, particulary relative to the linear model, confirming the nonlinear pattern in Figure 2. One may conclude that the specificity of the test tends to increase as the prevalence increases and that the increasing trend may be well described using the logistic link model.

7. DISCUSSION

Our focus has been on the dependence of the sensitivity and specificity on the prevalence. There are other intrinsic accuracy measures such as the receiver operating characteristic (ROC) curve and the area under the ROC curve (AUC) for a diagnostic test. Since ROC and AUC are derived from the sensitivity and specificity, their dependence on the prevalence can be inferred subsequently based on the known results for the sensitivity and specificity.

We propose our methodology mainly for studies where an estimate of p_i is available. In a retrospective study, the prevalence cannot be directly estimated. Lack of an estimator ${\widehat{p}}_i$ muddies the waters, especially when external or historical information for the prevalence is unattainable for the study. A potential statistical framework is to jointly model the distribution of S_i and p_i, which may enable the use of studies without ${\widehat{p}}_i$.

We have analyzed the prevalence dependence separately for sensitivity and specificity. It has been advised in Rutter and Gatsonis (1995, 2001) and Reitsma and others (2005) that a more coherent analysis might involve analyzing the dependence of sensitivity and specificity on the prevalence jointly. A limitation of existing joint modeling approaches is that they may not provide simple assessments of the association between diagnostic accuracy and prevalence. Random effects models have been studied (Arends and others, 2008; Chu and others, 2009; Reitsma and others, 2005), with the dependencies implicitly captured via latent variables. In general, data analysts who are interested in assessing the prevalence dependence of diagnostic accuracy measures may find the simplicity of interpretation and the ease of implementation of the proposed methods in the current paper. Another practical concern for the joint model is the potential model misspecification. If the joint model is incorrectly specified, nonignorable bias might enter the model-based parameter estimates.

SUPPLEMENTARY MATERIALS

Supplementary material is available at http://biostatistics.oxfordjournals.org.

FUNDING

Academic Research Funding (R-155-000-109-112) and National Medical Research Council (NMRC/NIG/0054/2009).