Contributions of Cell Growth and Biochemical Reactions to Nongenetic Variability of Cells

Abstract

Cell-to-cell variability in the molecular composition of isogenic, steady-state growing cells arises spontaneously from the inherent stochasticity of intracellular biochemical reactions and cell growth. Here, we present a general decomposition of the total variance in the copy number per cell of a particular molecule. It quantifies the individual contributions made by processes associated with cell growth, biochemical reactions, and their control. We decompose the growth contribution further into variance contributions of random partitioning of molecules at cell division, mother-cell heterogeneity, and variation in cell-cycle progression. The contribution made by biochemical reactions is expressed in variance generated by molecule synthesis, degradation, and their regulation. We use this theory to study the influence of different growth and reaction-related processes, such as DNA replication, variable molecule-partitioning probability, and synthesis bursts, on stochastic cell-to-cell variability. Using simulations, we characterize the impact of noise in the generation-time on cell-to-cell variability. This article offers a widely-applicable theory on the influence of biochemical reactions and cellular growth on the phenotypic variability of growing, isogenic cells. The theory aids the design and interpretation of experiments involving single-molecule counting or real-time imaging of fluorescent reporter constructs.

Introduction

Single-cell experiments show that isogenic cells generally differ markedly in the copy numbers of mRNA and protein molecules (1,2) and a multitude of other system properties, such as cell volume, growth rate, and phenotypic state (3–5). These experiments exploit single-molecule counting methods (6) or fluorescent reporter constructs (7) to quantify the levels of specific molecules in single cells. A wide range of processes have been shown to contribute to nongenetic cell-to-cell variability (8): e.g., fluctuation-induced imbalances in molecule synthesis and degradation (9,10), synthesis control (10), synthesis bursts (11), partitioning of molecules at cell division (12), bistable switching (13), and noise propagation (14).

In most single-cell studies, stochastic models are used to explain experimental findings. However, often those models highlight only a particular aspect of cellular stochasticity and they are highly simplified to overcome the problem of kinetic parameter uncertainty. As a consequence, it often remains unclear to what extent a particular stochastic phenomenon contributes to the total cell-to-cell variability because it is only one out of several and possibly many. Thus, the variance in the copy number of a molecule across a population of isogenic cells, growing in a balanced, exponential manner, results from several sources of stochasticity. For instance, cells that have just divided tend to have fewer molecules than cells that have progressed further along the cell cycle, because at the end of the cell cycle the volume of the cell and its molecular content should have doubled. Cells that have progressed in the cell cycle equally far can also differ in molecular content, because the number of molecules produced and degraded until this moment in time varies between cells, due to biochemical reaction stochasticity. In addition, two daughter cells that derive from the same mother cell can vary in molecular content due to partitioning stochasticity. Moreover, two daughter cells from different mother cells can vary because their two mother cells differed in molecule content at the time of division. Thus, the net variance of a molecule copy number is the result of the accumulation of various stochastic effects.

Different stochastic processes, associated with either biochemical reactions or cellular growth, contribute to total molecular noise. The relative sizes of those contributions will generally depend on the organism. For instance, Escherichia coli and Saccharomyces cerevisiae have completely different division statistics; E. coli divides symmetrically and S. cerevisiae asymmetrically. Genes encoded on plasmids, rather than genomes, may follow very different stochastic dynamics. Thus, being able to disentangle stochastic contributions to molecular noise allows for the identification, comparison, and characterization of mechanisms for specific organisms.

We present a variance decomposition in terms of the contributions of a wide range of cell growth and biochemical reaction processes. Such variance decomposition methods have recently been introduced to the field of stochastic cell biology (8,15–20). Here we generalize this method for cells engaging in exponential, steady-state growth. Our method offers a powerful method to analyze the causes of cell-to-cell variability without having to consider complex mechanistic models of underlying molecular reactions and the cellular growth process. Variance decomposition methods offer great potential for the analysis of experimental data and for experimental design.

Results

Steady-state growth of a population of cells

In this work, we decompose the variability in the copy number of a particular molecule $\mathbb{X}$—a protein or mRNA—across a population of growing, isogenic cells in terms of different processes. Generally, individual cells progress through the cell cycle asynchronously. Therefore, we find cells at different cell-cycle stages in a growing population; some cells have just divided, others have divided some time ago or are about to divide. The fraction of cells that have reached a particular cell-cycle progression status, a, is described by the probability distribution, u(a). Here a denotes the time that has passed since the last cell division. In balanced growth, this distribution, u(a), is completely determined by the interdivision time distribution (21), a probability distribution for the interdivision (or generation) time. T is the time period between subsequent cell divisions, which sets the population growth rate, denoted by μ (=(ln 2)/T).

Molecule turnover is a basic feature of a growing cell population (Fig. 1 A). While cells grow in volume and divide, new molecules need to be synthesized to compensate for their losses due to partitioning into daughter cells and their degradation. The entire molecular content of a just divided (daughter) cell needs to be doubled during the cell cycle (on average) before it has become a mature mother cell ready for cell division.

Figure 1.

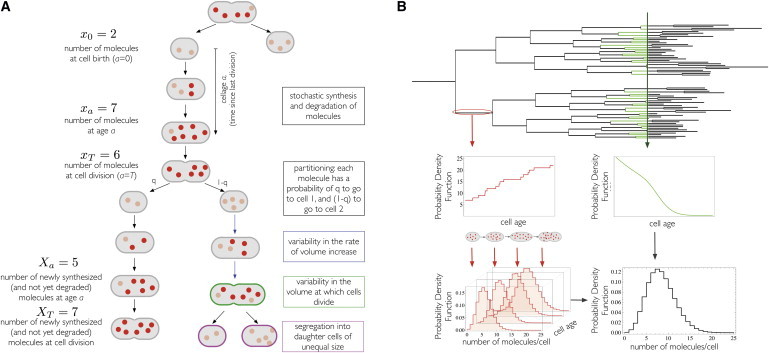
Overview of the biochemical reaction and cell-growth processes contributing to cell-to-cell variability. (A) Heterogeneity due to (i) biochemical reactions, i.e., fluctuations in rate of molecule synthesis and its regulation, and (ii) due to binomial partitioning of molecules at cell division, i.e., variability in molecule content of mother cells, and (iii) variability in partitioning. Molecules inherited from the mother cell are shown in faded red, newly synthesized molecules in bright red. (B) Heterogeneity due to the balanced growth process. At a specific cell-cycle stage, the molecule copy numbers of cells follow different probability distributions. Each cell-cycle stage has a certain probability of occurrence. The net distribution of molecule copy number per cell in a steady-state growing population of isogenic cells is given by marginalizing the conditional copy number distribution over the cell-cycle stage distribution. To see this figure in color, go online.

We consider the steady-state growth of the cell population, so-called balanced growth. Balanced growth requires that the intrinsic variables of the system—those expressed per unit cell mass or volume—follow a constant probability distribution (independent of time). Examples of such intrinsic variables are: the cell-cycle stage, the generation time, the molecule copy number per cell at a given stage, and the cell volume distribution.

Fig. 1 illustrates the key processes associated with cell growth and biochemical reactions that contribute together to variance in the molecule copy number across a population of isogenic cells at balanced growth. Fig. 1 A takes a single-cell perspective and emphasizes the processes at this level contributing to cell-to-cell heterogeneity. In this figure, four stochastic contributions are distinguished:

• 1.Molecular partitioning at cell division,
• 2.Cell volume growth,
• 3.Net molecule synthesis, and
• 4.Variability of mother cell volume and molecule copy number before division.

Fig. 1 B addresses the two main stochastic contributions arising at the population level, i.e.:

• 1.Cells at the same cell-cycle stage have differences in molecule content, and
• 2.The average molecule content varies with cell-cycle stage.

Those two sources are a direct consequence of the single-cell stochasticity mechanisms described in Fig. 1 A. Another source derives from the fact that cells pass through the cell cycle asynchronously and that different cell-cycle stages coexist at any moment in time. The resultant variability in molecule content across the population emerges from those two cell-cycle stage-dependent stochasticity contributions at the population level weighted by the probability distribution for the cell-cycle stage. Hence, decomposing the net variance into its causal components tells us how a certain degree of molecular noise is achieved for a given cell type at particular conditions.

Decomposition of molecule copy number variance into biochemical reaction and cell growth contributions

The mathematical notations that we use throughout this article are summarized in Table 1. The number of molecules at a certain cell-cycle stage, a, can be expressed as the sum of the number of molecules that have survived until stage a and that were either inherited from the mother cell or newly synthesized. Accordingly, the average copy number at stage a then equals

$$\langle x_a\rangle =p\left(a\right)\langle x_0\rangle +\langle X_a\rangle ,$$ (1)

where p(a) denotes the survival probability up to cell-cycle stage a for a molecule that was inherited from the mother cell. For independent first-order degradation with rate constant k_d, this probability equals $e^{-k_{d}a}$ and decays with cell-cycle progression. On average, 〈x₀〉 molecules were obtained from the mother. As cells progress through the cell cycle, the average copy number of any molecule doubles from cell birth to cell division: 〈x_T〉 = 2〈x₀〉. From this we can conclude that short-lived proteins require more synthesis, i.e., at most 〈X_T〉 = 〈x_T〉, whereas stable molecules (k_d = 0) require less; 〈X_T〉 = 1/2 〈x_T〉, because the molecules obtained at division are not degraded.

Table 1.

Notations

Notation	Explanation
〈⋅〉, 〈δ2⋅〉	Mean and variance
〈⋅|⋅〉, 〈δ2⋅|⋅〉	Mean and variance of a random variable conditional on a second random variable
T	Generation time
a	Cell-cycle stage (0 ≤ a ≤ T)
xa = x|a	Copy number per cell of molecule $\mathbb{X}$ at cell-cycle stage a
${\overline{x}}_0$	Number of molecules that were inherited from the mother cell and not yet degraded up to cell-cycle stage a
Xa = X|a	Number of newly synthesized $\mathbb{X}$ molecules because the last division up to cell-cycle stage a that have not been degraded.
u(a)	Cell-cycle stage distribution; $u\left(a\right)=\ln 2/T{2}^{1-\frac{a}{T}}$ for deterministic interdivision times
μ	Specific growth rate of the population; μ = ln2/T for deterministic interdivision times
p(a) = $e^{-k_{d}a}$	Survival probability of molecule $\mathbb{X}$
1/kd	Intrinsic lifetime of molecule $\mathbb{X}$
q	Probability that a molecule of $\mathbb{X}$ at cell division will be inherited by a particular daughter cell

Because cells at different cell-cycle stages have different molecule content, the variance in the molecule copy number has a contribution due to differences in cell-cycle stage and to differences in molecules content at a specific cycle stage (Fig. 1 B). Using the law of total variance, we can decompose the variance in the molecule copy number as

$$\langle {\delta }^{2}x\rangle =\underset{\text{variance}\text{due}\text{to}\text{differences}\text{in}\text{cell}\text{cycle}\text{stage}}{\underbrace{\langle {\delta }^2\langle x_a\rangle \rangle }}+\langle \langle {\delta }^2{x}_a\rangle \rangle .$$ (2)

Here 〈δ²〈x_a〉〉 is the variance in x due to fact that the average number of molecules increases with cell-cycle stage. We emphasize that 〈δ²〈x_a〉〉 is not indicating cell-to-cell variability due to stochastic fluctuations, rather it arises solely from molecule synthesis accompanying the growth process. The second variance term captures functional stochasticity, the variance in the copy number at a cell-cycle stage averaged over all possible stages. This term includes biochemical noise (contributions from molecule turnover) and partitioning at cell division.

We consider only systems without feedback, i.e., the number of newly synthesized molecules does not depend on currently available or past numbers of molecules. We limit ourselves to first-order, independent degradation of molecules. The synthesis process is completely general and can include bursts, cell-cycle-dependent synthesis rates, and sources of extrinsic noise. Regulation by upstream factors, multistep, or bursting synthesis is accounted for through the synthesis statistics of the molecule of interest (discussed in more detail below).

Derivation of the complete variance decomposition relation

The number of molecules at cell-cycle stage a equals the sum of molecules that were either obtained from the mother cell or newly synthesized and that have not yet been degraded. Accordingly, the variance in the number of molecules at cell-cycle stage a equals the variance of the sum of those random variables and their covariance,

$$\langle {\delta }^2{x}_a\rangle =\langle {\delta }^2{\overline{x}}_0\rangle +2\text{cov}\left({\overline{x}}_0,X_a\right)+\langle {\delta }^2{X}_a\rangle .$$ (3)

We note that even without feedback the covariance term need not be zero: the synthesis rate of new molecules and the number of molecules at birth can both depend on a hidden variable, e.g., an upstream regulatory factor.

The first term in Eq. 3 can be further decomposed. We assume independent degradation of molecules such that for a given number of molecules at cell birth the number of inherited molecules that survive at least up to cell-cycle stage a is distributed according to a binomial distribution with mean p(a)x₀ and variance p(a)(1 – p(a))x₀. Application of the law of total variance to $\langle {\delta }^2{\overline{x}}_0\rangle$ yields

$$\langle {\delta }^2{x}_a\rangle =p{\left(a\right)}^2\langle {\delta }^2{x}_0\rangle +p\left(a\right)\left(1-p\left(a\right)\right)\langle x_0\rangle +2p\left(a\right)cov\left(x_0,X_a\right)+\langle {\delta }^2{X}_a\rangle .$$ (4)

The variance in the number of inherited molecules, 〈δ²x₀〉, can be decomposed into a contribution from variance in the molecular composition of mother cells and variance deriving from the partitioning process:

$$\langle {\delta }^2{x}_0\rangle =\underset{\text{partitioning}\text{variance}}{\underbrace{\langle \langle {\delta }^2{x}_0|x_T\rangle \rangle }}+\underset{\text{variance}\text{due}\text{to}\text{mother}\text{cell}\text{variability}}{\underbrace{\langle {\delta }^2\langle x_0|x_T\rangle \rangle }}.$$ (5)

Combining Eqs. 2, 4, and 5 yields the complete variance decomposition relation,

$$\langle {\delta }^{2}x\rangle =\stackrel{\text{Growth}\text{-}\text{induced}\text{variance}}{\overbrace{\stackrel{\text{Decayed}\text{variance}\text{of}\text{molecules}\text{at}\text{cell}\text{birth},\langle p{\left(a\right)}^2\rangle \langle {\delta }^2{x}_0\rangle }{\overbrace{\underset{\text{partitioning}\text{variance}}{\underbrace{\langle p{\left(a\right)}^2\rangle \langle \langle {\delta }^2{x}_0|x_T\rangle \rangle }}+\underset{\text{variance}\text{due}\text{to}\text{mother}\text{cell}\text{variability}}{\underbrace{\langle p{\left(a\right)}^2\rangle \langle \langle {\delta }^2{x}_0|x_T\rangle \rangle }}}}+\underset{\text{variance}\text{due}\text{to}\text{differences}\text{in}\text{cell}\text{cycle}\text{stage}}{\underbrace{\langle {\delta }^2\langle x_a\rangle \rangle }}}}+\underset{\text{Reaction}-\text{induced}\text{variance}}{\underbrace{\underset{\text{variance in the degradation of}\text{molecules}\text{obtained at division}}{\underbrace{\langle p\left(a\right)\left(1-p\left(a\right)\right)\rangle \langle x_0\rangle }}+\underset{\text{variance}\text{in}\text{synthesis}\text{and}\text{extrinsic}\text{noise}\text{in}\text{newly}\text{synthesized}\text{molecules}\left(\text{networking}\right)}{\underbrace{\langle \langle {\delta }^2{X}_a\rangle \rangle }}+\underset{\text{covariance}\text{due}\text{to}\text{dependence}\text{on}\text{extrinsic}\text{factors}}{\underbrace{2\langle p\left(a\right)cov\left(x_0,X_a\right)\rangle }}}}.$$ (6)

The averages 〈p(a)²〉 and 〈p(a)(1 − (a))〉 can be expressed in terms of the dimensionless parameter ratio k_d/μ. This ratio describes the rate of loss of the memory of cell division variance and variance in the survived number of molecules obtained at division (see the Supporting Material). If this ratio is large, the molecule lives much shorter than the generation time and 〈p(a)²〉 ≈ 0 and 〈p(a)(1 − p(a))〉 ≈ 0. In this limit, the variance in x is determined only by the variance introduced during the synthesis of new $\mathbb{X}$ molecules and due to differences in cell-cycle progression.

We noted earlier that most of the theory developed in the field of stochastic cell biology concerned the analysis of noise creation and propagation in different biochemical circuits, independent of the growth process of cells. Those studies all concern the exact value of 〈〈δ²X_a〉〉 and express this in terms of biochemical kinetics. All the other terms either are due to the growth process alone or concern a coupling between biochemical reactions and the growth process and are not considered in most studies. In the following paragraphs, we will further discuss each of these contributions separately, and introduce several mechanisms relevant for cell biology.

Note that the terms 〈〈δ²x₀|x_T〉〉, 〈δ²〈x₀|x_T〉〉, 〈δ²〈x_a〉〉, and 〈x₀〉 can all be determined directly from time-lapse microscopy images with a fluorescent reporter construct. In combination with a separate measurement of the degradation rate, the first four terms on the right-hand side of Eq. 6 can therefore be determined. If using a stable protein, i.e., k_d ≈ 0, the last two terms can also be directly determined from time-lapse images: after background correction and possibly a correction for photobleaching, the newly accumulated fluorescence of a growing cell is due to new synthesis events. The variance at cell-cycle stage a equals the sum of the variance at cell birth, the variance in new synthesis, and twice their covariance. By conditioning on the amount of reporter protein at cell birth, x₀, the last two terms in Eq. 6 can be separated. If active degradation of the reporter construct is nonnegligible, these two terms can still be determined experimentally by bleaching all existing fluorescent molecules and then recording time-lapse images that should only show the net new synthesis. Conditioning on x₀ again allows for a separation of 〈δ²X_a〉 and p(a)cov(x₀,X_a).

Cell-division variance

One contribution to the variance in the copy number of a molecule stems from the variance introduced during cell division (discussed in detail by Huh and Paulsson (12)) and the extent by which this has decayed during the generation time of a cell. We found that this decay depends on the parameter ratio k_d/μ. Next, we will express the variance term in a newborn daughter cell, 〈δ²x₀〉, in terms of the mother cell variance and the mechanism of cell division. Here we limit ourselves to independent (binomial) partitioning of molecules but allow the partition probability, q (i.e., the probability for each molecule to end up in one daughter cell) to have a distribution by itself, denoted by g(q) (with 〈q〉 = 1/2).

The condition of balanced growth together with a partitioning mechanism leads to equations for the moments of the copy number distributions at cell birth and at cell division (see the Supporting Material). For the mean, we have 〈x₀〉 = 〈x_T〉/2 and to obtain the variance 〈δ²x₀〉, we apply the law of total variance twice (assuming that q and x_T are independent; see the Supporting Material):

$$\langle {\delta }^2{x}_0\rangle =\underset{\langle {\delta }^2\langle x_0|q\rangle \rangle ,\text{variance}\text{due}\text{to}q\text{fluctuations}}{\underbrace{\langle {\delta }^{2}q\rangle {\langle x_T\rangle }^2}}+\underset{\langle \langle {\delta }^2{x}_0|q\rangle \rangle \text{cell}\text{-}\text{division}\text{variance}}{\underbrace{\stackrel{\text{partitioning}\text{variance}}{\overbrace{\left(1/4-\langle {\delta }^{2}q\rangle \right)\langle x_T\rangle }}+\stackrel{\text{variance}\text{due}\text{to}\text{mother}\text{cell}\text{heterogeneity}}{\overbrace{\left(1/4+\langle {\delta }^{2}q\rangle \right)\langle {\delta }^2{x}_T\rangle }}}}.$$ (7)

We note that rearrangement of this equation leads to the same result as given in Huh and Paulsson (12). This equation indicates that fluctuations in the partitioning probability, for instance because of different volumes of two sister cells or intracellular organization (12), enhance 〈δ²x₀〉. For a molecule that is degraded rapidly (its half-life is short in comparison to the generation time; k_d/μ is high), the variance at cell division, 〈δ²x_T〉, is mainly determined by the variance of molecules that were newly synthesized during the last cell cycle. In contrast, for stable molecules (k_deg ≈ 0) 〈δ²x_T〉 = 〈δ²x₀〉 + 〈δ²X_T〉, i.e., the variance at cell division has a significant contribution from the variance at cell birth and therefore also from the fluctuations in q during previous divisions. Therefore, for a stable molecule, fluctuations in q are a significant contribution to the copy number noise. The population level copy number noise for a stable molecule that is synthesized by a zero-order reaction can be written as (see the Supporting Material for a derivation)

$$\frac{\langle {\delta }^{2}x\rangle }{{\langle x\rangle }^2}=\frac{1}{\langle x\rangle }+\underset{\text{noise}\text{due}\text{to}\text{distribution}\text{of}\text{cell}\text{cycle}\text{stages}\left(\text{see}\text{following}\text{paragraph}\right)}{\underbrace{1-2\text{ln}{\left(2\right)}^2}}+\underset{\text{noise}\text{due}\text{to}\text{fluctuations}\text{in}q}{\underbrace{\frac{16\text{ln}{\left(2\right)}^2\langle {\delta }^{2}q\rangle }{3-4\langle {\delta }^{2}q\rangle }}}.$$ (8)

For many microorganisms, the coefficient of variation of q is in the range of 3–7% (22,23) (i.e., 〈δ²q〉 = 0.0075–0.0175)). As a result, the last term in this equation lies between 0.019 and 0.046. For a molecule with high copy numbers, where intrinsic noise (1/〈x〉)) is low, this contribution can become quite significant.

Variance due to the distribution of cell-cycle stages

The third variance term in Eq. 6, 〈δ²〈x_a〉〉, quantifies the differences in the average copy numbers at different cell-cycle stages. Due to binary divisions, the average copy number per cell needs to double during a generation time (Fig. 2). Therefore, cells in an asynchronous population have different cell-cycle progression stages and older cells will, on average, have a higher copy number than younger cells. The variance deriving from these differences, 〈δ²〈x_a〉〉, does in general not constitute a source of functional noise and derives solely from the growth process. It does, however, make a serious contribution to copy number noise as we shall show in this section. This contribution becomes negligible when noises in molecular concentration are considered (shown in a later section).

Figure 2.

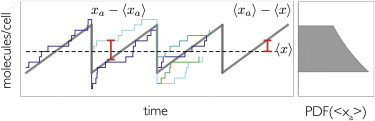
Cell-stage-dependent and independent noise contributions. (Thick gray line) Average copy number as function of cell-cycle stage; (blue and green) results of individual stochastic simulations. (Dashed black line) Population average copy number. Differences between the blue and gray lines at a fixed cell-cycle stage (x_a − 〈x_a〉) lead to functional noise, whereas the differences between the cell-cycle stage-dependent average and the total average (〈x_a〉 − 〈x〉) derive from the growth process alone. The distribution of the cell-cycle stage-dependent averages is shown on the right. To see this figure in color, go online.

If the synthesis rate is constant throughout the cell cycle, the average copy number of produced molecules at a certain cell-cycle stage can for a simple model be written as

$$\langle X_a\rangle =\frac{k_s}{k_d}\left(1-e^{-k_{d}a}\right),$$ (9)

$$\langle x_a\rangle =p\left(a\right)\langle x_0\rangle +\langle X_a\rangle ,$$ (10)

where k_s denotes the effective synthesis rate. These equations can, for instance, apply to mRNA but are equally valid for most proteins provided that the lifetime of their mRNA is short relative to the cell-cycle duration. Given these equations, the contribution of differences in cell-cycle stage to the variance in copy numbers equals

$$\langle {\delta }^2\langle x_a\rangle \rangle =\underset{0}{\overset{T}{\int }}u\left(a\right){\left(\langle x_a\rangle -\langle x\rangle \right)}^{2}da={\langle x\rangle }^{2}f\left(\frac{k_d}{\mu }\right),$$ (11)

where f(k_d/μ) is a monotonically decreasing function of k_d/μ (see the Supporting Material for complete expression; see Fig. S1 A in the Supporting Material). As we found earlier, the ratio k_d/μ is an essential parameter. In the limit of k_d/μ → 0, when the molecule is only diluted by growth, 〈δ²〈x_a〉〉 simplifies to

$$\langle {\delta }^2\langle x_a\rangle \rangle =\frac{k_s^2\left(1-2\text{ln}{\left(2\right)}^2\right)}{{\mu }^2}={\langle x\rangle }^2\left(1-2\text{ln}{\left(2\right)}^2\right)\approx 0.04{\langle x\rangle }^2,$$ (12)

with 〈x〉 = k_s/μ as the population-average copy number (and μ = ln(2)/T). For a stable molecule, differences in cell-cycle stage contribute 0.04 to the noise in copy numbers across a population of cells. This contribution can be expected to be very significant for moderately to highly expressed proteins while becoming negligible as compared to 〈〈δ²x|a〉〉 for molecules with low copy numbers because the intrinsic noise contribution 1/〈x〉 dominates.

If the synthesis rate changes during the course of the cell cycle, e.g., because the gene encoding the protein of interest is replicated, the cell-cycle stage noise contribution 〈δ²〈x_a〉〉 changes. Assuming again a stable molecule (k_d/μ → 0) and synthesis with rate k_s up to time t_r (time of replication) and a doubled synthesis rate between t_r and division at time T, the cell-cycle-dependent variance becomes a function of the ratio t_r/T (see the Supporting Material for complete expression; see Fig S1 B). It can take values in the range of ≈0.035〈x〉² and ≈0.046〈x〉², as was determined before numerically by Marathe et al. (24). In the limit of t_r → 0 or t_r → T, it reduces to 〈x〉² (1−2ln(2)²), as we found earlier.

Variance due to the biochemical reactions and (extrinsic) noise propagation

The term 〈δ²X_a〉 in the variance decomposition (Eq. 6) captures contributions from the synthesis of new molecules because of the last cell division event. This comprises contributions from intrinsic as well as extrinsic noise (15). We focus here on the variance decomposition for a single molecule and therefore consider all effects from upstream regulators to be part of the extrinsic noise. For a large number of models (considering various sources of extrinsic noise, as well as bursting) the variance of the net number of newly synthesized molecules (i.e., the number of newly made molecules that survive up to the time of interest) can be described by queuing theory. A very general bursting model with nonexponential waiting times between bursts and general distributions for burst size is described by a GI^X/M/∞ queue for which the transient moments can be calculated from recursive equations (25,26). Transient moments for two- and three-state models of gene expression have been solved in the Iyer-Biswas et al. (27) and Shahrezaei and Swain (28). Extrinsic noise can be modeled by using queues with input correlations (29,30). Here we demonstrate the use of queuing theory to describe the variance contribution from biochemical reactions with a simple model of bursting synthesis where the times between bursts are exponentially distributed and burst sizes have a general distribution (31). For simplicity we take the molecule to be stable, i.e., k_d = 0.

We denote the average burst size 〈b〉 and its variance 〈δ²b〉. With average time between bursts equal to 1/k_s the variance at cell-cycle stage a is given by 〈δ²X_a〉 = k_sa(〈δ²b〉 + 〈b〉²). With this, Eq. 6 becomes (for a derivation, see the Supporting Material)

$$\langle {\delta }^{2}x\rangle =\stackrel{\text{variance}\text{due}\text{to}\text{cell}\text{cycle}\text{stage}\text{distribution}}{\overbrace{{\langle x\rangle }^2\left(1-2\text{ln}{\left(2\right)}^2\right)}}+\stackrel{\text{variance}\text{due}\text{to}\text{synthesis}}{\overbrace{\left(1/\text{ln}2-1\right)k_{s}T\left(\langle {\delta }^{2}b\rangle +{\langle b\rangle }^2\right)}}+\underset{\langle {\delta }^2{x}_0\rangle \text{variance}\text{at}\text{cell}\text{birth}}{\underbrace{\frac{k_{s}T\left(\langle b\rangle \left(2+\langle b\rangle \right)+\langle {\delta }^{2}b\rangle +4\left(\langle b\rangle \left(-2+\langle b\rangle +4\langle b\rangle k_{s}T\right)+\langle {\delta }^{2}b\rangle \right)\langle {\delta }^{2}q\rangle \right)}{3-4\langle {\delta }^{2}q\rangle }}},$$ (13)

with 〈x〉 = k_sT〈b〉/ln(2) as the average copy number. This equation indicates that synthesis bursts enhance copy number variance and that variations in the burst size, 〈δ²b〉, and in the partition function, 〈δ²q〉, have a multiplicative contribution to overall copy number noise. If we remove the bursts by setting 〈b〉 = 1 and 〈δ²b〉 = 0, we recover Eq. 8. When we set the average burst size to five molecules (as has been measured for the lac promoter in E. coli (32,33)) and its variance to 20 (assuming a geometric burst size distribution), then the copy number variance increases 3.75-fold due to bursts only (〈δ²q〉 = 0) compared to a model with the same average copy number but without bursts. When 〈δ²q〉 = 0.01 (a typical value for many microorganisms), we find an increase in variance of 4.05-fold.

Extrinsic noise in the synthesis rate shapes the expressions for 〈δ²X_a〉 as well as cov(p(a)x₀|X_a): their dependence on the cell-cycle stage is a function of the lifetime of the molecule $\mathbb{X}$ under consideration as well as the lifetime and shape of the autocorrelation function of the extrinsic noise. If either lifetime is short, the covariance term quickly decreases to zero, because the number of molecules that were inherited from the mother cell and survived until cell-cycle stage a is small or because the synthesis rate at a is uncorrelated with the one during the previous cell cycle such that the number of newly synthesized molecules is independent of the number of inherited molecules. The variance of the net new synthesis as a function of the cell-cycle stage can be calculated from the average synthesis rate and its autocorrelation function as (30)

$$\langle {\delta }^2{X}_a\rangle =\underset{t=0}{\overset{a}{\int }}p\left(a-t\right)\left(1-p\left(a-t\right)\right)\langle k_s\left(t\right)\rangle dt+\underset{t_1=0}{\overset{a}{\int }}\underset{t_2=0}{\overset{a}{\int }}p\left(a-t_1\right)p\left(a-t_2\right)\text{cov}\left(k_s\left(t_1\right),k_s\left(t_2\right)\right)d{t}_{1}d{t}_2,$$ (14)

where k_s(t) denotes the synthesis rate at time t. For a modulated Poisson process the covariance term always equals a sum of a Dirac-delta function accounting for the shot noise of the synthesis process and the autocorrelation function of the upstream regulator (see the Supporting Material). The covariance term in Eq. 4, 2p(a)cov(x₀, X_a), derives from correlations in the synthesis rate that span more than one generation. Usually it is unclear from which exact factors the extrinsic noise derives and how those factors are themselves affected by the cell division. If there is no variance in the division fraction q, the cell-cycle stage-dependent copy number variance and the covariance term can be calculated as a function of the synthesis covariance during and across generations (see the Supporting Material).

The full copy number distribution for zero-order synthesis and first-order degradation (the Poisson limit)

If the partitioning probability q is fixed and equal to 1/2, the full copy number distribution at a cell-cycle progression stage a can be derived using probability generating functions (see the Supporting Material). The number of molecules at a equals the sum of the net synthesized molecules because the last division and those inherited from the mother cell that have not yet been degraded. To obtain the probability distribution of such a sum of independent random variables, one needs to calculate the convolution of the two associated probability distributions. This step simplifies when instead of these distributions their probability generating functions (PGFs) are considered, because the PGF of a sum of two independent random variables equals the product of the two associated generating functions. Moreover, the binomial partitioning at division as well as first-order degradation can be expressed in simple terms for generating functions: with F_x(z) as the generating function of some random variable x, the distribution of a binomial partitioning of x over two daughter cells is given by F_x(1−1/2 (1 − z)). Equivalently, the PGF for the number of molecules that remains after a period of time a, where each molecule has a probability (1 – p(a)) to be degraded, equals F_x(1 – p(a)(1 – z)). With this, we obtain an equation for the PGF of the number of molecules at cell-cycle stage a,

$$G_{\left(x,a\right)}\left(z\right)=\stackrel{\text{net}\text{new}\text{synthesis}}{\overbrace{F_{\left(X,a\right)}\left(z\right)}}\stackrel{\text{molecules}\text{remaining}\text{from}\text{previous}\text{cell}\text{cycles}}{\overbrace{\prod _{i=0}^{\infty }\underset{\text{molecules}\text{that}\text{were}\text{synthesized}i+1\text{generations}\text{ago}\text{and}\text{ended}\text{up}\text{in}\text{the}\text{cell}\text{of}\text{interest}}{\underbrace{F_{\left(X,T\right)}\left(1-\left(1/2p\left(a\right)\right){\left(1/2p\left(T\right)\right)}^i\left(1-z\right)\right)}}}},$$ (15)

where F_(X,a)(z) denotes the generating function of the number of newly synthesized molecules at cell-cycle stage a. The probability that a molecule that was present in the mother cell is inherited and not yet degraded at a is accounted for by p(a)/2, whereas (p(T)/2)ⁱ reflects the probability that a molecule that was synthesized i generations ago is not yet degraded and ended up in a particular daughter cell. The population wide copy number distribution can be obtained by marginalizing out the cell-cycle stage distribution:

$$G_x\left(z\right)=\underset{0}{\overset{T}{\int }}u\left(a\right)G_{\left(x,a\right)}\left(z\right)da.$$ (16)

As an example, we consider a model with zero-order synthesis and first-order degradation: the classical Poisson model. To solve the generating function given in Eq. 15 we only need to determine the generating function F_(X,a)(z) for the number of produced molecules that have not yet been degraded. F_(X,a)(z) is the generating function of the time-dependent probability distribution of the following stochastic process, starting from the initial condition with 0 molecules:

$$\mathrm{Ø}\stackrel{k_s}{\to }X\stackrel{k_d}{\to }\mathrm{Ø}.$$ (17)

The associated master equation can be solved analytically (34) and gives the following distribution for the number of molecules:

$$X_a\sim \text{Poisson}\left(\kappa \left(a\right)\right)\text{with}\kappa \left(a\right)=k_s/k_d\left(1-e^{-k_{d}a}\right).$$ (18)

F_(X,a)(z) then equals F_(X,a)(z) = e^κ(a)(z−1). Substituting this into Eq. 15 yields

$$\begin{array}{c}{G}_{\left(x,a\right)}\left(z\right)=e^{\kappa \left(a\right)\left(z-1\right)}\prod _{i=0}^{\infty }{e}^{\kappa \left(T\right)\left(\left(1-\left(1-z\right)p\left(a\right){1/2\left(p\left(T\right)1/2\right)}^i\right)-1\right)}\\ =e^{\left(z-1\right)\left(\kappa \left(a\right)+\frac{p\left(a\right)1/2\kappa \left(T\right)}{1-p\left(T\right)1/2}\right)}.\end{array}$$ (19)

This indicates that the copy number distribution at cell-cycle stage a is given by a Poisson distribution with average

$$\kappa \left(a\right)+\frac{p\left(a\right)1/2\kappa \left(T\right)}{1-p\left(T\right)1/2},$$

where the first term equals 〈X_a〉 and the second 〈x₀〉p(a).

For a stable molecule, i.e., k_d = 0, marginalizing out the cell-cycle stage distribution and taking appropriate limits yields

$$\begin{array}{c}p\left(x\right)=\underset{0}{\overset{T}{\int }}u\left(a\right)p\left(x|a\right)da\\ =\underset{0}{\overset{T}{\int }}u\left(a\right)\frac{e^{-k_s\left(a+T\right)}{\left(k_s\left(a+T\right)\right)}^x}{x!}da\\ =\frac{4{\left(k_{s}T\right)}^x\left(\text{Γ}\left[1+x,k_{s}T+\text{ln}\left(2\right)\right]-\text{Γ}\left[1+x,2k_{s}T+\text{ln}\left(4\right)\right]\right)}{x!}\frac{\ln \left(2\right){\left(k_{s}T+\ln \left(2\right)\right)}^{-1-x}}{x!},\end{array}$$ (20)

where Γ[⋅] denotes the incomplete gamma function (Fig. 3).

Figure 3.

Extrinsic noise can shape the distributions of concentrations and copy numbers. The distributions of concentrations (black) and copy numbers (gray) are shown for a stable molecule synthesized by a zero order reaction for different values of the synthesis rate k_s (Eq. 20). (A) Distributions without extrinsic noise. (B) Extrinsic noise in the synthesis rate, k_s. Extrinsic noise was modeled with a log-normal distribution of k with squared coefficient of variation of 0.1 and an autocorrelation time that much exceeds one generation time such that the resulting distributions are mixture distributions of the distributions obtained for different values of k_s drawn from the log-normal distribution. (Insets) Fits of the concentration and copy number distributions with intermediate k_s to normal (green), log-normal (blue), and gamma (red) distributions with the same average and variance. To see this figure in color, go online.

Under these conditions, the variance decomposition as given in Eq. 6 takes a simple form and gives the variance decomposition of the classical Poisson model,

$$\langle {\delta }^{2}x\rangle =\underset{=\langle x\rangle }{\underbrace{\underset{=1/2ln\left(2\right)\langle x\rangle }{\underbrace{\langle \langle {\delta }^2{x}_0|x_T\rangle \rangle }}+\underset{=1/2ln\left(2\right)\langle x\rangle }{\underbrace{\langle {\delta }^2\langle x_0|x_T\rangle \rangle }}+\underset{=\left[1-ln\left(2\right)\right]\langle x\rangle }{\underbrace{\langle \langle {\delta }^2{X}_a\rangle \rangle }}}}+\underset{\left[1-2ln{\left(2\right)}^2\right]{\langle x\rangle }^2}{\underbrace{\langle {\delta }^2\langle x_a\rangle \rangle }},$$ (21)

showing that under these conditions the variance contributions from partitioning, from variance in the mother cell, and from intrinsic noise in the synthesis process, are of comparable magnitude. The relative magnitude of the last term (variance deriving from the cell-cycle stage distribution) in comparison to the other three depends on the average copy number. Typically we associate with the Poisson model the result that 〈δ²x〉 = 1/〈x〉, and here we see that, in fact, the growth process also makes a contribution to this variance due to the cell-cycle dependency of x.

For the case that active degradation of molecules is on a comparable or faster timescale as the generation time, the Poisson model gives insight into how the different variance contributions change during the cell cycle. Because the copy number distribution at any cell-cycle stage is given by a Poisson distribution, the variance at a equals the average copy number at that cell-cycle stage. With this, we obtain

$$\stackrel{\text{decay}\text{of}\text{memory}\text{of}\text{cell}\text{division}\text{variance}}{\overbrace{\langle p{\left(a\right)}^2\rangle \langle \langle {\delta }^2{x}_0|x_T\rangle \rangle +\langle p{\left(a\right)}^2\rangle \langle {\delta }^2\langle x_0|x_T\rangle \rangle +\langle p\left(a\right)\left[1-p\left(a\right)\right]\rangle \langle x_0\rangle }}=p\left(a\right)\langle {\delta }^2{x}_0\rangle =p\left(a\right)\langle x_0\rangle .$$ (22)

Combining this with Eq. 4 yields the following expression for the variance at a:

$$\langle {\delta }^2{x}_a\rangle =\langle {\delta }^2{X}_a\rangle +p\left(a\right)\langle {\delta }^2{x}_0\rangle =\underset{\text{variance}\text{from}\text{newly}\text{synthesized}\text{molecules}}{\underbrace{k_s/k_d\left(1-e^{-k_{d}a}\right)}}+\underset{\text{decay}\text{of}\text{memory}\text{of}\text{cell}\text{division}\text{variance}}{\underbrace{e^{-k_{d}a}\langle {\delta }^2{x}_0\rangle }}=\langle x_a\rangle .$$ (23)

This illustrates that the contribution of the variance at cell birth decays exponentially with cell-cycle stage but that this decrease is balanced by the increasing variance from newly synthesized molecules.

Variance decomposition for concentrations

The results derived in the previous sections can be transferred to variance decompositions for concentrations directly if a fixed volume-age relationship is assumed. When volume, V, is expressed as a function of cell stage, the concentration variance at stage a can be expressed as 〈δ²c_α〉 = 〈δ²x_α〉/V_a² and the total variance can be expressed as

$$\begin{array}{c}\langle {\delta }^{2}c\rangle =\langle \langle {\delta }^2{c}_a\rangle \rangle +\langle {\delta }^2\langle c_a\rangle \rangle \\ =\langle \frac{\langle {\delta }^2{x}_a\rangle }{V_a^2}\rangle +\langle {\delta }^2\langle \frac{x_a}{V_a}\rangle \rangle .\end{array}$$ (24)

The first term can now be decomposed in an analogous manner as for copy numbers. The second term, denoting variance in concentrations from changes in concentration during the cell cycle, will in most cases be much smaller than the corresponding term for copy numbers: while the copy number inevitably doubles on average between subsequent divisions, the average concentration at stage 0 must equal that at stage T. For the case of a constant synthesis rate throughout the cell cycle and no active degradation, there is a linear increase in the average copy number with cell-cycle stage. Therefore, if volumes also increase linearly, stage 〈δ²〈c_α〉〉 will become zero, while with exponential volume growth 〈δ²〈c_α〉〉 ≈ 0.0003〈c〉².

For the simple model with zero-order synthesis and no active degradation, Fig. 3 compares the resulting distributions of copy numbers and concentrations. The difference in the magnitude of the cell-cycle stage distribution-dependent noise is also reflected in the distributions: whereas concentration distributions for this model have relatively small noise (close to the inverse of the mean copy number if the average volume is set to 1 unit) and can be fit reasonably by normal, log-normal, or gamma distributions, copy number distributions have a larger spread and can be fit with neither of those distributions (especially if the copy number average is >≈15). The shape of the copy number distributions is different from what has been reported in the literature based on FACS experiments with cells expressing a fluorescent protein. To illustrate the effect that extrinsic noise can have on the shapes of those distributions, we also show distributions for a stable protein with extrinsic noise in the synthesis rate. For extrinsic noise with log-normal distribution (35), squared coefficient of variation of 0.1, and a large autocorrelation time, the resulting copy number and concentration distributions are both best fit with gamma distributions in agreement with experiments (36,37).

Variability in interdivision times

In the previous sections, we assumed the interdivision times to be deterministic. However, in reality, the times between subsequent divisions would be better described by a random variable. For a number of symmetrically dividing microorganisms, the distributions of interdivision times have been measured, and were found to have coefficients of variation between 12 and 35% (38–45). However, few studies investigate how this variability in the generation time affects distributions of molecule copy numbers and concentrations (24,46–48).

With interdivision time heterogeneity, the analytical approach taken in the previous sections has only limited applicability. The reason for this is that three different types of population samples now need to be distinguished: extant cells (all cells that exist at a given moment in time), baby cells (all cells that were born during the same time interval), and mother cells (all cells that divide within the same interval). Those three types of samples differ in their interdivision time statistics, as well as the distributions of copy numbers at birth and division. With deterministic interdivision times, all three types of samples become identical, which allows the combination of Eqs. 4 and 7 to estimate the total variance. Denoting those different types of samples with subscripts of e (extant), b (baby), and m (mother) we obtain:

$$\langle {\delta }^2{x}_{a\left\{e\right\}}\rangle =p{\left(a\right)}^2\langle {\delta }^2{x}_{0\left\{e\right\}}\rangle +p\left(a\right)\left(1-p\left(a\right)\right)\langle x_{0\left\{e\right\}}\rangle +\langle {\delta }^2{X}_a\rangle +2p\left(a\right)\text{cov}\left(x_{0\left\{e\right\}},X_a\right),$$ (25)

$$\langle {\delta }^2{x}_{0\left\{b\right\}}\rangle =\langle {\delta }^{2}q\rangle {\langle x_{T\left\{m\right\}}\rangle }^2+\left(1/4-\langle {\delta }^{2}q\rangle \right)\langle x_{T\left\{m\right\}}\rangle +\left(1/4+\langle {\delta }^{2}q\rangle \right)\langle {\delta }^2{x}_{T\left\{m\right\}}\rangle .$$ (26)

This means that the variance decomposition remains the same (as applied to a sample of extant cells) but the variance at cell birth of a sample of extant cells can no longer be expressed in a straightforward way as a function of the copy number variance at the time of division. An alternative approach to calculate the copy number noise for a model with interdivision time heterogeneity is by use of cell population balance models (48–51). The disadvantage of the population balance equation is that it does not allow decomposition of variance into its different sources and that it can usually only be solved numerically.

Next, we use simulations to study the effect of interdivision time heterogeneity on copy number and concentration variations. There are different mechanisms that can cause heterogeneities in interdivision times:

• 1.Asymmetric or imprecise division,
• 2.A distribution of volumes at which cells divide, and
• 3.Variation in the rate of volume increase between cells.

Although living organisms will have contributions to interdivision time heterogeneity from all three sources, we first explore their effects separately by simulating production and degradation of a molecule for a population of cells that have only one of the above-mentioned sources of heterogeneity in interdivision time. To make those results comparable we determine distributions of division fraction, volume at division, and rate of volume increase such that the resulting interdivision time distribution remains approximately the same. For the first mechanism we choose a distribution of the division fraction that is peaked at q = 1/2 (symmetric but imprecise division). Simulation of these models (Fig. 4; for description of the simulation algorithm, see the Supporting Material) show that the effects on copy number and concentration distributions are rather small for the first two mechanisms whereas heterogeneity in the rate of volume increase changes the distribution of concentrations appreciably. This effect becomes more pronounced for high average concentrations when intrinsic noise is smaller.

Figure 4.

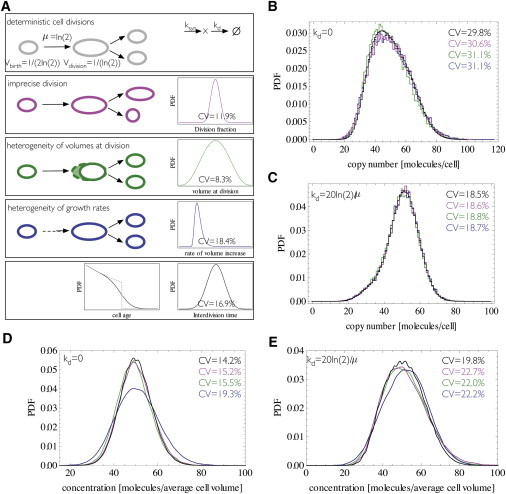
Variations in interdivision times have small effects on variability of copy numbers while fluctuations in rate of volume increase do change distributions of concentrations. (A) Schematic of the simulated scenarios for cell divisions: deterministic cell cycle (gray), variability in the division fraction (magenta), variability in the volume at which a cell divides (green), or variability in the rate of volume increase (blue). For the last three scenarios, the distributions of division fraction, volume at division, and rate of volume increase are depicted at the right and were chosen to yield the approximately same interdivision time distribution that is depicted at the bottom panel together with the resulting cell-cycle stage distribution. For comparison, the cell-cycle stage distribution for the scenario with deterministic interdivision times is shown (dashed gray). (B–E) Distributions of copy numbers and concentrations for molecule $\mathbb{X}$ produced through a zero order and degraded with first-order reaction for the four scenarios with the production rate set to give averages of 50 molecules per cell. (B and D) Simulations where k_d = 0; (C and E) where k_d = 20ln(2)/μ. To see this figure in color, go online.

If contributions of these different mechanisms that generate heterogeneity in interdivision times were independent, one would expect the squared coefficient of variation of the molecule concentrations to be a sum of noise terms:

$$\frac{\langle {\delta }^{2}c\rangle }{{\langle c\rangle }^2}={\frac{\langle {\delta }^{2}c\rangle }{{\langle c\rangle }^2}}_{\text{deterministic}\text{cell}\text{cycle}}+\sum _{i=1}^n{\frac{\langle {\delta }^{2}c\rangle }{{\langle c\rangle }^2}}_{\text{noise}\text{caused}\text{by}\text{mechanism}i}.$$ (27)

However, simulations with all three mechanisms combined show that the total noise is lower than this sum. This is not too surprising because the noise in the interdivision time distribution is less than three times that of the distribution used for the simulations with only one source of interdivision time heterogeneity.

If variations in the rate of volume increase persist over multiple generations, the squared coefficient of variation in concentrations can be expected to be the sum of intrinsic terms and the noise in the distribution of interdivision times: for the case in which heterogeneity in the rates of volume-increase is the only source of variation in interdivision times, the distribution of interdivision times can be derived from the distribution of rates of volume increase using the change-of-variable technique: with g(k) as the distribution of rates, f(τ) the distribution of times, and τ = 1/k as

$$f\left(\tau \right)=g\left(1/\tau \right)\frac{1}{{\tau }^2}$$ (28)

For deterministic interdivision times, the average protein concentration depends linearly on the interdivision time (c = k_s〈τ〉); according to the law of total variance for long autocorrelation times of the fluctuations in k (and therefore also in τ), the total noise in protein concentration equals the sum of noise in interdivision times and the average noise for a model with deterministic interdivision times. That this is indeed the case is shown in Fig. 5 for a Gaussian distribution of rates of volume increase. Here the rates were correlated over time with an exponentially decaying autocorrelation function. (Because the Gaussian distribution of rates in volume increase was applied to a sample of baby cells, enforcing the correlation leads to a slight increase in specific growth rate with increasing autocorrelation time; however, the effect of this on the squared coefficient of variation is small (<5%).)

Figure 5.

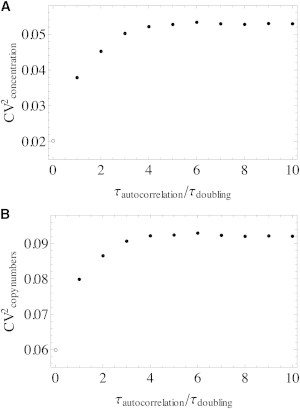
The squared coefficient of variation for copy numbers (A) and concentrations (B) increases with the correlation time of the rate of volume increase. Simulations were run for a stable protein (no degradation), average concentration of 50 molecules per average cell volume, with rates of volume increase sampled from a Gaussian distribution with CV = 0.15 and an exponentially decaying autocorrelation function. The specific growth rate of the population increases with increasing correlation because faster growth rates are overrepresented in a populations of extant cells.

Discussion

We provided a theory that integrates intrinsic and extrinsic noise of biochemical reactions with noise introduced during cell division and growth. Regarding the biochemical synthesis processes and its regulators, the model is completely general. Results from queuing theory can be used to describe various synthesis processes, including those regulated by upstream factors. Different levels of coarse graining can then be considered, such as descriptions solely characterized by a waiting-time and burst-size distribution (31), and involving extrinsic noise following different statistics. To allow for analytical results, the degradation mechanism is assumed to be first order without extrinsic noise. We note that nonexponential lifetimes have been observed experimentally (52), indicating more complex mechanisms. Application of this theory would therefore require testing whether degradation is indeed first-order.

The noise decomposition given in Eq. 6 remains valid when the assumption of deterministic interdivision times is relaxed. We emphasize that, in such a case, the copy-number noise can no longer be calculated as was done above (for a more detailed discussion, see the Supporting Material). Once the degradation rate of the molecule of interest has been measured, all terms in Eq. 6 can be quantified from time-lapse microscopy with fluorescent reporter constructs.

We decided to focus on the variance decomposition for a single molecule, considering regulatory factors only through their effect on the synthesis rate. As has been pointed out before (53), this alone does not allow for a distinction between different mechanisms that cause the variabilities in synthesis rate, such as noise in the copy number of an upstream regulator. We note that the way that the variance in newly synthesis molecules changes over the cell cycle, and how net synthesis correlates with the amount that is present at cell birth, can be used for model selection (54–58). A more detailed understanding of the mechanistic causes of variability in synthesis rates will require experiments using multiple (fluorescent) reporters.

The mathematical decomposition techniques used here can be applied to systems when more than one variable is monitored, although the equations then do quickly become lengthy. In such cases, regulatory interactions result in cross-correlations between net new synthesis of one molecule and the abundance of others. In addition, dependencies occur in the partitioning process, quantified as correlations in the molecule numbers at cell birth for given amounts of both species in the mother cell.

Another extension of the approach presented here is usage of higher moments. This can be advantageous because averages and variances are often poor discriminators of different noise sources, as they capture only part of the information contained in the full distribution (17,59). As shown in Eq. 15, the full distribution can be derived if partitioning is assumed to be binomial with probability q = 1/2. If this assumption does not apply, the moments of the distribution can be calculated from differentiation of Eq. S47 (see the Supporting Material). Higher moments can be obtained by using the equivalent of the law of total variance for higher moments: the law of total cumulance. However, the resulting decomposition terms no longer have intuitive interpretations.

Nongenetic heterogeneity in the molecular composition of cells in a growing population is a basic feature of cell biology. We have shown that this heterogeneity arises out of different processes and their relations, and they can be disentangled. The heterogeneity contributions of those processes likely vary among organisms, cell types, and across conditions; for instance, we would expect variations in the noise in cell volume at a given cell-cycle stage, the partitioning probability, and the reaction-induced noise. With this article, we presented a theoretical framework for quantifying and disentangling noise contributions, applicable to experimental data obtained with real-time fluorescent imaging of gene reporters and cell growth.