SUMMARY
How do neurons develop, control, and maintain their electrical signaling properties in spite of ongoing protein turnover and perturbations to activity? From generic assumptions about the molecular biology underlying channel expression, we derive a simple model and show how it encodes an “activity set point” in single neurons. The model generates diverse self-regulating cell types and relates correlations in conductance expression observed in vivo to underlying channel expression rates. Synaptic as well as intrinsic conductances can be regulated to make a self-assembling central pattern generator network; thus, network-level homeostasis can emerge from cell-autonomous regulation rules. Finally, we demonstrate that the outcome of homeostatic regulation depends on the complement of ion channels expressed in cells: in some cases, loss of specific ion channels can be compensated; in others, the homeostatic mechanism itself causes pathological loss of function.
INTRODUCTION
A mysterious yet essential property of the nervous system is its ability to self-organize during development and maintain function in maturity despite ongoing perturbations to activity and to the biochemical milieu upon which all cellular processes depend (Desai 2003; Marder and Goaillard 2006; Marder and Prinz 2002; Mease et al., 2013; Moody 1998; Moody and Bosma 2005; O’Donovan 1999; Spitzer et al., 2002; Turrigiano and Nelson 2004; van Ooyen 2011). Although we are beginning to understand the homeostatic mechanisms that underlie this robustness, there are many substantial open questions. First, conceptual and computational models of neuronal homeostasis assume a “set point” in activity that neurons and networks return to following perturbations (Davis 2006; LeMasson et al., 1993; Liu et al., 1998; Turrigiano 2007). Where does this set point come from? How can it be encoded biologically? Second, previous work has shown that phenomenological feedback control rules can maintain specific activity patterns in model neurons by regulating intrinsic and synaptic ion channel densities using intracellular Ca2+ as a monitor of cellular excitability (Desai 2003; LeMasson et al., 1993; Liu et al., 1998), but it remains to be shown how such rules can be implemented in a biologically plausible way that incorporates the underlying mechanisms of channel expression (Davis 2006; O’Leary and Wyllie 2011). Third, the nervous system is heterogeneous, with many distinct cell types that have specific combinations of ion channels that lend them their unique electrical properties (Marder 2011). How is this diversity achieved while ensuring that global levels of activity are maintained? Fourth, does homeostatic plasticity occur at the network level, or are nominally cell-autonomous homeostatic mechanisms sufficient to confer network stability (Maffei and Fontanini 2009)? Fifth, nervous systems do not always behave homeostatically; mutations in ion channel genes are the basis of many diseases, and genetic knockout animals often have measurable phenotypes. Is this a failure of regulatory mechanisms (Ramocki and Zoghbi 2008)? Or, is homeostatic regulation compatible with incomplete or aberrant compensation in certain situations? We specifically address these questions using theory and computational models.
Previous modeling and theory work has shown that feedback rules can sculpt and stabilize activity in single neurons and networks (Abbott and LeMasson 1993; Golowasch et al., 1999b; LeMasson et al., 1993; Liu et al., 1998; Soto-Treviño et al., 2001; Stemmler and Koch 1999). These models helped to establish that intrinsic properties and synaptic strengths can be subject to homeostatic regulation, but left questions of biological implementation, such as the nature of set points, largely unanswered. In addition, models that were intended to capture regulation of multiple intrinsic conductances either suppressed variability in conductance densities (Abbott and LeMasson 1993; LeMasson et al., 1993; Soto-Treviño et al., 2001) or produced such a high degree of variability that the model neurons were sometimes unstable (Liu et al., 1998). Underlying this problem is the fact that the set of conductance densities that produces a specific kind of activity comprises disparate solutions with a complicated distribution (Prinz et al., 2003; Taylor et al., 2006, 2009). Thus, a biologically plausible regulation rule needs to navigate this complex space so as to allow variability but maintain certain relations between conductances. Here, we achieve this from first principles, deriving a straightforward, biologically plausible model of gene regulation to show how neurons can use a single physiological variable–intracellular Ca2+−to robustly control their activity and develop specific electrophysiological properties that enable function at the circuit level.
RESULTS
The first part of the Results (Figures 1, 2, and 3) is a technical derivation of an activity-dependent regulation rule. The consequences and interpretation of this rule are covered in the latter part of the Results (Figure 4 onward).
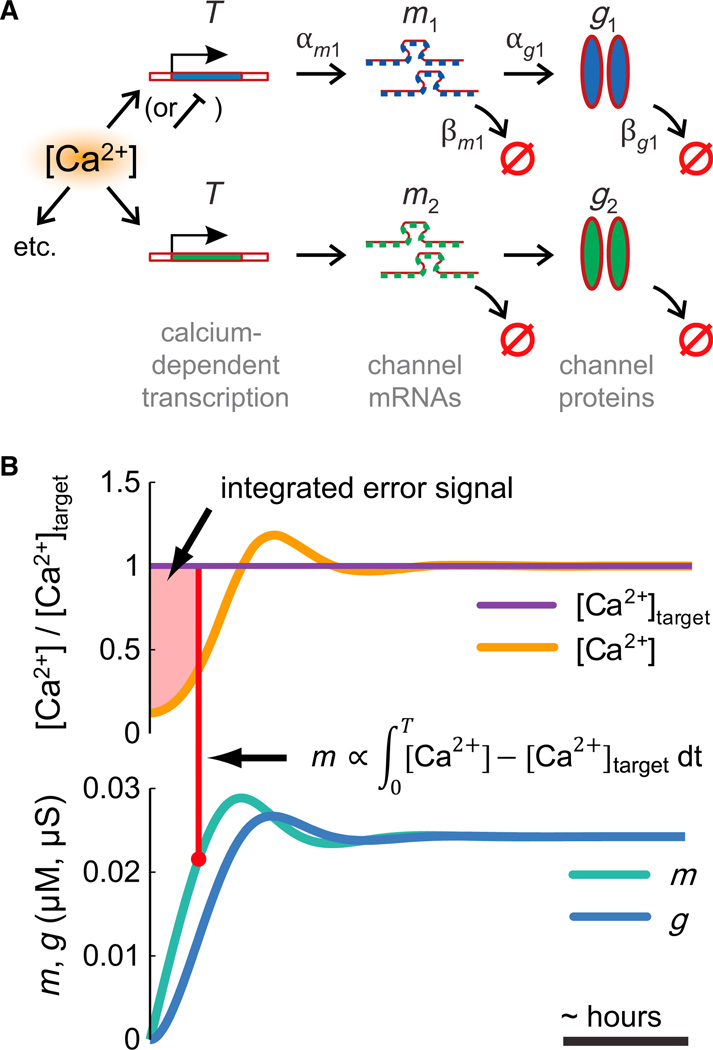
Figure 1. Integral Control from the Canonical Model of Gene Expression.
(A) A simple biochemical scheme for activity-dependent ion channel expression. Channel mRNAs are produced at a rate αm that depends on a Ca2+-activated factor, T, and degraded at rate βm Functional channel proteins are produced at a rate αg from mRNAs and degraded at a rate βg.
(B) The scheme in (A) is equivalent to an integral controller. Error (deviation from [Ca2+] target, [Ca2+]tgt) is accumulated in the mRNA (m) concentration (shaded region), which causes a change in ion channel expression (g).
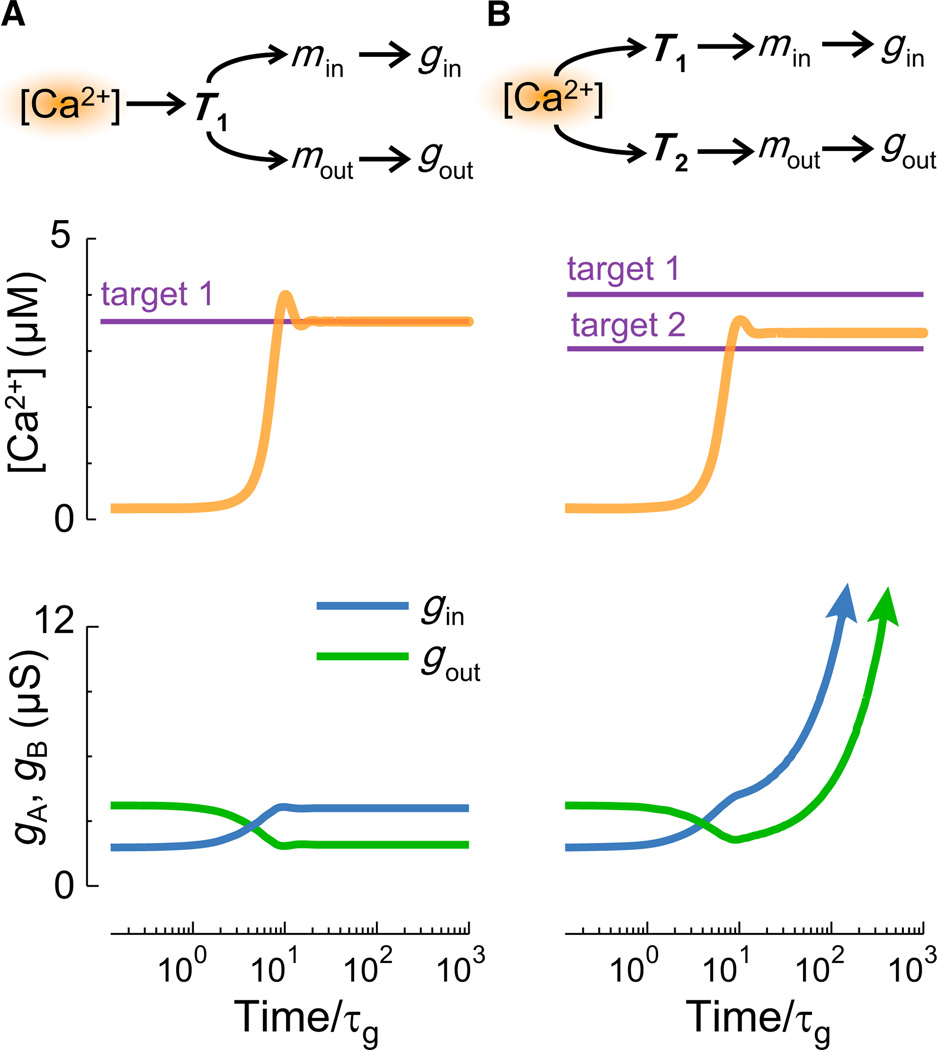
Figure 2. A Potential Problem with Multiple Regulators.
A model cell with one inward and one outward leak conductance implements integral control to maintain a target [Ca2+] (Supplemental Experimental Procedures). Time is normalized to conductance expression rate, τg.
(A) A single master regulator, T1, produces a stable model.
(B) Two separate regulators T1 and T2 with nonequal targets lead to an unbounded (arrows) increases in conductance.
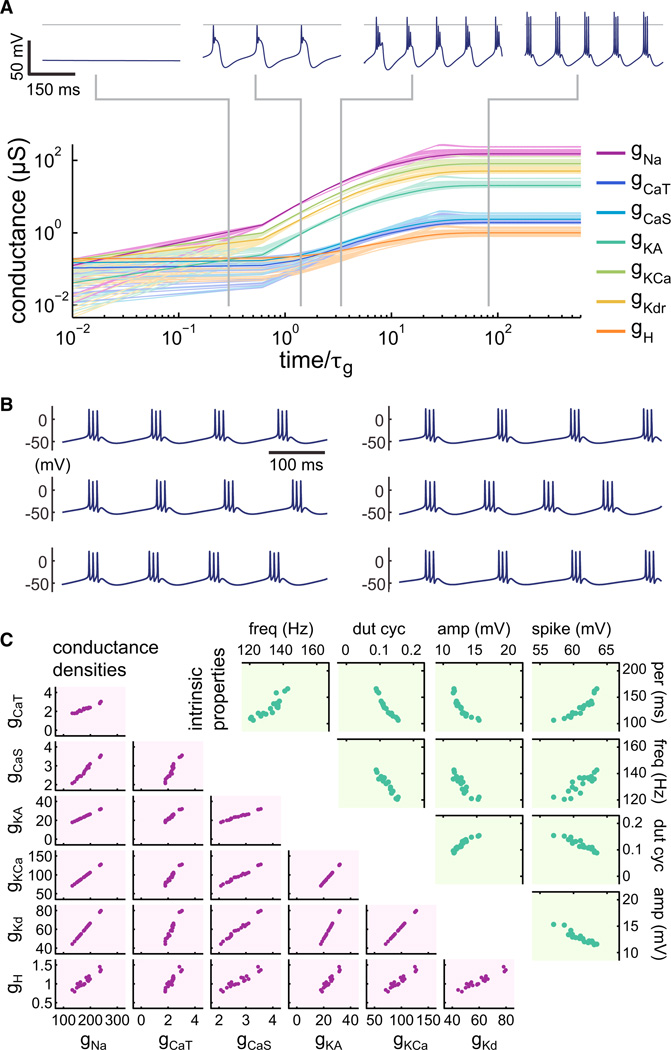
Figure 3. Regulation in a Complex Biophysical Cell Model.
(A) Time evolution of a self-regulating neuron implementing integral control for its seven voltage-dependent conductances (fast sodium, gNa; slow Ca2+gCaS; transient Ca2+gCaT; A-type/transient potassium, gKA; Ca2+-dependent potassium, gKCa; delayed-rectifier potassium, gKd; hyperpolarization-activated mixed-cation, gH). A total of 20 independent runs are shown with mean in bold; axes are log-log; timeis normalized to τg. (Top) Voltage traces for an example neuron at the stages indicated.
(B) Examples of steady-state behavior of the bursting pacemaker from six independent runs.
(C) Scatter plots of conductance distributions (bottom left) and intrinsic properties (top right) at steady state of the 20 neurons from the independent runs in (A). Intrinsic properties are as follows: intraburst spike frequency (freq), burst duty cycle (dut cyc), slow-wave amplitude (amp), spike height (spike), and burst period (per).
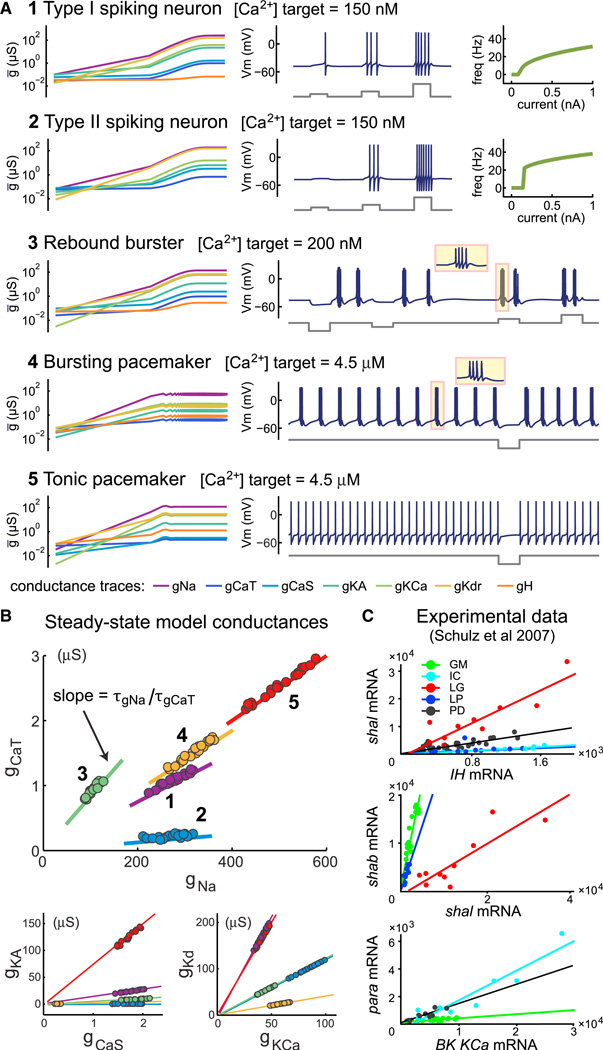
Figure 4. Specifying Different Cell Types with the Same Model.
(A) Example cell types produced from the same set of seven voltage-dependent conductances. (Left-hand plots) Log-log plots of conductance evolution over time. Each example has a different set of regulation time constants for the conductances (Experimental Procedures). Total duration for all simulations is 10×τg. (Right-hand plots) Membrane potential traces with current injection traces shown below. FI (frequency versus current amplitude) plots are shown for the type I/II neurons (1 and 2). Current injection amplitudes for each example are as follows: 100, 200, and 500 pA for 1 and 2; −200, −100, 100, and 200 pA for 3; −500 pA for 4 and 5. Time base for all membrane potential traces (from duration of current pulse): 500 ms.
(B) Scatter plots of steady-state conductances in each cell type (1–5) shown in (A) after 20 independent runs. Straight lines are calculated from the ratio of regulation time constants for each pair of conductances in each cell type; see Equation 4.
(C) Experimental data reproduced from Schulz et al. (2007) showing cell-type-specific correlations in ion channel gene expression. Quantitative PCR was performed on ion channel mRNAs obtained from single identified cells in the crab STG (cell types shown are GM, IC, LG, LP, and PD).
Integral Control from a Simple Model of Ion Channel Expression
Experiments have shown that the processes responsible for regulating intrinsic neuronal properties are slow relative to fluctuations in electrical activity (Desai et al., 1999; O’Leary et al., 2010; Thoby-Brisson and Simmers 2000). These processes behave as a feedback control mechanism that monitors average activity and adjusts membrane conductances to achieve some kind of target activity. An important readout signal appears to be intracellular [Ca2+], which correlates with electrical activity due to voltage-dependent Ca2+channels and buffering mechanisms that average out fluctuations in time and space (Berridge 1998; Wheeler et al., 2012). Moreover, long-term changes in [Ca2+] are found to regulate many ion channel types (Barish 1998; Mermelstein et al., 2000; O’Leary et al., 2010; Turrigiano et al., 1994; Wheeler et al., 2012).
Hence we developed a model of activity-dependent conductance regulation using intracellular [Ca2+] as a feedback control signal. There are many ways to implement feedback control of membrane conductances (Günay and Prinz 2010; LeMasson et al., 1993; Liu et al., 1998; Olypher and Prinz 2010; Stemmler and Koch 1999). We wanted to focus on a rule that captures essential biological principles and has experimentally testable properties. Ion channels are proteins, and their expression depends on the level of channel mRNA in the cell. A simple way of capturing this leads to a canonical model of regulation (also known as the “central dogma” of molecular biology):
| (1) |
Here, m is the concentration of mRNA for channel protein g and αx and βx are synthesis and degradation rates; dots denote time derivatives. The biochemical scheme underlying this model is shown in Figure 1A. In spite of its simplicity, this model has proven useful for understanding gene expression dynamics in systems biology (Alon 2007). Neurons possess a rich repertoire of other regulatory mechanisms, including alternative splicing, alternative promoter usage, RNA interference, regulated protein trafficking, and posttranslational modifications to channel proteins. Therefore, the simplified scheme we use is a first approximation that can be refined to take into account more intricate aspects of regulation when and where sufficient experimental data are available.
Where does activity dependence enter this model? mRNA expression rates depend on transcription factor activation. Many important transcription factors such as CREB are known to be Ca2+ dependent or dependent on other Ca2+-sensing enzymes (Finkbeiner and Greenberg 1998; Mermelstein et al., 2000; Mihalas et al., 2013; Wheeler et al., 2012). Furthermore, transcriptional changes in ion channel genes occur in response to activity perturbations (Kim et al., 2010) and may underlie homeostatic regulation of network activity (Thoby-Brisson and Simmers 2000). We therefore assume that mRNA production depends on some Ca2+-sensitive enzyme, or enzyme complex, T, whose production rate is Ca2+ dependent and whose rate of degradation is saturated (Drengstig et al., 2008). Incorporating this into the model, we have
| (2) |
We do not know in general how the forward rate, αT depends on [Ca2+]. The assumption that the degradation rate of T is saturated means the equilibrium of the system occurs at a unique value of [Ca2+]. Thus average [Ca2+] will be maintained at a specific “target” value, Catgt, given by solving the steady-state, 〈Ṫ〉 = 0. We do not know in general how the forward rate, αT depends on [Ca2+]. If this rate is determined by a single reaction involving Ca2+ binding, then it will typically have a monotonic dependence in the form of a Hill equation (Supplemental Experimental Procedures). Thus, for simplicity, we assume a linear approximation, αT([Ca2 +]) = αT·[Ca2+]. In this case the target [Ca2+] is simply the ratio of two rate constants: Catgt = βT/αT.
We can now show how mRNA and conductances are regulated to keep the system at Catgt. Inspection of Equation 2 reveals that T explicitly integrates the difference between [Ca2+] and Catgt overtime:
This integrated Ca2+ “error” signal is then fed into the synthesis term of the channel mRNA (αmT, Equation 2). Similarly, m directly controls the expression rate of g via the term αgm. Finally, g controls the membrane potential and Ca2+ dynamics. The scheme in Equation 2 therefore constitutes a feedback loop that maintains average [Ca2+] by continually modifying the expression rates of channels in the membrane. This is illustrated in Figure 1B, where the shaded area shows the accumulated error signal over time. If [Ca2+] is different from the target, error will accumulate and drive changes in the expression of mRNA and membrane conductances until the system reaches equilibrium at [Ca2+] = Catgt.
So far, we assumed that a global regulator (T) controls downstream precursors of membrane conductances. What if these conductances are controlled by independent pathways that have the same integrating mechanism acting on the same error signal? An immediate problem arises if the set points for each controller are not tuned so that they all agree precisely. In Figure 2A, an inward and outward conductance are under the control of a single Ca2+-integrating regulator, T1, with target t1. Now suppose (Figure 2B) that each conductance is controlled by separate regulators, T1, T2, with different targets, t1 ≠ t2. Two possibilities exist: either one target will become satisfied, in which case error will accumulate without bound in the other controller, or, as will be the case more generally, neither target will be satisfied and both controllers will accumulate error without bound. This is shown in Figure 2B, where the two conductances upregulate without bound. In control theory, this accumulation of error is known as “windup.” In biological terms, windup would result in unbounded (eventually saturating) production of mRNAs and channels and loss of regulatory control. This could be avoided in this scenario if the reaction rates determining the independent targets are precisely matched; however, precise tuning seems unlikely in biological systems. We therefore conclude that for this model to work across a set of conductances, a single master regulator pathway is preferable. In more complex schemes with several distinct regulatory signals, it is possible to have separate targets for each signal (Liu et al., 1998). However, windup can still occur if these multiple signals cannot be satisfied simultaneously.
Specifying and Maintaining Cell Types with Multiple Regulated Conductances
The above analysis shows how activity in neurons can be maintained using a simple model of gene regulation. Overall, the regulation scheme can be written in simplified form for a neuron with multiple conductances, gi:
| (3) |
In this simplified form, the equations for Ṫ and m are lumped together (Experimental Procedures), concentrations are scaled, and reaction rates are replaced by single time constants. τg represents the characteristic time constant of channel expression and τi represents the coupling of channel gene expression to [Ca2+]. We use this simplified system in what follows.
The model achieves target [Ca2+], but what combination of conductances will the neuron express at this target? There are typically many ways to reach the same average activity using different maximal conductances (Bhalla and Bower 1993; Golowasch et al., 2002; Olypher and Calabrese 2007; Prinz et al., 2003; Sobie 2009; Swensen and Bean 2005; Taylor et al., 2006, 2009). Recent mathematical work has made the relationships between conductances and excitability clearer and more precise and can be understood in terms of ratios of conductances that act on different timescales (Drion et al., 2012; Franci et al., 2012; Franci et al., 2013). We see next that the integral control rule produces “nice” conductance distributions with constant ratios that are qualitatively similar to those observed biologically and can thus generate “cell types.”
Previous work (O’Leary et al., 2013) showed how regulation time constants determine correlations in conductance expression at steady state. What is the relation between conductance ratios and the regulation time constants τi in the present model? From the simplified scheme (Equation 3), each mi converges to a value that depends on the time integral of average [Ca2+], scaled by the inverse expression time constant τi. Thus, we can estimate steady-state gi for positive time constants and small initial conductances:
When taking ratios, the integrals cancel, so that:
| (4) |
In summary, different ratios of the τi ’s specify correlations between each conductance. Correlations in conductance expression, in turn, promote defined electrophysiological characteristics, because ratios of different kinds of voltage-gated conductances largely determine single neuron dynamics (Drion et al., 2012; Franci et al., 2013; Hudson and Prinz 2010).
Figure 3 shows an example of a complex model neuron with seven voltage-dependent conductances, all regulated by the integral control rule. The time evolution of the membrane conductances for multiple, randomly initialized runs of the model is shown (Figure 3A) with the membrane potential of an example neuron at four different time points. Each model starts in a nonexcitable nascent state (left-most trace, Figure 3A), which is ensured by choosing the random initial distribution of conductances to be small relative to the leak conductance that is itself randomly distributed (Experimental Procedures). The steady-state behavior of the model neuron is stereotyped and develops a rhythmic bursting activity (right-most trace, Figure 3A). In spite of varying initial conditions, the models at steady state all have similar membrane potential activity, as can be seen in the example traces of six model neurons that developed from different initial conditions (Figure 3B).
Figure 3C (lower panel) shows steady-state conductance distributions and intrinsic properties of 20 independent runs of the model. The conductance densities vary several-fold over the population, but all of the neurons have a similar bursting phenotype. Both the conductances and the firing properties show clear pairwise correlations that are reminiscent of experimental data in identified crustacean as well as mammalian neurons (Amendola et al., 2012; Liss et al., 2001; Schulz et al., 2007; Tobin et al., 2009). In contrast to previous modeling work that used a less biologically realistic regulation rule (Liu et al., 1998; O’Leary et al., 2013), the conductance correlations are approximately linear. Second, the use of a single activity sensor in the present model differs from this previous work, which used three sensors with different timescales to promote bursting behavior. While we do not rule out the possibility that more than one activity sensor is used biologically, the current model shows that this is not necessary.
Generating Cell Types
The simple relationship between regulation time constants and conductance ratios in the model means we can determine arbitrary correlations between conductances and thus construct self-regulating cells with specific intrinsic properties using only a single activity sensor. These intrinsic properties can encompass any excitability type, provided we have a sufficiently rich set of available conductances (i.e., a sufficiently rich “genome” in the model). Figure 4 shows five distinct neuron types that are achieved using the same underlying model and random initial conditions but with appropriately chosen sets of regulation time constants and [Ca2+] targets. We can thus specify cells that establish and maintain specific input-output relations, as quantified by the Type I/II FI curves in the first two examples. Type I excitability is characterized by the existence of arbitrarily low firing frequencies at spiking threshold (Figure 4A, example 1); in contrast, Type II excitability does not support firing below a fixed nonzero rate (example 2, Figure 4A) (Rinzel and Ermentrout, 1989). Notably, in spite of having different firing properties, both of these models have the same [Ca2+] target. Similarly, we can specify cells that respond reliably to input, as exemplified by an excitable rebound bursting cell that generates action potentials coupled to slow membrane potential oscillations in response to both depolarizing and hyperpolarizing current (example 3, Figure 4A). Finally, we can specify cells that are active in either a tonic spiking mode or bursting mode (examples 4 and 5, Figure 4A). Each of these cell types has a unique correlation structure in its steady-state conductance distribution (Figure 4B) following multiple runs from the same initial conditions. Furthermore, the straight line calculated from the ratio of expression time constants in Equation 4 predicts the pairwise conductance distributions in each case (Figure 4B).
The conductance distributions produced by the model may explain cell-specific linear correlations that are found biologically. Figure 4C reproduces data from Schulz et al. (2007) in which the expression levels of multiple ion channel genes were measured in single stomatogastric ganglion (STG) neurons using quantitative PCR. This revealed linear correlations in the expression that are specific the cell type (Figure 4C). The model predicts that the slopes of the correlations in the data should equal the (time-averaged) expression rates of the respective mRNAs in each plot.
There are two important biological assumptions in this instantiation of the model. First, the leak conductance, which can be thought of as an aggregate of multiple conductances, is static but varies between cells. This serves as a model of conductances that are not regulated by the integral control rule and that may vary across a population of neurons. Second, we have assumed that expression rates are fixed. Biologically, this corresponds to steady values in average promoter activity, binding affinities of signaling enzymes, translation rates, protein trafficking, and degradation rates. While this may be a reasonable assumption at any given stage in nervous system development, it is entirely plausible that these relationships change over time. Neurons may thus cycle through several physiological “types” as they develop, and this process will be highly specific to the species and brain area in question. We have not explicitly attempted to model these transient stages as our goal is more general; they can however be incorporated by switching the rates in the regulatory rule–an idea we examine in the final part of this work.
Expression Rates versus Activity Targets as Determinants of Electrophysiological Properties
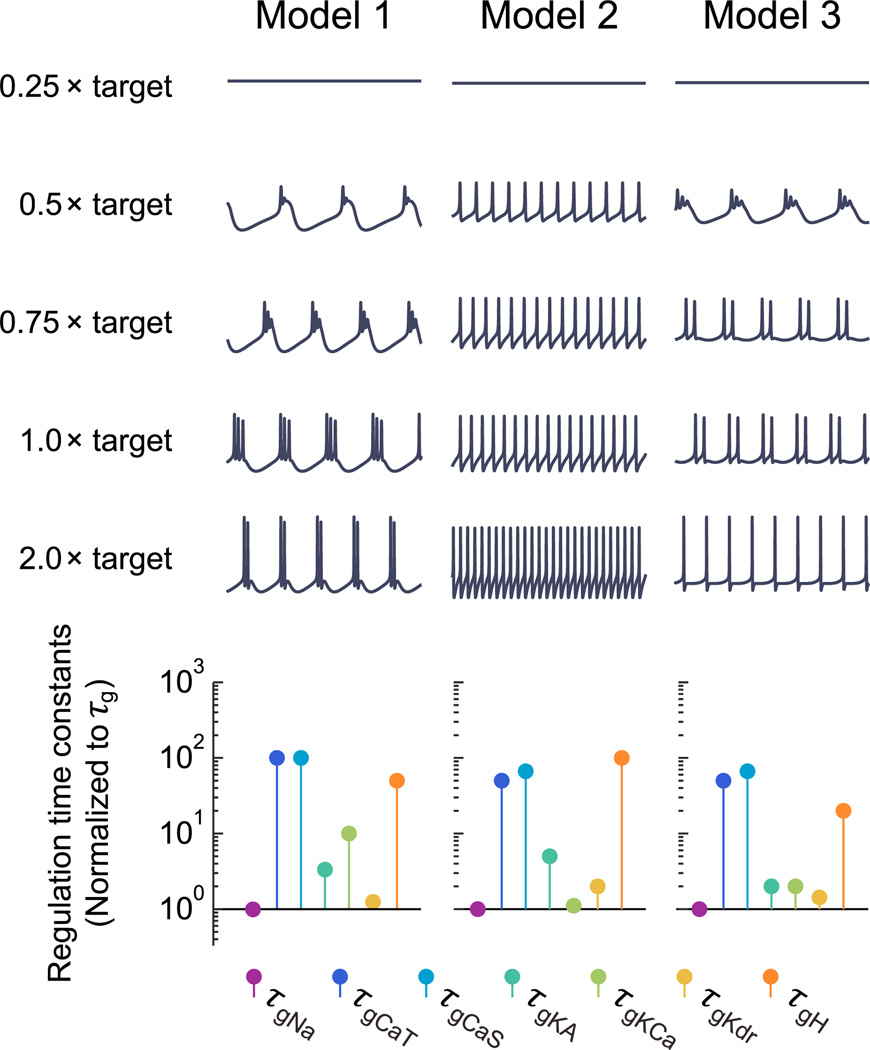
We have shown that different sets of regulation rates/time constants determine cell types and that distinct cell types can have the same [Ca2+] target in principle. What happens when the [Ca2+] target is scaled within a cell type? While the regulation time constants determine the direction in which the cell moves in conductance space, the target determines how far it travels along a trajectory before reaching equilibrium. Thus, targets can determine the location of the conductance distribution as well as scaling activity. Figure 5 shows the steady-state activity of three example neuron types as target [Ca2+] is scaled. Below the traces are plots showing the regulation time constants for each cell type. Typically, as the target is raised, spiking activity elevates because this corresponds to greater average Ca2+ influx, as can be seen in the first two examples. In some cases, moving the target can also cause a qualitative change in activity as seen in the third example, which transitions from bursting to spiking as [Ca2+] target is increased. Thus, the combined contributions of ion channel expression dynamics can be dissociated from activity set points in neurons, but both have a role in determining physiological properties.
Figure 5. Changing Targets within Cell Types.
Each column shows 500 ms segments of steady-state membrane potential activity in a different self-regulating model at steady state with the [Ca2+] target (= 4 µM) scaled. The regulation time constants for each conductance are shown below, normalized to τg.
A Self-Assembling Motor Circuit
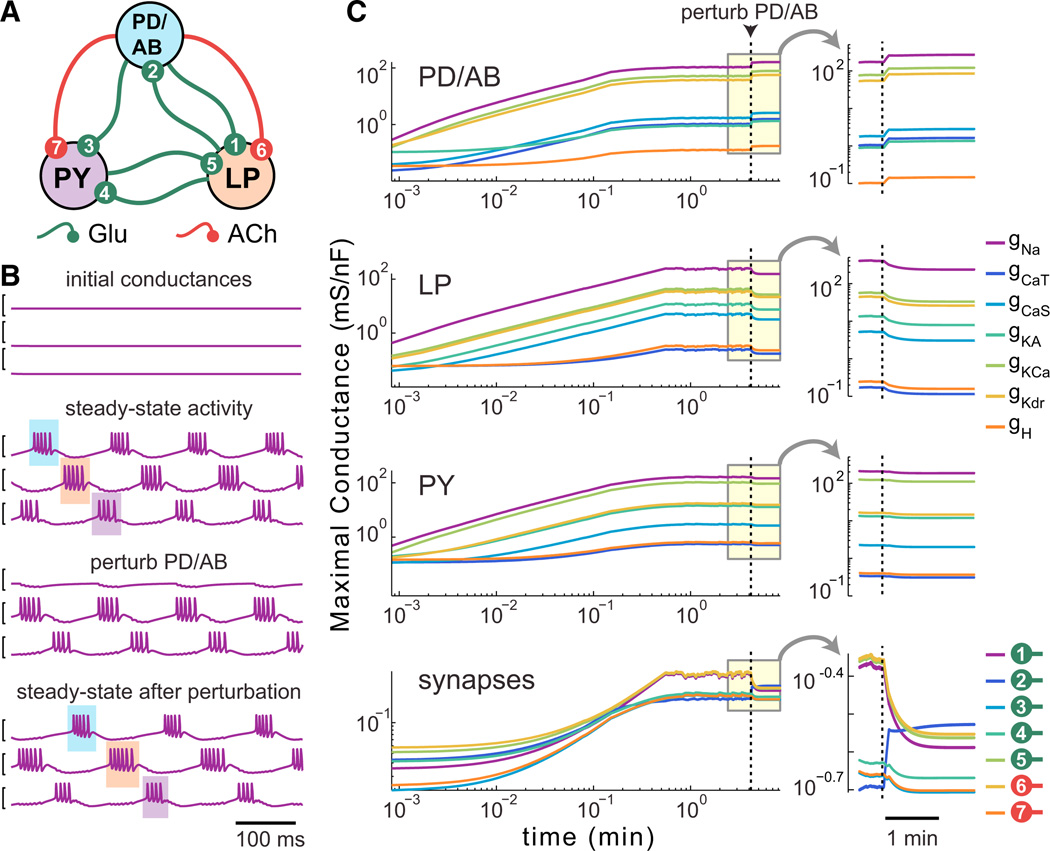
If we can reliably specify cell types using this model, it should be possible to construct a self-assembling, homeostatically regulated network whose activity depends on specific properties of the component cells (Golowasch et al., 1999b). The pyloric central pattern generating network of the crustacean STG consists of three distinct cell type modules: a pacemaker complex and two follower cell types that fire in successive phases. Activity in this network consists of a triphasic pattern of firing starting with the AB/PD complex, followed by the LP cell and then PY (Marder and Bucher 2007). The synaptic connectivity is known (Figure 6A) and consists of slow inhibitory cholinergic synapses as well as fast inhibitory glutamatergic synapses (Marder and Eisen 1984). We reasoned that by finding steady-state conductances and synaptic strengths that produced a triphasic pattern, we could then find regulation time constants for intrinsic conductances and synapses that would dynamically specify and maintain a characteristic network activity pattern.
Figure 6. A Self-Assembling, Self-Regulating Central Pattern Generating Network.
(A) Connectivity diagram of the model CPG, based on the synaptic connectivity of the pyloric network in the crustacean STG (PD/AB, pyloric dilator/ anterior burster; LP, lateral pyloric cell; PY, pyloric cell). The PD/AB pacemaker kernel is modeled as a single cell. All synapses are inhibitory and graded; glutamate (Glu) synapses are instantaneous, acetylcholine (ACh) synapses are slow (activation time constant = 50 ms).
(B) (Top) Example membrane potential traces for random initial conductances. (Second from top) Example steady-state behavior of the model. The triphasic order (PD, LP, PY) is highlighted with shaded boxes. (Third from top) Perturbation of network activity by addition of hyperpolarizing (reversal potential = −80 mV) conductance to PD. (Bottom) steady-state recovery of the network with hyperpolarizing conductance still present. All traces = 1 s.
(C) Example time evolution of intrinsic and synaptic conductances in a self-regulating pyloric network model for a single run. Onset of the PD/AB perturbation is indicated by the vertical line. Insets show detail of the conductance dynamics on a linear timescale.
After randomly searching conductance values to find combinations that produced bursting pacemaker cell types, we hand tuned an unregulated network to produce a qualitatively realistic triphasic rhythm. We then converted maximal conductances and synaptic conductances in the hand-tuned network to expression time constants using Equation 4. We next searched around this initial set of time constants using a log-normal distribution to find those that reliably produced triphasic networks from random initial conditions (Experimental Procedures).
The network always starts in a nonfunctional state (Figure 6B, top). The membrane potential activity of the cells after the network has reached steady state (Figure 6B, second from top) shows a regular triphasic rhythm. Furthermore, the network activity is robust to perturbations at steady state, as exemplified by recovery from the addition of a hyperpolarizing leak conductance (0.02 µS, Erev = −80 mV) that silences the PD/AB pacemaker cell (Figure 6B, third and fourth panels from top). Over multiple runs (n = 507) of this model, 99.6% produced stable triphasic rhythms. Of these, 93.5% recovered after the perturbation (which abolished rhythms in 99.2% of networks). Figure 6C shows the evolution of intrinsic and synaptic conductances in the example network of Figure 6B. Notably, the synaptic and intrinsic conductances in all cells respond to the perturbation in the PD/AB cell.
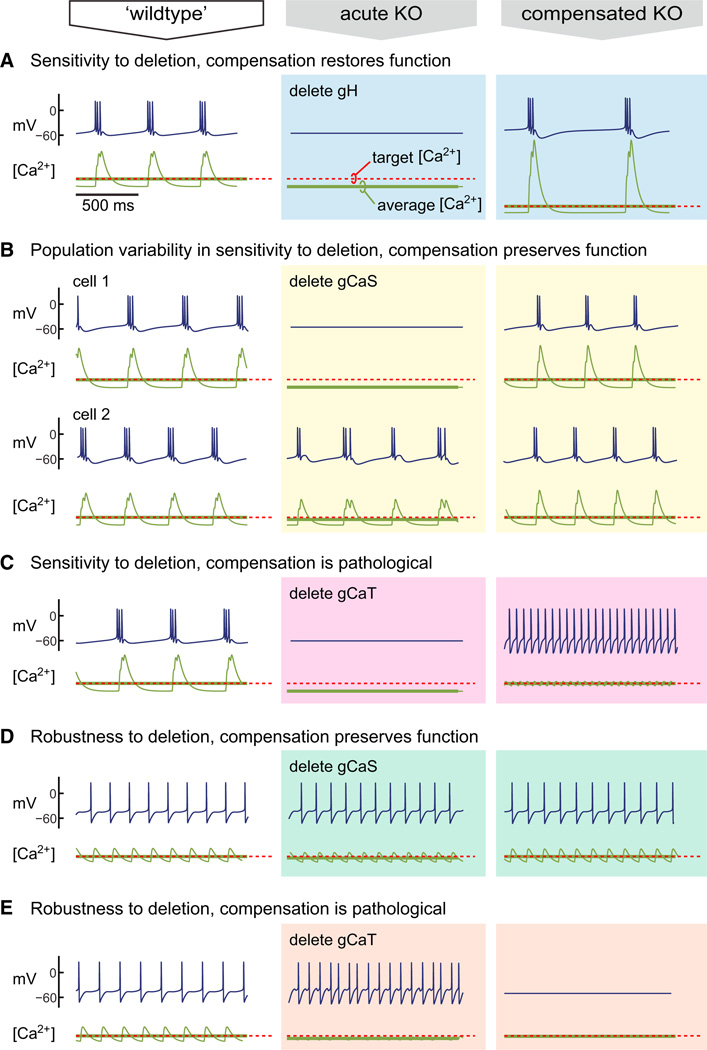
Activity-Dependent Regulation Can Be Compensatory or Pathological
Under what conditions does activity-dependent regulation compensate for mutation or pharmacological blockade? The conductances in the model neurons, as in biological neurons, overlap in some of their properties. Thus, if certain conductances are lost, others can be upregulated or downregulated to compensate. Figure 7A shows the steady-state behavior of a self-regulating bursting pacemaker neuron. Upon deletion of the Ih conductance, the models become silent, leading to a decrease in average [Ca2+]. Following deletion, the integral control rule restores bursting activity by altering conductance expression to achieve target [Ca2+]. Similar outcomes are possible when the deletion has variable effects owing to variability in the cells produced by the model. Figure 7B shows the effect of deleting a slow Ca2+ conductance in two different examples (that have converged to different maximal conductances) of the same cell type. In one example, the model increased in frequency; in the other, the model became silent. Again, average [Ca2+] encodes this increase or decrease in activity, and the resulting conductance regulation restores bursting.
Figure 7. Outcome of Homeostatic Compensation after Channel Deletion Depends on Cell and Channel Type.
Membrane potential activity for a self-regulating bursting ([A]–[C]) and tonic ([D] and [E]) pacemaker models in which specific conductances are deleted. The first column (“wild-type”) shows model behavior at steady state with all conductances present. Acute deletion of the indicated conductance produces the behavior shown in the middle column (“acute KO”). Following conductance deletion, each model is allowed to reach steady state (third column, “compensated KO”).
Can compensation lead to loss of function? The model assumes that neurons sense a gross physiological variable, [Ca2+], which cannot always distinguish specific activity patterns. Previous work identified this as a potential problem for regulation (Liu et al., 1998), but as we have shown here, it is nonetheless possible to use [Ca2+]to generate and maintain specific electrical properties using differential ion channel expression rates. However, this model will fail to preserve neuronal properties if the relationship between electrophysiological properties and [Ca2+] activity changes drastically. Such a change occurs in the example neuron in Figure 7C. Deletion of the transient Ca2+ conductance, gCaT, silences the neuron, but following compensation to target [Ca2+], the neuron no longer bursts and instead fires tonically. In this case, the deletion of gCaT resulted in changes in Ca2+ dynamics so that target [Ca2+] occurs for a fundamentally different pattern of membrane potential activity.
In a different tonic spiking model, deletion of one of the two Ca2+ currents has distinct effects. In Figure 7D, deletion of the slow Ca2+ conductance, gCaS, slightly alters the spiking frequency, and this is compensated by regulation. However, deletion of gCaT (Figure 7E) results in faster spiking, and compensation to the [Ca2+] target instead renders the cell silent.
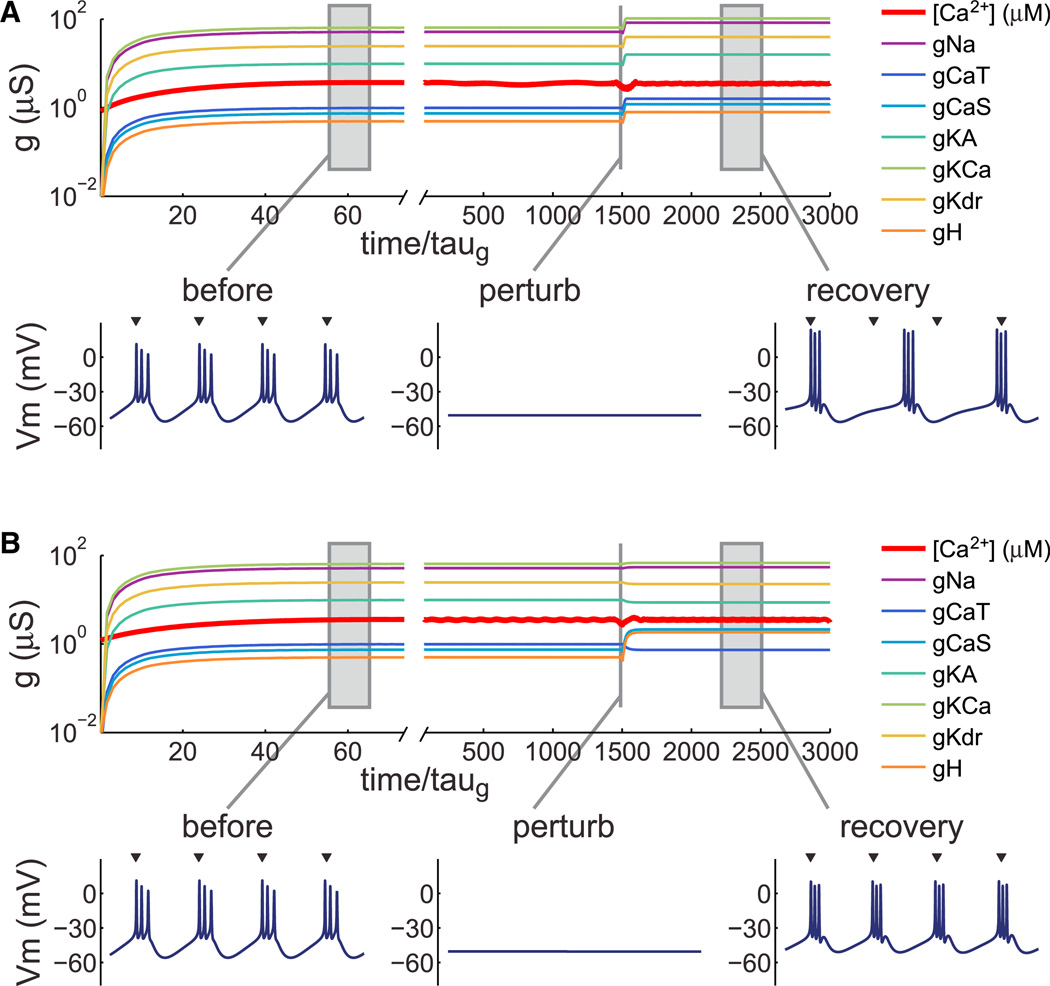
Switching Regulation Rates Can Preserve Specific Properties
The sets of regulation time constants we have studied so far are all fixed and positive. This achieves growth from random initial conditions but does not necessarily preserve all intrinsic properties when perturbations are compensated. Models with fixed positive regulation time constants predict that all conductances will upregulate or downregulate in the same direction in response to a perturbation. This is known to be false once neurons have more mature and stable properties (Desai et al., 1999; O’Leary et al., 2010), which suggests that a regulation rule suitable for growth may switch to one that is more appropriate for maintaining function in maturity.
We have previously shown (O’Leary et al., 2013) that self-regulating models are robust to changes in sign as well as magnitude of the conductance regulation rates. A negative regulation time constant/rate means the conductance is upregulated or downre-gulated in the opposite direction to those with positive rates as activity moves above or below target. We therefore examined whether regulation time constants could be switched in sign and magnitude to preserve a specific intrinsic property once a cell type has reached steady state. We began with a set of regulation time constants that encodes a bursting pacemaker cell (Figure 8A) with a characteristic burst period (mean ±SD = 123.1 ± 1.7 ms, n = 100 runs). Following perturbation with a hyperpolarizing leak conductance (0.02 µS, Erev = −80 mV), bursting activity recovered, but burst period increased by 47% (181.2 ±1.5 ms, n = 100 runs). We then searched sets of regulation time constants to find a set that could compensate burst period more accurately. After numerically searching 38,400 sets of time constants, we found a set that maintained burst period within 5% of the unperturbed value (128.8 ± 3.9 ms, n = 100 runs) during the perturbation. An example run is shown in Figure 8B. Notably, three of the time constants are negative (those regulating gCaT, gKA, and gKd) in the best “mature” set, and these parameters do not produce bursting cells if used exclusively from the initial conditions (data not shown). In summary, regulation time constants that promote development of specific physiological properties can be switched to mature time constants that preserve those properties better in response to specific kinds of perturbation.
Figure 8. Switching Regulation Rates in the Same Cell Can Preserve Specific Properties.
(A) Conductance regulation in a bursting pacemaker neuron. Membrane potential traces (500 ms duration) are shown at steady state, at the onset of a perturbation (hyperpolarizing leak), and at steady state following perturbation. Arrowheads above the rightmost trace indicate burst onset times of the unperturbed neuron, aligned to the first burst.
(B) Evolution of the same model as (A), but with regulation rule switched prior to the onset of the perturbation. Regulation time constants following the switch were chosen to preserve burst duration (see Experimental Procedures). Arrowheads as in (A). Membrane potential trace durations: 500 ms.
DISCUSSION
The proteins and other molecules that are found in neurons (or any other type of cell) are turned over continually and at any point in time exhibit variability in their quantity and structural relationships from cell to cell. In spite of this, and in spite of additional external perturbations, neurons must develop and maintain specific physiological properties. Otherwise the nervous system would be unable to learn, remember, process sensory information, produce movements, or perhaps function at all.
Ion channels underlie all electrical activity in the brain, and the relationship between ion channel expression and resulting activity is complex. We know from realistic biophysical models that sets of conductance parameters–which, in biological terms, represent the expression levels and enzymatic states of ion channels–can be wildly disparate and nevertheless give rise to highly specific physiological properties that are essential for a functioning nervous system (Bhalla and Bower 1993; Golowasch et al., 2002; Marder and Goaillard 2006; Prinz et al., 2003, 2004; Taylor et al., 2009). Small changes in some conductances can lead to catastrophic changes in excitability, while others can change several-fold without any noticeable effect. This does not mean that the underlying parameters in biological systems are as disparate as they can be in principle; rather, it conveys the necessity of navigating this wider parameter space in a robust way (Drion et al., 2012; Franci et al., 2013; Goldman et al., 2001; Hudson and Prinz 2010; Olypher and Calabrese 2007; Zhao and Golowasch 2012).
Experiments show that neurons use activity-dependent feedback to regulate membrane conductances and receptors (Amendola et al., 2012; Baines et al., 2001; Brickley et al., 2001; Desai et al., 1999; Golowasch et al., 1999a; Mee et al., 2004; O’Leary et al., 2010; Turrigiano et al., 1994, 1995). This allows ongoing perturbations or phenotypic variability in a cell population to be dynamically compensated. We showed how a regulatory scheme that captures the major events underlying ion channel expression gives riseto a simple, flexible, and robust model of activity-dependent conductance regulation. The model we derived differs from previous models (Abbott and LeMasson 1993; Golowasch et al., 1999b; LeMasson et al., 1993; Stemmler and Koch 1999) in several important ways that shed light on the biology of activity-dependent regulation. First, the origin of the activity set point is derived from biochemical principles in a way that depends on rates of enzymatic reactions. Second, the regulation mechanism is consistent with known biology. Third, the model shows biologically plausible levels of variability in the final conductance distributions without the conductances diverging or occasionally growing without bound. Fourth, the same model can be used to produce distinct cell types and only requires a single Ca2+ sensor to do so.
Biological neurons almost certainly possess more complex regulatory machinery than we have captured. However, this work shows how much can be done with minimal assumptions that are consistent with known biology. We thus view this model as a first approximation that can be refined rather than completely rewritten as experimental observations dictate.
Model Interpretation
A technical message of this work is that a canonical model of channel expression can be interpreted as a well-known control law: the integral controller. Integral control has been suggested as a mechanism of neuronal homeostasis based on the available molecular machinery for integrating Ca2+ signals in neurons (Davis 2006; O’Leary and Wyllie, 2011). We showed in this work how activity-dependent transcription can be an instantiation of integral control. The essential component of integral control is a variable whose rate of change depends on error. In the model presented here, error is deviation in [Ca2+] from a specific value, resulting in a change in the equilibrium of a putative regulator enzyme. The rate of change of ion channel mRNA is proportional to this error; consequently, ion channel mRNA concentration can be interpreted as the “accumulated error signal.” Biologically, the regulator enzyme could be a Ca2+-dependent transcription factor complex, or a Ca2+-binding enzyme upstream of a set of transcription factors. The biological counterpart of the [Ca2+] signal we consider is therefore a somatic or nuclear [Ca2+].
The form of the model placed a strong constraint on its implementation. If multiple, parallel integral control pathways using the same error signal exist within a cell, the targets for each pathway need to agree, otherwise the continual (and deleterious) accumulation of the molecules that encode error (such as mRNAs) will occur. While in principle it is possible that multiple parallel controllers are tuned so that their set points are equal, in biological reality, slight deviations are unavoidable. Thus for this model to work as a means of jointly regulating conductances in a neuron, a “master regulator” may be required. However, this does not rule out the possibility that other controllers using different error signals may coexist, provided there are conductance combinations that can simultaneously satisfy all controllers. For example, some currents could have targets specified by [Ca2+] transients or concentrations of other biological molecules provided these signals are sufficiently independent.
Integral control exists as a regulatory mechanism in simple organisms such as bacteria, where it permits sensitivity to environmental chemical cues and robust chemotaxis (Alon et al., 1999; Yi et al., 2000). It is thus a plausible and testable hypothesis that neurons have developed integral control pathways to regulate membrane conductances. Integral control implies perfect compensation in the control variable (average [Ca2+] in our case). Conversely, in systems that can be locally linearly approximated, perfect compensation implies integral control (Yi et al., 2000). Therefore, an experimental test of one assumption of this model is whether a relevant physiological variable such as average [Ca2+] is perfectly compensated over a range of perturbations. It is important that the perturbations do not exceed the capacity of the system to compensate, so a carefully controlled range of perturbations may be required along with precise monitoring of [Ca2+] to do this test.
The biochemical framework also allows a straightforward interpretation of an “activity target.” The nature of this target has been a source of speculation and even controversy since homeostatic regulation was first proposed (Maffei and Fontanini 2009; Marder and Prinz 2002).Weshowed that target [Ca2+] can be encoded by the rates of the underlying molecular mechanisms. Because these rates ultimately depend on chemical properties of enzymes, such as substrate binding affinity, the target can be reliably defined in a given cell or cell type.
How literally should one interpret this model? The mechanisms involved in regulating neuronal conductances are the focus of ongoing research and have many intricate components that we have omitted. Transcriptional control is involved in ion channel regulation (Weston and Baines 2007), and transcript editing, alternative splicing, and RNA interference can occur at the early stages of the process (Lin et al., 2012; Seeburg and Hartner 2003; Wang 2013). Similarly, at the stage when functional channels are expressed in the plasma membrane, phosphorylation and auxiliary subunit interactions can alter the biophysical properties of channels (Lipscombe et al., 2013). We did not attempt to model the effects of all such processes; instead we focus on the major events underlying channel expression that are encapsulated in the canonical model of gene expression: channel genes are activated, channel mRNA is transcribed, and channel protein is produced from mRNA. This simplification can be thought of as averaging out the contribution of more intricate processes, or as forming a backbone onto which the additional processes can be added. The task of refining the model will not be trivial; while we would expect the canonical model to hold across species and cell types, it would be surprising if more detailed models generalize without incorporating data that are specific to each experimental preparation.
Model Predictions
This work makes three general predictions. First, it predicts linear correlated variability in ion channel expression and that the slopes of the pairwise correlations between two ion channel expression measures should correspond to the ratio of their expression rates. For example, if one were to measure the average mRNA expression rates of two ion channels that are known to show a positive linear correlation in single-cell quantitative PCR measurements, then the ratio of the expression rates should equal the measured correlation slope (for example, the K+ channel genes shaw and shab in LP cells of the crab STG–see Figure 4B and 4C). Measuring mRNA expression dynamics is challenging and has not, to our knowledge, been performed in single neurons, although tools that may permit such measurements are being developed. On the other hand, single-cell quantification of steady-state ion channel gene expression does indeed show cell-type-specific correlations that are close to linear (Liss et al., 2001; Schulz et al., 2006, 2007; Temporal et al., 2012; Tobin et al., 2009).
Second, the model predicts that neurons do not necessarily perfectly compensate their electrical properties when perturbed, or when an ion channel type is knocked out, even if average [Ca2+] (or the relevant activity signal) is perfectly compensated over long timescales. This is illustrated in Figure 7, where we see that average [Ca2+] is always compensated, while the physiological behavior of the neuron can be compensated, partially compensated, or can even show pathological changes in behavior caused by the regulatory mechanism. In nonpathological cases, the model works because the regulation signal, [Ca2+], distinguishes different regions of conductance space. However, this sensing mechanism is dependent on certain combinations of conductances being present together. For example, if the ratio of delayed-rectifier K+ to fast Na+ conductances is within a certain (possibly large) range, then (ignoring other conductances and assuming a source of Ca2+ influx) low average [Ca2+] will correspond to silent cells, while high average [Ca2+] will only be achievable if the cell is firing tonically. Removal of one or more conductances can drastically alter the relationship between firing properties and [Ca2+], causing aberrant compensation. On the other hand, if the conductances overlap in their properties with other conductances, then removal may have only a subtle effect, or a substantial acute effect that can be compensated by the regulation mechanism.
This disconnect between nominally homeostatic behavior in one variable and nonhomeostatic behavior in the larger system has been suggested previously (O’Leary and Wyllie 2011) and illustrates the need for a careful definition of what homeo-stasis means. The safest definition is that homeostasis is an emergent phenomenon and occurs because the components in biological systems (such as ion channels) are often regulated using feedback. In general, the feedback signals can be a subset of those available and may act on a subset of the systems parameters (i.e., the system may be underactuated). Thus, neurons can exhibit firing rate set points (Hengen et al., 2013) or even maintenance of a coordinated motor pattern (Figure 6), but this does not necessarily mean the system directly measures and maintains these specific properties. This point is perhaps underappreciated but important because it is difficult to assess experimentally which are the controlled features of a homeostatic process.
The third broad prediction of this work is that changes in the regulatory rule itself may be part of nervous system development. The sets of regulation rates that define cell types in the model bring each cell to a steady state from random initial conditions with low conductance densities. This is a reasonable model of the early stage of differentiation from a nonneuronal cell with a nonexcitable (or weakly excitable) membrane (Moody and Bosma 2005; Spitzer et al., 2002). To reach mature levels of conductance expression, all conductances need to increase initially. This coordinated increase is inherent in the model of cell types (Figure 4) and predicts that the appearance of each ion channel type above some detection threshold will show a cell-type-specific ordering, in agreement with experimental observations in developing nervous systems (Baccaglini and Spitzer 1977; Moody and Bosma 2005; Spitzer 1991).
However, other experiments in nominally mature systems have shown that conductances can change their expression in opposite directions in response to perturbations in activity (Desai et al., 1999; O’Leary et al., 2010). Furthermore, while one rule may be sufficient for establishing a broad phenotype, changes to the rule could fine-tune conductances so the cell can preserve specific properties more effectively. We explored this idea speculatively in Figure 8, where we showed that tighter control of specific properties entails a switch in the regulation rates. Moving to a biological interpretation, this idea incorporates the observation that molecular switching events alter the expression rates of different genes (including ion channels) early in development and that some developmental changes have strictly sequential critical periods.
Network Homeostasis from Cell-Autonomous Regulation
Although the regulation model is local to each cell (i.e., it is “cell-autonomous”), the network model in Figure 6 shows coordinated responses across the network following perturbation of only one cell. Thus, when self-regulating cells are part of an interacting network, it is no longer sensible to label compensatory mechanisms as “cell-autonomous” or “non-cell-autonomous” by solely observing responses to perturbations.
The relative ease with which we constructed a self-regulating network is reassuring when we consider how biological nervous systems solve the analogous task. When systematically searched, the parameter space that produces a triphasic CPG in a similar model is found to be complex (Prinz et al., 2004). Biological systems thus need robust solutions to this problem (Morohashi et al., 2002; Stelling et al., 2004). Finding functional parameters in a complex space and reliably assembling a circuit is relatively straightforward with a well-behaved, biologically realistic feedback control mechanism. A key feature of this ease is modularity: in isolation, cell types can grow and self-regulate. Self-regulation ensures that when cells are combined in networks, the resulting perturbations due to network activity are compensated. The process of combining modular components would be impossibly fragile without some form of feedback control within the cells themselves or, as it is commonly known, homeostatic plasticity.
EXPERIMENTAL PROCEDURES
Single-compartment Hodgkin-Huxley models were used for all neuron models. The membrane potential, V, of a cell containing N conductances and membrane capacitance, C, is given by:
g̅i is maximal conductance, pi and qi are the number of “gates” in each conductance, and Ei is the reversal potential. m and h are the activation and inactivation variables. All models have unit capacitance (1 nF); maximal conductance values in the manuscript are therefore equivalent to conductances densities in units of µS/nF. The kinetic equations describing the seven voltage-gated conductances are taken from experimentally measured currents in isolated crab STG neurons, as described previously (Liu et al., 1998).
Numerical integration (exponential Euler) used a fixed timestep of 0.1 ms. Maximal conductances in all models were regulated using the integral control equations:
To avoid negative conductances, variables were bounded at 0; however, this condition was not required for the models presented. The parameters for neuron types were found by first identifying steady-state conductance densities that gave desired behavior from a random search of conductance space (2 × 106 models). The resulting conductance ratios were then scaled to give regulation time constants that were modified by hand where necessary to tune behavior. All parameters and initial conditions for all models are provided in Table S1 (available online). Additional simulation details and an example biochemical scheme that implements integral control are in Supplemental Experimental Procedures.
Supplementary Material
ACKNOWLEDGMENTS
The authors thank Michael Wright and Paul Miller for comments. Funding was provided by NIH 1P01NS079419 and the Charles A. King Trust.
Footnotes
SUPPLEMENTAL INFORMATION
Supplemental Information includes Supplemental Experimental Procedures and can be found with this article online at http://dx.doi.org/10.1016/j.neuron.2014.04.002.
REFERENCES
- Abbott L, LeMasson G. Analysis of neuron models with dynamically regulated conductances. Neural. Comput. 1993;5:823–842. [Google Scholar]
- Alon U. An Introduction to Systems Biology: Design Principles of Biological Circuits. Boca Raton: Chapman & Hall/CRC; 2007. [Google Scholar]
- Alon U, Surette MG, Barkai N, Leibler S. Robustness in bacterial chemotaxis. Nature. 1999;397:168–171. doi: 10.1038/16483. [DOI] [PubMed] [Google Scholar]
- Amendola J, Woodhouse A, Martin-Eauclaire MF, Goaillard JM. Ca2+/cAMP-sensitive covariation of I(A) and I(H) voltage dependences tunes rebound firing in dopaminergic neurons. J. Neurosci. 2012;32:2166–2181. doi: 10.1523/JNEUROSCI.5297-11.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baccaglini PI, Spitzer NC. Developmental changes in the inward current of the action potential of Rohon-Beard neurones. J. Physiol. 1977;271:93–117. doi: 10.1113/jphysiol.1977.sp011992. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baines RA, Uhler JP, Thompson A, Sweeney ST, Bate M. Altered electrical properties in Drosophila neurons developing without synaptic transmission. J. Neurosci. 2001;21:1523–1531. doi: 10.1523/JNEUROSCI.21-05-01523.2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barish ME. Intracellular calcium regulation of channel and receptor expression in the plasmalemma: potential sites of sensitivity along the pathways linking transcription, translation, and insertion. J. Neurobiol. 1998;37:146–157. [PubMed] [Google Scholar]
- Berridge MJ. Neuronal calcium signaling. Neuron. 1998;21:13–26. doi: 10.1016/s0896-6273(00)80510-3. [DOI] [PubMed] [Google Scholar]
- Bhalla US, Bower JM. Exploring parameter space in detailed single neuron models: simulations of the mitral and granule cells of the olfactory bulb. J. Neurophysiol. 1993;69:1948–1965. doi: 10.1152/jn.1993.69.6.1948. [DOI] [PubMed] [Google Scholar]
- Brickley SG, Revilla V, Cull-Candy SG, Wisden W, Farrant M. Adaptive regulation of neuronal excitability by a voltage-independent potassium conductance. Nature. 2001;409:88–92. doi: 10.1038/35051086. [DOI] [PubMed] [Google Scholar]
- Davis GW. Homeostatic control of neural activity: from phenomenology to molecular design. Annu. Rev. Neurosci. 2006;29:307–323. doi: 10.1146/annurev.neuro.28.061604.135751. [DOI] [PubMed] [Google Scholar]
- Desai NS. Homeostatic plasticity in the CNS: synaptic and intrinsic forms. J. Physiol. Paris. 2003;97:391–402. doi: 10.1016/j.jphysparis.2004.01.005. [DOI] [PubMed] [Google Scholar]
- Desai NS, Rutherford LC, Turrigiano GG. Plasticity in the intrinsic excitability of cortical pyramidal neurons. Nat. Neurosci. 1999;2:515–520. doi: 10.1038/9165. [DOI] [PubMed] [Google Scholar]
- Drengstig T, Ueda HR, Ruoff P. Predicting perfect adaptation motifs in reaction kinetic networks. J. Phys. Chem. B. 2008;112:16752–16758. doi: 10.1021/jp806818c. [DOI] [PubMed] [Google Scholar]
- Drion G, Franci A, Seutin V, Sepulchre R. A novel phase portrait for neuronal excitability. PLoS ONE. 2012;7:e41806. doi: 10.1371/journal.pone.0041806. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Finkbeiner S, Greenberg ME. Ca2+ channel-regulated neuronal gene expression. J. Neurobiol. 1998;37:171–189. [PubMed] [Google Scholar]
- Franci A, Drion G, Sepulchre R. An organizing center in a planar model of neuronal excitability. SIAM J. Appl. Dyn. Syst. 2012;11:1698–1722. [Google Scholar]
- Franci A, Drion G, Seutin V, Sepulchre R. A balance equation determines a switch in neuronal excitability. PLoS Comput. Biol. 2013;9:e1003040. doi: 10.1371/journal.pcbi.1003040. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goldman MS, Golowasch J, Marder E, Abbott LF. Global structure, robustness, and modulation of neuronal models. J. Neurosci. 2001;21:5229–5238. doi: 10.1523/JNEUROSCI.21-14-05229.2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Golowasch J, Abbott LF, Marder E. Activity-dependent regulation of potassium currents in an identified neuron of the stomatogastric ganglion of the crab Cancer borealis . J. Neurosci. 1999a;19:RC33. doi: 10.1523/JNEUROSCI.19-20-j0004.1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Golowasch J, Casey M, Abbott LF, Marder E. Network stability from activity-dependent regulation of neuronal conductances. Neural Comput. 1999b;11:1079–1096. doi: 10.1162/089976699300016359. [DOI] [PubMed] [Google Scholar]
- Golowasch J, Goldman MS, Abbott LF, Marder E. Failure of averaging in the construction of a conductance-based neuron model. J. Neurophysiol. 2002;87:1129–1131. doi: 10.1152/jn.00412.2001. [DOI] [PubMed] [Google Scholar]
- Günay C, Prinz AA. Model calcium sensors for network homeostasis: sensor and readout parameter analysis from a database of model neuronal networks. J. Neurosci. 2010;30:1686–1698. doi: 10.1523/JNEUROSCI.3098-09.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hengen KB, Lambo ME, Van Hooser SD, Katz DB, Turrigiano GG. Firing rate homeostasis in visual cortex of freely behaving rodents. Neuron. 2013;80:335–342. doi: 10.1016/j.neuron.2013.08.038. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hudson AE, Prinz AA. Conductance ratios and cellular identity. PLoS Comput. Biol. 2010;6:e1000838. doi: 10.1371/journal.pcbi.1000838. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim TK, Hemberg M, Gray JM, Costa AM, Bear DM, Wu J, Harmin DA, Laptewicz M, Barbara-Haley K, Kuersten S, et al. Widespread transcription at neuronal activity-regulated enhancers. Nature. 2010;465:182–187. doi: 10.1038/nature09033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- LeMasson G, Marder E, Abbott LF. Activity-dependent regulation of conductances in model neurons. Science. 1993;259:1915–1917. doi: 10.1126/science.8456317. [DOI] [PubMed] [Google Scholar]
- Lin WH, Gu¨nay C, Marley R, Prinz AA, Baines RA. Activity-dependent alternative splicing increases persistent sodium current and promotes seizure. J. Neurosci. 2012;32:7267–7277. doi: 10.1523/JNEUROSCI.6042-11.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lipscombe D, Allen SE, Toro CP. Control of neuronal voltagegated calcium ion channels from RNA to protein. Trends Neurosci. 2013;36:598–609. doi: 10.1016/j.tins.2013.06.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liss B, Franz O, Sewing S, Bruns R, Neuhoff H, Roeper J. Tuning pacemaker frequency of individual dopaminergic neurons by Kv4.3L and KChip3.1 transcription. EMBO J. 2001;20:5715–5724. doi: 10.1093/emboj/20.20.5715. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu Z, Golowasch J, Marder E, Abbott LF. A model neuron with activity-dependent conductances regulated by multiple calcium sensors. J. Neurosci. 1998;18:2309–2320. doi: 10.1523/JNEUROSCI.18-07-02309.1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maffei A, Fontanini A. Network homeostasis: a matter of coordination. Curr. Opin. Neurobiol. 2009;19:168–173. doi: 10.1016/j.conb.2009.05.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marder E. Variability, compensation, and modulation in neurons and circuits. Proc. Natl. Acad. Sci. USA. 2011;108(Suppl 3):15542–15548. doi: 10.1073/pnas.1010674108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marder E, Bucher D. Understanding circuit dynamics using the stomatogastric nervous system of lobsters and crabs. Annu. Rev. Physiol. 2007;69:291–316. doi: 10.1146/annurev.physiol.69.031905.161516. [DOI] [PubMed] [Google Scholar]
- Marder E, Eisen JS. Transmitter identification of pyloric neurons: electrically coupled neurons use different transmitters. J. Neurophysiol. 1984;51:1345–1361. doi: 10.1152/jn.1984.51.6.1345. [DOI] [PubMed] [Google Scholar]
- Marder E, Goaillard JM. Variability, compensation and homeostasis in neuron and network function. Nat. Rev. Neurosci. 2006;7:563–574. doi: 10.1038/nrn1949. [DOI] [PubMed] [Google Scholar]
- Marder E, Prinz AA. Modeling stability in neuron and network function: the role of activity in homeostasis. Bioessays. 2002;24:1145–1154. doi: 10.1002/bies.10185. [DOI] [PubMed] [Google Scholar]
- Mease RA, Famulare M, Gjorgjieva J, Moody WJ, Fairhall AL. Emergence of adaptive computation by single neurons in the developing cortex. J. Neurosci. 2013;33:12154–12170. doi: 10.1523/JNEUROSCI.3263-12.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mee CJ, Pym EC, Moffat KG, Baines RA. Regulation of neuronal excitability through pumilio-dependent control of a sodium channel gene. J. Neurosci. 2004;24:8695–8703. doi: 10.1523/JNEUROSCI.2282-04.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mermelstein PG, Bito H, Deisseroth K, Tsien RW. Critical dependence of cAMP response element-binding protein phosphorylation on L-type calcium channels supports a selective response to EPSPs in preference to action potentials. J. Neurosci. 2000;20:266–273. doi: 10.1523/JNEUROSCI.20-01-00266.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mihalas AB, Araki Y, Huganir RL, Meffert MK. Opposing action of nuclear factor κB and Polo-like kinases determines a homeostatic end point for excitatory synaptic adaptation. J. Neurosci. 2013;33:16490–16501. doi: 10.1523/JNEUROSCI.2131-13.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moody WJ. Control of spontaneous activity during development. J. Neurobiol. 1998;37:97–109. doi: 10.1002/(sici)1097-4695(199810)37:1<97::aid-neu8>3.0.co;2-3. [DOI] [PubMed] [Google Scholar]
- Moody WJ, Bosma MM. Ion channel development, spontaneous activity, and activity-dependent development in nerve and muscle cells. Physiol. Rev. 2005;85:883–941. doi: 10.1152/physrev.00017.2004. [DOI] [PubMed] [Google Scholar]
- Morohashi M, Winn AE, Borisuk MT, Bolouri H, Doyle J, Kitano H. Robustness as a measure of plausibility in models of biochemical networks. J. Theor. Biol. 2002;216:19–30. doi: 10.1006/jtbi.2002.2537. [DOI] [PubMed] [Google Scholar]
- O’Donovan MJ. The origin of spontaneous activity in developing networks of the vertebrate nervous system. Curr. Opin. Neurobiol. 1999;9:94–104. doi: 10.1016/s0959-4388(99)80012-9. [DOI] [PubMed] [Google Scholar]
- O’Leary T, Wyllie DJA. Neuronal homeostasis: time for a change? J. Physiol. 2011;589:4811–4826. doi: 10.1113/jphysiol.2011.210179. [DOI] [PMC free article] [PubMed] [Google Scholar]
- O’Leary T, van Rossum MCW, Wyllie DJA. Homeostasis of intrinsic excitability in hippocampal neurones: dynamics and mechanism of the response to chronic depolarization. J. Physiol. 2010;588:157–170. doi: 10.1113/jphysiol.2009.181024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- O’Leary T, Williams AH, Caplan JS, Marder E. Correlations in ion channel expression emerge from homeostatic tuning rules. Proc. Natl. Acad. Sci. USA. 2013;110:E2645–E2654. doi: 10.1073/pnas.1309966110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Olypher AV, Calabrese RL. Using constraints on neuronal activity to reveal compensatory changes in neuronal parameters. J. Neurophysiol. 2007;98:3749–3758. doi: 10.1152/jn.00842.2007. [DOI] [PubMed] [Google Scholar]
- Olypher AV, Prinz AA. Geometry and dynamics of activity-dependent homeostatic regulation in neurons. J. Comput. Neurosci. 2010;28:361–374. doi: 10.1007/s10827-010-0213-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Prinz AA, Billimoria CP, Marder E. Alternative to hand-tuning conductance-based models: construction and analysis of databases of model neurons. J. Neurophysiol. 2003;90:3998–4015. doi: 10.1152/jn.00641.2003. [DOI] [PubMed] [Google Scholar]
- Prinz AA, Bucher D, Marder E. Similar network activity from disparate circuit parameters. Nat. Neurosci. 2004;7:1345–1352. doi: 10.1038/nn1352. [DOI] [PubMed] [Google Scholar]
- Ramocki MB, Zoghbi HY. Failure of neuronal homeostasis results in common neuropsychiatric phenotypes. Nature. 2008;455:912–918. doi: 10.1038/nature07457. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rinzel J, Ermentrout GB. Analysis of neural excitability and oscillations. In: Koch C, Segev I, editors. In Methods in Neuron Modeling. Cambridge: MIT Press; 1989. [Google Scholar]
- Schulz DJ, Goaillard JM, Marder E. Variable channel expression in identified single and electrically coupled neurons in different animals. Nat. Neurosci. 2006;9:356–362. doi: 10.1038/nn1639. [DOI] [PubMed] [Google Scholar]
- Schulz DJ, Goaillard JM, Marder EE. Quantitative expression profiling of identified neurons reveals cell-specific constraints on highly variable levels of gene expression. Proc. Natl. Acad. Sci. USA. 2007;104:13187–13191. doi: 10.1073/pnas.0705827104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Seeburg PH, Hartner J. Regulation of ion channel/neurotrans-mitter receptor function by RNA editing. Curr. Opin. Neurobiol. 2003;13:279–283. doi: 10.1016/s0959-4388(03)00062-x. [DOI] [PubMed] [Google Scholar]
- Sobie EA. Parameter sensitivity analysis in electrophysiological models using multivariable regression. Biophys. J. 2009;96:1264–1274. doi: 10.1016/j.bpj.2008.10.056. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Soto-Treviño C, Thoroughman KA, Marder E, Abbott LF. Activity-dependent modification of inhibitory synapses in models of rhythmic neural networks. Nat. Neurosci. 2001;4:297–303. doi: 10.1038/85147. [DOI] [PubMed] [Google Scholar]
- Spitzer NC. A developmental handshake: neuronal control of ionic currents and their control of neuronal differentiation. J. Neurobiol. 1991;22:659–673. doi: 10.1002/neu.480220702. [DOI] [PubMed] [Google Scholar]
- Spitzer NC, Kingston PA, Manning TJ, Conklin MW. Outside and in: development of neuronal excitability. Curr. Opin. Neurobiol. 2002;12:315–323. doi: 10.1016/s0959-4388(02)00330-6. [DOI] [PubMed] [Google Scholar]
- Stelling J, Sauer U, Szallasi Z, Doyle FJ, Doyle J., 3rd Robustness of cellular functions. Cell. 2004;118:675–685. doi: 10.1016/j.cell.2004.09.008. [DOI] [PubMed] [Google Scholar]
- Stemmler M, Koch C. How voltage-dependent conductances can adapt to maximize the information encoded by neuronal firing rate. Nat. Neurosci. 1999;2:521–527. doi: 10.1038/9173. [DOI] [PubMed] [Google Scholar]
- Swensen AM, Bean BP. Robustness of burst firing in dissociated purkinje neurons with acute or long-term reductions in sodium conductance. J. Neurosci. 2005;25:3509–3520. doi: 10.1523/JNEUROSCI.3929-04.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Taylor AL, Hickey TJ, Prinz AA, Marder E. Structure and visualization of high-dimensional conductance spaces. J. Neurophysiol. 2006;96:891–905. doi: 10.1152/jn.00367.2006. [DOI] [PubMed] [Google Scholar]
- Taylor AL, Goaillard JM, Marder E. How multiple conductances determine electrophysiological properties in a multicompartment model. J. Neurosci. 2009;29:5573–5586. doi: 10.1523/JNEUROSCI.4438-08.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Temporal S, Desai M, Khorkova O, Varghese G, Dai A, Schulz DJ, Golowasch J. Neuromodulation independently determines correlated channel expression and conductance levels in motor neurons of the stomatogastric ganglion. J. Neurophysiol. 2012;107:718–727. doi: 10.1152/jn.00622.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thoby-Brisson M, Simmers J. Transition to endogenous bursting after long-term decentralization requires De novo transcription in a critical time window. J. Neurophysiol. 2000;84:596–599. doi: 10.1152/jn.2000.84.1.596. [DOI] [PubMed] [Google Scholar]
- Tobin AE, Cruz-Bermúdez ND, Marder E, Schulz DJ. Correlations in ion channel mRNA in rhythmically active neurons. PLoS ONE. 2009;4:e6742. doi: 10.1371/journal.pone.0006742. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Turrigiano G. Homeostatic signaling: the positive side of negative feedback. Curr. Opin. Neurobiol. 2007;17:318–324. doi: 10.1016/j.conb.2007.04.004. [DOI] [PubMed] [Google Scholar]
- Turrigiano GG, Nelson SB. Homeostatic plasticity in the developing nervous system. Nat. Rev. Neurosci. 2004;5:97–107. doi: 10.1038/nrn1327. [DOI] [PubMed] [Google Scholar]
- Turrigiano G, Abbott LF, Marder E. Activity-dependent changes in the intrinsic properties of cultured neurons. Science. 1994;264:974–977. doi: 10.1126/science.8178157. [DOI] [PubMed] [Google Scholar]
- Turrigiano G, LeMasson G, Marder E. Selective regulation of current densities underlies spontaneous changes in the activity of cultured neurons. J. Neurosci. 1995;15:3640–3652. doi: 10.1523/JNEUROSCI.15-05-03640.1995. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van Ooyen A. Using theoretical models to analyse neural development. Nat. Rev. Neurosci. 2011;12:311–326. doi: 10.1038/nrn3031. [DOI] [PubMed] [Google Scholar]
- Wang Z. miRNA in the regulation of ion channel/transporter expression. Compr. Physiol. 2013;3:599–653. doi: 10.1002/cphy.c110002. [DOI] [PubMed] [Google Scholar]
- Weston AJ, Baines RA. Translational regulation of neuronal electrical properties. Invert. Neurosci. 2007;7:75–86. doi: 10.1007/s10158-006-0037-8. [DOI] [PubMed] [Google Scholar]
- Wheeler DG, Groth RD, Ma H, Barrett CF, Owen SF, Safa P, Tsien RW. Ca(V)1 and Ca(V)2 channels engage distinct modes of Ca(2+) signaling to control CREB-dependent gene expression. Cell. 2012;149:1112–1124. doi: 10.1016/j.cell.2012.03.041. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yi TM, Huang Y, Simon MI, Doyle J. Robust perfect adaptation in bacterial chemotaxis through integral feedback control. Proc. Natl. Acad. Sci. USA. 2000;97:4649–4653. doi: 10.1073/pnas.97.9.4649. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhao S, Golowasch J. Ionic current correlations underlie the global tuning of large numbers of neuronal activity attributes. J. Neurosci. 2012;32:13380–13388. doi: 10.1523/JNEUROSCI.6500-11.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.