Scattered Hammond plots reveal second level of site-specific information in protein folding: φ′ (β^‡)

Abstract

Site-specific information about structural heterogeneities of the protein-folding transition-state ensemble is commonly derived from the scatter of the Brønsted plot through the individual values of φ = Δlogk_f/ΔlogK_D-N. Here, we provide a second level of site-specific detail in the transition-state analysis by demonstrating that the scatter of the Hammond plot is related to heterogeneities in the φ-value growth. That is, the extent of transition-state movement (Δβ^‡) is proportional to the free-energy gradient of the mutational perturbation across the top of the activation barrier, φ′(β^‡) ∝ ΔlogK_D-N. The analysis is applied to the two-state protein L23 where the site-specific free-energy gradients are used to identify the interactions that show the highest degree of consolidation after crossing the barrier top. These interactions are distributed as a shell around the high-φ initiation point and denote the side-chain contacts that add criticality to the folding nucleus.

Amajor challenge in experimental studies of protein folding is to deduce more detailed, high-dimensional information about the diffuse transition-state ensemble to aid the microscopic characterization of folding nucleation and the folding free-energy landscape (1, 2). One strategy has been to see how the structural features of the transition-state ensemble change upon perturbation by denaturants and mutation. A frequently encountered example of such transition-state changes is the Hammond postulate behavior (3). The phenomenon was first reported for barnase and CI2, whose transition-state structures became more native-like as the activation free energy for unfolding was decreased by protein engineering (4, 5). Detection of the transition-state shift was by changes of the kinetic m values, i.e., by small tilts of the v-shaped chevron plots. The Hammond behavior, which has subsequently appeared as a general feature of small proteins (6–16), indicates that the top of the activation barrier is smoothly curved and displays some breadth. Upon mutational perturbation, any slanting of this curvature will cause a movement of the barrier maximum along the folding trajectory (13). From second-order polynomial curvatures of the chevron plots (4), it is further apparent that the barrier tops display an approximately quadratic curvature (13). However, the magnitude of the Hammond shifts for proteins with v-shaped chevron plots is relatively subtle and covers typically <15% of the total folding distance as measured by β^‡ = m_f/(m_u - m_f). Deviation from this minimal behavior is sometimes seen for proteins with pronounced distortions of the v-shaped chevron plot, indicating much larger changes of the transition state position (13, 17). The phenomenon, however, can still be accounted for by low-dimensional movements along the barrier profile, but this time in the form of discrete shifts between consecutive pointed maxima along the folding free-energy profile (7, 14, 18–20). More complex transition-state alterations along secondary order parameters are not normally discerned by the gross parameter β^‡ (6), and seem also to require extensive mutational alterations (7, 21–23) or changes of the sequence connectivity through circular permutation (24–27).

In this study, we present a formalism that quantitatively relates mutational perturbations to the extent of Hammond shifts in protein folding, revealing another aspect of the structural events taking place in the transition-state ensemble: the site-specific growth of contact free energy along the experimental progress coordinate β. The analysis is applied to the ribosomal protein L23 (PDB ID code 1N88; ref. 28), which has not previously been subjected to folding studies. L23 shows v-shaped chevron plots and a classical nucleation-condensation distribution of fractional φ values in the transition state. The mutant-induced m-value changes show further that L23 describes moderate Hammond shifts, but no significant plasticity of the denatured or native ground states. The critical feature of the L23 Hammond plot is, however, that the individual m values are scattered beyond the experimental errors, allowing a detailed description of the contact growth within the critical nucleus as the protein traverses the barrier top.

Theory

General Features of Two-State Folding. In two-state folding, the equilibrium constant (K_D-N = [D]/[N]) has been shown to equal the ratio of the unfolding and refolding rate constants (29), K_D-N = k_u/k_f, where

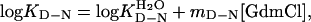[1]

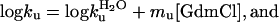[2]

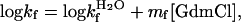[3]

according to the empirical observation of linear free-energy changes after the addition of chemical denaturants like GdmCl or urea (30). The parameters are derived experimentally from chevron plots; i.e., plots of log k_f and log k_u versus [GdmCl], fitting the equation

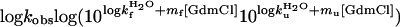[4]

The slopes m_u - m_f = m_D-N are commonly taken as measures of the change in solvent exposure in the activation process of unfolding and refolding, respectively. The m values are used to position the folding transition-state ensemble on the experimental progress coordinate β according to refs. 29 and 31:

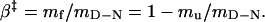[5]

Additional, site-specific information about the contacts present in the transition-state structure is obtained from the φ values (30)

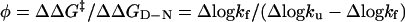[6]

that measure the effect of point mutation on the transition-state stability (ΔΔG^‡) relative to that of the native state (ΔΔG_D-N). A φ value of 1 indicates that the structure around the mutated side chain has grown fully native-like at the position of the transition state (β = β^‡), whereas a φ value of 0 indicates that it is still disordered.

Basic Rationale for Hammond Postulate Behavior in Protein Folding. The relation between mutational perturbation and transition-state movements; i.e., changes of β^‡, was deduced as follows. We have previously demonstrated, by monitoring the effect of individual mutations along the broad barrier region of U1A, that the stability loss on mutation increases progressively with β (15). That is, mutations have generally larger energetic effect on the late part of the reaction profile where the interactions are better consolidated. A general expression for this mutant-induced perturbation is given by

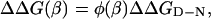[7]

where ΔΔG(β) is the stability loss as a function of β and φ(β) describes the φ-value growth along β (Fig. 1). Because ΔΔG(β) increases along the experimental progress coordinate, the free-energy profile is shifted up more near the native state and, in combination with any width of the barrier top, this biased perturbation will cause the transition state to shift closer to the native state. For quadratic curvatures of the barrier top, as is suggested experimentally from second-order polynomial dependence of logk_u on [GdmCl] (13), the folding free-energy profile near the transition state may be approximated with the function

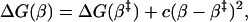[8]

where c < 0. The transition-state shift following the mutational perturbation ΔG^mut(β) = ΔG(β) + φ(β)ΔΔG_D-N is then given by 0 = ΔG′(β) + φ′(β)ΔΔG_D-N ⇒

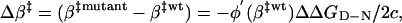[9]

and from Eq. 5

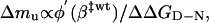[10]

assuming that the perturbation φ(β)ΔΔG_D-N is approximately linear in the narrow interval Δβ^‡. The corresponding barrier height at β^‡mut is

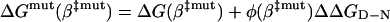[11]

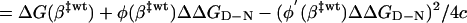Fig. 1.

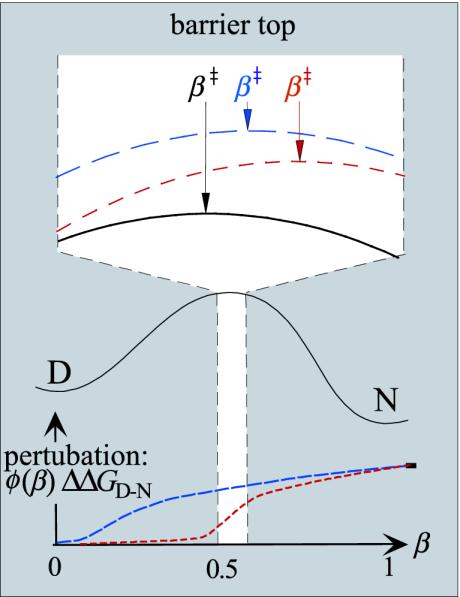
Schematic illustration of transition-state shift on a smooth folding free-energy profile, including an expanded view of the barrier top. After mutational perturbation, the barrier profile is offset by ΔΔG(β) = φ(β)ΔΔG_D-N (Eq. 7), describing the loss of interaction free energy along the experimental coordinate β. The resulting extent of transition-state shift is then determined by the slope of the perturbation across the barrier top (Eqs. 7, 8, 9, 10, 11). Exemplified are two mutations with different values of φ and different gradients of ΔΔG(β) across the narrow interval of the transition-state shift (blue and red). For simplicity, the mutations are assumed to have the same ΔΔG_D-N. The red mutation causes larger shifts of β^‡ than the blue because its relative effect of the early and late part of the barrier top is larger. Mutations with constant values of φ across the barrier top do not produce transition-state shifts.

In other words, the extent of transition-state movement (Δm_u) is proportional to the gradient of the mutational perturbation across the free-energy maximum. Hammond shifts are thus not expected for mutations with constant values of φ across the barrier top, because these mutations will just contribute to offset the barrier without affecting its tilt. β^‡ shifts arise only from mutation of interactions that undergo changes upon traversing the barrier top, i.e., interactions that are in the process of being formed (5). Preformed or fully unfolded parts of the protein are just carried over silently. Notably, it can be shown that the proportionality between Δm_u and φ′(β^{‡ wt})ΔΔG_D-N is qualitatively the same whether the barrier top is not perfectly smooth as assumed in Eq. 8, but riddled with fine structure. The values of Δm_u would then tend to change discretely with ΔΔG_D-N as the transition state shifts from one local maximum to the next. However, the approximately smooth distribution of the experimentally observed m_u values provides no evidence for the existence of such fine structure (compare Fig. 5). To this end, it may further be argued that, for the small β-windows studied here, the fine structure should be smoothened out by conformational heterogeneities of the transition-state ensemble. Another notable feature of the simplistic formalism in Fig. 1 is that it captures the experimental finding that, in protein folding, the Hammond shift (Δβ^‡ or Δm_u) is linearly related to ΔΔG_D-N (13) and not to changes in the barrier height (Eqs. 8, 9, 10, 11).

Fig. 5.

m values change after mutational perturbation of L23. (Upper). Hammond plot (m_u versus Δlogk_u) showing that the scatter of the m_u values is larger than the experimental errors. The fitted line is m_u = 0.7–0.077(±0.01)Δlogk_u, R = 0.82. (Lower) Comparison of the Hammond plots β^‡ versus ΔlogK_D-N from data in Table 1 (•) and the Brønsted slopes (<φ> in Fig. 3) versus ΔlogK_D-N = <m_D-N>[GdmCl] (○). β^‡ = 0.5 + 0.033(± 0.01)ΔlogK_D-N (R = 0.74) and <φ>= 0.14 + 0.053(± 0.004)ΔlogK_D-N (R = 0.99). Although the absolute values for the transition-state position are different, their dependence on ΔlogK_D-N is overall similar, providing additional evidence for transition state movements in L23.

Experiment

Materials. Mutagenesis was performed by standard procedures using the QuikChange kit (Stratagene). The protein was expressed in Escherichia coli (BL21 DE3) and purified with cation exchange (SP-Sepharose, Amersham Pharmacia) and gel filtration (S100, Amersham Pharmacia). The stopped-flow measurements were carried out on a SX-17MV instrument (Applied Photophysics, Surrey, U.K.) at 25°. Buffer was 50 mM Mes at pH 6.3 (Sigma) and 0.23 M Na₂SO₄ (Merck). The guanidinium chloride (GdmCl) was ultra pure from ICN Biomedicals.

Na₂SO₄ Allows Analysis of Marginally Stable Proteins. Because the stability of wild-type L23 is relatively low, the experiments were performed under mildly stabilizing conditions in the presence of 0.23 M Na₂SO₄ to assure accurate determination of the refolding rate constant and the refolding m value (Eqs. 2 and 3). Under these conditions, L23 displays a transition midpoint of 3.73 M GdmCl and ΔG_D-N = 7.4 kcal/mol, corresponding to a stabilizing power of Na₂SO₄ of ≈3 (kcal/mol) M. In the absence of Na₂SO₄, midpoint = 2.77 M and ΔG_D-N = 4.6 kcal/mol.

A side effect of subjecting proteins to Na₂SO₄, or other stabilizing agents, is that the increased contact strength may lead to premature collapse of the coil, revealed by rollovers in the refolding limb of the chevron plot (32, 33). Although such rollovers may be discerned >0.5 M Na₂SO₄, the effect is negligible at 0.23 M. As a control, the φ values for several mutants were determined in both 0 and 0.23 M Na₂SO₄ and found to be the same within the experimental errors. Moreover, the exclusion of chevron data <1 M GdmCl does not significantly affect the m value changes upon mutation.

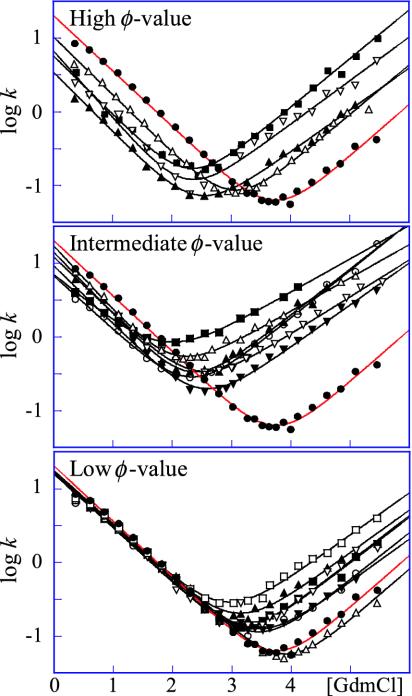
V-Shaped Chevrons and Diffuse Nucleus Suggest “Classical” Two-State Behavior. L23 consists of a central four-stranded β-sheet that is clamped by three helices forming a saddle-shaped hydrophobic core (28). A notable feature of this core is that the aromatic side chains are polarized toward the N-terminal side, whereas the C-terminal side consists mainly of aliphatic moieties. For the analysis, 17 conservative mutations were performed throughout the interior of the L23 structure, all of which showed approximately v-shaped chevron plots with overall similar, but not identical, m values (Fig. 2). By this criterion, L23 classifies as a classical two-state folder (34). Even so, the slightly different tilts of the chevron plots, i.e., changes in m_f and m_u (Table 1), will produce a slight GdmCl dependence of the φ value according to Eq. 6. The phenomenon is apparent to various extent in all two-state proteins and seems to reflect structural reorganizations of the transition state upon mutation (35). To minimize the consequences of these m-value changes, we have estimated the φ values near the transition midpoint at 1.5 M GdmCl, where the refolding rate constant (k_f) can be measured directly and the extrapolation of unfolding data (k_u) is minimal. All L23 mutations display fractional φ values, ranging from a highest value of 0.44 for V81A to nearly zero for V12A and I89A (Table 1). This diffuse nature of the L23 transition state is further apparent from the Brønsted plot (i.e., Δlogk_u versus ΔlogK_D-N), which yields <φ> = 0.18 (Fig. 3). When calculated at other GdmCl concentrations, the internal graduation of the φ values remains largely the same, showing that the deviation from “ideal” two-state behavior of L23 is too small to have any significant bearing on the structural analysis of the transition-state ensemble. The stability loss of the mutants in Table 1 varies from 1.1 kcal/mol (L57A) to >4 kcal/mol (Y26A), with the exception of the excluded mutation Y18A that shows too slight a stability change to allow accurate determination of its φ-value. Taken together, these straightforward experimental characteristics make L23 an ideal model system for tests of the formalism in Fig. 1.

Fig. 2.

Chevron plots for wild-type (•) and mutant L23, grouped according to their φ values. Units for the rate constants are in s^-1. (Top) Mutants with φ > 0.25. V30A (▪), V81A (▴), V43A (▿), and I39V (▵). (Middle) Mutants with 0.25 > φ > 0.10. Y26A (▪), V49A (▴), V51A (▿), V54A (▵), I80A (▾), and V83A (○). (Bottom) Mutants with φ < 0.10. I8V (▪), V12A (▴), L13A (▿), Y18A (▵), F21A (▾), L57A (○), and I89A (□). In Figs. 3 and 4, mutants with high, intermediate, and low φ values are red, orange, and yellow, respectively. In Table 1, mutants with high and intermediate φ values are bold and underlined, respectively.

Table 1. Parameters from kinetic measurements.

Mutant		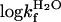	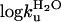Midpoint (M)	mf	mu	mD-N (mol-1·M-1)	ΔGD-N(kcal/mol-1)	ΔΔGD-N (kcal/mol-1)	ø1.5M	β‡	Δmu	Δmu/ΔlogKD-N
WT	1.31 ± 0.03	-4.13 ± 0.02	3.73 ± 0.05	-0.75 ± 0.02	0.70 ± 0.04	1.46 ± 0.05	7.39 ± 0.28			0.52
18V	1.22 ± 0.04	-3.10 ± 0.16	3.17 ± 0.07	-0.74 ± 0.03	0.62 ± 0.03	1.36 ± 0.04	5.87 ± 0.22	1.52 ± 0.36	0.08	0.55	0.09	0.11
V12A	1.25 ± 0.04	-2.76 ± 0.16	3.06 ± 0.07	-0.73 ± 0.03	0.58 ± 0.04	1.31 ± 0.04	5.45 ± 0.22	1.94 ± 0.36	0.02	0.56	0.12	0.14
L13A	1.21 ± 0.06	-3.10 ± 0.21	3.15 ± 0.09	-0.74 ± 0.04	0.62 ± 0.05	1.37 ± 0.06	5.87 ± 0.29	1.52 ± 0.41	0.08	0.54	0.08	0.10
Y18A	1.20 ± 0.03	-4.27 ± 0.23	3.91 ± 0.05	-0.70 ± 0.02	0.70 ± 0.05	1.40 ± 0.05	7.45 ± 0.31	-0.06 ± 0.42		0.50	0.01	-0.02
F21A	1.24 ± 0.03	-3.17 ± 0.14	3.39 ± 0.05	-0.72 ± 0.01	0.58 ± 0.03	1.30 ± 0.04	6.00 ± 0.20	1.39 ± 0.34	0.03	0.55	0.12	0.26
Y26A	0.84 ± 0.02	-1.20 ± 0.06	1.85 ± 0.05	-0.65 ± 0.03	0.45 ± 0.02	1.10 ± 0.03	2.78 ± 0.09	4.61 ± 0.29	0.11	0.59	0.25	0.10
V30A	0.76 ± 0.05	-2.58 ± 0.09	2.30 ± 0.06	-0.80 ± 0.04	0.66 ± 0.02	1.46 ± 0.05	4.55 ± 0.14	2.84 ± 0.31	0.29	0.55	0.04	0.02
I39V	1.02 ± 0.04	-3.40 ± 0.12	3.03 ± 0.05	-0.79 ± 0.02	0.67 ± 0.03	1.46 ± 0.04	6.00 ± 0.18	1.39 ± 0.33	0.33	0.54	0.03	0.03
V43A	0.83 ± 0.09	-2.53 ± 0.17	2.24 ± 0.10	-0.91 ± 0.07	0.59 ± 0.04	1.50 ± 0.08	4.58 ± 0.26	2.82 ± 0.38	0.34	0.61	0.11	0.06
V49A	1.15 ± 0.05	-2.20 ± 0.11	2.29 ± 0.06	-0.84 ± 0.04	0.62 ± 0.03	1.46 ± 0.05	4.56 ± 0.16	2.83 ± 0.32	0.14	0.57	0.08	0.04
V51A	1.09 ± 0.08	-1.97 ± 0.06	2.41 ± 0.06	-0.76 ± 0.05	0.50 ± 0.01	1.27 ± 0.05	4.15 ± 0.14	3.24 ± 0.31	0.12	0.60	0.20	0.11
V54A	1.24 ± 0.03	-1.46 ± 0.06	2.03 ± 0.05	-0.88 ± 0.03	0.45 ± 0.01	1.33 ± 0.04	3.66 ± 0.09	3.73 ± 0.29	0.10	0.66	0.25	0.11
L57A	1.19 ± 0.04	-3.42 ± 0.31	3.42 ± 0.09	-0.71 ± 0.03	0.64 ± 0.07	1.35 ± 0.07	6.28 ± 0.43	1.11 ± 0.51	0.08	0.53	0.07	0.15
I80A	0.97 ± 0.03	-2.42 ± 0.07	2.49 ± 0.05	-0.79 ± 0.03	0.57 ± 0.02	1.36 ± 0.03	4.60 ± 0.11	2.79 ± 0.30	0.21	0.58	0.13	0.08
V81A	0.54 ± 0.04	-2.82 ± 0.09	2.44 ± 0.05	-0.81 ± 0.03	0.57 ± 0.02	1.38 ± 0.04	4.57 ± 0.13	2.82 ± 0.31	0.44	0.59	0.14	0.08
V83A	0.83 ± 0.03	-2.32 ± 0.06	2.30 ± 0.04	-0.73 ± 0.03	0.65 ± 0.01	1.37 ± 0.03	4.29 ± 0.09	3.10 ± 0.29	0.21	0.53	0.06	0.03
I89A	1.22 ± 0.03	-2.49 ± 0.10	2.88 ± 0.05	-0.71 ± 0.02	0.57 ± 0.02	1.29 ± 0.03	5.04 ± 0.15	2.35 ± 0.32	0.02	0.55	0.13	0.11

ø^1.5M calculated from refolding and unfolding data at 1.5 M GdmCl (Eq. 6) High and intermediate values are bold and underlined, respectively.

Fig. 3.

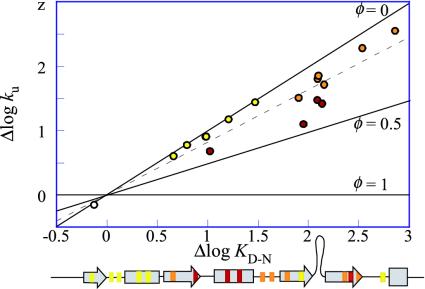
Brønsted plot, logk_u versus logK_D-N, of L23 at 1.5 M GdmCl. The φ values for the individual mutations are calculated from Eq. 6 and are colored as in Fig. 4. The dotted line is <φ> = 0.18. Below is the mutant position in the L23 primary sequence.

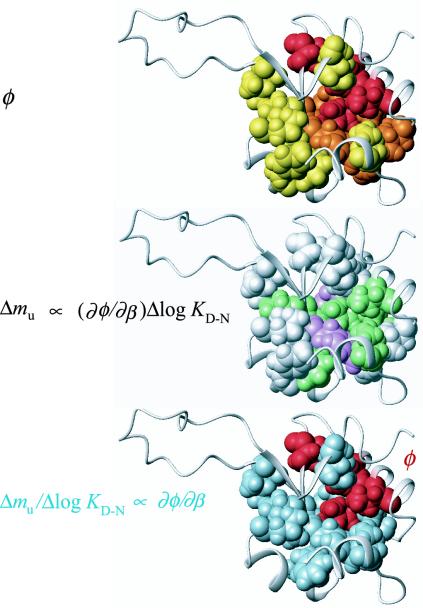
φ Value Analysis of the L23 Transition State. The positions of the mutated residues in the L23 structure are shown in Fig. 4, where the individual φ values are coded yellow (0<φ < 0.10), orange (0.10<φ < 0.25), and red (φ > 0.25). The thresholds have been chosen for clarity. Apparently, the L23 φ values describe an approximately radial graduation from the center of the hydrophobic core, which is in good agreement with the nucleation condensation mechanism for two-state folding (36, 37). The highest φ values (red) are observed for the triad Val-81 (φ = 0.44), Ile-39 (φ = 0.33) and Val-43 (φ = 0.34), linking the central strand 4 and helix 2 by contacts through the aliphatic side of the core, flanked by Val-30 (φ = 0.29) in strand 3 closing the loop to helix 2. In direct connection to this high-φ cluster is a contiguous group of residues with intermediate φ values (orange), closing up the central part of the β-sheet by connecting strands 2, 4, and 3; i.e., Tyr-26 (φ = 0.11), Val-49 (φ = 0.14), Val-51 (φ = 0.12), Val-54 (φ = 0.10), Ile-80 (φ = 0.21), and Val-83 (φ = 0.21). The lowest φ values (yellow) are found for the more peripheral residues Ile-8 (φ = 0.08), Val-12 (φ = 0.02), Leu-13 (φ = 0.08), Phe-21 (φ = 0.03), and Ile-89 (φ = 0.02), anchoring the N and C termini, and Leu-57 (φ = 0.08) near the disordered loop.

Fig. 4.

L23 structures showing spatial distribution of φ, Δm_u, and Δm_u/ΔΔG_D-N. (Top) The highest values of φ (red) are found in the aliphatic side of the L23 core, which is consistent with a prenucleus of long-range contacts between Val-81 in the central strand 4, and residues in the helix-2 region. (Middle) The highest values of Δm_u (magenta) are found for the sheet residues on either side of Val-81. Depicted are the residues that show the highest degree of free-energy gain after passing the barrier top. The intermediate values of Δm_u (green) are found in the central region of the L23 core, whereas the lowest values of Δm_u (white) are found at more peripheral positions, including the interfaces to the N and C termini. (Bottom) In the diffuse transition-state ensemble of L23, the highest φ-value growth, Δm_u/ΔlogK_D-N ∝ φ′(β^‡), is observed for residues just outside the initiation site (red). Blue residues are those with Δm_u//ΔlogK_D-N larger than within the high-φ cluster (red).

Matched m Value Changes Indicative of Transition-State Movements. Transition-state movements in protein folding are commonly inferred from changes in β^‡ (Eq. 5), following stability perturbations by either mutation or addition of denaturant (5, 13). However, the interpretation of these β^‡ changes is not always straightforward because they may also result from alterations of the ground states D or N (8, 19). To test for such ground-state alterations in the case of L23, we first replaced β^‡ with m_u that measures directly the “distance” between the native starting material and the transition state for unfolding (Eq. 2). The plot of m_u versus change in unfolding activation free energy (∝ Δlogk_u) for the 17 mutations in Table 1 shows a significant linear correlation (R = 0.82), which is in apparent agreement with the Hammond postulate (Fig. 5). Because the correlation is largely retained in a plot of β^‡ versus ΔlogK_D-N^mut (R = 0.74), we conclude that contributions from denatured-state plasticity is after all very small with L23 (Fig. 5). The increased values of m_f are matched by a decrease in m_u, as would be expected for transition-state movements (Table 1). As an alternative test, the average φ value (<φ >) derived from the slope of the Brønsted plot was used as a measure of transition-state position and plotted against ΔlogK_D-N^GdmCl = <m_D-N>[GdmCl], where <m_D-N> is the average value of m_D-N in Table 1. The result shows a linear correlation with a slope that is within the experimental error of that for β^‡ versus ΔlogK_D-N^mut (Fig. 5). It is thus apparent that <φ> and β^‡ produce coherent Hammond shifts although their overall values for the transition-state placement are very different at ≈0.18 and ≈0.5, respectively.

Scatter in Hammond Plot Exceeds Experimental Errors. In view of the smooth transition-state shifts observed upon addition of denaturant (13), the plot of m_u versus Δlogk_u reveals considerable scatter (Fig. 5). Notably, this scatter does not arise from experimental errors but shows mutant-specific deviations from the mean kinetic pattern. Compare, for example, I80A and V83A in Fig. 2 that have similar Δlogk_u but distinctly different m_u. It can further be noted that the outliers in the L23 Hammond plot are not correlated with their extent of interaction in the transition-state ensemble, i.e., anomalously small m_u changes are observed for both high and low φ values (Table 1). Scattered Hammond plots are not unique for L23 but have also been observed for barnase and CI2, where the susceptibility to undergo transition-state movements was found to be different in different parts of the structure (4, 5). Even so, these deviations from uniform Hammond behavior cannot a priori be attributed to transition state effects alone. One possibility is that they arise from partial unfolding of the native protein. Such ground-state fraying has been presented as an alternative explanation for kinked logk_u limbs of certain S6 mutations, based on their location at the late-forming interface between the N and C termini (19). However, this interpretation seems unlikely in the case of L23 because the largest m_u changes involve core mutations where native-state fraying seems incompatible with microscopic reversibility (Fig. 4). Moreover, the mutations at the seemingly late folding N- and C-terminal regions of L23 show the smallest m_u changes (Fig. 4). Another possibility is that the Hammond shifts describe redistributions between parallel folding pathways that extend beyond the minimal two-dimensional barrier model (4, 6). In accord with the prediction in Eq. 10, however, we opt for a more rational explanation: the scattered Hammond plots in protein folding emerge as an intrinsic consequence of nonuniform values of φ′ (β^{‡ wt}) ΔΔG_D-N (Fig. 1).

Discussion

The Diffuse Transition-State Ensemble. The φ-value data of L23 yields an overall diffuse impression of the transition state with a graduated distribution of fractional φ values that encompasses the majority of the native contacts (37). This delocalized nucleation pattern is a typical feature of two-state proteins (34, 36, 37) and is generally taken to indicate that the folding transition state is an ensemble of states whose average topology is native-like (38, 39). Consistently, the logarithm of the refolding rate constant across different two-state proteins is found to correlate with the topological parameter “contact order” of the native state (40), with some intrinsic modulation by protein stability and chain length (40–44). The native-like appearance of the transition-state ensemble suggests that the various parts of a protein fold with similar probability (38). At the extreme, such equalization would lead to a situation where all folding and unfolding trajectories are equally favorable, producing ideal Brønsted plots with uniform φ values and maximal cooperativity; local unfolding of the native structure is entropically prevented because all native interactions are fractionally present in the transition state (25). In practice, however, the graduated φ-value distribution indicates often a dominant initiation point that can be qualitatively predicted by simplistic topology-based folding models (45–48). Simulations suggest further that this initiation point, although it looks diffuse by φ values, could still be consistent with a subset of fully established contacts that are shared by the majority of species in the transition-state ensemble (49). With L23, the initiation point is the docking of the helix 2 and strand 4 regions by long-range contacts through the aliphatic side of the core (Fig. 4). Concomitant with this long-range hydrophobic association is probably the local trapping of hydrogen bonds in helix 2 that are “flickeringly” present in the denatured ensemble (37, 50). Structural rationalization of the subsequent layers of contacts becomes increasingly degenerate as the configurational dimensionality grows rapidly with decreasing values of φ (39). Even so, additional information about the folding nucleation events can be deduced from the m_u value changes in Fig. 5.

Variable Hammond Response Linked to Heterogeneous φ Value Growth. In contrast to the low-dimensional case of covalent bonds, it is evident that the Hammond behavior in protein folding is governed by multiple order parameters: the global progress coordinate β by which the transition-state shift is measured, and a large set of site-specific coordinates ΔΔG(β) = φ (β)ΔΔG_D-N that determine the energetic perturbations upon mutation. It follows that the individual data points in the Hammond plot (Δm_u versus ΔΔG_D-N), which are derived from site-specific free-energy perturbations, reflect local properties ∝φ′(β^‡). The common Hammond plot, based on a superposition of data from structurally dispersed mutations, is therefore expected to contain scatter unless the local values of φ′(β^‡) are the same throughout the transition-state structure. However, such uniform growth of the local progress coordinates seems incompatible with the way real proteins fold. The φ values are different throughout the protein structure and are bound to show nonlinear dependencies on β. Thus, the individual values of φ′(β^‡) are also likely to be different at any given point along the reaction profile, which is consistent with experimental data on U1A (15).

On this basis, we conclude that the scatter of the Hammond plot (Fig. 5) is related to site-specific variations in φ′(β^‡), similar to the way the scatter of the Brønsted plot is related to the site-specific values of φ(β^‡) (Fig. 3).

An Additional Facet of the Folding Nucleus: The Critical Contact Layer. To examine the mechanistic implications of the Hammond data, we have tentatively defined Δm_u ∝ φ′(β^‡) as the site-specific free-energy gradient, and the normalized ditto Δm_u/ΔΔG_D-Nφ′(β^‡) as the site-specific φ value gradient. Absolute estimates of these parameters require precise knowledge about the barrier curvature, i.e., the value of c in Eq. 8. Accordingly, Δm_u can be seen as a directional parameter indicating in which part of the transition-state structure the growth of interaction free energy is most downhill, i.e., the interactions that show the largest degree of consolidation after traversing the barrier top. Δm_u/ΔΔG_D-N, on the other hand, represents a local order parameter indicating heterogeneities in the structural growth as defined by Eq. 6. The graduation of these parameters throughout the L23 structure is shown in Fig. 4, where the individual values are coded: magenta (Δm_u > 0.21), green (0.1 < Δm_u< 0.20), white (Δm_u < 0.1), and pale blue (Δm_u/ΔΔG_D-N > 0.079). The result shows that the distribution of Δm_u values is different from that of the φ values. Whereas the center of the folding nucleus is in the aliphatic side of the core, the high values of Δm_u are, on the whole, shifted toward the aromatic side (Fig. 4). The implication of this spatial separation of the Δm_u and φ value distributions is that, at the barrier top, the local free-energy gradients are steeper at the interface to the folding nucleus than in its center. Looking at a more detailed level the pattern emerges even clearer. The two highest Δm_u values (> 0.21) are found for the sheet mutations Y26A (φ = 0.11, strand 2) and V54A (φ = 0.10, strand 3), flanking the initiation site V81 (φ = 0.44) in the central strand 4, whereas the next layer of residues with intermediate Δm_u values covers the aromatic part of the core. The lowest Δm_u values are observed at the interface to the N and C termini, and at positions peripheral to the sheet. Notably, this low-Δm_u set includes also the two residues in the high-φ cluster facing the C terminus, i.e., V30A (φ = 0.29) and I39V (φ = 0.33), emphasizing the polarization of high Δm_u values toward side chains closing up the β-sheet.

The accompanying values of Δm_u/ΔΔG_D-N yield a very similar picture. The φ value growth is higher for the residues distributed around the initiation point than in its center (Fig. 4), in apparent analogy with the “hydrophobic cloud” wetting the central nucleus in the capillarity description of protein folding (51).

Accordingly, the results allow us to make a crude distinction between a primary set of interactions that provides the gross topology for nucleation; i.e., those that form on the uphill side of the free-energy barrier, and a secondary set that brings the process downhill. In somewhat simplified terms, the latter, deterministic, interactions are those that make the embryonic nucleus critical: the interactions that undergo the highest free-energy change after passing the barrier top. For comparison, the critical nucleus of water condensation is solely defined by size, because the individual molecules within the emerging droplet are indistinguishable. In protein folding, the interactions that add criticality to the nucleus have identity: the critical contact layer.