Abstract
Risk-prediction models need careful calibration to ensure they produce unbiased estimates of risk for subjects in the underlying population given their risk-factor profiles. As subjects with extreme high or low risk may be the most affected by knowledge of their risk estimates, checking the adequacy of risk models at the extremes of risk is very important for clinical applications. We propose a new approach to test model calibration targeted toward extremes of disease risk distribution where standard goodness-of-fit tests may lack power due to sparseness of data. We construct a test statistic based on model residuals summed over only those individuals who pass high and/or low risk thresholds and then maximize the test statistic over different risk thresholds. We derive an asymptotic distribution for the max-test statistic based on analytic derivation of the variance–covariance function of the underlying Gaussian process. The method is applied to a large case–control study of breast cancer to examine joint effects of common single nucleotide polymorphisms (SNPs) discovered through recent genome-wide association studies. The analysis clearly indicates a non-additive effect of the SNPs on the scale of absolute risk, but an excellent fit for the linear-logistic model even at the extremes of risks.
Keywords: Case–control studies, Gene–gene and gene–environment interactions, Genome-wide association studies, Goodness-of-fit tests, Polygenic score, Risk stratification
1. Introduction
Many modern biomedical studies that use high-throughput technologies initially focus on discoveries of biomarkers that are associated with specific clinical outcomes. At this step, typically, the associations of individual biomarkers with the outcome are tested one at a time and the statistical significance of these associations are assessed after multiple testing adjustments to minimize the chance of false-positive discoveries. After the discovery of the biomarkers and possible validation in independent studies, many translational applications of the new knowledge require careful characterization of the risk of the outcome with respect to all the discovered biomarkers simultaneously. Although development of such a multivariable model may involve many complex intermediate steps, such as exploration of interactions and model selection, a key final step requires testing the “calibration” of the final model to ensure that it can produce unbiased estimates of risk for the underlying population for which prediction is desired.
Various existing goodness-of-fit testing procedures can be used for testing the calibration of a risk model in a new dataset. One can assess the significance of test statistics that are based on sums of squares of residuals or other types of deviance measures that capture the departures between observed and expected outcomes at the level of individual subjects (Windmeijer, 1990) or groups of subjects (Hosmer and Lemeshow, 2000; Tsiatis, 1980). Tests based on grouping of subjects into categories of risk, such as those defined by deciles of risk distribution, have been popular in practice although there is substantial subjectivity in the method due to the selection of the number and placement of the underlying risk categories.
In this report, motivated from the need for the development of polygenic risk-prediction models following discoveries of susceptibility single nucleotide polymorphisms (SNPs) from modern genome-wide association studies (GWASs) (Meigs and others, 2008; Wacholder and others, 2010; Khoury and others, 2013; Chatterjee and others, 2013), we re-evaluate optimal approaches for model calibration in a setting where the underlying risk could be defined by a combination of large number of risk markers, each with modest effect. We observe that while many standard models, such as linear logistic, can be adequate for describing the risk profiles of subjects in the intermediate range of risk where most of the risk distribution is concentrated, they are likely to show departure from empirical risk near the tails of risk distribution containing subjects with very high or low risks Moonesinghe and others, 2011. Recognizing the limitation of the standard goodness-of-fit tests that their power is driven by departure of the data from the null model in the range of intermediate risks where most of subjects reside, in this report, we propose a complementary approach to a goodness-of-fit test that focuses more on tails of risk distribution where the departure is more likely to be prominent.
We propose constructing goodness-of-fit statistics by summing individual level deviance statistics over subjects whose predicted risks are above or below an upper or lower threshold, respectively. We then maximize such test statistics by varying the threshold over a set of grid points. Based on a simple characterization of the correlation of the test statistic for different thresholds, we derive an asymptotic theory for the max-test statistics based on Gaussian process theory. We conduct extensive simulation studies mimicking models that seem realistic for describing joint effects of SNP markers emerging from modern GWASs. We also apply the proposed method to a large study of breast cancer involving 8035 cases and 10 525 controls from the Breast and Prostate Cancer Cohort Consortium (BPC3) to explore the adequacy of alternative models for describing the polygenic risk associated with 19 SNPs that have been previously associated with the disease. These analyses reveal several strengths of the proposed methods.
2. Methods
Let  be the binary indicator of presence,
be the binary indicator of presence, 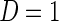 , or absence,
, or absence, 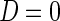 , of a disease and let
, of a disease and let 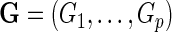 be a
be a 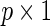 vector denoting a subject's genotype status for
vector denoting a subject's genotype status for 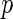 SNPs. Consider a risk model for the disease given
SNPs. Consider a risk model for the disease given 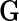 in the general form
in the general form
 |
(2.1) |
where 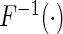 denotes a fixed link function,
denotes a fixed link function, 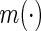 is a pre-specified function to reflect an assumed model for the joint risk of a disease associated with the genotype vector
is a pre-specified function to reflect an assumed model for the joint risk of a disease associated with the genotype vector 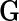 , and
, and 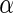 and
and 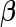 are unknown parameters of the model.
are unknown parameters of the model.
Here, we are interested in testing the null hypothesis that the multivariate risk of the disease given all the SNP markers has the model form given by (2.1). Let 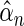 and
and 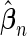 be estimates for
be estimates for 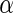 and
and 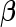 that can be assumed to be consistent so that
that can be assumed to be consistent so that 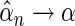 and
and 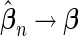 as sample size
as sample size 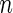 becomes larger. Given such estimates, one can test the null hypothesis using a standard goodness-of-fit test of the form
becomes larger. Given such estimates, one can test the null hypothesis using a standard goodness-of-fit test of the form
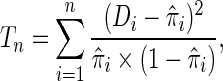 |
where 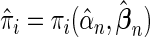 (Windmeijer, 1990). Below, we propose a modification of
(Windmeijer, 1990). Below, we propose a modification of 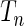 so that the power of the test statistics can be improved to detect departure of the null model from the true underlying model near tails of risk distribution. In particular, we propose, for any given pair of “thresholds”,
so that the power of the test statistics can be improved to detect departure of the null model from the true underlying model near tails of risk distribution. In particular, we propose, for any given pair of “thresholds”, 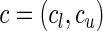 , a test statistic of the form
, a test statistic of the form
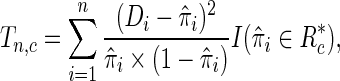 |
where 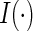 is the indicator function and
is the indicator function and 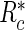 is a risk region such that
is a risk region such that  . In words,
. In words,  is a sum of squared Pearson residuals over only those individuals who achieve a certain high or low threshold for fitted disease risk. As we assume that
is a sum of squared Pearson residuals over only those individuals who achieve a certain high or low threshold for fitted disease risk. As we assume that  is a monotone function of
is a monotone function of 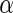 and
and 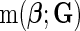 , the test statistics can be expressed equivalently as
, the test statistics can be expressed equivalently as
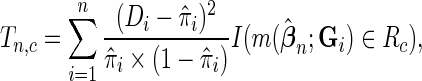 |
(2.2) |
where 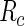 ranges over (
ranges over (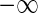 ,
, 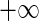 )
) 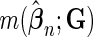 can take.
can take.
Since we do not know an optimal value for the threshold 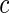 , we propose to maximize the normalized
, we propose to maximize the normalized 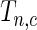 for a fixed set of grid points,
for a fixed set of grid points, 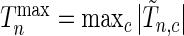 where
where 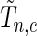 is the normalized
is the normalized 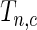 such that mean is 0 and variance is 1. In supplementary material available at Biostatistics online, we show that if we define
such that mean is 0 and variance is 1. In supplementary material available at Biostatistics online, we show that if we define 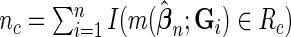 , then under the null hypothesis, for any given
, then under the null hypothesis, for any given 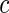 ,
, 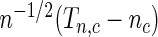 follows the normal distribution whose mean is 0 and the variance can be analytically characterized (see Section 1 of supplementary material available at Biostatistics online for details). Further, for any two values of the threshold, say
follows the normal distribution whose mean is 0 and the variance can be analytically characterized (see Section 1 of supplementary material available at Biostatistics online for details). Further, for any two values of the threshold, say 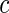 and
and 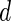 , the covariance between
, the covariance between 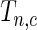 and
and 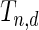 can be analytically characterized.
can be analytically characterized.
Once the mean and the covariance of multivariate distribution of Gaussian random variables are characterized, the 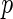 -value of our test,
-value of our test, 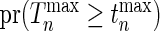 where
where 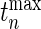 is the observed value of
is the observed value of 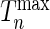 can be estimated through simulations. To compute the
can be estimated through simulations. To compute the 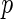 -value, we generate a multivariate Gaussian random variable from the covariance of
-value, we generate a multivariate Gaussian random variable from the covariance of 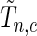 and mean of zero and obtain the maximum of the absolute values of the multivariate realization generated from the normal distribution. We then repeat the process and the
and mean of zero and obtain the maximum of the absolute values of the multivariate realization generated from the normal distribution. We then repeat the process and the 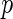 -value would be the ratio of the cases where the maxima from the simulations are larger than or equal to
-value would be the ratio of the cases where the maxima from the simulations are larger than or equal to 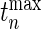 .
.
2.1. Analysis of joint effects of breast cancer susceptibility SNPs
GWASs with increasing sample size are continuing to discover common SNPs associated with a variety of complex traits and diseases, including breast cancer. Typically, for the discovery stage, the analysis has focused on the association of the traits with each individual SNP marginally. Following discovery, a major question is how to best characterize the joint association of the disease with multiple SNPs simultaneously. Although in principle a totally non-parametric approach where the probability of a disease could be estimated for each combination of the SNPs may be desirable, in practice reliance on some kind of parametric model becomes necessary as the sample size becomes inevitably sparse as the number of unique combination of risk factors become rapidly large.
We utilize data from the BPC3 (Hunter and others, 2005; Hüsing and others, 2012) to investigate the suitability of alternative models for joint effects of a set of known susceptibility SNPs for breast cancer. These data include 8035 cases and 10 525 controls of European ancestry from four cohort studies conducted in North America and Europe. The study includes genotype data on a total of 19 SNPs although not all subjects had data on all SNPs. As we attempted to analyze these data, we came across a number of additional challenging methodological issues related to the choice of alternative models, missing genotype data and case–control sampling. In the following, we describe these additional methods that could be relevant for other similar applications as well.
2.2. Choice of models for 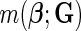
In our analysis, we focus on two common models for describing joint effects of multiple risk factors. One is the widely used logistic regression model where 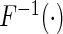 in (2.1) corresponds to logit link function. If we assume a linear-logistic model, i.e. the effects of the SNPs are additive under the logit link, then the joint odds ratio (OR) of the disease associated with multiple risk factors, i.e. the term
in (2.1) corresponds to logit link function. If we assume a linear-logistic model, i.e. the effects of the SNPs are additive under the logit link, then the joint odds ratio (OR) of the disease associated with multiple risk factors, i.e. the term 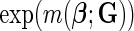 in (2.1), is given by the product of individual ORs associated with each SNP. For rare diseases, as the logit link approximates the log-link and ORs approximate relative-risk parameters, the model is often referred to as a “multiplicative” model because it implies a multiplicative effect of the different risk factors on the probability of the disease itself. As the breast cancer patients in our study were all incident cases from underlying cohorts for which the overall incident rates were low, the assumption of rare diseases is quite reasonable in our application. For cancer applications, the multiplicative model has been shown to be consistent with a multistage model for carcinogenesis where different risk factors act on different stages serially (Siemiatycki and Thomas, 1981).
in (2.1), is given by the product of individual ORs associated with each SNP. For rare diseases, as the logit link approximates the log-link and ORs approximate relative-risk parameters, the model is often referred to as a “multiplicative” model because it implies a multiplicative effect of the different risk factors on the probability of the disease itself. As the breast cancer patients in our study were all incident cases from underlying cohorts for which the overall incident rates were low, the assumption of rare diseases is quite reasonable in our application. For cancer applications, the multiplicative model has been shown to be consistent with a multistage model for carcinogenesis where different risk factors act on different stages serially (Siemiatycki and Thomas, 1981).
An alternative model, widely discussed in the epidemiologic literature (Rothman and Greenland, 1998, Chapter 18) but not often utilized in practice, is an “additive model” that implies multiple risk factors influence risk of the disease in an additive fashion on the scale of the probability of the disease itself. Although there are numerical difficulties in fitting such a model due to constraints required on parameters so that fitted probabilities remained bounded between 0 and 1, it has been shown that such models can be a natural starting point as they correspond to independence of the biological effects of the underlying risk factors. Further, for assessing gene-environment interaction in the context of certain public health applications such as targeted intervention, test for departure from the additive model is of direct relevance.
Given the above background, we assessed the adequacy of multiplicative and additive models for joint effects of the breast cancer SNPs. We assumed that each SNP genotype is coded as a dosage variable counting the number of a specific allele an individual carries at the specific locus. We fit the “multiplicative” model using standard logistic regression that includes a main-effect term for each SNP genotype variable. As we are dealing with case–control studies, we could not fit the additive model in the absolute-risk scale, but instead derived an alternative representation of the same model in the OR scale.
The additive model for the risk of the disease in the underlying population given the SNP genotype data for 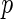 loci is given by
loci is given by
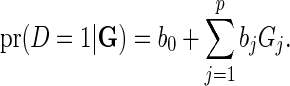 |
(2.3) |
We show in supplementary material available at Biostatistics online (Section 2), under the assumption of rare diseases, that allows us to approximate ORs by relative risks, the additive model can be expressed in the general form (2.1)
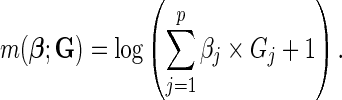 |
2.3. Case–control studies and missing genotype data
In the BPC3 study, case–control samples were selected for genotyping within the respective cohort studies. Since many biomarker-based studies employ such design, following we examine the proposed test in the context of case–control sampling.
For testing model calibration under case–control sampling, the proposed statistic can be simply modified as
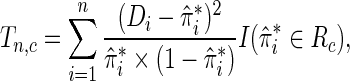 |
where 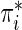 denotes the probability of the disease under the case–control sampling scheme, as opposed to the underlying population. Specifically,
denotes the probability of the disease under the case–control sampling scheme, as opposed to the underlying population. Specifically,
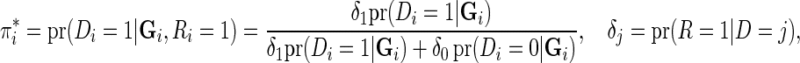 |
where 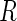 is the indicator of whether or not a subject has been selected in the case–control samples. For any model that could be in the logistic form,
is the indicator of whether or not a subject has been selected in the case–control samples. For any model that could be in the logistic form, 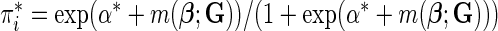 with
with 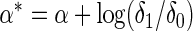 and thus the effect of sampling can be ignored as long as the model is fitted to the case–control data with a free-intercept parameter (Prentice and Pyke, 1979). Thus, for testing of both the multiplicative and additive models described above, which can be represented in the logistic form, the effect of case–control sampling can be ignored for calibration of relative risks.
and thus the effect of sampling can be ignored as long as the model is fitted to the case–control data with a free-intercept parameter (Prentice and Pyke, 1979). Thus, for testing of both the multiplicative and additive models described above, which can be represented in the logistic form, the effect of case–control sampling can be ignored for calibration of relative risks.
For fitting joint models with multiple SNPs or biomarkers, a common problem investigators often face is that many subjects may not have complete data on all of the variables. In our breast cancer dataset, for example, only 49% of subjects had complete genotype data for all 19 SNPs (Table 1 of supplementary material available at Biostatistics online). We propose incorporating individuals with missing genotype data using a modification of the test statistics in the form
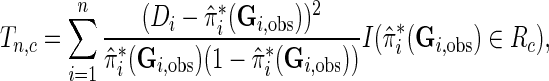 |
where 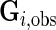 denotes the observed genotype data for the
denotes the observed genotype data for the 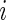 th subject and
th subject and
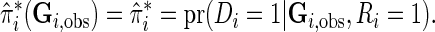 |
In supplementary material available at Biostatistics online (Section 3), we show how to compute 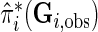 under different modeling assumptions and approximations.
under different modeling assumptions and approximations.
Table 1.
Statistical significance for the test of calibration of alternative models for joint effects of SNPs for breast cancer in the BPC3 study
| Multiplicative model |
Additive model |
||||||
|---|---|---|---|---|---|---|---|
| Complete case analysis |
Analysis including subjects with missing genotypes |
Complete case analysis |
|||||
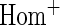 OR OR |
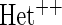 OR OR |
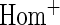 OR OR |
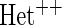 OR OR |
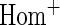 OR OR |
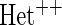 OR OR |
||
| HL test | 0.11 | 0.87 | — | — | 0.0003 | 0.01 | |
| Asymptotic | 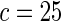 |
0.11 | 0.85 | 0.16 | 0.11 | 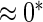 |
 |
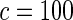 |
0.20 | 0.77 | 0.23 | 0.17 | 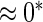 |
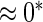 |
|
| Parametric bootstrap | 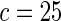 |
0.07 | 0.70 | 0.14 | 0.12 | 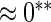 |
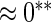 |
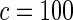 |
0.11 | 0.54 | 0.28 | 0.18 | 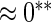 |
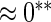 |
|
The proposed method is evaluated using 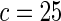 or
or 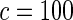 with the corresponding risk regions being defined by the combinations of evenly placed grid points at various upper and lower quintiles of the risk distribution.
with the corresponding risk regions being defined by the combinations of evenly placed grid points at various upper and lower quintiles of the risk distribution. 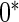 are based on
are based on 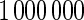 simulations.
simulations. 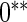 are based on
are based on 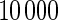 simulations.
simulations. 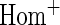 OR is the analysis assuming a homogeneous OR across cohorts.
OR is the analysis assuming a homogeneous OR across cohorts.  OR is the analysis assuming heterogeneous OR across cohorts.
OR is the analysis assuming heterogeneous OR across cohorts.
Finally, evaluation of the test statistic requires consistent estimates of the disease-model parameter, 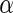 and
and 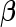 . In the presence of missing genotype data, the test statistic also requires estimates of genotype frequency parameters. For our application, we estimate the disease model parameters by fitting the corresponding “null” model of interest to subjects who have complete genotype data for all SNPs. Similarly, the allele frequency for each SNP was estimated using control subjects who have complete genotype data on all SNPs and the corresponding genotype frequencies were obtained assuming Hardy–Weinberg Equilibrium (HWE). The asymptotic theory for the test statistics incorporating subjects with missing genotype data is described in supplementary material available at Biostatistics online (Section 4).
. In the presence of missing genotype data, the test statistic also requires estimates of genotype frequency parameters. For our application, we estimate the disease model parameters by fitting the corresponding “null” model of interest to subjects who have complete genotype data for all SNPs. Similarly, the allele frequency for each SNP was estimated using control subjects who have complete genotype data on all SNPs and the corresponding genotype frequencies were obtained assuming Hardy–Weinberg Equilibrium (HWE). The asymptotic theory for the test statistics incorporating subjects with missing genotype data is described in supplementary material available at Biostatistics online (Section 4).
2.4. Simulation studies
We conducted extensive simulation studies to evaluate the validity and the power of the proposed methods. In our simulations, we generate data on 10 or 20 SNPs, each assumed to follow HWE in the underlying population with a minor allele frequency of 30%. We generated disease status for individuals conditional on multivariate genotype status based on a general logistic model of the form (2.1) where 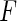 is the logit link and the intercept parameter was chosen in such a way so that the overall probability of the disease in the underlying population remains fixed at 5% in all different settings. To investigate type-I error of the proposed test under the multiplicative and additive “null” models, we simulated data from models that correspond to
is the logit link and the intercept parameter was chosen in such a way so that the overall probability of the disease in the underlying population remains fixed at 5% in all different settings. To investigate type-I error of the proposed test under the multiplicative and additive “null” models, we simulated data from models that correspond to 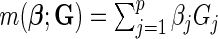 and
and  , respectively, assuming
, respectively, assuming 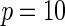 SNPs are under investigation. In each model, the parameters were chosen so that the marginal disease OR for each SNP is around 1.1. For evaluating power, we generated data under a “true” model that corresponds to
SNPs are under investigation. In each model, the parameters were chosen so that the marginal disease OR for each SNP is around 1.1. For evaluating power, we generated data under a “true” model that corresponds to 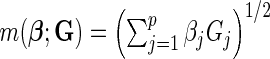 which generates a multivariate risk profile that is in between those generated from the additive and multiplicative models (Figure 1). In each model, we allowed the association parameters
which generates a multivariate risk profile that is in between those generated from the additive and multiplicative models (Figure 1). In each model, we allowed the association parameters 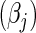 to be constant across the SNPs and chose a value for the constant so that the marginal disease OR for each SNP is approximately 1.15 and 1.1 under the 10-SNP
to be constant across the SNPs and chose a value for the constant so that the marginal disease OR for each SNP is approximately 1.15 and 1.1 under the 10-SNP 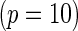 and 20-SNP
and 20-SNP 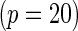 models, respectively.
models, respectively.
Fig. 1.
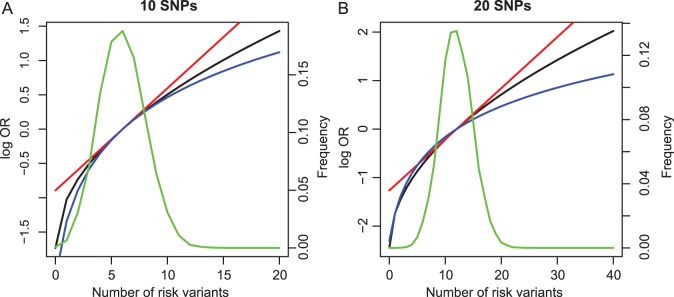
Variation in risk by cumulative number of risk variants under alternative model for simulation: (a) 10 SNPs and (b) 20 SNPs. The 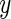 -axis is the log OR where the reference groups were the samples whose numbers of risk alleles at the 10 loci and the 20 loci are 6 and 12, respectively. Power was evaluated by generating data from an “alternative” model (black line). Fitted risks under the multiplicative (red) and additive (blue) models are plotted. The distribution of subjects by total number of risk variants is also shown (green line).
-axis is the log OR where the reference groups were the samples whose numbers of risk alleles at the 10 loci and the 20 loci are 6 and 12, respectively. Power was evaluated by generating data from an “alternative” model (black line). Fitted risks under the multiplicative (red) and additive (blue) models are plotted. The distribution of subjects by total number of risk variants is also shown (green line).
We conducted additional studies to investigate the potential utility of the proposed test statistics as a model selection tool. We simulated data either under the additive or the multiplicative models and then examined how many times the test statistics 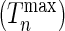 has a smaller value under the correct model from which the data were simulated compared with the value of it under the alternative model. As a benchmark, we also evaluated the performance of the standard goodness-of-fit test statistics
has a smaller value under the correct model from which the data were simulated compared with the value of it under the alternative model. As a benchmark, we also evaluated the performance of the standard goodness-of-fit test statistics 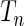 (Windmeijer, 1990) for selection of the correct model in the same manner.
(Windmeijer, 1990) for selection of the correct model in the same manner.
3. Results
3.1. Joint risk model in BPC3 study
Our analyses include 18 560 samples from four BPC3 cohorts which had at least some subjects with complete genotyping data on 19 known breast cancer risk SNPs (rs11249433, rs1045485, rs13387042, rs4973768, rs10941679, rs889312, rs2046210, rs1562430, rs1011970, rs865686, rs2380205, rs10995190, rs1250003, rs2981582, rs909116, rs614367, rs10483813, rs3803662, rs6504950) for estimation of study-specific model parameters.
We tested the calibration for a variety of different models (Table 1). First, using only the 9098 subjects (4168 cases and 4930 controls) who had complete genotype data, we tested for adequacy of additive and multiplicative models. Each model was tested assuming the underlying disease-association parameters are either homogeneous or heterogeneous across the four cohorts. For implementation of the proposed method, we chose 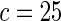 or
or 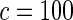 with the grid points being defined by the combination of evenly placed upper and lower quintiles of the risk distribution. The models for the additive effects were soundly rejected under both homogeneous and heterogeneous effects by all different methods considered. In contrast, tests for the multiplicative model under either homogeneous and heterogeneous effect parameters were generally non-significant or borderline significant.
with the grid points being defined by the combination of evenly placed upper and lower quintiles of the risk distribution. The models for the additive effects were soundly rejected under both homogeneous and heterogeneous effects by all different methods considered. In contrast, tests for the multiplicative model under either homogeneous and heterogeneous effect parameters were generally non-significant or borderline significant.
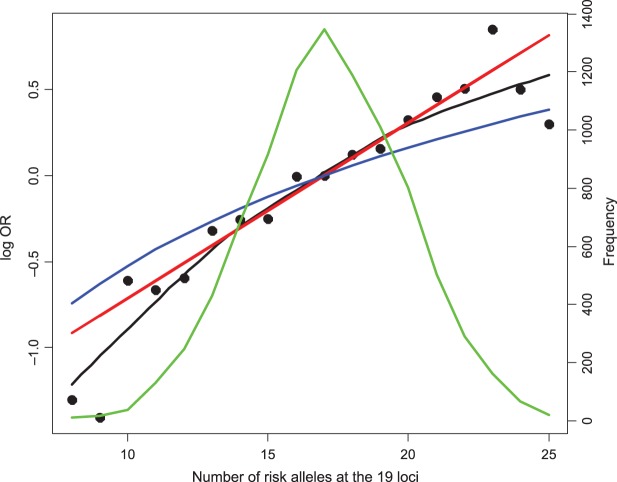
As a further exploratory analysis, we applied the non-parametric smoothing technique to inspect the empirical relationship between disease risk and a polygenic risk score (PRS) variable that counts the number of risk alleles carried by individuals without any regard to effect size of the individual SNPs (Figure 2). When we compare such “empirical risk” to fitted risks obtained from a “multiplicative” and “additive” model that assumes that the relationship between disease risk and PRS is linear in the logit or the absolute probability scale, respectively, it is quite evident that the additive model produces much more moderate variation of risk than the empirical risks. The fitted risks from the “multiplicative” model followed the empirical risks quite closely for the center of risk distribution where majority of subjects resided, but some departures from this trend are observed on both tails of the risk distribution.
Fig. 2.
Variation in the risk of breast cancer in the BPC3 study subjects by cumulative number of risk variants they carried. The  -axis is the log OR where the reference group were the samples whose number of risk alleles at the 19 loci is 17, which is the observed average in the number of risk alleles at the 19 loci. Fitted risk under the multiplicative (red) and additive (blue) models are plotted together with smoothed non-parametric estimates of risks (black). The distribution of subjects by total number of risk variants they carry is also shown (green line).
-axis is the log OR where the reference group were the samples whose number of risk alleles at the 19 loci is 17, which is the observed average in the number of risk alleles at the 19 loci. Fitted risk under the multiplicative (red) and additive (blue) models are plotted together with smoothed non-parametric estimates of risks (black). The distribution of subjects by total number of risk variants they carry is also shown (green line).
Simulation studies suggested that a study with only 4000 cases and comparable number of controls may not have adequate power to detect modest departure from non-multiplicative effects (see Table 2). To increase the power for the test of the multiplicative model, we extended our analysis to include all subjects 18 560 in 4 cohorts many of whom had incomplete genotype data for one or more SNPs. Even with substantially larger sample size, the test for departure from the multiplicative model remained statistically insignificant. Finally, to explore the clinical implications for different models, we assessed the proportion of the population that would be identified to be in a high-risk group, defined as subjects who are at 2-fold or higher risk compared with the average risk of the population, under the two alternative models. Assuming rare disease, we estimated these proportions empirically from the estimated risks of the controls under the two alternative models. The analysis shows while the multiplicative model identified 1.16% of the population to be at high risk, the additive model identifies only 0.02% to be at the high-risk group using the same threshold. Although in terms of absolute percentages both numbers are small, the differences clearly have major implications for applications of risk models for targeted intervention and screening.
Table 2.
Power of tests for detecting departures from multiplicative and additive models at the 5% nominal significance level
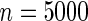 |
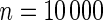 |
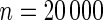 |
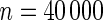 |
||||||
|---|---|---|---|---|---|---|---|---|---|
| Model | Power | 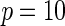 |
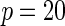 |
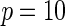 |
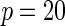 |
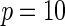 |
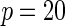 |
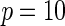 |
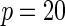 |
| Multiplicative | HL test | 0.09 | 0.07 | 0.12 | 0.08 | 0.28 | 0.12 | 0.57 | 0.27 |
| Windmeijer test | 0.05 | 0.06 | 0.07 | 0.06 | 0.05 | 0.05 | 0.06 | 0.04 | |
Proposed method 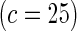
|
0.13 | 0.08 | 0.22 | 0.12 | 0.47 | 0.20 | 0.86 | 0.44 | |
Proposed method 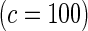
|
0.13 | 0.08 | 0.19 | 0.10 | 0.42 | 0.17 | 0.83 | 0.39 | |
| Additive | HL test | 0.06 | 0.21 | 0.09 | 0.41 | 0.13 | 0.76 | 0.23 | 0.99 |
| Windmeijer test | 0.13 | 0.96 | 0.20 | 0.99 | 0.35 | 1 | 0.62 | 1 | |
Proposed method 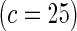
|
0.10 | 0.94 | 0.16 | 0.99 | 0.25 | 1 | 0.50 | 1 | |
Proposed method 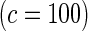
|
0.10 | 0.94 | 0.14 | 0.99 | 0.23 | 1 | 0.45 | 1 | |
The proposed method is evaluated using 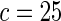 or
or 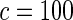 with the corresponding risk regions being defined by the combinations of evenly placed grid points at various upper and lower quintiles of the risk distribution. Results are based on
with the corresponding risk regions being defined by the combinations of evenly placed grid points at various upper and lower quintiles of the risk distribution. Results are based on 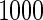 simulated datasets each involving a total of
simulated datasets each involving a total of 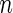 subjects with equal number of cases and controls. In each simulation, data are generated with models involving
subjects with equal number of cases and controls. In each simulation, data are generated with models involving 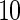 SNPs
SNPs 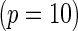 or
or 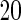 SNPs
SNPs 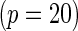 .
.
3.2. Simulation studies
As seen in Table 3, the proposed methods maintain the nominal type-I error under both the multiplicative and the additive null models. For evaluating power, in addition to the proposed test, we implemented Hosmer–Lemeshow (HL) and Windmeijer tests as two possible alternatives. When the HL test was applied throughout all the simulation studies and BPC3 data analysis, the grouping method was based on 10% quantiles which leads to a more accurate asymptotic distribution (Hosmer and Lemeshow, 2000). Power simulation results displayed in Table 2 suggest that substantial power gain is achievable by the proposed method compared with both the HL and Windmeijer tests when the multiplicative model is assumed. It is particularly striking that, for the test for departure from the multiplicative null model, the Windmeijer test suffered from very poor power even when the sample size was as large as 40 000. The result is intuitive given that Windmeijer test sums model residuals over all individuals diluting the signal that comes from the departure of the true risk from the multiplicative model only near the tails of risk distribution (see Figure 1). The HL test performed better than Windmeijer test as it was able to separate the signals coming from different categories of risk, but compared with the proposed method it still loses substantial power as it discards individual level information. For testing additive null, which departed from the true risk throughout the whole risk distribution (Figure 1), the proposed methods are much more powerful than the HL test but experience some loss of power compared with the Windmeijer test. Considering all the different scenarios, the proposed method clearly was the most robust among all the methods considered. Finally, results in Table 4 reveal that the proposed method performs well as a model selection tool. In particular, when data were generated under the additive model, the proposed test statistic  selected the correct model substantially more often than the standard test statistic that corresponds to the Windmeijer procedure. When data were generated under the multiplicative model, both methods perform comparably in selecting the correct model.
selected the correct model substantially more often than the standard test statistic that corresponds to the Windmeijer procedure. When data were generated under the multiplicative model, both methods perform comparably in selecting the correct model.
Table 3.
Type-I error of proposed tests under additive and multiplicative “null” models
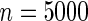 |
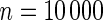 |
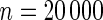 |
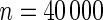 |
||||||
|---|---|---|---|---|---|---|---|---|---|
| Model | Type-I error rate | 0.05 | 0.01 | 0.05 | 0.01 | 0.05 | 0.01 | 0.05 | 0.01 |
| Multiplicative | 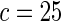 |
0.054 | 0.012 | 0.058 | 0.012 | 0.050 | 0.013 | 0.046 | 0.008 |
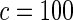 |
0.053 | 0.013 | 0.058 | 0.013 | 0.055 | 0.010 | 0.046 | 0.008 | |
| Additive | 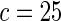 |
0.050 | 0.009 | 0.047 | 0.005 | 0.053 | 0.011 | 0.054 | 0.013 |
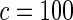 |
0.051 | 0.008 | 0.042 | 0.007 | 0.049 | 0.011 | 0.055 | 0.011 | |
The proposed method is evaluated using 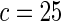 or
or 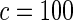 with the corresponding risk regions being defined by the combinations of evenly placed grid points at various upper and lower quintiles of the risk distribution. Results are based on
with the corresponding risk regions being defined by the combinations of evenly placed grid points at various upper and lower quintiles of the risk distribution. Results are based on 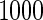 simulated datasets each involving a total of
simulated datasets each involving a total of 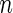 subjects with equal number of cases and controls. In each simulation, data are generated with models involving
subjects with equal number of cases and controls. In each simulation, data are generated with models involving 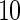 SNPs
SNPs 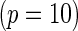 .
.
Table 4.
The proportion of cases where the correct model is selected by the different goodness-of-fit test statistics
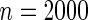 |
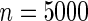 |
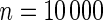 |
||||
|---|---|---|---|---|---|---|
| Correct model | Windmeijer test | Proposed method | Windmeijer test | Proposed method | Windmeijer test | Proposed method |
| Multiplicative | 0.558 | 0.472 | 0.568 | 0.530 | 0.697 | 0.617 |
| Additive | 0.495 | 0.639 | 0.527 | 0.744 | 0.503 | 0.842 |
The proposed method is evaluated using 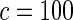 with the corresponding risk regions being defined by the combinations of evenly placed grid points at various upper and lower quintiles of the risk distribution. Data were generated with models involving
with the corresponding risk regions being defined by the combinations of evenly placed grid points at various upper and lower quintiles of the risk distribution. Data were generated with models involving 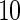 SNPs
SNPs 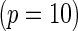 . Results are based on
. Results are based on 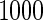 simulated data sets.
simulated data sets.
4. Discussion
Linear-logistic model is widely used in practice for analysis of binary disease outcome data. The popularity of this model stems from its elegant statistical properties, and not necessarily because it corresponds to more natural model for biological mechanisms for action of multiple risk factors of a disease. In fact, in the epidemiologic literature, there is long-standing debate about whether an “additive” or a “multiplicative” model is more appropriate as the starting point for the investigation of interaction between multiple risk factors (Rothman and Greenland, 1998; Weinberg, 1986; Thompson, 1991; Siemiatycki and Thomas, 1981). In this context, the fact that analysis of a very large case–control study with a powerful test for model diagnosis targeted towards extremes of risks provides strong support for “multiplicative” effects of common SNPs of breast cancer is quite intriguing. Irrespective of their implications for mechanisms of etiology, the results are relevant for risk prediction and stratification as the multiplicative model implies much stronger variation of risk in the population compared with the additive and other sub-multiplicative models. In particular, number of subjects in the population who can be identified to be at extreme risk categories can be vastly higher under the multiplicative than the additive model.
One can use the proposed methodology to test for alternative models for multiple risk factors as well. We, for example, investigated a model for the additive effects of the SNPs on the probit scale, also popularly known the liability-threshold model in the genetics community (Zaitlen and others, 2012). We used information about the disease rate in the underlying population for fitting the probit model to case–control data. This analysis (results not shown) suggested that the fitted probability under the logistic and the probit model are almost identical. Thus, these two models cannot be distinguished in the range of polygenic risk distribution that is seen in the breast cancer dataset.
Development of a risk-prediction model may often involve selecting the best model among possible alternatives as opposed to testing the goodness-of-fit of a particular model. Our simulation studies show that the 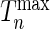 statistics can be used as a powerful criterion for model selection as well when the underlying models have a comparable number of parameters. For comparing models with varying number of parameters, the proposed statistic can be modified in principle to account for model complexity using penalty terms similar to those used in popular criteria such as Akaike information criterion and Bayesian information criterion. Future research is merited for more rigorous development of these extensions so that the methodology can be used more widely as a model selection tool.
statistics can be used as a powerful criterion for model selection as well when the underlying models have a comparable number of parameters. For comparing models with varying number of parameters, the proposed statistic can be modified in principle to account for model complexity using penalty terms similar to those used in popular criteria such as Akaike information criterion and Bayesian information criterion. Future research is merited for more rigorous development of these extensions so that the methodology can be used more widely as a model selection tool.
In conclusion, we develop a powerful approach for testing calibration of a risk model specially targeted toward the extremes of risk distribution. The method when applied to a large case–control study of breast cancer indicates non-additive effects of common SNPs on the absolute risk of the disease, but an excellent fit for an additive model on the logistic scale. Extensive simulation studies suggest good numerical properties of the method. As GWASs and other types of large-scale genomic studies continue to yield new biomarkers of risks for complex diseases, the method could become a useful tool for assembling the cumulative information into well-calibrated risk-prediction models.
5. Software implementation
Tests for calibration of the binary risk model using different goodness-of-fit statistics described here are implemented in the R software package and are freely available for download at http://dceg.cancer.gov/tools/analysis/cbrm.
Supplementary material
Supplementary material is available at http://biostatistics.oxfordjournals.org.
Funding
Drs M.S. and N.C.'s research was supported by the Intramural Research Program of the Division of Cancer Epidemiology and Genetics of the National Cancer Institute. The breast cancer dataset was funded by the U.S. National Institutes of Health, National Cancer Institute (cooperative agreements U01-CA98233 and U19-CA148065 to David J. Hunter, U01-CA98710 to Michael J. Thun, U01-CA98216 to Elio Riboli and Rudolf Kaaks, and U01-CA98758 to Brian E. Henderson, and Intramural Research Program of NIH/NCI, Division of Cancer Epidemiology and Genetics).
Supplementary Material
Acknowledgements
Conflict of Interest: None declared.
References
- Chatterjee N., Wheeler B., Sampson J., Hartge P., Chanock S. J., Park J.-H. Projecting the performance of risk prediction based on polygenic analyses of genome-wide association studies. Nature genetics. 2013;45(4):400–405. doi: 10.1038/ng.2579. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hosmer D. W., Lemeshow S. Applied Logistic Regression. New York: John Wiley & Sons; 2000. [Google Scholar]
- Hunter D. J., Riboli E., Haiman C. A., Albanes D., Altshuler D., Chanock S. J., Haynes R. B., Henderson B. E., Kaaks R., Stram D. O. A candidate gene approach to searching for low-penetrance breast and prostate cancer genes. Nature Reviews. Cancer. 2005;5(12):977–985. doi: 10.1038/nrc1754. and others. [DOI] [PubMed] [Google Scholar]
- Hüsing A., Canzian F., Beckmann L., Garcia-Closas M., Diver W. R., Thun M. J., Berg C. D., Hoover R. N., Ziegler R. G., Figueroa J. D. Prediction of breast cancer risk by genetic risk factors, overall and by hormone receptor. Journal of Medical Genetics. 2012;49:601–608. doi: 10.1136/jmedgenet-2011-100716. and others. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Khoury M. J., Janssens A. C., Ransohoff D. F. How can polygenic inheritance be used in population screening for common diseases? Genetics in Medicine. 2013;15(6):437–443. doi: 10.1038/gim.2012.182. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meigs J. B., Shrader P., Sullivan L. M., McAteer J. B., Fox C. S., Dupuis J., Manning A. K., Florez J. C., Wilson P. W. F., D'Agostino R. B., Sr, Cupples L. A. Genotype score in addition to common risk factors for prediction of type 2 diabetes. New England Journal of Medicine. 2008;359(21):2208–2219. doi: 10.1056/NEJMoa0804742. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moonesinghe R., Khoury M. J., Liu T., Janssens A. C. Discriminative accuracy of genomic profiling comparing multiplicative and additive risk models. European Journal of Human Genetics. 2011;19(2):180–185. doi: 10.1038/ejhg.2010.165. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Prentice R. L., Pyke R. Logistic disease incidence models and case-control studies. Biometrika. 1979;66(3):403–411. [Google Scholar]
- Rothman K. J., Greenland S. Modern Epidemiology. Philadelphia: Lippincott Williams & Wilkins; 1998. [Google Scholar]
- Siemiatycki J., Thomas D. C. Biological models and statistical interactions: an example from multistage carcinogenesis. International Journal of Epidemiology. 1981;10(4):383–387. doi: 10.1093/ije/10.4.383. [DOI] [PubMed] [Google Scholar]
- Thompson W. D. Effect modification and the limits of biological inference from epidemiologic data. Journal of Clinical Epidemiology. 1991;44:221–232. doi: 10.1016/0895-4356(91)90033-6. [DOI] [PubMed] [Google Scholar]
- Tsiatis A. A. A note on a goodness-of-fit test for the logistic regression model. Biometrika. 1980;67(1):250–251. [Google Scholar]
- Wacholder S., Hartge P., Prentice R., Garcia-Closas M., Feigelson H. S., Diver W. R., Thun M. J., Cox D. G., Hankinson S. E., Kraft P. Performance of common genetic variants in breast-cancer risk models. New England Journal of Medicine. 2010;362(11):986–993. doi: 10.1056/NEJMoa0907727. and others. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weinberg C. R. Applicability of the simple independent action model to epidemiologic studies involving two factors and a dichotomous outcome. American journal of epidemiology. 1986;123(1):162–173. doi: 10.1093/oxfordjournals.aje.a114211. [DOI] [PubMed] [Google Scholar]
- Windmeijer F. A. G. The asymptotic distribution of the sum of weighted squared residuals in binary choice models. Statistica Neerlandica. 1990;44(2):69–78. [Google Scholar]
- Zaitlen N., Pasaniuc B., Patterson N., Pollack S., Voight B., Groop L., Altshuler D., Henderson B. E., Kolonel L. N., Le Marchand L. Analysis of case–control association studies with known risk variants. Bioinformatics. 2012;28(13):1729–1737. doi: 10.1093/bioinformatics/bts259. and others. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.