Phosphatase Specificity and Pathway Insulation in Signaling Networks

Abstract

Phosphatases play an important role in cellular signaling networks by regulating the phosphorylation state of proteins. Phosphatases are classically considered to be promiscuous, acting on tens to hundreds of different substrates. We recently demonstrated that a shared phosphatase can couple the responses of two proteins to incoming signals, even if those two substrates are from otherwise isolated areas of the network. This finding raises a potential paradox: if phosphatases are indeed highly promiscuous, how do cells insulate themselves against unwanted crosstalk? Here, we use mathematical models to explore three possible insulation mechanisms. One approach involves evolving phosphatase K_M values that are large enough to prevent saturation by the phosphatase’s substrates. Although this is an effective method for generating isolation, the phosphatase becomes a highly inefficient enzyme, which prevents the system from achieving switch-like responses and can result in slow response kinetics. We also explore the idea that substrate degradation can serve as an effective phosphatase. Assuming that degradation is unsaturatable, this mechanism could insulate substrates from crosstalk, but it would also preclude ultrasensitive responses and would require very high substrate turnover to achieve rapid dephosphorylation kinetics. Finally, we show that adaptor subunits, such as those found on phosphatases like PP2A, can provide effective insulation against phosphatase crosstalk, but only if their binding to substrates is uncoupled from their binding to the catalytic core. Analysis of the interaction network of PP2A’s adaptor domains reveals that although its adaptors may isolate subsets of targets from one another, there is still a strong potential for phosphatase crosstalk within those subsets. Understanding how phosphatase crosstalk and the insulation mechanisms described here impact the function and evolution of signaling networks represents a major challenge for experimental and computational systems biology.

Introduction

Signaling networks allow cells to sense changes in their environment and respond adaptively. One of the most common motifs in eukaryotic signaling networks consists of a kinase that phosphorylates another protein in the network. Phosphorylation often alters the function of the target protein; for instance, the target itself might be a kinase that only becomes active when it is phosphorylated. A second enzyme, called a phosphatase, generally catalyzes the removal of the phosphoryl group. Although they are generally less well studied than kinases, phosphatases play a crucial role in controlling the phosphorylation levels of target proteins and thus the response of signaling networks to external stimuli (1–3).

Metazoan signaling networks are often very complex, exhibiting a high degree of crosstalk where many enzymes are shared among multiple pathways (3–9). Crosstalk studies have generally concentrated on the interactions made by kinases, and the potential for phosphatases to contribute to signaling complexity has been largely overlooked (10). For instance, when developing mathematical models of signaling networks, and a phosphatase has not yet been identified for a particular phosphoprotein, investigators will often add an anonymous, independent, and often unsaturatable phosphatase to the model to fill in the gap (11–17). This approach obviously ignores any contribution that phosphatase-mediated crosstalk might make to the behavior of the network.

We recently used a set of mathematical models to explore whether phosphatases acting on multiple substrates could impact signaling dynamics. We found that the responses of substrates to incoming signals can be strongly coupled if they share a phosphatase (2). In particular, we considered a case in which two different substrate proteins in the network, S₁ and S₂, have two completely independent kinases but share a single phosphatase. In this case, signals that activate only one of the kinases can cause both substrates to respond in a switch-like manner. This occurs because the phosphorylated substrate (say S₂^∗) will act as a competitive inhibitor of the phosphatase, causing the other substrate to become active. This significantly increases S₁ phosphorylation even when the kinase specific to that substrate has very low activity.

Although more than 500 distinct kinases have been identified in the human genome, there are only ∼150 phosphatases (18,19). Thus, there are not even enough phosphatases to assign a unique one to each kinase, let alone to each unique substrate in the network, as has commonly been assumed in modeling studies (11–17). In fact, it is well established that phosphatases are often inherently promiscuous: well-characterized phosphatases have been shown to act on tens, if not hundreds, of substrates (20–22). This fact suggests a potential paradox: since by virtue of their relatively small numbers, each phosphatase must act on a large number of targets, it is unclear how the cell avoids rampant phosphatase-mediated crosstalk between distinct parts of the network (2).

In this work, we used mathematical models to investigate a variety of mechanisms that cells could deploy to prevent shared phosphatases from resulting in unwanted crosstalk. These models focus on a simplified scenario in which substrates share a single phosphatase but are otherwise unrelated (e.g., Fig. 1 A). Although this ignores crosstalk at the kinase level (2–9) and the fact that phosphatase activity is often itself regulated by the signaling network (23,24), it allows us to isolate a particular source of crosstalk and characterize various mechanisms the cell might use to prevent it.

Figure 1.

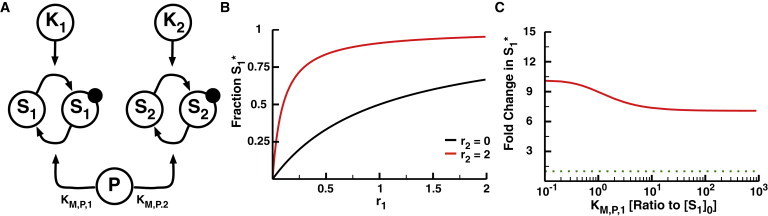
The 2-Kinase/1-Phosphatase loop. (A) Two independent kinases (K₁ and K₂) phosphorylate their respective substrates (S₁ and S₂). The solid circles indicate the phosphorylation of the substrates. A single shared phosphatase, P, dephosphorylates both substrates. (B) The fraction of phosphorylated S₁ (denoted as S₁^∗) as a function of response parameter r₁ when r₂ = 0 (black) and r₂ = 2 (red). r₁ and r₂ represent the ratio of the maximum velocity of the respective kinase to the maximum velocity of the phosphatase and are the dominant response parameters for the system. The initial concentrations of both S₁ and S₂ are set at 10 μM, K_M,P,1 at 1 mM, and K_M,P,2 at 1 μM. As such, S₁ does not saturate either the kinase K₁ or phosphatase, whereas S₂ saturates K₂ and P. Note the increase in phosphorylated S₁ in response to activation of the second loop, as described previously for this motif (2). (C) The fold change in S₁^∗ as a function of K_M,P,1. The fold change in S₁^∗ is calculated as the fraction S₁^∗ at r₂ = 2 divided by the fraction S₁^∗ at r₂ = 0. The dotted green line represents no change in S₁^∗. To see this figure in color, go online.

Since phosphatases can only couple substrate responses if they are saturated (2), one natural approach to limiting the impact of the phosphatase crosstalk would be to evolve phosphatases with Michaelis constants (K_M) so large that they essentially cannot be saturated by their substrates. We showed that in this scenario, the substrates can no longer respond ultrasensitively to incoming signals, and the phosphatases become highly inefficient enzymes that must be expressed at high levels to ensure rapid substrate responses. A second mechanism that cells might employ involves disposing of specific phosphatases altogether and instead employing degradation of the substrate as a means of removing phosphorylated molecules from the system. This alternative approach to effective dephosphorylation would have the benefit of reducing the required number of targets per phosphatase, decreasing the potential for phosphatase coupling in the rest of the network. We found that this dephosphorylation mechanism also cannot generate ultrasensitive responses. Additionally, in order for degradation to yield rapid response kinetics, the phosphorylated substrate would have to be highly unstable, with half-lives on the order of tens of minutes, which would involve high energetic costs to the cell.

Phosphatase promiscuity is likely a larger problem for serine/threonine phosphatases than it is for tyrosine phosphatases (20,21,25–27). Interestingly, serine/threonine phosphatases such as PP2A often act as holoenzymes comprised of a catalytically active subunit, a scaffolding subunit, and an adaptor subunit that recruits specific substrates to the complex (20,27–33). Using our models, we demonstrated that these adaptor subunits can insulate signaling pathways from phosphatase crosstalk while still allowing each independent substrate to respond ultrasensitively. We found that the ability of adaptor subunits to insulate signals between different substrates depends upon the manner of adaptor binding. In particular, the adaptor must be able to bind the substrate independently of whether or not it is already bound in an active holoenzyme complex with the catalytic subunit. Focusing on the example of PP2A, it is likely that the substrate specificities of its adaptor subunits have evolved to functionally couple subsets of targets within the signaling network (20,27–33).

Overall, our work demonstrates that although certain mechanisms can allow cells to avoid widespread phosphatase crosstalk, each of these mechanisms involves a set of functional trade-offs that likely dictate which mechanism will evolve in any given situation. Although these mechanisms almost certainly reduce the overall level of crosstalk in the cell, our analysis of the PP2A example indicates that at least some phosphatase coupling likely remains. Characterizing the functional role of phosphatase-mediated crosstalk in shaping network dynamics represents a major experimental and theoretical challenge in systems biology.

Materials and Methods

Our models of 2-Kinase/1-Phosphatase dynamics, the corresponding systems of ordinary differential equations (ODEs), and details regarding the simulations are described in the Supporting Material. We used the CVODE library from SUNDIALS (34) to numerically integrate the systems of ODEs. The analytical solutions and subsequent derivations are also provided in the Supporting Material.

The half-lives of signaling proteins were taken from a published data set of the half-lives of proteins in mouse C2C12 cells (35). We analyzed the UniProt entry for each protein in this data set and checked for Gene Ontology (GO) annotations describing the protein as being a phosphoprotein. We also obtained the density curve for signaling protein half-lives using the default density estimator in R (36).

Results

The promiscuity of phosphatases

As mentioned above, kinases vastly outnumber phosphatases in the human genome (18,19). To characterize the generality of this kinase/phosphatase mismatch across different species, we searched the UniProt database for ratios of kinases to phosphatases, and phosphoproteins to phosphatases (see Supporting Material for details) (37). We found that for most eukaryotes, there is no way to achieve a single, independent phosphatase per kinase, let alone substrate (as is often assumed, if implicitly, in modeling studies) (27). These findings are consistent with a variety of experimental studies in which phosphatases were shown to target tens to hundreds of phosphoproteins (20,21,25–27).

We previously demonstrated that phosphatases acting on multiple substrates could contribute to network crosstalk. Using a mathematical model in which a phosphatase is shared between two substrates with independent kinases (diagrammed in Fig. 1 A), one can show that the shared phosphatase couples the responses of the substrates so that the activation of one kinase increases the phosphorylation of both substrates through phosphatase inhibition (2). It is straightforward to derive the fraction of phosphorylated substrate S₁ at steady state for this system:

$$S_1^{\ast }=\frac{\left(r_1-1\right)-\left(K_{K,1}+r_1{\alpha }_{P,1}{K}_{P,1}\right)+\sqrt{{\left(\left(r_1-1\right)-\left(K_{K,1}+r_1{\alpha }_{P,1}{K}_{P,1}\right)\right)}^2+4\left(r_1-1\right)r_1{\alpha }_{P,1}{K}_{P,1}}}{2\left(r_1-1\right)},$$ (1)

where S₁^∗ ≡ [S₁^∗]/[S₁]₀ is the mole fraction of phosphorylated substrate S₁; K_K,1 ≡ K_M,K,1/[S₁]₀ and K_P,1 ≡ K_M,P,1/[S₁]₀ are the Michaelis constants of the substrate S₁ for the kinase K₁ and the shared phosphatase P divided by the total concentration of S₁; and r₁ ≡ k_cat,K,1[K₁]₀/k_cat,P,1[P]₀. Since protein concentrations remain constant over relevant timescales, r₁ serves as the response parameter that drives S₁ phosphorylation (2,38). The α_P,1 ≡ 1 + [S₂^∗]/K_M,P,2 term represents the influence of S₂ on the phosphorylation of S₁. The solution for the fraction of phosphorylated S₂ at steady state is the same as Eq. 1 with different indices (e.g., r₂ ≡ k_cat,K,2[K₂]₀/k_cat,P,2[P]₀). Upon activation of the second loop (K₂-S₂), the phosphorylated S₂ acts as a competitive inhibitor of the phosphatase, increasing α_P,1 if [S₂^∗] is large relative to K_M,P,2. This phosphatase inhibition results in an increase in S₁ phosphorylation (Fig. 1 B). The difference in S₁ phosphorylation due to K₂-S₂ activity can be illustrated as the fold change in S₁ phosphorylation upon K₂ stimulation, defined here as the concentration of phosphorylated S₁ at r₂ = 2 divided by the concentration of phosphorylated S₁ at r₂ = 0. Give this definition, we observe up to a 10-fold increase in phosphorylation of the first substrate at low values of r₁. Additionally, making P a poor phosphatase for S₁ by increasing K_M,P,1 does not remove the crosstalk, since α_P,1 depends only on the saturation of the phosphatase by S₂^∗ (Fig. 1 C). Although the results in Fig. 1 focus on a case in which there is a single competing substrate S₂, multiple substrates can collectively saturate the phosphatase, leading to indirect activation of S₁ even when none of the competing substrates is at a high enough concentration to individually saturate the enzymes (see Supporting Material for details) (2).

The findings above indicate that on average, phosphatases are quite promiscuous, with tens to hundreds of substrates, and that this promiscuity can cause indirect activation of substrates due to phosphatase crosstalk (Fig. 1). In the following sections, we characterize a number of possible mechanisms that cells could use to minimize the impact of this crosstalk on the response of the network.

Removing coupling with unsaturatable phosphatases

Since phosphatase coupling is dependent upon the collective saturation of the phosphatase by its substrates, it follows that an unsaturatable phosphatase could insulate substrate responses. To investigate the effects of phosphatase saturation on crosstalk, we simultaneously increased both K_M,P,1 and K_M,P,2 in our 2-Kinase/1-Phosphatase model (Fig. 1 A). When the K_M,P values are smaller than the total concentrations of the substrates, we see that the phosphorylation of S₁ at a low value of r₁ is increased ∼10-fold upon activation of the second kinase. As the phosphatase K_M values are increased, however, the fold increase in S₁ phosphorylation drops until it reaches one, indicating that S₁ becomes insensitive to K₂ activity at K_M,P values above ∼10 times the total substrate concentration (Fig. 2 A).

Figure 2.

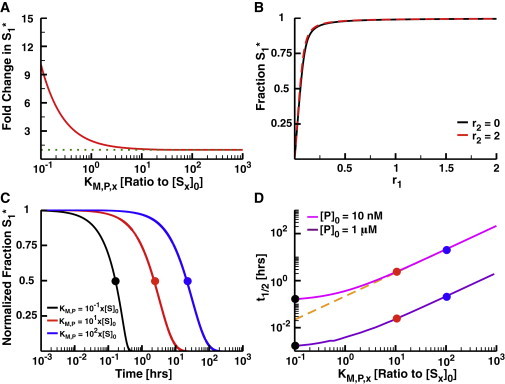
Removing coupling with unsaturatable phosphatases. (A) The fold increase in S₁ phosphorylation as a function of the K_M,P of the shared phosphatase for both substrates in a 2-Kinase/1-Phosphatase loop. (B) The fraction S₁^∗ as a function of r₁ at r₂ = 0 (black) and r₂ = 2 (red) when K_M,P = 10x[S]₀. Note that there is very little difference between these curves. (C) The normalized fraction of phosphorylated substrate S₁^∗ as a function of time after the removal of input signal. In these simulations, the concentration of S₂ and K₂ are 0. The systems were allowed to run to steady state at high K₁ activity (r₁ = 2); at t = 0, the activity of the kinase was set to 0 (i.e., r₁ = 0). The y axes were normalized by y₁ = (y – min_y) / (max_y – min_y), where min_y is the fraction S₁^∗ at r₁ = 0 and max_y is the fraction S₁^∗ at r₁ = 2 at steady state. (D) The half-life of S₁ phosphorylation as a function of K_M,P with two total concentrations of P (10 nM, green, and 1 μM, purple). Note that the black, red, and blue dots are shown to illustrate the relationship between (D) and (C). The dashed orange line shows the linear approximation of t_1/2 for highly unsaturated phosphatases (t_1/2 = K_M,P/k_cat,P[P]₀). To see this figure in color, go online.

The insulation provided by an unsaturated phosphatase comes at the cost of the loss of an ultrasensitive response of the substrates to incoming signal (2,39). The unsaturated phosphatase can no longer operate at its maximum velocity, and as such it takes very little active kinase to phosphorylate a significant fraction of S₁ at steady state (Fig. 2 B). One can understand these results by treating the system analytically. With an unsaturated phosphatase, the solution for the fraction of phosphorylated substrate becomes

$$S_1^{\ast }=\frac{\left(1+K_{K,1}+r_1{K}_{P,1}\right)-\sqrt{{\left(1+K_{K,1}+r_1{K}_{P,1}\right)}^2-4r_1{K}_{P,1}}}{2}.$$ (2)

Note the lack of the α inhibition term from the shared phosphatase, since K_M,P,2 >> [S₂]₀, α_P,1 ≈ 1, resulting in a lack of phosphatase-mediated crosstalk. One can show that the analytical solution in Eq. 2 is strictly hyperbolic in r₁ regardless of the values of the kinetic parameters, confirming the lack of any possible ultrasensitive response (see Supporting Material for derivation) (39).

Another complication with an unsaturated phosphatase is the timescale on which it can dephosphorylate a pool of substrate molecules. To explore this issue, we initialized our system with a fully phosphorylated pool of S₁ molecules and no activity for the second kinase (i.e., r₂ = 0). This represents a pathway that has been fully activated by an incoming signal. We then ran this system with absolutely no kinase activity (r₁ = 0) to simulate the system after the removal of input. When K_M,P is small, it takes <1 h to fully dephosphorylate all substrate. However, it takes longer as the phosphatase becomes unsaturated; for example, it takes >100 h to completely dephosphorylate the substrate when the K_M,P is 100 times the total substrate concentration (Fig. 2 C). When K_M,P is large, the time it takes to dephosphorylate half the substrates (t_1/2) follows

$$t_{1/2}=\frac{\log 2\cdot K_{M,P,1}}{k_{cat,P}{\left[P\right]}_0}.$$ (3)

The dependence of t_1/2 on K_M,P,1 is thus linear, which can result in very long timescales when the enzyme becomes highly unsaturated. In cases where fast dephosphorylation of the substrate is important (say, in tightly controlling the duration of a cellular response, or when fast oscillations are necessary), the system can compensate for this increase in timescale by expressing more phosphatase (Fig. 2 D).

Interestingly, overexpression of the phosphatase alone can insulate substrate responses even when the K_M values are small, as long as the concentration of phosphatase becomes so high that the traditional Michaelis-Menten assumption that the enzymes are at much lower concentration than their substrates is broken (1). In this regime, however, the enzymes tend to sequester their substrates, reducing the concentration of unbound, phosphorylated substrate available to participate in downstream reactions within the network (see Fig. S1). Thus, while phosphatase overexpression can result in insulation and reduce dephosphorylation timescales (Fig. 2 D), it can also reduce the capacity of the system to respond to incoming signals. As a result, many phosphatases (such as Msg5, which dephosphorylates the MAPK Fus3 in yeast) are at least an order of magnitude lower in concentration than their substrates (40,41).

An increased phosphatase K_M is the only mechanism cells could use to unsaturate the phosphatase. Previous experimental studies have demonstrated that binding of phosphorylated sites by SH-2 domain-containing or 14-3-3 proteins can shield the phosphoprotein from dephosphorylation, creating a reservoir phosphorylated substrate (42,43). The presence of such proteins would effectively reduce the concentration of substrate available to the phosphatase (and thus its saturation level) without influencing the saturation of the kinase. To consider the effects of this shielding phenomenon, we added substrate-specific reservoir proteins to our 2-Kinase/1-Phosphatase model. As expected, these reservoir proteins do insulate the substrates from crosstalk even when the K_M values are relatively small (see Fig. S2, A and B). However, since the phosphatase is effectively unsaturated, the substrates always respond hyperbolically to inputs. The dephosphorylation kinetics are also very slow in the presence of high concentrations of reservoir proteins, since the phosphatase must essentially wait for a substrate to be unbound long enough for it to bind and catalyze the dephosphorylation reaction (Fig. S2 C).

Thus, although unsaturating the phosphatase can insulate a substrate from the response of another substrate, this mechanism clearly involves a set of trade-offs. For one, none of the substrates can respond in a switch-like manner to incoming signals, so this mechanism cannot be deployed in cases where ultrasensitive responses are crucial (11,16,44–47). In addition, achieving fast dephosphorylation timescales may require high levels of phosphatase expression, which may become impractical (or limit the capacity of the system to respond at all) in cases where the K_M needed to achieve insulation is very large (Figs. 2 D and S1 A). These trade-offs likely limit the number of cases in which insulation via an unsaturated phosphatase represents an evolutionarily favored mechanism.

Degradation as a phosphatase substitute

The vast majority of work on modeling signal transduction has assumed that dephosphorylation occurs through the catalytic activity of a phosphatase (1,2,11–17). Although there are many clear cases in which phosphatases play this role, it is also possible for substrate degradation to serve as a dephosphorylation mechanism. The idea in this case is straightforward: phosphoproteins are synthesized in their unphosphorylated state, but both the unphosphorylated and phosphorylated states of the protein may be lost from the system due to degradation. When the total protein concentration (regardless of state) remains constant in time, the effect of synthesis and degradation effectively amounts to a first-order dephosphorylation term (see the Supporting Material for details). Substrates that rely on degradation as their phosphatase would not need a separate phosphatase enzyme, which would reduce the number of substrates upon which each phosphatase would have to act.

To characterize degradation as a phosphatase substitute, we built a mathematical model with a substrate responding to a single kinase without a phosphatase. In this model, we assume that the degradation process is completely unsaturatable. As a result, the degradation terms are all taken to be first order, and there is no degradation- or phosphatase-mediated crosstalk between pathways. In some cases, phosphorylation of a protein changes its half-life; for instance, the phosphorylated state of the protein may be less stable than the unphosphorylated state (48,49). To capture this possibility in our model, the unphosphorylated and phosphorylated substrates are degraded at different rates (k_deg,U and k_deg,P for the unphosphorylated and phosphorylate states, respectively). When the substrate is bound to a kinase, we assume that the kinase falls off the complex as the substrate is degraded. Unphosphorylated substrate is synthesized at a rate necessary to maintain a constant total substrate concentration at steady state (see Supporting Material for details). To parameterize the model, we obtained a range of half-lives by using UniProt to identify phosphoproteins from a published data set of protein half-lives in mouse C2C12 cells (35,37). Phosphoproteins in this data set have half-lives ranging from ∼10 to 187 h, with a median of 31 h (Fig. 3 A). We used these values to set the range of biologically relevant degradation rates for the substrates.

Figure 3.

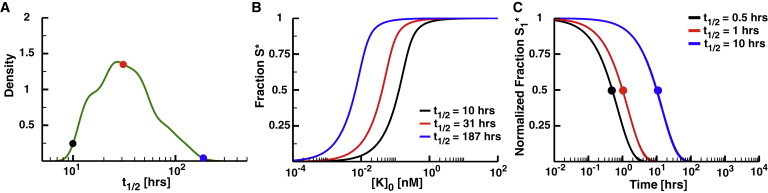
Degradation as a phosphatase. (A) The range of signaling protein half-lives in mouse C2C12 cells (35). The minimum reported half-life is 10 h (black dot), maximum is 187 h (blue), and median is 31 h (red). (B) The fraction S^∗ as a function of the concentration of active kinase, [K]₀. Note that the model for these panels includes only the kinase and degradable substrate. [K]₀ directly affects the parameter r_deg, which represents the ratio of the maximum velocity of the kinase to the maximum velocity of degradation (k_deg×[S]₀). The value of r_deg will thus change for a constant concentration of kinase as the half-life changes. As such, any r_deg for a protein with a longer half-life will involve a lower concentration of kinase than that for a protein with a shorter half-life. (C) The normalized fraction S^∗ as a function of the time after setting kinase activity to 0 for substrates with half-lives of 0.5, 1, and 10 h. To see this figure in color, go online.

We then ran this model to steady state using each of the phosphoprotein half-lives for a range of kinase concentrations. For these initial simulations, we assumed that the phosphorylation state does not influence the degradation rate (i.e., k_deg,U = k_deg,P). The response of the substrate to incoming signal is dependent on the half-life of the substrate (e.g., more stable phosphoproteins are more highly phosphorylated than less stable phosphoproteins; Fig. 3 B). However, substrates with any half-life in the mouse data set become completely phosphorylated when the kinase concentration is ≥1 nM, making these substrates highly sensitive to incoming signal. Note that the catalytic rate of the kinase in these simulations is 0.9 s⁻¹, which is close to the kinase catalytic rates that have been determined experimentally (50,51). Faster kinase catalytic rates would further reduce the kinase concentrations necessary to completely phosphorylate substrates with the observed half-lives.

To understand how the different degradation rates may affect substrate phosphorylation and sensitivity, we derived a solution for the fraction of phosphorylated S^∗ in this model:

$$S_1^{\ast }=\frac{\left(1+r_{\mathit{deg}}+K_{\mathit{deg}}\right)-\sqrt{{\left(1+r_{\mathit{deg}}+K_{\mathit{deg}}\right)}^2-4r_{\mathit{deg}}}}{2},$$ (4)

where r_deg ≡ k_cat,K[K]₀/k_deg,P[S]₀ is the ratio of the maximum velocity of the kinase to the maximum velocity of substrate degradation. This solution includes a modified Michaelis constant K_M,deg ≡ (k_-,K + k_cat,K + k_deg,U)/k_+,K, taking into account the degradation of the kinase-bound substrate, which is divided by the total substrate concentration to obtain K_deg. As expected based on our results for an unsaturatable phosphatase, one can show that the phosphorylation response of the substrate in this model can only be hyperbolic in r_deg (see Supporting Material for the derivation). As such, a signaling pathway that relies on degradation to remove phosphorylated substrate could never respond ultrasensitively to incoming signals.

Finally, the timescales required to degrade a pool of phosphorylated substrate based on the half-lives of phosphoproteins from the C2C12 data set would be very long. To demonstrate this, we ran the model at high levels of kinase activity (r_deg = 2) to steady state. We then set r_deg = 0 to simulate the system after removal of the input. Even with the shortest substrate half-life, the system requires ∼100 h to completely dephosphorylate the substrate (Fig. 3 C). Complete dephosphorylation of the substrate in <1 h would require the phosphorylated state to have a half-life on the order of minutes. If the system needs to recover quickly from incoming signals, utilizing degradation as a phosphatase subunit would likely be quite inefficient, requiring a very unstable phosphorylated substrate. Maintaining a reasonable concentration of total substrate would in turn require a high rate of protein synthesis, resulting in a high energetic cost for the cell. Thus, although degradation could reduce the total substrate burden of phosphatases in the cell, it is likely to be employed only in cases where an ultrasensitive response is not necessary and when either slow dephosphorylation kinetics or the energetic costs of high protein turnover are functionally acceptable.

Role of phosphatase regulatory subunits in pathway isolation

Serine phosphatases such as PP1 and PP2A exist as holoenzymes: the catalytic subunit of PP2A binds to a scaffold subunit, which makes up the catalytic core. This core can then bind to one of many possible regulatory adaptor subunits, with each adaptor recruiting PP2A to a specific set of substrates (Fig. 4 A) (20,27–33). A previous study examined the mechanism of targeting of substrates by a regulatory subunit, as well as the effects of concentration and binding constants (52). However, that study did not consider whether regulatory subunits might provide insulation from phosphatase-mediated crosstalk. To investigate the role of these adaptors in isolating different pathways that share the same phosphatase catalytic core, we built two models, one ordered and one unordered, for binding of the phosphatase adaptor subunits. In the ordered model, the phosphatase catalytic core can bind two one of two adaptor subunits, creating two distinct holoenzymes. This holoenzyme can then specifically bind to and dephosphorylate a cognate substrate (diagrammed in the inset of Fig. 4 B). This model represents the standard case in which the holoenzyme first assembles and then acts on its substrates (30,33).

Figure 4.

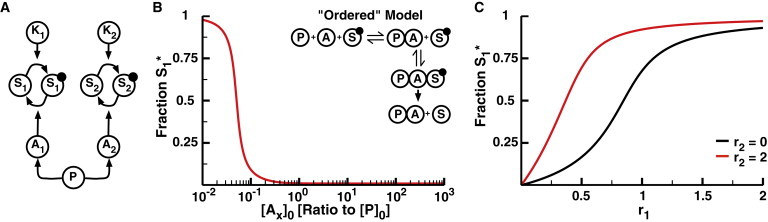
Ordered model of phosphatase regulatory adaptor subunits. (A) Diagram of the regulatory adaptor model. The previously described 2-Kinase/1-Phosphatase model (Fig. 1A) was expanded to include two regulatory adaptor subunits, A₁ and A₂, that target the phosphatase to substrates S₁ and S₂, respectively. The phosphatase must bind an adaptor domain to bind and dephosphorylate either substrate. (B) The fraction S₁^∗ as a function of the initial concentration of each adaptor subunit with low levels of K₁ activity (r₁ = 0.05) and high levels of K₂ activity (r₂ = 2). The concentrations of both adaptor subunits are equal and are varied simultaneously. Inset: Diagram of the ordered model. The phosphatase must first bind to an adaptor subunit. This complex can then bind to and dephosphorylate a phosphorylated substrate. (C) The fraction S₁^∗ as a function of r₁ at r₂ = 0 (black) and r₂ = 2 (red) with [A_x]₀ = 100 nM. In this model, the adaptor subunits do not eliminate the potential for phosphatase-mediated crosstalk even though they are perfectly specific for their respective substrates. To see this figure in color, go online.

We first tested the ordered model to determine whether the interaction specificity of adaptor subunits is sufficient to isolate the responses of different substrates. To examine how the concentrations of the adaptor subunits affect substrate phosphorylation, we ran this model to steady state with a range of total adaptor concentrations (keeping the concentrations of the two adaptors equivalent, i.e., [A₁] = [A₂]) and measured the fraction of phosphorylated S₁ at low levels of kinase 1 activation (r₁ = 0.05) and high levels of kinase 2 activity (r₂ =2) (Fig. 4 B). In this model, a phosphatase can only act on its substrate when bound to an adaptor subunit. When the concentration of adaptors is less than that of the catalytic core, the total number of active phosphatases is thus limited by the adaptor concentration. As that concentration decreases, so does the concentration of active phosphatases, making the apparent value of r very high for both substrates and leading to an increase in S₁ phosphorylation (Fig. 4 B). Once the concentration of the adaptors exceeds that of the catalytic core, however, the concentration of the adaptors has little influence on S₁ phosphorylation (Fig. 4 B). At higher levels of kinase 1 activity, adaptor subunits provide no insulation between different substrates in this model: S₁ phosphorylation increases considerably as r₂ goes from 0 to 2 (Fig. 4 C). This indicates that although regulatory adaptor domains may help to target different phosphoproteins, their specificity cannot insulate substrates from phosphatase-mediated crosstalk in the ordered model. This is because the large pool of phosphorylated S₂ makes it far more likely that the holoenzyme will remain intact in order to bind and further dephosphorylate S₂. As such, the catalytic core is prevented from disassociating from its S₂-specific adaptor subunit and forming the holoenzyme specific to S₁, decreasing the concentration of phosphatase available to act on S₁.

The unordered model differs in that the adaptor subunit can bind its specific phosphoprotein without being bound to the catalytic core first. The adaptor-substrate dimer can then bind the catalytic core, resulting in substrate dephosphorylation (diagrammed in the inset of Fig. 5 A). This removes the ability of one substrate to sequester the catalytic core in the holoenzyme, since the core can dissociate from the regulatory adaptor subunit even in the presence of the phosphorylated substrate. At low concentrations of the adaptor subunits, the unordered model acts similarly to the ordered model (Fig. 5 A). However, as the adaptor concentration becomes very large, there is an increase in substrate phosphorylation. This is due to the prozone effect, i.e., as the concentration of adaptor increases, the system starts to produce many phosphatase-adaptor dimers and phosphorylated substrate-adaptor dimers. These dimers cannot bind to one another, which prevents the catalytic core from interacting with the substrate (41,52–57). Even though the prozone effect can influence the response at high adaptor concentrations, there is still a wide range of adaptor concentrations (>2 orders of magnitude) that provide robust phosphatase activity (Fig. 5 A). The unordered model also provides effective pathway insulation since there is essentially no change in S₁ phosphorylation as the second kinase switches between inactive and active (r₂ = 0 and r₂ = 2, respectively) (Fig. 5 B). Additionally, S₁ can respond ultrasensitively in r₁, although the apparent r₁ is about half of what is expected since the adaptor subunits split the available phosphatase between the two substrates.

Figure 5.

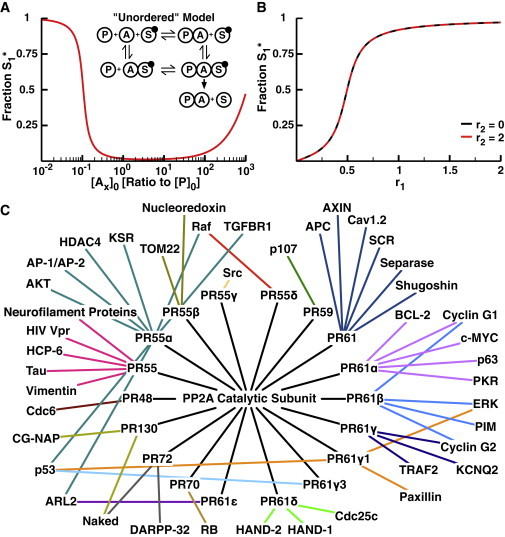
Unordered model of phosphatase regulatory adaptor subunits. (A) The fraction S₁^∗ as a function of initial concentration of each adaptor subunit with low levels of K₁ activity (r₁ = 0.05) and high levels of K₂ activity (r₂ = 2). Inset: diagram of the unordered adaptor model. In this case, the adaptor subunit can bind to the substrate without previously binding to the phosphatase (lower path). (B) The fraction S₁^∗ as a function of r₁ at r₂ = 0 (black) and r₂ = 2 (red) with [A_x]₀ = 100 nM. Note that this model provides insulation between the substrates. (C) Network diagram of the interactions of the PP2A catalytic subunit with each of 18 identified regulatory subunits (20). The PP2A holoenzyme formed by binding a regulatory subunit then interacts with a subset of the proteins in the network. To see this figure in color, go online.

PP2A is known to interact with a large number of substrates, yet only ∼18 different regulatory subunits have been identified. To understand how this handful of subunits could allow the PP2A catalytic core to dephosphorylate so many substrates while maintaining a degree of pathway insulation, we built a network based on previously identified interactions between the regulatory subunits and the substrates of PP2A (Fig. 5 C) (20). This network depicts the interactions between 42 PP2A substrates and 18 regulatory subunits. Strikingly, only six of the substrates have interactions with more than one of the adaptors, and of these, only p53 interacts with three. The remaining substrates are all specific to a single regulatory subunit. According to our findings, these subsets of phosphoproteins would be insulated from one another, assuming the regulatory subunits can bind the phosphorylated substrates without binding the catalytic core. However, this insulation would not work within any given subset. Since they all share a single regulatory adaptor, the phosphoproteins in that subset would act as if they have a single, shared phosphatase. The coupling within groups of substrates could have positive phenotypic effects. For instance, PR55α interacts with AKT, AP-1/AP-2, HDAC4, and KSR, all of which are involved in the same signaling cascade (58–61). We previously showed that sharing a phosphatase among multiple members of the same signaling cascade increases the sensitivity of the cascade (2), so sharing the same PP2A holoenzyme within a subsection of a signaling network could increase its local responsiveness to external signals.

Discussion

Although it is understood that both kinases and phosphatases act on a large number of targets, phosphatases have classically been considered to be more promiscuous than kinases. For example, although more than 20 phosphoproteins have been identified as substrates of the EGF/ErbB receptor tyrosine kinase (62), phosphatases such as PP2A dephosphorylate hundreds of substrates within the cell (20–22). Although the fact that phosphatases can be promiscuous has been appreciated for some time (20–22), it was only recently demonstrated that shared phosphatases can actually couple the responses of their substrates (2). Since phosphatases must act on large numbers of substrates, it is unclear how cells can ensure at least some degree of specificity in downstream responses to incoming signals. In this work, we extended our previous modeling efforts to consider three possible mechanisms whereby cells might insulate substrates from the possibility of phosphatase crosstalk. We found that each mechanism involves a set of unavoidable functional trade-offs that likely influence where and when they have evolved in eukaryotic signaling networks.

Perhaps the simplest mechanism would be to evolve phosphatases whose K_M values are so large that they cannot be saturated by their substrates. Although this mechanism is indeed effective in isolating the responses of substrates that share a particular phosphatase (Fig. 2, A and B), it inherently creates phosphatases that are highly inefficient enzymes. As a result, the response of a substrate to upstream signals can no longer exhibit a switch-like, ultrasensitive character. Thus, it is unlikely that phosphatase inefficiency would be employed in cases where ultrasensitivity is a key component of the functional response (1,2,11,16,44–47). A second consequence of this inefficiency is slow dephosphorylation kinetics, which in turn means that high phosphatase expression levels are required before a particular substrate can quickly return to baseline activity levels after a signal is removed (Fig. 3, C and D). Other mechanisms that effectively desaturate the phosphatase, such as the expression of high levels of reservoir proteins that bind the phosphorylated state and prevent phosphatase binding, could also provide insulation but would have similar effects on the ultrasensitivity and dephosphorylation kinetics.

Protein degradation can also assume the role of an effective phosphatase, reducing the number of substrates that phosphatase enzymes might have to act upon in the cell. If we assume that degradation is both efficient and unsaturatable, then degradation can indeed prevent phosphatase crosstalk between substrates. As with the inefficient phosphatase mechanism, however, the lack of an ultrasensitive response and slow dephosphorylation kinetics might represent an issue for this particular mechanism in some cases. Even the least stable phosphoprotein in mouse cells would still require >100 h to return to baseline after removal of the signal (Fig. 3 C). Using degradation to fill the role of a phosphatase would thus require a very high (and very costly) rate of protein turnover in cases where fast response kinetics are necessary.

The final mechanism we considered here involved separate regulatory subunits recruiting a catalytic core to particular substrates. Although these subunits can clearly provide substrate specificity, it is not clear that they can actually insulate those substrates from one another. Indeed, if the phosphatase preassembles into a holoenzyme before interacting with the substrate (which is essentially the classical picture for this sort of enzyme (20,27–32)), even perfectly specific regulatory subunits cannot prevent phosphatase-mediated crosstalk (Fig. 4). If the regulatory subunits can bind their substrates independently of binding the catalytic core, however, this mechanism could provide insulation while still maintaining the possibility of an ultrasensitive response and fast dephosphorylation kinetics (Fig. 5). Deploying this mechanism, however, would require the evolution and expression of a distinct regulatory subunit for every set of phosphoproteins that the cell needs to isolate, which could represent a costly and evolutionarily complex solution to the problem of phosphatase coupling.

Our findings thus demonstrate that cells have a considerable degree of flexibility in the mechanisms they might use to insulate substrates from one another, despite the (relatively) small number of phosphatases in eukaryotic genomes. The question then arises: which of these mechanisms are deployed in any given situation, and to what extent are substrates truly isolated from one another? For instance, the well-characterized serine/threonine phosphatase PP2A acts as a holoenzyme with a regulatory subunit (20,27–32), and it is currently unclear whether the assembly of this holoenzyme follows the ordered or unordered model. Our results suggest that an experiment in which the adaptor concentration is increased (either directly in an in vitro setting or through overexpression in vivo) could establish which of these mechanisms is utilized by PP2A (Figs. 4 B and 5 A). Even if the assembly mechanism is unordered, PP2A-mediated crosstalk is still a strong possibility. Although the data presented in Fig. 5 C are certainly not complete (for instance, KSR and Akt share an additional regulatory subunit (63,64)), PP2A clearly does not have a distinct regulator for every substrate with which it interacts. Instead, these regulators have clearly evolved to interact with a specific subset of proteins, possibly coupling their responses in functionally meaningful ways (Fig. 5 C).

A major component of systems biology is the construction of formal mathematical or computational models of cellular regulatory systems, with the goal of understanding how cells process information from their environment and respond appropriately (65–68). In the case of complex eukaryotic signaling networks, a major barrier to this goal is the fact that dephosphorylation, whether by phosphatases or through some other mechanism, has been comparatively poorly characterized for most phosphoproteins in the network. The addition of anonymous and perfectly specific phosphatases to cover this gap may produce effective models of individual cascades or pathways (11–17), but it is unlikely that this practice will remain effective as larger, more genome-wide models of signaling networks are formulated. Experimentally determining the phosphatase structure of signaling systems and gaining a theoretical understanding of how that structure has evolved to generate and regulate crosstalk among pathways (Fig. 5 C) thus represents a major challenge for systems biology.