Structured Functional Principal Component Analysis

Summary

Motivated by modern observational studies, we introduce a class of functional models that expand nested and crossed designs. These models account for the natural inheritance of the correlation structures from sampling designs in studies where the fundamental unit is a function or image. Inference is based on functional quadratics and their relationship with the underlying covariance structure of the latent processes. A computationally fast and scalable estimation procedure is developed for high-dimensional data. Methods are used in applications including high-frequency accelerometer data for daily activity, pitch linguistic data for phonetic analysis, and EEG data for studying electrical brain activity during sleep.

1. Introduction

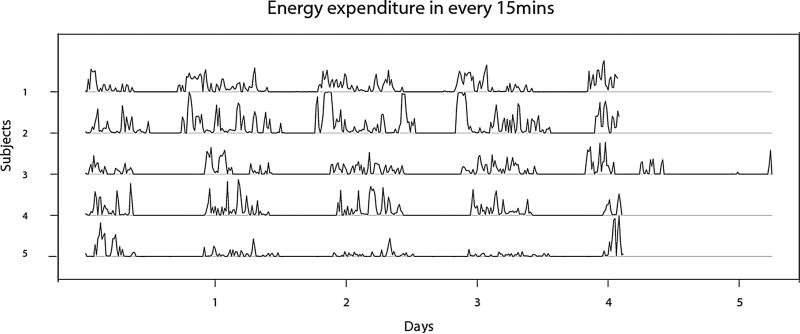
In many current studies, functional measurements have well-defined stochastic structures induced either by the experimental design or by the scientific meaning of the data. For example, the Sleep Heart Health Study (SHHS) (Quan et al., 1997; Crainiceanu et al., 2009; Di et al., 2009) collected electroencephalograms (EEG) data for thousands of subjects at two visits, roughly 5 years apart. At every visit, EEG data were recorded at a frequency of 125 Hz during sleep. Thus, for each subject and visit, data consist of 125 observations per second. Crainiceanu et al. (2009) applied a Fourier transformation to the original data and obtained the normalized δ-power as a densely sampled stationary time series. These data have a natural hierarchical structure induced by the replicated visits within each subject. More precisely, one can denote the δ-power function for visit j of subject i at time t after sleep onset by Y_ij(t), which can be decomposed into a subject-specific process X_i(t) and a visit-within-subject process U_ij(t) that quantifies the deviation from the subject-specific mean. A second example is provided by Bai et al. (2012) in a recent study of physical activity in an elderly population. In this study, each subject wears an accelerometer that records three-axis accelerations during in-home activities at a sampling frequency of 10 Hz. Bai et al. (2012) introduced activity intensity, a measure of activity expressed in multiple of signal standard deviations of inactive periods. Activity intensity is calculated in every tenth of one second interval. Figure 1 displays the activity intensity for five subjects during a 5-day period averaged over 15 minutes for improved display clarity. One possibility of analyzing these data is to focus on activity intensity in non-overlapping one-hour intervals. Thus, the data for each subject on every day contains 36,000 activity measurements per hour for 24 hours. This can be viewed as a three-level hierarchical structure: hour within day within subject. More specifically, let Y_ijk(t) be the activity intensity at time t within hour k on day j for subject i. In addition to the subject-specific process X_i(t) and the day-within-subject process U_ij(t), the remaining part of the variation in Y_ijk(t) can be explained by the hour-specific process W_ijk(t) that quantifies the deviation of hour k from the average of day j for subject i.

Figure 1.

Activity intensity measurements over 5 days for 4 subjects. Original data contain 10 observations per second. This plot shows the average of activity intensity in non-overlapping 15 minute intervals for improved display clarity.

Aston, Chiou, and Evans (2010) described a different study of phonetic analysis where the authors were interested in studying the fundamental frequency (F0, “pitch”) of spoken languages. In particular, they recorded the F0-contours of syllables from 19 nouns pronounced by 8 native speakers of the Luobuzhai Qiang dialect in China. Suppose that we use Y_ijk(t) to denote the pitch of syllables within the jth word that are pronounced by subject i. Each (i, j) contains more than one curves, indicated by k, because there are multiple syllables within a word and every word was spoken under three different contexts. Each curve was normalized by the total duration of the corresponding vowel and was sampled at 11 equidistant time points. Figure 2 displays an example of F0-contours for vowels that compose three different words spoken by three speakers. We observe that: (a) the shapes of the curves are strongly associated with the vowels; (b) there are substantial variations across the speakers and words. For example, speaker “a” has, on average, a lower pitch than the other two. Given vowel “i”, curves from word 3 display a steep rising pattern and decay at the end of the vowel. But curves from word 2 (labeled by the triangle symbol) are all arch-shaped. Y_ijk(t) is jointly affected by at least two random components: the word-generic effect X_i(t) and the speaker-inherent effect Z_j(t). Unlike the hierarchical models, the two random components are mutually independent, yet interact on the pitch contours.

Figure 2.

F0-contours for 3 words (triangles for word 2, dots for word 3, and multiplication signs for word 4) spoken by 3 speakers (the lightest color for speaker “a”, a slightly darker color for speaker “c”, and the darkest color for speaker “g”). Each contour was measured at 11 equal distant time points within a vowel (“ə”, “a”, “e”, “i”, or “u”) when a particular word was spoken by one of the eight speakers. Every word was repeated under three different contexts.

Although these three studies have different designs, they share some common features: (1) the fundamental observational unit is a function that can be high-dimensional; (2) data have a known structure induced by the sampling design; and (3) analysis of individual levels of variability is of interest. One goal of this article is to define a wide class of structured functional models with explicit functional effect components; in particular, the model class will contain the observed structures in the three examples. We will focus on the common structures and provide a consistent statistical framework for all these models. A second goal is to characterize the observed variability by uncorrelated latent processes. Through estimating and diagonalization of these covariance operators, we will achieve both dimensionality reduction of the original data and statistical modeling on the induced linear spaces. From an intuitive perspective, this article shows how to conduct principal component analysis (PCA) when data have a particular known and common latent correlation structure.

The structured functional models in this article fall into functional linear mixed model (FLMM) framework. Early work (Guo, 2002; Herrick and Morris, 2006; Morris and Carroll, 2006) mainly use splines or wavelets smoothing in model fitting. Brumback and Rice (1998) and Guo (2004) have specifically studied functional nested and crossed designs. More recent work like Staicu, Crainiceanu, and Carroll (2010) and Zhou et al. (2010) consider spatial correlation in the nested model. While all these models can be viewed as particular cases of FLMM, model fit and inference remains difficult, and is currently done on a model-by-model basis. We conclude that none of these previous articles have addressed the class of complex functional structures discussed here. Moreover, very fast algorithms for high-dimensional data had not been available. We aim to introduce a data-driven approach that applies to both nested and crossed designs, but is generalizable to a much broader model space. We introduce latent processes to capture explicit levels of variability using the same concept from standard mixed effects models. The only difference is that random effects are now replaced with random processes. Computational feasibility is achieved via principal component decomposition of covariance operators for latent processes, and by loss-less projections of high-dimensional data. The approaches are methodologically related to PCA decomposition (Staniswalis and Lee, 1998; Yao et al., 2003; Yao, Müller, and Wang, 2005; Di et al., 2009; Aston et al., 2010; Greven et al., 2010). Among those, Aston et al. (2010) project the whole function onto a vector space, where the vector entries are the first few principal scores of the function. Through multiple linear mixed effects models which link principal scores with the covariates, they are able to assess the effect of covariates on the outcome function. Alternatively, multilevel functional PCA (MFPCA, Di et al. [2009]) decomposes the intra-subject and inter-subject covariance operators in the two-way nested model, while inference is based on the scores separated by levels of variability. Longitudinal functional PCA (LFPCA, Greven et al. [2010]) uses a similar approach to model the longitudinal dynamics of functional observations at multiple visits. In this article, we generalize these ideas to analyze functional observations collected under the most common nested and crossed designs, and expand the number and type of models for functional data. We propose structured functional principal component analysis (SFPCA) as a method to decompose the variability via PCA for any functional model with a particular linear structure. We claim SFPCA to be the first algorithm for FLMM to efficiently handle dense and high-frequency measurements.

We organize the article as follows: in Section 2, we provide a list of structured functional models that SFPCA is applied to and connect them with the symmetric sum method of moments (MoM) estimators described in Koch (1968); Section 3 discusses SFPCA and its implementation, with extension to high-dimensional settings; Section 4 describes simulation studies for low-dimensional, high-dimensional and noisy settings; Section 5 applies SFPCA to the scientific questions described in Section 1.

2. Structured Functional Models

Koch (1967) provides a comprehensive list of linear models for scalar data that emerge from various experimental designs. We contend that these models have natural extensions to functional data and that the models may be analyzed by decomposing the corresponding covariance operators. Table 1 lists the proposed designs that are grouped based on sampling schemes (Brumback and Rice, 1998; Guo, 2002; Yao et al., 2005; Morris and Carroll, 2006; Baladandayuthapani et al., 2008; Di et al., 2009; Staicu et al., 2010; Zhou et al., 2010; Liu and Guo, 2012).

Table 1.

Structured functional models. For nested models, i = 1, 2,..., I; j = 1, 2,..., J_i; k = 1, 2,..., K_ij; i₁ = 1, 2,..., I₁, i₂ = 1, 2,..., I_2i1,..., i_r = 1, 2,..., I_{ri1i2...ir–1}. For crossed designs, i = 1, 2,..., I; j = 1, 2,..., J; k = 1, 2,..., n_ij; (C2s) “Two-way sub” stands for “Two-way crossed design with subsampling”; (CM) contains combinations of any s (s = 1, 2,..., r) subset of the r latent processes, as 'well as repeated measurements within each cell. ${\mathcal{S}}_1,{\mathcal{S}}_2,\dots ,{\mathcal{S}}_d\in \{i_{k_1}{i}_{k_2}\cdots i_{k_s}u:k_1,k_2,\dots ,k_s\in (1,2,\dots ,r),u\in (\varnothing ,1,2,\dots ,I_{i_1{i}_2\dots i_r}),s\le r\}$, u is the index for repeated observation in cell (i_k1,i_k2,...i_kr). ε_.t, is the white noise distributed as (0, σ²).

Nested	(N1) One-way	Yi(t) = μ(t) + Xi(t) + εit
	(N2) Two-way	Yij(t) = μ(t) + Xi(t) + Uij(t) + εijt
	(N3) Three-way	Yijk(t) = μ(t) + Xi(t) + Uij(t) + Wijk (t) + εijkt
	(NM) Multi-way	$Y_{i_1{i}_2\cdot i_r}\left(t\right)=\mu \left(t\right)+R_{i_1}^{\left(1\right)}\left(t\right)+\cdots +R_{i_1\cdots i_r}^{\left(r\right)}\left(t\right)+{∊}_{i_1{i}_2\cdots i_{r}t}$
Crossed	(C2) Two-way	Yij(t) = μ(t) + Xi(t) + Zj(t) + Wij(t) + εijt
	(C2s) Two-way sub	Yijk(t) = μ(t) + Xi(t) + Zj(t) + Wij(t) + Uijk(t) + εijkt
	(CM) Multi-way	$Y_{i_1{i}_2\cdots i_{r}u}\left(t\right)=\mu \left(t\right)+R_{{\mathcal{S}}_1}\left(t\right)+\cdots +R_{{\mathcal{S}}_d}\left(t\right)+{∊}_{i_1{i}_2\cdots i_{r}ut}$

Let Y(t) indicate the observed outcome function. The most general model format is that $Y\left(t\right)=\mu \left(t\right)+\sum$ latent processes + ε_t, where μ(t) is the mean curve of fixed effect, ${∊}_t\stackrel{\mathrm{i}.\mathrm{i}.\mathrm{d}.}{\sim }(0,{\sigma }^2)$ (0, σ²) is the white noise. The latent processes are assumed to be zero-mean and square integrable, so that they are identifiable and the standard statistical assumptions for scalar outcomes can mirror to functional data. Consequently, the total variability of a functional outcome is decomposed into sum of process-specific variations plus σ². These models capture a wide variety of correlation structures in modern functional data studies. In the following, we build up the intuition behind the functional nested and crossed designs, and connect them to the data examples that are discussed in the Introduction. For presentation purpose, we first assume “noise-free” models where σ = 0. Our methods are extended to “noisy” scenarios in Section 3.4.

2.1. Nested Designs

A one-way nested model (N1) is the simplest variance component model for functional data. In (N1), the observed outcome Y_i(t) is represented as a sum of a deterministic mean function, μ(t), and a level-specific stochastic process X_i(t). X_i(t) are assumed to be i.i.d., with mean zero and covariance operator K_X(t, s) = Cov{X_i(t), X_i(s)}; K_X may be thought of as the functional counterpart of scalar covariance. The variability of Y_i(t) is completely determined by that of X_i(t), that is, K_Y = K_X. In conventional functional data analysis (Ramsay and Silverman, 2005), X_i(t) would be expressed via a set of spline or wavelet basis, or data-driven principal components (Ramsay and Silverman, 2005; Di et al., 2009; Greven et al., 2010). Irrespective of the basis functions, K_X is determined by the first two moments of the representation coefficients and a quadratic form of the basis functions.

The two-way functional nested design (N2) is the functional equivalent of a one-way analysis of variance (ANOVA) model. Originally motivated by the two-way sampling design of EEG data in SHHS (Di et al., 2009), the model expands (N1) with a subject-visit specific process U_ij(t) that has covariance K_U(t, s) = Cov{U_ij(t), U_ij(s) . Thus, the observed total variability of Y_ij(t)} is decomposed into subject-specific and subject-visit specific variability. These two parts are modeled through K_X and K_U – the functional covariance operators of X_i(t) and U_ij(t). To ensure identifiability, the random processes X_i(t) and U_ij(t) are assumed to have mean zero and be uncorrelated. This assumption also guarantees that K_Y = K_X + K_U.

Additional levels of nesting can be included in the model to accommodate higher hierarchies. For example, the three-way nested model (N3) provides an appropriate framework for modeling the activity intensity data described in Section 1. In addition to the subject-specific process X_i(t) and the subject-visit specific process, U_ij(t), the remaining variation in Y_ijk(t) is modeled through W_ijk(t), which quantifies the hourly deviation from the average activity intensity level of day j for subject i. The most general functional nested model (NM) admits arbitrarily many levels of nesting. If the activity intensity is followed for weeks or months, a four-way or five-way model may be more descriptive, given the possible repeated patterns of activity from week to week or from month to month. As in the preceding models, mutual independence is imposed for model identifiability. The total variability is decomposable into level-specific functional variance components as K_Y = K₁ + K₂ + ··· + K_r, where $K_r(t,s)=\mathrm{Cov}\{R_{i_1\cdots i_r}^{\left(r\right)}\left(t\right),R_{i_1\cdots i_r}^{\left(r\right)}\left(s\right)\}$. Here we use the notation from Table 1 for the multilevel hierarchical model with an arbitrary number of levels (NM).

2.2. Crossed Designs

Another group of designs admits crossing between levels. For example, the two-way crossed design (C2) is a functional analog of two-way ANOVA with an interaction term. It emphasizes a joint effect of two uncorrelated processes X_i(t) and Z_j(t), as well as their interaction W_ij(t), on the outcome Y_ij(t). The two-way crossed model with sub-sampling (C2s) applies to experimental designs where repeated measurements occur within each combination (i, j) induced by the first-level processes X_i(t) and Z_j(t). In addition to the first-level crossing W_ij(t) as in (C2), U_ijk(t) accounts for variation in the replicates. For the phonetic example, X_i(t) and Z_j(t) model the main effects of speakers and words, while W_ij(t) models their interaction. Since multiple F0-contours may fall in category (i, j), we use U_ijk(t) to capture the residual variation.

In general, we can consider an m-way crossed functional model (CM) with arbitrary number of crossings. In this model, r (r > 2) uncorrelated latent processes have exchangeable first-level effects on Y(t). Any subset of s (s ≤ r) processes out of r may have interactions, resulting in d functional additive terms in the model. For notational convenience, we express this model using d sub-index sets, $\{{\mathcal{S}}_1,{\mathcal{S}}_2,\dots ,{\mathcal{S}}_d\}$ that define the model structure. For example, (C2s) with four terms can be written as $\{{\mathcal{S}}_1,{\mathcal{S}}_s,{\mathcal{S}}_3,{\mathcal{S}}_4\}=\{i,j,ij,ijk\}$ and $R_{{\mathcal{S}}_1}\left(t\right)=X_i\left(t\right)$, $R_{{\mathcal{S}}_2}\left(t\right)=Z_j\left(t\right)$, $R_{{\mathcal{S}}_3}\left(t\right)=W_{ij}\left(t\right)$, and $R_{{\mathcal{S}}_4}\left(t\right)=U_{ijk}\left(t\right)$. The assumptions on correlation structures stay the same as the previous designs. We now show how to efficiently estimate these models.

3. Structured Functional PCA

We develop SFPCA to efficiently reduce dimensionality and extract signals for the class of functional models introduced in Section 2. This approach models latent processes parsimoniously via principal components (PCs) by Karhunen–Loéve expansion. SFPCA starts with estimating the covariance operators of latent processes. Following Koch (1968), we employ the MoM approach based on symmetric sums. By extending his approach to functional settings, we construct unbiased estimators of covariance matrices on a grid of p points $\mathcal{T}=\{t_1,t_2,\dots ,t_p\}$. After estimating the covariance operators, we conduct spectral decomposition to obtain eigenfunctions and principal scores that serve as coordinates in the space spanned by eigenfunctions. Note that the fixed effect is not of our main interest and can be estimated using existing methods. Without loss of generality, we assume that the data are already demeaned and we mainly focus on the random effects.

We use two-way crossed design (C2) as the main example. Details for other models in Table 1 can be found in Appendix B. Let X_i(t), Z_j(t) and W_ij(t) be mutually uncorrelated mean-zero random processes as described in Section 2. Their covariance operators are K_X, K_Z, and K_W, respectively, where K_X(t, s) = E{X_i(t)X_i(s)}, K_Z(t, s) = E{Z_j(t)Z_j(s)} and K_W(t, s) = E{W_ij(t)W_ij(s)}. Using the Karhunen–Loéve expansion for X_i(t), Z_j(t)}, and W_ij(t), model (C2) becomes

$$Y_{ij}\left(t\right)=\sum _{k=1}^{\infty }{\varphi }_k^X\left(t\right){\xi }_{ik}^X+\sum _{l=1}^{\infty }{\varphi }_l^Z\left(t\right){\xi }_{jl}^Z+\sum _{m=1}^{\infty }{\varphi }_m^W\left(t\right){\xi }_{ijm}^W,$$ (1)

where ${\varphi }_k^X\left(t\right)$, ${\varphi }_l^Z\left(t\right)$, and ${\varphi }_m^W\left(t\right)$ are the eigenfunctions of the covariance operators K_X, K_Z, and K_W. The scores ${\xi }_{ik}^X=\int X_i\left(s\right){\varphi }_k^X\left(s\right)\mathrm{d}s$, ${\xi }_{il}^Z=\int Z_j\left(s\right){\varphi }_l^Z\left(s\right)\mathrm{d}s$, and ${\xi }_{ijm}^W=\int W_{ij}\left(s\right){\varphi }_m^W\left(s\right)\mathrm{d}s$ are mutually independent random variables with mean 0 and variance ${\lambda }_k^X$, ${\lambda }_l^Z$, and ${\lambda }_m^W$, respectively, where ${\lambda }_k^X\ge {\lambda }_{k+1}^X$, ${\lambda }_l^Z\ge {\lambda }_{l+1}^Z$, and ${\lambda }_m^W\ge {\lambda }_{m+1}^W$ for every k, l, and m Normality of scores not necessary for the results in this article, but may be a convenient mild assumption.

3.1. Level-Specific Spectral Decomposition

Consider the case when most variability of each latent process is captured by the first N₁, N₂, and N₃ principal components of X_i(t), Z_j(t), and W_ij(t), model (1) can then be approximated as $Y_{ij}\left(t\right)={\sum }_{k=1}^{N_1}{\varphi }_k^X\left(t\right){\xi }_{ik}^X+{\sum }_{l=1}^{N_2}{\varphi }_l^Z\left(t\right){\xi }_{jl}^Z+{\sum }_{m=1}^{N_3}{\varphi }_m^W\left(t\right){\xi }_{ijm}^W$. We vectorize the functional outcome on the discrete sampling points $\mathcal{T}$, and define Y = (Y₁₁, . . . , Y_1J1, . . . , Y_I1, . . . , Y_IJI) to be a p × n matrix with Y_ij := {Y_ij(t₁), Y_ij(t₂), . . . , Y_ij(t_p)}^T and $n={\sum }_{i=1}^l{J}_i$. For notational simplicity we assume a balanced design where J_i = J, though such assumption is not necessary. Let ${\xi }_i^X={({\xi }_{i1}^X,\dots ,{\xi }_{i{N}_1}^X)}^{\mathrm{T}}$ and ${\Phi }_X=[{\Phi }_1^X\left(\mathcal{T}\right),{\Phi }_2^X\left(\mathcal{T}\right),\dots ,{\Phi }_{N_1}^X\left(\mathcal{T}\right)]$ be the first N₁ principal components observed at time grid $\mathcal{T}$. Similar definitions apply to $({\xi }_j^Z,{\Phi }_Z)$ and $({\xi }_{ij}^W,{\Phi }_W)$. Hence the truncated model is further expressed into matrix form as ${\mathbf{Y}}_{ij}={\Phi }_X{\xi }_i^X+{\Phi }_Z{\xi }_j^Z+{\Phi }_W{\xi }_{ij}^W$.

We will show in the next section how to obtain K̂_X, K̂_Z and K̂_W. Given the availability of such estimators, we obtain ${\widehat{\Phi }}_X^{N_1}$, ${\widehat{\Phi }}_Z^{N_2}$, and ${\widehat{\Phi }}_W^{N_3}$ to be their first N₁, N₂, and N₃ eigenvectors, where N_k (k = 1, 2, 3) is selected so that $N_k=\min \{L,\mathrm{s}.\mathrm{t}.\frac{{\sum }_l^L\widehat{{\lambda }_l}}{{\sum }_{l=1}^p\widehat{{\lambda }_l}}\ge q\}$ and q is a threshold between (0, 1). $\widehat{{\lambda }_i}$ denotes the estimated eigenvalues for the corresponding covariance matrix. Let ${\widehat{\Lambda }}_X^{N_1}$, ${\widehat{\Lambda }}_Z^{N_2}$, and ${\widehat{\Lambda }}_W^{N_3}$ be the diagonal matrices for the first N₁, N₂, and N₃ eigenvalues. We can estimate the truncated set of principal scores as the best linear unbiased predictor (BLUP) of the mixed effect model ${\mathbf{Y}}_{ij}={\widehat{\Phi }}_X^{N_1}{\xi }_i^X+{\widehat{\Phi }}_Z^{N_2}{\xi }_j^Z+{\widehat{\Phi }}_W^{N_3}{\xi }_{ij}^W$, where ${\xi }_i^X\sim N(0,{\widehat{\Lambda }}_X^{N_1})$, ${\xi }_j^Z\sim N(0,{\widehat{\Lambda }}_Z^{N_2})$ and ${\xi }_{ij}^W\sim N(0,{\widehat{\Lambda }}_W^{N_3})$. The BLUP estimators for two-way crossed model (C2) and three-way nested model (N3) are provided in Appendix A.

3.2. MoM Covariance Operator Estimation

By extending the idea of symmetric sum MoM estimators in Koch (1968), we show that our estimated covariance matrices will be of the form K̂_X = YG_XY^T, K̂_Z = YG_ZY^T, and K̂_W = KG_WY^T, where G_X, G_Z, are G_W are design-specific matrices of dimension n × n. In fact, for all the structured functional models, MoM estimators of covariance operator are representable in the “sandwich” form, YGY^T. We illustrate the detailed calculation for the covariance operators for the two-way crossed design (C2) and three-way nested design (N3). Results for other design schemes are provided in Appendix B.

3.2.1. Two-way crossed design (C2)

For model (C2), we have

$$E\{Y_{ij}\left(t\right)-Y_{kl}\left(t\right)\}{\{Y_{ij}\left(s\right)-Y_{kl}\left(s\right)\}}^{\mathrm{T}}=\{\begin{array}{cc}2\{K_W(t,s)+K_Z(t,s)\}\hfill & \text{if}i=k,j\ne l\hfill \\ 2\{K_W(t,s)+K_X(t,s)\}\hfill & \text{if}i\ne k,j=l\hfill \\ 2\{K_W(t,s)+K_Z(t,s)+K_X(t,s)\}\hfill & \text{if}i\ne k,j\ne l.\hfill \end{array}\phantom{\}}$$

Let n_ij = 1 if Y_ij is observed and 0 otherwise; $n_{i0}={\sum }_j{n}_{ij}$, $n_{0j}={\sum }_i{n}_{ij}$, $n={\sum }_{i,j}{n}_{ij}$, $k_1={\sum }_i{n}_{i0}^2$, and $k_2={\sum }_j{n}_{0j}^2$. Define D_n×n = diag{N₁, N₂, . . . , N_I} with N_i = n_i0I_ni0, ${\mathbf{E}}_{I\times n}=\mathrm{diag}\{1_{{\mathrm{n}}_{10}}^{\mathrm{T}},\dots ,1_{{\mathrm{n}}_{\mathrm{I}0}}^{\mathrm{T}}\}$, and $1_{n_{i0}}={(1,1,\dots ,1)}_{n_{i0}}^{\mathrm{T}}$. P_n×n = diag{P₁, . . . , P_I} with P_i = diag{n₀₁, . . . , n_0ni0} of dimension n_i0 × n_i0, F_J×n = (f₁, . . . , f_J)^T is the second-level analogy E, where f_j is a vector with value 1 on observations with second-level process Z_j(t) and 0 otherwise. If H_Z = 2(K_W + K_Z), H_X = 2(K_W + K_X), and H_XZ = 2(K_W + K_Z + K_X), then the results above indicate the following explicit MoM estimators

$$\begin{array}{cc}\hfill {\widehat{H}}_Z=& \frac{1}{k_1-n}\sum _{i=1}\sum _{j\ne l}({\mathbf{Y}}_{ij}-{\mathbf{Y}}_{il}){({\mathbf{Y}}_{ij}-{\mathbf{Y}}_{il})}^{\mathrm{T}}\hfill \\ \hfill =& \frac{2}{k_1-n}\mathbf{Y}(\mathbf{D}-{\mathbf{E}}^{\mathrm{T}}\mathbf{E}){\mathbf{Y}}^{\mathrm{T}}\hfill \\ \hfill {\widehat{H}}_X=& \frac{1}{k_2-n}\sum _{i\ne k}\sum _j({\mathbf{Y}}_{ij}-{\mathbf{Y}}_{kj}){({\mathbf{Y}}_{ij}-{\mathbf{Y}}_{kj})}^{\mathrm{T}}\hfill \\ \hfill =& \frac{2}{k_2-n}\mathbf{Y}(\mathbf{P}-{\mathbf{F}}^{\mathrm{T}}\mathbf{F}){\mathbf{Y}}^{\mathrm{T}}\hfill \\ \hfill {\widehat{H}}_{XZ}=& \frac{1}{n^2-k_1-k_2+n}\sum _{i\ne k}\sum _{j\ne l}({\mathbf{Y}}_{ij}-{\mathbf{Y}}_{kl}){({\mathbf{Y}}_{ij}-{\mathbf{Y}}_{kl})}^{\mathrm{T}}\hfill \\ \hfill =& \frac{2}{n^2-k_1-k_2+n}\mathbf{Y}(n\mathbf{I}-{11}^{\mathrm{T}}-\mathbf{D}+{\mathbf{E}}^{\mathrm{T}}\mathbf{E}-\mathbf{P}+{\mathbf{F}}^{\mathrm{T}}\mathbf{F}){\mathbf{Y}}^{\mathrm{T}}.\hfill \end{array}$$

Thus, the covariance operators can be estimated as K̂_Z = (Ĥ_XZ – Ĥ_X)/2 =: YG_XY^T, K̂_X = (Ĥ_XZ – Ĥ_Z)/2 =: YG_XY^T and K̂_W = (Ĥ_X + Ĥ_Z – Ĥ_XZ)/2 =: YG_WY^T.

3.2.2. Three-way nested model

Consider model (N3), where Y_ijk(t) = X_i(t) + U_ij(t) + W_ijk(t), i = 1, 2, . . . , I; j = 1, 2, . . . , J_i; k = 1, 2, . . . , n_ij, and W, U, and X are the three latent processes nested in orders. Similar to the approach for (C2), we have

$$E\{Y_{ijk}\left(t\right)-Y_{luv}\left(t\right)\}{\{Y_{ijk}\left(s\right)-Y_{luv}\left(s\right)\}}^{\mathrm{T}}=\{\begin{array}{cc}2K_W(t,s)\hfill & \text{if}i=l,j=u,k\ne v\hfill \\ 2\{K_W(t,s)+K_U(t,s)\}\hfill & \text{if}i=l,j\ne u\hfill \\ 2\{K_X(t,s)+K_W(t,s)+K_U(t,s)\}\hfill & \text{if}i\ne l.\hfill \end{array}\phantom{\}}$$

Let Y_ijk = {Y_ijk(t₁), . . . , Y_ijk(t_p)}^T, $n={\sum }_{i,j}^I{n}_{ij}$, $n_{i.}={\sum }_{j=1}^{J_i}{n}_{ij}$, $k_1={\sum }_{i=1}^I{\sum }_{j=1}^{J_i}{n}_{ij}^2$, $k_2={\sum }_i{n}_i^2$, ${\mathbf{D}}_1=\mathrm{diag}\{{\mathrm{N}}_{11},\dots ,{\mathrm{N}}_{{\mathrm{IJ}}_{\mathrm{I}}}\}$. D₁ diag {N₁₁, . . . , N_IJI} where N_ij = n_ijI_nij, and D₂ diag N₁, . . . , N_I}, where N_i = n_i. I_ni.; ${\mathbf{E}}_1=\mathrm{diag}\{1_{{\mathrm{n}}_{11}}^{\mathrm{T}},\dots ,1_{{\mathrm{n}}_{{\mathrm{IJ}}_{\mathrm{I}}}}^{\mathrm{T}}\}$, ${\mathbf{E}}_2=\mathrm{diag}\{1_{{\mathrm{n}}_{1.}}^{\mathrm{T}},\dots ,1_{{\mathrm{n}}_{\mathrm{I}.}}^{\mathrm{T}}\}$. If H_W = 2K_W, H_U = 2(K_W + K_U) and H_x = 2(K_W + K_Z + K_X), we obtain

$$\begin{array}{cc}\hfill {\widehat{H}}_W=& \frac{1}{k_1-n}\sum _{i,j}\sum _{k,v}(Y_{ijk}-Y_{ijv}){(Y_{ijk}-Y_{ijv})}^{\mathrm{T}}\hfill \\ \hfill =& \frac{2}{k_1-n}\mathbf{Y}({\mathbf{D}}_1-{\mathbf{E}}_1^{\mathrm{T}}{\mathbf{E}}_1){\mathbf{Y}}^{\mathrm{T}}\hfill \\ \hfill {\widehat{H}}_U=& \frac{1}{k_2-k_1}\sum _i\sum _{j\ne u}\sum _{k,v}(Y_{ijk}-Y_{iuv}){(Y_{ijk}-Y_{iuv})}^{\mathrm{T}}\hfill \\ \hfill =& \frac{2}{k_2-k_1}\mathbf{Y}({\mathbf{D}}_2-{\mathbf{E}}_2^{\mathrm{T}}{\mathbf{E}}_2-{\mathbf{D}}_1+{\mathbf{E}}_1^{\mathrm{T}}{\mathbf{E}}_1){\mathbf{Y}}^{\mathrm{T}}\hfill \\ \hfill {\widehat{H}}_X=& \frac{1}{n^2-k_2}\sum _{i\ne l}\sum _{j,u,k,v}(Y_{ijk}-Y_{iuv}){(Y_{ijk}-Y_{iuv})}^{\mathrm{T}}\hfill \\ \hfill =& \frac{2}{n^2-k_2}\mathbf{Y}(n\mathbf{I}-{11}^{\mathrm{T}}-{\mathbf{D}}_2+{\mathbf{E}}_2^{\mathrm{T}}{\mathbf{E}}_2){\mathbf{Y}}^{\mathrm{T}}.\hfill \end{array}$$ (2)

Hence, K̂_W = Ĥ_W/2, K̂_U = (Ĥ_U – Ĥ_W/2, and K̂_X = (Ĥ_X – Ĥ_U/2 all have the form YGY^T. In general, multi-way nested and crossed designs can be estimated through a similar work flow (see Appendix B for details).

3.3. Structured High-Dimensional Data

Given the current research emphasis on high-dimensional data, linear models are still difficult to fit. Here we show that the entire model class described in Table 1 can be fitted using fast approaches. Note that the estimation procedures in the previous sections assume that the MoM estimators of the covariance operators can be constructed and decomposed. When the dimension of observations, p, is moderate, the methods described in Section 3 are straightforward. However, if the observations are high-dimensional, such as p > 10,000, the approach is no longer feasible. Calculating and storing a p-dimensional covariance operator K̂_p×p is computationally expensive, and conducting spectral decomposition will become prohibitive. One could possibly smooth and down-sample the data assuming that the data are generated from low-rank intrinsic features. But in many scenarios, data are densely sampled for us to explore finer information and we would like to preserve the high resolution. Thus, we propose an alternative approach based on a rank-preserving transformation. This algorithm allows efficient calculation of the eigenfunctions and eigenvalues without requiring either storing or diagonalizing the estimated covariance matrices in high-dimensional space.

We outline the algorithm as follows. Throughout this section, we assume that $p\gg n$. Hence, the induced covariance matrix is at most of rank n. Zipunnikov et al. (2011) propose an approach that avoids calculating the covariance operators in the original p-dimensional space. Consider (C2) as an example: the idea is to map the model onto a lower-dimensional space and obtain ${\tilde{\mathbf{Y}}}_{ij}≔{\mathbf{CY}}_{ij}=\mathbf{C}{\Phi }^X{\xi }_i^X+\mathbf{C}{\Phi }^Z{\xi }_j^Z+\mathbf{C}{\Phi }^W{\xi }_{ij}^W$, where the matrix C should be of dimension m × p and $m\ll p$. An arbitrarily chosen C will lose information from the p-dimensional data. However, we can show that we are able to find a C such that Ỹ_ij span a space that preserve the ordering and important features from the original data space. One possible choice would be to start with the whole data matrix, Y, which can be obtained by column binding individual data vectors, Y_ij. Suppose that Y = VS^1/2U^T is the singular value decomposition (SVD) of Y, let C = V^T. Given that Y_ij = VỸ_ij, the data in the reduced-dimensional space Ỹ_ij contain enough information from the original space.

Model becomes ${\mathbf{S}}^{1∕2}{\mathbf{U}}^{\mathrm{T}}={\mathbf{V}}^{\mathrm{T}}{\Phi }^X{\xi }_i^X+{\mathbf{V}}^{\mathrm{T}}{\Phi }^Z{\xi }_j^Z+{\mathbf{V}}^{\mathrm{T}}{\Phi }^W{\xi }_{ij}^W≔{\mathbf{A}}^X{\xi }_i^X+{\mathbf{A}}^Z{\xi }_j^Z+{\mathbf{A}}^W{\xi }_{ij}^W$. Theorem 1 in Zipunnikov et al. (2011) shows that this transformation preserves full information for the linear PCA model. The eigenfunctions for the original model can be recovered by left multiplying V to the eigenfunctions obtained in the new model, and the eigenvalues remain unchanged. This is straightforward to implement, as the number of operations involved in the SVD of Y is linear in p. After obtaining the SVD of Y, each column Y_ij can be represented as Y_ij = VS^1/2U_ij, where U_ij is a corresponding column of matrix U^T. Therefore, the vectors Y_ij differ only via the factors U_ij of length n, which is much lower-dimensional. Comparing this SVD representation of Y_ij with the original model (C2), it follows that the structured separation of the variability modeled by high-dimensional latent processes X_i, Z_j, and W_ij is identical in the structured separation of the low-dimensional vectors U_ij. This is the key observation which motivates our approach. This model has an “intrinsic” dimensionality that is induced by the sample size n. The low-dimensional model is estimable using SFPCA in Section 3 and requires only O(n³) calculations.

We obtain ${\tilde{\xi }}_i^X$, ${\tilde{\xi }}_j^Z$, and ${\tilde{\xi }}_{ij}^W$ as the induced BLUP in the lower-dimensional model, with the matrices A^X, A^Z, and A^W replaced by their corresponding estimates ${\mathbf{A}}_{N_1}^X$, ${\mathbf{A}}_{N_2}^Z$, and ${\mathbf{A}}_{N_3}^W$. Furthermore, ${\Phi }_{N_1}^X$, ${\Phi }_{N_2}^Z$, and ${\Phi }_{N_3}^W$ in the original space may be recovered by left multiplying V onto ${\mathbf{A}}_{N_1}^X$, ${\mathbf{A}}_{N_2}^Z$, and ${\mathbf{A}}_{N_3}^W$. We provide the formula for final estimates and their detailed derivation for two-way crossed model (C2) and three-way nested model (N3) in Appendix A. Up until the last step, all the calculations can be conducted in O(n³) complexity. Therefore, fitting the model in a reduced-dimensional space guarantees the high-dimensional principal components in a p-linear time. This means that complex statistical models for high-dimensional data sets can be fitted quickly.

3.4. Model with Noise

So far we have assumed that the data are measured without noise. However, the algorithm can be naturally extended to “noisy models.” When the noise component has a smooth covariance structure on the functional domain and can be expressed as another latent process such as U_ij(t) in model (N2) and W_ijk(t) in model (N3), SFPCA directly applies. When there is white noise ε ~ (0, σ²) along the function and σ² > 0, we propose several approaches to smooth either the raw data or the covariance matrix estimators.

Take model (N3) as an example, suppose that the observed data are Ỹ_ijk(t) = Y_ijk(t) + ε_ijkt. The symmetric sum MoM estimators as in equation 2 become H̃ ỸGỸ^T and EH̃ = EH̃ + σ²I, where H̃ = YGY^T. For low-dimensional data where rank preserved projection in Section 3.3 is not necessary, we estimate EĤ by smoothing the off-diagonal surface of H̃ as in Staniswalis and Lee (1998), and proceed with SFPCA algorithm as in the “noise-free” scenarios. However, we encounter multiple difficulties when applying this approach to high-dimensional functional data. First, it is computationally infeasible to conduct bivariate smoothing on the p × p covariance matrix when say, p ≥ 10,000. Second, although the white noises remain to be i.i.d. when projected onto the lower-dimensional space, the one-to-one mapping of the eigenvalues and principal scores between the p-dimensional model and the reduced n-dimensional model no longer holds after smoothing the covariance matrix in the reduced-dimensional space.

Therefore, we recommend a pre-processing by smoothing the raw data before conducting SFPCA. There is a trade-off between the signal from the raw data and the smoothness in the pre-processed data. As we have observed in our simulation settings, the first eigenvalues from the smoothed data are usually under-estimated. An alternative approach for the high-dimensional functional data is to apply a “structured” twist of the fast covariance estimation (FACE) algorithm (Xiao, Li, and Ruppert, 2013; Xiao et al. 2014). Their algorithm implements a computationally fast sandwich smoother on the sample covariance matrix YY^T, and directly provides the eigenvalues and eigenfunctions without explicitly constructing the smoothed covariance matrix. Since the covariance matrix for each latent process in SFPCA techniques has the uniform sandwich expression YGY^T, we are able to define the new data matrix Ỹ := YG^1/2 and directly apply FACE to Ỹ. We refer to that article for more details.

4. Simulations

To better understand how SFPCA performs in practice, we conduct simulation studies for both low- and high-dimensional functional data, under various experimental designs and signal-to-noise ratios.

$$\{\begin{array}{c}{Y}_{ijk}\left(t\right)=\sum _{l=1}^{N_1}{\varphi }_l^X\left(t\right){\xi }_{il}+\sum _{m=1}^{N_2}{\varphi }_m^U\left(t\right){\zeta }_{ijm}+\sum _{h=1}^{N_3}{\varphi }_h^W\left(t\right){\eta }_{ijkh}+{∊}_{ijkt},\hfill \\ {\xi }_{il}\stackrel{\mathrm{i}.\mathrm{i}.\mathrm{d}.}{\sim }N(0,{\lambda }_l^X),{\zeta }_{ijm}\stackrel{\mathrm{i}.\mathrm{i}.\mathrm{d}.}{\sim }N(0,{\lambda }_m^U),{\eta }_{ijkh}\stackrel{\mathrm{i}.\mathrm{i}.\mathrm{d}.}{\sim }N(0,{\lambda }_h^W),\hfill \\ {∊}_{ijkt}\stackrel{\mathrm{i}.\mathrm{i}.\mathrm{d}.}{\sim }N(0,{\sigma }^2).\hfill \end{array}\phantom{\}}$$ (3)

For the three-way nested model (N3), we generate the high-dimensional data based on the true model 3, where i = 1, . . . , I; j = 1, . . . , J; k = 1, . . . , K; N₁ = N₂ = N₃ = 4, ${\lambda }_k^X={\lambda }_k^U={\lambda }_k^W={0.5}^{k-1}$, 1, 2, 3, 4; $t\in \mathcal{T}=\{1∕p,2∕p,\dots ,1\}$; p = 50,000, I = 50, J = 5, and K = 5. The eigenfunctions are specified as

${\varphi }_l^X\left(t\right)$	${\varphi }_m^U\left(t\right)$	${\varphi }_h^W\left(t\right)$
sin(2πt)	$1∕\sqrt{2}$	l
cos(2πt)	sin(6πt)	$\sqrt{3}(2t-1)$
sin(4πt)	cos(6πt)	$\sqrt{5}(6t^2-6t+1)$
cos(4πt)	sin(8πt)	$\sqrt{5}(20t^3-30t^2+12t-1)$

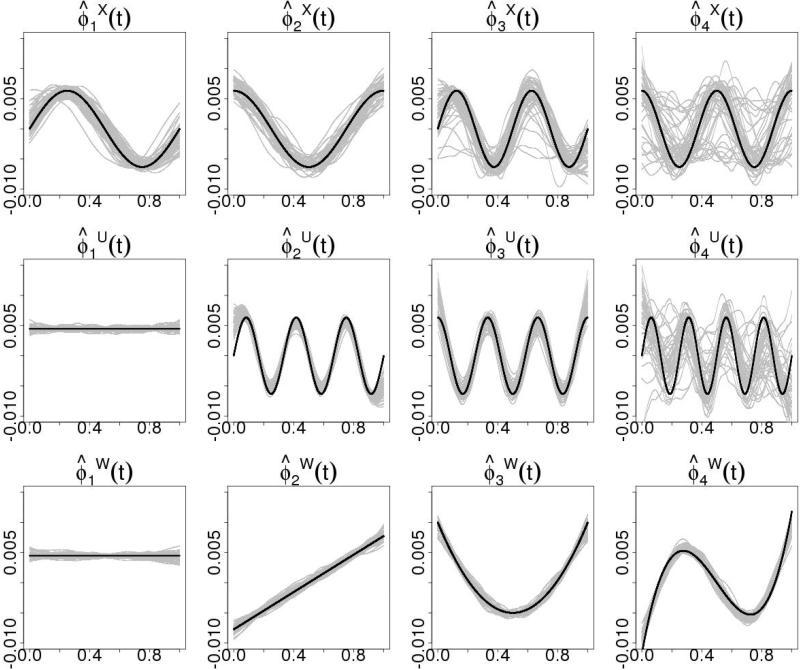
We vary the standard deviation of the white noise σ to be 0, 0.1, 0.5, and 1, and conduct 100 simulations under each scenario. To compare the estimation accuracy, the number of PCs N₁, N₂, and N₃ are treated as known. Figure 3 shows the estimated eigenfunctions when σ = 0.5. Overall the shape of the functions are well recovered. As we go from lower (X_i) to higher (W_ijk) hierarchies, the estimation gets better because the level-specific sample size increases. Within each latent process, the first few eigenfunctions with larger eigenvalues are better estimated than the later ones. Table 2 lists the mean square errors (MSEs) of estimated $\widehat{\sigma }$ and eigenvalues under different signal-to-noise ratio. More results for this simulation can be found in Appendix C.

Figure 3.

The estimated eigenfunctions for three latent processes over 100 simulations when σ 0.5 are shown in gray (we randomly plot 50 out of 100 estimates). The true eigenfunctions are displayed in black curves.=The first- and second-level hierarchies X and U are captured by two sets of trigonometric basis. The third-level process W is polynomial. Within each process, the first few eigenfunctions in correspondence with larger percentages of variance explanation are better estimated than the later eigenfunctions. The eigenfunctions for W are better estimated than X and U because we observe more levels of independent realizations for W.

Table 2.

Average MSEs over 100 simulations for estimating σ, the eigenvalues and the principal scores under various signal-to-noise ratios. The values are augmented 100 times for better presentation.

σ	MSEλX (10−2)				MSEλU (10−2)				MSEλW (10−2)
	${\lambda }_1^X$	${\lambda }_2^X$	${\lambda }_3^X$	${\lambda }_4^X$	${\lambda }_1^U$	${\lambda }_2^U$	${\lambda }_3^U$	${\lambda }_4^U$	${\lambda }_1^W$	${\lambda }_2^W$	${\lambda }_3^W$	${\lambda }_4^W$
0	3.2	0.9	0.2	0.1	1.2	0.3	0.1	0.02	0.2	0.1	0.01	2E-3
0.1	4.5	0.9	0.2	0.1	1.3	0.7	0.2	0.2	0.2	0.1	0.02	8E-3
0.5	5	1.6	1.4	0.4	1.3	9.3	3.2	1.0	6.5	6.7	3.5	2.7
1	8	5	2.8	0.6	2	15.5	4.1	0.8	102	101	33.6	21.7

${\mathrm{MSE}}_{\widehat{\sigma }}\left({10}^{-2}\right)$	MSEξ (10−2)				MSEθ (10−2)				MSEζ (10−2)
	ξ 1	ξ 2	ξ 3	ξ 4	θ 1	θ 2	θ 3	θ 4	ζ 1	ζ 2	ζ 3	ζ 4
2E-17	14.7	11.2	7.6	136	120	4.5	2.5	2	20.2	8.1	0.5	2.6
3E-8	42.7	18.2	5.5	34.7	305	5.6	3.2	2	280	30.5	9.9	15.8
4E-7	267	129.2	17.7	22.2	1660	22.8	12	19.1	1623	226	161	102
1E-6	370	159	36.1	22.5	1657	50.1	58.3	31.7	1677	466	245	153

We have also conducted simulation studies for (C2) model under different sample sizes and by smoothing the off-diagonal matrix. The results are also presented in Appendix C.

5. Data Applications

SFPCA can be applied to various types of structured data including the three examples discussed in the Introduction. The SHHS data were analyzed in details in Di et al. (2009) with MFPCA, which is a special case of the methodology considered in this article. Here we provide results for the phonetic study and the accelerometer data.

5.1. Phonetic Study

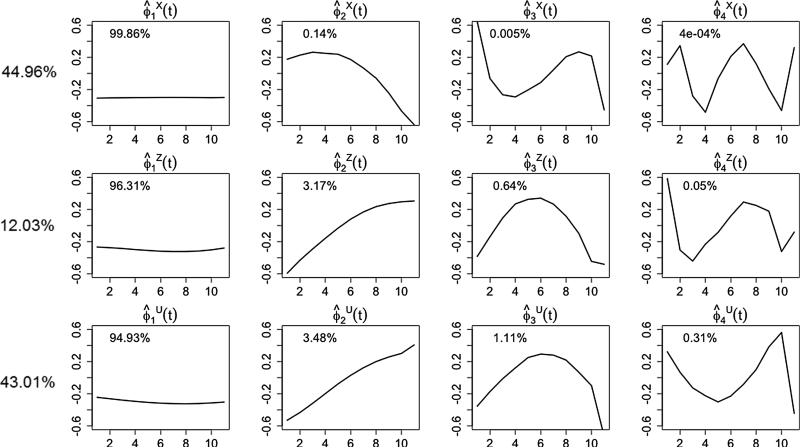
The phonetic study of Luobuzhai Qiang dialect consists of F0-contours from 8 subjects speaking 19 words under 3 contexts. Every word contains up to 4 syllables, each corresponding to one of the five vowels: “ə”, “a”, “e”, “i”, and “u”. The pitch values of the contours are measured at 11 equidistant time points that are standardized based on the total duration of the vowel. As previously observed, given the balanced study design, the marginal shapes of the contours are correlated with the associated vowels. In addition, each curve demonstrates speaker-specific and word-generic variations. To assess the effect of these covariates with relatively simple specification, Aston et al. (2010) assume that all the latent processes are on the same space expanded by a common set of eigenfunctions, and that covariates are associated with pitch levels through the principal scores – weights of the eigenfunctions. Here we relax these assumptions and attempt to fully evaluate the variability of each latent process as indicated by the data structure. We fit a two-way crossed model with subsampling (C2s) as in Table 1, but absorb the speaker-word interaction W_ij(t) into U_ijk(t). More specifically, the observed pitch contours Y_ijk(t) is modeled as μ(t, v_ijk) + X_i(t) + Z_j(t) + U_ijk(t), where μ(t, v_ijk) is the fixed effect determined by vowel v_ijk ∈ {“ə”, “a”, “e”, “i”, “u”}, X_i(t) and Z_j(t) are two independent first-level random effects for speaker i = 1, 2, . . . , 8 and word j = 1, 2, . . . , 19, respectively. U_ijk(t) accounts for all the remaining variability such as the tone, stress and intonation of the syllables. By applying the SFPCA algorithm, we extract the PCs as shown in Figure 4.

Figure 4.

Principal components for process X_i(t), Z_j(t), and U_ijk(t) using two-way crossed model with sub-sampling (C2s) to analyze the phonetic data. The top row show the first four PCs for the speaker-specific effect X_i(t), while the second row display PCs for word effect Z_j(t). The proportion of variation explained by every principal component within each latent process is listed inside the plotting window. The estimated percentages of total variation explained by the latent processes are shown in front of the rows.

The speaker-specific deviation from the population average explains 45% of the total variation in the data, among which the majority (99.86%) is captured by the first PC that indicates equal weights over time. Similarly, PC 1 for the word-specific process Z_j(t) also stays constant over time. This is consistent with the findings in Aston et al. (2010): most of the variations across speakers or words arise from the “shift” in the average pitch level. However, instead of further modeling the overall principal scores to determine whether the “shift” is speaker- or word-dependent as in Aston et al. (2010), we can claim that ${\Phi }_1^X\left(t\right)$ corresponds to speaker heterogeneity and ${\Phi }_1^Z\left(t\right)$ accounts for word difference. Under the threshold of 99%, we only keep one PC for X_i(t), two for Z_j(t) and three for U_ijk(t). The fact that more PCs are selected to represent the features of Z_j(t) and U_ijk(t) implies greater complexity induced by the inherent word and syllables effects. To further evaluate the effects of speaker- or word-related covariates, we can conduct regression analysis specifically to principal scores of each latent process.

Furthermore, with SFPCA we can quantify the relative effect size (Shou et al., 2013) of speakers versus words based on the portion of variation explained by X_i(t) or Z_j(t) (45% vs. 12% in Figure 4), indicating that subject heterogeneity is about 3 times larger than that of word-to-word difference. In fact, it also helps us to select the current model over model μ(t, v_ijk) + X_i(t) + Z_j(t) + W_ij(t) + U_ijk(t) because the estimated variation explained by W_ij(t) is negligible compared to other latent processes. Such assessment cannot be obtained using the very interesting analysis from Aston et al. (2010), as it would require an explicit modeling of the functional space. The two approaches are complementary and should be pondered in particular applications.

5.2. Accelerometer Data

In the accelerometer study, each participant has their activity intensity values recorded for 5 days during active periods (after waking up and before bedtime), which are identified using methods developed by Bai et al. (2012). Bai et al. (2012) mainly focuses on predicting movement type based on the three-axis accelerometer records. Here we are more interested in using the same data set to assess the variability of energy expenditure in the population and from day to day. As Figure 1 indicates a periodic pattern every hour, we model the observed curves into three hierarchies: hours within days within each subject.

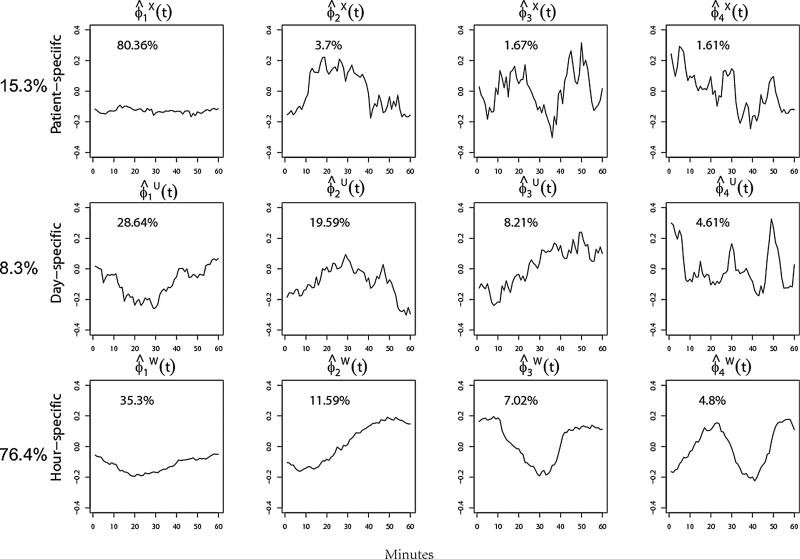
The three-way nested model (N3) is applied to decompose the variance of the data. For the original data set which contain 36,000 measurements per hour, we can implement SFPCA using methods described in Section 3.3 for high-dimensional data. However, with the interest of understanding the circadian patterns of daily activity, it is more informative to smooth the data by averaging energy expenditure within every minute and conduct SFPCA on the summarized data. For simplicity, we also truncate the observations at the end of the study that do not complete an entire hour. Therefore, there are 60 measurements for every curve with a maximum of 19 curves per day for each subject. The first four principal components for the three levels of latent processes are displayed in Figure 5. The first component for the patient-specific process X_i(t) accounts for the heterogeneity of average activity level in the population. While the remaining few demonstrate either one-peak or double-peak energy expenditure pattern within one hour. Compared to subject-specific and hour-specific effects, the day-to-day variation (8.3%) accounts for a much smaller portion of the total variability. The majority (about 76%) of the total variability is contained in the hour-to-hour heterogeneity. This indicates in a quantitative way that people follow a similar routine everyday, but their energy expenditures change dramatically within one day, depending on the type of activity they are involved in during a particular hour. The relative effect size of different processes can also be evaluated as in the previous example.

Figure 5.

Principal components for process X_i(t), U_ij(t), and W_ijk(t) using three-way nested model (N3) to analyze the accelerometer data. The proportion of variation explained by each PC component is listed in the plots. The top row show the first four PC components for the patient-specific effect X(t), the second row display results for the day-specific effect U(t) and the third row are estimated principal components for hour-specific effect W(t). The proportion of variation explained by each latent process is labeled on the left side.

6. Discussion

The defining characteristic of many functional studies is the existence of a specific structure in correlations with regard to the experimental design, which can directly affect inference. Thus, there is an increasing demand for methods that (1) respect study design; (2) model multiple levels of variation; (3) are computationally feasible in high dimensions. In response to this demand, we have introduced a class of structured functional models that include nested and crossed designs, and proposed a statistical framework, SFPCA, that analyzes these models. Given the independence assumption of latent processes, the covariance structures of the observed outcome are fully captured by the variance operators of the random processes. SFPCA is a set of efficient tools that estimate and analyze the covariance structures using a uniform protocol for all the models. It uses functional PCA for dimensionality reduction and feature extraction.

The extensive simulation studies clearly demonstrate a great potential of the methodology to recover level-specific features of the latent processes. When we apply SFPCA to two studies that collected accelerometeric and phonetic data, we are able to distinguish various layers of effects that are inherent in the data. Similar to Section 5 in Koch (1967), our methods are extendable to the cases when the covariance matrices differ across levels.

Future work should focus on developing more efficient unbiased method of moments estimators that are adaptable to unbalanced designs. The development of combined methodology that infuses both “naked” (nested/crossed) design-induced structures, with covariate-driven parts such as the one proposed in Greven et al. (2010), is an important, although challenging step in generalizing this framework. Our methodology has a few potential limitations. Two most important ones are more rigorous treatment of noise (Di et al., 2009), and possible accommodation of sparsity in the functional observations (Di, Crainiceanu and Jank, 2014).