Heritable Environmental Variance Causes Nonlinear Relationships Between Traits: Application to Birth Weight and Stillbirth of Pigs

Abstract

There is recent evidence from laboratory experiments and analysis of livestock populations that not only the phenotype itself, but also its environmental variance, is under genetic control. Little is known about the relationships between the environmental variance of one trait and mean levels of other traits, however. A genetic covariance between these is expected to lead to nonlinearity between them, for example between birth weight and survival of piglets, where animals of extreme weights have lower survival. The objectives were to derive this nonlinear relationship analytically using multiple regression and apply it to data on piglet birth weight and survival. This study provides a framework to study such nonlinear relationships caused by genetic covariance of environmental variance of one trait and the mean of the other. It is shown that positions of phenotypic and genetic optima may differ and that genetic relationships are likely to be more curvilinear than phenotypic relationships, dependent mainly on the environmental correlation between these traits. Genetic correlations may change if the population means change relative to the optimal phenotypes. Data of piglet birth weight and survival show that the presence of nonlinearity can be partly explained by the genetic covariance between environmental variance of birth weight and survival. The framework developed can be used to assess effects of artificial and natural selection on means and variances of traits and the statistical method presented can be used to estimate trade-offs between environmental variance of one trait and mean levels of others.

IN the classic model of quantitative genetics, the phenotype is assumed to be the sum of an effectively infinite number of genes and environmental effects; i.e., $P=G+E$ (Falconer and Mackay 1996; Lynch and Walsh 1998). The phenotypic variance is the sum of the genetic ($V_{\text{G}}$) and environmental ($V_{\text{E}}$) variance. It is assumed that the environmental variance is homogeneous across genotypes, but recently there is evidence from laboratory experiments and analysis of livestock populations that not only the phenotype itself, but also its $V_{\text{E}}$, is under genetic control (Hill and Mulder 2010). This might be expressed as genetic heterogeneity in the within-individual variance of a trait with repeat measurements, such as weight of individual piglets in a litter or total litter weight across parities, or as a difference in within-family variance for traits such as juvenile body weight expressed once.

The median genetic coefficient of variation for $V_{\text{E}}$ (${\text{GCV}}_{V_{\text{E}}}={\sigma }_{{\mathrm{A}}_{\text{v}}}/V_{\text{E}},$ where ${\sigma }_{{\mathrm{A}}_{\text{v}}}$ is additive genetic variance in $V_{\text{E}}$) is ∼0.3 based on a review of 14 studies with estimates of genetic variance in $V_{\text{E}}$ primarily on livestock populations (Hill and Mulder 2010). This indicates that $V_{\text{E}}$ could be increased or decreased by 30% if changed by one genetic standard deviation. These analyses were mainly based on genetic analysis of pedigreed livestock populations; but with 300 isofemale lines of Drosophila melanogaster, thereby avoiding possible confounding by within-line genetic heterogeneity, Mackay and Lyman (2005) showed a significant genetic variance in CV and $V_{\text{E}}$. In a selection experiment in rabbits, selection on estimated breeding value for $V_{\text{E}}$ of birth weight successfully changed the within-litter variability of birth weight (Garreau et al. 2008). There are more recent data on genetic control of $V_{\text{E}}$ at the level of individual loci from genome-wide association studies (see review by Geiler-Samerotte et al. 2013). Those in experimental species are very clear cut: for example, Jimenez-Gomez et al. (2011) and Nelson et al. (2013) located QTL for phenotypic variability in gene expression in Arabidopsis and yeast, respectively, and Shen et al. (2012) identified regions controlling the phenotypic variability of traits in Arabidopsis. In vertebrates, the FTO genotype was shown to be associated with phenotypic variability in body mass index in humans, with the two homozygotes differing 7% in standard deviation (SD) (Yang et al. 2012). In laying hens, a QTL region on chromosome 4 was identified that explained 30% and 16% of the genetic variance in mean and within-individual SD, respectively, of egg weight (Wolc et al. 2012); and in dairy cattle the phenotypic variability of somatic cell score, an indicator for mastitis, was shown to be determined by many loci, while that with the largest effect explained ∼3% of the genetic variance in $V_{\text{E}}$ (Mulder et al. 2013a). It has been argued that findings such as those of Yang et al. (2012) can also be explained in terms of a scale effect (Sun et al. 2013), but the extreme transformations required are not biologically plausible (Shen and Rönnegård 2013).

In agriculture, there is interest in reducing phenotypic variance to improve uniformity of animals and animal products. For instance, penalties are imposed by slaughterhouses for meat animals delivered with excessive variability because uniform products are demanded by retailers and packing efficiency of products is higher (Hennessy 2005). It has been shown both in theory (SanCristobal-Gaudy et al. 1998; Sorensen and Waagepetersen 2003; Mulder et al. 2007, 2008) and from experiment (Garreau et al. 2008) that uniformity can be increased by selection.

Before implementing selection to reduce $V_{\text{E}}$ in livestock breeding programs it is necessary to know what correlated changes in means of the target trait and other traits of interest would be expected. A particular concern is that animals with small $V_{\text{E}}$ would not have the capacity to react to unpredictable environments, i.e., have reduced plasticity. There is some evidence that plasticity and $V_{\text{E}}$ are positively correlated, i.e., that genotypes with higher $V_{\text{E}}$ have higher plasticity (Mulder et al. 2013b; Tonsor et al. 2013). Whether plastic genotypes with high $V_{\text{E}}$ or stable genotypes with small $V_{\text{E}}$ are better capable of handling unpredictable environments is under debate. In livestock little is known about trade-offs between $V_{\text{E}}$ and means of other traits, except that uniformity of birth weight in litter-bearing animals does increase the survival of the offspring, e.g., in pigs (Kapell et al. 2011) and rabbits (Garreau et al. 2008).

Genetic variation in $V_{\text{E}}$ of a trait has been shown analytically to lead to a nonlinear relationship between the breeding value of $V_{\text{E}}$ and the phenotypic deviation from the mean (Mulder et al. 2007). Therefore, if there is a genetic correlation between the mean of one trait and $V_{\text{E}}$ of another, which we term an M-V genetic correlation between traits, the phenotypic relationship between them is expected to be nonlinear. Nonlinear parent–offspring regression and nonlinear regression of one trait on another within half-sib groups have been employed to explore nonlinearity between traits by Sölkner and Fuerst-Waltl (1996) and Fuerst-Waltl et al. (1997, 1998), who assumed this was caused by nonlinearity between additive genetic effects of different traits. They also showed that phenotypic relationships were often more linear than the genetic relationships due to dilution with environmental covariance. Nonlinear relationships might also be expected when one of the traits, for example fitness, has an optimum value (Lande and Arnold 1983; Falconer and Mackay 1996; Kingsolver et al. 2001, 2012). Such nonlinear relationships are often observed or hypothesized in natural populations, typically as “fitness profiles” between trait values and fitness (e.g., Falconer and Mackay 1996) that show whether phenotypes on one side of the distribution (directional), in the middle (stabilizing), or at extremes (disruptive) have highest fitness. If there is an optimum phenotype, a maximum would imply a negative covariance between $V_{\text{E}}$ and fitness; i.e., families with small variance would have selective advantage if there is stabilizing selection, and correspondingly families with a large variance would have an advantage if there is disruptive or strong directional selection (Hill and Zhang 2004; Mulder et al. 2007). Examples of nonlinear trait relationships include that between birth weight and survival of infants in humans in historic data when medical care was less optimized (Karn and Penrose 1951 in Schluter 1988), survival and size in house sparrows (Schluter and Smith 1986; Schluter 1988), and between litter size and birth weight in piglets (Varona and Sorensen 2014). These nonlinear relationships might be due in part to a nonnormality of at least one of the traits such as survival (binomial). To our knowledge no studies have yet been undertaken of the degree to which nonlinearity between traits is caused by an M-V genetic correlation between them. It is possible that low $V_{\text{E}}$ may yield better fitness in some environments (a conservative bet-hedging strategy) or high $V_{\text{E}}$ in others (a coin-flipping strategy) (Olofsson et al. 2009). Therefore, while insight into the nonlinear relationships between traits should increase understanding of the existence and if so of the position of phenotypic and genetic optima, no framework is available to study the role of M-V genetic correlations between traits and the consequent effects of selection.

The objectives this article are to (1) derive mathematically nonlinear relationships between traits when one exhibits genetic variance in $V_{\text{E}}$, (2) predict responses to selection in mean and variance of both traits, (3) predict genetic and phenotypic optima, (4) predict changes in genetic parameters consequent on selection shifting the population mean toward the fitness optimum, and (5) investigate the relationship between piglet birth weight and survival in pigs as a practical application of the theory. We assumed multivariate normality for deriving the expressions, whereas survival is binomially distributed. Therefore, we extended the predictions toward assuming that survival has an underlying normal distribution and predictions can be transformed to the observed binomial scale.

Quantitative Genetic Model

Consider two traits for which the phenotypic deviations from the mean are the sum of additive genetic and environmental effects, with no dominance or epistasis (Falconer and Mackay 1996). The first trait, with phenotypic value $P_1$, is also subject to additive genetic differences in its environmental variance, so-called genetic heterogeneity of environmental variance (SanCristobal-Gaudy et al. 1998), whereas the second trait (phenotypic value $P_2$) has homogeneous environmental variance. Here we assume the exponential model for environmental variance (SanCristobal-Gaudy et al. 1998; Hill and Mulder 2010), because of its statistical tractability, as the environmental variance cannot be negative and the model appears linear on the log scale. Different models to model genetic differences in environmental variance appear similar when genetic variance in $V_{\text{E}}$ is small. Further discussion and comparison of models for genetic analysis of the environmental variance are given elsewhere (Hill and Mulder 2010). The genetic model is

$${\mathit{P}}_1={\mu }_1+{\mathit{A}}_{\mathit{m},1}+{\mathit{E}}_1={\mu }_1+{\mathit{A}}_{\mathit{m},1}+\chi \exp \left[\frac{1}{2}\left(\text{ln}\left({\sigma }_{{\mathit{e}}_1}^2\right)+{\mathit{A}}_{\mathit{v},1}\right)\right]$$ (1)

$$P_2={\mu }_2+A_{m,2}+E_2,$$ (2)

where ${\mu }_i$ is the population mean, $A_{m,i}$ is the breeding value, and $E_i$ is the environmental deviation for trait i. The environmental variance for trait 2 is assumed constant, ${\sigma }_{e_2}^2,$ whereas ${\sigma }_{e_1}^2$ is the expected environmental variance for trait 1 when $A_{v,1}=0,$ but varies among individuals according to their breeding value $A_{v,1}.$ The standard normal deviate χ is the standardized environmental deviation for trait 1. The breeding values $A_{m,1},$ $A_{v,1},$ and $A_{m,2}$ are assumed to be the sum of effects of an infinite number of additive loci and are multivariate normally distributed,

$$\left[\begin{array}{c}{\mathit{A}}_{\mathit{m},1}\\ {\mathit{A}}_{\mathit{v},1}\\ {\mathit{A}}_{\mathit{m},2}\end{array}\right]\sim \mathit{N}\left(\begin{array}{c}0\\ 0\\ 0\end{array},\left[\begin{array}{ccc}{\sigma }_{{\mathit{A}}_{\mathit{m},1}}^2& {\mathit{cov}}_{{\mathit{A}}_{\mathit{m},1},{\mathit{A}}_{\mathit{v},1}}& {\mathit{cov}}_{{\mathit{A}}_{\mathit{m},1},{\mathit{A}}_{\mathit{m},2}}\\ & {\sigma }_{{\mathit{A}}_{\mathit{v},1}}^2& {\mathit{cov}}_{{\mathit{A}}_{\mathit{v},1},{\mathit{A}}_{\mathit{m},2}}\\ \text{symmetric}& & {\sigma }_{{\mathit{A}}_{\mathit{m},2}}^2\end{array}\right]\otimes \mathbf{A}\right),$$

where A is the additive genetic or numerator relationship matrix; ${\sigma }_{{\mathit{A}}_{\mathit{m},1}}^2,$${\sigma }_{{\mathit{A}}_{\mathit{v},1}}^2,$ and ${\sigma }_{{\mathit{A}}_{\mathit{m},2}}^2$ are the additive genetic variances in ${\mathit{A}}_{\mathit{m},1},$ ${\mathit{A}}_{\mathit{v},1},$ and ${\mathit{A}}_{\mathit{m},2};$ and ${\mathit{cov}}_{{\mathit{A}}_{\mathit{m},1},{\mathit{A}}_{\mathit{v},1}},$ ${\mathit{cov}}_{{\mathit{A}}_{\mathit{m},1},{\mathit{A}}_{m,2}},$ and ${\mathit{cov}}_{{\mathit{A}}_{\mathit{v},1},{\mathit{A}}_{\mathit{m},2}}$ are the corresponding additive genetic covariances. The environmental effects ${\mathit{E}}_1\left(=\chi \exp \left[(1/2)\left(\text{ln}\left({\sigma }_{{\mathit{e}}_1}^2\right)+{\mathit{A}}_{\mathit{v},1}\right)\right]\right)$ and ${\mathit{E}}_2$ are bivariate normally distributed,

$$\left[\begin{array}{c}{\mathit{E}}_1\\ {\mathit{E}}_2\end{array}\right]\sim \mathit{N}\left(\begin{array}{c}0\\ 0\end{array},\left[\begin{array}{cc}{\sigma }_{{\mathit{e}}_1}^2\exp \left({\mathit{A}}_{\mathit{v},1}\right)& {\mathit{r}}_{\mathit{e}}{\sigma }_{{\mathit{e}}_1}\exp \left(\frac{1}{2}{\mathit{A}}_{\mathit{v},1}\right){\sigma }_{{\mathit{e}}_2}\\ \text{symmetric}& {\sigma }_{{\mathit{e}}_2}^2{}_{}^{}\end{array}\right]\right),$$

where ${\sigma }_{e_2}^2$ is the environmental variance of trait 2 and $r_e$ is the environmental correlation.

Methodological Framework for Nonlinear Relationships

Multiple-regression framework

We used a multiple-regression framework to predict the nonlinear relationship between traits caused by M-V genetic correlations between them and to predict responses in mean and variance due to selection, following the methodology of Mulder et al. (2007). In Mulder et al. (2007), breeding values and selection responses for mean and variance were predicted using linear, quadratic, and cubic regression on the phenotypic deviation of an individual phenotype. This methodology formally requires multivariate normality, which holds only approximately because genetic variance in $V_{\text{E}}$ for $P_1$ causes small deviations from normality (Mulder et al. 2007). We also used selection index theory (Hazel 1943), which is essentially an application of multiple regression assuming that fixed effects are known without error.

Monte Carlo simulation

To check the accuracy of derived relationships and predicted responses to selection, we simulated 1000 replicates each with 1 million animals according to the genetic models in Equations 1 and 2 and calculated the expected value of trait 2 given trait 1 by calculating the average $P_2$ given $P_1$ within 601 successive intervals of 0.01${\sigma }_{P,1}$ between −3 and 3${\sigma }_{P,1}.$ Selection responses to directional mass selection on $P_1$ and $P_2$ were calculated as the mean $A_{m,1},$ $A_{v,1},$ and $A_{m,2}$ of all selected animals with $P\ge x$ in each replicate and averaged over replicates, where x is the truncation point.

Deriving the phenotypic relationship between P₂ and P₁

The phenotypic relationship between $P_2$ and $P_1$ was derived as the multiple regression of $P_2$ on $P_1$ and $P_1^2,$ because genetic variance in $V_{\text{E}}$ causes genetic variance in $P_1^2$ (Mulder et al. 2007). The regression can be written as

$$\mathrm{E}(P_2|P_1,P_1^2)=b_1{P}_1+b_2{P}_1^2,$$ (3)

where

$$\left[\begin{array}{c}{\mathit{b}}_1\\ {\mathit{b}}_2\end{array}\right]=P^{-1}c,$$ (4)

$$P=\left[\begin{array}{cc}\text{var}\left({\mathit{P}}_1\right)& \text{cov}\left({\mathit{P}}_1,{\mathit{P}}_1^2\right)\\ \text{cov}\left({\mathit{P}}_1,{\mathit{P}}_1^2\right)& \text{var}\left({\mathit{P}}_1^2\right)\end{array}\right],$$

and

$$c=\left[\begin{array}{c}\text{cov}\left({\mathit{P}}_2,{\mathit{P}}_1\right)\\ \text{cov}\left({\mathit{P}}_2,{\mathit{P}}_1^2\right)\end{array}\right].$$

The elements of P and c were derived using the higher-order moments of the normal distribution (Stuart and Ord 1994) and using the laws of total (co)variance and standard variance–covariance rules (see Appendix A for full derivations),

$$\text{var}\left(P_1\right)={\sigma }_{A_{m,1}}^2+{\sigma }_{e_1}^2\exp \left(\frac{1}{2}{\sigma }_{A_{v,1}}^2\right)={\sigma }_{P_1}^2$$ (5)

$$\text{cov}\left(P_1,P_1^2\right)=3{\mathit{cov}}_{A_{m,1},A_{v,1}}{\sigma }_{e_1}^2\exp \left(\frac{1}{2}{\sigma }_{A_{v,1}}^2\right)$$ (6)

$$\begin{array}{l}\text{var}\left(P_1^2\right)=2{\sigma }_{P_1}^4+6{\mathit{cov}}_{A_{m,1},A_{v,1}}^2{\sigma }_{e_1}^2\exp \left(\frac{1}{2}{\sigma }_{A_{v,1}}^2\right)\\ +3{\sigma }_{e_1}^4\exp \left({\sigma }_{A_{v,1}}^2\right)\left(\exp \left({\sigma }_{A_{v,1}}^2\right)-1\right)\end{array}$$ (7)

$$\text{cov}\left(P_2,P_1\right)=co{v}_{A_{m,1},A_{m,2}}^{}+co{v}_{e_1{e}_2}^{}$$ (8)

$$\text{cov}\left(P_2,P_1^2\right)= {\mathit{cov}}_{A_{v,1},A_{m,2}}^{}{\sigma }_{e_1}^2\exp \left(\frac{1}{2}{\sigma }_{A_{v,1}}^2\right)+{\mathit{cov}}_{e_1{e}_2}^{}{\mathit{cov}}_{A_{m,1},A_{v,1}},$$ (9)

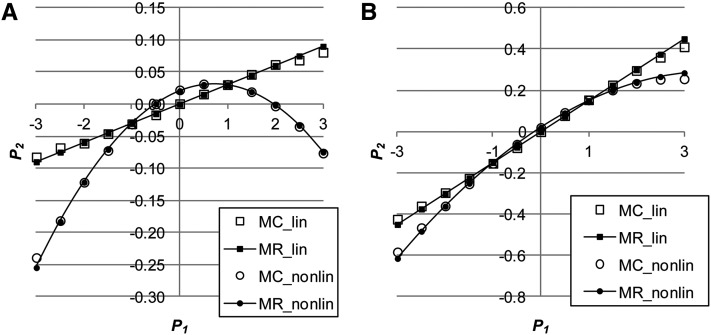
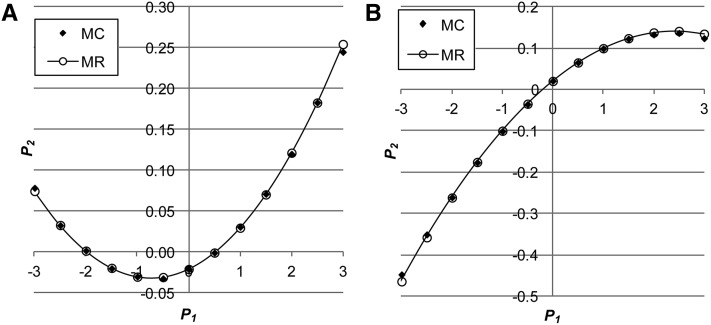
where ${\mathit{cov}}_{e_1{e}_2}^{}=r_e{\sigma }_{e_1}^{}\exp \left((1/4){\sigma }_{A_{v,1}}^2\right){\sigma }_{e_2}.$ Note that Equation 3 is about the relationship between single observations of $P_2$ and $P_1.$ In Equation 7, the two rightmost terms are related to the skewness (Equation 6) and kurtosis of the distribution, respectively. All elements of P and c (equal to Equations 5–9) were checked using Monte Carlo simulation. The multiple-regression prediction of $P_2$ from $P_1$ shows very good agreement with the Monte Carlo simulation (Figure 1 and Figure 2), with R² > 0.995 for all cases evaluated. Appendix C shows a natural extension to multiple random effects, such as permanent and common environmental effects.

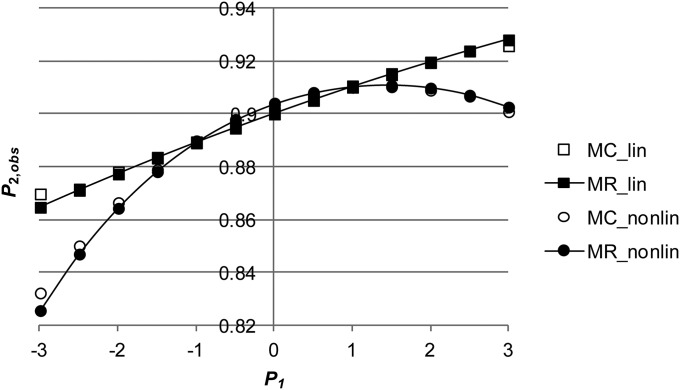
Figure 1.

(A and B) The relationship between $P_2$ and $P_1$ either assuming no genetic correlation ($r_{A_{v,1},A_{m,2}}=0$) between environmental variance in $P_1$ and the mean of $P_2$ using Monte Carlo simulation (MC_lin) and multiple regression (MR_lin) or assuming a negative genetic correlation ($r_{A_{v,1},A_{m,2}}=-0.5$) between them (MC_nonlin, MR_nonlin) when $r_{A_{m,1},A_{m,2}}=0.1$ (A) or when $r_{A_{m,1},A_{m,2}}=0.5$ (B) (${\sigma }_{A_{m,1}}^2={\sigma }_{A_{m,2}}^2=0.3,{\sigma }_{A_{v,1}}^2=0.05,{\sigma }_{e_1}^2\text{exp}\left(\left(1/2\right){\sigma }_{A_{v,1}}^2\right)=0.7,$ ${\sigma }_{e_2}^2=0.7,$ $r_{A_{m,1},A_{m,2}}=0.1,$ $r_{A_{m,1},A_{v,1}}=0,$ $r_e=0$).

Figure 2.

(A and B) The relationship between $P_2$ and $P_1,$ using Monte Carlo simulation (MC) and multiple regression (MR) either with positive genetic correlation (A: $r_{A_{v,1},A_{m,2}}=0.5,$$r_e=0$) between environmental variance in $P_1$ and the mean of $P_2$ or with negative genetic correlation (B: when $r_{A_{v,1},A_{m,2}}=-0.5,$$r_e=0.1$) (${\sigma }_{A_{m,1}}^2={\sigma }_{A_{m,2}}^2=0.3,{\sigma }_{A_{v,1}}^2=0.05,{\sigma }_{e_1}^2\text{exp}\left(\left(1/2\right){\sigma }_{A_{v,1}}^2\right)=0.7$, ${\sigma }_{e_2}^2=0.7,$ $r_{A_{m,1},A_{m,2}}=0.1,$ $r_{A_{m,1},A_{v,1}}=0$).

Deriving response to mass selection

Deterministic predictions:

Response to selection (R) is predicted as the mean deviation of offspring from the population mean regressed on the selection differential of the parents $\mathit{R}=\mathit{bS},$ which is equal to the regression of the breeding value (A) on the selection differential (S) $\mathrm{\Delta }\mathit{A}=\mathit{bS}$ (Falconer and Mackay 1996). We showed previously that response to selection in ${\mathit{A}}_{\mathit{m},1}$ and ${\mathit{A}}_{\mathit{v},1}$ could be predicted for different kinds of mass selection, e.g., directional, stabilizing, or disruptive (Mulder et al. 2007). Here we extend this framework to the correlated responses in (1) ${\mathit{P}}_2$ from mass selection on ${\mathit{P}}_1$ and (2) ${\mathit{A}}_{\mathit{m},1}$ and ${\mathit{A}}_{\mathit{v},1}$ from mass selection on ${\mathit{P}}_2.$ In both cases, the general equation to predict selection responses in

$$\mathrm{\Delta }\mathbf{a}=\left[\begin{array}{c}\mathrm{\Delta }{\mathit{A}}_{\mathit{m},1}\\ \mathrm{\Delta }{\mathit{A}}_{\mathit{v},1}\\ \mathrm{\Delta }{\mathit{A}}_{\mathit{m},2}\end{array}\right]$$

in terms of selection differentials $\left(\mathrm{\Delta }\mathbf{x}\right)$ is

$$\mathrm{\Delta }a=P^{\mathbf{-1}}G\mathrm{\Delta }x=B^{\prime }\mathrm{\Delta }x,$$ (10)

where P is the variance–covariance matrix among selection differentials in $\mathrm{\Delta }\mathbf{x}$, because selection differentials are random variables under the quantitative genetic model assumed; G is the covariance matrix between $\mathrm{\Delta }\mathbf{a}$ and $\mathrm{\Delta }\mathbf{x}$; and B is a matrix of regression coefficients. First, if mass selection on ${\mathit{P}}_1$ is performed, then the selection differentials on ${\mathit{P}}_1$ and ${\mathit{P}}_1^2$ are

$$\mathrm{\Delta }\mathbf{x}=\left[\begin{array}{c}\overline{{\mathit{P}}_{1\mathrm{,}\mathit{s}}}-{\mu }_1\\ \overline{{\mathit{P}}_{1,s}^2}-{\sigma }_{{\mathit{P}}_1}^2\end{array}\right]=\left[\begin{array}{c}\overline{{\mathit{P}}_{1,\mathit{s}}}-\mathrm{E}\left({\mathit{P}}_1\right)\\ \overline{{\left({\mathit{P}}_{1,\mathit{s}}-\mathrm{E}\left({\mathit{P}}_1\right)\right)}^2}-\mathrm{E}\left\{{\left({\mathit{P}}_1-\mathrm{E}\left({\mathit{P}}_1\right)\right)}^2\right\}\end{array}\right].$$ (11)

If it is assumed that ${\mu }_1=0,$

$$\left[\begin{array}{c}\mathrm{\Delta }{\mathit{A}}_{\mathit{m},1}\\ \mathrm{\Delta }{\mathit{A}}_{\mathit{v},1}\\ \mathrm{\Delta }{\mathit{A}}_{\mathit{m},2}\end{array}\right]={B^{\prime }}_{P_1}\left[\begin{array}{c}\overline{{\mathit{P}}_{1\mathrm{,}\mathit{s}}}\\ \overline{{\mathit{P}}_{1,\mathit{s}}^2}-{\sigma }_{{\mathit{P}}_1}^2\end{array}\right]={B^{\prime }}_{P_1}\left[\begin{array}{c}\mathit{i}{\sigma }_{{\mathit{P}}_1}\\ \mathit{ix}{\sigma }_{{\mathit{P}}_1}^2\end{array}\right],$$ (12)

where ${B^{\prime }}_{P_1}$ is the transpose of $B_{P_1}=P^{-1}{G}_{P_1},$ P is the same as in Equation 3, and

$$\begin{array}{l}{G}_{P_1}\\ =\left[\begin{array}{ccc}{\sigma }_{{\mathit{A}}_{\mathit{m},1}}^2& {\mathit{cov}}_{{\mathit{A}}_{\mathit{m},1},{\mathit{A}}_{\mathit{v},1}}& {\mathit{cov}}_{{\mathit{A}}_{\mathit{m},1}{\mathit{A}}_{\mathit{m},2}}\\ {\mathit{cov}}_{{\mathit{A}}_{\mathit{m},1},{\mathit{A}}_{\mathit{v},1}}{\sigma }_{{\mathit{e}}_1}^2\exp \left(\frac{1}{2}{\sigma }_{{\mathit{A}}_{\mathit{v},1}}^2\right)& {\sigma }_{{\mathit{A}}_{\mathit{v},1}}^2{\sigma }_{{\mathit{e}}_1}^2\exp \left(\frac{1}{2}{\sigma }_{{\mathit{A}}_{\mathit{v},1}}^2\right)& {\mathit{cov}}_{{\mathit{A}}_{\mathit{v},1}{\mathit{A}}_{\mathit{m},2}}{\sigma }_{e_1}^2\text{exp}\left(\frac{1}{2}{\sigma }_{{\mathit{A}}_{\mathit{v},1}}^2\right)\end{array}\right],\end{array}$$

i.e., the covariance matrix between

$$\left[\begin{array}{c}\overline{{\mathit{P}}_{1,\mathit{s}}}\\ \overline{{\mathit{P}}_{1,\mathit{s}}^2}-{\sigma }_{{\mathit{P}}_1}^2\end{array}\right]\hspace{1em}\text{and}\hspace{1em}\left[\begin{array}{c}\mathrm{\Delta }{\mathit{A}}_{\mathit{m},1}\\ \mathrm{\Delta }{\mathit{A}}_{\mathit{v},1}\\ \mathrm{\Delta }{\mathit{A}}_{\mathit{m},2}\end{array}\right],$$

i is the selection intensity when selecting the best p animals, and x is the truncation point corresponding to p based on a normal distribution (Mulder et al. 2007).

Second, if mass selection is on ${\mathit{P}}_2,$ Equation 10 becomes

$$\left[\begin{array}{c}\mathrm{\Delta }{\mathit{A}}_{\mathit{m},1}\\ \mathrm{\Delta }{\mathit{A}}_{\mathit{v},1}\\ \mathrm{\Delta }{\mathit{A}}_{\mathit{m},2}\end{array}\right]={{\mathrm{b}}^{\prime }}_{P_2}\left[\overline{{\mathit{P}}_{2,\mathit{s}}}\right]={{\mathrm{b}}^{\prime }}_{P_2}i{\sigma }_{P_2}$$ (13)

where $b_{P_2}=\mathrm{var}{\left({\mathit{P}}_2\right)}^{-1}{g}_{P_2}$ and $g_{P_2}=\left[\begin{array}{c}{\mathit{cov}}_{{\mathit{A}}_{\mathit{m},1}{\mathit{A}}_{\mathit{m},2}}{\mathit{cov}}_{{\mathit{A}}_{\mathit{v},1}{\mathit{A}}_{\mathit{m},2}}{\sigma }_{{\mathit{e}}_1}^2\text{exp}\left((1/2){\sigma }_{{\mathit{A}}_{\mathit{v},1}}^2\right){\sigma }_{{\mathit{A}}_{\mathit{m},2}}^2\end{array}\right],$ the covariance vector between $\overline{{\mathit{P}}_{2,\mathit{s}}}$ and

$$\left[\begin{array}{c}\mathrm{\Delta }{\mathit{A}}_{\mathit{m},1}\\ \mathrm{\Delta }{\mathit{A}}_{\mathit{v},1}\\ \mathrm{\Delta }{\mathit{A}}_{\mathit{m},2}\end{array}\right].$$

Evaluation of predictions:

Genetic selection differentials in $A_{m,1},$ $A_{v,1},$ and $A_{m,2}$ with directional mass selection on either $P_1$ (Equation 12) or $P_2$ (Equation 13) were shown by Monte Carlo simulation to be very accurately predicted, with differences only at the third decimal (Table 1). Correlated responses in both $A_{v,1}$ and $A_{m,2}$ are expected following mass selection on P₁, even if genetic correlations between $A_{m,1}$ and $A_{v,1}$ or $A_{m,2}$ are zero, provided that the genetic correlation between $A_{v,1}$ and $A_{m,2}$ is nonzero. This is because, with strong directional selection (e.g., P ≥ 20%), animals with higher $A_{v,1}$ (i.e., environmental variance in $P_1$) have a higher probability of selection (Hill and Zhang 2004; Mulder et al. 2007). In other words, with directional selection genotypes with a higher variance are more likely to be parents of the next generation than genotypes with a low variance.

Table 1. Genetic selection differentials in $A_{m,1},$ $A_{v,1},$ and $A_{m,2}$ when selecting on $P_1$ or on $P_2$ for different selected proportions (p) and when $r_{A_{m,1},A_{v,1}}$ and $r_{A_{m,1},A_{m,2}}$ are the same (0 or 0.5).

			$A_{m,1}$		$A_{v,1}$		$A_{m,2}$
Selection	$r_{A_{m,1},A_{v,1}}=r_{A_{m,1},A_{m,2}}$	p	MR	MC	MR	MC	MR	MC
$P_1$	0	0.80	0.105	0.105	−0.005	−0.005	0.006	0.006
		0.50	0.239	0.242	0.000	0.000	0.000	0.000
		0.20	0.420	0.421	0.020	0.020	−0.024	−0.025
	0.5	0.80	0.104	0.103	0.017	0.017	0.063	0.061
		0.50	0.239	0.241	0.048	0.049	0.123	0.121
		0.20	0.422	0.430	0.099	0.102	0.180	0.179
$P_2$	0	0.80	0.000	0.000	−0.021	−0.021	0.105	0.105
		0.50	0.000	0.000	−0.049	−0.049	0.239	0.239
		0.20	0.000	0.000	−0.086	−0.086	0.420	0.420
	0.5	0.80	0.052	0.052	−0.021	−0.021	0.105	0.105
		0.50	0.120	0.120	−0.049	−0.049	0.239	0.239
		0.20	0.210	0.210	−0.086	−0.086	0.420	0.420

Values were obtained analytically [multiple regression (MR): Equations 12 and 13] and with Monte Carlo simulation (MC) (${\sigma }_{A_{m,1}}^2={\sigma }_{A_{m,2}}^2=0.3, {\sigma }_{A_{v,1}}^2=0.05,{\sigma }_{e_1}^2\text{exp}\left(\left(1/2\right){\sigma }_{A_{v,1}}^2\right)=0.7,$ ${\sigma }_{e_2}^2=0.7,$ $r_{A_{v,1},A_{m,2}}=-0.5,$ $r_e=0$).

Response to selection on estimated breeding value

In animal breeding, selection is often on predicted breeding values rather than on raw phenotypes. For instance, if the breeding goal is to increase trait 2, then the predicted breeding value ${\widehat{A}}_{m,2}$ using information of $P_1$ and $P_1^2$ is

$${\widehat{A}}_{\mathit{m},2}={{\mathrm{b}}^{\prime }}_{{\mathit{a}}_2}\left[\begin{array}{c}{\mathit{P}}_1-{\mu }_1\\ {\mathit{P}}_1^2-{\sigma }_{{\mathit{P}}_1}^2\end{array}\right],$$ (14)

where ${\mathrm{b}}_{{\mathit{a}}_2}=P^{\mathbf{-1}}{g}_{{\mathit{a}}_2},$ P is given in Equation 3, and

$$g_{{\mathit{a}}_2}=\left[\begin{array}{c}{\mathit{cov}}_{{\mathit{A}}_{\mathit{m},1},{\mathit{A}}_{\mathit{m},2}}\\ {\mathit{cov}}_{{\mathit{A}}_{\mathit{v},1},{\mathit{A}}_{\mathit{m},2}}{\sigma }_{{\mathit{e}}_1}^2\text{exp}\left(\frac{1}{2}{\sigma }_{{\mathit{A}}_{\mathit{v},1}}^2\right)\end{array}\right].$$

The expected response to selection would be equal to that using the generalized form of the breeders equation (Hazel 1943):

$$\mathrm{\Delta }{\mathit{A}}_{\mathit{m},2}=\frac{\mathit{i}{{\mathrm{b}}^{\prime }}_{{\mathit{a}}_2}{\mathrm{g}}_{{\mathit{a}}_2}}{\sqrt{{{\mathrm{b}}^{\prime }}_{{\mathit{a}}_2}{P}^{\mathbf{-1}}{\mathrm{b}}_{{\mathit{a}}_2}}}.$$ (15)

An alternative to using squared phenotypic deviations is to use squared residuals of $P_1$ corrected for its leverage (l), which is the diagonal element of the “hat matrix” for each observation (Hoaglin and Welsh 1978) as used in the double-hierarchical generalized linear model (DHGLM) (Rönnegård et al. 2010):

$$\frac{{\mathit{e}}_1^2}{\left(1-\mathit{l}\right)}=\frac{\left[{\left(\left(1-{\mathit{b}}_{{\mathit{A}}_{\mathit{m},1}}\right){\mathit{P}}_1\right)}^2\right]}{\left[1-\mathit{l}\right]}.$$ (16)

In the absence of any fixed effects, $1-l=1-b_{A_{m,1}},$ Equation 16 reduces to $e_1^2/\left(1-l\right)=\left(1-b_{A_{m,1}}\right)P_1^2 \text{and}$

$${\widehat{A}}_{\mathit{m},2}={{\mathrm{b}}^{\prime }}_{{\mathit{a}}_2\mathit{e}}\left[\begin{array}{c}{\mathit{P}}_1\\ {\mathit{e}}_1^2/\left(1-\mathit{l}\right)\end{array}\right],$$ (17)

where $b_{{\mathit{a}}_2\mathit{e}}=P_{\mathit{e}}^{-1}{g}_{{\mathit{a}}_2\mathit{e}},$

$$P_e=\left[\begin{array}{cc}\text{var}\left({\mathit{P}}_1\right)& \text{cov}\left({\mathit{P}}_1,{\mathit{e}}_1^2/\left(1-\mathit{l}\right)\right)\\ \text{cov}\left({\mathit{P}}_1,{\mathit{e}}_1^2/\left(1-\mathit{l}\right)\right)& \text{var}\left({\mathit{e}}_1^2/\left(1-\mathit{l}\right)\right)\end{array}\right]=WPW,$$

and $g_{{\mathit{a}}_2\mathit{e}}=W{g}_{{\mathit{a}}_2},$ where

$$W=\left[\begin{array}{cc}1& 0\\ 0& \left(1-{\mathit{b}}_{{\mathit{A}}_{\mathit{m},1}}\right)\end{array}\right]$$

(see derivation in Appendix B). Use of either ${\mathit{P}}_1^2$ or ${\mathit{e}}_1^2/\left(1-\mathit{l}\right)$ would yield identical accuracy of prediction ${\widehat{A}}_{\mathit{m},2}$ and of response to selection $\mathrm{\Delta }{\mathit{A}}_{\mathit{m},2}$ in this case where only their own phenotypes provide information and there are no fixed effects; otherwise squared residuals corrected for leverages are expected to give higher accuracy and response than using squared phenotypic deviations.

Determining whether the parabola have a maximum or a minimum

The multiple-regression Equation 3 is quadratic and therefore has a parabolic shape. Such quadratic relationships may indicate a biological optimum, for instance birth weight and survival in humans prior to modern medical intervention (Karn and Penrose 1951 in Schluter 1988). Expressions for $b_1$ and $b_2$ (from Equation 3) are given by

$${\mathit{b}}_1=\frac{\left[\text{var}\left({\mathit{P}}_1^2\right){\mathit{c}}_1-\mathrm{cov}\left({\mathit{P}}_1,{\mathit{P}}_1^2\right){\mathit{c}}_2\right]}{\text{det}\left(P\right)}$$ (18)

$${\mathit{b}}_2=\frac{\left[-\text{cov}\left({\mathit{P}}_1,{\mathit{P}}_1^2\right){\mathit{c}}_1+\text{var}\left({\mathit{P}}_1\right){\mathit{c}}_2\right]}{\text{det}\left(P\right)},$$ (19)

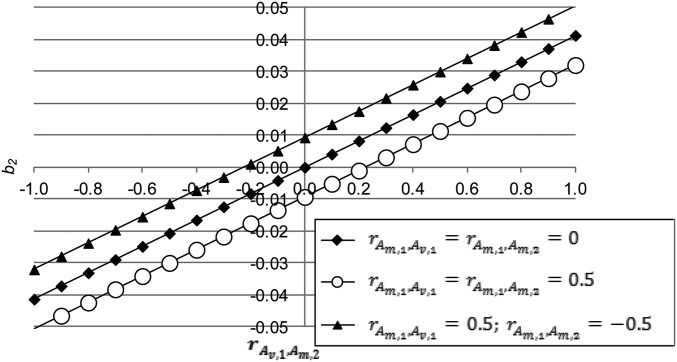
where $c_1=\text{cov}\left(P_2,P_1\right)$ (Equation 8) and $c_2=\text{cov}\left(P_2,P_1^2\right)$ (Equation 9) and P is shown below Equation 4. Whether there is a maximum or a minimum depends on the sign of the quadratic regression coefficient ($b_2$), i.e., $P_1^2.$ If $b_2>0,$ it has a minimum and if $b_2<0,$ it has a maximum. The sign of the regression coefficient depends on multiple parameters (Equations 18 and 19). As Figure 3 shows, $b_2$ is linear in $r_{A_{v,1},A_{m,2}}$ because it is a linear function of $c_2$ (Equation 19) and $c_2$ is the genetic covariance between $A_{v,1}$ and $A_{m,2}.$ When $r_{A_{v,1},A_{m,2}}=0$ and other correlations are zero, $b_2=0,$ i.e., when the straight-line relationship between $P_2$ and $P_1$ passes through (0, 0). If other correlations are nonzero, $b_2=0$ shifts to a point dependent mainly on $r_{A_{v,1},A_{m,2}},$ with other parameters having less influence on $b_2.$ In summary, a moderate to strong negative M-V genetic correlation between traits ($r_{A_{v,1},A_{m,2}}$) yields a parabola with a maximum, e.g., animals with phenotypes close to the optimum have maximum fitness, a fitness optimum; while a moderate to strong positive genetic correlation yields one with a minimum; e.g., animals with phenotypes largely deviating from the minimum have the highest fitness.

Figure 3.

The quadratic regression coefficient $b_2$ as a function of the genetic correlation $r_{A_{v,1},A_{m,2}}$ for different values of $r_{A_{m,1},A_{v,1}}$ and $r_{A_{m,1},A_{m,2}}$ (${\sigma }_{A_{m,1}}^2={\sigma }_{A_{m,2}}^2=0.3,{\sigma }_{A_{v,1}}^2=0.05,{\sigma }_{e_1}^2\text{exp}\left(\left(1/2\right){\sigma }_{A_{v,1}}^2\right)=0.7,$ ${\sigma }_{e_2}^2=0.7,$ $r_e=0$).

Similarly, Equation 14 shows whether the genetic parabola has a maximum or a minimum. The regression coefficients now are

$${\mathit{b}}_{{\mathit{a}}_{2}1}=\frac{\left[\text{var}\left({\mathit{P}}_1^2\right){\mathit{g}}_{{\mathit{a}}_{2}1}-\text{cov}\left({\mathit{P}}_1,{\mathit{P}}_1^2\right){\mathit{g}}_{{\mathit{a}}_{2}2}\right]}{\text{det}\left(P\right)}$$ (20)

$${\mathit{b}}_{{\mathit{a}}_{2}2}=\frac{\left[-\text{cov}\left({\mathit{P}}_1,{\mathit{P}}_1^2\right){\mathit{g}}_{{\mathit{a}}_{2}1}+{\sigma }_{{\mathit{P}}_1}^2{\mathit{g}}_{{\mathit{a}}_{2}2}\right]}{\text{det}\left(P\right)},$$ (21)

where $g_{{\mathit{a}}_{2}1}$ and $g_{{\mathit{a}}_{2}2}$ are the elements of $g_{{\mathit{a}}_2}$ (just below Equation 14). Equations 20 and 21 differ from Equations 18 and 19 only in $g_{{\mathit{a}}_{2}1}$ and $g_{{\mathit{a}}_{2}2}.$ If $r_e=0,$ then $g_{{\mathit{a}}_{2}1}=c_1$ and $g_{{\mathit{a}}_{2}2}=c_2$ and consequently $b_{{\mathit{a}}_{2}1}=b_1$ and $b_{{\mathit{a}}_{2}2}=b_2.$

Can phenotypic and genetic parabolas have different shapes?

The interest here is in whether there are conditions when the phenotypic parabola has a maximum and the genetic parabola a minimum or vice versa. Because $r_e$ affects only the phenotypic parabola, it determines the relative shapes of the parabolas, and so it is helpful to calculate the magnitude of $r_e$ when $b_2=0$ and switches to a different sign than that of $b_{{\mathit{a}}_{2}2}.$ The most obvious situation is when the environmental correlation $r_e$ and the genetic correlation $r_{A_{m,1},A_{m,2}}$ have opposite signs, but $b_2=0$only when ${\mathit{cov}}_{A_{m,1},A_{v,1}}\ne 0.$ Calculations show that, for the parabolas to be of different shape, $r_e$ has to be strong, in which case the regression is almost linear. So in practice, parabolas of opposite sign are likely to occur only rarely, if at all.

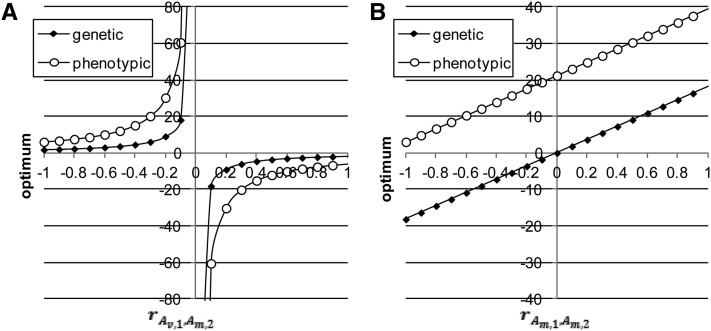
Determining the phenotypic and genetic stationary points

The maximum (minimum) phenotype $P_2$ can be found at the stationary point of $P_1$ ($P_{1_{\text{stat}}}$). The stationary point is mathematically the point where the first derivative is zero, e.g., a minimum or maximum. The stationary point of the quadratic relationship of $P_2$ as a function of $P_1$ can be calculated as

$$P_{1_{\text{stat}}}=\frac{-b_1}{2b_2}=\frac{-\text{var}\left(P_1^2\right)c_1+\text{cov}(P_1,P_1^2)c_2}{-2\hspace{0.17em}\text{cov}\left(P_1,P_1^2\right)c_1+2{\sigma }_{P_1}^2{c}_2}.$$ (22)

If we assume for simplicity that $\text{cov}\left(P_1,P_1^2\right)=0$ when ${\mathit{cov}}_{A_{m,1},A_{v,1}}=0,$ then $P_{1_{\text{stat}}}=-\text{var}\left(P_1^2\right)c_1/2{\sigma }_{P_1}^2{c}_2.$ The population mean is at a stationary point of zero when $c_1=r_{A_{m,1},A_{m,2}}=0.$ A positive (negative) stationary point implies that the current population mean is lower (higher) than it is. In general, $P_{1_{\text{stat}}}$ = 0 if $\text{var}\left(P_1^2\right)c_1=\text{cov}\left(P_1,P_1^2\right)c_2.$

The genetic stationary point can be determined similarly:

$$P_{1_{g\text{\_stat}}}=\frac{-b_{{\mathit{a}}_{2}1}}{2b_{{\mathit{a}}_{2}2}}=\frac{-\text{var}\left(P_1^2\right)g_{{\mathit{a}}_{2}1}+\text{cov}(P_1,P_1^2)g_{{\mathit{a}}_{2}2}}{-2\hspace{0.17em}\text{cov}\left(P_1,P_1^2\right)g_{{\mathit{a}}_{2}1}+2{\sigma }_{P_1}^2{g}_{{\mathit{a}}_{2}2}}.$$ (23)

The genetic and phenotypic stationary points differ unless $r_e=0.$ They are shown in Figure 4 as functions of $r_{A_{v,1},A_{m,2}}$ (Figure 4A) and $r_{A_{m,1},A_{m,2}}$ (Figure 4B), and although they differ, their shapes do not. Both are near zero when $r_{A_{v,1},A_{m,2}}$ is close to −1 or 1, but large in absolute terms when $r_{A_{v,1},A_{m,2}}\sim 0$ (Figure 4A), i.e., a hyperbolic form, because $r_{A_{v,1},A_{m,2}}$ largely determines the curvature of the parabolas; and both increase linearly with $r_{A_{m,1},A_{m,2}}$ (Figure 4B). These phenotypic and genetic stationary points can be interpreted as phenotypic and genetic optima in the case of stabilizing selection.

Figure 4.

(A and B) Phenotypic and genetic optima as functions of $r_{A_{v,1},A_{m,2}}$ (A) and $r_{A_{m,1},A_{m,2}}$ (B) when $r_e=0.5$ $({\sigma }_{A_{m,1}}^2={\sigma }_{A_{m,2}}^2=0.3,{\sigma }_{A_{v,1}}^2=0.05,{\sigma }_{e_1}^2\text{exp}\left(\left(1/2\right){\sigma }_{A_{v,1}}^2\right)=0.7,$ ${\sigma }_{e_2}^2=0.7,$ $r_{A_{m,1},A_{v,1}}=0;$ A, $r_{A_{m,1},A_{m,2}}=0.5;$ B,$r_{A_{v,1},A_{m,2}}=-0.2$).

Effects of selection on genetic parameters

Both natural and artificial selection may bring the population mean to a fitness optimum. As shown in Figure 4, there is a relationship between the distance between the stationary point and the current population mean and the genetic correlations, such that the genetic correlations may change as selection shifts the population toward the stationary point. The formulas underlying Figure 4 can also be expressed to show how genetic correlations depend on the distance between the current population mean and the stationary point, e.g., a fitness optimum (Ω), assuming that the parabola has fixed shape. The regression equation can be written as

$$P_2=b_2{(P_1-\text{Ω})}^2+d,$$ (24)

where d is a constant. If we assume $d=0$ and $\text{cov}\left(P_1,P_1^2\right)=0,$ then $b_2=c_2/\text{var}\left(P_1^2\right).$ From Equation 22, $b_1=-2b_2\text{Ω,}$ substituting $b_2=c_2/\text{var}\left(P_1^2\right)$ and equating to the expression for $b_1$ in Equation 18 assuming $\text{cov}\left(P_1,P_1^2\right)=0,$

$$b_1=\frac{-2c_2\text{Ω}}{\text{var}\left(P_1^2\right)}=\frac{c_1}{{\sigma }_{P_1}^2}.$$ (25)

The change in genetic correlation $r_{A_{m,1},A_{m,2}}$ can be predicted as the population mean moves to the stationary point. For instance, if all other parameters stay equal,

$$c_1=\frac{-2{\sigma }_{P_1}^2{c}_2\text{Ω}}{\text{var}\left(P_1^2\right)}$$ (26)

$$\begin{array}{l}{r}_{A_{m,1},A_{m,2}}\\ =\frac{-2{\sigma }_{P_1}^2{c}_2\text{Ω}}{\text{var}\left(P_1^2\right){\sigma }_{A_{m,1}}{\sigma }_{A_{m,2}}}\\ =\frac{-2{\sigma }_{P_1}^2\text{Ω}\left({\mathit{cov}}_{A_{v,1},A_{m,2}}^{}{\sigma }_{e_1}^2\exp \left(\left(1/2\right){\sigma }_{A_{v,1}}^2\right)+{\mathit{cov}}_{e_1{e}_2}^{}{\mathit{cov}}_{A_{m,1},A_{v,1}}\right)}{\text{var}\left(P_1^2\right){\sigma }_{A_{m,1}}{\sigma }_{A_{m,2}}}.\end{array}$$ (27)

Equation 27 shows that $r_{A_{m,1},A_{m,2}}$ and Ω are linearly related.

Similarly, for the genetic correlation between $r_{A_{v,1},A_{m,2}},$

$$c_2=\frac{c_1\text{var}\left(P_1^2\right)}{-2{\sigma }_{P_1}^2\text{Ω}}$$ (28)

$$r_{A_{v,1},A_{m,2}}=\frac{c_1\text{var}\left(P_1^2\right)}{-2{\sigma }_{P_1}^2\text{Ω}{\sigma }_{A_{v,1}}{\sigma }_{A_{m,2}}}-\frac{{\mathit{cov}}_{e_1{e}_2}^{}{\mathit{cov}}_{A_{m,1},A_{v,1}}}{{\sigma }_{A_{v,1}}{\sigma }_{A_{m,2}}},$$ (29)

showing that $r_{A_{v,1},A_{m,2}}$ has a hyperbolic relationship with Ω (Figure 4A).

Example: index selection with changing genetic correlation ${\mathit{r}}_{{\mathit{A}}_{\mathit{m},1},{\mathit{A}}_{\mathit{m},2}}$

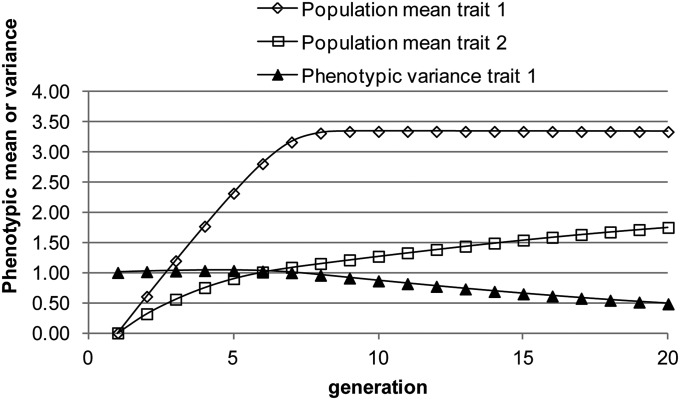
If index selection is applied to improve trait 2 using the phenotypic deviation of trait 1 and its square, i.e., Equations 14 and 15, the mean of trait 1 will tend to move to the optimum value (Figure 5). If only $r_{A_{m,1},A_{m,2}}$ changes according to Equation 27, the genetic correlation will become smaller as the population mean approaches the optimum. The response in trait 1 is nearly linear up to generation seven and becomes almost zero after generation eight, whereas the response in trait 2 is curvilinear. The response in trait 2 in the first seven generations is due mainly to bringing the population mean for trait 1 to the optimum and subsequently is due to reducing the phenotypic variance in trait 1.

Figure 5.

Population mean for traits 1 and 2 and the phenotypic variance of trait 1 as a function of generation when applying index selection for trait 2 using the phenotype deviation of trait 1 and the squared phenotypic deviation of trait 1 in the index (starting values are as follows: selected proportion is 5%, ${\sigma }_{A_{m,1}}^2={\sigma }_{A_{m,2}}^2=0.3,$ ${\sigma }_{A_{v,1}}^2=0.05,$ ${\sigma }_{e_1}^2\text{exp}\left(\left(1/2\right){\sigma }_{A_{v,1}}^2\right)=0.7,$ ${\sigma }_{e_2}^2=0.7,$ $r_{A_{m,1},A_{m,2}}=0.5,$ $r_{A_{m,1},A_{v,1}}=0.1,$ $r_e=0,$ $r_{A_{v,1},A_{m,2}}=-0.5$).

Deriving the phenotypic relationship between P₂ and P₁ when P₂ is a binary trait

Until now, we assumed multivariate normality but nonlinear relationships between traits occur when one of the traits is not normally distributed, such as survival or presence/absence of disease. Therefore we extend the prediction of $P_2$ on $P_1$ (Equation 3) when $P_2$ is a 0/1 binomial trait. We assume that $P_2$ is normally distributed on the underlying/liability scale ($P_{\text{2,liab}})$ (Gianola 1982; Foulley 1992) and therefore, $\widehat{P_{\text{2,liab}}}$ can be predicted using Equation 3. On the observed scale ($P_{\text{2,obs}}$), the proportion of animals that survive (dead = 0; alive =1) is predicted as

$${\mathit{P}}_{\text{2,obs}}={\mathit{p}}_{\text{survival}}={\displaystyle {\int }_{\mathit{x}-\widehat{{\mathit{P}}_{\text{2,liab}}}}^{\mathrm{\infty }}\phi \left(\mathit{t}\right)\mathit{dt}},$$ (30)

where x is the truncation point of the normal distribution corresponding to the average survival in the population ($\overline{p_{\text{survival}}}$), $x-P_{\text{2,liab}}\widehat{P_{\text{2,liab}}}$ represents the predicted truncation point given $P_1,$ and $\phi \left(t\right)$ is the standard normal density function. Using Equation 30 together with Equation 3 to predict $P_{\text{2,obs}}$ from $P_1$ shows very good agreement with results from Monte Carlo simulation (Figure 6), with R² > 0.995 for all cases evaluated. (Fortran scripts for all theoretical predictions and Monte Carlo simulations are provided in Supporting Information, File S3).

Figure 6.

The relationship between the proportion of surviving animals $P_{\text{2,obs}}$ and $P_1$ using Monte Carlo simulation (MC_lin) and multiple regression (MR_lin) either with no genetic correlation ($r_{A_{v,1},A_{m,2}}=0$) or with a negative genetic correlation ($r_{A_{v,1},A_{m,2}}=-0.5$) (MC_nonlin, MR_nonlin) between environmental variance in $P_1$ and the mean of $P_{\text{2,liab}}$ on the underlying scale (${\sigma }_{A_{m,1}}^2={\sigma }_{A_{m,2}}^2=0.3,{\sigma }_{A_{v,1}}^2=0.05,{\sigma }_{e_1}^2\text{exp}\left(\left(1/2\right){\sigma }_{A_{v,1}}^2\right)=0.7,$ ${\sigma }_{e_2}^2=0.7,$ $r_{A_{m,1},A_{m,2}}=0.2,$ $r_{A_{m,1},A_{v,1}}=0,$ $r_e=0,$ average proportion for $P_{\text{2,obs}}$ = 0.9).

Application to Birth Weight and Stillbirth in Pigs

The theoretical framework developed above shows that an M-V genetic correlation between traits leads to a nonlinear relationship between their phenotypes. The subsequent analyses demonstrated that the genetic and phenotypic optima could differ in position, but that selection could bring the population mean to the genetic optimum. As a practical example, we investigate such a nonlinear relationship between birth weight and stillbirth in pigs. We used 32,450 birth weight records from 2129 litters from 813 sows. Piglets were crossbred whereas the sows were purebred Landrace pigs from TOPIGS. Piglet survival at birth was recorded for each piglet as one (alive) or zero (dead). More details on the data are given elsewhere (Sell-Kubiak et al. 2015). Data are provided in Supporting Information, File S2.

Statistical analysis

We analyzed piglet birth weight, its environmental variance ($V_{\text{E}}$), and piglet survival at birth as three traits with a DHGLM in ASReml4 (Rönnegård et al. 2010; Felleki et al. 2012; Gilmour et al. 2014). For piglet survival we assumed a linear model with homogeneous residual variance because combining a logistic model for piglet survival with DHGLM for birth weight is not yet feasible and indeed outside the scope of this article. Fixed effects fitted were herd–year–season, parity of the sow, and sex of the piglet for all three traits. The random effects included were maternal genetic effects, litter effects, and residuals for all three traits, with each random effect trivariate normally distributed. The model is

$$\begin{array}{l}\left[\begin{array}{c}{y}_{m,1}\\ y_{v,1}\\ y_{m,2}\end{array}\right]=\left[\begin{array}{ccc}X& 0& 0\\ 0& X& 0\\ 0& 0& X\end{array}\right]\left[\begin{array}{c}{b}_{m,1}\\ b_{v,1}\\ b_{m,2}\end{array}\right]+\left[\begin{array}{ccc}Z& 0& 0\\ 0& Z& 0\\ 0& 0& Z\end{array}\right]\left[\begin{array}{c}{a}_{m,1}\\ a_{v,1}\\ a_{m,2}\end{array}\right]\\ +\left[\begin{array}{ccc}W& 0& 0\\ 0& W& 0\\ 0& 0& W\end{array}\right]\left[\begin{array}{c}{c}_{m,1}\\ c_{v,1}\\ c_{m,2}\end{array}\right]+\left[\begin{array}{c}{e}_{m,1}\\ e_{v,1}\\ e_{m,2}\end{array}\right],\end{array}$$ (31)

where $y_{m,1},$ $y_{v,1},$ and $y_{m,2}$ are the vectors of observations for piglet birth weight, the response variable for ${\mathit{V}}_{\text{E}}$ of birth weight, and piglet survival; and X, Z, and W are the incidence matrices relating fixed effects $\left(b\right),$ random breeding values, and random litter effects to observations. The vectors $a_{m,1},$${\mathbf{a}}_{v,1},$ and ${\mathbf{a}}_{m,2}$ are maternal breeding values for birth weight, its ${\mathit{V}}_{\text{E}},$ and survival

$$\left[\begin{array}{c}{a}_{m,1}\\ a_{v,1}\\ a_{m,2}\end{array}\right]\sim \text{N}\left(\left[\begin{array}{c}0\\ 0\\ 0\end{array}\right],\left[\begin{array}{ccc}{\sigma }_{{\mathit{A}}_{\mathit{m},1}}^2& {\mathit{cov}}_{{\mathit{A}}_{\mathit{m},1},{\mathit{A}}_{\mathit{v},1}}& {\mathit{cov}}_{{\mathit{A}}_{\mathit{m},1},{\mathit{A}}_{\mathit{m},2}}\\ & {\sigma }_{{\mathit{A}}_{\mathit{v},1}}^2& {\mathit{cov}}_{{\mathit{A}}_{\mathit{v},1},{\mathit{A}}_{\mathit{m},2}}\\ \text{symmetric}& & {\sigma }_{{\mathit{A}}_{\mathit{m},2}}^2\end{array}\right]\otimes A\right);$$

$c_{m,1}$, $c_{v,1},$ and $c_{m,2}$ are the corresponding vectors for random litter effects

$$\left[\begin{array}{c}{c}_{m,1}\\ c_{v,1}\\ c_{m,2}\end{array}\right]\sim \text{N}\left(\left[\begin{array}{c}0\\ 0\\ 0\end{array}\right],\left[\begin{array}{ccc}{\sigma }_{{\mathit{C}}_{\mathit{m},1}}^2& {\mathit{cov}}_{{\mathit{C}}_{\mathit{m},1},{\mathit{C}}_{\mathit{v},1}}& {\mathit{cov}}_{{\mathit{C}}_{\mathit{m},1},{\mathit{C}}_{\mathit{m},2}}\\ & {\sigma }_{{\mathit{C}}_{\mathit{v},1}}^2& {\mathit{cov}}_{{\mathit{C}}_{\mathit{v},1},{\mathit{C}}_{\mathit{m},2}}\\ \text{symmetric}& & {\sigma }_{{\mathit{C}}_{\mathit{m},2}}^2\end{array}\right]\otimes I\right),$$

where I is the identity matrix; ${\sigma }_{{\mathit{C}}_{\mathit{m},1}}^2,$${\sigma }_{{\mathit{C}}_{\mathit{v},1}}^2,$ and ${\sigma }_{{\mathit{C}}_{\mathit{m},2}}^2$are the litter variances; and ${\mathit{cov}}_{{\mathit{C}}_{\mathit{m},1},{\mathit{C}}_{\mathit{v},1}},$ ${\mathit{cov}}_{{\mathit{C}}_{\mathit{m},1},{\mathit{C}}_{\mathit{m},2}},$ and ${\mathit{cov}}_{{\mathit{C}}_{\mathit{v},1},{\mathit{C}}_{\mathit{m},2}}$ are the corresponding covariances of $c_{m,1},$ $c_{v,1},$ and $c_{m,2}.$ Although sows had repeated observations, at the risk of biasing estimates of genetic covariance estimates, permanent sow effects were excluded from the model because their inclusion yielded estimates at the lower boundaries. Subsequently, these estimates of parameters were used to predict the regression of piglet survival on birth weight and were compared to the averages of survival rate for each of 20 ranked bins with equal numbers of piglet birth weight records. Because the statistical model included litter effects, the extension in Appendix C was used to predict the regression equation when the residual covariances between $V_{\text{E}}$ and birth weight and survival are ignored.

Results

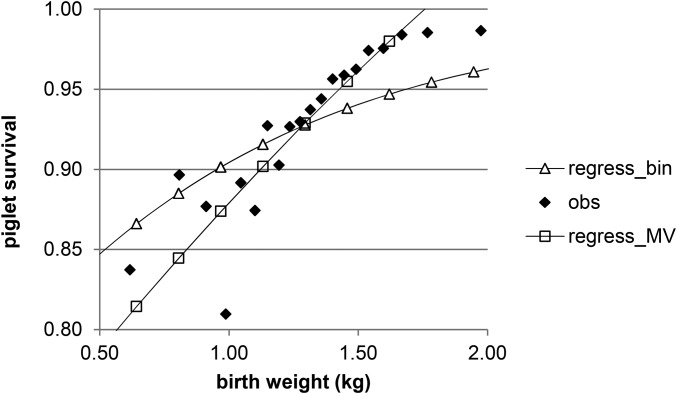
The parameter estimates (Table 2 and Table 3) indicate that the genetic correlation between mean piglet birth weight and survival is negative, as is that between $V_{\text{E}}$ of birth weight and survival, the M-V genetic correlation between traits. This implies that lower birth weight or lower $V_{\text{E}}$ is genetically associated with a higher survival rate and, importantly, that uniform litters have higher mean survival rates. The multiple-regression equation based on the estimated variance components describes the nonlinear relationship between individual survival rate and individual birth weight quite well (Figure 7). Because a linear model for survival is used, the regression equation goes beyond a survival rate of 1.0. Accounting for the binomial nature of survival, using Equation 30, solves the problem of predicting a survival rate beyond 1.0, but the goodness of fit was slightly worse (R² = 0.78) than for the regression assuming multivariate normality (R² = 0.79). The relationship between individual birth weight and individual survival rate is, however, almost linear because the residual covariance between birth weight and survival substantially dilutes the nonlinear genetic relationship. Similarly Sölkner and Fuerst-Waltl (1996) found that environmental or residual correlations can greatly reduce the nonlinearity of the genetic relationship such that the phenotypic relationship is almost linear. From a biological point of view, a nonlinear relationship between piglet birth weight and survival rate at litter level can arise because extremely small piglets decrease survival rate, as also do very large piglets but to a lesser extent, because the very large piglets induce early farrowing.

Table 2. Estimates of genetic, litter, and residual variance for birth weight (kg) (BW), its environmental variance $V_{\text{E}}$ (BWv), and survival rate (SU) in pigs (standard error in parentheses).

Variance component	BW (×10−3)	BWv (×10−3)	SU (×10−3)
Genetic variance	16.4 (1.51)	46.5 (7.55)	0.968 (0.22)
Litter variance	15.0 (0.80)	75.0 (7.53)	2.74 (0.26)
Residual variancea	74.9 (0.61)	1803 (14.7)	63.4 (0.50)

^aResidual variance for BW is based on a model with homogeneous residual variance.

Table 3. Estimates for traits as in Table 2 of genetic correlations (above diagonal) and litter correlations (below diagonal) in pigs (standard errors in parentheses).

Trait	BW	BWv	SU
BW		0.51 (0.08)	−0.24 (0.11)
BWv	0.20 (0.05)		−0.19 (0.14)
SU	0.35 (0.05)	0.06 (0.07)

Note that residual correlation between BW and SU was 0.18.

Figure 7.

The phenotypic relationship between survival and individual piglet birth weight (kg) when averages were calculated for 20 bins after sorting on birth weight (obs), regression based on Equation 3 assuming multivariate normality (regress_MV), and regression based on Equations 3 and 30 to account for the binomial nature of survival (regress_bin).

Discussion

Methodological framework and quantitative genetic aspects of nonlinear relationships

This study shows that a genetic covariance between the environmental variance of one trait and the mean of another trait, i.e., an M-V genetic correlation between them, can lead to nonlinear relationships between these traits and presented a framework based on multiple regression to investigate the consequences of selection in the presence of such an M-V genetic correlation. Although all relationships between breeding values are assumed to be linear, the phenotypic relationship between traits becomes curvilinear because the breeding value for environmental variance for the first trait $A_{v,1}$ is associated with the squared phenotype $P_1^2$ and its covariance to the mean of trait 2. Most quantitative genetic machinery is based on multivariate normality and thus linear relationships (Bulmer 1980), but we show that it can be extended to incorporate nonlinear relationships using methods of Mulder et al. (2007) for predicting breeding values and selection responses when there is genetic variation in $V_{\text{E}}$. Mulder et al. (2007) used the additive model for genetic heterogeneity of $V_{\text{E}}$, but here the exponential model was used because of its statistical tractability and implementation in the DHGLM methodology to estimate genetic variance in $V_{\text{E}}$. The additive and exponential models are similar, assuming that the genetic variance in $V_{\text{E}}$ is small and parameters can be converted from one model to the other (Mulder et al. 2007; Hill and Mulder 2010). Here the focus is on the principles rather than the details and therefore the choice of model does not have a major impact on the nonlinear relationships caused by M-V genetic correlations between traits.

We extended the DHGLM methodology to estimate genetic and environmental variances and the correlations between piglet birth weight, its $V_{\text{E}}$, and survival. The current algorithm can be run in ASREML4 (code provided in Supporting Information, File S1). It could, for example, also be used to estimate the trade-offs between $V_{\text{E}}$ and other traits and thereby help further unravel the biological mechanisms and causes of genetic differences in $V_{\text{E}}$. Genetic correlations may change due to selection, as predicted in this study, even under infinitesimal model assumptions, and therefore reestimation of genetic parameters seems important if there are curvilinear relationships between traits. Large family sizes are required to get accurate estimates for genetic variance in $V_{\text{E}}$ (Hill 2004; Hill and Mulder 2010), and consequently very large data sets are required for estimating M-V genetic correlations between traits with sufficient precision (inferred from Robertson 1959).

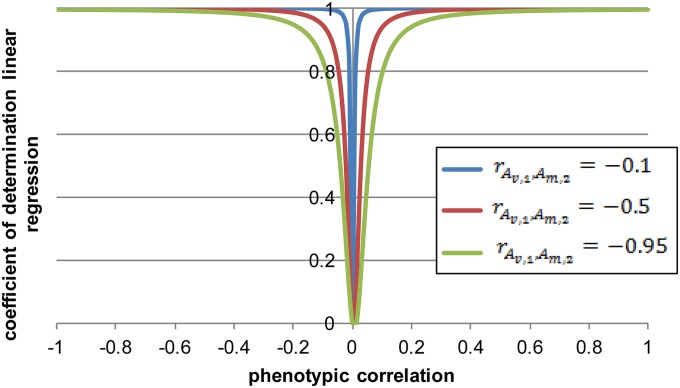
The regression in Figure 1 shows substantial nonlinearity, but in our examples the coefficient of determination ($R^2$) would not be greatly reduced if a linear regression was applied even though the true relationship is quadratic because of an M-V genetic correlation between traits. The linear regression would generally explain ≥90% of the variation, except when the phenotypic correlation between the traits is close to zero (i.e., −0.15 < phenotypic correlation < 0.15) (Figure 8). Therefore, a linear regression between traits is sufficient when the population is far from the optimum, but if there is a nonzero M-V genetic correlation between them and the population mean is close to the optimum, quadratic regression should be used.

Figure 8.

The coefficient of determination (R²) of a linear regression when the true relationship is quadratic as a function of the phenotypic correlation ($=r_{A_{m,1},A_{m,2}}=r_e$) between trait 1 and trait 2 for different values of $r_{A_{v,1},A_{m,2}}$ (${\sigma }_{A_{m,1}}^2={\sigma }_{A_{m,2}}^2=0.3,$ ${\sigma }_{A_{v,1}}^2=0.05,$ ${\sigma }_{e_1}^2\text{exp}\left(\left(1/2)\right){\sigma }_{A_{v,1}}^2\right)=0.7,$ ${\sigma }_{e_2}^2=0.7,$ $r_{A_{m,1},A_{v,1}}=0$).

A related question is how much of the nonlinearity observed is due to an M-V genetic correlation between the traits. In the pig example, the quadratic relationship improved $R^2$ only from 0.787 to 0.793, whereas the best-fitting quadratic regression $R^2$ would explain 0.794. Assuming that the true relationship is equal to the best-fitting quadratic regression, it can be concluded that the genetic covariance between $V_{\text{E}}$ of birth weight and survival is the main driver for the quadratic relationship, and no other factors need to be invoked. The environmental correlations seem to have a dominant influence on diluting the nonlinearity, which accords with findings of Sölkner and Fuerst-Waltl (1996) who investigated the effect of nonlinear relationships between traits due only to nonlinearity of their breeding values for trait means. If the environmental relationship between traits is approximately linear, the phenotypic relationship will also be approximately linear, especially when the heritabilities are small.

In this study, we investigated the contribution of M-V genetic correlations between traits to nonlinearity between them. Nonnormality of at least one of the traits can cause a nonlinear relationship between them (Varona and Sorensen 2014). Survival is binomially distributed, although we assumed multivariate normality of birth weight and survival, but estimates of additive genetic correlations on the linear scale are expected to be equal to those on the underlying scale (Vinson et al. 1976; Gianola 1982) and therefore not biased by the current procedure. Furthermore, we showed that the prediction assuming multivariate normality fitted the observed survival rates better than when assuming that survival is binomially distributed. Nevertheless, Equation 30 is a useful extension of the framework to predict phenotypes of traits that are not normally distributed, but have an underlying liability scale that is normally distributed. More research is needed to explore the effects of nonnormality on estimation of such M-V correlations.

The focus in the present study was on understanding the nonlinear relationship between traits caused by M-V correlations between traits and its consequences for artificial and natural selection. We focused on mass selection, but the same framework could be used to predict responses to selection when using information of relatives, e.g., sibs or offspring as shown by Mulder et al. (2007, 2008). With progeny testing, accuracy will be greatly improved, especially for the breeding value for $V_{\text{E}}$. In Mulder et al. (2008) we showed that when profit has an optimum value, artificial selection will first bring the population mean to the optimum and subsequently selection will be to reduce the variance, similar to that in Figure 5. It should be noted that current calculations as well as those in Mulder et al. (2007, 2008) do not take into account reduced genetic variance due to gametic phase disequilibrium (Bulmer 1971).

The framework provides estimates of positions and heights of phenotypic and genetic optima, which are functions of genetic and nongenetic (co)variances. As standard errors, particularly on genetic (co)variances, are moderate to high, those on optima are also likely to be large, especially when the M-V genetic correlation between traits is close to zero (Figure 5). The calculated location of optima gives insight into where the current population mean is compared to the optimum. The piglet example shows that phenotypic and genetic optima may be very different: the current population mean is far from the phenotypic optimum (∼13 phenotypic SD), because higher birth weight still yields higher survival on average based on the regression, although observed survival rate flattens at ∼1.8–2.0 kg. The high prediction for the phenotypic optimum is likely due to neglecting the binomial nature of survival. In contrast, the genetic optimum is ∼6 phenotypic SD below the current population mean, with the discrepancy between the phenotypic and the genetic optimum due to the opposite signs of the genetic vs. litter and environmental correlations between birth weight and survival. Yoshimura and Shields (1995) indicate that environmental uncertainty is the driver between differences in optima. If genetic/nongenetic (co)variances differ among environments, the optima, i.e., fitness profiles, would also differ among environments (e.g., Dewitt and Yoshimura 1998).

Phenotypic variability and fitness in natural populations

Nonlinear relationships are often observed or hypothesized in natural populations, typically as “fitness profiles” between trait values and fitness (Lande and Arnold 1983; Falconer and Mackay 1996; Kingsolver et al. 2001, 2012). If the optimum phenotype is intermediate, there would be a negative covariance between ${\mathit{V}}_{\text{E}}$ and fitness, such that families with small variance would contribute more survivors, and correspondingly families with a large variance would have an advantage with disruptive or strong directional selection (Hill and Zhang 2004; Mulder et al. 2007). The strength of natural selection (i.e., the selection gradient) can be determined by regressing relative fitness on phenotypic value if it is directional or on the squared deviation of phenotypic value from the mean if it is stabilizing or disruptive (Lande and Arnold 1983). Thus if fitness is taken as trait 2, the regression coefficients in Equation 3 indicate the strength of selection. For instance, the strength of stabilizing selection is obtained as ${\mathit{V}}_{\text{S}}=-1/2{\mathit{b}}_2$ (Falconer and Mackay 1996), where ${\mathit{b}}_2$ is the regression of fitness on the squared deviation of the trait under selection, i.e., trait 1 in this study. Applying this to our study and assuming ${\mathit{r}}_{{\mathit{A}}_{\mathit{m},1}{\mathit{A}}_{\mathit{v},1}}=0,$ ${\mathit{r}}_{\mathit{e}}=0,$ ${\mathit{r}}_{{\mathit{A}}_{\mathit{m},1}{\mathit{A}}_{\mathit{m},2}}=0,$ i.e., the population mean is at the optimum, the strength of stabilizing selection (expressed as the “variance” of the fitness profile standardized by ${\mathit{V}}_{\text{E}}$ on trait 1, so small values imply strong selection) would be ${\mathit{V}}_{\text{S}}=-1/2{\mathit{b}}_2=\left[2{\sigma }_{{\mathit{P}}_1}^4+3{\sigma }_{{\mathit{e}}_1}^4\exp \left({\sigma }_{{\mathit{A}}_{\mathit{v},1}}^2\right)\left(\exp \left({\sigma }_{{\mathit{A}}_{\mathit{v},1}}^2\right)-1\right)\right]/[-2{\mathit{cov}}_{{\mathit{A}}_{\mathit{v},1},{\mathit{A}}_{\mathit{m},2}}{\sigma }_{{\mathit{e}}_1}^4\exp \left({\sigma }_{{\mathit{A}}_{\mathit{v},1}}^2\right)]$ (Falconer and Mackay 1996). The estimate of $V_{\text{S}}$ $\left({\mathit{V}}_{\text{S}}=-1/2{\mathit{b}}_2\right)$ for the example of piglet survival and piglet birth weight is 435${\mathit{V}}_{\text{E}}.$

Based on early estimates of the strength of stabilizing selection, Falconer and Mackay (1996) suggested that strong selection would be $V_{\text{S}}$ = 10 and weak selection $V_{\text{S}}$ = 100, with “typical” estimates of the order of 20–25 (Falconer and Mackay 1996; Zhang and Hill 2005). Kingsolver et al. (2001, 2012), however, reviewed selection gradients estimated in a range of natural populations and found that in only a few studies negative quadratic regression coefficients ($b_2$) were actually obtained, indicating that strong stabilizing selection is rarely detected. The value obtained here for the piglet data implies very weak stabilizing selection. Indeed, as fitness typically has a low heritability (<0.1) and ${\sigma }_{A_{v,1}}^2<0.1$ (${\text{GCV}}_{V_{\text{E}}}\cong {\sigma }_{A_{v,1}}<0.32$) in most recent estimates using DHGLM or MCMC (Felleki et al. 2012; Mulder et al. 2013a; Rönnegård et al. 2013), the stabilizing selection driven by the M-V genetic correlation between $V_{\text{E}}$ and fitness is likely to be weak (examples in Table 4).

Table 4. The strength of stabilizing selection ($V_{\text{s}}$) standardized by $V_{\text{E}}$ for different combinations of the heritability of relative fitness (${\sigma }_{P\text{,fitness}}^{\text{2}}=0.25$), the genetic correlation between $V_{\text{E}}$ of trait 1 and fitness ($r_{A_{v,1},A_{m,2}}$), and the genetic variance in $V_{\text{E}}$ (${\sigma }_{A_{v,1}}^2$).

		${\sigma }_{A_{v,1}}^2$
${\mathit{h}}^2$ fitness	$r_{A_{v,1},A_{m,2}}$	0.05	0.1
0.02	−0.1	1339	983
	−0.5	268	197
	−1.0	134	98
0.1	−0.1	599	440
	−0.5	120	88
	−1.0	60	44

Implications and applications in agriculture

In agriculture, a frequent objective is to increase uniformity of animals and plants for some traits because these may have an optimum with respect to profit, for instance for slaughter traits in livestock because slaughterhouses prefer low variability in carcass weight and meat quality to optimize processing and to provide homogeneous products to retailers (Hennessy 2005). Some conformation traits such as udder depth or front teat placement may have a nonlinear relationship with respect to fitness traits, such as longevity (Larroque and Ducrocq 2001), or with milk production (Fuerst-Waltl et al. 1998). In contrast, there is also concern that animals with small $V_{\text{E}}$ would not have the capacity to react to unpredictable environments, i.e., lack robustness, so it is likely to be worthwhile to explore the relationship between $V_{\text{E}}$ and fitness traits in different environments. While very little is known about trade-offs between $V_{\text{E}}$ and means of traits, the current study provides insight in showing that a negative genetic covariance between $V_{\text{E}}$ and fitness is advantageous for piglet survival and birth weight. Furthermore, selection on $V_{\text{E}}$ can increase accuracy of selection provided the population is at the optimum and the genetic correlation between trait means is close to zero. Therefore, inclusion of $V_{\text{E}}$ in index selection is mainly of interest for traits that have a direct economic value for uniformity or where $V_{\text{E}}$ has a strong genetic correlation with an economically important trait that has a low heritability and is not strongly correlated to other economic traits.

In conclusion, this study provides a framework to study nonlinear relationships between traits caused by M-V genetic correlations between them and to assess the effects of artificial and natural selection on their means and variances. It is shown that phenotypic and genetic optima may differ; that genetic relationships are often more curvilinear than phenotypic relationships, especially for environmentally correlated traits; and that genetic correlations may change when population means change relative to the optimal phenotypes. The analysis of piglet birth weight and survival shows that the nonlinearity can be partly explained by such an M-V genetic correlation between $V_{\text{E}}$ of birth weight and survival.

Appendix A

Derivation of Elements in the Multiple-Regression Equation of P₂ on P₁ and P₁²

The elements of the P matrix and the c vector were derived as follows for the genetic model in Equation 1 $\left({\mathit{P}}_1={\mu }_1+{\mathit{A}}_{\mathit{m},1}+{\mathit{E}}_1\right),$ in which ${\mathit{E}}_1=\chi \exp \left[\left(1/2\right)\left(\text{ln}\left({\sigma }_{{\text{e}}_1}^2\right)+{\mathit{A}}_{\mathit{v},1}\right)\right]$ and $\text{E}\left({\chi }^2\exp ({\mathit{A}}_{\mathit{v},1}\right)=\exp \left(\left(1/2\right){\sigma }_{A_{v,1}}^2\right),$ where the roman E denotes expectation.

The elements of P are

$$\text{E}\left(P_1\right)=0$$

$$\text{E}\left({\mathit{P}}_1^2\right)=\text{E}\left({\mathit{A}}_{\mathit{m},1}^2\right)+2\text{E}\left({\mathit{A}}_{\mathit{m},1}{\mathit{E}}_1\right)+\text{E}\left({\mathit{E}}_1^2\right)={\sigma }_{{\mathit{A}}_{\mathit{m},1}}^2+{\sigma }_{{\mathit{e}}_1}^2\exp \left(\frac{1}{2}{\sigma }_{{\mathit{A}}_{\mathit{v},1}}^2\right)={\sigma }_{\mathit{P}}^2$$

$$\text{E}\left(P_1^3\right)=\text{ E}\left(A_{m,1}^3\right)+3\text{E}\left(A_{m,1}^2{E}_1\right)+3\text{E}\left(A_{m,1}^{}{E}_1^2\right)+\text{E}\left(E_1^3\right)=3{\mathit{cov}}_{A_{m,1},A_{v,1}}{\sigma }_{e_1}^2\exp \left(\frac{1}{2}{\sigma }_{A_{v,1}}^2\right)$$

$$\text{E}\left(P_1^4\right)=\text{E}\left(A_{m,1}^4\right)+4\text{E}\left(A_{m,1}^3{E}_1\right)+6\text{E}\left(A_{m,1}^2{E}_1^2\right)+4\text{E}\left(A_{m,1}{E}_1^3\right)+\text{E}\left(E_1^4\right)$$

$$=3{\sigma }_{A_{m,1}}^4+6{\mathit{cov}}_{A_{m,1},A_{v,1}}^2{\sigma }_{e_1}^2\exp \left(\frac{1}{2}{\sigma }_{A_{v,1}}^2\right)+3{\sigma }_{e_1}^4\exp \left(2{\sigma }_{A_{v,1}}^2\right),$$

where

$$\text{E}\left(A_{m,1}^2{E}_1^2\right)=2{\text{cov}}^2\left(A_{m,1}{E}_1\right)=(2)(\frac{1}{2}){\mathit{cov}}_{A_{m,1},A_{v,1}}^2{\sigma }_{e_1}^2\exp \left(\frac{1}{2}{\sigma }_{A_{v,1}}^2\right),$$

and $1/2$ comes from the coefficient of ${\mathit{A}}_{\mathit{v},1}$ in ${\mathit{E}}_1=\chi \exp \left[\left(1/2\right)\left(\text{ln}\left({\sigma }_{e_1}^2\right)+{\mathit{A}}_{\mathit{v},1}\right)\right];$

$$\text{var}\left({\mathit{P}}_1\right)=\text{E}\left({\mathit{P}}_1^2\right)-{\left[\text{E}\left({\mathit{P}}_1\right)\right]}^2={\sigma }_{\mathit{P}}^2$$

$$\text{cov}\left(P_1,P_1^2\right)=\text{E}\left(P_1^3\right)-\text{E}\left(P_1\right)\text{E}\left(P_1^2\right)=3{\mathit{cov}}_{A_{m,1},A_{v,1}}{\sigma }_{e_1}^2\exp \left(\frac{1}{2}{\sigma }_{A_{v,1}}^2\right)$$

$$\text{var}\left(P_1^2\right)=\text{E}\left(P_1^4\right)-{\left[\text{E}\left(P_1^2\right)\right]}^2=2{\sigma }_{P_1}^4+6{\mathit{cov}}_{A_{m,1},A_{v,1}}^2{\sigma }_{e_1}^2\exp \left(\frac{1}{2}{\sigma }_{A_{v,1}}^2\right)+3{\sigma }_{e_1}^4\exp \left({\sigma }_{A_{v,1}}^2\right)\left(\exp \left({\sigma }_{A_{v,1}}^2\right)-1\right).$$

The elements of c are

$$\text{cov}\left(P_2,P_1\right)=\text{E}\left(A_{m,2}{A}_{m,1}\right)+\text{E}\left(E_2{E}_1\right)={\mathit{cov}}_{A_{m,1},A_{m,2}}+{\mathit{cov}}_{e_1{e}_2}^{}$$

$$\begin{array}{c}\text{cov}\left(P_2,P_1^2\right)=\text{E}\left(A_{m,2}{A}_{m,1}^2\right)+2\text{E}\left(A_{m,2}{A}_{m,1}{E}_1\right)+\text{E}\left(A_{m,2}{E}_1^2\right)+\text{E}\left(E_2{A}_{m,1}^2\right)+2\text{E}\left(E_2{A}_{m,1}{E}_1\right)+\text{E}\left(E_2,E_1^2\right)\\ ={\mathit{cov}}_{A_{v,1},A_2}{\sigma }_{e_1}^2\exp \left(\frac{1}{2}{\sigma }_{A_{v,1}}^2\right)+{\mathit{cov}}_{A_{m,1},A_{v,1}}{\mathit{cov}}_{e_1{e}_2}^{}.\end{array}$$

Appendix B

Derivation of Elements of P and g When Using Squared Residuals Corrected for Leverages

Instead of using $P_1^2$ directly, squared residuals of $P_1$ corrected for its leverage (l) can be used to predict breeding values for the second trait $A_{m,2}$ (see Equation 17 in main text). The leverage is the diagonal element of the hat matrix for each observation (Hoaglin and Welsh 1978) as used in the DHGLM (Rönnegård et al. 2010).

Assuming that only information of the animal itself is used for breeding value estimation and in the absence of fixed effects, $b_{A_{m,1}}=l$ and hence the elements of $P_e$ in Equation 17 are

$$\text{var}\left(\frac{e_1^2}{1-l}\right)=\text{var}\left(\left(1-b_{A_{m,1}}\right)P_1^2\right)={\left(1-b_{A_{m,1}}\right)}^2\text{var}\left(P_1^2\right)$$

$$\text{cov}\left(P_1,\frac{e_1^2}{1-l}\right)=\text{cov}\left(P_1,\left(1-b_{A_{m,1}}\right)P_1^2\right)=\left(1-b_{A_{m,1}}\right)\text{cov}\left(P_1,P_1^2\right)$$

and similarly the elements of $g_{a_{2}e\mathit{ }}$ are

$$\text{cov}\left(A_{v1},\frac{e_1^2}{1-l}\right)=\left(1-b_{A_{m,1}}\right)\text{cov}\left(A_{v1},P_1^2\right)$$

$$\text{cov}\left(A_{m,2},\frac{e_1^2}{1-l}\right)=\left(1-b_{A_{m,1}}\right)\text{cov}\left(A_{m,2},P_1^2\right).$$

If $\left(1-{\mathit{b}}_{{\mathit{A}}_{\mathit{m},1}}\right)$ is put into a scaling matrix

$$\mathbf{W}=\left[\begin{array}{cc}1& 0\\ 0& \left(1-{\mathit{b}}_{{\mathit{A}}_{\mathit{m},1}}\right)\end{array}\right],$$

the derived elements in Appendix A can be used together with the scaling matrix (see main text below Equation 17). It can be shown that the accuracy of the estimated breeding value $\widehat{{\mathit{A}}_{\mathit{m},2}}$ $\left({\mathit{r}}_{{\mathit{A}}_{\mathit{m},2},\widehat{{\mathit{A}}_{\mathit{m},2}}}\right)$ is the same as with using squared phenotypic deviations instead of squared residuals corrected for leverages:

$$r_{A_{m,2},\widehat{A_{m,2}}}=\frac{\sqrt{{(W^{-1}{P}^{-1}{W}^{-1}Wg)}^{\prime }Wg}}{{\sigma }_{A_{m,2}}}=\frac{\sqrt{{(P^{-1}g)}^{\prime }g}}{{\sigma }_{A_{m,2}}}.$$

Appendix C

Generalization of Equations Involved in Multiple Regression with Multiple Random Effects

Assume the statistical model for trait 1 (= y), its $V_{\text{E}},$ and trait 2 contains fixed effects and a number of random effects ($n-1$) in addition to the residual,

$$\mathbf{y}=\mathbf{Xb}+{\displaystyle \sum _{\mathit{i}=1}^{\mathit{n}-1}{\mathbf{Z}}_{\mathbf{i}}{\mathbf{u}}_{\mathbf{i}}+\mathbf{e}},$$

and $P_2$ is predicted from $P_1$ and $P_1^2.$ The (co)variances in the P matrix are ${\mathit{V}}_{11}={\displaystyle {\sum }_{\mathit{i}=1}^{\mathit{n}-1}\mathit{v}{\mathit{c}}_{{\mathit{i}}_{11}}},$ ${\mathit{V}}_{12}={\mathit{V}}_{21}={\displaystyle {\sum }_{\mathit{i}=1}^{\mathit{n}-1}\mathit{v}{\mathit{c}}_{{\mathit{i}}_{12}}},$ ${\mathit{V}}_{22}={\displaystyle {\sum }_{\mathit{i}=1}^{\mathit{n}-1}\mathit{v}{\mathit{c}}_{{\mathit{i}}_{22}}},$ where $v{c}_{i_{11}}$ ($v{c}_{i_{22}}$) is the variance for random effect i for trait 1 ($V_{\text{E}}$ of trait 1) and $v{c}_{i_{12}}$ is the covariance for random effect i between trait 1 and its $V_{\text{E}}$:

$$\text{var}\left(P_1\right)=V_{11}+{\sigma }_{e_1}^2\exp \left(\frac{1}{2}{V}_{22}\right)$$

$$\text{cov}\left(P_1,P_1^2\right)=3V_{12}{\sigma }_{e_1}^2\exp \left(\frac{1}{2}{V}_{22}\right)$$

$$\text{var}\left(P_1^2\right)=2{\left(V_{11}+{\sigma }_{e_1}^2\exp \left(\frac{1}{2}{V}_{22}\right)\right)}^2+6V_{12}^2{\sigma }_{e_1}^2\exp \left(\frac{1}{2}{V}_{22}\right)+3{\sigma }_{e_1}^4\exp \left(V_{22}\right)\left(\exp \left(V_{22}\right)-1\right).$$

The covariances in c are ${\mathit{V}}_{13}={\displaystyle {\sum }_{\mathit{i}=1}^{\mathit{n}-1}\mathit{v}{\mathit{c}}_{{\mathit{i}}_{13}}},$ ${\mathit{V}}_{23}={\displaystyle {\sum }_{\mathit{i}=1}^{\mathit{n}-1}\mathit{v}{\mathit{c}}_{{\mathit{i}}_{23}}},$ where $v{c}_{i_{13}}$ is the covariance for random effect i for trait 1 and trait 2 and $v{c}_{i_{23}}$ is the covariance for random effect i between trait 1 and its $V_{\text{E}}:$

$$\text{cov}\left(P_2,P_1\right)=V_{13}+{\mathit{cov}}_{e_1{e}_2}^{}$$

$$\text{cov}\left(P_2,P_1^2\right)=V_{23}{\sigma }_{e_1}^2\exp \left(\frac{1}{2}{V}_{22}\right)+V_{12}{\mathit{cov}}_{e_1{e}_2}^{}.$$