Joint Models for a Primary Endpoint and Multiple Longitudinal Covariate Processes

Summary

Joint models are formulated to investigate the association between a primary endpoint and features of multiple longitudinal processes. In particular, the subject-specific random effects in a multivariate linear random effects model for multiple longitudinal processes are predictors in a generalized linear model for primary endpoints. Li et al. (2004, Biometrics 60, 1–7) proposed an estimation procedure that makes no distributional assumption on the random effects but assumes independent within-subject measurement errors in the longitudinal covariate process. Based on an asymptotic bias analysis, we found that their estimators can be biased when random effects do not fully explain the within-subject correlations among longitudinal covariate measurements. Specifically, the existing procedure is fairly sensitive to the independent measurement error assumption. To overcome this limitation, we propose new estimation procedures that require neither a distributional or covariance structural assumption on covariate random-effects nor an independence assumption on within-subject measurement errors. These new procedures are more flexible, readily cover scenarios that have multivariate longitudinal covariate processes and can be calculated using available software. Through simulations and an analysis of data from a hypertension study, we evaluate and illustrate the numerical performances of the new estimators.

1. Introduction

It is often of scientific interest to investigate the association between a primary endpoint and features of longitudinal profiles. Joint models for these types of problems are being increasingly applied to situations in which the primary endpoint is a time-to-event outcome (e.g., Henderson et al., 2000; Xu and Zeger, 2001; Tsiatis and Davidian, 2001; Song et al., 2002; Tsiatis and Davidian, 2004) or a single non-survival type outcome (e.g., Wang et al., 2000; Wang and Huang, 2001; Li et al., 2004). A relevant framework for a non-survival primary endpoint, which is the focus of this article, is a generalized linear model (GLM; McCullagh and Nelder, 1989) in which the predictors consist of some observed explanatory variables and certain underlying random effects that characterize the salient features of subject-specific longitudinal processes. We refer to these two types of predictors as observed covariates and random-effect covariates, respectively.

The major challenge in making inferences on the generalized linear model parameters is that the random-effect covariates are not available directly but are observed only through longitudinal measurements and often at different time points. A naive approach which replaces random-effect covariates by the individual ordinary least squares estimates leads to biased estimation (Wang et al., 2000). To reduce these biases, several authors have proposed parametric methods including regression calibration (RC), refined RC (RRC) (Wang et al., 2000) and likelihood-based approaches (Wang et al., 2000, for a non-survival primary endpoint and Wulfson and Tsiatis, 1997 and Xu and Zeger, 2001, for a survival endpoint). These approaches rely heavily on the normality assumption of random effects and inferences may be compromised when this assumption is violated (Verbeke and Lesaffre, 1997; Heagerty and Kurland, 2001; Li et al., 2004). Song et al. (2002) and Tsiatis and Davidian (2001, 2004), among others, proposed joint modeling approaches to relax the normality assumption on random effects for time-to-event responses.

Equivalently, Li et al. (2004) developed sufficiency score (SS) and conditional score (CS) methods under the joint modeling GLM framework. These methods provide valid inferences without specifying the random effects distribution. Like other approaches in the literature, Li et al. (2004)’s approach assumes that within-subject measurement errors in the longitudinal covariate process are independent and identically distributed (IID) and follow a mean zero normal distribution. This assumption implies that the dependence of the longitudinal measurements is explained solely by the random effects. However, in many situations, an additional random component exists which causes the correlation between two error terms to decrease as the time lag between them increases; such error covariance behaviors for longitudinal measurements have been previously reported and commonly observed in practice (e.g., Diggle, 1988). When the IID measurement error assumption is violated, the consequences of making inferences on regression parameters using methods that require this assumption have not been well understood. Unfortunately, the bias analysis we conducted in Section 3 suggests that the potential biases of the SS and the CS can be substantial. Hence, new procedures are needed to address this concern.

The SS and CS estimators of Li et al. (2004) were constructed under the additional assumption that there is a single scalar measurement error variance; this assumption may be unrealistic when multiple longitudinal processes are of interest. In many studies, two or more longitudinal covariates of interest may exist. For example, in the Johns Hopkins Precursors Study (e.g., Golden et al., 2003), a prospective cohort study of former medical students, the investigators were interested in whether the underlying change in longitudinal body mass index (BMI) profiles prior to hypertension was associated with the risk of hypertension later in life, after accounting for the underlying average baseline systolic blood pressure (SBP) in young adulthood. In the dataset, the primary endpoint was the presence or absence of hypertension later in life (say, after age 40), and two longitudinal covariate processes were considered: SBP measurements taken between ages 25 and 35 and BMI measurements taken between age 25 and either the age at which hypertension was diagnosed or age 60, whichever was earlier. Other noticeable features of the longitudinal covariate processes were that SBP variation was much larger than BMI variation, and that the within-subject correlations remained after accounting for the random effects.

Motivated by the above example, we incorporate multiple longitudinal covariate processes into a joint model framework. The main features of the proposed score functions are that the distribution and dependence structure of the random effect covariates are entirely unspecified and that the independence assumption on the within-subject measurement errors is relaxed. As the random effects for distinct longitudinal processes may be correlated, so may be their corresponding measurement errors. We estimate the within-subject measurement error covariance via a robust estimator that is easily computed using available software. Though the proposed approach is slightly more complicated than that of Li et al. (2004), it enables removal of a potentially troublesome assumption. We feel its use is warranted even for situations in which only one longitudinal covariate process exists.

2. Joint Model

To outline the problem, suppose there are n randomly selected subjects and g distinct covariate variables such that for the i^th subject, $m_i^{\left(k\right)}$ observations of the k^th variable are obtained longitudinally. Let $W_{\mathit{ij}}^{\left(k\right)}$ denote such a longitudinal measurement taken at the j^th time point, $j=1,\dots m_i^{\left(k\right)}$. Define ${\mathit{W}}_i^{\left(k\right)}={\left(W_{i1}^{\left(k\right)},\dots ,W_{{\mathit{im}}_i^{\left(k\right)}}^{\left(k\right)}\right)}^{\mathrm{T}}$, a vector that contains all measurements for the k^th longitudinal covariate variable on subject i. Assume ${\mathit{W}}_i^{\left(k\right)}$ follows a linear random effects model of the form,

$${\mathit{W}}_i^{\left(k\right)}={\mathit{D}}_i^{\left(k\right)}{\mathit{X}}_i^{\left(k\right)}+{\mathit{U}}_i^{\left(k\right)},$$ (1)

where ${\mathit{D}}_i^{\left(k\right)}$ is a known full rank design matrix, ${\mathit{X}}_i^{\left(k\right)}$ is a q^(k) × 1 vector of random effects that captures the latent features of the k^th longitudinal process on subject i, and ${\mathit{U}}_i^{\left(k\right)}$ are the within-subject measurement errors and independent of ${\mathit{X}}_i^{\left(k\right)}$. Let ${\mathit{W}}_i={\left({\mathit{W}}_i^{{\left(1\right)}^{\mathrm{T}}},\dots ,{\mathit{W}}_i^{{\left(g\right)}^{\mathrm{T}}}\right)}^{\mathrm{T}}$, X_i and U_i be analogous for ${\mathit{X}}_i^{\left(k\right)}$’s and ${\mathit{U}}_i^{\left(k\right)}$’s, respectively, and denote D_i = block diagonal(${\mathit{D}}_i^{\left(1\right)},\dots ,{\mathit{D}}_i^{\left(g\right)}$). Then the g separate random effects models (1) can be combined into one

$${\mathit{W}}_i={\mathit{D}}_i{\mathit{X}}_i+{\mathit{U}}_i,i=1,\dots ,n.$$ (2)

The distribution and the covariance matrix for X_i are left unspecified. Further, we assume that ${\mathit{U}}_i^{\left(k\right)}~\mathcal{N}(0,{\Omega }_i^{\left(k\right)})$ and that the covariance of U_i is Σ_i = block diagonal(${\Omega }_i^{\left(1\right)},\dots ,{\Omega }_i^{\left(g\right)}$), an M × M covariance matrix, where $M={\sum }_{k=1}^g{m}_i^{\left(k\right)}$. We impose the latter assumption to avoid assuming a potentially high dimensional dependence structure among measurement errors across different longitudinal processes. This assumption is reasonable for measurement errors from different processes. The proposed methods given in Sections 4 and 5 do not require it either provided that all parameters in Σ_i can be consistently estimated. Consequently, the assumption can be easily removed when the need of a more complex dependent structure is warranted. Section 8 discusses additional considerations and potential future work regarding this assumption. Given X_i, W_i has the density function,

$$f({\mathit{W}}_i\mid {\mathit{X}}_i;{\Sigma }_i)={\left(2\pi \right)}^{-M∕2}{\mid {\Sigma }_i\mid }^{-1∕2}\text{exp}\left\{-{({\mathit{W}}_i-{\mathit{D}}_i{\mathit{X}}_i)}^{\mathrm{T}}{\Sigma }_i^{-1}({\mathit{W}}_i-{\mathit{D}}_i{\mathit{X}}_i)∕2\right\}.$$ (3)

In addition to W_i, a primary response, Y_i, and a p-vector of observed covariate, Z_i, which may include a one that corresponds to the intercept, are observed on each subject. We assume that the primary outcome and the multivariate random effect covariates are related via a generalized linear model in canonical form; i.e., the conditional distribution of Y_i given X_i (and Z_i; conditioning on Z_i is dropped throughout for notational convenience) is

$$f(Y_i\mid {\mathit{X}}_i;\theta )=\text{exp}\left\{\frac{Y_i({\alpha }^{\mathrm{T}}{\mathit{Z}}_i+{\beta }^{\mathrm{T}}{\mathit{X}}_i)-b({\alpha }^{\mathrm{T}}{Z}_i+{\beta }^{\mathrm{T}}{\mathit{X}}_i)}{a\left(\varphi \right)}+c\left(Y_{i,}\varphi \right)\right\},$$ (4)

where θ = (α^T, β^T, ϕ)^T are the parameters of primary interest; α and β are regression parameters and ϕ is a dispersion parameter; and a(·), b(·), c(·, ·) are known functions. β is of particular interest because it represents the relationship between the primary endpoint and features of longitudinal profiles. The joint model of primary outcomes Y = (Y₁, … , Y_n)^T and multivariate longitudinal measurements W, equivalently defined, is constructed based on (4) and (2). Following the surrogacy assumption in Carroll et al. (1995), Y_i and W_i are assumed to be independent, conditional on X_i.

3. Bias Analysis

Under the IID normal assumption ${\mathit{U}}_i~\mathcal{N}(0,{\sigma }^2{\mathit{I}}_M)$ where I_l denotes the l × l identity matrix, the re-defined joint model setting of (2) and (4) fits in the the joint model format considered in Li et al. (2004). A natural question arises: will inferences still be valid if we make such an IID assumption and directly apply the methods of Li et al. (2004) when the correlations among within-subject measurement errors are not zero? To illustrate the impact of ignoring these types of correlations on the estimation of θ, we perform a bias analysis. Our findings regarding the sensitivity of the existing methods to a mild violation of the IID measurement error assumption motivated the development of the new methods.

For simplicity let g = 1, m_i = m, and X_i, α and β be scalars. Assume the n longitudinal data W_i follow a random intercept model, as in (2), that W_i = 1X_i + U_i, where 1 is a vector of 1’s, Σ_i, the covariance of U_i, is σ²{(1 – ρ)I_m + ρJ_m} with J_m = 11^T. That is, the true Σ_i has a compound symmetry structure. Let the primary outcome Y_i be binary and follow a logistic model pr(Y_i = 1∣X_i; θ) = H(α + βX_i), where H(u) = (1 + e^−u)⁻¹. Suppose the true Σ_i is incorrectly specified as Σ_iA = σ²I_m (equivalently, correlation is ignored by setting ρ = 0). Let θ_* = (α_*, β_*)^T denote the asymptotic limit of ${\widehat{\theta }}_{\ast }={({\widehat{\alpha }}_{\ast },{\widehat{\beta }}_{\ast })}^{\mathrm{T}}$ which solves the estimating equation based on the SS of Li et al. (2004). Although there is no closed form expression for θ_*, we can numerically calculate θ_* and the asymptotic bias of ${\widehat{\theta }}_{\ast }$ when n → ∞; see Web Appendix A for technical details of the bias calculations.

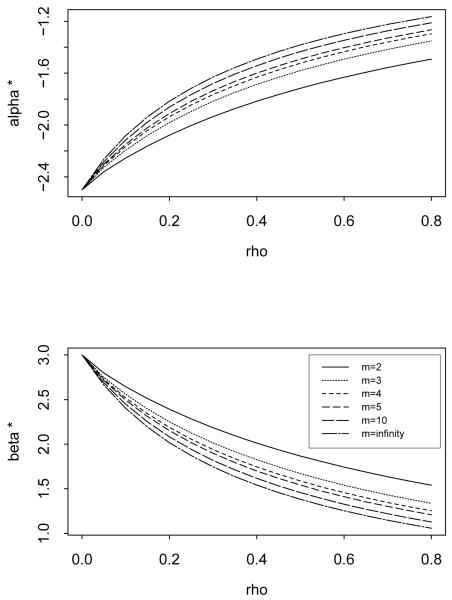
We performed a numerical illustration for this computation of θ_* for ρ varying between 0 and 0.8 and for m ranging from 2 to ∞. The parameter configurations are θ = (α, β)^T = (−2.5, 3)^T and σ² = 1. Figure 1 plots the calculated θ_* = (α_*, β_*)^T against ρ for different cluster size m; this illustrates that α_* is greater than α while β_* is less than β, and the biases worsen for larger ρ. An interesting special case is when the number of longitudinal observations m is large. A common conception is that the effect of measurement errors is eliminated when m → ∞. However, this is not the case here. As m increases, the biases of both naive estimators of α and β become more considerable, which leads us to believe that cluster size is an important factor in the asymptotic biases of the estimators.

Figure 1.

Asymptotic values of parameters α_* and β_* obtained in the asymptotic bias analysis for the SS of Li et al. (2004) versus the true within-subject measurement error correlation parameter ρ. The true values are α = −2.5 and β = 3.0. m denotes the cluster size of longitudinal measurements.

4. Proposed Score Functions

The bias analysis in Section 3 proves that direct application of the SS or the CS to our joint model leads to biased estimation when the IID measurement error assumption is violated. The key development in this section is the establishment of estimators for θ that require neither distributional or dependence structural assumptions on random effects X_i nor an IID assumption on measurement errors U_i. For simplicity, we tentatively treat Σ_i, the covariance matrix for U_i, as if it is known.

4.1 Generalized Sufficiency Score (GSS)

To remove the dependence on X_i, we use conditioning argument after finding a parameter-dependent sufficient statistic for X_i. Consider the functional version of (3) and (4) when X_i are viewed as unknown constants. Under the surrogacy assumption, the joint density of (Y_i, W_i) given X_i is f(Y_i, W_i∣X_i; θ) = f(Y_i∣X_i; θ)f(W_i∣X_i). By viewing X_i as parameters in a an exponential family, we obtain that ${\mathit{S}}_i={\mathit{D}}_i^{\mathrm{T}}{\Sigma }_i^{-1}{\mathit{W}}_i+Y_i\beta ∕a\left(\varphi \right)$ is a complete and sufficient “statistic” for X_i when β and ϕ are fixed. Consequently, the conditional distribution of Y_i given S_i, denoted by f(Y_i∣S_i; θ), is independent of X_i; that is, f(Y_i∣S_i; θ) depends only on Y_i, W_i, and θ. Score functions derived from this conditional distribution will not depend on unobserved X_i. In contrast to Li et al. (2004) which considered the conditional distribution of Y_i and W_i given S_i, we focus on is f(Y_i∣S_i; θ). The Jacobian of transformation taking (Y_i, W_i) into (Y_i, S_i) has a determinant which involves only D_i and Σ_i, which we treat as fixed, thus f(Y_i, S_i∣X_i; θ) ∝ f(Y_i, W_i∣X_i; θ). Hence

$$f(Y_i\mid {\mathit{S}}_i;\theta )=\frac{f(Y_i,{\mathit{S}}_i\mid {\mathit{X}}_i;\theta )}{\int f(y,{\mathit{S}}_i\mid {\mathit{X}}_i;\theta )\mathit{dm}\left(y\right)}=\frac{f(Y_i,{\mathit{W}}_i\mid {\mathit{X}}_i;\theta )}{\int f(y,{\mathit{W}}_i\mid {\mathit{X}}_i;\theta )\mathit{dm}\left(y\right)},$$ (5)

where m(y) is the dominating measure of Y_i and does not depend on θ. Deleting the terms that do not involve Y_i from the numerator and denominator of (5) yields

$$f(Y_i\mid {\mathit{S}}_i;\theta )=\text{exp}\left[Y_i{\eta }_i-\frac{Y_i^2{\beta }^{\mathrm{T}}{\left({\mathit{D}}_i^{\mathrm{T}}{\Sigma }_i^{-1}{\mathit{D}}_i\right)}^{-1}\beta }{2a^2\left(\varphi \right)}+c(Y_i,\varphi )-\log \left\{Q\right({\eta }_i,\beta ,\varphi \left)\right\}\right],$$ (6)

where $Q({\eta }_i,\beta ,\varphi )=\int \text{exp}\left[y{\eta }_i-y^2{\beta }^{\mathrm{T}}{\left({\mathit{D}}_i^{\mathrm{T}}{\Sigma }_i^{-1}{\mathit{D}}_i\right)}^{-1}\beta ∕\left\{2a^2\right(\varphi \left)\right\}+c(y,\varphi )\right]\mathit{dm}\left(y\right)$ and ${\eta }_i=\{{\alpha }^{\mathrm{T}}{\mathit{Z}}_i+{\mathit{S}}_i^{\mathrm{T}}{\left({\mathit{D}}_i^{\mathrm{T}}{\Sigma }_i^{-1}{\mathit{D}}_i\right)}^{-1}\beta \}∕a\left(\varphi \right)$.

The GSS is defined to be ψ_S(Y_i, W_i, θ) = ∂/∂θ{log f(Y_i∣S_i; θ)} evaluated at ${\mathit{S}}_i={\mathit{D}}_i^{\mathrm{T}}{\Sigma }_i^{-1}{\mathit{W}}_i+Y_i\beta ∕a\left(\varphi \right)$. Using the exponential family property in (6) we show that ∂/∂ η_i{logQ(η_i, β, ϕ)} = E(Y_i∣S_i). After some derivations, we deduce GSS, ψ_S(Y_i, W_i, θ), evaluated at ${\mathit{S}}_i={\mathit{D}}_i^{\mathrm{T}}{\Sigma }_i^{-1}{\mathit{W}}_i+Y_i\beta ∕a\left(\varphi \right)$ to be

$$\left(\begin{array}{c}\{Y_i-E(Y_i\mid {\mathit{S}}_i\left)\right\}{\mathit{Z}}_i∕a\left(\varphi \right)\hfill \\ \{Y_i-E(Y_i\mid {\mathit{S}}_i\left)\right\}{\left({\mathit{D}}_i^{\mathrm{T}}{\Sigma }_i^{-1}{\mathit{D}}_i\right)}^{-1}{\mathit{S}}_i∕a\left(\varphi \right)-\{Y_i^2-E(Y_i^2\mid {\mathit{S}}_i\left)\right\}{\left({\mathit{D}}_i^{\mathrm{T}}{\Sigma }_i^{-1}{\mathit{D}}_i\right)}^{-1}\beta ∕a^2\left(\varphi \right)\hfill \\ -\{Y_i-E(Y_i\mid {\mathit{S}}_i\left)\right\}\{{\alpha }^{\mathrm{T}}{\mathit{Z}}_i+{\mathit{S}}_i^{\mathrm{T}}{\left({\mathit{D}}_i^{\mathrm{T}}{\Sigma }_i^{-1}{\mathit{D}}_i\right)}^{-1}\beta \}\partial ∕\partial \varphi \left\{a\right(\varphi \left)\right\}∕a^2\left(\varphi \right)\hfill \\ +\{Y_i^2-E(Y_i^2\mid {\mathit{S}}_i\left)\right\}{\beta }^{\mathrm{T}}{\left({\mathit{D}}_i^{\mathrm{T}}{\Sigma }_i^{-1}{\mathit{D}}_i\right)}^{-1}\beta \partial ∕\partial \varphi \left\{a\right(\varphi \left)\right\}∕a^3\left(\varphi \right)+\partial ∕\partial \varphi \left\{c\right(Y_i,\varphi \left)\right\}\hfill \\ -E[\partial ∕\partial \varphi \{c(Y_i,\varphi )\}\mid {\mathit{S}}_i]\hfill \end{array}\right).$$ (7)

Because E{ψ_S(Y_i, W_i, θ)∣S_i} = ∫ ∂/∂θ{f(y∣S_i; θ)}dm(y) = ∂/∂θ ∫ f(y∣S_i; θ)dm(y) = 0, we have E{ψ_S(Y_i, W_i, θ)} = E [E{ψ_S(Y_i, W_i, θ)∣S_i}] = 0, which means that the GSS is unbiased. Consequently, without any assumption on X_i, we can construct an unbiased estimating equation for θ of the form ${\sum }_{i=1}^n{\psi }_S(Y_i,{\mathit{W}}_i,\theta )=0$.

Under the popular logistic regression model, a(ϕ) = 1, b(u) = log(1+e^u), c(y, ϕ) = 0, and m(·) is the counting measure on (0, 1), (4) becomes pr(Y_i = 1∣X_i; θ) = H(α^TZ_i + β^TX_i), where H(u) = (1+e^−u)⁻¹ and θ = (α^T, β^T)^T; the entry for ϕ in the score function is ignored because there is no ϕ in the model. From (6), it can be shown that Y_i∣S_i follows a logistic model, $\text{pr}(Y_i=1\mid {\mathit{S}}_i;\theta )={\mu }_i=H\{{\alpha }^{\mathrm{T}}{\mathit{Z}}_i+{({\mathit{S}}_i-\beta ∕2)}^{\mathrm{T}}{\left({\mathit{D}}_i^{\mathrm{T}}{\Sigma }_i^{-1}{\mathit{D}}_i\right)}^{-1}\beta \}$ and, from (7), the GSS for the logistic model is

$${\psi }_S(Y_i,{\mathit{W}}_i,\theta )={\left(\begin{array}{c}(Y_i-{\mu }_i){\mathit{Z}}_i\hfill \\ (Y_i-{\mu }_i){\left({\mathit{D}}_i^{\mathrm{T}}{\Sigma }_i^{-1}{\mathit{D}}_i\right)}^{-1}({\mathit{S}}_i-\beta )\hfill \end{array}\right)}_{{\mathit{S}}_i={\mathit{D}}_i^{\mathrm{T}}{\Sigma }_i^{-1}{\mathit{W}}_i+Y_i\beta }.$$ (8)

4.2 Generalized Conditional Score (GCS)

Following McCullagh and Nelder(1989, Section 7.2.2), we define the bias-corrected score as ∂/∂θ{log f(Y_i, W_i∣X_i; θ)} −E[∂/∂θ{log f(Y_i, W_i∣X_i; θ)}∣S_i]. This score function still involves unknown X_i, thus replacing X_i with a ${\sum }_{k=1}^g{q}^{\left(k\right)}$-dimensional vector-valued function of S_i, denoted by t(S_i), leads to the GCS, ψ_C(Y_i, W_i, θ), evaluated at ${\mathit{S}}_i={\mathit{D}}_i^{\mathrm{T}}{\Sigma }_i^{-1}{\mathit{W}}_i+Y_i\beta ∕a\left(\varphi \right)$, to be

$$\left(\begin{array}{c}\{Y_i-E(Y_i\mid {\mathit{S}}_i\left)\right\}{\mathit{Z}}_i∕a\left(\varphi \right)\hfill \\ \{Y_i-E(Y_i\mid {\mathit{S}}_i\left)\right\}\mathit{t}\left({\mathit{S}}_i\right)∕a\left(\varphi \right)\hfill \\ -\{Y_i-E(Y_i\mid {\mathit{S}}_i\left)\right\}\{{\alpha }^{\mathrm{T}}{\mathit{Z}}_i+{\beta }^{\mathrm{T}}\mathit{t}({\mathit{S}}_i\left)\right\}\partial ∕\partial \varphi \left\{a\right(\varphi \left)\right\}∕a^2\left(\varphi \right)+\partial ∕\partial \varphi \left\{c\right(Y_i,\varphi \left)\right\}\hfill \\ -E[\partial ∕\partial \varphi \{c(Y_i,\varphi )\}\mid {\mathit{S}}_i]\hfill \end{array}\right).$$ (9)

Clearly, the GCS is unbiased if E[{Y_i – E(Y_i∣S_i)}t(S_i)] = 0, or equivalently E(E[{Y_i – E(Y_i∣S_i)}t(S_i)]∣S_i) = 0, which can be satisfied when the dependence of t(S_i) on (Y_i, W_i) comes only through S_i. Similar to the reasoning of Lindsay (1985) and Stefanski and Carroll (1987), we achieve the semiparametric efficiency bound of the GCS estimator when t(S_i) = E(X_i∣S_i). Considering ${\widehat{\mathit{X}}}_i={\left({\mathit{D}}_i^{\mathrm{T}}{\Sigma }_i^{-1}{\mathit{D}}_i\right)}^{-1}{\mathit{D}}_i^{\mathrm{T}}{\Sigma }_i^{-1}{\mathit{W}}_i$, the generalized least squares estimator and an unbiased estimator for X_i, and noticing that S_i is sufficient for X_i and that ${\widehat{\mathit{X}}}_i={\left({\mathit{D}}_i^{\mathrm{T}}{\Sigma }_i^{-1}{\mathit{D}}_i\right)}^{-1}\{{\mathit{S}}_i-Y_i\beta ∕a(\varphi \left)\right\}$, we can derive the uniformly minimum variance unbiased estimator (UMVUE) of X_i: $E({\widehat{\mathit{X}}}_i\mid {\mathit{S}}_i)={\left({\mathit{D}}_i^{\mathrm{T}}{\Sigma }_i^{-1}{\mathit{D}}_i\right)}^{-1}\{{\mathit{S}}_i-E(Y_i\mid {\mathit{S}}_i)\beta ∕a(\varphi \left)\right\}$, as a suitable choice for t(S_i). Consequently, we can form an unbiased estimating equation for θ as ${\sum }_{i=1}^n{\psi }_C(Y_i,{\mathit{W}}_i,\theta )=0$, regardless of the distribution of X_i.

For the special case of a logistic primary model pr(Y_i = 1∣X_i; θ) = H(α^TZ_i + β^TX_i), when the UMVUE $\mathit{t}\left({\mathit{S}}_i\right)={\left({\mathit{D}}_i^{\mathrm{T}}{\Sigma }_i^{-1}{\mathit{D}}_i\right)}^{-1}({\mathit{S}}_i-{\mu }_i\beta )$ is chosen, from (9), the GCS is

$${\psi }_C(Y_i,{\mathit{W}}_i,\theta )={\left(\begin{array}{c}(Y_i-{\mu }_i){\mathit{Z}}_i\hfill \\ (Y_i-{\mu }_i){\left({\mathit{D}}_i^{\mathrm{T}}{\Sigma }_i^{-1}{\mathit{D}}_i\right)}^{-1}({\mathit{S}}_i-{\mu }_i\beta )\hfill \end{array}\right)}_{{\mathit{S}}_i={\mathit{D}}_i^{\mathrm{T}}{\Sigma }_i^{-1}{\mathit{W}}_i+Y_i\beta }.$$ (10)

The GSS and the GCS differ in general, but provide very similar inferences; the simulations in Section 6 and the data analysis in Section7 exemplify this observation.

5. Covariance Estimator and Implementation

Both the GSS and the GCS are M-estimators (Huber, 1967). Followed by M-estimator asymptotic (e.g., Carroll et al., 1995, Section A.3.1), with Σ_i in the proposed estimating equations replaced by its consistent estimator, the proposed estimators for θ remain consistent. We now find a consistent estimator for Σ_i to accomplish the new methods.

5.1 Estimation of Within-subject Measurement Error Covariance

As discussed in Section 2, when there is no structural restriction on the covariance matrix Σ_i in practice, the number of unknown parameters in it may be quite large relative to the sample sizes. Consequently, putting a reasonable structure on Σ_i helps stabilize estimation. As stated earlier, we assume that the correlation between ${\mathit{U}}_i^{\left(k\right)}$ and ${\mathit{U}}_i^{\left(k^{\prime }\right)}$ for any k ≠ k’ is negligible. This assumption does not rule out the dependence between any two longitudinal covariate processes because such dependence can exist through the dependence among corresponding random effects. The violation of this assumption may have minimum consequences when structure within (1) is correctly specified; see Section 8.

There exist various meaningful covariance matrices for ${\Omega }_i^{\left(k\right)}$ in which the structures are motivated by applications; examples include m-dependence, Markov structure (or autoregressive of order 1 for equally-spaced times), and completely unstructured. It is well known that when the random effects are normal, under a given covariance structure assumption, ${\Omega }_i^{\left(k\right)}$ can be estimated based on the random effects model (1) for the k^th longitudinal process using maximum likelihood (ML) or restricted maximum likelihood (REML) methods. Then the appropriate estimator of ${\Omega }_i^{\left(k\right)}$, denoted by ${\widehat{\Omega }}_i^{\left(k\right)}$, may be chosen via information criteria such as Akaike’s information criterion (AIC) and Schwarz’s Bayesian information criterion (BIC) using available software (e.g., Diggle et al., 1994; Vonesh and Chinchilli, 1997). ${\widehat{\Sigma }}_i=\text{block}({\widehat{\Omega }}_i^{\left(1\right)},\dots ,{\widehat{\Omega }}_i^{\left(g\right)})$ represents the estimator of Σ_i obtained this way. Asymptotic consistency under general random effect distributions was reported in Verbeke and Lesaffre (1997). Assuming a variety of true random effects distributions, we conducted simulations to investigate the finite sample performance of ${\widehat{\Sigma }}_i$ under non-normal random effects.

We generated longitudinal data from the random effects model W_ij = X_1i + X_2it_ij + U_ij, where the random effects X_i = (X_1i, X_2i)^T represent subject-specific intercept and slope; t_ij = j – 1, j = 1, … , m, (m = 10); i = 1, … , n, (n = 500). The measurement error covariance Σ_i ≡ Σ_i(ρ, σ²) has a Markov structure in which the (j, j’)^th element is equal to σ²ρ^{∣t_ij–t_ij’∣} with σ² = 0.5, −1 ≤ ρ ≤ 1, and for both j, j’ = 1, … , m. We designed four scenarios of the true X_i distribution: (1) a bivariate normal; (2) a bimodal mixture of normals with mixing proportion 30-70; (3) a bivariate skew-normal with coefficients of skewness −0.10 and 0.85 for X_1i and X_2i, respectively; and (4) a bivariate t₅ distribution. For all X_i distribution scenarios, E(X_1i) = E(X_2i) = 0.5, var(X_1i) = 1.0, var(X_2i) = 0.64, and cov(X_1i, X_2i) = −0.2. One thousand data sets were generated for each combination of X_i distribution and choice of ρ.

We used SAS proc mixed (SAS Institute, 2003) to obtain ML estimates of ρ and σ² under the normal random effects assumption. Table 1 shows the results. In all cases and for all datasets, AIC and BIC correctly selected the Markov structure from several candidates of the covariance structure. Estimators for both ρ and σ² show negligible bias and achieve nominal coverage probabilities. Similar features were observed for other true covariance structures, for smaller m (e.g., m = 5), and for smaller n (e.g., n = 100), as well as when REML of ρ and σ² are used. The simulation results indicate that ${\widehat{\Sigma }}_i$ obtained under normality assumption for random effects is insensitive to violations of the normal random effects assumption even for relatively small m and n. Similar robustness findings have been reported by others (Beal and Sheiner, 1988; Butler and Louis, 1992) for longitudinal data with univariate random effects. Here, we have demonstrated satisfactory numerical performances for finite samples and under a wide range of true multivariate random effects distributions.

Table 1.

Simulation results for the MLE of within-subject measurement error covariance parameters ρ and σ² in a random effects model obtained under the normal random effects X_i assumption. True σ² = 0.50 and four underlying X_i distributions are considered. Reported values are Mean, Monte Carlo average of estimate; RB, estimated relative bias (presented as percentages), as the difference between the Monte Carlo average of estimates and the true parameter, divided by the true parameter; SD, Monte Carlo standard deviation; SE, average of estimated standard errors; CP, Monte Carlo coverage probability of 95% Wald confidence interval.

True ρ		Mean	RB (%)	SD	SE	CP	Mean	RB	SD	SE	CP
Xi Normal							Xi Bimodal mixture
0.25	$\widehat{\rho }$	0.25	0.6	0.02	0.02	0.96	0.25	−0.2	0.02	0.02	0.96
	${\widehat{\sigma }}^2$	0.50	0.1	0.02	0.02	0.95	0.50	0.1	0.02	0.02	0.95
0.50	$\widehat{\rho }$	0.50	0.3	0.02	0.02	0.95	0.50	−0.2	0.03	0.02	0.94
	${\widehat{\sigma }}^2$	0.50	0.4	0.03	0.03	0.95	0.50	0.1	0.03	0.03	0.95
−0.25	$\widehat{\rho }$	−0.25	−0.5	0.02	0.02	0.95	−0.25	0.0	0.02	0.02	0.96
	${\widehat{\sigma }}^2$	0.50	−0.1	0.01	0.01	0.95	0.50	0.1	0.01	0.01	0.93
−0.50	$\widehat{\rho }$	−0.50	−0.2	0.01	0.01	0.94	−0.50	0.0	0.01	0.01	0.96
	${\widehat{\sigma }}^2$	0.50	−0.2	0.01	0.01	0.94	0.50	0.1	0.01	0.01	0.94
Xi Skew-normal							Xi Bivariate t5
0.25	$\widehat{\rho }$	0.25	0.1	0.02	0.02	0.97	0.25	0.0	0.02	0.02	0.96
	${\widehat{\sigma }}^2$	0.50	0.0	0.02	0.02	0.96	0.50	0.1	0.02	0.02	0.96
0.50	$\widehat{\rho }$	0.50	0.0	0.02	0.02	0.97	0.50	0.0	0.03	0.03	0.95
	${\widehat{\sigma }}^2$	0.50	0.2	0.03	0.03	0.96	0.50	0.3	0.03	0.03	0.96
−0.25	$\widehat{\rho }$	−0.25	0.0	0.02	0.02	0.96	−0.25	−0.2	0.02	0.02	0.96
	${\widehat{\sigma }}^2$	0.50	0.0	0.01	0.01	0.95	0.50	0.1	0.01	0.01	0.96
−0.50	$\widehat{\rho }$	−0.50	0.0	0.01	0.01	0.95	−0.50	−0.1	0.01	0.01	0.95
	${\widehat{\sigma }}^2$	0.50	0.0	0.01	0.01	0.95	0.50	0.0	0.01	0.01	0.95

5.2 Inference and Implementation

To implement the GSS and the GCS after Σ_i is replaced by ${\widehat{\Sigma }}_i$, we use the Newton-Raphson algorithm to solve the estimating equations. Although the estimating equations technically may have multiple roots, the “correct” consistent solution $\widehat{\theta }$ may be identified via the use of a naive or RC estimate as the starting value. Such $\widehat{\theta }$ is asymptotically normal because the GSS and GCS estimators are M-estimators, and thus the empirical sandwich method (e.g., Carroll et al., 1995, Section A.3.1) may be used to calculate standard errors; see Web Appendix B for the first order derivatives of the GSS (8) and the GCS (10) for the logistic primary model discussed in Section 4.

Consider a reparameterization by defining ${\tilde{\mathit{W}}}_i={\Sigma }_i^{-1∕2}{\mathit{W}}_i$, ${\tilde{\mathit{D}}}_i={\Sigma }_i^{-1∕2}{\mathit{D}}_i$, and ${\tilde{\mathit{U}}}_i={\Sigma }_i^{-1∕2}{\mathit{U}}_i$, then model (2) is equivalent to ${\tilde{\mathit{W}}}_i={\tilde{\mathit{D}}}_i{\mathit{X}}_i+{\tilde{\mathit{U}}}_i$, where ${\tilde{\mathit{U}}}_i~\mathcal{N}(0,\mathit{I})$. This reparameterization yields a joint model under the exact framework considered by Li et al. (2004) with σ² = 1. Hence, we can alternatively implement the proposed approaches using a combination of reparameterization and the methods of Li et al. (2004). When we leave σ² to be estimated, the estimate should be very close to 1; this can be used to check potential covariance structural mis-specification. Our numerical experiences suggest that the direct implementation of the GSS and GCS on (4) and (2) using the Newton-Raphson algorithm and the reparameterization alternative provide virtually identical results. A summary of the complete estimation procedure is provided in Web Appendix B.

6. Simulation

To evaluate the performances of the proposed methods, we conducted simulations. We generated longitudinal data using the same scheme as in the simulations in Section 5.1 and considered the same four scenarios for the true random effects distribution. Binary observations Y_i were generated from logistic model H(α + β^TX_i) with α = −2.5, β = (β₁, β₂)^T = (3.0, 2.0)^T. For each scenario of X_i distribution and a choice of ρ, one thousand datasets were simulated. For each data set, we examined six estimators for θ = (α, β₁, β₂)^T: (i) the RRC, the refined regression calibration estimator in Wang et al. (2000), which has better performance for logistic primary model than do other estimators in the literature (e.g., the naive and RC estimators) that require normal X_i when this assumption holds; (ii) a generalized version of the RRC (GRRC) which applies the RRC after parameterization of W_i and D_i as in Section 5.2; (iii) the SS; (iv) the GSS; (v) the CS; and (vi) the GCS. The RRC and the GRRC are available only for the logistic and probit models. The RRC and the GRRC depend on normality of X_i and the RRC, the SS and the CS impose the IID assumption on U_i, but the proposed GSS and GCS require neither of these restrictions. Tables 2–3 show the results including relative bias, Monte Carlo standard deviation, average of estimated standard errors, and 95% Wald coverage probability. Web Tables S.1-2 present results of additional simulations with negative ρ values. In all cases, the proposed GSS and GCS always exhibit negligible bias, attain nominal coverage probabilities, and yield similar results, regardless of the underlying X_i distribution and whether the within-subject measurement error correlation is small or large, negative or positive; these findings are consistent with our theory. In general, performance degradation is observed for the competing estimators when the departures from normal X_i exist and when measurement errors are correlated. The RRC, the SS and the CS show substantial bias through underestimating θ when ρ is positive and overestimating θ when ρ is negative; further, their biases and failures to achieve nominal coverage become much more severe for larger absolute value of ρ, except that the RRC has acceptable performance for bimodal X_i when ρ is small and positive. Accounting for the correlation of measurement errors, the GRRC demonstrates expected good performance similar to that of the GSS and the GCS when the normal X_i is true or slightly violated by mild skewness. However, under bimodal X_i, the GRRC noticeably overestimates θ and its coverage is off nominal, and under heavy-tailed X_i, it underestimates θ with coverage falling short of nominal level. The overall poor performances of the competing estimators are more pronounced for positive ρ, which is often the case in practice, than for negative ρ.

Table 2.

Simulation results for the joint model with ρ = 0.25 under four underlying X_i distributions. In the logistic model, true α = −2.5 and β = (β₁, β₂)^T = (3.0, 2.0)^T. Reported values are RB, relative bias (%); SD, Monte Carlo standard deviation; SE, average of estimated standard errors; CP, Monte Carlo coverage probability of 95% Wald confidence interval.

ρ = 0.25	Method	RB (%)	SD	SE	CP	RB (%)	SD	SE	CP
Xi Normal						Xi Bimodal mixture
$\widehat{\alpha }$	RRC	−14.2	0.26	0.27	0.70	−1.6	0.39	0.39	0.95
	GRRC	1.9	0.38	0.38	0.96	36.0	0.87	0.81	0.99
	SS	−13.5	0.27	0.28	0.71	−11.2	0.34	0.34	0.81
	GSS	3.6	0.42	0.42	0.96	4.4	0.52	0.48	0.97
	CS	−13.5	0.27	0.28	0.72	−11.4	0.34	0.34	0.79
	GCS	3.5	0.42	0.43	0.96	4.6	0.51	0.50	0.96
${\widehat{\beta }}_1$	RRC	−16.8	0.27	0.28	0.52	6.7	0.43	0.42	0.97
	GRRC	1.9	0.44	0.43	0.96	44.8	1.06	0.95	0.99
	SS	−16.1	0.28	0.29	0.52	−7.3	0.30	0.30	0.83
	GSS	3.8	0.50	0.49	0.96	3.5	0.44	0.40	0.96
	CS	−16.1	0.28	0.29	0.55	−7.5	0.30	0.29	0.82
	GCS	3.7	0.49	0.50	0.96	3.7	0.43	0.42	0.96
${\widehat{\beta }}_2$	RRC	−10.3	0.23	0.24	0.83	1.8	0.32	0.31	0.96
	GRRC	1.9	0.31	0.31	0.96	28.0	0.61	0.57	0.98
	SS	−9.6	0.24	0.24	0.85	−5.5	0.29	0.28	0.90
	GSS	3.4	0.34	0.33	0.96	3.8	0.39	0.36	0.96
	CS	−9.6	0.24	0.24	0.85	−5.7	0.29	0.28	0.89
	GCS	3.3	0.33	0.34	0.96	4.0	0.38	0.36	0.96
Xi Skew-normal						Xi Bivariate t5
$\widehat{\alpha }$	RRC	−14.3	0.27	0.27	0.68	−20.6	0.25	0.25	0.46
	GRRC	1.7	0.38	0.38	0.95	−7.7	0.33	0.33	0.86
	SS	−13.7	0.27	0.28	0.70	−16.5	0.27	0.27	0.63
	GSS	2.9	0.41	0.41	0.95	3.9	0.46	0.45	0.96
	CS	−13.7	0.27	0.28	0.70	−16.5	0.27	0.27	0.62
	GCS	2.9	0.41	0.42	0.95	3.8	0.43	0.45	0.95
${\widehat{\beta }}_1$	RRC	−17.0	0.27	0.28	0.52	−24.0	0.25	0.26	0.22
	GRRC	1.5	0.43	0.43	0.95	−8.8	0.37	0.37	0.82
	SS	−16.5	0.27	0.28	0.52	−19.6	0.28	0.29	0.44
	GSS	2.8	0.47	0.48	0.96	4.1	0.55	0.53	0.96
	CS	−16.5	0.27	0.28	0.53	−19.5	0.28	0.29	0.44
	GCS	2.8	0.46	0.49	0.95	4.0	0.51	0.54	0.95
${\widehat{\beta }}_2$	RRC	−10.2	0.24	0.24	0.82	−15.7	0.23	0.23	0.69
	GRRC	1.8	0.31	0.31	0.96	−6.3	0.29	0.28	0.89
	SS	−9.7	0.24	0.24	0.84	−12.1	0.25	0.24	0.81
	GSS	2.9	0.32	0.33	0.96	3.6	0.38	0.36	0.96
	CS	−9.7	0.24	0.24	0.84	−12.1	0.25	0.24	0.81
	GCS	2.9	0.32	0.33	0.96	3.5	0.36	0.36	0.95

Table 3.

Simulation results for the joint model with ρ = 0.50 under four underlying X_i distributions. The rest of the setup is identical to that of Table 2.

ρ = 0.50	Method	RB (%)	SD	SE	CP	RB (%)	SD	SE	CP
Xi Normal						Xi Bimodal mixture
$\widehat{\alpha }$	RRC	−28.8	0.21	0.22	0.13	−25.5	0.27	0.29	0.38
	GRRC	1.0	0.45	0.42	0.94	57.2	2.38	3.26	1.00
	SS	−28.5	0.21	0.22	0.14	−28.9	0.26	0.27	0.26
	GSS	2.8	0.49	0.50	0.96	2.9	0.57	0.55	0.96
	CS	−28.5	0.21	0.22	0.14	−29.2	0.26	0.27	0.25
	GCS	1.5	0.41	0.47	0.94	2.5	0.53	0.56	0.95
${\widehat{\beta }}_1$	RRC	−33.9	0.19	0.20	0.01	−15.4	0.27	0.29	0.59
	GRRC	0.7	0.53	0.49	0.94	69.0	2.94	4.02	1.00
	SS	−33.6	0.20	0.21	0.02	−20.9	0.23	0.24	0.28
	GSS	3.0	0.62	0.60	0.95	2.2	0.47	0.47	0.95
	CS	−33.6	0.20	0.21	0.02	−21.1	0.23	0.24	0.26
	GCS	1.3	0.48	0.55	0.94	1.9	0.44	0.48	0.94
${\widehat{\beta }}_2$	RRC	−21.5	0.19	0.20	0.40	−13.5	0.24	0.25	0.75
	GRRC	0.9	0.35	0.34	0.95	45.6	1.60	2.22	1.00
	SS	−21.2	0.20	0.20	0.42	−16.2	0.24	0.24	0.68
	GSS	2.7	0.40	0.39	0.96	2.9	0.41	0.40	0.96
	CS	−21.2	0.20	0.20	0.41	−16.4	0.23	0.24	0.67
	GCS	1.5	0.34	0.37	0.96	2.6	0.38	0.40	0.95
Xi Skew-normal						Xi Bivariate t5
$\widehat{\alpha }$	RRC	−28.9	0.22	0.22	0.13	−34.5	0.20	0.21	0.03
	GRRC	0.5	0.44	0.42	0.93	−11.5	0.35	0.34	0.78
	SS	−28.6	0.22	0.22	0.14	−32.9	0.21	0.22	0.06
	GSS	2.3	0.49	0.49	0.94	3.1	0.56	0.57	0.95
	CS	−28.6	0.22	0.22	0.14	−32.9	0.21	0.22	0.06
	GCS	1.9	0.50	0.49	0.94	1.3	0.45	0.50	0.94
${\widehat{\beta }}_1$	RRC	−34.0	0.20	0.20	0.01	−40.1	0.18	0.19	0.00
	GRRC	0.2	0.51	0.48	0.93	−12.9	0.39	0.39	0.72
	SS	−33.8	0.20	0.21	0.01	−38.4	0.19	0.20	0.00
	GSS	2.1	0.58	0.58	0.95	3.2	0.69	0.68	0.94
	CS	−33.8	0.20	0.21	0.01	−38.4	0.19	0.20	0.00
	GCS	1.7	0.60	0.59	0.94	1.2	0.53	0.60	0.93
${\widehat{\beta }}_2$	RRC	−21.3	0.21	0.20	0.43	−26.3	0.20	0.20	0.25
	GRRC	0.8	0.35	0.33	0.95	−9.6	0.30	0.29	0.84
	SS	−21.0	0.21	0.20	0.45	−24.7	0.21	0.20	0.30
	GSS	2.3	0.38	0.38	0.95	3.2	0.45	0.44	0.95
	CS	−21.0	0.21	0.20	0.45	−24.7	0.21	0.20	0.30
	GCS	2.2	0.40	0.38	0.95	1.6	0.38	0.39	0.95

7. Application

The main interest of the hypertension study discussed in Section 1 was to investigate the effects of lifetime longitudinal processes on latter-in-life health outcomes, particularly the association between the risk of hypertension later in life (age > 40) and features of longitudinal BMI profiles, and the association between the risk of hypertension later in life and the underlying mean SBP in young adulthood. The study included 782 individuals from the Johns Hopkins Precursors Study who were less than 30 years old at enrollment and who had not developed hypertension by age 40. Among those individuals, 192 never developed hypertension. Let Y_i = 1 and 0 denote the presence and absence of hypertension for individual i, respectively, i = 1, … , n, (n = 782). The two longitudinal covariate processes were longitudinal SBP readings in young adulthood between ages 25 and 35 and longitudinal BMI measurements prior to the occurrence of hypertension or between ages 25 and 60. For each individual, the number of SBP observations ranged from 1 to 8 and the number of BMI observations ranged from 1 to 24. Web Figure S.1 contains scatter plots and fitted lines of longitudinal BMI measurements from several individuals. The covariates of interest were the baseline SBP, the baseline BMI, and the BMI trend.

We consider a random intercept model for the longitudinal SBP observations and a random intercept-slope model for the BMI measurements,

$$W_{\mathit{ij}}^{\mathit{SBP}}=X_i^{\mathit{SBP}}+U_{\mathit{ij}}^{\mathit{SBP}},W_{\mathit{ij}}^{\mathit{BMI}}=X_{1i}^{\mathit{BMI}}+X_{2i}^{\mathit{BMI}}{\text{age}}_{\mathit{ij}}+U_{\mathit{ij}}^{\mathit{BMI}},$$ (11)

where $X_i^{\mathit{SBP}}$, $X_{1i}^{\mathit{BMI}}$ and $X_{2i}^{\mathit{BMI}}$ are the individual-specific “true” average SBP in young adulthood, BMI intercept and slope, respectively. Letting ${\mathit{W}}_i={(W_{i1}^{\mathit{SBP}},\dots ,W_{{\mathit{im}}_i^{\mathit{SBP}}}^{\mathit{SBP}},W_{i1}^{\mathit{BMI}},\dots ,W_{{\mathit{im}}_i^{\mathit{BMI}}}^{\mathit{BMI}})}^{\mathrm{T}}$, D_i = block diagonal($1,{\mathit{D}}_i^{\mathit{BMI}}$) with ${\mathit{D}}_i^{\mathit{BMI}}$ having 1’s in the first column and ages of individual i at which BMI was measured in the second column, and ${\mathit{U}}_i={(U_{i1}^{\mathit{SBP}},\dots ,U_{{\mathit{im}}_i^{\mathit{SBP}}}^{\mathit{SBP}},U_{i1}^{\mathit{BMI}},\dots ,U_{{\mathit{im}}_i^{\mathit{BMI}}}^{\mathit{BMI}})}^{\mathrm{T}}~\mathcal{N}(0,{\Sigma }_i)$, we combine the two models in (11) into the format given in (2). The relationship between the risk of hypertension and ${\mathit{X}}_i={(X_i^{\mathit{SBP}},X_{1i}^{\mathit{BMI}},X_{2i}^{\mathit{BMI}})}^{\mathrm{T}}$ is described by the logistic model:

$$P(Y_i=1\mid {\mathit{X}}_i)={[1+\text{exp}\{-(\alpha +{\beta }_1{X}_i^{\mathit{SBP}}+{\beta }_2{X}_{1i}^{\mathit{BMI}}+{\beta }_2{X}_{2i}^{\mathit{BMI}})\left\}\right]}^{-1}.$$ (12)

We fit the joint model using the proposed GSS and GCS under three scenarios of the covariance structure of U_i: (a) IID with the same σ² for SBP and BMI, i.e., Σ_i = σ²I — fitting model (11) under this structure results in ${\widehat{\sigma }}^2=9.2552$; (b) independent errors but with different σ² for SBP and BMI, i.e., Σ_i = block (σ^{2 SBP}I, σ^{2 BMII}I) — fitting the models in (11) yields ${\widehat{\sigma }}^{2\text{SBP}}=61.8480$ and ${\widehat{\sigma }}^{2\text{BMI}}=0.7813$, respectively; and (c) preferred structure of Σ_i = block diagonal (${\Omega }_i^{\text{SBP}}$, ${\Omega }_i^{\text{BMI}}$) by the information criteria AIC and BIC based on the goodness of fits of models in (11) among various covariance structures. Specifically, the outcomes of our analysis lead to the preferred structure for ${\Omega }_i^{\text{SBP}}$ being the Markov structure, as described in Section 5.1, with ${\widehat{\rho }}^{\text{SBP}}=0.4220$ and ${\widehat{\sigma }}^{2\text{SBP}}=68.7562$, and the preferred structure for ${\Omega }_i^{\text{BMI}}$ being the Markov structure with ${\widehat{\rho }}^{\text{BMI}}=0.6278$ and ${\widehat{\sigma }}^{2\text{BMI}}=1.0212$.

Table 4 displays $\widehat{\theta }={(\widehat{\alpha },{\widehat{\beta }}_1,{\widehat{\beta }}_2,{\widehat{\beta }}_3)}^{\mathrm{T}}$ and estimated standard errors. The difference in variance components (σ²) between SBP and BMI is very sizable. When we completely ignore the existence of correlation among within-subject measurement errors and the heterogeneity between SBP and BMI by using structure (a), which is equivalent to a direct application of the SS and the CS, inferences are flawed. For example, the estimated coefficients for BMI intercept (or slope) differ considerably when we apply the SS and the CS. The coefficient for BMI intercept is negative using one method but significantly positive using the other. This phenomenon no longer exists when the covariance structure is less poorly specified, as in structures (b) and (c). In the absolute scale, the relative changes of the four estimated coefficients using models (b) and (c) are, 13%, 25%, 100% and 2%, respectively. That is, if one model is correct, the estimates assumed the other could bear substantial biases. Based on the knowledge gained from our numerical studies, the most reliable inferences should be those using structure (c).

Table 4.

Analysis of the hypertension data under three scenarios of the within-subject measurement error covariance: (a) IID with same σ² for SBP and BMI: Σ_i = σ²I for ${\widehat{\sigma }}^2=9.2552$; (b) Independent with different σ² for SBP and BMI: Σ_i = block (σ^{2 SBP}I, σ^{2 BMI}I) for ${\widehat{\sigma }}^{2\mathit{SBP}}=61.8480$ and ${\widehat{\sigma }}^{2\mathit{BMI}}=0.7813$; (c) Following a structure preferred by information criteria: Σ_i = block (${\Omega }_i^{\mathit{SBP}}$, ${\Omega }_i^{\mathit{BMI}}$) where ${\Omega }_i^{\mathit{SBP}}$ has Markov structure with ${\widehat{\rho }}^{\mathit{SBP}}=0.4220$ and ${\widehat{\sigma }}^{2\mathit{SBP}}=68.7562$, and ${\Omega }_i^{\mathit{BMI}}$ has Markov structure with ${\widehat{\rho }}^{\mathit{BMI}}=0.6278$ and ${\widehat{\sigma }}^{2\mathit{BMI}}=1.0212$. Estimated standard errors are in parentheses below each estimate.

	Intercept		SBPyoung adulthood		BMIintercept		BMIslope
	Estimate	p-value	Estimate	p-value	Estimate	p-value	Estimate	p-value
(a) Σi = σ2I
SS	−28.30 (7.62)	0.00	0.28 (0.07)	0.00	−0.35 (0.26)	0.17	49.17 (11.98)	0.00
CS	−103.20 (15.51)	0.00	0.63 (0.15)	0.00	1.73 (0.23)	0.00	82.78 (11.23)	0.00
(b) Σi = block (σ2 SBPI, σ2 BMII)
GSS	−18.03 (2.86)	0.00	0.12 (0.02)	0.00	0.08 (0.05)	0.07	6.81 (1.76)	0.00
GCS	−18.36 (2.94)	0.00	0.13 (0.03)	0.00	0.08 (0.05)	0.09	6.80 (1.77)	0.00
(c) Σi = block (${\Omega }_i^{\text{SBP}}$,${\Omega }_i^{\text{BMI}}$) where both ${\Omega }_i^{\text{SBP}}$ and ${\Omega }_i^{\text{BMI}}$ have preferred Markov structures
GSS	−20.84 (3.72)	0.00	0.16 (0.03)	0.00	0.04 (0.06)	0.46	6.94 (1.99)	0.00
GCS	−21.96 (4.25)	0.00	0.17 (0.04)	0.00	0.03 (0.06)	0.61	7.03 (2.11)	0.00

The analysis using the proposed GSS and GCS and the preferred Σ_i structure (c) suggests that the risk of having hypertension later in life may remain highly positively associated with baseline SBP in young adulthood, after adjusting for the effects from BMI measurements. Inferences also indicate a strong positive association between presence of hypertension later in life and the rate of change in BMI prior to developing hypertension, after adjusting for other covariates such as baseline SBP and baseline BMI. This suggests that the rate of change in BMI may be an important covariate for predicting the risk of developing hypertension.

In terms of verifying the assumptions made in structure (c), an examination of histograms of SBP and BMI residuals suggests that the normality assumption for $U_{\mathit{ij}}^{\mathit{SBP}}$ and $U_{\mathit{ij}}^{\mathit{BMI}}$ is reasonable. The correlations between the SBP and BMI residuals taken from the same time points are very small, which suggests the conditional independence between the longitudinal covariate processes given X_i. To verify the surrogacy assumption, we compared the histograms of the covariate processes residuals for Y_i = 1 with those for Y_i = 0. Their bell-shapes and first several moments, including mean, standard deviation and skewness, were similar; this indicates the conditional independence between Y_i and W_i given X_i.

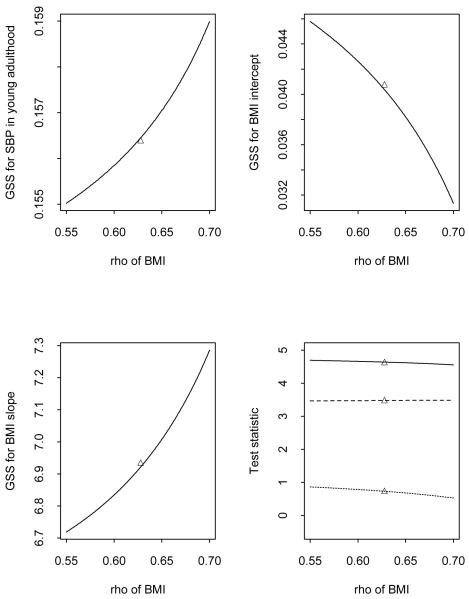
Although asymptotic results indicate that the estimators of θ remain consistent when the GSS and the GCS are implemented by substituting ${\widehat{\Sigma }}_i$ in the score functions, it is desirable to check how insensitive the inferences on θ are to changes of covariance in a neighborhood of ${\widehat{\Sigma }}_i$. Figure 2 presents results that correspond to one such sensitivity analysis in which we let ρ^BMI vary in a neighborhood of ${\widehat{\rho }}^{\text{BMI}}=0.6278$. The analysis was conducted by fixing ${\widehat{\rho }}^{\text{SBP}}=0.4220$ and ${\widehat{\sigma }}^{2\text{SBP}}=68.7562$, letting ρ^BMI vary between 0.55 and 0.70, and estimating ${\widehat{\sigma }}^{2\text{BMI}}$ accordingly. Figure 2 shows that when ρ ^BMI decreases, the GSS estimated coefficients for baseline SBP and BMI slope decrease while the estimated coefficient for average BMI increases. This reflects the complex interplay between measurement errors and multivariate correlated covariate processes. Although these GSS estimates have slight changes, their corresponding test statistics (estimated coefficient divided by the estimated standard error) are nearly insensitive to small changes in ρ^BMI. We observe similar behavior using the GCS and in the sensitivity analysis with respect to slight changes in ρ^SBP.

Figure 2.

Sensitivity of the GSS estimates and their test statistics (estimate divided by estimated standard error) in the hypertension data analysis with respect to changes of withinsubject measurement error correlation parameter ρ in a neighborhood of ${\widehat{\rho }}^{\text{BMI}}=0.6196$. In the plot of test statistics, the solid line is the test statistic for SBP in young adulthood, the dashed line is that for the BMI slope, and the dotted line is that for the BMI intercept. △ denotes the results from actual data analysis.

8. Discussion

We have proposed a joint modeling framework to accommodate outcomes for which a primary endpoint follows a generalized linear model whose covariates are the random effects from multiple longitudinal processes. We have demonstrated that when there are departures from the IID assumption for within-subject measurement errors, direct application of the SS and the CS of Li et al. (2004) leads to considerable biases and that the magnitude of these biases increases as cluster sizes and correlations increase. The proposed GSS and GCS need neither a distributional nor a covariance structural assumption on random effect covariates and allow flexible measurement error covariance structures chosen by objective information criteria. Compared with competing estimators that rely on the normality assumption of random effects and/or the IID assumption of within-subject measurement errors, the GSS and the GCS yield sound inferences when these assumptions are violated. The model framework is applicable to unbalanced longitudinal data; that is, neither the same number of observations per subject nor the same number of observations from different longitudinal covariate processes is required. To be scientifically meaningful, different numbers or types of random effects can be posited to depict the specific features of different longitudinal processes.

The establishment of the GSS and the GCS does not require conditional independence among longitudinal covariate processes given the random effects, as illustrated in Section 4. However, it is reasonable to assume that measurement errors from different longitudinal processes are independent. Further, since individual process would contain sufficient information for the distribution of ${\mathit{X}}_i^{\left(k\right)}$ provided that model (1), particularly the structure of ${\Omega }_i^{\left(k\right)}$, can be correctly specified, we conjecture that the misspecification of the covariance structure of two sets of measurement errors from two different processes would cause only inefficiency. Our numerical study described in Web Appendix C seems to support this conjecture, or at least show the insensitivity of the proposed methods toward this type of model misspecification. The establishment of theoretical consistency is currently under study. For computational convenience, we suggest that the within-subject measurement error covariance within each longitudinal process be estimated using the covariance estimator obtained by the MLE or the REML with the normal random effects via available software for mixed effects models. The covariance estimator performs well and stably as long as the number of longitudinal observations per subject is not too small on average (m ≥ 5) or the number of subjects n is moderate. Implementation of the GSS and the GCS is easy and fast (less than 1 minute for our data set) via the Newton-Raphson algorithm or, alternatively, via a reparameterization of data and an application of the SS and the CS.

Although we focused on generalized linear models, this methodology can be applied to time-to-event endpoints. For instance, model (4) can be replaced by a Cox proportional hazards model and a conditional score function with known Σ_i can be derived similar to Tsiatis and Davidian (2004); Σ_i in the score function is substituted by a consistent estimator. Further, fixed effects can be included in distinct random effects models (1), i.e., ${\mathit{W}}_i^{\left(k\right)}={\mathit{C}}_i^{\left(k\right)}{\gamma }^{\left(k\right)}+{\mathit{D}}_i^{\left(k\right)}{\mathit{X}}_i^{\left(k\right)}+{\mathit{U}}_i^{\left(k\right)}$ for observed covariates ${\mathit{C}}_i^{\left(k\right)}$. The proposed methodology remains the same by viewing ${\mathit{W}}_i^{\left(k\right)}-{\mathit{C}}_i^{\left(k\right)}{\gamma }^{\left(k\right)}$ as the ${\mathit{W}}_i^{\left(k\right)}$ in this paper and adding another set of estimating equations that yield consistent estimation of γ^(k).

Likelihood-based methods with relaxed distributional assumptions on random effects proposed for proportional hazards model (Song et al., 2001) and for generalized linear model (Li et al., 2006), which may gain some efficiency (e.g., 2%–38% efficiency gains in generalized linear model parameter estimates as shown in Li et al., 2006), were developed under the IID measurement error assumption and thus may result in biased inference when this assumption is violated. Moreover, computational complexity is another major concern for these approaches, especially when multiple longitudinal processes are included and each has multidimensional random effects.