There Goes the Neighborhood Effect: Bias Due to Non-Differential Measurement Error in the Construction of Neighborhood Contextual Measures

Abstract

BACKGROUND

Multilevel studies of neighborhood impacts on health frequently aggregate individual-level data to create contextual measures. For example, percent of residents living in poverty and median household income are both aggregations of Census data on individual-level household income. Because household income is sensitive and complex, it is likely to be reported with error.

METHODS

To assess the impact of such error on effect estimates for neighborhood contextual factors, we conducted simulation studies to relate neighborhood measures derived from Census data to individual body mass index, varying the extent of non-differential misclassification/measurement error in the underlying Census data. We then explored the relationship between the form of variables chosen for neighborhood measure and outcome, modeling technique used, size and number of neighborhoods, and categorization of neighborhoods to the magnitude of bias.

RESULTS

For neighborhood contextual variables expressed as percentages (e.g. % of residents living in poverty), non-differential misclassification in the underlying individual-level Census data always biases the parameter estimate for the neighborhood variable away from the null. However, estimates of differences between quantiles of neighborhoods using such contextual variables are unbiased. Aggregation of the same underlying individual-level Census income data into a continuous variable, such as median household income, also introduces bias into the regression parameter. Such bias is non-negligible if the sampled groups are small.

CONCLUSIONS

Decisions regarding the construction and analysis of neighborhood contextual measures substantially alter the impact on study validity of measurement error in the data used to construct the contextual measure.

Within epidemiology there is a large literature on the effects of non-differential measurement error or misclassification of individuals’ exposures on the magnitude of statistical association: such error usually biases an epidemiological effect estimate to the null¹. For instance, in a study of the effect of personal income on body mass index (BMI) (e.g. ²), non-differential measurement error in income assessment would decrease the apparent association between income and BMI. There is a smaller literature on the effects of exposure measurement error in cross-sectional ecologic studies, such as a study relating the proportion of residents living below poverty across counties to the proportion of people in those counties who are obese^3,4. For this type of study, data on individual poverty status is aggregated to determine the proportion of residents in each county who live in poverty; if there is misclassification of individuals’ poverty status, effect estimates are biased away from the null⁴.

However, there is almost no literature on how non-differential measurement error or misclassification of exposure affects multilevel studies of neighborhood health effects on individual’s health outcomes. Multilevel neighborhood health effect studies typically include individual level outcome measures in a study population (e.g. individual’s BMI), individual level predictors measured from the study participants (e.g. age, race/ethnicity, gender, income) and neighborhood level contextual predictors derived from Census data (e.g. neighborhood poverty rates). One of the goals of such studies is to quantify the effect of a neighborhood context feature (e.g. neighborhood poverty) on individual outcomes after adjusting for individual covariates. Neighborhood contextual measures are often computed by aggregating data collected from individuals during the Decennial Census, American Community Survey, or another large social survey. Sensitive information, including income, is likely to be measured with error in these surveys⁵. A detailed review has suggested that under-reporting and over-reporting are about equally common⁶; for many outcomes, researchers might reasonably expect such error to be non-differential. It has previously been argued that non-differential measurement error in survey data causes bias away from the null for effect estimates relating outcome variables measured at the individual level in a study population to a neighborhood contextual variable created by aggregating individual-level survey data from respondents who live in each neighborhood⁷. However, the potential magnitude of the bias has not been documented, nor has the quantitative relationship between the extent of measurement error and bias.

For a given neighborhood context measure created by aggregating data collected from individuals, an investigator may have several options as to how to create a contextual variable⁸. For instance, ‘median household income’ and ‘proportion of residents living in poverty’ are both commonly used neighborhood contextual variables derived from the same individual-level Census data on income. Similarly, the investigator has several options for categorizing neighborhoods by a contextual variable⁹. For example, an investigator may choose to compare neighborhoods with less than 5% of residents living in poverty with neighborhoods where more than 20% of residents live in poverty or may choose to compare highest quintile to the lowest quintile of neighborhoods ranked by the percent of residents living in poverty. The effects of these choices on the extent of bias in calculated effect estimates when the underlying data includes measurement error have not been documented.

Here we demonstrate the bias that occurs in the effect estimate for the influence of neighborhood contextual variables on individual level outcomes when there is measurement error or misclassification in the individual level data that is used to create the contextual variable. We demonstrate how choices an investigator makes in creation of contextual variables, such as the use of proportions as opposed to means, impact bias in the effect estimate, and how further manipulating the data to express continuous measures as categories affects bias.

METHODS

Overview

We use a combination of health survey data, Census data, mathematical derivation, and simulations to explore bias in effect estimates for neighborhood contextual variables derived from the aggregation of individual-level data that is likely to have been measured with error. We use as our model the association between survey respondent’s BMI and zip code-level socio-economic status (SES), accounting for individual-level covariates, as assessed in the New York City (NYC) Community Health Survey (CHS), a population based health survey of residents of NYC conducted by the New York City Department of Health and Mental Hygiene that collected self-reported data on height and weight and zip code¹⁰.^11-13. We simulate error in the Census data, then assess the bias created by that error given several study design options: 1) form (continuous or dichotomous) of outcome variable, 2) form (continuous or dichotomous) of the household-level variable aggregated by the Census to create the zip code SES estimate, 3) modeling technique (GEE vs. Mixed), and 4) population size of neighborhoods and number of neighborhoods used in the study and, 5) categorization of neighborhoods (none, quantile-based, or external cut-point) for final effect estimation. Non-differential misclassification of a neighborhood-level variable aggregated from dichotomous measures can be simulated without needing to access underlying per-household Census data; analyses focused on zip code poverty rate were performed using the CHS dataset linked to zip code level Census data. However, since simulations of measurement error of a neighborhood-level variable aggregated from an underlying continuous measure (e.g. zip code median household income) require the individual-level continuous data, we created completely simulated datasets to study the effects of measurement error in continuous data. These datasets were simulated to resemble the CHS dataset in general distribution of variables, though population sizes were typically smaller than zip codes to avoid computational overload (NYC zip codes vary widely but average about 40,000 residents). Our simulation was adapted from work by Clarke, et al¹⁴; SAS code for the simulation is included in eAppendix 1. Details of the scenarios investigated are provided as Table 1.

Table 1. Analyses Performed to Assess the Effect of Non-Differential Measurement Error in Individual-level Variables Aggregated to Create Neighborhood Contextual Measures in Multi-level Studies.

Form of measurement error	Dataset	Variations Tested
Dichotomous individual-level variable: (e.g. non-differential misclassification of household-level poverty)	New York City Community Health Survey	Magnitude of measurement error Modeling strategy (GEE vs. mixed models) Outcome form (continuous vs. dichotomous) Effect estimation (quantile comparison vs. direct interpretation of slope)
	Multiple Simulated Datasets Modeled on the New York City Community Health Survey	Effect estimation (externally-defined cut-points)
Continuous individual-level variable: (e.g. non-differential error in household-level income)	Multiple Simulated Datasets Modeled on the New York City Community Health Survey	Magnitude of measurement error Number of neighborhoods Number of residents per neighborhood Effect estimation (quantile comparison vs. direct interpretation of slope)

Survey Data Source

We used data from the 2002 to 2004 NYC Community Health Survey (CHS) and the 2000 US Census to provide a baseline estimate of association between neighborhood poverty rates and body mass index and obesity status^12,13. Using the residential zip code, individual-level outcome and covariate data were linked to Census data on the proportion of zip code residents living below the poverty line. Analyses of BMI, individual demographic variables, and appended neighborhood characteristics were approved by the Columbia University Medical Center Institutional Review Board.

Measures

The BMI of CHS respondents was computed from self-reported height and weight data, and obesity was defined as BMI of 30 or more¹⁵. The respondents also reported their age, gender, and race, which for this exercise was coded as black or non-black. The CHS measures respondent’s SES as the ratio of reported family income to the US poverty threshold as reported by the US Census.

Contextual Variables Aggregated from Dichotomous Individual-Level Census Measures

To assess the effects of non-differential misclassification error in Census data used to estimate the proportion of residents in each zip code living in poverty, we first used mixed models to assess the association between zip code poverty rate and CHS respondent’s individual-level BMI after adjusting for individual age, sex, race, and poverty status. Treating the actual Census data as the truth, we created data sets in which in the poverty rate (PR) was assumed to have been measured with error using the formula:

$${\mathit{PR}}_{\text{observed}}={\mathit{PR}}_{\text{true}}\ast \mathit{Se}+(1-{\mathit{PR}}_{\text{true}})\ast (1-\mathit{Sp})$$

where Se = sensitivity and Sp = specificity for the determination of whether an individual Census respondent lived in poverty. We modeled the association between neighborhood poverty rate observed with varying amounts of misclassification in the underlying Census data and CHS respondent’s individual-level BMI after adjusting for individual age, sex, race and poverty status. Analyses were conducted for Se and Sp ranging from 50% to 100%, and effect estimates calculated from zip code level data that incorporated error were compared to the effect estimate at 100% Se and Sp to calculate magnitude of bias. Analyses were repeated with obesity status rather than BMI as the outcome and using GEE based approaches with clustering on zip codes and robust standard error estimation¹⁶ rather than mixed models. Finally, we repeated analyses with neighborhood poverty rates further transformed into categories based on quintile cut-points across the distribution of zip codes.

Researchers sometimes use externally-defined cut-points to categorize neighborhoods (e.g. neighborhoods with a greater than 20% poverty rate are classified as high poverty). Since misclassification of individual-level measures can result in re-categorization of neighborhoods with respect to the cut-points, the impact of misclassification on neighborhood effect estimates is dependent on the distribution of neighborhoods with respect to the cut-points. For example, a neighborhood whose underlying poverty rate is 19.9% is more likely to be re-categorized above a 20% cut-point than one whose underlying poverty rate is 10%. Because we did not want our analysis to be affected by the specifics of NYC zip codes, we analyzed this scenario using simulated datasets rather than the CHS. Each dataset had 200 neighborhoods with 4,000 residents each, for a total of 800,000 observations, and individuals followed approximately the same distribution of socio-demographic predictors and associations between BMI and age, race, sex, and income as the CHS data. Using this framework, we simulated 100 datasets. Within each dataset, we varied sensitivity and specificity in the individual poverty measurements, aggregated individual measurements that reflected varying degrees of error to create estimates of neighborhood poverty rates, and computed the estimated effect on BMI of living in a neighborhood with a poverty rate measured at over 20% compared to living in a neighborhood with a poverty rate measured at under 5%. Finally, we compared estimates calculated using neighborhood poverty rates aggregated from erroneous individual-level measures to estimates calculated using perfectly measured individual-level measures to estimate magnitude of bias due to measurement error.

Contextual Variables Aggregated from Continuous Individual-Level Census Measures

Publicly available Census data does not include individuals’ or households’ incomes, and so simulations of measurement error in reported income could not be conducted directly using Census data. Therefore we estimated the effects of measurement error in income data within a simulated dataset with 200 neighborhoods with 4,000 residents each; we then sampled 200 individuals from each neighborhood to serve as study subjects. Within the simulated dataset, we used mixed models to assess the effect of neighborhood mean income on individual-level BMI after adjusting for individual age, sex, race, and income to poverty line. We introduced random measurement error into the measure of income in the simulated Census data as follows:

$${\text{IndividualIncome}}_{\text{noise}}={\text{IndividualIncome}}_{\text{true}}\ast (\theta -0.5)\ast \text{noise},\text{where}\theta \sim \text{Uniform}(0,1)$$

We re-computed mean income within each neighborhood with the erroneous measure and modeled the association between neighborhood mean income and BMI after adjusting for individual-level age, sex, race, and income to poverty line. We repeated the introduction of random error for varying degrees of error 50 times each at each level from 1% noise to 50% noise and compared the resulting effect estimate to the estimate computed at 0% noise. To assess the effect of categorization of neighborhood mean income, we repeated the introduction of measurement error but computed effects of mean income on BMI comparing neighborhoods categorized as the highest and lowest quintiles of observed mean income. To assess the effect of neighborhood population size from which neighborhood mean income was estimated, we simulated datasets with 20% noise and 100 neighborhoods, and varied the number of residents per neighborhood from 20 to 4000. Finally, to assess the effect of number of neighborhoods on magnitude of bias due to random measurement error, we simulated datasets with individual income measured at 20% noise while number of study neighborhoods ranged from 5 to 400.

Software

All analyses were conducted using SAS 9.2, using PROC MIXED for mixed models with BMI as an outcome, PROC GLIMMIX using a logit link for mixed models with obesity as an outcome, and PROC GENMOD for all GEE models. All models within the CHS dataset were clustered on zip code, and all models in the simulated datasets were clustered on the simulated neighborhood designation.

RESULTS

Effect of Misclassification when Dichotomous Individual Level Data are Used to Create Contextual Variables

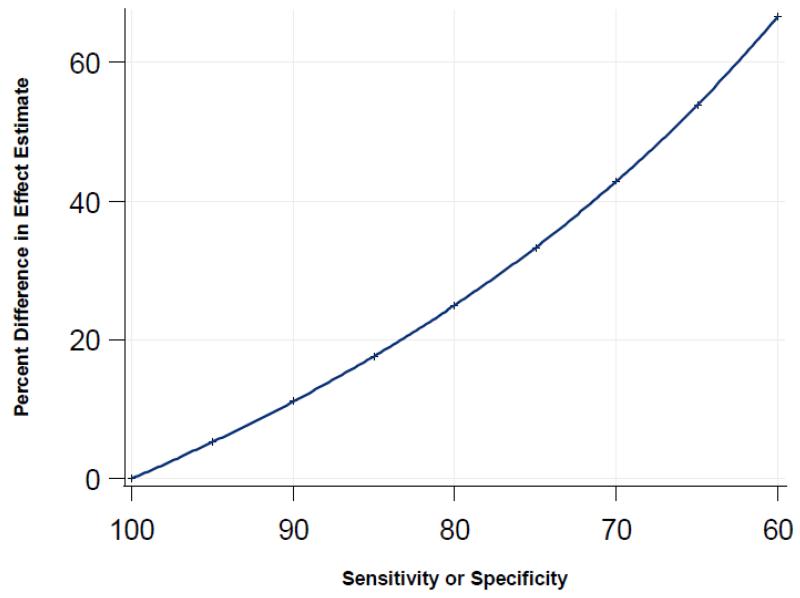
When analyzed using a mixed model, the proportion of zip code residents living in poverty was significantly positively associated with higher BMI among CHS respondents after adjustment for individual level covariates. As increasing amounts of non-differential misclassification of individual-level poverty status was factored into the Census data derived measure of the proportion of zip code residents living in poverty, the estimated association between neighborhood poverty rate and individual-level BMI increased (Figure 1) as did the standard error of the estimate. The extent of inflation in both the group-level parameter estimate and the estimate’s standard error was $\frac{1}{\mathit{Se}+\mathit{Sp}-1}$ times its true value, where Se and Sp are sensitivity and specificity of the designation of an individual in the Census data living in poverty. The algebraic basis for this formula is presented in eAppendix 2.

Figure 1. Bias in effect estimate for the association between neighborhood poverty rate and Body Mass Index among residents of New York City for decreasing sensitivity or specificity in the measurement of individual-level poverty in population Census data.

When obesity status was used as the outcome variable, misclassification in the underlying Census data similarly caused a bias away from the null. Analyses of the BMI and obesity outcomes using GEE models resulted in the same extent of bias as analyses using mixed models. The model intercept estimate was unaffected by variation in sensitivity but was biased away from the null under conditions of imperfect specificity for both GEE and mixed models. Parameter estimates for other variables in the model were not affected by measurement error in the neighborhood contextual variable. Because inflation in the parameter estimate was matched by an inflation in the standard error, significance tests were unaffected by the bias.

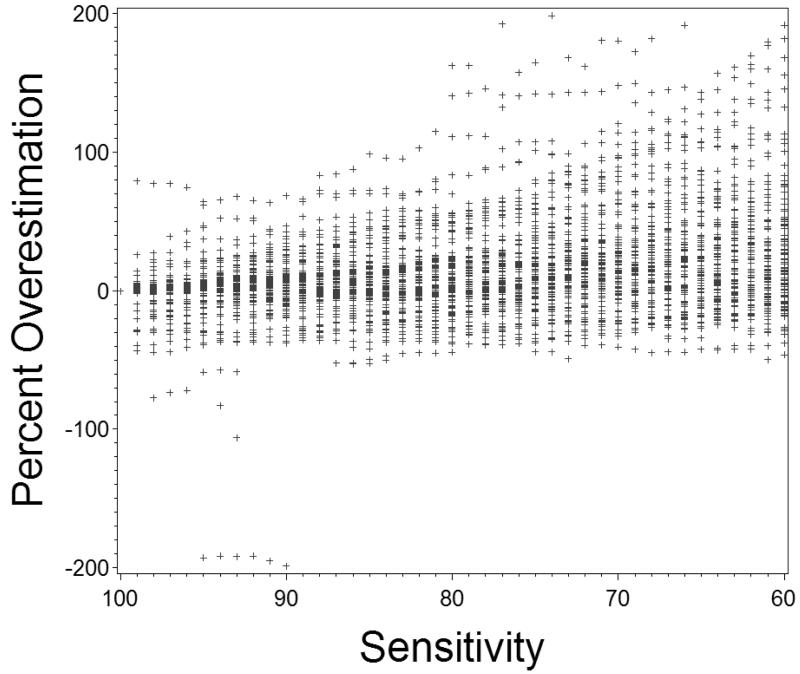
In many studies, neighborhoods are categorized for analysis either using cut-points based on the distribution of the data itself, such as quintiles of poverty rate, or using externally defined cut-points, such as above or below 20% poverty. When the data were analyzed categorizing neighborhoods into quintiles of poverty rate, misclassification in the underlying Census data used to estimate poverty rate did not cause bias in estimates of the effect of neighborhood poverty on BMI. That is, associations between quintiles of zip code poverty rate and BMI under circumstances of misclassification in the individual level Census data were the same as for associations between quintiles of zip code poverty rate measured with no misclassification in the underlying Census data. The algebraic basis for this result is presented in eAppendix 3. When neighborhoods were categorized based on externally defined cut-points, bias was generally away from the null. Figure 2 shows bias in effect estimates comparing individual’s BMI in neighborhoods with 5% or fewer households living in poverty to neighborhoods with 20% or more households living in poverty for varying levels of sensitivity in classifying individuals in regards to poverty status in the underlying Census data.

Figure 2. Bias in estimated difference in Body Mass Index for subjects living in a neighborhood with > 20% of residents living in poverty compared to living in a neighborhood with < 5% of residents living in poverty for a range of sensitivity in the individual-level poverty measure used to estimate neighborhood poverty rate.

Effect of Measurement Error when Continuous Individual Level Data are Used to Create Contextual Variables

Simulation analyses showed that non-differential measurement error in the underlying individual level income data used to estimate mean neighborhood income did not consistently bias the estimated effect of mean neighborhood income on BMI – both bias towards the null and bias away from the null occurred across simulations. In simulations in which measurement error in the individual-level income data caused an expansion in the range of the zip code-level mean income data, bias towards the null occurred, conversely when the range was compressed, bias away from the null occurred. However, non-differential measurement error in the underlying income data did not systematically expand or compress the range of the zip code-level mean income values.

Generally, the magnitude of bias was: positively correlated with the extent of noise in the individual-level data used to estimate mean neighborhood income; inversely correlated with the number of neighborhoods included in the analysis; and inversely correlated with number of individuals used to estimate neighborhood mean income. When the number of individuals used to create the neighborhood estimate exceeded 4,000 (the approximate number of residents in a US Census tract), estimates were never biased more than 0.5% towards or away from the null. However, studies estimating neighborhood context from sources less comprehensive than the Census may be more substantially biased. For example, in a study with 15 neighborhoods for which neighborhood income is estimated from only 30 surveyed residents each, noise levels at 25% resulted in effect estimates biased as high as 100% above and as low as 100% below the true value. eFigures 1 to 3 illustrate these three relationships over repeated simulations. Categorizing neighborhoods in quintiles for comparison did not remove the bias.

DISCUSSION

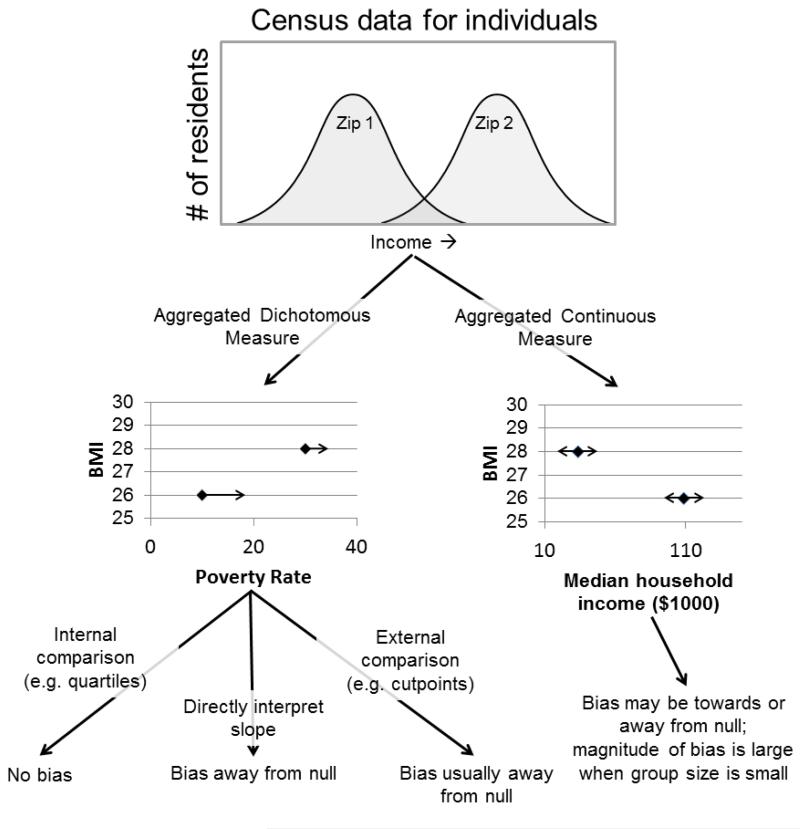
This paper explores the effects of non-differential misclassification and measurement error in individual-level data that are used to create estimates of neighborhood-level contexts for neighborhood health effects studies. It is common for investigators to use Census data to create measures of neighborhood income/poverty, educational attainment and ethnic composition and then to assess whether the neighborhood level contextual variable predicts individual-level outcomes in a study population. Due to the wealth of data available for download from the Census the researcher has many options as to the form these contextual measures might take. Blakely previously asserted that measurement error in the individual-level data that underlie these types of contextual measures would cause bias away from the null in the contextual variable’s beta coefficients⁷. Here we document the extent of the bias described by Blakely and additionally show that: the presence of bias in the beta coefficient is determined by the form of the contextual variable; standard errors of beta coefficients are also affected by this type of non-differential measurement error; that the model intercept can also be affected by this type of non-differential measurement error; and that the bias is identical for continuous and dichotomous outcomes and when data are analyzed with GEE and mixed models. Figure 3 summarizes the effects of the various choices a researcher might make in constructing neighborhood contextual measures when there is measurement error or misclassification in the data being aggregated to create the contextual measure.

Figure 3. A summary of the results of choices researchers make operationalizing neighborhood constructs on bias in effect estimates. The top graph depicts individual-level Census data for income for two hypothetical zip codes and two common aggregations of these data to create zip-code level contextual measures. The black arrows extending from the data points on the two lower graphs depict the effects of non-differential measurement error in the Census income data on estimates of the zip code-level contextual measures, and the black arrows below the graphs illustrate the bias resulting from analytic decisions under these conditions.

The form a researcher selects for a neighborhood-level contextual variable has implications for how measurement error in the individual-level data that underlies the contextual measure impact the effect estimates derived from a study. When the neighborhood-level variable is expressed as a proportion of residents having a dichotomous individual-level state, the beta coefficient for the contextual measure will be biased away from the null in the presence of misclassification error for the individual-level state (e.g. as in ¹⁷). If a contextual measure expressed as a proportion is further transformed into a quantiled categorical variable (e.g. quintile categories across the observed distribution of proportion of residents living in poverty, as in ^8,18), non-differential misclassification error in the underlying individual-level Census data does not produce bias in the estimated association between the dependent variable and increasing quantiles of the contextual variable. However, when neighborhoods are categorized using pre-defined cut-points (e.g. neighborhoods with >20% poverty classified as high poverty and neighborhoods with ≤ 20% poverty classified as low poverty ⁸) non-differential misclassification in the underlying Census data will usually cause a bias away from the null. Analyses using internal versus external cut-points to categorize neighborhoods behave differently in the presence of non-differential misclassification in the underlying Census data because misclassification causes re-categorization of neighborhoods when external cut-points are used but not when internal cut-points are used. Suppose that when ranked by true poverty rate, the 20^th percentile neighborhood has a 5% poverty rate and the 80^th percentile neighborhood has a 20% poverty rate, but the Census actually measures individuals’ poverty status with 90% sensitivity and 100% specificity. With this imperfect measure, the first quintile cut-point will be 4.5% and the fifth quintile will be 18%, but the rank order of neighborhoods by poverty rate is unchanged. Thus, misclassification of individuals’ poverty status in the Census data does not alter which neighborhoods will be classified as being in the lowest and highest quintile of poverty rate. However, when neighborhoods are defined as low poverty if their poverty rate is < 5% and high poverty if their poverty rate is >20%, misclassification of individuals’ poverty status in the Census data alters some neighborhood’s classifications: a neighborhood whose true poverty rate is 5.1% will be included in the low-poverty group and a neighborhood whose true poverty rate is 21% will be excluded from the high poverty group. This shuffling of neighborhoods across categories defined by externally set cut-points can cause bias towards or away from the null; bias away from the null was more common in our simulations (Figure 2).

Measurement error in individual-level Census data expressed as a continuum (e.g. income) and aggregated to a contextual variable also expressed as a continuum (e.g. mean household income) does not cause a consistent direction of bias in the beta coefficient relating the neighborhood contextual variable to the dependent variable. Random error in the underlying individual-level Census income data produces random error in the neighborhood-level mean income data for each neighborhood, but when the number of residents sampled to derive the neighborhood mean income measure is large, the random error in the neighborhood estimate is small. As a result, the magnitude of bias in the resulting effect estimate is likely to be negligible if the number of measurements per neighborhood aggregated to create the neighborhood measure is as large as a Census tract.

Our analysis focused on the simplified view of measurement error that investigators frequently hope for: that measurement error is non-differential with respect to true exposure level, true outcome level, and error in measured outcome. We show that even under these assumptions, bias away from the null can occur. We note, however, that such assumptions often do not hold in reality; measurement error may be correlated with the true value (e.g., income may be disproportionately under-reported by those with higher incomes) or with measurement error in the outcome¹⁹. Such scenarios may cause bias towards or away from the null and warrant more complex simulations than we have presented here.

Our simulations of misclassified dichotomous individual-level data assumed deterministic misclassification across all neighborhoods. If misclassification is treated as random error (i.e. the misclassification rate may vary between neighborhoods, though the variability is unrelated to the outcome), as explored in the simulations of Jurek, et al²⁰, re-ordering of neighborhoods may occur, though because the proportion of individuals misclassified is related to the true proportion of individuals with a trait, rank order changes are minimal and so quantiling still minimizes the effects of non-differential misclassification.

Outside of the area of neighborhood health effects research there are several areas of research worth noting where these types of contextual variables created through the aggregation of individual-level data are commonly used. For example, no individual-level income data is available in the Surveillance, Epidemiology, and End Results (SEER), database, so it has been suggested that measures derived from Census data on the patient’s Census tract of residence are the best available indicator of socioeconomic status²¹. Though such analyses frequently assess the resulting tract measures in quantiles (e.g.²²), analyses that do not may be affected by non-differential measurement error in the underlying Census data. It is likely that the validity of studies of educational and health outcomes in schools in which classroom or school level contextual measures are created by aggregating student level data is threatened by the measurement issues identified here as well. The socio-economic context of a school or classroom is often of interest as a predictor of outcomes and is often operationalized as the proportion of students receiving free or reduced price school lunch (e.g. ^23,24). This measure has been criticized as including measurement error²⁵. Within a classroom only a small number of students may contribute to continuously distributed contextual measures (e.g. mean family income (e.g. ²⁶)) and these studies often only study a modest number of classrooms or schools (e.g. ²⁷). Thus, such studies fall within the design parameters where measurement error in the estimation of a contextual variable will produce considerable bias.

In conclusion, measurement error in the individual-level data that underlie the construction of neighborhood level contextual variables can significantly impact estimates of neighborhood effects on individual-level health outcomes. However, by carefully choosing the form of the contextual variable and/or transforming the contextual data into quantiles bias can be reduced.