Fine Mapping Causal Variants with an Approximate Bayesian Method Using Marginal Test Statistics

Abstract

Two recently developed fine-mapping methods, CAVIAR and PAINTOR, demonstrate better performance over other fine-mapping methods. They also have the advantage of using only the marginal test statistics and the correlation among SNPs. Both methods leverage the fact that the marginal test statistics asymptotically follow a multivariate normal distribution and are likelihood based. However, their relationship with Bayesian fine mapping, such as BIMBAM, is not clear. In this study, we first show that CAVIAR and BIMBAM are actually approximately equivalent to each other. This leads to a fine-mapping method using marginal test statistics in the Bayesian framework, which we call CAVIAR Bayes factor (CAVIARBF). Another advantage of the Bayesian framework is that it can answer both association and fine-mapping questions. We also used simulations to compare CAVIARBF with other methods under different numbers of causal variants. The results showed that both CAVIARBF and BIMBAM have better performance than PAINTOR and other methods. Compared to BIMBAM, CAVIARBF has the advantage of using only marginal test statistics and takes about one-quarter to one-fifth of the running time. We applied different methods on two independent cohorts of the same phenotype. Results showed that CAVIARBF, BIMBAM, and PAINTOR selected the same top 3 SNPs; however, CAVIARBF and BIMBAM had better consistency in selecting the top 10 ranked SNPs between the two cohorts. Software is available at https://bitbucket.org/Wenan/caviarbf.

UNTIL recently, there have been >2000 genome-wide association studies (GWAS) published with different traits or disease status (Hindorff et al. 2014). Most of them reported only regions of association, represented by SNPs with the lowest P-values in each region. Only a few provide further information of likely underlying causal variants. A noted exception is refinement based on Bayesian methods (Maller et al. 2012). Fine mapping the causal variants from the verified association regions is an important step toward understanding the complex biological mechanisms linking the genetic code to various traits or phenotypes.

Fine-mapping methods can be roughly divided into two groups. The first group was developed before the availability of high-density genotype data. These fine-mapping methods assume the causal variants are not genotyped in the data and aim to identify a region as close as possible to the causal variants (Morris et al. 2002; Durrant et al. 2004; Liang and Chiu 2005; Zollner and Pritchard 2005; Minichiello and Durbin 2006; Waldron et al. 2006). Because the causal variants are not observed in the data, these methods usually rely on various strong assumptions to model the relationship of the causal and the observed variants. Examples include models based on the coalescent theory (Morris et al. 2002; Zollner and Pritchard 2005; Minichiello and Durbin 2006) or statistical assumptions about the patterns of linkage disequilibrium (LD) (Liang and Chiu 2005). There are at least two limitations of these methods. First, the result is usually a region with a confidence value rather than candidate causal variants. Second, the result may be unreliable if the model assumptions are too strict and deviate far away from the real data, or the inferred region may be too wide to be useful if the model assumptions are too general.

The second group of fine-mapping methods assumes that the causal variants are among those measured. As the sequencing technology advances and with the availability of the HapMap Project (Altshuler et al. 2010) and the 1000 Genomes Project (Abecasis et al. 2012), it is feasible to obtain the sequence data of the association regions or impute almost all common variants with high quality. Now it is plausible to assume the causal variants exist in the data, either measured or imputed. How to best prioritize the candidate causal SNPs for follow-up functional studies becomes the aim of fine mapping (Faye et al. 2013). One simple way to prioritize variants is based on P-values. However, there are at least two limitations of this method. First, P-values do not give a comparable measure of the likelihood that a variant is causal across loci or across studies (Stephens and Balding 2009). Second, a noncausal variant could have the lowest P-value due to LD with a causal SNP and statistical fluctuation. This may also happen when a noncausal variant is in LD with multiple causal SNPs.

There have been several methods developed to address the above problems. For example, in Maller et al. (2012), a Bayesian method was developed to refine the association signal for 14 loci. This method circumvents the first limitation of using P-values by using the posterior inclusion probability (PIP). However, it assumes only a single causal variant for each locus. Recently, two fine-mapping methods, CAVIAR (Hormozdiari et al. 2014) and PAINTOR (Kichaev et al. 2014), were proposed, which lift the restriction of a single causal variant in a locus and show much better performance than other fine-mapping methods. Another advantage is that only the marginal test statistics and the correlation coefficients among SNPs are required, instead of the original genotype data, which makes it easier to share data among different groups. When only marginal test statistics are available, which is not uncommon, the correlation among SNPs in a study can be approximately computed from an appropriate reference population panel, e.g., from the 1000 Genomes Project. We noted that BIMBAM (Servin and Stephens 2007; Guan and Stephens 2008), a Bayesian method, can be used for fine mapping multiple causal variants by setting the maximal number of causal variants allowed in the model. Both CAVIAR and PAINTOR use the marginal test statistics directly and are likelihood based. The relationship with other Bayesian methods, such as BIMBAM, which takes the original genotype data as input, is not clear. In this study, we derive and explain the relationship between CAVIAR/PAINTOR and BIMBAM, which leads to a unified Bayesian framework for both fine mapping and association testing using marginal test statistics. We call our proposed method CAVIAR Bayes factor (CAVIARBF). We also compared the performance of different fine-mapping methods in simulations with multiple causal variants.

Compared to CAVIAR, PAINTOR has an additional option to include extra functional annotations about the variants. Even though it is important to include the annotations when they are available, we focus on the scenario where no annotation is available and discuss functional annotations in the Discussion. There are other Bayesian-based methods in fine mapping, such as those in Wilson et al. (2010) and Guan and Stephens (2011). These methods are based on sampling techniques, such as the Markov chain Monte Carlo (MCMC) algorithm. Because MCMC methods can require more computation time than BIMBAM or CAVIARBF, where the Bayes factors are calculated analytically and exhaustively enumerated, MCMC methods have computational limitations. We further discuss these issues in the Discussion.

Materials and Methods

Approximate equivalence between BIMBAM and CAVIAR

In this section we derive the equivalence between BIMBAM using a D₂ prior and CAVIAR. Suppose X is an n × m SNP matrix. It is coded additively as 0, 1, and 2 for the number of a specified allele for each SNP, where n is the number of individuals and m is the number of putative causal SNPs. First, we scale X so that each column of X has mean 0 and variance 1; i.e., $\left(1/n\right){\displaystyle {\sum }_{i=1}^n{X}_{ij}}=0,\left(1/n\right){\displaystyle {\sum }_{i=1}^n{X}_{ij}^2}=1,j=1,2,\dots ,n$. X_ij is the element of row i and column j in X. The quantitative phenotype y is a n × 1 vector. We also center y so that we can use the linear model without the intercept as

$$y=X\beta + \epsilon ,$$ (1)

where β is the effect size and $\epsilon \sim N(0,\left(1/\tau \right)I_n$). Here $I_n$ denotes the n × n identity matrix.

Bayes factor from BIMBAM using the D₂ prior given τ:

The D₂ prior from Servin and Stephens (2007; Guan and Stephens 2008) assumes that β has a prior normal distribution N(0, $v\left(1/\tau \right)$), where v is a diagonal matrix and β and ε are independent. Assume all SNPs have the same variance ${\sigma }_a^2\left(1/\tau \right)$; i.e., $v={\sigma }_a^2{I}_m$. Then we have

$$E\left(y\text{|}\tau , X\right)=E\left(E\left(y\text{|}\tau , X,\beta \right)\right)=E\left(X\beta \right)=0,$$

$$\begin{array}{c}\mathrm{Var}\left(y\text{|}\tau , X\right)=E\left(\mathrm{Var}\left(y\text{|}\tau ,X,\beta \right)\right)+\mathrm{Var}\left(E\left(y\text{|}\tau ,X,\beta \right)\right)\\ =E\left(\frac{1}{\tau }{I}_n\right)+\mathrm{Var}\left(X\beta \right)\end{array}$$

$$=\frac{1}{\tau }(I_n+Xv{X}^{\mathrm{T}}).$$

Note that $X^{\text{T}}$ means the transpose of X. Since y is a linear transformation of the multivariate normal random vector ${\left(\beta , \epsilon \right)}^{\mathrm{T}}$, y has a normal distribution

$$y|\tau ,X\sim N(0,\frac{1}{\tau }\left(I_n+Xv{X}^{\mathrm{T}}\right)).$$ (2)

The likelihood of model (1) is $P\left(y\text{|}\tau , X\right)={\left(2\pi \right)}^{-\left(n/2\right)}{\left|D\right|}^{-\left(1/2\right)}\exp \left(-\left(1/2\right)y^{\mathrm{T}}{D}^{-1}y\right)$, where $D=\left(1/\tau \right)(I_n+Xv{X}^{\mathrm{T}})$. The null model is that $\beta =0;$ i.e., $v=0$ $I_m$ or ${\sigma }_a^2=0.$ Therefore the likelihood of the null model is $P_0\left(y\text{|}\tau , X\right)={\left(2\pi \right)}^{-\left(n/2\right)}{\left|D_0\right|}^{-\left(1/2\right)}\exp \left(-\left(1/2\right)y^T{D}_0^{-1}y\right)$, where $D_0=\left(1/\tau \right)I_n$. Then the Bayes factor is

$$\begin{array}{c}\mathrm{B}{\mathrm{F}}_1=\frac{{\left(2\pi \right)}^{-\left(n/2\right)}{\left|D\right|}^{-\left(1/2\right)}\exp \left(-\left(1/2\right)y^{\mathrm{T}}{D}^{-1}y\right)}{{\left(2\pi \right)}^{-\left(n/2\right)}{\left|D_0\right|}^{-\left(1/2\right)}\exp \left(-\left(1/2\right)y^{\mathrm{T}}{D}_0^{-1}y\right)}\\ ={\left|I_n+Xv{X}^{\mathrm{T}}\right|}^{-\left(1/2\right)}\exp (-\frac{1}{2}{y}^{\mathrm{T}}{\left(I_n+Xv{X}^{\mathrm{T}}\right)}^{-1}y\tau +\frac{1}{2}{y}^{\mathrm{T}}y\tau ).\end{array}$$

From the Woodbury matrix identity (Harville 2008), ${\left(I_n+Xv{X}^{\mathrm{T}}\right)}^{-1}=I_n-X{\left(v^{-1}+X^{\mathrm{T}}X\right)}^{-1}{X}^{\mathrm{T}}$, resulting in

$$\mathrm{B}{\mathrm{F}}_1={\left|I_n+Xv{X}^{\mathrm{T}}\right|}^{-\left(1/2\right)}\exp (\frac{1}{2}{y}^{\mathrm{T}}X{\left(v^{-1}+X^{\mathrm{T}}X\right)}^{-1}{X}^{\mathrm{T}}y\tau ).$$

Bayes factor from CAVIAR given τ:

Suppose X has full column rank. From result (2), we have

$$\frac{1}{\sqrt{n}}{X}^{\mathrm{T}}y|\tau ,X\sim N\left(0,\frac{1}{\tau }\left(\frac{X^{\mathrm{T}}X}{n}+\frac{X^{\mathrm{T}}Xv{X}^{\mathrm{T}}X}{n}\right)\right).$$

Let ${\text{Σ}}_x=X^{\mathrm{T}}X/n$, which is the correlation matrix among SNPs in X. We can write

$$\begin{array}{l}\frac{1}{\sqrt{n}}{X}^{\mathrm{T}}y|\tau ,X\sim N\left(0,\frac{1}{\tau }\left({\text{Σ}}_x+{\text{Σ}}_x\left(nv\right){\text{Σ}}_x\right)\right)\iff \frac{1}{\sqrt{n}}\frac{X^{\mathrm{T}}y}{{\left(1/\tau \right)}^{1/2}}\\ \sim N\left(0,{\text{Σ}}_x+{\text{Σ}}_x\left(nv\right){\text{Σ}}_x\right).\end{array}$$

Let $u=nv$ and $z=\left(1/\sqrt{n}\right)\left(X^{\mathrm{T}}y/{\left(1/\tau \right)}^{1/2}\right);$ then $z\sim N\left(0,{\text{Σ}}_x+{\text{Σ}}_{x}u{\text{Σ}}_x\right)$. If the variance $1/\tau$ is replaced by the maximum-likelihood estimate from the linear model (1) when keeping one SNP in the model at a time, the resulting vector $\widehat{z}={\left(z_1,z_2,\dots , z_m\right)}^{\mathrm{T}}$ consists of exactly the marginal test statistics for each SNP used in CAVIAR (Hormozdiari et al. 2014). The likelihood of z is

$$\begin{array}{l}P\left(z\text{|}\tau , X\right)={\left(2\pi \right)}^{-\left(n/2\right)}{\left|{\text{Σ}}_x+{\text{Σ}}_{x}u{\text{Σ}}_x\right|}^{-\left(1/2\right)}\\ \times \exp \left(-\frac{1}{2}{z}^{\mathrm{T}}{\left({\text{Σ}}_x+{\text{Σ}}_{x}u{\text{Σ}}_x\right)}^{-1}z\right).\end{array}$$

For the null model, u = 0, the likelihood of z is

$$P_0\left(z\text{|}\tau , X\right)={\left(2\pi \right)}^{-\left(n/2\right)}{\left|{\text{Σ}}_x\right|}^{-\left(1/2\right)}\exp \left(-\frac{1}{2}{z}^{\mathrm{T}}{\left({\text{Σ}}_x\right)}^{-1}z\right).$$

Then the Bayes factor based on z is

$$\mathrm{B}{\mathrm{F}}_2=\frac{{\left|{\text{Σ}}_x+{\text{Σ}}_{x}u{\text{Σ}}_x\right|}^{-\left(1/2\right)}\exp (-\left(1/2\right)z^{\mathrm{T}}{\left({\text{Σ}}_x+{\text{Σ}}_{x}u{\text{Σ}}_x\right)}^{-1}z)}{{\left|{\text{Σ}}_x\right|}^{-\left(1/2\right)}\exp (-\left(1/2\right)z^{\mathrm{T}}{\left({\text{Σ}}_x\right)}^{-1}z)}.$$

Because X has full column rank m, ${\text{Σ}}_x$ also has rank m and is nonsingular. Therefore,

$$\begin{array}{l}\left|{\text{Σ}}_x+{\text{Σ}}_{x}u{\text{Σ}}_x\right|=\left|{\text{Σ}}_x\left(I_m+u{\text{Σ}}_x\right)\right|=\left|{\text{Σ}}_x\right|\left|I_m+u{\text{Σ}}_x\right|\\ =\left|{\text{Σ}}_x\right|\left|I_m+v{X}^{\mathrm{T}}X\right|.\end{array}$$

From Sylvester’s determinant theorem (Harville 2008), $\left|I_m+v{X}^{\mathrm{T}}X\right|=\left|I_n+Xv{X}^{\mathrm{T}}\right|$. Therefore,

$$\left|{\text{Σ}}_x+{\text{Σ}}_{x}u{\text{Σ}}_x\right|=\left|{\text{Σ}}_x\right|\left|I_n+Xv{X}^{\mathrm{T}}\right|.$$

From Woodbury matrix identity, ${\left({\text{Σ}}_x+{\text{Σ}}_{x}u{\text{Σ}}_x\right)}^{-1}={\text{Σ}}_x^{-1}-{\left(u^{-1}+{\text{Σ}}_x\right)}^{-1}$, resulting in the Bayes factor

$$\mathrm{B}{\mathrm{F}}_2={\left|I_n+Xv{X}^{\mathrm{T}}\right|}^{-\left(1/2\right)}\exp \left(\frac{1}{2}{z}^{\mathrm{T}}{\left(u^{-1}+{\text{Σ}}_x\right)}^{-1}z\right).$$

By plugging in the definition of z and u,

$$\mathrm{B}{\mathrm{F}}_2={\left|I_n+Xv{X}^{\mathrm{T}}\right|}^{-\left(1/2\right)}\exp \left(\frac{1}{2}\frac{1}{n}{y}^{\mathrm{T}}X{\left(\frac{1}{n}{v}^{-1}+\frac{1}{n}{X}^{\mathrm{T}}X\right)}^{-1}{X}^{\mathrm{T}}y\tau \right)$$

$$={\left|I_n+Xv{X}^{\mathrm{T}}\right|}^{-\left(1/2\right)}\exp \left(\frac{1}{2}{y}^{\mathrm{T}}X{\left(v^{-1}+X^{\mathrm{T}}X\right)}^{-1}{X}^{\mathrm{T}}y\tau \right)=\mathrm{B}{\mathrm{F}}_1.$$

Therefore, given τ, BIMBAM (using D₂ prior) and CAVIAR have the same Bayes factor. In practice, τ is unknown. BIMBAM uses a noninformative prior for τ and integrates it out. On the other hand, CAVIAR uses the maximum-likelihood estimate (MLE) of $1/\tau$ by putting one SNP at a time in model (1); i.e., only one column of X is used each time. There are two approximations here. First the MLE is used instead of the true unknown $1/\tau$. Second, different MLEs of $1/\tau$ from different columns of X are used for each element of z. The second approximation makes the result of CAVIAR farther away from a true Bayes factor. An alternative approximation is to use the MLE of $1/\tau$ from model (1) with the full X matrix. However, this loses the ability to directly use marginal test statistics. For fine mapping of a region, because SNPs in a region usually explain only a very small portion of the total variance of y, e.g., <5%, the MLEs from different columns of X may be all close to the true parameter. In practice, the calculated Bayes factors from CAVIAR and BIMBAM are usually similar to each other, given that the same v is used.

In the CAVIAR article (Hormozdiari et al. 2014), all SNPs in a region are used in calculating Bayes factors. The variances of the SNPs not in the putative causal model are set to a very small positive value. When this value approaches 0, the result approaches the case where only putative causal SNPs are used as above. Using only putative causal SNPs to compute the Bayes factor can also be faster. Another advantage of the above derivation is that even when X is not full column rank, which is very common for SNPs in high LD, we can still use the following formula to calculate the Bayes factor:

$$\mathrm{B}{\mathrm{F}}_2={\left|I_m+nv{\text{Σ}}_x\right|}^{-\left(1/2\right)}\exp \left(\frac{1}{2}{z}^{\mathrm{T}}{\left({(nv)}^{-1}+{\text{Σ}}_x\right)}^{-1}z\right).$$ (3)

For small $u=nv$, e.g., $u^{-1}>{10}^{-3}$, this avoids the need to add a small positive value to the diagonal of ${\text{Σ}}_x$, which is required in the current CAVIAR implementation. When u gets larger and ${\text{Σ}}_x$ is singular, the exponent in Equation 3 may be unstable. In this case we still need to add a small positive value to the diagonal of ${\text{Σ}}_x$, e.g., ${10}^{-3}$. This may have some shrinkage effect on the Bayes factors compared to that from BIMBAM based on our simulations. Our implementation of CAVIARBF is based on Equation 3.

BIMBAM can naturally incorporate a dominance effect by adding an extra column to X for each SNP, which is coded as 1 for the heterozygous genotype and 0 for others. The same could be used for CAVIAR to extend it to incorporate a dominance effect. In this case, each SNP will have two z statistics calculated, one for the SNP column of additive effects and the other for the heterozygous indicator. The correlation matrix also needs the correlations with these heterozygous indicators.

In the above proof, we assumed that the SNP matrix X is scaled to have variance 1 for each SNP. This is not assumed in the BIMBAM article (Servin and Stephens 2007; Guan and Stephens 2008). In the following we consider the impact of scaling. As noted in Guan and Stephens (2011), scaling to variance 1 corresponds to a prior assumption that SNPs with lower minor allele frequency have larger effect size. Specifically, suppose $\tilde{X}$ is the original centered SNP matrix, but not scaled, with the model

$$y=\tilde{X}\gamma + \epsilon ,$$

where $\gamma \sim N(0,w\left(1/\tau \right))$. Then the scaled SNP matrix $X=\tilde{X}{s}^{-\left(1/2\right)}$, where s is the diagonal matrix with the variance of each SNP on the diagonal. From $X\beta =\tilde{X}{s}^{-\left(1/2\right)}\beta =\tilde{X}\gamma$ and $\beta \sim N(0,v\left(1/\tau \right))$, we have the correspondence that $v_i=s_i{w}_i;$ subscript i denotes the ith diagonal elements. If we assume a common prior $v_i={\sigma }_a^2$ for all SNPs in the scaled SNP matrix X, then $w_i={\sigma }_a^2/s_i$, which is proportional to the inverse of the SNP i’s variance in the original $\tilde{X}$. On the other hand, if we assume a common prior $w_i={\sigma }_a^2$ in the original $\tilde{X}$, then $v_i=s_i{\sigma }_a^2$, which has a smaller value if the minor allele frequency is low. Since there is no strong reason to prefer one to the other, in our software we provide the option to set the weight $s_i$ for each SNP in the implementation of CAVIARBF. To get results similar to those of BIMBAM, we just need to set the weight $s_i$ to the variance of the corresponding SNPs.

PAINTOR (Kichaev et al. 2014) is a recently proposed method to prioritize causal variants that can optionally include additional function data. Without function data, PAINTOR is similar to CAVIAR. Both use marginal test statistics and SNP correlations and leverage the multivariate normal distribution. However, PAINTOR does not model the uncertainty of the effect size (or noncentrality parameter) as in CAVIAR. Instead, it uses the observed test statistic as the true underlying effect size if the observed test statistic is larger than a threshold. This may result in a decrease in performance when the observed data deviate largely from the true values.

Model space, Bayes factors, and posterior inference

To compute the probabilities of SNPs being causal, we need to consider the set of possible models to evaluate and their related Bayes factors. Suppose the total number of SNPs in a candidate region is p. Let $c=(c_1, c_2, \cdots ,c_p)$ with each component being either 0 or 1, indicating whether the corresponding SNP is in a causal model. The total number of possible causal models is $2^p$. It is usually prohibitive to enumerate all models when p is relatively large, e.g., for p > 20. Similarly as in Hormozdiari et al. (2014), we set a limit on the number of causal variants in the model, denoted by l; e.g., l = 5. This reduces the total number of models to evaluate in the model space M to ${\displaystyle {\sum }_{i=0}^l\left(\begin{array}{c}p\\ i\end{array}\right)}$, where $\left(\begin{array}{c}p\\ i\end{array}\right)$ denotes the number of i combinations from p elements. For any causal model M_c in the model space M, we can calculate the posterior probability as

$$p\left(M_{\mathrm{c}}\text{|}D\right)=\frac{p(M_{\mathrm{c}}, D)}{p(D)}=\frac{p\left(D\text{|}{M}_{\mathrm{c}}\right)p(M_{\mathrm{c}})}{{{\displaystyle \sum }}_{M_{\mathrm{t}}\in M}p\left(D\text{|}{M}_{\mathrm{t}}\right)p(M_{\mathrm{t}})},$$

where D denotes the data. For example, for BIMBAM, $D=(y, X_{\text{full}})$, where $X_{\text{full}}$ represents all SNP data. For CAVIAR/CAVIARBF, $D=(z_{\text{full}}, {\text{Σ}}_{\text{full}})$, where now the marginal test statistics and the correlation matrix represent the data. The prior probabilities of M_c and M_t are $p\left(M_{\mathrm{c}}\right)$ and$p(M_{\mathrm{t}})$, respectively. Denote by M₀ the null model where no SNP is included; i.e., $c=(0, 0, \cdots ,0)$. Define the Bayes factor comparing model $M_{\mathrm{c}}$ with the null model by $\mathrm{BF}\left(M_{\mathrm{c}}:M_0\right)=p\left(D\text{|}{M}_{\mathrm{c}}\right)/p\left(D\text{|}{M}_0\right)$. The posterior probability of each model can be calculated as

$$p\left(M_{\mathrm{c}}\text{|}D\right)=\frac{\mathrm{BF}(M_{\mathrm{c}}:M_0)p(M_{\mathrm{c}})}{{{\displaystyle \sum }}_{M_{\mathrm{t}}\in M}\mathrm{BF}(M_{\mathrm{t}}:M_0)p(M_{\mathrm{t}})}.$$ (4)

The posterior probability of the global alternative $M_{\mathrm{g}}$ that at least one SNP is causal in the region can be calculated as

$$p\left(M_{\mathrm{g}}\text{|}D\right)=\frac{{{\displaystyle \sum }}_{M_{\mathrm{t}}\in M_{\mathrm{g}}}\mathrm{BF}(M_{\mathrm{t}}:M_0)p(M_{\mathrm{t}})}{{{\displaystyle \sum }}_{M_{\mathrm{t}}\in M}\mathrm{BF}(M_{\mathrm{t}}:M_0)p(M_{\mathrm{t}})}.$$

We can also use Bayes factors to compare the global alternative $M_{\mathrm{g}}$ with the null model $M_0$ (Wilson et al. 2010), which can be calculated as

$$\mathrm{BF}\left(M_{\mathrm{g}}:M_0\right)=\frac{{{\displaystyle \sum }}_{M_{\mathrm{t}}\in M_{\mathrm{g}}}\mathrm{BF}(M_{\mathrm{t}}:M_0)p(M_{\mathrm{t}})}{{{\displaystyle \sum }}_{M_{\mathrm{t}}\in M_{\mathrm{g}}}p(M_{\mathrm{t}})}.$$

As advocated in Servin and Stephens (2007; Stephens and Balding 2009; Wilson et al. 2010), the Bayesian method provides a natural way to answer both the association question (Which regions are most likely associated with the phenotype?) and the fine-mapping question (If a region shows evidence of association, which are the potential causal SNPs in the region?). In the following we focus on the fine-mapping question.

Marginal PIP

The probability of including a SNP as causal in a model is commonly used to prioritize SNPs (Stephens and Balding 2009). The marginal PIP for each SNP j is defined as

$$p\left(c_j=1|D\right)={\displaystyle \sum }_{M_{\mathrm{c}}\in M, c_j=1}p(M_{\mathrm{c}}|D).$$

Here we provide a justification of using marginal posterior probability to rank SNPs. Suppose we want to select k SNPs from p SNPs, and our objective is to maximize the number of causal SNPs among these k SNPs. Denote the indexes of the selected k SNPs by $I_k$. The objective value is then $q={\displaystyle {\sum }_{j\in I_k}{c}_j}$. Because each $c_j$ is a random variable, it is natural to use the expectation $E\left(q|D\right)$ as the objective function. It turns out that $E\left(q|D\right)$ is the sum of marginal PIPs of the selected k SNPs as follows:

$$E\left(q|D\right)=E\left({\displaystyle \sum }_{j\in I_k}{c}_j|D\right)={\displaystyle \sum }_{j\in I_k}E(c_j|D)={\displaystyle \sum }_{j\in I_k}p\left(c_j=1|D\right).$$

To maximize $E\left(q|D\right)$, we need only to sort all p SNPs based on their marginal PIPs and choose the top k SNPs. In other words, prioritizing SNPs based on marginal PIPs maximizes the expected number of causal SNPs for a fixed number of SNPs selected. There are two implications from this result. First, when selecting SNPs from multiple loci, we need to pool all of the SNPs in these loci together and choose the top k SNPs. This is also the better way as demonstrated in Kichaev et al. (2014). Second, we can use the sum of the marginal PIPs as a measure of our expected number of causal SNPs. This could be used to decide the number of SNPs to be followed in subsequent functional studies. For example, choose the number that maximizes an objective function that considers both the cost and benefits of finding a causal SNP as in Kichaev et al. (2014).

ρ-Level confidence set

The ρ-level confidence set (or ρ confidence set) was proposed in Hormozdiari et al. (2014), where ρ is the probability that all causal SNPs are included in a selected SNP set. Specifically, for a SNP set with indexes $I_k$, the probability ρ is defined as

$$\rho ={\displaystyle \sum }_{M_{\mathrm{c}}\in M,c_j=0\text{for}\forall j\notin I_k,}p(M_{\mathrm{c}}|D).$$

Different from the definition in Hormozdiari et al. (2014), we do not include the null model $M_0$ in the above summation. When all SNPs are included in the set, the probability ρ is the posterior probability that there is at least 1 causal SNP in the region. Because direct maximization of ρ by selecting k SNPs from p SNPs is computationally prohibitive, we follow the same stepwise selection as in Hormozdiari et al. (2014). For each step, the SNP that increases ρ the most is selected. In Results, we compare the performance of prioritizing SNPs based on ρ and that based on PIP.

Priors

Choosing a reasonable prior is important for a Bayesian model (Stephens and Balding 2009). There are different ways to set the model priors. For example, we can use a binomial prior for the number of causal SNPs, which assumes that the probability of each SNP being causal is independent and equal (Guan and Stephens 2011; Hormozdiari et al. 2014). Denote the probability of each SNP being causal by π, then $p\left(M_{\mathrm{c}}\right)={\pi }^{\left|M_{\mathrm{c}}\right|}{\left(1-\pi \right)}^{p-\left|M_{\mathrm{c}}\right|}$, where $\left|M_{\mathrm{c}}\right|$ is the model size, i.e., the number of SNPs in the model. BIMBAM (Servin and Stephens 2007; Guan and Stephens 2008) uses another way to specify the priors. Specifically, for any model $M_{\mathrm{c}}$ with $\left|M_{\mathrm{c}}\right|\ge 1$, $p\left(M_{\mathrm{c}}\right)={\left(1/2\right)}^{\left|M_{\mathrm{c}}\right|}/\#(|M_{\mathrm{c}}|)$, where $\#(|M_{\mathrm{c}}|)$ is the total number of models with model size $\left|M_{\mathrm{c}}\right|$. We can also use a Beta-binomial distribution to introduce uncertainty on π, as discussed in Scott and Berger (2010). Different implications between the binomial prior and the Beta-binomial prior were also discussed and summarized in table 2 of Wilson et al. (2010). For all the comparisons in this study we used the binomial prior and assumed the average number of causal SNPs is 1; i.e., $\pi =1/p$.

The value of ${\sigma }_a$ reflects the distribution of the effect size. Using a “large” value places almost all the mass on large effect sizes (Servin and Stephens 2007). There are different ways to set it, for example, based on a mixture of 0.1, 0.2, and 0.4 (Guan and Stephens 2008) or based on the proportion of variation in phenotype explained (Guan and Stephens 2011). For simplicity, we use 0.1 for ${\sigma }_a$ in all comparisons. We found that the performance is quite robust; see Results.

Implementation details

The implementation of fine mapping consists of two components. The first component is the computation of Bayes factors. The output format of the Bayes factors from CAVIARBF is the same as that from BIMBAM. The second component is model search, which can compute PIPs and the ρ-level confidence set based on the computed Bayes factors and the specified model priors. The second component can also be used to process the Bayes factors output from BIMBAM. We also note that CAVIAR (Hormozdiari et al. 2014) uses the ρ-level confidence set to prioritize variants, in contrast to PAINTOR (Kichaev et al. 2014) that uses PIPs. When pairing CAVIARBF with the ρ-level confidence set, in principle it is the same as CAVIAR. However, our implementation is much faster than CAVIAR. One reason is that in our implementation the Bayes factors for each model are calculated once and stored, but the CAVIAR implementation recomputes the likelihoods of different models when it tries to find the best next SNPs to include.

Methods for comparison and settings

It has been shown that assuming only 1 causal SNP results in suboptimal performance in prioritizing causal variants (Hormozdiari et al. 2014; Kichaev et al. 2014). A comprehensive evaluation was done in Kichaev et al. (2014), where PAINTOR has shown better performance than many other methods compared. Therefore we decided to compare only the following methods in this study.

CAVIARBF and BIMBAM:

We assume the prior normal distribution of the effect size is on the original scale with SNPs coded as 0, 1, and 2 with respect to the count of the alternate allele. This makes CAVIARBF and BIMBAM comparable because BIMBAM uses only the original scale of SNPs. For both CAVIARBF and BIMBAM, the maximal number of causal SNPs is set to 5. The option “-a” is used for BIMBAM because only the additive model is considered in this study. Once the Bayes factors were calculated, PIPs were calculated and used to prioritize SNPs. For BIMBAM with binary traits, we use the “-cc” option, which uses the Laplace approximation in calculating Bayes factors. BIMBAM version 1.0 was used. CAVIAR was not compared here because the implementation is very slow and the method is essentially equivalent to CAVIARBF. Because often only the marginal test statistics for individual SNPs are available, the true correlation matrix among SNPs needs to be estimated from existing reference populations. Therefore we also evaluated the performance of CAVIARBF with the estimated correlation matrix, denoted by CAVIARBF(ref), using the Utah Residents (CEPH) with Northern and Western European Ancestry (CEU) population panel of the 1000 Genomes Project that was also the reference panel used in the simulated data set.

PAINTOR:

Since we do not consider functional annotations in this study, we assigned the same baseline annotation value of 1 to all SNPs in the data. We used the default iteration number 10. We set the maximal number of causal SNPs to 3. We also tried to set it to 5. However, the performance based on the proportion of causal SNPs included was not as good as that using 3. PAINTOR version 1.1 was used.

LASSO and elastic net:

LASSO (Tibshirani 1996) and elastic net (ENET) (Zou and Hastie 2005) are two widely used penalized methods for variable selection. LASSO uses the norm-1 penalization for coefficients in the model with a penalty parameter λ. When the penalty parameter λ varies, the model size (nonzero coefficients) can change from 0 to p (assuming n is larger than p), resulting in a series of models. Elastic net combines both norm-1 and norm-2 penalizations with a mixing parameter α and the penalty parameter λ. For quantitative traits, R package lars (v1.2) and elasticnet (v1.1) were used for LASSO and elastic net, respectively, due to a slightly better performance than using the R package glmnet. For binary traits, R package glmnet (v1.9-8) was used for LASSO (fixing the parameter α to 1) and elastic net. For elastic net, we first did a grid search for both α and λ with 10-fold cross-validation and chose the pair with the minimum cross-validation error. Then we fixed the mixing parameter α and varied the penalty parameter λ to generate a series of models. Even though LASSO and ENET output a series of models, the size (number of variables included in the model) difference between two neighboring models may not be exactly 1, e.g., more than one SNP may be added in the next model. To make sure the increase of model size is 1 so that it can be compared with other methods for each number of selected SNPs, we interpolated the intermediate models if the model size difference between two neighboring models was >1. Specifically, if the current model is a subset of the next model, we randomly choose the order of those to-add SNPs to form the intermediate models. If the current model is not a subset of the next model, which was not common, we removed the SNPs in the current but not in the next model and then did the interpolation. Finally, we started with the last model (the largest model) and worked backward to pick models with each model size. Once a model was chosen, other models with the same size would not be selected.

For CAVIARBF and PAINTOR, the inputs are marginal test statistics for each SNP and the pairwise correlation among SNPs. For quantitative traits the marginal test statistic is the t-statistic from the linear regression model. For binary traits, it is the Armitage trend test statistic with additive coding (Armitage 1955). For other methods, the inputs are the genotypes and phenotypes.

Data simulation and evaluation

We used HAPGEN (Su et al. 2011) to simulate genotypes, using the CEU population from the 1000 Genomes Project (Abecasis et al. 2012) as the reference panel. For each simulated data set, we randomly selected a region of 35 common SNPs (minor allele frequency >0.05) on chromosome 8 and simulated 2000 individuals (1000 cases and 1000 controls for binary traits). We simulated data sets with the number of causal SNPs ranging from 1 to 5. The causal SNPs were selected randomly. In assigning the effect size to each causal SNP, we made sure the power of detecting each causal SNP using the individual SNP-based test was in a certain range, e.g., power no less than 0.5. The underlying logic is that true causal SNPs should be replicated in other independent studies and thus the power of detecting the true causal SNPs should not be too small. Specifically, we randomly sampled the effect size β for each causal SNP from a normal distribution, with mean 0 and standard deviation 1 for quantitative traits and mean 0 and standard deviation 0.5 for binary traits. Then we accepted only those combinations where the noncentrality parameters of the marginal test statistics for causal SNPs fell in the range of (30.457, 61.856). Using an approximate ${\chi }_1^2$ distribution, this corresponds to the power range of (0.527, 0.992) when using the marginal test statistics with significance level 5 × 10⁻⁸. The formulas of the noncentrality parameters of marginal test statistics with multiple causal SNPs are given in Supporting Information, File S1. Another requirement for each data set is that there is at least one SNP with a P-value <5 × 10⁻⁸. We simulated 100 data sets for each number of causal SNPs. To compare different methods, we calculated the proportion of causal SNPs included among 100 data sets by selecting k SNPs, $k=1\cdots 35.$

One distinguishing characteristic of sequence data is that many SNPs are exactly the same; i.e., the correlation coefficient is 1 or −1. This will create some ambiguity on the number of causal variants. For example, five causal SNPs, which are identical, with the same effect size e will influence the phenotype in the same way as one of these five SNPs being causal with the effect size 5e. Therefore there can be some data sets overlapping for different numbers of causal SNPs.

Results

Marginal PIPs vs. P-values

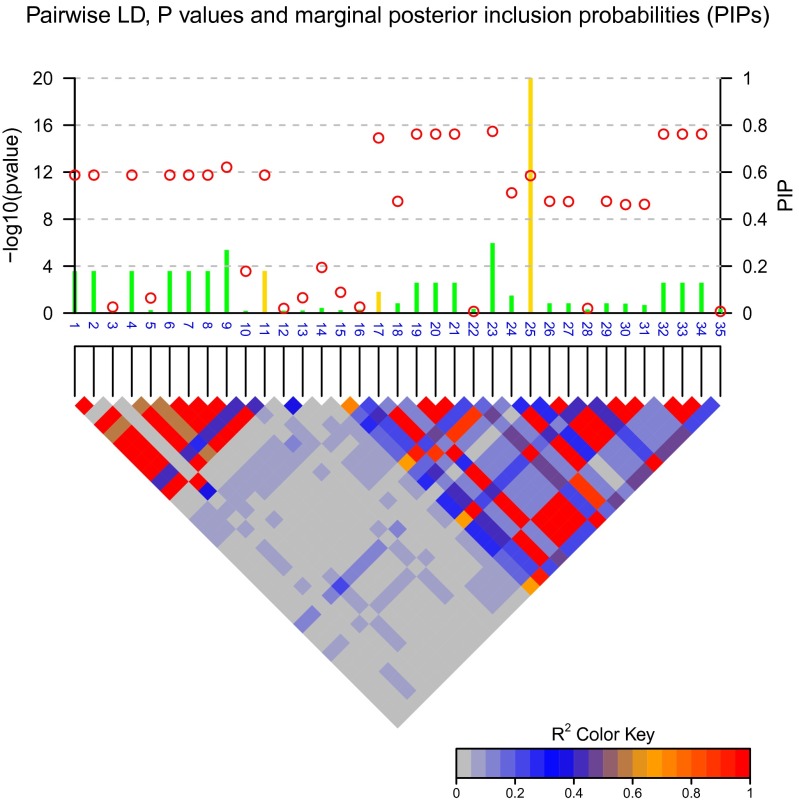
First we demonstrate the advantage of marginal PIPs over P-values in identifying candidate causal SNPs. Figure 1 shows the result of fine mapping on a simulated data set with 3 causal SNPs. PIPs were computed based on Bayes factors calculated from CAVIARBF. Circles represent the individual SNP-based P-value levels and lines represent the PIPs. The gold color indicates the true causal SNPs. The noncausal variant SNP23 had the smallest P-value, but this is purely due to high LD with the causal variant SNP17 and statistical fluctuation. The causal variant SNP25 did not achieve the smallest P-value, but it was correctly captured by the highest PIP. It seems that the causal variant SNP17 was ranked higher by P-values than by PIPs. However, from the perspective of the number of causal variants identified, ranking by P-values will include the first causal variant (SNP17) when 8 SNPs are selected, and ranking by PIPs will include on average 1 + 4/7 causal variants (SNP25 and SNP11) when 7 SNPs are selected (due to the same PIPs among SNP1, -2, -4, -6, -7, -8, and -11). If the correlation among SNPs is 1 or −1, for example between the causal variant SNP11 and SNP1, -2, -4, -6, -7, -8, and -11, these SNPs will have the same P-values and PIPs. To further distinguish them, extra information, such as functional annotation, may be helpful.

Figure 1.

P-values and posterior inclusion probabilities (PIPs). Circles represent the individual SNP-based P-values on the left y-axis and lines represent the PIPs on the right y-axis. The gold color indicates the true causal SNPs. The color-coded LD pattern is shown below. The noncausal variant (SNP23) has the smallest P-values, but is purely due to high LD with the causal variant (SNP17) and statistical fluctuation. The causal variant (SNP25) does not achieve the smallest P-values but is correctly captured by the highest PIP.

Proportion of causal SNPs included by different methods

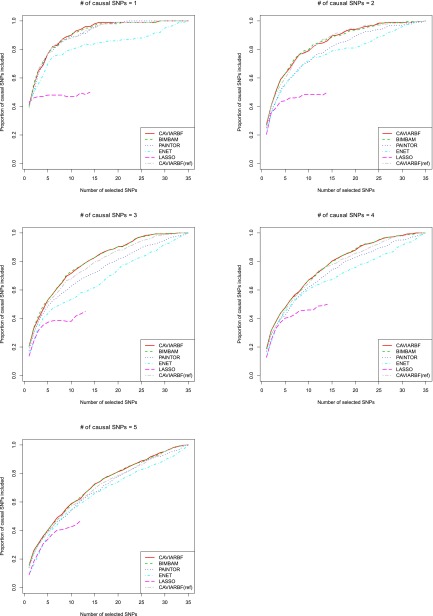
Figure 2 shows the proportion of causal SNPs included for different numbers of selected SNPs in 100 simulated data sets with quantitative traits. CAVIARBF, BIMBAM, and PAINTOR all use PIPs to rank SNPs and select the top SNPs. CAVIARBF and BIMBAM had similar performance as expected. Note that this similar performance does not require a very large sample size, e.g., 2000 here. Similar performance between CAVIARBF and BIMBAM was also observed when the sample size was 200 (data not shown). When there was only 1 causal SNP, CAVIARBF, BIMBAM, and PAINTOR had similar performance. However, when there was >1 causal SNP, CAVIARBF and BIMBAM showed better performance than PAINTOR. One reason may be that PAINTOR uses the observed test statistics as the true underlying effect size, and therefore it does not account for the uncertainty of the effect size. On the other hand, CAVIARBF and BIMBAM incorporate the uncertainty by averaging (integrating) over the prior distributions of effect sizes. ENET had better performance than LASSO, but worse performance than CAVIARBF, BIMBAM, or PAINTOR. One reason for the worst performance of LASSO is that when a causal variant has correlation 1 or −1 with other noncausal variants, LASSO will pick only one and ignore the rest. If the causal variant is not picked, it will not have the chance to be picked again as the model size increases. As expected, CAVIARBF had better performance than CAVIARBF(ref) because of using the true correlation matrix. However, CAVIARBF(ref) still had good performance, and in general it was the third best method among all compared, following CAVIARBF and BIMBAM. The differences among methods were small when only few SNPs were selected, but the differences became larger in the middle, i.e., around half of the total number of SNPs, and were small again when almost all SNPs were selected. In each plot, if we fix the proportion of causal SNPs included (the y-axis), we can compare the number of SNPs needed to reach that proportion, which is linearly interpolated based on the discrete numbers on the x-axis. Table 1 shows the average number of SNPs needed to include 50% or 90% of the causal SNPs among 100 simulated data sets. For example, when there were 3 causal SNPs, to include 90% of the causal SNPs, the average numbers of SNPs needed were 19.80 for CAVIARBF and BIMBAM, 25.25 for PAINTOR, 29.00 for ENET, and 22.00 for CAVIARBF(ref). The results were similar for binary traits, which are shown in Figure S1 and Table S1.

Figure 2.

Comparison of different fine-mapping methods on quantitative traits. The y-axis is the proportion of causal SNPs included and the x-axis is the number of selected SNPs. There are 35 SNPs in total. The proportions are calculated over 100 data sets. The proportion (y-value) is not calculated if >5 data sets do not reach the specified number of SNPs (x-value). This is why some proportions are not available for LASSO as the number of selected candidate SNPs becomes large. Each plot corresponds to a different number of causal SNPs.

Table 1. Average number of SNPs needed to include 50% and 90% causal SNPs among 100 simulated data sets under different numbers of causal SNPs for continuous traits.

Methods	1a		2		3		4		5
	50%	90%	50%	90%	50%	90%	50%	90%	50%	90%
CAVIARBF	1.69	10.00	2.95	16.00	4.53	19.80	5.47	20.80	7.42	26.18
BIMBAM	1.63	9.75	3.00	17.00	4.25	19.80	5.50	20.55	7.86	26.25
PAINTOR	2.00	11.50	3.75	20.33	5.36	25.25	6.50	25.67	8.77	26.83
ENET	2.00	27.00	4.00	26.20	7.80	29.00	6.41	29.00	8.39	30.33
LASSO	NA	NA	NA	NA	NA	NA	13.75	NA	NA	NA
CAVIARBF(ref)	1.73	12.00	3.17	15.00	4.76	22.00	5.88	23.17	7.82	26.77

^aThe number of causal SNPs in the data. The smallest number for each column is in boldface type. NA: data not available for the calculation. CAVIARBF(ref): CAVIARBF with the correlation among SNPs estimated from the CEU population of the 1000 Genomes Project.

Choices and robustness of ${\sigma }_a$

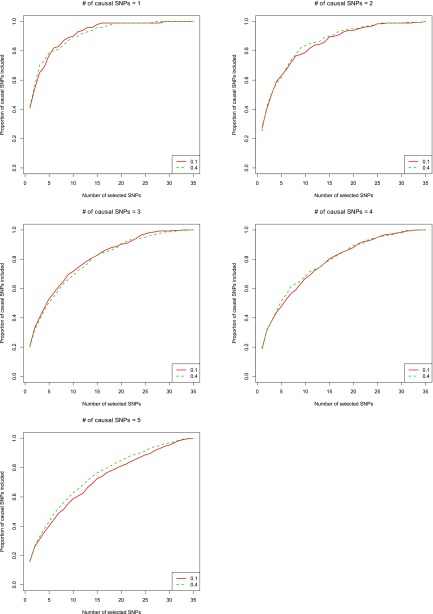
For both CAVIARBF and BIMBAM, we needed to specify ${\sigma }_a$. We found that the results were robust with different values of ${\sigma }_a$. Figure 3 shows the result of CAVIARBF on quantitative traits by setting ${\sigma }_a$ to 0.1 and 0.4, which are common values used from BIMBAM’s manual. The results were similar except for the case of five causal SNPs where setting ${\sigma }_a$ to 0.4 showed a slightly better performance. Similar robustness was observed for binary traits (see Figure S2). Another possible way to choose ${\sigma }_a$ is to try several values and choose the one that maximizes the likelihood of the given data. This is similar to the empirical Bayesian method. When computation time is not an issue, this may result in a more robust and improved performance.

Figure 3.

Comparison of different prior values ${\sigma }_a$ on quantitative traits. CAVIARBF is used to calculate the Bayes factors. The description of the x-axis and y-axis is the same as in Figure 2.

ρ-Level confidence set vs. marginal PIP

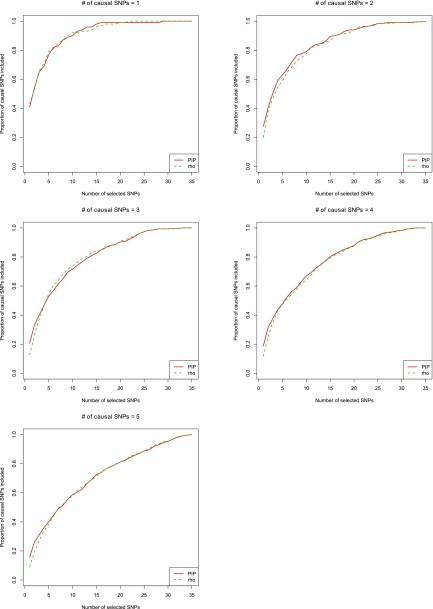
Even though choosing SNPs with the top marginal PIPs maximizes the expected number of causal SNPs, we want to compare this criterion with the ρ-level confidence set, as proposed in CAVIAR (Hormozdiari et al. 2014). Figure 4 and Figure S3 show the results for quantitative traits and binary traits, respectively. In general, the results from the two different selection criteria were very similar if the number of selected SNPs was not too small. Specifically, it seems that selecting SNPs using marginal PIPs usually had better performance than the ρ-level confidence set at the first few steps. This is reasonable. Take the first step, for example. For each candidate SNP, the ρ-level confidence set considers only the causal model that is composed of the candidate SNP. In contrast, the marginal PIP considers all models that include the candidate SNP. The marginal PIP gives the likelihood that a candidate SNP is causal among all possible causal models, while the ρ-level confidence set gives the likelihood that a candidate SNP is causal, assuming there is only one causal SNP. Obviously, marginal PIP is what we want when there are multiple causal SNPs. Interestingly, when the number of selected SNPs was large enough, e.g., no less than five, the two methods showed similar results. Given that the marginal PIP is much easier and faster to compute and ranking by PIP maximizes the expected number of causal variants, we recommend using it first. In our implementation, we still provide an option to calculate the ρ-level confidence set if the user wants to have an estimate of the probability that all causal SNPs have been included in each selection step. The forward stepwise selection to construct a ρ-level confidence set may have some advantages when there are interactions among causal SNPs. There might be more flexible stepwise procedures that allow previously selected SNPs to be removed from the model or swapped with others. These could be a topic for further study.

Figure 4.

Comparison of different criteria to prioritize variants on quantitative traits. CAVIARBF is used to calculate the Bayes factors. The green dashed line represents prioritizing SNPs using marginal posterior inclusion probabilities (PIPs). The red solid line represents prioritizing SNPs using the ρ-level confidence set. The description of the x-axis and y-axis is the same as in Figure 2.

Estimated probability of ρ-level confidence set

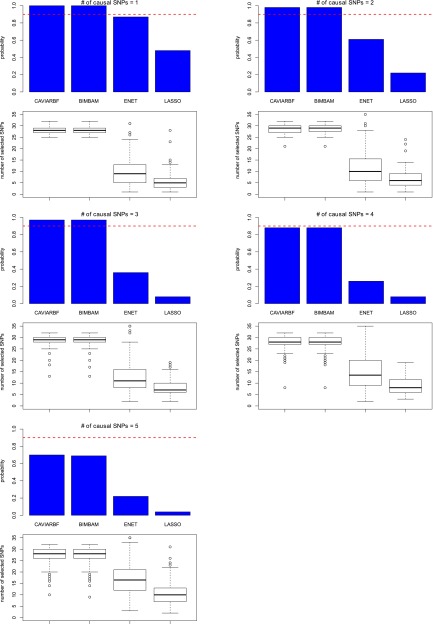
In this section we estimate the probability of including all causal SNPs. Figure 5 shows the estimated probability and the distribution (boxplot) of the number of selected SNPs for quantitative traits. The nominal ρ level was set to 0.9. For CAVIARBF and BIMBAM, when the number of causal SNPs was no more than three, the estimated probability was larger than the nominal level, which means more SNPs than needed were selected. When the number of causal SNPs was five, the estimated probability was ∼0.7, lower than the nominal level. This inaccurate ρ-level estimation was because we used a model that assumed the expected number of causal SNPs in the data was one, much smaller than five. Therefore in real data analysis, even though the estimated probability ρ for each SNP set can usually give a rough indication of the probability of including all causal SNPs, it should be interpreted with some caution. For ENET and LASSO, we first used cross-validation to select the best parameters and then used the selected parameters to build the best model, using the full data. It was obvious that both ENET and LASSO cannot guarantee a high probability of including all causal SNPs based on the best model built from the data, even though the number of the selected SNPs was much smaller than those from CAVIARBF and BIMBAM. For binary traits, similar patterns were observed (see Figure S4).

Figure 5.

Estimated probabilities of the ρ-level confidence set and boxplots of the number of selected SNPs. The phenotypes are quantitative traits. The bar graph is plotted above the corresponding boxplot. The red dashed line shows the nominal level of the confidence set. The bars show the estimated proportion where the selected SNPs include all causal SNPs among 100 data sets. For ENET and LASSO, the best model selected by cross-validation is used for each data set.

The results show that CAVIARBF or BIMBAM selected more SNPs than ENET or LASSO but achieved a higher probability of including all causal SNPs. We questioned whether this was due to the high correlation between SNPs in the simulated data set or other factors. To answer this, we simulated data sets with quantitative traits where SNPs were independent from each other. Results are shown in Figure S5. For data sets with less than five causal SNPs, CAVIARBF and BIMBAM selected more SNPs than needed; i.e., the reported level of confidence was conservative even in the case of independent SNPs. We think that this is due to the uncertainty on the number of causal SNPs. For example, for the data set with only one causal SNP, allowing a maximum of five causal SNPs with CAVIARBF and BIMBAM may also take into account other possible small effects, resulting in more SNPs needed to reach a nominal level than that assuming only one causal SNP. For data sets with five causal SNPs, which was also the maximal number of causal SNPs allowed in the analysis, most of the time CAVIARBF and BIMBAM selected exactly the five causal SNPs because no extra small effects needed to be considered. This number was also lower than that from ENET or LASSO. The single ρ level of a candidate set provides limited information about the selected SNPs; another informative way is to look at the marginal PIPs, as shown in Figure S6. There were three causal SNPs in the data set, which correspond to the marginal PIPs close to 1 (gold lines). Compared to Figure 1, the pattern here is much simpler and reflects the independence among SNPs.

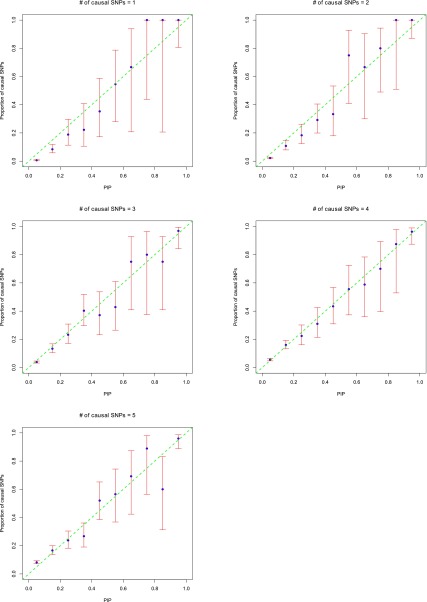
Calibration of the PIPs

PIPs are more useful if they are well calibrated. To assess the accuracy of estimated PIPs, following Guan and Stephens (2011), we put SNPs into 10 bins according to their PIPs. Each bin’s width was 0.1. We chose 10 bins instead of 20 due to the small number of counts in some bins. Then we compared the proportion of causal SNPs in each bin with the center PIP of that bin. Figure 6 shows the plots using quantitative traits. Except those bins with very large confidence intervals, due to small total counts in the bins, in general the points lie near the diagonal line. This indicates that the PIPs are reasonably calibrated. Therefore PIPs can be used not only to rank SNPs, but also as an indication of the expected number of SNPs in the candidate set. Similar results for binary traits are shown in Figure S7.

Figure 6.

Calibration of the posterior inclusion probabilities (PIPs) on quantitative traits. CAVIARBF is used to calculate the Bayes factors. SNPs were put into 10 bins of width 0.1 according to their PIPs. In each bin, the proportion of causal SNPs was then calculated. The x-axis shows the center of each bin. The y-axis is the proportion of causal SNPs. The blue points show the proportion of causal SNPs in each bin. The red bars show the 95% Wilson score confidence interval of the proportion assuming a binomial distribution in each bin. One hundred data sets were used in each plot. Except those points with very large confidence intervals due to small total counts in the bins, usually <10, in general the points lie near the line y = x. This indicates that the PIPs are reasonably calibrated.

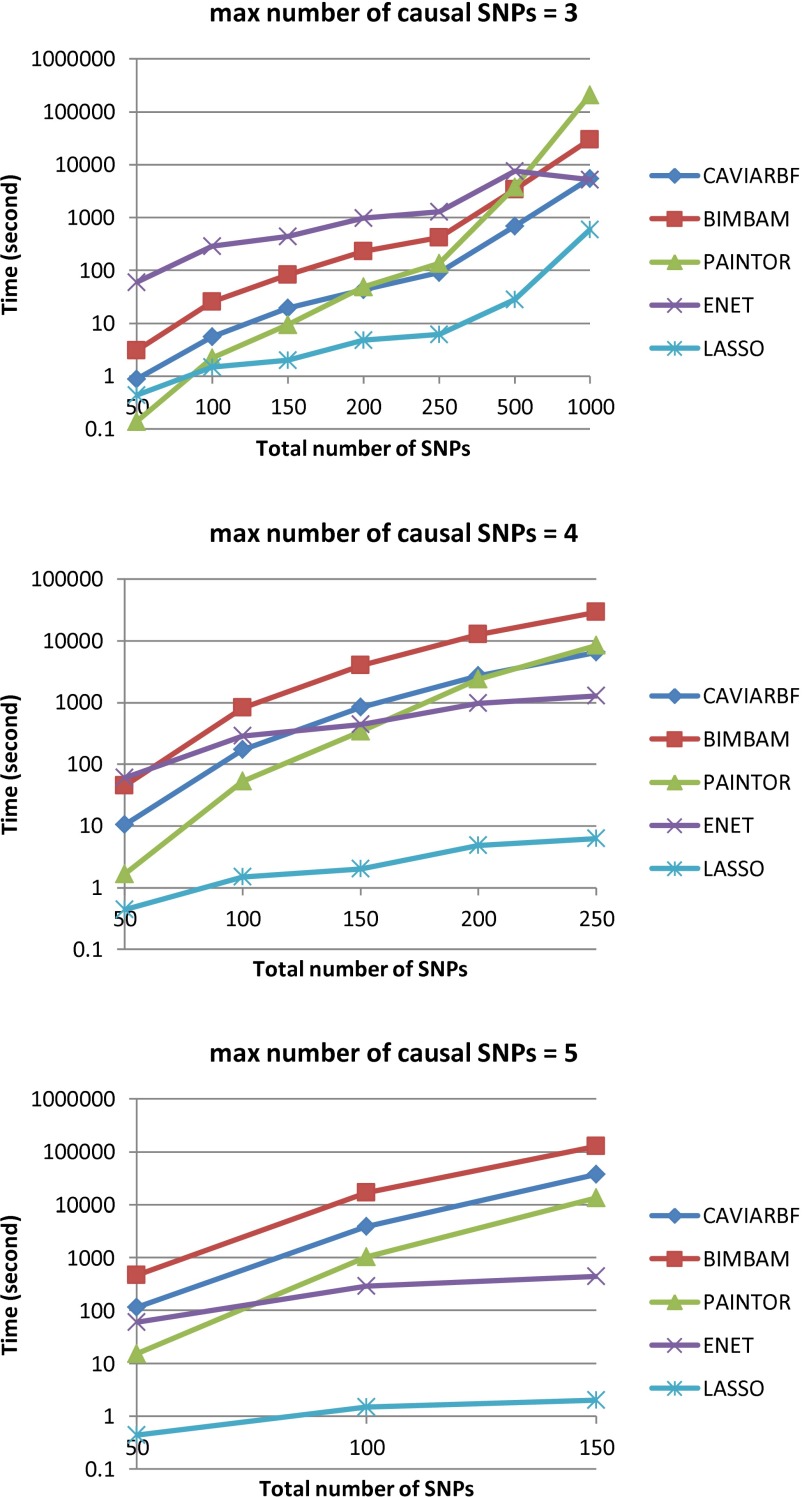
Time cost

For CAVIARBF and BIMBAM, the time cost depends on the total number of SNPs p and the maximal number of causal SNPs allowed, l. The total number of causal models is ${\displaystyle {\sum }_{i=0}^l\left(\begin{array}{c}p\\ i\end{array}\right)}$, which is dominated by the combinatorial term $\left(\begin{array}{c}p\\ l\end{array}\right)$. Because ${\left(p/l\right)}^l\le \left(\begin{array}{c}p\\ l\end{array}\right)\le p^l/l!\le {\left(\left(p\cdot e\right)/l\right)}^l$, if we fix p, for small l much less than p, $\left(\begin{array}{c}p\\ l\end{array}\right)$ increases approximately exponentially with respect to l. If we fix l, it is bounded above by a polynomial complexity of degree l. For a reasonable running time, l is usually small, e.g., no more than 5. The total number of SNPs p can be relatively larger. Figure 7 shows the actual time cost for quantitative traits with different p when l = 3, 4, and 5. ENET was based on the R package elastic net with 10-fold cross-validation and LASSO was based on the R package lars. For PAINTOR, we set the number of iterations to two because after that the likelihood changed little. CAVIARBF takes about one-quarter to one-fifth of the time of BIMBAM. For example for l = 3, when the number of SNPs was 200, the time was ∼44 sec for CAVIARBF and 229 sec for BIMBAM. CAVIARBF was slower than PAINTOR when p < 200 but faster than PAINTOR when p became larger. This is because PAINTOR always uses all the SNPs in the computation of the likelihood for each model while CAIVARBF uses only those SNPs included in each model to calculate the likelihood.

Figure 7.

Time cost of different methods. Different maximal numbers of causal SNPs are tested for CAVIARBF, BIMBAM, and PAINTOR. The y-axis is on a log10 scale. The x-axis shows the total number of SNPs in the input data.

Application of methods

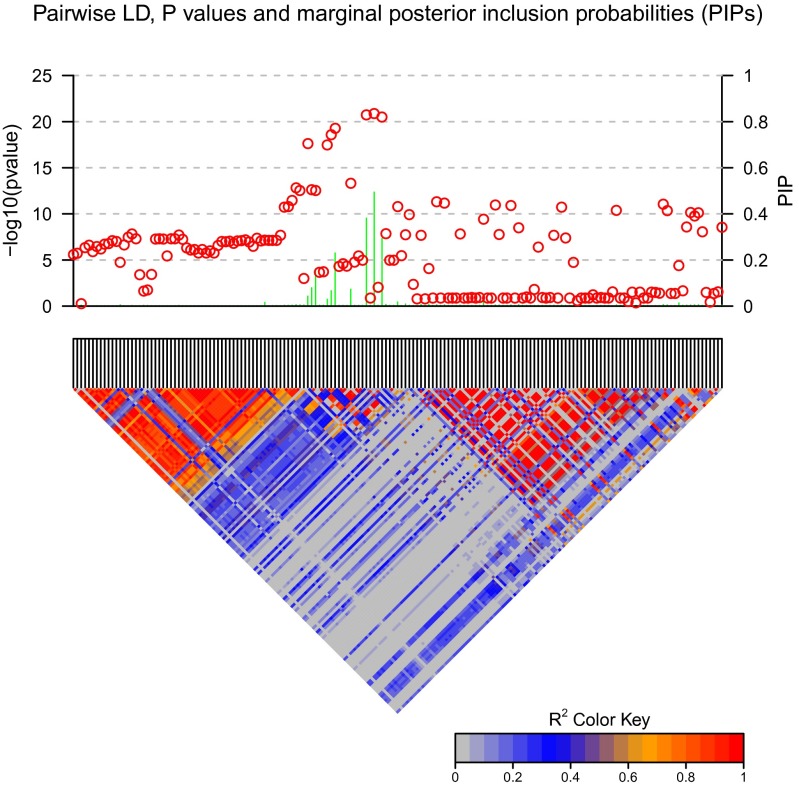
To compare different methods on real data, we used two GWAS cohorts designed to identity genetic variants associated with variation in smallpox vaccine-induced immune responses. The phenotype of interest is vaccinia virus-induced IFN-α production detected in peripheral blood mononuclear cells (PBMCs) from first-time recipients of smallpox vaccine. More details about the study cohorts can be found in Ovsyannikova et al. (2011, 2012, 2014) and Kennedy et al. (2012). The first cohort, called the San Diego cohort, included 1076 recipients of Dryvax, of which 488 were Caucasian and had the IFN-α outcome available and genotypes measured by the Illumina HumHap 550 platform. Genotypes were imputed using IMPUTE2 (Howie et al. 2009) with the reference panel from the 1000 Genomes Phase 1 haplotypes. The second cohort, called the U.S. cohort, included 1058 recipients of ACAM2000, of which 734 were Caucasian and 713 of them had the IFN-α outcome available. The genotypes were measured by the Omni 2.5S genome-wide SNP chip. For the U.S. cohort (mainly Caucasian), the European (EUR) population was used as the reference panel. For the San Diego cohort (a mix of different race and ethnic groups), the EUR, East Asian (ASN), African (AFR), and Admixed American (AMR) populations were used as the reference panel. For both cohorts, the analyses were restricted to Caucasians. For the U.S. cohort, the phenotype was regressed on the following covariates: gender, time from immunization to blood draw, vaccination date, immune assay batch, and the first principal component to adjust for potential population stratification. For the San Diego cohort, the phenotype was regressed on the following covariates: date of IFN-α assay, date of blood draw, shipping temperature of the sample, site the sample was drawn from, and the second principal component (the first is not included because it is not significant). The residuals from these regressions were used as the analysis phenotype. We focused on a region of chromosome 5 where multiple SNPs reached the genome-wide significance level of 5 × 10⁻⁸ for both cohorts. We chose the region based on a cluster of peak signals and included ∼100 SNPs on both sides of the target region. Furthermore, SNPs with minor allele frequency (MAF) <5% in each cohort were removed, leaving 167 SNPs in the U.S. cohort and 200 SNPs in the San Diego cohort for fine-mapping analysis. The mode of posterior probabilities from IMPUTE2 for each SNP averaged over all individuals was >0.8, and the overall average across all SNPs was >0.97. We set the maximal number of causal SNPs to 3 and 4. Because they showed similar results, there was no need to use a larger maximal number of causal SNPs. We present the results corresponding to a maximum of 4 causal SNPs. For BIMBAM and CAVIARBF, we set σ_a to 0.1 and used the original SNP matrix (not scaled) in the model. The prior probability of being causal for each SNP is set to 1/m, where m is the number of SNPs.

The overall Bayes factor $\mathrm{BF}\left(M_{\mathrm{g}}:M_0\right)$ measures the evidence strength of at least one causal variant in the region. For the U.S. cohort, it was 2.5 × 10¹³, which is very strong evidence favoring the model that there is at least one causal variant. For the San Diego cohort it was 8.1 × 10⁷, which is much smaller than the U.S. cohort but is still suggestive even if we use a very conservative prior, say 10⁻⁷. One obvious reason for the smaller Bayes factor is the smaller sample size in the San Diego cohort. The overall evidence of the region also makes the prior assumption of 1 expected causal SNP in the region reasonable. Figure 8 shows the PIPs from CAVIARBF on the U.S. cohort. PIPs of many SNPs in the plot are very small and can be excluded from the candidate causal set. Some of these excluded SNPs have P-values <10⁻¹⁰; however, this is likely due to their being in close LD with causal variants. PIPs from BIMBAM and PAINTOR on the U.S. cohort are shown in Figure S8 and Figure S9, respectively. As in the simulation results, CAVIARBF and BIMBAM showed similar results. PAINTOR identified the same top 3 SNPs as CAVIARBF and BIMBAM; however, the pattern of the remaining SNPs was different. CAVIARBF and BIMBAM still included other SNPs with relatively large PIPs, while PAINTOR-selected SNPs had very small PIPs. This may be due to treating a fixed or estimated noncentrality parameter (effect size) as the true value in PAINTOR, while in CAVIARBF and BIMBAM a prior distribution of the effect size is assumed. Similar patterns are shown on the San Diego cohort (see Figure S10, Figure S11, and Figure S12). The top 10 SNPs from each method on two cohorts are presented in Table 2 and Table 3. For both cohorts, CAVIARBF and BIMBAM identified the same top 10 SNPs and ranked them identically. PIPs are similar between BIMBAM and CAVIARBF. On the other hand, PAINTOR included some different SNPs. Some of the top 10 SNPs selected by BIMBAM and CAVIARBF were ranked >50 by PAINTOR. Next we examined the number of SNPs shared in the top 10 SNPs picked by each method between two cohorts. These SNPs are indicated in boldface type in Table 2 and Table 3. For BIMBAM and CAVIARBF, 8 of 10 SNPs are shared while there are only 3 SNPs shared for PAINTOR. We also found that one of the shared SNPs picked by PAINTOR seems counterintuitive. This SNP (rs11744917) was ranked 10th with a P-value of 0.555 in the U.S. cohort, and ranked 4th with a P-value of 0.152 in the San Diego cohort. The same SNP was ranked 47 by CAVIARBF and 48 by BIMBAM in the U.S. cohort and 49 by CAVIARBF and 57 by BIMBAM in the San Diego cohort. Because no functional study has been performed yet to verify the underlying causal variants, no conclusion can be made on the performance of different methods. However, the PIP patterns and the sharing of the top 10 SNPs may shed some light on the characteristics of different methods. One advantage of CAVIARBF is the use of summary statistics. We also tried to use only the z test statistics and estimated LD pattern (the correlation coefficient matrix among SNPs) from the 1000 Genomes Project, using EUR samples. Figure S13 shows the PIPs and LD plots on the U.S. cohort. Compared to the result from using the LD matrix calculated from the U.S. cohort, even though there are some distortions, the general patterns are similar. As the numbers of samples in the study and in the reference panel increase, assuming a good match of ancestry background, the estimation of the correlation matrix will become more stable and accurate. Therefore, we anticipate the PIPs from using only the z test statistic and correlations from reference panels will become more accurate in studies with large samples.

Figure 8.

P-values and posterior inclusion probabilities (PIPs) from CAVIARBF on the U.S. cohort. Circles represent the individual SNP-based P-values on the left y-axis and lines represent the PIPs on the right y-axis. The color-coded LD pattern is shown below.

Table 2. Top 10 variants ranked by PIPs from different methods and the corresponding P-values on the U.S. cohort.

BIMBAM			CAVIARBF			PAINTOR
SNP	P-value	PIP	SNP	P-value	PIP	SNP	P-value	PIP
rs13166214	1.32E-21	0.470	rs13166214	1.32E-21	0.496	rs13166214	1.32E-21	0.431
rs7447927	1.83E-21	0.354	rs7447927	1.83E-21	0.383	rs7447927	1.83E-21	0.305
rs7444313	3.21E-21	0.283	rs7444313	3.21E-21	0.295	rs7444313	3.21E-21	0.177
rs55792153	5.28E-20	0.226	rs55792153	5.28E-20	0.232	rs113451531	8.29E-05	0.064
rs10875554	2.88E-13	0.204	rs10875554	2.88E-13	0.163	rs1131769	4.94E-14	0.047
rs28419191	2.44E-13	0.099	rs28419191	2.44E-13	0.081	rs112269266	3.94E-05	0.038
rs1131769	4.94E-14	0.091	rs1131769	4.94E-14	0.074	rs7380272	3.59E-06	0.031
rs13153461	2.67E-19	0.072	rs13153461	2.67E-19	0.068	rs55792153	5.28E-20	0.019
rs9716069	2.36E-18	0.048	rs9716069	2.36E-18	0.044	rs10875554	2.88E-13	0.012
rs13181561	3.39E-18	0.035	rs13181561	3.39E-18	0.031	rs11744917	5.55E-01	0.011

The SNPs in boldface type are shared in the top 10 SNPs between two cohorts for each method.

Table 3. Top 10 variants ranked by PIPs from different methods and the corresponding P-values on the San Diego cohort.

BIMBAM			CAVIARBF			PAINTOR
SNP	P-value	PIP	SNP	P-value	PIP	SNP	P-value	PIP
rs13181561	6.43E-17	0.596	rs13181561	6.43E-17	0.651	rs13181561	6.43E-17	0.707
rs13153461	1.62E-16	0.374	rs13153461	1.62E-16	0.391	rs13153461	1.62E-16	0.284
rs9716069	8.45E-15	0.108	rs9716069	8.45E-15	0.094	rs9716069	8.45E-15	0.006
rs7447927	5.03E-14	0.062	rs7447927	5.03E-14	0.054	rs11744917	1.52E-01	0.004
rs7444313	1.16E-13	0.048	rs7444313	1.16E-13	0.041	rs28419191	4.03E-10	0.001
rs7446197	7.76E-12	0.047	rs7446197	7.76E-12	0.040	rs7447927	5.03E-14	0.001
rs28419191	4.03E-10	0.037	rs28419191	4.03E-10	0.031	rs28396805	1.27E-06	1E-03
rs55792153	5.92E-13	0.036	rs55792153	5.92E-13	0.030	rs73257323	1.20E-04	4E-04
rs13166214	6.36E-13	0.032	rs13166214	6.36E-13	0.027	rs7444313	1.16E-13	4E-04
rs36137978	5.26E-12	0.030	rs36137978	5.26E-12	0.026	rs7380062	1.58E-04	4E-04

The SNPs in boldface type are shared in the top 10 SNPs between two cohorts for each method.

Discussion

By proving that BIMBAM and CAVIAR are approximately equivalent, we provided a Bayesian framework of fine mapping using marginal test statistics and correlation coefficients among SNPs. We also provided a fast implementation, CAVIARBF. Compared to CAVIAR, CAVIARBF has the following main advantages: (1) it is much faster largely because it uses only the SNPs in each causal model to calculate Bayes factors; (2) it unifies the fine-mapping and association tests in a consistent Bayesian framework; and (3) it is Bayes factor centered, so the output Bayes factors can be used for other analysis, e.g., calculating the evidence of at least 1 causal SNP in the region. Our simulation showed that the performances of BIMBAM and CAVIARBF are almost the same, as expected. CAVIARBF had better performance than PAINTOR, which has been shown to be a very competitive method to other fine-mapping methods (Kichaev et al. 2014). Our implementation is about four to five times as fast as BIMBAM. Application to real data showed that BIMBAM and CAVIARBF identified the same top 10 SNPs with the same ranking. PAINTOR identified 3 of the same top 10 SNPs (those with large PIPs) as BIMBAM and CAVIARBF. BIMBAM and CAVIARBF may be more consistent than PAINTOR in prioritizing causal SNPs because 8 of the 10 top SNPs were shared between two cohorts on the same phenotype.

The approximate equivalence between BIMBAM using the full data $(y, X)$ and CAVIAR/CAVIARBF using only the marginal test statistics and the correlation coefficient matrix $(z, {\Sigma }_x)$ can also be explained in terms of sufficient statistics. For example, for quantitative traits, let $D_1=(y, X)$. If we assume the variance of y is known, we can equivalently write the input $(z, {\Sigma }_x)$ as $D_2=\left(X^{\mathrm{T}}y, X^{\mathrm{T}}X\right)$. The likelihood function $l\left(y, X\text{|}\beta \right)=p\left(X\right)p(y|X,\beta )$. The conditional probability $p(y|X,\beta )$ depends only on ${\left(y-X\beta \right)}^{\mathrm{T}}\left(y-X\beta \right)=y^{\mathrm{T}}y+{\beta }^{\mathrm{T}}{X}^{\mathrm{T}}X\beta -2{\beta }^{\mathrm{T}}{X}^{\mathrm{T}}y$, where the part involving both parameter β and data is ${\beta }^{\mathrm{T}}{X}^{\mathrm{T}}X\beta -2{\beta }^{\mathrm{T}}{X}^{\mathrm{T}}y$. Therefore $D_2=(X^{\mathrm{T}}y, X^{\mathrm{T}}X)$ is the sufficient statistic for the model parameter β. Then it can be shown that the Bayes factor depends only on the sufficient statistics. More details of proving the equivalence for binary traits are given in File S1.

The analytic Bayes factor is also derived in Wen (2014). For example, Equation 3 can be derived from equation 9 in Wen (2014), even though the marginal test statistics are not used directly. In Wen (2014), it also proves the approximation when the error variance $1/\tau$ is unknown. Similar derivations could be applied for the marginal test statistics.

All derivations assume no covariates in the model. When there are covariates, for quantitative traits, as suggested in the manual of BIMBAM, we can regress the trait on all covariates first and use the residual as the new trait. Because CAVIARBF needs only the input of marginal test statistics, a natural way is to calculate the test statistic for each SNP adjusted for other covariates. This method can be applied to both quantitative traits and binary traits. Further analysis is needed to fully validate the effectiveness of this handling of covariates.

For a well-powered GWAS, there are usually multiple loci with potential causal variants for further fine mapping. Usually these loci can be assumed to be independent of one another. In this case we can first do fine mapping of each locus and then pool all PIPs of the SNPs in these loci together and choose the top k SNPs as recommended in Kichaev et al. (2014).

We considered only common variants in this study. For common variants, it might be practical to assume a maximal number of causal variants in a locus, e.g., no more than five. When the maximal number of causal SNPs in a model is limited, all possible models can be enumerated exhaustively in a reasonable time if the number of SNPs in a locus is not too large. This is different from typical Bayesian methods where sampling methods, such as MCMC, are often used to sample models from the model space (Wilson et al. 2010; Guan and Stephens 2011). The sampling methods would be useful if more than five causal variants are expected in a large region with high LD among SNPs. On the other hand, if a large region can be divided into multiple uncorrelated or weakly correlated regions, we can perform fine mapping in each region, and then combine the results together. For rare variants, there may be many rare causal variants in a region, and therefore sampling methods may be required to explore the model space. Some Bayesian-based methods have been proposed for rare variants, such as in Quintana et al. (2011, 2012).

Because the Bayesian framework can also answer the association question, in principle the proposed method can be used for genome-wide association scans. Because of the consideration of multiple causal SNPs in a region, it may achieve higher power to discover the association regions than the traditional individual SNP-based test. This has already been demonstrated in Wilson et al. (2010) and Guan and Stephens (2011), using the true positive vs. false positives plot. However, the time cost may be much larger compared to that of individual SNP-based tests. Further reduction in time cost will be helpful for this application.

We assumed the effects of multiple causal SNPs are additive (for binary traits, additive on logit scale) and the effect of each causal genotype is additive. We believe these assumptions are reasonable for most cases. In principle, the dominance effect of each SNP can be included by adding an extra column indicating the genotype heterozygosity as implemented in BIMBAM. How to include a nonadditive combination of effects from multiple causal SNPs will be an interesting topic of further study.

We assumed that functional annotations of SNPs are not included in fine mapping. As pointed out in Kichaev et al. (2014) and Pickrell (2014), a large amount of annotation information of genomic elements has been generated, such as the Encyclopedia of DNA Elements (ENCODE Project Consortium 2012). Including informative functional annotations into fine-mapping analysis will further increase the chance to filter out the underlying causal variants (Quintana and Conti 2013; Kichaev et al. 2014; Pickrell 2014). In principle, the same EM algorithm proposed in Kichaev et al. (2014) can be applied to extend our method to handle functional annotations. We leave this as a future direction to pursue.