Abstract
Meta-analysis of genetic data must account for differences among studies including study designs, markers genotyped, and covariates. The effects of genetic variants may differ from population to population, i.e., heterogeneity. Thus, meta-analysis of combining data of multiple studies is difficult. Novel statistical methods for meta-analysis are needed. In this article, functional linear models are developed for meta-analyses that connect genetic data to quantitative traits, adjusting for covariates. The models can be used to analyze rare variants, common variants, or a combination of the two. Both likelihood-ratio test (LRT) and F-distributed statistics are introduced to test association between quantitative traits and multiple variants in one genetic region. Extensive simulations are performed to evaluate empirical type I error rates and power performance of the proposed tests. The proposed LRT and F-distributed statistics control the type I error very well and have higher power than the existing methods of the meta-analysis sequence kernel association test (MetaSKAT). We analyze four blood lipid levels in data from a meta-analysis of eight European studies. The proposed methods detect more significant associations than MetaSKAT and the P-values of the proposed LRT and F-distributed statistics are usually much smaller than those of MetaSKAT. The functional linear models and related test statistics can be useful in whole-genome and whole-exome association studies.
Keywords: meta-analysis, rare variants, common variants, association mapping, quantitative trait loci, complex traits, functional data analysis
META-ANALYSIS is a statistical method to combine multiple studies for a unified analysis and it plays an important role in genetic studies (de Bakker et al. 2008; Zeggini and Ioannidis 2009; Cantor et al. 2010; Evangelou and Ioannidis 2013). One obvious advantage of meta-analysis is that the sample size is large (Liu et al. 2014). Therefore, meta-analysis should lead to more significant results. It is argued that most of the reported complex disease associations came from large-scale meta-analysis of genome-wide association studies (GWASs) (Zeggini and Ioannidis 2009; Evangelou and Ioannidis 2013; Liu et al. 2014). Therefore, there has been great interest in developing novel statistical methods to perform GWAS meta-analysis (Ioannidis et al. 2007; Hu et al. 2013; Liu et al. 2014). Meta-analysis combines studies with different study designs. The genotype data and covariates may vary from study to study. Moreover, the effects of genetic variants in different populations may not be the same, i.e., the heterogeneity (Tang and Lin 2014). Thus, meta-analysis of combining data of multiple studies is difficult. Novel statistical methods for meta-analysis are needed.
The statistical methods for meta-analysis fall into two classes: (1) single genetic variant-based approaches and (2) gene-based variant analysis approaches. The single genetic variant approaches only use one genetic variant at a time and are usually based on fixed-effect linear regression models for quantitative traits, -tests, or score tests for qualitative traits. The single genetic variant approaches are mainly applied to analyze common variants (Zeggini et al. 2008; Hindorff et al. 2009; Stahl et al. 2010). Gene-based approaches use multiple genetic variants in genetic regions in the analysis and can analyze rare variants, common variants, or combinations of the two. Developing gene-based approaches for association analysis is a major area of interest. A few recent studies have targeted analysis of rare variants.
Three types of tests are available for gene-based association analysis of complex diseases. The first type is burden tests that are based on collapsing rare variants in a genetic region to be a single variable that is then used to test for association with the phenotypes (Li and Leal 2008; Madsen and Browning 2009; Morris and Zeggini 2010; Price et al. 2010). Burden tests were built to analyze rare variants by aggregating statistics of multiple rare variants for an analysis.
The second type is variance-component tests such as the sequence kernel association test (SKAT) and its optimal unified version (SKAT-O) (Lee et al. 2012). In Lee et al. (2012), it was shown that SKAT-O has higher power than some burden tests, such as the combined collapsing and multivariate method (Li and Leal 2008) and the nonparametric weighted sum test (Madsen and Browning 2009). By extending SKAT and SKAT-O to perform meta-analysis, Lee et al. (2013) developed meta-analysis SKAT and SKAT-O (MetaSKAT and MetaSKAT-O) to carry out meta-analysis for rare variants in multiple studies. Both SKAT and MetaSKAT are score tests based on mixed-effect models.
The third type is tests based on fixed-effect models that include (1) traditional additive effect models that are well studied (Cordell and Clayton 2002; Fan and Xiong 2002; Fan et al. 2006) and (2) functional regression models as shown in our previous research (Luo et al. 2012; Fan et al. 2013, 2014; Wang et al. 2015). Note that functional regression models are fixed-effect models, which extend traditional population genetics models to analyze multiple genetic variants and can analyze rare variants, common variants, or combinations of the two. For individual studies with small and moderate sample sizes, functional linear models (FLMs) were proposed to analyze quantitative traits. The FLMs lead to -score tests and F-distributed statistics, which are more powerful than SKAT and SKAT-O while controlling type I error correctly (Luo et al. 2012; Fan et al. 2013; Wang et al. 2015). For dichotomous traits, generalized FLMs were developed to perform gene-based association analysis (Fan et al. 2014).
In functional regression models, we treat multiple genetic variants of an individual as a realization of an underlying stochastic process (Ross 1996). Therefore, the genome of an individual in a chromosome region is a continuum of sequence data rather than discrete observations. The genome of an individual is viewed as a stochastic function that contains both genetic position and linkage disequilibrium (LD) information of the genetic markers. In short, the functional regression models have a number of advantages: (1) the genetic effects at the major gene locus are modeled as fixed effects, which fit traditional population genetics theory and modern genetic data very well; (2) the models fully utilize LD and genetic position information; and (3) the models test for a joint effect of genetic variants, including both common and rare.
It is worth of noting that SKAT and SKAT-O were found to perform better than C-alpha (Neale et al. 2011) and burden tests (Li and Leal 2008; Madsen and Browning 2009; Morris and Zeggini 2010; Price et al. 2010). Hence, FLMs are potentially very powerful in association analysis of complex quantitative traits. The superior performance of the FLMs motivates us to extend them to perform meta-analysis.
In this article, FLMs are developed for meta-analysis of multiple studies to connect genetic data to quantitative traits, adjusting for covariates. We allow that different studies may have different environmental factors/covariates, and genetic variants may differ among studies. The effects of genetic variants may differ from population to population, i.e., heterogeneity. This makes it possible for us to build flexible models for meta-analysis of multiple studies. We assume that individual genotype data are available from all studies.
Both likelihood-ratio test (LRT) and F-distributed statistics of FLMs are introduced to test association between quantitative traits and multiple genetic variants in one gene region. Extensive simulations are performed to evaluate the empirical type I error rates and power performance of the proposed models and tests. The proposed methods are applied to analyze four blood lipid levels in data from meta-analysis of eight European studies.
Materials and Methods
Consider a meta-analysis with L studies in a genomic region. For the ℓth study, we assume that there are individuals who are sequenced in the genomic region at variants. We assume that the variants are located with ordered genetic positions . To make the notation simpler, we normalized the region to be [0, 1]. For the ith individual in the ℓth study, let denote her/his quantitative trait, denote her/his genotypes of the variants, and denote her/his covariates. Hereafter, ′ denotes the transpose of a vector or matrix. For the genotypes, we assume that is the number of minor alleles of the individual i at the jth variant.
General functional linear model
In this section, we view the ith individual’s genotype data as a genetic variant function (GVF) . Note that the sample includes discrete realizations or observations of the human genome. By using the genetic variant information , we may estimate the related GVF , which is discussed below. To relate the GVF to the phenotypic trait adjusting for covariates, we consider the following functional linear model,
| (1) |
where is the overall mean, is a column vector of regression coefficients of covariates, is the genetic effect of GVF at the position t, and is an error term. For each ℓ and i, the error term is normally distributed with a mean of zero and a variance . Moreover, are independent variables, and are independent vectors of variables, . Similar to the GVF, we assume that the genetic effect is a function of the genetic position t.
Expansion of genetic effect function:
The genetic effect function is assumed to be smooth. One may expand it by B-spline or Fourier basis functions. Formally, let us expand the genetic effect function by a series of basis functions as , where is a vector of coefficients . We consider two types of basis functions: (1) the B-spline basis, and (2) the Fourier basis, , and . Here for the Fourier basis, is taken as a positive odd integer (de Boor 2001; Ramsay and Silverman 2005; Ferraty and Romain 2010; Horváth and Kokoszka 2012).
Estimation of genetic variant function:
To estimate the genetic variant functions from the genotypes , we use an ordinary linear square smoother (Ramsay and Silverman 2005; Ramsay et al. 2009; Fan et al. 2013). Let , be a series of K basis functions, such as the B-spline basis and Fourier basis functions. Denote . Let Φ denote the by the K matrix containing the values , where . Using the discrete realizations , we may estimate the GVF , using an ordinary linear square smoother as follows (Ramsay and Silverman 2005, Chap. 4):
| (2) |
Revised functional linear model:
We expand by the ordinary linear square smoother. Assume that the genetic effect is expanded by a series of basis functions as . Replacing in the functional linear model (1) by in (2) and by the expansion, we have a revised linear regression model
| (3) |
where . In the above revised regression model, one needs to calculate and to get . In the statistical packages R or Matlab, there are readily available codes to calculate them (Ramsay et al. 2009).
β-smooth only functional linear models
Model (1) is a theoretical FLM in functional data analysis literature (Ramsay and Silverman 2005). For analysis of dense genetic data, one may use a simplified model,
| (4) |
where is the genetic effect at the position for the ℓth study, and the other terms are similar to those in the general model (1). In the above model, the integration term in model (1) is replaced by the summation term . It turns out that model (4) performs very similarly to model (1) in real data analysis and simulations due to high resolution of genotype data (Fan et al. 2013, 2014; Wang et al. 2015).
In model (4), is introduced as the genetic effect at the position . We assume that the genetic effect function is a function of the genetic position t. Therefore, , are the values of function at the genetic positions. The genetic effect function is assumed to be smooth. One may expand it by B-spline or Fourier basis functions as above. Replacing by the expansion, model (4) can be revised as
| (5) |
where . In model (4) and its revised version (5), we use the raw genotype data directly in the analysis. The genetic effect function is assumed to be smooth. Hence, the models are called β-smooth only.
Traditional additive effect models
Traditionally, an additive effect model can be used to analyze the relation between the trait and the variants in the ℓ study as
| (6) |
(Fan and Xiong 2002; Fan et al. 2006), where is the additive genetic effect of variant j for the ℓth study, and the other terms are similar to those in the functional linear models (1) and (4). There is only one difference between model (4) and model (6); i.e., the genetic effect coefficients in model (6) do not depend on the genetic position , while in model (4) depend on the genetic position . The genetic effect coefficients in model (6) are discrete, while in model (4) are the values of function at the genetic positions .
The number of parameters of model (6) can be large, and so it may not be powerful. Moreover, model (6) can model only the LD between the trait and each of the genetic variants as well as the pairwise LD between the genetic variants, but it cannot model higher-order LD among the genetic variants (Fan and Xiong 2002; Fan et al. 2006). In spite of the potential drawbacks, model (6) can be easily implemented by standard statistical software such as R, and we use it to make comparison with models (1) and (4). To facilitate the computation in applications, the QR decomposition can be applied to the genotype data to remove the redundancy if the number of genetic variants is large, i.e., to decompose the genotype matrix into the product of an orthogonal matrix Q and a triangular matrix R via Gram-Schmidt process.
One common feature of models (1), (4), and (6) is that they are all fixed-effect models. The novel part of models (1) and (4) is that we may revise them to be models (3) and (5) by functional data analysis techniques, in which the numbers K and of basis functions do not depend on the numbers of genetic variants. This makes models (1) and (4) able to conveniently analyze high-dimension genetic variant data.
LRT and F-distributed statistics
We consider the revised regression models (3) and (5) as usual multiple linear regressions. First, assume that the genetic effects among the L studies are different/heterogeneous. To test the association between the genetic variants and the quantitative trait, the null hypothesis is . By using the standard statistical approach, we may test the null by a LRT and an F-distributed statistics. The LRT statistic is distributed with d.f. and is denoted as Het-LRT. The F-distributed statistic’s degrees of freedom (d.f.) are (Weisberg 2005). The F-distributed statistic is denoted as Het-F.
If the genetic effects are homogeneous, i.e., , we may test the association between the genetic variants and the quantitative trait by testing a simplified null Again, a LRT and an F-distributed statistics can be used to test the null The F-distributed statistic has d.f. . The F-distributed statistic is denoted as Hom-F. The LRT is distributed with d.f. and is denoted as Hom-LRT.
For the additive effect model (6), the null hypothesis of no association between the genetic variants and the quantitative trait is , under an assumption of heterogeneous genetic effect. The corresponding LRT statistic is distributed with d.f., and the corresponding F-distributed statistic has d.f. as . The tests are denoted as Het-LRT and Het-F.
Assume that each individual of the L studies is sequenced at the same variants located at and so . In addition, assume that the genetic effects are homogenous; i.e., . Then, model (6) is simplified as
| (7) |
The null hypothesis of no association between the genetic variants and the quantitative trait is The corresponding LRT statistic is distributed with m d.f., and the corresponding F-distributed statistic has d.f. as . The tests are denoted as Hom-LRT and Hom-F.
Parameters of functional data analysis
In the data analysis and simulations, we used the functional data analysis procedure in the statistical package R. We use two functions in library fda of the R package as follows to create basis:
basis = create.bspline.basis(norder = order, nbasis = bbasis)
basis = create.fourier.basis(c(0,1), nbasis = fbasis).
The three parameters were taken as order = 4, bbasis = 15, fbasis = 25 in all data analysis. In the simulations, the three parameters were taken as order = 4, bbasis = 15, fbasis = 21 for the heterogeneous genetic effect model and order = 4, bbasis = 15, fbasis = 25 for the homogeneous genetic effect model. Specifically, the order of B-spline basis was 4, the number of basis functions of B-spline was and the number of Fourier basis functions was for the heterogeneous genetic effect model, and similarly the number of basis functions of B-spline was and the number of Fourier basis functions was for the homogeneous genetic effect model.
To make sure that the results are valid and stable, we tried a wide range of parameters: (1) for the heterogeneous genetic effect model and (2) for the homogeneous genetic effect model. The results are similar to each other.
Results
Meta-analysis of lipid traits in eight European cohorts
Lipid traits from eight European cohorts were analyzed: five from Finnish (FUSION Stage 2, D2d-2007, DPS, METSIM, and DRs EXTRA), two from Norway (HUNT and Tromso), and one from Germany (DIAGEN). The two Norwegian cohorts are combined as one study for a joint analysis. The genotype data were from Metabochip genotyping, which was designed to fine map regions that have been associated to metabolic traits (Altshuler et al. 2010). For each cohort, 54,741 genetic variants were genotyped.
For our analysis, we utilized the existing literature as a reference for gene selection and found that 22 gene regions were fine mapped (Liu et al. 2014). We used Builder Mar. 2006 (NCBI36/hg18) to determine gene positions and 5 kb was used to extend the gene region on each side of a gene. The summary of 22 genes and the number of genetic variants in each gene region are given in Supporting Information, Table S1.
Four lipid traits were analyzed: high-density lipoprotein (HDL) levels, low-density lipoprotein (LDL) levels, triglycerides (TG), and total cholesterol (CHOL). The sample sizes for each trait are provided in Table S2. For each trait, inverse normal rank transformation was performed to make sure that normality is valid. For all studies except for METSIM, age, sex, and type 2 diabetes status were used as covariates. For METSIM, age and type 2 diabetes status were used as covariates since no female was included in the study. A significance threshold of was taken from Liu et al. (2014) (corresponding to 0.05/16,153 and allowing for the number of genes tested therein). In addition, a covariate for Norwegian study origin was created, since the two Norwegian cohorts were analyzed jointly.
Table 1 reports results of association analysis of the eight European cohorts by homogeneous LRT (Hom-LRT), Hom-MetaSKAT-O, and Hom-MetaSKAT; and Table 2 reports results by heterogeneous LRT (Het-LRT), Het-MetaSKAT-O, and Het-MetaSKAT. The results of Hom-F and Het-F are reported in Table S3 and Table S4. At the significance threshold of , we observe the following associations by both Hom-LRT and Hom-F of functional regression models (3) and (5): (1) at the LPL for HDL levels; (2) at the APOB, APOE, LDLR, and PCSK9 for LDL levels; (3) at the APOE and LPL for TG levels; and (4) at the APOB, APOE, HNF1A, and LDLR for CHOL levels. Hom-MetaSKAT and Hom-MetaSKAT-O detect the following associations: (1) at the APOE, LDLR, and PCSK9 for LDL levels and (2) at the APOE and LDLR for CHOL levels.
Table 1. Association analysis of lipid traits in eight European cohorts by homogeneous likelihood-ratio tests (Hom-LRT), Hom-MetaSKAT-O, and Hom-MetaSKAT.
| P-values of Hom-LRT | ||||||||
|---|---|---|---|---|---|---|---|---|
| Basis of both GVF and | Basis of β-smooth only | P-values of Hom-Meta- | ||||||
| Traits | Gene | B-spline basis | Fourier basis | B-spline basis | Fourier basis | Additive model (7) | SKAT | SKAT-O |
| HDL | LPL | |||||||
| LDL | APOB | |||||||
| APOE | ||||||||
| LDLR | ||||||||
| PCSK9 | ||||||||
| TG | APOE | |||||||
| LPL | ||||||||
| CHOL | APOB | |||||||
| APOE | ||||||||
| HNF1A | ||||||||
| LDLR | ||||||||
The associations that attain a threshold significance of are boldface (Liu et al. 2014). The results of “Basis of both GVF and ” were based on smoothing both GVF and genetic effect functions of model (3), the results of “Basis of β-smooth only” were based on the smoothing only approach of model (5), the results of “Additive model (7)” were based on the additive effect model (7), and the P-values of Hom-MetaSKAT and Hom-MetaSKAT-O were based on the R package MetaSKAT. GVF, genetic variant function.
Table 2. Association analysis of lipid traits in eight European cohorts by heterogeneous likelihood-ratio tests (Het-LRT), Het-MetaSKAT-O, and Het-MetaSKAT.
| P-values of the Het-LRT | ||||||||
|---|---|---|---|---|---|---|---|---|
| Basis of both GVF and | Basis of β-smooth only | P-values of Het-Meta- | ||||||
| Traits | Gene | B-spline basis | Fourier basis | B-spline basis | Fourier basis | Additive model (6) | SKAT | SKAT-O |
| LDL | APOB | |||||||
| APOE | ||||||||
| CDC123 | ||||||||
| CDKAL1 | ||||||||
| CDKN2B | ||||||||
| FTO | ||||||||
| HNF1A | ||||||||
| LDLR | ||||||||
| OASL | ||||||||
| PCSK9 | ||||||||
| TSPAN8 | ||||||||
| TG | LPL | |||||||
| CHOL | APOB | |||||||
| APOE | ||||||||
| CDC123 | ||||||||
| CDKAL1 | ||||||||
| CDKN2B | ||||||||
| FTO | ||||||||
| HNF1A | ||||||||
| IDE | ||||||||
| JAZF1 | ||||||||
| KIF11 | ||||||||
| LDLR | ||||||||
| MTNR1B | ||||||||
| OASL | ||||||||
| PCSK9 | ||||||||
| TSPAN8 | ||||||||
The associations that attain a threshold significance of are boldface (Liu et al. 2014). The results of “Basis of both GVF and ” were based on smoothing both GVF and genetic effect functions of model (3), the results of “Basis of β-smooth only” were based on the smoothing only approach of model (5), the results of “Additive model (6)” were based on the additive effect model (6), and the P-values of Het-MetaSKAT and Het-MetaSKAT-O were based on the R package MetaSKAT. GVF, genetic variant function.
By both Het-LRT and Het-F of functional regression models (3) and (5) shown in Table 2 and Table S4, we observe the following associations: (1) at the APOB, APOE, CDC123, CDKAL1, CDKN2B, FTO, HNF1A, LDLR, OASL, PCSK9, and TSPAN8 for LDL levels; (2) at the LPL for TG levels; and (3) at the APOB, APOE, CDC123, CDKAL1, CDKN2B, FTO, HNF1A, IDE, JAZF1, KIF11, LDLR, MTNR1B, OASL, PCSK9, and TSPAN8 for CHOL levels. Het-MetaSKAT and Het-MetaSKAT-O detect the following associations: (1) at the APOE and LDLR for LDL levels and (2) at the APOE for CHOL levels.
In addition to the results of functional regression models (3) and (5), MetaSKAT, and MetaSKAT-O, Table 1, Table 2, Table S3, and Table S4 report the results of the traditional additive effect models (6) and (7). The additive effect models (6) and (7) detect more association signals than MetaSKAT and MetaSKAT-O, but less than the functional regression models (3) and (5).
Generally, the P-values of Hom-LRT in Table 1 are slightly smaller than those of Hom-F in Table S3, and the P-values of Het-LRT in Table 2 are slightly smaller than those of Het-F in Table S4. Hence, the LRT statistics are slightly more powerful than the F-distributed statistics. In addition, Het-LRT and Het-F detect more association signals than Hom-LRT and Hom-F. Overall, the P-values of Hom-MetaSKAT-O and Hom-MetaSKAT are bigger than those of Hom-LRT and Hom-F, and the P-values of Het-MetaSKAT-O and Het-MetaSKAT are bigger than those of Het-LRT and Het-F. Therefore, MetaSKAT is less sensitive than the proposed LRT and F-distributed statistics.
When we analyze the data sets separately for each study, significant association is detected only at APOE for LDL and CHOL, levels for a few studies and at LDLR for CHOL levels in the study of METSIM (Table S5). No significant association is detected for TG and HDL levels in any separate study. The P-values of separate analysis in Table S5 are much bigger than those of meta-analysis in Table 1, Table 2, Table S3, and Table S4. Thus, it is more advantageous to perform meta-analysis of multiple studies.
A simulation study
To evaluate the performance of the proposed methods, we carried out simulation analyses for two cases: (1) the causal variants are all rare and (2) the causal variants are both rare and common. Simulations were performed for three scenarios listed in Table 3 (Lee et al. 2013). For scenarios 1 and 2, we used the European-like (EUR) sequence data used in Lee et al. (2012). For scenario 3, we used both the EUR and African–American-like (AA) sequence data. Specifically, the EUR sequence data were generated using COSI’s (available at: http://www.broadinstitute.org/∼sfs/) calibrated best-fit models, and the generated European haplotypes mimick Centre d'Etude du Polymorphisme Humain (CEPH) Utah individuals with ancestry from northern and western Europe in terms of site frequency spectrum and LD pattern (figure 4 in Schaffner et al. 2005; International HapMap Consortium 2007). Similarly, the AA sequence data mimick individuals with a 20:80 mixture of Europeans and Africans, together with parameters calibrated to model realistic demographic history (including bottleneck, population expansion, and migration events). The EUR sequence data included 10,000 chromosomes covering 1-Mb regions, and the AA sequence data included 45,000 chromosomes covering 0.1-Mb regions. Genetic regions of 3-kb length were randomly selected in the simulations for type I error and power calculations.
Table 3. Simulation study settings.
| Sample sizes | Covariates | ||||||
|---|---|---|---|---|---|---|---|
| Scenario | Population | Study 1 | Study 2 | Study 3 | Study 1 | Study 2 | Study 3 |
| 1 | EUR | 1600 | 2200 | 3200 | |||
| 2 | EUR | 1600 | 2200 | 3200 | |||
| 3 | EUR + AA | 1600 | 2200 | 3200 | |||
Sample sizes are total sample sizes in each study. Covariates represent covariates in each study. EUR refers to the scenario where all three studies had EUR samples. EUR + AA refers to the scenario where studies 1 and 2 had EUR samples and study 3 had AA samples. is a binary covariate taking values 0 and 1 each with probability 0.5, and and are continuous covariates and distributed as standard normal.
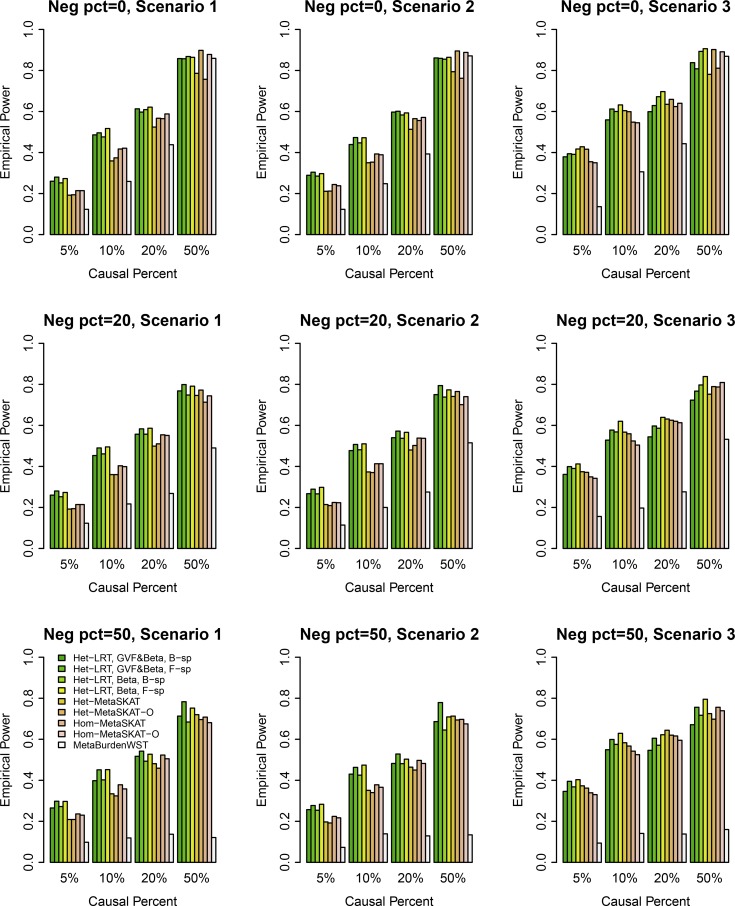
Figure 4.
The empirical power of the homogeneous LRT statistics (Hom-LRT) of models (3) and (5), MetaSKAT, and MetaBurdenWST at , when causal variants were only rare and the genetic effect is simulated as heterogeneous. When Neg pct = 0, all causal variants had positive effects; when Neg pct = 20, 20%/80% of causal variants had negative/positive effects; when Neg pct = 50, 50%/50% of causal variants had negative/positive effects.
Type I error simulations:
To evaluate the type I error rates of the proposed models and tests, we generated phenotype data sets by using the model
| (8) |
for scenario 1 in Table 3 and
| (9) |
for scenarios 2 and 3 in Table 3, where is a dichotomous covariate taking values 0 and 1 with an equal probability of 0.5, and are continuous covariates from standard normal distributions , and follows a standard normal distribution . To obtain genotype data, 3-kb subregions were randomly selected in the 1-Mb region of EUR-like data and the 0.1-Mb region of AA-like data. The ordered genotypes were these SNPs in the 3-kb subregions. Note that the trait values are not related to the genotypes, and so the null hypothesis holds. The sample sizes of the data sets were taken as 1600 (study 1), 2200 (study 2), and 3200 (study 3), respectively. The simulation settings are summarized in Table 3. For each sample size combination, phenotype–genotype data sets were generated to fit the proposed models and to calculate the test statistics and related P-values. Then, an empirical type I error rate was calculated as the proportion of P-values that were smaller than a given α-level (i.e., 0.05, 0.01 and 0.001, 0.0001, respectively).
Empirical power simulations:
To evaluate the power performance of the proposed tests, we simulated data sets under the alternative hypothesis by randomly selecting 3-kb subregions to obtain causal variants for the phenotype values as follows. Once a 3-kb subregion was selected, a subset of p causal variants located in the 3-kb subregion was then randomly selected to obtain ordered genotypes . Then, we generated the quantitative traits by
for scenario 1 and for scenarios 2 and 3,
where and are the same as in the type I error models (8) and (9), and the β’s are the additive effect for the causal variants defined as follows. We used , where was the minor allele frequency (MAF) of the jth variant. Three genetic effect scenarios were used to perform power calculations: (1) all causal variants had positive effects, (2) 20%/80% causal variants had negative/positive effects, and (3) 50%/50% causal variants had negative/positive effects. As in Lee et al. (2013), four different settings were considered: 5%, 10%, 20%, and 50% of variants in the 3-kb subregion are chosen as causal variants. When 5%, 10%, 20%, and 50% of the variants were causal, two parameter settings of genetic effects were considered for (1) homogeneous and (2) heterogeneous (Table 4). In the homogeneous case, the genetic effects are the same for the three studies; i.e., . In the heterogeneous case, the genetic effects are different for the three studies; i.e., For each setting, 1000 data sets were simulated to calculate the empirical power as the proportion of P-values that are smaller than a given level. The homogeneous settings of genetic effect are taken from Lee et al. (2013).
Table 4. Simulation parameter settings.
| Causal % | |||||
|---|---|---|---|---|---|
| Genetic effect | Study | 5 | 10 | 20 | 50 |
| Homogeneous | 1 | 0.475 | 0.375 | 0.25 | 0.175 |
| 2 | 0.475 | 0.375 | 0.25 | 0.175 | |
| 3 | 0.475 | 0.375 | 0.25 | 0.175 | |
| Heterogeneous | 1 | 0.475 | 0.375 | 0.25 | 0.175 |
| 2 () | |||||
| 3 | |||||
The constants in of power simulations, , are given for two cases: (1) homogeneous genetic effect and (2) heterogeneous genetic effect.
Type I error simulation results:
The empirical type I error rates are reported in Table 5 when the causal variants are only rare and in Table 6 when the causal variants are both rare and common. For each entry of empirical type I error rates, we generated data sets. Results of four different , and 0.0001 levels are reported. For both the proposed F-distributed tests and LRT statistics of the functional linear models, all empirical type I error rates are around the nominal α-levels for both B-spline basis and Fourier basis (columns 4–11 of Table 5 and Table 6). Therefore, both the F-distributed tests and LRT statistics of the functional linear models controlled type I error rates correctly for all scenarios at all significance levels. The functional linear models and related F-distributed tests and LRT statistics can be useful in both whole-genome and whole-exome association studies.
Table 5. Empirical type I error rates of F-distributed statistics and LRT statistics at different α-levels based on simulated data sets, when the causal variants are only rare.
| F-distributed statistics | LRT statistics | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Basis of both GVF and | Basis of β-smooth only | Basis of both GVF and | Basis of β-smooth only | |||||||
| Type of tests | Scenario | Level α | B-spline | Fourier | B-spline | Fourier | B-spline | Fourier | B-spline | Fourier |
| Het-F and Het-LRT | 1 | 0.05 | 0.049876 | 0.049922 | 0.050093 | 0.049924 | 0.050611 | 0.050895 | 0.050819 | 0.050916 |
| 0.01 | 0.009932 | 0.010006 | 0.009987 | 0.010029 | 0.010173 | 0.010407 | 0.010225 | 0.010422 | ||
| 0.001 | 0.000991 | 0.000974 | 0.001000 | 0.000971 | 0.001055 | 0.001056 | 0.001065 | 0.001056 | ||
| 0.0001 | 0.000089 | 0.000097 | 0.000091 | 0.000095 | 0.000094 | 0.000107 | 0.000097 | 0.000105 | ||
| 2 | 0.05 | 0.049838 | 0.050189 | 0.050077 | 0.050194 | 0.050546 | 0.051163 | 0.050789 | 0.051164 | |
| 0.01 | 0.009944 | 0.009848 | 0.009998 | 0.009851 | 0.010239 | 0.010251 | 0.010305 | 0.010253 | ||
| 0.001 | 0.001024 | 0.001021 | 0.001036 | 0.001025 | 0.001079 | 0.001082 | 0.001090 | 0.001088 | ||
| 0.0001 | 0.000094 | 0.000101 | 0.000094 | 0.000102 | 0.000103 | 0.000118 | 0.000105 | 0.000118 | ||
| 3 | 0.05 | 0.049886 | 0.050002 | 0.050081 | 0.049940 | 0.050593 | 0.050934 | 0.050789 | 0.050906 | |
| 0.01 | 0.009948 | 0.010084 | 0.009989 | 0.010090 | 0.010255 | 0.010454 | 0.010294 | 0.010446 | ||
| 0.001 | 0.000981 | 0.001044 | 0.000985 | 0.001035 | 0.001029 | 0.001104 | 0.001033 | 0.001098 | ||
| 0.0001 | 0.000106 | 0.000093 | 0.000108 | 0.000097 | 0.000116 | 0.000105 | 0.000118 | 0.000108 | ||
| Hom-F and Hom-LRT | 1 | 0.05 | 0.049834 | 0.049795 | 0.049948 | 0.049906 | 0.050131 | 0.050221 | 0.050240 | 0.050337 |
| 0.01 | 0.009932 | 0.009901 | 0.009896 | 0.010018 | 0.010050 | 0.010062 | 0.010012 | 0.010216 | ||
| 0.001 | 0.000987 | 0.001039 | 0.001030 | 0.000996 | 0.001000 | 0.001070 | 0.001054 | 0.001022 | ||
| 0.0001 | 0.000091 | 0.000102 | 0.000077 | 0.000108 | 0.000098 | 0.000104 | 0.000078 | 0.000112 | ||
| 2 | 0.05 | 0.050140 | 0.050340 | 0.050057 | 0.050050 | 0.050459 | 0.050784 | 0.050349 | 0.050475 | |
| 0.01 | 0.009995 | 0.010131 | 0.010001 | 0.009911 | 0.010103 | 0.010308 | 0.010141 | 0.010078 | ||
| 0.001 | 0.000965 | 0.001029 | 0.000977 | 0.000998 | 0.000984 | 0.001061 | 0.001001 | 0.001031 | ||
| 0.0001 | 0.000095 | 0.000106 | 0.000085 | 0.000092 | 0.000099 | 0.000111 | 0.000088 | 0.000097 | ||
| 3 | 0.05 | 0.049900 | 0.049757 | 0.050173 | 0.049742 | 0.050201 | 0.050213 | 0.050453 | 0.050180 | |
| 0.01 | 0.010043 | 0.010068 | 0.010047 | 0.009950 | 0.010157 | 0.010260 | 0.010161 | 0.010138 | ||
| 0.001 | 0.001025 | 0.001002 | 0.001010 | 0.001017 | 0.001045 | 0.001023 | 0.001035 | 0.001060 | ||
| 0.0001 | 0.000090 | 0.000121 | 0.000098 | 0.000118 | 0.000092 | 0.000128 | 0.000100 | 0.000125 | ||
The results of “Basis of both GVF and ” were based on smoothing both GVF and genetic effect functions of model (3), and the results of “Basis of β-smooth only” were based on the smoothing only approach of model (5). GVF, genetic variant function.
Table 6. Empirical type I error rates of F-distributed statistics and LRT statistics at different α-levels based on simulated data sets, when the causal variants are both rare and common.
| F-distributed statistics | LRT statistics | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Basis of both GVF and | Basis of β-smooth only | Basis of both GVF and | Basis of β-smooth only | |||||||
| Type of tests | Scenario | Level α | B-spline | Fourier | B-spline | Fourier | B-spline | Fourier | B-spline | Fourier |
| Het-F and Het-LRT | 1 | 0.05 | 0.050146 | 0.049931 | 0.050220 | 0.049953 | 0.050853 | 0.050913 | 0.050928 | 0.050936 |
| 0.01 | 0.009964 | 0.009942 | 0.009983 | 0.009945 | 0.010250 | 0.010303 | 0.010268 | 0.010308 | ||
| 0.001 | 0.000993 | 0.000996 | 0.000997 | 0.000996 | 0.001057 | 0.001078 | 0.001061 | 0.001078 | ||
| 0.0001 | 0.000108 | 0.000088 | 0.000109 | 0.000088 | 0.000116 | 0.000097 | 0.000117 | 0.000097 | ||
| 2 | 0.05 | 0.049942 | 0.050298 | 0.050014 | 0.050324 | 0.050705 | 0.051303 | 0.050786 | 0.051330 | |
| 0.01 | 0.009974 | 0.009993 | 0.010001 | 0.010001 | 0.010268 | 0.010396 | 0.010291 | 0.010402 | ||
| 0.001 | 0.000960 | 0.000970 | 0.000967 | 0.000970 | 0.001013 | 0.001046 | 0.001017 | 0.001046 | ||
| 0.0001 | 0.000079 | 0.000092 | 0.000080 | 0.000093 | 0.000089 | 0.000099 | 0.000090 | 0.000099 | ||
| 3 | 0.05 | 0.050100 | 0.050012 | 0.050159 | 0.050008 | 0.050844 | 0.051006 | 0.050911 | 0.051000 | |
| 0.01 | 0.010060 | 0.010008 | 0.010089 | 0.010010 | 0.010328 | 0.010367 | 0.010360 | 0.010375 | ||
| 0.001 | 0.000989 | 0.001022 | 0.000989 | 0.001021 | 0.001032 | 0.001098 | 0.001034 | 0.001096 | ||
| 0.0001 | 0.000109 | 0.000099 | 0.000111 | 0.000099 | 0.000117 | 0.000111 | 0.000118 | 0.000110 | ||
| Hom-F and Hom-LRT | 1 | 0.05 | 0.049899 | 0.049875 | 0.050077 | 0.050165 | 0.050193 | 0.050331 | 0.050374 | 0.050595 |
| 0.01 | 0.010127 | 0.010135 | 0.010014 | 0.010043 | 0.010225 | 0.010309 | 0.010135 | 0.010230 | ||
| 0.001 | 0.001004 | 0.001031 | 0.001007 | 0.001001 | 0.001017 | 0.001050 | 0.001027 | 0.001047 | ||
| 0.0001 | 0.000084 | 0.000113 | 0.000092 | 0.000085 | 0.000087 | 0.000119 | 0.000095 | 0.000089 | ||
| 2 | 0.05 | 0.049982 | 0.050054 | 0.050017 | 0.049746 | 0.050267 | 0.050461 | 0.050289 | 0.050168 | |
| 0.01 | 0.010037 | 0.010105 | 0.009901 | 0.009977 | 0.010170 | 0.010280 | 0.010020 | 0.010157 | ||
| 0.001 | 0.001025 | 0.001019 | 0.000993 | 0.000982 | 0.001048 | 0.001056 | 0.001016 | 0.001018 | ||
| 0.0001 | 0.000108 | 0.000101 | 0.000098 | 0.000096 | 0.000111 | 0.000109 | 0.000104 | 0.000101 | ||
| 3 | 0.05 | 0.050401 | 0.049749 | 0.050276 | 0.050243 | 0.050693 | 0.050187 | 0.050551 | 0.050694 | |
| 0.01 | 0.009975 | 0.009920 | 0.010148 | 0.009904 | 0.010097 | 0.010082 | 0.010272 | 0.010088 | ||
| 0.001 | 0.000993 | 0.000993 | 0.000966 | 0.000997 | 0.001019 | 0.001039 | 0.000995 | 0.001037 | ||
| 0.0001 | 0.000116 | 0.000100 | 0.000097 | 0.000089 | 0.000119 | 0.000108 | 0.000097 | 0.000093 | ||
The results of “Basis of both GVF and ” were based on smoothing both GVF and genetic effect functions of model (3), and the results of “Basis of β-smooth only” were based on the smoothing only approach of model (5). GVF, genetic variant function.
Statistical power results:
We compared the power performance of the proposed tests with MetaSKAT and MetaBurden tests based on the simulated COSI sequence data. The empirical power levels of the proposed LRT statistics at the level are plotted in Figure 1, Figure 2, Figure 3, Figure 4, Figure S1, Figure S2, Figure S3, and Figure S4. In the legends of all the figures, “GVF&Beta, B-sp” (or “GVF&Beta, F-sp”) means that both genetic variant function and genetic effect function were smoothed by B-spline (or Fourier) basis functions, and “Beta, B-sp” (or “Beta, F-sp”) means that only the genetic effect function was smoothed by B-spline (or Fourier) basis functions (i.e., β-smooth only). Moreover, the results of “Het-MetaSKAT,” “Het-MetaSKAT-O,” “Hom-MetaSKAT,” “Hom-MetaSKAT-O,” and the metaburden weighted sum test (MetaBurdenWST) using the R package MetaSKAT are reported for power comparison (Madsen and Browning 2009; Lee et al. 2012, 2013).
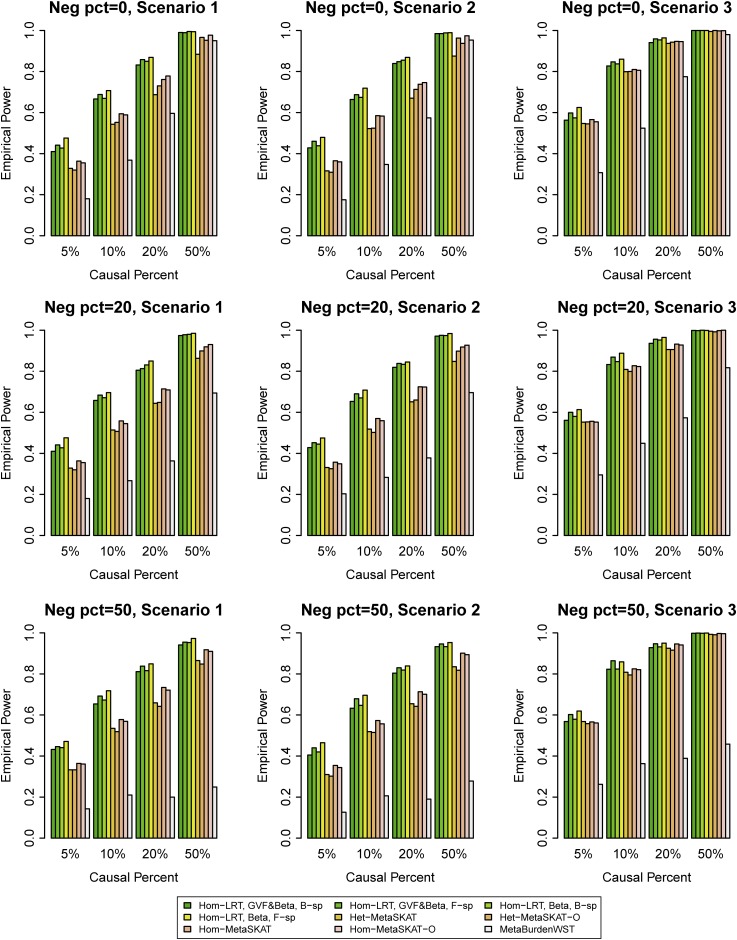
Figure 1.
The empirical power of the homogeneous LRT statistics (Hom-LRT) of models (3) and (5), MetaSKAT, and MetaBurdenWST at , when causal variants were both rare and common and the genetic effect is simulated as homogeneous. When Neg pct = 0, all causal variants had positive effects; when Neg pct = 20, 20%/80% of causal variants had negative/positive effects; when Neg pct = 50, 50%/50% of causal variants had negative/positive effects.
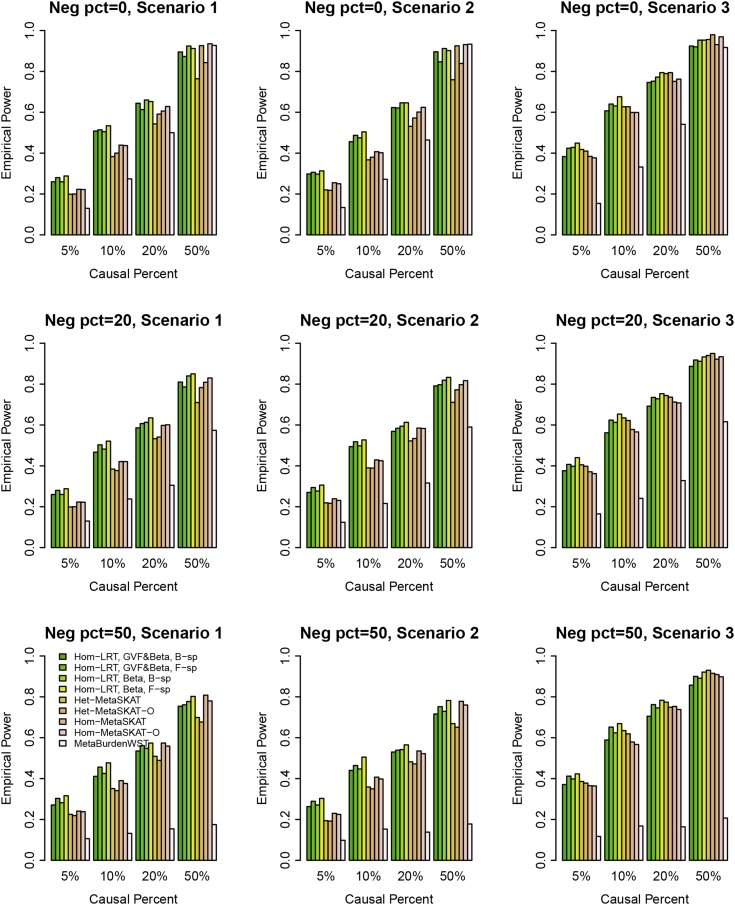
Figure 2.
The empirical power of the homogeneous LRT statistics (Hom-LRT) of models (3) and (5), MetaSKAT, and MetaBurdenWST at , when causal variants were only rare and the genetic effect is simulated as homogeneous. When Neg pct = 0, all causal variants had positive effects; when Neg pct = 20, 20%/80% of causal variants had negative/positive effects; when Neg pct = 50, 50%/50% of causal variants had negative/positive effects.
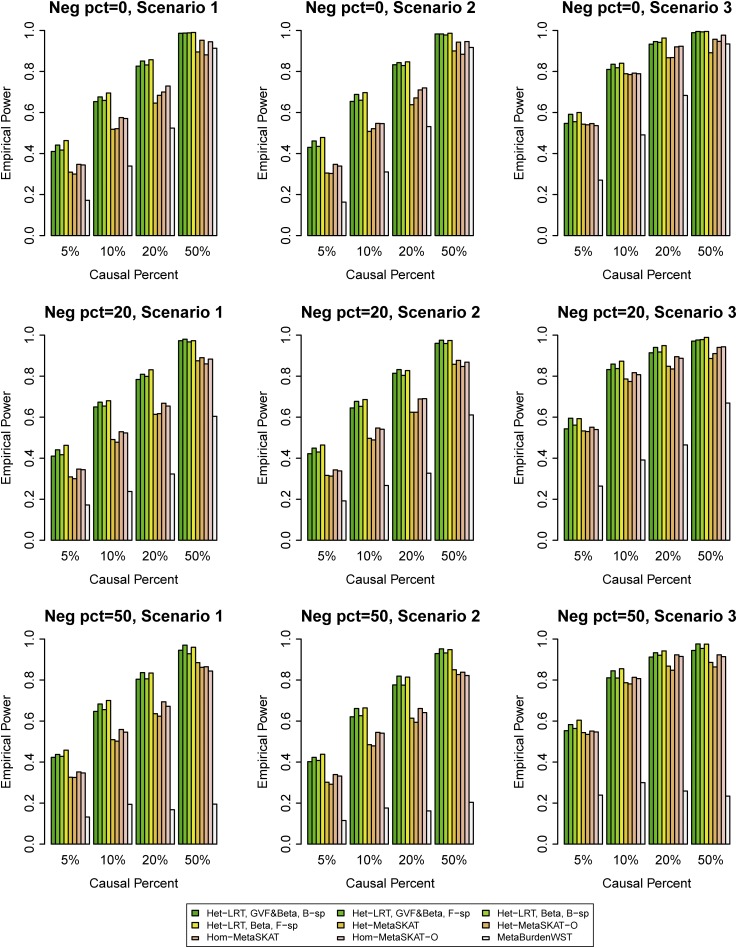
Figure 3.
The empirical power of the homogeneous LRT statistics (Hom-LRT) of models (3) and (5), MetaSKAT, and MetaBurdenWST at , when causal variants were both rare and common and the genetic effect is simulated as heterogeneous. When Neg pct = 0, all causal variants had positive effects; when Neg pct = 20, 20%/80% of causal variants had negative/positive effects; when Neg pct = 50, 50%/50% of causal variants had negative/positive effects.
In Figure 1, Figure 2, Figure 3, and Figure 4, the results of “Hom-LRT” are reported, where the LRT statistics are constructed using the homogeneous effect model that assumes . In Figure S1, Figure S2, Figure S3, and Figure S4, the results of “Het-LRT” are reported, where the LRT statistics are constructed using the heterogeneous effect model in which the regression coefficients , and are different from each other. In Figure 1, Figure 2, Figure S1, and Figure S2, the simulated data are generated under the assumption of homogeneous genetic effect; and in Figure 3, Figure 4, Figure S3, and Figure S4, the simulation data are generated under the assumption of heterogeneous genetic effect (Table 4).
The proposed homogeneous LRT statistics (Hom-LRT) of the functional linear models have higher power than that of MetaSKAT and MetaSKAT-O in Figure 1, Figure 2, Figure 3, and Figure 4. The heterogeneous LRT statistics (Het-LRT) of the functional linear models also have higher power than that of MetaSKAT and MetaSKAT-O in Figure S1, Figure S2, Figure S3, and Figure S4, except for a few cases in Figure S2 when 20% or 50% of variants were causal. Therefore, the proposed LRT statistics of the functional linear models have superior performance in most cases. In Figure S2, the simulated data were generated using the homogeneous genetic effect (Table 4), but the data were analyzed by the heterogeneous effect model and the test is Het-LRT. Thus, it is not strange that there is power loss by Het-LRT in Figure S2.
As shown in Lee et al. (2013, p. 44), MetaSKAT-O takes the minimum P-value of a weighted average of MetaSKAT and the metaburden weighted sum test for a range of ρ values over and the metaburden weighted sum test corresponds to in the construction of SKAT-O. Therefore, the power of MetaBurdenWST is generally lower than that of MetaSKAT-O. This is consistent with the results of Lee et al. (2013).
In Figure 1 and Figure 2, the simulated data were generated under the assumption of homogeneous genetic effect and the data were analyzed by the homogeneous effect model and the test was Hom-LRT. In Figure S3 and Figure S4, the simulated data were generated under the assumption of heterogeneous genetic effect and the data were analyzed by the heterogeneous effect model and the test was Het-LRT. Therefore, “correct models” were used in analyzing the simulated data in Figure 1, Figure 2, Figure S3, and Figure S4, in which the proposed LRT statistics have significantly higher power levels than those of MetaSKAT. Even when “wrong models” were used to analyze the simulated data in Figure 3, Figure 4, Figure S1, and Figure S2, the empirical power levels of the proposed LRT statistics were much higher than those of MetaSKAT in most cases except a few in Figure S2.
In total, we compared four LRT statistics of the functional linear models in each graph: two are based on B-spline basis functions, and two are based on Fourier basis functions. In the two LRT statistics to use B-spline (or Fourier) basis functions, one is to smooth both the genetic variant functions and the genetic effect function , and the other is to smooth only the genetic effect function (i.e., β-smooth only). Generally, the four LRT statistics of the functional linear models have similar power. The power levels of β-smooth only are almost identical to those of smoothing both the genetic variant functions and the genetic effect function by B-spline basis (or Fourier basis). Thus, the tests do not strongly depend on whether the genotype data are smoothed or not. In addition, the LRT statistics do not strongly depend on which basis functions are used.
In addition to the LRT statistics, we calculated the empirical power levels of the F-distributed statistics, which provide very similar empirical power levels as the LRT statistics (data not shown).
Discussion
In this article, FLMs are developed to perform gene-level meta-analysis of quantitative traits for a combined analysis of multiple studies. By using functional data analysis techniques, the theoretical FLMs (1) and (4) are transformed to be traditional multiple linear regressions (3) and (5) (de Boor 2001; Ramsay and Silverman 2005; Ramsay et al. 2009; Ferraty and Romain 2010; Horváth and Kokoszka 2012). The null hypothesis of association is tested by LRT and F-distributed statistics. We show that the proposed LRT and F-distributed statistics control the type I error very well and have higher empirical power levels than the existing methods such as MetaSKAT and MetaBurdenWST in most simulations. By applying the proposed methods to analyze four blood lipid levels in data from a meta-analysis of eight European studies, it is found that the proposed methods detect more significant association than MetaSKAT and MetaSKAT-O, and the P-values of the proposed LRT and F-distributed statistics are usually much smaller than those of MetaSKAT and MetaSKAT-O.
One reason that the proposed functional linear models perform better is that SKAT and MetaSKAT do not model LD among genetic markers sufficiently. Specifically, the test statistic of SKAT is given by , where is the trait value column vector, is the genotype matrix, and is an diagonal weight matrix using the notations of Lee et al. (2012). Let . Then, is the score test statistic for testing in the single genetic variant model with only the jth genetic variant
Thus, models the pairwise LD between the jth genetic variant and the trait locus. Note that is a weighted summation of the squared score test statistics . Therefore, the test statistics of SKAT and MetaSKAT model pairwise LD only between each individual marker and the trait locus, while the LD among genetic markers are not modeled.
Note that Lee et al. (2012) used dichotomous traits to present the test statistic , but the formulation of is also the same for continuous traits or survival traits (Chen et al. 2014). SKAT and MetaSKAT were constructed as score tests on the variance component parameter for the genetic random variations in linear or logistic mixed-effects models. The reason that the regression coefficients of genetic terms were assumed to be random in the models of SKAT and MetaSKAT is that the number of genetic variants in a genetic region is usually large. For instance, there are 660 genetic variants in the region of the KCNQ1 gene in data of European cohorts, Table S1. Due to a large number of genetic terms in a regression model, it is hard to estimate the genetic effects of all genetic variants by ordinary fixed-effect regression models. By making the regression coefficients of the genetic terms to be random, the theory of mixed models was used to build the test statistics of SKAT and MetaSKAT (Lee et al. 2012, 2013).
In association studies, association between phenotypic traits and major gene loci is tested. If the number of causal genetic variants at a major gene locus is very large and each causal variant makes a small contribution to the phenotype, the assumption of mixed models will be satisfied and SKAT and MetaSKAT should perform well (Fisher 1918). On the other hand, if the number of causal genetic variants at a major gene locus is not large and the contribution of a few causal variants to the phenotype is reasonably large, fixed-effect models should work well. In our simulation studies and real data analysis, the proposed functional linear models perform better than SKAT and MetaSKAT in most cases. Thus, the mixed models of SKAT and MetaSKAT could be statistically convenient and attractive but not necessarily biologically reasonable. We argue that the fixed-effect models are useful in most cases. In practice, it makes sense to perform analysis by both the fixed- and mixed-effect models and make a comparison, and this can be readily done using our R codes and SKAT and MetaSKAT packages.
The proposed FLMs are fixed-effect models that can analyze large numbers of genetic variants and extend traditional population genetics models naturally. Unlike other methods such as SKAT or MetaSKAT and burden tests that treat genetic variants as discrete variables, FLMs treat the genetic variant data as continuous stochastic functions or realizations of an underlying stochastic process (Ross 1996). Since genetic variant data are treated as functions, the genetic effects are modeled as functions. One advantage of treating genetic variant data as functions is that the LD information and genetic positions of genetic variant data are contained in the genetic variant functions. The regression coefficients of genetic terms in the models of SKAT and MetaSKAT do not depend on the genetic position, while our genetic effect function depends on the genetic position and is actually a function of genetic position. Hence, the proposed models can fully utilize LD and genetic position information.
The functional linear models (1) and (4) are built to analyze data of multiple studies that may have different covariates and genetic variants. If all studies are genotyped at the same markers and they have the same covariates, then models (1) and (4) are the same as those of Fan et al. (2013) if the genetic effects are homogeneous; i.e., . In reality, the homogeneity assumption may not be valid in which case the functional linear models (1) and (4) are not a trivial extension of the models of Fan et al. (2013). In the analysis of the eight European cohorts, more association signals are detected by Het-LRT and Het-F than by Hom-LRT and Hom-F, reflecting the presence of heterogeneity of the genetic effects.
In single studies with sample sizes of ≤1000, LRT statistics of FLMs were found to inflate the type I error rates while F-distributed statistics controlled type I error rates correctly (Fan et al. 2013). Hence, F-distributed statistics are recommended for small and moderate sample size single studies. In this article, we show that both F-distributed and LRT statistics control the type I error rates correctly and their empirical power levels are similar when the sample sizes of combined multiple studies are large. In Fan et al. (2013), the LRT statistics were found to have correct type I error rates when the sample sizes were ≥1500 in a single study. Therefore, the conclusion that both LRT and F-distributed statistics can be used for large sample meta-analysis in this article is consistent with the result of Fan et al. (2013).
The proposed method requires full genotype data; i.e., we assume that individual genotype data are available from all studies. One reason is that we have this type of data in the eight European cohorts. The proposed approach is more powerful than MetaSKAT and MetaSKAT-O when genotype data are available from all studies, and the proposed method cannot meta-analyze summary statistics while MetaSKAT can. If summary statistics of functional regression models are available from different studies only using Fan et al. (2013), it is still an open question if those statistics can be used to meta-analyze the data of multiple studies. Note that the functional regressions are simply ordinary regressions after revising the theoretical functional models by functional data analysis techniques, and so the strategy of usual meta-analysis would be useful. Hence, it should be possible to use results from functional regression models for a meta-analysis across cohorts. However, the details are still waiting for further work.
With the rapid advance of high-throughput sequencing technologies (Mardis 2008; Ansorge 2009), more sequencing data from large cohorts will be collected and more meta-analyses will be performed in different populations. Association analysis has been increasingly carried out to identify risk or protective genetic variants of complex traits. It is important to develop powerful and efficient statistical methods to test for associations. Our meta-analysis FLMs provide an effective approach for the association analysis of complex traits.
Supplementary Material
Acknowledgments
Two anonymous reviewers and the editors, Chiara Sabatti and Gary Churchill, provided very good and insightful comments for us to improve the manuscript. We greatly thank the European cohort investigators for letting us analyze the data and use them as examples. Heather M. Stringham and Tanya M. Teslovich kindly sent us the data of the European cohorts and patiently answered many questions about the cohorts, which we greatly appreciated. We thank Seunggeun Lee for sending us the simulation program of SKAT and sequence data generated by Yun Li using the program COSI. This study utilized the high-performance computational capabilities of the Biowulf Linux cluster at the National Institutes of Health (http://biowulf.nih.gov). The methods proposed in this article are implemented by using the procedure of functional data analysis (fda) in the statistical package R. The R codes for data analysis and simulations are available at http://www.nichd.nih.gov/about/org/diphr/bbb/software/fan/Pages/default.aspx. This study was supported by the Intramural Research Program of the Eunice Kennedy Shriver National Institute of Child Health and Human Development, National Institutes of Health (NIH) (Ruzong Fan and Yifan Wang); by Wei Chen’s NIH grants R01EY024226 and R01HG007358 and the University of Pittsburgh (Ruzong Fan is an unpaid collaborator on the grant R01EY024226); and by NIH grants R01HG006292 and R01HG006703 (to Yun Li).
Footnotes
Communicating editor: C. Sabatti
Supporting information is available online at www.genetics.org/lookup/suppl/doi:10.1534/genetics.115.178343/-/DC1.
Literature Cited
- Altshuler, D. M., E. S. Lander, L. Ambrogio, T. Bloom, K. Cibulskis et al., 2010 A map of human genome variation from population scale sequencing. Nature 467: 1061–1073. [DOI] [PMC free article] [PubMed]
- Ansorge W. J., 2009. Next-generation DNA sequencing techniques. New Biotechnol. 25: 195–203. [DOI] [PubMed] [Google Scholar]
- Cantor R. M., Lange K., Sinsheimer J. S., 2010. Prioritizing GWAS results: a review of statistical methods and recommendations for their application. Am. J. Hum. Genet. 86: 6–22. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen H., Lumley T., Brody J., Heard-Costa N. L., Fox C. S., et al. , 2014. Sequence kernel association test for survival traits. Genet. Epidemiol. 38: 191–197. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cordell H. J., Clayton D. G., 2002. A unified stepwise regression procedure for evaluating the relative effects of polymorphisms within a gene using case/control or family data: application to HLA in type 1 diabetes. Am. J. Hum. Genet. 70: 124–141. [DOI] [PMC free article] [PubMed] [Google Scholar]
- de Bakker P. I. W., Ferreira M. A. R., Jia X., Neale B. M., Raychaudhuri S., et al. , 2008. Practical aspects of imputation-driven meta-analysis of genome-wide association studies. Hum. Mol. Genet. 17: 122–128. [DOI] [PMC free article] [PubMed] [Google Scholar]
- de Boor C., 2001. Applied Mathematical Sciences 27, A Practical Guide to Splines, Revised Version. Springer-Verlag, New York. [Google Scholar]
- Evangelou E., Ioannidis J. P. A., 2013. Meta-analysis methods for genome-wide association studies and beyond. Nat. Rev. Genet. 14: 379–389. [DOI] [PubMed] [Google Scholar]
- Fan R. Z., Xiong M. M., 2002. High resolution mapping of quantitative trait loci by linkage disequilibrium analysis. Eur. J. Hum. Genet. 10: 607–615. [DOI] [PubMed] [Google Scholar]
- Fan R. Z., Jung J. S., Jin L., 2006. High resolution association mapping of quantitative trait loci, a population based approach. Genetics 172: 663–686. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fan R. Z., Wang Y. F., Mills J. L., Wilson A. F., Bailey-Wilson J. E., et al. , 2013. Functional linear models for association analysis of quantitative traits. Genet. Epidemiol. 37: 726–742. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fan R. Z., Wang Y. F., Mills J. L., Carter T. C., Lobach I., et al. , 2014. Generalized functional linear models for case-control association studies. Genet. Epidemiol. 38: 622–637. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ferraty F., Romain Y., 2010. The Oxford Handbook of Functional Data Analysis. Oxford University Press, New York. [Google Scholar]
- Fisher R. A., 1918. The correlation between relatives on the supposition of Mendelian inheritance. Philos. Trans. R. Soc. Edinb. 52: 399–433. [Google Scholar]
- Hindorff L. A., Sethupathy P., Junkins H. A., Ramos E. M., Mehta J. P., et al. , 2009. Potential etiologic and functional implications of genome-wide association loci for human diseases and traits. Proc. Natl. Acad. Sci. USA 106: 9362–9367. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Horváth, L., and P. Kokoszka, 2012 Inference for Functional Data With Applications. Springer-Verlag, New York.
- Hu Y. J., Berndt S. I., Gustafsson S., Ganna A.; Genetic Investigation of ANthropometric Traits (GIANT) Consortium et al, 2013. Meta-analysis of gene-level associations for rare variants based on single-variant statistics. Am. J. Hum. Genet. 93: 42–53. [DOI] [PMC free article] [PubMed] [Google Scholar]
- International HapMap Consortium , 2007. A second generation human haplotype map of over 3.1 million SNPs. Nature 449: 851–861. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ioannidis J. P. A., Patsopoulos N. A., Evangelou E., 2007. Heterogeneity in meta-analyses of genome-wide association investigations. PLoS ONE 2: e841. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee S., Emond M. J., Bamshad M. J., Barnes K. C., Rieder M. J., et al. , 2012. Optimal unified approach for rare-variant association testing with application to small-sample case-control whole-exome sequencing studies. Am. J. Hum. Genet. 91: 224–237. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee S., Teslovich T. M., Boehnke M., Lin X., 2013. General framework for meta-analysis of rare variants in sequencing association studies. Am. J. Hum. Genet. 93: 42–53. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li B., Leal S. M., 2008. Methods for detecting associations with rare variants for common diseases: application to analysis of sequence data. Am. J. Hum. Genet. 83: 311–321. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu D. J., Peloso G. M., Zhan X., Holmen O. L., Zawistowski M., et al. , 2014. Meta-analysis of gene-level tests for rare variant association. Nat. Genet. 46: 200–204. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Luo L., Zhu Y., Xiong M., 2012. Quantitative trait locus analysis for next-generation sequencing with the functional linear models. J. Med. Genet. 49: 513–524. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Madsen B. E., Browning S. R., 2009. A groupwise association test for rare mutations using a weighted sum statistic. PLoS Genet. 5: e1000384. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mardis E. R., 2008. Next-generation DNA sequencing methods. Annu. Rev. Genomics Hum. Genet. 9: 387–402. [DOI] [PubMed] [Google Scholar]
- Morris A. P., Zeggini E., 2010. An evaluation of statistical approaches to rare variant analysis in genetic association studies. Genet. Epidemiol. 34: 188–193. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Neale B. M., Rivas M. A., Voight B. F., Altshuler D., Devlin B., et al. , 2011. Testing for an unusual distribution of rare variants. PLoS Genet. 7: e1001322. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Price A. L., Kryukov G. V., de Bakker P. I. W., Purcell S. M., Staples J., et al. , 2010. Pooled association tests for rare variants in exon-resequencing studies. Am. J. Hum. Genet. 86: 832–838. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ramsay J. O., Silverman B. W., 2005. Functional Data Analysis, Ed. 2 Springer-Verlag, New York. [Google Scholar]
- Ramsay J. O., Hooker G., Graves S., 2009. Functional Data Analysis With R and Matlab. Springer-Verlag, New York. [Google Scholar]
- Ross S. M., 1996. Stochastic Processes, Ed. 2 John Wiley & Sons, New York. [Google Scholar]
- Schaffner S. F., Foo C., Gabriel S., Reich D., Daly M. J., et al. , 2005. Calibrating a coalescent simulation of human genome sequence variation. Genome Res. 15: 1576–1583. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stahl E. A., Raychaudhuri S., Remmers E. F., Xie G., Eyre S., et al. , 2010. Genome-wide association study meta-analysis identifies seven new rheumatoid arthritis risk loci. Nat. Genet. 42: 508–514. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tang Z. Z., Lin D. Y., 2014. Meta-analysis of sequencing studies with heterogeneous genetic associations. Genet. Epidemiol. 38: 389–401. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang Y. F., Liu A. Y., Mills J. L., Wilson A. F., Bailey-Wilson J. E. et al, 2015. Pleiotropy analysis of quantitative traits at gene level by multivariate functional linear models. Genet. Epidemiol. 39: 259–275. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weisberg S., 2005. Applied Linear Regression, Ed. 3 (Wiley Series in Probability and Statistics). Wiley Interscience, Hoboken, NJ. [Google Scholar]
- Zeggini E., Ioannidis J. P. A., 2009. Meta-analysis in genome-wide association studies. Pharmacogenomics 10: 191–201. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zeggini E., Scott L. J., Saxena R., Voight B. F., Marchini J. L., et al. , 2008. Meta-analysis of genome-wide association data and large-scale replication identifies additional susceptibility loci for type 2 diabetes. Nat. Genet. 40: 638–645. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.