Transcription factor competition allows embryonic stem cells to distinguish authentic signals from noise

Abstract

Stem cells occupy variable environments where they must distinguish stochastic fluctuations from developmental cues. Here, we use optogenetics to investigate how the pluripotency network in embryonic stem (ES) cells achieves a robust response to differentiation cues but not to gene expression fluctuations. We engineered ES cells in which we could quantitatively ontrol the endogenous mechanism of neural differentiation through a light-inducible Brn2 transgene and monitor differentiation status through a genome-integrated Nanog-GFP reporter. By exposing cells to pulses of Brn2, we find that the pluripotency network rejects Brn2 inputs that are below specific magnitude or duration thresholds, but allows rapid differentiation when both thresholds are satisfied. The filtering properties of the network arise through its positive feedback architecture and the intrinsic half-life of Nanog, which determines the duration threshold in the network. Together our results suggest that the dynamic properties of positive-feedback networks might determine how inputs are classified as signal or noise by stem cells.

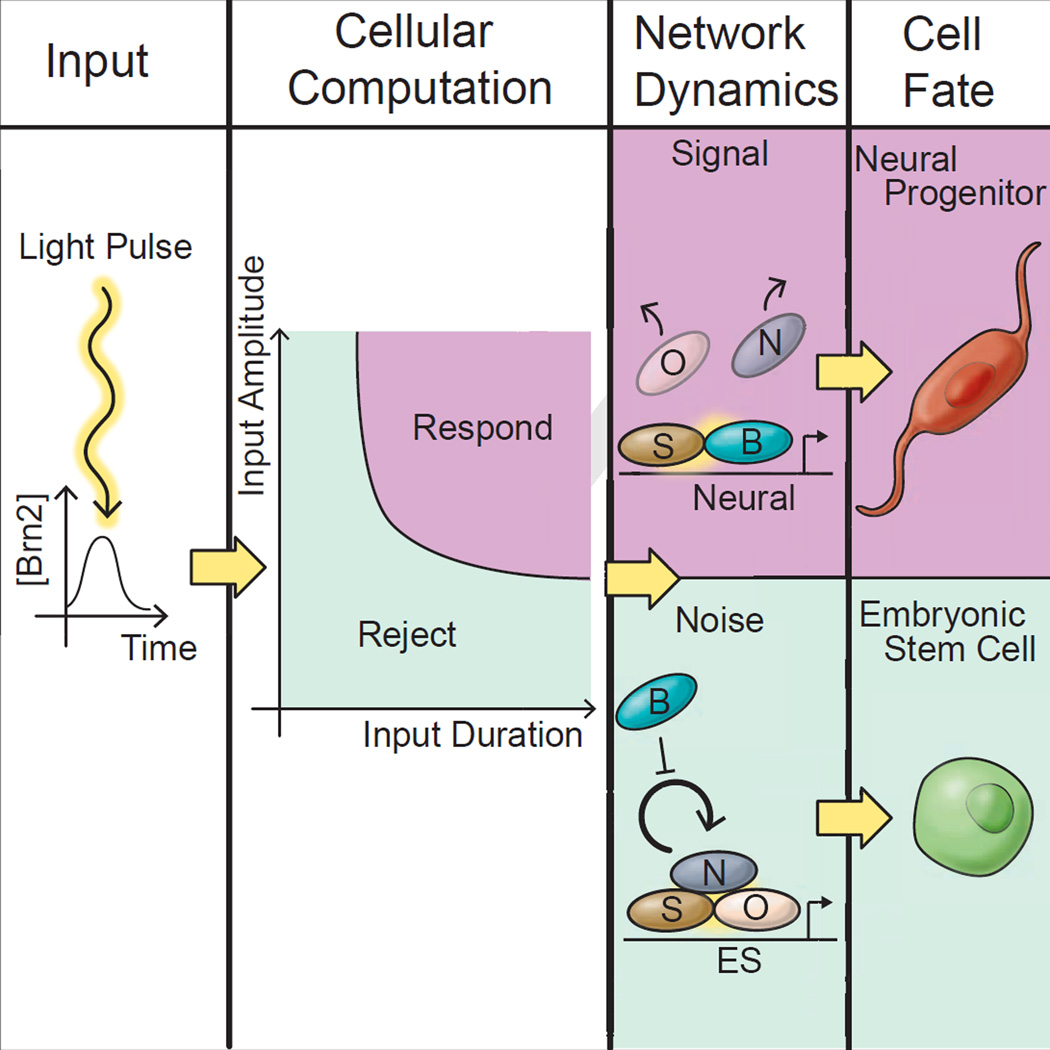
Graphical abstract

All cells experience fluctuations in the concentrations of internal regulatory molecules and external molecular cues (Kumar ME et al., 2014; Ohnishi et al., 2014; Raj et al., 2006; Raj and van Oudenaarden, 2008). In undifferentiated stem cells, internal gene expression fluctuations are particularly strong due to a permissive chromatin configuration that allows stochastic, unregulated bursts of transcription to occur broadly across the genome. Transcriptional bursting leads to the premature expression of differentiation-promoting genes in stem cells even prior to differentiation (Chang et al., 2008; Hu et al. 1997; Kumar RM et al 2014; Weishaupt et. al 2010;). Embryonic stem cells, as an example, stochastically express a number of lineage specific transcription factors including core regulators of neural differentiation in the pluripotent state (Kumar RM et al 2014). Stem cells, therefore, confront a critical challenge: cells must simultaneously avoid responding to these stochastic fluctuations while retaining a capacity to differentiate in response to appropriate developmental cues (Fig 1A)(Hornung and Barkai, 2008).

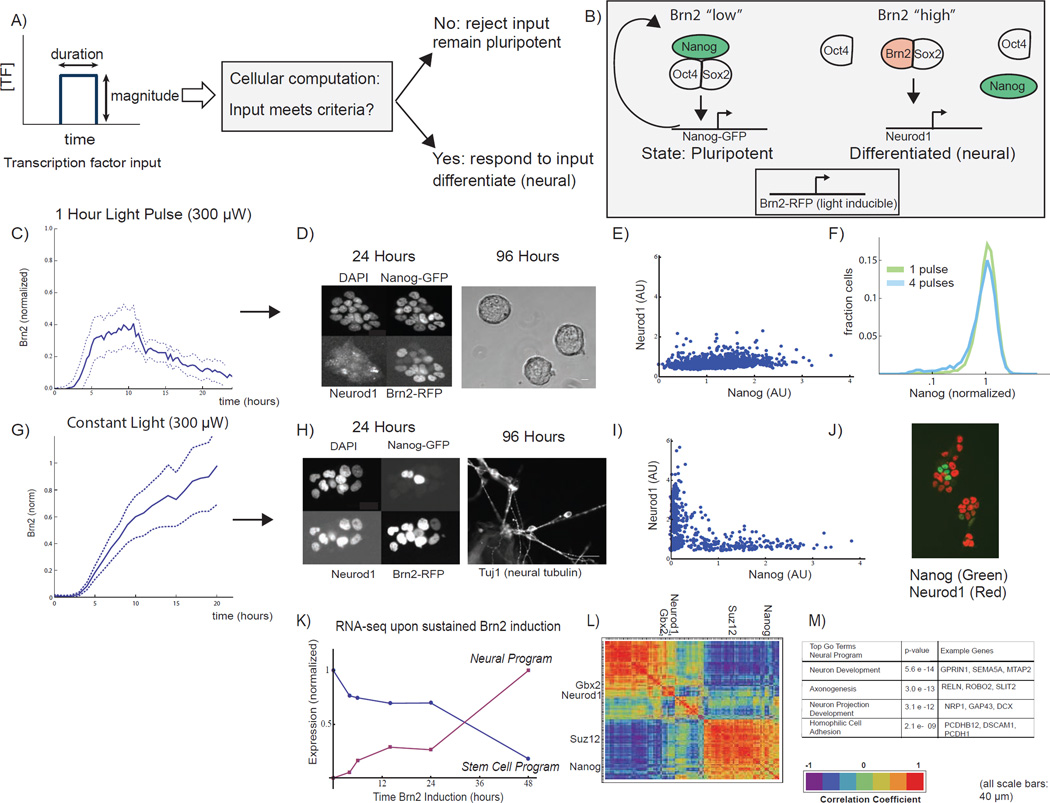
Fig 1. Sustained optical induction of Brn2 drives transition from pluripotency to neural differentiation.

A) In this work, we ask how embryonic stem cells distinguish gene expression fluctuations from development cues. B) The pluripotency network, an auto-regulatory network of transcription factors including Oct4, Sox2, and Nanog, maintains ES cells in a pluripotent state. Neural lineage entry occurs through a competitive binding mechanism where Brn2 binds Sox2, displacing Oct4, to activate neural lineage specific genes including Neurod1. We optically induce Brn2-RFP with the GAVPO system and tag both genomic copies of Nanog with GFP. C) Cells exposed to 1-hour light pulse activate Brn2 but do not differentiate. Brn2-RFP time-course (mean +/− standard deviation of 10 single-cell traces, normalized to constant light maximum, Fig 1G, see also Fig S1E) following a 1-hour blue light pulse (300uW). D) Left: Images of cells 24 hours after 1-hour light pulse, showing DAPI, Nanog-GFP, Neurod1 (IF), and Brn2-RFP. Right: Phase contrast image of ES cell colonies 96 hours after 1-hour light pulse. Cells retain the characteristic ESC circular colony morphology. Scale bars 40um. E) Neurod1 (IF) and Nanog-GFP for >1000 single cells 24 hours following the 1-hour light pulse. F) Nanog-GFP expression following a single 1-hour light pulse (green) or a series of four 1-hour light pulses spaced by 12 hours (blue) (n>10,000, sampled from two biological replicates). G) Sustained activation of Brn2 drives neural differentiation. Brn2-RFP intensity during sustained light exposure (mean +/− standard deviation of 20 cell traces, normalized to max) H) Left: Dapi, Nanog-GFP, Neurod1 (IF), and Brn2-RFP in cells exposed to 24 hours of constant light. Nanog and Brn2/Neurod1 are mutually exclusive. Scale bars 40um. Right: Tuj1 (neuron marker) staining of cells following 96 hours of sustained light exposure. Scale bar 40um. I) Nanog-GFP and Neurod1 (IF) in n >1000 single cells following 24 hours of Brn2 induction. J) Nanog-GFP and Neurod1 images from experiments in I. K) Normalized expression for gene expression programs derived from RNA-seq time course (6 time points, constant light input). L) The hierarchically clustered correlation matrix for 300 sampled genes following Brn2 induction, showing the two programs from Figure 1K as well as key ES (Nanog, Suz12) and neural (Neurod1,Gbx2) genes. M) The neural program’s most statistically significant GO terms and sample genes (see also SI Fig 1,2).

In control theory and engineering, the problem of distinguishing fluctuations (noise) from input commands (signal) is typically solved by feedback control (Bechhoefer, 2015; Yi et al 2000). The regulatory principles and network architectures that facilitate this process in stem cells are not well understood (Figure 1A). Microorganisms typically employ auto-regulatory negative-feedback loops to (Becskei and Serrano, 2000; Hornung and Barkai, 2008; Yi et al 2000) stabilize transcriptional regulatory networks against the stochastic activation of key regulatory molecules (Becskei and Serrano, 2000; Dublanche et al., 2006; Prill et al., 2005; Simpson et al., 2003; Thieffry et al., 1998; Yi et al 2000). However, metazoans present a quandary: instead of negative feedback, stem cell regulatory networks are dominated by positive feedback regulation (Fong and Tapscott, 2013; Hnisz et al., 2013; Jaenisch and Young, 2008; Kueh et al., 2013; Niwa, 2007; Whyte et al., 2013). It is not clear how positive feedback networks allow stem cells to reject fluctuations but also differentiate in response to developmental cues. Rather, in stem cell biology, discussions of noise tolerance have focused on models of cell fate regulation through “Waddington landscapes” (Fig. 2E depicts such a landscape) where abstract energy barriers between cell types prevent transitions due to stochastic fluctuations (Ferrell, 2012; Francois and Siggia, 2012; Pujadas and Feinberg, 2012;). Despite the intuitive appeal of landscape models of cell fate regulation, they have not been validated, and it is not clear how cell fate landscapes are implemented by underlying protein regulatory networks (Ferrell, 2012; Francois and Siggia, 2012).

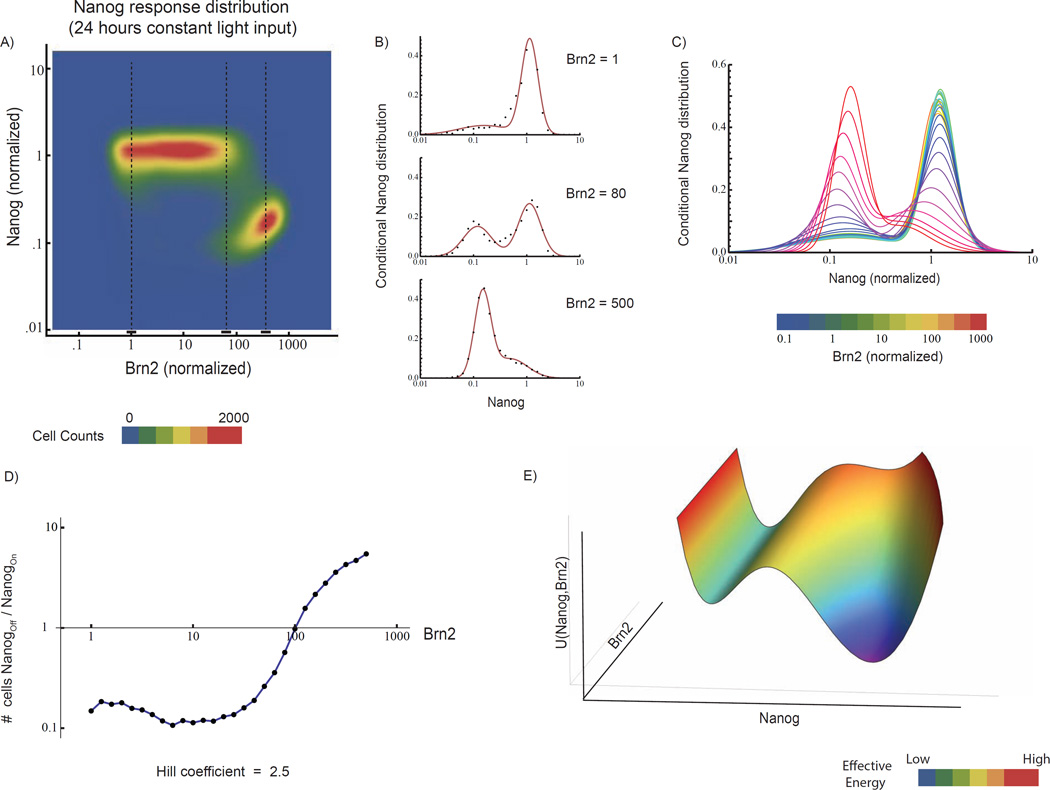
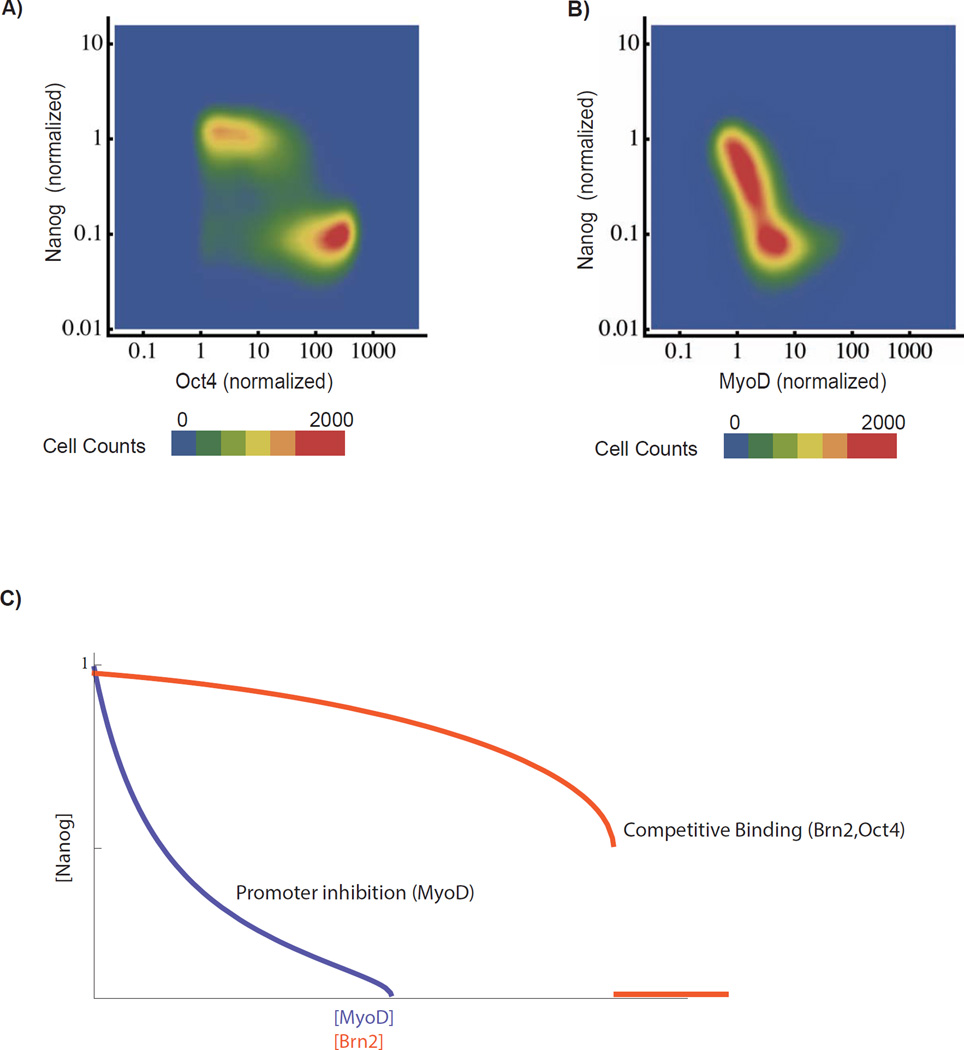
Fig 2. Switch-like response of Nanog to Brn2 provides magnitude thresholding of Brn2 input.

A) Joint distribution of Nanog and Brn2, 24 hours after light induction, as constructed from FACS of >250,000 cells exposed to nine light powers, sampled from two biological replicates. Dotted lines indicate Brn2-RFP levels analyzed in B. B) Steady-state conditional distributions of Nanog-GFP intensity for three Brn2-RFP levels (dots) with fits to Gaussian mixture model (line). C) Gaussian mixture model fits to Nanog-GFP distribution at a series of Brn2-RGP levels. D) The Nanog-off/Nanog-on cell ratio as a function of Brn2 level, as extracted from Gaussian fits. Beyond 100-fold Brn2 activation above baseline, the cell population abruptly transitions from predominantly Nanog-on to Nanog-off (Hill coefficient = 2.5 Nanog-GFP and Brn2-RFP are normalized to mean intensity in the unperturbed ES cell population. E) Schematic depiction of a bi-stable energy landscape, U(Nanog,Brn2), where the two energy minima represent distinct states of Nanog expression, and Brn2 activation shifts the landscape to favor the Nanog-off (differentiated) state over the Nanog-on (pluripotent) state (see Figure 5). See also SI Fig 3

Embryonic stem (ES) cells provide a well-characterized model system for quantitative analysis of stem cell differentiation and cell fate regulation. In the pluripotent state, a group of transcription factors including Oct4, Sox2, and Nanog form a complex that blocks the expression of differentiation-specific genes (Fig 1B) (Jaenisch and Young, 2008; Niwa, 2007). These pluripotency factors also activate their own expression, thus forming a positive feedback loop that stabilizes the undifferentiated state. The architecture of this “pluripotency network” is similar in topology to networks in a wide variety of stem cell types (ranging from the MyoD network in myoblasts to the Pu.1 network in monocytes) where a central group of auto-activating transcription factors stabilizes stem cell identity through positive feedback (Fong and Tapscott, 2013; Hnisz et al., 2013; Kueh et al., 2013; Whyte et al., 2013).

The pluripotency network is involved in both stabilization of the pluripotent state and lineage selection (26–28). Lineage selection occurs through a transcription factor competition mechanism (i.e., seesaw model), whereby lineage-specific transcriptional regulators compete for binding with the components of the pluripotency protein complex (Fig 1A) (Loh and Lim, 2011; Niwa et al., 2000; Shu et al., 2013;Thomson et al., 2011;). During neural lineage entry, Oct4 and Brn2 (Brain2), a pro-neural Oct4 homologue, compete for Sox2 binding (Fig 1B) (Jin et al., 2009; Lodato et al., 2013; Martello and Smith, 2014). Effective competition destabilizes the pluripotency network and drives neural progenitor differentiation. An analogous transcription factor competition mechanism controls endoderm differentiation of ES cells (where Sox17 competes with Sox2 for Oct4 binding) as well as differentiation events in a range of stem cell types in the immune (Graf and Enver, 2009; Niakan et al., 2010;).

To ask how ES cells respond to signal but not to noise, we engineered an optogenetic experimental system that co-opts the endogenous mechanism of neural lineage entry through Brn2/Oct4 competition (Fig 1B). Specifically, we modulate the timing and level of Brn2 expression and monitor differentiation through a quantitative, genome-integrated Nanog reporter (Fig 1B). Using this approach we show that the pluripotency network can reject fluctuations in Brn2 expression that are below sharp magnitude and duration thresholds, allowing differentiation only when both thresholds are met. Through modeling, we identify two properties of the pluripotency network, positive feedback subject to direct biochemical competition and the intrinsic Nanog protein lifetime, that determine whether an input is interpreted as a signal or as noise. In the model, the ability to distinguish signal from noise arises through a shifting epigenetic landscape. Together, our results demonstrate that the dynamic properties of positive feedback networks can provide both noise tolerance and cell fate switching in a wide range of cellular contexts.

Results

Optical induction and monitoring of neural differentiation in embryonic stem cells

To determine how embryonic stem cells distinguish fluctuations from developmental signals (Fig 1A), we constructed an optogenetic experimental system in which we could temporally-modulate the expression of Brn2 (tagged with RFP) using the light-inducible gene expression system GAVPO (Fig 1B, Fig S1, SI Movie 1) (Wang et al., 2012). Expression of Brn2 optically engages the endogenous mechanism of neural lineage entry in the ES cell where Brn2 competes with Oct4 to drive neural differentiation (Jin et al., 2009; Tanaka et al., 2004; Fujii and Hamada, 1993; Smit et al., 2000) (Fig 1B). Additionally, we monitored cellular differentiation using a genome-integrated Nanog-GFP reporter (Fig S2, Experimental Procedures) (Chambers et al., 2007; Mitsui et al., 2003). This approach allowed us to induce pulses of Brn2-RFP expression with light, and then analyze the ES cell’s response as a function of the magnitude and duration of the Brn2 pulse (Toettcher et al., 2011). We verified that optical induction could be carried out with minimal cell toxicity or photobleaching on the experimental time-scales considered in this paper (Fig S3).

Sustained, but not transient, induction of Brn2 drives neural differentiation

We first analyzed the response of ES cells to light inputs of a constant power (300 µW) but varying temporal duration. We found that cells could ignore short, one-hour light inputs but that sustained optical activation of Brn2 drove rapid neural differentiation (Fig 1C–F vs Fig 1G–M). Figure 1C shows the dynamics of Brn2 protein expression in a cell population following a one-hour light pulse. Although individual cells activate Brn2, they continue to express the Nanog protein (Fig 1D, E), and could be maintained for many days in standard ES cell media without showing signatures of differentiation; they also and retain the characteristic circular colony morphology of undifferentiated ES cells (Fig 1D, right panel). In fact, ES cells could tolerate a series of short but temporally-spaced light pulses without differentiating; Nanog protein levels were unperturbed in cells exposed to four one-hour light pulses separated by 12 hours in time (Figure 1F).

In contrast a constant 24-hour light input of the same intensity (300 µW) drove rapid neural differentiation (Fig 1G–M, SI Movie 2). Single cells activated Brn2 and down-regulated Nanog (Fig 1H–J, left panel). RNA-seq analysis (Fig 1K–M, Fig S4) demonstrated that cells also down-regulated many key stem cell factors including members of the Polycomb protein family that silence differentiation genes in the pluripotent cell state (Fig S4, Figure 1L). Cells subsequently activated a neural gene expression program that included the neural transcription factor Neurod1, a master regulator of committed neural progenitor cells (Fig S4) (Gao et al., 2009; Kuwabara et al., 2009; Vanderhaeghen, 2009). Nanog and Neurod1 were expressed in a mutually exclusive pattern following 24 hours of Brn2 induction with Neurod1 present in greater than 70% of cells (Fig 1I–J). Neurod1 and Gbx2 are also induced during standard, small molecule in vitro differentiation of embryonic stem cells into the neural lineage (Fig S5A).

After longer periods of sustained Brn2 induction, cell morphology changed dramatically; cells generated long projections that formed an interconnected network (Fig S1D,F, SI Movie 2) and expressed markers of terminal neuron development (Fig 1 K–M). After 96 hours, approximately ~20% of cells stained positive for Tuj1 (Tubb3), a well-established neural marker (Gaspard et al., 2008) (Fig 1H, right). These results are consistent with Brn2’s role in neural development where the protein regulates both neural progenitor differentiation and terminal neuron development (Kuwabara et al., 2009).

Therefore, by controlling Brn2 expression, our optogenetic system could induce a neural cell fate transition in the embryonic stem cell. Notably, the cell’s response to Brn2 depended upon the duration of the light input. A one-hour light pulse induced Brn2 protein expression of lower magnitude and shorter temporal duration (~ 5 hours) than the Brn2 protein expression induced by sustained light induction. Therefore, we wanted to understand systematically how cells respond to Brn2 as a function of its magnitude and temporal dynamics (Fig 1A) and how this response might emerge through dynamics of the pluripotency network.

A two-state Nanog switch sets the magnitude threshold for Brn2

To understand how single ES cells decide whether to reject or respond to the Brn2 “input” as a function of its magnitude, we first performed a systematic analysis of the input-output response of the pluripotency circuit to light inputs of equivalent duration but different intensities. We exposed cell populations to 24 hours of constant intensity of light, and then measured the level of Brn2-RFP and Nanog-GFP in single cells using FACS (at the 24 time point) analyzing 9 different light powers (Experimental Procedures) in two biological replicates and over 250,000 single cells. At each fixed light power the cell population was heterogeneous with respect to Brn2 protein level, but the Nanog-GFP and Brn2-RFP fluorescent reporters allowed us to extract quantitative single cell information from otherwise convoluted population data (Fig S6A).

We found that cells transition sharply between two, discrete states of Nanog-GFP as a function of Brn2-RFP level (Figure 2A). Pooling data across all light powers, we constructed a two-dimensional Nanog/Brn2 joint distribution that quantifies the Nanog response in single cells as a function of the Brn2-RFP level at the 24-hour time point. At low levels of Brn2, the conditional Nanog-GFP distribution is (Fig 2B top) peaked at the mean of the unperturbed cell population (Nanog-on, pluripotent state). With increasing Brn2, cells begin to occupy a second state (Nanog-off, differentiated), and the Nanog-GFP distribution is bimodal (Fig 2B, middle). At high levels of Brn2, the distribution peaks at the Nanog-off state (differentiated) (Fig 2B top vs. bottom; 2C). Importantly, cells switch between the two states of Nanog expression without adopting intermediate values of Nanog.

To determine the switching threshold, we fit the conditional Nanog distributions to a Gaussian mixture model (Fig 2C), and calculated the ratio of Nanog-off (differentiated) to Nanog-on (pluripotent) cells. While low levels of Brn2 induction (relative to background) do not alter the Nanog-GFP distribution (Figure 2D), the cell population shifts towards the Nanog-off (differentiated) state at a threshold of ~100-fold Brn2 induction over background (Hill coefficient = 2.5). Because cells could tolerate sub-threshold levels of Brn2 for greater than 24 hours without down-regulating Nanog, we infer that this switching threshold is stable in time (Fig S7). At Brn2 levels near the switch threshold (Brn2~100), the Nanog-GFP distribution is bimodal, suggesting that the decision to down-regulate Nanog is stochastic. The stochastic response of the cell population at intermediate Brn2 levels could emerge, for example, due to cell-to-cell variation in the precise concentration of Brn2 need to switch a cell from the pluripotent to the differentiated state.

The Nanog distributions in Fig 2C are reminiscent of the equilibrium distribution of an ensemble of particles on a shifting bi-stable energy landscape. The two energy minima represent distinct states of Nanog expression, and Brn2 activation shifts the landscape to favor the Nanog-off (differentiated) state over the Nanog-on (pluripotent) state. Analogies between energy landscapes and differentiation are common in the literature on cell fate regulation; our experiments make the connection precise, as the Nanog distribution in Fig 2A implies an effective energy landscape for the Brn2-induced transition from a Nanog-on (pluripotent) to Nanog-off (differentiated) cell (Figure 2E; also See Supporting Materials).

In this way, we found that Nanog responds to Brn2 like a two-state switch. In the pluripotent state, cells can assess Brn2 expression as a function of its magnitude, so that below the 100-fold induction threshold, cells tolerate Brn2 expression as noise and do not down-regulate Nanog. Above the 100-fold induction threshold, cells generate a sharp response to Brn2 expression, switching from a Nanog-on (pluripotent) to Nanog-off (differentiated) state. We hypothesized that a two-state switching mechanism might enable ES cells to distinguish signal from noise. Therefore, we asked how dynamic properties of the switch impact its response to different durations of Brn2 expression.

Mathematical model connects two-state switching to pluripotency circuit architecture and Brn2 binding competition

We constructed a simple mathematical model to ask: (i) how a two-state switch arises through the pluripotency network and its interaction with Brn2; ii) how the network might respond to dynamically-varying Brn2 inputs. The coarse-grained mathematical model focuses on the key topological features of the network (positive feedback and competitive binding) rather than detailed biochemical interactions. Despite this simplicity, the model makes quantitative predictions about system behavior.

The pluripotency circuit is composed of the core Oct4-Nanog-Sox2 auto-regulatory loop (Fig 3A) (Chen et al., 2008; Jaenisch and Young, 2008; Niwa, 2007). Brn2, an Oct4 homologue, can bind to both Sox2 and Oct4 and titrate the factors away from the pluripotency complex (Lodato et al., 2013; Martello and Smith, 2014; Tanaka et al., 2004). Therefore, we considered the kinetic and steady-state behavior of a single auto-regulatory node that is destabilized by the competitive binding of an outside component. In the Supplemental Information, we show that competitive binding leads to Nanog dynamics that evolve according to:

$$\frac{dN}{dt}=\frac{V{N}^m}{K{[B]}^m+N^m}-\frac{N}{\tau },$$ (1)

where N and B are the concentrations of Nanog and Brn2 respectively. The first term on the right hand side represents the positive feedback loop, where V parameterizes the strength of auto-activation; K[B] models the threshold for induction of the positive feedback loop; m is the Hill coefficient describing the cooperativity of the auto-regulatory circuit. The second term models first order Nanog degradation with lifetime τ. The critical feature of the competitive binding model is that K, the threshold for triggering the Nanog positive feedback loop, is a function of Brn2 concentration: K[B] = γ(1+B), due to competitive binding. The parameter γ represents the threshold for positive feedback loop activation in cells in the absence of Brn2 induction. In the SI, we show how the competitive binding model leads to this functional dependence (see SI Mathematical Model).

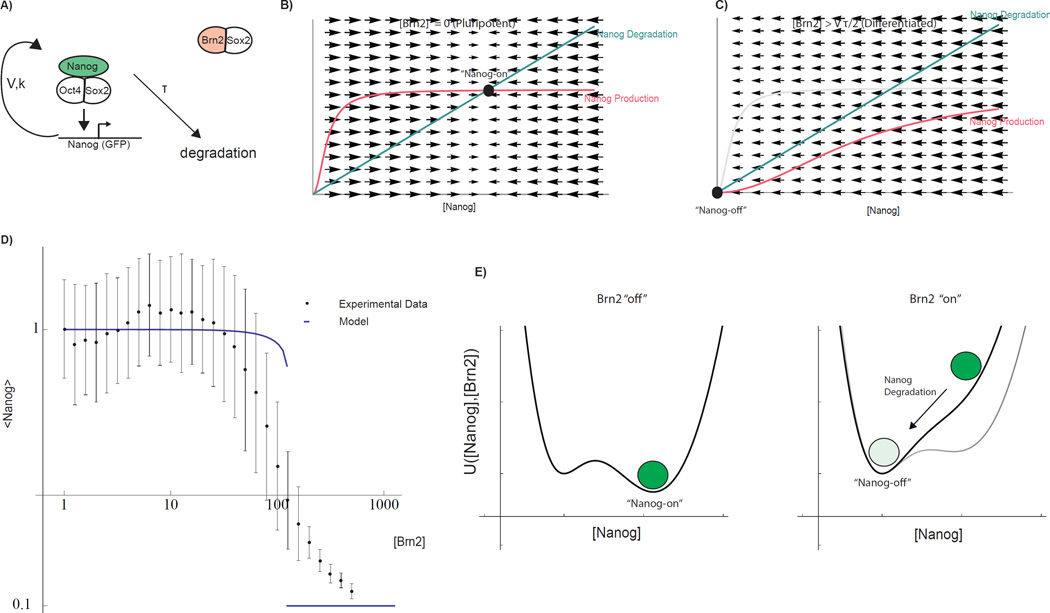
Fig 3. Mathematical model of pluripotency network and Brn2-induced cell fate switch.

A) Topology of the coarse-grained mathematical model. Pluripotency complex is engaged in an auto-regulatory positive feedback loop. Components are subject to first-order degradation. Through competitive binding, Brn2 interferes with the core auto-regulatory loop. Parameters V, K, and τ (Equation 1) parameterize Nanog promoter strength, promoter threshold, and Nanog life-time. B) Geometric analysis of steady states demonstrating the mechanism by which Brn2 can induce a switch-like transition from a Nanog-on to Nanog-off state (see SI for mathematical details). Curves indicate Nanog production (which depends upon [Nanog] due to auto-regulation) and degradation rates as a function of Nanog concentration. Black disk: stable Nanog-on steady state. C) Competitive binding effectively increases the threshold for Nanog promoter activation, sliding to the right the sigmoidal curve representing the Nanog production rate. At a threshold of [Brn2], the Nanog-on state becomes destabilized (intersection point vanishes) and the system collapses towards a Nanog-off state due to Nanog degradation. D) Steady-state Nanog as a function of Brn2 from experiments (mean as well as inter-quartile range) and model fit (thick line) with parameters fit to experimental data. E) Underlying energy landscape U(N,B) for regulatory network derived through direct integration of Eqn 1 and plotted for fixed V, τ, K[B] for a indicated Brn2 levels (Functional form SI, Equation 23). See also SI Fig 4

Figures 3B and C illustrate that competitive destabilization of a positive feedback loop can generate a sharp switch. In the absence of Brn2, balanced Nanog production (pink curve) and degradation (green curve) holds the unperturbed regulatory network in a Nanog-on (pluripotent) steady state (Fig 3B, black circle). Binding competition from Brn2 disrupts the production of Nanog (Fig 3C) by interfering with the pluripotency complex, thus shifting the pink production curve to the right (by increasing K[B]). In the model, the Nanog-on (pluripotent) steady state abruptly loses stability and disappears at a sharp Brn2 threshold (K[B] = V τ/2) through a saddle node bifurcation in the underlying dynamical system (see SI Mathematical Model) inducing a sharp transition in steady state Nanog level as a function of Brn2 (Figure 3D). Dynamically, following destabilization of the Nanog-on (pluripotent) state (Fig 3C, left, black circle), the network transitions to a Nanog-off (differentiated) state due to intrinsic and unbalanced Nanog protein degradation.

In our mathematical model, the cell fate switch can also be directly and rigorously interpreted as being controlled by an underlying energy landscape that governs the dynamics of Nanog expression (Supplemental Information, Thomson, 2015). The dynamical system described by equation 1 is identical in form to the equation of motion for a particle on potential energy landscape (over-damped regime), where undulations in the underlying energy landscape control the dynamic behavior of the particle. Therefore by analogy, we interpret the concentration of Nanog protein as being governed by an underlying energy landscape, U(N,B) where dN/dt = −dU(N, B)/dN, and U(N,B) is determined through integration of the right hand side of Equation 1 (Fig 3E). The local minima of U(N,B) represent the stable steady states of Nanog expression for each Brn2 concentration. Brn2 expression shifts the bi-stable potential destabilizing the Nanog-on (pluripotent) state, and the Nanog concentration decays towards the Nanog-off (differentiated) state. U(N,B) can also be used to model fluctuations in the Nanog concentration during the cell fate transition (Supporting Information, SI 8). The geometric interpretation of the model provides intuition for understanding the response of the pluripotency network to dynamic Brn2 expression, as considered in later sections of this study.

The mathematical model makes several testable predictions. First, the model predicts that the sharpness of the Nanog switch emerges due to the Brn2 competitive binding mechanism, so that additional transcription factors that can competitively bind the pluripotency complex should induce a similar switch-like response. Second, in the model, the dynamics by which cells transition from the Nanog-on (pluripotent) to Nanog-off (differentiated) state is determined by the intrinsic degradation rate of the Nanog protein, so that switching dynamics of the intrinsic lifetime of the Nanog protein in the unperturbed pluripotent ES cell should be matched. We verified these key predictions of the model before using it to analyze the response of the pluripotency network to dynamic, transient Brn2 expression.

Switch-like response of Nanog to competitive binding factor, Oct4

The model predicts that the switch-like response of Nanog to Brn2 occurs biochemically due to competitive binding, so that other competitive binding factors should have a similar switch-like impact on Nanog expression. Oct4 itself has been shown to form a homodimer in addition to its heterodimeric interaction with Sox2 (Botquin et al., 1998; Remenyi et al., 2001). The homodimeric and heterodimeric forms of Oct4 are mutually exclusive; Oct4 homodimers cannot form complexes with Sox2. Therefore, Oct4 also acts competitively with the pluripotency complex.

To test whether the Nanog response to Oct4 is also switch-like, we constructed an optically inducible Oct4 cell line and performed similar light-titration experiments as shown in Fig 2 for Brn2. We found that Oct4, like Brn2, induces down-regulation of Nanog at a threshold level of Brn2 where cells transition sharply from a Nanog-on (pluripotent) to Nanog-off (differentiated) state (Figure 4A). Therefore, the two-state switch response observed for Brn2 can be generalized to additional competitive binding factors

Fig 4. Competitive binding factor Oct4 induces a discrete Nanog-on to Nanog-off switch.

A) Response of Nanog to Oct4 induction. Oct4 was optically induced in cells for 24 hours at 4 distinct light powers (10 µW, 50 µW, 100 µW, 300 µW) and sampled from two biological replicates (N>80,000 cells). B) Response of Nanog to MyoD (a master muscle transcription factor) Response distribution constructed as for Oct4. C) Nanog response in mathematical model to decreases in V (modeling inhibition) compared with linear increase in K’ (modeling competitive binding) for fixed initial values of V, K, and τ. See also SI Fig 5

In contrast, Nanog responds to MyoD, a strong inducer of muscle differentiation not known to bind competitively to the pluripotency factors, in a continuous and gradual rather than switch-like fashion. At intermediate MyoD inductions, cells occupy intermediate Nanog levels and shift gradually from high Nanog to low Nanog expression (see also Fig S9). Accordingly, in the mathematical model (Fig 4C) decreasing V, modeling direct promoter inhibition (vs competitive binding), leads to a linear decrease in Nanog and a qualitatively distinct graded Nanog response (see SI for more detailed analysis).

Switch dynamics predict Nanog half-life in unperturbed ES cells

In the mathematical model, the dynamics of the cell fate switch are controlled by the intrinsic Nanog protein lifetime. When Brn2 crosses the switching threshold, single cells transition from the Nanog-on (pluripotent) to Nanog-off (differentiated) state through intrinsic Nanog protein degradation. Mathematically, the positive feedback term in Equation (1) approaches zero, and Nanog falls exponentially to zero with a switching time set by the intrinsic Nanog half-life [log(2) τ]. Thus, in the model, Nanog degradation is rate limiting, and the switching time of the ES cell from the Nanog-on to Nanog-off state following Brn2 induction provides an upper bound on the Nanog half-life.

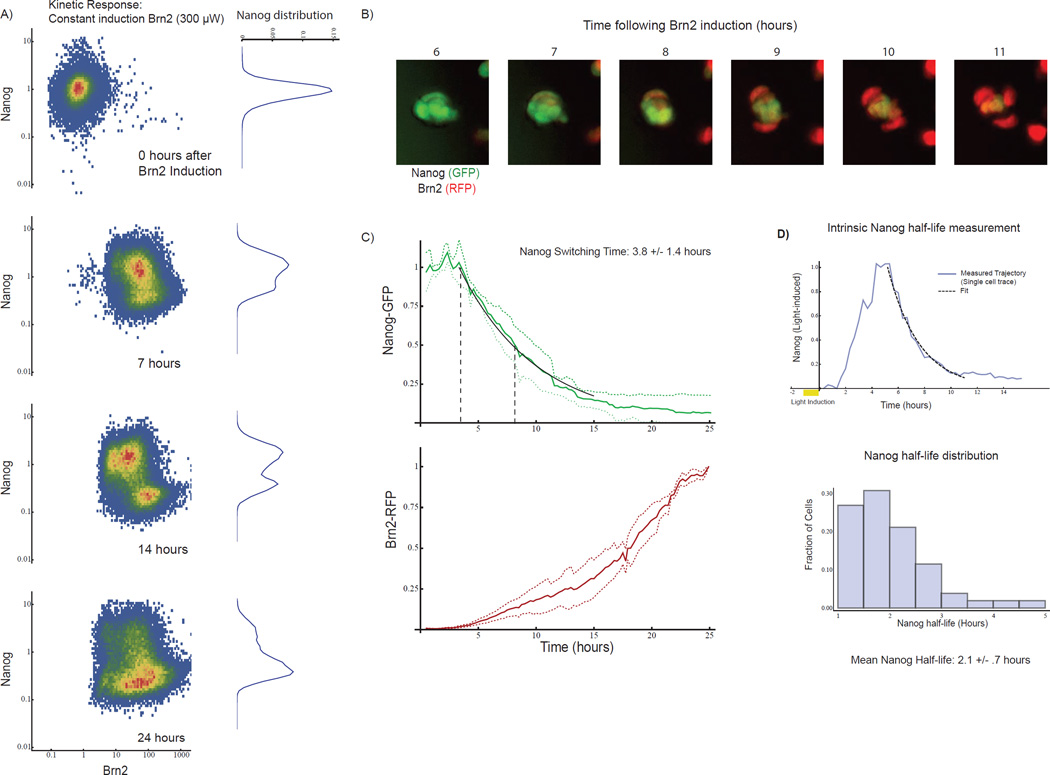
Single cell imaging and FACS (Fig 5A–C) measurements revealed that cells transition from the Nanog-on (pluripotent) to Nanog-off (differentiated) states with a switching half-life of just 3.8 +/− 1.2 hours (Fig 5B–C, SI Movie 3), predicting a <3.8 hour Nanog half-life. This half-life is short compared with other mammalian proteins where the mean protein half-life in human cells is 9 hours (Eden et al., 2011). Therefore, by connecting switch dynamics with Nanog’s intrinsic half-life in unperturbed ES cells, the model made a strong and non-obvious prediction.

Fig 5. Switch dynamics predict intrinsic Nanog half-life in unperturbed cells.

A) Two-dimensional histograms of Nanog-GFP and Brn2-RFP intensity in ES cell populations as measured by FACS at 0, 7, 14, and 24 hours during constant 300uW light stimulation. Each histogram represents >40,000 single cells. The marginal distribution of Nanog-GFP is shown on the right of each plot. Cells begin transitioning from Nanog-on to Nanog-off state at 7 hours, and by 14 hours the cell population breaks into two subpopulations. B) Nanog-GFP and Brn2-RFP images at one-hour intervals. (20um scale bars) C) Distribution of > 50 single-cell time-courses of Nanog-GFP and Brn2-RFP (mean and standard deviation, normalized to max). From Exponential fit (black line) yielded a switching time of 3.8 +/− 1.4 hours. D) Measurement of Nanog lifetime using optically-inducible Nanog-RFP construct (optical pulse chase). Top: Nanog-RFP dynamics (blue curve) in a light-inducible Nanog cell following a 1-hour light pulse, with exponential fit (black curve). Blue curve is an example single cell trace. Bottom: histogram of Nanog half-life from 50 single-cell time-courses (mean half-life 2.1 +/− .75 hours). See also SI Fig 6

We tested the prediction by measuring the Nanog half-life in unperturbed ES cells through optical pulse chase experiments using a light inducible Nanog-RFP cell line (Fig 5D, SI Movie 4). In unperturbed ES cells we measured a mean Nanog half-life of 2.1 +/− 0.8 hours, consistent with predictions and confirming the short intrinsic Nanog lifetime. Through proteasome inhibition, we found that rapid Nanog production balances this rapid Nanog degradation in unperturbed ES cells (Figure S10A), so that the ES cell generates approximately 100% of the steady-state Nanog protein pool every four hours (Fig S10A).

Model predicts quantitative response of pluripotency network to transient Brn2 inputs

With core features of the model validated, we sought to use the model to explain the response of the pluripotency network to transient Brn2 expression. In the model, the ability to distinguish a differentiation cue from noise arises from two properties of the dynamical system: the sharp Brn2 threshold and the switching time-scale due to Nanog degradation. To drive differentiation, Brn2 expression must be high enough in magnitude to surpass the Brn2 threshold and long enough in duration to allow the network to transition from the Nanog-on (pluripotent) to Nanog-off (differentiated) state.

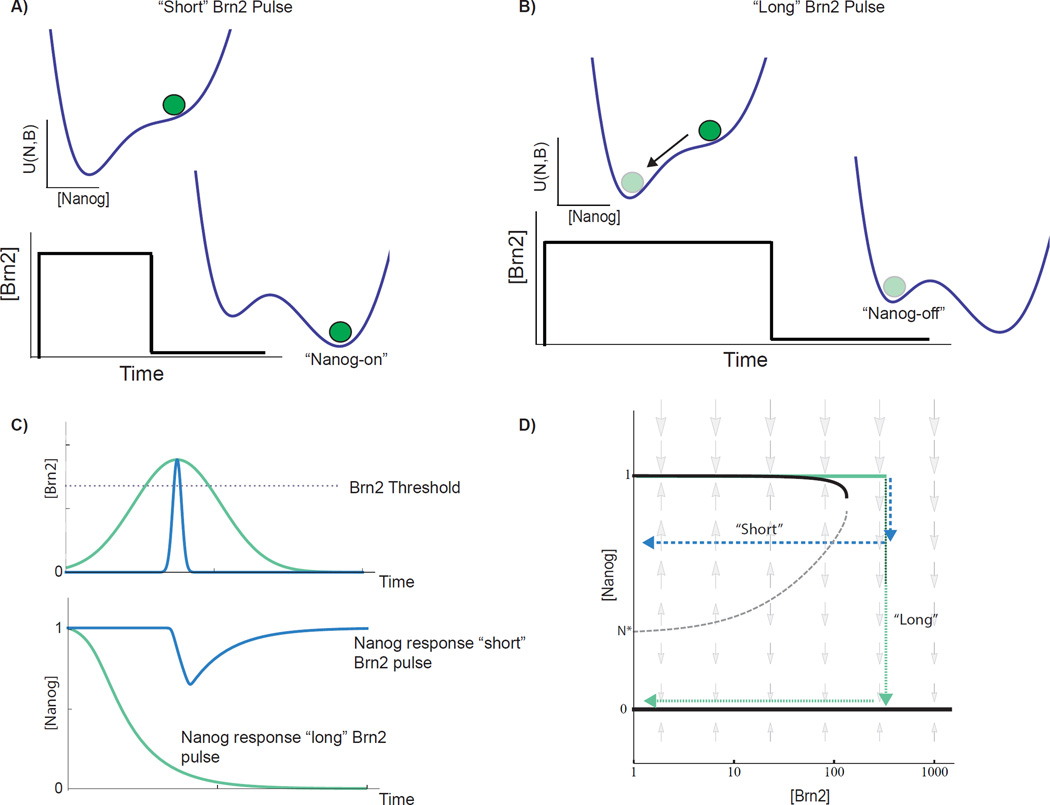
The landscape formalism provides a qualitative, intuitive description of Brn2’s role in promoting differentiation: above the 100-fold induction threshold, Brn2 shifts the underlying cell fate landscape (Fig 6A), and Nanog begins to decay towards the Nanog-off (differentiated) state. However, when the duration of Brn2 expression is short relative to the Nanog lifetime, the network cannot complete the transition from the “on” to the “off” state before the pulse subsides, and the landscape returns to its original form. Therefore, the cell is retained in the Nanog-on state (pluripotent) when the duration of Brn2 expression is below the switching threshold. For longer pulses (Fig 6B), cells complete the transition from Nanog-on (pluripotent) to Nanog-off (differentiated) and remain in the Nanog-off state even when Brn2 subsequently drops below the switching threshold (Fig 6B). Dynamically, the Nanog lifetime sets a duration threshold in the network, so that Brn2 expression below a minimum temporal duration does not drive Nanog down-regulation (Fig 6C).

Fig 6. Mathematical model predicts filtering of Brn2 inputs based upon their duration.

A) Energy landscape depiction of duration thresholding through the dynamics of two-state Nanog switch. Brn2 induction destabilizes Nanog-on (pluripotent) state, and cell begins to transition to Nanog-off (differentiated) state through intrinsic Nanog degradation. For an input that is “short” relative to the Nanog half-life, Brn2 begins to fall before the cell can transition past a critical point, and the cell returns to the Nanog-on state following the light pulse. For a long pulse, B) the cell transitions beyond the critical Nanog concentration during the pulse and so transitions to and remains in the Nanog-off state following the pulse. C) Nanog and Brn2 dynamics from mathematical model for “short” and “long” Brn2 pulses. D) 2D depiction of Nanog steady states and dynamic flows vs Brn2 input level. Stable Nanog concentrations (black curves) and dynamic Nanog flows (gray arrows) indicated as a function of [Brn2]. The Nanog-on stable state is lost at a sharp Brn2 threshold due to a saddle node bifurcation. Schematic Nanog/Brn2 trajectories for “short” (blue arrow) and “long” (green arrow) square Brn2 pulses. For short pulse, Brn2 exceeds switching threshold but returns below the threshold before Nanog passes a “critical concentration” defined by presence of an unstable fixed point (dotted gray curve).

Quantitatively, the minimum Brn2 duration required for switching is determined by the position of an unstable fixed point (the hill separating the two valleys in the energy landscape). This minimum value can also be seen in the diagram in Figure 6D (gray dotted line) that shows the steady state Nanog concentration (black lines) as a function of Brn2 expression and also shows the “flow” of Nanog away from the stable concentration (indicated by gray arrows). Above the Brn2 threshold, Nanog flows towards the Nanog-off (differentiated) state. However, if excursions beyond the Brn2 threshold are brief, then Nanog begins to decay, but does not reach the critical Nanog concentration (gray dotted line) to trigger differentiation before the Brn2 pulse subsides. The network, thus, ignores or rejects as noise any Brn2 expression pulse that breaches the magnitude threshold but is shorter than the duration threshold (Figure 6C). The analytic lower bound for the minimum duration of Brn2 expression required to switch Nanog from on to off is τ log(Nanog_on/Nanog*) where Nanog_on/Nanog* is the ratio of the Nanog-on concentration to the Nanog concentration at the unstable fixed point (N* in 4D) and τ is the Nanog lifetime in (1).

Figure 7 shows the experimentally-measured dynamics of a cell population responding to a 3-hour light pulse. The level of Brn2 in the cell population rises, and the mean level transiently reaches the switch-threshold (Figure 7A, gray line, Brn2~100). However, the population begins relaxing due to Brn2 degradation before cells can transition to the Nanog-off (differentiated) steady state. The population breaches the switching threshold but returns below this threshold on a time scale that is not sufficient for switching (~ 3 hours). Fig S10C indicates the switching threshold for a constant light control experiment performed simultaneously for comparison. The distributions in Figure 7A illustrate in real-time the ability of the network to reject transient Brn2 expression as noise.

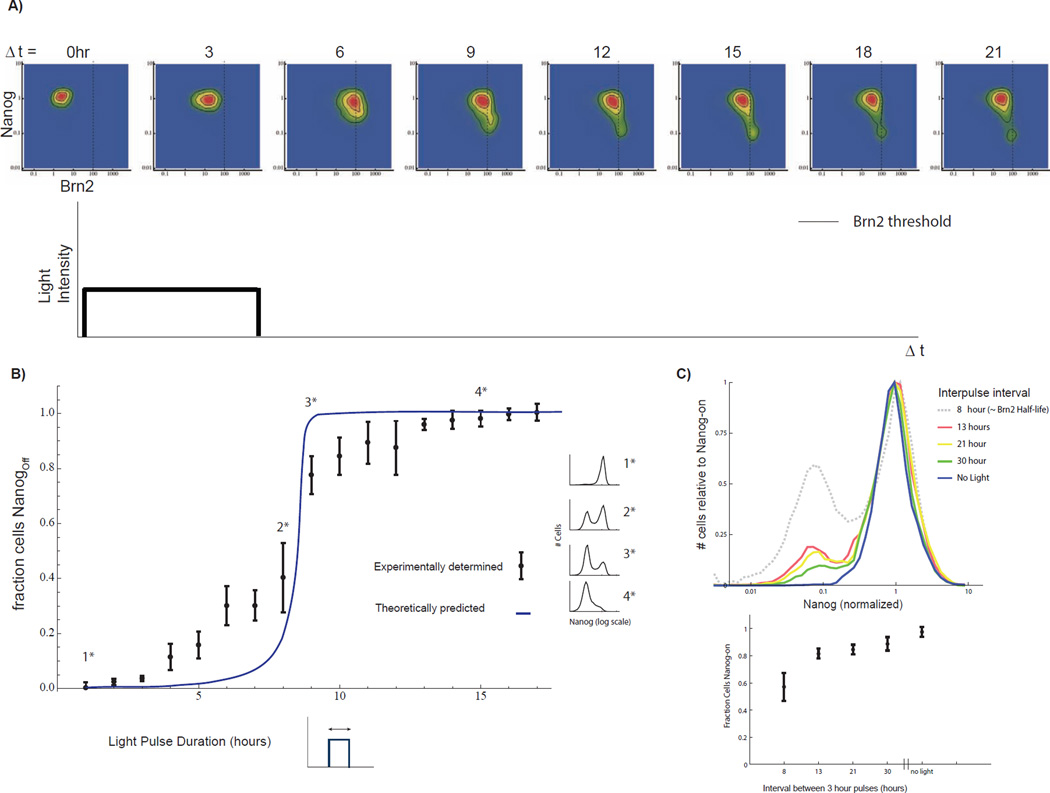
Fig 7. Nanog-half life determines duration filtering properties of the pluripotency network.

A) Brn2 vs. Nanog distribution for >20,000 single cells at each of eight time points. Time is measured in units of hours following light pulse initiation. A dashed line indicates the Brn2 switching threshold (validated by constant input control in SI 10C). The Brn2 level exceeds the threshold in approximately half of the cells at 6 hours following pulse initiation. However, only a fraction of these cells (<20% of the cell sub-population) switch to the Nanog-off state. B) Predictions of model (blue line) and the experimentally-measured Nanog-off fraction (mean and standard deviation) for cells exposed to 300µW light pulses of 0 to 17 hours. For pulses of less than 5 hours >80% of cells maintain Nanog in the on state. Half of the cell population switches for a 8.5-hour light pulse. Example Nanog distributions shown in the margin. C) Top: Histograms of Nanog-GFP following repeated 3-hour light pulses with variable inter-pulse spacing as indicated. Experiment performed over 48 hours and n>10,000 cells measured for each experiment. Brn2 half-life is approximately 8 hours. Histograms normalized to height of Nanog-on peak for comparative purposes. Total number of pulses delivered is: 3 pulses, 13 hour interval; 2 pulses 21 hour interval; 1.5 30 hour interval). Bottom: fraction of Nanog-on cells, mean +/− standard deviation for three biological replicates. See also SI Fig 7

Model predicts quantitative buffering and switching regimes

To quantitatively predict the filtering properties of the network, we fully parameterized a model of Nanog dynamics using the steady-state and relaxation-time data in Figures 2 and 4. To parameterize a model of Brn2 dynamics, we performed time-lapse imaging and FACS experiments to measure the half-life of Brn2 as well as to parameterize the dynamic and steady-state induction of Brn2 in response to light inputs of varying magnitude (Figure S11 A–D).

With all the free parameters fixed, the model quantitatively predicted the response of Nanog to pulses of Brn2 expression. The predicted Brn2 pulse-response contains two regimes of behavior, a buffering regime and a switching regime, separated by a boundary (Fig 7B, blue curve). The model predicted that cells tolerate 5-hour light inputs without switching to the Nanog-off (differentiated) state. We emphasize that Figure 7B shows a prediction of the model that is based upon parameters fixed through the steady state and dynamic measurements made previously without further parameter adjustment or fitting.

The optogenetic system enabled us to measure the response of cells to varying durations of Brn2 expression and to compare a switch from Nanog-on (pluripotent) to Nanog-off (differentiated) with the theoretical predictions. We exposed cells to light pulses of 17 different durations and measured the fraction of Nanog-off (differentiated) and Nanog-on (pluripotent) cells in cell populations 24 hours after the termination of the light pulse. In agreement with model predictions, the experimentally-determined differentiation-response curve (Fig 7B, dots and error bars) contains a buffering regime and a switching regime quantitatively consistent with the regimes predicted by the mathematical model. Even at these saturating light powers, more than 80% of cells tolerate Brn2 induction pulses of up to ~5 hours without down-regulating Nanog (or activating Neurod1, Fig S12). Indeed, a large fraction of cells (~50%) tolerate light pulses of 8 hours without switching to the Nanog-off (differentiated) state. Further, the cells can tolerate a series of light pulses when the pulses are separated by a temporal durations longer than the Brn2 half-life, so that Brn2 has time to decay following each round of activation (Figure 7C). Three, three-hour light pulses, delivered over two days and spaced by 13 hours drove differentiation in less than 20% of cells.

Discussion

In this work, we analyzed mechanisms by which embryonic stem cells distinguish differentiation cues (signals) from gene expression fluctuations (noise). Using an optogenetic approach, we find that the pluripotency network evaluates inputs based upon both magnitude (Figure 2) and duration (Figure 7) thresholds. Inputs that fall below either threshold are filtered as noise (Figure 1A). Inputs that satisfy both thresholds trigger efficient differentiation. The filtering properties of the network emerge due to the dynamics of an underlying two-state switch (Figures 4, 6). Brn2 induction disrupts the Oct4/Nanog/Sox2 pluripotency complex and positive-feedback loop, and the Nanog concentration of the cell begins to fall due to reduced Nanog production. In our model, Nanog acts like a timer, and pulses of Brn2 expression must exceed a minimum duration set by the intrinsic degradation rate of Nanog in order to switch the network. The Nanog half-life is short relative to the lifetime of typical mammalian proteins. This short half-life allows the cell to respond to pulses on an hours (vs days) time scale, and to quickly reject short time-scale fluctuations in Brn2 levels.

In the context of recent global analyses of cell fate regulatory networks, our results suggest that positive auto-regulatory networks might provide a general and tunable strategy for stem cells to differentiate in response to authentic signals but not to noise (Dublanche et al., 2006; ; Prill et al., 2005; Simpson et al., 2003; Thieffry et al., 1998). Recent work has shown that circuits with positive-feedback architecture underlie cell fate regulation in a large number of stem cell and differentiated cell types (Fong and Tapscott, 2013; Hnisz et al., 2013; Kueh et al., 2013; Whyte et al., 201;). Our work highlights the ability of such auto-regulatory positive feedback networks, through their dynamic behavior, to distinguish signal from noise and also to trigger fate switching. Prior theoretical work, in fact, showed the positive feedback regulation is an optimal architecture for noise filtering (Hornung and Barkai, 2008) while allowing a network to maintain sensitivity to sustained changes in an input.

Further, critical properties of the network, including the duration threshold, can be simply tuned by modifying underlying biochemical rates. For example, scaling the Nanog degradation rate in our mathematical model linearly scales the duration of the minimum Brn2 pulse required for differentiation (Figure S13) suggesting that auto-regulatory networks provide a simple and tunable regulatory architecture for tolerating noise but while also responding robustly to signals. Indeed, the half-life of master cell fate regulators varies widely (Kueh et al., 2013), suggesting that a simple circuit topology might be exploited to provide tunable envelopes of stability in a wide variety of stem cell populations. It will be interesting to ask how the degradation rates of core cell fate regulators vary between stem cells of different types to meet specific physiological criteria (Sivak and Thomson, 2014).

Waddington’s work on epigenetic landscapes has long been viewed as a qualitative metaphor for cell fate regulation (Ferrell, 2012; Francois and Siggia, 2012; Pujadas and Feinberg, 2012;). Here, we find that a mathematical model based upon an underlying Waddington-like energy landscape additionally provides a quantitative mathematical framework for dissecting a simple cell fate transition. The sufficiency of an energy landscape for modeling the dynamics of a regulatory circuit has important implications. It implies that the behavior of a regulatory network (on experimentally observed timescales) is "memoryless": the future state of the network can be directly predicted (in a statistical sense) from the current state of the network while ignoring potentially complex history-dependent effects like adaptation (Yi et al., 2000). For example, in our experimental system, the landscape model implies that the current Brn2 and Nanog protein concentrations predict the future behavior of the pluripotency network, and the past dynamics of Brn2 can be ignored.

Energy landscape models can be applied efficiently to model much larger networks of genes than considered here. In such cases, the energy landscape will exist in a high dimensional space with one dimension for each gene in the network. Statistical mechanics provides mathematical tools that can be adapted to extract landscape models directly from large single cell data sets. Once parameterized, the dynamics of a cell population evolving on the landscape can be modeled (Zwanzig, 2001). It will be interesting to extend this approach to more complicated cell fate transitions where multiple states can be accessed as a function of transcription factor expression levels (Graf and Enver, 2009; Gaspard et al., 2008; Thomson and Gunawardena, 2009). In this way, the experimental and mathematical approaches described here might be extended to the genome scale to provide a global view of mechanisms for buffering and gating differentiation.

Experimental Procedures

Full experimental procedures can be found in the Supplemental Information. Briefly: mESCs were cultured under standard conditions but maintained in the dark and passaged under red illumination. The Nanog-GFP knock-in cell line was generated from E14 mouse embryonic stem cells (gift from Chong Park) through Cas9 mediated homologous recombination of eGFP into the C terminus of the endogenous Nanog gene. Optogenetic induction of Brn2 in E14 mES cells was accomplished using the GAVPO blue-light activate-able transcription factor. Expression of Brn2 was induced by an addressable LED matrix, the illumination of each LED was controlled in space and time and isolated from the others by a custom 3D printed mask. All imaging experiments were performed with a Nikon Ti-E Microscope with Hamamatsu Flash 4.0 camera controlled by Nikon Elements software NIS-Elements 4.2. FACS and RNA-seq experiments were performed and analyzed using standard methods. The mathematical model is described in detail in the supporting information. Numerical integration of the model was performed using NDSolve in Mathematica.