On random-effects meta-analysis

Summary

Meta-analysis is widely used to compare and combine the results of multiple independent studies. To account for between-study heterogeneity, investigators often employ random-effects models, under which the effect sizes of interest are assumed to follow a normal distribution. It is common to estimate the mean effect size by a weighted linear combination of study-specific estimators, with the weight for each study being inversely proportional to the sum of the variance of the effect-size estimator and the estimated variance component of the random-effects distribution. Because the estimator of the variance component involved in the weights is random and correlated with study-specific effect-size estimators, the commonly adopted asymptotic normal approximation to the meta-analysis estimator is grossly inaccurate unless the number of studies is large. When individual participant data are available, one can also estimate the mean effect size by maximizing the joint likelihood. We establish the asymptotic properties of the meta-analysis estimator and the joint maximum likelihood estimator when the number of studies is either fixed or increases at a slower rate than the study sizes and we discover a surprising result: the former estimator is always at least as efficient as the latter. We also develop a novel resampling technique that improves the accuracy of statistical inference. We demonstrate the benefits of the proposed inference procedures using simulated and empirical data.

1. Introduction

Meta-analysis compares and combines results from multiple independent studies, with the hope of identifying consistent patterns and sources of disagreement. It has been routinely used in all areas of statistical applications, from astronomy to zoology. The meta-analysis literature has grown exponentially over the past three decades, owing to the need for reliable summarization of the vast and expanding volume of scientific research. According to the Web of Science, there were 2006 meta-analysis publications during the years 1985–1994, 13 154 during 1995–2004, and more than 55 000 during 2005–2014. The impact of meta-analysis on medical research and clinical practice has been enormous (see, e.g., Whitehead, 2002; Sutton & Higgins, 2008). Most of the recent discoveries about genetic variants associated with complex human diseases and traits have been made through meta-analysis (e.g., McCarthy et al., 2008; Evangelou & Ioannidis, 2013). Meta-analysis is likely to play an even greater role in the current big-data era.

Conventional meta-analysis relies on summary statistics, such as estimated effect sizes and standard errors, from relevant studies. Advances in technology and communications have made it increasingly feasible to access data on individual participants (e.g., Sutton et al., 2000). Indeed, joint analysis of individual patient data is considered the gold standard in systematic reviews of randomized clinical trials (e.g., Chalmers et al., 1993). Recently, a number of consortia have been formed to share individual participant data from genetic association studies (e.g., Psychiatric GWAS Consortium Steering Committee, 2009; Evangelou & Ioannidis, 2013; Lin et al., 2013).

Suppose that there are K independent studies, with n_k participants for the kth study. The data consist of {𝒪_ki : k =1,…, K; i =1,…, n_k}, where 𝒪_ki represents the observation, including the response variable and explanatory variables, on the ith participant of the kth study. Assume that the density function of 𝒪_ki is proportional to f_k(·; β_k, η_k), where β_k is the parameter of interest, namely the effect size for a new treatment or genetic mutation, and η_k is a set of nuisance parameters, such as the error variance and the regression effects of demographic variables. Let β̂_k be the maximum likelihood estimator of β_k based on the likelihood $L_k({\beta }_k,{\eta }_k)={\prod }_{i=1}^{n_k}{f}_k({\mathcal{O}}_{ki};{\beta }_k,{\eta }_k)$, and let V̂_k be the estimated variance of β̂_k. We assume that standard regularity conditions (Cox & Hinkley, 1974, p. 281) hold and that the n_k are large enough that β̂_k is approximately normal with mean β_k and variance V̂_k.

Under the fixed-effects model, β_k =β for all k =1,…, K. The familiar inverse-variance estimator of β is

$$\widehat{\beta }={\left(\sum _{k=1}^K{\widehat{V}}_k^{-1}\right)}^{-1}\sum _{k=1}^K{\widehat{V}}_k^{-1}{\widehat{\beta }}_k,$$

which is approximately normal with mean β and variance ${(\sum {\widehat{V}}_k^{-1})}^{-1}$. Let β̂^† be the maximum likelihood estimator of β found by maximizing the joint likelihood ${\prod }_{k=1}^K{L}_k(\beta ,{\eta }_k)$. Olkin & Sampson (1998) and Mathew & Nordstrom (1999) showed that, in the case of comparing multiple treatments and a control for a continuous outcome with known error variances, β̂ is the same as β̂^†. Recently, Lin & Zeng (2010) proved that the two estimators are asymptotically equivalent for all commonly used parametric and semiparametric models.

We focus on the random-effects model

$${\beta }_k=\beta +{\xi }_k(k=1,\dots ,K),$$

where ξ_k ~ N(0, τ²). Because β̂_k is approximately normal with mean β and variance V̂_k + τ², it is natural to estimate β by

$${\widehat{\beta }}_{\text{MA}}={\left(\sum _{k=1}^K{\widehat{w}}_k\right)}^{-1}\sum _{k=1}^K{\widehat{w}}_k{\widehat{\beta }}_k,$$ (1)

where ${\widehat{w}}_k={({\widehat{V}}_k+{\widehat{\tau }}_{\text{MA}}^2)}^{-1}$, with (DerSimonian & Laird, 1986)

$${\widehat{\tau }}_{\text{MA}}^2=max\left\{0,\frac{{\sum }_{k=1}^K{\widehat{V}}_k^{-1}{({\widehat{\beta }}_k-\widehat{\beta })}^2-(K-1)}{{\sum }_{k=1}^K{\widehat{V}}_k^{-1}-{\sum }_{k=1}^K{\widehat{V}}_k^{-2}/{\sum }_{k=1}^K{\widehat{V}}_k^{-1}}\right\}.$$ (2)

Inference on β is typically based on the normal approximation

$${\widehat{\beta }}_{\text{MA}}~N\left\{\beta ,{\left(\sum {\widehat{w}}_k\right)}^{-1}\right\}.$$ (3)

For finite K, the estimator ${\widehat{\tau }}_{\text{MA}}^2$ involved in the ŵ_k is random and correlated with the β̂_k, so the normal approximation given in (3) can be very crude. Indeed, it is well documented that confidence intervals based on (3) have very poor coverage for small and moderate K (see, e.g., Biggerstaff & Tweedie, 1997; Brockwell & Gordon, 2001). Various methods have been proposed to improve the confidence intervals (e.g., Hardy & Thompson, 1996; Biggerstaff & Tweedie, 1997; Brockwell & Gordon, 2001; Sidik & Jonkman, 2002; Henmi & Copas, 2010); however, none of these methods has been rigorously justified or widely accepted.

When individual participant data are available, one can maximize the loglikelihood

$$\sum _{k=1}^{K}log{\int }_{{\xi }_k}\prod _{i=1}^{n_k}{f}_k({\mathcal{O}}_{ki};\beta +{\xi }_k,{\eta }_k){(2\pi {\tau }^2)}^{-1/2}exp(-{\xi }_k^2/2{\tau }^2)\mathrm{d}{\xi }_k.$$ (4)

Denote the resulting estimators of β, τ² and (η₁,…, η_K) by β̂_ML, ${\widehat{\tau }}_{\text{ML}}^2$ and (η̂₁,…, η̂_K). It is challenging to establish the theoretical properties of the maximum likelihood estimators, because the n_k are typically larger than K. This problem is similar to that encountered in the analysis of large clusters. The existing theory for random-effects models with large clusters requires that the variance component be known (Bellamy et al., 2005). The fact that the variance component needs to be estimated from the data poses major theoretical challenges.

In the present paper, we establish the asymptotic properties of the meta-analysis estimators β̂_MA and ${\widehat{\tau }}_{\text{MA}}^2$ and the maximum likelihood estimators β̂_ML and ${\widehat{\tau }}_{\text{ML}}^2$ for the situations of a fixed K and diverging K. We then investigate the asymptotic relative efficiency of β̂_MA to β̂_ML and reveal that the former is at least as efficient as the latter. In addition, we develop a novel resampling technique that yields substantially more accurate inference than the normal approximation given in (3). Finally, we demonstrate the advantages of the new inference procedures by applying them to data from clinical trials on the treatment of cancer-associated anaemia.

2. Asymptotic theory

We assume that the n_k (k =1,…, K) are comparable and denote their median by n. We write τ² =σ²/n, where σ² is a constant, such that the between-study variability is of the order n⁻¹ and thus comparable to the within-study variability V̂_k. We estimate σ² by ${\widehat{\sigma }}_{\text{MA}}^2=n{\widehat{\tau }}_{\text{MA}}^2$ and ${\widehat{\sigma }}_{\text{ML}}^2=n{\widehat{\tau }}_{\text{ML}}^2$ in the meta-analysis and maximum likelihood estimation, respectively. Note that ${\widehat{\sigma }}_{\text{MA}}^2$ is a consistent method-of-moments estimator.

We assume the following regularity conditions.

• Condition 1. The parameters (β, η_k, σ²) lie in the interior of a compact set 𝒞₁ × 𝒞_2k × 𝒞₃ within the parameter domain.

• Condition 2. For (β_k, η_k) ∈ 𝒞₁ × 𝒞_2k, the function log f_k(𝒪; β_k, η_k) is thrice continuously differentiable.

• Condition 3. For k =1,…, K, n_k = p_kn for some constant p_k within a compact interval in (0,∞).

• Condition 4. The information matrix of f_k(𝒪; β, η_k) is continuous in a neighbourhood of the true parameter value (β₀, η_k0), and its eigenvalues have positive lower and upper bounds uniformly for k =1,…, K.

In practice, K is small relative to n. Therefore, we investigate the asymptotic properties of the meta-analysis estimators and maximum likelihood estimators in the cases where K is fixed or diverges to ∞ at a slower rate than n. The results for the first case are stated below.

Theorem 1

Under Conditions 1–4,

$${\widehat{\sigma }}_{\text{ML}}^2\to {\mathcal{A}}_{\text{ML}}=\underset{{\sigma }^2}{argmax}\left\{-\frac{1}{2}\sum _{k=1}^{K}log({\mathcal{I}}_{{\beta }_k}^{-1}+p_k{\sigma }^2)-\frac{1}{2}\sum _{k=1}^K\frac{{\mathcal{Z}}_k^2}{v_k+p_k{\sigma }^2}+\frac{1}{2}{\left(\sum _{k=1}^K\frac{p_k}{v_k+p_k{\sigma }^2}\right)}^{-1}{\left(\sum _{k=1}^K\frac{{p_k}^{1/2}{\mathcal{Z}}_k}{v_k+p_k{\sigma }^2}\right)}^2\right\}$$

in distribution, where ${\mathcal{I}}_{{\beta }_k}=-E\{{\partial }^{2}log{f}_k(\mathcal{O};{\beta }_0,{\eta }_{k0})/\partial {\beta }_k^2\}$, 𝒵₁,…,𝒵_K are independent zero-mean normal random variables with variances $v_k+p_k{\sigma }_0^2$, v_k is the limit of n_kV̂_k, and ${\sigma }_0^2$ is the true value of σ². In addition,

$$n^{1/2}({\widehat{\beta }}_{\text{ML}}-{\beta }_0)\to {\left(\sum _{k=1}^K\frac{p_k}{v_k+p_k{\mathcal{A}}_{\text{ML}}}\right)}^{-1}\sum _{k=1}^K\frac{{p_k}^{1/2}{\mathcal{Z}}_k}{v_k+p_k{\mathcal{A}}_{\text{ML}}}$$

in distribution. Furthermore,

$$\begin{array}{l}{\widehat{\sigma }}_{\text{MA}}^2\to {\mathcal{A}}_{\text{MA}}\\ =max\left[0,\frac{{\sum }_{k=1}^K{\stackrel{\sim }{v}}_k^{-1}{\{{\mathcal{Z}}_k/{p_k}^{1/2}-{({\sum }_{k=1}^K{\stackrel{\sim }{v}}_k^{-1})}^{-1}{\sum }_{k=1}^K{\stackrel{\sim }{v}}_k^{-1}{\mathcal{Z}}_k/{p_k}^{1/2}\}}^2-(K-1)}{{\sum }_{k=1}^K{\stackrel{\sim }{v}}_k^{-1}-{\sum }_{k=1}^K{\stackrel{\sim }{v}}_k^{-2}/{\sum }_{k=1}^K{\stackrel{\sim }{v}}_k^{-1}}\right]\end{array}$$

in distribution, where ṽ_k =v_k/p_k, and

$$n^{-1/2}({\widehat{\beta }}_{\text{MA}}-{\beta }_0)\to {\left(\sum _{k=1}^K\frac{p_k}{v_k+p_k{\mathcal{A}}_{\text{MA}}}\right)}^{-1}\sum _{k=1}^K\frac{{p_k}^{1/2}{\mathcal{Z}}_k}{v_k+p_k{\mathcal{A}}_{\text{MA}}}$$

in distribution.

This theorem indicates that neither the maximum likelihood estimator β̂_ML nor the metaanalysis estimator β̂_MA is asymptotically normal. Their asymptotic distributions are mixtures of normal random variables, the mixing probabilities being random and correlated with the normal random variables. This phenomenon is different from the usual asymptotic theory (Cox & Hinkley, 1974, § 9.2) and is caused by the fact that K is fixed.

Before stating the asymptotic results for divergent K, we make two additional assumptions.

• Condition 5. We have n→∞, K → ∞, and Kn^−1/2→0.

• Condition 6. For any σ² ∈ 𝒞₃, the following limit exists:

  $$g({\sigma }^2)=-\underset{K\to \infty }{lim}\frac{1}{K}\sum _{k=1}^K\left\{\frac{v_k+p_k{\sigma }_0^2}{v_k+p_k{\sigma }^2}+log\left({\mathcal{I}}_{{\beta }_k}^{-1}+p_k{\sigma }^2\right)\right\},$$

  where g(σ²) has a unique maximum at ${\sigma }_{\mathrm{r}}^2$ in 𝒞₃.

Remark 1

Condition 5 implies that the number of studies increases to infinity but not as fast as the study sizes. The function g(·) is the limit of the profile likelihood function for σ², so Condition 6 guarantees the convergence of ${\widehat{\sigma }}_{\text{ML}}^2$ to some unique value as K → ∞.

Theorem 2

Under Conditions 1–6, ${\widehat{\sigma }}_{\text{ML}}^2\to {\sigma }_{\mathrm{r}}^2$ and β̂_ML→β₀ in probability. In addition,

$${(Kn)}^{1/2}({\widehat{\beta }}_{\text{ML}}-{\beta }_0)\to N\{0,\mathrm{\sum }{({\sigma }_{\mathrm{r}}^2,{\sigma }_0^2)}^{-1}\mathrm{\sum }({\sigma }_{\mathrm{r}}^2,{\sigma }_{\mathrm{r}}^2)\mathrm{\sum }{({\sigma }_{\mathrm{r}}^2,{\sigma }_0^2)}^{-1}\}$$

in distribution, where

$$\mathrm{\sum }({\sigma }_1^2,{\sigma }_2^2)=\underset{K\to \infty }{lim}\frac{1}{K}\sum _{k=1}^K\frac{p_k(v_k+p_k{\sigma }_0^2)}{(v_k+p_k{\sigma }_1^2)(v_k+p_k{\sigma }_2^2)},$$

which is assumed to exist for any ${\sigma }_1^2$ and ${\sigma }_2^2$ in 𝒞₃. Under Conditions 1–5, ${\widehat{\sigma }}_{\text{MA}}^2\to {\sigma }_0^2$ and β̂_MA → β₀ in probability, and ${(Kn)}^{1/2}({\widehat{\beta }}_{\text{MA}}-{\beta }_0)\to N\{0,\mathrm{\sum }{({\sigma }_0^2,{\sigma }_0^2)}^{-1}\}$ in distribution. Furthermore, var(β̂_ML) ≥ var(β̂_MA) asymptotically, with equality if and only if ${\sigma }_{\mathrm{r}}^2={\sigma }_0^2$ or ṽ₁ =···=ṽ_K.

Theorem 2 provides some intriguing results. First, the maximum likelihood estimator for σ² may not even be consistent; it converges to ${\sigma }_{\mathrm{r}}^2$ as defined in Condition 6. Second, the metaanalysis estimator β̂_MA is at least as efficient as the maximum likelihood estimator β̂_ML. Both results contradict standard likelihood theory, which is applicable only to a large number of small clusters with fixed parameters. In our case, K is relatively small compared to n, and the variance component τ² changes with n.

3. A special case

To gain some insights into the asymptotic properties of the maximum likelihood estimators described in Theorems 1 and 2, we consider the special case of simple linear regression:

$$Y_{ki}={\alpha }_k+(\beta +{\xi }_k)X_{ki}+{\epsilon }_{ki}(i=1,\dots ,n_k;k=1,\dots ,K),$$

where ξ_k ~ N(0, σ²/n), ε_ki ~ N(0, 1), and ξ_k is independent of ε_ki. Define

$$m_{x1k}=\sum _{i=1}^{n_k}{X}_{ki},m_{x2k}=\sum _{i=1}^{n_k}{X}_{ki}^2,m_{yk}=\sum _{i=1}^{n_k}{Y}_{ki},m_{\mathit{yxk}}=\sum _{i=1}^{n_k}{Y}_{ki}{X}_{ki}.$$

The loglikelihood function is, up to some constant,

$$-\frac{1}{2}\sum _{k=1}^{K}log\left(\frac{n}{m_{x2k}}+{\sigma }^2\right)-\frac{1}{2}\sum _{k=1}^K\sum _{i=1}^{n_k}{(Y_{ki}-{\alpha }_k-\beta X_{ki})}^2+\frac{1}{2}\sum _{k=1}^K\frac{1}{n/{\sigma }^2+m_{x2k}}{\left(m_{\mathit{yxk}}-{\alpha }_k{m}_{x1k}-\beta m_{x2k}\right)}^2.$$

After maximization over the α_k and β, we obtain the profile loglikelihood function for σ²,

$$\begin{array}{c}{l}_n({\sigma }^2)=-\frac{1}{2}\sum _{k=1}^{K}log\left(\frac{n}{m_{x2k}}+{\sigma }^2\right)-\frac{1}{2}\frac{n}{{\sigma }^2}\sum _{k=1}^K\frac{{(n_k{m}_{\mathit{yxk}}-m_{yk}{m}_{x1k})}^2/(n_k{m}_{x2k}-m_{x1k}^2)}{(n_{k}n/{\sigma }^2+n_k{m}_{x2k}-m_{x1k}^2)}\\ +\frac{1}{2}\frac{n}{{\sigma }^2}\frac{{\{{\sum }_{k=1}^K(n_k{m}_{\mathit{yxk}}-m_{yk}{m}_{x1k})/(n_k^2/{\sigma }^2+n_k{m}_{x2k}-m_{x1k}^2)\}}^2}{{\sum }_{k=1}^K(n_k{m}_{x2k}-m_{x1k}^2)/(n_{k}n/{\sigma }^2+n_k{m}_{x2k}-m_{x1k}^2)}.\end{array}$$

Note that ${\widehat{\beta }}_k=(n_k{m}_{\mathit{yxk}}-m_{yk}{m}_{x1k})/(n_k{m}_{x2k}-m_{x1k}^2)$ with variance v_k/n_k, where $v_k=n_k^2/(n_k{m}_{x2k}-m_{x1k}^2)$. We can rewrite the profile loglikelihood function as

$$l_n({\sigma }^2)=-\frac{1}{2}\sum _{k=1}^{K}log\left(\frac{n}{m_{x2k}}+{\sigma }^2\right)-\frac{n}{2}\sum _{k=1}^K\frac{{({\widehat{\beta }}_k-{\beta }_0)}^2}{{\stackrel{\sim }{v}}_k+{\sigma }^2}+\frac{n}{2}\frac{{\left\{{\sum }_{k=1}^K({\widehat{\beta }}_k-{\beta }_0)/({\stackrel{\sim }{v}}_k+{\sigma }^2)\right\}}^2}{{\sum }_{k=1}^{K}1/({\stackrel{\sim }{v}}_k+{\sigma }^2)}.$$

If K is fixed while n goes to ∞, then ${\widehat{\beta }}_k={\beta }_0+{({\sigma }_0^2/n+v_k/n_k)}^{1/2}{Z}_k$, where Z₁,…, Z_K are independent standard normal. It follows that

$$l_n({\sigma }^2)=-\frac{1}{2}\sum _{k=1}^{K}log\left(\frac{n}{m_{x2k}}+{\sigma }^2\right)-\frac{1}{2}\sum _{k=1}^K\frac{({\stackrel{\sim }{v}}_k+{\sigma }_0^2)Z_k^2}{{\stackrel{\sim }{v}}_k+{\sigma }^2}+\frac{1}{2}\frac{{\left\{{\sum }_{k=1}^K{({\stackrel{\sim }{v}}_k+{\sigma }_0^2)}^{1/2}{Z}_k/({\stackrel{\sim }{v}}_k+{\sigma }^2)\right\}}^2}{{\sum }_{k=1}^{K}1/({\stackrel{\sim }{v}}_k+{\sigma }^2)},$$

which is the result for ${\widehat{\sigma }}_{\text{ML}}^2$ given in Theorem 1. When K diverges, Theorem 2 implies that the argument maximizing K⁻¹l_n(σ²), i.e., ${\widehat{\sigma }}_{\text{ML}}^2$, converges to ${\sigma }_{\mathrm{r}}^2$, which maximizes the function

$$\underset{K\to \infty }{lim}\frac{1}{K}\left[-\frac{1}{2}\sum _{k=1}^{K}log\left\{\frac{1}{p_{k}E(X_{k1}^2)}+{\sigma }^2\right\}-\frac{1}{2}\sum _{k=1}^K\frac{var{(X_{k1})}^{-1}/p_k+{\sigma }_0^2}{var{(X_{k1})}^{-1}/p_k+{\sigma }^2}\right].$$ (5)

Suppose that p_k =1 for k =1,…, K and that the X_ki all have the same distribution with mean m_x and variance v_x. Then (5) becomes

$$-\frac{1}{2}log\{{(v_x+m_x^2)}^{-1}+{\sigma }^2\}-\frac{1}{2}\frac{v_x^{-1}+{\sigma }_0^2}{v_x^{-1}+{\sigma }^2}.$$

Let ${\sigma }_{\mathrm{m}}^2$ and ${\sigma }_{\mathrm{M}}^2$ denote, respectively, the minimum and maximum of σ² in 𝒞₃. It can be shown that if ${\sigma }_0^2<4m_x^2{v}_x^{-1}{(v_x+m_x^2)}^{-1}-v_x^{-1}$, then ${\sigma }_{\mathrm{r}}^2={\sigma }_{\mathrm{m}}^2$; otherwise, ${\sigma }_{\mathrm{r}}^2$ can be ${\sigma }_{\mathrm{m}}^2,{\sigma }_{\mathrm{M}}^2$ or a value that maximizes the above limit, and the maximizer has to be

$$-\frac{1}{2}(v_x^{-1}-{\sigma }_0^2)+\frac{1}{2}{\left[(v_x^{-1}+{\sigma }_0^2)\{v_x^{-1}+{\sigma }_0^2-4m_x^2{v}_x^{-1}{(v_x+m_x^2)}^{-1}\}\right]}^{1/2},$$

which is ${\sigma }_0^2$ if m_x =0. In particular, if X_ki ~ 2 × Ber(0·5) − 1 + m_x, ${\sigma }_0^2=1,{\sigma }_{\mathrm{m}}^2=0·001$ and ${\sigma }_{\mathrm{M}}^2=2$, then the above derivation implies that ${\sigma }_{\mathrm{r}}^2={\sigma }_{\mathrm{m}}^2=0·001$ under m_x =2^1/2 and ${\sigma }_{\mathrm{r}}^2={\{(1-m_x^2)/(1+m_x^2)\}}^{1/2}=0·6^{1/2}$ under m_x =0·5. In both cases, ${\sigma }_{\mathrm{r}}^2\ne {\sigma }_0^2$; however, the asymptotic variances of β̂_ML and β̂_MA are the same since the ṽ_k (k =1,…, K) are equal.

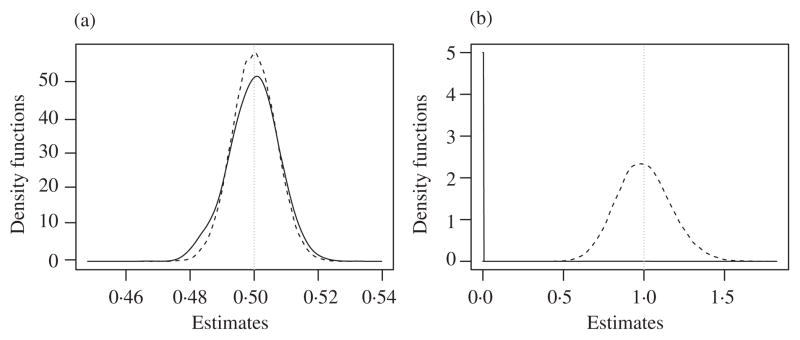
To induce unequal variances, we let n_k =50, 100, 400 and 800 for every four studies, and let X_ki take the value 0 with probability a Un(0·05, 0·5) random variable in each study and the value 2 otherwise. We set α_k =0 (k =1,…, K), β₀ =0·5, ${\sigma }_0^2=1,{\sigma }_{\mathrm{m}}^2=0,{\sigma }_{\mathrm{M}}^2=\infty$ and n =200. Then the asymptotic relative efficiency of β̂_MA to β̂_ML is approximately 1·2 according to Theorem 2. Using Monte Carlo simulation, we found the empirical relative efficiencies to be approximately 1·037, 1·083, 1·125, 1·171 and 1·218 for K =100, 200, 300, 400 and 500, respectively. The distributions of β̂_ML, β̂_MA, ${\widehat{\sigma }}_{\text{ML}}^2$ and ${\widehat{\sigma }}_{\text{MA}}^2$ for K =300 are displayed in Fig. 1. The empirical means of β̂_ML, β̂_MA, ${\widehat{\sigma }}_{\text{ML}}^2$ and ${\widehat{\sigma }}_{\text{MA}}^2$ are 0·50, 0·50, 0·00076 and 1·00, respectively, and the corresponding standard errors are 0·0073, 0·0069, 0·0263 and 0·169.

Fig. 1.

Estimated density functions of: (a) β̂_ML and β̂_MA; (b) ${\widehat{\sigma }}_{\text{ML}}^2$ and ${\widehat{\sigma }}_{\text{MA}}^2$ in simple linear regression. In each panel, the solid curve corresponds to the maximum likelihood estimator and the dashed curve to the meta-analysis estimator.

4. Inference procedures

When K is large, we make inference about β₀ by using the asymptotic normality of β̂_ML and β̂_MA described in Theorem 2. The asymptotic variance of (nK)^1/2(β̂_ML − β₀) can be consistently estimated by $\widehat{\mathrm{\sum }}{({\widehat{\sigma }}_{\text{ML}}^2,{\widehat{\sigma }}_{\text{MA}}^2)}^{-1}\widehat{\mathrm{\sum }}({\widehat{\sigma }}_{\text{ML}}^2,{\widehat{\sigma }}_{\text{ML}}^2)\widehat{\mathrm{\sum }}{({\widehat{\sigma }}_{\text{ML}}^2,{\widehat{\sigma }}_{\text{MA}}^2)}^{-1}$, where

$$\widehat{\mathrm{\sum }}({\sigma }_1^2,{\sigma }_2^2)=\frac{1}{K}\sum _{k=1}^K\frac{p_k(n_k{\widehat{V}}_k+p_k{\widehat{\sigma }}_{\text{MA}}^2)}{(n_k{\widehat{V}}_k+p_k{\sigma }_1^2)(n_k{\widehat{V}}_k+p_k{\sigma }_2^2)}.$$

The asymptotic variance of (nK)^1/2(β̂_MA − β₀) can be consistently estimated by $\widehat{\mathrm{\sum }}{({\widehat{\sigma }}_{\text{MA}}^2,{\widehat{\sigma }}_{\text{MA}}^2)}^{-1}$. The normal approximation based on this variance estimator is equivalent to the normal approximation given in (3), which is the DerSimonian–Laird method.

When K is small, the normal approximations to the distributions of β̂_ML and β̂_MA are no longer accurate, so we appeal to Theorem 1. Without knowledge of ${\sigma }_0^2$, however, it is not possible to estimate the asymptotic distributions given in Theorem 1. To deal with this problem, we propose a double resampling approach to meta-analysis. Theorem 1 shows that, for fixed K, the asymptotic distribution of n^1/2(β̂_MA − β₀) depends on the asymptotic distribution of ${\widehat{\sigma }}_{\text{MA}}^2$. Thus, we first simulate σ² from the distribution of 𝒜_MA, in which ${\mathcal{Z}}_k~N(0,n_k{\widehat{V}}_k+p_k{\widehat{\sigma }}_{\text{MA}}^2)$. For each sampled σ², say ${\sigma }_{\mathrm{s}}^2$, we then generate β as

$${\widehat{\beta }}_{\text{MA}}+n^{-1/2}{\left(\sum _{k=1}^K\frac{p_k}{n_k{\widehat{V}}_k+p_k{\sigma }_{\mathrm{s}}^2}\right)}^{-1}\sum _{k=1}^K\frac{{p_k}^{1/2}{\mathcal{Z}}_k}{n_k{\widehat{V}}_k+p_k{\sigma }_{\mathrm{s}}^2},$$

where ${\mathcal{Z}}_k~N(0,n_k{\widehat{V}}_k+p_k{\sigma }_{\mathrm{s}}^2)$. Operationally, this resampling procedure is equivalent to the following: simulate τ² from equation (2), in which ${\widehat{\beta }}_k~N({\widehat{\beta }}_{\text{MA}},{\widehat{V}}_k+{\widehat{\tau }}_{\text{MA}}^2)$; for each sampled τ², say ${\tau }_{\mathrm{s}}^2$, simulate β from equation (1), in which ${\widehat{\beta }}_k~N({\widehat{\beta }}_{\text{MA}},{\widehat{V}}_k+{\tau }_{\mathrm{s}}^2)$ and ${\widehat{w}}_i={({\widehat{V}}_k+{\tau }_{\mathrm{s}}^2)}^{-1}$. We repeat this process B times to obtain B² values of β. The empirical distribution of those values is used to make inference about β.

5. Simulation studies

We used simulation to evaluate the proposed inference procedures. To facilitate comparisons with existing methods, we adopted the simulation set-up of Brockwell & Gordon (2001), which corresponds to a typical scenario of estimating a log odds ratio. Specifically, we generated the parameter estimates as

$${\widehat{\beta }}_k=\beta +N(0,{\tau }^2+{\widehat{V}}_k)(k=1,\dots ,K),$$

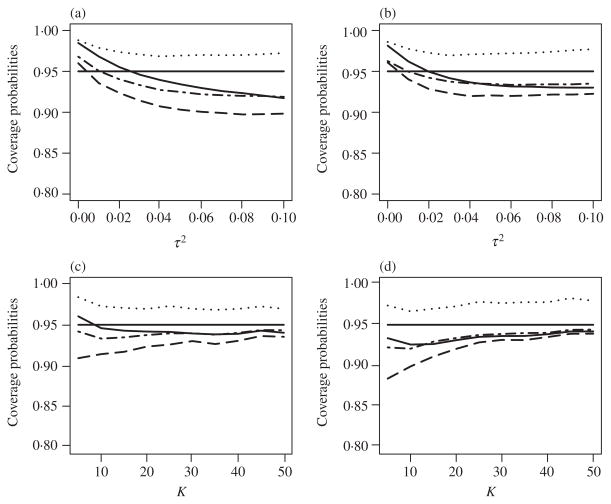
where β = 0·5 and the V̂_k (k = 1, …, K) are realizations from a ${\chi }_1^2$ distribution multiplied by 0·25 and then restricted to lie within the interval (0·009, 0·6). We varied τ² from 0 to 0·1 and K from 5 to 50. The corresponding values of I² (Higgins et al., 2003) are displayed in the Supplementary Material. For each simulated dataset, we obtained the 95% confidence intervals for β using the new resampling approach with B = 1000, the DerSimonian–Laird method, the profile likelihood method of Hardy & Thompson (1996), and the resampling method of Jackson & Bowden (2009). The coverage probabilities based on 10 000 replicates are shown in Fig. 2 and the Supplementary Material; the corresponding mean widths are shown in the Supplementary Material.

Fig. 2.

Empirical coverage probabilities of nominal 95% confidence intervals plotted against τ² for (a) K = 10 and (b) K = 20, and plotted against K for (c) τ² = 0·03 and (d) τ² = 0·07. In each panel, the different curves correspond to the new resampling method (solid), the DerSimonian–Laird method (dashed), the Jackson–Bowden method (dotted), and the Hardy–Thompson method (dot-dash).

The new method has reasonable coverage probabilities, especially when τ² is small or K is large. Its coverage probabilities are always higher than those of the DerSimonian–Laird method. The differences between the two methods become smaller as K increases. Indeed, both methods have correct coverage probabilities when K is 50. The Jackson–Bowden method is very conservative. The new method has better coverage than the profile likelihood method when K is small and τ² is not too small. By comparing our Fig. 1 with Fig. 4 of Brockwell & Gordon (2001), Fig. 1 of Sidik & Jonkman (2002), and Fig. 1 of Henmi & Copas (2010), we see that the new method outperforms the other methods. The widths of the confidence intervals are similar for the new and profile likelihood methods, which are bigger than those of the DerSimonian–Laird method.

6. Real-data example

The erythropoiesis-stimulating agents erythropoietin and darbepoetin are approved to treat chemotherapy-associated anaemia in patients with nonmyeloid malignancies. To evaluate mortality rates associated with the administration of these agents for the treatment of anaemia in cancer patients, Bennett et al. (2008) conducted a systematic review of 52 phase III clinical trials with 13 611 patients that compared the erythropoiesis-stimulating agents with placebo or standard care with respect to mortality. The estimated hazard ratios and 95% confidence intervals are shown in Fig. 2 of Bennett et al. (2008). Using the DerSimonian–Laird method, Bennett et al. (2008) obtained a hazard ratio estimate of 1·10 with a 95% confidence interval of (1·01, 1·20), which raised concerns about the safety of administering these agents to patients with cancer. Our resampling method yields a 95% confidence interval of (1·006, 1·201), which is very close to the DerSimonian–Laird counterpart. The corresponding intervals are (0·973, 1·242) and (0·986, 1·230) for the Jackson–Bowden and Hardy–Thompson methods, respectively.

Bennett et al. (2008) also applied the DerSimonian–Laird method to a subset of six trials consisting of 2089 patients who did not receive chemotherapy or radiation therapy and obtained a hazard ratio estimate of 1·29 with a 95% confidence interval of (1·00, 1·67). Our resampling method yields a 95% confidence interval of (0·851, 1·963), which is considerably wider. In this case, ${\widehat{\tau }}_{\text{MA}}^2=0$, so the DerSimonian–Laird method is actually the same as the fixed-effects method. By contrast, our resampling approach accounts for the variation in the estimation of τ² and thus will not reduce to the fixed-effects method even when the point estimate of τ² is zero. The Jackson–Bowden and Hardy–Thompson methods yield intervals of (0·798, 2·094) and (0·703, 1·792), respectively.

7. Remarks

Effect sizes tend to vary among study populations because of differences in demographic and environmental factors. Furthermore, the treatments or outcomes may not be identical across clinical trials, so the treatment effects may differ even for similar patient populations. In genetic association studies, different definitions and measurements of phenotypes, as well as different collections and manipulations of genotype data, also contribute to between-study heterogeneity. Thus, it is important to allow for heterogeneity through the use of random-effects models, especially when one is interested in parameter estimation rather than hypothesis testing. The confidence intervals under fixed-effects models have extremely poor coverage under even mild heterogeneity (e.g., Brockwell & Gordon, 2001; Henmi & Copas, 2010).

The prevailing approach to random-effects meta-analysis is the DerSimonian–Laird method. Indeed, DerSimonian & Laird’s 1986 paper has been cited more than 10 000 times in the Web of Science database. Our paper provides a rigorous asymptotic theory for the DerSimonian–Laird estimator in cases where the number of studies is fixed or divergent. In addition, we propose a resampling technique that yields more accurate inference than the commonly adopted normal approximation.

In most applications, the number of studies is much smaller than the study sizes, so that Condition 5 holds. It would be interesting to consider situations in which K diverges at the same rate as n or n^r for some r ≥ 1/2. Such an extension would require careful examination of the higher-order expansion in the quadratic approximation to the profile loglikelihood of each study.

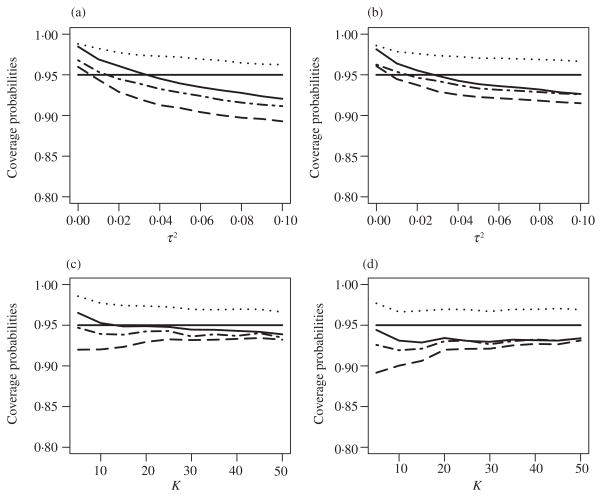
The random-effects model proposed by DerSimonian & Laird (1986) and considered in this paper assumes that the random effect is normally distributed. Additional simulation studies have revealed that our resampling procedure performs satisfactorily under other random-effects distributions; see Fig. 3. Recently, Wang et al. (2010) proposed a nonparametric inference procedure for the percentiles of the random-effects distribution. Their method works well for small K but may not be statistically efficient.

Fig. 3.

Empirical coverage probabilities of nominal 95% confidence intervals when the random effects are from the τ × Ga(1, 1) distribution centred at its mean, plotted against τ² for (a) K = 10 and (b) K = 20, and plotted against K for (c) τ² = 0·03 and (d) τ² = 0·07. In each panel, the different curves correspond to the new resampling method (solid), the DerSimonian–Laird method (dashed), the Jackson–Bowden method (dotted), and the Hardy–Thompson method (dot-dash).

For ethical and logistical reasons, individual participant data are not as easily accessible as summary statistics. Our work shows that it is not necessary to collect individual participant data. In fact, maximum likelihood analysis of individual participant data can give worse results than meta-analysis of summary statistics: the maximum likelihood estimator of σ² may not be consistent as K → ∞, and the maximum likelihood estimator of β is always less efficient than the meta-analysis estimator.

We have assumed that β is a scalar; however, all our results can be extended to multivariate random-effects models (e.g., Jackson et al., 2010; Chen et al., 2012). Specifically, the meta-analysis estimator of β still takes the form of (1), whereas expression (2) is replaced by an estimator of the covariance matrix of the random effects (e.g., Chen et al., 2012). The basic conclusions of Theorems 1 and 2 continue to hold; a key change in the proofs is to approximate the profile likelihood function by a quadratic function based on the multivariate version of the Laplace approximation. Our resampling procedure remains the same except that multivariate versions of the estimators are used.

Our work can be applied to the analysis of large clusters in other contexts. The most rigorous theory for the analysis of large clusters was provided by Bellamy et al. (2005), who quantified the bias of the penalized quasilikelihood estimator of the cluster-level covariate effect in generalized linear mixed models for group-randomized trials under the assumption of a known variance component. Our framework covers this case with an unknown variance component upon setting β_k = X_kγ + ξ_k (k = 1, …, K), where X_k is a group-level treatment indicator. More generally, we may assume that β_k = X_kγ_k (k = 1, …, K), where γ_k = γ + ξ_k and X_k is a cluster-level covariate. Our theory suggests that meta-analysis of summary statistics is preferable to maximum likelihood analysis of individual participant data in such situations.

Appendix. Proofs of Theorems 1 and 2

The proofs of both theorems rely on a local expansion of the loglikelihood function around the maximum likelihood estimators. By Condition 2 and Theorem 2.83 of van der Vaart & Wellner (1996), the class of functions {log f_k (𝒪; β_k, η_k) : (β_k, η_k) ∈ 𝒞₁ × 𝒞_2k } and the corresponding classes of first and second derivatives are uniformly Donsker and Glivenko–Cantelli with respect to any probability measure. We will use this fact repeatedly. Let ℘_nk denote the empirical measure for (𝒪_k1, …, 𝒪_{k, nk})conditional on ξ_k, and let ℘_k be the conditional expectation under the density f_k (· ; β_k0, η_k0), where β_k0 is the true value of β_k. Then the kth summand in (4) can be written as

$$l_k(\beta ,{\sigma }^2,{\eta }_k)=-\frac{1}{2}log\frac{2\pi {\sigma }^2}{n}+log{\int }_{{\xi }_k}exp\left(-n_k\left[{\mathcal{P}}_{nk}\{-log{f}_k(\mathcal{O};\beta +{\xi }_k,{\eta }_k)\}+\frac{n{\xi }_k^2}{2n_k{\sigma }^2}\right]\right)\mathrm{d}{\xi }_k.$$

Consider an open set 𝒩 for (β, η₁, …, η_K, σ²) with |β −β₀| ≤ M(nK)^−1/2, ||η_k − η_k0|| ≤ Mn^−1/2 (k = 1, …, K) for some large M to be chosen later, and σ² ∈ 𝒞₃. We will show that with probability tending to 1, there exists a local maximizer of ${\sum }_{k=1}^K{l}_k(\beta ,{\sigma }^2,{\eta }_k)$ in this neighbourhood. The proof of existence consists of four main steps. First, we obtain a Laplace approximation to the integral in l_k (β, σ², η_k). Second, we show that for each (β, σ²) there exist estimators η̂_k (β, σ²) (k = 1, …, K) which maximize ${\sum }_{k=1}^K{l}_k(\beta ,{\sigma }^2,{\eta }_k)$, and we obtain the profile loglikelihood function ${\sum }_{k=1}^K{\text{pl}}_k(\beta ,{\sigma }^2)$, where pl_k (β, σ²) = l_k{β, σ², η̂_k (β, σ²)}. Third, we show that there exists an estimator β̂_ML(σ²) which maximizes ${\sum }_{k=1}^K{\text{pl}}_k(\beta ,{\sigma }^2)$ for each σ². Finally, we show that there exists an estimator for σ², denoted by ${\widehat{\sigma }}_{\text{ML}}^2$, which maximizes ${\sum }_{k=1}^K{\text{pl}}_k\{{\widehat{\beta }}_{\text{ML}}({\sigma }^2),{\sigma }^2\}$, so we obtain ${\widehat{\beta }}_{\text{ML}}={\widehat{\beta }}_{\text{ML}}({\widehat{\sigma }}_{\text{ML}}^2)$ and ${\widehat{\eta }}_k={\widehat{\eta }}_k({\widehat{\beta }}_{\text{ML}},{\widehat{\sigma }}_{\text{ML}}^2)$. These four steps are detailed in the Supplementary Material.

Proof of Theorem 1

When K is fixed, ${\widehat{\sigma }}_{\text{ML}}^2$ does not converge to any constant. It follows from equation (S5) in the Supplementary Material and the arg max continuous mapping theorem (van der Vaart & Wellner, 1996, Theorem 3.2.2) that

$${\widehat{\sigma }}_{\text{ML}}^2\to argmax\{-\frac{1}{2}\sum _{k=1}^{K}log({\mathcal{I}}_{{\beta }_k}^{-1}+p_k{\sigma }^2)-\frac{1}{2}\sum _{k=1}^K\frac{{\mathcal{Z}}_k^2}{v_k+p_k{\sigma }^2}+\frac{1}{2}{\left(\sum _{k=1}^K\frac{p_k}{v_k+p_k{\sigma }^2}\right)}^{-1}{\left(\sum _{k=1}^K\frac{{p_k}^{1/2}{\mathcal{Z}}_k}{v_k+p_k{\sigma }^2}\right)}^2\}$$

in distribution. It then follows from equation (S4) in the Supplementary Material that

$$n^{1/2}({\widehat{\beta }}_{\text{ML}}-{\beta }_0)\to {\left(\sum _{k=1}^K\frac{p_k}{v_k+p_k{\mathcal{A}}_{\text{ML}}}\right)}^{-1}\sum _{k=1}^K\frac{{p_k}^{1/2}{\mathcal{Z}}_k}{v_k+p_k{\mathcal{A}}_{\text{ML}}}$$

in distribution. Likewise, the asymptotic distribution for ( ${\widehat{\sigma }}_{\text{MA}}^2$, β̂_MA) can be obtained from the arg max continuous mapping theorem.

Proof of Theorem 2

We examine the random process Q_n(σ²) given in (S5) of the Supplementary Material. Let

$${\mathcal{Z}}_{nk}({\sigma }^2)=\frac{n_k\{{\xi }_{k0}+v_k({\mathcal{P}}_{nk}-{\mathcal{P}}_k)(S_k^{\ast })\}}{n^{1/2}(v_k+p_k{\sigma }^2)}.$$

Then

$$Q_n({\sigma }^2)=-\frac{1}{2}\sum _{k=1}^{K}log(p_k{\sigma }^2{\mathcal{I}}_{{\beta }_k}+1)-\frac{1}{2}\sum _{k=1}^K\frac{n}{n_k}{\mathcal{Z}}_{nk}^2({\sigma }^2)(v_k+p_k{\sigma }^2)+\frac{n}{2}{\left(\sum _{k=1}^K\frac{n_k}{v_k+p_k{\sigma }^2}\right)}^{-1}{\left\{\sum _{k=1}^K{\mathcal{Z}}_{nk}({\sigma }^2)\right\}}^2.$$

Consider the random process $K^{-1/2}{\sum }_{k=1}^K{\mathcal{Z}}_{nk}({\sigma }^2)$ ndexed by σ². We verify the conditions in Theorem 2.11.1 of van der Vaart & Wellner (1996). First, we verify the Lindeberg condition,

$$\sum _{k=1}^K{K}^{-1}E\left[\underset{{\sigma }^2\in ({\sigma }_{\mathrm{m}}^2,{\sigma }_{\mathrm{M}}^2)}{max}{\mathcal{Z}}_{nk}^2({\sigma }^2)I\left\{K^{-1/2}\underset{{\sigma }^2\in ({\sigma }_{\mathrm{m}}^2,{\sigma }_{\mathrm{M}}^2)}{max}\mid {\mathcal{Z}}_{nk}({\sigma }^2)\mid >\delta \right\}\right]\to 0,\delta >0.$$

By the Markov inequality, the left-hand side is bounded by ${\sum }_{k}E\{{\mathcal{Z}}_{nk}^4({\sigma }_{\mathrm{m}}^2)\}/{(\sigma K)}^2$. In addition,

$$\begin{array}{ll}\hfill E({\xi }_{k0}^4)& =2{\sigma }^4/n^2,\hfill \\ \hfill E\{{\mid ({\mathcal{P}}_{nk}-{\mathcal{P}}_k)(S_k^{\ast })\mid }^4\}& =n_k^{-4}\{E({\mid S_k^{\ast }\mid }^4)n_k+n_k(n_k-1)v_k\}\{1+O(n^{-1})\},\hfill \\ \hfill E\left[{\xi }_{k0}^2{\{({\mathcal{P}}_{nk}-{\mathcal{P}}_k)(S_k^{\ast })\}}^2\right]& =E\left({\xi }_{k0}^{2}E\left[{\{({\mathcal{P}}_{nk}-{\mathcal{P}}_k)(S_k^{\ast })\}}^2\mid {\xi }_{k0}\right]\right)\hfill \\ \hfill & =E\{{\xi }_{k0}^{2}var(S_k^{\ast }\mid {\xi }_{k0})/n_k\}\hfill \\ \hfill & =v_k{\sigma }^2{(n{n}_k)}^{-1}\{1+O(n^{-1})\},\hfill \\ \hfill E\{{\xi }_{k0}^3({\mathcal{P}}_{nk}-{\mathcal{P}}_k)(S_k^{\ast })\}& =E\left[{\xi }_{k0}^{3}E\{({\mathcal{P}}_{nk}-{\mathcal{P}}_k)(S_k^{\ast })\mid {\xi }_{k0}\}\right]=0,\hfill \\ \hfill \left|E\left[{\xi }_{k0}{\{({\mathcal{P}}_{nk}-{\mathcal{P}}_k)(S_k^{\ast })\}}^3\right]\right|& =\left|E\left({\xi }_{k0}E\left[{\{({\mathcal{P}}_{nk}-{\mathcal{P}}_k)(S_k^{\ast })\}}^3|{\xi }_{k0}\right]\right)\right|\hfill \\ \hfill & \le E\{\mid {\xi }_{k0}\mid n_k^{-2}E({\mid S_k^{\ast }\mid }^3\mid {\xi }_{k0})\}\le c_3{n}^{-5/2}\hfill \end{array}$$

for some constant c₃. Thus, ${\sum }_{k}E\{{\mathcal{Z}}_{nk}^4({\sigma }_{\mathrm{m}}^2)\}/{(\delta K)}^2\le c_4{K}^{-1}\to 0$, where c₄ is a constant. For the second condition in Theorem 2.11.1 of van der Vaart & Wellner (1996), we note that, by the mean value theorem,

$$K^{-1}\sum _{k=1}^{K}E\left[{\{{\mathcal{Z}}_{nk}({\sigma }_1^2)-{\mathcal{Z}}_{nk}({\sigma }_2^2)\}}^2\right]\le {\mid {\sigma }_1^2-{\sigma }_2^2\mid }^2\sum _{k=1}^{K}E\left[\frac{p_k^2{n}_k{\{{\xi }_{k0}+v_k({\mathcal{P}}_{nk}-\mathcal{P})(S_k^{\ast })\}}^2}{{(v_k+p_k{\sigma }_{\mathrm{m}}^2)}^2}\right]\to 0$$

as $\mid {\sigma }_1^2-{\sigma }_2^2\mid \to 0$. Since 𝒞₃ is one-dimensional, it is easy to see that the random entropy condition in Theorem 2.11.1 holds. In light of Condition 6, Theorem 2.11.1 implies that $K^{-1/2}{\sum }_{k=1}^K{\mathcal{Z}}_{nk}({\sigma }^2)$ converges weakly to a zero-mean Gaussian process with covariance function $\mathrm{\sum }({\sigma }_1^2,{\sigma }_2^2)$ between ${\sigma }_1^2$ and ${\sigma }_2^2$. Thus, the third term of Q_n(σ²) is o_p(K) uniformly in σ². Similarly, for the second term of Q_n(σ²),

$$-\frac{1}{2K}\sum _{k=1}^K\frac{n}{n_k}{\mathcal{Z}}_{nk}^2({\sigma }^2)(v_k+p_k{\sigma }^2)\to -\frac{1}{2}\underset{K\to \infty }{lim}\frac{1}{K}\sum _{k=1}^K\frac{v_k+p_k{\sigma }_0^2}{v_k+p_k{\sigma }^2}$$

in probability. Combining the above results, we conclude that, in probability,

$$\frac{1}{K}\left\{Q_n({\sigma }^2)+\frac{1}{2}\sum _{k=1}^{K}log({\mathcal{I}}_{{\beta }_k})\right\}\to \frac{1}{2}g({\sigma }^2),$$

which has a unique maximum at ${\sigma }_{\mathrm{r}}^2$ according to Condition 6.

We are ready to show that ${\widehat{\sigma }}_{\text{ML}}^2\to {\sigma }_{\mathrm{r}}^2$ in probability. Since ${\widehat{\sigma }}_{\text{ML}}^2$ is bounded, we can always choose a further subsequence from any subsequence, still denoted by ${\widehat{\sigma }}_{\text{ML}}^2$, such that ${\widehat{\sigma }}_{\text{ML}}^2\to {\stackrel{\sim }{\sigma }}^2$. Because ${\sum }_{k=1}^K{\text{pl}}_k\{{\widehat{\beta }}_{\text{ML}}({\widehat{\sigma }}_{\text{ML}}^2),{\widehat{\sigma }}_{\text{ML}}^2\}\ge {\sum }_{k=1}^K{\text{pl}}_k\{{\widehat{\beta }}_{\text{ML}}({\sigma }_{\mathrm{r}}^2),{\sigma }_{\mathrm{r}}^2\}$, it follows from equation (S5) in the Supplementary Material that

$$\frac{1}{K}\left\{Q_n({\widehat{\sigma }}_{\text{ML}}^2)+\frac{1}{2}\sum _{k=1}^{K}log({\mathcal{I}}_{{\beta }_k})\right\}\ge \frac{1}{K}\left\{Q_n({\sigma }_{\mathrm{r}}^2)+\frac{1}{K}\sum _{k=1}^{K}log({\mathcal{I}}_{{\beta }_k})\right\}-O_{\mathrm{p}}(1)n^{-1/2}.$$

Taking the limit on both sides yields $g({\stackrel{\sim }{\sigma }}^2)\ge g({\sigma }_{\mathrm{r}}^2)$. Therefore ${\stackrel{\sim }{\sigma }}^2={\sigma }_{\mathrm{r}}^2$.

In light of (S4) in the Supplementary Material, for the local maximum likelihood estimator ${\widehat{\beta }}_{\text{ML}}={\widehat{\beta }}_{\text{ML}}({\widehat{\sigma }}_{\text{ML}}^2)$, we have

$$\begin{array}{l}{(Kn)}^{1/2}({\widehat{\beta }}_{\text{ML}}-{\beta }_0)={(Kn)}^{1/2}{\left(\sum _{k=1}^K\frac{n_k}{v_k+p_k{\sigma }^2}\right)}^{-1}\left[\sum _{k=1}^K\frac{n_k}{v_k+p_k{\sigma }^2}\{{\xi }_{k0}+v_k({\mathcal{P}}_{nk}-{\mathcal{P}}_k)(S_k^{\ast })\}\right]+o_{\mathrm{p}}(1)\\ ={\left(\frac{1}{nK}\sum _{k=1}^K\frac{n_k}{v_k+p_k{\widehat{\sigma }}_{\text{ML}}^2}\right)}^{-1}\left\{\sum _{k=1}^K{K}^{-1/2}{\mathcal{Z}}_{nk}({\widehat{\sigma }}_{\text{ML}}^2)\right\}+o_{\mathrm{p}}(1).\end{array}$$

By Theorem 2.11.1 of van der Vaart & Wellner (1996) and the convergence of ${\widehat{\sigma }}_{\text{ML}}^2$ to ${\sigma }_{\mathrm{r}}^2$,

$${(Kn)}^{1/2}({\widehat{\beta }}_{\text{ML}}-{\beta }_0)\to N\{0,\mathrm{\sum }{({\sigma }_{\mathrm{r}}^2,{\sigma }_0^2)}^{-1}\mathrm{\sum }({\sigma }_{\mathrm{r}}^2,{\sigma }_{\mathrm{r}}^2)\mathrm{\sum }{({\sigma }_{\mathrm{r}}^2,{\sigma }_0^2)}^{-1}\}$$

in distribution.

We now derive the asymptotic distribution of β̂_MA. Because ${\widehat{\sigma }}_{\text{MA}}^2\to {\sigma }_0^2$ in probability as K → ∞, we have sup_k |ŵ_k/ n −w_k | = o_p(1), where $w_k=p_k{(v_k+p_k{\sigma }_0^2)}^{-1}$. Thus,

$$\begin{array}{l}{(Kn)}^{1/2}({\widehat{\beta }}_{\text{MA}}-{\beta }_0)=\frac{{\sum }_{k=1}^K{K}^{1/2}({\widehat{w}}_k/n)n^{1/2}({\widehat{\beta }}_k-{\beta }_0)}{{\sum }_{k=1}^K({\widehat{w}}_k/n)}\\ =\frac{{\sum }_{k=1}^K{K}^{1/2}{w}_k{n}^{1/2}({\widehat{\beta }}_k-{\beta }_0)}{{\sum }_{k=1}^K{w}_k}\{1+o_{\mathrm{p}}(1)\}.\end{array}$$

Since max_k w_k /Σ_k w_k → 0 by Condition 4, the Lindeberg–Feller central limit theorem yields that, in distribution,

$$\frac{{\sum }_{k=1}^K{K}^{1/2}{w}_k{n}^{1/2}({\widehat{\beta }}_k-{\beta }_0)}{{\sum }_{k=1}^K{w}_k}\to N\{0,\mathrm{\sum }{({\sigma }_0^2,{\sigma }_0^2)}^{-1}\}.$$

By the Cauchy–Schwarz inequality, $\mathrm{\sum }{({\sigma }_{\mathrm{r}}^2,{\sigma }_0^2)}^{-1}\mathrm{\sum }({\sigma }_{\mathrm{r}}^2,{\sigma }_{\mathrm{r}}^2)\mathrm{\sum }{({\sigma }_{\mathrm{r}}^2,{\sigma }_0^2)}^{-1}\ge \mathrm{\sum }{({\sigma }_0^2,{\sigma }_0^2)}^{-1}$, and equality holds if and only if ( ${\stackrel{\sim }{v}}_k+{\sigma }_{\mathrm{r}}^2$) is proportional to ( ${\stackrel{\sim }{v}}_k+{\sigma }_0^2$) for k = 1, …, K. This condition is met if ${\sigma }_{\mathrm{r}}^2={\sigma }_0^2$ or the ṽ_k (k = 1, …, K) are all equal. The lower bound is the asymptotic variance of β̂_MA. Thus β̂_MA has a smaller asymptotic variance than β_ML, unless ${\sigma }_{\mathrm{r}}^2={\sigma }_0^2$ or the ṽ_k are all the same.