Using Decision Lists to Construct Interpretable and Parsimonious Treatment Regimes

Summary

A treatment regime formalizes personalized medicine as a function from individual patient characteristics to a recommended treatment. A high-quality treatment regime can improve patient outcomes while reducing cost, resource consumption, and treatment burden. Thus, there is tremendous interest in estimating treatment regimes from observational and randomized studies. However, the development of treatment regimes for application in clinical practice requires the long-term, joint effort of statisticians and clinical scientists. In this collaborative process, the statistician must integrate clinical science into the statistical models underlying a treatment regime and the clinician must scrutinize the estimated treatment regime for scientific validity. To facilitate meaningful information exchange, it is important that estimated treatment regimes be interpretable in a subject-matter context. We propose a simple, yet flexible class of treatment regimes whose members are representable as a short list of if-then statements. Regimes in this class are immediately interpretable and are therefore an appealing choice for broad application in practice. We derive a robust estimator of the optimal regime within this class and demonstrate its finite sample performance using simulation experiments. The proposed method is illustrated with data from two clinical trials.

1. Introduction

Treatment regimes formalize clinical decision making as a function from patient information to a recommended treatment. Proponents of personalized medicine envisage the widespread clinical use of evidence-based, i.e., data-driven, treatment regimes. The potential benefits of applying treatment regimes are now widely recognized. By individualizing treatment, a treatment regime may improve patient outcomes while reducing cost and the consumption of resources. This is important in an era of growing medical costs and an aging global population. However, the widespread integration of data-driven treatment regimes into clinical practice is, and should be, an incremental process wherein: (i) data are used to generate hypotheses about optimal treatment regimes; (ii) the generated hypotheses are scrutinized by clinical collaborators for scientific validity; (iii) new data are collected for validation and new hypothesis generation, and so on. Within this process, it is crucial that estimated treatment regimes be interpretable to clinicians. Nevertheless, optimality, not interpretability, has been the focal point in the statistical literature on treatment regimes.

A treatment regime said to be optimal if it maximizes the expectation of a pre-specified clinical outcome when used to assign treatment to a population of interest. There is a large literature on estimating optimal treatment regimes using data from observational or randomized studies. Broadly, these estimators can be categorized as regression-based or classification-based estimators. Regression-based estimators model features of the conditional distribution of the outcome given treatment and patient covariates. Examples include estimators of the regression of an outcome on covariates, treatment, and their interactions (e.g., Su et al., 2009; Qian and Murphy, 2011; Tian et al., 2014), and estimators of point treatment effects given covariates (e.g., Robins, 1994; Vansteelandt et al., 2014). Regression-based methods rely on correct specification of some or all of the modeled portions of the conditional distribution of the outcome. Thus, a goal of many regression-based estimators is to ensure correct model specification under a large class of generative models (Zhao et al., 2009; Qian and Murphy, 2011; Moodie et al., 2013; Laber et al., 2014; Taylor et al., 2014). However, as flexibility is introduced into the model, interpretability tends to diminish, and in the extreme case the estimated treatment regime becomes an unintelligible black box.

Classification-based estimators, also known as policy-search or value-search estimators, estimate the marginal mean of the outcome for every treatment regime within a pre-specified class and then take the maximizer as the estimated optimal regime. Examples include marginal structural mean models (Robins et al., 2008; Orellana et al., 2010); robust marginal mean models (Zhang et al., 2012); and outcome weighted learning (Zhang et al., 2012; Zhao et al., 2012, 2015). Classification-based estimators often rely on fewer assumptions about the conditional distribution of the outcome given treatment and patient information and thus may be more robust to model misspecification than regression-based estimators (Zhang et al., 2012,?). Furthermore, because classification-based methods estimate an optimal regime within a pre-specified class, it is straightforward to impose structure on the estimated regime, e.g., interpretability, by restricting this class. We use robust marginal mean models with a highly interpretable yet flexible class of regimes to estimate a high-quality regime that can be immediately understood by clinical and intervention scientists.

To obtain an interpretable and parsimonious treatment regime, we use the concept of decision list, which was developed in the computer science literature for representing flexible but interpretable classifiers (Rivest, 1987; Clark and Niblett, 1989; Marchand and Sokolova, 2005; Letham et al., 2012; Wang and Rudin, 2014); see Freitas (2014) for a recent position paper on the importance of interpretability in predictive modeling and additional references on interpretable classifiers. As a treatment regime, a decision list comprises a sequence of “if-then” clauses that map patient covariates to a recommended treatment. Figure 1 shows a decision list for patients with chronic depression (see Section 4.2). This decision list recommends treatments as follows: if a patient presents with somatic anxiety score above 1 and retardation score above 2, the list recommends nefazodone; otherwise, if the patient has Hamilton anxiety score above 23 and sleep disturbance score above 2, the list recommends psychotherapy; and otherwise the list recommends nefazodone + psychotherapy (combination). Thus, a treatment regime represented as a decision list can be conveyed as either a diagram or text and is easily understood, in either form, by domain experts. Indeed, decision lists have frequently been used to display estimated treatment regimes (Shortreed et al., 2011; Moodie et al., 2012; Shortreed et al., 2014; Laber and Zhao, 2015) or to describe theory-based, i.e., not data-driven, treatment regimes (Shiffman, 1997; Marlowe et al., 2012).

Figure 1.

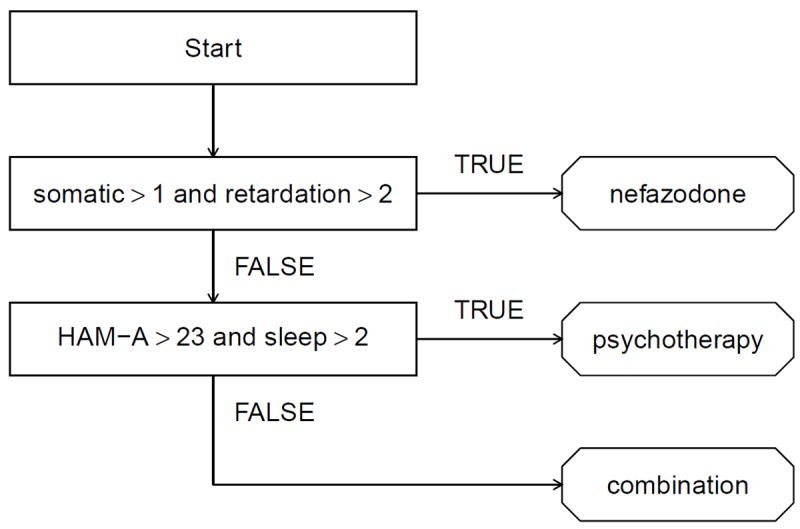
Estimated decision list for treating patients with chronic depression.

Another important attribute of a decision list is that it “short circuits” measurement of patient covariates; e.g., in Figure 1, the Hamilton anxiety score and sleep disturbance score do not need to be collected for patients with somatic anxiety score above 1 and retardation score above 2. This is important in settings where patient covariates are expensive or burdensome to collect (e.g., Gail et al., 1999; Gail, 2009; Baker et al., 2009; Huang et al., 2015). We provide an estimator of the treatment regime that minimizes an expected cost among all regimes that optimize the marginal mean outcome.

2. Methodology

2.1 Framework

We assume that the observed data are ${\{(X_i,A_i,Y_i)\}}_{i=1}^n$, which comprise n independent identically distributed observations, one for each subject in an experimental or observational study. Let (X, A, Y) denote a generic observation. Then X ∈ ℝ^p are baseline patient covariates; A ∈ A = {1, …, m} is the treatment assigned; and Y ∈ ℝ is the outcome, coded so that higher values are better. A treatment regime, π, is a function from ℝ^p into A, so that under π a patient presenting with X = x is recommended treatment π(x).

The value of a regime π is the expected outcome if all patients in the population of interest are assigned treatment according to π. To define the value, we use the set of potential outcomes {Y*(a)}_a∈A, where Y*(a) is the outcome that would be observed if a subject were assigned treatment a. Define Y*(π) =Σ_a∈A Y*(a)I {π(X) = a} to be the potential outcome under regime π, and R(π) = E{Y*(π)} to be the value of regime π. An optimal regime, say π^opt, satisfies R(π^opt) ≥ R(π) for all π. Let ∏ denote a class of regimes of interest. Classification-based estimation methods form an estimator of R(π), say R̂(π), and then estimate π^opt using π̂ = arg max_π∈∏ R̂(π). The success of this approach requires: (i) a high-quality estimator of R(π); (ii) a sufficiently rich class ∏; and (iii) an efficient algorithm for maximizing R̂(π) over ∏. We discuss these topics in the next three sections.

2.2 Estimation of R(π)

We make several standard assumptions: (A1) consistency: Y = Y*(A); (A2) no unmeasured confounders: {Y*(a)}_a∈A are conditionally independent of A given X; and (A3) positivity: there exists δ > 0 so that ℙ(A = a∣X) ≥ δ for all a ∈ A. Assumption (A2) is automatically satisfied in a randomized study but is untestable in observational studies (Robins et al., 2000). Under (A1)–(A3), it can be shown (Tsiatis, 2006) that

$$R(\pi )=\mathrm{E}\left(\sum _{a=1}^m\left[\frac{I(A=a)}{\omega \left(X,a\right)}\{Y-\mu (X,a)\}+\mu (X,a)\right]I\{\pi (X)=a\}\right),$$ (1)

where ω(x, a) = ℙ(A = a∣X = x) and μ(x, a) = E(Y∣X = x, A = a). Alternate expressions for R(π) exist (Zhang et al., 2012); however, estimators based on (1) possess a number of desirable properties (see below).

To construct an estimator of R(π) from (1) we replace ω(x, a) and μ(x, a) with estimated working models and replace the expectation with its sample analog. If treatment is randomly assigned independently of subject covariates, then ω(x, a) can be estimated by $n^{-1}{\sum }_{i=1}^{n}I(A_i=a)$. Otherwise, we posit a multinomial logistic regression model of the form $\omega (x,a)=\exp (u^{\mathrm{T}}{\gamma }_a)/\{1+{\sum }_{j=1}^{m-1}\exp (u^{\mathrm{T}}{\gamma }_j)\}$, a = 1, …, m – 1, where u = u(x) is a known feature vector, and γ₁, …, γ_m–1 are unknown parameters. Let ω̂(x, a) denote the maximum likelihood estimator of ω(x, a), where γ₁, …, γ_m–1 are replaced by maximum likelihood estimators γ̂₁, …, γ̂_m–1. We posit a generalized linear model for μ(x, a), g{μ(x, a)} = z^Tβ_a, where g(·) is a known link function, z = z(x) is a known feature vector constructed from x, and β₁, …, β_m are unknown parameters. We use μ̂(x, a) = g⁻¹ (z^Tβ̂_a) as our estimator of μ(x, a), where β̂₁, …, β̂_m are the maximum likelihood estimators of β₁, …, β_m.

Given estimators ω̂(x, a) and μ̂(x, a), an estimator of R(π) based on (1) is

$$\widehat{R}(\pi )=\frac{1}{n}\sum _{i=1}^n\sum _{a=1}^m\left[\frac{I(A_i=a)}{\widehat{\omega }(X_i,a)}\{Y_i-\widehat{\mu }(X_i,a)\}+\widehat{\mu }(X_i,a)\right]I\{\pi (X_i)=a\}.$$ (2)

For any fixed π, R̂(π) is doubly robust in the sense that it is a consistent estimator of R(π) if either the model for ω(x, a) or μ(x, a) is correctly specified (Tsiatis, 2006; Zhang et al., 2012). As a direct consequence, R̂(π) is guaranteed to be consistent in a randomized study, as ω(x, a) is known by design. Furthermore, if both models are correctly specified, then R̂(π) is semiparametric efficient; i.e., it has the smallest asymptotic variance among the class of regular, asymptotically linear estimators (Tsiatis, 2006).

2.3 Regimes representable as decision lists

Gail and Simon (1985) present an early example of a treatment regime using data from the NSABP clinical trial. The treatment regime they propose is

$$\begin{array}{l}\mathbf{If}\mathrm{age}\le 50\mathrm{and\; PR}\le 10\mathbf{then}\mathrm{chemotherapy\; alone};\\ \mathbf{else}\mathrm{chemotherapy\; with\; tamoxifen},\end{array}$$

where age (in years) denotes the age of the patient and PR denotes the progesterone receptor level (in fmol). The simple if-then structure of the foregoing treatment regime makes it immediately interpretable.

Formally, a treatment regime, π, that is representable as a decision list of length L is described by {(c₁, a₁), …, (c_L, a_L), a₀}, where c_j is a logical condition that is true or false for each x ∈ ℝ^p, and a_j ∈ A is a recommended treatment, j = 0, …, L. As a special case, L = 0 is allowed. The corresponding treatment regime {a₀} gives the same treatment a₀ to every patient. Hereafter, let ∏ denote the set of regimes that are representable as a decision list. Clearly, the regime proposed by Gail and Simon (1985) is a member of ∏.

Define T(c_j) = {x ∈ ℝ^p : c_j is true for x}, j = 1, …, L; R₁ = T (c₁), R_j = {∩_ℓ<jT (c_ℓ)^c}∩ T(c_j), j = 2, …, L; and $R_0={\cap }_{\ell =1}^{L}T{(c_{\ell })}^c$, where S^c is the complement of the set S. Then a regime π ∈ ∏ can be written as $\pi (x)={\sum }_{\ell =0}^L{a}_{\ell }I(x\in R_{\ell })$, which has structure

$$\begin{array}{l}\mathbf{If}{c}_1\mathbf{then}{a}_1;\\ \mathbf{else\; if}{c}_2\mathbf{then}{a}_2;\\ \cdots \\ \mathbf{else\; if}{c}_L\mathbf{then}{a}_L;\\ \mathbf{else}{a}_0.\end{array}$$ (3)

In principle, the conditions c_j, and hence the sets T(c_j), can be arbitrary. To ensure parsimony and interpretability, we restrict c_j so that T(c_j) is one of the following sets:

$$\begin{array}{llll}[1]:& \{x\in {ℝ}^p:x_{j_1}\le {\tau }_1\},& \hfill [6]:& \{x\in {ℝ}^p:x_{j_1}\le {\tau }_1\mathrm{or}{x}_{j_2}\le {\tau }_2\},\\ [2]:& \{x\in {ℝ}^p:x_{j_1}\le {\tau }_1\mathrm{and}{x}_{j_2}\le {\tau }_2\},& \hfill [7]:& \{x\in {ℝ}^p:x_{j_1}\le {\tau }_1\mathrm{or}{x}_{j_2}>{\tau }_2\},\\ [3]:& \{x\in {ℝ}^p:x_{j_1}\le {\tau }_1\mathrm{and}{x}_{j_2}>{\tau }_2\},& \hfill [8]:& \{x\in {ℝ}^p:x_{j_1}>{\tau }_1\mathrm{or}{x}_{j_2}\le {\tau }_2\},\\ [4]:& \{x\in {ℝ}^p:x_{j_1}>{\tau }_1\mathrm{and}{x}_{j_2}\le {\tau }_2\},& \hfill [9]:& \{x\in {ℝ}^p:x_{j_1}>{\tau }_1\mathrm{or}{x}_{j_2}>{\tau }_2\},\\ [5]:& \{x\in {ℝ}^p:x_{j_1}>{\tau }_1\mathrm{and}{x}_{j_2}>{\tau }_2\},& \hfill [10]:& \{x\in {ℝ}^p:x_{j_1}>{\tau }_1\},\end{array}$$ (4)

where j₁ < j₂ ∈ {1, …, p} are indices and τ₁, τ₂ ∈ ℝ are thresholds. We believe that the conditions that dictate the sets in (4), e.g., x_j1 ≤ τ₁ and x_j2 ≤ τ₂, are more easily interpreted than those dictated by linear thresholds, e.g., α₁x_j1 + α₂x_j2 ≤ α₃, as the former are more commonly seen in clinical practice.

In the proposed setup, at most two variables are involved in any single condition. Having a small number of variables in each clause yields two important properties. First, the resulting treatment regime is parsimonious, and the most important variables for treatment selection are automatically identified. Second, application of the treatment regime allows for patient measurements to be taken in sequence so that the treatment recommendation can be short-circuited. For example, consider a decision list described by {(c₁, a₁), (c₂, a₂), a₀}. It is necessary to measure the variables that compose c₁ on all subjects, but the variables composing c₂ need only be measured for those who do not satisfy c₁.

2.3.1 Uniqueness and minimal cost of a decision list

For a decision list π described by {(c₁, a₁), …, (c_L, a_L), a₀}, let N_ℓ denote the cost of measuring the covariates required to check logical conditions c₁, …, c_ℓ. Hereafter, for simplicity, we assume that this cost is equal to the number of covariates needed to check c₁, …, c_ℓ, but it can be extended easily to a more complex cost function reflecting risk, burden, and availability. The expected cost of applying treatment rule $\pi (x)={\sum }_{\ell =0}^L{a}_{\ell }I(x\in R_{\ell })$ is $N(\pi )={\sum }_{\ell =1}^L{N}_{\ell }\mathbb{P}(X\in R_{\ell })+N_L\mathbb{P}(X\in R_0)$, which is smaller than $N_L=N_L{\sum }_{\ell =0}^L\mathbb{P}(X\in R_{\ell })$, the cost of measuring all covariates in the treatment regime. This observation reflects the benefit of the short-circuit property.

A decision list π described by {(c₁, a₁), …, (c_L, a_L), a₀} need not be unique in that there may exist an alternative decision list π′ described by $\{(c_1^{\prime },a_1^{\prime }),\dots ,(c_{L^{\prime }}^{\prime },a_{L^{\prime }}^{\prime }),a_0^{\prime }\}$ such that π(x) = π^′ (x) for all x but L ≠ L′ or L = L′ but $c_j\ne c_j^{\prime }$ or $a_j\ne a_j^{\prime }$ for some j ∈ {1, …, L}. This is potentially important because the expected costs N(π) and N(π′) might differ substantially. Figure 2 shows two representations, π and π′, of the same decision list both with L = L′ = 2 but with different clauses. The cost of the decision list in the middle panel, π, is N(π) = N₁ℙ(X₁ > τ₁) + N₂ℙ(X₁ ≤ τ₁), whereas the cost of the decision list in the right panel, π′ is N(π′) = N₂ ≥ N (π) with strict inequality if N₂ > N₁ and ℙ(X₁ > τ₁) > 0. Thus, π is preferred to π′ in settings where X₂ is a biomarker that is expensive, burdenome, or potentially harmful to collect (e.g., Huang et al., 2015, and references therein).

Figure 2.

Left: diagram of a decision list dictated by regions R₁ = {x ∈ ℝ² : x₁ > τ₁}, R₂ = {x ∈ ℝ² : x₁ ≤ τ₁, x₂ > τ₂}, and R₀ = {x ∈ ℝ² : x₁ ≤ τ₁, x₂ ≤ τ₂}, and treatment recommendations a₁, a₂, and a₀. Middle: representation of the decision list that requires only x₁ in the first clause. Right: alternative representation of the same decision list that requires both x₁ and x₂ in the first clause.

Therefore, among all decision lists achieving the value R(π^opt), where π^opt is an optimal regime as defined previously, we seek to estimate the one that minimizes the cost. Defining L_r to be the level set {π ∈ Π : R(π) = r}, then the goal is to estimate a regime in the set arg min_{π∈L{R(π^opt)}} N (π). Define L̂(r) = {π ∈ Π : R̂(π) = r}. Let π̃ be an estimator of an element in the set arg max_π∈Π R̂ (π). In the following we provide an algorithm that ensures our estimator, π̂, belongs to the set arg min_{π∈L̂ {R̂ (π̂)}} N̂(π), where N̂(π) is defined by replacing the probabilities in N(π) with sample proportions.

2.4 Computation

Estimation proceeds in two steps: (i) approximate an element π̃ ∈ arg max_π∈Π R̂(π), where R̂(π) is constructed using (2); and (ii) find an element π̂ ∈ arg min_{π∈L̂ {R̂ (π̃) }} N̂(π).

2.4.1 Approximation of arg max_π∈Π R̂(π)

Maximizing R̂(π) over π ∈ Π is computationally burdensome in problems with more than a handful of covariates because of the indicator functions in (2) and the discreteness of the decision list. However, the tree structure of decision lists suggests a greedy algorithm in the spirit of classification and regression trees (CART, Breiman et al., 1984). Assume that for the jth covariate, there is a candidate set of finitely many possible cutoff values χ_j. These cutoffs might be dictated by clinical guidelines, e.g., if the covariate is a comorbid condition then the thresholds might reflect low, moderate, and high levels of impairment; alternatively, these cutoffs could be chosen to equal empirical or theoretical percentiles of that covariate. There is no restriction imposed on these cutoffs. Let C denote the set of all conditions that induce regions of the form in (4) with the cutoffs τ_jk ∈ χ_jk for k = 1, 2, j_k ∈ {1, …, p}.

Before giving the details of the algorithm, we provide a conceptual overview. The algorithm first uses exhaustive search to find a decision list with exactly one clause, of the form π = {(c₁, a₁), $a_1^{\prime }$}, which maximizes R̂(π). Let {(c̃₁, ã₁), ${\stackrel{\sim }{a}}_1^{\prime }$} denote this decision list. The algorithm then uses exhaustive search to find the decision list that maximizes R̂(π) over decision lists with exactly two clauses, the first of which must be either (c̃₁, ã₁) or ( ${\stackrel{\sim }{c}}_1^{\prime }$, ${\stackrel{\sim }{a}}_1^{\prime }$), where ${\stackrel{\sim }{c}}_1^{\prime }$ is the negation of c̃₁ such that $T({\stackrel{\sim }{c}}_1^{\prime })=T{({\stackrel{\sim }{c}}_1)}^c$; e.g., if c̃₁ has the form x_j1 ≤ τ₁ and x_j2 ≤ τ₂, then ${\stackrel{\sim }{c}}_1^{\prime }$ would be x_j1 > τ₁ or x_j2 > τ₂. Although the decision lists {(c̃₁, ã₁), ${\stackrel{\sim }{a}}_1^{\prime }$} and {( ${\stackrel{\sim }{c}}_1^{\prime }$, ${\stackrel{\sim }{a}}_1^{\prime }$), ã₁} yield identical treatment recommendations and have the same value, their first clauses are distinct, and may lead to substantially different final decision lists. Hence it is necessary to consider both possibilities for the first clause. The algorithm proceeds recursively by adding one clause at a time until some stopping criterion (described below) is met.

Hereafter, for a decision list π described by {(c₁, a₁), …, (c_L, a_L), a₀} for some L ≥ 0, write R̂[{(c₁, a₁), …, (c_L, a_L), a₀}] to denote R̂(π); e.g., for L = 0, R̂[{a₀}] is the estimated value of the regime that assigns treatment a₀ to all patients. For any decision list with a vacuous condition, e.g.,{∩_ℓ<j T (c_ℓ)^c} ∩ T (c_j) = ∅ for some j, define R̂[{(c₁, a₁), …, (c_L, a_L), a₀}] = −∞. Let z_ρ be the 100_ρ percentile of the standard normal distribution. Let Π_temp denote the set of regimes to which additional clauses can be added, and let Π_final denote the set of regimes that have met one of the stopping criteria. The algorithm is as follows, and an illustrative example with a step-by-step run of the algorithm is given in the Web Appendix.

• Step 1Choose a maximum list length L_max and a critical level α ∈ (0, 1). Compute ã₀ = arg max_a0∈A R̂[{a₀}]. Set Π_temp = ∅, and Π_final = ∅.
• Step 2Compute $({\stackrel{\sim }{c}}_1,{\stackrel{\sim }{a}}_1,{\stackrel{\sim }{a}}_1^{\prime })={\mathrm{arg\; max}}_{(c_1,a_1,a_1^{\prime })\in C\times A\times A}\widehat{R}[\{(c_1,a_1),a_1^{\prime }\}]$ and ${\widehat{\mathrm{\Delta }}}_1=\widehat{R}[\{({\stackrel{\sim }{c}}_1,{\stackrel{\sim }{a}}_1),{\stackrel{\sim }{a}}_1^{\prime }\}]-\widehat{R}[\{({\stackrel{\sim }{a}}_0\}]$. If ${\widehat{\mathrm{\Delta }}}_1<z_{1-\alpha }{\{\widehat{\mathrm{Var}}({\widehat{\mathrm{\Delta }}}_1)\}}^{1/2}$ then let π = {ã₀}, set Π_final = {π}, and go to Step 5; otherwise let $\pi =\{({\stackrel{\sim }{c}}_1,{\stackrel{\sim }{a}}_1),{\stackrel{\sim }{a}}_1^{\prime }\},{\pi }^{\prime }=\{({\stackrel{\sim }{c}}_1^{\prime },{\stackrel{\sim }{a}}_1^{\prime }),{\stackrel{\sim }{a}}_1\}$ set Π_temp = {π, π′}, and proceed to Step 3, where ${\stackrel{\sim }{c}}_1^{\prime }$ is the negation of c̃₁.
• Step 3Pick an element π̄ ∈ Π_temp, say, $\overline{\pi }=\{({\overline{c}}_1,{\overline{a}}_1),\dots ,({\overline{c}}_{j-1},{\overline{a}}_{j-1}),{\overline{a}}_{j-1}^{\prime }\}$ where j − 1 is the length of π̄. Remove π̄ from Π_temp. With the clauses (c̄₁, ā₁), …, (c̄_j−1, ā_j−1) held fixed, compute $({\stackrel{\sim }{c}}_j,{\stackrel{\sim }{a}}_j,{\stackrel{\sim }{a}}_j^{\prime })={\arg \max }_{(c_j,a_j,a_j^{\prime })\in C\times A\times A}\widehat{R}[\{({\overline{c}}_1,{\overline{a}}_1),\dots ,({\overline{c}}_{j-1},{\overline{a}}_{j-1}),(c_j,a_j),a_j^{\prime }\}]$ and ${\widehat{\mathrm{\Delta }}}_j=\widehat{R}[\{{\overline{c}}_1,{\overline{a}}_1),\dots ,({\overline{c}}_{j-1},{\overline{a}}_{j-1}),({\stackrel{\sim }{c}}_j,{\stackrel{\sim }{a}}_j),{\stackrel{\sim }{a}}_j^{\prime }\}]-\widehat{R}[\{({\overline{c}}_1,{\overline{a}}_1),\dots ,({\overline{c}}_{j-1},{\overline{a}}_{j-1}),{\overline{a}}_{j-1}^{\prime }\}]$. If ${\widehat{\mathrm{\Delta }}}_j<z_{1-\alpha }{\{\widehat{\mathrm{Var}}({\widehat{\mathrm{\Delta }}}_j)\}}^{1/2}$, then let $\pi =\{({\overline{c}}_1,{\overline{a}}_1),\dots ,({\overline{c}}_{j-1},{\overline{a}}_{j-1}),{\overline{a}}_{j-1}^{\prime }\}$, and set Π_final = Π_final ∪ {π}, otherwise if j = L_max, let $\pi =\{({\overline{c}}_1,{\overline{a}}_1),\dots ,({\overline{c}}_{j-1},{\overline{a}}_{j-1}),({\stackrel{\sim }{c}}_j,{\stackrel{\sim }{a}}_j),{\stackrel{\sim }{a}}_j^{\prime }\}$, and set Π_final = Π_final ∪ {π}; otherwise set Π_temp = Π_temp ∪ {π, π′}, where ${\stackrel{\sim }{c}}_j^{\prime }$ is the negation of c̃_j, $\pi =\{({\overline{c}}_1,{\overline{a}}_1),\dots ,({\overline{c}}_{j-1},{\overline{a}}_{j-1}),({\stackrel{\sim }{c}}_j,{\stackrel{\sim }{a}}_j),{\stackrel{\sim }{a}}_j^{\prime }\}$ and ${\pi }^{\prime }=\{({\overline{c}}_1,{\overline{a}}_1),\dots ,({\overline{c}}_{j-1},{\overline{a}}_{j-1}),({\stackrel{\sim }{c}}_j^{\prime },{\stackrel{\sim }{a}}_j^{\prime }),{\stackrel{\sim }{a}}_j\}$.
• Step 4Repeat Step 3 until Π_temp becomes empty.
• Step 5Compute π̃ = arg max_π∈Πfinal R̂(π). Then π̃ is the estimated optimal decision list.

The above description is simplified to illustrate the main ideas. The actual implementation of this algorithm avoids exhaustive searches by pruning the search space C × A × A. It also avoids explicit construction of Π_temp and Π_final. Complete implementation details are provided in the Web Appendix. In the algorithm, the decision list stops growing if either the estimated increment in the value, Δ̂_j, is not sufficiently large compared to an estimate of its variation, ${\{\widehat{\mathrm{Var}}({\widehat{\mathrm{\Delta }}}_j)\}}^{1/2}$, or if it reaches the pre-specified maximal length L_max. We estimate Var(Δ̂_j) using large sample theory; the expression is given in the Web Appendix. This variance estimator is a crude approximation, as it ignores uncertainty introduced by the estimation of the decision lists; however, it can be computed quickly, and in simulated experiments it appears sufficient for use in a stopping criterion. The significance level α is a user-chosen tuning parameter. In our simulation experiments, we chose α = 0.05; results were not sensitive to this choice (see Web Appendix). To avoid lengthy lists, we set L_max = 10. Nevertheless, in our simulations and applications the estimated lists never reach this limit. Finally, it may be desirable in practice to restrict the set of candidate clauses so that, for each j, the number of subjects in R̂_j = {∩_ℓ<j T (ĉ_ℓ)^c} ∩ T (ĉ_j) exceeds some minimal threshold. This can be readily incorporated into the above algorithm by simply discarding candidate clauses that induce partitions that contain an insufficient number of observations.

The time complexity of the proposed algorithm is O [2^L_maxmp² {n + (max_j # χ_j)²}] (see Web Appendix), where #χ_j is the number of cutoff values in χ_j. Because 2^L_max and m are constants that are typically small relative to p² {n + (max_j # χ_j)²}, the time complexity is essentially O(np²) provided that max_j # χ_j is either fixed or diverges more slowly than n^1/2. Hence, the time complexity is the same as a single least squares fit, indicating that the proposed algorithm runs very fast and scales well in both dimension p and sample size n.

2.4.2 Finding an element of arg min_{π∈L̂{R̂(π̃)}} N̂(π)

To find an element within the set min_{π∈L̂{R̂(π̃)}} N̂(π), we enumerate all regimes in L{R̂(π̃)} with length no larger than L_max and select among them the list with the minimal cost. The enumeration algorithm is recursive and requires a substantial amount of bookkeeping; therefore, we describe the basic idea here and defer implementation details to the Web Appendix. Suppose π̃ is described by {(c̃₁, ã₁), …, (c̃_L, ã_L), ã₀}. Call a condition of the form x_j ≤ τ_j an atom. There exist K ≤ 2L atoms, say d₁, …, d_K, such that each clause c̃_ℓ, ℓ = 1, …, L, can be expressed using the union, intersection, and/or negation of at most two of these atoms. The algorithm proceeds by generating all lists with clauses representable using the foregoing combinations of at most two atoms. To reduce computation time, we use a branch-and-bound scheme (Brusco and Stahl, 2006) that avoids constructing lists with vacuous conditions or those that are provably worse than an upper bound on min_{π∈L̂{R̂(π̃)}} N(π) In the simulation experiments in the next section, the average runtime for the enumeration algorithm was less than one second running on a single core of a 2.3GHz AMD Opteron™ processor and 1GB of DDR3 RAM.

3. Simulation Experiments

We use a series of simulated experiments to examine the finite sample performance of the proposed method. The average value E{R(π̂)} and the average cost E{N(π̂)} are the primary performance measures. We consider generative models with (i) binary and continuous outcomes; (ii) binary and trinary treatments; (iii) correctly and incorrectly specified models; and (iv) low- and high-dimensional covariates. The class of data-generating models that we consider is as follows. Covariates are drawn from a p-dimensional Gaussian distribution with mean zero and autoregressive covariance matrix such that cov(X_k, X_ℓ) = 4(1/5)^|k−ℓ|, and the treatments are sampled uniformly so that P(A = a∣X = x) = 1/m for all x ∈ ℝ^p and a ∈ A. Let ϕ(x, a) be a real-valued function of x and a; given X = x and A = a, continuous outcomes are normally distributed with mean 2 + x₁ + x₃ + x₅ + x₇ + ϕ(x, a) and variance 1, whereas binary outcomes follows a Bernoulli distribution with success probability expit {2 + x₁ + x₃ + x₅ + x₇ + ϕ(x, a)}, where expit(u) = exp(u)/{1 + exp(u)}. Table 1 lists the expressions of ϕ used in our generative models and the number of treatments, m, in A. Under these outcome models, the optimal regime is π^opt(x) = arg max_a ϕ(x, a).

Table 1.

The second column gives the number of treatment options m. The third column gives the set of ϕ functions used in the outcome models. The fourth column specifies the form of the optimal regime π^opt (x) = arg max_a ϕ(x, a) where: “linear” indicates that π^opt(x) = arg max_a{(1, x^T)β_a} for some coefficient vectors β_a ∈ ℝ^p+1, a ∈ A, “decision list” indicates that π^opt is representable as a decision list; and “nonlinear” indicates that π^opt(x) is neither linear nor representable as a decision list.

Setting	m	Expression of ϕ	Form of πopt
I	2	ϕ1(x, a) = I(a = 2){3I(x1 ≤ 1, x2 > −0.6) −1}	decision list
II	2	ϕ2(x, a) = I(a = 2)(x1 + x2 − 1)	linear
III	2	ϕ3(x, a) = I(a = 2) arctan(exp(1+x1) −3x2 −5)	nonlinear
IV	2	ϕ4(x, a) = I(a = 2)(x1 − x2 + x3 − x4)	linear
V	3	ϕ5(x, a) = I(a = 2){4I(x1 > 1) −2} + I(a = 3)I(x1 ≤ 1){2I(x2 ≤ −0.3) −1}	decision list
VI	3	ϕ6(x, a) = I(a = 2)(2x1) + I(a = 3)(−x1x2)	nonlinear
VII	3	ϕ7(x, a) = I(a = 2)(x1 − x2)+ I(a = 3)(x3 − x4)	linear

For comparison, we estimate π^opt by parametric Q-learning, nonparametric Q-learning, outcome weighted learning (OWL, Zhao et al., 2012) and modified covariate approach (MCA, Tian et al., 2014). For parametric Q-learning, we use linear regression when Y is continuous and logistic regression when Y is binary. The linear component in the regression model has the form ${\sum }_{a=1}^{m}I(A=a)(1,X^{\mathrm{T}}){\beta }_a$, where β₁, …, β_m are unknown coefficient vectors. A LASSO penalty (Tibshirani, 1996) is used to reduce overfitting; the amount of penalization is chosen by minimizing 10-fold cross-validated prediction error. For nonparametric Q-learning, we use support vector regression when Y is continuous and support vector machines when Y is binary (Zhao et al., 2011), both are implemented using a Gaussian kernel. Tuning parameters for non-parametric Q-learning are selected by minimizing 10-fold cross-validated prediction error. For OWL, both linear and Gaussian kernels are used and we follow the same tuning strategy as in Zhao et al. (2012). For MCA, we incorporate the efficiency augmentation term described in Tian et al. (2014). Both OWL and MCA are limited to two treatment options.

To implement our method, the mean model, μ(x, a), in (1), is estimated as in parametric Q-learning. The propensity score ω(x, a) is estimated by $n^{-1}{\sum }_{i=1}^{n}I(A_i=a)$. All the comparison methods result in treatment regimes that are more difficult to interpret than a decision list; thus, our intent is to show that decision lists are competitive in terms of the achieved value of the estimated regime, E{R(π̂)}, while being significantly more interpretable and less costly.

Results in Table 2 are based on the average over 1000 Monte Carlo replications with data sets of size n = 500 if m = 2 and Y is continuous; n = 750 if m = 3 and Y is continuous; n = 1000 if m = 2 and Y is binary; and n = 1500 if m = 3 and Y is binary. The value R(π̂) and cost N(π̂) were computed using an independent test set of size 10⁶.

Table 2.

The average value and the average cost of estimated regimes in simulated experiments. In the header, p is the dimension of patient covariates; DL refers to the proposed method using decision list; Q₁ refers to parametric Q-learning; Q₂ refers to nonparametric Q-learning; OWL₁ and OWL₂ refer to outcome weighted learning with linear kernel and Gaussian kernel, respectively; MCA refers to modified covariate approach with efficiency augmentation. OWL and MCA are not applicable under Setting V, VI and VII.

p	Setting	Value						Cost
		DL	Q1	Q2	OWL1	OWL2	MCA	DL	Q1	MCA
Continuous response
10	I	2.78	2.53	2.53	2.33	2.29	2.54	1.64	9.0	5.1
	II	2.70	2.80	2.79	2.61	2.54	2.80	1.64	9.0	5.1
	III	2.59	2.54	2.53	2.29	2.24	2.55	1.68	9.1	4.9
	IV	2.89	3.37	3.35	3.16	3.09	3.37	2.50	9.5	7.4
	V	2.90	2.67	2.59	–	–	–	1.90	9.5	–
	VI	3.98	3.46	3.95	–	–	–	1.61	9.2	–
	VII	3.22	3.75	3.73	–	–	–	2.56	9.7	–
50	I	2.76	2.51	2.36	2.21	2.19	2.53	1.80	21.3	9.2
	II	2.70	2.79	2.73	2.26	2.27	2.79	1.64	21.4	9.3
	III	2.59	2.52	2.35	2.16	2.12	2.54	1.71	23.1	9.0
	IV	2.89	3.36	3.27	2.76	2.70	3.36	2.53	25.4	14.9
	V	2.87	2.63	2.33	–	–	–	2.14	28.5	–
	VI	3.95	3.43	3.47	–	–	–	1.69	26.6	–
	VII	3.21	3.74	3.61	–	–	–	2.55	30.8	–
Binary response
10	I	0.77	0.74	0.69	0.73	0.73	0.74	1.94	8.9	4.1
	II	0.71	0.72	0.60	0.71	0.71	0.72	1.69	9.2	5.3
	III	0.73	0.73	0.68	0.72	0.72	0.73	2.10	9.2	4.7
	IV	0.71	0.76	0.66	0.75	0.74	0.75	2.40	9.6	8.4
	V	0.75	0.73	0.62	–	–	–	2.52	9.6	–
	VI	0.79	0.75	0.64	–	–	–	2.09	9.5	–
	VII	0.77	0.81	0.69	–	–	–	2.83	9.9	–
50	I	0.76	0.73	0.69	0.71	0.70	0.73	2.64	21.9	8.3
	II	0.71	0.72	0.60	0.70	0.69	0.71	1.87	26.2	6.4
	III	0.73	0.72	0.67	0.70	0.69	0.72	2.53	25.0	7.3
	IV	0.71	0.76	0.66	0.73	0.72	0.74	2.55	31.0	13.8
	V	0.74	0.72	0.61	–	–	–	3.15	30.4	–
	VI	0.78	0.75	0.63	–	–	–	2.41	29.6	–
	VII	0.76	0.81	0.68	–	–	–	2.97	35.7	–

Table 2 shows that the decision list is competitive in terms of the value obtained across the entire suite of simulation experiments. If π^opt can be represented as a decision list, the proposed method produces the best value. However, even in settings in which the optimal regime is not a decision list, the estimated decision list appears to perform well. Recall that the proposed algorithm attempts to find the best approximation of the optimal regime within the class of regimes that are representable as a decision list. Figure 3 shows the average estimated decision list in misspecified settings II and III with continuous outcome and p = 10. In these settings, the estimated decision list provides a reasonable approximation of the true optimal regime. In addition, the cost of the decision list is notably smaller than the cost of the parametric Q-learning estimator or the MCA estimator. Nonparametric Q-learning OWL always use all covariates, so their costs are always equal to p.

Figure 3.

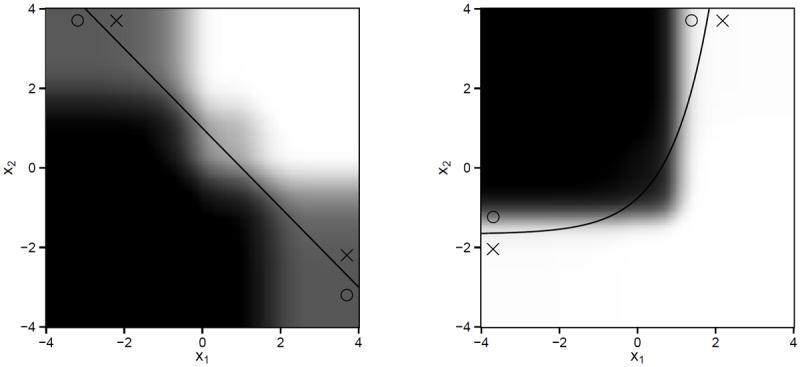
Left: average estimated regimes under setting II. Right: average estimated regimes under setting III. In both settings π^opt cannot be represented as decision list. The solid line is the treatment decision boundary under π^opt. The region where treatment 1 is better than treatment 2 is marked by circles, while the region where treatment 2 is better than treatment 1 is marked by crosses. For every point (x₁, x₂)^T, we compute the proportion of 1000 replications that the estimated regime recommends treatment 1 to a patient with covariate (x₁, x₂, 0, …, 0) ∈ ℝ¹⁰. The larger the proportion, the darker the shade.

In the Web Appendix, we derive point estimates and prediction intervals for R(π̂). We also present simulation results to illustrate the accuracy of variable selection for the decision list.

4. Applications

4.1 Breast Cancer Data

Gail and Simon (1985) compared the treatment effects of chemotherapy alone and chemotherapy with tamoxifen using data collected from the NSABP trial. Their regime recommended chemotherapy alone to patients with age ≤ 50 and PR ≤ 10 and chemotherapy plus tamoxifen to all others. Because the variables involved in the treatment regime constructed by Gail and Simon were chosen using clinical judgment, it is of interest to see what regime emerges from a more data-driven procedure. Thus, we use the proposed method to estimate an optimal treatment regime in the form of a decision list using data from the NSABP trial.

As in Gail and Simon (1985), we take three-year disease-free survival as the outcome, so that Y = 1 if the subject survived disease-free for three years after treatment, and Y = 0 otherwise. Patient covariates are age (years), PR (fmol), estrogen receptor level (ER, fmol), tumor size (centimeters), and number of histologically positive nodes (number of nodes, integer). We estimated the optimal treatment regime representable as a decision list using data from the 1164 subjects with complete observations on these variables. Because treatment assignment was randomized in NSABP, we estimated ω(x, a) by the sample proportion of subjects receiving treatment a. Based on exploratory analyses, we estimated μ(x, a) using a logistic regression model with transformed predictors z = z(x) = {age, log(1 + PR), log(1 + ER), tumor-size, log(1 + number-of-nodes)}^T.

The estimated optimal treatment regime representable as a decision list is given in the top panel of Figure 4; the regime estimated by Gail and Simon is given in the bottom panel of this figure. The structure of the two treatment regimes is markedly similar. The treatment recommendations from the two regimes agree for 92% of the patients in the NSABP data. In this data set, 33% of the patients have a PR value less than 3; 13% of the patients have a PR values between 3 and 10; and 54% of the patients have a PR value greater than 10.

Figure 4.

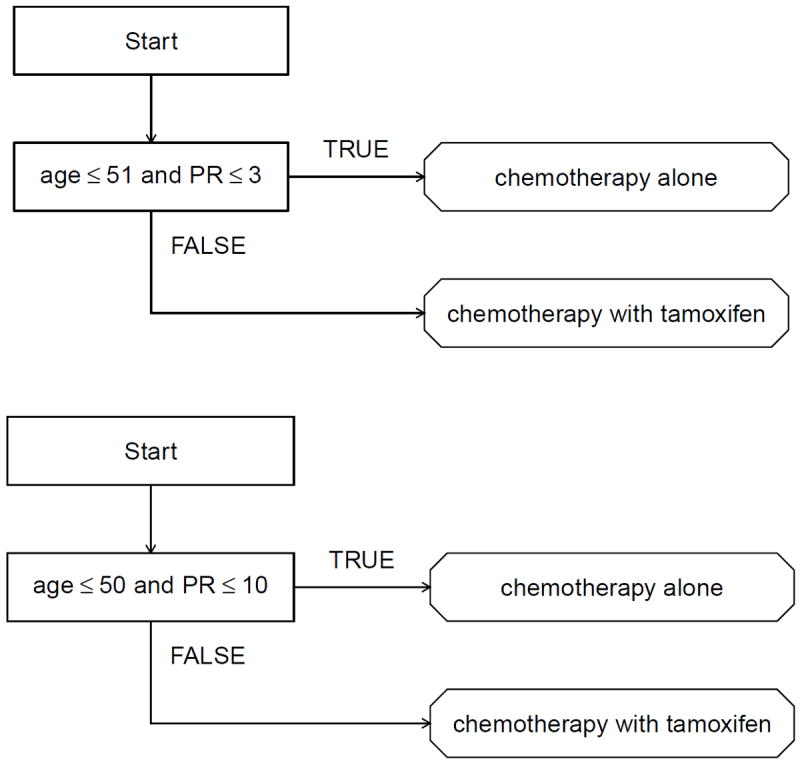
Top: estimated optimal treatment regime representable as a decision list. Bottom: treatment regime proposed by Gail and Simon (1985).

In a previous analysis of the NSABP data, Zhang et al. (2012) recommended that patients with age + 7.98 log(1 + PR) ≤ 60 receive chemotherapy alone and all others receive chemotherapy plus tamoxifen. However, this regime was built using only age and PR as potential predictors with no data-driven variable selection. In contrast, the proposed method selects age and PR from the list of potential predictors. For completeness, we also implemented parametric Q-learning using a logistic regression model with covariate vector z. The estimated regime recommends chemotherapy alone if 1.674 – 0.021 age − 0.076 log(1+PR) – 0.116 log(1 + ER) − 0.024 tumor-size − 0.274 log(1 + number-of-nodes) ≥ 0 and chemotherapy with tamoxifen otherwise. The treatment recommendation dictated by parametric Q-learning agrees with that dictated by decision list for 86% of the subjects in the data set.

To estimate the survival probability under each estimated regime, we use cross-validation. The data set was randomly divided into a training set containing 80% of the subjects and a test set containing 20% of the subjects. The optimal regime was estimated using both approaches on the training set, and its value was computed using (2) (with μ̂ ≡ 0) on the test set. To reduce variability, this process was repeated 100 times. The estimated survival probability is 0.65 for the regime representable as decision list and 0.66 for the regime obtained from parametric Q-learning. Thus, the proposed method greatly improves interpretability while preserving quality.

4.2 Chronic Depression Data

Keller et al. (2000) compared nefazodone, psychotherapy, and combination of nefazodone and psychotherapy for treating patients with chronic depression in a three-arm randomized clinical trial. Among the three treatments considered, combination therapy was shown to be the most beneficial in terms of efficacy as measured by the Hamilton Rating Scale for Depression score (HRSD). However, the combination treatment is significantly more expensive and burdensome than monotherapy. Therefore, it is of interest to construct a treatment regime that recommends combination therapy only to subjects for whom there is a significant benefit over monotherapy.

Because lower HRSD indicates less severe symptoms, we define outcome Y = –HRSD to be consistent with our paradigm of maximizing the mean outcome. Patient covariates comprise 50 pretreatment variables, including personal habits and difficulties, medication history and various scores from several psychological questionnaires; a list of these variables is given in the Web Appendix. We estimate an optimal regime using data from the n = 647 (of 680 enrolled) subjects in the clinical trial with complete data. Because treatments were randomly assigned, we estimated ω(x, a) by the sample proportion of subjects receiving treatment a. We estimated μ(x, a) using a penalized linear regression model with all patient covariates and treatment by covariate interactions. Penalization was implemented with a LASSO penalty tuned using 10-fold cross-validated prediction error.

The estimated optimal treatment regime representable as a decision list is displayed in Figure 1. One explanation for this rule is as follows. Those with strong physical anxiety symptoms (somatic) and significant cognitive impairment (retardation) may be unlikely to benefit from psychotherapy alone or in combination with nefazodone and are therefore recommended to nefazodone alone. Otherwise, because psychotherapy is a primary tool for treating anxiety (HAM-A) and nefazodone is associated with sleep disturbance (sleep), it may be best to assign subjects with moderate to severe anxiety and severe sleep disturbance to psychotherapy alone. All others are assigned to the combination therapy.

The estimated regime contains only four covariates. In contrast, the regime estimated by parametric Q-learning using linear regression and LASSO penalty involves a linear combination of twenty-four covariates, making it difficult to explain and expensive to implement. To compare the quality of these two regimes, we use random-split cross-validation as in Section 4.1. The estimated HRSD score under the regime representable as decision list is 12.9, while that under the regime estimated by parametric Q-learning is 11.8. Therefore, by using decision lists we are able to obtain a remarkably more parsimonious regime with high quality, which facilitates easier interpretation.

5. Discussion

Data-driven treatment regimes have the potential to improve patient outcomes and generate new clinical hypotheses. Estimation of an optimal treatment regime is typically conducted as a secondary, exploratory analysis aimed at building knowledge and informing future clinical research. Thus, it is important that methodological developments are designed to fit this exploratory role. Decision lists are a simple yet powerful tool for estimation of interpretable treatment regimes from observational or experimental data. Because decision lists can be immediately interpreted, clinical scientists can focus on the scientific validity of the estimated treatment regime. This allows the communications between the statistician and clinical collaborators to focus on the science rather than the technical details of a statistical model.

Due to the “if-then” format and the conditions given in (4), the estimated regime, as a function of the data, is discrete. Thus, a theoretical proof of the consistency of the treatment recommendations using decision lists is heavily technical and will be presented elsewhere. We provide some empirical evidence in the Web Appendix that the estimated regime gives consistent treatment decisions.