Survival analysis with high-dimensional covariates

Abstract

In recent years, breakthroughs in biomedical technology have led to a wealth of data in which the number of features (for instance, genes on which expression measurements are available) exceeds the number of observations (e.g. patients). Sometimes survival outcomes are also available for those same observations. In this case, one might be interested in (a) identifying features that are associated with survival (in a univariate sense), and (b) developing a multivariate model for the relationship between the features and survival that can be used to predict survival in a new observation. Due to the high dimensionality of this data, most classical statistical methods for survival analysis cannot be applied directly. Here, we review a number of methods from the literature that address these two problems.

1 Introduction

In the past decade, new experimental technologies in the field of genomics have led to an explosion of biomedical data. Gene expression and single nucleotide polymorphism (SNP) data have revolutionised our understanding of biological processes and diseases such as cancer. These new types of data share a common characteristic: the number of covariates or features (p) greatly exceeds the number of observations (n). We will refer to this setting as ‘high dimensional’. As a result, many classical statistical methods cannot be applied to these data without substantial modifications.

When, in addition to genomic data, (possibly censored) survival times are available for each observation, two questions arise naturally:

1. Which of the features (e.g. genes or SNPs) in the genomic data are individually most associated with the survival outcome? The classical statistical approach involves testing the null hypothesis {H₀: feature j is not associated with survival} for each feature j. In this article, we present alternatives that are better-suited to high-dimensional data.

2. How can one predict survival based on the genomic data? A standard approach for predicting survival in the n > p framework is to fit a Cox proportional hazards model; however, this model cannot be applied directly in a high-dimensional setting and performs poorly when p ≈ n. In this article, we present some methods for adapting the proportional hazards model to high-dimensional problems.

In Section 2, we discuss examples of high-dimensional data in genomics, as well as the statistical considerations that arise in the analysis of high-dimensional data. Section 3 contains a brief review of some classical methods for survival analysis. In Section 4, we present some methods for identification of features that are associated with a survival outcome. In Section 5, we present a number of methods for prediction of survival times in high-dimensional settings, and in Section 6 we discuss ways to evaluate the relative performances of the aforementioned prediction methods. Section 7 contains the Discussion. Throughout this article, we will consider for illustration the gene expression data set of Zhao et al.,¹ which consists of measurements for 14,814 genes taken on 177 patients with renal cell carcinoma. For each patient, there is an associated survival outcome. In the original article, these patients are split into two groups: a training set of 88 cases, and a test set of 89 cases.

2 High-dimensional data with a survival outcome

2.1 High-dimensional genomic data

In the past decade, new technologies have emerged that have changed the face of biomedical research. These methods have made it possible for biologists to perform experiments that once would have been many orders of magnitude too time consuming. It is now possible to measure the expression of tens of thousands of genes in a tissue sample in a single experiment and to determine the identities of half a million base-pairs of an individual’s DNA at once. In order to motivate the development of statistical methods for survival analysis in high-dimensional settings, we will discuss these two types of data in turn.

Genes are segments of an individual’s DNA sequence that encode proteins, which carry out the functions of the cell. In different tissues and disease states and between individuals, the same gene will have different levels of expression – that is, different amounts of mRNA (an intermediary along the way to protein production) will be present. Gene expression data has been successfully used to identify previously unknown cancer subtypes, to classify new patients into cancer subtypes, and to predict survival time; early articles in this area include Perou et al.,² Golub et al.,³ Sorlie et al.,⁴ Hedenfalk et al.,⁵ van’t Veer et al.,⁶ and Ramaswamy et al.⁷ A typical gene expression data set involves measurements of expression of tens of thousands of genes for a single tissue sample; usually, between a couple dozen and a couple hundred samples are available. Often, in addition to this genetic or biological data, clinical data is also available. This clinical data might relate to the tissue sample itself: for instance, if tumour and normal tissue samples are extracted from the same individual, then the clinical data might be the tumour/normal labels for each sample. Alternatively, the clinical data could consist of a (possibly censored) survival time for the patient from which the tissue sample was extracted. In this situation, the clinical data can be considered the outcome, and the genes are the variables. Allison et al.⁸ provide a review of issues related to gene expression data measured on microarrays.

A SNP is a DNA base-pair at which there is sequence variability in a population. SNPs are of interest in part because it is believed that they can determine predispositions to certain diseases (see, e.g. Hirschhorn and Daly,⁹ Duerr et al.,¹⁰ Rioux et al.,¹¹ Samani et al.,¹² and Sladek et al).¹³ It is now possible to assay many hundreds of thousands of SNPs for an individual at a given time. It is becoming increasingly common to collect SNP data and clinical data for a set of individuals in order to seek SNPs that are associated with the clinical outcome. While gene expression data involves continuous measurements for each gene, SNP data is discrete. An individual carries two copies of each chromosome, one from each parent; therefore, for each SNP, an individual can have no copies of the common variant, one copy of the common variant, or two copies of the common variant. (These possibilities are usually coded as 0, 1 and 2). In a SNP data set with an associated clinical measurement for each observation, the clinical data is considered the outcome, and the SNPs are the features. An overview of statistical methods for SNP (also known as genome-wide association) data is given in Balding.¹⁴

Most of the methods that we will discuss are applicable to gene expression data and SNP data, as well as many other types of high-dimensional data.

2.2 Statistical issues that arise in high dimensions

When the number of features p is very large, classical statistical methods for performing both of the goals mentioned in Section 1 cannot be applied directly.

Consider first the goal of identifying features that are associated with survival. The classical statistical approach is to perform a hypothesis test for each feature: one could test the hypothesis that in a Cox proportional hazards model for survival (explained in the next section) using that feature as a predictor, the coefficient β is zero. We would then consider to be associated with survival all features for which the p-value for that hypothesis test is small. When p is large, we expect some of the p hypothesis tests to have small p-values due to chance; correcting for multiple hypothesis testing gives poor results. This problem is discussed in e.g. Dudoit et al.¹⁵ A method of identifying important features that is better-suited to a high-dimensional setting is required.

The problems that arise in building a prognostic model with p ≫ n are even more dire. Recall that in the case of linear regression, if the covariance matrix of the features is not full rank then the least squares regression coefficients are not unique. Some form of regularisation is required in order to reduce the dimensionality of the feature space. Even if regularisation is performed so that the regression coefficients are unique, overfitting is a major concern – one risks fitting not just the signal, but also the noise in the data, so that the model will not fit a new observation well. Much care is required in order to avoid overfitting, which can occur even if p < n. The same problems and considerations arise in the case of survival data.

Moreover, in building a prognostic model that will be of use in evaluating future patients, an important consideration is the simplicity of the model. All else being equal, one would prefer a model that uses only a small subset of the features, rather than a model that uses all of the features. This is the case for several reasons. First, a smaller (or sparse) model will be more useful in predicting survival for future patients. It is much cheaper and easier for a doctor to measure expression of 30 genes for a new patient than it is to measure 30,000. In addition, a sparser model is simpler to interpret. It is easier for a biologist to understand the way in which 30 genes affect survival than it is to understand the way in which 30,000 genes affect survival. Also, if one believes that the true underlying biology that determines survival involves only a small number of genes, then a method that yields a sparse model might be more accurate. Therefore, when we present methods for prediction of survival in Section 5, we will make special note of whether each method results in sparsity.

3 Basic tools for survival analysis

We now briefly review a few basic tools in survival analysis, as they will arise repeatedly in the next sections. Kalbfleisch and Prentice¹⁶ provide a helpful overview of these methods and many others.

Let X denote an n × p data matrix, where n is the number of observations and p the number of covariates, or features. For each observation xⁱ ∈ ℝ^p there is an associated survival time y_i and censoring status δ_i, where δ_i = 1 if the observation is complete and δ_i = 0 if it is censored. In other words, if δ_i = 1, then individual i failed at time y_i, and if δ_i = 0, then individual i survived until at least time y_i. We assume that censoring is non-informative and that given xⁱ, y_i and δ_i are independent. Let t₁ < t₂ < ⋯ < t_k denote the failure times.

To estimate a survivor function P(y > t) we can use the product limit estimate or Kaplan–Meier estimate, which is

$$P(y>t)=\prod _{j|t_j<t}\left(\frac{n_j-d_j}{n_j}\right)$$ (1)

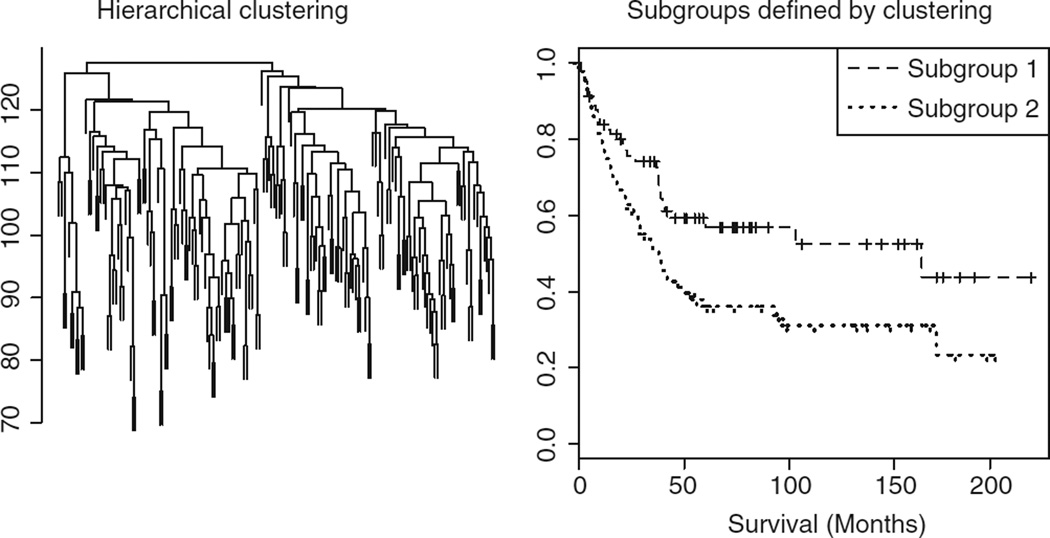
where d_j is the number of failures at time t_j and n_j is the number of observations at risk just prior to time t_j. A plot of the Kaplan–Meier estimate yields the Kaplan–Meier survival curve; this is a popular tool for visualizing survival data. Examples of Kaplan–Meier survival curves can be seen in Figures 2 and 3. A log-rank test can be used to determine if two or more samples could have arisen from the same survivor function.

Figure 2.

Hierarchical clustering of the patients is shown on the left. Kaplan–Meier survival curves for the two largest subgroups defined by hierarchical clustering are shown on the right; the p-value for the log-rank test is 0.0102.

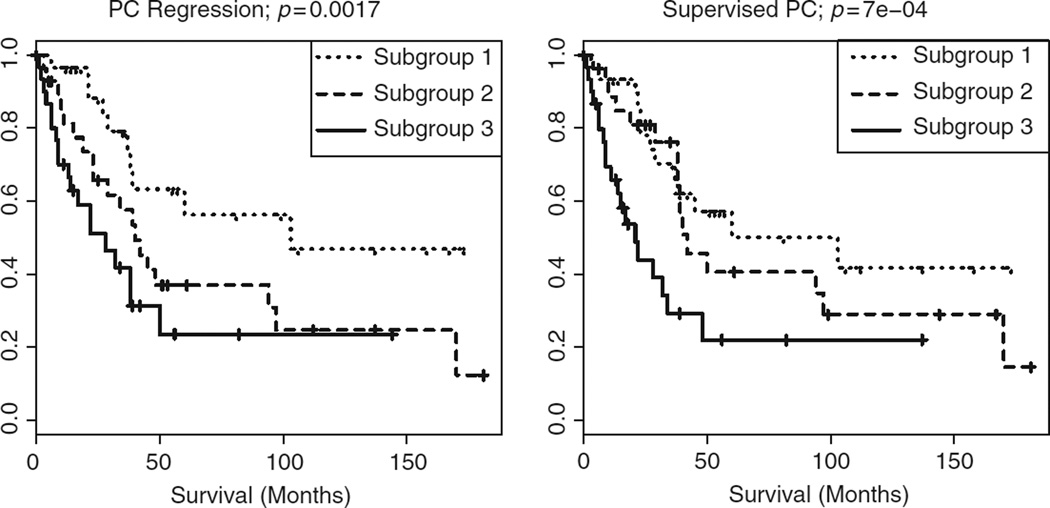
Figure 3.

For the Zhao et al.¹ data, predictors obtained via PC regression and SPC on the training set were used to define three subgroups on the test set. For these subgroups, Kaplan–Meier survival curves and p-values for the log rank test statistic are shown.

The Cox proportional hazards model is commonly used to model survival data. It is non-parametric in that the baseline hazard function can take an arbitrary form. The model is as follows:

$$\lambda (t|{\mathbf{x}}^i)={\lambda }_0(t)\text{exp }(\sum _{j=1}^p{x}_j^i{\beta }_j)$$ (2)

where λ(t|xⁱ) is the hazard at time t for observation xⁱ, and β ∈ ℝ^p is a vector of regression coefficients. λ₀(t) is the unspecified hazard function. The partial likelihood for β can be written as

$$L(\beta )=\prod _{r\in D}\frac{\text{exp}({\beta }^T{\mathbf{x}}^r)}{{\sum }_{i\in R_r}\text{exp}({\beta }^T{\mathbf{x}}^i)}$$ (3)

where D is the set of indices of the events (deaths), and R_r is the set of the individuals at risk at time t_r − 0.

To fit the model in Equation (2), we maximise the partial likelihood in Equation (3). When n < p, this can be done by using iteratively re-weighted least squares (IRLS) to implement the Newton–Raphson method. Let l(β) denote the log partial likelihood. We wish to solve

$$\frac{\partial l}{\partial \beta }=0;$$ (4)

given an initial estimate β, we can obtain an update β* by solving

$$(-\frac{{\partial }^{2}l}{\partial \beta {\beta }^T})({\beta }^{*}-\beta )=\frac{\partial l}{\partial \beta }.$$ (5)

This update is repeated until convergence. Letting η = Xβ and $A=-\frac{{\partial }^{2}l}{\partial \eta {\eta }^T}$, Equation (5) can be re-written as

$${\mathbf{X}}^T\mathbf{A}\mathbf{X}({\beta }^{*}-\beta )={\mathbf{X}}^T\frac{\partial l}{\partial \eta },$$ (6)

which is simply a least squares problem.

However, in the case that p > n, this approach cannot be used to estimate β; in particular, note that β that maximises the partial likelihood is not even unique. In the context of the IRLS procedure, the matrix X^TAX is singular. Thus, in high-dimensional settings, some type of dimension reduction is required in order to use the Cox proportional hazards model to predict survival times. Given that Equation (6) can be solved via least squares, it is clear that the problem that arises in high-dimensional survival problems is similar to the problem that arises in high-dimensional regression problems. Therefore, it is not surprising that many of the methods presented in Section 5 for prediction of survival in high dimensions are closely related to analogous high-dimensional regression methods.

4 Methods to identify features that are individually associated with survival

Consider a gene expression study involving patients with a given type of cancer, in which the researcher seeks genes that are associated with survival time. Such genes might be candidates for follow-up experiments in order to better understand the disease mechanism. In what follows, we will sometimes refer to genes truly associated with survival as ‘significant’.

The most straightforward way to identify features that are associated with survival is using univariate Cox scores, given in Equation (7). For each feature x_j, a univariate Cox proportional hazards model is fit; the score statistic or Cox score for that model quantifies how well that feature predicts survival. The score statistic is

$$S_j=\left(\frac{dl(0)}{d{\beta }_j}\right)/{\left(\frac{d^{2}l(0)}{d{\beta }_j^2}\right)}^{\frac{1}{2}}=\frac{{\sum }_{r\in D}(x_j^r-\frac{1}{n_r}{\sum }_{i\in R_r}{x}_j^i)}{{[{\sum }_{r\in D}\frac{1}{n_r}{\sum }_{i\in R_r}{(x_j^i-\frac{1}{n_r}{\sum }_{k\in R_r}{x}_j^k)}^2]}^{1/2}}.$$ (7)

A large value of S_j suggests that feature j is associated with the survival outcome, i.e. that one can reject the null hypothesis. The sign of the Cox score indicates whether overexpression of that gene is associated with increased or decreased survival. Cox scores are used to identify significant genes in Beer et al.¹⁷ Note that instead of Cox scores, one could use Wald scores in order to quantify each feature’s significance; however, when the number of features is very large, this method has the disadvantage that computation of β̂_j requires iteratively fitting a Cox model for each j.

Tusher et al.¹⁸ propose the significance analysis of microarrays (SAM) procedure for the identification of significant features. It involves the use of a modified Cox score, obtained by adding a small constant d₀ to the denominator of the Cox score in order to stabilise the variance, as follows:

$$S_j^{d_0}=\frac{{\sum }_{r\in D}(x_j^r-\frac{1}{n_r}{\sum }_{i\in R_r}{x}_j^i)}{{\left[{\sum }_{r\in D}\frac{1}{n_r}{\sum }_{i\in R_r}{(x_j^i-\frac{1}{n_r}{\sum }_{k\in R_r}{x}_j^k)}^2\right]}^{1/2}+d_0}.$$ (8)

Modified Cox scores generally perform better than Cox scores.

The lassoed principal components (LPC) method, proposed by Witten and Tibshirani,¹⁹ seeks to ‘borrow strength’ by using information about all of the features in order to determine whether a given feature is significant. The motivation for this approach is that in a gene expression data set, sets of genes tend to have correlated expression. One might be more willing to believe that a given gene is associated with the survival outcome if it is correlated with a large set of genes that all appear to be associated with survival. Let T denote a vector of Cox or modified Cox scores, and let v₁, …, v_n ∈ ℝ^p denote the right singular vectors of X. Then the LPC scores T̂ are given by the equation $\hat{\mathbf{T}}={\hat{\beta }}_0+{\sum }_{i=1}^n{\mathbf{v}}_i{\hat{\beta }}_i$, where

$$\hat{\beta }={\text{argmin}}_{\beta }\{{\Vert \mathbf{T}-{\beta }_0-\sum _{i=1}^n{\mathbf{v}}_i{\beta }_i\Vert }^2+\lambda \sum _{i=1}^n|{\beta }_i|\}.$$ (9)

That is, T̂ are the fitted values obtained by regressing the Cox or modified Cox scores onto the eigenvectors of the data matrix, subject to an L₁ penalty; this regression serves to de-noise the scores for the features. The tuning parameter λ ≥ 0 is chosen adaptively.

Each of the three methods just mentioned – Cox scores, modified Cox scores, and LPC scores – is used to obtain a ranking for the significance of the features. The higher a feature’s absolute score, the more significant it is believed to be. The top K features on this ranked list are suspected to be associated with survival; however, we need a way to choose K. More generally, we require some way to evaluate the level of significance of the features at the top of this ranking. In classical statistics, one would assess significance by testing, for each feature j, the null hypothesis of no association with survival. Features corresponding to a sufficiently small p-value for the hypothesis test would be deemed significant. But in the context of high-dimensional genomic data, the number of features is extremely large, and necessary correction of the p-values for multiple testing often leads to disappointing results. Moreover, in the case of gene expression or SNP data, a researcher may be willing to accept a list of candidate features that contains some small number of false positives. Therefore, a false discovery rate (FDR) approach is preferred. That is, we are interested in estimating the expected fraction of features at the top of our ranked list that truly are associated with survival; the complement of this fraction is the FDR. Table 1 displays the possible outcomes from p hypothesis tests of a set of features and the connection to FDR; more detailed discussions of FDR can be found in Benjamini and Hochberg²⁰ and Storey and Tibshirani.²¹ In the case of Cox and modified Cox scores, where each feature’s significance is assessed based only on the measurements for that feature, FDRs can be easily estimated by permuting the survival outcomes for the n observations. The procedure is as follows:

1. Compute scores for each feature, where the score for feature j is denoted S_j = f (x_j, y, δ), to indicate that it is a function of that feature, the vector of survival times, and the vector of censoring statuses.

2. For i ∈ 1, …, M where M is large (for instance, 1000):

   1. Permute the pairs (y₁, δ₁), (y₂, δ₂), …, (y_n, δ_n); let (y*, δ*) denote the vectors of permuted values.
   2. Compute feature scores for the permuted data, $S_j^{*i}=f({\mathbf{x}}_j,{\mathbf{y}}^{*},{\delta }^{*})$.
3. To estimate the FDR at a given threshold c, compute the ratio

   $$\widehat{FDR(c)}=\frac{\frac{1}{M}{\sum }_{i=1}^M{\sum }_{j=1}^{p}1(|S_j^{*i}|\ge c)}{{\sum }_{j=1}^{p}1(|S_j|\ge c)},$$ (10)

   where 1(·) is an indicator variable. The numerator is the expected number of features that exceed the threshold under the null hypothesis, and the denominator is the observed number of features that exceed the threshold.

This is done in the SAM procedure and is a ‘plug-in’ estimate of FDR: see Tusher et al.,¹⁸ and Storey and Tibshirani.²¹ Because the LPC score for a given feature is a function of all of the features, estimation of FDR for LPC is more involved. A discussion is given in Witten and Tibshirani.¹⁹ In the context of gene expression data, often genes with FDR less than some fixed cut-off (say, 0.1 or 0.2) are reported.

Table 1.

Possible outcomes from p hypothesis tests for a set of features. The FDR is defined as $E(\frac{V}{R})$. If the statistic used to test each hypothesis is a function of that feature only, then permutations can be used to estimate the FDR

	Called not significant	Called significant
Null	U	V
Non-null	T	S
Total	p −R	R

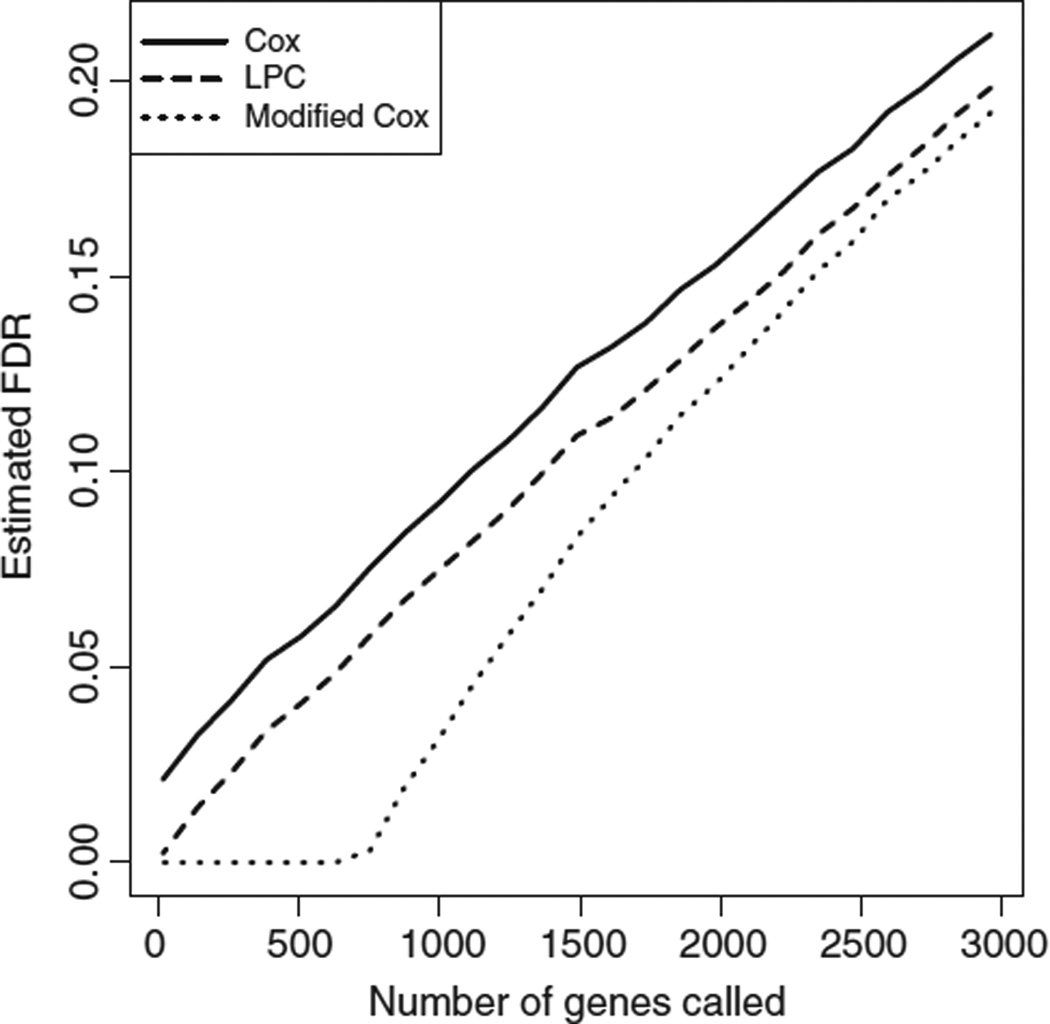
The estimated FDRs for Cox scores, modified Cox scores, and LPC scores for the renal cell carcinoma data set of Zhao et al.¹ are shown in Figure 1. In this example, the use of modified Cox scores results in a slight improvement in FDR over ordinary Cox scores. LPC provides an additional improvement.

Figure 1.

Estimated FDR for Cox scores, modified Cox scores, and LPC scores are shown for the renal cell carcinoma data set of Zhao et al.¹

While there are a great number of methods in the literature for identification of significant genes in a microarray experiment with a two-class outcome (see e.g. Lonnstedt and Speed,²² Cui and Churchill,²³ Cui et al.,²⁴ Storey et al.²⁵), the topic of identification of significant genes with a survival outcome is still relatively unexplored.

5 Methods for prediction of survival time

As previously discussed, a Cox proportional hazards model cannot be fit to the data when p ≫ n. For this reason, many methods have been developed that are better suited for prediction in high-dimensional settings. We separate the methods presented here into four types: methods that involve discrete feature selection (Section 5.1), shrinkage-based methods (Section 5.2), methods that involve clustering the data (Section 5.3) and methods that involve a variance criterion (Section 5.4). Most of these methods involve one or more tuning parameters for which values must be chosen; we will take care in the descriptions below to point these out. For simplicity, we will assume that the columns of X have been standardised to have mean zero and standard deviation one.

5.1 Methods that involve discrete feature selection

5.1.1 Univariate selection

The simplest method for selecting a subset of features for use in a proportional hazards model is univariate selection. This method involves computing Cox scores (7) for each feature; the K < n features with the highest Cox scores are then used as features in a Cox proportional hazards model. In this method,K is a tuning parameter. (Analogously, modified Cox scores or LPC scores could be used to determine which features to include in the model.)

The obvious drawback of univariate feature selection is that while each of the features included in the multivariate model will be predictive of survival (at least in the training set), there is no guarantee that the multivariate model predicts survival substantially better than the features with highest Cox scores do individually. In particular, if the features with highest Cox scores are very highly correlated with each other (as is often the case for gene expression data) then the multivariate model may not provide much information beyond what is present in the univariate models. In this case, it is clear that another method for feature selection is preferable.

5.1.2 Stepwise selection

Stepwise selection for survival models is the exact analog of stepwise selection for linear regression. It is similar to univariate selection, but the correlation between the features is taken into account. Forward stepwise selection is performed as follows: first, Cox scores are computed for each feature, and a model is created using only the feature with the highest absolute Cox score. Then, a local score test is used to determine which of the remaining p − 1 features will lead to the greatest improvement if added to the model. This process is continued until K features have been included. Note that stepwise methods find local optima; that is, they do not yield the best model with K features. The tuning parameter K must be selected in order to use stepwise selection (or a p-value threshold for the local score test can be used).

5.2 Shrinkage-based methods

5.2.1 L_p shrinkage of coefficients

The methods presented thus for have involved making a discrete decision for each feature: whether or not to include it in the model. An alternative to this all-or-nothing approach is to use a more continuous method for regularisation, with shrunken coefficients for each feature.

Consider the case of linear regression, with y a n-vector of outcome measurements, and X as defined earlier. Assume that y has been centred. Linear regression seeks to minimise

$${(\mathbf{y}-{\mathbf{X}}_{\beta })}^T(\mathbf{y}-{\mathbf{X}}_{\beta }).$$ (11)

As mentioned earlier, if p > n, then some type of regularisation or shrinkage of the β vector is required. This can be done by penalizing the magnitudes of the elements of β. Using an L₂ penalty yields ridge regression²⁶

$$\hat{\beta }={\text{argmin}}_{\beta }\{{(\mathbf{y}-\mathbf{X}\beta )}^T(\mathbf{y}-\mathbf{X}\beta )+\lambda \sum _{j=1}^p{\beta }_j^2\},$$ (12)

whereas an L₁ penalty gives the lasso²⁷

$$\hat{\beta }={\text{argmin}}_{\beta }\{{(\mathbf{y}-\mathbf{X}\beta )}^T(\mathbf{y}-\mathbf{X}\beta )+\lambda \sum _{j=1}^p|{\beta }_j|\}.$$ (13)

Ridge regression results in elements of β̂ that are small (relative to their values in the absence of the ridge penalty) but, in general, non-zero. Therefore, the resulting model solves the p > n problem and can avoid overfitting, but it involves all of the features. On the other hand, the lasso results in (for an appropriate choice of λ) a vector β̂ that is sparse – that is, some of its elements are zero. Depending on the context, and whether one seeks a model that is sparse in the features, one might choose to use an L₁ or an L₂ penalty.

These L_p shrinkage methods can be extended directly to the survival framework. Recall from Section 3 that the Cox proportional hazards model is fit by maximizing Equation (3). If we again let l(β) denote the log partial likelihood, then we can instead maximise

$$l(\beta )-\lambda \sum _j{\beta }_j^2$$ (14)

or

$$l(\beta )-\lambda \sum _j|{\beta }_j|;$$ (15)

these are presented in Verweij and van Houwelingen²⁸ and Tibshirani,²⁹ respectively. This is done by replacing Equation (6) with a penalised least squares procedure. As in the linear regression case, Equation (14) results in p non-zero but shrunken coefficients and Equation (15) results in the selection of a subset of the coefficients for an appropriate range of λ. Gui and Li³⁰ and Park and Hastie³¹ present efficient algorithms for estimating β in the L₁ case. For L₁ and L₂ regularisation, λ is a tuning parameter that must be chosen based on the data.

Tibshirani³² presents a variation on the Cox proportional hazards model with an L₁ penalty. Consider the form of the log partial likelihood in Equation (3); note that (exp(β^Tx^r)/ ∑_i∈Rr exp(β^Txⁱ)) is the probability that individual r fails when it does, given the observations in the risk set and their feature vectors. The Cox univariate shrinkage method assumes that the features are independent of each other, both marginally and conditionally on each risk set. Therefore, the partial likelihood factors,

$$L(\beta )=\prod _{r\in D}\prod _{j=1}^p\frac{\text{exp}(x_j^r{\beta }_j)}{{\sum }_{i\in R_r}\text{exp}(x_j^i{\beta }_j)}.$$ (16)

An L₁ penalty is added to the resulting log partial likelihood, as in (15), in order to obtain a shrunken and sparse estimate of β. This very simple method is the analog of univariate soft thresholding (described in e.g. Zou and Hastie³³) in the regression case.

As in the regression case, L_p-penalised proportional hazards models perform well in practice. In addition to the L₁ and L₂ penalties discussed here, other penalties exist; for instance, the elastic net penalty³³ can be extended to the survival setting. Candes and Tao³⁴ present the Dantzig selector, an attractive method for regression in high-dimensional settings that is closely related to L₁-regularised regression. It is extended to the Cox proportional hazards model in Antoniadis et al.³⁵ L_p regularisation is a flexible framework for coping with the p > n problem.

5.2.2 L_p shrinkage of inverse covariance matrix

In Section 5.2.1, we presented methods that shrink the coefficients for each feature via an L_p penalty on the log partial likelihood in the Cox model. Witten and Tibshirani³⁶ propose a different approach to shrinkage of the coefficients. We first explain this method in the regression setting. Rather than applying an L_p penalty to the sum of squared errors as in Equations (12) and (13), we can instead estimate the inverse covariance matrix of the data, under a multivariate normal model, subject to an L_p penalty on its elements. More specifically, if we assume that y has been centered, then β̂ is derived via this two-step procedure, called covariance-regularised regression:

1. $\hat{\mathbf{\Theta }}\leftarrow {\text{argmax}}_{\mathbf{\Theta }}\{\text{log}(\text{det}\mathbf{\Theta })-\text{tr}(\frac{1}{n}{\mathbf{X}}^T\mathbf{X}\mathbf{\Theta })-{\lambda }_1{\Vert \mathbf{\Theta }\Vert }^{p_1}\}$. The p × p matrix Θ̂ is a regularised estimate of the inverse of the population covariance matrix of X under a multivariate normal model.

2. $\hat{\beta }\leftarrow {\text{argmin}}_{\beta }({\beta }^T{\hat{\mathbf{\Theta }}}^{-1}\beta -\frac{2}{n}{\beta }^T{\mathbf{X}}^{T}y+{\lambda }_2{\Vert \beta \Vert }^{p_2}\}$.

Here, λ₁, λ₂ ≥ 0 are tuning parameters. It is clear that if λ₁ = 0, then this method reduces to the form of the L_p coefficient shrinkage methods of Section 5.2.1; however, with λ₁ > 0, shrinkage of the inverse covariance matrix also takes place. Whenp₁ = 1, the elements of Θ̂ are sparse. When p₂ = 1, the method results in sparse regression coefficients. This method can be extended to the Cox proportional hazards model by replacing the linear regression step in the Newton–Raphson procedure with a covariance-regularised regression. This method is also called the scout, and the choice of p₁ and p₂ can be indicated with the notation Scout(p₁, p₂).

5.3 Clustering-based methods

The methods described thus far have been supervised: the dimensionality of the data was reduced using knowledge about the survival time for each observation. However, some methods for predicting survival from gene expression data involve an unsupervised approach: first, the dimension of the gene expression data is reduced without using the outcome, and then the reduced version of the data is used in conjunction with survival times to build a predictive model of survival. The canonical unsupervised method for data analysis is clustering: using some metric of distance, the pairwise distances between the observations or features can be computed. Then, sets of observations or features with small pairwise distances form clusters.

Hierarchical clustering³⁷ of the observations has been used to identify cancer subtypes associated with survival in a number of studies, including Alizadeh et al.³⁸ and Zhao et al.¹ In these studies, the clustering dendrograms were used to define subgroups of patients, which were then found to differ in terms of survival. The drawback of this approach is that, in general, the subgroups obtained by clustering may not differ in terms of survival, even if some of the features present in the original (unclustered) data set are strong predictors of survival.

We illustrate this method on the renal cell carcinoma data set of Zhao et al.¹ We cluster the patients using correlation-based distance, average linkage, and only the25%of genes with highest variance. The clustering dendrogram and the Kaplan–Meier survival curves for the two largest subgroups that result from this clustering are shown in Figure 2; the p-value for the log rank test is 0.0102.

A more sophisticated method that uses hierarchical clustering to predict survival is the tree harvesting approach of Hastie et al.³⁹ The p features are clustered hierarchically; this results in a total of 2p − 1 clusters (one cluster contains all of the features, p clusters contain one feature each, and the remaining p − 2 clusters contain between 2 and p − 1 features each). Let x̅_Ck denote the n-vector corresponding to the average expression of the features in cluster C_k. Now, the vectors x_C1, …, x_C2p−1 are treated as possible features in a Cox proportional hazards model (with interaction terms) to predict survival. The features to be included are selected via stepwise selection (described previously), with a slight modification such that the inclusion of larger clusters in the model is favoured. This method is linear and possibly sparse in the original features (depending on the clusters included).

5.4 Variance-based methods

We now discuss methods that involve the selection of features using a criterion based on the variance: that is, these methods seek features that capture much of the variation present in the data. Some of these methods create new features in a supervised way, and others do so in an unsupervised way.

5.4.1 Methods based on principal components analysis

Principal components analysis (PCA) is an important unsupervised statistical method for dimension reduction. The first principal component v₁ of the data matrix X is the unit vector such that Xv₁ has greatest variance. The subsequent principal components v_j maximise the variance of Xv_j, subject to being orthogonal to the previous ones:

$${\mathbf{v}}_j={\text{argmax}}_{{\mathbf{v}}_j}{\mathbf{v}}_j^T{\mathbf{X}}^T\mathbf{X}{\mathbf{v}}_j\text{ subject to }{\mathbf{v}}_j^T{\mathbf{v}}_j=1,{\mathbf{v}}_j^T{\mathbf{v}}_k=0\forall k<j.$$ (17)

It turns out that the principal components v_j are given by the columns of the matrix V in the singular value decomposition of X:

$$\mathbf{X}=\mathbf{U}\mathbf{D}{\mathbf{V}}^T$$ (18)

where D is diagonal and U and V have orthonormal columns.

In many data sets, much of the variability in X is contained in the first few principal component directions, and so projecting X onto the first principal components does not lead to much loss of information. Suppose that much of the variation in the data is contained in the first K principal components, and that y is a centered quantitative outcome. Then, rather than performing ordinary least squares regression (which minimises Equation (11)), one can instead regress y onto Xv₁, …, Xv_k:

$$\hat{\beta }={\text{argmin}}_{\beta }\{{(\mathbf{y}-\sum _{k=1}^K\mathbf{X}{\mathbf{v}}_k{\beta }_k)}^T(\mathbf{y}-\sum _{k=1}^K\mathbf{X}{\mathbf{v}}_k{\beta }_k)\}.$$ (19)

If one chooses K < rank(X), then this can solve the multicollinearity problem that arises in regression if p > n. This method is known as principal components regression (PC regression).⁴⁰ An analogous approach to PC regression can be taken in the case of survival data, using Xv_j as predictors in a Cox proportional hazards model. Even for K small, PC regression is not sparse in the features, since v_j is in general non-zero for each feature.

Bair and Tibshirani⁴¹ and Bair et al.⁴² point out a drawback of the use of principal components for regression and survival models: while the first few principal components may summarise a large proportion of the variance present in the data, there is no guarantee that these principal components are associated with the outcome of interest. The problem is that the principal components are computed in an unsupervised manner. Thus, Bair and Tibshirani⁴¹ and Bair et al.⁴² propose a semi-supervised approach, which they call supervised principal components (SPC). In the survival case, the method proceeds as follows. First, univariate Cox scores are computed for each feature. Let X̃ denote the n × K matrix consisting of the K < p features with highest absolute Cox scores, and let X̃ = Ũ D̃ Ṽ^T denote the SVD of this matrix. Then, one can fit a Cox proportional hazards model with the first few columns of X̃Ṽ, termed ‘supervised principal components’, as predictors. This model can be written in terms of the original data X, and can also be used to obtain predictions for a future observation. The number of supervised principal components used, and the number of features K included in the reduced data matrix, are tuning parameters for the supervised principal components method. (For simplicity and to avoid having to select two tuning parameters, often only the first supervised principal component is used). Supervised principal components results in a sparse model that involves only K of the features.

To illustrate PC regression and SPC on the renal cell carcinoma data set, we used cross-validation (discussed in Section 6) on the training set in order to select tuning parameter values for the two methods. Cross-validation selected 10 principal components for PC regression, and 39 genes for SPC. We then assessed how well X_test β̂_train predicts survival on the test set (see Section 6); PC regression and SPC resulted in p-values of 0.003 and 0.0005, respectively. The predictor X_test β̂_train was then discretised based on the tertile to which each element belonged. This new categorical variable defined three groups on the test set, for which Kaplan–Meier survival curves and p-values are shown in Figure 3. In this example, both PC regression and SPC perform quite well.

Li and Li⁴³ propose combining principal component regression with an additional dimension reduction technique, sliced inverse regression (SIR). The SIR method, proposed in Li,⁴⁴ involves the model

$$\mathbf{y}=f(\mathbf{X}{\gamma }_1,\mathbf{X}{\gamma }_2,\dots ,\mathbf{X}{\gamma }_d,\epsilon )$$ (20)

where d < n, ε; is independent of X, γ_j are unknown column vectors, and f is an arbitrary unknown function on ℝ^d+1. Equivalently, the underlying assumption is that the conditional distribution of y given X depends on X only through (Xγ₁, …, Xγ_d). The goal is to reduce the dimension of the data X by estimating the vectors γ_j. Roughly speaking, the SIR procedure is as follows, after standardizing the data:

1. The range of y is divided into H slices.

2. Compute m_h, the mean of the observations corresponding to the y_i in slice h.

3. The principal components of (m₁, …, m_H) are computed, after weighting the m_h by the proportion of y_i that fall in slice h.

4. A linear transformation of the first d principal components gives (γ₁, …, γ_d).

The value of d is chosen by hypothesis testing. In many applications, d will be quite small, leading to a significant reduction in model complexity. The method of Li and Li⁴³ is as follows: since SIR requires that the covariance matrix of the data have full rank, they compute the first K principal components of the data in order to achieve dimension reduction. They then apply a version of SIR that is modified for survival outcomes,⁴⁵ using the principal components as the features. The resulting d-dimensional subspace can be fit to the outcome using a Cox proportional hazards model. For this method, K is a tuning parameter. The resulting model is linear in X and uses all of the features.

5.4.2 Methods based on partial least squares

Partial least squares (PLS) is a popular method for regression in high-dimensional settings. It is similar to PC regression, except that while the principal components in PC regression are selected in an unsupervised way, PLS selects these features using the outcome variable for guidance. In the regression case, with y the centered outcome, we seek a matrix W with columns w₁, …, w_k that solve

$${\mathbf{w}}_i={\text{argmax}}_{{\mathbf{w}}_i}{\mathbf{w}}_i^T{\mathbf{X}}^T\mathbf{y}{\mathbf{y}}^T\mathbf{X}{\mathbf{w}}_i\text{ subject to }{\mathbf{w}}_i^T{\mathbf{w}}_i=1,{\mathbf{w}}_i^T{\mathbf{X}}^T\mathbf{X}{\mathbf{w}}_j=0\forall j<i.$$ (21)

Then, the columns of T = XW are used as the predictors in a regression model for y.⁴⁶ A latent variable model underlies this approach. Comparing Equations (17) and (21), it is clear that PC regression and PLS are closely related. The number K of columns of T used in the regression model is a tuning parameter for the method; for K small, dimensionality reduction results. As with PC regression, PLS results in a model that is linear in X but not sparse in the features.

Many authors have extended the PLS method to the survival setting.⁴⁷⁻⁴⁹ The approach of Nguyen and Rocke⁴⁷ is quite simple: it involves treating the survival time y (which may or may not be censored) as a regression outcome, and finds the PLS components as described above for the regression case. (In other words, they make no use of whether an observation was censored in reducing the dimensionality of the data.) These components are then used as predictors in a proportional hazards model.

On the other hand, Park et al.⁴⁸ and Li and Gui⁴⁹ adapt the PLS procedure to the survival setting. Park et al.⁴⁸ do this by reformulating the failure time problem into a generalised linear model. Here, we focus instead on the simpler method of Li and Gui;⁴⁹ their adaptation of PLS to survival data is called partial Cox regression (PCR). Their algorithm, which generalises to PLS when the Cox proportional hazards models in Step 2(a) are replaced with least squares regressions, is as follows:

1. V¹ ← X.

2. For k ∈ 1, …, K:

   1. Fit a Cox proportional hazards model for each j, using as features ${\mathbf{V}}_j^k$ (column j of V^k) and (if k > 1) T₁, …, T_k−1. Let β̂_kj denote the coefficient of ${\mathbf{V}}_j^k$.
   2. Let $T_k={\sum }_j{\hat{\beta }}_{kj}{\mathbf{V}}_j^k$.
   3. V^k+1 is the matrix of residuals obtained after regressing each column of V^k onto T_k.

3. Now, T₁, …, T_K are the features in a Cox proportional hazards model; the resulting model can be re-written in terms of X because T_k is linear in X for all k.

This method makes use of the censoring status of each observation.

5.5 Other methods for prediction of survival

Most of the methods described for prediction of survival in previous sections have been linear in the features of X. Many non-linear models for prediction of survival in high-dimensional settings also have been developed. We might wish to model the data as

$$\lambda (t|\mathbf{X})={\lambda }_0(t)\text{exp}[F(\mathbf{X})],$$ (22)

where F(X) is not necessarily linear in X. Li and Luan⁵⁰ propose the use of a boosting procedure with smoothing splines in order to model non-linear effects in the data. In addition, all of the aforementioned methods could be performed after transforming the features as desired.

Moreover, the methods that we have discussed thus far have involved the use of a Cox proportional hazards model. Other options exist; for instance, Ma et al.⁵¹ and Martinussen and Scheike⁵² propose the use of an additive risk model.

A summary of the methods discussed for prediction of survival is given in Table 2.

Table 2.

Summary of methods discussed for predicting survival

Method	Sparsity	Description	Reference
Cox prop. hazards	No	Only applies if columns of X not multicollinear	Kalbfleisch and Prentice16
Univariate selection	Yes	Does not find best multivariate model	Klein and Moeschberger63
Stepwise selection	Yes	Computationally intensive; not global optimum	Klein and Moeschberger63
L2 shrinkage	No	Resulting coefficients can be small, but non-zero	Verweij and van Houwelingen28
L1 shrinkage	Yes	Dimension reduction and feature selection are integrated into one step	Tibshirani29
Covariance-regularised regression	Yes	Sparsity results if p2 = 1	Witten and Tibshirani36
Tree harvesting	Maybe	In general, not sparse; depends on clusters included in model	Hastie et al.39
Principal component regression	No	Outcome is regressed onto high-variance subspace of features	Massy40
SIR + PC	No	PC is followed by SIR44in order to reduce dimension before fitting survival model	Li and Li43
Supervised PC	Yes	PC is performed only on the features with highest Cox scores	Bair and Tibshirani41
PLS + Cox prop. hazards	No	PLS used to reduce dimension before fitting a survival model	Nguyen and Rocke47
PCR (PLS for Cox model)	No	PLS regression adapted to the survival setting	Park et al.48

6 Evaluation of methods for prediction of survival time

In Section 5, we presented a number of methods for predicting survival time in high-dimensional settings. However, two issues remain:

1. None of the aforementioned methods will dominate the others in every circumstance, so an approach is needed to determine which method is best for a given data set.

2. All of the methods described involve one or more tuning parameters. An approach for the selection of tuning parameter values is required.

These two tasks are closely related. In general, when one wishes to determine how well a model fits a given data set, one can split the observations in the data set into a training set and a test set. The model can then be fit on the training set and tested on the test set. In order to select the optimal value of a tuning parameter, cross-validation on the training set is commonly performed.

For both of these tasks, we require a method for evaluating the test set performance of a model developed on a training set. In the case of a quantitative outcome, one might use squared error to evaluate a model’s test set performance, and for a categorical outcome, misclassification error could be used. An analogous quantity is required for survival data, for which squared error is inappropriate due to censoring. In fact, as discussed in Graf et al.,⁵³ prognostic models for survival generally are not accurate at predicting time-to-event for a test observation. However, alternatives exist. Some possibilities for quantifying the performance of a model are as follows; these methods assume that the model is linear in the features.

1. Split the data into training and test sets; let the subscript ‘train’ denote the training data and ‘test’ denote the test data. In addition, let β̂_train denote the estimated coefficients based on X_train. Stratify X_test β̂_train based on some quantiles of its distribution. Then, a log-rank test can be used in order to determine whether there is a significant difference between the Kaplan–Meier survival curves for the resulting groups. This was done in Figure 3. This method has the drawback that information is lost in stratifying X_test β̂_train, but it has the advantage that it results in interpretable figures.

2. A continuous version of the previous method is to treat X_test β̂_train as a continuous predictor of test set survival in a univariate Cox proportional hazards model; a large log likelihood for the resulting model reflects a good fit.

3. The model’s test set performance can be quantified by evaluating the test set Cox log partial likelihood at β̂_train. This is done in e.g. Bovelstad et al.⁵⁴ The difference between this method and the previous one is subtle but important. In this method, we are taking β̂_train and plugging it into the formula for the Cox partial likelihood on the test set (see Equation (3)), whereas in the previous method, we fit a new Cox proportional hazards model on the test data with X_test β̂_train as the only predictor.

4. Let β̂_−i denote the coefficients obtained from a given model when observation i is excluded, and again let xⁱ denote observation i. Then the vector ${({\hat{\beta }}_{-1}^T{\mathbf{x}}^1,\dots ,{\hat{\beta }}_{-n}^T{\mathbf{x}}^n)}^T$ can be used as a predictor in a Cox model with outcome (y, δ); a large value of the resulting log likelihood indicates a good fit to the new observations (and, therefore, a good model). This method was proposed in Verweij and Van Houwelingen,⁵⁵ and does not require splitting the data into training and test sets. It can be interpreted as a form of leave-one-out cross-validation, and is closely related to the ‘pre-validation’ approach of Tibshirani and Efron.⁵⁶ It is computationally expensive, since it requires fitting n models, each containing n − 1 observations.

5. Another possibility proposed by Verweij and Van Houwelingen,⁵⁵ is as follows: one can compute the quantity

   $$\sum _{i=1}^n{l}_i({\hat{\beta }}_{-i})$$ (23)

   where l_i(β) = l(β) − l_(−i)(β) is the contribution of observation i to l(β), the Cox log partial likelihood of the full data set with coefficient vector β (l_(−i)(β) is the log partial likelihood when observation i is left out). A large value of the quantity (23) indicates a model that fits new observations well. Again, the data need not be split into training and test sets in order to use this method, which is computationally expensive.

In addition, Heagerty et al.⁵⁷ propose the use of ROC curves and Graf et al.⁵³ propose time-dependent measures of inaccuracy to assess predictive models for survival.

Bovelstad et al.⁵⁴ provide a comprehensive comparison of seven methods for prediction of survival: univariate selection, forward stepwise selection, principal components regression, supervised principal components regression, PLS regression, L₂ penalisation of the Cox partial likelihood and L₁ penalisation of the Cox partial likelihood. Based on the performance of these methods on three published gene expression data sets – Rosenwald et al.,⁵⁸ Sorlie et al.,⁵⁹ and van Houwelingen et al.⁶⁰ – they determine that L₂ penalisation of the partial likelihood yields the best predictions. However, as mentioned earlier, L₂ penalisation suffers from the major drawback that it does not result in a sparse model. Segal⁶¹ considers again the data set of Rosenwald et al.,⁵⁸ and compares the L₁-penalised proportional hazards model, SPC, and tree harvesting. The conclusion is that L₁ penalisation performs best, although gene expression ‘delivers only modest predictions of … survival’. Schumacher et al.⁶² also consider the performance of three prediction methods - univariate selection, L₁ shrinkage, and PCR - on the Rosenwald et al.⁵⁸ data set, and also find that L₁ shrinkage gives the best performance.

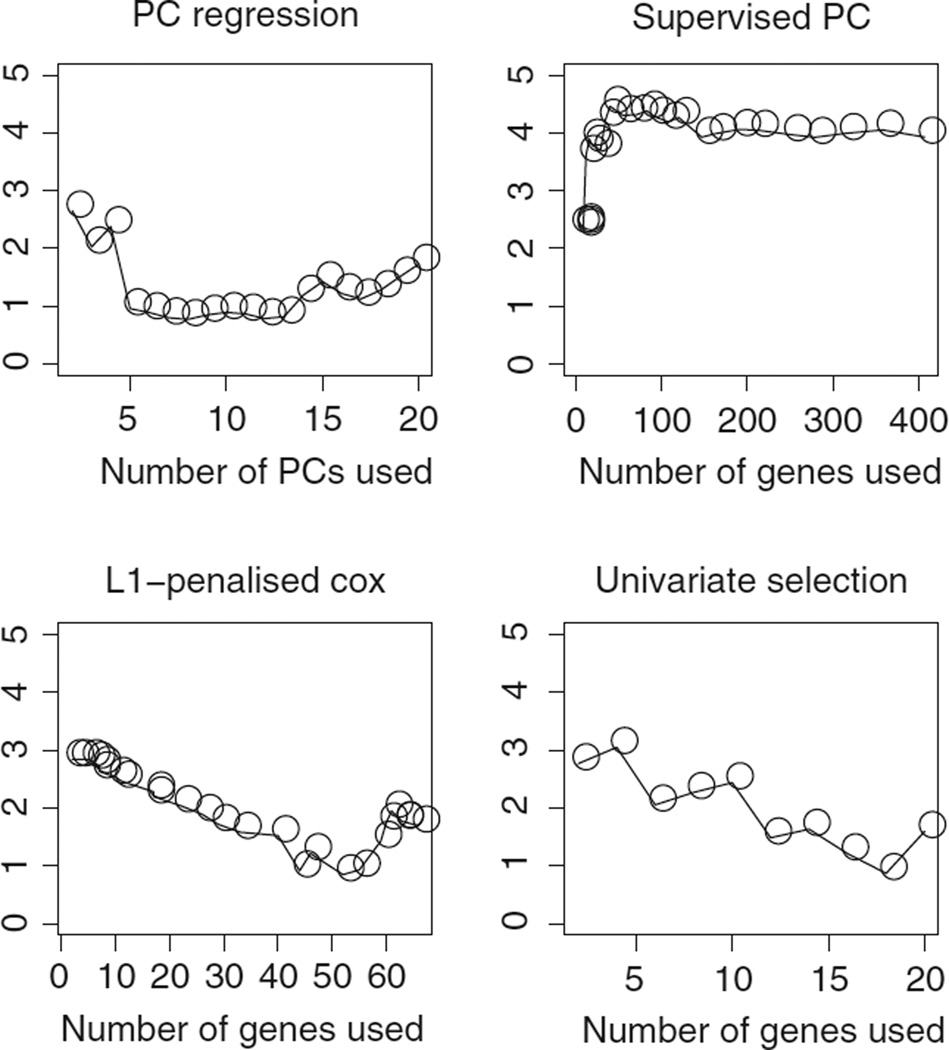
We compare the performances of PC regression, SPC, L₁ shrinkage, Scout(2, 1), and univariate feature selection on the 10% of genes with highest training set variance in the renal cell carcinoma data set of Zhao et al.¹ The training set and test set defined in the original article were used; models fit on the training set were evaluated on the test set using the second method for evaluating models proposed above. Tuning parameter values were selected by cross-validation on the training set. Cross-validation plots for each method can be seen in Figure 4. Test set results are reported in Table 3.

Figure 4.

For the Zhao et al.¹ data, the y-axes show the average value of 2(l(X_test β̂_train, y_test, δ_test)− l(0, y_test, δ_test)) across cross-validation folds; a large value indicates a good fit on independent data. The notation l(γ, y, δ) indicates the log partial likelihood of the Cox model with outcome (y, δ) and predictor γ. Scout(2, 1) is not shown in this figure because it involves two tuning parameters.

Table 3.

Five methods are compared on the data set of Zhao et al.¹For each method, tuning parameter values were selected via cross-validation on the training set. Models were evaluated on the test set. The notation l(γ, y, δ) indicates the log partial likelihood of the Cox model with outcome (y, δ) and predictor γ. The predictors developed on the training set are highly significant on the test set

Method	2(l(Xtest β̂train, ytest, δtest) − l(0, ytest, δtest))	p-value	Tuning parameter
PC regression	8.489	0.0037	2 PCs
SPC	12.70	0.00035	40 genes
L1-penalised Cox	4.402	0.0317	3 genes
Scout(2, 1)	11.307	0.0006	27 genes
Univar. feature selection	16.04	3.69 × 10−5	4 genes

7 Discussion

With the emergence of new, high-throughput biomedical technologies, statistical methods for the analysis of high-dimensional survival data have become increasingly important. We have presented a number of methods for survival analysis in high-dimensional settings, with a focus on identification of features that are associated with survival and construction of predictive models that perform well on independent test data.