Collective space sensing coordinates pattern scaling in engineered bacteria

Summary

Scale invariance refers to the maintenance of a constant ratio of developing organ size to body size. Though common, its underlying mechanisms remain poorly understood. Here we examined scaling in engineered E. coli that can form self-organized core-ring patterns in colonies. We found that the ring width exhibits perfect scale invariance to the colony size. Our analysis revealed a collective space-sensing mechanism, which entails sequential actions of an integral feedback loop and an incoherent feedforward loop. The integral feedback is implemented by the accumulation of a diffusive chemical produced by a colony. This accumulation, combined with nutrient consumption, sets the timing for ring initiation. The incoherent feedforward is implemented by the opposing effects of the domain size on the rate and duration of ring maturation. This mechanism emphasizes a role of timing control in achieving robust pattern scaling and provides a new perspective in examining the phenomenon in natural systems.

Introduction

Scale invariance, or the maintenance of constant relative size of an organ with respect to the whole body during animal development, or between individuals, is a common phenomenon in biology (Lesne and Lagues, 2012; Weymouth et al., 1942). For example, in the Drosophila embryo, the imaginal discs are segmented to scale with the embryo size (Bollenbach et al., 2008); in the vertebrate neural tube, the ventral neuroepithelium subdivides into neural progenitor domains with precise positional information (Balaskas et al., 2012; Dessaud et al., 2008). For natural systems, scale invariance of pattern to size is a major, but unsolved, problem in developmental biology. Several reviews have noted the difficulties of studying pattern scaling (Barkai and Ben-Zvi, 2009; Fried and Iber, 2014; Gisiger, 2001). A major challenge is the limited number of experimentally tractable systems to enable precise perturbation and quantification of pattern scaling. Less than a quarter of the animal models used for studying pattern formation are used to study scale invariance (Lander, 2011). Moreover, the networks underlying pattern formation or scaling in existing model organisms are often highly complicated, making it difficult to tease out generally applicable design principles. Most proposed mechanisms that explain pattern scaling are theoretically based.

When pattern formation is driven by one or more morphogen gradients, scale invariance can be explained by several mechanisms (Averbukh et al., 2014; Ben-Zvi et al., 2011b; Gurdon and Bourillot, 2001). Analogous mechanisms have been proposed to examine the scale invariance of system responses to varying inputs (Skataric et al., 2015). In a source-sink mechanism (Wolpert, 1969), a diffusible morphogen is generated from a source at the center of the system and degraded at the system boundary, which can establish a linear gradient from source to sink regardless of the system size. When two opposing gradients are involved, their ratio as a function of the spatial coordinate can exhibit scale invariance, which in turn can generate scale-invariant patterns (McHale et al., 2006). Alternatively, a system may adopt feedback to adjust the scaling of a morphogen gradient. In particular, the expansion-repression mechanism, whereby a system produces fast-diffusing chemicals that suppress the morphogen, can lead to a gradient that scales with the body size (Ben-Zvi and Barkai, 2010; Ben-Zvi et al., 2008).

Studies have indicated that pattern formation may not require morphogen gradients (Chen et al., 2012; Roth and Lynch, 2012). Such patterns are much less studied in comparison to those relying on morphogen gradients. It remains unknown whether and how scale invariance might emerge in such systems. Addressing this question is challenging, in part due to the complexity of natural systems, where many confounding factors complicate quantitative experiments and data interpretation. To overcome this limitation, we set out to examine the scaling dynamics of pattern formation in E. coli programmed by a synthetic gene circuit that we previously developed (Figure 1A) (Payne et al., 2013). The circuit consists of a mutant T7 RNA polymerase (Tan et al., 2009) (T7RNAP) that activates its own expression and that of LuxR and LuxI. LuxI synthesizes an acyl-homoserine lactone (AHL), a membrane-diffusible chemical that upon binding and activating LuxR, can induce expression of T7 lysozyme. Lysozyme inhibits T7RNAP by forming a stable complex with it. The T7-lysozyme complex inhibits the transcription of T7RNAP as well (Stano and Patel, 2004). CFP and mCherry fluorescent proteins are co-expressed with T7RNAP and lysozyme, respectively, to report the circuit dynamics.

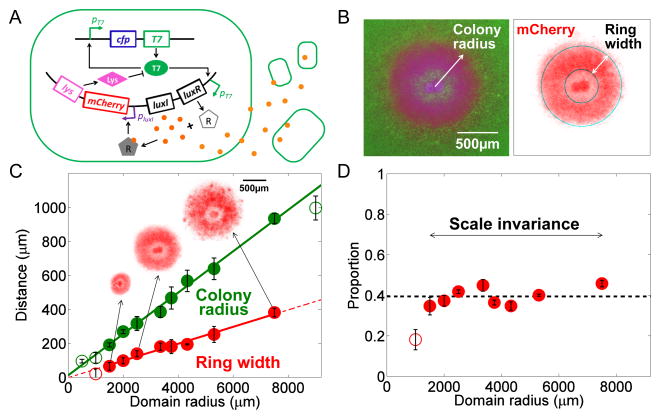
Figure 1. Scale invariance in self-organized pattern formation in engineered bacteria.

A. Circuit logic. The circuit consists of a T7 RNA polymerase that activates its own expression as well as the expression of LuxR and LuxI. Upon activation by T7RNAP (T7), LuxI mediates synthesis of AHL (A), which can diffuse across the cell membrane. When the global AHL concentration surpasses a threshold, intracellular AHL binds to LuxR to activate the synthesis of T7 lysozyme (L). Lysozyme then binds to the T7RNAP and forms a T7-lysozyme complex, therefore inhibiting the T7RNAP binding to the T7 promoter. This T7- lysozyme complex also inhibits T7RNAP transcription. In this process, the AHL concentration is affected by its initial concentration and the domain size. The expression rates of T7RNAP, lysozyme, and AHL are all controlled by the spatially dependent gene expression capacity.

B. Self-organized pattern formation in engineered bacteria. Left: A composite fluorescent image. Right: mCherry image extracted by MATLAB code from left composite image. Images of a 1.2mm × 1.2mm field of colony at 2500 μm domain radius after 24 h of incubation. The experimental platform used here was described in Figure S1A.

C. Scale invariance in self-organized pattern formation. The mCherry ring width (red circle) and the colony radius (green circle) are plotted as a function of the domain radius. Measurements were done in microcolonies after 32 h incubation. The error bars represent the standard error from ≥5 replicates for each domain radius. The solid lines represent the linear regression of the data points (green: colony radius; red: ring width) for intermediate domain radii (between 1500 μm and 7500 μm), where scale invariance emerges (the R-square value for ring width vs. domain radius linear regression is 0.9828; the R-square value for colony radius vs. domain radius linear regression is 0.9943). The purple block corresponds to domain radii<1500 μm; the yellow block corresponds to domain radii >7500 μm. The insets show mCherry images for domain radii of 1500 μm, 2500 μm, and 3750 μm, respectively. For all of the presented figures, if unnoted, filled circles represent the data where ring width vs. colony radius follows a linear regression with domain radius.

D. Ratio of mCherry ring width to colony radius for different domain radii. The ratio was calculated from the data in Figure 1C. The dashed line shows the average ratio for data points within the range of domain radii where the scale invariance emerges. The standard deviation of the ratio values between 1500 and 7500 μm is 0.0448 (~10% of the total constant ratio).

As AHL is highly diffusible, its spatial gradient is negligible over the length scale of pattern formation in this system. All else being equal, the time required for AHL to reach a critical concentration is inversely proportional to the size of the growth environment. Therefore, the production and accumulation of AHL enables a growing colony to collectively sense the domain size and to time the pattern formation accordingly (Payne et al., 2013). This sensing property suggests an opportunity to quantify pattern scaling in a well-defined experimental platform. Indeed, by using this system, we found a simple mechanism by which scale invariance can emerge without the need to scale the gradient of a diffusible morphogen.

Results

Scale invariance emerges from programmed pattern formation

We adopted an inkjet-printing technique to precisely control the inoculum size and the location of the initial seeding cells (Figures S1A–C) (Cohen et al., 2009). Briefly, bacterial culture was used as “ink” and printed onto the surface of soft agar in a multi-well device. This technique ensured precise control over the initial spatial arrangement of colonies and the initial cell number (~20) in each colony. By changing the configuration of initial cell placements, we were able to modulate the effective domain size of the growth environment available for each colony (Figure S1D).

Figure 1B shows a typical self-organized pattern in a microcolony at 24 h after incubation. The pattern consists of a core of high CFP and mCherry expression, as well as a wide peripheral ring of mCherry expression (see Figure S1E). This patterning process was reproducible (Figure S1F). In contrast, E. coli MG1655 cells not carrying the circuit did not generate these patterns under the same experimental conditions (Figure S1G).

The domain size plays a critical role in the observed patterning dynamics. No mCherry ring formed when the domain size was too small (<500 μm) or too large (>9000 μm). For intermediate domain sizes (between 1500 and 7500 μm), however, the ring width exhibited scale invariance with respect to the colony radius. Both were proportional to the domain radius (Figure 1C), leading to a constant ratio between them (Figure 1D).

Modeling reveals the essential requirements for scale invariance

The observed scale invariance is surprising, considering all of the diverse factors contributing to the patterning dynamics. Its simplicity suggests two possibilities. One is that the system parameters are extremely fine-tuned to generate such a simple outcome. Alternatively, beneath the apparent complexity of the circuit dynamics may be a simple regulatory core motif that ensures the observed outcome. If the latter is true, such a motif may define a generally applicable mechanism to generate robust scale invariance.

To address these issues, we formulated a set of partial differential equations (PDEs) to account for the circuit dynamics (see Supplemental Information), including intracellular gene expression and protein-protein interactions, bacterial growth and colony expansion (Figure S1H), and transport of intracellular components by cell movement (Edelstein-Keshet, 1988). Due to their fast diffusion and the geometry of device, AHL and nutrient were assumed to have uniform concentrations across space (Figure S2B). In our model, the term nutrient is used to refer to one or more factors that limit the overall colony growth. Our model also accounted for the spatial variation in gene expression capacity across the colony: this capacity was highest near the colony edge (defined as the location where cell density is 95% of the carrying capacity) and decreased toward the interior of the colony. This empirical function lumps potential contribution of multiple factors, such as mechanical stress (Jozefczuk et al., 2010), cell-cell contact inhibition (Morse et al., 2012), and oxygen concentrations (Prindle et al., 2015; Salmon et al., 2003).

The model has 22 parameters; we chose their initial values based on the literature data or biologically realistic estimates. Given the high dimensional parameter space, however, we did not attempt to determine one parameter set that best fits the experimental data - it would likely represent an overfit. Instead, we sought to determine the likelihood of finding some parameter sets able to generate the observed scale invariance, and then identify the commonalities among these parameter sets. To address these questions, we developed a search algorithm (see Supplemental Information) to explore the parameter space. We examined 18,231 parameter sets, in which we fixed all parameters that had been measured experimentally (Table S1) and varied the remaining nine parameters randomly in a pre-defined range of biologically meaningful values. For each parameter set, we simulated the patterning dynamics for varying domain sizes. We identified 409 parameter sets that produced mCherry core-ring patterns for varying domain sizes (Figure 2A, blue polygons). Of these 409 sets, 55 supported scale invariance (Figure S2C). This result underscores the notion that conditions underlying scale invariance are much more stringent than those underlying pattern formation (Lander, 2011; Rogers and Schier, 2011; Tomlin and Axelrod, 2007). To determine the conditions underlying scale invariance, for each of the 409 parameter sets, we performed a local optimization to generate a parameter set that produced scale invariance (see Supplemental Information, and Figure S2D for further details on the optimization).

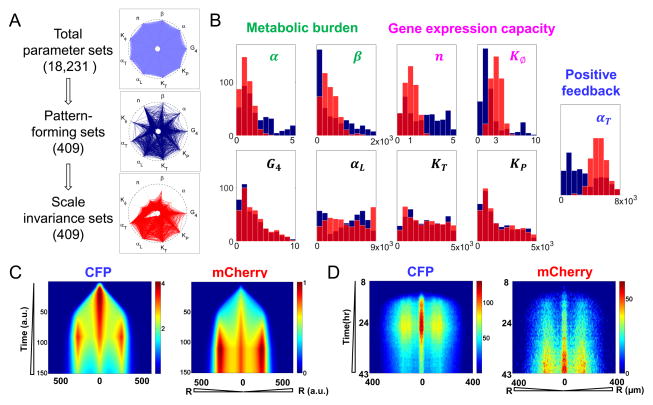
Figure 2. Pattern formation dynamics in engineered bacteria.

A. Parameter search. Each spike represents the range of a parameter, ranging from 0 to its maximum value (the intersect with the outer circle) (Von Dassow et al., 2000). G₄ was explored between 0 and 10; other parameters’ search ranges are listed in Table S1. Each polygon represents a parameter set. We started with 18,231 parameter sets (light blue). Dark blue lines indicate 409 parameter sets that generated core-ring patterns for varying domain radii (from 1 to 3). A local search on each of these 409 sets led to an optimal parameter set that generated scale invariance (red curves). α and β are the inhibition factors of T7RNAP and T7 lysozyme on cell growth, respectively. n is the Hill coefficient for distance-dependent gene expression capacity. K_φ is the half activation distance for gene expression capacity. α_T and α_L are synthesis rates of T7RNAP and T7 lysozyme, respectively. K_T and K_P are half-inhibition concentration of T7RNAP and T7-lyszome complex, respectively. G₄ is the synthesis rate of AHL, after non-dimensionalized.

B. Conditions underlying scale invariance. Five parameters shifted systematically during the optimization step: α and β characterize circuit mediated metabolic burden; n and K_φ determine the shape of gene expression capacity; and α_T characterize the strength of T7RNAP feedback. In contrast, the four other parameters, G₄, α_L, K_T and K_P did not change significantly during optimization. The blue histograms represent values from the 409 pattern-forming sets in Figure 2A before optimization. The red histograms represent values of the 409 sets resulting from the optimization. The light red is the overlap between blue and red histogram.

C. Simulated spatio-temporal profiles of CFP and mCherry intensity. Left: Average CFP intensity over colony cross-section from 1 to 150 in arbitrary unit. Right: Average mCherry intensity over colony cross-section from 1 to 150 in arbitrary unit.

D. Experimentally measured spatio-temporal profiles of CFP and mCherry. Left: average CFP intensity of bacterial colony at different radii from 8 h to 43 h. Right: Average mCherry intensity of bacterial colony at different radii from 8 h to 43 h. The experiments were measured at domain radius of 2500 μm.

Altogether, our parameter search and further optimization identified 409 parameter sets that generated scale invariance (Figure 2A). These parameter sets differed drastically from each other in terms of the range of the values we have searched for. This diversity suggests that scale invariance is a robust property that can be achieved by many combinations of parameters. We inspected the change of the parameter range during the optimization from pattern-forming sets to scale-invariance sets. Five parameters shifted in a consistent manner (Figure 2B). The final distributions of these parameters reveal three conditions for scale invariance. First, T7RNAP and lysozyme had minimal metabolic burden on cell growth, as indicated by reduced α and β values. Second, the gene expression capacity decreased slowly as a function of distance to the colony edge, as indicated by an optimal Hill coefficient (n) of around 1.0 and moderate width K_φ, which approximately matches the half-width of the colony wavefront. Third, the T7RNAP positive feedback needed to be sufficiently strong, as indicated by increased α_T values. When these conditions were satisfied, the search algorithm identified a much greater fraction of parameter sets able to generate scale invariance, without further local optimization (Figure S2E).

The first two conditions distinguish the patterns reported here from those described previously (Payne et al., 2013). This distinction is indeed consistent with the differences between the two experimental conditions, in terms of cell strains and experimental platforms (see the Supplemental Information for a detailed comparison). In particular, we measured growth of MC4100Z1 (the strain used in the previous study) and MG1655 (current study) cells carrying the pattern-formation circuit and its variants. These variants include the positive-feedback module, the pattern-formation circuit with the luxI gene knocked out, and the pattern-formation circuit with an effector gene co-expressed with the T7 lysozyme. Compared with MG1655 cells, MC4100Z1 cells experienced a higher metabolic burden when different circuits were induced. Furthermore, the pattern-formation circuit carrying an effector gene caused a higher metabolic burden than did the pattern-formation circuit by itself (Figure S2F). According to our simulation results, a high metabolic burden and a sharp gene expression profile would generate a narrow mCherry ring whose width does not show scale invariance with the colony size (Figure S2G, green boxed figure on left panel). These predictions are consistent with the experimental observation in the previous study (Payne et al., 2013).

Figure 2C shows simulated patterning dynamics from an optimal parameter set, which recapitulated the experimentally observed temporal dynamics of the CFP and mCherry pattern formation from 8 to 43 h (Figure 2D, also see Movie S1). Before the colony stopped expanding at ~12 h, CFP had accumulated to form a core at the center of the microcolony and a weak ring close to the colony edge. Its intensity continued to increase until ~26 h, when it began to decrease. Eventually, CFP decayed into a low and relatively flat profile (43 h). Because mCherry is controlled by T7RNAP via the LuxR/LuxI module, its dynamics lagged behind that of CFP. The mCherry core and ring emerged at ~16 h and kept increasing in intensity until the end of measurement. As a result, the mCherry pattern was much more sustained than that of CFP.

Scale invariance is mediated by a collective sensing mechanism

Inspection of the simulations reveals a collective space-sensing mechanism that underlies the patterning process and the resulting scale invariance. The growth environment acts both as a nutrient reservoir for colony growth and as a sink for AHL produced by the colony (Figure 3A). Everything else being equal, the rate of AHL accumulation decreases with the domain size. Therefore, the production and accumulation of AHL enables a colony to sense the domain size and to coordinate patterning. In other words, the domain size controls the pace and extent of colony expansion by determining nutrient availability. It also controls the timing of ring initiation by determining the accumulation of AHL produced by the colony. Meanwhile, the spatially dependent gene expression capacity provides the spatial cue to drive pattern formation. Scale invariance requires a proper coordination between the spatial and temporal cues, which are modulated by the domain size and circuit parameters. We now illustrate this notion by examining the key events during the mCherry patterning process, which can be divided into two phases: core formation and ring formation (Figures 2C, 2D, 3B).

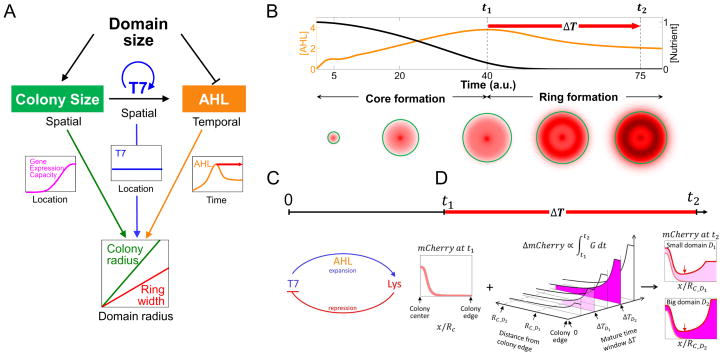
Figure 3. A collective space sensing mechanism underlies scale invariance.

A. A collective space sensing mechanism. The domain size controls the pace and extent of colony expansion by determining nutrient availability. The domain size also controls the timing of ring initiation by determining the accumulation rate of AHL. The interplay of the gene expression capacity (magenta curve), T7RNAP profile (blue curve), and AHL concentration (orange curve) leads to the scale invariance of ring width to colony size. The gene expression capacity and T7RNAP profiles are drawn as functions of the distance to the colony center at the final time point. The red arrow indicates the time window for ring maturation.

B. Simulated emergence of a core-ring pattern. Top: AHL (orange curve) and nutrient (black curve) concentrations over time. Bottom: Simulated mCherry distributions at different time points. The time points were labeled on x-axis. The mCherry ring initiates when AHL reaches its maximum concentration (t₁), which coincides with a pause of colony expansion (t₂). The ring matures during the time window, ΔT, between ring initiation and system stabilization (red arrow).

C. Emergence of scale invariance during core formation. When the colony is at fast expanding phase, the pattering process is mainly governed by an integral feedback topology which is similar to the expansion-repression model (Ben-Zvi and Barkai, 2010). In our model, the T7RNAP can be considered the expander that drives morphogen (AHL) synthesis, whereas the T7 lysozyme serves as the repressor. At time point t₁, the mCherry profile scales with the colony radius.

D. Emergence of scale invariance during ring maturation. All the x-axes are normalized to the domain radius. The units of y-axes are all on a per cell basis. Left: At different domain radii, the mCherry profile (pink) at the ring initiation time (t₁) approximately scales with domain size. R_C is the colony radius, and it is a function of domain radius. Middle: mCherry accumulation during maturation time (ΔT) is mainly determined by the gene expression capacity. The x-axis represents the distance from the colony edge. D₁ and D₂ are two different domain radii, D₁ < D₂. R_{C_D1} and R_{C_D2} are the colony radius for domain radii D₁ and D₁, respectively. The y-axis is ΔT, the maturation time window. ΔT_D1 and ΔT_D2 are the maturation time windows when the domain radii are D₁ (light magenta) and D₂ (dark magenta). The intersect of x- and y- axes represent that the mCherry accumulation rate is 0 at the colony edge at ring initiation time, t₁. The z-axis indicates the mCherry accumulation during the given time window. Right: mCherry at t₂ is a combination of that at t₁ (pink) and that accumulated during ΔT (color code is the same with that in middle panel). Its minimum is at the same relative location on the normalized axis (red pointer), indicating proportionality between the inner edge position and the domain radius. The outer edge of the ring pattern is roughly the colony edge, which is also proportional to the domain radius. Combining these two aspects leads to a ring width that scales with the colony size.

At the beginning stage of colony expansion, the T7RNAP positive feedback is active in all cells, leading to global CFP expression. AHL is building up to activate moderate mCherry expression. The gene expression capacity is uniformly high due to the small colony size. Due to the dilution from cell growth at the colony edge, CFP and mCherry are higher in the core at the single cell level. When the colony becomes sufficiently large, such that the colony width is greater than K_φ, it manifests effects of the spatial dependence of the gene expression capacity. This spatial dependence combined with a strong T7RNAP positive feedback leads to formation of a CFP ring near the colony edge. However, because the expression of mCherry is weaker than that of CFP and insufficient to overcome the dilution due to fast cell growth at the colony edge, there is no mCherry ring formed yet. This phase defines the mCherry core formation. Near the colony edge, the advection of T7RNAP by colony growth and expansion negates effects of the high gene expression capacity, preventing accumulation of T7RNAP or the lysozyme near the edge. The T7 lysozyme profile is thus mainly determined by circuit logic and growth dilution. This phase is reminiscent of the expansion-repression mechanism (Averbukh et al., 2014; Ben-Zvi and Barkai, 2010). In our system, cell growth establishes a gradient by contributing to transport and dilution of a target molecule. The T7RNAP can be considered the expander that drives morphogen (AHL) synthesis, whereas the T7 lysozyme serves as the repressor. As a result of this feedback, the mCherry profile scales with colony radius at the end of first stage (Figure 3C).

As AHL keeps increasing, the metabolic burden and nutrient depletion together slows down colony growth and expansion. Due to the interplay between the T7RNAP positive feedback and the AHL-mediated negative feedback (via lysozyme), T7RNAP has also become approximately uniform across space (Figures S3A–C). Therefore, the spatial dependence of mCherry is primarily determined by the gene expression capacity, which triggers initiation of the mCherry ring near the colony edge. This process is facilitated by the slowdown in overall cell growth. Conversely, the accumulation of mCherry (and thus the lysozyme) further enhances repression of T7RNAP, which contributes to the down regulation of AHL. Afterwards, the mCherry continues to be expressed across the colony, at rates constrained by the gene expression capacity. The maturation of the mCherry ring is characterized by its widening toward the colony center (Figure 3D).

The collective space-sensing mechanism provides a simple interpretation of the three critical requirements for scale invariance identified by our search algorithm. A low metabolic burden by the circuit components ensures that the colony expansion is limited not by the accumulation of a circuit species but rather by nutrient availability, which in turn is limited by the domain size. This coupling allows a perfect coordination between the stop of colony expansion and initiation of the ring at the colony edge.

To generate scale invariance, AHL and T7RNAP both need to be sufficiently uniform across space. The uniform distribution of AHL results from its fast diffusion. The uniform distribution of T7RNAP results from the interplay between the T7RNAP positive feedback and AHL-mediated negative feedback. Strong T7 positive feedback is critical for buffering against the varying gene expression capacity, ensuring a flat T7RNAP profile along the domain.

Finally, scale invariance requires a moderate gene expression capacity gradient, which has to decrease significantly toward the colony center. If the gene expression did not decrease, mCherry would be uniform across the entire colony. If the gene expression decreased too sharply, only a narrow mCherry ring would emerge and its width would not scale with the colony width (Figure S2G).

These insights provide an intuitive interpretation for the emergence of scale invariance. When the ring initiates, the mCherry profile scales with the domain size. Thanks to the flat T7RNAP and AHL profiles, maturation of the mCherry ring is driven by gene expression capacity, which has a constant half-width K_φ. When K_φ matches the half-width of the colony wavefront and when the duration of maturation time window scales with the domain size, the change in mCherry during maturation will also scale with the domain size. As a result, the final mCherry profile scales with the domain size (See Supplemental Information and Figure 3D, Figures S3D–G for detailed reasoning).

The scale invariance is disrupted by perturbing temporal or spatial cues

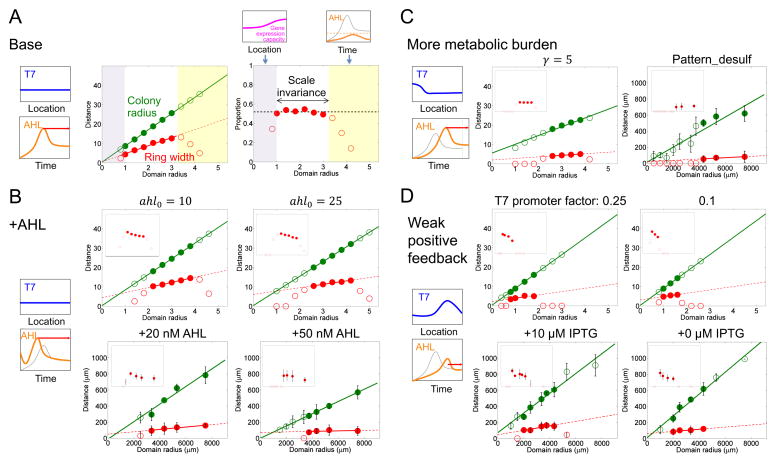
Using the base parameter set (Table S2), simulations (Figure 4A) recapitulate the experimentally observed scaling properties (Figures 1C, D), where perfect scale invariance emerged for an intermediate range of domain sizes. According to this mechanism, the pattern formation or scale invariance can be disrupted by perturbing the temporal or spatial cues. When the domain size is too small, the colony size is too small for a distinct ring to emerge. In other words, the ring merges with the core to manifest no distinguishable pattern (Figure 4A, purple region). If the domain size is too large, AHL cannot accumulate to a high enough concentration to trigger ring initiation (Figure 4A, yellow region), again leading to the loss of scale invariance. Both aspects are consistent with experimental data (purple and yellow shaded regions in Figures 1C, D).

Figure 4. Modulation of scaling property by environmental factors.

A. Simulated scale invariance (base case). Left: Illustration of T7RNAP and gene expression capacity shape in the scale invariance range. Middle: Dependence of the ring width (red circles) and the colony radius (green circles) on the domain radius. The solid lines represent the linear regression of the colony radius and the ring width with respect to the domain radius in the white region. Solid circles represent the linear range of the dependence of the ring width and colony radius on the domain radius. Right: The ratio of mCherry ring width to the colony radius for different domain radii. The dashed line shows the average ratio for the values in the white region. Top left: Illustration of gene expression capacity profile when the domain is too small (purple shaded regions in Top and Middle panels). Top right: Illustration of the AHL profile over time when the domain is too large (yellow shaded regions in Top and Middle panels). The thinner gray curve corresponds to the AHL profile in the left panel; the thicker orange curve corresponds to a larger domain. These results correspond to time point t₂.

B. Modulating the scaling property by adding exogenous AHL. Left: T7RNAP and gene expression capacity profiles were the same with those in base case. Adding exogenous AHL changes the temporal cue. The thinner gray line indicates the AHL concentration over time in the base case; the thicker orange line indicates the AHL concentration over time in the presence of initial exogenous AHL. The ring maturation window is longer (red arrow) compared with the base case. Right top: Simulated scaling property when the parameter of initial exogenous AHL (ahl₀) were set to 10 and 25 (from left to right). The two figures show relationships of the colony radius and of the ring width to the domain radius with different initial AHL concentrations. The insets represent the ratio of the ring width to the colony radius. The x-axes for the insets are on the same scale as the corresponding figure panels; the y-axes range from 0 to 1. Right bottom: Experimentally measured scaling property in the presence of 20 nM AHL and 50 nM AHL (from left to right). The two figures are plotted as in Figures 1C, D. The error bars represent the standard error or range of 2–5 replicates. Each data point was obtained at 32h after start of experiment.

C. Modulating the scaling property by having a higher metabolic burden. Cell growth is slowed down at a high metabolic burden, so AHL reaches its peak value later than in the base case. At that time, T7RNAP distribution over space is not flat yet; instead, it has a higher distribution near the center of the colony, which will increase the mCherry core accumulation during the ring maturation stage. Because the maturation time is shorter, the ring cannot catch up with the core formation and the eventual ring width is smaller. The figure symbols are the same as those in Figure 4B. Simulated scaling properties with γ, the metabolic burden from an effector gene, at a value of 5 (γ = 0 for the base case).

D. Modulating the scaling property by using weak T7RNAP positive feedback. Due to the weak feedback, the T7RNAP distribution over space is no longer flat but instead reflects that of the gene expression profile. The weak feedback also slows down accumulation of AHL, thus delaying the ring initiation in comparison with the base case. Therefore, the ring maturation time (red arrow) is shorter than that in the base case. The figure symbols are the same as those in Figure 4B. The scaling property was simulated with varying positive-feedback strength (the T7 promoter rate is 0.25 or 0.1 fold of promoter rate when circuit is fully induced).

The timing cue can be modulated by adding exogenous AHL, which accelerates ring initiation (Figure 4B, Figure S4E). Our model predicts that the ring width remains a linear function of an intermediate domain size. In comparison with the base case, however, this range of domain sizes conferring the linear dependence is narrower and shifts toward large domain sizes with increasing AHL concentrations. In addition, the linear function has a positive intercept, leading to loss of scale invariance. Both predictions were validated by our observed patterning dynamics in the presence of 10–50 nM exogenously added AHL. The loss of scale invariance is due to two consequences of exogenous AHL (Supplemental Information, Figures S4A–D). First, the maturation time window no longer scales with the domain size, as the ring initiation time is decoupled with the domain size, unlike the base case. Second, the half-width of the colony wavefront becomes wider due to a slight increase in metabolic burden, resulting from accelerated expression of lysozyme and mCherry. This causes a mismatch with the half-width of the gene expression capacity profile. The combination of these effects cause loss of scaling of the mCherry accumulation with respect to the domain size during the maturation phase.

Another key condition for generating scale invariance is the low metabolic burden from gene expression on growth. The metabolic burden controls the pace of cell growth and gene expression. With a higher metabolic burden, the AHL synthesis rate is smaller because of the slower growth rate, so it takes a longer time to reach the peak concentration. This provides a shorter time window for ring maturation (Figure 4C, Figure S4F). Thus, we would expect the ring width to become smaller than the base case. Furthermore, a high metabolic burden cannot maintain a flat T7RNAP profile when the ring initiates. Our model predicts that the combination of these effects would lead to loss of scale invariance. We tested this prediction using an extended circuit containing a cysteine desulfhydrase gene co-expressed with the T7 lysozyme, which caused a greater metabolic burden than did the pattern-formation circuit itself (Figure S2F). When induced, cells carrying the extended circuit indeed exhibited dynamics predicted by modeling (Figure 4C). Compared with the base case, the ring width became smaller. It remained a linear function of the domain size over a narrower range of domain sizes, and this range shifted toward larger domain sizes. These changes in dynamics led to loss of scale invariance.

The strength of the T7RNAP positive feedback controls both temporal and spatial cues. With a weak positive feedback, the AHL synthesis rate is smaller, and it takes a longer time to reach the peak concentration. This provides a shorter time window for ring maturation (Figure 4D, Figure S5E). Thus, we would expect the ring width to become smaller than the base case. In addition, the model predicts that, in comparison to the base case, the range of the domain sizes that allow pattern formation will shrink and shift toward small domain sizes. Furthermore, a weak positive feedback cannot maintain a flat T7RNAP profile when the ring initiates, as T7RNAP expression itself will be primarily determined by the profile of the gene expression capacity (Supplemental Information, Figure S5A–D). Our model predicts that the combination of these effects would lead to loss of scale invariance. Experimentally, the strength of the positive feedback can be controlled by the strength of the promoter driving T7RNAP, which is induced by isopropyl β-D-1-thiogalactopyranoside (IPTG). The T7RNAP feedback weakens when IPTG concentration is low. Under these conditions (100 μM, 10 μM, 1 μM and 0 μM IPTG), the circuit generated a corering pattern that was substantially weakened in fluorescent intensity (Figure S2A) compared with that resulting from a strong positive feedback. The ring width remained a linear function of the domain size over a narrow range of domain sizes. As predicted by modeling, however, this range was narrower and shifted toward smaller domain sizes in comparison with the base case when the IPTG concentration was reduced (Figure 4D).

Discussion

In comparison with pattern formation, pattern scaling is more challenging to study due to its intrinsically more stringent requirements, in terms of both the underlying regulatory network architecture and the associated reaction mechanisms and parameters. This greater challenge is reflected in the scarcity of well-established, generally applicable mechanisms to explain pattern scaling, in comparison with other aspects of biological patterning (Lander, 2011; Stathopoulos and Iber, 2013). Most mechanisms proposed to explain scale invariance rely on the scaling of morphogen gradients. Our results reveal a collective space sensing mechanism to coordinate colony growth and patterning dynamics to generate scale invariance. Our circuit logic resembles that of the expansion-repression model (Ben-Zvi and Barkai, 2010; Ben-Zvi et al., 2011a). However, the dynamic constraints underlying the scale invariance are different from the expansion-repression model. Our mechanism does not require a gradient of the morphogen, but instead relies on the morphogen as a timing cue to trigger pattern initiation.

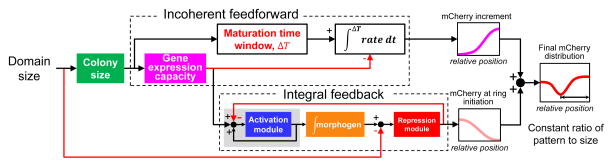
From a control perspective, our mechanism entails sequential actions of an integral feedback loop and an incoherent feedforward loop (Figure 5). The integral feedback is implemented through the simultaneous sensing of the domain size using two species, AHL and nutrient. The combined effects of AHL accumulation and nutrient consumption set the timing for the core formation and the ring initiation. As a result, the integral feedback plays a critical role in generating the mCherry distribution at ring initiation time that scales with the colony size.

Figure 5. Sequential actions of integral feedback and incoherent feedforward underlie the scale invariance.

The overall system input is the domain size; the output is the mCherry pattern in a colony scaled with respect to the domain size. The integral feedback underlies a scale-invariant mCherry distribution at ring initiation. In our system, the activation module represents the strong T7RNAP positive feedback; morphogen represents AHL; the repression module represents T7 lysozyme. The incoherent feedforward controls the mCherry increment during maturation time window of ring formation. ΔT is a proportional function of domain size; rate represents mCherry accumulation rate, which is dominated by gene expression capacity during ring maturation. At the same relative location, a larger domain results in smaller gene expression capacity and thus a reduced accumulation rate in mCherry. This reduction is compensated by the increase in ΔT, leading to the same increment in mCherry at the same relative position for different domain sizes. The sum of the mCherry distribution at ring initiation and the increment during maturation leads to the final mCherry ring (red) that scales with the domain size. The color code is the same as in previous figures.

The incoherent feedforward loop is implemented through the opposing effects of the domain size on two aspects of mCherry accumulation across space. A larger domain size leads to a larger colony, thus reducing the rate of mCherry gene expression at the same relative position on a scaled axis. However, this reduction is compensated by an extended maturation time, leading to an increment of mCherry that is equivalent at the same relative position within the colony (Figure 3D, 5). The combination of the mCherry profiles at the ring initiation and after ring maturation leads to the final pattern that scales with the colony size. This last step resembles the opposing gradient model (McHale et al., 2006), which relies on the combination (Houchmandzadeh et al., 2005) or annihilation (Howard and Wolde, 2005) of two gradients to generate scaling patterns. However, in our system, the two opposing profiles are not due to molecular diffusion. In addition, the two gradients are sequentially super-imposed.

It is increasingly appreciated that synthetic gene circuits can serve as well-defined model systems to elucidate “design principles” of biological networks (Brophy and Voigt, 2014; Slusarczyk et al., 2012; Tanouchi et al., 2012). The simplicity of the reduced systems enables a high degree of experimental control, which facilitates the deduction of definitive conclusions (Jessup et al., 2004). Therefore, studies based on synthetic systems can advance the understanding of the underlying mechanisms or processes that are too complicated to study in natural systems (Elowitz and Lim, 2010). To this end, studies have demonstrated engineering of gene circuits to examine formation of diverse patterns in response to autonomously generated or externally imposed morphogen gradients (Basu et al., 2005; Liu et al., 2011; Schaerli et al., 2014; Tabor et al., 2009). In contrast, our study focuses on deducing a mechanism underlying the scaling properties of self-organized patterns. Our mechanism underscores the role of temporal control in both generating and scaling patterns.

Geometrically, the patterning process in our system resembles that during the embryonic development in birds and reptiles that occurs in a hard-shell egg. The egg is a self-contained life-supporting system (Sinervo, 1992), where the shell defines the domain size. Among same species, the vitelline (yolk) weight before embryotic development and hatchling sizes increase isometrically with the egg size (Brawand et al., 2008; Dzialowski and Sotherland, 2004). Mechanisms analogous to what we present here could be responsible for generating the scaling property in these systems.

The overall simplicity of our mechanism in terms of the underlying dynamic constraints suggests its applicability to the interpretation of scaling properties of natural biological systems. For example, in the vertebrate neuron tubes, Sonic Hedgehog (Shh) is a morphogen that controls the pattern of neuronal subtype formation (Briscoe and Ericson, 2001; Dessaud et al., 2008). Interestingly, the Shh concentration in the neural tube is found to be much higher than that required to trigger pattern formation (Chen et al., 2012), and, the duration of Shh plays a critical role in controlling the pattern size (Ahn and Joyner, 2004; Pages and Kerridge, 2000). Since cells are known to become insensitive to Shh after prolonged exposure (Dessaud et al., 2007), it is conceivable that the duration of elevated Shh concentration may serve as a timing cue to initiate patterning and to time pattern maturation. Also, both the nutrient and AHL are critical in driving pattern formation and scaling in our system. In general, their roles can be fulfilled by other factors controlling tissue growth and gene expression, such as those proposed in the chalone hypothesis (Bullough, 1962; Gamer et al., 2003).

Experimental procedures

Plasmids, cell strains, and growth media

The full circuit consists of two plasmids: pET15bLCFPT7 and pTuLys2CMR2 (Payne et al., 2013). We used ptetmCherry (Payne et al., 2013) for constitutive expression of mCherry. Unless noted otherwise, MG1655 cells carrying the circuit or the control plasmids and 2×YT medium (Sambrook and Russell, 2001) (with pH adjusted to 6.5 using 1M KOH) were used for all experiments.

Experimental set-up

We used the Epson Stylus Photo R280 Ultra Hi-Definition Photo Printer (C11C691201), along with PrintPayLess Empty Refillable Ink Cartridges, for printing experiments (Cohen et al., 2009). To facilitate manipulation, the outer shell of the printer was disassembled and removed. Print heads were cleaned before and after each experiment. First, the printer head box was repositioned to the middle of the printer trail and absorbent paper towels were placed under the printer head to collect the liquid flushing through the printer heads. Second, the printer heads were flushed with 75% ethanol once, followed with washing with deionized water three times using a syringe. The paper towels were removed and the printer head box was then placed back in its original spot.

0.3% 2 ×YT agar was prepared in microwave. We then cooled the agar below 50°C at room temperature, and supplemented it with 75 μg/mL carbenicillin, 50 μg/mL chloramphenicol, and 1000 μM β-D-1-thiogalactopyranoside (IPTG). We next pipetted 170 μL of the agar into each culture well (Grace Bio-Labs; Bend, OR, USA; Item #103310), and let it solidify at room temperature.

An overnight culture of MG1655 cells carrying the full circuit was diluted to 0.2 absorbance (measured by Victor 3 plate reader) and then diluted another 50 fold into fresh LB broth. The diluted culture was transferred into a tone empty ink cartridge using a sterile syringe. The other five cartridges were filled with deionized water with a 0.2 μm filter (VWR® Syringe Filters, # 28145-477).

Printing templates were designed in software GIMP using 1-pixle diameter spots. Each template was exported to an Epson CD printer program to direct printing of bacteria onto the agar surface. After printing, a 24 mm×50 mm glass coverslip was placed on the top of the culture well. All of the inkjet-printed samples were incubated at 30 °C for 16–43 h. After incubation, the samples were imaged under a Leica DM16000B fluorescence microscope with a mercury excitation lamp at 5X.

Mathematical modeling

The PDE model used in the current study corresponds to the hydrodynamic limit of the stochastic agent-based model from (Payne et al., 2013). The PDE formulation has two advantages. First, it is computationally less expensive to solve the PDE model numerically than the stochastic agent-based model. This increased computational efficiency enables extensive parameter. Second, the PDE formulation better facilitates development of mechanistic insights into the patterning dynamics. Because the air pocket between glass plate and dense agar is only 20 μm high (Figure S1H), we model the system in two spatial dimensions and neglect vertical variations in gene expression profiles. The circuit dynamics can be described by the following PDEs:

$$\{\begin{array}{l}\frac{\partial C}{\partial t}={\kappa }_C\mathrm{\Delta }C+{\alpha }_C\frac{1}{1+\alpha T+\beta L}·\frac{N}{K_N+N}C\left(1-\frac{C}{\overline{C}}\right),\hfill \\ \frac{dN}{dt}=-\frac{{\alpha }_N}{\mid \mathit{\Omega }\mid }{\int }_{\mathit{\Omega }}C\left(1-\frac{C}{\overline{C}}\right)\frac{N}{K_N+N}d\sigma ,\hfill \\ \frac{dA}{dt}=\frac{{\alpha }_A}{\mid \mathit{\Omega }\mid }{\int }_{\mathit{\Omega }}C\frac{T}{K_T+T}\frac{K_P}{K_P+P}\phi (x,C)d\sigma -d_{A}A,\hfill \\ \frac{\partial T}{\partial t}={\kappa }_C\frac{\nabla \mathrm{T}·\nabla \mathrm{C}}{C}-{\alpha }_{C}T\frac{N}{K_N+N}\left(1-\frac{C}{\overline{C}}\right)-d_{T}T+{\alpha }_T\theta (C)\frac{T}{K_T+T}\frac{K_P}{K_P+P}\phi (x,C)\hfill \\ \frac{\partial L}{\partial t}={\kappa }_C\frac{\nabla \mathrm{L}·\nabla \mathrm{C}}{C}-{\alpha }_{C}L\frac{N}{K_N+N}\left(1-\frac{C}{\overline{C}}\right)+{\alpha }_L\theta (C)\frac{T}{K_T+T}\frac{A^m}{K_A^M+A^m}\phi (x,C)-d_{L}L\hfill \\ \frac{\partial P}{\partial t}={\kappa }_C\frac{\nabla \mathrm{P}·\nabla \mathrm{C}}{C}-{\alpha }_{C}P\frac{N}{K_N+N}\left(1-\frac{C}{\overline{C}}\right)+k_{1}TL-k_{2}P,\hfill \end{array}$$ (1)

where C(t, x) is the cell density; N(t) is the nutrient concentration; A(t) is the AHL concentration; T(t, x), L(t, x), P(t, x) are cellular T7RNAP, lysozyme and the T7-lysozyme complex density respectively. See Table S1 for description of all model parameters.

In deriving the above equations, we made the following assumptions:

1. Cells are assumed to perform an unbiased random walk and their movement is modeled as diffusion (Kenkre, 2004; Maini, 2004; Murray et al., 1998). We considered “diffusion” as an approximation of the observed colony expansion, so that cell movement can be described by a single lumped parameter. Intracellular components are modeled with passive-tracer equations (see Supplemental Information for detailed derivation).

2. Cell growth is modeled with a logistic term, along with a Monod function. The Monod function is to account for contribution of nutrient to cell growth. The logistic term accounts for the limit of cell growth in a particular location. This carrying capacity is unlikely to be limited by nutrient availability; instead, it is limited by the spatial confinement imposed by our device, e.g. the colony height is confined to be ~20 μm between the coverslip and the agar surface.

3. Fast diffusion of AHL and nutrient.

4. Gene expression capacity:

$$\phi (x,C)=\{\begin{array}{rr}\hfill \frac{K_{\phi }^n}{K_{\phi }^n+{\left(R_{\phi }-x\right)}^n},& \hfill x\le R_{\phi }\\ \hfill 1,& \hfill x>R_{\phi }\end{array}$$ (2)

where R_φ is defined as the distance between colony center and the location where cell density is 95% of the carrying capacity (parameters are all described in Table S1).