A Bayesian Model for the Identification of Differentially Expressed Genes in Daphnia Magna Exposed to Munition Pollutants

Summary

In this paper we propose a Bayesian hierarchical model for the identification of differentially expressed genes in Daphnia Magna organisms exposed to chemical compounds, specifically munition pollutants in water. The model we propose constitutes one of the very first attempts at a rigorous modeling of the biological effects of water purification. We have data acquired from a purification system that comprises four consecutive purification stages, which we refer to as “ponds”, of progressively more contaminated water. We model the expected expression of a gene in a pond as the sum of the mean of the same gene in the previous pond plus a gene-pond specific difference. We incorporate a variable selection mechanism for the identification of the differential expressions, with a prior distribution on the probability of a change that accounts for the available information on the concentration of chemical compounds present in the water. We carry out posterior inference via MCMC stochastic search techniques. In the application, we reduce the complexity of the data by grouping genes according to their functional characteristics, based on the KEGG pathway database. This also increases the biological interpretability of the results. Our model successfully identifies a number of pathways that show differential expression between consecutive purification stages. We also find that changes in the transcriptional response are more strongly associated to the presence of certain compounds, with the remaining contributing to a lesser extent. We discuss the sensitivity of these results to the model parameters that measure the influence of the prior information on the posterior inference.

1. Introduction

Quality of water is a very important issue for modern society. The number and diversity of chemicals discharged into the environment is increasing with the size of the population and its diversity, posing a largely unknown hazard to the ecosystem and the human health. In the year 2000, a Water Framework Directive of the European Parliament and Council has committed European countries to achieve good surface water quality by 2015. Evaluating the effects of waste waters on aquatic organisms has therefore become an interesting challenge.

In the last decade, new water purification systems have been introduced and studied. Their aim is to improve the biological and chemical quality of the waters discharged from waste water treatment plants, before they are released into the fresh water ecosystem. One example is the Waterharmonica Improving Purification Effectiveness (WIPE) project (Kampf and Claassen, 2004; Kampf et al., 2005), in the Netherlands, which consists of artificially constructed wetland environments. The advantage of such bioremediation systems lies in their low costs and in the additional ecological value. Indeed, Sebire et al. (2011) give evidence that purification systems greatly reduce the risk for the environment.

In the past, whole-organism responses, such as mortality and reproduction, have been used in order to evaluate the biological effects of industrial pollutants (De Schamphelaere et al., 2004; Jemec et al., 2007). However, such responses are only the endpoints of variations at a molecular level and, as such, provide only limited information. For this reason, more recent studies have focused on evaluating changes in gene expression on various organisms, as caused by the presence of chemicals in the water. Daphnia magna, a cladoceran freshwater flea, has been largely used for testing toxicity of water (Soetaert et al., 2006; Jo and Jung, 2008). This organism plays a key role in the aquatic food chain, it is highly sensitive to chemicals, easy to culture in laboratory and it is a widely spread species.

Daphnia magna has been intensively studied using functional genomics techniques, which allow measuring thousands of cellular molecular components in single experiments. Jo and Jung (2008) studied the effect of exposure to rubber waste water on gene expression in Daphnia magna, while Scanlan et al. (2013) investigated the effects of the exposure to silver nanowire. Also, Antczak et al. (2013) used molecular toxicity identification evaluation to predict chemical exposure. In this paper, we investigate the effect of chemicals, in particular munition pollutants, on the gene expression of Daphnia magna using the data introduced by Garcia-Reyero et al. (2012) and available at the NCBI GEO site (http://www.ncbi.nlm.nih.gov/geo/) with accession number GSE13169. The bioremediation system we use comprises of 4 consecutive purification stages (which we refer to as “ponds”) of progressively more contaminated water. We look at the exposure to mixtures of six chemical constituents and consider an order of the ponds from the most pure water to the pond with the highest concentration of chemicals. Even though relatively simple, the model we present in this paper constitutes one of the very first attempts at a rigorous modeling of the biological effects of water purification.

The major interest of a water purification experiment is in the identification of the differentially expressed genes in consecutive ponds. For this, we propose a hierarchical Bayesian model of the expected change in expression. The model further incorporates a variable selection prior that accounts for the available information on the concentration of chemical compounds present in the water. This allows us to estimate the relative influence of single chemicals on the probability of a change in expression. In order to simplify the complexity of the gene expression profiling data, we group genes by their functional characteristics (defined by the biological pathway database KEGG) and then express the transcriptional activity of each pathway by means of its principal components. Our model successfully identifies a number of pathways that show differential expression between consecutive ponds. These mainly represent membrane, signaling, and translational and transcription pathways. We also find that changes in the transcriptional response are more strongly associated to the presence of TNT and 2,4-DNT, with the remaining compounds contributing to a lesser extent. We discuss the sensitivity of these results to the model parameters that measure the influence of the prior information on the posterior inference. We also compare the performances of our method with those obtained using the significance analysis of microarrays (SAM) method. Our model succeeds in identifying additional important pathways not identified by SAM, in addition to providing estimates of the effects of specific chemicals on the observed transcriptional response.

The model we propose in this paper constitutes one of the very first attempts at a rigorous modeling of the biological effects of water purification. The approach we take is general and can be applied in a variety of experimental settings. Unlike most of the common approaches, that look at the effect of single compounds (Falciani et al., 2008; Garcia-Reyero et al., 2012; Gust et al., 2013), our method considers mixtures of multiple compounds and helps identifying not only the associated molecular responses but also which compound is dominant in the mixture. This approach can be used not only to understand how water purification systems work, but also how dissipation of chemicals into the environment are affecting different areas of the ecosystem, possibly even biodiversity.

The rest of the paper is organized as follows: In Section 2 we introduce the hierarchical model of the expected change in expression between consecutive ponds. We also describe the variable selection prior and the MCMC algorithm for posterior inference. Section 3 gives details on the Daphnia magna experimental study and the results from the data analysis. Section 4 contains some final remarks.

2. Methods

In this paper, we propose a Bayesian hierarchical model to investigate the effect of chemical compounds, in particular munition pollutants, on the gene expression of Daphnia magna. The bioremediation system we use comprises of 4 consecutive purification stages (which we refer to as “ponds”) of progressively more contaminated water. We model the expected change in the expression of a gene between subsequent ponds. We further incorporate a variable selection mechanism for the identification of the differential expressions, with a prior distribution on the probability of a change that accounts for the available information on the concentration of chemical compounds present in the water.

2.1 Hierarchical Model

Let Y_igt denote the expression measurement for gene g (g = 1, …, G) in pond t (t = 0, …, T ), from sample i (i = 1, …, N_t). Note that we allow each pond to have a different sample size. Let t = 0 indicate the blank pond, i.e., the purest one, and let us assume that the ponds are ordered from the cleanest water to the most dirty. We assume that the gene expression measurements Y_igt are normally distributed,

$$Y_{\mathit{igt}}~\mathcal{N}({\mu }_{gt},{\sigma }_g^2),$$ (1)

with μ_gt a gene-pond specific mean and ${\sigma }_g^2$ a gene specific variance. The gene-pond specific mean μ_gt is then modeled as a function of the mean of the same gene in the previous pond plus a gene-pond specific difference in mean expression, α_gt, as

$${\mu }_{gt}={\mu }_{g(t-1)}+{\alpha }_{gt},$$ (2)

for t = 1, …, 4. Without loss of generality, we assume the mean of the blank pond μ_g0 to be zero and, for each gene in each pond, we center the expression data with respect to the mean of the same gene in the blank pond, i.e. Y_igt − Ȳ_g0 for g = 1, …, G and t = 0, …, T.

2.2 Variable Selection Prior

We incorporate in the model a variable selection prior that accounts for the available information on the concentration of chemical compounds present in the water.

Let A the (G × T) matrix with elements α_gt. For each gene we wish to find whether its mean expression in a specific pond changes with respect to the previous one. This is equivalent to inferring which α_gt in model (2) are non-zero with high confidence. To address this goal, we introduce a (G × T) matrix Ω of binary indicators, that is, ω_gt = 1 indicates that the corresponding α_gt is different from zero. Otherwise, ω_gt = 0 indicates that gene g in pond t has not changed its mean expression with respect to the previous pond, i.e., α_gt = 0. Conditional on this latent matrix Ω, we assume that the elements of the matrix A are stochastically independent and have the following mixture prior distribution,

$$\pi ({\alpha }_{gt}\mid {\omega }_{gt},{\sigma }_g^2)={\omega }_{gt}\mathcal{N}(0,c_{\alpha }^{-1}{\sigma }_g^2)+(1-{\omega }_{gt}){\delta }_0({\alpha }_{gt}),$$ (3)

with δ₀ a Dirac spike and c_α > 0 a hyperparameter to be set. We complete the prior model by assuming ${\sigma }_g^{-2}~\text{Ga}(\frac{\delta }{2},\frac{d}{2})$. In the variable selection literature the conjugate choice is often made for computational convenience, as it allows to marginalize some of the model parameters. Mixture priors of type (3) are known as spike and slab in the Bayesian variable selection literature, and have been used extensively in univariate and multivariate linear regression settings (George and McCulloch, 1997; Brown et al., 1998; Sha et al., 2004).

Model (3) requires a prior on ω_gt. A simple choice in variable selection is to assume independent Bernoulli priors, i.e. ω_gt ~ Bern(p), where p can be either a fixed hyperparameter or a random variable itself. Recently, some authors have suggested prior models that incorporate external information about the predictors, for example via Markov random field or logistic priors that capture correlation among the variables (Li and Zhang, 2010; Stingo et al., 2010). Here we use a probit-like prior that allows us to incorporate the information we have available on the concentrations of the chemical compounds present in the water. Probit-like priors have been recently proposed in the literature on Bayesian variable selection as a convenient way to incorporate external information to guide the selection of the predictors (Quintana and Conti, 2013; Cassese et al., 2014).

Let D be the (Q × T) matrix whose elements are the normalized absolute values of the difference in concentration of the individual chemical compounds with respect to the previous pond, that is,

$$d_{qt}=\frac{\mid c_{qt}-c_{q(t-1)}\mid }{{\sum }_{j=1}^T{c}_{qj}},$$ (4)

where c_qt is the concentration of chemical q in pond t, and where c_q0 = 0, for every chemical. Given the matrix D, we model the prior probability of a change in the mean expression of a gene as a function of D,

$$\pi ({\omega }_{gt}=1\mid \mathit{\theta })=\mathrm{\Phi }(\eta +\sum _{q=1}^Q{D}_{qt}{\theta }_q),$$ (5)

with Φ the c.d.f. of a standard Normal distribution and η a hyperparameter to be chosen, and where we allow for different prior probabilities for each pond. The parameter θ_q in (5) captures the effect of a change in the concentration of the q-th chemical. Since we expect a change in concentration to result in a change in the expression of some genes, and thus, we expect π(ω_gt = 1|θ) only to increase, we constrain θ_q > 0 by assuming θ_q ~ Ga(a_q, b_q). The choice of normalized absolute difference in (4) allows us to more reliably estimate θ even in situations where one chemical may dominate the others. Furthermore, it is worth noting that, in estimating θ, the number of ponds T plays the role of the sample size. The hyperparameter η in (5) regulates the prior probability of a change in gene expression when ignoring (or in the absence of) any information on the concentrations of the chemical compounds. More specifically, if θ = 0, or if all the chemicals do not change their concentration (i.e. D_qt = 0 for every q = 1, …, Q), equation (5) reduces to Φ(η).

2.3 Posterior inference

Our full joint model can be summarized as

$$\pi (\mathit{Y},\mathit{A},\mathbf{\Omega },\mathit{\theta },\mathit{\sigma })=f(\mathit{Y}\mid (\mathit{A},\mathbf{\Omega }),\mathit{\sigma })\pi (\mathit{A}\mid \mathbf{\Omega },\mathit{\sigma })\pi (\mathbf{\Omega }\mid \mathit{\theta })\pi (\mathit{\theta })\pi (\mathit{\sigma })$$ (6)

Our primary interest lies in the estimation of the presence/absence of a change in the mean expression of a gene between two adjacent ponds, i.e. the estimation of the matrix Ω. Since the posterior distribution is not available in closed form, we design a Markov Chain Monte Carlo algorithm based on stochastic search variable selection (SSVS) procedures (Savitsky et al., 2011). To simplify the sampling algorithm we integrate ${\sigma }_g^2$ out and work with the marginalised likelihood,

$$f(Y_{gt}\mid \mathit{A},\mathbf{\Omega })=\frac{\mathrm{\Gamma }(\frac{\delta +1}{2})}{\mathrm{\Gamma }(\frac{\delta }{2})}\sqrt{\frac{(N_t+{\omega }_{gt}{c}_{\alpha })}{\pi d}}{\left(1+\frac{(N_t+{\omega }_{gt}{c}_{\alpha })}{d}{({\alpha }_{gt}-q_{gt})}^2\right)}^{-\frac{\delta +1}{2}},$$ (7)

where

$$q_{gt}=\frac{{\sum }_{i=1}^{N_t}{Y}_{\mathit{igt}}-{\mu }_{g(t-1)}}{N_t+{\omega }_{gt}{c}_{\alpha }}.$$

Note that f(Y_gt|A, Ω) is the p.d.f. of a non standard non central t-distribution and that (N_t + ω_gtc_α) reduces to N_t when ω_gt = 0.

A generic iteration of the MCMC algorithm consists of the following updates:

• Update (A, Ω): We perform a between-model step by updating these two parameters jointly. First, a new value of Ω is proposed by either an add/delete (A/D), with probability ρ, or swap (S), with probability (1 − ρ), step. If an A/D step is chosen we simply select at random one element and change its value. If an S step is chosen we select independently at random a 1 and a 0 element and swap their values. When ${\omega }_{gt}^{\mathit{new}}=0$, we set the corresponding ${\alpha }_{gt}^{\mathit{new}}=0$, otherwise if ${\omega }_{gt}^{\mathit{new}}=1$ we propose a new value of α_gt by sampling it from a Normal distribution. The mean of the proposal distribution is calculated with a random walk procedure, as the mean of the B previous iterations during the burn-in phase, and it is fixed to the last computed value afterwards, while the variance is fixed throughout the MCMC (Roberts and Rosenthal, 2009). The proposed values ${\omega }_{gt}^{\mathit{new}}$ and ${\alpha }_{gt}^{\mathit{new}}$ are then accepted with probability

  $$min[\frac{f(Y_{gt}\mid {\alpha }_{gt}^{\mathit{new}},{\omega }_{gt}^{\mathit{new}})\pi ({\omega }_{gt}^{\mathit{new}}\mid \theta )q({\alpha }_{gt}^{\mathit{old}};{\alpha }_{gt}^{\mathit{new}},{\omega }_{gt}^{\mathit{old}})}{f(Y_{gt}\mid {\alpha }_{gt}^{\mathit{old}},{\omega }_{gt}^{\mathit{old}})\pi ({\omega }_{gt}^{\mathit{old}}\mid \theta )q({\alpha }_{gt}^{\mathit{new}};{\alpha }_{gt}^{\mathit{old}},{\omega }_{gt}^{\mathit{new}})},1].$$

  Note that the proposal distribution of ω_gt drops out from the previous ratio since all moves are symmetric.

• Update A: This within-model step is performed via a Gibbs sampler with the purpose of improving mixing. It consists of updating each α_gt corresponding to ω_gt = 1 by sampling from $\mathrm{t}(\nu ,{\mu }_t,{\sigma }_t^2)$, with t() a non standard not central t-distribution, and where the degrees of freedom ν, the location parameter μ_t and the dispersion parameter ${\sigma }_t^2$ are set to δ, ${\sum }_{i=1}^{N_t}\frac{Y_{\mathit{igt}}-{\mu }_{g(t-1)}}{N_t+c_{\alpha }}$ and $=\frac{d}{\delta (N_t+c_{\alpha })}$, respectively.

• Update θ: We propose a new value for each θ_q by sampling from a Gamma distribution. As for step 1, the parameters of the Gamma proposal are chosen following a random walk procedure, during the burn-in, and are fixed to the last computed value afterwards. In particular, the mean of the Gamma distribution is set to the mean of θ_q in the previous B iterations, while the variance is fixed to .1. The proposed values are then accepted with probability

  $$min[\frac{{\prod }_{g=1}^G{\prod }_{t=1}^T\pi ({\omega }_{gt}\mid {\theta }_q^{\mathit{new}})\pi ({\theta }_q^{\mathit{new}})q({\theta }_q^{\mathit{old}};{\theta }_q^{\mathit{new}})}{{\prod }_{g=1}^G{\prod }_{t=1}^T({\omega }_{gt}\mid {\theta }_q^{\mathit{old}})\pi ({\theta }_q^{\mathit{old}})q({\theta }_q^{\mathit{new}};{\theta }_q^{\mathit{old}})},1].$$

  Given the MCMC output, we perform posterior inference on Ω by calculating the marginal posterior probability of inclusion (PPI) for each element, which we estimate as the number of iterations where that element was set to 1, after burn-in. Point estimates of each θ_q are computed as the mean of the sampled values, after burn-in.

3. Case Study

We are interested in investigating the effects of munition pollutants on the gene expression of Daphnia magna. We consider a purification system with four stages of contaminated water. Exposures are to four chemical mixtures considered by Garcia-Reyero et al. (2012). Below we describe the experiment in some details and then present the results from our analysis.

3.1 The Daphnia magna experiment

Daphnia magna, a cladoceran freshwater flea, has been largely used for testing toxicity of water (Soetaert et al., 2006; Jo and Jung, 2008). This organism plays a key role in the aquatic food chain, it is highly sensitive to chemicals, easy to culture in laboratory and it is a widely spread species. We have data available from an experiment that looks at the exposure to four mixtures, each characterising the chemical concentrations of a pond, of six munitions constituents. The six contaminants under study are 1,3,5-trinitroperhydro-1,3,5-tiazine (RDX), 2,4,6-trinitrotoulene (TNT), 2,4 and 2,6-dinitrotoulene (2,4-DNT and 2,6-DNT), 1,3,5-trinitrobenzene (TNB) and 1,3-dinitrobenzene (DNB). Table 1 reports their concentrations. We consider an order of the four ponds from the most pure water to the pond with the highest concentration of chemicals.

Table 1.

Case study: Concentrations of the six chemicals under study in the four ponds. We consider an order of the ponds from the most pure water (blank) to the pond with the highest concentration of chemicals (Mix 4).

Chemical	Blank	Mix 1	Mix 2	Mix 3	Mix 4
TNT	0	.498	.999	1.269	1.012
2,4-DNT	0	0	1.242	.044	1.245
2,6-DNT	0	0	0	0	1.13
DNB	0	0	0	.157	1.107
TNB	0	0	0	.159	.67
RDX	0	0	0	.093	.334

Daphnia magna exposures were conducted on 6–8 old daphnids in 1L glass beakers with a 750ml exposure volume. After 24h of exposure RNA was isolated using RNeasy kits (Qiagen, Valencia, CA, USA). Quality was assessed with an Agilent 2100 Bioanalyzer (Agilent, Palo Alto, CA, USA) and quantified using a Nanodrop ND-1000 spectrophotometer (Nanodrop Technologies, Wilmington, DE, USA). Microarray data were normalized using the normalize.quantile function of the preprocessCore package of the R programming language. More details can be found in the supplementary material of Garcia-Reyero et al. (2012).

In order to simplify the complexity of the gene expression profiling data, we grouped genes by their functional characteristics, as defined by the biological pathway database KEGG (Kanehisa and Goto, 2000), and then expressed the transcriptional activity of each pathway by means of its principal components. Methods that employ pathway-based scores of gene expression data have become quite popular in genomics as an effective way to reduce the dimensionality of the data, see for example Su et al. (2009); Drier et al. (2013). Here we used the same annotation and data reduction as published in Antczak et al. (2013). Specifically, 92 KEGG pathways were identified and associated to the microarray chip design. Then, for each pathway, we applied principal component analysis (PCA) to the gene expression data in each pond, using the prcomp function available in R, and selected the components that explained at least 75% of the observed variance. This choice accomplishes a good reduction of the complexity of the gene expression profiling data (from 1379 genes to 630 pathway components) while still retaining a large percentage of the observed variance.

3.2 Parameter settings

In our model formulation, the expression data are captured via the matrix Y in (1), with G = 92 × 2, T = 4 and N_t = (5, 3, 4, 3, 3). In each pond, we centered the data with respect to the purest one, i.e., the blank pond, as described in Section 2.1. In addition, given the concentrations in Table 1, we computed each element of the matrix D as in (4).

Results we report below were obtained by starting the MCMC chain from a matrix Ω with all its elements set to zero and by sampling the initial values for the parameters θ_q from their prior distributions. As for hyperparameter settings, we specified the shrinkage parameter c_α of prior (3) in the range of variability of the data, so as to control the ratio of prior to posterior precision (Sha et al., 2004). Specifically, we set c_α = .1. Furthermore, we specified a vague prior on ${\sigma }_g^2$ by setting δ = 3, and choosing d such that the expected value of the variance parameter ${\sigma }_g^2$ represents a fraction of the observed variance (5% for the results in this paper). In our model, the parameter η in (5) reflects the prior belief of a change in mean expression, in the absence of any information on the concentration of the chemical compounds, i.e. θ = 0. We performed sensitivity analysis to different settings of η. More specifically, we investigated η =−3.72, −3.09 and −2.32, which correspond to a 0.01%, 0.1% and 1% prior probability. Finally, we specified vague priors on θ_q by setting a_q = b_q = 1.

We ran the MCMC chains for 2, 000, 000 iterations, with a burn-in of 1, 000, 000 and random walk proposals centered on values calculated over the previous B = 50 iterations. Our C++ code performed 1,000 MCMC iterations in about 6 seconds on a double core Intel®Xeon®processor with 16GB of memory, 2.2GHz. We assessed convergence by visually inspecting the MCMC sample traces. Additionally, we tested convergence by applying the diagnostic test of Geweke (1992) for the equality of the means, based on the first 10% and the last 50% of the chain. We also used the Heidelberger and Welch (1981) test on the stationarity of the distribution to determine a suitable burn-in.

3.3 Results

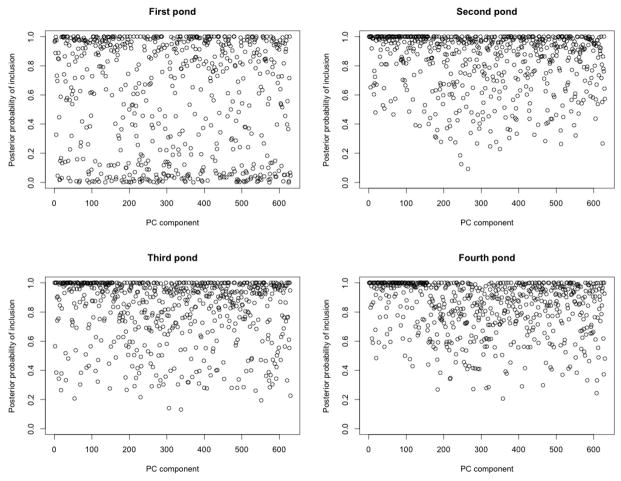
We report results obtained with η = −3.09, i.e. a prior probability of 0.1%, and later comment on the sensitivity to this choice. Figure 1 shows plots of the PPIs of the elements ω_gt of Ω. Each sub figure refers to the comparison of a given pond (t = 1, …, 4) with the previous one, with the x-axis showing the set of pathway components. Changes in expression across consecutive ponds can by detected by looking at the components with large PPI values. We notice that, as exposure to any given chemical compound can have a variety of effects on the molecular state of an organism, it is generally expected that a large number of pathway components will be significantly perturbed, as our results show (Williams et al., 2009; Hernndez et al., 2013; Antczak et al., 2013). Many more significant changes are observed in the third and fourth sub figures, as indicated by the large PPIs values, since there is more variation in the chemical compounds in the last two ponds (see the concentrations reported in Table 1).

Figure 1.

Case study: PPIs of the elements of Ω. Each sub figure refers to the comparison of a given pond (t = 1, …, 4) with the previous one, with the x-axes showing the set of pathway components.

A threshold of .99 on the PPIs identified 92, 156, 152 and 142 pathway components in the four consecutive ponds transitions, moving from the least to the most polluted. We analyzed the selected pathways by grouping them according to the top two levels of the KEGG pathway hierarchy (general terms and potential additional terms). The detailed breakdown is shown in the Supplementary Material. This analysis revealed that the transcriptional response linked to the transition between the blank and the first pond contains a large number of genetic information processing pathways, specifically in protein folding, sorting and degradation (18.1%), followed by translation (9%) and transcription (4.5%). In addition, a number of metabolic (22%), transport (20%) and signal transduction pathways (11.7%) were identified. The transition between ponds 1 and 2 follows a similar trend but with a greater focus on signal transduction (20%) and transcription pathways (9%). In the transition between ponds 2 and 3 we found an increased prevalence of metabolism pathways (31%), which mainly include carbohydrate metabolism (7.5%) and lipid (5%) and amino acid metabolism (7%). In addition, the number of signaling molecule pathways increased (5.8%) while transport and catabolism and nucleotide metabolism pathways were constant compared to the previous transition (20% and 1% respectively). Lastly, the transition between ponds 3 and 4 showed a decreased prevalence of genetic processing pathways (18%), and a similar profile for the others, with a high amount of metabolic pathways (30%), signal transduction (17%) and transport pathways (20%).

Our results contain a number of interesting findings. First, all 4 pond transitions showed same level of endocrine system related pathways (1.5%), including the first transition, where only TNT is present. This suggests an effect of TNT on the endocrine system. Similar links have already been observed in other species (Haerry et al., 1997; Kraut, 2011; Torre et al., 2008) but not yet in Daphnia magna. Another interesting result is that the number of identified membrane related pathways increases with the number of compounds within a pond, suggesting that mixtures of compounds have an increased effect on membrane components, and particularly on signal transduction pathways.

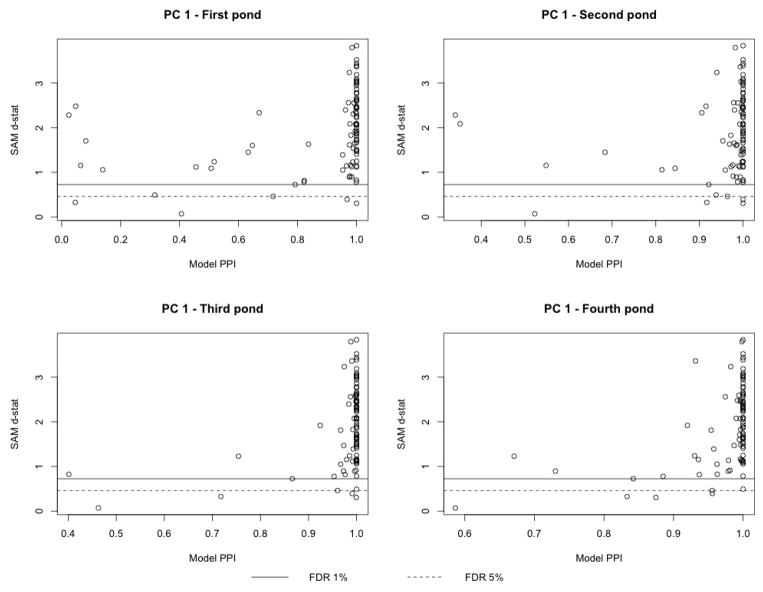
As a point of comparison with other methods, we looked at the results obtained using the significance analysis of microarrays (SAM) d-statistic of Tusher et al. (2001). This is a distribution free permutation based technique that measures the strength of the relationship between gene expression and a response variable. Figure 2 summarises the results, with each sub-plot showing a scatter-plot of the PPIs obtained with our method (x-axis) against the d-statistics obtained with SAM (y-axis), for the first pathway components only. Horizontal solid and dashed lines correspond to 1% and 5% FDR thresholds on the d-statistic, respectively. The figure shows that the performance of the two methods is broadly similar, as there is a large concordance in the selection. For example, looking at the modal model selected by our method, that is the set of pathway components that have PPIs greater than .5 (Barbieri and Berger, 2004), we find an overlap with those selected by SAM of 93.75% and 95.29%, using the FDR thresholds of 1% and 5%, respectively. However, there are also important differences in the selection done by the two methods. For example, Glycosphingolipid biosyntheses were among the pathways identified by our method but not by SAM. Genes involved in the Glycosphingolipid are important membrane building blocks and may play an important role in the composition of the membrane. As we have shown above, a number of membrane pathways are highly affected by exposure to the compounds we considered, and this effect could be facilitated through additional perturbation of the Glycosphingolipid biosynthesis pathway.

Figure 2.

Case study: Comparison of our method with SAM, on the first pathway components. For each pond, PPIs are plotted against the SAM d-statistics. Horizontal solid and dashed lines are located at a 1% and 5% FDR threshold on the d-statistic, respectively.

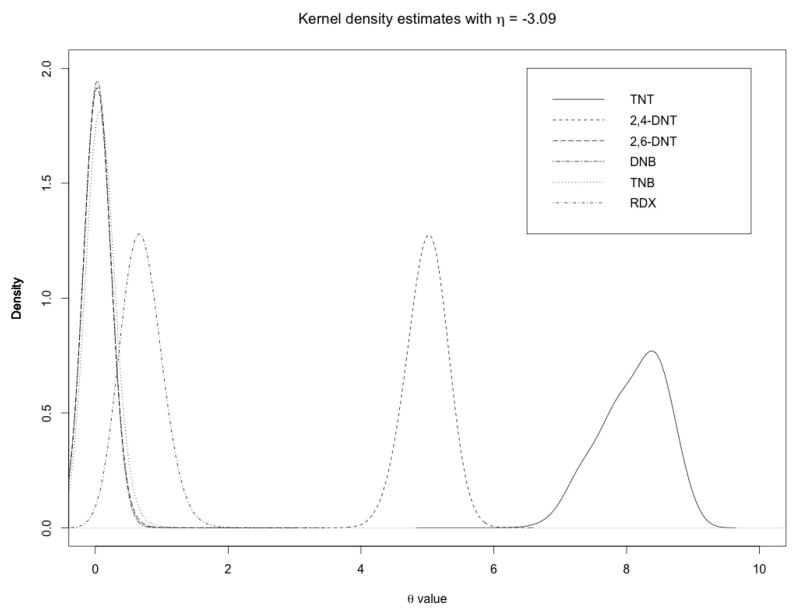
In addition to the inference on Ω, which allows to detect differential expressions, our model also returns the posterior distribution of the θ_q elements. These parameters measure the relative influence of the individual chemical compounds on the posterior inference. Figure 3 shows the kernel density estimates of all six parameters. Results clearly suggest that chemical TNT has the strongest influence, followed by 2,4-DNT and RDX. TNB, 2,6-DNT and DNB all have very little to negligible influence.

Figure 3.

Case study: Kernel density estimate of the posterior distribution of θ.

As for the results on the selected pathway expressions, our results are in line with what is known about the individual chemical compounds. Indeed, several studies have shown that TNT can cause oxidative stress (Cenas et al., 2001; Nemeikaite-Ceniene et al., 2004). Also, RDX is related with the nervous system and can cause seizures in vertebrates and invertebrates (Gust et al., 2009; Garcia-Reyero et al., 2011), while 2,4-DNT affects lipid metabolism in liver and oxygen transport (Wintz et al., 2006). Additional validation came from a one-class SAM analysis, with an FDR threshold at 20%, that we performed on gene expression data on exposures to single compounds, which we also have available from Garcia-Reyero et al. (2012). This analysis showed that TNT had the highest normalised count, followed by 2,4-DNT (result not shown).

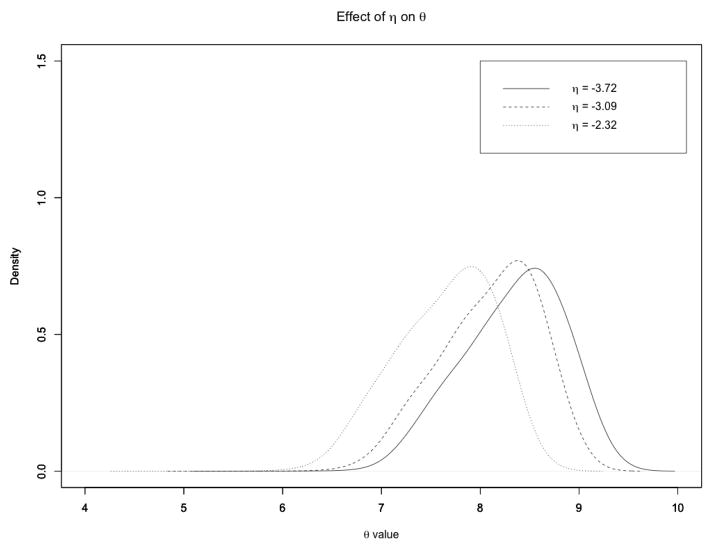
Let us now comment on the sensitivity of the results to the choice of the parameter η in (5). This parameter represents the weight assigned to the data, as our prior belief of a change in expression in the absence of any information on the concentration of the chemical compounds. Some sensitivity to this parameter is therefore to be expected. In particular, since the parameters θ₁, …, θ₆ are the weights of the prior information derived from changes in the chemical concentrations, we expect that higher values of η will result in values of the θ_q parameters that are concentrated around smaller values. Indeed, as an example, Figure 4 shows the effect of different choices of η on the density kernel estimate of θ₁ (the parameter associated to TNT). Notice how the posterior distribution tends to concentrate on lower values when η increases. We observed the same behavior for the other θ_q parameters (result not shown).

Figure 4.

Case study: Kernel density estimate of the posterior distribution of θ₁, for different settings of η.

In spite of the evident sensitivity of the individual θ_q estimates to the choice of the η parameters, we found that the overall effect of the estimates on the posterior inference did not depend on the chosen η value. For example, in the second pond (the one where we observed the largest increases in posterior probability) we observed a 67.29% increase on the prior probability of p(ω_gt = 1) for η = −3.72, of 66.56% for η = −3.09 and of 64.70% for η = −2.32. Of course, these probability values should be interpreted with caution, as inference on the θ_q parameters also depends on the sample size and the number of parameters to estimates, as well as the concordance between the data and the prior information.

4. Discussion

In this paper we have presented a simple approach to a rigorous modeling of the biological effects of water purification. For this, we have proposed a hierarchical Bayesian model of the expected change in gene expression between consecutive purification stages. We have also incorporated a variable selection prior that accounts for available information on the concentration of chemical compounds present in the water. Our modeling approach is general and can be applied to a variety of settings used in experimental studies to estimate the biological effects of water purification. Here we have presented an application to the identification of differentially expressed genes in Daphnia Magna organisms exposed to munition pollutants in water.

In order to simplify the complexity of the gene expression profiling data, we have grouped genes by KEGG pathways and then expressed the transcriptional activity of each pathway by means of its principal components. When applied to gene expression data from Daphnia Magna organisms exposed to munition pollutants, our model has successfully identified a number of pathways that show differential expression between consecutive purification stages. These mainly represent membrane, signaling, and translational and transcription pathways. In addition, our model allows for the estimation of the relative influence of single chemicals on the probability of a change in expression. We have found, in particular, that changes in the transcriptional response are more strongly associated to the presence of TNT and 2,4-DNT, with the remaining compounds contributing to a lesser extent. We have discussed the sensitivity of these results to the model parameters that measure the influence of the prior information on the posterior inference.

In the application, we have also looked into results of the SAM method, although it should be pointed out that this comparison only addressed one feature of the method we have developed, which is the ability to identify genes differentially expressed across a series of samples. Our method, in addition, allows to estimate the effect of individual chemicals on the observed transcriptional response. This feature of our model could be particularly important in the growing application of adverse outcome pathways (AOPs). At the moment, these AOPs are derived on a single exposure level - where one looks at the single effect that a compound with a set of characteristics may have on the organism. Our approach would allow to estimate the effects of multiple compounds and to prioritize pathways as a result of their interactions with the compounds. Our approach can be used not only to understand how water purification systems work, but also how dissipation of chemicals into the environment are affecting different areas of the ecosystem, possibly even biodiversity.

The modeling approach we have considered in this paper is general and can be applied to data collected, for example, from artificially constructed wetland environments, such as the WIPE project (Kampf and Claassen, 2004; Kampf et al., 2005). Such datasets typically involve a large number of chemical compounds. Also, it could be interesting to include interactions between compounds, as well as chemical features that can be calculated to provide a more informed assessment of how strong the chemical is affecting the pathways. With a large number of possible covariates, an interesting methodological extension of the methods would then be to also employ selection priors at the second stage of the model, for the identification of those chemicals inducing changes in the transcriptional response.