Approach to the unfolding and folding dynamics of add A-riboswitch upon adenine dissociation using a coarse-grained elastic network model

Abstract

Riboswitches are noncoding mRNA segments that can regulate the gene expression via altering their structures in response to specific metabolite binding. We proposed a coarse-grained Gaussian network model (GNM) to examine the unfolding and folding dynamics of adenosine deaminase (add) A-riboswitch upon the adenine dissociation, in which the RNA is modeled by a nucleotide chain with interaction networks formed by connecting adjoining atomic contacts. It was shown that the adenine binding is critical to the folding of the add A-riboswitch while the removal of the ligand can result in drastic increase of the thermodynamic fluctuations especially in the junction regions between helix domains. Under the assumption that the native contacts with the highest thermodynamic fluctuations break first, the iterative GNM simulations showed that the unfolding process of the adenine-free add A-riboswitch starts with the denature of the terminal helix stem, followed by the loops and junctions involving ligand binding pocket, and then the central helix domains. Despite the simplified coarse-grained modeling, the unfolding dynamics and pathways are shown in close agreement with the results from atomic-level MD simulations and the NMR and single-molecule force spectroscopy experiments. Overall, the study demonstrates a new avenue to investigate the binding and folding dynamics of add A-riboswitch molecule which can be readily extended for other RNA molecules.

I. INTRODUCTION

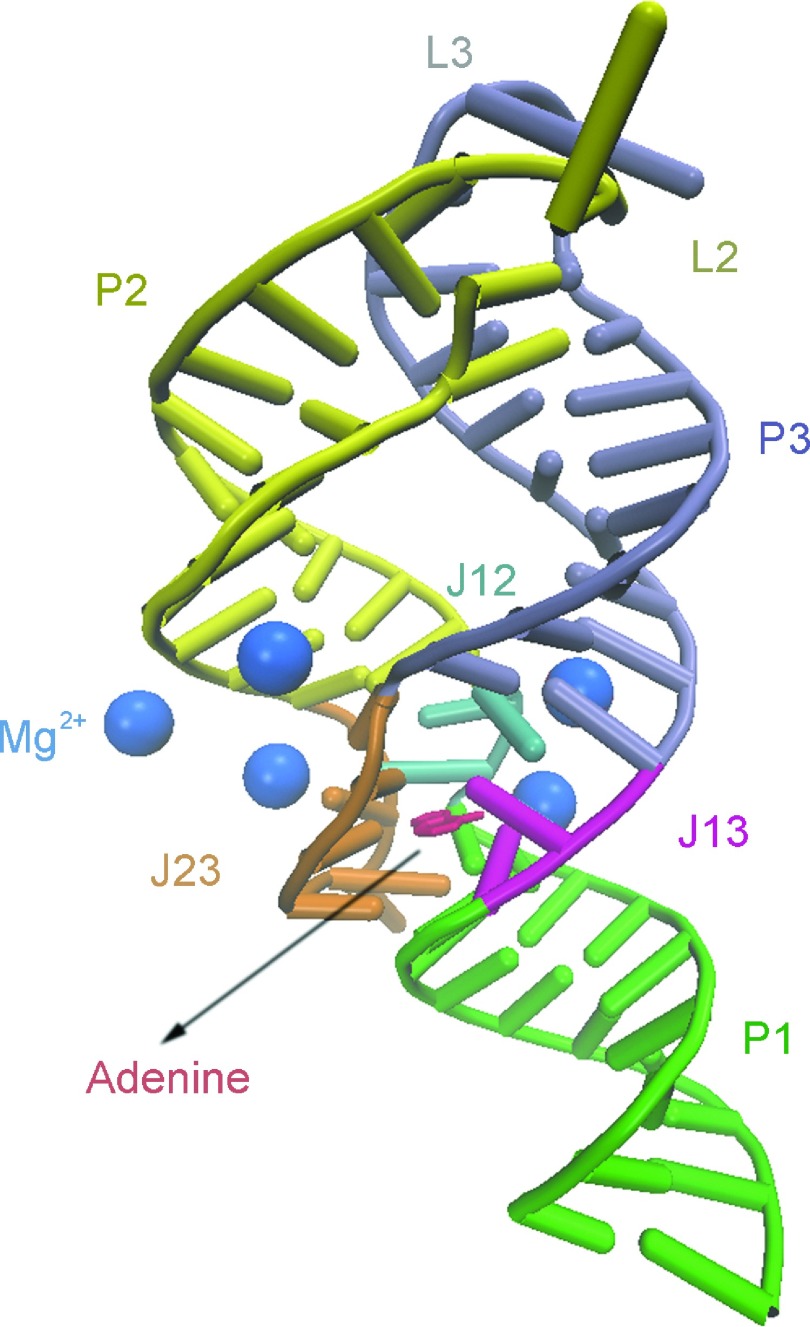
In recent years, the studies of functional noncoding RNAs have received unprecedented attention.^1–3 Riboswitches are the natural genetic control segments found in the 5′ untranslated regions (UTRs) of many mRNAs of bacteria and fungi. They can regulate gene expression at the level of transcription or translation that is highly sensitive to the cellular concentrations of specific metabolites.^2–4 So far, various riboswitches have been discovered which can specifically recognize a large variety of ligands, such as adenine, glycine, lysine, and glucosamine-6-phosphate.^5–8 Riboswitches are generally composed of two domains: the aptamer domain and the downstream expression platform. The former can fold into an intricate three-dimensional structure upon binding to a specific metabolite when the concentration of the metabolite exceeds a threshold. The latter switches a gene on/off through its structural changes triggered by metabolite-induced large-scale conformational changes in the aptamer domain.⁸ The adenosine deaminase (add) A-riboswitch is one of the structurally simplest riboswitches and has been widely studied.^9–12 The folded aptamer domain of the add A-riboswitch bound with the ligand adenine was structurally characterized by X-ray crystallography with Protein Data Bank (PDB) code 1Y26 (Fig. 1).¹³ It forms a tuning-fork-like architecture assembled by three helical stems, two of which are hairpins (P2 and P3) interacting via kissing loops (L2 and L3) and aligned on top of the third helix P1. The ligand-binding pocket is formed through stacked bases interconnecting the junctions J12, J13, and J23, with two base pairs (U75-A21 and A76-U20) at the end of P1 stem. The adenine ligand forms a Watson-Crick (WC) type of interaction with U74. In the crystal structure, there are five Mg²⁺ ions binding to the add A-riboswitch, one of which is on the surface, and the other four are positioned deep within the grooves primarily formed by the junction-connecting segments. The binding of adenine ligand to the aptamer domain results in the change of its folding pattern, which alters the conformation of the expression platform and activates the gene expression.¹⁴ Thus, the functional performance of the add A-riboswitch depends on the conformational transformation of the aptamer between the folded and unfolded states. Therefore, characterizing and elucidating its folding/unfolding process is important for the understanding of its regulatory mechanism.

FIG. 1.

Three-dimensional structure of add A-riboswitch with five Mg²⁺ ions and a ligand adenine (PDB code 1Y26). The ligand and Mg²⁺ ions are colored with red and blue, respectively. The secondary structures of the system are labelled correspondingly with P1, P2, and P3 for stems, L2 and L3 for loops, and J12, J13, and J23 for junctions.

In the past few years, several experimental and theoretical investigations have been conducted on the folding/unfolding process of the add A-riboswitch system. Rieder et al.¹⁵ reported that the folding process of the aptamer is induced by adenine ligands and metal ions. Neupane et al.¹¹ have explored its unfolding pathway using single molecule force measurements and observed a series of intermediates during its unfolding process. Using a self-organized polymer model with the Langevin dynamics, Lin and Thirumalai¹⁴ described force-triggered unfolding of this system and obtained the same unfolding sequence as the experimental observation. Priyakumar and MacKerell¹⁶ performed a 40 ns all-atom molecular dynamics (MD) simulation to investigate the unfolding behavior in both presence and absence of ligand, but the complete unfolding process was not produced and only structural deviations were observed in the J23 junction and P1 stem. In addition, some investigations have concentrated on the roles of adenine ligand on the structural stability of add A-riboswitch. Researchers found that the ligand binding plays a critical role in stabilizing the binding pocket, especially for the folded P1 stem.^11,16,17 While the all-atom MD simulation can provide useful information on the fluctuations and conformational changes of biomacromolecules, it is generally difficult to obtain a complete folding/unfolding picture through MD due to the prohibitive computational costs.

The coarse-grained method has proved to be an efficient tool to explore the large-scale functional motions of biomolecular systems. Recently, we proposed a Gaussian network model (GNM) method, which was successfully applied to protein folding/unfolding studies.^18,19 In this method, the unfolding process of proteins is modeled through gradually breaking the non-covalent native contacts according to the distance fluctuations of residue pairs. This process can be considered to be composed of a series of quasi-equilibrium states corresponding to a slowly increasing temperature, during which the molecule has sufficient time to search for the state with a maximum entropy increase at each unfolding step.

In this work, we extended the iterative GNM approach to explore the unfolding process of the add A-riboswitch, with the changes of cross-correlations between nucleotide fluctuations and the fluctuations in the fast modes analyzed in detail. Additionally, we tried to interpret the roles of the adenine ligand in stabilizing the folded aptamer from a topological point of view.

II. METHODS

A. Gaussian network model

In the Gaussian network model, the three-dimensional structure of a molecule is described as an elastic network of nodes that are connected by harmonic springs with a certain cutoff distance.^20,21 In this work, the RNA chain is represented by a set of linked nodes, with each node standing for a nucleotide, where the interactions of backbone-backbone, base-base, and backbone-base, and the effects of Mg²⁺ ions and adenine are considered in the construction of the nucleotide networks. In addition to the backbone links, the nucleotide nodes are connected in the model when one of the following requirements is satisfied:

• I.The distance between P atoms ≤8.5 Å.
• II.The distance between mark atoms ≤8.0 Å.
• III.The distance between the P and mark atoms from different nucleotides ≤8.0 Å.
• IV.Both distances of two P atoms from the same Mg²⁺ ion ≤8.5 Å.
• V.Both distances of two mark atoms from the mark atom of the ligand adenine ≤8.0 Å.

The mark atoms refer to the four atoms (N6 for adenine, O6 for guanine, N4 for cytosine and O4 for uracil), representing the four kinds of bases, respectively, all of which participate in the formation of hydrogen bonds in canonical base pairs.²² The requirements I, II, and III are designed to take into account the interactions of backbone-backbone, base-base, and backbone-base, respectively, and V for considering the mediating role of the ligand.

It should be pointed out that as Mg²⁺ ions are important for structure stabilization and folding of the system, all the five Mg²⁺ ions are considered in the network construction. Mg²⁺ ions mainly play a role in mediating the interactions among the negative charges of the highly acidic phosphate backbone, permitting the system to form and retain the folded structures. Thus, in the network construction we consider the mediating roles of Mg²⁺ ions (not treated as separated nodes) by connecting the nucleotide nodes when both distances of their P atoms from the same Mg²⁺ ion ≤8.5 Å, as shown in requirement IV.

Different from the conventional GNM in which the force constants are identical for the springs of covalent and noncovalent pairs, the spring constants of non-bonded nucleotides are set as γ while those of the covalently bonded pairs along the chain backbone are chosen as cγ. The values of c and γ are determined by fitting the predicted fluctuations against the crystallographic B-factors. This setting allows us to consider the heterogeneity of RNA chain interactions, since the covalent bonding is generally much stronger than the non-covalent ones.

The internal Hamiltonian of the RNA molecule system can be written as²³

$${\displaystyle H=\frac{1}{2}\gamma \left[\mathrm{\Delta }{R}^{\text{T}}\left(\mathrm{\Gamma }\otimes E\right)\mathrm{\Delta }R\right],}$$ (1)

where $\mathrm{\Delta }R=\left\{\mathrm{\Delta }{R}_1,\mathrm{\Delta }{R}_2,\dots \mathrm{\Delta }{R}_N\right\}$ represents the 3N-dimensional column vectors of fluctuations of the nodes in the network, where N is the number of nucleotides; the superscript T denotes the transpose; E is the third-order identity matrix; ⊗ is the direct product; and Γ is the N × N symmetric matrix in which the elements are given by

$${\displaystyle {\mathrm{\Gamma }}_{ij}=\left\{\begin{array}{ll}-c\hfill & \mathit{if}\left|i-j\right|=1\hfill \\ -1\hfill & \mathit{if}\left|i-j\right|>1\text{and}\text{nucleotides}i\text{and}j\text{are}\text{connected}\hfill \\ 0\hfill & \mathit{if}\left|i-j\right|>1\text{and}\text{nucleotides}i\text{and}j\text{are}\text{not}\text{connected}\hfill \\ -\sum _{i,j\ne i}{\mathrm{\Gamma }}_{ij}\hfill & \mathit{if}i=j\hfill \end{array}\right..}$$ (2)

The mean-square fluctuation (MSF) of each nucleotide node and the cross-correlation fluctuations between different nucleotide nodes are in proportion to the diagonal and off-diagonal elements of the pseudo-inverse of the Γ matrix. The inverse of the matrix can be decomposed as

$${\displaystyle {\mathrm{\Gamma }}^{-1}=U{\mathrm{\Lambda }}^{-1}{U}^{\text{T}},}$$ (3)

where U is an orthogonal matrix whose columns u_i (1 < i ≤ N) are the eigenvectors of Γ, and Λ is a diagonal matrix of eigenvalues λ_i of Γ. The cross-correlation fluctuations between the ith and jth nucleotides are written as

$${\displaystyle 〈\mathrm{\Delta }{R}_i\cdot \mathrm{\Delta }{R}_j〉=\frac{3k_{B}T}{\gamma }{\left[{\mathrm{\Gamma }}^{-1}\right]}_{ij},}$$ (4)

where k_B is the Boltzmann constant and T is the absolute temperature. When i = j, the MSF of the ith nucleotide can be obtained. The B-factor, also called temperature factor, which is related to the MSF, can be computed with the expression

$${\displaystyle B_i=\frac{8{\pi }^2}{3}〈\mathrm{\Delta }{R}_i\cdot \mathrm{\Delta }{R}_i〉=\frac{8{\pi }^2{k}_{B}T}{\gamma }{\left[{\mathrm{\Gamma }}^{-1}\right]}_{ii}.}$$ (5)

The MSF of the ith nucleotide associating with the kth mode is obtained by

$${\displaystyle {〈\mathrm{\Delta }{R}_i\cdot \mathrm{\Delta }{R}_i〉}_k=\frac{3k_{B}T}{\gamma }{\lambda }_k^{-1}{\left[u_k\right]}_i{\left[u_k\right]}_i.}$$ (6)

The MSF in the distance vector R_ij between the nucleotides i and j can be calculated with the expression²⁴

$${\displaystyle 〈{\left(\mathrm{\Delta }{R}_{ij}\right)}^2〉=〈{\left(R_{ij}-R_{ij}^0\right)}^2〉=〈{\left(\mathrm{\Delta }{R}_i-\mathrm{\Delta }{R}_j\right)}^2〉=〈\mathrm{\Delta }{R}_i\cdot \mathrm{\Delta }{R}_i〉+〈\mathrm{\Delta }{R}_j\cdot \mathrm{\Delta }{R}_j〉-2〈\mathrm{\Delta }{R}_i\cdot \mathrm{\Delta }{R}_j〉=\frac{3k_{B}T}{\gamma }\left({\left[{\mathrm{\Gamma }}^{-1}\right]}_{ii}+{\left[{\mathrm{\Gamma }}^{-1}\right]}_{jj}-2{\left[{\mathrm{\Gamma }}^{-1}\right]}_{ij}\right),}$$ (7)

where R_ij and $R_{ij}^0$ are the instantaneous and equilibrium separation vectors between nucleotides i and j. In the GNM, the cross-correlation is normalized as

$${\displaystyle C_{ij}=\frac{〈\mathrm{\Delta }{R}_i\cdot \mathrm{\Delta }{R}_j〉}{{\left[〈\mathrm{\Delta }{R}_i^2〉\cdot 〈\mathrm{\Delta }{R}_j^2〉\right]}^{1/2}}.}$$ (8)

B. Iterative Gaussian network model

The unfolding process of the riboswitch molecules is modeled based on the thermodynamic fluctuations. Generally, with a higher fluctuation the native contacts of riboswitches between nucleotides are expected to break in a higher possibility, which results in unfolded structures. The fluctuations in the distance between all nucleotides are calculated by the GNM. The nonlinear elasticity during RNA unfolding is considered via iterative normal mode calculations, i.e.,¹⁸

• I.The MSFs of the distances in all nucleotide pairs are calculated according to the native structure topology with Eq. (7).
• II.The contact in the nucleotide pair with the largest distance fluctuation is broken. Then, a new matrix Γ is constructed, which represents a new topology during RNA unfolding.
• III.The MSFs of the distances in all nucleotide pairs are recalculated based on the new matrix Γ with Eq. (7).
• IV.The above steps II and III are repeated until all the noncovalent contacts are broken.
• V.All the topologies of different conformations during RNA unfolding are obtained and the unfolding pathway can be derived from the above data.

It should be noted that many previous studies have been conducted on examining the roles of Mg²⁺ ions on the add A-riboswitch, indicating that they mainly affect the pre-organization and stabilization of the folded conformation rather than the intervention of the unfolding process.^12,15 Therefore, we did not specifically examine the unfolding behavior induced by Mg²⁺ release. Here, the contacts mediated by Mg²⁺ are not treated specially and the unfolding process is simulated purely in a fluctuation-dependent manner.

III. RESULTS AND DISCUSSION

A. Force constants for the covalent and noncovalent interactions

The add A-riboswitch is modeled by the Gaussian network model system with each node representing a nucleotide and the interaction network formed by the adjoining atomic contacts (see Sec. II). The spring constant values of covalent and noncovalent interactions, i.e., cγ and γ, are determined by matching the calculated and experimental B-factor values. As the absolute value of γ does not affect the relative size of nucleotide fluctuations, it has no influence on the correlation between the calculated and experimental B-factors. Therefore, we first set γ = 1 to determine the value of c via maximizing the correlation between the computed and experimental B-factors. The value of γ was then determined through normalizing the calculated fluctuation with the experimental B-factors. According to this method, we obtained c = 8.0 and γ = 0.125 k_BT/Ų, where the correlation coefficient between the theoretical and experimental B-factors is 0.728.

Compared to the traditional GNM with uniform spring contacts, the introduction of heterogeneity in the covalent and noncovalent spring contacts in our model improves the correlation coefficient of B-factors from 0.606 to 0.728. Part of the effect is due to the consideration of the mediating roles of Mg²⁺ ions in our network construction. Without considering the Mg²⁺ ions, the correlation coefficient of B-factors will reduce to 0.717, which partly highlights the roles of Mg²⁺ ions in the stabilization and folding of the molecule.

We also computed this correlation coefficient using the conventional RNA single-point GNM, in which one node represents one nucleotide and the connections between them are determined only based on the distances between P atoms;²⁵ this gives an even lower correlation coefficient 0.587. The results indicate that the new iterative GNM approach, which considers the RNA backbone-backbone, backbone-base, base-base interactions, and Mg²⁺ ion binding, and meanwhile distinguishes the covalent from noncovalent interactions, can help generate a better accordance with experimental fluctuation data.

B. Roles of ligand adenine and Mg²⁺ ions on the dynamics of add A-riboswitch

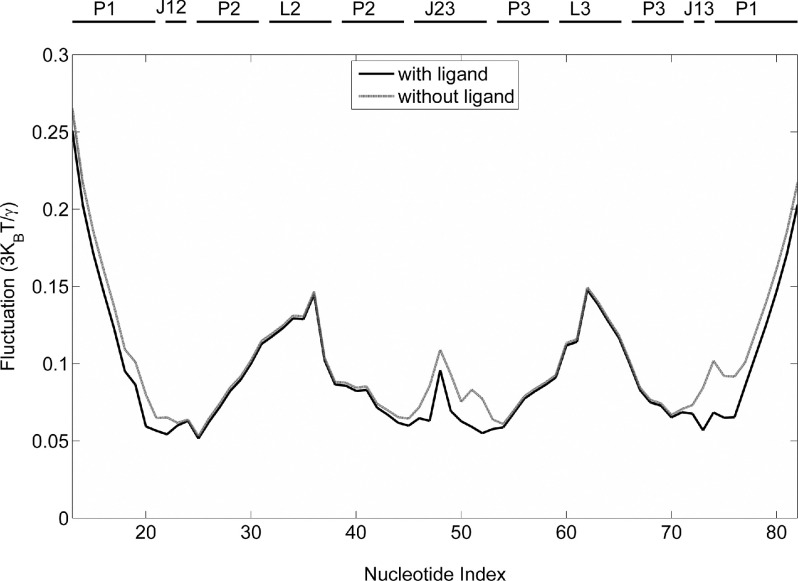
The ligand adenine was found to be important for the structure and function of add A-riboswitch.²⁶ To examine the specific role of the ligand adenine on the dynamics of the system, we computed the MSF of each nucleotide in the GNM with and without adenine. Fig. 2 shows that the nucleotides have a relatively higher MSF in the adenine-free state than in the adenine-binding state, although the difference in MSFs varies along the sequence. The most significant increase in MSFs occurs in the three junctions (J12, J13, and J23) associated with the binding pockets as well as the nucleotides at the terminal P1 stem that are near the binding pocket. In particular, the region from U74-A76 pairing with the adenine has the highest MSF increase. Similar MSF changes have been observed in the former atomic MD and experimental studies,^12,16,17,27 suggesting that the adenine ligand-binding indeed plays an important role in stabilizing the binding pocket, especially for the folded P1 stem and J23 junction regions. Functionally, binding with the adenine ligand leads to a change in the stability of P1 stem, which in effect, constitutes a structural switch in the expression platform, since the 3′ strand of P1 stem is involved in alternative base pairing with the Shine-Dalgarno sequence of the expression platform in the absence of adenine binding, which masks the Shine-Dalgarno sequence and causes the stop of translation.^8,28,29

FIG. 2.

Fluctuations of nucleotides of add A-riboswitch in ligand-bound state (solid line) and ligand-free one (shaded line), respectively.

The ligand dissociation leads to a marked rise in MSF at J23 U51 (base pairing with ligand), which causes further instability of its neighbors C50 and U49 that are involved in the formation of base triplets with the top base pairs of P1 stem: U75-A21 and A76-U20, respectively.¹² This explains the causal relationship between the fluctuations of P1 stem and J23 junction, observed by Sharma et al.¹² Additionally, the data imply that the transmission pathway of structural changes caused by ligand dissociation may start from ligand-bound U51, and then to its neighbors, finally to the P1 stem. Also, the high flexibility of J23 in the absence of the adenine ligand suggests that the ligand should associate and dissociate from the riboswitch in the vicinity of J23.

Recently, the experimental and theoretical researches have reported that Mg²⁺ ions appear to be important in preorganizing and stabilizing the aptamer fold.^12,15 In order to detect the roles of Mg²⁺ ions on the dynamics of the system, we calculated the MSF of each nucleotide in the GNM of the system with and without Mg²⁺ ions (see Figure S1 of the supplementary material³⁸). Overall, the nucleotides have relatively higher MSFs in the Mg²⁺ ion free state than in the Mg²⁺ ion binding state, especially for the regions around the ligand-binding pocket: J12, J23, and the junction proximal ends of three stems P1 (U20-A21), P2 (G42-A45), and P3 (C69-U71), which was also observed in the previous MD simulation study.¹²

In conclusion, both ligand adenine and Mg²⁺ ions show their importance in stabilizing the folded conformation of the riboswitch. Ligand adenine mainly contributes to the stabilization of P1 and J23, and the effect of Mg²⁺ ions is mainly reflected in stabilizing the ligand binding pocket.

C. Pathway of add A-riboswitch unfolding

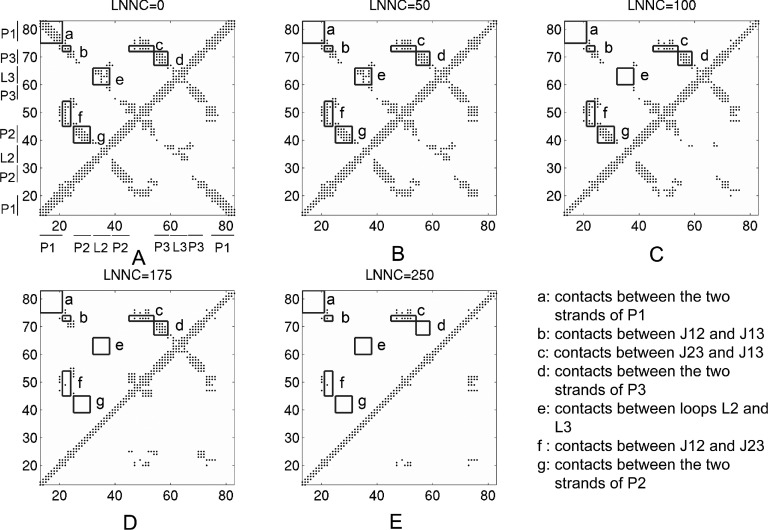
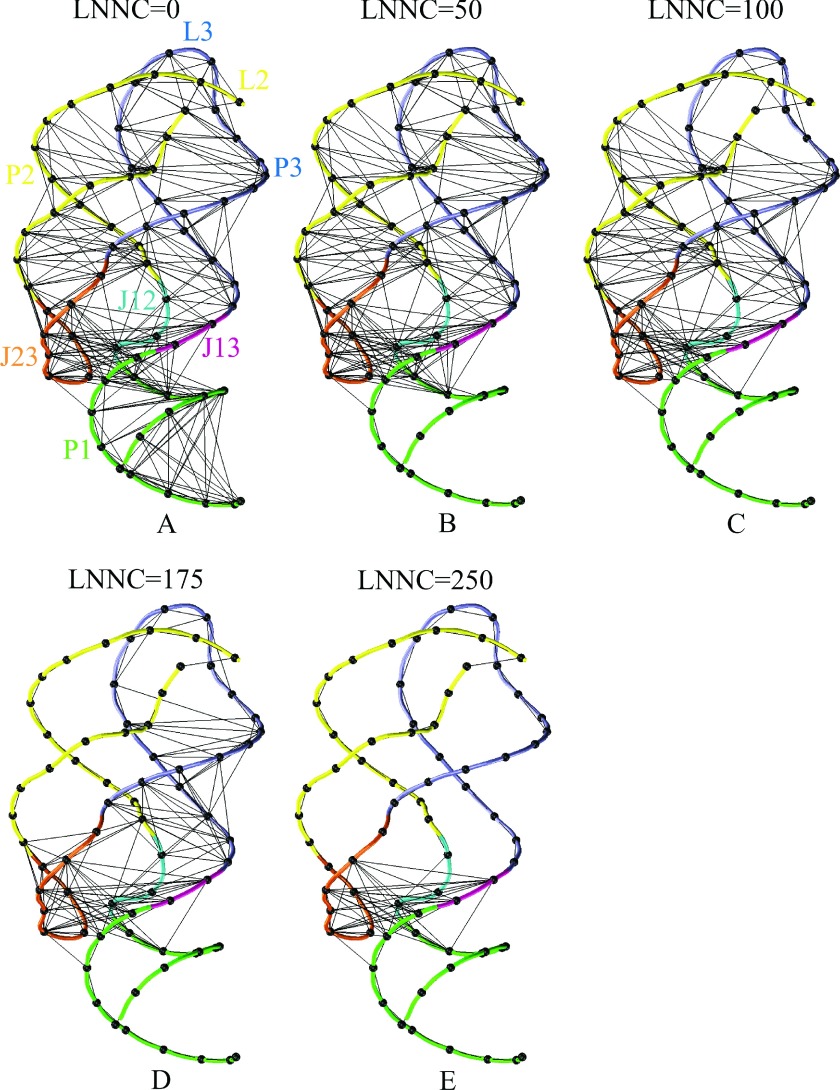
The GNM based calculations showed that the riboswitch molecule becomes unstable and tends to unfold in the absence of adenine. To examine the unfolding pathway of the riboswitch, we monitored the loss of the native contacts between nucleotides in the course of unfolding simulation based on the iterative GNM, which starts from the native riboswitch structure but removing the adenine ligand. Fig. 3 shows the snapshots of the native contact maps with each native contact marked by a dot in the maps, where Figs. 3(a)-3(e) run from the loss-number-of-native-contact (LNNC) equal to 0, 50, 100, 175, and 250, respectively. In Figure 4, we present 3D conformation for each of the snapshots, with the connections and nodes of the networks mapped on the molecule (see Fig. 4).

FIG. 3.

The contact maps of the native conformation (a) and the conformations with the LNNC to be 50 (b), 100 (c), 175 (d), and 250 (e) for add A-riboswitch, respectively. Each native contact is marked by a dot in the maps. The rectangles labelled with letters (a)–(g) represent the contacts between different secondary structures that are indicated in the lower right corner.

FIG. 4.

The connections (black lines) and nodes (black balls) of the networks mapped on the three-dimensional structures with the LNNC to be 0 (a), 50 (b), 100 (c), 175 (d), and 250 (e) for add A-riboswitch, respectively.

The first unfolding event is the loss of the native contacts within P1 stem, as shown in Figs. 3(b) and 4(b). Similar observations were also made in the NMR experiment^9,30 and MD simulation,^12,16 i.e., the main conformational change upon ligand dissociation is the unfolding of P1 helix. This result means that P1 is probably easier to unfold compared to the other parts of the riboswitch.

Next, the native tertiary contacts between L2 and L3 loops are lost (Figs. 3(c) and 4(c)), indicating that the two loops separate from each other. Therefore, the removal of the ligand not only destabilizes P1 directly but also causes a slight collapse of the kissing loops (L2-L3) as indicated by the MD studies.^9,12 Allner et al.,⁹ further suggested that along with the L2-L3 opening process, a key event is that the stacking interactions between A24 and G72/A73 are lost and A24 becomes exposed to the solvent, losing its function as a hook between helices P2 and P3. This insight was also observed in our modeling in which the native contacts between junction J12 A23/A24 and J13 A73 disappear, causing the structural instability and exposure of the hydrophobic core. After the disruption of L2-L3 interactions, the native contacts within P2 stem, as well as several contacts between J12 and J23 are lost (Figs. 3(d) and 4(d)), which is followed by the unfolding of P3 stem (Figs. 3(e) and 4(e)). Finally, the add A-riboswitch is fully unwound and the hydrophobic binding pocket is completely exposed. There are several contacts among the three junctions (J12, J23, and J13) remaining till the unfolding event is almost over. These retained parts which unfold last may fold first in a refolding process due to their lower free-energy basins, which was also proposed by Allnér et al.⁹ for add A-riboswitch with all-atom MD simulations. Overall, despite the simplified modeling, the unfolding pathway of the add A-riboswitch calculated here is in close agreement with the experimental data obtained by the single-molecule force spectroscopy.¹¹

It should be mentioned that the detailed interactions among nucleotides have been replaced by constant springs in our coarse-grained GNM and the topological structure is therefore the determinant factor for the results. The close agreement between the modeling results and the experimental data implies that the topology plays an important role in the folding and unfolding process of add A-riboswitch. Similarly, the topology-driven view of folding has been put forth for protein folding.³¹ A variety of experimental and theoretical evidences has suggested that proteins, especially small fast-folding proteins, have selected the sequences with minimal energetic frustration under evolutionary pressure, leaving the topology as the main source of the frustration in protein folding/unfolding.^18,32–35 Yet an analogous definite statement has not been made for RNA molecules, most likely due to the strong coupling between the ionic environment and conformational energetics that make RNA folding more complex than protein folding. Recently, Sorin et al.³⁶ have found that the native tRNA topology serves as a dominant predictor of the bulk folding mechanism. The detailed comparison between protein and RNA hairpin structures indicated that the native topology defines the folding landscape for nucleic acids in a manner analogous to that suggested for proteins, with the specific interactions within the polymer determining the relative weighting between parallel pathways.³⁷ These insights are again consistent with our results here that the structural topology is a critical factor for determining the folding/unfolding dynamics of the add A-riboswitch.

D. Robustness of unfolding process against noise

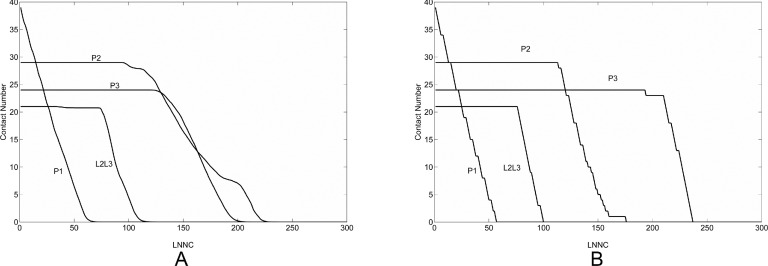
In our iterative GNM approach, we identify and remove the nucleotide pairs of the highest MSF at each step. To examine the robustness of the unfolding process, we introduced a stochastic noise to the model by randomly selecting and removing a contact from those with the top-three highest MSFs. The unfolding process with such noise was simulated 500 times and the average result of the contact losing process is shown in Fig. 5(a). As a comparison, the unfolding process without noise is displayed in Fig. 5(b). It can be seen that the two figures are very similar except for a small difference in the unfolding order of P2 and P3 domains. In both simulations, the stem P1 unfolds first, followed by the separation between L2 and L3. But in the simulation without noise, P3 starts to unfold after P2 completes the unfolding, while in the model with noise the unfolding of P3 completes slightly prior to P2 although P2 breaks earlier than P3. Indeed, the P2 stem is not as stable as P3, but the free energy difference between them is merely 1 kcal/mol.^9,14 This small free energy difference can explain why introducing some randomness into the thermal denaturation can result in a light effect on the unfolding order of P2 and P3. But the overall unfolding pathway of add A-riboswitch is quite robust against external random disturbances (Fig. 5).

FIG. 5.

The process of losing of native contacts during unfolding of add A-riboswitch. The unfolding process with some perturbation is simulated 500 times and the average result is shown in panel A. In contrast, the unfolding process without perturbation is represented in panel B.

E. Change of MSFs in the fast modes during add A-riboswitch unfolding process

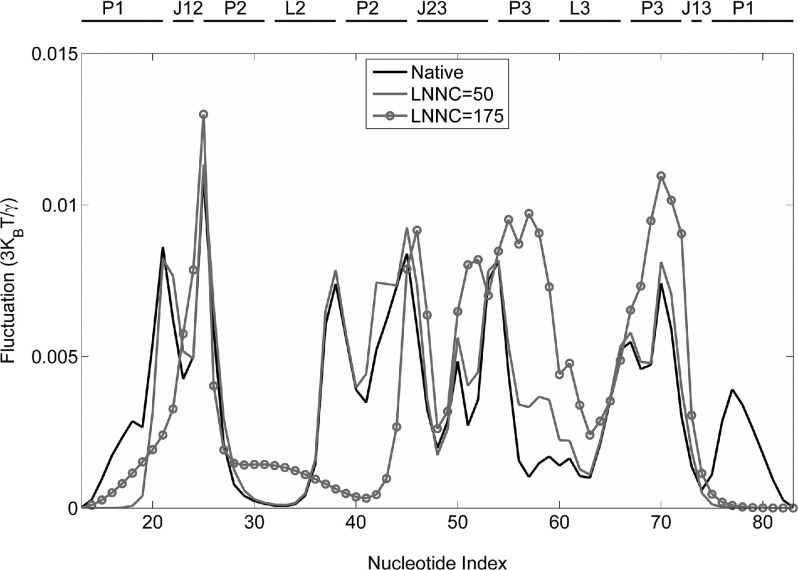
It has been well-established that the fast motion modes in protein system correspond to geometric irregularity in the local structure, and the residues acting in the fast modes are considered as kinetically hot residues that are crucially important for the stability of the tertiary fold.¹⁸ In RNA, however, the problem whether nucleotides acting in fast modes play the same role remains unclear. To attack this problem, we select multiple conformations from the unfolding process and calculate the fluctuations of all nucleotides in these conformations using the iterative GNM approach (Eq. (6)). Fig. 6 gives the fluctuations of nucleotides in the eight fastest modes for the conformations during the unfolding of the system. It is shown that the peaks of the fluctuations are mainly situated in junctions J12 (U22-A24), J23 (U49-A50, A52-C53), and stems P1 (U20-A21, A76), P2 (U25, G42-A45), and P3 (A56, A66-C67, C69-U70) which are close to the junctions. Most of these nucleotides are considered to constitute the hydrophobic binding pocket.^11,12,15 Interestingly, the peaks of the fluctuations largely overlap for the conformations selected from different stages in the unfolding process, which indicates that these nucleotides retain most of their contacts until the end of the unfolding process. Thus, similar to protein system, these relative high fluctuation nucleotides acting in fast modes are critical to maintain the stability of the tertiary fold of add A-riboswitch.

FIG. 6.

The fluctuations of the nucleotides in the fast eight modes from GNM analysis for several conformations visited during the unfolding of add A-riboswitch. The solid, shaded, and shaded circled lines represent the native conformation, the conformations with LNNC = 50 and LNNC = 175, respectively.

F. Change of cross-correlation between the fluctuations of nucleotides during unfolding process

The correlation between fluctuations can reveal information related to the spatial motion and interaction. The pair-wise cross-correlations between nucleotides can be calculated using Eq. (8), with the values ranging from −1 to 1. The positive values represent the motions of nucleotides are in the same direction, and the negatives represent that they move in the opposite direction. The higher the absolute value is, the more the two nucleotides are correlated. The value C_ij = 0 means that the motions of nucleotides are completely uncorrelated.

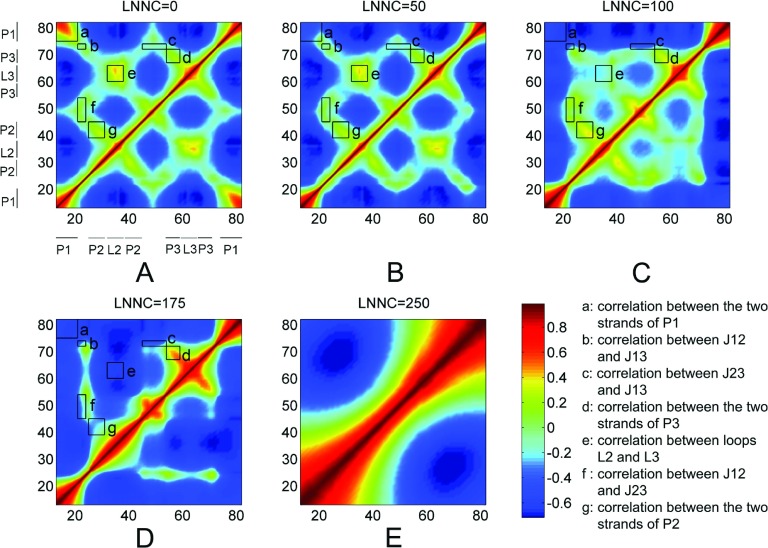
Fig. 7 presents the change of the cross-correlation maps of the nucleotide fluctuations along the course of unfolding. Prior to the unfolding (Fig. 7(a)), the opposite strands in the helical stems (P1, P2, P3) form strong positive correlations, due to the stable folded structure and strong base pairing interactions. Similarly, the contacts between loops (L2 and L3) and junctions (J12, J13, and J23) also dictate the positive correlations in these regions, consistent with the structural feature of the binding pocket.^11,12,15

FIG. 7.

The cross-correlation maps calculated using all modes for native conformation (a) and several conformations with LNNC to be 50 (b), 100 (c), 175 (d), and 250 (e) during the unfolding process of add A-riboswitch. As shown in the color bar, the blue regions in the figure indicate negative correlation and the green-yellow-red regions present positive correlation. The rectangles labelled with letters a–g represent the correlations between different secondary structures that are indicated in the lower right corner.

After the removal of the ligand, the system becomes unstable and the structure starts to unfold. Accordingly, the strong positive correlations, which were formed in the helical stems, loops, and junctions, are gradually converted to weak and then strong negative, as shown from Figs. 7(b)-7(d) which corresponds to LNNC = 50, 100, and 175, respectively. The results imply that these structural segments move away from each other to expose the hydrophobic binding pocket during the unfolding process of the RNA molecule. Interestingly, when the contacts within P2 are disrupted, P2 and L2 form negative correlations with P3 and L3 as shown in Fig. 7(d), and the correlations among the three junctions remain weak, indicating that P2 and L2 move apart from P3 and L3 but some contacts still exist among junctions due to the low free-energy basin involved in the binding pocket region.

When the contacts among the junctions are lost, the structure of add A-riboswitch is finally divided into two parts that fluctuate in the opposite directions (Fig. 7(e)). The unfolded RNA molecule does not behave as a random coil, suggesting that long-range correlations still exist in the denatured state probably due to the cooperative motion. Maybe the highly cooperative motion can help and promote the add A-riboswitch refold into the native state speedily through reducing the population searched in the conformational space.

IV. CONCLUSIONS

We have proposed a general coarse-grained Gaussian network model to describe the structure and folding dynamics of the functional noncoding RNA molecules. The network construction and introduction of heterogeneous spring constants for covalent and noncovalent interactions resulted in significantly improved correlation of modeled nucleotide fluctuations compared to experimental data.

The model was extended to examine the folding dynamics of the adenosine deaminase (add) A-riboswitch. It was found that the ligand adenine and Mg²⁺ ions play a critical role in stabilizing the structural fold of the molecule and the removal of adenine can result in unfolding due to the increased thermodynamic fluctuations in the junction and stem areas. The iterative GNM simulations show that the unfolding process of the add A-riboswitch starts with the denature of terminal P1 helix stem, followed by the loop and junction regions that are relevant to hooking the central helix domains and the ligand binding pocket, and then the central helix domains. Although the iterative GNM is an overly simplified model involving only two types of node interactions, the unfolding dynamics and pathway are in close agreement with the results from expensive atomic-level MD simulations^12,16 and NMR and single-molecule force spectroscopy experiments.^9,11 This result suggests that the topology of the RNA structures is responsible for the folding and unfolding dynamics, an analog to the observation made in the topology-driven folding process of proteins.³¹ Nevertheless, it should be mentioned that the spring constants in the GNM model are based on B-factors, which are not necessarily the best measure of the conformational flexibility. In particular, many experimental effects, including crystal packing and ligand binding, have not been taken into account, description of which should request for more detailed modeling.

Finally, we examined the impact of the stochastic noise on the unfolding pathway by allowing nucleotides with slightly lower thermodynamic fluctuations to unfold. It shows that the unfolding pathway is largely robust to the noise except for the switch of the unfolding order between two central helix domains that involves similar free energy basins. The calculations on the cross-correlation between nucleotide fluctuations further confirmed the unfolding pathway revealed by fluctuation-based simulations. Additionally, the nucleotides near the hydrophobic pocket with higher fluctuations in fast modes remain a high number of contacts throughout the unfolding process and are very important for maintaining the stability of the folded state. Overall, this study demonstrates a new simplified but efficient Gaussian network modeling approach to reveal the binding and folding dynamics of the adenosine deaminase A-riboswitch which can be readily extended for other RNA molecules.