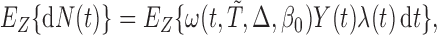Abstract
Right-censored time-to-event data are sometimes observed from a (sub)cohort of patients whose survival times can be subject to outcome-dependent sampling schemes. In this paper, we propose a unified estimation method for semiparametric accelerated failure time models under general biased estimating schemes. The proposed estimator of the regression covariates is developed upon a bias-offsetting weighting scheme and is proved to be consistent and asymptotically normally distributed. Large sample properties for the estimator are also derived. Using rank-based monotone estimating functions for the regression parameters, we find that the estimating equations can be easily solved via convex optimization. The methods are confirmed through simulations and illustrated by application to real datasets on various sampling schemes including length-bias sampling, the case–cohort design and its variants.
Keywords: Accelerated failure time model, Case–cohort design, Counting process, Estimating equations, Importance sampling, Length-bias, Regression, Survival data
1. Introduction
Length/size-biased sampling has been recognized in statistics for decades in the studies of ecology (McFadden, 1962; Muttlak and McDonald, 1990), fiber length (Cox, 1969), and economic duration data (Kiefer, 1988). This kind of biased sampling arises when a positive-valued outcome variable is sampled with selection probability proportional to its size/survival time. The one-sample problem of estimating the survivor function has been studied in Vardi (1982, 1985). Further results can be found in Asgharian and others (2002) and Asgharian and Wolfson (2005).
Under the scope of semiparametric inference, Tsai (2009) carefully studied two intrinsically different types of length-biased sampling, depending on the assumption made on the recruitment/censoring procedure under the Cox proportional hazards model. Shen and others (2012) proposed two likelihood approaches for the estimation and assessment of the difference between two survival distributions under length-biased sampling. While there has been extensive effort to develop survival models in the context of length-biased sampling, e.g. proportional hazards and linear transformation models, less attention has been paid to the accelerated failure time (AFT) model. More recently, Chen (2010) and Shen and others (2009) specifically studied the AFT model for data that are length/size-biased.
Another outcome sampling scheme is the case–cohort design which has first proposed by Prentice (1986). Such a design is developed in order to provide a more cost-efficient sampling method, especially in large-scale (epidemiological) studies on rare diseases with certain covariate information that is difficult or costly to obtain. Recent works that study inference on survival data from the case–cohort design include Lu and Tsiatis (2006), Nan and others (2009), and Kong and Cai (2009); the first of these developed inference procedure on a general class of semiparametric transformation models, while the latter two proposed solutions on inferring regression parameters of the AFT model.
The AFT model, as a common alternative to linear transformation models, relates the logarithm of the failure time linearly to the covariates; see Tsiatis (1990), Wei and others (1990), Kalbfleisch and Prentice (2002), and Cox and Oakes (1984) among others. Under the AFT model, the effect of the covariates on the failure time is directly related to the acceleration or deceleration of time to failure. This feature facilitates an easy interpretation for clinicians and hence the model provides an alternative to the celebrated (Cox, 1972) proportional hazards model for the regression analysis of censored failure time data.
Several estimation and inferential procedures have been proposed for the estimation of the regression parameters, including rank-based estimating equations and martingale estimating equations for unbiased data; see Prentice (1978) and Buckley and James (1979). The large-sample properties of the Buckley–James-type and rank estimators were then studied by Ritov (1990), Tsiatis (1990), Ying (1993), and Jin and others (2003). Furthermore, Zeng and Lin (2007) proposed a kernel-smoothed profile likelihood function for the AFT model.
Despite the theoretical advances, semiparametric methods for the AFT model have rarely been developed to deal with various biased sampling schemes, either due to natural setting or trial design, under one general framework. This paper aims at proposing a unified approach that can handle many commonly encountered biased sampling schemes such as length-biased sampling, the case–cohort design as well as its variants. We show that our approach leads to estimators that are consistent and asymptotically normal and we provide consistent variance estimators. The one-size-fit-all solution introduced in this paper should benefit a wide range of practitioners who have to tackle problems on biased samples.
The approach presented in this paper is related to that of Kim and others (2013), which deals with biased sampling under the semiparametric linear transformation models. However, it is by no means straightforward to apply their framework directly to the AFT model setting. This is due to the fact that the bias involved in sampling is usually characterized via the event time, whereas inference for the regression parameter of the AFT model is carried out through the residual term. Furthermore, it has still been unclear about the feasibility of extending the existing rank-based inference procedure for censored data (Jin and others, 2003, 2006) including finding equivalent objective functions and resampling schemes for variance estimation to datasets with sampling bias. Our main contribution in this paper is to provide a careful treatment that extends (Jin and others, 2003) methodology to a biased sampling setting so that the corresponding estimator is still numerically tractable, while its standard error can also be estimated via a resampling scheme as discussed in Jin and others (2006). Ignoring the sampling bias or uniqueness of the point estimates may result in substantial bias in estimating the survival time distribution and hence potentially fallacious inference.
The rest of the article is organized as follows: Section 2 specifies the model setup, necessary notation as well as the estimating procedures. The asymptotic properties of the proposed estimator are studied. In particular, we presented a Gehan-type estimating equation whose root can be obtained via convex optimization. We present a resampling procedure for variance estimation. Solution to a more general weighting scheme will also be elaborated. Simulation studies under practical sample sizes and real data analyses are conducted to assess the performance of the proposed estimator; the corresponding discussion is included in Section 3. Section 4 concludes the paper. In addition to specific simulation settings and results, all the technical details are presented in supplementary materials (available at Biostatistics online).
2. Proposed methods
We shall assume throughout this paper that there are two underlying random variables 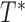 and
and 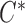 that correspond to unbiased time to failure and time to censoring as seen in typical right-censored data problems. Only
that correspond to unbiased time to failure and time to censoring as seen in typical right-censored data problems. Only 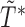 , the minimum between
, the minimum between 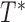 and
and  , is observed. The AFT model relates the logarithm of the failure time linearly to the concomitant covariates, say
, is observed. The AFT model relates the logarithm of the failure time linearly to the concomitant covariates, say 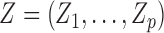 in the following sense:
in the following sense:
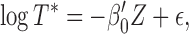 |
(2.1) |
where 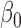 is a
is a 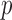 -vector of regression coefficients and
-vector of regression coefficients and 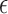 , in contrast to the transformation models, has an unknown distribution. The parameter
, in contrast to the transformation models, has an unknown distribution. The parameter 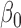 appears to be easy to interpret because it directly relates to the level of
appears to be easy to interpret because it directly relates to the level of 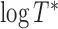 . The primary goal of this paper is to find semiparametric estimates of
. The primary goal of this paper is to find semiparametric estimates of 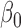 , denoted by
, denoted by 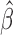 , under a generalized biased sampling scheme. The data observed will consist of
, under a generalized biased sampling scheme. The data observed will consist of 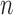 biased iid random vectors
biased iid random vectors 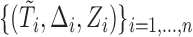 , where
, where 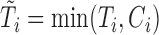 and
and 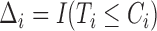 . Following Kim and others (2013), we introduce
. Following Kim and others (2013), we introduce 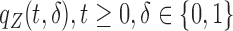 , the joint conditional density of
, the joint conditional density of 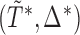 given the covariates
given the covariates 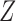 , where
, where 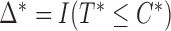 . Since
. Since 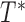 and
and 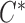 are assumed to be conditionally independent given
are assumed to be conditionally independent given 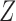 , we can write
, we can write
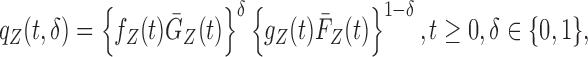 |
where 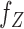 (
(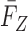 ) and
) and 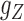 (
(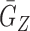 ) denote the conditional density (survival) functions of
) denote the conditional density (survival) functions of 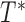 and
and 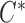 , respectively. Under a biased sampling scheme, i.e. the data collected are subject to a certain type of biased sampling, which is characterized by a biasing function
, respectively. Under a biased sampling scheme, i.e. the data collected are subject to a certain type of biased sampling, which is characterized by a biasing function 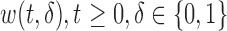 , the conditional joint density of
, the conditional joint density of 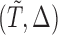 given
given  then changes to
then changes to
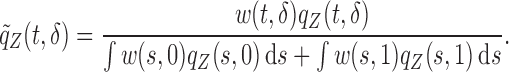 |
(2.2) |
Typical examples of biasing functions include: (a) length-biased sampling, where 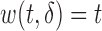 and (b) case–cohort sampling, where
and (b) case–cohort sampling, where 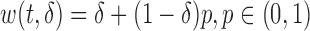 is a predefined constant. Readers should be noted that the biasing function can be generalized so that it depends on
is a predefined constant. Readers should be noted that the biasing function can be generalized so that it depends on 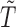 ,
, 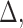 or both.
or both.
2.1. Notation and background
For our purposes, it will be convenient to consider the counting process approach; see Gill (1980). Here, and in the sequel, we shall use the notation 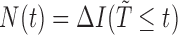 to represent the counting process which jumps by one when a failure occurs. Hazard and cumulative hazard functions of
to represent the counting process which jumps by one when a failure occurs. Hazard and cumulative hazard functions of 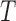 are denoted by
are denoted by 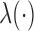 and
and 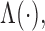 respectively. Let
respectively. Let 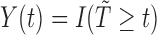 denote the at-risk indicator. Moreover, for the AFT model, it is helpful to re-express the counting process via the residual term. Specifically, we define
denote the at-risk indicator. Moreover, for the AFT model, it is helpful to re-express the counting process via the residual term. Specifically, we define 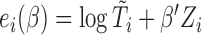 ,
, 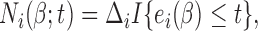 and
and 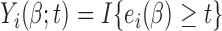 for
for 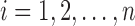 . Unless there exists ambiguity, the subscript
. Unless there exists ambiguity, the subscript 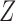 that appears in
that appears in 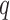 and
and 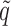 will be suppressed.
will be suppressed.
In full cohort design, the regression parameters can be estimated via the weighted log-rank estimating function (Ying, 1993; Jin and others, 2003):
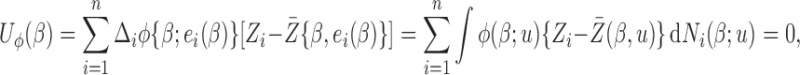 |
where 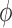 is a (data-dependent) weight function,
is a (data-dependent) weight function, 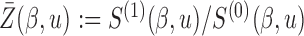 with
with 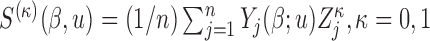 ;
; 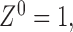 and
and 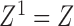 . The choices of
. The choices of 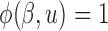 and
and 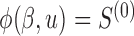 correspond to log-rank and Gehan statistics, respectively.
correspond to log-rank and Gehan statistics, respectively.
One of the technical issues that needs to be tackled for the above root-finding problem is that the estimating equation 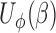 is not necessarily component-wise monotone in
is not necessarily component-wise monotone in 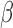 . Non-differentiability and non-monotonicity involved with respect to
. Non-differentiability and non-monotonicity involved with respect to 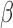 also lead to the potential of having multiple solutions to the equation, amongst which some of them are inconsistent. Such a problem is even more prominent when
also lead to the potential of having multiple solutions to the equation, amongst which some of them are inconsistent. Such a problem is even more prominent when 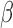 is of higher dimension. In the following subsections, apart from introducing the estimation procedure for
is of higher dimension. In the following subsections, apart from introducing the estimation procedure for 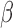 , we shall also investigate the numerical issues involved in this root-finding procedure.
, we shall also investigate the numerical issues involved in this root-finding procedure.
2.2. Estimation procedure
Biased sampling appears in many applications, either naturally or by design. To the best of our knowledge, there has not yet been any unified inference procedure for the regression parameter in the AFT model (2.1) under general biased sampling schemes. A key element in the counting process approach is the use of 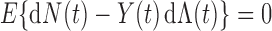 as the basis for constructing an unbiased estimating equation. Under the biased sampling setting (2.2), however, the above quantity is no longer a zero-mean process. In fact, Kim and others (2013) derived the following lemma that shows that the compensator of the counting process
as the basis for constructing an unbiased estimating equation. Under the biased sampling setting (2.2), however, the above quantity is no longer a zero-mean process. In fact, Kim and others (2013) derived the following lemma that shows that the compensator of the counting process 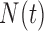 requires an extra adjustment term to achieve the mean-zero property.
requires an extra adjustment term to achieve the mean-zero property.
Lemma 2.1. —
Under the biased sampling scheme, i.e.
follows
given by (2.2) and
, we have
(2.3) where
denotes the conditional expectation given
and
.
The inclusion of the adjustment term 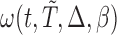 in (2.3) can be regarded as the Radon–Nikodym derivative between the true and the biased densities for the risk set and the counting process, respectively. Due to the fact that both the counting process and the risk set are observed under a biased probability measure, whereas the hazard function is expressed with respect to the true density, we have to adjust both
in (2.3) can be regarded as the Radon–Nikodym derivative between the true and the biased densities for the risk set and the counting process, respectively. Due to the fact that both the counting process and the risk set are observed under a biased probability measure, whereas the hazard function is expressed with respect to the true density, we have to adjust both 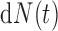 and the at-risk indicator
and the at-risk indicator 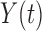 so that all the components in estimating equation (2.3) are evaluated under the same measure. The proof of this lemma is presented in Kim and others (2013).
so that all the components in estimating equation (2.3) are evaluated under the same measure. The proof of this lemma is presented in Kim and others (2013).
Due to (2.3), we can obtain the following set of estimating equations:
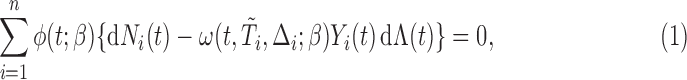 |
(2.4) |
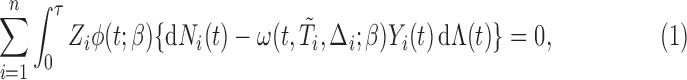 |
(2.5) |
where 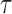 is constant such that
is constant such that 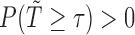 . By choosing
. By choosing 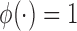 for (2.4), we obtain
for (2.4), we obtain 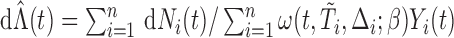 . It follows that if we consider a transformation on the time scale:
. It follows that if we consider a transformation on the time scale: 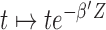 , then (2.5) can be written as
, then (2.5) can be written as
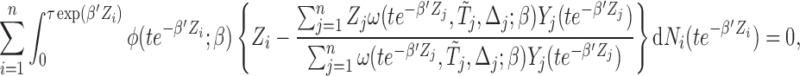 |
or equivalently,
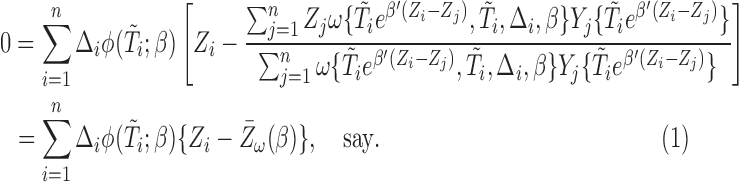 |
(2.6) |
The unbiasedness property exhibited in (2.6) is important in obtaining an asymptotically unbiased estimator for 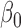 . It is noteworthy that since the weight function
. It is noteworthy that since the weight function 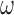 , which may contain
, which may contain 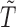 and/or
and/or 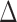 , is not necessarily
, is not necessarily 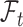 -measurable, the process
-measurable, the process  is not a martingale but a mean-zero process instead.
is not a martingale but a mean-zero process instead.
Before discussing more general weight functions 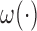 in Section 2.4, we first study the special case of
in Section 2.4, we first study the special case of 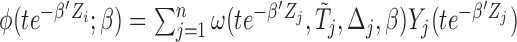 , which is regarded as the Gehan-type weight function. Such a formulation can considerably simplify (2.6) and lead to
, which is regarded as the Gehan-type weight function. Such a formulation can considerably simplify (2.6) and lead to
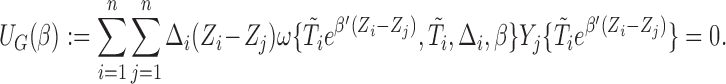 |
(2.7) |
There are a number of typical biasing sampling designs that can be covered under the purposed generalized framework. Common examples include (i) length-biased sampling, (ii) case–cohort design, (iii) case–cohort sampling on a length-biased sampling, and (iv) generalized case–cohort design. Readers are referred to Kim and others (2013) for a more elaborated description of the weight function 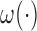 formulation. We shall elaborate the subtlety of the proposed method and its difference between that discussed in Kim and others (2013) via two examples.
formulation. We shall elaborate the subtlety of the proposed method and its difference between that discussed in Kim and others (2013) via two examples.
Length-biased sampling. In the length-biased sampling case, since the density of 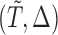 is proportional to
is proportional to 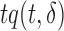 , the weight function is given by
, the weight function is given by
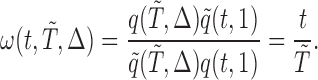 |
Due to the fact that the time horizon considered in (2.7) is viewed from the perspective of 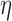 , the time variable
, the time variable 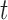 expressed in the above weight function should be adjusted to
expressed in the above weight function should be adjusted to 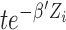 for subject
for subject 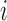 (
(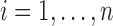 ), instead. With specifically
), instead. With specifically 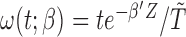 and hence
and hence 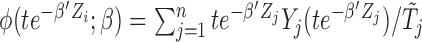 , we can rewrite (2.7) into the following estimating equation that corresponds to the length-biased sampling setting:
, we can rewrite (2.7) into the following estimating equation that corresponds to the length-biased sampling setting:
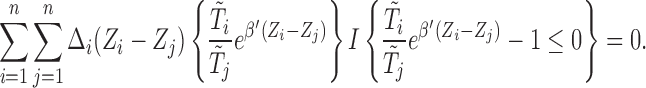 |
(2.8) |
We cannot, however, directly adopt the approach of Jin and others (2003) in solving (2.8) via linear programming due to the extra term 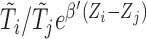 involved for the bias correction.
involved for the bias correction.
It can be shown in the supplementary material (available at Biostatistics online) that the root of (2.8) is still a solution of a monotone estimating equation. In fact, the root-finding problem presented in (2.8) can be translated into an optimization problem of a convex function:
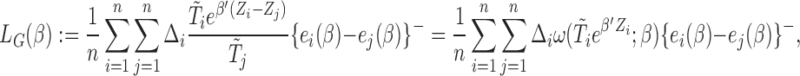 |
where 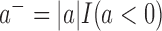 . The minimizer of
. The minimizer of 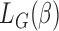 is denoted by
is denoted by 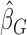 . Note that although
. Note that although 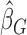 is not necessarily unique, all these minimizers are asymptotically equivalent.
is not necessarily unique, all these minimizers are asymptotically equivalent.
We would like to emphasize that our estimation procedure is different from that proposed in Chen (2010). In particular, Chen (2010) only considered the uncensored case and made use of the invariance principle (see Property 1 of Chen, 2010, p. 150) to provide an inference procedure for the regression covariates. Shen and others (2009) proposed the estimating equation 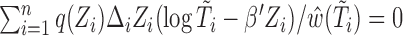 , where
, where 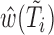 is a consistent estimator of
is a consistent estimator of 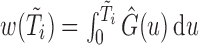 with
with 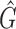 the Kaplan–Meier estimator for the censoring variable
the Kaplan–Meier estimator for the censoring variable 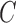 . For the cases where censoring times are dependent on a large number of covariates, the estimation of
. For the cases where censoring times are dependent on a large number of covariates, the estimation of 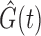 may not be stable, so will be the estimates of the regression parameters.
may not be stable, so will be the estimates of the regression parameters.
While the weight function introduced for bias-adjustment resembles the risk set resampling proposed in Wang (1996), our methodology is developed upon an estimating equation derived from the joint density of 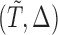 and hence the problem of censoring, which is not covered under the pseudo-likelihood framework as considered in Wang (1996), can be properly tackled.
and hence the problem of censoring, which is not covered under the pseudo-likelihood framework as considered in Wang (1996), can be properly tackled.
As an additional remark, the current setup is designed for handling censoring first and followed by length-biased sampling. In fact, this setting coincides with the first type of length-biased sampling considered in Tsai (2009). Adopting the notation used in Tsai (2009), we let 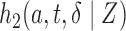 be the conditional probability density function of the observed data
be the conditional probability density function of the observed data 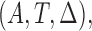 where
where 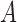 denotes the truncation time. Under the assumption that
denotes the truncation time. Under the assumption that 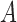 follows a uniform distribution marginally, one can write
follows a uniform distribution marginally, one can write 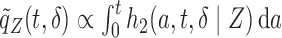 . This formulation occurs naturally when a cross-sectional sampling (censoring) is performed in which the probability for a sample to be selected is proportional to the follow-up period
. This formulation occurs naturally when a cross-sectional sampling (censoring) is performed in which the probability for a sample to be selected is proportional to the follow-up period 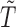 instead of the event time
instead of the event time 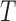 . Under such a model assumption, subjects with short follow-up times, which may be the result of dropouts or death due to other unrelated causes, will be selected with lower probabilities. For the second type of censoring discussed in Tsai (2009), we shall introduce the corresponding treatment in Section 3.2.
. Under such a model assumption, subjects with short follow-up times, which may be the result of dropouts or death due to other unrelated causes, will be selected with lower probabilities. For the second type of censoring discussed in Tsai (2009), we shall introduce the corresponding treatment in Section 3.2.
Classical case–cohort sampling and its variants. For those weight functions that do not involve time, it can be easily proved that the estimating equations for these cases are also monotonically non-decreasing as there is no time-transformation involved in the bias-adjustment term 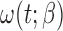 . Similar estimation procedure as shown above can be applied to obtain
. Similar estimation procedure as shown above can be applied to obtain 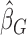 . In particular, for the traditional case–cohort biased sampling setting, the corresponding
. In particular, for the traditional case–cohort biased sampling setting, the corresponding 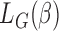 is given by
is given by
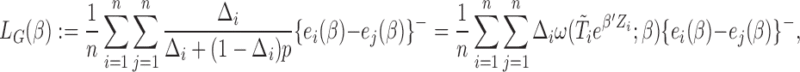 |
where 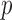 denotes the sampling probability amongst the censored subjects. Furthermore, in our model,
denotes the sampling probability amongst the censored subjects. Furthermore, in our model, 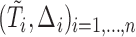 refer to the samples selected in the subcohort. For case–cohort data on the AFT model, Kong and Cai (2009) also proposed an estimation procedure based on the convergence result of Wei and others (1990). Their method covers the case of sampling without replacement, which is slightly different from the current setting. It is noteworthy that Nan and others (2006) and Nan and others (2009) view case–cohort sampling from the missing data perspective. Indeed, one can actually derive (2.3) by considering
refer to the samples selected in the subcohort. For case–cohort data on the AFT model, Kong and Cai (2009) also proposed an estimation procedure based on the convergence result of Wei and others (1990). Their method covers the case of sampling without replacement, which is slightly different from the current setting. It is noteworthy that Nan and others (2006) and Nan and others (2009) view case–cohort sampling from the missing data perspective. Indeed, one can actually derive (2.3) by considering 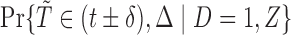 , where
, where 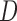 denotes the indicator of observing an individual or not as demonstrated in Kim and others (2013). While our formulation coincides with the construction of Nan and others (2009) with a non-predictable weight function for the classical case–cohort sampling, such a generalization enables us to handle variants of case–cohort sampling, including stratified case–cohort sampling, generalized case–cohort sampling, and case–cohort sampling on length-biased samples; see Section 3.1 and Kim and others (2013) for further details. Neither of the previously mentioned last two settings has been studied in the existing literature to the best of our knowledge.
denotes the indicator of observing an individual or not as demonstrated in Kim and others (2013). While our formulation coincides with the construction of Nan and others (2009) with a non-predictable weight function for the classical case–cohort sampling, such a generalization enables us to handle variants of case–cohort sampling, including stratified case–cohort sampling, generalized case–cohort sampling, and case–cohort sampling on length-biased samples; see Section 3.1 and Kim and others (2013) for further details. Neither of the previously mentioned last two settings has been studied in the existing literature to the best of our knowledge.
Before concluding this subsection, the authors would like to emphasize that the translation from Kim and others (2013) to the current model setting is not as direct as it appears to be. In addition to the fine treatment for the time variable 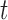 due to a different counting process considered, the proposed method, under a relatively high-dimensional setting, requires extra attention for cases like left truncation. Recall that for the case where there is left truncation for the sampled data, the weight function needed for bias correction is given by
due to a different counting process considered, the proposed method, under a relatively high-dimensional setting, requires extra attention for cases like left truncation. Recall that for the case where there is left truncation for the sampled data, the weight function needed for bias correction is given by 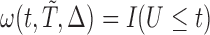 , where
, where 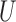 is the truncation threshold. In order to be selected into the sample, subjects must survive until at least
is the truncation threshold. In order to be selected into the sample, subjects must survive until at least  . Correspondingly, the estimating equation, under the AFT model setting, will become
. Correspondingly, the estimating equation, under the AFT model setting, will become
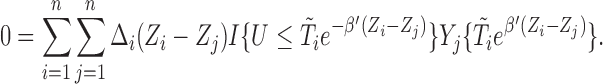 |
It can be shown that the right-hand side of the above equation is not a monotonic non-decreasing field. There can be multiple inconsistent roots, especially for relatively high-dimensional 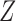 's. For other sampling procedures that introduce biases, which include case–cohort, stratified/generalized and combo of case–cohort with length-biased sampling, we can still obtain a monotone estimating equation. Once we have such a desirable numerical property, the root-finding procedure can be carried out via convex optimization.
's. For other sampling procedures that introduce biases, which include case–cohort, stratified/generalized and combo of case–cohort with length-biased sampling, we can still obtain a monotone estimating equation. Once we have such a desirable numerical property, the root-finding procedure can be carried out via convex optimization.
2.3. Variance estimation
The random vector 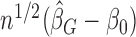 is asymptotically mean zero with covariance matrix of the form
is asymptotically mean zero with covariance matrix of the form 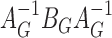 , where
, where 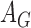 and
and 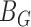 are functions of
are functions of 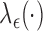 , the unknown hazard of the residual:
, the unknown hazard of the residual:
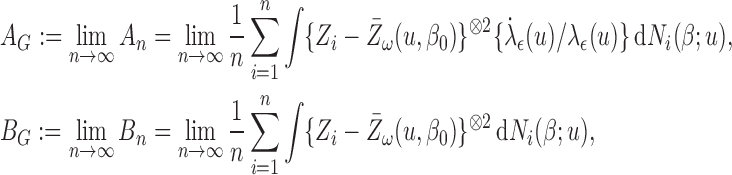 |
where 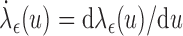 . It is therefore challenging to obtain an analytical expression for the covariance matrix. In this subsection, we will adopt a resampling scheme discussed in Jin and others (2006). Since the perturbation method proposed in Jin and others (2003) is developed upon a martingale structure, the weight function
. It is therefore challenging to obtain an analytical expression for the covariance matrix. In this subsection, we will adopt a resampling scheme discussed in Jin and others (2006). Since the perturbation method proposed in Jin and others (2003) is developed upon a martingale structure, the weight function 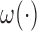 that adjusts the bias makes the direct adaptation of Jin and others (2003) not possible.
that adjusts the bias makes the direct adaptation of Jin and others (2003) not possible.
We, therefore, define a loss function
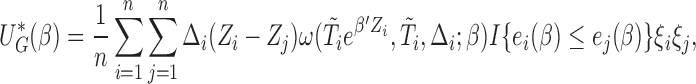 |
where 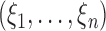 are independent positive random variables with
are independent positive random variables with 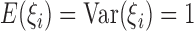 ,
, 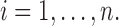 Denote by
Denote by 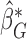 a root that solves
a root that solves 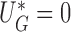 , which can be obtained from the convex optimization discussed in Section 2.2. Note that
, which can be obtained from the convex optimization discussed in Section 2.2. Note that 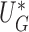 has the same mean and approximately the same variance as its unperturbed counterpart
has the same mean and approximately the same variance as its unperturbed counterpart 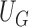 as defined in (2.7). It can be shown that the asymptotic distribution of
as defined in (2.7). It can be shown that the asymptotic distribution of 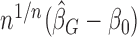 can be approximated by the conditional distribution of
can be approximated by the conditional distribution of 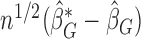 given the data
given the data 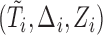 . In order to approximate the distribution of
. In order to approximate the distribution of 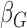 , a large number of realizations of
, a large number of realizations of 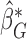 are generated by randomizing the perturbation
are generated by randomizing the perturbation 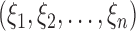 while holding the data at their observed values. The asymptotic variance of
while holding the data at their observed values. The asymptotic variance of 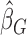 can then be estimated by the empirical covariance matrix of
can then be estimated by the empirical covariance matrix of 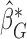 , enabling construction of Wald-type confidence intervals for
, enabling construction of Wald-type confidence intervals for 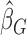 . This procedure is applicable to cases in which there are high censoring rates and hence is useful for the biased sampling schemes that our framework can cover.
. This procedure is applicable to cases in which there are high censoring rates and hence is useful for the biased sampling schemes that our framework can cover.
2.4. General weight functions
Upon the basis of 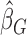 , we introduce the following modification that allows the construction of weighted Gehan-type loss functions. It is a modified version of Jin and others (2003) with the variable
, we introduce the following modification that allows the construction of weighted Gehan-type loss functions. It is a modified version of Jin and others (2003) with the variable 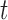 due to the bias-adjusting weight function which may involve time. The most popular weight functions, for example log-rank, Prentice–Wilcoxon and
due to the bias-adjusting weight function which may involve time. The most popular weight functions, for example log-rank, Prentice–Wilcoxon and 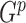 class of Harrington and Fleming (1982), are special cases of this framework. Let
class of Harrington and Fleming (1982), are special cases of this framework. Let 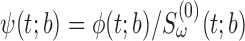 ; one can write
; one can write
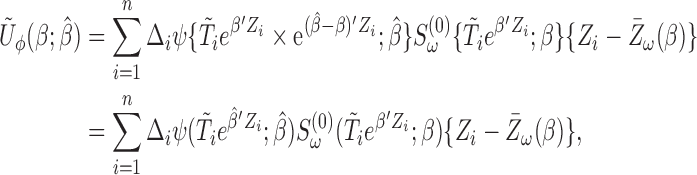 |
where 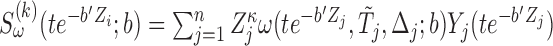 ,
, 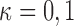 . The resulting
. The resulting 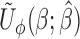 is similar to that of (2.7) except for the additional weights
is similar to that of (2.7) except for the additional weights 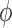 introduced. This term is, however, free of
introduced. This term is, however, free of 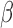 . Hence,
. Hence, 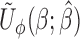 is still monotone in each component of
is still monotone in each component of 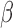 and the root-finding procedure can be carried out in a similar fashion as discussed in Section 2.2. The estimate
and the root-finding procedure can be carried out in a similar fashion as discussed in Section 2.2. The estimate 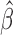 has to be estimated iteratively with
has to be estimated iteratively with 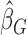 as the initial value. Numerical results suggest that the number of iterations can be as small as three in order to achieve the convergence; see Jin and others (2003). Similar to the discussion in Section 2.2, despite the fact that
as the initial value. Numerical results suggest that the number of iterations can be as small as three in order to achieve the convergence; see Jin and others (2003). Similar to the discussion in Section 2.2, despite the fact that 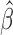 can be easily obtained via iterations, it is difficult to obtain an analytical expression for the limiting covariance matrix. As in the case of
can be easily obtained via iterations, it is difficult to obtain an analytical expression for the limiting covariance matrix. As in the case of 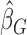 , one can adopt the resampling approach and carry out inference on
, one can adopt the resampling approach and carry out inference on 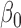 based on the empirical distribution of
based on the empirical distribution of 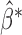 , the set of estimates under perturbation.
, the set of estimates under perturbation.
3. Numerical results
3.1. Simulations
Results of simulations of four study designs are detailed in the supplementary material available at Biostatistics online. In particular, we considered four biased sampling designs that are under the scope of the proposed framework, namely (i) length-biased sampling, (ii) case–cohort design, (iii) generalized case–cohort design, and (iv) a combo biased sampling: case–cohort analysis on length-biased data. For generalized case–cohort design (Kim and others, 2013), case–cohort samples are selected from the full cohort by sampling from cases with a probability of 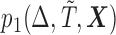 and controls with a possibly different probability of
and controls with a possibly different probability of 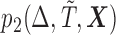 , where
, where 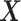 denotes covariates that may include (part of) the model covariates
denotes covariates that may include (part of) the model covariates 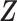 . Such a design can be regarded as a generalization of the stratified case–cohort design; see Borgan and others (2000). In all the examples presented, our method produces nearly unbiased parameter estimates with empirical coverage probabilities of the confidence intervals constructed close to their nominal values. As suggested by an anonymous referee, we also compared our results on length-biased data with Mandel and Ritov (2010); for various case–cohort settings, our approach was compared with that proposed in Nan and others (2009). Our approach, in general, provides more desirable estimates in terms of lower biasedness and/or smaller standard errors incurred.
. Such a design can be regarded as a generalization of the stratified case–cohort design; see Borgan and others (2000). In all the examples presented, our method produces nearly unbiased parameter estimates with empirical coverage probabilities of the confidence intervals constructed close to their nominal values. As suggested by an anonymous referee, we also compared our results on length-biased data with Mandel and Ritov (2010); for various case–cohort settings, our approach was compared with that proposed in Nan and others (2009). Our approach, in general, provides more desirable estimates in terms of lower biasedness and/or smaller standard errors incurred.
3.2. Real examples
In this subsection, we analyze three datasets, namely (i) a shrub dataset of Muttlak and McDonald (1990) for size-biased data, (ii) a dementia study carried out by Canadian Study of Health and Aging, and (iii) South Wales Nickel Refinery Study on nasal sinus. The first two sets of data correspond to length-/size-biased data, while the last one involves case–cohort analysis and its variants.
The original dataset of shrub with contains data on 89 shrub samples. According to Wang (1996), the dataset includes 46 samples. Data were collected using a line-intercept sampling method for vegetation. Under this sampling technique, the probability a shrub was included in the sample was proportional to the width. Two indicator covariates were used to denote the three groups of transects to which the shrubs belonged. In the analysis with results reported in Table 1(a), we defined 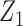 and
and 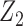 to be indicators that the shrub belonged to transect I and transect III, respectively, in which case the second transect was the reference group. A total of 500 resamplings were carried out for estimating the standard errors of the estimators. The estimates obtained are in concordance with the conclusion drawn in Kim and others (2013) for the Cox proportional hazards model and show the proportional hazards model provides a better fit to the dataset.
to be indicators that the shrub belonged to transect I and transect III, respectively, in which case the second transect was the reference group. A total of 500 resamplings were carried out for estimating the standard errors of the estimators. The estimates obtained are in concordance with the conclusion drawn in Kim and others (2013) for the Cox proportional hazards model and show the proportional hazards model provides a better fit to the dataset.
Table 1.
(a) Estimates and standard errors for regression parameters in Shrub Dataset; see Muttlak and McDonald (1990). (b) Estimates and standard errors for regression parameters CSHA Dataset. (c) Analysis of time from the first employment to the nasal sinus cancer death for the Welsh Nickel Refiners Study; Breslow and Day (1987)
| (a) | ||||||
|---|---|---|---|---|---|---|
| Parameter | Gehan | Log-rank | Parameter | Gehan | Log-rank | |
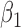 |
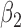 |
|||||
| Est. | 0.580 | 0.624 | Est. |
 0.182 0.182 |
 0.221 0.221 |
|
| SE | 0.213 | 0.235 | SE | 0.210 | 0.231 | |
| (b) | ||||||
| Parameter | Gehan | Log-rank | Parameter | Gehan | Log-rank | |
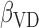 |
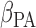 |
|||||
| Est. |
 0.043 0.043 |
0.014 | Est. |
 0.060 0.060 |
 0.050 0.050 |
|
| SE | 0.044 | 0.030 | SE | 0.050 | 0.060 | |
| (c) | ||||||
| Full cohort | Case–cohort | Gen. Case–cohort | ||||
| Parameter | Gehan | Log-rank | Gehan | Log-rank | Gehan | Log-rank |
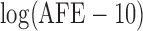 | ||||||
| Est. | 0.612 | 0.598 | 0.706 | 0.768 | 0.604 | 0.589 |
| SE | 0.110 | 0.103 | 0.122 | 0.148 | 0.126 | 0.137 |
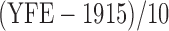 | ||||||
| Est. | 0.014 | 0.017 | 0.168 | 0.223 | 0.044 | 0.041 |
| SE | 0.077 | 0.075 | 0.101 | 0.116 | 0.083 | 0.086 |
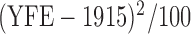 | ||||||
| Est. |
 0.173 0.173 |
 0.304 0.304 |
0.019 |
 0.054 0.054 |
 0.230 0.230 |
 0.322 0.322 |
| SE | 0.103 | 0.130 | 0.129 | 0.181 | 0.104 | 0.126 |
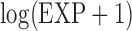 | ||||||
| Est. | 0.168 | 0.210 | 0.254 | 0.324 | 0.147 | 0.183 |
| SE | 0.041 | 0.042 | 0.052 | 0.066 | 0.044 | 0.047 |
The second example covers another version of length-biased sampling discussed in Vardi (1989), Wang (1991), and Shen and others (2009). It also corresponds to the second type of censoring under the length-bias setting studied in Tsai (2009). This configuration involves censoring of the residual lifetime after the data are sampled with bias. Under this setting, individuals' unbiased failure times can be observed only when they are event-free before the unbiased truncation time 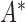 , i.e.
, i.e. 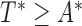 . For the observed (biased) data, we define
. For the observed (biased) data, we define 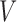 as the time measured from the initiation time
as the time measured from the initiation time 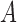 to failure, which is regarded as the residual survival time. We assume that
to failure, which is regarded as the residual survival time. We assume that 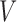 is censored by
is censored by 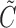 , the residual potential censoring variable, and that
, the residual potential censoring variable, and that 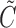 is independent of
is independent of 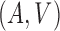 conditional on
conditional on 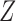 . Then the observed survival and censoring times,
. Then the observed survival and censoring times, 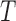 and
and 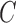 , can be expressed, respectively, as
, can be expressed, respectively, as 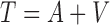 and
and 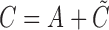 ; again
; again 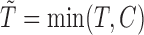 and
and 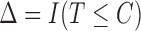 .
.
It can be shown that, conditional on the truncation time 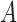 , the weight function
, the weight function 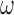 is
is
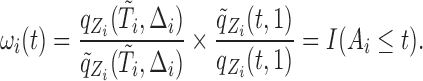 |
This weight function leads to
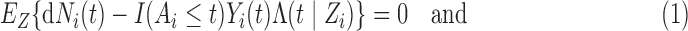 |
(3.1) |
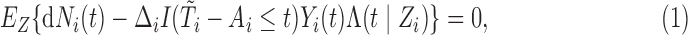 |
(3.2) |
where (3.2) is due to the stationarity assumption, see Vardi (1989). We can, therefore, define a family of subject-specific weight functions by combining (3.1) and (3.2):
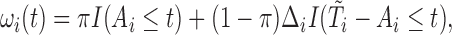 |
(3.3) |
where 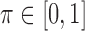 . We recommend the choice of
. We recommend the choice of 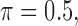 which can strike a balance between (3.1) and (3.2). The indicator functions included, however, may not necessarily lead to a monotone estimating equation as discussed at the end of Section 2.2. Our numerical experience, however, shows that this non-monotone structure does not affect the estimation accuracy significantly for 2D cases. To handle this problem for a more general setting, one may adopt the induced smoothing approach for the AFT model proposed in Chiou and others (2015) to avoid the multiple-root problem. This is, however, beyond the scope of this paper.
which can strike a balance between (3.1) and (3.2). The indicator functions included, however, may not necessarily lead to a monotone estimating equation as discussed at the end of Section 2.2. Our numerical experience, however, shows that this non-monotone structure does not affect the estimation accuracy significantly for 2D cases. To handle this problem for a more general setting, one may adopt the induced smoothing approach for the AFT model proposed in Chiou and others (2015) to avoid the multiple-root problem. This is, however, beyond the scope of this paper.
The dataset collected in the Canadian Study of Health and Aging (CSHA) study identified 1132 seniors aged 65 or above having the disease. All the dementia patients had undergone a follow-up procedure up to 1996. Entries with missing attributes are removed, resulting in the final dataset of size 818. Each individual can be categorized into three groups, namely (i) probable Alzheimer's disease (393 patients), (ii) possible Alzheimer's disease (252 patients), and (iii) vascular dementia (173 patients). The censoring rate is slightly over 22%. Table 1(b) reports the estimated values of 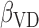 and
and 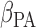 based on (3.3). They can be interpreted as the marginal effect on the log-survival times of vascular disease and possible Alzheimer patients, respectively. Neither of these indicator variables is statistically significant. In other words, there is no significant difference in survival times amongst the three groups of patients. Our finding agrees with the conclusion made in Shen and others (2009).
based on (3.3). They can be interpreted as the marginal effect on the log-survival times of vascular disease and possible Alzheimer patients, respectively. Neither of these indicator variables is statistically significant. In other words, there is no significant difference in survival times amongst the three groups of patients. Our finding agrees with the conclusion made in Shen and others (2009).
In addition to length-/size-biased data, we also analyze a case–cohort sampling-related sample called the South Welsh Nickel Refiners Study dataset. It contains altogether 679 subjects employed in a nickel refinery. The records of these workers are registered in Appendix VIII of Breslow and Day (1987). The study continued the follow-up until 1981 when 56 deaths were observed from cancer of the nasal sinus. The corresponding censoring rate is 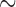 92%. Previous studies discover three significant risk factors, which include AFE (age at first employment), YFE (year at first employment), and EXP (exposure level). In Kim and others (2013), specifically, they set up the following four variables as regression covariates:
92%. Previous studies discover three significant risk factors, which include AFE (age at first employment), YFE (year at first employment), and EXP (exposure level). In Kim and others (2013), specifically, they set up the following four variables as regression covariates: 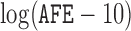 , log of the age of the first employment minus 10 years,
, log of the age of the first employment minus 10 years, 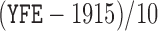 ,
, 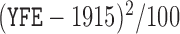 , two transformed versions of number of years working in the refinery since 1915 and
, two transformed versions of number of years working in the refinery since 1915 and 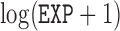 , the log exposure level; some of the subjects had zero exposure and hence
, the log exposure level; some of the subjects had zero exposure and hence 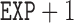 is considered so that its logged value is non-negative and well-defined.
is considered so that its logged value is non-negative and well-defined.
In Table 1(c), the first column presents the estimated parameter values obtained from the full cohort dataset. In this case,  for all observations. The second column displays the results from fitting the same model to data obtained from a randomly drawn, hypothetical subcohort. Such a subcohort contains all the observed failures and some censored subjects that make up two-thirds of the size of the subcohort. We also performed an analysis on another hypothetical subcohort which was drawn from the generalized case–cohort sampling scheme. We used selection probability
for all observations. The second column displays the results from fitting the same model to data obtained from a randomly drawn, hypothetical subcohort. Such a subcohort contains all the observed failures and some censored subjects that make up two-thirds of the size of the subcohort. We also performed an analysis on another hypothetical subcohort which was drawn from the generalized case–cohort sampling scheme. We used selection probability 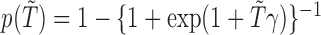 , where
, where 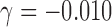 and
and 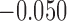 for
for 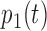 and
and 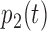 , respectively. The estimated values of
, respectively. The estimated values of 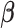 and their standard deviations are summarized in the third column of Table 1(c). All of these studies indicate that the covariates
and their standard deviations are summarized in the third column of Table 1(c). All of these studies indicate that the covariates 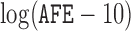 and
and 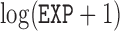 are statistically significant. Compared with the full cohort study, the estimated standard deviation of
are statistically significant. Compared with the full cohort study, the estimated standard deviation of 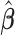 presented for the two case–cohort studies are slightly inflated. The estimates obtained from this generalized case–cohort sampling scheme are closed to the corresponding values obtained by using a full cohort. Under the generalized case–cohort setting, however, only 65% of the cases were included in the subcohort with the sample size only about 30% of that of the original samples.
presented for the two case–cohort studies are slightly inflated. The estimates obtained from this generalized case–cohort sampling scheme are closed to the corresponding values obtained by using a full cohort. Under the generalized case–cohort setting, however, only 65% of the cases were included in the subcohort with the sample size only about 30% of that of the original samples.
4. Conclusion
In this paper, we propose an inference procedure for the regression parameter and the distribution function of the error term in the AFT model under general biased sampling schemes. This is a parallel of Kim and others (2013) to the AFT counterpart. This methodology again covers special cases of general biased sampling schemes in which the sampling probability depends on the outcome variable 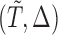 under one unified framework. The weight function
under one unified framework. The weight function 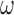 introduced that adjust the bias due to various sampling schemes plays a major role. As we have demonstrated, the corresponding weight functions for many common sampling schemes are readily available. This adds versatility and usefulness to the proposed method.
introduced that adjust the bias due to various sampling schemes plays a major role. As we have demonstrated, the corresponding weight functions for many common sampling schemes are readily available. This adds versatility and usefulness to the proposed method.
Supplementary material
Supplementary Material is available at http://biostatistics.oxfordjournals.org.
Funding
T.S. acknowledges the financial support of the Research Grants Council of Hong Kong ECS 24300514. Z.Y. research is supported in part by the National Science Foundation DMS-1308566 and the National Institutes of Health R37GM047845.
Supplementary Material
Acknowledgments
The authors would like to thank anonymous referees for their valuable comments which have significantly improved the paper, in particular for our treatments for the length-biased sampling case. Acknowledgement should also be dedicated to the CSHA for permission for usage of part of the data collected for the dementia study. Conflict of Interest: None declared.
References
- Asgharian M., M'Lan C. E. Wolfson D. B. (2002). Length-biased sampling with right censoring: an unconditional approach. Journal of the American Statistical Association 95, 888–902. [Google Scholar]
- Asgharian M., Wolfson D. B. (2005). Asymptotic behavior of the unconditional NPMLE of the length-biased survivor function from right censored prevalent cohort data. The Annals of Statistics 33, 2109–2131. [Google Scholar]
- Borgan Ø., Langholz B., Samuelsen S. O., Goldstein L. Pogoda J. (2000). Exposure stratified case–cohort designs. Lifetime Data Analysis 6, 39–58. [DOI] [PubMed] [Google Scholar]
- Breslow N. E., Day N. E. (1987) Statistical Methods in Cancer Research, Vol. II: The Design and Analysis of Cohort Studies. Lyon, France: IARC. [PubMed] [Google Scholar]
- Buckley J., James I. (1979). Linear regression with censored data. Biometrika 66, 429–436. [Google Scholar]
- Chen Y. Q. (2010). Semiparametric regression in size-biased sampling. Biometrics 66, 149–158. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chiou S., Kang S. Yan J. (2015). Rank-based estimating equations with general weight for the accelerated failure time model: an induced smoothing approach. Statistics in Medicine 34, 1495–1510. [DOI] [PubMed] [Google Scholar]
- Cox D. R. (1969). Some sampling problems in technology. In: Johnson and Smith (editors), New Developments in Survey Sampling. New York: Wiley.
- Cox D. R. (1972). Regression models and life-tables (with Discussion). Journal of the Royal Statistical Society. Series B 34, 187–220. [Google Scholar]
- Cox D. R., Oakes D. (1984) Analysis of Survival Data. London: Chapman and Hall. [Google Scholar]
- Gill R. D. (1980). Censoring and Stochastic Integrals, Mathematical Center Tract 124 Amsterdam: Mathematische Centrum. [Google Scholar]
- Harrington D. P., Fleming T. R. (1982). A class of rank test procedures for censored survival data. Biometrika 69, 133–143. [Google Scholar]
- Jin Z., Lin D. Y., Wei L. J. Ying Z. (2003). Rank-based inference for the accelerated failure time model. Biometrika 90, 341–353. [Google Scholar]
- Jin Z., Lin D. Y. Ying Z. (2006). Rank regression analysis of multivariate failure time data based on marginal linear models. Scandinavian Journal of Statistics 33, 1–23. [Google Scholar]
- Kalbfleisch J. D., Prentice R. L. (2002) The Statistical Analysis of Failure Time Data, 2nd edition New York: Wiley. [Google Scholar]
- Kiefer N. M. (1988). Economic duration data and hazard functions. Journal of Economic Literature 26, 646–679. [Google Scholar]
- Kim J. P., Lu W., Sit T. Ying Z. (2013). A unified approach to semiparametric transformation models under generalized biased sampling schemes. Journal of the American Statistical Association 108, 217–227. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kong L., Cai J. (2009). Case–cohort analysis with accelerated failure time model. Biometrics 65, 135–142. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lu W. B., Tsiatis A. A. (2006). Semiparametric transformation models for case–cohort study. Biometrika 93, 207–214. [Google Scholar]
- Mandel M., Ritov Y. (2010). The accelerated failure time model under biased sampling. Biometrics 66, 1306–1308. [DOI] [PubMed] [Google Scholar]
- McFadden J. A. (1962). On the lengths of intervals in a stationary point process. Journal of the Royal Statistical Society. Series B 24, 364–382. [Google Scholar]
- Muttlak H. A., McDonald L. L. (1990). Ranked set sampling with size-biased probability of selection. Biometrics 46, 435–446. [Google Scholar]
- Nan B., Kalbfleisch J. D. Yu M. (2009). Asymptotic theory for the semiparametric accelerated failure time model with missing data. The Annals of Statistics 37, 2351–2376. [Google Scholar]
- Nan B., Yu M. Kalbfleisch J. D. (2006). Censored linear regression for case–cohort studies. Biometrika 93, 747–762. [Google Scholar]
- Prentice R. L. (1978). Linear rank tests with right-censored data. Biometrika 65, 167–179. [Google Scholar]
- Prentice R. L. (1986). A Case–cohort design for epidemiologic cohort studies and disease prevention trials. Biometrika 73, 1–11. [Google Scholar]
- Ritov Y. (1990). Estimation in a linear regression model with censored data. The Annals of Statistics 18, 303–328. [Google Scholar]
- Shen Y., Ning J. Qin J. (2009). Analyzing length-biased data with semiparametric transformation and accelerated failure time models. Journal of the American Statistical Association 104, 1192–1202. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shen Y., Ning J. Qin J. (2012). Likelihood approaches for the invariant density ratio model with biased-sampling data. Biometrika 99, 363–378. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tsai W.-Y. (2009). Pseudo-partial likelihood for proportional hazards models with biased-sampling data. Biometrika 96, 601–615. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tsiatis A. A. (1990). Estimating regression parameters using linear rank tests for censored data. The Annals of Statistics 18, 354–372. [Google Scholar]
- Vardi Y. (1982). Nonparametric estimation in the presence of length bias. The Annals of Statistics 10, 616–620. [Google Scholar]
- Vardi Y. (1985). Empirical distributions in selection bias models. The Annals of Statistics 13, 178–203. [Google Scholar]
- Vardi Y. (1989). Multiplicative censoring, renewal processes, deconvolution and decreasing density: nonparametric estimation. Biometrika 76, 751–761. [Google Scholar]
- Wang M.-C. (1991). Nonparametric estimation from cross-sectional survival data. Journal of the American Statistical Association 86, 751–761. [Google Scholar]
- Wang M.-C. (1996). Hazards regression analysis for length-biased data. Biometrika 83, 343–354. [Google Scholar]
- Wei L. J., Ying Z. Lin D. Y. (1990). Linear regression analysis of censored survival data based on rank tests. Biometrika 77, 845–851. [Google Scholar]
- Ying Z. (1993). A large sample study of rank estimation for censored regression data. The Annals of Statistics 21, 76–99. [Google Scholar]
- Zeng D., Lin D. Y. (2007). Efficient estimation for the accelerated failure time model. Journal of the American Statistical Association 102, 1387–1396. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.