Abstract
Studies often follow individuals until they fail from one of a number of competing failure types. One approach to analyzing such competing risks data involves modeling the cause-specific hazards as functions of baseline covariates. A common issue that arises in this context is missing values in covariates. In this setting, we first establish conditions under which complete case analysis (CCA) is valid. We then consider application of multiple imputation to handle missing covariate values, and extend the recently proposed substantive model compatible version of fully conditional specification (SMC-FCS) imputation to the competing risks setting. Through simulations and an illustrative data analysis, we compare CCA, SMC-FCS, and a recent proposal for imputing missing covariates in the competing risks setting.
Keywords: Competing risks, Missing covariates, Missing at random, Multiple imputation
1. Introduction
In competing risks analysis, individuals are followed up until they “fail” from one of a set of possible causes of failure, e.g. cause-specific death. In such situations, it is often of interest to model how the hazard of failure from the different causes depends on a set of covariates recorded at cohort entry. Arguably, the most direct approach to analyzing competing risks data is to specify models for the cause-specific hazard functions (Andersen and others, 2002).
A problem that arises in practice is that one or more covariates contain missing values. While extensive research has been conducted into missing covariates in the context of generalized linear models (Ibrahim and others, 2005) and the Cox model for single failure type data (Herring and Ibrahim, 2001; White and Royston, 2009), little has been done on competing risks. Recently, Escarela and others (2013) proposed a likelihood-based approach for handling incomplete covariates in competing risks analysis, based on models for the conditional survival distributions. They focused on the case of two partially observed discrete covariates, and developed a copula-based approach to model specification, under both missing at random (MAR) and missing not at random (MNAR) mechanisms (Rubin, 1976).
The simplest and most commonly used approach to handling missing covariates is to fit models of interest excluding those with missing covariate values, in a so-called complete case analysis (CCA). In Section 3, we establish a condition under which CCA is valid, and discuss how the observed data can be used to assess compatibility with this condition. An increasingly popular approach for handling missing data is to use multiple imputation (MI), usually under the MAR assumption (Carpenter and Kenward, 2013). In Section 4, we describe recent proposals for imputing covariates in the competing risks setting using standard software. We then propose an approach that ensures covariates are imputed using models that are compatible with the analyst's specified cause-specific hazard models. We compare CCA with the MI approaches in simulations in Section 5. In Section 6, we apply CCA and MI to handle missing covariates in an analysis of data from the NHANES III study. We conclude with a discussion in Section 7.
2. Setup and full data analysis
We assume a sample of 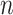 independent individuals. For each, we observe vectors of time-independent baseline covariates
independent individuals. For each, we observe vectors of time-independent baseline covariates 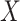 and
and 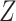 . For the moment, we assume both are fully observed. For each individual, we assume the existence of a time to failure
. For the moment, we assume both are fully observed. For each individual, we assume the existence of a time to failure 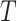 and failure indicator
and failure indicator 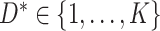 , where
, where 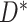 indicates the type of failure. As described by Prentice and others (1978), the basic estimable quantities in the competing risks setting are the cause-specific hazard functions. For cause
indicates the type of failure. As described by Prentice and others (1978), the basic estimable quantities in the competing risks setting are the cause-specific hazard functions. For cause 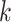 , the cause-specific hazard function is defined as
, the cause-specific hazard function is defined as
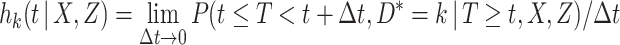 |
Often the time to failure is censored, and so we further assume the existence of a time to censoring 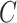 for each individual. We observe
for each individual. We observe 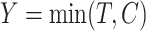 and
and 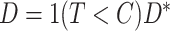 , which indicates either the observed cause of failure or that the individual is censored (
, which indicates either the observed cause of failure or that the individual is censored (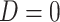 ). We assume that censoring is independent, in the sense that
). We assume that censoring is independent, in the sense that 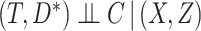 . An individual's contribution to the likelihood function, conditional on
. An individual's contribution to the likelihood function, conditional on 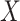 and
and 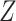 , is then equal to
, is then equal to
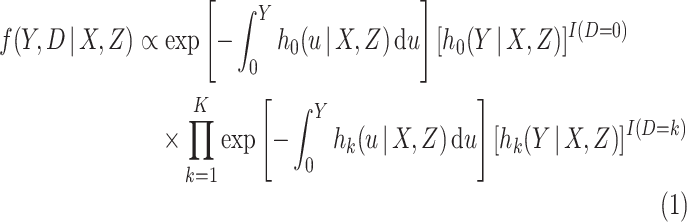 |
(2.1) |
where 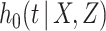 denotes the hazard for the censoring process, given
denotes the hazard for the censoring process, given 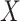 and
and 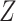 . When covariates are fully observed, as described by Prentice and others (1978), inference for a particular (say
. When covariates are fully observed, as described by Prentice and others (1978), inference for a particular (say 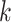 th) cause-specific hazard function can proceed by using standard survival analysis procedures, treating both censoring events and failures from causes other than
th) cause-specific hazard function can proceed by using standard survival analysis procedures, treating both censoring events and failures from causes other than 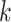 as censored at their time of failure. A popular approach is to assume a Cox proportional hazards model
as censored at their time of failure. A popular approach is to assume a Cox proportional hazards model
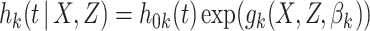 |
(2.2) |
where 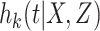 denotes the cause-specific hazard function for cause
denotes the cause-specific hazard function for cause 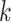 ,
, 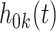 denotes the baseline hazard function for cause
denotes the baseline hazard function for cause 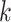 ,
, 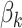 denotes a vector of cause-specific regression coefficients, and
denotes a vector of cause-specific regression coefficients, and 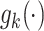 denotes a known function, indexed by
denotes a known function, indexed by 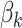 . The baseline hazard functions
. The baseline hazard functions 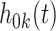 can either be assumed to follow a parametric form or as is more commonly done in the absence of missing covariates, left arbitrary. In this case, as in Cox's proportional hazards model, the cumulative baseline hazard
can either be assumed to follow a parametric form or as is more commonly done in the absence of missing covariates, left arbitrary. In this case, as in Cox's proportional hazards model, the cumulative baseline hazard 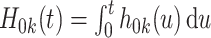 can be viewed as an infinite dimensional parameter.
can be viewed as an infinite dimensional parameter.
An alternative formulation of the competing risks problem involves postulating the existence of latent failure times for each cause of failure. This formulation and analyses based on it relies on strong untestable assumptions surrounding independence of competing risks (Prentice and others, 1978; Andersen and others, 2002), and so we do not pursue it further here.
3. Complete case analysis
We now consider inference when 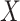 is partially observed (
is partially observed (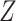 remains fully observed). We let
remains fully observed). We let 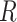 denote whether all components of
denote whether all components of 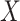 are observed (
are observed ( ) or some are missing (
) or some are missing (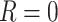 ). Without loss of generality, we assume interest lies in fitting a model for the first cause-specific hazard function. In CCA, we fit a model for this using only those individuals with
). Without loss of generality, we assume interest lies in fitting a model for the first cause-specific hazard function. In CCA, we fit a model for this using only those individuals with 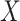 completely observed and who therefore have
completely observed and who therefore have  . In Appendix A of the Supplementary Materials (available at Biostatistics online), we show that this will be valid if
. In Appendix A of the Supplementary Materials (available at Biostatistics online), we show that this will be valid if 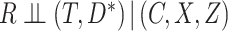 . This assumption encompasses both MAR mechanisms (e.g. missingness dependent only on
. This assumption encompasses both MAR mechanisms (e.g. missingness dependent only on 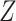 ) and MNAR mechanisms (e.g. missingness dependent on
) and MNAR mechanisms (e.g. missingness dependent on 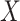 , or missingness dependent on
, or missingness dependent on 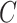 ).
).
In the special case of single failure type data (i.e. 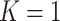 ), Rathouz (2007) established sufficient conditions under which CCA gives valid inferences. Specifically, he showed that valid inferences are obtained if
), Rathouz (2007) established sufficient conditions under which CCA gives valid inferences. Specifically, he showed that valid inferences are obtained if 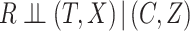 . We note that since single failure time data are a special case of competing risks with
. We note that since single failure time data are a special case of competing risks with 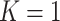 , our result extends that of Rathouz (2007) in that missingness in
, our result extends that of Rathouz (2007) in that missingness in 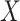 can be dependent on
can be dependent on 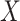 . This extension intuitively makes sense in light of the fact that CCA makes no distinction between which covariates are fully observed and which are partially observed in the full sample.
. This extension intuitively makes sense in light of the fact that CCA makes no distinction between which covariates are fully observed and which are partially observed in the full sample.
A special case of the sufficient missingness assumption is when 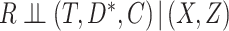 , in which case missingness in
, in which case missingness in 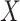 is covariate dependent. As discussed by Bartlett and others (2014), such an assumption may sometimes be plausible when, as here, the covariates temporally preceed the outcome. This is because in order for
is covariate dependent. As discussed by Bartlett and others (2014), such an assumption may sometimes be plausible when, as here, the covariates temporally preceed the outcome. This is because in order for 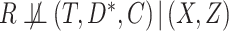 , there would have to exist another baseline variable
, there would have to exist another baseline variable 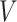 which itself has an independent effect on
which itself has an independent effect on 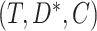 and on
and on 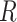 .
.
As with the MAR assumption, in general, it is not possible to verify the assumption 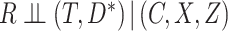 from the observed data. It is, however, possible to check whether the observed data are compatible with a stronger version of the assumption. Specifically, consider the stronger assumptions that
from the observed data. It is, however, possible to check whether the observed data are compatible with a stronger version of the assumption. Specifically, consider the stronger assumptions that 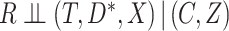 and that
and that 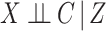 (this condition being unnecessary if there is no censoring). Then by ignoring the actual cause of failure, the results of Rathouz (2007) imply that: (1)
(this condition being unnecessary if there is no censoring). Then by ignoring the actual cause of failure, the results of Rathouz (2007) imply that: (1) 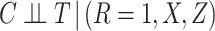 , (2)
, (2) 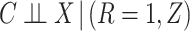 , (3)
, (3) 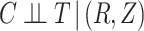 , and (4)
, and (4) 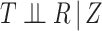 . One can then check whether the observed data are compatible with these implications of the stronger assumptions. Specifically, (1) implies one can check whether (2) holds by fitting a model for the hazard of censoring (treating failures as censoring events) conditional on
. One can then check whether the observed data are compatible with these implications of the stronger assumptions. Specifically, (1) implies one can check whether (2) holds by fitting a model for the hazard of censoring (treating failures as censoring events) conditional on 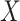 and
and 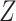 within the complete cases. If the stronger assumptions hold, one should find that the hazard for censoring in this model does not depend on
within the complete cases. If the stronger assumptions hold, one should find that the hazard for censoring in this model does not depend on 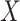 (i.e. (2) is satisfied). Next, (3) implies that censoring is independent conditional on
(i.e. (2) is satisfied). Next, (3) implies that censoring is independent conditional on 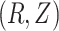 . Thus, (4) can be checked by fitting a model for the hazard of any failure (i.e. combining the failure types), conditional on
. Thus, (4) can be checked by fitting a model for the hazard of any failure (i.e. combining the failure types), conditional on 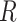 and
and 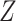 . If (4) is satisfied, one should find that the hazard of any failure does not depend on
. If (4) is satisfied, one should find that the hazard of any failure does not depend on 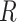 , conditional on
, conditional on 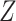 . It is important to note, however, that if the observed data are not consistent with the implications of the stronger assumptions, this does not necessarily mean that the CCA is invalid.
. It is important to note, however, that if the observed data are not consistent with the implications of the stronger assumptions, this does not necessarily mean that the CCA is invalid.
4. MI assuming MAR
As described in the introduction, MI assuming data are MAR is a commonly adopted approach for handling missing covariates. In this section, we first consider the plausibility of MAR. We then describe a recently proposed MI approach for the competing risks setting. Lastly, we propose an approach that imputes covariates from models which are compatible with the analyst's specified models for the cause-specific hazard functions.
4.1. Plausibility of MAR
For the moment, suppose that 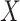 is either scalar or a vector of covariates which is either entirely missing or entirely observed. The MAR assumption here means that
is either scalar or a vector of covariates which is either entirely missing or entirely observed. The MAR assumption here means that 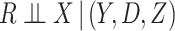 . MAR is plausible if missingness in
. MAR is plausible if missingness in 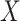 is thought to be dependent on
is thought to be dependent on 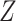 . Alternatively, if missingness depends on
. Alternatively, if missingness depends on 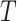 and/or
and/or 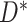 , then MAR holds in the absence of censoring (since then
, then MAR holds in the absence of censoring (since then 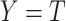 and
and 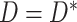 ). However, if censoring is present, and missingness depends on
). However, if censoring is present, and missingness depends on 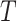 and/or
and/or 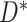 , following the results of Rathouz (2007) for time-to-event data, MAR does not hold. Nevertheless, MAR is a useful assumption, since it enables information to be extracted from the incomplete cases, and provides a starting point for possible MNAR sensitivity analyses.
, following the results of Rathouz (2007) for time-to-event data, MAR does not hold. Nevertheless, MAR is a useful assumption, since it enables information to be extracted from the incomplete cases, and provides a starting point for possible MNAR sensitivity analyses.
4.2. Directly specified imputation models
Imputation models are in practice almost always specified directly as conditional models for the incomplete variable(s), conditional on the fully observed variables. In the present context, this means directly specifying a model for 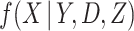 . In the simpler context of incomplete covariates in survival analysis, White and Royston (2009) previously derived imputation models for incomplete covariates which are approximately compatible with a Cox proportional hazards model for the hazard of failure, assuming the latter contains main effects of
. In the simpler context of incomplete covariates in survival analysis, White and Royston (2009) previously derived imputation models for incomplete covariates which are approximately compatible with a Cox proportional hazards model for the hazard of failure, assuming the latter contains main effects of 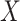 and
and 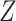 . Specifically, they proposed that the incomplete
. Specifically, they proposed that the incomplete 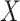 be imputed using an imputation model with
be imputed using an imputation model with 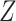 ,
, 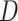 (the binary event indicator) and the baseline cumulative hazard function, as covariates. A better approximation additionally includes interactions between
(the binary event indicator) and the baseline cumulative hazard function, as covariates. A better approximation additionally includes interactions between 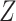 and the baseline cumulative hazard function. Since the baseline cumulative hazard function is not available prior to analysis, they proposed its approximation by the Nelson–Aalen estimator of the marginal cumulative hazard function. Through simulations, they demonstrated that their approach gives estimates that typically have little or small bias, although larger biases can occur with strong covariate effects.
and the baseline cumulative hazard function. Since the baseline cumulative hazard function is not available prior to analysis, they proposed its approximation by the Nelson–Aalen estimator of the marginal cumulative hazard function. Through simulations, they demonstrated that their approach gives estimates that typically have little or small bias, although larger biases can occur with strong covariate effects.
Recently, Resche-Rigon and others (2012) proposed an extension of the results of White and Royston (2009) to the competing risks setting. Assuming Cox proportional hazards models for each cause-specific hazard, they showed using a Taylor series expansion that an approximately compatible imputation model for 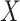 uses
uses 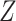 ,
, 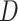 (as a factor variable) and
(as a factor variable) and 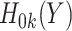 ,
, 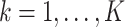 as covariates. Resche-Rigon and others (2012) further showed that this approximation could be improved by including the interactions
as covariates. Resche-Rigon and others (2012) further showed that this approximation could be improved by including the interactions 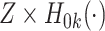 ,
, 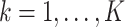 . Since the cumulative baseline hazard functions are not available prior to imputation, they proposed their approximation by the corresponding Nelson–Aalen estimates of the (marginal) cumulative cause-specific hazard functions. Simulation results suggested that the approach led to estimates with little bias, and confidence intervals with nominal coverage. They also demonstrated that applying the approach of White and Royston (2009) treating failures from competing risks which were not of primary interest as censoring, led to bias. When
. Since the cumulative baseline hazard functions are not available prior to imputation, they proposed their approximation by the corresponding Nelson–Aalen estimates of the (marginal) cumulative cause-specific hazard functions. Simulation results suggested that the approach led to estimates with little bias, and confidence intervals with nominal coverage. They also demonstrated that applying the approach of White and Royston (2009) treating failures from competing risks which were not of primary interest as censoring, led to bias. When 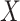 is vector valued, and there are multiple missingness patterns, Resche-Rigon and others (2012) proposed using the fully conditional specification MI approach (van Buuren, 2007).
is vector valued, and there are multiple missingness patterns, Resche-Rigon and others (2012) proposed using the fully conditional specification MI approach (van Buuren, 2007).
The approach proposed by Resche-Rigon and others (2012) is attractive since it can be readily implemented using existing software for MI. A potential drawback, however, is that the imputation model used is only approximately compatible with the assumed models for the cause-specific hazard functions. It is, therefore, expected that in certain situations (e.g. large covariate effects), the approach may lead to estimates with appreciable biases. Moreover, as described in detail by Bartlett and others (2015), more generally it is difficult to choose directly specified imputation models for incomplete covariates that are compatible with outcome models when the incomplete covariates are assumed to have non-linear effects or interactions in the substantive model. These difficulties can, however, be overcome by constructing an imputation model that is compatible with the assumed models for the cause-specific hazard functions.
4.3. Substantive model compatible covariate imputation
Suppose for the moment that 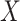 is scalar, and is MAR. We further assume that for each cause-specific hazard function, a proportional hazards model conditional on
is scalar, and is MAR. We further assume that for each cause-specific hazard function, a proportional hazards model conditional on 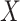 and
and 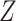 has been specified, as given in equation (2.2). To ensure the imputation model for
has been specified, as given in equation (2.2). To ensure the imputation model for 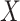 is compatible with the substantive model, we note that
is compatible with the substantive model, we note that 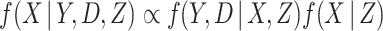 . The first part of this is the likelihood contribution given by equation (2.1). Thus a substantive model compatible imputation distribution for
. The first part of this is the likelihood contribution given by equation (2.1). Thus a substantive model compatible imputation distribution for 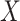 is, up to a constant of proportionality, equal to
is, up to a constant of proportionality, equal to
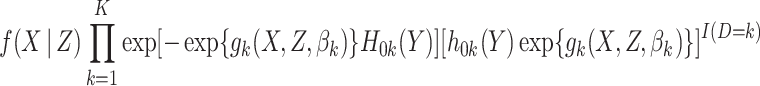 |
(4.1) |
where we omit the terms corresponding to the censoring process on the assumption that 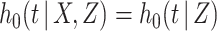 . If in a particular application such an assumption is deemed inappropriate, for example based on a preliminary model fit for the censoring process, this can be handled by treating censoring as an additional cause of failure and specifying a proportional hazards model for the censoring process conditional on
. If in a particular application such an assumption is deemed inappropriate, for example based on a preliminary model fit for the censoring process, this can be handled by treating censoring as an additional cause of failure and specifying a proportional hazards model for the censoring process conditional on 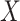 and
and 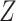 .
.
Thus, having specified models for the cause-specific hazards, the imputation distribution specification is completed by specifying a model 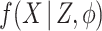 . The model for
. The model for 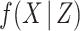 can be chosen to be an appropriate model depending on the variable type of
can be chosen to be an appropriate model depending on the variable type of 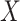 . For example, we may use linear, logistic, ordinal, or multinomial logistic regression models for continuous, binary ordered categorical, and unordered categorical variables, respectively. Count variables can be imputed using Poisson or negative binomial models. In Appendix B.1 of the Supplementary Materials (available at Biostatistics online), we describe how a Gibbs sampler can be constructed using this imputation approach, and give details about prior choice. In Appendix B.2 (see supplementary material available at Biostatistics online), we describe methods for sampling from the required conditional distributions.
. For example, we may use linear, logistic, ordinal, or multinomial logistic regression models for continuous, binary ordered categorical, and unordered categorical variables, respectively. Count variables can be imputed using Poisson or negative binomial models. In Appendix B.1 of the Supplementary Materials (available at Biostatistics online), we describe how a Gibbs sampler can be constructed using this imputation approach, and give details about prior choice. In Appendix B.2 (see supplementary material available at Biostatistics online), we describe methods for sampling from the required conditional distributions.
In practice, 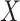 is commonly vector valued, with multiple missingness patterns. In this case, a joint model could in principle be specified for
is commonly vector valued, with multiple missingness patterns. In this case, a joint model could in principle be specified for 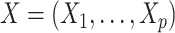 , and imputations be drawn from the posterior distribution of the missing data using a Gibbs sampler. One approach in this case is to factorize the joint distribution as a series of univariate conditional models, as proposed by Ibrahim and others (1999).
, and imputations be drawn from the posterior distribution of the missing data using a Gibbs sampler. One approach in this case is to factorize the joint distribution as a series of univariate conditional models, as proposed by Ibrahim and others (1999).
Here, following the popular chained equations or fully conditional specification approach to MI, we instead adopt the substantive model compatible fully conditional specification (SMC-FCS) approach recently proposed by Bartlett and others (2015). Rather than specifying a joint model for 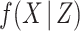 , this approach involves specifying, for each partially observed variable
, this approach involves specifying, for each partially observed variable 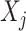 , a model
, a model 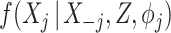 , where
, where 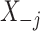 denotes the components of
denotes the components of 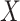 except the
except the 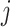 th. The partially observed
th. The partially observed 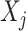 are then imputed one at a time. Further details for the algorithm are given in Appendix B.3 of the Supplementary Materials (available at Biostatistics online).
are then imputed one at a time. Further details for the algorithm are given in Appendix B.3 of the Supplementary Materials (available at Biostatistics online).
The SMC-FCS approach ensures that each partially observed variable is imputed from a model that is compatible with the substantive model, and at the same time permits flexibility since different model types can be specified for each 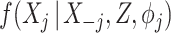 ,
, 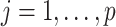 . A drawback of the SMC-FCS algorithm is that these models may themselves be mutually incompatible, such that the resulting sampler does not draw imputations from a well-defined Bayesian joint model. However, given recent theoretical developments regarding the properties of standard FCS MI (Liu and others, 2013; Hughes and others, 2014), we believe the possibility of such incompatibility may not be such a great practical concern for SMC-FCS, provided the models
. A drawback of the SMC-FCS algorithm is that these models may themselves be mutually incompatible, such that the resulting sampler does not draw imputations from a well-defined Bayesian joint model. However, given recent theoretical developments regarding the properties of standard FCS MI (Liu and others, 2013; Hughes and others, 2014), we believe the possibility of such incompatibility may not be such a great practical concern for SMC-FCS, provided the models 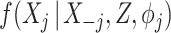 ,
, 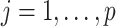 fit well.
fit well.
5. Simulations
In this section, we report the results of simulations to evaluate the performance of CCA and the MI approaches described previously.
5.1. Simulation 1: covariate-dependent missingness
For datasets of size 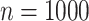 , we first generated three covariates
, we first generated three covariates 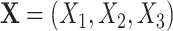 as
as 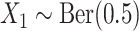 ,
, 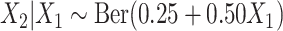 ,
, 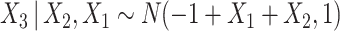 . Event times for two competing causes were then generated. The first was generated with hazard
. Event times for two competing causes were then generated. The first was generated with hazard 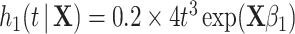 , with
, with 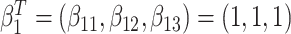 . The second was generated with hazard
. The second was generated with hazard 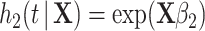 , with
, with 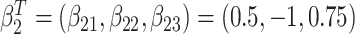 . Censoring times were generated from a uniform distribution between 0.5 and 2. This led to 25% of individuals being censored, 25% failing from cause 1 and 50% from cause 2.
. Censoring times were generated from a uniform distribution between 0.5 and 2. This led to 25% of individuals being censored, 25% failing from cause 1 and 50% from cause 2.
Values in 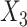 were then made missing (at random) with probability
were then made missing (at random) with probability 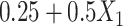 , leading to 50% missing values. We imputed the missing values in
, leading to 50% missing values. We imputed the missing values in 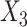 using three different directly specified conditional imputation models for
using three different directly specified conditional imputation models for 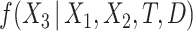 using the R package MICE. First, following the results of Resche-Rigon and others (2012),
using the R package MICE. First, following the results of Resche-Rigon and others (2012), 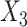 was imputed using a normal linear regression imputation model, using the event indicator
was imputed using a normal linear regression imputation model, using the event indicator 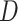 as a categorical predictor, the Nelson–Aalen estimates of the (marginal) cumulative hazard functions (i.e. ignoring covariates),
as a categorical predictor, the Nelson–Aalen estimates of the (marginal) cumulative hazard functions (i.e. ignoring covariates), 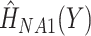 and
and 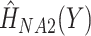 , and
, and 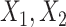 as covariates (FCS competing). Secondly, we used an imputation model based on the more accurate approximation derived by Resche-Rigon and others (2012), by additionally including interaction terms between each of
as covariates (FCS competing). Secondly, we used an imputation model based on the more accurate approximation derived by Resche-Rigon and others (2012), by additionally including interaction terms between each of 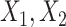 and each of
and each of 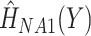 and
and 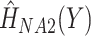 (FCS competing int.). Thirdly, to explore the impact of ignoring the second cause of failure at the imputation stage, we also imputed
(FCS competing int.). Thirdly, to explore the impact of ignoring the second cause of failure at the imputation stage, we also imputed 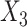 as if it were (single failure type) survival data, by treating failures from the second cause as if they were censorings when defining
as if it were (single failure type) survival data, by treating failures from the second cause as if they were censorings when defining 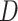 and calculating
and calculating 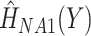 , and omitting
, and omitting 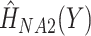 from the imputation model (FCS survival). Note that here we did not include the interactions between
from the imputation model (FCS survival). Note that here we did not include the interactions between 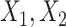 , and
, and 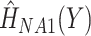 .
.
Next we imputed 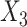 using the substantive model compatible approach described in Section 4.3, assuming (correctly here) that
using the substantive model compatible approach described in Section 4.3, assuming (correctly here) that 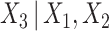 is normal linear regression, and assuming Cox models with linear covariate effects for both causes of failure (SMC-FCS competing). We then imputed again using the substantive model compatible approach, acting as if the data were single failure type data, considering failures only due to cause one (SMC-FCS survival).
is normal linear regression, and assuming Cox models with linear covariate effects for both causes of failure (SMC-FCS competing). We then imputed again using the substantive model compatible approach, acting as if the data were single failure type data, considering failures only due to cause one (SMC-FCS survival).
For all the imputation methods, five imputations were generated for each dataset. With each imputed dataset, we fitted Cox proportional hazards models for each cause of failure, and combined estimates of the two sets of regression coefficients 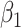 and
and 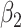 using Rubin's rules. Using each imputation, we also estimated the cumulative cause-specific hazard function for cause one at
using Rubin's rules. Using each imputation, we also estimated the cumulative cause-specific hazard function for cause one at 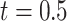 , and obtained standard errors using the R function survfit. These were similarly combined across the five imputations using Rubin's rules.
, and obtained standard errors using the R function survfit. These were similarly combined across the five imputations using Rubin's rules.
Table 1 shows the results of the simulations. First, we note the considerable efficiency loss due to missing data as shown by the larger empirical SDs for complete case estimates compared with full data. In line with the results of Section 3, CCA is unbiased since missingness is covariate dependent. Estimates based on FCS MI, accounting for competing risks (FCS competing), showed moderately large biases for most parameters, and consequently low confidence interval coverage for some parameters. This can be attributed to the fact that the imputation model used is only approximately compatible with the cause-specific hazard models, and the baseline cumulative hazards are estimated by the marginal Nelson–Aalen cumulative hazard estimator. The estimate of the first cumulative baseline hazard function at 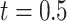 was also biased upward. Including interactions between the estimated cumulative hazard functions and
was also biased upward. Including interactions between the estimated cumulative hazard functions and 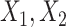 (FCS competing inter) reduced the biases considerably. Moreover, confidence interval coverage was improved, although for
(FCS competing inter) reduced the biases considerably. Moreover, confidence interval coverage was improved, although for 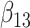 coverage was still poor. In line with the simulation results of Resche-Rigon and others (2012), performance was worse when the second cause of failure was treated as if it were censoring (FCS survival), with larger biases and lower confidence interval coverage.
coverage was still poor. In line with the simulation results of Resche-Rigon and others (2012), performance was worse when the second cause of failure was treated as if it were censoring (FCS survival), with larger biases and lower confidence interval coverage.
Table 1.
Mean (empirical SD) of estimates across 1000 simulations, with covariate-dependent missingness in 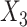
| Method | 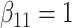 |
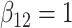 |
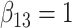 |
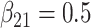 |
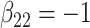 |
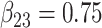 |
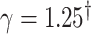 |
|---|---|---|---|---|---|---|---|
| Mean | |||||||
| Full data | 1.01 | 1.01 | 1.01 | 0.50 |
 1.00 1.00 |
0.75 | 1.25 |
| Complete case | 1.02 | 1.01 | 1.01 | 0.50 |
 1.01 1.01 |
0.76 | 1.24 |
| FCS competing | 0.87 | 1.18 | 0.59 | 0.51 |
 0.88 0.88 |
0.62 | 1.65 |
| FCS compet inter | 0.99 | 1.10 | 0.75 | 0.54 |
 0.98 0.98 |
0.68 | 1.43 |
| FCS survival | 0.84 | 1.21 | 0.56 | 0.63 |
 0.70 0.70 |
0.43 | 1.58 |
| SMC-FCS competing | 1.05 | 1.01 | 1.00 | 0.53 |
 1.01 1.01 |
0.75 | 1.25 |
| SMC-FCS survival | 0.83 | 1.13 | 1.00 | 0.75 |
 0.58 0.58 |
0.34 | 1.13 |
| SD | |||||||
| Full data | 0.16 | 0.18 | 0.08 | 0.11 | 0.11 | 0.05 | 0.29 |
| Complete case | 0.24 | 0.26 | 0.13 | 0.18 | 0.18 | 0.07 | 0.44 |
| FCS competing | 0.17 | 0.19 | 0.09 | 0.13 | 0.13 | 0.07 | 0.36 |
| FCS compet inter | 0.19 | 0.20 | 0.09 | 0.13 | 0.13 | 0.07 | 0.33 |
| FCS survival | 0.17 | 0.19 | 0.08 | 0.12 | 0.12 | 0.06 | 0.35 |
| SMC-FCS competing | 0.19 | 0.21 | 0.13 | 0.13 | 0.14 | 0.07 | 0.32 |
| SMC-FCS survival | 0.19 | 0.21 | 0.13 | 0.11 | 0.10 | 0.04 | 0.30 |
| Coverage | |||||||
| Full data | 95 | 95 | 96 | 95 | 96 | 94 | 94 |
| Complete case | 95 | 95 | 96 | 97 | 95 | 94 | 92 |
| FCS competing | 91 | 89 | 11 | 95 | 88 | 66 | 92 |
| FCS compet inter | 97 | 95 | 55 | 94 | 96 | 90 | 98 |
| FCS survival | 88 | 86 | 3 | 84 | 40 | 2 | 95 |
| SMC-FCS competing | 94 | 96 | 95 | 94 | 94 | 95 | 94 |
| SMC-FCS survival | 85 | 92 | 94 | 49 | 6 | 0 | 87 |
CI indicates empirical coverage of nominal 95% confidence intervals.
 .
.
Estimates from SMC-FCS accounting for the competing risks showed little bias and confidence interval coverage close or slightly below the nominal 95% level. Of particular note, the cumulative baseline hazard function at 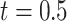 for the first cause of failure was estimated with little bias, and confidence intervals had only slight under coverage. Comparing empirical standard deviations, we see that SMC-FCS recovers considerable information for the coefficients of the fully observed covariates
for the first cause of failure was estimated with little bias, and confidence intervals had only slight under coverage. Comparing empirical standard deviations, we see that SMC-FCS recovers considerable information for the coefficients of the fully observed covariates 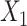 and
and 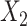 , while for the coefficient of the partially observed
, while for the coefficient of the partially observed 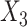 there is no efficiency gain. As expected, imputing treating the second cause of failure as censoring (SMC-FCS survival) led to biased estimates and confidence interval coverage below the nominal level, particularly (as one might expect) for
there is no efficiency gain. As expected, imputing treating the second cause of failure as censoring (SMC-FCS survival) led to biased estimates and confidence interval coverage below the nominal level, particularly (as one might expect) for 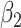 .
.
5.2. Simulation 2: multiple missingness patterns and interactions
In a second set of simulations, we explored imputation of two covariates with multiple missingness patterns, and the ability of the two imputation approaches to accommodate interactions in the competing hazards models. Here 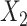 was made missing with probability
was made missing with probability 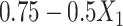 , while
, while 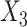 was made missing with probability
was made missing with probability 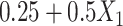 , leading to 50% missingness in each variable. The two cause-specific hazard functions were also modified, additionally including the term
, leading to 50% missingness in each variable. The two cause-specific hazard functions were also modified, additionally including the term 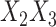 in each, with coefficient vectors
in each, with coefficient vectors 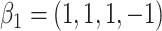 ,
, 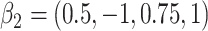 . This led to 33% of individuals failing due to cause 1, and 67% failing from cause 2. No censoring was imposed.
. This led to 33% of individuals failing due to cause 1, and 67% failing from cause 2. No censoring was imposed.
In the FCS approaches, 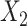 was imputed using logistic regression, conditioning on
was imputed using logistic regression, conditioning on 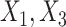 and the event indicator and Nelson–Aalen cumulative hazard estimators as before. In “FCS competing inter” as before we included interactions between
and the event indicator and Nelson–Aalen cumulative hazard estimators as before. In “FCS competing inter” as before we included interactions between 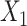 and the Nelson–Aalen cumulative hazard estimates, and similarly between
and the Nelson–Aalen cumulative hazard estimates, and similarly between 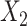 (
(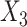 ) and the cumulative hazard estimates when imputing
) and the cumulative hazard estimates when imputing 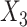 (respectively,
(respectively, 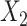 ). Note, however, that no further modifications were made to attempt to allow for the
). Note, however, that no further modifications were made to attempt to allow for the 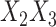 interactions in the cause-specific hazard models, with these interaction values simply being passively imputed at the end in the final imputed datasets.
interactions in the cause-specific hazard models, with these interaction values simply being passively imputed at the end in the final imputed datasets.
In the SMC-FCS approaches, 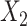 was imputed using a logistic model conditional on
was imputed using a logistic model conditional on 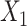 and
and 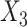 , and the
, and the 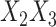 interactions were included in the cause-specific Cox models. The number of iterations for SMC-FCS was increased from its default of 10 to 20, since MCMC convergence plots of initial simulations suggested more than 10 were required for convergence due to the presence of the interaction term.
interactions were included in the cause-specific Cox models. The number of iterations for SMC-FCS was increased from its default of 10 to 20, since MCMC convergence plots of initial simulations suggested more than 10 were required for convergence due to the presence of the interaction term.
Table 2 shows the results. The FCS approaches led to biased estimates and confidence intervals with very poor coverage for the interaction parameters because FCS (at least as implemented here) does not account for the interactions in the cause-specific hazard models. In contrast, SMC-FCS accounting for both competing causes led to valid inferences, while SMC-FCS treating the second cause as censoring as expected led to very biased estimates of 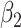 (as expected), although biases for
(as expected), although biases for 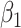 were smaller.
were smaller.
Table 2.
Mean 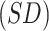 of estimates across 1000 simulations, with missingness in
of estimates across 1000 simulations, with missingness in 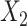 and
and 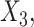 and
and 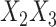 interactions present in cause-specific hazard models
interactions present in cause-specific hazard models
| Method | 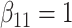 |
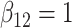 |
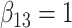 |
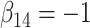 |
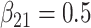 |
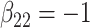 |
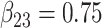 |
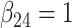 |
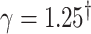 |
|---|---|---|---|---|---|---|---|---|---|
| Mean | |||||||||
| Full data | 1.01 | 1.01 | 1.01 |
 1.01 1.01 |
0.50 |
 1.01 1.01 |
0.75 | 1.00 | 1.23 |
| Complete case | 1.07 | 1.06 | 1.04 |
 1.05 1.05 |
0.51 |
 1.04 1.04 |
0.77 | 1.01 | 1.15 |
| FCS competing | 0.79 | 1.14 | 0.69 |
 0.45 0.45 |
0.45 |
 0.39 0.39 |
0.73 | 0.15 | 1.23 |
| FCS compet inter | 0.96 | 1.12 | 0.64 |
 0.40 0.40 |
0.53 |
 0.63 0.63 |
0.78 | 0.31 | 1.14 |
| FCS survival | 0.76 | 1.27 | 0.62 |
 0.54 0.54 |
0.48 |
 0.23 0.23 |
0.65 |
 0.01 0.01 |
1.14 |
| SMC-FCS competing | 1.02 | 1.04 | 1.01 |
 1.02 1.02 |
0.51 |
 1.03 1.03 |
0.77 | 1.01 | 1.20 |
| SMC-FCS survival | 0.81 | 1.23 | 1.01 |
 0.94 0.94 |
0.70 | 0.02 | 0.40 |
 0.08 0.08 |
1.12 |
| SD | |||||||||
| Full data | 0.15 | 0.16 | 0.10 | 0.15 | 0.10 | 0.12 | 0.06 | 0.10 | 0.34 |
| Complete case | 0.37 | 0.44 | 0.27 | 0.39 | 0.25 | 0.31 | 0.16 | 0.25 | 0.81 |
| FCS competing | 0.17 | 0.23 | 0.10 | 0.11 | 0.12 | 0.19 | 0.08 | 0.07 | 0.37 |
| FCS compet inter | 0.18 | 0.27 | 0.15 | 0.17 | 0.13 | 0.20 | 0.10 | 0.09 | 0.36 |
| FCS survival | 0.17 | 0.23 | 0.09 | 0.10 | 0.11 | 0.17 | 0.07 | 0.07 | 0.34 |
| SMC-FCS competing | 0.19 | 0.28 | 0.14 | 0.27 | 0.14 | 0.22 | 0.10 | 0.17 | 0.38 |
| SMC-FCS survival | 0.22 | 0.27 | 0.14 | 0.22 | 0.09 | 0.08 | 0.05 | 0.06 | 0.36 |
| Coverage | |||||||||
| Full data | 94 | 96 | 96 | 95 | 96 | 96 | 94 | 94 | 93 |
| Complete case | 94 | 95 | 94 | 95 | 94 | 95 | 94 | 95 | 82 |
| FCS competing | 83 | 95 | 38 | 26 | 94 | 25 | 97 | 0 | 95 |
| FCS compet inter | 97 | 95 | 51 | 44 | 96 | 61 | 96 | 2 | 89 |
| FCS survival | 80 | 86 | 14 | 28 | 96 | 5 | 80 | 0 | 89 |
| SMC-FCS competing | 94 | 94 | 94 | 96 | 95 | 95 | 94 | 94 | 92 |
| SMC-FCS survival | 84 | 87 | 94 | 92 | 60 | 0 | 0 | 0 | 87 |
CI indicates empirical coverage of nominal 95% confidence intervals.
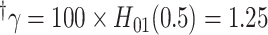 .
.
Three sets of additional simulations are reported in Appendix C of the Supplementary Materials (available at Biostatistics online). In the first set, missingness was dependent on 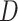 , such that CCA was biased, while SMC-FCS gave valid inferences. In the second set,
, such that CCA was biased, while SMC-FCS gave valid inferences. In the second set, 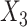 was made missing with missingness dependent on
was made missing with missingness dependent on 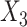 (MNAR), such that CCA was unbiased, while the MI approaches were biased. In the final set, missingness in
(MNAR), such that CCA was unbiased, while the MI approaches were biased. In the final set, missingness in 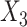 was again dependent on
was again dependent on 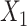 , but with the hazard for the second failure type not dependent on
, but with the hazard for the second failure type not dependent on 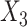 . Here both SMC-FCS approaches were unbiased, with SMC-FCS survival being slightly more efficient.
. Here both SMC-FCS approaches were unbiased, with SMC-FCS survival being slightly more efficient.
6. Illustrative analysis
To illustrate the two MI approaches, we consider data from the third US National Health and Nutrition Examination Survey (NHANES III), which was conducted between 1988 and 1994. The overall study involved around 40 000 individuals, and consisted of an in-depth survey of their health and nutrition status, obtained from physical examinations and interview. Mortality status at the end of 2011 is available through linkage to the US National Death Index. Here we consider the subset of individuals aged between 60 and 70 at the time of the original survey, which consists of 2583 individuals. By the end of 2011, 1492 (57.8%) had died. Cause of death was classified using the ICD-10 system. For the illustrative analyses, here we focus on how the hazard for death due to cardiovascular disease (CVD) relates to the risk factors shown in Table 3. Here death due to CVD is of primary interest, and deaths due to other causes are competing causes. We categorize deaths as due to CVD, cancer, and other causes, separating out cancer as it represents a large proportion of deaths and may have quite different associations with the risk factors than other causes. There were 358 CVD deaths, 379 cancer deaths, and 755 deaths due to other causes.
Table 3.
Descriptive statistics for baseline risk factors in NHANES III
| Variable | Mean (SD)/no. (%) | Number of missing (%) |
|---|---|---|
| Sex, female | 1302 (50.4) | 0 |
| Age (years) | 64.4 (2.9) | 0 |
| Current smoker | 597 (38.9) | 1048 (40.6) |
| Diabetes | 427 (16.6) | 3 (0.1) |
Alcohol consumer
|
992 (55.0) | 778 (30.1) |
| Systolic blood pressure (mmHg) | 137.8 (19.4) | 297 (11.5) |
| Total cholesterol (mg/dL) | 225.6 (45.2) | 355 (13.7) |
C-reactive protein 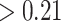 mg/dL mg/dL |
946 (42.7) | 368 (14.2) |
| Fibrinogen (mg/dL) | 330.8 (96.0) | 387 (15.0) |
 Reported to have had at least 12 alcoholic drinks in the last 12 months.
Reported to have had at least 12 alcoholic drinks in the last 12 months.
We assumed a Cox proportional hazards model for the hazard of death due to CVD, with main effects of each of the risk factors listed in Table 3, and assuming linear effects (on the log hazard scale) of continuous variables. The first column of Table 4 shows estimated log hazard ratios for each risk factor based on the 1106 (42.8%) complete cases. This shows statistically significant evidence for independent associations of each risk factor with hazard of death due to CVD, except for diabetes, with directions of association as expected based on the prior knowledge of CVD. A global test of the proportional hazards assumption using Schoenfeld residuals revealed no evidence (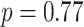 ) against the assumption.
) against the assumption.
Table 4.
Estimated log hazard ratios 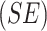 for death due to CVD from NHANES III data
for death due to CVD from NHANES III data
| SMC-FCS | SMC-FCS | ||||
|---|---|---|---|---|---|
| Complete case | FCS competing | FCS survival | competing | survival | |
| Male | 0.51 (0.18) | 0.69 (0.12) | 0.69 (0.12) | 0.69 (0.12) | 0.70 (0.12) |
| Age (per 10 years) | 0.86 (0.27) | 0.90 (0.19) | 0.91 (0.19) | 0.92 (0.19) | 0.90 (0.19) |
| Current smoker | 0.59 (0.15) | 0.63 (0.13) | 0.60 (0.13) | 0.63 (0.13) | 0.56 (0.13) |
| Diabetic | 0.26 (0.20) | 0.74 (0.13) | 0.74 (0.13) | 0.75 (0.13) | 0.75 (0.13) |
| Alcohol consumer | 0.38 (0.16) | 0.37 (0.14) | 0.38 (0.14) | 0.35 (0.14) | 0.35 (0.14) |
| SBP (per 10 mmHg) | 0.96 (0.38) | 1.38 (0.28) | 1.35 (0.28) | 1.36 (0.29) | 1.35 (0.28) |
| Cholesterol (mg/mL) | 0.34 (0.16) | 0.31 (0.12) | 0.31 (0.12) | 0.31 (0.12) | 0.31 (0.12) |
CRP (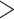 0.21 mg/dL) 0.21 mg/dL) |
0.45 (0.17) | 0.45 (0.12) | 0.45 (0.13) | 0.45 (0.12) | 0.44 (0.12) |
| Fibrinogen (mg/dL) | 0.19 (0.08) | 0.13 (0.06) | 0.13 (0.06) | 0.13 (0.06) | 0.13 (0.06) |
To investigate whether the CCA is valid, following Section 3, we first argue that the assumption that 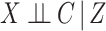 is satisfied here because censoring is almost exclusively due to the length of available follow-up. Next we fitted a Cox model where events were taken as death from any cause, with fully observed sex, age, diabetes (dropping the three observations with diabetes missing) and an indicator
is satisfied here because censoring is almost exclusively due to the length of available follow-up. Next we fitted a Cox model where events were taken as death from any cause, with fully observed sex, age, diabetes (dropping the three observations with diabetes missing) and an indicator 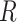 of whether the other risk factors were all available or not, as covariates. Unfortunately, this showed evidence (
of whether the other risk factors were all available or not, as covariates. Unfortunately, this showed evidence (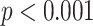 ) that being a complete case was associated with increased hazard of death, conditional on sex, age, and diabetes. The data are thus not consistent with an assumption that
) that being a complete case was associated with increased hazard of death, conditional on sex, age, and diabetes. The data are thus not consistent with an assumption that 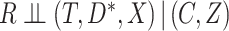 . Nevertheless, the CCA may still be valid, if for example missingness in the partially observed covariates is dependent only on
. Nevertheless, the CCA may still be valid, if for example missingness in the partially observed covariates is dependent only on 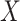 and
and 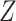 . This is arguably quite plausible for variables such as smoking and alcohol consumption.
. This is arguably quite plausible for variables such as smoking and alcohol consumption.
Next we applied the FCS and SMC-FCS approaches to multiply impute the missing covariate values, using 50 imputations for each method. As in the simulation study, we applied each either accounting for or ignoring (as censoring) failures from causes of death other than the one of interest (CVD).
Table 4 shows the estimated log hazard ratios and corresponding standard errors. Estimates and standard errors were very similar across all four MI methods, suggesting that the approximations being made in the directly specified FCS approach are here quite reasonable. The MI standard errors were uniformly smaller than those from CCA, even for the coefficients of fully observed covariates. However, the MI estimates differed materially from the CCA estimates for some risk factors, such as gender, diabetes, and SBP. Unfortunately, we do not believe it is possible to establish here from the observed data whether the CCA assumption or MAR (or neither) is true. From considerations of the nature of the variables, a covariate-dependent MNAR missingness mechanism, under which CCA is valid, is arguably more plausible than MAR.
7. Discussion
We have explored approaches for handling missing covariates in competing risks analysis when one is interested in modeling the cause-specific hazard functions. We have shown under what assumptions CCA is valid, and suggested how the observed data can be checked for compatibility with a stronger version of this assumption. Even when CCA is valid, it is however inefficient. Recently Bartlett and others (2014) developed an approach for improving upon the efficiency of CCA for conditional mean models when a covariate-dependent MNAR mechanism is assumed, and further work is warranted to extend this to survival and competing risks settings.
Under an MAR assumption, we have proposed a flexible approach to multiply impute missing covariates in competing risks data, based on proportional hazards models for cause-specific hazards. The approach automatically handles user-specified covariate effects in these models, including interactions and non-linear covariate effects. Through simulation we have demonstrated its good finite sample performance, for both the regression coefficients indexing models for cause-specific hazards and for estimation of the cumulative cause-specific baseline hazard functions. In contrast, we have empirically shown that directly specified approximately compatible imputation models in general lead to biased estimates.
The SMC-FCS approach we have described relies on the analyst specifying appropriate models for the cause-specific hazard functions and the covariate models 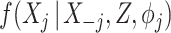 . The assessment of model fit in the context of MI approaches, or indeed when data are incomplete more generally, is challenging. In the present setting, we would recommend that analysts assess the fit of the covariate
. The assessment of model fit in the context of MI approaches, or indeed when data are incomplete more generally, is challenging. In the present setting, we would recommend that analysts assess the fit of the covariate 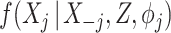 models fitted to those corresponding complete cases. While these fits may themselves be biased (when missingness is not completely at random), if the model appears to fit well in the complete cases, it is arguably plausible that the models are reasonable for the entire sample. For the cause-specific hazard models, if missingness can be assumed to be at most covariate dependent, then again model assessment and selection could be applied to corresponding complete case fits prior to imputation of missing covariates. Alternatively, one could impute missing covariates using SMC-FCS, and then apply model diagnostics for the cause-specific hazard models to the imputed datasets. The obvious limitation with such a strategy is that the missing covariates will have been imputed assuming that the analyst's specified cause-specific models are correctly specified, which would be expected to weaken the potential to detect misspecification in the cause-specific hazard models.
models fitted to those corresponding complete cases. While these fits may themselves be biased (when missingness is not completely at random), if the model appears to fit well in the complete cases, it is arguably plausible that the models are reasonable for the entire sample. For the cause-specific hazard models, if missingness can be assumed to be at most covariate dependent, then again model assessment and selection could be applied to corresponding complete case fits prior to imputation of missing covariates. Alternatively, one could impute missing covariates using SMC-FCS, and then apply model diagnostics for the cause-specific hazard models to the imputed datasets. The obvious limitation with such a strategy is that the missing covariates will have been imputed assuming that the analyst's specified cause-specific models are correctly specified, which would be expected to weaken the potential to detect misspecification in the cause-specific hazard models.
In the context of single failure time data, Qi and others (2010) found that using directly specified conditional MI methods for missing covariates gave estimates with large bias when the partially observed covariate was related to the censoring time. Our results explain their finding, and show that if 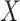 and
and 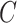 are related, the censoring process must be modeled as an additional competing risk when imputing missing covariates.
are related, the censoring process must be modeled as an additional competing risk when imputing missing covariates.
Often in competing risks settings, primary interest will be in modeling the hazard of failure due to just one cause. In this case, in the absence of missing covariates, models need not be specified for the causes of failure which are not of interest. An advantage of CCA is that similarly a model need only be specified for the cause(s) of interest. In contrast, if missing covariates are imputed, models must be specified for these causes, (unless the analyst is willing to assume that the cause-specific hazards for the causes not of interest are unrelated to 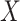 conditional on
conditional on 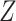 ). In this situation, one must choose how to define the competing causes. At one extreme, all of the causes of failure that are not of interest could be combined to form a second cause of failure (in addition to the cause of interest). However, this may be statistically inefficient when the partially observed covariate(s) have different effects on the causes that have been combined. Moreover, if missingness in
). In this situation, one must choose how to define the competing causes. At one extreme, all of the causes of failure that are not of interest could be combined to form a second cause of failure (in addition to the cause of interest). However, this may be statistically inefficient when the partially observed covariate(s) have different effects on the causes that have been combined. Moreover, if missingness in 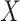 is related to failure type, amalgamating the causes not of interest into a single cause may render the MAR assumption invalid, leading to biased estimates.
is related to failure type, amalgamating the causes not of interest into a single cause may render the MAR assumption invalid, leading to biased estimates.
A closely related approach to handling missing covariates is to fit a single Bayesian joint model, allowing for missingness in the covariates, as described in the case of single failure type data by Chen and others (2006). The strengths of such an approach are that one uses a coherent joint model for the data, and uses well-defined priors for all model parameters. However, with multiple partially observed variables, arguably specifying joint models becomes more challenging. Moreover, the Gibbs sampler developed by Chen and others (2006) is more involved than the SMC-FCS algorithm, and unlike SMC-FCS, is not currently available in software.
A further alternative approach to handling missing data is based on inverse probability weighting (IPW). IPW and doubly robust estimators assuming MAR have been developed for the Cox model with single failure time data (Wang and Chen, 2001; Qi and others, 2010), and further work is warranted on extending these to the competing risks setting. Lastly, we note that an alternative approach to competing risks analysis is based on modeling covariate effects on the cumulative incidence function (Fine and Gray, 1999), and further research is similarly warranted to explore missing covariates within this framework.
Supplementary materials
Supplementary Material is available at http://biostatistics.oxfordjournals.org.
Funding
This work was supported by a UK Medical Research Council Fellowship (MR/K02180X/1) [to J.W.B.] and by grant CA129102 from the US National Institutes of Health [to J.M.G.T.]. Funding to pay the Open Access publication charges for this article was provided by the UK Medical Research Council.
Supplementary Material
Acknowledgments
The work was partly undertaken while J.W.B. was kindly hosted at the Department of Biostatistics and Institute for Social Research at the University of Michigan. Conflict of Interest: None declared.
References
- Andersen P. K., Abildstrom S. Z., Rosthøj S. (2002). Competing risks as a multi-stage model. Statistical Methods in Medical Research 11, 203–215. [DOI] [PubMed] [Google Scholar]
- Bartlett J. W., Carpenter J. R., Tilling K., Vansteelandt S. (2014). Improving upon the efficiency of complete case analysis when covariates are MNAR. Biostatistics 15, 719–730. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bartlett J. W., Seaman S. R., White I. R., Carpenter J. R. (2015). Multiple imputation of covariates by fully conditional specification: accommodating the substantive model. Statistical Methods in Medical Research 24, 462–487. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carpenter J. R., Kenward M. G. (2013) Multiple Imputation and its Application. Chichester, UK: John Wiley & Sons, Ltd. [Google Scholar]
- Chen M., Ibrahim J. G., Shao Q. (2006). Posterior propriety and computation for the Cox regression model with applications to missing covariates. Biometrika 93, 791–807. [Google Scholar]
- Escarela G., de Chavez J. R., Castillo-Morales A. (2013). Addressing missing covariates for the regression analysis of competing risks: prognostic modelling for triaging patients diagnosed with prostate cancer. Statistical Methods in Medical Research doi:10.1177/0962280213492406. [DOI] [PubMed] [Google Scholar]
- Fine J. P., Gray R. J. (1999). A proportional hazards model for the subdistribution of a competing risk. Journal of the American Statistical Association 94, 496–509. [Google Scholar]
- Herring A. H., Ibrahim J. G. (2001). Likelihood-based methods for missing covariates in the Cox proportional hazards model. Journal of the American Statistical Association 96453, 292–302. [Google Scholar]
- Hughes R. A., White I. R., Seaman S. R., Carpenter J. R., Tilling K., Sterne J. A. C. (2014). Joint modelling rationale for chained equations. BMC Medical Research Methodology 141, 28. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ibrahim J. G., Chen M. H., Lipsitz S. R. (1999). Monte-Carlo EM for missing covariates in parametric regression models. Biometrics 55, 591–596. [DOI] [PubMed] [Google Scholar]
- Ibrahim J. G., Chen M. H., Lipsitz S. R., Herring A. H. (2005). Missing-data methods for generalized linear models: a comparative review. Journal of the American Statistical Association 100, 332–346. [Google Scholar]
- Liu J., Gelman A., Hill J., Su Y. S., Kropko J. (2013). On the stationary distribution of iterative imputations. Biometrika 101, 155–173. [Google Scholar]
- Prentice R. L., Kalbfleisch J. D., Peterson A. V. Jr., Farewell V. T. (1978). The analysis of failure times in the presence of competing risks. Biometrics 344, 541–554. [PubMed] [Google Scholar]
- Qi L., Wang Y., He Y. (2010). A comparison of multiple imputation and fully augmented weighted estimators for Cox regression with missing covariates. Statistics in Medicine 29, 2592–2604. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rathouz P. J. (2007). Identifiability assumptions for missing covariate data in failure time regression models. Biostatistics 8, 345–356. [DOI] [PubMed] [Google Scholar]
- Resche-Rigon M., White I., Chevret S. (2012). Imputing missing covariate values in presence of competing risk. Presentation at the International Society for Clinical Biostatistics Conference.
- Rubin D. B. (1976). Inference and missing data. Biometrika 63, 581–592. [Google Scholar]
- van Buuren S. (2007). Multiple imputation of discrete and continuous data by fully conditional specification. Statistical Methods in Medical Research 16, 219–242. [DOI] [PubMed] [Google Scholar]
- Wang C. Y., Chen H. Y. (2001). Augmented inverse probability weighted estimator for Cox missing covariate regression. Biometrics 57, 414–419. [DOI] [PubMed] [Google Scholar]
- White I. R., Royston P. (2009). Imputing missing covariate values for the Cox model. Statistics in Medicine 28, 1982–1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


