Evolution of Cell-to-Cell Variability in Stochastic, Controlled, Heteroplasmic mtDNA Populations

Abstract

Populations of physiologically vital mitochondrial DNA (mtDNA) molecules evolve in cells under control from the nucleus. The evolution of populations of mixed mtDNA types is complicated and poorly understood, and variability of these controlled admixtures plays a central role in the inheritance and onset of genetic disease. Here, we develop a mathematical theory describing the evolution of, and variability in, these stochastic populations for any type of cellular control, showing that cell-to-cell variability in mtDNA and mutant load inevitably increases with time, according to rates that we derive and which are notably independent of the mechanistic details of feedback signaling. We show with a set of experimental case studies that this theory explains disparate quantitative results from classical and modern experimental and computational research on heteroplasmy variance in different species. We demonstrate that our general model provides a host of specific insights, including a modification of the often-used but hard-to-interpret Wright formula to correspond directly to biological observables, the ability to quantify selective and mutational pressure in mtDNA populations, and characterization of the pronounced variability inevitably arising from the action of possible mtDNA quality-control mechanisms. Our general theoretical framework, supported by existing experimental results, thus helps us to understand and predict the evolution of stochastic mtDNA populations in cell biology.

Introduction

Molecules of mitochondrial DNA (mtDNA) form dynamic evolutionary populations within cells, replicating and degrading according to cellular control signals.^{1, 2} mtDNA can vary due to mutation or artificial manipulation;³ the proportion of mutant mtDNA in a cell is referred to as heteroplasmy. mtDNA encodes vital aspects of the bioenergetic machinery of eukaroytic cells; mtDNA variability can thus have dramatic cellular consequences, including devastating genetic diseases and numerous other conditions,³ making a theoretical understanding of this complex evolutionary system important. Understanding the natural feedback control acting on mtDNA populations is also a vital step in the development of artificial approaches to control mitochondrial behavior with genetic tools.^{4, 5} Cell-to-cell variances of mtDNA copy number and heteroplasmy are of particular importance, owing to their implications for maternal transmission of dangerous mutations⁶ and the manifestation of pathologies dependent on the range of heteroplasmies present in a tissue⁷—even a very small proportion of cells exceeding a heteroplasmy threshold can lead to pathologies.⁸

Stochastic behavior underlies much of cell biology and contributes to this cell-to-cell variability; cellular processes including gene expression,^{9, 10, 11} DNA replication,¹² and mitochondrial and mtDNA dynamics^{13, 14, 15, 16} are subject to fundamentally stochastic influences. Variability in mitochondria can be a leading contributor to cell physiological behavior, making mitochondria an important target for explanatory stochastic models.¹⁵ Existing studies have included stochastic modeling and numerical treatments of mitochondrial¹⁷ and mtDNA populations, making quantitative progress with the assumption of specific control mechanisms.^{1, 14, 18, 19, 20} Other theoretical studies have drawn on classical statistical genetics, notably including the well-known Wright formula,^{21, 22} to produce a description of partitioning of mtDNA populations at cell divisions, but the role of stochastic mtDNA dynamics between cell divisions is largely omitted. Although recent experimental studies are starting to shed light on cellular control of mtDNA,^{14, 16} a general theoretical framework is currently absent. Here we address this open question by constructing a general, bottom-up stochastic description of mtDNA populations subject to arbitrary cellular control mechanisms, providing analytic results for the predicted behavior associated with any mtDNA control mechanism, and adapting the classic Wright formula to account for and interpret stochastic mtDNA dynamics. Notably, our approach and results hold independently of the details of specific regulatory mechanisms underlying mtDNA feedback signaling, providing a general theoretical framework for control of stochastic mtDNA populations across different species and environments.

As we develop the theoretical framework to address mtDNA dynamics below, we will consider a set of applications of the theory, linking with existing experimental data from a variety of studies to validate our approach and obtain quantitative results and predictions on the processes governing mtDNA dynamics. We will focus on two questions arising from the study of mtDNA diseases: (1) how and at what rate does cell-to-cell heteroplasmy variance increase and (2) how selective pressure against a particular mtDNA mutation affects cellular mtDNA populations. The single-cell measurements required to address these questions directly remain challenging: we aim to show that mathematical theory, appropriately validated and refined with available data, provides a powerful alternative route to make quantitative progress understanding this important behavior. Box 1 summarizes the central biological messages arising from development and analysis of our theory.

Box 1. Key Biological Findings from Our Mathematical Model.

These results arise when the assumptions of our modeling approach hold: that cells are heteroplasmic, mtDNA replication and degradation are Poisson processes with the same rates for mutant and wild-type mtDNA, and feedback mechanisms depend only on the current state of the system. We justify these assumptions with reference to experimental data in the text and in Appendix A.

• I.When mean copy numbers are constant, at least one variance (wild-type or mutant) increases linearly with time (Equations 8, 9, and 10).
• II.When mean copy numbers are constant, heteroplasmy variance increases linearly with time with a rate that depends only on mtDNA copy numbers and the rate of mtDNA turnover, and not on any details of mechanism or signaling (Equation 12); many copy-number control mechanisms are therefore indistinguishable even from dynamical measurements of heteroplasmy (Figures 1 and 2).
• III.Control applied through (1) biogenesis rates and (2) degradation rates induce comparable behavior in the cellular mtDNA population (Figure 1; Supplemental Data Section 2).
• IV.A modified Wright formula (Equation 14; Figure 4) gives a general method to establish a quantitative link between observed normalized heteroplasmy variance 〈h²〉 ’ and observable (as opposed to effective) quantities (Figure 4).
• V.Quality control does not guarantee the clearing or stabilization of mutant load and can induce substantial variance in wild-type mtDNA (potentially challenging cells with diminished populations; Figures 5 and 6).

Material and Methods

We will consider mtDNA populations in cells that are heteroplasmic with two non-recombining haplotypes, though this treatment can readily be extended to more mtDNA types. We write a state with w wild-type mtDNAs and m mutant mtDNAs as {w,m}. We first consider the class of systems where both haplotypes are subject to the same degradation rate ν and the same replication rate λ, both of which may be general functions of both haplotype copy numbers. This model thus represents the situation where no direct selective difference exists between mutant and wild-type. This assumption holds for only some biological cases (see Burgstaller et al.²³ and references therein for a review of studies where mtDNA types segregate unevenly) and will be relaxed later. We also assume that cellular control is based only on the current state of the cellular mtDNA population and not its history. The dynamics governing the system then consist of a set of Poisson processes:

$$\left\{w,m\right\}\stackrel{w\lambda \left(w,m\right)}{\to }\left\{w+1,m\right\},$$ (Equation 1)

$$\left\{w,m\right\}\stackrel{m\lambda \left(w,m\right)}{\to }\left\{w,m+1\right\},$$ (Equation 2)

$$\left\{w,m\right\}\stackrel{w\nu \left(w,m\right)}{\to }\left\{w-1,m\right\},$$ (Equation 3)

$$\left\{w,m\right\}\stackrel{m\nu \left(w,m\right)}{\to }\left\{w,m-1\right\}.$$ (Equation 4)

This formalism captures a wide range of models for mtDNA dynamics (see below). We will begin with the assumption that the system does not undergo cell divisions and has a stationary state in the population mean of both haplotype copy numbers, and we will write this steady state as $\left\{\tilde{w},\tilde{m}\right\}$. This initial picture is more appropriate for quiescent cell types or mtDNA “set points” than for the pronounced changes in mtDNA copy number that occur during development.^{2, 14} We will later generalize this picture to allow for arbitrary changes in copy number.

We will first consider general results from this formalism, applicable to a wide variety of possible cellular behaviors. We will then illustrate its application with a range of previously proposed and new feedback mechanisms.

Results

Copy-Number Variance with Stable Population Means

Any control mechanism of the form in Equations 1, 2, 3, and 4 (including manifestations of feedback control) can be represented to linear order by a Taylor expansion of its rates about $\left\{\tilde{w},\tilde{m}\right\}$ (the steady state exists by construction from our previous assumption):

$$\lambda \left(w,m\right)\simeq {\beta }_0+{\beta }_w\left(w-\tilde{w}\right)+{\beta }_m\left(m-\tilde{m}\right),$$ (Equation 5)

$$\nu \left(w,m\right)\simeq {\delta }_0+{\delta }_w\left(w-\tilde{w}\right)+{\delta }_m\left(m-\tilde{m}\right).$$ (Equation 6)

It will readily be seen that to support a stable population mean at $\left\{\tilde{w},\tilde{m}\right\}$, ${\delta }_0={\beta }_0$. Assuming that w and m can be written as the sum of a deterministic and a fluctuating component, we use Van Kampen’s system size expansion to find a Fokker-Planck equation describing the behavior of w and m governed by Equations 5 and 6.^{24, 25} From this equation we extract expressions for the time behavior of the mean and variance of w and m (see Supplemental Data Sections 1 and 2).

We show in Supplemental Data Section 4 that attempting to identify a stable state for population variances and covariance yields the condition

$$\frac{2\tilde{m}\left(\tilde{m}+\tilde{w}\right){\beta }_0}{\tilde{w}}=0;$$ (Equation 7)

hence, any population mean state in which mutant content $\tilde{m}$ is nonzero does not admit a stationary solution for variances, unless ${\beta }_0=0$. If ${\beta }_0=0$ then there is no further change to the system once steady state has been reached (no stochastic turnover occurs) and the system remains frozen thereafter. In other words, for a nonzero mutant population and nonzero mtDNA turnover, the variance of at least one mtDNA population will change with time.

The Fokker-Planck equation we derive can be used to compute the expected behaviors of $\langle w^2\rangle$ (wild-type variance), $\langle m^2\rangle$ (mutant variance), and $\langle wm\rangle$ (wild-type mutant covariance) for a given control mechanism. The variance and covariance solutions display some transient behavior, involving terms on the timescale $t^{\prime }\equiv \text{exp}\left(\left(\left({\beta }_m-{\delta }_m\right)\tilde{m}+\left({\beta }_w-{\delta }_w\right)\tilde{w}\right)t\right)$. Because, for stability, ${\beta }_i$ are nonpositive and ${\delta }_i$ are nonnegative, $t^{\prime }$ is either a constant or an exponentially decaying function of time t. The expressions thus subsequently converge to linear trends for large t:

$$\langle w^2\rangle =F_1^{decay}\left(t^{\prime }\right)+{\theta }_{1}t+{\varphi }_1,$$ (Equation 8)

$$\langle wm\rangle =F_2^{decay}\left(t^{\prime }\right)+{\theta }_{2}t+{\varphi }_2,$$ (Equation 9)

$$\langle m^2\rangle =\stackrel{F_3^{decay}\left(t^{\prime }\right)}{\underset{\begin{array}{c}\text{transient}\\ \text{behaviour}\end{array}}{︸}}+\stackrel{{\theta }_{3}t+{\varphi }_3}{\underset{\begin{array}{c}\text{long}-\text{term}\text{linear}\\ \text{behaviour}\end{array}}{︸}}.$$ (Equation 10)

The forms of the transient functions $F_i^{decay}$ and the constants ${\theta }_i$ and ${\varphi }_i$ are given in Supplemental Data Section 2 and are functions only of the difference between replication and degradation rates $\left({\beta }_i-{\delta }_i\right)$, steady-state copy numbers $\tilde{m}$ and $\tilde{w}$, and mitophagy rate ${\beta }_0$. Furthermore, the structure of these expressions is such that for ${\beta }_0\ne 0$ and nonzero w and m, at most one of the ${\theta }_i$ can be zero, ${\theta }_1\ge 0$, and ${\theta }_3\ge 0$. Thus, around the mean $\left(\tilde{w},\tilde{m}\right)$, either wild-type variance or mutant variance or both increase linearly with time (Box 1, I). As time continues, the increasing variance means that extinction of one mtDNA becomes increasingly likely; implications of this behavior are explored below.

The mathematical structure of the solutions only ever involves the difference between replication and degradation rates $\left({\beta }_i-{\delta }_i\right)$, showing that control of (1) biogenesis rates and (2) degradation rates induce comparable behavior in the cellular mtDNA population (Box 1, III).

Heteroplasmy Statistics

As shown in Supplemental Data Section 5, a first-order Taylor expansion gives an approximation for the variance of $h=m/\left(w+m\right)$:

$$\langle h^2\rangle =\frac{{\langle w\rangle }^2\langle m^2\rangle +{\langle m\rangle }^2\langle w^2\rangle -2\langle wm\rangle \langle w\rangle \langle m\rangle }{{\left(\langle m\rangle +\langle w\rangle \right)}^4},$$ (Equation 11)

and we can then use previously obtained expressions for $\langle w\rangle ,\langle m\rangle ,\langle w^2\rangle ,\langle m^2\rangle ,\langle wm\rangle$ to compute this approximate heteroplasmy variance. Neglecting transient terms and using $\langle w\rangle =\tilde{w}$ and $\langle m\rangle =\tilde{m}$ in Equation 11 gives, after some algebra,

$$\langle h^2\rangle =\frac{2{\beta }_0}{n}h\left(1-h\right)t;\frac{\langle h^2\rangle }{\langle h\rangle \left(1-\langle h\rangle \right)}\equiv {\langle h^2\rangle }^{\text{′}}=\frac{2{\beta }_{0}t}{n},$$ (Equation 12)

where $n=\tilde{w}+\tilde{m}$, with $\tilde{w}=\left(1-h\right)n$ and $\tilde{m}=hn$; thus, h is (mean) heteroplasmy and n is (mean) total copy number (recall that ${\beta }_0={\delta }_0$ in steady state). In Equation 12 we have used normalized heteroplasmy variance ${\langle h^2\rangle }^{\text{′}}$, accounting for the dependence of $\langle h^2\rangle$ on the magnitude of h; ${\langle h^2\rangle }^{\text{′}}$ is the quantity most often reported in experimental studies.

In other words, when the system size expansion is valid (see below), for any control mechanism, heteroplasmy variance in the copy number steady state increases linearly with time with a rate that depends only on the copy numbers of the system and the timescale of random turnover (Box 1, II) (Equation 12 is independent of the β and δ terms in Equations 5 and 6). As we discuss later, this observation implies that many possible mechanisms could be responsible for the same observed trend in heteroplasmy variance, meaning that measurements of heteroplasmy variance alone, even if repeated at different time points, place only a limited mechanistic constraint on mtDNA dynamics.¹⁴ In Supplemental Data Section 7, we discuss experimental strategies that can more efficiently discriminate between different control mechanisms.

Transient Behavior and Cell Divisions and Validity of the Expansion

To obtain analytic insight, we have thus far focused on modeling mtDNA behavior using the system size expansion when a steady-state assumption had already been applied. Transient behavior can also be explored by employing the system size expansion directly on the appropriate master equation, using the full expressions for $\lambda \left(w,m\right)$ and $\nu \left(w,m\right)$ (see Supplemental Data Sections 2 and 6). Relaxing the steady state assumption means that the ODEs describing variance behavior are analytically intractable for many forms of $\lambda \left(w,m\right),\nu \left(w,m\right)$. However, they can simply be solved numerically and, as shown in subsequent sections, well match stochastic simulation (which of course is numerically far more intensive). This ODE approach fully accounts for non-equilibrium behavior—including transient relaxation, cell cycling, and so on—while the system size expansion remains appropriate (see below).

This analysis can readily be used to characterize the effect of partitioning mtDNAs at cell divisions. To compute the time behavior of variance where cell divisions occur at arbitrary times, we invoke a linear noise assumption,^{24, 25} first using the ODEs above to compute the variance behavior within one cell cycle. Partitioning rules for copy-number statistics are then applied, and the resulting post-partition statistics are used as the initial condition for a next phase of ODE solution. We here illustrate this process for binomial partitioning of mtDNAs to connect with recent studies in mice¹⁴ and HeLa,¹⁵ although with an appropriate choice of partitioning rules, this approach can be used to address any partitioning regime (for example, the sub-binomial case recently reported in fission yeast¹⁶). In the case of binomial partitioning, the appropriate partitioning rules are $\langle w\rangle \to \langle w\rangle /2,\langle m\rangle \to \langle m\rangle /2,\langle w^2\rangle \to \langle w^2\rangle /4+\langle w\rangle /4,\langle wm\rangle \to \langle wm\rangle /4,\langle m^2\rangle \to \langle m^2\rangle /4+\langle m\rangle /4$, following straightforwardly from the variance of a binomial distribution with p = 1/2. We will see below that this picture well describes the behavior of stochastic populations in dividing cells: hence, the total variance contributions of turnover between divisions and partitioning at divisions can be modeled as a linear sum, and the behavior of mechanisms across cell cycles is comparable to that within a cell cycle.

The results above hold for a nonzero mutant population. As copy-number variance increases, we expect extinction of one mtDNA type to become increasingly likely. To address this behavior, we must consider when the system size expansion itself, which is reliant on the validity of the linear noise approximation, holds. An important threat to this validity is a non-negligible extinction probability for one mtDNA type, whereupon a normal distribution no longer adequately models the copy-number distribution. Heuristically, this situation arises when, for example, $\sqrt{\langle m^2\rangle }\sim \langle m\rangle$. Another challenge arises due to the fact that, when λ and ν are functions of w and m, our linear theory is an approximation to the nonlinear dynamics that result. Highly nonlinear behavior (for example, pronounced discrete steps in rates occurring at critical copy numbers) will therefore not be perfectly captured, but the ability of our theory to reproduce simulation of the fully nonlinear dynamics (in Figures 1, 3, and 5 and Supplemental Data Section 3) suggests that the linear theory provides valuable insight into a wide range of biologically plausible behaviors. Treatments of fully nonlinear cases represent a substantial technical challenge that will be addressed in future work.

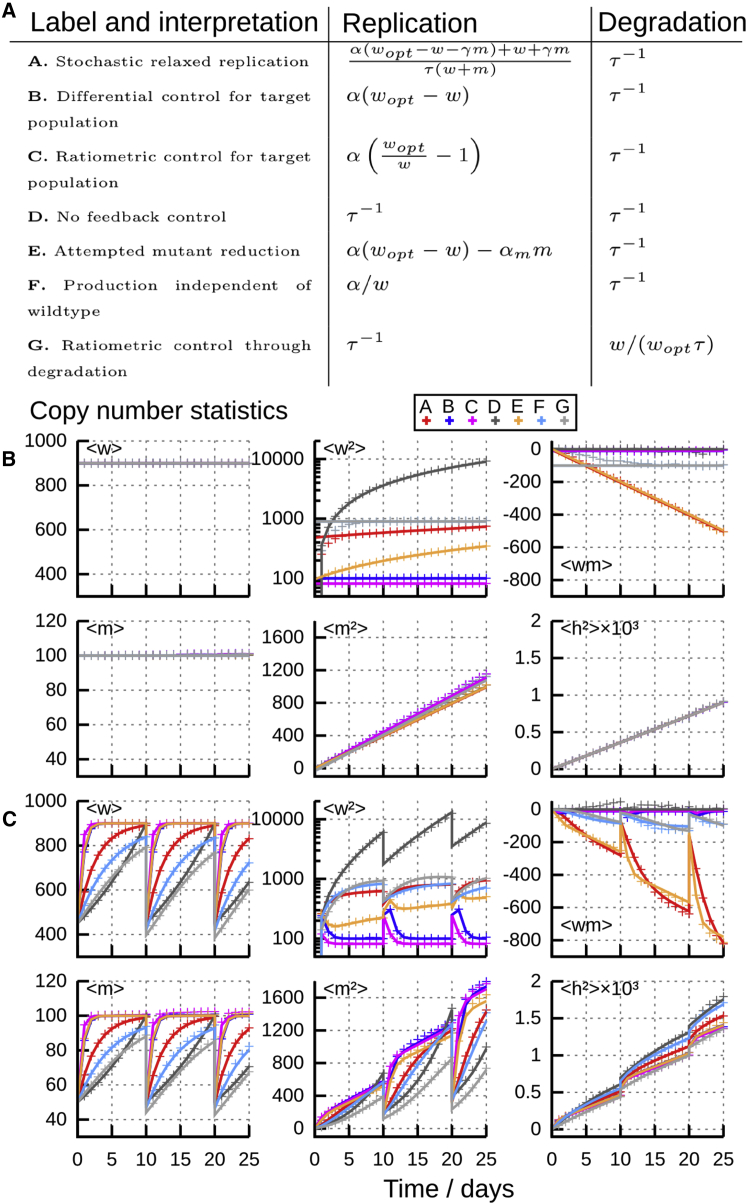
Figure 1.

Behavior of Different Specific Control Mechanisms

All control mechanisms have at least one population with time-increasing variance and so have increasing heteroplasmy variance; mean heteroplasmy $\langle h\rangle$ remains constant through these simulations.

(A) Replication $\lambda \left(w,m\right)$ and degradation $\nu \left(w,m\right)$ rates for model control mechanisms explored in the text, from existing studies and newly proposed here.

(B and C) Copy number and heteroplasmy moments with time for these control mechanisms, (B) in the absence of cell divisions and (C) with binomial cell divisions every 10 days. Analytic results (lines; full expressions in Supplemental Data Section 3) match stochastic simulation (crosses) throughout. Parameters used are chosen to support the same steady state $\left(\tilde{w}=900,\tilde{m}=100\right)$ and with a turnover timescale of $\tau =5$ days. Other parameters: $\gamma =0,{\alpha }_m=0.001,\alpha =2$ (except for models B, E, and F, for which $\alpha =0.002,0.002,200$ respectively); 10⁵ stochastic simulations used.

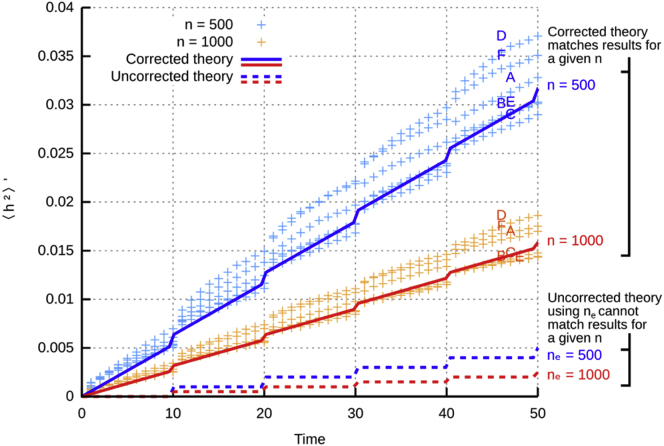
Figure 3.

Correcting the Wright Formula to Include mtDNA Turnover and Connect to Biological Observables

Application of the Wright formula Equation 13 to stochastic mtDNA populations subject to division is only semiquantitative: the Unadjusted Theory lines (dashed) for given effective population sizes n_e do not describe the behavior of simulations of mtDNA populations of that size (crosses). Correcting for mtDNA turnover with Equation 14 quantitatively connects Theory lines (solid) and simulation (crosses); further improvement can be achieved using the ODE approach in Figure 2.

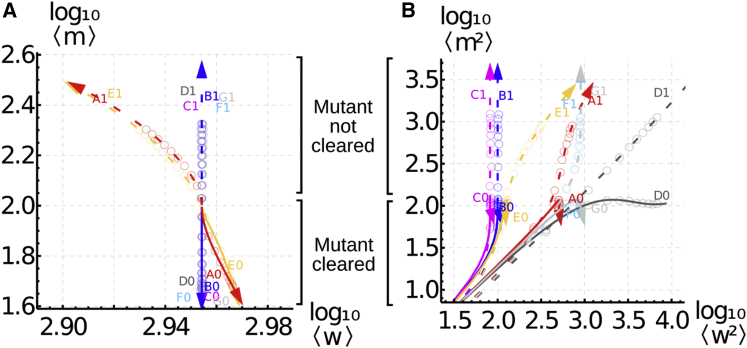
Figure 5.

Variability in Quality Control Clearing of Mutants from Replication Errors

Co-evolution of (A) means and (B) variances of mutant m and wild-type w mtDNA in cells where replication errors occur. Solid lines (downward trajectories; labels A0–F0) give the case where quality control is sufficiently strong to clear the resulting mutant molecules (hence decreasing $\langle m\rangle$ in A); dashed lines (upward trajectories; labels A1–F1) give the case where quality control cannot clear mutants (hence increasing $\langle m\rangle$). Colors and labels correspond to different control models (see text and Figure 2). Points show stochastic simulation. Importantly, regardless of the success of quality control in clearing mutants, wild-type mtDNA variability $\langle w^2\rangle$ can increase substantially during the action of quality control (rightward movement in B), and some strategies lead to order-of-magnitude differences in this increase (starred arrow).

In cases where the validity of the system size expansion is challenged, the mean and variance of mtDNA populations are likely to be underestimated by the preceding analysis (see Supplemental Data Section 3), and the heteroplasmy variance will likely be overestimated, with the true increase in $\langle h^2\rangle$ with time gradually becoming sublinear. Fixation is also neglected by the deterministic version of the mean equations of motion, which allow only an asymptotic descent to zero. Thus, the more general statement of our findings are that (1) for the period when extinction of either type is unlikely, variances and covariances change linearly (after transients), (2) as extinction of one type becomes more likely due to this increased variance, the increasing trend continues but departs from those linear forms (in particular, the increase of $\langle h^2\rangle$ slows to become sublinear), and (3) when extinction of one type is almost certain, the system tends toward the behavior expected if only one type was present (ultimately stalling variance increase, as if $\tilde{m}=0$ in Equation 7). The results we focus on in the remainder of this report can be viewed as describing the “quasi-stationary state” where extinction is negligible; further quantitative details can be derived using, for example, adaptations of the system size expansion that address extinction.²⁶

Specific Control Mechanisms and Comparison with Simulation

The previous results make no assumptions about the specific form of control applied to the mtDNA population, other than the fact that it depends only on current state and is manifest through the rates of Poissonian replication and degradation that are equal for both mtDNA species (and can be described with the system size expansion, as discussed above). We can exploit the generality of the preceding formalism to obtain results for any given (feedback) control mechanism, defined by a specific form of $\lambda \left(w,m\right)$ and $\nu \left(w,m\right)$ in Equations 1, 2, 3, and 4.

We first consider the well-known “relaxed replication” model,^{1, 19} which involves stochastic mtDNA degradation, coupled with mtDNA replication that is physically modeled as a deterministic process. We propose that, if degradation is regarded as a stochastic process (due to its microscopic reliance on complicated processes and colocalizations in the cell), picturing replication (which also relies on complicated interactions on the microscopic scale) as a stochastic process leads to a consistent stochastic generalization (see Appendix A). The corresponding model has exactly the same expressions for rates as in Capps et al.¹ (type A in Figure 1A), but replication rate is now interpreted as the rate of a stochastic, rather than a deterministic, process.

We also introduce several other models for mtDNA control to consider a range of potential functional forms, including differential and ratiometric control based on a target wild-type copy number, an absence of any feedback control, and others (types B–G in Figure 1A). The presence or absence of w and m in these expressions reflects what quantity is being sensed by the cell (wild-type mtDNA alone, mutant mtDNA alone, or a combination of the two). We further note that this general formalism can also incorporate physical constraints on the mtDNA population. For example, the hypothesis that mitochondrial concentration is controlled between cell divisions¹⁵ (recently confirmed in fission yeast¹⁶) could correspond to w_opt, the “target” mtDNA number, being a linear function of cell volume in the models above, or could arise through passive birth-death dynamics (model D) with control implemented at the cell division stage (see previous section). Interpretations of these control mechanisms in terms of cellular sensing and the language of stochastic population processes are given in Supplemental Data Section 3.

Figure 1B illustrates the application of our analysis to these example control mechanisms in the absence of cell divisions. The close agreement between stochastic simulation and analytic results in steady state demonstrates the ability of our general theory to describe a wide range of different potential cellular control mechanisms. The long-term linear increases in one or both mtDNA variances are clear (Box 1, I), and trajectories of $\langle h^2\rangle$ with the same steady state and turnover timescale are identical (Box 1, II). Figure 1C, including cell divisions, demonstrates close agreement between ODE solutions and stochastic simulation, further showing that the linear noise treatment successfully captures stochastic behavior over cell divisions. The close similarity of $\langle h^2\rangle$ trajectories across divisions is a consequence of their aforementioned identity in steady-state conditions with no cell divisions (Figure 1B); the slow divergence is due to differences in mechanism behavior away from the steady state.

Applications I: Heteroplasmy Variance Increases at Constant Mean Copy Number

The increase of heteroplasmy variance $\langle h^2\rangle$ with time is of profound importance in determining the inheritance and onset of mtDNA diseases. Because disease symptoms often manifest only when heteroplasmy exceeds a certain threshold,⁷ increasing heteroplasmy variance with time can lead to pathologies even if mean heteroplasmy does not change (because a higher cell-to-cell variance implies a greater probability of a given cell exceeding a threshold).¹⁴

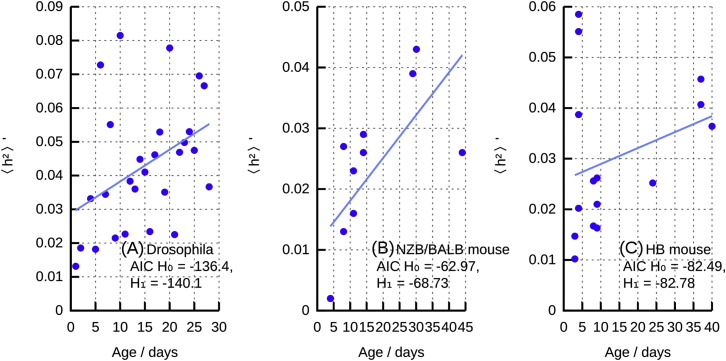
We sought experimental evidence to support the linear increase of $\langle h^2\rangle$ predicted by our theory. Time course measurements of single-cell heteroplasmy values remain limited; we identified results from the Drosophila germline²⁷ and in the mouse germline for the NZB/BALB model^{28, 29} and the HB model.¹⁴ For these data, we compared the ability to fit the data of a null model involving constant ${\langle h^2\rangle }^{\text{′}}$ (${\mathcal{H}}_0:{\langle h^2\rangle }^{\text{′}}=\alpha +\mathit{\epsilon }$, where α is a constant) and an alternative model $\left({\mathcal{H}}_1:{\langle h^2\rangle }^{\text{′}}=\alpha +\beta t+\mathit{\epsilon }\right)$, where ${\langle h^2\rangle }^{\text{′}}$ changes linearly with time as our theory predicts (Equation 12; Box 1, II). Using the Akaike information criterion (AIC) and assuming normally distributed noise on mean ${\langle h^2\rangle }^{\text{′}}$ ($\mathit{\epsilon }\sim \mathcal{N}\left(0,{\sigma }^2\right)$, an assumption consistent with our linear approximation but which can be further refined as in Wonnapinij et al.²⁹), we found that the alternative, time-varying model was favored in all cases, providing support for our theory (Figures 2A–2C).

Figure 2.

Experimental Support for Linear $\langle h^2\rangle$ Increase

Normalized heteroplasmy variance ${\langle h^2\rangle }^{\text{′}}$ in model organism germlines over time (points); lines show maximum-likelihood linear fit for $\langle h^2\rangle$ as a function of time. Insets give Akaike information criterion (AIC) values for ${\mathcal{H}}_0$ (${\langle h^2\rangle }^{\text{′}}$ is constant) and ${\mathcal{H}}_1$ (${\langle h^2\rangle }^{\text{′}}$ increases linearly with time). Model organism and reference(s): Drosophila²⁷ (A), NZB/BALB mice²⁸, ²⁹ (B), and HB mice¹⁴ (C).

These results are quantitatively consistent with a previous study on the dynamics of heteroplasmy variance during the mtDNA bottleneck in mice¹⁴ where a mechanism involving random mtDNA turnover and random mtDNA partitioning at cell divisions was found to best explain experimental observations. mtDNA in mice and rats often has a half-life of 10–100 days.²³ This corresponds to ${\beta }_0={\delta }_0=\text{log}2/t_{1/2}=0.03-0.003$ day^-1 and $\tau =t_{1/2}/\text{log}2=5-50$ days. In Figure 1 we show the patterns of copy number and heteroplasmy means and variances for $\tau =5$ days and 10³ mtDNA molecules per cell under different specific control strategies. The increase of $\langle h^2\rangle$ from 0 to 10⁻³, corresponding for h = 0.1 to an increase in ${\langle h^2\rangle }^{\text{′}}$ from 0 to 0.011, matches the scale of change observed in the mtDNA bottleneck (though the bottleneck is complicated by changing population size n and compensatory changing turnover ${\beta }_0$).¹⁴ Previous work has shown that the case with no feedback (D in Figure 1) describes well the behavior of mtDNA with cell divisions in mouse development.¹⁴ In Appendix A we discuss further connections with previous theoretical studies; experimental cell-to-cell measurements in more quiescent cell types, although currently lacking, will provide valuable further tests of our theory.

mtDNA Turnover in the Wright Formula

Powerful existing analyses of mtDNA population variance^{22, 29} with widespread influence³ have drawn upon a classical theory by Wright (and Kimura)^{21, 30} describing stochastic sampling of a population of elements between generations. The resulting expression for expected heteroplasmy variance is the well-known equation sometimes referred to as the Wright formula (though other equations also bear this name):^{3, 22}

$${\langle h^2\rangle }^{\text{′}}=1-{\left(1-{\left(2n_e\right)}^{-1}\right)}^g,$$ (Equation 13)

where n_e is an effective population size and g is a number of generations. The mapping of this effective theory to the complicated mtDNA system is valuable to develop intuition but cannot capture the detailed dynamics of individual mtDNA molecules, due to assumptions (see Appendix B) that mean the effective parameters of the theory (n_e and g) cannot generally be interpreted as biological observables,^{22, 31} preventing quantitative analyses of mechanisms and dynamics.³ In particular, n_e does not generally correspond to a minimum mtDNA copy number (see Appendix B), and, being a genetic rather than a physical parameter, “is unlikely ever to correspond closely to the number of anything.”³¹

The Wright formula, however, does accurately describe the heteroplasmy variance due to binomial sampling of 2n_e real elements at cell divisions for an observable population size, and, as seen in the previous section, the additional effect of mtDNA turnover based on observable values can be included as an extra linear contribution. In general, this term will depend on the dynamics controlling the mtDNA population and can easily be calculated via the ODE approach above (Figure 1).

In the case where no systematic change in mtDNA population size occurs with time, we can use the observation that $\langle h^2\rangle$ trajectories are often comparable across a variety of different possible cellular control mechanisms (and identical in the steady state; Figure 1 and Equation 12) to produce a simple approximate description linking ${\langle h^2\rangle }^{\text{′}}$ to observables. The simple steady-state behavior is given by Equation 12. To construct an approximation, we use a simple estimate of mean population size over a cell cycle, writing $n^{\prime }=3/2n$, where n is the mtDNA population size immediately after division and $n^{\prime }$ thus gives a population size “average” over the changes within a cell cycle. Using the above analysis with $w_0=\left(1-\langle h\rangle \right)n^{\prime }$, $m_0=\langle h\rangle n^{\prime }$ (representing the “average” populations of wild-type and mutant mtDNA), and ${\beta }_0=1/\tau$ (so that τ is the timescale of mtDNA degradation), the corresponding expression in terms of h and n is then given by a “turnover-adjusted” Wright formula (see Appendix B):

$${\langle h^2\rangle }^{\text{′}}=1-{\left(1-{\left(2n\right)}^{-1}\right)}^g+4t/\left(3n\tau \right),$$ (Equation 14)

where g is the number of cell divisions that have occurred and t is the amount of time that has expired since an initial state with ${\langle h^2\rangle }^{\text{′}}=0$. This expression is subject to the conditions for system size expansion validity described above; thus, as fixation probability increases, the increase of ${\langle h^2\rangle }^{\text{′}}$ will drop below this prediction.

Figure 3 illustrates the agreement between Equation 14 and stochastic simulation for the range of control mechanisms we consider under different population sizes and heteroplasmies. It is worth reiterating that more exact solutions for a given control mechanism can easily be computed using the preceding ODE approach, and stochastic analysis can also be used to quantitatively describe the effects of more specific circumstances (for example, the systematically varying population size through the mtDNA bottleneck¹⁴). In the case of no such systematic variation, and, crucially, if the Poissonian model of Equations 1, 2, 3, and 4 holds, then Equation 14, a modified Wright formula, represents a simpler, approximate way to establish a quantitative link between observed normalized heteroplasmy variance ${\langle h^2\rangle }^{\text{′}}$ and observable quantities (Box 1, IV), i.e., n (mtDNA copy number immediately after division), g (number of cell divisions), and τ (timescale of mtDNA turnover).

Applications II: Linking Physical and Genetic Rates with the Modified Wright Formula

The Wright formula is traditionally used to compare a heuristic, effective “bottleneck size” across experimental systems (for example, in studies of different organisms²² and of human disease³²). In its uncorrected form, this bottleneck size can only be semiquantitatively treated—bottleneck sizes can be ranked, but absolute values and differences cannot be straightforwardly interpreted. Our adaptation allows us to use this formula to connect the rates of physical subcellular processes with the resulting rates of genetic change.

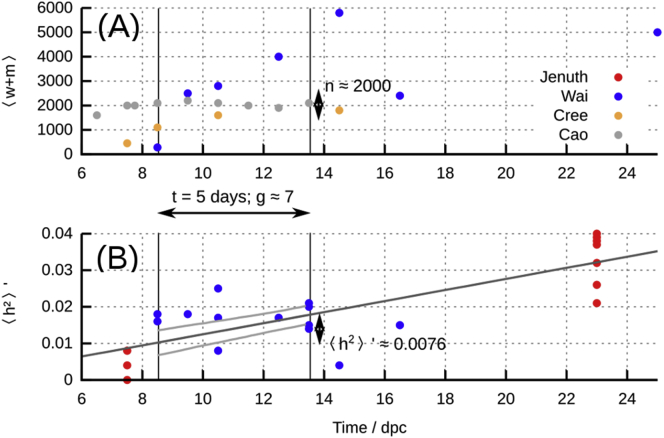
To illustrate this connection, we focus on a particular period during mouse development. Between 8.5 and 13.5 days post conception (dpc) in the developing mouse germline, cell divisions occur with a period of about 16 hr,³³ giving g = 7 or 8 cell divisions in this period (of length t = 5 days). Copy-number measurements during this period show that the mean total number of mtDNA molecules per cell remains of the order of n = 2,000 (Figure 4A).^{28, 34, 35} During this period, heteroplasmy variance ${\langle h^2\rangle }^{\text{′}}$ increases on average (but with substantial variability) from around 0.01 to 0.02 (Figure 4B).^{28, 36} Figure 4B shows a best-fit line to ${\langle h^2\rangle }^{\text{′}}$ data, with slope 1.52 × 10⁻³ day⁻¹ (5%–95% confidence intervals (1.11–1.92) × 10⁻³ day⁻¹).

Figure 4.

Using the Adapted Wright Formula to Estimate mtDNA Turnover

(A) mtDNA copy number n, taken to correspond to $\langle w+m\rangle$, in the mouse germline during development. Data from several existing studies, referred to by first author.²⁸, ³⁴, ³⁵, ³⁶

(B) Normalized heteroplasmy variance ${\langle h^2\rangle }^{\text{′}}$ in this time period (points). Dark gray line is the mean inferred increase (which is linear, in agreement with our theoretical predictions, as in Figure 3). Light gray lines give the 95% confidence intervals in the 8.5–13.5 dpc window, from a linear model fit. Values used in the turnover-adjusted Wright formula (Equation 14) are given.

We can use these measurements in conjunction with the turnover-adjusted Wright formula (Equation 14) to obtain estimates for the rate of mtDNA turnover during this period. Using Equation 14 with the best-fit ${\langle h^2\rangle }^{\text{′}}=1.52\times {10}^{-3}\times 5=7.6\times {10}^{-3}$, and g = 7 divisions, n = 2,000 mtDNA molecules, t = 5 days gives the resulting estimate $\tau \simeq 0.57$ days (5%–95% confidence intervals 0.43–0.88 days, using the same values for n, g, t) for the characteristic timescale of mtDNA degradation. This increase in mtDNA turnover (relative to the $\tau \simeq 5-50$ day timescale in differentiated tissues²³) in the germline during this developmental period matches quantitative results from a more detailed study of the bottleneck reporting τ within the range 0.38–2.1 days (based on posteriors for $\nu =1/\tau$ between 0.02 and 0.11 hr⁻¹)¹⁴ and illustrates how a suitable mathematical model can be used to estimate biological quantities that are challenging to directly address with experiment.³⁷

Influence of Mutations, Replication Errors, and Selective Differences: Quality Control of Replication Errors

Our approach is easily generalized to include other processes than those described by Equations 1, 2, 3, and 4: in Supplemental Data Section 6 we demonstrate that adding and changing appropriate processes allows us to analyze the effects on mtDNA mean and variance due to de novo mutations, replication errors, and multiple selective pressures. Our approach can be thus used to characterize variability arising from selection and mutation under any control mechanisms, without requiring stochastic simulation.

We can use this ability to explore a particular scientific question: if mtDNA replication errors occur and the cell attempts to clear the resulting mutant mtDNA through selective quality control, how do cellular mtDNA populations change? To investigate this question, we introduce the process $\left\{w,m\right\}\stackrel{\mu w}{\to }\left\{w,m+1\right\}$ (replication errors—leading to the production of a new mutant mtDNA—occurring with rate μ) and reparameterize Equation 4 as $\left\{w,m\right\}\stackrel{\left(1+\mathit{\epsilon }\right)m\nu \left(w,m\right)}{\to }\left\{w,m-1\right\}$ (an increase of ε in mutant degradation rate compared to wild-type degradation). We thus model the situation where replication errors arise and the cell attempts to clear them through quality control, while a control strategy for mtDNA populations is also in place.

Figure 5 illustrates the mean and variance of w and m in two different cases, distinguished by the relative magnitude of the selective difference (ε) and error rate (μ). This ratio is crucial in determining whether mutant mtDNA is cleared or increased: Figure 5A shows that mutant is cleared when $\left(1+\mathit{\epsilon }\nu \right)\gg \mu$ (selection is sufficiently strong to overcome errors), but when selective difference ε is insufficiently high, mutant mtDNA mean and variance (and heteroplasmy) increase with time. In both cases, we also observe substantial differences in mtDNA behavior depending on the control model in place. Control models lacking an explicit target copy number (D, no feedback; F and G, immigration-like) experience substantial increases in wild-type variance while mutant is being removed. Models involving a target wild-type copy number and weak or no coupling to mutant mtDNA (B, C, E) admit an order-of-magnitude lower increase in wild-type variance as mutant is cleared. Relaxed replication (model A), which combines a target copy number with a strong coupling between mutant and wild-type mtDNA, displays an intermediate increase on wild-type variance as mutant is cleared.

Theoretical approaches that consider only the mean behavior of mtDNA populations (Figure 5A) cannot account for this cellular heterogeneity and the important fact that quality control acting to remove mutant mtDNA can also induce variability in wild-type mtDNA (Figure 5B). The action of quality control may therefore yield a subset of cells with wild-type mtDNA substantially lower than the mean value across cells—potentially placing a physiological challenge on those cells where wild-type mtDNA is decreased. In addition to the important point that the simple presence of quality control does not guarantee the clearing or stabilization of mutant load, we thus find that quality control may have substantial effects on wild-type as well as mutant mtDNA if cellular control couples the two species (Box 1, V).

Applications III: Variance Induced through Mutant Clearing

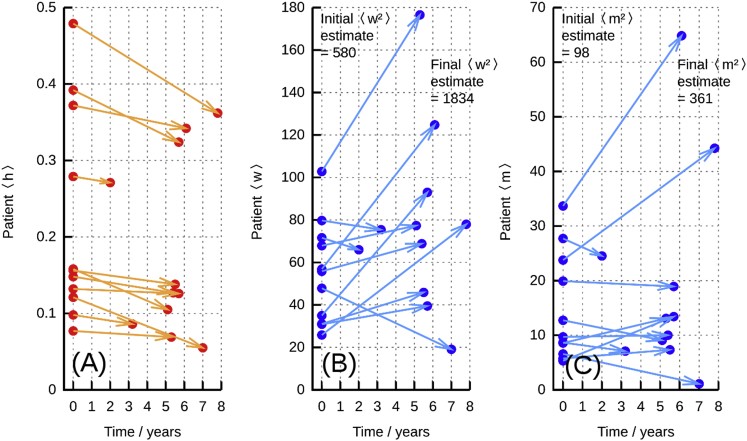
The A>G mutation at position 3243 in human mtDNA is the most common heteroplasmic pathological mtDNA mutation, giving rise to MELAS (mitochondrial encephalomyopathy, lactic acidosis, and stroke-like episodes), a multi-system disease. The dynamics of c.3243A>G heteroplasmy are complex and tissue dependent; its behavior in blood has been characterized in particular detail using a fluorescent PCR assay for heteroplasmy³⁸ in a way that allows us to explore our theoretical predictions about mtDNA statistics with mutant clearing.

Pyle et al.³⁸ took two blood samples, several years apart, from human patients, and quantified c.3243A>G heteroplasmy (h) and mean mtDNA copy number per cell for both samples. Although single-cell data are not presented in the publication, progress can be made with the averaged quantities. A strong decrease in (h) with time is observed for all patients, confirming that mutant mtDNA is being cleared (Figure 6A). The behavior of total mtDNA molecules per cell (w + m) is less consistent, with a range of large increases and moderate decreases in total number. As shown in Figures 6B and 6C, patient-to-patient variance in both w and m increases with time in conjunction with h decreases.

Figure 6.

mtDNA Evolution in MELAS Patients from Pyle et al.³⁸

(A) Changes in mean heteroplasmy $\langle h\rangle$ between two samples from patient blood, showing a general decrease in $\langle h\rangle$ over time.

(B) Changes in mean cellular wild-type content w between these samples.

(C) Changes in mean cellular mutant content m.

In both (B) and (C), an overall increase in variance over time is observed: hence $\langle w^2\rangle$ and $\langle m^2\rangle$ increase while $\langle h\rangle$ decreases, consistent with Figure 6.

Although the measurements in Pyle et al.³⁸ are averages over groups of cells, an approximate quantitative comparison of these data with the predictions of our theory can be made. In the spirit of “back-of-the-envelope” calculations,³⁹ we estimate that each sample of cells giving rise to a measurement corresponds to approximately 10³ cells (see Supplemental Data Section 8). Then, using an estimate of $\tau =5$ days (by comparison with other mammalian species, as above), we find that a selective pressure of ${\mathit{\epsilon }}_8\simeq 1.2\times {10}^{-4}$ day⁻¹ matches the observed decrease in heteroplasmy, corresponding, for example, to a decrease from 0.15 to 0.14 over 8 years, as in Figure 6A. Solving the ODEs resulting from this system, using control model D as the simplest case, predicts increases in cell-to-cell copy-number variance of approximate magnitude $\langle w^2\rangle \sim {10}^5$ and $\langle m^2\rangle \sim 2\times {10}^4$ over 8 years. We can translate these cell-to-cell values into the variance expected across samples of cells by dividing by the number of samples (taken as 10³ as above). The resulting variance corresponds, for example, to expected standard deviations in wild-type and mutant copy number after 8 years of 10.0 and 4.0, respectively, for a sample with $\langle w\rangle =85$ and $\langle m\rangle =15$ (consistent with the increasing spread of values in Figures 6B and 6C). We used the Kolmogorov-Smirnov test to test the alternative hypotheses that the experimentally observed $\langle w\rangle$ and $\langle m\rangle$ at the later time point differed from those predicted by our model; no test yielded p < 0.05 (see Supplemental Data Section 8). Of course, an absence of support for an alternative hypothesis cannot be taken as support for a null hypothesis, but shows that the existing experimental data are not incompatible with our model.

The observations in Figure 6 support the predictions made in Figure 5, where mutant load is decreased but variance in wild-type copy number (and mutant copy number) increases. The bottom-left quadrant of Figure 5B shows that different control mechanisms display similar initial behavior; follow-up studies on these subjects could be used to distinguish possible mechanisms for mtDNA control. For example, if the rate of wild-type variance increase decreases over time, models B, C, and E are more likely; if wild-type variance continues to increase, models A, D, F, and G are more likely. More detailed model discrimination based on the time behavior of w and m variances are possible (Figure 1) and can be performed using statistical methods accounting for mean and variance behavior.^{29, 40}

Discussion

A general, bottom-up theory has been produced to describe the time behavior of cell-to-cell variance in mtDNA populations subject to controlled biogenesis and/or degradation, mutation, selection, and cell divisions. This theory is based around the microscopic behavior of mtDNA molecules, allowing a hitherto absent connection between widely used “effective” statistical genetics approaches (Equation 13) and measurable biological quantities, and motivating experiments to further elucidate the mechanisms acting to control mtDNA (described in Supplemental Data Section 7). We have shown that the predictions of this theory agree with experimental observations of mixed mtDNA populations and that the application of appropriately validated mathematical theory allows us to make estimates of important biological quantities that remain challenging to directly address with experiments. Our theory describes the cell-to-cell variability in mtDNA populations and thus provides a framework with which to understand the inheritance and onset of mtDNA diseases.^{6, 14}

Our theoretical platform unifies several existing modeling approaches that have driven advances in the study of mtDNA populations. We have specifically demonstrated that the “relaxed replication” model^{1, 19, 34} (our model A), simple birth-death models^{14, 20} (our model D), and cellular controls based on homeostatic principles^{15, 16} (our models B, C, and G) can naturally be represented within our framework. As a result, analytic expressions for the expected behavior of heteroplasmy variance and other population statistics can readily be extracted for these and other mtDNA models (see Supplemental Data Section 3), allowing the detailed characterization of mtDNA dynamics, including the probability of crossing disease thresholds,⁷ which can be computed from heteroplasmy statistics.¹⁴ We have also used the theoretical ideas developed herein to refine a widely used model for mtDNA populations of changing size (the Wright formula), explicitly connecting it with cellular processes and allowing a link between physical and genetic quantities (Equation 14, Figure 4).

Further, our theory also describes the dynamics of heteroplasmy change with time in the presence of selective pressure for one mtDNA type. Given an initial heteroplasmy h₀ and a selective pressure β (positive β corresponding to positive selection for the mutant mtDNA type), we find (see Supplemental Data Section 5) that heteroplasmy evolves according to:

$$h=\frac{1}{1+\frac{1-h_0}{h_0}{e}^{-\beta t}}.$$ (Equation 15)

This behavior immediately motivates a transformation, allowing the evolution of heteroplasmy to be compared across different starting values h₀:

$$\text{Δ}{h}^{\prime }\equiv \beta t=\text{log}\left(\frac{h\left(h_0-1\right)}{h_0\left(h-1\right)}\right),$$ (Equation 16)

allowing, as in our previous work,²³ heteroplasmy results from different biological samples to be compared together, accounting for different initial heteroplasmies (in other words, the same selective pressure will produce the same $\text{Δ}{h}^{\prime }$ regardless of h₀).

It is likely that control mechanisms found in biology have nonlinear forms (for example, sigmoidal response curves are common in cellular signaling). We have shown that a linearization satisfactorily describes some non-equilibrium behavior (for example, in the case of our cell division model), but further investigation of more general nonlinear behavior and modulation of wider cell behavior by mtDNA populations (for example, by influencing cell cycle progression¹⁵) are important future developments. In Supplemental Data Section 1 we discuss a linear stability analysis of our expressions for mean mtDNA behavior, which highlights a link between the “sensing” of an mtDNA species (in the sense that the presence of that species modulates replication or degradation rates) and the ability to control the mean level of that species.

The control of stochastic systems is a well-established field within control theory.⁴¹ Optimal control mechanisms addressing the mean and variance of stochastic processes have been derived in a variety of contexts (see, for example, Borkar⁴² and citations therein), particularly in financial applications,⁴³ and often find tradeoffs between controlling the mean and variance of a process. We observe a comparable tradeoff, that tight control on moments of one species leads to loose control on another. We have focused on providing a general theoretical formalism with which to treat any given control mechanism; it is anticipated that the above treatment may also be of value in describing heterogeneity in other systems where replication and/or death rates of individuals depend on feedback from current numbers of individuals (for example, through terms describing competition for resources in ecology). Within the context of mtDNA populations, we anticipate that this theoretical framework will assist in understanding natural processes of mtDNA inheritance and evolution within an organismal lifetime (including segregation and increasing variance with age)^{14, 23} and informing applied approaches to control mitochondrial behavior with genetic tools.^{4, 5}

Published: October 27, 2016

Appendix A. Interpretation of Relaxed Replication

The relaxed replication model¹, ¹⁹ describes a cellular population of mtDNA molecules according to the following algorithm. mtDNAs randomly degrade as a Poisson process with rate $1/\tau$. Every time step $\text{Δ}t$, the value of C(w,m), a deterministic function of w and m, is computed, then $\text{Δ}tC\left(w,m\right)$ mtDNAs are added to the population. The genetic properties of these added mtDNAs are random—each is assigned a genetic type based on a random sampling of the existing populations—but their physical properties (i.e., the total copy number added at each step) are deterministic. We argue that, as both replication and degradation of mtDNAs depend on complicated behavior and thermal, microscopic interactions, it makes more sense to model both processes as stochastic. Thus, C(w,m) is interpreted as the rate of a Poisson process describing replication, just as $1/\tau$ is the rate of a Poisson process describing degradation. This interpretation reconciles the nature of the two processes.

Although this feature is less interesting than the underlying scientific behavior, the original algorithm also raises a (not insurmountable) technical problem with implementation. If a time step $\text{Δ}t<1/C\left(w,m\right)$ is chosen, the algorithm will never add any mtDNA to the system. But, in order to suitably characterize the stochastic degradation without using the Gillespie algorithm,⁴⁴ it is desirable to choose a time step $\text{Δ}t$ as low as possible. There is therefore a risk that one or other of the deterministic replication and stochastic degradation processes is inadequately captured in a given simulation protocol.

We have illustrated the excellent agreement between our theoretical approaches and stochastic simulation (for example, Figure 1). To quantitatively connect with previous analyses of specific control strategies, we confirm that the behavior for model A (relaxed replication) matches that observed in previous simulation studies¹⁹ with a back-of-the-envelope calculation.³⁹ The rate of variance increase with time with $\tau =5$ days (comparable in magnitude to the (1 − 10)× log 2 days used in Chinnery and Samuels¹⁹) and w_opt = 1,000 from Figure 1 is roughly 40 day⁻¹. Considering 50 years of evolution of this system, we expect a standard deviation of roughly $\sqrt{40\times 50\times 365}\simeq 850$ in mutant copy number. This value is consistent with the simulations in Chinnery and Samuels.¹⁹

We connect to an additional numerical result in Capps et al.¹ In the absence of a mutant population, the variance of the wild-type population was reported to be stable at $w_{opt}/\left(2\alpha \right)$, with the original model interpretation of mtDNA replication as deterministic. Under the interpretation of stochastic replication, an absent mutant population (m_ss = 0) permits stability in the wild-type population variance, which after a little algebra is calculated to be $w_{opt}/\alpha$. Intuitively, modeling both replication and degradation as stochastic does not affect mean copy number but does increase variance.

Appendix B. Interpretation of Wright Formula for mtDNA

The Wright formula

$$\langle h^2\rangle =\langle h\rangle \left(1-\langle h\rangle \right)\left(1-{\left(1-{\left(2n_e\right)}^{-1}\right)}^g\right)$$ (Equation 17)

has been proposed as a model for the time evolution of heteroplasmy variance $\langle h^2\rangle$ in a population with effective size n_e subject to random partitioning at each of g generations. This picture has been successfully employed to investigate heteroplasmy distributions in real systems,²² with n_e and g interpreted as parameters of the theory without immediate biological interpretation.

The mapping of the original genetic system considered by Wright²¹ to cellular populations of mtDNA requires some discussion. If “generations” are interpreted as cell divisions, the mechanism by which mtDNA copy number is redoubled between divisions is assumed by the model to be deterministic. Cell divisions will result in a halving of the mtDNA population. Application of the Wright model assumes that the original population is thenceforth recovered with no increased variance in the population. In other words, the mtDNA population is assumed to exactly double between divisions with no stochasticity in the process. As we underline in the main text, the effects of (inevitable) stochasticity due to mtDNA turnover are not explicitly captured by the Wright formula. Other complications exist, as described in Wonnapinij et al.,²² but play less important roles here. As a result, the “bottleneck size” n_e cannot immediately be interpreted as an observable minimum cellular copy number of mtDNA molecules (a quantity that is reported by, for example, a qPCR experiment measuring cellular mtDNA content), but rather the size of an effective “founder” population.