ISLES 2015 - A public evaluation benchmark for ischemic stroke lesion segmentation from multispectral MRI

Abstract

Ischemic stroke is the most common cerebrovascular disease, and its diagnosis, treatment, and study relies on non-invasive imaging. Algorithms for stroke lesion segmentation from magnetic resonance imaging (MRI) volumes are intensely researched, but the reported results are largely incomparable due to different datasets and evaluation schemes. We approached this urgent problem of comparability with the Ischemic Stroke Lesion Segmentation (ISLES) challenge organized in conjunction with the MICCAI 2015 conference. In this paper we propose a common evaluation framework, describe the publicly available datasets, and present the results of the two sub-challenges: Sub-Acute Stroke Lesion Segmentation (SISS) and Stroke Perfusion Estimation (SPES). A total of 16 research groups participated with a wide range of state-of-the-art automatic segmentation algorithms. A thorough analysis of the obtained data enables a critical evaluation of the current state-of-the-art, recommendations for further developments, and the identification of remaining challenges. The segmentation of acute perfusion lesions addressed in SPES was found to be feasible. However, algorithms applied to sub-acute lesion segmentation in SISS still lack accuracy. Overall, no algorithmic characteristic of any method was found to perform superior to the others. Instead, the characteristics of stroke lesion appearances, their evolution, and the observed challenges should be studied in detail. The annotated ISLES image datasets continue to be publicly available through an online evaluation system to serve as an ongoing benchmarking resource (www.isles-challenge.org).

Graphical abstract

1. Introduction

Ischemic stroke is the most common cerebrovascular disease and one of the most common causes of death and disability worldwide (WHO, 2012). In ischemic stroke an obstruction of the cerebral blood supply causes tissue hypoxia (underperfusion) and advancing tissue death over the next hours. The affected area of the brain, the stroke lesion, undergoes a number of disease stages that can be subdivided into acute (0-24h), sub-acute (24h-2w), and chronic (>2w) according to the time passed since stroke onset (González et al., 2011). Magnetic resonance imaging (MRI) of the brain is often used to assess the presence of a stroke lesion, it’s location, extent, age, and other factors as this modality is highly sensitive for many of the critical tissue changes observed in stroke.

Time is brain is the watchword of stroke units worldwide. Possible treatment options are largely restricted to reperfusion therapies (thrombolysis, thrombectomy), which have to be administered not later than four to six hours after the onset of symptoms. Unfortunately, these interventions are associated with an increasing risk of bleeding the longer the lesion has been underperfused. To this end, considerable effort has gone into finding image descriptors that predict stroke outcome (Wheeler et al., 2013), treatment response (Albers et al., 2006; Lansberg et al., 2012), or the patients that would benefit from a treatment even beyond the regular treatment window (Kemmling et al., 2015).

At present, only a qualitative lesion assessment is incorporated in the clinical workflow. Stroke research studies, which require quantitative evaluation, depend on manually delineated lesions. But the manual segmentation of the lesion remains a tedious and time consuming task, taking up to 15 minutes per case (Martel et al., 1999), with low inter-rater agreement (Neumann et al., 2009). Developing automated methods that locate, segment, and quantify the stroke lesion area from MRI scans remains an open challenge. Suitable image processing algorithms can be expected to have a broad impact by supporting the clinicians’ decisions and render their predictions more robust and reproducible.

In the treatment decision context, an automatic method would provide the medical practitioners with a reliable and, above all, reproducible penumbra estimation, based on on which quantitative decision procedures can be developed to weight the treatment risks against the potential gain. For medical trials, the results would become more reliable and reproducible, hence strengthening the finding and reducing the required amount of subjects for credible results. Another beneficiary would be cognitive neuroscientists, who often perform studies where cerebral injuries are correlated with cognitive function and for whom lesion segmentation is an important pre-requisite for statistical analysis.

Still, segmenting stroke lesions from MRI images poses a challenging problem. First, the stroke lesions’ appearance varies significantly over time, not only between but even within the clinical phases of stroke development. This holds especially true for the sub-acute phase, which is studied in the SISS sub-challenge: At the beginning of this interval, the lesion usually shows strongly hyperintense in the diffusion weighted imaging (DWI) sequence and moderately hyperintense in fluid attenuation inversion recovery (FLAIR). Towards the second week, the hyperintensity in the FLAIR sequence increases while the DWI appearance converges towards isointensity (González et al., 2011). Additionally, a ring of edema can build up and disappear again. In the acute phase, the DWI denotes the infarcted region as hyperintensity. The magnitude of the actual under-perfusion shows up on perfusion maps. The mismatch between these two is often considered the potentially salvageable tissue, termed penumbra (González et al., 2011). Second, stroke lesions can appear at any location in the brain and take on any shape. They may or may not be aligned with the vascular supply territories and multiple lesions can appear at the same time (e.g. caused by an embolic shower). Some lesions may have radii of few millimeters while others encompass almost a complete hemisphere. Third, lesion structures may not appear as homogeneous regions; instead, their intensity can vary significantly within the lesion territory. In addition, automatic stroke lesion segmentation is complicated by the possible presence of other stroke-similar pathologies, such as chronic stroke lesions or white matter hyperintensities (WMHs). The latter is especially prevalent in older patients which constitute the highest risk group for stroke. Finally, a good segmentation approach must comply with the clinical workflow. That means working with routinely acquired MRI scans of clinical quality, coping with movement artifacts, imaging artifacts, the effects of varying scanning parameters and machines, and producing results within the available time window.

1.1. Current methods

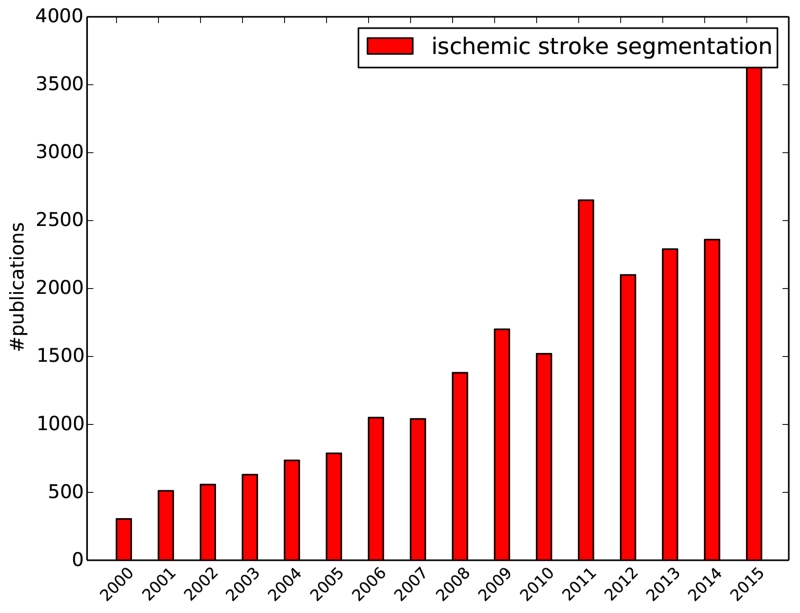
The quantification of stroke lesions has gained increasing interest during the past years (Fig. 1). Nevertheless, only few groups have started to develop automatic image segmentation techniques for this task in recent years despite the urgency of this problem. A recent review of non-chronic stroke lesion segmentation (Rekik et al., 2012) summarizes the most important works until 2008, reporting as few as five automated stroke lesion segmentation algorithms. A collection of more recent approaches not included in Rekik et al. (2012) are listed in Table 1. While an increasing number of automatic solutions are presented, there are also a number of semi-automatic methods indicating the difficulty of the task. Among the automatic algorithms, only a few employ pattern classification techniques to learn a segmentation function (Prakash et al., 2006; Maier et al., 2014, 2015c) or design probabilistic generative models of the lesion formation (Derntl et al., 2015; Menze et al., 2015; Forbes et al., 2010; Kabir et al., 2007; Martel et al., 1999).

Figure 1.

Increasing count of publications over the years as returned by Google scholar for the search terms ischemic stroke segmentation on 2016-05-17.

Table 1.

Listing of publications describing non-chronic stroke lesion segmentation in MRI with evaluation on human image data since Rekik et al. (2012). Column A denotes the lesion phase, i.e., (A)cute, (S)ub-acute or (C)hronic. Column T denotes the method type, i.e., (A)utomatic or (S)emi-automatic. Column N denotes the number of testing cases (mostly leave-one-out evaluation scheme is employed). Column Sequences denotes the used MRI sequences. Column DC denotes the reported Dice’s coefficient score if available. Column Metrics denotes the metrics used in the evaluation.

Method	A	T	N	Sequences	DC	Metrics
Prakash et al. (2006)	A	A	57	DWI	0.72	DC,+
Soltanian-Zadeh et al. (2007)	ASC	A	2	T1,T2,DWI,PD		+
Seghier et al. (2008)	SC	A	8	T1	0.64	DC
Forbes et al. (2010)	?	A	3	T2,FLAIR,DWI	0.63	DC
Saad et al. (2011)	AC	A	?	DWI		V
Mujumdar et al. (2012)	A	S	41	DWI,ADC	0.81	DC
Artzi et al. (2013)	AS	S	10	FLAIR,DWI		ASSD,HD,VE
Maier et al. (2014)	S	A	8	T1,T2,FLAIR,DWI,ADC	0.74	DC,ASSD,HD
Tsai et al. (2014)	AS	A	22	DWI,ADC	0.9	DC,PPV
Mah et al. (2014)	S	A	38	T2,DWI	0.73	DCm,+
Nabizadeh et al. (2014)	AS	S	6	DWI	0.80	DC,+
Ghosh et al. (2014)	S	A	2	ADC		VE
Maier et al. (2015c)	S	A	37	T1,T2,FLAIR,DWI,ADC	0.63	DC,ASSD,HD
Muda et al. (2015)	AC	A	20	DWI	0.73	DC
Derntl et al. (2015)	S	A	13	T1,T1c,T2,FLAIR	0.42	DC
Menze et al. (2015)	AS	A	18	T1,T1c,T2,FLAIR,DWI	0.78	DC
Maier et al. (2015b)	S	A	37	FLAIR	0.44-0.67	DC,ASSD,HD
Maier et al. (2015b)	S	A	37	T1,T2,FLAIR,DWI,ADC	0.54-0.73	DC,ASSD,HD

Abbreviations are: V=visual evaluation, VE=volume error, PPV=positive prediction value,

⁺=other metrics,

^m=median reported.

Note that the lesion phases were adapted to our definition if sufficient information was available.

While all approaches make an e ort to quantify segmentation accuracies, most lack detailed descriptions of the employed dataset, which is a critical matter as stroke lesion shape and appearance changes rapidly during the first hours and days, significantly altering the difficulty of the segmentation task. Information about the stroke evolution phase is sometimes omitted (Seghier et al., 2008; Forbes et al., 2010) or, if mentioned, not clearly defined (Saad et al., 2011; Muda et al., 2015). Where provided, the definition of acute stroke often mixes with the sub-acute phase (Ghosh et al., 2014; Mah et al., 2014; Tsai et al., 2014). Only a few studies give details on pathological inclusion and exclusion criteria of the data (James et al., 2006; Maier et al., 2015c), although these are important characteristics: Results obtained on right-hemispheric stroke only (Dastidar et al., 2000) are not comparable to ones omitting small lesions (Mah et al., 2014) nor to those obtained from two central axial slices of each volume (Li et al., 2004). Comparability is further impeded by a wide range of dataset sizes (N ∈ [2, 57]), employed MRI sequences and quantitative evaluation measures. All this renders the interpretation of the results difficult and explains the wide range of segmentation accuracies reported over the years. A very recent work (Maier et al., 2015b) compares a number of classification algorithms on a common dataset, but these do not fully represent the state-of-the-art nor are they implemented by their respective authors.

In the present benchmark study, we approach the urgent problem of comparability. To this end, we planned, organized, and pursued the Ischemic Stroke LEsion Segmentation (ISLES) challenge: A direct, fair, and independently controlled comparison of automatic methods on a carefully selected public dataset. ISLES 2015 was organized as a satellite event of the International Conference on Medical Image Computing and Computer Assisted Intervention (MICCAI) 2015, held in Munich, Germany. ISLES combined two sub-challenges dealing with different phases of the stroke lesion evolution: First, the Stroke Perfusion EStimation (SPES) challenge dealing with the image interpretation of the acute phase of stroke; second, the Sub-acute Ischemic Stroke lesion Segmentation (SISS) challenge dealing with the later stroke image patterns. In both tasks we aim at answering a number of open questions: What is the current state-of-the-art performance of automatic methods for ischemic stroke lesion segmentation? Which type or class of algorithms is most suited for the task? Which difficulties are overcome and which challenges remain? And what are the recommendations we can give to researchers in the field after the extensive evaluation conducted?

2. Setup of ISLES

Image segmentation challenges aim at an independent and fair comparison of various segmentation methods for a given segmentation task. In these de-facto benchmarks participants are first provided with representative training data with associated ground truth, on which they can adjust their algorithms. Later, a testing dataset without ground truth is distributed and the participants submit their results to the organizers, who score and rank the submissions.

Previous challenges in the medical image processing communities dealt with the segmentation of tumors (Menze et al., 2015) or multiple sclerosis lesions (Styner et al., 2008) in MRI brain data; complete lungs (Murphy, 2011) or their vessels (Rudyanto et al., 2014) in computed tomography scans; 4D ventricle extraction (Petitjean et al., 2015) as well as myocardial tracking and deformation (Tobon-Gomez et al., 2013); prostate segmentation from MRI (Litjens et al., 2014); and brain extraction in adults (Shattuck et al., 2009) and neonatals (Išgum et al., 2015).

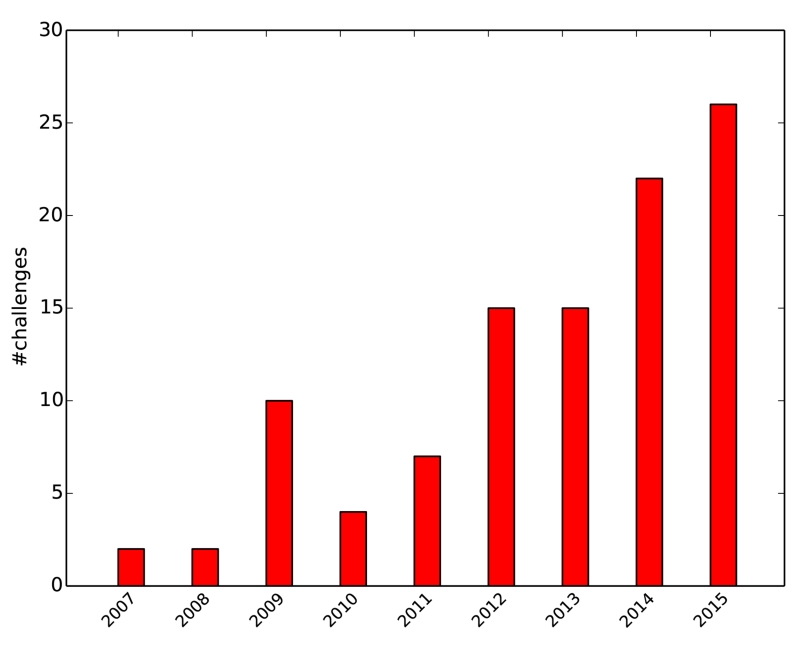
The number of challenges has been steadily increasing over the past years (Fig. 2) as visible from the events listed on http://grand-challenge.org. Many of these have become the de-facto evaluation standard for new algorithms, in particular when adhering to some standards listed on the same web resource: Both training and testing dataset are representative for the task, well described, and large enough to draw significant conclusions from the results; the associated ground truth is created by experts following a clearly defined set of rules; the evaluation metrics chosen capture all aspects relevant for the task; and, ideally, challenges remain open for future contestants and serve as an ongoing benchmark for algorithms in the field.

Figure 2.

Increasing count of challenges over the years as collected on http://grand-challenge.org on 2016-05-17.

With ISLES 2015, we introduce for the first time a benchmark for the growing but inaccessible collection of stroke lesion segmentation algorithms. The challenge was launched in February 2015 and potential participants were contacted directly following an extensive literature review on stroke segmentation or via suitable mailing lists. The training datasets for SISS and SPES were released in April 2015 using the the SICAS Medical Image Repository (SMIR) platform² (Kistler et al., 2013). The participants were able to download the testing datasets from September 14, 2015, and had to submit their results within a week. The ground truth for this second set is kept private with the organizers. Repeated submissions were allowed, but only the last one counted. The organizers evaluated the submitted results and presented them during a final workshop at the international MICCAI conference 2015 in Munich, Germany. All conclusions presented in this paper are drawn from these testing results.

We refrained from an on-site evaluation as previous attempts (Murphy et al., 2011; Menze et al., 2015; Petitjean et al., 2015) have shown that such endeavors may be prone to complications unrelated to the actual algorithms’ performances. Instead, the results obtained on the evaluation set were hidden from the participants to avoid tuning on the testing dataset.

The ISLES benchmark is open post-challenge for researchers to continue evaluating segmentation performance through the SMIR evaluation platform. The results and rankings of the initial participants remain as a frozen table on the challenge web page³ while the SMIR platform supplies an automatically generated listing of these and all future results.

Interested research teams could register for one or both sub-challenges. All submitted algorithms were required to be fully automatic; no other restrictions were imposed. Until the day of the challenge, the SMIR platform listed over 120 registered users for the ISLES 2015 challenge and a similar count of training dataset downloads. Of these, 14 teams provided testing dataset results for SISS and 7 algorithms participated in SPES. Their affiliations and methods can be found in Table 2. For a detailed description of the algorithms please refer to Appendix A.

Table 2.

List of all participants in the ISLES challenge. All teams are color coded for easier reference in all further listings. The ML column denotes whether the submitted algorithm is based on machine learning. Refer to the SISS and SPES columns for the sub-challenges each team participated in. Additionally, a very short summary of each method is provided. For a detailed description of each algorithm and used abbreviations see Appendix A.

Team	FN	SN	ML	SISS	SPES
UK-Imp1	Liang	Chen	Y	Y
	Regional RFs (dorsal, medial, ventral)
DE-Dkfz	Michael	Goetz	Y	Y
	Image selector RF + online lesion ET
FI-Hus	Hanna	Halme	Y	Y
	RF (deviation from global average) + Contextual Clustering (CC)
CA-McGill	Andrew	Jesson	Y	Y
	Local classifiers (554 GMM) + regional RF
UK-Imp2	Konstantinos	Kamnitsas	Y	Y
	2-path 3D CNN + CRF
US-Jhu	John	Muschelli	Y	Y
	RF (e.g. SD, skew, kurtosis)
SE-Cth	Qaiser	Mahmood	Y	Y
	RF (e.g. gradient, entropy)
US-Odu	Syed	Reza	Y	Y
	RF (many features, e.g., texture)
TW-Ntust	Ching-Wei	Wang	Y	Y
	RF (many features, e.g., edge)
CN-Neu	Chaolu	Feng	N	Y	Y
	Bias-correcting Fuzzy C-Means + Level Set
BE-Kul1	Tom	Haeck	N	Y	Y
	Tissue priors + EM-opt MRF + Level Set on sequence subset
CA-USher	Francis	Dutil	Y	Y	Y
	2-path 2D CNN
DE-UzL	Oskar	Maier	Y	Y	Y
	RF (anatomically and appearance motivated features)
BE-Kul2	David	Robben	Y	Y	Y
	Cascaded ETs
DE-Ukf	Elias	Kellner	N		Y
	Rule-based hemisphere-comparing approach
CH-Insel	Richard	McKinley	Y		Y
	RF (case bootstrapped forest of forests)

3. Data and methods

3.1. SISS image data and ground truth

We gathered 64 sub-acute ischemic stroke cases for the training and testing sets of the SISS challenge. A total of 56 cases were supplied by the University Medical Center Schleswig-Holstein in Lübeck, Germany. They were acquired in diagnostic routine with varying resolutions, views, and imaging artifact load. Another eight cases were scanned at the Department of Neuroradiology at the Klinikum rechts der Isar in Munich, Germany. Both centers are equipped with 3T Phillips systems. The local ethics committee approved their release under Az.14-256A. Full data anonymization was ensured by removing all patient information from the files and the facial bone structure from the images.

Considered for inclusion were all cases with a diagnosis of ischemic stroke for which at least the set of T1-weighted (T1), T2-weighted (T2), DWI (b = 1000) and FLAIR MRI sequences had been acquired. Additional pathological deformation, such as, e.g., non-stroke WMHs, haemorrhages, or previous strokes, did not lead to the exclusion of a case. Scans performed outside the sub-acute stroke development phase were rejected. As the exact time passed since stroke onset is not known in most cases, lesions were visually classified as sub-acute infarct if a pathologic signal was found concomitantly in FLAIR and DWI images (presence of vasogenic and cytotoxic edema with evidence of swelling due to increased water content).

In order to focus the analysis on the participating algorithms rather than assessing the preprocessing techniques employed by each team, all cases were consistently preprocessed by the organizers: The MRI sequences are skull-stripped using BET2 (Jenkinson et al., 2005) with a manual correction step where required, b-spline-resampled to an isotropic spacing of 1 mm³, and rigidly co-registered to the FLAIR sequences with the elastix toolbox (Klein et al., 2010).

Acquired in a routine diagnostic setting and representing the clinical reality, these data sets are a afflicted by secondary pathologies, such as stroke similar deformations and chronic stroke lesions, as well as imaging artifacts, varying acquisition orientations, differing resolutions, or movement artifacts.

In addition to the wide range of acquisition and clinically related variety, the sub-acute lesions themselves display a wide range of variability (Table 3). Great care has been taken to preserve the diversity of the stroke cases when splitting the data into testing and training datasets: both contain single- and multi-focal cases, small and large lesions, and were divided by further criteria (Table 3). The main difference between the sets is the addition of the eight cases from Munich to the testing dataset only; hence, this second center data was not available during the training phase (Table 4).

Table 3.

Stroke lesion characteristics of the 64 SISS cases. The strong diversity is representative for stroke lesions and emphasizes the difficulty of the task. μ denotes the mean value, [min, max] the interval and n the total count. Abbreviations are: anterior cerebral artery (ACA), middle cerebral artery (MCA), posterior cerebral artery (PCA) and basilar artery (BA).

Lesion count	μ = 2.46 [1, 14]
Lesion volume	μ = 17.59 ml [1.00, 346.06]
Haemorrhage present	n1 = 12 0=no, 1=yes
Non-stroke WMH load	μ = 1.34 0=none, 1=small, 2=medium, 3=large
Lesion localization (lobes)	n1 = 11 , n2 = 24, n3 = 42, n4 = 17, n5 = 2, n6 = 6 1=frontal, 2=temporal, 3=parietal, 4=occipital, 5=midbrain, 6=cerebellum
Lesion localization	n1 = 36, n2 = 49 1 =cortical, 2=subcortical
Affected artery	n1 = 6, n2 = 45, n3 = 11 , n4 = 5, n5 = 0 1 =ACA, 2=MCA, 3=PCA, 4=BA, 5=other
Midline shift	n0 = 51, n1 = 5, n2 = 0 0=none, 1=slight, 2=strong
Ventricular enhancement	n0 = 38, n1 = 15, n2 = 3 0=none, 1=slight, 2=strong
Laterality	n1 = 18, n2 = 35, n3 = 3 1=left, 2=right, 3=both

Table 4.

Details of the SISS data.

number of cases	28 training and 36 testing
number of medical centres	1 (train), 2 (test)
number of expert segmentations for each case	1 (train), 2 (test)
MRI sequences	FLAIR, T2 TSE, T1 TFE/TSE, DWI

All expert segmentations used in ISLES were prepared by experienced raters. For SISS, two ground truth sets (GT01 and GT02) were created and the segmentations were performed on the FLAIR sequence, which is known to exhibit lower inter-rater differences as, e.g., T2 (Neumann et al., 2009). The guidelines for expert raters were as follows:

1. The segmentation is performed on the FLAIR sequence

2. Other sequences provide additional information

3. Only sub-acute ischemic stroke lesions are segmented

4. Partially surrounded sulci/fissures are not included

5. Very thin/small or largely surrounded sulci/fissures are included

6. Surrounded haemorrhagic transformations are included

7. The segmentation contains no holes

8. The segmentation is exact but spatially consistent (no sudden spikes or notches)

Acute infarct lesions (DWI signal for cytotoxic edema only, no FLAIR signal for vasogenic edema) or residual infarct lesions with gliosis and scarring after infarction (no DWI signal for cytotoxic edema, no evidence of swelling) were not included. For the training, only GT01 was made available to the participants, while the testing data evaluation took place over both sets.

3.2. SPES image data and ground truth

All patients included in the SPES dataset were treated for acute ischemic stroke at the University Hospital of Bern between 2005 and 2013. Patients included in the dataset received the diagnosis of ischemic stroke by MRI with an identifiable lesion on DWI as well as on perfusion weighted imaging (PWI), with a proximal occlusion of the middle cerebral artery (MCA) (M1 or M2 segment) documented on digital subtraction angiography. An attempt at endovascular therapy was undertaken, either by intra-arterial thrombolysis (before 2010) or by mechanical thrombectomy (since 2010). The patients had a minimum age of 18 and the images were not subject to motion artifacts.

The stroke MRI was performed on either a 1.5T (Siemens Magnetom Avanto) or 3T MRI system (Siemens Magnetom Trio). The stroke protocol encompassed whole brain DWI (24 slices, thickness 5 mm, repetition time 3200 ms, echo time 87 ms, number of averages 2, matrix 256 × 256) yielding isotropic b1000 images. For PWI the standard dynamic-susceptibility contrast enhanced perfusion MRI (gradient-echo echo-planar imaging sequence, repetition time 1410 ms, echo time 30 ms, field of view 230 × 230 mm, voxel size: 1.8 × 1.8 × 5.0 mm, slice thickness 5 mm, 19 slices, 80 acquisitions) was acquired. PWI scans were recorded during the first pass of a standard bolus of 0.1 mmol/kg gadobutrol (Gadovist, Bayer Healthcare). Contrast medium was injected at a rate of 5 ml/s followed by a 20 ml bolus of saline at a rate of 5 ml/s. Perfusion maps were obtained by block-circular singular value decomposition using the Perfusion Mismatch Analyzer (PMA, from Acute Stroke Imaging Standardization Group ASIST) Ver.3.4.0.6. The arterial input function is automatically determined by PMA based on histograms of peak concentration, time-to-peak and mean transit time.

Sequences and derived maps made available to the participants are T1 contrast enhanced (T1c), T2, DWI, cerebral blood flow (CBF), cerebral blood volume (CBV), time-to-peak (TTP), and time-to-max (Tmax) (Table 5).

Table 5.

Details of the SPES data.

number of cases	30 training and 20 testing
number of medical centres	1
number of expert segmentations for each case	1
MRI sequences	T1c, T2, DWI, CBF, CBV, TTP, Tmax

For preprocessing, all images were rigidly registered to the T1c with constant resolution of 2 × 2 × 2 mm and automatically skull-stripped (Bauer et al., 2013). This resolution was chosen in regard to the low 1.8.8 × 5.0 mm resolution of the PWI images. Together with the removal of all patient data from the files, full anonymization was achieved.

To determine the eligibility of a patient for treatment or to assess a treatment response in clinical trials, the pretreatment estimation of the potentially salvageable penumbral area is crucial. A 6 second threshold applied to the Tmax map has been suggested (Straka et al., 2010) and successfully applied in large multi-center trials (Lansberg et al., 2012) to determine the area of hypoperfusion (i.e. penumbra + core). But this approach requires the manual setting of a region of interest as well as considerable manual postprocessing. For SPES, we are interested in whether advanced segmentation algorithms could replace manual correction of thresholded perfusion maps, yielding faster and reproducible estimation of tissue at risk volume.

The hypoperfused tissue was segmented semi-manually with Slicer 3D Version 4.3.1 by a medical doctor with a preadjusted threshold for Tmax of 6 seconds applied to regions of interest as described in Straka et al. (2010) and Lansberg et al. (2012), followed by a manual correction step consisting in removing sulci, non-stroke pathologies and previous infarcts by taking into account the other perfusion maps and anatomical images. The label represents the stroke-affected regions with restricted perfusion, which is the first requirement to determine the penumbral area via a perfusion-diffusion mismatch approach.

The collected data therefore includes a variety of acute MCA cases (Table 6) that were split into training and testing cases by an experienced neuroradiologist using as criteria the complexity in visually defining the extent of the penumbral area.

Table 6.

Stroke lesion characteristics of the 50 SPES cases. The cases are restricted to MCA stroke eligible for cerebrovascular treatment. μ denotes the mean value, [min, max] the interval and n the total count.

Lesion count	μ = 1 Not always connected, but single occlusion as source.
Lesion volume	μ = 133.21 ml [45.62, 252.20]
Affected artery	all MCA
Laterality	n1 = 22, n2 = 28, n3 = 0 1=left, 2=right, 3=both

The training dataset is additionally equipped with a manually created DWI segmentation ground truth set, which roughly denotes the stroke’s core area. These are not considered in the challenge.

3.3. Evaluation metrics

As measures we employ (1) Dice’s coefficient (DC), which describes the volume overlap between two segmentations and is sensitive to the lesion size; (2) the average symmetric surface distance (ASSD), which denotes the average surface distance between two segmentations; and (3) the Hausdor distance (HD), which is a measure of the maximum surface distance and hence especially sensitive to outliers.

The DC is defined as

$$\mathit{DC}=\frac{2\mid A\cap B\mid }{\mid A\mid +\mid B\mid }$$ (1)

with A and B denoting the set of all voxels of ground truth and segmentation respectively. To compute the ASSD we first define the average surface distance (ASD), a directed measure, as

$$\mathrm{AS}D(A_S,B_S)=\frac{{\Sigma }_{a\in A_S}{\mathit{min}}_{b\in B_S}d(a,b)}{\mid A_S\mid }$$ (2)

and then average over both directions to obtain the ASSD

$$ASSD(A_S,B_S)=\frac{ASD(A_S,B_S)+ASD(B_S,A_S)}{2}$$ (3)

Here A_S and B_S denote the surface voxels of ground truth and segmentation respectively. Similar, the HD is defined as the maximum of all surface distances with

$$HD(A_S,B_S)=\max \left\{\underset{a\in A_S}{\max }\underset{b\in B_S}{\min }d(a,b),\underset{b\in B_S}{\max }\underset{a\in A_S}{\min }d(a,b)\right\}$$ (4)

The distance measure d(·) employed in both cases is the Euclidean distance, computed taking the voxel size into account.

3.4. Ranking

After selecting suitable evaluation metrics, we face the problem of establishing a meaningful ranking for the competing algorithms as the different measures are neither in the same range nor direction.

In the simplest case, metrics are evaluated individually and different rankings are offered (Menze et al., 2015). But this would mean neglecting the aspects revealed by the remaining measures and is hence a bad choice for most challenges.

A second approach taken by some challenges (Styner et al., 2008) is to compare two expert segmentations against each other. The resulting evaluation values are then assumed to indicate the upper limit and hence denote the 100 percent mark of each measure. New segmentations are then evaluated and the values compared to their respective 100 percent marks, resulting in a percentage rating for each measure. Drawback is that for measure with an infinite range, such as the ASSD, one has to define an arbitrary zero percent mark.

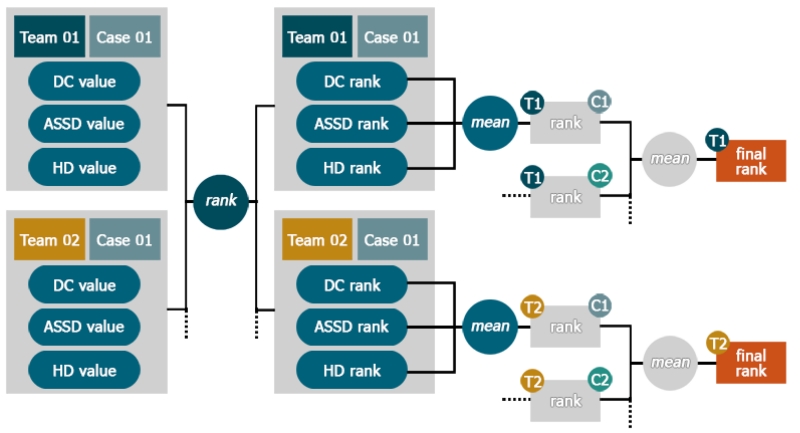
We chose a third approach based on the ideas of Murphy et al. (2011) that builds on the concept that a ranking reveals only the direction of a relationship between two items (i.e. higher, lower, equal) but not its magnitude. Basically, each participant’s results are ranked per case according to each of the three metrics and then the obtained ranks are averaged. For a more detailed account see Appendix B.

3.5. Label fusion

The specific design of each automatic segmentation algorithm will result in certain strengths and weaknesses for particular challenges in the present image data. Multiple strategies have been proposed in the past to automatically determine the quality of several raters or segmentation algorithms (Xu et al., 1992; Warfield et al., 2004; Langerak et al., 2010). These algorithms enable a suitable selection and/or fusion to best combine complementary segmentation approaches. To study and compensate the potential varying segmentation accuracy of all methods for individual cases, we apply the following three popular label fusion algorithms to their test results (see Tab 7, bottom): First, majority vote (Xu et al., 1992), which simply counts the number of foreground votes over all classification results for each voxel separately and assigns a foreground label if this number is greater than half the number of algorithms. Second, the STAPLE algorithm (Warfield et al., 2004), which performs a simultaneous truth and performance level estimation, that calculates a global weight for each rater and attempts to remove the negative influence of poor algorithms during majority voting. Third, the SIMPLE algorithm (Langerak et al., 2010), which employs a selective and iterative method for performance level estimation by successively removing the algorithms with poorest accuracy as judged by their respective Dice score against a weighted majority vote, where the weights are determined by the previously estimated performances.

4. Results: SISS

4.1. Inter-observer variance

Comparing the two ground truths of SISS against each other provides (1) the baseline above which an automatic method can be considered to produce results superior to a human rater and (2) a measure of the task’s difficulty (Table 7, last row). The two expert segmentations overlap at least partially for all cases. Compared to similar tasks, such as, e.g., brain tumor segmentation, for which inter-observer DC values of 0.74 ± 0.13 to 0.85 ± 0.08 are reported (Menze et al., 2015), the ischemic stroke lesion segmentations problem can be considered difficult with a mean DC score of 0.70 ± 0.20.

Table 7.

SISS challenge leaderboard after evaluating the 14 participating methods on the testing dataset. The rank is the final measure for ordering the algorithms’ performances relative to each other. The cases column denotes the number of successfully (i.e., all DC> 0) segmented cases. All evaluation measures are given in mean±STD. Please note that the ASSD and HD values were computed excluding the failed cases (they do, however, incur the lowest vacant rank for these cases). The three next-to-last rows display the results obtained with different fusion approaches. The last row shows the inter-observer results for comparison.

Rank	Method	Cases	ASSD (mm)	DC [0,1]	HD (mm)
3.25	UK-Imp2	34/36	05.96 ± 09.38	0.59 ± 0.31	37.88 ± 30.06
3.82	CN-Neu	32/36	03.27 ± 03.62	0.55 ± 0.30	19.78 ± 15.65
5.63	FI-Hus	31/36	08.05 ± 09.57	0.47 ± 0.32	40.23 ± 33.17
6.40	US-Odu	33/36	06.24 ± 05.21	0.43 ± 0.27	41.76 ± 25.11
6.67	BE-Kul2	33/36	11.27 ± 10.17	0.43 ± 0.30	60.79 ± 31.14
6.70	DE-UzL	31/36	10.21 ± 09.44	0.42 ± 0.33	49.17 ± 29.6
7.07	US-Jhu	33/36	11.54 ± 11.14	0.42 ± 0.32	62.43 ± 28.64
7.54	UK-Imp 1	34/36	11.71 ± 10.12	0.44 ± 0.30	70.61 ± 24.59
7.66	CA-USher	27/36	09.25 ± 09.79	0.35 ± 0.32	44.91 ± 32.53
7.92	BE-Kul1	30/36	12.24 ± 13.49	0.37 ± 0.33	58.65 ± 29.99
7.97	CA-McGill	31/36	11.04 ± 13.68	0.32 ± 0.26	40.42 ± 26.98
9.18	SE-Cth	30/36	10.00 ± 06.61	0.38 ± 0.28	72.16 ± 17.32
9.21	DE-Dkfz	35/36	14.20 ± 10.41	0.33 ± 0.28	77.95 ± 22.13
10.99	TW-Ntust	15/36	07.59 ± 06.24	0.16 ± 0.26	38.54 ± 20.36
	majority vote	34/36	11.47 ± 19.89	0.51 ± 0.30	38.11 ± 30.45
	STAPLE	36/36	12.90 ± 10.64	0.44 ± 0.32	71.08 ± 25.03
	SIMPLE	34/36	07.83 ± 14.97	0.57 ± 0.29	29.40 ± 28.11
	inter-observer	36/36	02.02 ± 02.17	0.70 ± 0.20	15.46 ± 13.56

4.2. Leaderboard

The main result of the SISS challenge is a leaderboard for state-of-the-art methods in sub-acute ischemic stroke lesion segmentation (Table 7). The evaluation measures and ranking system employed are described in the method part of this article (Sec. 3.4). No participating method succeeded in segmenting all 36 testing cases successfully (DC> 0) and the best scores are still substantially below the human rater performance. Note that for all following experiments, we will focus on DC averages only as the ASSD and HD values cannot be readily computed for the failed cases and are thus not suitable for a direct comparison of methods with differing numbers of failure cases.

4.3. Statistical analysis

We performed a statistical analysis of the results to rule out random influences on the leaderboard ranking. Each pair of methods is compared with the two-sided Wilcoxon signed-rank test (Wilcoxon, 1945), a nonparametric test of the null hypothesis that two samples come from the same population against an alternative hypothesis (Fig. 3).

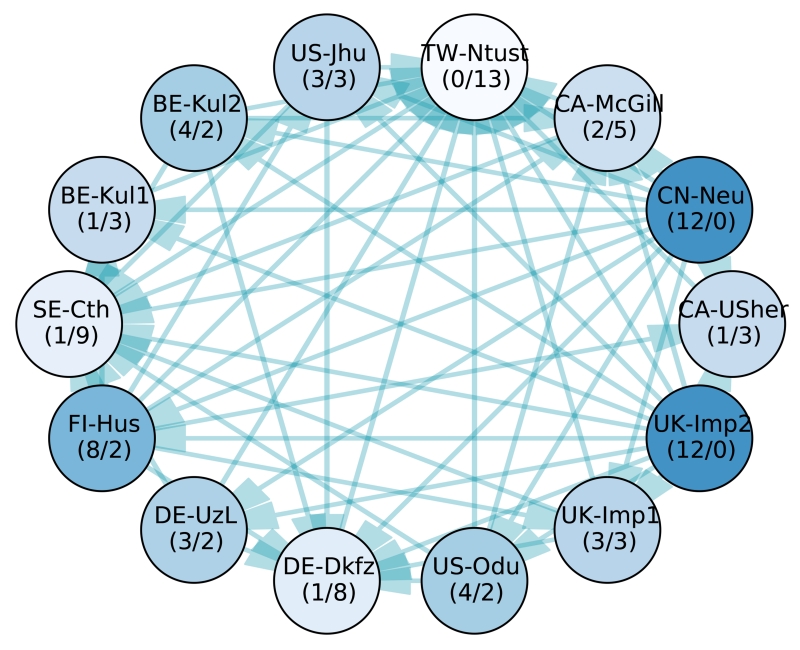
Figure 3.

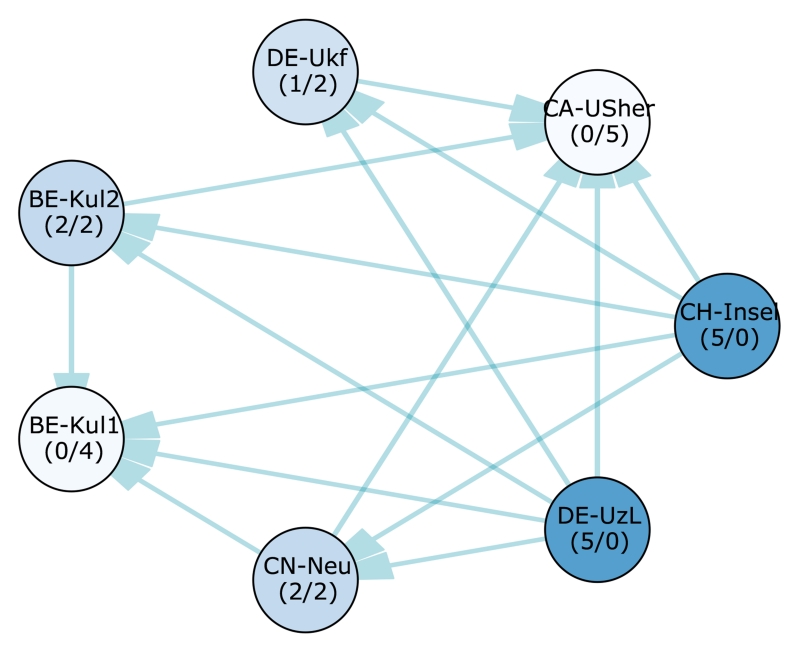
Significant differences between the 14 participating methods’ case ranks according to a two-sided Wilcoxon signed-rank test (p < 0.025). Each node represents a team, each edge a significant difference of the tail side team over the head side team. Therefore, the less outgoing and the more incoming edges a team has (denoted by numbers in brackets (#out/#in) for easier interpretation), the weaker its method compared to the others. The saturation of the node colors indicates the strength of a method, where better methods are highlighted with more saturated colors. Note that all teams with the same number of incoming and outgoing edges perform, statistically spoken, equally well. A higher importance of incoming over outgoing edges or vice-versa cannot be readily established.

The two highest ranking methods, UK-Imp2 and CN-Neu, show no statistically significant differences with a confidence of 95% (i.e. p < 0.025). No other algorithm performs better than them, and they both are better than the 12 remaining ones. Next comes a group of four methods (FI-Hus, BE-Kul2, US-Odu, De-UzL) to which only the two winners prove superior. But among these, FI-Hus takes the highest position as it is statistically better than eight other methods, while the other three only prove superior to at most four competitors. The established leaderboard ranking is largely confirmed by the statistical analysis.

4.4. Impact of multi-center data

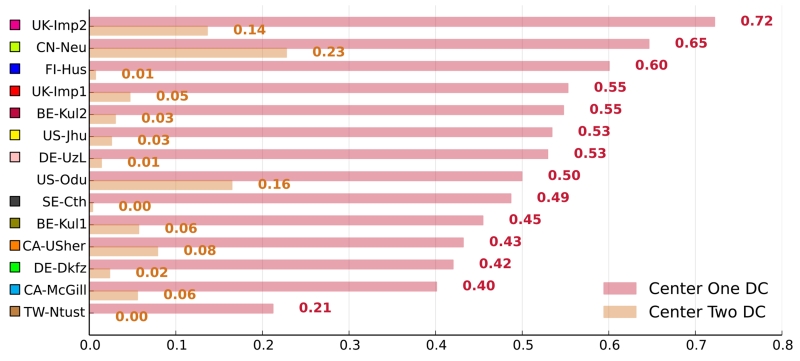
Cases acquired at different medical centers can differ greatly in appearance. A good automatic stroke lesion segmentation method should be able to cope with these variations. We broke down each method’s results by medical center (Fig. 4) to test whether this holds true for the participating algorithms.

Figure 4.

Adaptation to the data from the second medical center. The graph shows each method’s average DC scores on the 28 cases from the first and the eight cases from the second medical center. The methods are color coded.

Since the training dataset contained only cases from the first center, the difference in performance should reveal the methods’ generalization abilities. We observed that not a single algorithm reached second center scores comparable to its first center scores. This is a strong hint towards a difficult adaptation problem.

4.5. Combining the participants’ results by label fusion

Applying the three label fusion algorithms presented in Sec. 3.5 lead to the results presented in Table 7 at the bottom. We found that the SIMPLE algorithm performed best and could reduce outliers as evident by a lower Hausdor distance. When using majority voting or STAPLE, the negative influence of multiple failed segmentations that are correlated yielded a lower accuracy than at least the two top ranked algorithms.

4.6. Dependency on observer variations

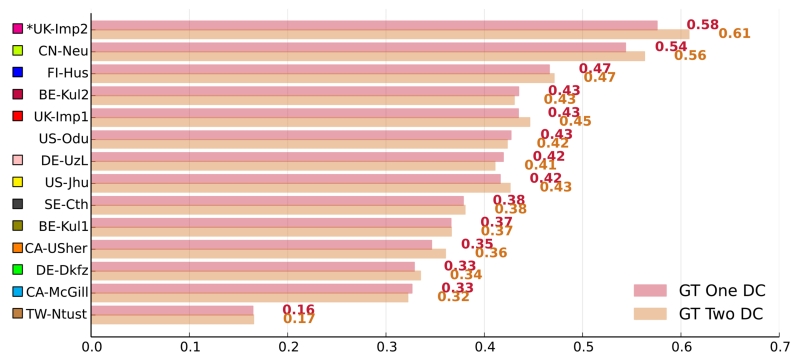
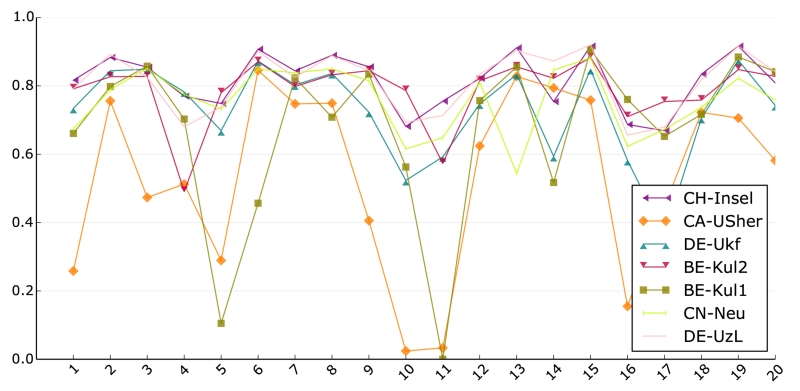
A good segmentation method does not only adapt well to second center data but equally to another observer’s ground truth. Only the GT01 ground truth set was made available to the participating teams during the training/tuning phase. Hence, particularly machine learning solutions could be expected to show deficits on the second rater ground truth GT02. To test how well the methods generalize, we compared their performance on the testing sets GT01 ground truth against their performance on the formerly unseen GT02 set (Fig. 5).

Figure 5.

Differences in performance on the two ground truth sets. The graph shows each methods average DC scores on the 36 testing dataset cases broken down by ground truth set. A star (*) before a team’s name denotes statistical significant difference according to a paired Student’s t-test with p < 0.05. The methods are color coded.

The average DC scores of each method differed only slightly over the ground truth sets. Only in a single case, UK-Imp2, the difference was significant (paired Student’s t-test with p < 0.05), but the higher results were obtained for the, formerly unseen, GT02 set. We can hence conclude that all algorithms generalized well with respect to expert segmentations of different raters. An additional data analysis showed that the ranking of the methods does not change if only one or the other of the ground truth sets is employed for evaluation.

4.7. Outlier cases

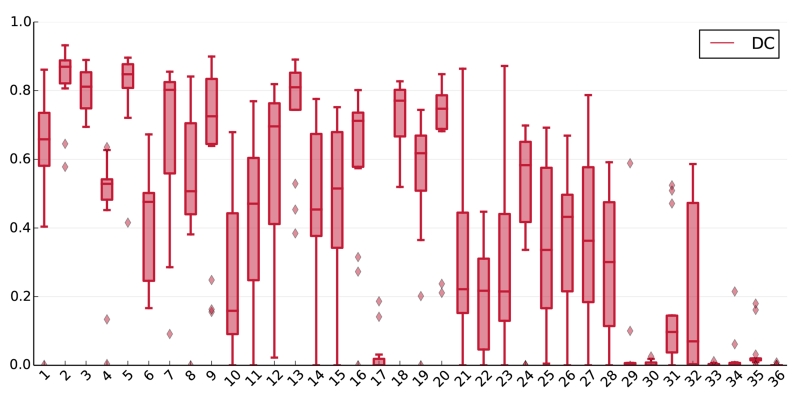
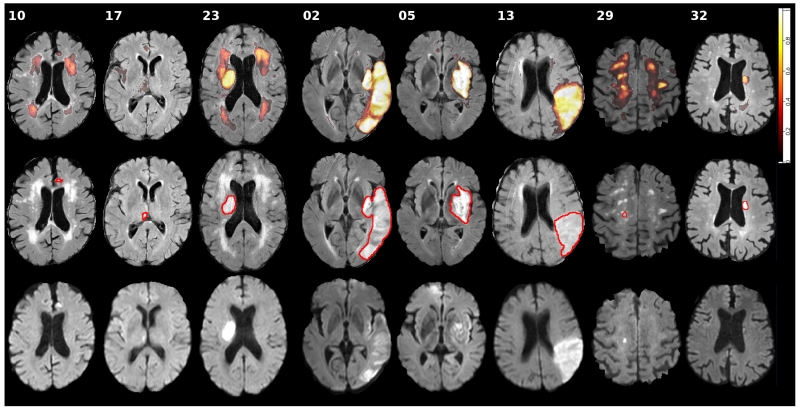
A benchmark is only as good as its data. The average scores obtained on the different cases of the testing dataset differed widely and some proved especially difficult or easy to segment (Fig. 6). For cases 29 to 36, this variation can be explained through the different acquisition parameters at the second medical center. But the weak performance of most methods on cases such as 10, 17 and 23 must have other reasons. We compared these visually to the overall most successful cases 2, 5 and 13 to detect possible commonalities (Fig. 7).

Figure 6.

Box plots of the 14 teams’ DC results on all testing dataset cases, i.e., the first box was computed from all teams’ results on the first case. The band in the box denotes the median, the upper and lower limits the first and third quartile. Outliers are plotted as diamonds.

Figure 7.

Visual results for selected difficult (10, 17, 23), easy (2, 5, 13), and second center (29, 32) cases from the SISS testing dataset. The first row shows the distribution of all 14 submitted results on a slice of the FLAIR volume. The second row shows the same image with the ground truth (GT01) outlined in red. And the third row shows the corresponding DWI sequence. Please refer to the online version for colors.

The three cases that were successfully processed by nearly all algorithms show large, clearly outlined lesions with a strongly hyperintense FLAIR signal. In two of these cases, the DWI signal is relatively weak, in some areas nearly isointense. Still, for these cases the algorithms displayed the highest confidence. One of the most difficult cases (17) contains only a single small lesion with marginal FLAIR and strong DWI hyperintensities. Another case (10), equally showing a small lesion, has a stronger FLAIR support, but also displays large periventricular WMHs that seem to confuse most algorithms despite missing DWI hyperintensities. This behavior was also visible for the third of the failed cases (17): Here, the actual lesion is correctly segmented by most methods as it is clearly outlined with strong FLAIR and DWI support. But many algorithms additionally delineated parts of the periventricular WMHs, which again only show up in the FLAIR sequence.

4.8. Correlation with lesion characteristics

The properties of the cases might have an influence on the segmentation quality as some are clearly easier to segment than others. To find such correlations, we related various lesion characteristics to the average DC scores obtained over all teams using suitable statistics (Table 8).

Table 8.

Correlation between the SISS case characteristics and the average DC values over all teams. A ρ denotes a Spearman correlation, a t a Student’s t-test. All p-values are two tailed (p₂). Significant results according to a 95% confidence interval are denoted by a *. Secondary tests appearing in the table were performed against the lesion volume rather than the average DC values.

Characteristic	Test	p 2
Lesion count	ρ = −0.21	0.23
Lesion volume	ρ = +0.76	0.00*
Haemorrhage present	t = +2.29	0.03*
vs. lesion volume	t = +4.33	0.00*
Non-stroke WMH load	ρ = −0.01	0.97
Midline shift	t = +0.51	0.62
Ventricular enhancement	t = +1.56	0.13
Laterality	t = +2.66	0.01*
vs. lesion volume	t = +2.12	0.03*
Movement artifacts	ρ = −0.30	0.08
Imaging artifacts	ρ = +0.24	0.15

Significant moderate correlation was found between the lesion volume and the average DC values. A statistically significant difference of means was found when comparing cases with haemorrhage present and cases without, as well as between left hemispheric and right hemispheric lesions. Since the characteristics cannot be assumed to be independent, we furthermore tested the last two groupings for significant differences in lesion volumes between the groups. This was found in both cases (see secondary test for each of these two characteristics). We could not reliably establish a significant influence on the results for any single parameter. Even the influence of lesion volume is not certain as we will detail in the discussion.

5. Results: SPES

5.1. Leaderboard

To establish an overall leaderboard for state-of-the-art methods in automatic acute ischemic stroke lesion segmentation, all submitted results were ranked relatively as described in Sec.3.4 (Table 9).

Table 9.

SPES challenge leaderboard after evaluating the 7 participating methods on the testing dataset. The rank is the final measure for ordering the algorithms’ performances relative to each other. The cases column denotes the number of successfully (i.e., all DC> 0) segmented cases. All evaluation measures are given in mean±STD. Since no method failed completely on a single case, the reported ASSD values are suitable for a direct comparison between methods. The three next-to-last rows display the results obtained with different fusion approaches. The last two rows denote thresholding methods employed in clinical studies.

rank	method	cases	ASSD (mm)	DC [0,1]
2.02	CH-Insel	20/20	1.65 ± 1.40	0.82 ± 0.08
2.20	DE-UzL	20/20	1.36 ± 0.74	0.81 ± 0.09
3.92	BE-Kul2	20/20	2.77 ± 3.27	0.78 ± 0.09
4.05	CN-Neu	20/20	2.29 ± 1.76	0.76 ± 0.09
4.60	DE-Ukf	20/20	2.44 ± 1.93	0.73 ± 0.13
5.15	BE-Kul1	20/20	4.00 ± 3.39	0.67 ± 0.24
6.05	CA-USher	20/20	5.53 ± 7.59	0.54 ± 0.26
	majority vote	20/20	1.75 ± 0.39	0.82 ± 0.08
	STAPLE	20/20	2.40 ± 1.22	0.82 ± 0.06
	SIMPLE	20/20	1.69 ± 0.50	0.83 ± 0.07
Tmax> 6s (Christensen et al., 2010)		20/20	13.02 ± 4.15	0.27 ± 0.10
Tmax> 6s & size> 3 ml (Straka et al., 2010)		20/20	7.04 ± 4.99	0.32 ± 0.13

We opted not to calculate the HD for SPES as it does not reflect the clinical interest of providing volumetric information of the penumbra region. In addition, since some lesions in SPES contained holes, the HD was not a useful metric for gauging segmentation quality. This ranking is the outcome of the challenge event and was used to determine the competition winners. No completely failed segmentation (DC< 0) was submitted for any of the algorithms and the evaluation results of the highest ranking teams denote a high segmentation accuracy.

5.2. Statistical analysis

A strict ranking is suited to determine the winners of a competition, but average performance scores are ignoring the spread of the results. To this end, we pursued a statistical analysis that takes into account the dispersion in the distribution of case-wise results, and we compare each pair of methods with the two-sided Wilcoxon signed-rank test (Fig. 8).

Figure 8.

Visualization of significant differences between the 7 participating methods’ case ranks. Each node represents a team, each edge a significant difference of the tail side team over the head side team according to a two-sided Wilcoxon signed-rank test (p < 0.025). Therefore, the less outgoing and the more incoming edges a team has (denoted by numbers in brackets (#out/#in) for easier interpretation), the weaker its method compared to the others. The saturation of the node colors roughly denotes the strength of a method, where better methods are depicted with stronger colors. Note that all teams with the same number of incoming and outgoing edges perform, statistically spoken, equally well.

In this test, we do not observe significant differences between the two first ranked methods nor between the third and fourth place. Hence, SPES has two first ranked, two second ranked, and one third ranked method according to the statistical analysis.

5.3. Results per case and method

A similarity in performance based on statistical tests and average scores between the first two and second two methods was already established. To test whether these pairs behave similarly for all of the testing dataset cases, we plotted the DC scores of each team against the cases (Fig. 9).

Figure 9.

DC score result of all 7 SPES teams for each of the testing dataset cases. Most methods show a similar pattern. Please refer to the online version for color.

The performance lines of the highest ranked methods, CH-Insel and DE-UzL, display a very similar pattern and, except for some small variation, reach mostly very similar DC values. It seems like both methods are doing roughly the same. This observation does not hold true for the two runner-ups, BE-Kul2 and CN-Neu. Both methods display outliers towards the lower end and their performances for the testing dataset cases are not as near to each other as observed for the first two methods, i.e., while similar in average performance, the methods seem to represent different segmentation functions. The lowest ranked methods mainly differ from the others in the sense that they fail to cope with the more difficult cases.

Overall, most algorithms exhibit the same tendencies, i.e., imaging and/or pathological differences between the cases seem to influence all methods in a similar fashion. In other words, the methods agree largely on what could be considered difficult and easy cases.

The outcome of combining all participants’ results by means of label fusion (c.f. Sec.3.5) yielded the highest Dice scores when using the SIMPLE algorithm, but (for the SPES data) applying STAPLE and majority vote produce a similar outcome (see Table 9, bottom)

5.4. Outlier cases

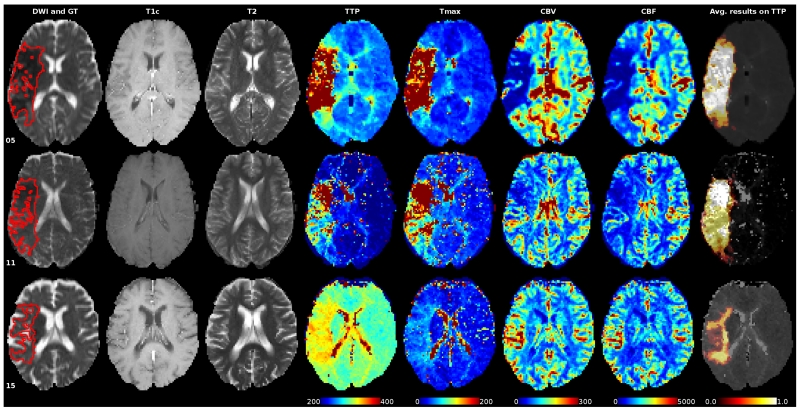
We took a close look at two cases with overall low average DC scores, cases 05 and 11, to establish a rationale behind the lower performance of the algorithms (Fig. 10). For case 05, we can be observed two previous embolisms that cause a compensatory perfusion change, depicted as two hyperintensity regions within the lesion area in the diffusion image and as hypoperfused areas in the Tmax map. The difficulties associated to the segmentation of case 11 are related to an acute infarct presenting a mismatch with a intensity pattern similar on the Tmax and in the borderline intensity range of 6 seconds. In summary, the main difficulties faced by the algorithms are related to physiological aspects, such as collateral flow, previous infarcts, etc.

Figure 10.

Sequences of some cases with a low (05 and 11) and high (15) average DC score over all 7 teams participating in SPES. The ground truth is painted red into the DWI sequence slices in the first column. The last column shows the distribution of the resulting segmentations on the gray-scale version of the TTP. All perfusion maps are windowed equally for direct comparison. Please refer to the online version for colors.

6. Discussion: SISS

With the SISS challenge, we provided a public dataset with a fair and independent automatic evaluation system to serve as a general benchmark for automatic sub-acute ischemic stroke lesion segmentation methods. As main result of the challenge event, we are able to assess the current state of the art performance in automatic sub-acute ischemic stroke lesion segmentation and to give well-founded recommendations for future developments. In this section, we review the results of the experiments conducted, discuss their potential implications, and try to answer the questions posed in the introduction.

Foremost, we aimed to establish if the task can be considered solved: The answer is a clear no. Even the best methods are still far from human rater performance as set by the inter-rater results. And while the observers agreed at least partially in all cases, no automatic method segmented all cases successfully. Many issues remain and a target-oriented community effort is required to improve the situation.

The best accuracy reached is an average DC of 0.6 with an ASSD of 4 mm. The high average HD of at least 20 mm reveals many outliers and/or missed lesions. An STD of 0.3 DC denotes high variations; indeed, we observe many completely or largely failed cases for each method.

Previously published DC results on sub-acute data (Table 1) are all slightly to considerably better. This underlines the need for a public dataset for stroke segmentation evaluation that encompasses the entire complexity of the task as private datasets are often too selective and the reported results differ greatly without providing the information required to identify the causes behind these variations.

The low scores obtained by all participating algorithms show that sub-acute ischemic stroke lesion segmentation is a very difficult task. This is furthermore supported by the high inter-rater variations obtained, an observation that has been made before: Neumann et al. (2009) report median inter-rater agreement of DC = 0.78 and HD = 23.4 mm over 14 subjects and 9 raters and Fiez et al. (2000) volume differences of 18 ± 16%.

6.1. The most suitable algorithm and the remaining challenges

The benchmark results were reviewed to identify the type of algorithm most suitable for sub-acute ischemic stroke lesion segmentation, but no definite winner could be determined. While there are clear methodological differences between the submitted methods, the same methodological approach (used in different algorithms) may lead to substantially different performance. We were not even able to determine clear performance differences between types of approaches: The two statistically equally well performing winners include one machine learning algorithm based on deep learning (UK-Imp2 with a convolutional neural network (CNN)) and one non-machine learning approach (CN-Neu with fuzzy C-means). We have to conclude that many of the participating algorithms are equally suited and that the devil is in the detail. This finding is supported by the wide spread of performances for random forest (RF) methods, including the third and the next to last position in the ranking. Adaptation to the task and tuning of the hyperparameters is the key to good results. An observation made is that the three winners all use a combination of two algorithms, possibly compensating the weak points of one with the other.

All participating methods showed good generalization abilities regarding the second rater. Since the inter-rater variability is high, we can assume that even the machine learning algorithms did not suffer from overfitting or, in other words, managed to avoid the inter-rater idiosyncrasies. Another explanation could be that the differences between the two raters fall into regions where little image information supports the presence of lesions.

Quite contrary, not a single algorithm adapted well to the second medical center data. differences in MRI acquisition parameters and machine dependent intensity variations are known to pose a challenge for all automatic image processing methods (Han et al., 2006). Seemingly, the center-dependent differences are difficult to learn or model. Regrettably, we did not have enough second center data in the testing dataset to draw a conclusive picture as the observed high variations might equally be caused by the considerably smaller lesion sizes in the second center dataset or other factors not attributable to multi-center variations (Jovicich et al., 2009). Special attention should be paid to this point when developing applications.

Cases for which all methods obtained good results show mostly large and well delineated lesions with a strong FLAIR signal while small lesions with only a slightly hyperintense FLAIR support posed difficulties. Surprisingly, quite a number of algorithms have trouble differentiating between sub-acute stroke lesions and periventricular WMHs despite the fact that the latter shows an isointense DWI signal. This might be attributable to the strongly hyperintense DWI artifacts and often inhomogeneous lesion appearance, reducing the methods’ confidence in the DWI signal. It is hard to judge whether these findings hold true for other state-of-the-art methods because most publications provide only limited information and discussions on the particularities of their performance or failure scenarios.

None of our collected lesion characteristics was found to exhibit a significant influence on the results (Table 8): The lesion volume correlates significantly with the scores, but the DC is known to reach higher values for larger volumes. The apparent performance differences in the presence of haemorrhages and the dependency on laterality could both be explained by differences in the respective group’s lesion sizes. To investigate combinations of characteristics with, e.g., multifactorial ANOVAs, a larger number of cases would be required.

The conclusions drawn here are meant to be general and valid for most of the participating methods. A method-wise discussion is out of the scope of this article. Any interested reader is invited to download the participants’ training dataset results and perform her/his own analysis to test whether these findings hold true for a particular algorithm.

6.2. Recommendations and limitations

When developing new methods, no particular algorithm should be excluded a-priori. Instead, the characteristics of stroke lesion appearances, their evolution, and the observed challenges should be studied in detail. Based on this information, new solutions targeting the specific problems can be developed. A specific algorithm can then be selected depending on how well the envisioned solutions can be integrated. Where possible, the strength of different approaches should be combined to counterbalance their weaknesses.

Evaluation should never be solely conducted on a private dataset as the variation between the cases is too large for a small set to compensate for all of them and, hence, renders any fair comparison impossible. We believe that with SISS we supplied a testing dataset which suitably reflects the high variation in stroke lesions characteristics and encompassed the complexity of the segmentation task.

Special attention should be put on the adaptation to second center data, which proved to be especially difficult. One could either concentrate on single-center solutions, try to develop a method that can encompass the large inter-center variations, or aim for an approach that can be specifically adapted. The whole subject requires further investigation and should not be handled lightly.

Considering that multiple complete failures were exhibited, it would be interesting to develop solutions that allow automatic segmentation algorithms to signal a warning when they assume to have failed on a segmentation. This problem is related to multi-classifier competence, which few publications have dealt with to date (Woloszynski and Kurzynski, 2011; Galar et al., 2013).

Label fusion (see Sec. 3.5) and automatic quality rating may be a potential avenue to compensate for different shortcomings of multiple algorithms that have been applied to the same data. We found that up to some degree the SIMPLE algorithm (Langerak et al., 2010) was able to improve over the average participants’ results by automatically assigning a higher weight to the respective algorithm that performed best for a given image. The weights obtained with the SIMPLE algorithm for each method may be used as an a priori selection of effective algorithms in the absence of manual segmentations. There is, however, a risk of a negative influence of multiple failed segmentations that are correlated as evident by the generally lower accuracy of the STAPLE fusion (tables 7 and 9).

Physicians and clinical researchers should not expect a fully automatic, reliable, and precise solution in the near future; the task is simply too complex and variable for current algorithms to solve. Instead, the findings of this investigation can help them to identify suitable solutions that can serve as support tools: In particular clearly outlined, large lesions are already segmented with good results, which are usually tedious to outline by hand. For smaller and less pronounced lesions the manual approach is still recommended. Furthermore, they should be aware that individual adaptations to each data source are most likely required - either by tuning the hyperparameters or through machine learning.

7. Discussion: SPES

All the best ranking methods show high average DC, low ASSD and only minimal STD, denoting accurate and robust results. A linear regression analysis furthermore revealed a good volume fit for the best methods (CH-Insel: r = 0.87 and DE-UzL: r = 0.93). We can say that reliable and robust perfusion lesion estimation from acute stroke MRI is in reach. For a final answer, a thorough investigation of the inter- and intra-rater scores would be required, which lies out of the scope of this work.

In clinical context a Tmax thresholding at > 6s was established to correlate best with other cerebral blood flow measures (Takasawa et al., 2008; Olivot et al., 2009b) and final lesion outcome (Olivot et al., 2009a; Christensen et al., 2010; Forkert et al., 2013). It is already used in large studies (Lansberg et al., 2012). We started out with the same method when creating the ground truth for SPES, but followed by considerable human correction. The comparison against the simple thresholding (Table 9, second to last row) hence gives an idea of the intervention in creating the ground truth. Compared against the participating methods, it becomes clear that these managed to capture the physicians intention when segmenting the perfusion lesion quite well and that simple thresholding might not suffice.

An improved version proposed by Straka et al. (2010), where binary objects smaller than 3 ml are additionally removed, leads to better results (Table 9, last row) than simple thresholding but still far from SPES’ algorithms. Thresholding is clearly not a suitable approach for penumbra estimation.

The discrepancy between the relatively good results reported by Olivot et al. (2009a), Christensen et al. (2010) and Straka et al. (2010) and the poor performance observed in this study can be partially explained by the different end-points (expert segmentation on PWI-MRI vs. follow-up FLAIR/T2), the different evaluation measures (DC/ASSD vs. volume similarity), and the different data. This only serves to highlight the need for a public evaluation dataset. From an image processing point of view, the volume correlation is not a suitable measure to evaluate segmentations as it can lead to good results despite completely missed lesions.

7.1. The most suitable algorithm and the remaining challenges

Both of the winning methods are based on machine learning (RFs) and both additionally employ expert knowledge (e.g. a prior thresholding of the Tmax map). Their results are significantly better than those of all other teams. The other methods in order of decreasing rank are: another RF method, a modeling approach, a rule based approach, another modeling approach, and a CNN.

Although the number of participating methods is too small to draw a general conclusion, the results suggest that RFs in their various configurations are highly suitable algorithms for the task of stroke penumbra estimation. Furthermore, they are known to be robust and allow for a computational effective application, both of which are strong requirements in clinical context.

An automated method has to fulfill the strict requirements of clinical routine. Since time is brain when treating stroke, it has to fit tightly into the stroke protocol, i.e., is restricted to a few minutes of runtime (Straka et al. (2010) state ±5min as an upper limit). With 6min (CH-Insel) and 20sec (DE-UzL), including all pre- and post-processing steps, the two winning methods fit the requirements, DE-UzL even leaving room for overhead.

7.2. Recommendations and limitations

New approaches for perfusion estimation should move away from simple methods (e.g. rule-based or thresholding). These are easy to apply, but our results indicate that they cannot capture the whole complexity of the problem. Machine learning, especially RFs, seem to be more suitable for the task: They can model non-linear functional relationship between data and desired results that a simpler approach cannot. Domain knowledge is likely required to achieve state-of-the-art results as the Tmax map thresholding of the two winning methods indicates. Evaluation should in any case be performed via a combination of suitable, quantitative measures. Simple volume difference or qualitative evaluation are of limited expressiveness and render the presented results incomparable. Where possible, the evaluation and training data should be publicly released. Finally, it has to be kept in mind that the segmentation task is a time-critical one and application times are always to be reported alongside the quantitative results.

The presented algorithms are close to clinical use. However, intensive work is further needed to increase their robustness for the variety of confounding factors appearing in clinical practice. In this direction, a clear direct improvement seems to be the incorporation of knowledge regarding collateral flow, which is also used in the clinical workflow to stratify selection of patient treatment. It remains to be shown that the diffusion lesion can be segmented equally well and whether the resulting perfusion-diffusion mismatch agrees with follow-up lesions. To this end, a benchmark with manually segmented follow-up lesions would be desirable.

SPES suffers from a few limitations: While MCA strokes are most common and well suited for mechanical reperfusion therapies (Kemmling et al., 2015), the restriction to low-noise MCA cases limits the result transfer to clinical routine. The generality of the results is additionally reduced by providing only single-center, single-ground truth data. Finally, voxel-sized errors in the ground truth prevented the evaluation of the HD, which would have provided additional information.

8. Conclusion

With ISLES, we provide an evaluation framework for the fair and direct comparison of current and future ischemic stroke lesion segmentation algorithms. To this end, we prepared and released well described, carefully selected, and annotated multi-spectral MRI datasets under a research license; developed a suitable ranking system; and invited research groups from all over the world to participate. An extensive analysis of 21 state-of-the-art methods’ results presented in this work allowed us to derive recommendations and to identify remaining challenges. We have shown that segmentation of acute perfusion lesions in MRI is feasible. The best methods for sub-acute lesion segmentation, on the other hand, still lack the accuracy and robustness required for an immediate employment. Second-center acquisition parameters and small lesions with weak FLAIR-support proved the main challenges. Overall, no type of segmentation algorithm was found to perform superior to the others. What could be observed is that approaches using combinations of multiple methods and/or domain knowledge performed best.

A valuable addition to ISLES would be a similarly organized benchmark based on CT image data, enabling a direct comparison between the modalities and the information they can provide to segmentation algorithms.

For the next version of ISLES, we would like to focus on the acute segmentation problem from a therapeutical point of view. By modeling a benchmark reflecting the time-critical decision making processes for cerebrovascular therapies, we hope to promote the transfer from methods to clinical routine and further the exchange between the disciplines. A multi-center dataset with hundreds of cases will allow the participants to develop complex solutions.

Highlights.

• Evaluation framework for automatic stroke lesion segmentation from MRI

• Public multi-center, multi-vendor, multi-protocol databases released

• Ongoing fair and automated benchmark with expert created ground truth sets

• Comparison of 14+7 groups who responded to an open challenge in MICCAI

• Segmentation feasible in acute and unsolved in sub-acute cases

Appendix A. Participating algorithms

This section includes short descriptions of the participating algorithms. For a more detailed description please refer to the workshop’s postproceeding volume (Crimi et al., 2016) or the challenge proceedings (Maier et al., 2015a).

Used abbreviations are: white matter (WM), gray matter (GM), cerebral spinal fluid (CSF), random forest (RF), extremely randomized trees (ET), contextual clustering (CC), gaussian mixture models (GMM), convolutional neural network (CNN), Markov Random Field (MRF), Conditional Random Field (CRF) and expectation maximization (EM).

Appendix A.1. UK-Imp1 (Liang Chen et al.)

We propose a multi-scale patch-based random forest algorithm for sub-acute stroke lesion segmentation. In the first step, we perform an intensity normalization under the exclusion of outliers. Second, we extract features from all images: Patch-wise intensities of each modality are extracted at multiple scales obtained with Gaussian smoothing. We parcellate the whole brain into three parts, including top, middle, and bottom. To keep an equilibrated class balance in the training set, only a subset of background patches is samples from locations all over the brain. Subsequently, we train three standard RF (Breiman, 2001) classifiers based on the patches selected from three parts of the brain. Finally, we perform some postprocessing operations, including smoothing the outputs of the RFs, applying a threshold, and performing some morphological operations to obtain the binary lesion map.

Appendix A.2. DE-Dkfz (Michael Götz et al.)

The basic idea of this approach is that a single classifier might not be able to learn all possible appearances of stroke lesions. We therefore use ‘Input-Data Adaptive Learning’ to train an individual classifier for every input image. The learning is done in two steps: First, we learn the similarity between two images to be able to find similar images for unseen data. We define the similarity between two images as the DC that can be achieved by a classifier trained on the first image with the second image. Neighborhood Approximation Forests (NAF) (Konukoglu et al., 2013) are used to predict similar images for images without a ground-truth label (e.g. without the possibility to calculate the DC). We use first-order statistic description of the complete images as features for the learning algorithm. While the first step is done offline, the second step is done online, when a new and unlabeled image should be segmented. A specific, voxel-wise classifier is trained from the closest three images, selected by the previous trained NAF. For the voxel classifier we use ETs (Geurts et al., 2006) which incorporate DALSA to show the general applicability of our approach (Goetz et al., 2016). In addition to the intensity values we use Gaussian, Difference of Gaussian, Laplacian of Gaussian (3 directions), and Hessian of Gaussian with Gaussian sigmas of 1, 2, 3mm for every modality, leading to 82 features per voxel.

Appendix A.3. FI-Hus (Hanna-Leena Halme et al.)

The method performs lesion segmentation with a RF algorithm and subsequent CC (Salli et al., 2001). We utilize the training data to build statistical templates and use them for calculation of individual voxel-wise differences from the voxel-wise cross-subject mean. First, all image volumes are warped to a common template space using Advanced Normalization Tools (ANTS). Mean and standard deviation over subjects are calculated voxel-by-voxel, separately for T1, T2, FLAIR and DWI images; these constitute the statistical templates. The initial lesion segmentation is calculated using RF classification and 16 image features. The features include normalized voxel intensity, spatially filtered voxel intensity, intensity deviation from the mean specified by the template, and voxel-wise asymmetry in intensities across hemispheres, calculated separately for each imaging sequence. For RF training, we only use a random subset of voxels in order to decrease computational time and avoid classifier overfitting, As a last phase, the lesion probability maps given by the RF classifier are subjected to CC to spatially regularize the segmentation. The CC algorithm takes the neighborhood of each voxel into account by using a Markov random field prior and iterated conditional modes algorithm.

Appendix A.4. CA-McGill

The authors of this method decided against participating in this article. A description of their approach can be found in the challenge’s proceedings on http://www.isles-challenge.org/ISLES2015/

Appendix A.5. UK-Imp2 (Konstantinos Kamnitsas et al.)

We developed an automatic segmentation system, based on a 11-layers deep, multi-scale, 3D CNN. The network classifies voxels after processing a multi-modal 3D patch around them. To achieve e cient processing of greater image context, we developed a network architecture with two parallel convolutional pathways that processes the image at different scales. To train our system we build upon the work in Urban et al. (2014) and form batches with large image segments, equally sampled from the two classes. We exploit our network’s fully convolutional nature to densely train on multiple voxels in the central part of the segments. By utilizing small 3³ kernels that lead to deeper architectures with less trainable parameters, as well as adopting Dropout, Batch Normalization (Ioffe and Szegedy, 2015) and augmenting the database using reflection along the sagittal axis, we heavily regularize our network and show that it is possible to train such a deep and wide network on a limited database. Training our CNN takes approximately one day on a GeForce GTX Titan Black, while inference on a brain volume requires 3 minutes. We applied only minimum preprocessing, normalizing the modalities of each patient to zero mean and unit variance. For our final submission in the testing phase of the challenge, the outputs of 3 similar CNNs were averaged, to reduce noise caused by randomness during training. Additionally, we implemented a 3D, densely connected CRF by extending the work of Krähenbuhl and Koltun (2012), which can efficiently postprocess a multi-modal scan in 2 minutes. Finally, connected components smaller than 20 voxels are eliminated.

Appendix A.6. US-Jhu (John Muschelli)

As rigid registration may not correct local differences between spatial locations across sequences, we re-register images to the FLAIR using Symmetric Normalization (Avants et al., 2008). We normalize the voxel intensities to a z-score using the 20% trimmed mean and standard deviation from each image. To train an algorithm, we create a series of predictors, including the x-y flipped voxel intensity, local moments (mean, sd, skew, kurtosis), and the images smoothed with large Gaussian filters. We trained a RF from 9 images, downsampled to 300, 000 voxels, with the manual segmentation as the outcome (Breiman, 2001). From the RF, we obtained the probability of lesion and determined the threshold for these probabilities using the out-of-sample voxels from the training images, optimizing for the DC.

Appendix A.7. SE-Cth (Qaiser Mahmood et al.)

The proposed framework takes the multi-spectral MRI brain images as input and includes two preprocessing steps: (1) Correction of bias field using the N3 bias field correction algorithm (Sled et al., 1998) and (2) normalization of the intensity values of each MRI modality to the interval [0, 1], done by applying linear histogram stretching. For each voxel of multi-spectral MRI images, the following set of meaningful features is extracted: intensities, smooth intensities, median intensities, gradient, magnitude of the gradient and local entropy. All these features were normalized to zero mean and unit deviation. These features are then employed to train the RF (Criminisi and Shotton, 2013) classifier and segment the sub-acute ischemic stroke lesion. In this work, we set the RF parameters to: number of trees=150 and depth of each tree=50. A total of 999, 000 data samples (i.e. 37, 000 randomly selected from each training case) is used to train the RF classifier. Finally, the postprocessing is performed using dilation and erosion operations in order to remove small objects falsely classified as stroke lesion.

Appendix A.8. US-Odu (Syed M S Reza et al.)

This work proposes fully automatic ischemic stroke lesion segmentation in multispectral brain MRI by innovating on our prior brain tumor segmentation work (Reza and Iftekharuddin, 2014). The method starts with the standard MRI preprocessing steps: intensity inhomogeneity correction and normalization. Next step involves two primary sets of feature extraction from T1, T2, FLAIR and DWI imaging sequences. The first set of features includes the pixel intensities (I_FL, I_T1, I_T2, I_DWI) and differences of intensities (d₁ = I_FL − I_T1, d₂ = I_FL − I_T2, d₃ = I_FL − I_DWI) that represents the global characteristics of brain tissues. In the second set, local texture features such as piece-wise triangular prism surface area, multi-fractal Brownian motion (Islam et al., 2013) and structure tensor based local gradients are extracted to capture the surface variation of the brain tissues. We use a mutual information based implementation of minimum redundancy maximum relevance feature ranking technique and choose the 19 top ranked features. A classical RF classifier is employed to classify the brain tissues as lesion or background. Finally, a binary morphological filter is used to reduce the false positives from the original detections. We observe a few remaining false positives that compromise the overall performance. Our future works will include the study of more e ective features, sophisticated feature selection techniques and an e ective false positive reduction technique.

Appendix A.9. TW-Ntust (Ching-Wei Wang et al.)

A fully automatic machine learning based stroke lesion three-dimensions segmentation system is built, which consists of a feature selection method, a multi-level RF model and a simple 3D registration approach. Only the FLAIR sequence was used and 275 features, which can be categorized into 24 types, are extracted for building RF models. To deal with the three dimensional data, a multi-RF model is developed and for stacks of five slices in the Z direction, a random forest model is built. The RF model generates probability maps. After obtaining the potential candidates from the RFs, we build a three-dimensional registration framework with backward and forward searching (Wang et al., 2015). It is applied to generate optimal three-dimensional predictions and too remove larger outliers. The system finds the largest object among all stacks and uses the stack with the largest object as the referenced stack. Then, the system performs backward and forward registration to maintain spatial consistency and remove the objects with no overlap to the detected objects in the neighboring stacks.

Appendix A.10. CN-Neu (Chaolu Feng)

We propose a framework to automatically extract ischemic lesions from multi-spectral MRI images. We suppose that the input images of different modalities have already been rigidly registered in the same coordinate system and non-brain tissues have already been removed from the images (Gao et al., 2014). Lesion segmentation is then performed by the proposed framework in three major steps: 1) preliminary segmentation, 2) segmentation fusion, and 3) boundary refinement. No training data is needed and no preprocessing and postprocessing steps involved. In the proposed framework, MRI images of each modality are first segmented into brain tissues (WM, GM and CSF) and ischemic lesions by weighting suppressed fuzzy c-means. Preliminary lesion segmentation results are then fused among all the imaging modalities by majority voting. The judge rule is that candidate voxels are regarded as lesions only if 1) they are considered as brain lesions in FLAIR images, and 2) they are viewed as brain lesions in more than 1 imaging modality beside FLAIR. The fused segmentation results are finally refined by a three phase level set method. The level set formulation is defined on multi-spectral images with the capability of dealing with intensity inhomogeneities (Feng et al., 2013).

Appendix A.11. BE-Kul1 (Tom Haeck et al.)

We present a fully-automated generative method that can be applied to individual patient images without need for a training data set. An EM-approach is used for estimating intensity models (GMMs) for both normal and pathological tissue. The segmentation is represented by a level-set that is iteratively updated to label voxels as either normal or pathological, based onwhich intensity model explains the voxels’ intensity the best. A convex level-set formulation is adopted (Goldstein et al., 2009), that eliminates the need for manual initialization of the the level-set. For each iteration to update the level-set, a full EM-estimation of the GMM parameters is done.

As a preprocessing step, spatial priors of WM, GM and CSF are non-rigidly registered to the patient image. The prior information is relaxed by smoothing the spatial priors with a Gaussian kernel. For SPES, we make use of the T2-weighted and TTP-weighted MR images and for SISS the diffusion weighted and FLAIR-weighted MR images. For SPES, the modalities are used in a completely multivariate way, i.e., with bivariate Gaussian models. For SISS, the modalities are segmented separately and a voxel is only labeled as lesion if it is a lesion in both modalities.

Appendix A.12. CA-USher (Francis Dutil et al.)

We propose a fully-automatic CNN approach which is accurate while also being computationally e cient, a balance that existing methods have struggled to achieve. We approach the problem by solving it slice by slice from the axial view. The segmentation problem is then treated by predicting the label of the center of all the overlapping patches. We propose an architecture with two pathways: one which focuses on small details of the tissues and one focusing on the larger context. We also propose a two-phase patch-wise training procedure allowing us to train models in a few hours and to account for the imbalanced classes. We first train the model with a balanced dataset which allows us to learn features impartial to the distribution of classes. We then train the second phase by only training on₁ the classification layer with a distribution closer to the ground₁ truth’s. This way we learn good features and introduce the cor-₁ rect class prior to the model. Fully exploiting the convolutional₁ nature of our model also allows to segment a complete brain₁ image in 25 seconds. To test the ability of CNNs to learn useful₁ features from scratch, we employ only minimal preprocessing.₁ We truncate the 1% highest and lowest intensities and applied₁ N4ITK bias correction. The input data is then normalized by₁ subtracting the channel mean and dividing by its standard de-₁ viation. A postprocessing method based on connected compo-₁ nents is also implemented to remove small blobs which might₁ appear in the predictions.

Appendix A.13. DE-UzL (Oskar Maier et al.)

We propose a novel voxel-wise RF classification method with features chosen to model a human observers discriminative criteria when segmenting a brain lesion. They are based on intensity, hemispheric difference, local histograms and center distances as detailed in (Maier et al., 2015c, 2016). First, the already co-registered, isotropic voxel-spacing and skull-stripped sequences are preprocessed with bias field correction and intensity range standardization (Maier, 2016) (SISS) resp. the Tmax capped at 10s (SPES). A total of 1, 000, 000 voxels are randomly sampled, keeping each case’s class ratio intact (i.e. imbalanced). With this training set, 50 trees are trained using Gini impurity and $\sqrt{163}$ features for node optimization. For SISS, the a-posteriori forest probability map is thresholded at 0.4 and objects smaller than 1ml removed. For SPES, the threshold is 0.35 and only the largest connected component is kept. Both are followed by an hole closing in sagittal slices. The proposed method was equally successfully applied to BRATS challenge data (Maier et al., 2016), underlining the generality of our approach.

Appendix A.14. BE-Kul2 (David Robben et al.)

A single segmentation method for both the SISS and SPES sub-challenges is proposed (Robben et al., 2016). First, all data is preprocessed, including bias-field correction, linear intensity standardization, and affine registration to MNI space. Then, each voxel is probabilistically classified as lesion or background within the native image space. The classifier consists of 3 cascaded levels, in which each level extends the feature set and uses a more complex extremely randomized forest (Geurts et al., 2006). The first level only uses the T1 intensity. The second level uses all modalities, smoothed in a local neighborhood at different radii, as well as voxel coordinates in atlas space. The third level additionally uses the probabilities estimated in level 2, smoothed locally. Classifier hyperparameters were tuned using 5-fold cross-validation. Testing data is preprocessed similarly and the voxelwise probabilities are predicted by the classifier. A technique to select the threshold that optimizes the DC is presented and applied to the predicted probability map in order to obtain the final binary segmentation.

Appendix A.15. DE-Ukf (Elias Kellner et al.)

In almost all cases of acute embolic anterior circulation stroke only one hemisphere is affected. We exploit this fact to (i) restrict the segmentation to only the affected hemisphere and (ii) to preselect the potential lesion by comparing local histograms of the affected side with the contralateral counter-part used as reference. Our approach is based on the evaluation of just the Tmax and ADC-maps. First, we automatically find the plane which separates the left and right hemisphere by co-registration with a mirrored Tmax-image, and identify the affected hemisphere as the one with the higher median value. For each voxel at position $\overrightarrow{x}$, a normalized, regional histogram $H(\overrightarrow{x},t_i)$ is calculated in a 20 × 20 × 12mm³ neighborhood with a bin-width of t_i+1 − t_i = 1.5s. The difference to the corresponding contralateral histogram $\tilde{H}(\overrightarrow{x},t_i)$, taken from the mirrored part of the brain is calculated via $D\left(\overrightarrow{x}\right)=1∕2{\Sigma }_i\mid H(\overrightarrow{x},t_i)-\tilde{H}(\overrightarrow{x},t_i)\mid$. The resulting map of histogram differences is thresholded by 0.5 to find the regions with unusual Tmax values. This pre-selection is thresholded with the generally accepted value of Tmax > 6s. The histogram neighborhood size and the morphological operation parameters are globally fine-tuned based on the training dataset. To clean the mask, morphological erosion and dilation is applied. Finally, the segmentation is multiplied with ADC > 1700mm²/s to remove CSF voxels.

Appendix A.16. CH-Insel (Richard McKinley et al.)

The model is trained only using data from the SPES dataset is used. The method makes use of all seven imaging modalities. Before learning takes place, the following preprocessing steps are employed: TMax values are censored below zero and above 100, and all imaging modalities are then scaled to lie in the interval [0, 256]. Simple image texture features, based on those first used in Porz et al. (2014) are extracted from each imaging modality. The resulting data points are used to train a decision forest model which assigns to each volume element a label indicating if it should be considered part of the perfusion lesion. The training algorithm is a modification of RF (Breiman, 2001), in which bootstrapping of the training data is performed first at the patient level, and only then at the voxel level. This avoids the effects of patient-level clustering and leads to out-of-sample patients. This out-of-sample data is then used to empirically discover a threshold at which the DC of the segmentation is maximized, avoiding the need for holding out training data to tune the classifier. After segmenting with this threshold, no further postprocessing was applied. The method takes approximately six minutes to segment a new case.

Appendix B. Ranking schema

Our ranking system builds on the concept that a rank reveals only the direction of a relationship between two items (i.e. higher, lower, equal), but not its magnitude. After obtaining from each participating team the segmentation results for each case, the following steps are executed:

1. Compute the DC, ASSD & HD values for each case

2. Establish each team’s rank for DC, ASSD & HD separately for each case

3. Compute the mean rank over all three evaluation measures/case to obtain the team’s rank for the case

4. Compute the mean over all case-specific ranks to obtain the team’s final rank

Graphically, the schema looks like displayed in Fig. B.11. The outcome of the procedure is a final rank (real number) for each participant, which defines its standing in the leaderboard relative to all others. For SISS, with two ground truth sets for the testing dataset, their respective final ranks are averaged. For SPES, only the DC and the ASSD were used.

This approach can be applied to any number of measures, independent of their range, type or direction. Its outcome denotes only the differences between algorithms and hence serves its purpose. For any interpretation of the results, the distinct evaluation measure values obtained have to be considered too.

A challenge with winners requires an absolute ranking; an ongoing benchmark does not. For the online, ongoing leaderboard, the rank is not computed. Rather, each user is invited to sort the result table according to their favorite evaluation measure.

Failed cases and resolving ties

In one step of our algorithm, we have to rank the performance of each team on one case regarding a single evaluation metric. Such a situation can lead to ties, which have to be handled specially. We chose to decorate both tied teams with the upper rank and leaving the following empty (see Table B.10 for an example).

Table B.10.

Example of resolving ties for ISLES.

Team	DC	Rank	Team
T-A	0.33	1	T-C
T-B	0.33	2	T-A, T-B, T-D
T-C	0.50	3
T-D	0.33	4
T-E	0.31	5	T-E
(a) Before…		(b) …after

This behavior has an interesting effect for very difficult cases, where most teams fail to produce a valid segmentation, as can be seen in the example of Table B.11.

Table B.11.

Tie resolving for difficult cases.

Team	DC	Rank	Team
T-A	0.00	1	T-C
T-B	0.00	2	T-A, T-B, T-D, T-E
T-C	0.10	3
T-D	0.00	4
T-E	0.00	5
(a) Before…		(b) …after.

Thus, difficult cases do not alter the mean as they would do when simply averaging, e.g., the DC values over all cases. Instead, only the performance relative to all other algorithms is compared, resulting in a more expressive ranking.

Beside resolving ties, we decided to introduce a concept of failed cases: When faced with (1) a missing segmentation mask or (2) a DC value of 0.00 (i.e. no overlap at all), the concerned case was declared failed and all metric evaluation values subsequently set to infinity. Combined with the employed ranking approach and above described treatment of ties, this allows to incorporate missing segmentations in the ranking in a natural and fair manner. It could be argued that a DC of 0.00 could well mean that another part of the brain has been segmented. But the case has nevertheless to be considered a failed one, as the target structure has not been detected. Not declaring the case a failure would lead methods submitting a single random voxel segmentation to be ranked higher than an empty segmentation mask.

Figure B.11.

Ranking schema as employed in the ISLES challenge.