Dynamical transition and proteinquake in photoactive yellow protein

Abstract

Conformational dynamics in protein functioning covers a wide range of time scales from nanosecond fluctuations around a conformation to the large-amplitude conformational changes of milliseconds or longer. We illustrate a picture of cooperative coupling among such motions of different time scales in a model protein, photoactive yellow protein, by proposing a model that can consistently explain the experimental results on the photocycle of photoactive yellow protein. The model provides a scenario in which the global collective motion induced by the unfolding of the N-terminal domain promotes the loosening of the atomistic packing around the chromophore, which produces the favorable molecular environment for the photoexcited chromophore, thereby stabilizing the partially unfolded intermediate in the photocycle. The proteinquake, the large conformational change triggered by the local structural disturbance, plays a decisive role in controlling the kinetics of functioning.

Elucidating roles of dynamical structural fluctuations in protein functioning has been a major topic in protein science (1, 2). Rates of chemical reactions are significantly perturbed by dynamical fluctuations of conformations (3), and efficiency of binding depends on the flexibility of structures (4). Important insights on structural fluctuations have been obtained from the equilibrium quasiharmonic picture for the nonharmonic potential surface around the native structure. In the quasiharmonic picture the equilibrium distribution of fluctuating structures has been characterized by a few low-frequency modes calculated by applying the normal mode or principal component analyses (5, 6) or by using coarse-grained elastic network models (7, 8). It has been suggested that these low-frequency collective modes play a dominant role in functional processes (6). When protein takes multiple conformational states, however, its dynamics are not confined in a single potential well, but the nonlinearity associated with the transition between different free energy valleys has to be explicitly taken into account. The energy landscape picture describes such dynamics as the stochastic motion on a multivalley free energy surface. Energy landscape models have been applied to protein binding (9, 10), allosteric transformation (11), molecular recognition (12, 13), and molecular motor (14). Through these applications, new scenarios of functioning have been proposed such that “proteinquakes” (15) involving the total or partial unfolding/refolding events can take part in functional processes.

Two pictures, the quasiharmonic and energy landscape pictures, are based on observations of different time scales. The Gaussian distribution of structures in the quasiharmonic picture reflects the equilibrium fluctuations of fast side-chain motions or backbone distortions around the folded conformation. The statistical weight in the energy landscape picture, on the other hand, reflects the distribution of conformations that are equilibrated through the slow rearrangement of the backbone conformation. Fast vibrational motions and slow conformational rearrangement, however, are not completely separable but should be coupled across different time scales. Indeed, the low-frequency vibrational modes should guide a large conformational change, and the consequent conformational change should alter the amplitude and frequency of vibration modes. Thus, the unification of two pictures has been most desired to understand dynamics in the functional processes. Here, a key observation is that topology of the native structure governs both vibrational (7, 8) and diffusive (16) dynamics. The purpose of this article is to propose a unified view of the conformational dynamics by developing a framework based on the topology of the native structure to shed light on how the cooperative communication among local and global motions works in the functional process.

As an example system, we focus on photoactive yellow protein (PYP) (ref. 17 and references therein and ref. 18). PYP is a relatively small (125 residues) and highly water-soluble blue-light receptor in the bacterium Ectothiorhodospira halophila (19), which displays negative phototaxis toward blue light. PYP is considered to be the photoreceptor for this response. As shown in Fig. 1a, PYP is composed of four segments, the N-terminal cap (residues 1–28), the PAS core (residues 29–69), the helical connector (residues 70–87), and the β-scaffold (residues 88–125). A chromophore, p-coumaric acid (pCA), is linked to Cys-69 by means of a thiol-ester linkage. PYP is a structural prototype of the PAS domain superfamily, which is a ubiquitous and versatile signaling module involved in regulation, sensing, the circadian rhythm, and a number of human diseases (20). For this reason PYP has been extensively studied as a model protein. We propose a scenario that PYP exhibits a dynamical transition involving partial unfolding induced by cooperative effects in dynamics of multiple time scales and show that the scenario can consistently explain the experimental results on the photocycle of PYP.

Fig. 1.

Structure and photocycle of PYP. (a) Structure of PYP [Protein Data Bank (PDB) ID code 2PHY] is composed of four segments: the N-terminal cap (yellow), the PAS core (red), the helical connector (orange), and the β-scaffold (green). The chromophore, pCA (blue), attaches to Cys-69 of PYP. pCA is stabilized through H bonds involving the residues Tyr-42 (light blue), Glu-46 (black), and Thr-50 (gray). (b) The photocycle of PYP. After absorbing a 446-nm photon, the dark state (^transpCA), pG, transforms to pR through the isomerization of pCA to the cis configuration (^cispCA_deprot) on the nanosecond time scale. pR then turns into pB through the protonation of pCA (^cispCA_prot) on the microsecond time scale, and pB returns to pG on the millisecond-to-second time scale. pB is the signaling intermediate.

The photocycle of PYP is illustrated in Fig. 1b. In the ground state, which is called the pG state, pCA resides in the trans configuration and is negatively charged, which is stabilized through hydrogen bonds involving the residues Tyr-42, Glu-46, and Thr-50 (Fig. 1a). Absorption of a blue-light photon triggers a photocycle by isomerizing pCA from the trans-to-cis configuration in the picosecond-to-nanosecond time scales. With this isomerization the ground state is transformed into an intermediate called pR in which the absorption spectrum is red-shifted. In the microsecond time scale, the pR state is transformed into a blue-shifted intermediate called pB. During the transition from pR to pB, a proton is transferred from Glu-46 to pCA. The pB intermediate is considered to be the functionally active signaling state of PYP, recognized by the partner protein, thereby transmitting the signal into the cell. Through deprotonation and reisomerization of pCA, pB is transformed into pG on the millisecond-to-second time scale, which completes the photocycle. When the photocycle is examined in crystal, the structure of pB is not significantly different from that of pG (21, 22). An interesting point here is that the structure of pB in water solution, i.e., in its functional environment, is largely different from that of pG. In solution, NMR (23, 24), Fourier transform infrared (25, 26), small-angle x-ray scattering (27), CD (28), fluorescence (29), thermodynamic, and kinetic (30–32) studies showed that the pB state is partially unfolded or structurally disordered. In this paper, we develop a model to explain how the global conformational disorder is induced by the photoabsorption at pCA.

Methods

The Extended Wako–Saito–Muñoz–Eaton (WSME) Model. In order to describe the global conformation change, it is convenient to use a coarse-grained variable, m_i = 1 or 0, which represents the configuration at the ith residue: m_i takes unity when two dihedral angles of the backbone at the ith residue are within some narrow range around values in the ground state conformation and zero otherwise. The model with such a two-valued coarse-grained variable was developed by Wako and Saito (33, 34) to analyze the folding pathway of proteins, and much later the same model was developed by Muñoz and Eaton (35). Muñoz and Eaton compared their results with the modern experimental data on protein folding and showed that the model can reasonably describe the free energy surface of folding and quantitatively explain the folding speed and the φ value distribution in many proteins (35). The model is in a class of Gō-like models (36), which are energetically minimally frustrated. Success of this model in explaining the folding process of many proteins convinced us that proteins are indeed minimally frustrated and folding is primarily determined by topology of the native conformation (16). The model includes multibody interactions taking into account the cooperativity in structural formation, and this point is discussed in detail in ref. 37. Here, in our problem, the WSME model is modified and is extended to describe both the large-scale conformational changes and the local packing fluctuations in the photocycle. The photoexcited states, pR and pB, should have higher energy than the dark state, pG, so that pG is regarded as the “native state.”

The partition function is formally written as Z = ∑_{mi} ∫ ∏_i dr_i exp[–H/k_BT], where r_i is the position of the C^α atom of the ith residue with i = 1–125. We consider that interactions of the effective Hamiltonian H = H ({r_i}, {m_i}) are renormalized by formally integrating the rest degrees of freedom, coordinates of solvent molecules, side chains, and other backbone atoms so that modulations in parameters of Hamiltonian indirectly reflect perturbations in those degrees of freedom. We define the effective Hamiltonian as H = H_int + H_s + H_chain + V_chrom. The first term, H_int, accounts for the stabilization in energy upon the formation of the native segment in which consecutive residues from i to j take the pG backbone configuration as m_ij ≡∏^j_k=i m_k = 1. We suppose that the native segment is more sufficiently stabilized in energy than the nonnative segment specified by m_ij = 0 (38). This assumption leads to the energy landscape that is energetically biased toward the native structure, the pG conformation. Here, stabilization of the native segment is expressed by defining the “native contact,” which is regarded to be formed Δ_ij = 1 when Å for |i – j| ≥ 2, where the superscript zero indicates the coordinate at the pG conformation [Protein Data Bank (PDB)/ID 2PHY] and Δ_ij = 0 otherwise. Then, the effective stabilization of native segments can be approximated by with r_ij = r_i – r_j. Here, the effective interaction is expanded in terms of r_ij – r_ij with ε_ij < 0 and γ_ij > 0 by assuming that local fluctuations of r_ij obey an isotropic Gaussian distribution as in the Gaussian network model (8). The spring constant, γ_ij, reflects how well the local atomistic packing is formed in the contact, so that the loosening of the packing should result in a smaller value of γ_ij. H_s represents the backbone conformational entropy: H_s = – T ∑_i S_i (1 – m_i), where S_i is the residue type-dependent entropic factor arising from disordered residues of m_i = 0 with S_i ≈ 0.5 k_B for compact globules (39). We assume S_i = 0.25 k_B for Pro, 1.51 k_B for Gly, and 0.50 k_B for other residues. H_chain is the elastic energy of the chain: H_chain =∑_{i ≤ j} K_ij Δr_i·Δr_j with . We adopt the stiff chain model (40) of K_{ii + 1} =–K < 0, K₁₂ = K_N–1N =–1/(1 + g)K, K_{ii + 2} = g/(1 + g)² K and K_ii =∑_j(≠i) (–1)^{δ_{|i – j|,1}} K_ij with g = 0.8, which gives rise to a correlation, 〈d_i·d_{i + l}〉∝ g^l with . The last term of H, V_chrom, comes from the electronic structure of the chromophore, and, for simplicity, we assume that V_chrom has different constant values for different pCA configurations.

Chromophore–Residue Interactions. By regarding the chromophore as the side chain of Cys-69, interaction between pCA and a residue is described as the virtual interaction between Cys-69 and the residue, so that additional contacts of Δ_ij = 1 are defined between the j = 69th residue and the ith residue, which interacts with pCA in the pG conformation.

Partition Function. The partition function can be written as Z = e^{–V_chrom/kbT} ∑_M Z_WSME (M) Z_G (M) Z_residual (M), where M =∑_i m_i = 0 – 125 is the number of native residues, which is used as an order parameter of folding to the pG conformation. Z_WSME (M) = ∑_∑imi=M exp (–H_WSME/k_BT) is the partition function calculated under the constraint of a given value of M by using the WSME Hamiltonian (33–35), 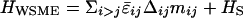. Z_WSME(M) can be exactly calculated by using the transfer matrix method (41). Z_G(M) =∫∏_i dr_ie^{–[Hg(M) +Γ (M)]/kbT} is the partition function for the Gaussian network model (8) with and (M), where the spring constant is renormalized by m̄_ij (M), which is the expectation value of m_ij with a given M calculated by using Z_WSME(M). The parameter was chosen to make Z_residual (M) – 1 ≥ 0 small (see Supporting Text, which is published as supporting information on the PNAS web site). With this mean-field-like treatment, free energy at a given temperature with a given number of native residues, M is calculated as F(M) = – k_BT ln [Z_WSME (M) Z_G (M)] + V_chrom.

Model of the Photocycle. Corresponding to three chromophore configurations appearing in the photocycle (see Fig. 1b), we suppose that interactions among residues in the vicinity of pCA are perturbed in the following way.

The trans configuration (^transpCA). The dark state, pCA, and its vicinity are not perturbed, and ε_ij and γ_ij are assumed to be independent of iand j; ε_ij = ε and γ_ij = γ = K.

The cis and deprotonated configuration (^cispCA_deprot). This state is structurally strained, and, in it, contact energies between pCA and residues are weakened owing to the steric hindrance. We put ε_ij = ε₁ > ε, when i is the residue directly interacting with pCA labeled by j = 69. The structural disturbance in residues leads to the loosening and rearrangement of the side-chain packing, which should invoke jumping among local energy minima (5) and thus broaden the distribution of . In our Hamiltonian, such broadening is represented by the nonlinear diminishing of the spring constant. As in the density functional model of the liquid–glass transition (42), we describe the nonlinear dependence of the spring constant on fluctuations with a density function ρ (Δr_i, Δr_j). The direct interaction coefficient for springs, γ, between the disturbed ith residue and pCA, j = 69 is perturbed as γ_ij = 〈ρ(Δr_i, Δr_j)〉_Mγ, where 〈...〉_M is the average taken by using Z(M) = exp [–F(M)/k_BT] at fixed M. The similar renormalization of the effective spring constant has been discussed in studies of the dynamical transition at low temperature (43) and during protein folding (44). Because the atomistic packing is of a multibody nature and is affected by the solvent motion, the structural disturbance should be enhanced not only by the fluctuation of Δr_i + Δr_j but also the translational fluctuation of Δr_i + Δr_j through motions of the side-chain atoms and the solvent molecules. We assume a Gaussian form for ρ (Δr_i, Δr_j) as

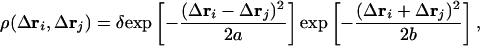[1]

with δ ≤ 1 (see Fig. 6, which is published as supporting information on the PNAS web site). Through Eq. 1, the structural disturbance weakens the interactions, which further enhances the structural fluctuations of disturbed residues. Such nonlinear effects can be taken into account by calculating γ_ij in a self-consistent way. Substituting γ into the Hamiltonian H_G(M), a new value of γ_ij is derived. By iterating this operation up to convergence, one can obtain the self-consistent solution of γ_ij.

The cis and protonated configuration (^cispCA_prot). A proton is transferred from Glu-46 to pCA, adding a positive charge to pCA and leaving a negative charge at Glu-46. This change in the charge distribution should further destabilize residues around the pCA. In addition to the modification of ε_ij and γ_ij introduced in ^cispCA_deprot, we modify the contact energy between the kth and ith residues as ε < ε_ki = ε₂ < ε₁ and the spring constant γ_ki as γ_ki =〈ρ(Δr_k, Δr_i)〉_M γ, when the ith residue directly interacts with pCA or Glu-46. On the way to recovering the dark state, interaction parameters are reset to the nonperturbed values at ^transpCA.

Constant values were given to V_chrom depending on the chromophore configurations; V_chrom(^transpCA) = 0, V_chrom-(^cispCA_deprot) = 30 k_BT₀, V_chrom(^cispCA_prot) = 20 k_BT₀, so as to make the isomerization energy and the energy gain on the protonation of pCA roughly agree with values obtained by the quantum chemical calculation (45, 46), where k_BT₀ is the thermal energy at room temperature, k_BT₀ = 0.6 kcal/mol (1 cal = 4.18 J).

The spring constant γ is adjusted to reproduce the observed x-ray B-factors of pG; γ = 1.8 k_BT₀Å^–2. The interaction energies ε, ε₁, and ε₂ are determined under the constraint that ε₂/ε should not be much smaller than 1. ε, ε₁, and ε₂ are adjusted to reproduce the experimental data of the stabilization energy gaps of pG and pB against unfolded states obtained from the chevron analysis of the equilibrium titrations (31) as ε = –1.4 k_BT₀, ε₁ = 0.15 ε, and ε₂ = 0.75 ε.

Results and Discussion

Free Energy Surfaces. Free energy surfaces along the one-dimensional coordinate M at room temperature are shown in Fig. 2a for three different chromophore configurations in the photocycle, ^transpCA, ^cispCA_deprot, and ^cispCA_prot. Here, the parameters used were δ = 0.5, a = 0.67 Ų, and b = 2.0 Ų (discussed in detail below). With this parameterization, the lowest free energy minimum in the ^transpCA configuration is at M ≈ 119, which corresponds to the pG state. The lowest free energy minimum in the ^cispCA_deprot configuration is also at M ≈ 119, which corresponds to the pR state. Free energy profiles of all three pCA configurations have a large barrier at M ≈ 95, which separates the folded or partially unfolded (M ≈ 104) state from the fully unfolded state. The PAS core and the helical connector are stable even at M ≈ 80, but the β-sheets near the C terminus largely fluctuate approximately at the transition state of M ≈ 95.

Fig. 2.

Free energy profiles. (a and b) Free energy surfaces (a) and equilibrium populations (b) at room temperature (k_BT₀ = 0.6 kcal/mol) for three different configurations of pCA are shown as functions of the number of residues that take approximately the pG backbone configuration, M = ∑_i m_i, for ^transpCA (black), ^cispCA_deprot (red), and ^cispCA_prot (blue). (c) Comparison between free energies of the pB intermediate with the protonated (black line) and deprotonated (broken line) chromophores. The free energy of deprotonated pB is drawn by using the same interaction parameters as in ^cispCA_deprot except for V_chrom, which mimics the free energy surface of the Glu-46-Gln mutant. (d) Dependence of the free energy gap, ΔF = F(104) – F(119), on the parameter b in Eq. 1 with a fixed a at 0.67 Ų for the ^cispCA_prot configuration.

Transition to the pB Intermediate. When pCA is protonated from ^cispCA_deprot to ^cispCA_prot, the free energy minimum moves from the state at M ≈ 119 of pR to the partially unfolded state at M ≈ 104. We refer to this partially unfolded state as pB_partial. By regarding pB_partial as the dominant component in the pB intermediate, we show below that many experimental data on pB can be explained. At this partially unfolded state, 28 residues near the N terminus are disordered; 〈m_i〉₁₀₄ ≤ 0.3 for i = 1–28, whereas 〈m_i〉₁₀₄ ≈ 0.7 for i = 29 and 〈m_i〉₁₀₄ ≈ 1 in the remainder of PYP. This partial unfolding at the N-terminal domain is consistent with the observed data (23–32). The change of the population appears to be a cooperative transition from the folded conformation in pR to the partially unfolded state (Fig. 2b). Fig. 3a shows the rms deviation (RMSD) of the C^α position at each residue, . In pB_partial, in addition to the intense increase in RMSD at the N-terminal domain, RMSDs are ≈0.3 Å larger than those in pG in the core domain (the PAS core, the helical connector, and the β-scaffold). The increase in RMSD in the core domain coincides with the increase of the radius of gyration observed in the small-angle x-ray scattering data (27). As shown in Fig. 3a and b, RMSD is increased everywhere in the core domain, indicating that the shape of the core domain is not significantly altered; only dimensional change is expected, which also agrees with previous experimental observations (27). These features of pB_partial indicate that pB resembles a molten globule. The possibility of regarding pB as the molten globule state was also suggested based on CD and 8-anilino-1-naphthalene sulfonate fluorescence (28). As shown in Fig. 3b, RMSD is relatively large at residues surrounding pCA. This local growth of fluctuation indicates the loosening of the atomistic packing around pCA and agrees with the observed change in the backbone amide ¹⁵N heteronuclear single quantum coherence cross-peaks data of NMR (24).

Fig. 3.

Structural fluctuation at each residue. (a) RMSDs from the x-ray crystalline structure of pG are shown as functions of the residue index: black line, pG; red line, pR; blue line, pB at M = 104 (pB_partial); blue broken line, pB at M = 119. Green line represents RMSD of pG obtained from the x-ray B-factors. Red bars are helical parts and green arrows are β-strands. (b) Difference in RMSD of pB_partial from that of pG (black line) is compared with intensity of heteronuclear single quantum coherence peak of NMR in pB relative to that in pG (24, 49) (orange vertical bars), where the zero values of the bars indicate that the peak was too weak to detect or could not be represented because of ambiguity or spectral overlap.

Dependence of the free energy gap, ΔF = F(104) – F(119), in the ^cispCA_prot configuration on parameter b of Eq. 1 is shown in Fig. 2d. pB_partial at M = 104 is stabilized as ΔF < 0 when the coupling of the local spring constant to the translational displacement motion Δr_i + Δr_j is in a range of 0.1 Ų < b < 3.7 Ų. ΔF is much less sensitive to the coupling to Δr_i – Δr_j, and pB_partial is stable in a relatively wide parameter range of a > 0.04 Ų. ΔF is insensitive to δ of Eq. 1; thus, the self-consistent coupling between the translational displacement motion and the conformational disorder is a most important factor in the model to explain the transition from pR to pB. With a moderate value of b = 0.5–2 Ų, the difference in free energy between two minima, M ≈ 104 and M ≈ 119, is about k_BT₀, and the activation energy for the transition between minima is a few k_BT₀ as shown in Fig. 2c. Because this activation energy is sufficiently smaller than a gap in V_chrom, pB is approximately in equilibrium as a mixture of the pB_partial state and the folded state at M ≈ 119, in which the system converts from one state to the other on a time scale faster than milliseconds, which can be estimated from the folding rate of comparative small proteins (35). The two-state picture of the pB intermediate is consistent with the two-state model of pB proposed by Craven et al. (24), which was supported by NMR (24), Fourier transform infrared (26), CD (28) and Nile red fluorescence (29) studies.

The model used here is a simplified model based on the topology of PYP without relying on the sequential details. The agreement between the model and experiments indicates that, given such a topological reason, the N-terminal domain, which is not directly interacting with pCA, is unfolded in pB upon destabilization of pG. For the same reason, we can expect that the state at M ≈ 104 in the dark state of ^transpCA should resemble pB. Indeed, the unfolding intermediate generated from pG by changing pH or adding denaturants in the dark condition shares many common features with pB and is referred to as pB_dark (47–49). The similarity between pB and pB_dark suggests that transitions in PYP are primarily governed by the cooperative effects arising from its topology.

Dynamical Transition and Proteinquake: A Unified Picture of Hierarchical Functioning Dynamics. By comparing Figs. 3 and 4a, we can see that changes in the low-frequency normal modes at a fixed M dominate the net change in the C^α fluctuations. The slowest mode largely contributes to both the N-terminal unfolding and the global increase in mean square deviation in the core domain (Fig. 4a, black line). Other low-frequency modes make dominant contribution in the local fluctuation in the region surrounding pCA (Fig. 4a, red and blue lines), whereas high frequency modes are localized in the rigid regions (Fig. 4a, green bars).

Fig. 4.

Normal mode analysis and crosscorrelation. (a) Difference in mean square deviation of the pB_partial (M = 104) from pG. Contribution of the slowest mode n = 1 (black line), the sum of n = 2–6 (red line) and the sum of n = 7–11 (blue line) modes, and the sum of the fastest 10 modes (×10), n = 115–124 (green vertical bars), where n denotes the mode number. (b) Crosscorrelation maps. The upper triangle is for the pG state, and the lower triangle is for the partially unfolded intermediate, pB_partial.

Further insights on the role of vibrational motions are obtained by examining their correlations. Fig. 4b shows the crosscorrelation of fluctuations in pG and pB_partial defined by C_ij = 〈Δr_i·Δr_j〉_M/[〈Δr_i·Δr_i〉_M 〈Δr_j·Δr_j〉_M]^1/2. C_ij > 0 when the ith and jth residues tend to move in the same direction, whereas C_ij < 0 when they tend to move in opposite directions. In pG, there are positive distinct correlations only in the vicinity of native contacts and C_ij ≈ 0 for the rest parts, whereas in pB_partial the correlation between the N-terminal domain and the core domain is significantly negative and the correlation within the N-terminal domain or within the core domain is largely positive. This clear difference in correlations in pG and pB_partial indicates that the unfolding of the N-terminal domain induces a collective motion extending globally across the N-terminal and core domains.

This collective motion plays decisive roles in the transition from pR to pB in the model. Because unfolding at the N-terminal domain and the collective motion are strongly coupled, as shown in Fig. 4a, unfolding and the collective motion should be concurrently induced. Because the collective motion is not localized in the N-terminal domain but extends over the global region and enhances the translational displacement around pCA as shown in Fig. 4b, it should reduce the spring constant γ_ij through the factor ρ (Δr_i, Δr_j) in the vicinity of pCA when b in Eq. 1 has a moderate value as designated in Fig. 2d. This reduction of γ_ij reflects the loosening of packing around pCA, which produces a favorable molecular environment for the isomerized and protonated pCA. Entropy gain around pCA is earned in the thusly generated pB state with the partial unfolding at the N-terminal domain and the structural loosening around pCA, which makes pB_partial more stable than the tightly folded state. The dynamical communication between the N-terminal unfolded region and residues around pCA cooperatively stabilizes the pB state, so that we may call the transition to pB the “dynamically mediated transition” or “dynamical transition.”

In the crystalline environment, the amplitude of the collective motion should be reduced, which prohibits communication between the N-terminal domain and the core domain and suppresses partial unfolding at the pB state, which can explain the lack of unfolded structure in the crystalline pB state (21, 22). The dashed line in Fig. 2c mimics the free energy surface of the mutant Glu-46-Gln. In this mutant Gln-46 cannot provide a proton, so that pCA has to be stabilized in a different way (25, 49) in which the structural disturbance around pCA might be confined in a narrower region in space and the partial unfolding should be suppressed. We may be able to assume that reisomerization of pCA is catalyzed in a rather structured environment of pB. Then, the returning rate to pG should be roughly proportional to the population of the folded pB, which is controlled by the equilibrium balance between the unfolded and folded states in pB. Thus, the recovery of pG in the crystalline PYP or in Glu-46-Gln, in which pB is dominated by the folded conformation, should be much faster than in the wild type in solution. This expectation is consistent with experimental results of kinetics of the crystalline wild type (21, 22) and Glu-46-Gln (50).

It is interesting to note that the dynamical transition from pR to pB in the present model has some analogy to the universal dynamical transition in proteins in the low temperature regime of 150–220 K (51): Hierarchically distributed motions of different amplitudes on different time scales are cooperatively coupled to induce a transition between the rigidly frozen state and the loosely fluctuating state upon changing temperature. We may be able to expect also in the present system that the dynamical transition to the partially unfolded state is sensitive to temperature. Such temperature dependence will be observed as the nonlinear temperature dependence in kinetics of pG recovery.

The dynamical transition from pR to pB is a process of proteinquake, in which the global conformational changes are triggered by a local structural “fault” (15, 25). We may be able to expect that this proteinquake mechanism due to the coupling among hierarchically distributed motions works in other allosteric systems. Because the scenario presented here is largely based on the topology of the native structure, other proteins having PAS or PAS-related domains, (18, 52) such as the light-oxygen-voltage domain (53) or GAF (54) domain, may have the common mechanism of conformational dynamics with PYP.

Protein Photochemistry: A New Scenario. The photocycle of PYP is schematically illustrated in Fig. 5. Upon absorption of a blue-light photon, pCA in the pG state is electronically excited to a higher energy state. The excited chromophore, then, relaxes to the pR state through the trans to cis isomerization (ref. 17 and references therein and refs. 45 and 46). In the course of this isomerization the ground and excited electronic states cross each other in a nonadiabatic way. After relaxing to pR, PYP goes back to pG in an adiabatic way by tracing the lowest electronic surface. This process at a glance resembles the usual photochemical cycle found in many other molecular systems (55). The present PYP photocycle, however, is profoundly different from the typical photochemical process in having additional huge degrees of freedom of the protein conformational dynamics. The protonation of pCA triggers the proteinquake, involving the partial unfolding at the N-terminal domain. The returning path from pR to pG thus takes a detour, passing the partially unfolded intermediate, pB_partial. The pB state is entropically stabilized to have a prolonged lifetime. Indeed, in crystal in which the proteinquake is suppressed, the returning rate to pG is much larger than in solution (22, 25). The partially unfolded pB in solution consists of many different conformations, and the detour returning to pG should take multiple pathways connecting those conformations. It would be interesting to pursue the possibility of the similar scenario in other proteins by assuming that intermediates in solution are different from those in crystal. Considering the analogy between photochemistry and allostery (11), it should also be important to examine the possibility whether the proteinquake mediated by the collective motions as discussed here plays important roles in allosteric systems.

Fig. 5.

Schematic illustration of the coupling between the photochemical reaction of the chromophore, pCA, and the protein unfolding/refolding processes in the photocycle of PYP. Arrows indicate pathways of the photocycle in the energy landscape: orange arrows, the photo-excitation and the trans to cis isomarization of pCA; green arrow, the protonation of pCA; yellow arrows, the dynamical transition between the folded and partially unfolded pB states; purple arrows, the reisomarization of pCA and the recovery of pG; red arrow, the pathway from pR to pB in crystalline environment.

Conclusions

The conformational change from the folded pR to the partially unfolded pB in the photocycle of PYP is a dynamical transition induced by a cooperative effect between the loosening of packing around the chromophore and the unfolding of the N-terminal domain through the global collective motion. The pB intermediate consists of multiple conformational states and converts from one state to the other. The present model indicates that the coupling among structural fluctuations on the hierarchically distributed time scales controls the kinetic features of the functioning process of PYP.