Model for anaphase B: Role of three mitotic motors in a switch from poleward flux to spindle elongation

Abstract

It has been proposed that the suppression of poleward flux within interpolar microtubule (ipMT) bundles of Drosophila embryonic spindles couples outward forces generated by a sliding filament mechanism to anaphase spindle elongation. Here, we (i) propose a molecular mechanism in which the bipolar kinesin KLP61F persistently slides dynamically unstable ipMTs outward, the MT depolymerase KLP10A acts at the poles to convert ipMT sliding to flux, and the chromokinesin KLP3A inhibits the depolymerase to suppress flux, thereby coupling ipMT sliding to spindle elongation; (ii) used KLP3A inhibitors to interfere with the coupling process, which revealed an inverse linear relation between the rates of flux and elongation, supporting the proposed mechanism and demonstrating that the suppression of flux controls both the rate and onset of spindle elongation; and (iii) developed a mathematical model using force balance and rate equations to describe how motors sliding the highly dynamic ipMTs apart can drive spindle elongation at a steady rate determined by the extent of suppression of flux.

Chromosome segregation depends upon the action of the spindle, a protein machine that uses ensembles of kinesin and dynein motors plus microtubule (MT) dynamics to move chromatids polewards (anaphase A) and to elongate the spindle (anaphase B) (1). Anaphase B is driven in part by a bipolar kinesin-dependent sliding filament mechanism (2–9), with the extent of spindle elongation determined by MT polymerization in the overlap zone (2). Poleward flux, the movement of tubulin subunits from the MT plus ends facing the spindle equator to their minus ends at the poles (10–14), is proposed to constrain the length of metaphase spindles, with subsequent inhibition of depolymerization at the poles converting metaphase flux to anaphase spindle elongation (12, 15, 16).

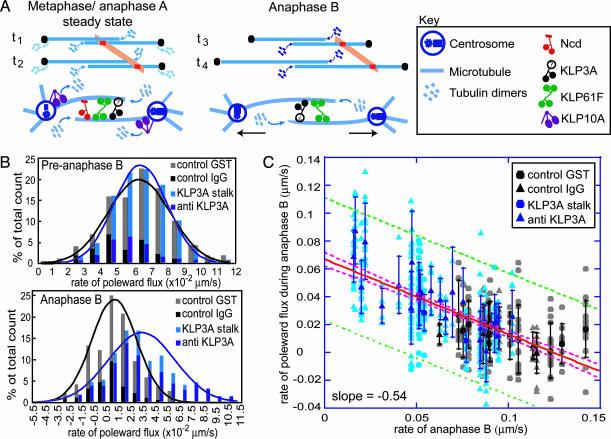
In support of this hypothesis, we observed that a suppression of poleward flux occurs at anaphase B onset: tubulin speckles within interpolar MTs (ipMTs) of Drosophila embryonic spindles fluxed toward the stationary poles of preanaphase B (herein meaning metaphase–anaphase A) spindles, but during anaphase B the speckles moved apart at the same rate as the poles (12). Here, we propose that three mitotic motors play critical roles in this process, based on previous studies (Fig. 1A). First, the bipolar kinesin KLP61F drives a sliding filament mechanism that underlies spindle elongation, because inhibiting KLP61F (in an Ncd-null mutant to circumvent the collapse of prometaphase spindles) inhibits anaphase B (9). Second, the kin I kinesin KLP10A depolymerizes ipMTs at the poles of preanaphase spindles, converting sliding to poleward flux; its inhibition leads to the premature suppression of flux and spindle elongation (14), suggesting that it is down-regulated at the onset of anaphase B. Finally, the chromokinesin KLP3A organizes ipMTs into bundles and is required for efficient anaphase spindle elongation (17).

Fig. 1.

Qualitative model for anaphase B and experimental test of the model. (A) Dynamics of spindle poles (black dots), ipMTs (overlapping blue lines) that add or lose tubulin subunits (blue), and tubulin speckles (orange) at time points t1 and t2 (preanaphase B) and t3 and t4 (anaphase B). In preanaphase B, pole–pole spacing remains constant, and opposite end assembly/disassembly is associated with poleward flux (orange). In anaphase B, depolymerization at the poles ceases, and ipMT sliding drives pole–pole separation; thus, speckles move away from the equator at the same rate as the poles. In the molecular model of anaphaseB, the turning off of depolymerization at the poles by inhibiting KLP10A allows KLP61F-driven ipMT sliding to push the poles apart. KLP3A organizes ipMTs into bundles, whereas the braking action of Ncd is turned off before anaphase B onset. (B) Histograms of the rates of flux in preanaphase B (Upper) and anaphase B(Lower) spindles in control (gray) and KLP3A-inhibited (blue) embryos. The number of counts was normalized to the total number. Note that there are large variations in the flux rate, and when the mean is near zero, some values are negative. (C) During anaphase B, the rates of poleward flux and spindle elongation are linearly inversely related. Data points display the behavior of individual fluorescent tubulin speckles within individual spindles of control (gray) and KLP3A-inhibited (blue) embryos; darker symbols represent the mean for each spindle. The red line is the best fit to the data; the pink and green dashed lines are the 95% confidence intervals for the best fit line and data points, respectively.

Here, we report experimental and theoretical results that provide a quantitative description of anaphase B dynamics in terms of these molecular mechanisms and reveal that the rate of anaphase spindle elongation is determined by (i) the unloaded rate of ipMT sliding and (ii) the extent of reduction of ipMT depolymerization at the poles.

Materials and Methods

Drosophila Stocks and Embryo Preparation. Flies were maintained and 0- to 2-h embryos were collected as described (9, 17). Embryos expressing GFP::tubulin were provided by Allan Spradling (Carnegie Institution, Washington, DC). Embryos were microinjected with rhodamine-conjugated bovine tubulin (Cytoskeleton, Denver), allowed to recover for 5 min, and microinjected with affinity-purified anti-KLP3A tail antibodies or purified recombinant KLP3A stalk proteins at concentrations ranging from 20 to 30 mg/ml (17). Control embryos were injected with identical concentrations of preimmune IgG or rabbit IgG (Sigma) or GST proteins.

Fluorescent Speckle Microscopy (FSM) and 3D Reconstructions. MT flux was imaged and measured as described (12), by using an Olympus (Melville, NY) microscope equipped with an Ultra-View spinning disk confocal head (Perkin–Elmer) and a 100× 1.35-numerical aperture objective with a time interval of 1.5 sec. Images were analyzed by using metamorph imaging software (Universal Imaging, West Chester, PA). Kymography was used to quantify speckle movement. Calculations and statistical analyses were done on Microsoft excel. For 3D reconstructions, embryos were injected with rhodamine tubulin, and z-stacks were acquired at 0.2-μm steps. The stacks were deconvolved, and projections and cross sections were generated by using autovisualize and autodeblur (Auto-Quant Imaging, Watervliet, NY).

Fluorescence Recovery After Photobleaching (FRAP). Embryos expressing GFP-tubulin were imaged on a Zeiss 510 Meta confocal microscope with a 63× 1.40-numerical aperture objective at 23°C. Areas of 12–20 μm² in the center of the spindle were bleached and time-lapse images were acquired. Total fluorescence intensity in the bleached area was measured as a function of time and fit to an exponential recovery by using kaleidagraph (Synergy Software, Reading, PA).

Computational Modeling Methods. We used random number generators to simulate the initial ipMT configurations and fluctuations in polymerization/depolymerization rates. The explicit Euler method [in matlab (Mathworks, Natick, MA)] was used to solve the equations of motion for the ipMTs on a desktop computer.

Supporting Information. Supporting Text, which provides details of the calculations, and movies of computer simulations are available as supporting information, which is published on the PNAS web site.

Results

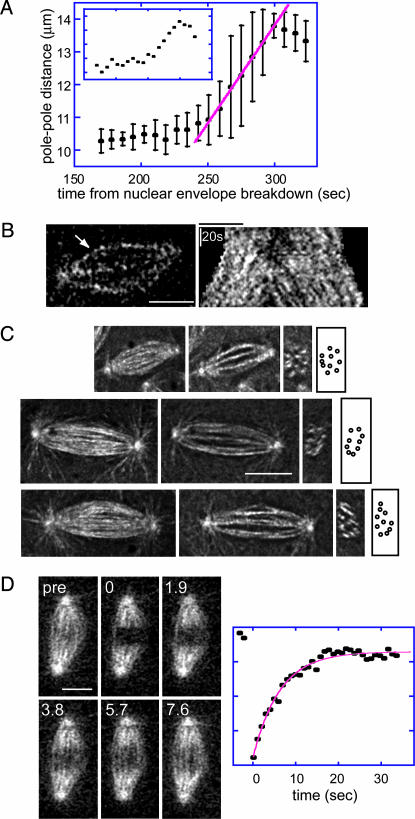
Experimental Results. The rates of poleward flux and anaphase spindle elongation are inversely related. We examined the relationship among poleward flux, ipMT sliding, and spindle length in Drosophila embryos. Plots of spindle pole separation versus time (Fig. 2A) reveal that the preanaphase B spindle maintains a constant length, and FSM (18) shows that tubulin speckles flux persistently poleward within ipMT bundles (Fig. 2B). During anaphase B, the spindle elongates at a linear rate (Fig. 2 A), and speckles move away from the equator at the same rate as the poles, consistent with ipMT sliding (Fig. 2B). To explain these dynamic events, we hypothesized that the suppression of flux couples ipMT sliding to spindle elongation (Fig. 1 A).

Fig. 2.

Organization and dynamics of ipMT bundles in Drosophila embryonic anaphase B spindles. (A) Pole–pole separation versus time during preanaphase B (160–250 sec) and anaphase B (250–300 sec). Spindle elongation is linear. Main graph, average data from multiple spindles; the standard deviation arises from variations in the linear rate between different spindles. (Inset) Typical spindle. Red line, regression line fit to the mean. (B) FSM of ipMT bundles. The kymograph (Right) during preanaphase B and anaphase B [for the bundle indicated by the arrow (Left) during anaphase B] shows that tubulin speckles flux away from the equator throughout. (C) ipMTs. Longitudinal projections (Left), XY sections (Center Left), transverse sections (Center Right), and cartoons of transverse sections (Right) reveal approximately nine ipMT bundles per spindle. (D) MT turnover determined by FRAP. Micrographs of a spindle before (pre) and after (time in seconds) photobleaching (Left) and the plot of fluorescence intensity (arbitrary units) versus time after photobleaching (Right) reveal that tubulin turnover in the central spindle is fast (recovery half time of 4.5 sec in this example). (Bar, 5 μm.)

We were able to test this hypothesis by microinjecting embryos with antibody and dominant negative protein inhibitors of the chromokinesin KLP3A, which interfere with spindle elongation during anaphase (17). These inhibitors have no effect on the rates of poleward flux during preanaphase B but surprisingly cause poleward flux to persist after anaphase B onset (Table 1 and Fig. 1B), suggesting that inhibiting KLP3A somehow inhibits the down-regulation of ipMT depolymerization at the poles that normally occurs at anaphase B onset. These experiments reveal that the rate of poleward flux within ipMT bundles displays an inverse linear relation with the rate of pole–pole separation (Fig. 1C), so that low flux rates correlate with high anaphase B rates. This provides evidence that the suppression of poleward flux within ipMT bundles (plausibly resulting from a loss of KLP10A activity) couples ipMT sliding to spindle elongation, thereby controlling the onset and rate of anaphase B.

Table 1. Poleward flux during the preanaphase B steady state and anaphase B.

	Preanaphase B flux, μm/s	Anaphase B poleward flux, μm/s
Control IgG	0.053 ± 0.017 (93/13/3)	0.008 ± 0.016 (51/8/3)
Anti-KLP3A	0.055 ± 0.016 (107/19/5)	0.035 ± 0.030 (258/30/6)
Control GST	0.066 ± 0.021 (295/12/2)	0.014 ± 0.020 (136/11/2)
KLP3A stalk	0.066 ± 0.017 (365/18/3)	0.034 ± 0.021 (83/7/3)

Parentheses indicate the number of speckles, spindles, and embryos, respectively, that were analyzed.

Dynamics of ipMTs in the central spindle. 3D reconstructions of deconvolved spinning disk confocal images (Fig. 2C) reveal approximately nine robust-looking ipMT bundles in a Drosophila embryonic spindle. Previous electron microscopies (8) reveal that these ipMT bundles, which are not highly ordered, have an average overlap of ≈1 μm in early anaphase B and contain ≈30 MTs per bundle per half spindle. We used FRAP to study the dynamics of these ipMTs in the anaphase B central spindle and observed a surprisingly rapid recovery of GFP::tubulin fluorescence (Fig. 2D; recovery half time of a 2-μm bleach zone was 3–6 sec). This recovery is much faster than observed in other systems (19) but is an order of magnitude slower than the characteristic diffusion time of free tubulin dimers, assuming a diffusion coefficient of ≈8 μm²/sec (20), and presumably reflects turnover due to dynamic instability of ipMT plus ends displaying overall growth, combined with the poleward translocation of bleached and unbleached ipMT segments into and out of the bleach zone, in accordance with FSM data (Fig. 2B). How does such a dynamic array of ipMTs elongate the spindle at the steady linear rate observed?

Mathematical Model for Anaphase Spindle Elongation. We developed a model to address the above question, to provide a quantitative description of anaphase B dynamics in terms of the underlying molecular events, and to identify testable predictions.

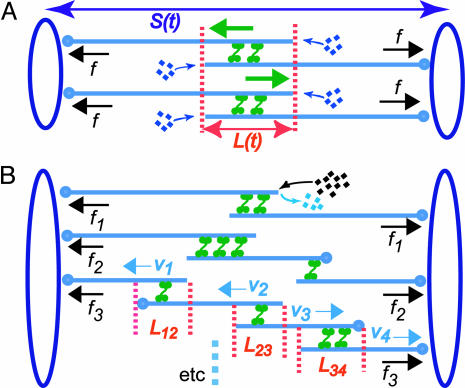
Model definitions and assumptions. (i) The state variables, S(t) and L(t), are pole–pole and ipMT overlap distances at time t, respectively (Fig. 3A), and their time derivatives are the rate of change of these distances. (ii) V_sliding(t) denotes the time-dependent rate of sliding apart of ipMTs, which, we propose, corresponds to the observed rate of speckle movement away from the spindle equator. We assume that each sliding motor is characterized by a linear force–velocity relationship (ref. 21; Fig. 5, which is published as supporting information on the PNAS web site) that the action of multiple motors is linearly additive, and that the number of force-generating motors is proportional to the overlap length L(t). We assume that the sliding motors work against an effective viscous drag imposed by the separating spindle poles (effective drag coefficient, μ). (iii) 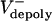is the average rate of depolymerization of ipMT minus ends, which, we propose, corresponds to the flux rate. In the model, we assume that ipMT minus end depolymerization is confined to the poles and does not occur in the spindle itself. 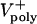is the mean rate of polymerization of the dynamic plus ends of ipMTs, determined by dynamic instability parameters. (iv) The validity of the quantitative model presented below is independent of the identity of the sliding and depolymerizing motors involved, even though its development and interpretation proceeded in the context of a specific molecular model (Fig. 1 A). Therefore, in the model results, we assume that ipMT sliding is driven predominantly by KLP61F motors, based on evidence that the antagonistic motor, Ncd, is turned off before anaphase B, and the complementary motor, cortical dynein, acts only during late stages of anaphase B (9), but we cannot rule out contributions from unknown force generators. We also assume that minus end depolymerization of ipMTs is due to KLP10A activity at the poles (14).

Fig. 3.

Model spindle geometry. (A) A simplified spindle with two identical arrays of ipMTs, each composed of two overlapping antiparallel MTs. Here, ipMTs have the same overlap, and their plus ends polymerize at the same rate. S(t) is the pole–pole distance, and L(t) is the length of the ipMT overlap. Green arrows indicate sliding of ipMTs by bipolar motors; black arrows indicate the motor-generated forces, equal to f for both ipMT arrays. (B) A realistic spindle with ipMT arrays composed of two, three, and four overlapping MTs. In the lower ipMT array, the overlap length between the parallel (L₁₂ and L₃₄) and antiparallel (L₂₃) MTs and the sliding velocity of each MT (V₁, V₂, V₃, and V₄) is indicated. The dynamic instability of the plus ends, resulting in an average net polymerization, is shown only for the left MT in the top ipMT array. Forces generated by bipolar motors in different ipMT arrays (e.g., f₁, f₂, and f₃) are different.

Model equations. The model consists of a system of multiple coupled differential equations, based on three core equations that pertain to a simplified spindle composed of identical and stable ipMTs (Fig. 3A), where anaphase B spindle dynamics (Fig. 2 A and B) can be explained by the simple kinematic equation

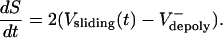[1]

Let us assume that the sliding of ipMTs occurs at a constant average rate throughout metaphase and anaphase, i.e., V_sliding(t) = V_sliding. If in preanaphase B spindles V_sliding = 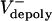, then dS/dt = 0, and the spindle maintains a constant length; if at anaphase B onset the flux rate and thus 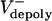decrease to almost zero, the spindle elongates at a linear rate (Fig. 2 A).

Although this equation is adequate for an idealized highly ordered spindle (Fig. 3A), where flux and sliding exactly balance to maintain the isometric preanaphase B spindle, and sliding coupled to polymerization of stable ipMTs elongates the anaphase B spindle at a linear rate, the assumption that the sliding velocity is constant rather than being a time-dependent variable is an oversimplification. In reality, the sliding rate could vary due to fluctuations in the load per motor caused by changes in the overlap region, L(t), and to the increase in viscous drag that occurs as the poles start to move at anaphase B onset.

To account for this complication, Eq. 1 is coupled with the following two equations that describe the dynamics of the overlap region and the force–velocity relations of the ipMT sliding motors:

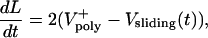[2]

and

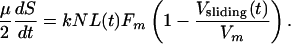[3]

The kinematic equation (Eq. 2) describes the rate of change of the antiparallel overlap region in each ipMT array (Fig. 3A) and is needed because the number of motors sliding ipMTs apart depends on the overlap length, L(t). The force–balance equation (Eq. 3) states that the resistance to spindle elongation at rate dS/dt (left-hand side) is equal to the net outward force on the poles (right-hand side) generated by motors sliding apart ipMTs at rate V_sliding(t). It incorporates the assumed linear force–velocity relationship for one motor, f = F_m (1 – V_sliding(t)/V_m), where F_m is the maximal “stall” force, and V_m is the maximal “unloaded” motor velocity. k is the number of motors per ipMT overlap length, kL is the total number of engaged motors, N is the number of ipMT arrays, and kNL is the total number of motors.

Realistic situation. The spindle has a complicated architecture (Fig. 3B), with ipMT arrays composed of a few interconnected MTs of variable parallel and antiparallel overlaps (4, 8). In addition, the plus ends of MTs undergo dynamic instability, resulting in rapid and asynchronous changes in each overlap. Therefore, individual MTs are likely to slide at different rates, and different ipMT arrays may generate forces of different magnitude. The kinematics of the spindle poles and the overlap regions, as well as the force-generating and dynamic properties of each ipMT, can be described by using equations similar to those introduced above. Consider, for example, the lower ipMT array in Fig. 3B, which pushes the poles apart at a rate determined by the sliding velocities, V₁(t) and V₄(t), combined with the MT depolymerization rate at the poles, thus

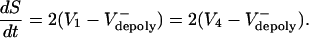[4]

The kinematics of the overlap regions in this ipMT array depend upon the polymerization rate of the MT plus ends and their sliding velocities, e.g., for L₂₃,

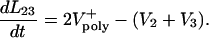[5]

To accommodate the highly dynamic nature of the interzone, we use dynamic instability parameters consistent with our FRAP and FSM data (Table 2, which is published as supporting information on the PNAS web site).

Finally, the force generated by the lower ipMT array is given by

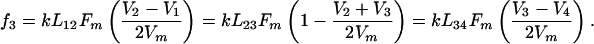[6]

(See Supporting Text). Assuming that the forces are additive, we calculate the total motor-generated sliding force as the sum of the force generated in the ith ipMT array over all ipMTs, F_total= Σ_i f_i, balanced by the viscous resistance on the poles:

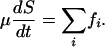[7]

Consideration of the kinematics (Eqs. 4 and 5) and forces (Eq. 6) associated with each ipMT, together with the force–balance equation (Eq. 7), yields a large system of coupled equations describing the elongation of a realistic spindle (Fig. 3B).

Model Results. The system of equations was repeatedly solved numerically (see Supporting Text) to calculate the dynamic evolution of realistic ipMTs (typically up to 90 ipMT arrays), varying the model parameter values (Table 2) and initial conditions (see Supporting Text). Solutions are displayed as computer animations (Movies 1–5, which are published as supporting information on the PNAS web site) and graphs (Fig. 4).

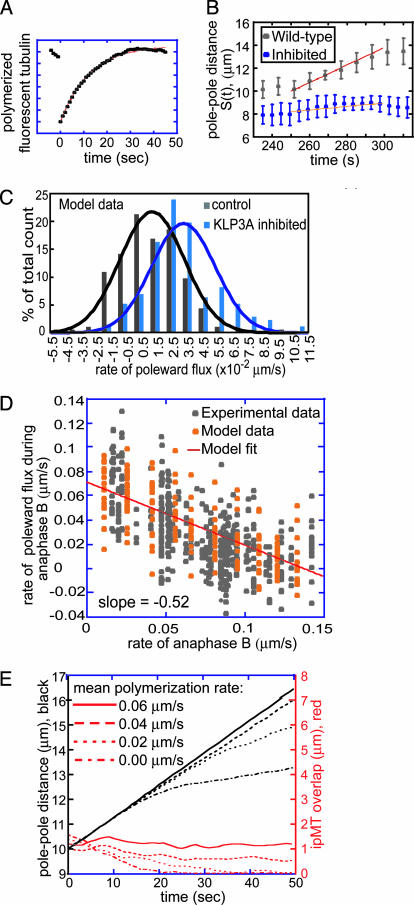
Fig. 4.

Model results. (A) FRAP simulation. 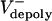= 0 μm/sec. (B) Experimental and theoretical plots of pole–pole separation [S(t)] versus time during anaphase B. Control (gray) and KLP3A-inhibited (blue) data and theoretical curves (red, control; orange, KLP3A-inhibited). 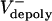= 0.015 and 0.055 μm/sec for control and KLP3A-inhibited embryos, respectively. (C) Histograms of the rates of flux in anaphase B in control (gray) and KLP3A-inhibited embryos (blue) obtained by numerical solutions. 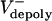= 0–0.03 and 0.02–0.07 μm/sec for control and KLP3A-inhibited embryos, respectively. The flux rate exhibits large variances similar to the experimental data (Fig. 1B). (D) Numerical results for the flux and spindle elongation rates in spindles where 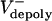alone has been varied ( 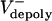= 0–0.07 μm/sec). The model solutions (orange) are superimposed on the data from Fig. 1C (gray). (E) Plots of pole–pole distance [S(t), black] and ipMT overlap [L(t), red] for various rates of 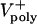. During the first half of anaphase B, the poles separate steadily at a velocity independent of the polymerization rate (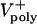). However, the ipMT overlap is affected by 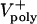. Note the small fluctuations in L(t) due to dynamic instability. The catastrophe frequency was varied as 0.04, 0.08, 0.16, and 0.2/sec to yield the indicated polymerization rates. 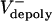= 0 μm/sec. The initial average overlap is 1–1.5 μm, n = 30, f_rescue = 0.2/sec, and f_catastrophe = 0.02/sec, unless indicated otherwise. All unspecified parameter values are given in Table 2.

The animations (Movies 1–4) vividly display the dynamic relationship among poleward flux, dynamic instability of ipMT ends, ipMT sliding, and spindle elongation at large flux rates (high 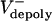, corresponding to preanaphase B or KLP3A-inhibited anaphase B spindles), or at low flux rates (low 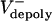, corresponding to control anaphase B spindle elongation). At high flux rates, the spindle maintains a constant length, because the outward sliding apart of ipMTs, growing and shrinking at their plus ends, is converted to flux by depolymerization at the poles. At low flux rates, ipMT sliding drives spindle elongation at a steady rate despite the highly dynamic nature of the overlap.

The model provides a very good description of the fast ipMT turnover within the elongating spindle interzone (Fig. 2D). Movie 5 shows a simulation of FRAP in a 2-μm-wide region of the central spindle and yields recovery kinetics in good agreement with the experimental FRAP data (Fig. 4A).

The solutions to the model equations displayed as graphs of S(t) versus time, histograms, and anaphase B–flux rate relationship (Fig. 4) were all in good agreement with the experimental data, supporting the idea that our molecular model can account for anaphase B dynamics. Plots of S(t) versus time show that, despite the dynamic nature of the overlap zone and the increase in load as the poles start moving at anaphase B onset, KLP61F motors continue to work in the “unloaded” regime throughout (see Supporting Text) and are capable of sliding apart ipMTs and elongating the spindle at a steady linear rate (Fig. 4B). This rate is determined only by the unloaded rate of KLP61F-driven sliding and the extent of suppression of flux (Fig. 4D).

Variations of up to an order of magnitude in other model parameters, e.g., the maximal motor force, number of ipMTs, number of motors, viscous drag, dynamic instability of ipMT plus ends, and the mean ipMT plus end polymerization rate, as well as deviations from linearity in the force–velocity curves, have no significant effect on the rate of spindle elongation, at least initially. Fig. 4E, for example, shows that reasonable values of the mean ipMT plus end polymerization rate (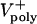) support a steady, linear rate of pole–pole separation throughout anaphase B. However, decreasing the polymerization rate does influence the spindle elongation rate during the second half of anaphase B(>25 sec), but in the embryo this could be compensated by the pulling activity of cortical dynein (14). Note that, even when the mean polymerization rate is zero, the spindle can elongate, albeit at a reduced rate, plausibly due to KLP61F (now working close to stall), pushing apart those ipMTs that happen to be growing (Supporting Text). Consequently, under conditions of low 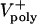, a small increase in the drag or any other external load should slow down KLP61F-driven spindle elongation.

Discussion

This work provides a quantitative description of the observed dynamics of anaphase spindle elongation in terms of a simple molecular mechanism (Fig. 1 A), in which the ipMTs are slid apart by KLP61F motors plausibly working close to their free sliding rate, in both the elongating spindle and the preanaphase spindle, Remarkably, despite the dynamic, somewhat disorganized nature of the ipMTs, the sliding motors can develop a total force an order of magnitude greater than the characteristic viscous resistance to spindle pole movement, enabling them to drive steady, linear spindle elongation. The rate at which the persistently sliding ipMTs elongate the spindle depends on the extent of suppression of KLP10A activity, and KLP3A plays an unexpected coupling role in the switch from poleward flux to spindle elongation.

Predictions of the Model. The model predicts that experimentally perturbing the mean ipMT growth rate or increasing the drag force up to an order of magnitude should not affect the rate of spindle elongation, but changing the unloaded sliding velocity of KLP61F motors should. The idea that KLP61F slides ipMTs at a constant velocity throughout predicts that it contributes to poleward flux within ipMTs, and an obvious prediction of our model is that KLP10A is down-regulated at anaphase B onset. Finally, the model predicts that when V_sliding = 0, and spindle length does not change, there should be no flux. These predictions are under investigation.

Role of KLP3A. KLP3A appears to couple ipMT sliding to spindle elongation by a mechanism more complex than simply facilitating KLP61F-driven sliding (17). We propose that, by organizing ipMTs into robust bundles, it influences the critical ratio of active KLP10A to ipMT minus ends at the poles. In controls, this ratio decreases substantially at anaphase B onset, when some hypothetical signal turns off KLP10A activity, so depolymerization is suppressed and the spindle elongates. In KLP3A-inhibited embryos, ipMT bundles are disorganized, and fewer minus ends are focused at the poles. In preanaphase B spindles, the rate of depolymerization remains at control levels, because the rate at which ipMTs are slid and fed into the poles is limiting, but at anaphase B onset, the ratio of residual KLP10A to ipMT ends remains high, allowing depolymerization and flux to persist, inhibiting spindle elongation. Although this remains to be tested experimentally, computer simulations using varying ratios of KLP10A to ipMT minus ends support the hypothesis (see Fig. 6, which is published as supporting information on the PNAS web site).

Variance in the Flux Rates. On individual spindles, we observed high variance in the rates of poleward flux (Fig. 1C) but not in the rates of spindle elongation (Fig. 2 A Inset), which depends on multiple MTs acting on each pole at once, thus averaging out the variance. A quantitative analysis of the variance in flux rates reveals that it may be due to fluctuations in KLP10A activity and/or Poisson fluctuations in the number of subunits disassembled from the MT minus ends at the poles. Other potential causes, such as tracking errors, velocity variance due to the motor-dependent shearing of parallel MT segments within ipMT bundles (refs. 4 and 8; Fig. 3B), or fluctuations in the rate constants of mechanochemical coupling by the sliding motors, appear insufficient to account for the large variance (see, Supporting Text).

Limitations of the Model. Our model does not address the formation or function of preanaphase B spindles or the contribution of additional mechanisms to anaphase B, e.g., KLP61F sliding ipMTs against a spindle matrix, or dynein/astral MTs pulling the poles apart (see Movies 6 and 7, which are published as supporting information on the PNAS web site). It does show that, despite the highly dynamic nature of the central spindle, our sliding filament-based model can account for steady anaphase spindle elongation, at least initially, and additional mechanisms are not necessary. However, if there is no ipMT polymerization (V⁺_poly) at the equator, linear spindle elongation during the second half of anaphase B (Fig. 4E) may require an additional component, plausibly cortical dynein (9).

Implications for the Rate of Mitosis. The Drosophila early embryo carries out multiple mitoses very rapidly (cell cycle duration, ≈10 min). Accordingly, both anaphase B spindle elongation and anaphase spindle ipMT turnover occur faster than in other systems (e.g., refs. 19 and 22), yet KLP61F motors work at the same slow rate as bipolar kinesins from diverse organisms (23). Based on our data (Figs. 1C, 4D, and Fig. 7, which is published as supporting information on the PNAS web site), we propose that the rate of elongation of different spindles may be governed by the extent of down-regulation of depolymerization at the poles. This would be completely turned off in Drosophila embryos, providing maximal coupling and allowing ipMT sliding to drive elongation at the maximum rate, but, in other spindles, the partial down-regulation of flux may produce a slower elongation rate. In contrast, in different muscle fibers, changes in sliding motor activity via changes in the rate of ADP release by myosin II governs the rate of fiber shortening (24).

Conclusion

This model, supported by experimental data, describes the dynamics of anaphase B in terms of a plausible molecular mechanism in which the onset and rate of spindle elongation are controlled by the suppression of poleward flux. The model is an advance toward a quantitative description of mitosis and can be generalized to describe spindle length-determining mechanisms operating elsewhere (25).