Human Facial Shape and Size Heritability and Genetic Correlations

Abstract

The human face is an array of variable physical features that together make each of us unique and distinguishable. Striking familial facial similarities underscore a genetic component, but little is known of the genes that underlie facial shape differences. Numerous studies have estimated facial shape heritability using various methods. Here, we used advanced three-dimensional imaging technology and quantitative human genetics analysis to estimate narrow-sense heritability, heritability explained by common genetic variation, and pairwise genetic correlations of 38 measures of facial shape and size in normal African Bantu children from Tanzania. Specifically, we fit a linear mixed model of genetic relatedness between close and distant relatives to jointly estimate variance components that correspond to heritability explained by genome-wide common genetic variation and variance explained by uncaptured genetic variation, the sum representing total narrow-sense heritability. Our significant estimates for narrow-sense heritability of specific facial traits range from 28 to 67%, with horizontal measures being slightly more heritable than vertical or depth measures. Furthermore, for over half of facial traits, >90% of narrow-sense heritability can be explained by common genetic variation. We also find high absolute genetic correlation between most traits, indicating large overlap in underlying genetic loci. Not surprisingly, traits measured in the same physical orientation (i.e., both horizontal or both vertical) have high positive genetic correlations, whereas traits in opposite orientations have high negative correlations. The complex genetic architecture of facial shape informs our understanding of the intricate relationships among different facial features as well as overall facial development.

HUMAN appearance is comprised of a remarkably variable set of physical traits. Of all externally visible characteristics, facial appearance is both the most morphologically variable and the most distinctive and recognizable. Facial appearance involves a major genetic component, with each of the many structural features that define facial shape and appearance themselves likely determined by a multiplicity of genes, with environmental variables such as nutrition and environmental toxins, exerting increasing influence over time (Fitzgerald et al. 2010). Nevertheless, the striking similarity of facial appearance within families, often across many generations, suggests that certain key genes exert particularly large effects on facial shape and appearance.

Facial shape is measured in various ways, including specific linear measurements between defined morphological points as well as complex quantitative measurements of the entire face. Previous estimates of the heritability of facial shape distances and angles were principally derived by direct measurements between common facial morphometric landmarks on human faces, cephalograms, and skulls. These estimates vary widely; in general, facial height dimensions tend to be more heritable than width (Manfredi et al. 1997; Carson 2006; Amini and Borzabadi-Farahani 2009; AlKhudhairi and AlKofide 2010), in contrast with the rest of the skull, for which heritability of width tends to be greater than for height (Martínez-Abadías et al. 2009a,b, 2012).

The genetic architecture of facial shape variation has been studied more extensively in mice than in humans. In the mouse, measures of craniofacial morphology are highly heritable (Leamy 1977; Klingenberg and Leamy 2001; Klingenberg et al. 2001; Percival et al. 2016). Further, the mouse skull is highly integrated in terms of phenotypic and genetic correlations (Leamy 1977; Cheverud 1982). Genetic and environmental correlations also tend to be similar, likely due to their basis in similar developmental connections among traits (Cheverud 1982).

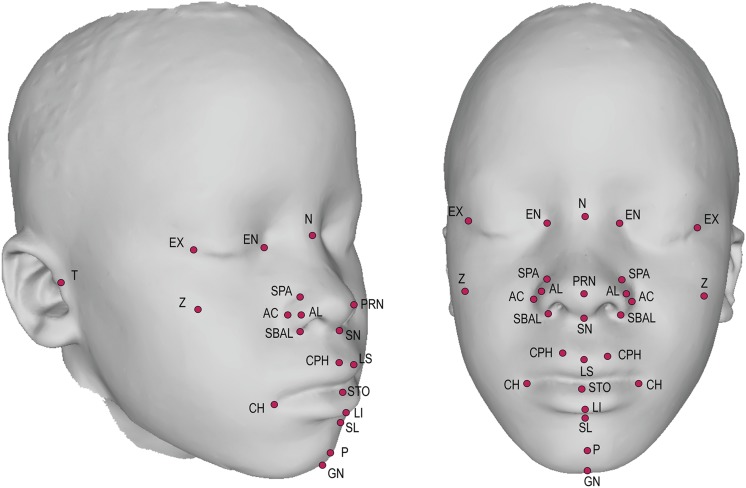
Morphological assessment of facial variation has typically required manual landmarking, an approach that is slow, labor intensive, and error prone; complicating its application to large-scale studies as well as comparisons across multiple studies. As an advance toward standardized, replicable phenotyping of human facial traits, we combined advanced three-dimensional (3D) imaging technology with a novel automated landmarking method (Li et al. 2016) to derive precise, detailed, and informative facial phenotypes from 29 standard facial morphometric landmarks (Supplemental Material, Table S1) (Bookstein 1997).

Our study, based on Bantu children from Tanzania, avoids facial shape variation that occurs later in life due to injury, weight gain, and disease. Moreover, these African children are very lean, with minimal variation related to facial adiposity, and furthermore have significant occult relatedness, providing the opportunity to formally analyze the heritability of facial shape phenotypes in this population.

To assess heritability, we analyzed genotypes of >15 million common SNPs with minor allele frequencies >1% using Genome-wide Complex Trait Analysis (GCTA) (Yang et al. 2010, 2011). We estimated narrow-sense heritability (h²); heritability explained by common genetic variation (h²_g); and pairwise genetic correlations of 38 facial phenotypes, incorporating close family structures into a joint linear mixed model with two variance components, one representing the genetic relatedness between close relatives and the other representing the genetic relatedness between all individuals in the study (Zaitlen et al. 2013). The phenotypic variance was then partitioned into variance explained by common genetic variation, variance explained by close genetic relationships but not common genetic variation, and the remaining residual variance explained by the environment.

We found that facial shape and size phenotypes are highly heritable, and additionally are highly genetically correlated, and that a large fraction of the genetic component of facial differences can be explained by common variation genome-wide. Our findings help elucidate the complex genetic relationships and pathways underlying facial shape, augment basic biological understanding of facial development, enable better modeling of facial shape based on genetic correlations, and may assist in delineation and diagnosis of facial dysmorphism syndromes.

Materials and Methods

Study subjects

Samples and data were collected from 3631 Bantu African children aged 3–21 over a 3-year period in the Mwanza region of Tanzania. Subjects with a known birth defect or a relative with known orofacial cleft or facial birth defect were excluded. Additional data collected were age, sex, height, weight, head circumference, school, and detailed parental and grandparental ethnicity, and tribe information. Subjects with non-Bantu tribal ancestry in one or more grandparents were excluded from the study. Written informed consent was obtained from all study subjects or their parents as appropriate.

3D facial imaging and automated landmarking

3D images were obtained using the Creaform MegaCapturor 3D photogrammetry imaging system. Each subject was imaged twice at six standard positions. Meshes were reconstructed at the highest possible resolution and assembled using Inspeck software to form a complete 3D mesh of the face (Figure 1).

Figure 1.

3D facial scan with annotated landmarks. Landmarks annotated are defined in Table S1.

A set of 29 morphometric facial landmarks (Figure 1 and Table S1) was applied to each individual facial mesh using a novel automated landmarking method (Li et al. 2016). Briefly, this method morphs a 29-landmark template (created from a training set of manually landmarked faces) to each individual face through the guidance of anchor points defined by the local curvature features of the face. Presenting the same image to the automated landmarking system twice generates identical landmark positions. Errors, when they occur, tend to be fairly large, readily detectible, and easily removed.

Derivation of phenotypic variables

Landmarks were subjected to Procrustes superimposition for geometric morphometric analysis (Bookstein 1997; Dryden and Mardia 1998; Mitteroecker and Gunz 2009). Superficial artifacts (smiling, squinting, mouth open, lateral nasal deformity, etc.) were identified by manual quality inspection of each facial mesh, and were corrected using a multiple linear model in which all factors and their interactions were considered. For each correction, we determined the significance of the artifact using a Procrustes distance permutation test on age- and size-adjusted data. We performed the corrections jointly using a linear model in R to avoid overcorrection caused by overlap among the artifacts. Additionally, we determined whether the corrections affected biological signals such as the estimates of ontogenetic or static allometry and the heritabilities of the traits. For all artifacts, we performed canonical variate analysis both before and after to visualize the effect of the correction (Figure S1 and Figure S2).

An additional artifact in 3D photogrammetry is “skew,” defined as coordinated asymmetric displacement of landmarks due either to variation in assembly of the facial views to produce the assembled mesh or from parallax. Most landmarks are affected by skew when it occurs, but individuals are not equally affected. Therefore, we regressed the landmark data on the principal component (PC) scores for PCs corresponding to skew variation. Skew corrections have minimal effects on most subjects but graded effects on those toward the ends of the skew PC. Figure S2 shows morphs that correspond to the extreme skew values in the sample. Skew corrections were applied to the linear distances as this improved heritability, but not to the multivariate measures as this did not affect heritability. We validated artifact and skew corrections by determining their influences on the estimates of allometric shape variation and on heritabilities.

We obtained 25 linear distance phenotypes representing heights, widths, and depths of different facial structures from the fully corrected landmark coordinates after restoring size. Size was calculated as centroid size, as is standard in geometric morphometrics (Mitteroecker and Gunz 2009). Table S2 lists means and standard deviations for all linear distances and centroid size.

Multivariate measures were calculated from artifact but not skew-corrected data. We removed variation related to age and size in symmetrized landmark data using multiple multivariate regression and centering the residuals on the sample mean (Klingenberg and Zimmermann 1992; Klingenberg 1998). Symmetrizing the data removes facial asymmetry variation. While there is biological variation in asymmetry, this did not significantly affect the first 10 PCs, aside from the skew artifacts discussed above. The age-shape relationship is nonlinear, particularly when an analysis includes both young children and adults. Within our sample, however, polynomial fits for age or centroid size did not significantly improve the fit (Figure S3). As our sample mostly excludes the major shape changes occurring early in facial growth and the slowing of changes that occur in late ontogeny, linear regression sufficiently captures the shape variation associated with age and centroid size. Shape variation related to size, or static allometry, was estimated using the regression scores corresponding to size independent of age. We obtained the scores for the first 10 PCs based on the age and size-standardized landmark coordinate data (Figure S4). All references to PCs in the results refer to the PC scores derived from the phenotypic data.

We used Klingenberg’s permutation test for Escoffier’s RV coefficient to identify the set of spatially contiguous landmarks that maximized the ratio of covariation among themselves to covariation with landmarks outside of that set (Klingenberg 2009). This method does not consider overlapping determinants of covariation structure (Hallgrímsson et al. 2009), but it reveals sets of strongly covarying, spatially adjacent landmarks. The resulting set, defined by the nasal region and upper lip (Figure S5), was subjected to separate Procrustes alignment, and a principal component analysis (PCA). The first PC (40% of variance) served as a measure of variation within this “module.”

The final phenotype values then adjusted for biological covariates as follows: multivariate measures including all PCs and allometry were adjusted for sex; linear distances were adjusted for age, sex, and centroid size (after age-sex adjustment); and centroid size was adjusted for age and sex. In this way, all multivariate measures and linear distances were corrected for age, sex, and size prior to downstream analysis. Phenotypic correlations used throughout are based on phenotype residual correlations on a subset of unrelated individuals. All morphometric analyses were done in MorphoJ (Klingenberg 2011) or in R using the Geomorph (Adams and Otárola-Castillo 2013; Adams et al. 2014) and Morpho (Schlager 2016) packages.

Genome-wide genotyping and quality control

Genome-wide genotyping, quality control, and imputation of 3480 study subjects used in these analyses were described previously (Cole et al. 2016). The final postquality-control dataset included 3480 individuals with complete phenotyping information and imputed genotypes at >15 million markers with INFO scores >0.30. A sensitivity analysis comparing heritability estimates from the full imputed data set and from a data set of only genotyped markers demonstrated no bias in using imputed genotypes (Figure S6).

Heritability estimates

Both h² and h²_g were estimated using GCTA software (Yang et al. 2010, 2011). We fit a joint linear mixed model with two variance components for each phenotype as described (Zaitlen et al. 2013). Briefly, one variance component represented close relatives only, in which any pairwise genetic correlation in the full genetic relatedness matrix as calculated by GCTA <0.05 was set to 0. Specifically, our variance component highlighting close relationships contained 4425 pairwise relationships ≥0.05 from a total of 2937 individuals in each triangle half of the matrix. While this variance component represents a small proportion of all pairwise relationships in our sample (0.07%), it includes 84% of our total sample. Therefore the “missing heritability” explained by this additional variance component of close relatives is based on a large number of independent nuclear families, and thus is not biased by a small number of large families (Figure S7). Heritability estimates obtained using different relatedness thresholds demonstrated that 0.05 was both unbiased and conservative when compared to 0.00 and 0.025. The other variance component represented the full genetic relatedness matrix for all individuals. The joint model uses 4,307,014 more pairwise comparisons from 3480 individuals to estimate h²_g than the traditional GCTA unrelateds only model (n = 1869), using their recommended relatedness threshold cutoff value of 0.025 (Table S3) (Yang et al. 2010). GCTA uses restricted maximum likelihood to estimate the variance of each component, the sum of which represents total genetic variance, used for calculating h². By default, GCTA estimates that escape from the parameter space were set to 1.0 × 10⁻⁶ × phenotypic variance. To adjust our significance threshold for multiple testing of correlated phenotypes, we performed PCA of the 38 phenotype residuals in unrelated individuals to determine the number of effectively independent phenotypes. The first 11 eigenvectors had eigenvalues >1, making them each representative of at least one phenotype. We divided the traditional P < 0.05 threshold by 11, making our significance threshold P < 0.0045.

To calculate heritabilities and genetic variances for each landmark, we obtained the genetic and phenotypic variance-covariance matrices for the symmetrized landmarks. This leaves out one dimension for midline landmarks and treats the landmark coordinates for both sides as a single variable. Heritabilities are calculated as the ratio of genetic to phenotypic variance for each landmark coordinate. We then used a heatmap method to visualize these variance components across the face. Here, each component is represented as a vector that has a length proportional to the variance component, an origin at each landmark, and a direction parallel to a vector that connects each landmark to the landmark centroid. These vectors are then used to produce a face morph using the thin-plate-spline method that is then superimposed on the unmorphed mean face to generate a heatmap.

Genetic correlation

Genetic correlations between all phenotypes were also estimated using GCTA software (Yang et al. 2011). We eliminated PC8 and LS_STO, for which the joint heritability LRT models were not significant (Table 2), from the genetic correlation matrix. Due to nonconvergence of such a large parameter space, 148/630 bivariate analyses failed the joint analysis and instead, for the sake of having a complete genetic correlation matrix, were fit by the standard GCTA approach, using a single genetic relatedness matrix of only unrelated individuals (n = 1869). Of those 148 bivariate models, 36 failed the single component model of unrelateds due to constraining genetic or environmental components. To construct a complete genetic correlation matrix, we estimated these 36 values based on both univariate and bivariate models of the traits affected. If the bivariate model’s genetic component was constrained or the univariate model’s heritability estimate was less than the SE of that estimate, we set the genetic covariance to 1.0 × 10⁻⁶ × phenotypic covariance. If the bivariate model’s environmental component was constrained or the univariate model’s heritability was essentially equal to one, we set the genetic covariance as equal to the total phenotypic covariance between the two traits. Therefore, the genetic correlation matrix represents only the shared genetic correlation which can be explained by >15 million common variants. Table S4 includes all h²_g genetic correlation estimates, SE, and models in which those values were derived.

Table 2. Heritability of 38 facial traits.

Trait	h2g	SE (h2g)	h2	SE (h2)	LRT P-valuea	h2g/h2	SE (h2g/h2)
PC7	0.669	0.138	0.669	0.072	1.00 × 10−17b	1.000	0.560
T_R_T_L	0.521	0.138	0.662	0.075	1.00 × 10−17b	0.786	0.482
Allometry	0.643	0.132	0.643	0.072	1.00 × 10−17b	1.000	0.562
Centroid Size	0.277	0.134	0.641	0.076	3.66 × 10−15	0.432	0.335
N_MEN	0.260	0.134	0.639	0.075	3.89 × 10−16	0.406	0.322
AL_R_AL_L	0.623	0.131	0.623	0.076	1.00 × 10−17b	1.000	0.575
PC4	0.604	0.131	0.604	0.075	5.55 × 10−17	1.000	0.583
PC2	0.579	0.139	0.579	0.074	1.00 × 10−17b	1.000	0.607
EX_R_EX_L	0.421	0.141	0.566	0.076	8.11 × 10−14	0.744	0.509
N_PRN	0.456	0.142	0.544	0.075	3.94 × 10−15	0.839	0.562
EN_EX	0.208	0.140	0.522	0.078	4.35 × 10−10	0.399	0.360
N_T	0.419	0.136	0.512	0.076	4.52 × 10−14	0.819	0.564
PC5	0.211	0.138	0.491	0.077	6.33 × 10−10	0.430	0.385
N_STO	0.443	0.140	0.490	0.076	2.22 × 10−13	0.903	0.621
GN_T	0.487	0.140	0.487	0.076	2.97 × 10−12	1.000	0.663
SN_LS	0.486	0.130	0.486	0.077	5.26 × 10−11	1.000	0.651
SN_T	0.469	0.139	0.486	0.076	2.97 × 10−13	0.966	0.650
PC3	0.308	0.139	0.478	0.078	2.03 × 10−10	0.643	0.504
PC1	0.477	0.140	0.477	0.076	5.76 × 10−13	1.000	0.672
PC8	0.074	0.137	0.471	0.079	2.50 × 10−8	0.158	0.223
N_SN	0.244	0.137	0.456	0.075	1.95 × 10−10	0.535	0.455
PC9	0.431	0.125	0.452	0.076	1.16 × 10−13	0.953	0.643
MidfaceModPC1	0.433	0.138	0.433	0.078	2.23 × 10−9	1.000	0.706
N_GN	0.159	0.137	0.426	0.078	1.11 × 10−7	0.373	0.380
EN_R_EN_L	0.392	0.142	0.411	0.076	2.09 × 10−9	0.952	0.699
AC_PRN	0.311	0.140	0.410	0.079	1.47 × 10−7	0.758	0.604
SN_GN	0.239	0.139	0.386	0.079	8.70 × 10−7	0.619	0.546
CH_R_CH_L	0.378	0.137	0.378	0.077	7.99 × 10−6	1.000	0.747
SBAL_R_SBAL_L	0.373	0.134	0.373	0.080	2.76 × 10−6	1.000	0.754
LI_SL	0.177	0.134	0.342	0.077	5.61 × 10−6	0.518	0.510
SN_PRN	0.242	0.139	0.340	0.074	1.37 × 10−6	0.711	0.629
CPH_R_CPH_L	0.337	0.126	0.337	0.077	3.45 × 10−6	1.000	0.775
STO_LI	0.324	0.139	0.324	0.075	2.48 × 10−5	1.000	0.810
SN_STO	0.314	0.131	0.314	0.079	1.57 × 10−5	1.000	0.819
PC10	0.291	0.140	0.291	0.080	0.000570	1.000	0.860
STO_SL	0.283	0.134	0.283	0.078	0.000102	1.000	0.863
PC6	0.169	0.131	0.169	0.077	0.0152	1.000	1.10
LS_STO	0.076	0.116	0.076	0.077	0.259	1.000	1.61

h², h²_g, and the proportion of narrow-sense heritability explained by common genetic variants (h²_g/h²), all with SE.

^aLRT P-value for the joint model vs. the null model (H₀: h² = 0).

^bLRT P-value was reported as 0, indicating it was less than the GCTA limit 1 × 10⁻¹⁷.

Data availability

Phenotype data were deposited in FaceBase (https://www.facebase.org/; accession number: FB00000667.01). Genotype data were deposited in the Database of Genotypes and Phenotypes (dbGaP) (http://www.ncbi.nlm.nih.gov/gap; accession number: phs000622.v1.p1). This study was carried out with overall approval and oversight of the Colorado Multiple Institutional Review Board (protocol #09-0731), was additionally approved by the institutional review boards of the University of Calgary, Florida State University, the University of California San Francisco, and the Catholic University of Health and Allied Sciences (Mwanza, Tanzania), and was carried out with the approval of the National Institute for Medical Research (Tanzania).

Results

Study population and phenotypes

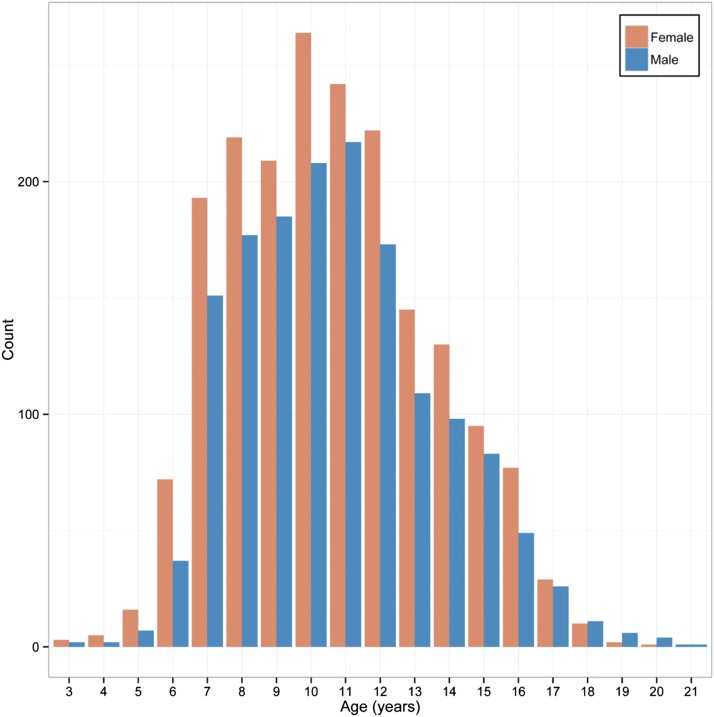
The study population consisted of 3480 normal African Bantu children and adolescents ages 3–21 from the Mwanza region of Tanzania. Over 70% of subjects were aged 7–12, and 44.4% were male and 55.6% female (Figure 2). As described previously (Cole et al. 2016), PCA of population substructure demonstrated minimal genetic clustering and an analysis of fixation index demonstrated no apparent subgroups by school or tribe.

Figure 2.

Study age distribution by sex.

For each subject, we captured 3D facial scans, applied 29 standard facial morphometric landmarks (Figure 1 and Table S1) (Bookstein 1997), derived 38 facial shape phenotypes based on the landmarks, carried out genome-wide SNP genotyping, and used these data to estimate h² and h²_g for each phenotype. These facial phenotypes represent several different classes, including 3D summary variables in the form of PCs derived from PCA of the whole face and PCA of the most highly correlated landmarks positioned around the midface, interlandmark linear distances, and global measures of overall facial size and the relationship between size and shape (Table 1). In addition, for each subject we obtained height and weight, from which we calculated body mass index (BMI). Analysis of these data showed that the mean BMI of the study population was ∼1 SD below the 2007 World Health Organization world standards (Figure S8). Furthermore, the correlations between all age- and sex-adjusted facial traits with age- and sex-adjusted BMI in unrelated individuals are small (r² = −0.18 to 0.14), suggesting that BMI is not a confounding factor in our study population.

Table 1. The 38 facial phenotypes derived from landmarks on 3D facial scans.

Phenotype abbreviation	Physical description
PCA
PC1	upper facial height, midfacial width
PC2	overall facial height, lower facial height
PC3	upper and middle facial width
PC4	width of the nose, mandible height
PC5	nose shape, height of the mouth
PC6	nasal width, maxillary prognathism
PC7	nasal root shape, mouth width
PC8	cheek protrusion
PC9	midface protrusion, upper facial height
P10	chin height, nasion protrusion
PC1 from a PCA of the midfacial landmark  network (MidfaceModPC1)	midfacial landmark network around the nose and mouth
Size-related measurements
Centroid size	facial size
Allometry	variation in shape due to size
Linear distancesa
AL_R_AL_L	nasal width
AC_PRN	nasal ala length (average)
CH_R_CH_L	mouth width
CPH_R_CPH_L	philtrum width
EN_EX	palpebral fissure length (average)
EN_R_EN_L	inner canthal width
EX_R_EX_L	outer canthal width
GN_T	lower facial depth (average)
LI_SL	cutaneous lower lip height
LS_STO	upper vermilion height
N_GN	morphological facial height
N_MEN	nasion to midendocanthion
N_PRN	nasal bridge length
N_SN	nasal height
N_STO	upper facial height
N_T	upper facial depth (average)
SBAL_R_SBAL_L	subnasal width
SN_GN	lower facial height
SN_LS	philtrum length
SN_PRN	nasal protrusion
SN_STO	upper lip height
SN_T	midfacial depth (average)
STO_LI	lower vermilion height
STO_SL	lower lip height
T_R_T_L	facial width

^aLinear distances are the distance between two landmarks (e.g., AL_R and AL_L).

Heritability of facial phenotypes

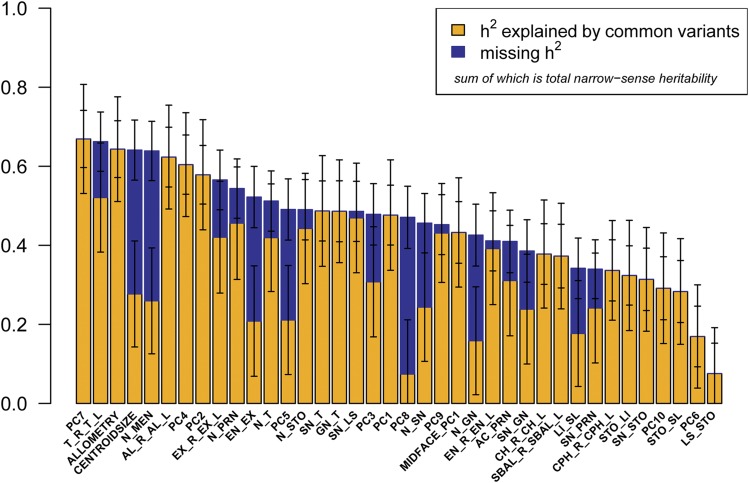
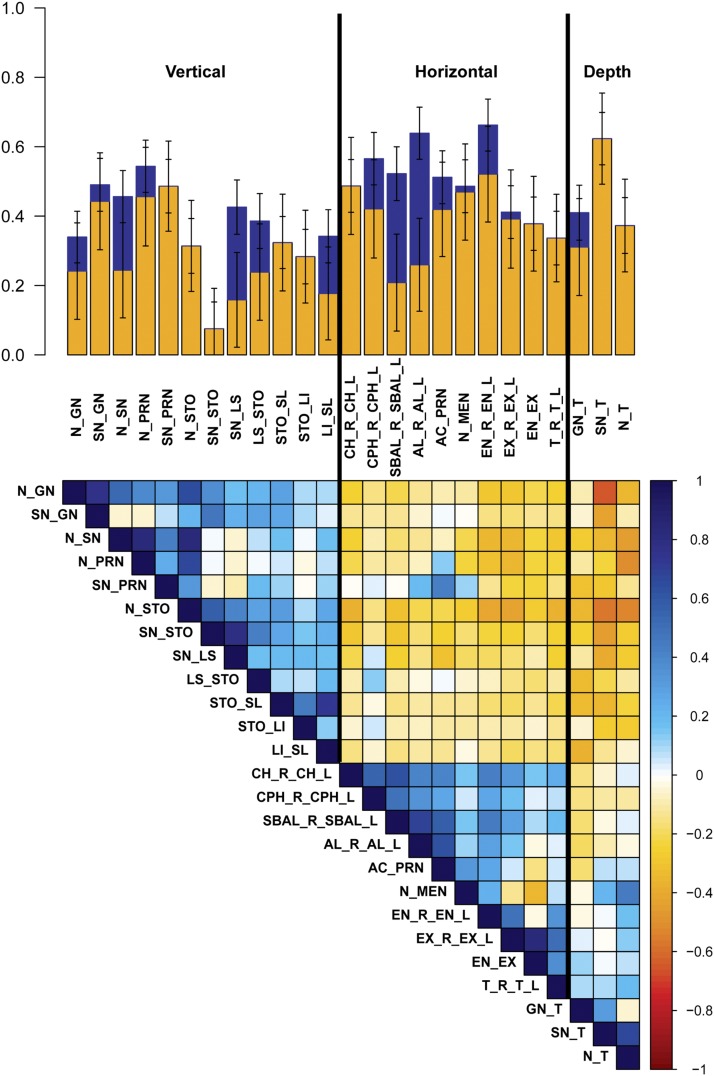
As shown in Figure 3 and Table 2, 36 of our 38 phenotypes were significantly heritable (P < 0.0045), with h² 28.3–66.9%. The most heritable facial traits include PC7, representing nasal root shape and mouth width (h² = 66.9%, SE = 7.2%); total facial width (T_R_T_L) (h² = 66.2%, SE = 7.5%); the allometric variable (h² = 64.3%, SE = 7.2%); centroid size (h² = 64.1%, SE = 7.6%); and nasion to midendocanthion distance (N_MEN) (h² = 63.9%, SE = 7.5%). Furthermore, by combining genetic variance across all 10 orthogonal PCs, which explain >87% of total shape variation captured by sparse landmarking (Figure S4), we obtained a single global estimate of total facial shape of h² = 50.1%. Previous studies have suggested that vertical measures have greater heritability than horizontal measures (Manfredi et al. 1997; Carson 2006; Amini and Borzabadi-Farahani 2009; AlKhudhairi and AlKofide 2010). However, we observed a trend toward horizontal facial measures having greater heritability than vertical measures. Figure 4 depicts h² and h²_g estimates for the 25 linear distances, clustered by physical orientation and phenotypic correlation. The three facial depth measurements, lower facial depth (GN_T), midfacial depth (SN_T), and upper facial depth (N_T), share the tragion landmark and have very similar h² estimates (h² = 48.6%, SE = 7.6%; h² = 48.7%, SE = 7.6%; and h² = 51.2%, SE = 7.6%; respectively), but exhibit very different phenotypic correlations (GN_T:SN_T = 0.31, GN_T:N_T = −0.04, and SN_T:N_T = 0.67). Similarly, the three horizontal eye measurements, inner canthal distance (EN_R_EN_L), outer canthal distance (EX_R_EX_L), and average palpebral fissure length (EN_EX), likewise share some landmarks in common and have fairly similar h² estimates, (h² = 41.1%, SE = 7.6%; h² = 52.2%, SE = 7.6%; and h² = 56.6%, SE = 7.8%; respectively), but exhibit very different phenotypic correlations (EN_R_EN_L:EX_R_EX_L = 0.49, EN_R_EN_L:EN_EX = −0.03, and EX_R_EX_L:EN_EX = 0.82). In contrast, three midfacial horizontal measures, mouth width (CH_R_CH_L), philtrum width (CPH_R_CPH_L), and subnasal width (SBAL_R_SBAL_L), share no overlapping landmarks, have similar h² estimates (h² = 37.8%, SE = 7.7%; h² = 33.7%, SE = 7.7%; and h² = 37.2%, SE = 8.0%; respectively), and also exhibit fairly high phenotypic correlations (CH_R_CH_L:CPH_R_CPH_L = 0.55, CH_R_CH_L:SBAL_R_SBAL_L = 0.62, and CPH_R_CPH_L:SBAL_R_SBAL_L = 0.48). It appears that facial traits of similar orientation that either share overlapping morphological points or have high phenotypic correlations are influenced by additive genetic effects and environmental effects to similar degrees.

Figure 3.

Heritability of 38 facial traits. The bar plot represents h²_g (yellow), missing h² (blue), and total h² (yellow + blue) with error bars for all 38 facial phenotypes analyzed. Bars that apparently have no missing h² (blue) indicate that h²_g equals h²; therefore, narrow-sense heritability of that phenotype can be explained fully by common genetic variation.

Figure 4.

Heritability of linear distances by measurement orientation. The bar plot represents h²_g (yellow), missing h² (blue), and total h² (yellow + blue) with error bars for 25 linear distances. Traits are first clustered by orientation, then by facial structure with between-trait phenotypic correlations seen in the colored matrix in the bottom half of the figure.

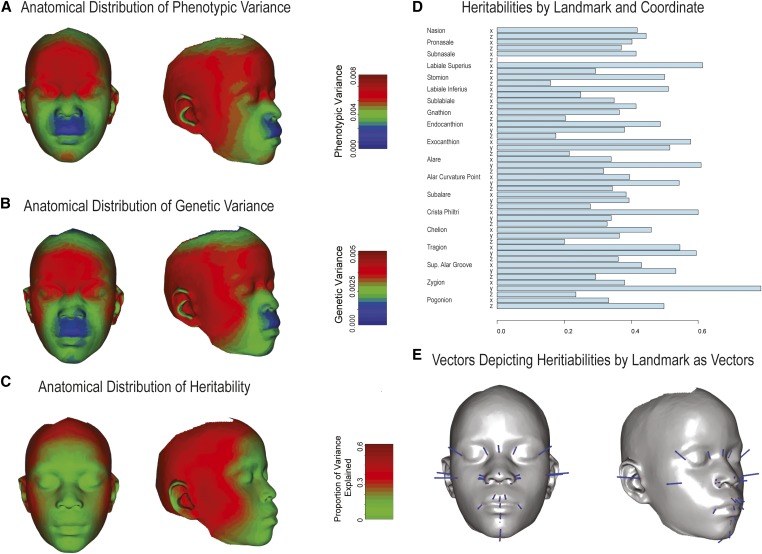
Figure 5 shows the anatomic distribution of phenotypic and genetic variance as well as heritability by landmark. The pattern is consistent with Figure 3 and Figure 4 in that the landmarks defining facial width and the orbital region tend to have higher genetic variances and heritabilities.

Figure 5.

Distribution of variance components across the face. (A–C) The anatomical distribution of phenotypic and genetic variances as well as heritabilities is shown. These are represented as heatmaps based on a thin-plate-spine morph as described in Materials and Methods. (D) The heritability estimates or the Procrustes-superimposed symmetrized landmarks are shown. (E) The vectors, magnified 10-fold, used to generate the heritability heatmap are depicted.

Genetic basis of observed heritability

For 22 of the 38 facial phenotypes analyzed, >90% of the narrow-sense heritability (h²) can be explained by the effects of common genetic variation (h²_g/h²). However, for a number of other traits, common variation (h²_g) accounts for <50% of h²; indicating significant additional genetic contributions beyond common variants that can be imputed for Africans from the Illumina HumanOmni 2.5-8 array, which captures 54% of common African variation (minor allele frequency >1%; http://www.illumina.com/content/dam/illumina-marketing/documents/products/datasheets/datasheet-human-omni2.5-exome-8.pdf). However, we caution that these conclusions are based on estimates of h²_g/h² that have high SE (Table 2). These traits include centroid size, nasion to midendocanthion (N_MEN), palpebral fissure length (EN_EX), PC5 representing nose shape and height of the mouth, PC8 representing cheek protrusion, and morphological facial height (N_GN).

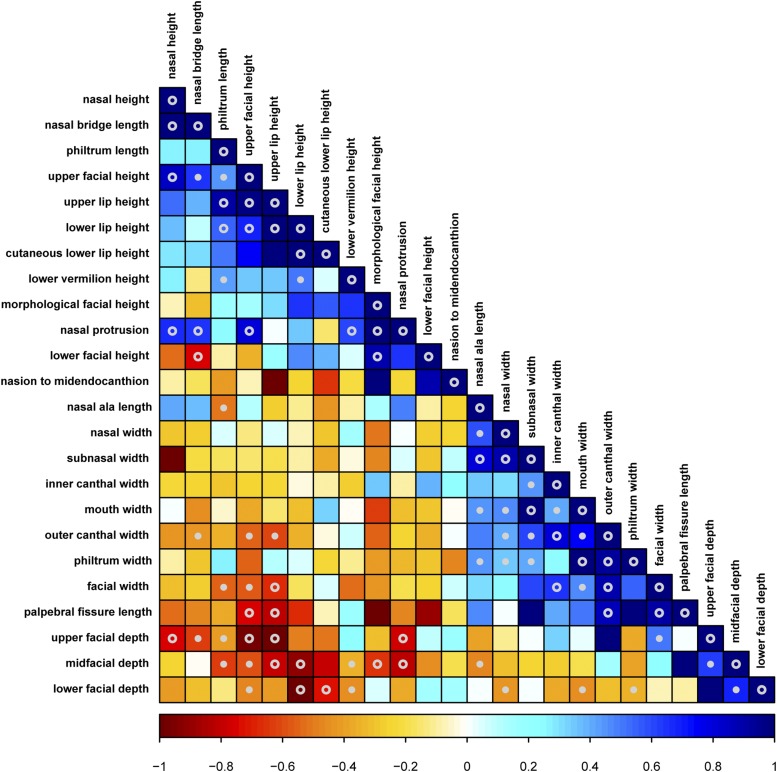
To elucidate underlying genetic relationships between different facial traits, we estimated pairwise genetic correlations between all significantly heritable traits (Table S4) and constructed a genetic correlation matrix of all significantly heritable linear distances (Figure 6). Due to lack of power to detect h² in joint bivariate models between all traits (Visscher et al. 2014), these genetic correlations are based on the genetic covariance calculated from >15 million common variants and not total genetic covariance, resulting in higher SE. Although not all genetic correlation estimates are significantly different from 0 (P < 0.05), Figure 6 depicts striking patterns of shared heritability among distinct facial traits. A number of horizontal measurements mostly defined by nonoverlapping landmarks have high positive genetic correlations with each other. These phenotypes include palpebral fissure length (EN_EX), outer canthal width (EX_R_EX_L), facial width (T_R_T_L), mouth width (CH_R_CH_L), subnasal width (SBAL_R_SBAL_L), philtrum width (CPH_R_CPH_L), and two PCs that both account for midfacial width (PC1 and MidfaceModPC1). We observed a similar pattern of high positive genetic correlations, though to a lesser extent, among midline vertical measurements. These include upper lip height (SN_STO), morphological facial height (N_GN), upper facial height (N_STO), PC2 representing both overall and lower facial height, lower lip height (STO_SL), and philtrum length (SN_LS). Importantly, the horizontal and vertical measurements exhibit large negative genetic correlations with each other, indicating that phenotypic variation along both horizontal and vertical measurements are largely caused by the same genetic variation acting to increase one direction while decreasing the other. In a simple sense, this means that the same alleles that cause an individual to have a broad face also cause that individual to have a short face, and vice versa.

Figure 6.

Pairwise genetic correlation matrix of the linear distances. Genetic correlation was calculated from >15 million common genetic variants. Traits that have high positive genetic correlations with each other are shown in blue, indicating that the same genetic loci alter the magnitude of those traits in the same direction. Traits that have high negative genetic correlations with each other are shown in red, indicating that the same genetic loci are contributing to each phenotype in opposite directions, increasing one while decreasing the other. Genetic correlation estimates that are significantly different (P < 0.05) from 0 to +1 or 0 to −1 are marked with ○ and genetic correlation estimates that are significantly different (P < 0.05) than 0, +1, and −1 are marked with ○.

Discussion

We report here the first estimates of both heritability and genetic correlation of facial shape phenotypes derived from 3D facial scans and true genome-wide genetic correlations between 1000s of individuals. Facial scans provide far more accurate measurements than previous approaches based on direct manual measurements between prominent facial features (Ozsoy et al. 2009). Furthermore, direct calculation of genome sharing from genome-wide data are more accurate than kinship coefficients used in traditional heritability analyses, which represent the average genetic sharing for any given relationship and not the actual genetic correlation for any specific pair of relatives (Hayes et al. 2009).

Our analysis, carried out in Bantu children from Tanzania, provides the opportunity to assess heritability of facial shape and size in a young, lean population. The choice of population is both a strength and a limitation of this analysis. In any population, heritability is determined by a combination of genetic variance and environmental influences. Variation in facial adiposity, for instance, is small in this population while it may be large in others (Figure S8) (Cole et al. 2016). The focus on children creates the need to adjust for age and size but also avoids facial shape changes that occur later in life due to injury, weight gain, and disease.

Not surprisingly, we found that many quantitative facial-shape phenotypes, derived with high accuracy from 3D facial scans, are highly heritable. Furthermore, most of these quantitative facial phenotypes can be explained by common genetic variants across the genome. In particular, based on h², several horizontal measurements including facial width (T_R_T_L; h² = 66.2%, SE = 7.5%), nasal width (AL_R_AL_L; h² = 62.3%, SE = 7.6%), outer canthal width (EX_R_EX_L; h² = 56.6%, SE = 7.6%), and palpebral fissure length (EN_EX; h² = 52.2%, SE = 7.8%) appear to be among the most heritable facial features; contrary to findings of previous heritability studies of the face. There are several obvious potential explanations for this difference. First, heritability of some facial attributes may be population specific, driven by different underlying genetic variants in different populations; thus reflecting differing underlying biological bases of facial shape and size. Second, the present study population, Tanzanian Bantu children, is a much leaner population than has been studied previously. BMI in our cohort of Tanzanian Bantu children is significantly lower than world standards (Figure S8) (de Onis et al. 2004) and is uncorrelated with our measures of facial shape after adjusting for age, sex, and centroid size (see Materials and Methods). Linear measures, particularly horizontal distances, collected in populations with higher BMI, may be more affected by excess subcutaneous fat, reflecting a greater environmental component, and thus proportionately smaller genetic component. Third, genetic influences on horizontal facial distances may be proportionately greater at younger ages, as in our cohort of children and adolescents ages 3–21, whereas these distances may become proportionately more affected by environmental components with increasing age. This model of age-related shape differences fits well with what is already known about how the face matures and morphs into the adult form. As the face reaches adult shape at ∼16 years of age (as determined in males of European descent), the midface undergoes a strong vertical expansion and becomes relatively taller than the rest of the face (Bastir et al. 2006).

The 10 PCs displayed similar heritabilities as the linear distances. PCs represent axes of covariation within the data and most combine variation from multiple if not most landmarks. A limitation of PCA is that the assumption that each PC is orthogonal to the previous may not map well onto the underlying biological determinants of covariation structure. In the absence of knowledge about those determinants, however, PCA is a widely accepted and rational approach to multivariate data. In this context, each PC represents a distinct facial shape transformation that emerges from the covariance structure of the data and can be treated as a univariate trait.

Interestingly, global facial size appears to be among the most heritable of facial traits. Allometry, a measure of the variation in shape due to size, has h² of 64.3% (SE = 7.2%). Centroid size, a measure of overall face size, has h² of 64.1% (SE = 7.6%). These findings indicate that there may be a strong genetic basis underlying global size of the face and how size drives shape variation; whereas facial shape per se, irrespective of size, may be somewhat more influenced by environmental factors. Although our findings also indicate that the majority of facial shape variation can be explained by the effects of common genetic variation, there were several facial phenotypes, including centroid size, for which h²_g did not explain the majority of h². Potential explanations for such missing heritability include variants not in linkage disequilibrium with variants on our array, rare causal genetic variants, uncharacterized structural variation, and epistatic effects. Our genome-wide association studies (GWAS) of these same facial traits in Africans identified two loci that were significantly associated with either centroid size or allometry (Cole et al. 2016); traits with high h² but variable h²_g. While these heritability estimates support an overall genetic contribution, the specific estimate of h²_g does not provide information on the magnitude of effect of contributing loci, and thus is not necessarily an indicator of GWAS success. Irrespective of the specific h²_g estimates for centroid size and allometry, our GWAS of 6300 individuals had the power to detect genetic determinants with relatively large effect sizes for both traits.

We observed high positive genetic correlations among variables that represent similar orientations on the face, and rather high negative genetic correlations among variables that represent different orientations. The highest genetic correlations, of horizontal measures across the facial midline, likely correspond to related genetic effects on biological relationships underlying facial structure during development, in which the two sides of the face meet and fuse at the midline (Sperber et al. 2001). The negative genetic correlations we observe between horizontal and vertical facial measures are consistent with overall phenotypic correlations between these measures. Furthermore, high positive and negative genetic correlations between a wide array of facial traits support the presence of a finite set of underlying genes involved in overall facial development.

Finally, our analysis of genetic variance and covariance structure shows that genetic variation in the face is both highly integrated and modular. Integration refers to the developmentally based tendencies for traits to covary (Hallgrímsson et al. 2009; Klingenberg 2013), while modularity refers to suites of traits connected by development (Wagner et al. 2007). We find a large number of both positive and negative correlations among traits, attesting to highly structured patterns of variation. For craniofacial morphology more generally, somatic growth, chondrocranial growth, and brain growth are known to drive such patterns of integrated variation in both mouse and human crania (Cooper et al. 2004; Hallgrímsson et al. 2006, 2009; Marcucio et al. 2011; Martínez-Abadías et al. 2012). Here, both facial size and facial shape allometry exhibit a pattern of genetic correlations with facial measures that capture aspects of facial height, midfacial width, and lower facial prognathism. This pattern of genetic correlations likely reflects the overall influence of somatic growth on facial shape, forming a developmentally based module within the face. Further work integrating developmental studies with results such as these will shed light on the mechanistic basis for the structure of variation in the face.

Supplementary Material

Supplemental material is available online at www.genetics.org/lookup/suppl/doi:10.1534/genetics.116.193185/-/DC1.