Cytoplasmic RNA-Protein Particles Exhibit Non-Gaussian Subdiffusive Behavior

Abstract

The cellular cytoplasm is a complex, heterogeneous environment (both spatially and temporally) that exhibits viscoelastic behavior. To further develop our quantitative insight into cellular transport, we analyze data sets of mRNA molecules fluorescently labeled with MS2-GFP tracked in real time in live Escherichia coli and Saccharomyces cerevisiae cells. As shown previously, these RNA-protein particles exhibit subdiffusive behavior that is viscoelastic in its origin. Examining the ensemble of particle displacements reveals a Laplace distribution at all observed timescales rather than the Gaussian distribution predicted by the central limit theorem. This ensemble non-Gaussian behavior is caused by a combination of an exponential distribution in the time-averaged diffusivities and non-Gaussian behavior of individual trajectories. We show that the non-Gaussian behavior is a consequence of significant heterogeneity between trajectories and dynamic heterogeneity along single trajectories. Informed by theory and simulation, our work provides an in-depth analysis of the complex diffusive behavior of RNA-protein particles in live cells.

Introduction

The central limit theorem states that the mean of a large number of independent identically distributed random variables with finite mean and variance will approximate a Gaussian distribution. Furthermore, the random variables need not be statistically identical if they satisfy certain conditions (such as the Lyapunov or Lindeberg conditions) (1). As a consequence of this theorem, random walk systems whose discrete steps are defined by random variables with finite mean and variance will exhibit a Gaussian distribution in the limit of many such steps. In the context of single-particle tracking, the Gaussian distribution is thus defined by its probability density function as

$$P_{\text{Gauss}}\left(\Delta x;\mu ,\sigma \right)=\frac{1}{\sigma \sqrt{2\pi }}\text{exp}\left[-\frac{{\left(\Delta x-\mu \right)}^2}{2{\sigma }^2}\right],$$ (1)

where Δx is the particle displacement in one dimension (1D) and μ and σ are the displacement’s mean and standard deviation values, respectively.

The classic works of Fick, Einstein, and Smulochowski define a diffusion equation for particles in solution whose only free parameter is the diffusivity $D=k_{\text{B}}T/\xi$, which is related to the solution temperature T by the Boltzmann constant $k_{\text{B}}$ and the drag coefficient ξ of the particle (2, 3, 4). Thus, diffusion of the particle is a consequence of random, thermally driven collisions with the solvent molecules, resulting in the particle displacement variance ${\sigma }^2=2D\Delta t$, where Δt is the length of time over which the displacements Δx occur (Eq. 1). Perrin (5) (and many others) experimentally confirmed the validity of this framework by showing that particle displacements in simple Newtonian solutions indeed exhibit a Gaussian distribution.

Despite the implications of the central limit theorem, there are many instances of experimental systems where particle diffusion exhibits non-Gaussian displacement behavior. In soft-matter systems, examples include beads diffusing on lipid tubes (6), in actin and agarose networks (6, 7, 8, 9, 10), in concentrated colloidal suspensions (11, 12), and in suspension with eukaryotic swimmers (13). For particles inside living cells, examples include RNA-protein particles and protein aggregates in Escherichia coli (14, 15) and Saccharomyces cerevisiae (16) and submicron colloidal tracers in the cytoplasm of human cell lines (17, 18). We suspect that there are many more examples to be found in biological systems, but studies involving single-particle tracking experiments in biological systems frequently do not report displacement distributions. The cause of the non-Gaussian behavior is generally thought to be due to the heterogeneity of the material’s environment and its fluctuations, resulting in a wide distribution of diffusivities whose behavior can span orders of magnitude of time (19).

In addition to the non-Gaussian behavior noted above, the cellular cytoplasm often displays viscoelastic properties (20). Particles moving passively in such an environment frequently exhibit subdiffusive behavior, defined as a mean-square displacement (MSD = $\langle {\left[x\left(t+\Delta t\right)-x\left(t\right)\right]}^2\rangle$) scaling as a power law ${\left(\Delta t\right)}^{\alpha }$, where $\alpha <1$. Examples include $\alpha \approx 0.7$ for RNA-protein particles in E. coli (14, 21) and S. cerevisiae (22), $\alpha \approx 0.7$ for lipid granules in fission yeast (23), $\alpha \approx 0.5$ for gold nanoparticles in several human and mammalian cell lines (24), and $\alpha \approx 0.5-0.8$ for dextrans in HeLa cells (25). Chromosomal loci also exhibit subdiffusive behavior, with $\alpha \approx 0.4-0.5$ for E. coli (26, 27), $\alpha \approx 0.5-0.7$ in budding yeast (28, 29), and $\alpha \approx 0.3$ for mammalian telomeres at timescales <10 s (30). Note that subdiffusive behavior does not necessarily imply non-Gaussian behavior, as models such as fractional Brownian motion exhibit Gaussian, anticorrelated increments resulting in anomalous diffusion (31). Conversely, non-Gaussian behavior can still exhibit normal diffusive dynamics (19).

In this study, we examine the trajectories of MS2-GFP bound mRNA as effective tracer particles in the cytoplasm of the bacterium E. coli and the eukaryote Saccharomyces cerevisiae (budding yeast). We use this system to better understand the local heterogeneity of the cytoplasm. We find non-Gaussian, subdiffusive behavior at all timescales measured in both organisms. Using individual-trajectory analyses, analytical theory, and simulation, we show that the non-Gaussian behavior is due to a combination of a wide distribution in the trajectory average diffusivities and local spatiotemporal heterogeneities in the individual trajectories, which are also non-Gaussian.

Materials and Methods

Strains

The E. coli strain used (a gift from I. Golding) is DH5α-Z1 carrying two plasmids, the first containing a GFP-MS2 protein fusion (pIG-K133) and the second encoding an mRNA molecule with a 96-tandem repeat of binding sites for the RNA-binding protein MS2 (pIG-BAC2) (21). The S. cerevisiae used was a haploid JCY66 strain (MATa ade2-1 trp1-1 can1-100 leu2-3,112 his3-11,15 ura3) with the sequence for 12 MS2 hairpins inserted at the ARG3 coding region as described in Thompson et al. (32) and Haim-Vilmovsky and Gerst (33).

Growth conditions and microscopy

See Stylianidou et al. (14) for details of experimental methods and data acquisition of the MS2-mRNA trajectories in E. coli cells. In short, overnight cultures grown in Luria Broth media with Kanamycin and Chloramphenicol were diluted and grown to approximately midlog phase. The cells were then induced with Isopropyl β-D-1-thiogalactopyranoside (1 mM) and anhydrotetracycline (10 ng/mL) for 15 min at 30C. Cells were rinsed and grown in fresh media for 1 h at 30°C. 2 μL of cells were spotted onto 2% wt/wt agarose pads with growth media and sealed with VALP. Time-lapse phase-contrast and wide-field fluorescence microscopy images were collected at 1 min or 1 s time intervals using a large-format sCMOS camera (Andor Neo; Andor Technology/Oxford Instruments, Belfast, Northern Ireland) attached to a TiE microscope (Nikon Instruments, Melville, NY) with a 60× Plan-Apo oil immersion objective with a 1.4 numerical aperture and equipped with an environmental chamber and controlled by NIS-Elements (Nikon Instruments). Mean localization precision of particles was calculated to be ∼57 nm. Trajectory data were analyzed using the custom MATLAB software (The MathWorks, Natick, MA) SuperSegger (34).

See Thompson et al. (32) for details of experimental methods and data acquisition of the MS2-mRNA trajectories in S. cerevisiae cells. In short, overnight cultures were grown in synthetic complete (SC) his-media with glucose (2% wt/vol) and adenine hemisulfate (40 μg/mL) to early log phase and transferred into SC media without methionine for induction of MS2-3xEGFP for 3 h at 30°C and then removed to SC media for 3 h. After rinsing, roughly 2 μL of cells were spotted onto 1.5% wt/wt agarose pads with SC media and sealed with paraffin wax. Fluorescence microscopy images were taken at 15 ms intervals using an iXon+ electron-multiplying charge-coupled device camera (Andor Technology/Oxford Instruments) attached to an inverted IX71 fluorescence microscope (Olympus, Melville, NY) using a 100× oil immersion objective with a 1.4 numerical aperture and fitted with a double helix point spread function (DH-PSF) image processing section. The DH-PSF uses a spatial light modulator that transforms a single fluorescent focus into two spots, angle of which between them, relative to the spatial light modulator, enables calculation of the focus z coordinate (32, 35, 36, 37). Mean localization precision of particles was calculated to be ∼25 and 28 nm in the x and y directions, respectively (the DH-SPF is not symmetric to 90° rotations). Images of putative RNA-protein particles were identified by hand and x,y,z coordinates were calculated according to the DH-PSF using custom MATLAB software (32).

Trajectory analysis

RNA-protein particle trajectories were converted to tables of position coordinates and analyzed using custom MATLAB software.

Trajectory simulations

Trajectories of simulated Brownian and fractional Brownian motion were generated using the wfbm function in MATLAB, which uses the fractional ARIMA process (38).

Results and Discussion

RNA-protein particle tracking

We examine fluorescent RNA-protein particles that are diffusing in the cytoplasm of E. coli and S. cerevisiae. The E. coli data sets span 136 min with a time interval of 1 min between position measurements (14) and 100 s with a time interval of 1 s (reported in this study), and the S. cerevisiae data set spans 45 s with a time interval of 0.015 s (32). In the E. coli data sets, the RNA-protein particles consist of noncoding mRNA with no ribosomal binding site or degradation tag and a 96× repeat of the MS2 binding sequence that binds an MS2-GFP fusion protein under the control of the tetracycline promoter (39). In the S. cerevisiae data set, the ARG3 mRNA was selected for its low expression level and its lack of localization behavior and labeled using a 12× repeat of the MS2 binding sequence that binds to an MS2 protein fused to three EGFPs (32). The majority of trajectories analyzed in this study belong to cells containing one particle (>95%). For cells containing two particles whose paths could potentially cross, trajectories from E. coli are only included if particles are at opposite ends of the cell, and crossing was not observed in the S. cerevisiae data set (32).

For E. coli, we analyze the particle trajectories in 1D along the long axis of the cell, starting in the middle 95% of the cell for the 1 s data set (1807 trajectories, average of 97 data points per trajectory) and the middle 50% of the cell for the 1 min data set (892 trajectories, average of 45 data points per trajectory) to reduce the influence of the confining cell edges in biasing the motion. The effects of the confining cell wall can be included in analyzing and modeling the motion of RNA-protein particles (14), but in this work we are only interested in studying the freely diffusing behavior. We include sample trajectories in Fig. S1, a and b, in the Supporting Material. For S. cerevisiae, we analyze particle dynamics in the x and y directions (252 trajectories, average of 663 data points per trajectory). Data for the z direction is also available, but not included in this study due to less spatial resolution leading to more uncertainty in the position relative to the x and y coordinates (32). We include sample trajectories in the Supporting Material placed arbitrarily in a circle with the typical diameter of an S. cerevisiae cell (3 μm) to show the comparison between the trajectory exploration area and the size of the cell Fig. S1 c). We note that mRNA-protein particles are not free to move throughout the entire cell volume. Particles in E. coli are generally excluded from the nucleoid, which biases their position to the cell center and poles (14). In S. cerevisiae the nucleus and other organelles can obstruct particle motion, which could cause the particles to feel an effective confinement at shorter timescales.

RNA-protein particles exhibit subdiffusive motion

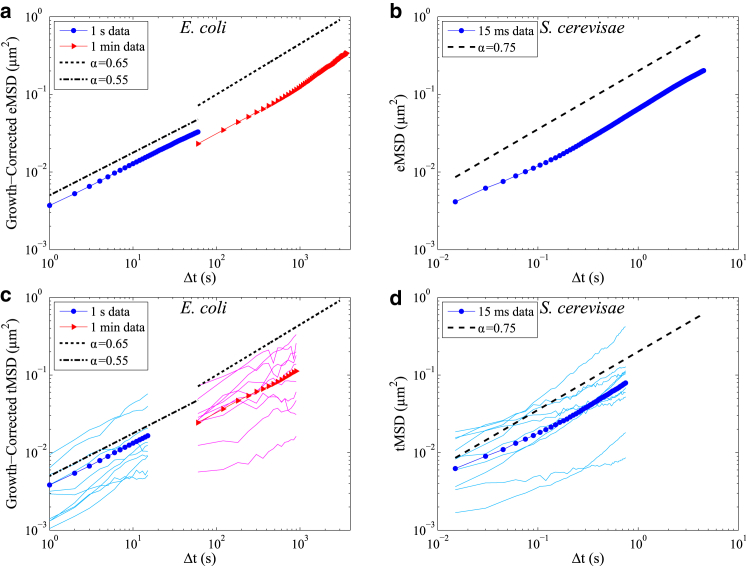
RNA-protein particles in the E. coli and S. cerevisiae cytoplasm exhibit ergodic subdiffusive behavior as both their ensemble-averaged MSD (eMSD, $\langle {\left[x\left(t+\Delta t\right)-x\left(t\right)\right]}^2\rangle$) and time-averaged MSD (tMSD, $\langle \overline{{\left[x\left(t+\Delta t\right)-x\left(t\right)\right]}^2}\rangle$, where the overbar denotes a time average over each trajectory before taking the ensemble average) exhibit power-law behavior MSD ∼(Δt)^α (Fig. 1). In the E. coli data sets, we measure α = 0.54 (standard error of 0.001) for Δt of 1–60 s and α = 0.68 (standard error of 0.007) for Δt of 1–60 min using a simple power law fit to the ensemble-averaged MSD (Fig. 1 a). We note that the MSD curves at the shorter and longer timescales do not quite line up with one another (Fig. 1 a), but it is common to see a slight day-to-day variation in the mean diffusivity between experiments even when using the same medium and strain of cells (40). We note that the measurement of α = 0.54 for Δt of 1–60 s is shallower than previous measurements. However, the single effective power law behavior suggests that its origin is not localization error (41) and analyzing trajectories in the middle 50% of cell far away from the cell edges results in α = 0.56, eliminating weak confinement by the cell edge as the cause. For particles in S. cerevisiae we observe a shallower slope at short timescales, which is indicative of localization error (Fig. 2, b and d), and which can be accounted for in the fitting of α by using the appropriate statistical model that corrects for localization error (42). Using this correction, we measure α = 0.75 (standard error of 0.004) for Δt of 0.015–4.5 s (Fig. 1 b).

Figure 1.

RNA-protein particles exhibit ergodic subdiffusive behavior. (a) eMSD and (c) tMSD of RNA-protein particles in E. coli for particle position measurements taken at 1 s intervals (blue circles) and 1 min intervals (red triangles (14)) and corrected for drift due to cell growth using an affine expansion model (14). Ten example tMSD curves for individual trajectories are also shown (light-blue lines and magenta lines). (b) eMSD and (d) tMSD of RNA-protein particles in S. cerevisiae (32). Ten example tMSD curves for individual trajectories are also shown (light-blue lines). Error bars for standard error of the mean are smaller than the symbol sizes. To see this figure in color, go online.

Figure 2.

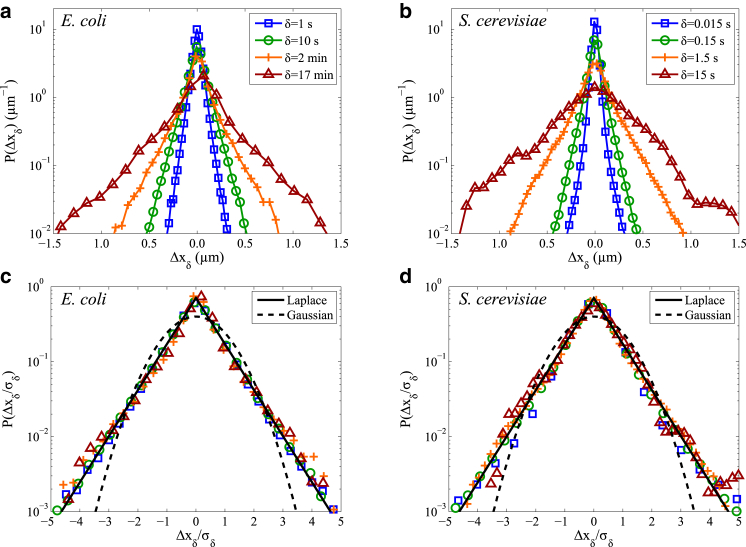
Displacement distributions of RNA-protein particles in E. coli. (a) Ensemble of 1D displacement (Δx) distributions over multiple timescales (δ) along the long axis of E. coli. (b) Ensemble of 1D displacement distributions (Δx and Δy combined) over multiple timescales (δ) in the S. cerevisiae cytoplasm. (c and d) Same as (a) and (b), but with each displacement distribution rescaled by its standard deviation σ_δ for direct comparison to Laplace and Gaussian distributions. Particle displacement measurements for E. coli are from two different data sets spanning 1–100 s used for δ = 1 s and 10 s (this study) and 1–136 min used for δ = 2 min and 17 min (from Stylianidou et al. (14)). Particle displacement measurements for S. cerevisiae are from a single data set spanning 0.015–45 s (from Thompson et al. (32)). To see this figure in color, go online.

We observe negative correlation peaks in the velocity autocorrelation function (Fig. S2), which along with the ergodic MSD indicates that the particle dynamics are most consistent with motion in a viscoelastic medium that is described by fractional Brownian motion, as opposed to other models such as the subdiffusive continuous time random walk, scaled Brownian motion, or ergodicity breaking heterogeneous diffusion models (43, 44, 45, 46). In particular, the subdiffusive continuous time random walk and heterogeneous diffusion models often exhibit a wide spread in the tMSD like that seen in Fig. 2, c and d (though with α = 1) (47, 48). We notice that there is a trend in the velocity autocorrelation function where the correlation becomes more positive for larger timescales of measurement (Fig. S2, c and d), likely due to the bias in RNA-particle motion toward the cell poles at these longer timescales (14, 49).

We note that the confinement imposed by the cell membrane can have a strong effect on the tracer particle dynamics at long enough timescales. The typical feature observed is a plateau in the MSD, as has been previously shown for proteins and chromosome loci in the E. coli cytoplasm (41, 50) and the fractional Brownian motion model (51). For the fractional Brownian motion the approach to the plateau in the MSD can be significantly delayed relative to the standard Brownian motion due to the slower dynamics (48, 51), while a subdiffusive continuous time random walk would exhibit a second, shallower slope on the tMSD (47, 51). We do not see the plateau signature in the MSD for the timescales and cellular regions analyzed in this study (Fig. 1), therefore we assume that the confinement does not have a strong effect on our statistical analysis in the following sections.

RNA-protein particle displacements exhibit a Laplace distribution

In Fig. 2, we plot the histograms of the 1D displacement distribution for the RNA-protein particles. Displacements are defined as $\Delta x_{\delta }=x\left(t+\delta \right)-x\left(t\right)$, where x(t) is the particle position at time t and δ is the time between particle position measurements. For E. coli, we show displacements along the cell’s long axis spanning δ = 1 s to 17 min (Fig. 2, a and b). For S. cerevisiae, displacements in the x and y directions are treated independently and pooled together for timescales of δ = 0.015–15 s (Fig. 2, c and d).

The ensemble of trajectory displacements exhibit non-Gaussian behavior at all observed timescales and are well predicted by a Laplace distribution (sometimes known as a two-sided or double exponential distribution). The probability density function of the Laplace random variable is defined as

$$P_{\text{Laplace}}\left(\Delta x;\mu ,\sigma \right)=\frac{1}{\sigma \sqrt{2}}\text{exp}\left(-\frac{\left|\Delta x-\mu \right|\sqrt{2}}{\sigma }\right).$$ (2)

Fig. 2, c and d, further shows that the Laplace distribution with mean $\mu =0$ describes the histogram shape that is self-similar over three orders of magnitude of time when displacements $\Delta x_{\delta }$ are normalized by their standard deviation ${\sigma }_{\delta }=\sqrt{{\langle \left[\Delta x_{\delta }-\langle \Delta x_{\delta }\rangle \right]\rangle }^2}$. This is in stark contrast to other soft-matter systems, whose particle displacements generally follow a Gaussian distribution at low displacements and exhibit exponential tails at large displacements, although often also in a self-similar manner (19). Given the expectation that particle displacements should exhibit at least partially Gaussian behavior at long enough time intervals, we perform further analysis to investigate the statistical and physical origins of the non-Gaussian behavior.

On generating a Laplace distribution

It has been previously reported that particles diffusing in agarose and actin networks and the S. cerevisiae cytoplasm exhibited a non-Gaussian ensemble displacement distribution (8, 16). However, further investigation revealed that each particle trajectory exhibited a nearly Gaussian displacement distribution, thought to be due to the probe only sampling a local region during the timescale of observation (8, 16). Thus, a natural starting point for our analysis is to assume that each particle assumes a Gaussian displacement distribution from exploring a local region of cytoplasm, and search for statistical relationships that can generate a Laplace random variable starting from a Gaussian random variable. From a statistical analysis, it can be shown that

$$X\stackrel{d}{=}Z\sqrt{W},$$ (3)

where the Laplace random variable X (mean of 0 and variance of 1) is the product of the Gaussian random variable Z (mean of 0 and variance of 1) and the square root of the exponential random variable W (mean of 1) and the $\stackrel{d}{=}$ notation indicates that the two sides are identically distributed (52). The exponential distribution is defined by its probability distribution function as

$$P_{\text{Exp}}\left(w;\sigma \right)=\frac{1}{\sigma }\text{exp}\left(-\frac{w}{\sigma }\right)$$ (4)

for w ≥ 0 and both a mean and standard deviation of σ.

We note that there exist many other mathematical combinations of random variables that can generate the Laplace variable (52). The simple framework of Eq. 3 makes a testable prediction that the observed Laplace-distributed displacement behavior could be generated by trajectories exhibiting fractional Brownian motion whose diffusivity parameter D is chosen from an exponential distribution. Each trajectory then exhibits a time-averaged MSD $\left(\Delta t\right)=2dD\Delta t^{\alpha }$, where d is the dimension of the random walk and D has units of $\left[{\text{Length}}^2/{\text{Time}}^{\alpha }\right]$. The added complexity of random diffusivities does not affect the subdiffusive behavior observed in the ensemble-averaged MSD, which is then defined as MSD $\left(\Delta t\right)=2d\langle D\rangle \Delta t^{\alpha }$, where $\langle D\rangle$ is the mean of the trajectory diffusivities. We check the prediction for the diffusivity distribution after an exponential distribution by examining the individual trajectory diffusivities and displacement distributions in the subsequent sections.

An alternative strategy equivalent to Eq. 3 that generates a Laplace displacement distribution uses the probability distribution functions. Using $P_{\text{Gauss}}\left(\Delta x;\mu =0,\sigma \right)$, $P_{\text{Laplace}}\left(\Delta x;\mu ,\sigma \right)$, and $P_{\text{Exp}}\left(D;\langle D\rangle \right)$ as defined in Eqs. 1, 2, and 4, the displacement distribution over the ensemble of all trajectories can be described by integrating the Gaussian probability density function weighted by the exponentially distributed diffusivities over all possible values of the diffusivity, $D\in \left[0,\infty \right)$. The equation describing this integral for ${\sigma }^2=\text{MSD}\left(\Delta t\right)$ can be solved as

$$\begin{array}{c}{\int }_0^{\infty }dD\left[P_{\text{Exp}}\left(D;\langle D\rangle \right)P_{\text{Gauss}}\left(\Delta x;\mu =0,\sigma =\sqrt{2D\Delta t^{\alpha }}\right)\right]\\ ={\int }_0^{\infty }dD\left[\frac{1}{\langle D\rangle }\text{exp}\left(-\frac{D}{\langle D\rangle }\right)\frac{1}{2\sqrt{\pi D\Delta t^{\alpha }}}\text{exp}\left(-\frac{\Delta x^2}{4D\Delta t^{\alpha }}\right)\right]\\ =\frac{1}{2\sqrt{\langle D\rangle \Delta t^{\alpha }}}\text{exp}\left(-\frac{\left|\Delta x\right|}{\sqrt{\langle D\rangle \Delta t^{\alpha }}}\right)\\ =P_{\text{Laplace}}\left(\Delta x;\mu =0,\sigma =\sqrt{2\langle D\rangle \Delta t^{\alpha }}\right).\end{array}$$

A similar derivation for $\sigma =\sqrt{2\langle D\rangle t}$ corresponding to Fickian diffusion was shown in Chubynsky and Slater (53).

One potential alternative model for Laplacian displacement distribution is the fractional Laplace motion, a process that subordinates fractional-Brownian motion to a gamma process (54). This process exhibits power law correlation between steps like fractional Brownian motion but has a Laplace displacement distribution instead of the Gaussian distribution. However, fractional Laplace motion exhibits self-similarity at random transformations of scale in time defined by a stochastic process (54). This cannot explain the self-similarity in time of the displacement distributions in Fig. 2, which is done by dividing displacements by the distribution’s standard deviation.

RNA-protein particle diffusivities exhibit an exponential distribution

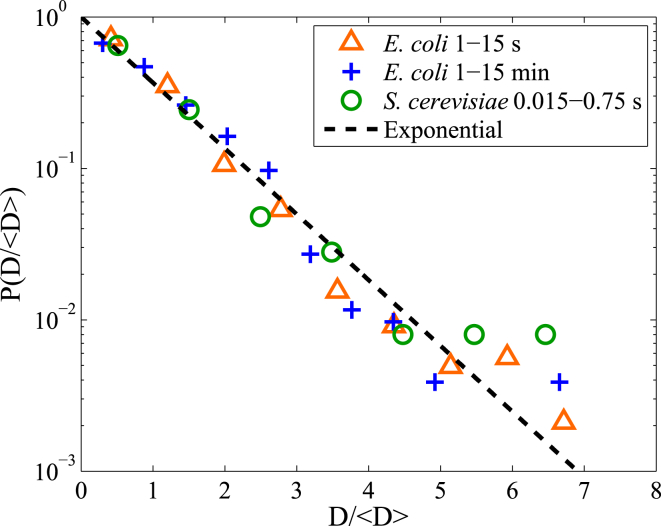
We extract the diffusivities from the time-averaged MSD of individual RNA-particle trajectories using a two-parameter fit to a power-law function. In Fig. 3, we show that the distribution of diffusivities of the E. coli and S. cerevisiae data sets are well approximated by an exponential distribution defined by

$$P_{\text{Exp}}\left(D;\langle D\rangle \right)=\frac{1}{\langle D\rangle }\text{exp}\left(-\frac{D}{\langle D\rangle }\right)$$ (5)

for D ≥ 0 and both a mean and standard deviation of $\langle D\rangle$. This is consistent with the hypothesis we proposed for the origin of the Laplace distribution in the previous section and generally consistent with the broader hypothesis that non-Gaussian distributions in particle displacements are caused by a broad spectrum of diffusivities (19).

Figure 3.

Diffusivity distributions of RNA-protein particles. The probability distribution of diffusivities normalized by their mean for E. coli and S. cerevisiae data sets. Diffusivities are calculated using a two-parameter fit of the individual time-averaged MSDs to a power law function over the time intervals indicated in the figure legend. To see this figure in color, go online.

It is important to note that the statistical effects of finite track length can cause a broadening of the diffusivity distribution, making this a critical feature for which to control. To account for this, we performed fractional Brownian motion simulations of varying track lengths and calculated their diffusivities from the time-averaged MSD of individual trajectories. We find that the observed distributions for D in the RNA-protein particle data in Fig. 3 are significantly wider than would be predicted simply due to the finite track length effects (Fig. S3).

Another possible source of broadening of the diffusivity distribution is variation in the number of MS2-GFP proteins bound to the RNA, which would affect its size and effective drag. We examine the mean fluorescence intensity during single trajectories as a proxy for the particle’s effective size and drag to investigate its potential to explain the broader than expected distributions. In Fig. S4, we plot each particle’s mean fluorescence intensity versus its calculated diffusivity. Because the diffusivity should be inversely related to the particle’s drag coefficient, we attempt to fit a simple mathematical model where intensity (I) and diffusivity exhibit an inverse relationship D = A/I, where A is a constant parameter fit to the data. Calculating the Pearson correlation coefficient indicates that there is generally a weak to moderate inverse relationship between these variables (ρ = −0.48 for E. coli 1 s, ρ = −0.16 for E. coli 1 min, and ρ = −0.06 for S. cerevisiae; Fig. S4). However, further analysis calculating R² values (0.13 for E. coli 1 s, −0.15 for E. coli 1 min, and −0.33 for S. cerevisiae) indicates that the simple inverse model cannot explain the large variation in the observed diffusivities (Fig. S4). We further note that using fluorescence intensity as a proxy for particle size and drag can be complicated by the effects of photobleaching and the particle’s z position relative to the focus plane (14, 32). Even fluorescent cytoplasmic particles that have been rigorously examined to control for size effects can exhibit behaviors with broader-than-expected distributions (15).

Individual particle trajectories exhibit non-Gaussian displacement distributions

The remaining prediction from our framework is that the individual trajectory displacement distributions should exhibit a Gaussian distribution for timescales short enough that the particle does not sample the spatial or temporal heterogeneity of its environment. This distribution is defined by

$$P_{\text{Gauss}}\left(\Delta x;\mu =0,\sigma \right)=\frac{1}{\sigma \sqrt{2\pi }}\text{exp}\left(-\frac{\Delta x^2}{2{\sigma }^2}\right),$$ (6)

where Δx are the particle displacements in 1D, the mean μ = 0, and the variance σ². Setting σ² = 2dDΔt^α results in Eq. 6 becoming the propagator for fractional Brownian motion (55, 56).

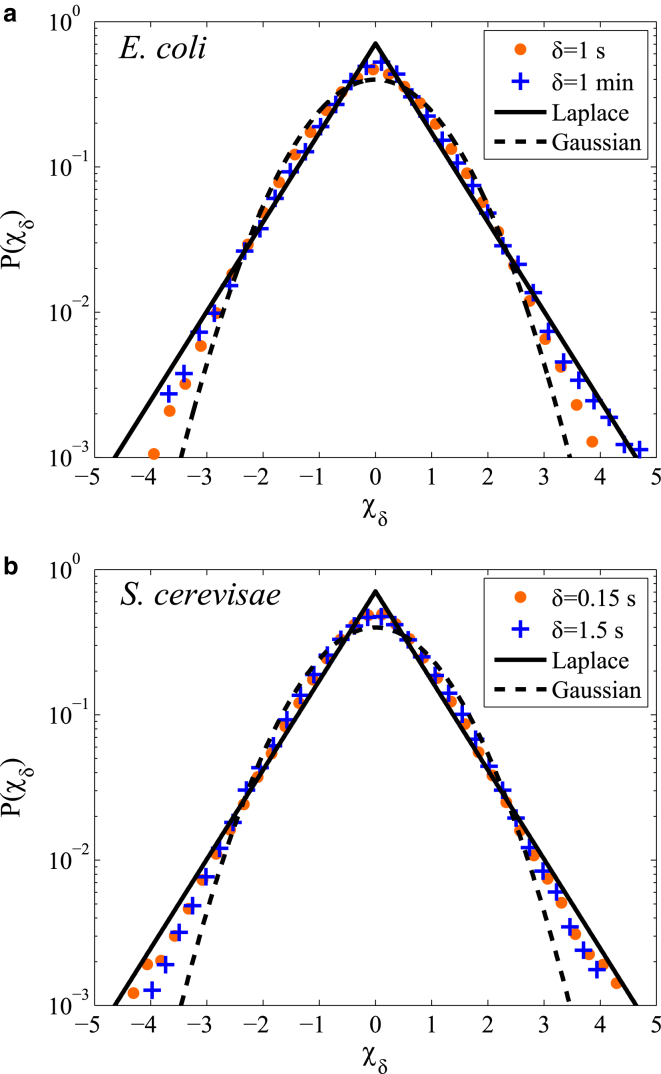
To test our prediction that the trajectories are Gaussian, we normalize the 1D displacements of each individual trajectory by their standard deviation and then pool the displacements into an ensemble distribution that is normalized for a parameter-free comparison to the Gaussian and Laplace distributions. In Fig. 4, we show that the distribution for the normalized displacements, χ_δ, are non-Gaussian, falling between the Gaussian and Laplace distributions. Each individual distribution exhibits a positive excess kurtosis (narrower than Gaussian in the center and wider than Gaussian at the tails).

Figure 4.

Standard deviation normalized displacement distribution of RNA-protein particles. (a and b) Displacement distributions over multiple timescales along the long axis of (a) E. coli and the pooled x and y displacements in (b) S. cerevisiae. Each individual trajectory is normalized by its standard deviation before being pooled into the ensemble distribution. Distributions are then made dimensionless by the overall standard deviation to show the parameter-free comparison of the normalized displacement, χ_δ, to the Gaussian and Laplace distributions. To see this figure in color, go online.

The non-Gaussian behavior is commonly quantified using the non-Gaussian parameter (NGP), which in 1D is defined as

$$\text{NGP}=\frac{{\langle \left(\Delta x\right)\rangle }^4}{3{\langle {\left(\Delta x\right)}^2\rangle }^2}-1.$$ (7)

This parameter has a value of 0 for a Gaussian distribution and a value of 1 for a Laplace distribution. The NGP for the RNA-particle trajectories in E. coli is 0.32 for δ = 1 s and 0.67 for δ = 1 min, indicating that the trajectories are less Gaussian at larger timescales. The S. cerevisiae trajectories exhibit NGP of 0.71 for δ = 1.5 s and 0.42 for δ = 1.5 s, which indicates that the trajectories are actually becoming more Gaussian at larger timescales, the opposite of the trend in E. coli. Our hypothesis that the individual trajectories would exhibit Gaussian behavior at some timescale is not observed, and likely indicates that in addition to a broad distribution of diffusivities between different trajectories, there may also be significant dynamic heterogeneity experienced by individual particle trajectories at the observed timescales. It was previously reported that RNA-protein particles in the S. cerevisiae cytoplasm can exhibit different dynamic regimes and transitions during single trajectories, even including directed and confined motion (32, 57). The heterogeneity likely manifests for a very wide range of timescales, yet nevertheless results in a self-similar Laplace distribution for the combined ensemble of particle displacements.

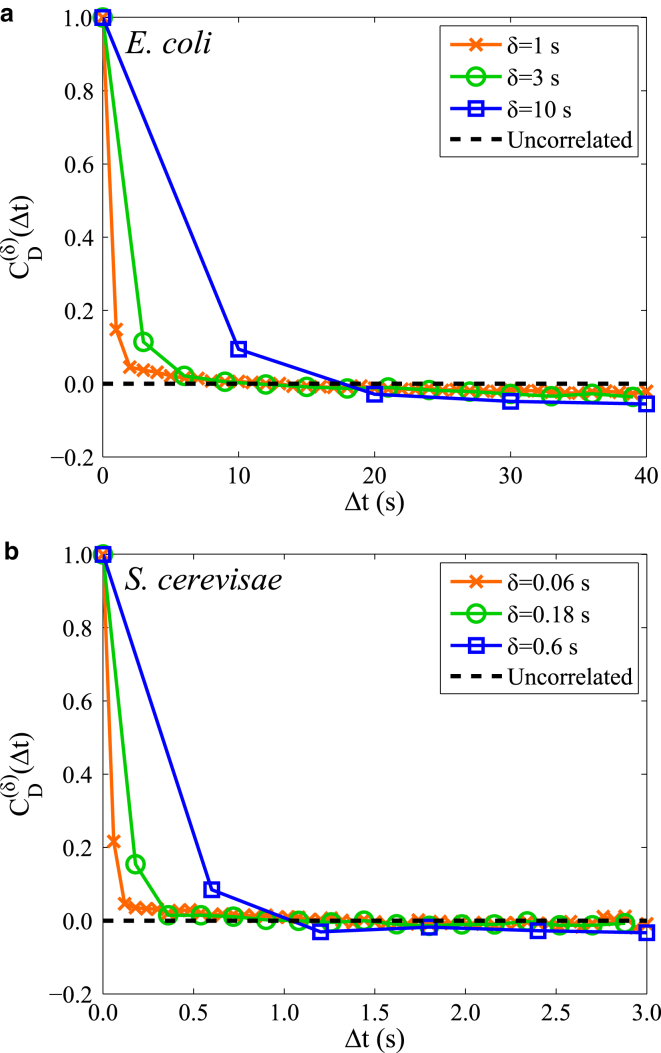
Diffusivity autocorrelation function shows correlated, heterogeneous behavior

To further understand why the heterogeneity between and within trajectories results in non-Gaussian displacement behavior, we examine the dynamic evolution of the single-trajectory behavior. Toward this effort, we define a diffusivity autocorrelation function that is similar to the trajectory-amplitude autocorrelation function defined by Duits et al. (58) and the square-displacement correlation function defined by Cao (59). The diffusivity autocorrelation function $C_D^{\left(\delta \right)}\left(\Delta t\right)$ is thus defined as

$$C_D^{\left(\delta \right)}\left(\Delta t\right)=C_D^{\left(\delta ,m\right)}={\langle C_D^{\left(\delta ,m,i\right)}\rangle }_i,$$ (8)

where

$$C_D^{\left(\delta ,m,i\right)}=\frac{\overline{\Delta D_{i,j}^{\left(\delta \right)}\Delta D_{i,j+m\delta }^{\left(\delta \right)}}}{\overline{{\left(\Delta D_{i,j}^{\left(\delta \right)}\right)}^2}},$$ (9)

with a relative diffusivity

$$\Delta D_{i,j}^{\left(\delta \right)}=D_{i,j}^{\left(\delta \right)}-\overline{D_{i,j}^{\left(\delta \right)}}$$ (10)

and

$$D_{i,j}^{\left(\delta \right)}={\left(\Delta x_{i,j}^{\left(\delta \right)}-\overline{\Delta x_{i,j}^{\left(\delta \right)}}\right)}^2/\left(2\delta \right).$$ (11)

The overline $\overline{A_{i,j}}$ indicates a time average over the time index j for a given trajectory index i, while ${\langle B^{\left(\delta ,m,i\right)}\rangle }_i$ indicates an ensemble average over all trajectory indices i. We define the diffusivity $D_{i,j}^{\left(\delta \right)}$ locally using the drift-corrected displacements, with $\Delta x_{i,j}^{\left(\delta \right)}=x_{i,\delta \left(j+1\right)}-x_{i,\delta j}$. This enables examination of the average dynamic correlation as a function of $\Delta t=m\delta$ (where m is an integer). This formulation of the autocorrelation function employs a time average of each trajectory before taking an ensemble average to normalize each trajectory by the average amplitude of the fluctuations. This step is essential to removing artifacts that are due to different tracks having different average diffusivities (58).

In Fig. 5, we plot the diffusivity autocorrelation function for several different values of time δ of displacements. A fractional Brownian motion in the limit of infinite track length would exhibit a diffusivity correlation of 1.0 at Δt = 0.0 and be uncorrelated at all nonzero times. While the steps are anticorrelated with one another at all timescales for this model, the diffusivity is a constant and thus the relative diffusivity $\Delta D_{i,j}^{\left(\delta \right)}$ cannot display any variation or correlation on average. Furthermore, if other models or the data contain variation in the diffusivity with heterogeneity that is temporally uncorrelated at certain timescales, we would also expect the correlation value to be zero. Thus, any deviation from zero indicates the presence of correlated, dynamic heterogeneity in the local value of the particle diffusivity that can lead to non-Gaussian displacement behavior.

Figure 5.

Diffusivity autocorrelation function of RNA-protein particles. (a and b) Diffusivity autocorrelation function $C_D^{\left(\delta \right)}\left(\Delta t\right)$ for different timescales of RNA-protein particle displacement measurements δ for (a) E. coli and (b) S. cerevisiae. To see this figure in color, go online.

One artifact to control for is that any trajectories analyzed must have a finite track length, whose statistical noise introduces a slight negative correlation at larger time separations Δt (58). Negative correlations could also be interpreted as the particle entering a new environment with, on average, a different diffusivity value. In either case, a relative diffusivity $\Delta D_{i,j_1}^{\left(\delta \right)}$ calculated over a segment of time δ will, on average, have an opposite sign to a relative diffusivity $\Delta D_{i,j_2}^{\left(\delta \right)}$ calculated over another nonoverlapping segment. We perform fractional Brownian motion simulations whose track length and sparsity is determined by that of the experimental data set for a direct comparison to examine the correlation contribution from the statistical noise (Fig. S4). These simulations show that the slight negative correlation observed in Fig. 5 can be explained by the statistical noise from the finite track length and data sparsity. Furthermore, the degree of positive correlation observed at smaller values of Δt is not predicted by the simulations, indicating the presence of temporal correlations in the diffusion heterogeneity in both E. coli and S. cerevisiae (Figs. 5 and S4). This initial positive correlation is seen over a full order of magnitude of time for both E. coli and S. cerevisiae, decaying slightly as δ increases, and reveals that deviations from the average diffusivity of the trajectory are correlated weakly and last only a few seconds (Fig. 5).

We note that static and dynamic errors can introduce additional correlations such that anomalous behavior is observed in statistics such as the MSD or the velocity autocorrelation function (41, 42, 60). Likewise, static and dynamic errors can introduce additional correlation into the diffusivity autocorrelation function. However, because these errors are generally uncorrelated with one another over time, they can only affect the first datapoint Δt = δ, and thus these errors cannot be responsible for the positive correlation beyond the first datapoint of the lower values of δ seen in Fig. 5.

Conclusions

In this article, we have shown that RNA-protein particles in the cytoplasm of living cells exhibit non-Gaussian displacement distributions due to a combination of heterogeneity between particle trajectories and dynamic heterogeneity within single trajectories. The RNA-protein particle ensemble displacement distribution exhibits a Laplace distribution at all observed timescales, falling on a universal curve when displacements are normalized by σ_δ (Fig. 2). Previous studies have reported particles in complex media exhibiting exponential tails and self-similarity, but often the center of the distribution would be more rounded or Gaussian-like (19). We do not see relaxation, because no relaxation regime is observed in the subdiffusive MSD either (Fig. S1). Instead, it has been observed in bacteria that the limiting regime of particle or chromosome locus dynamics at long timescales of Δt is the confinement imposed by the cell membrane (14, 41).

The distribution of particle diffusivities measured from time-averaging single trajectories exhibits an exponential distribution that is much broader than is predicted by finite-track length effects (Figs. 3 and S3). The source of the exponential distribution is currently unknown and is an interesting avenue of future inquiry. The exponential distribution is the maximal entropy distribution on the positive support, $D\in \left[0,\infty \right)$, although it is unclear if a principle akin to a limit theorem is at work. Chubynsky and Slater (53) developed a purely mathematical diffusing-diffusivity model, where the diffusivity evolves according to an advection-diffusion equation that results in an exponential diffusivity distribution for certain conditions. Wide distributions in the diffusivities of probe trajectories have been reported before for labeled cell-surface receptors (45, 61). In many studies, this broad spectrum of diffusivities has been attributed to there being discrete states of mobility sampled by the probe, examples of which are RNA polymerases in E. coli (62), cell-surface receptors (45), and Cas9 proteins searching for a target site in the cell nucleus (63). Other studies are unable to directly detect distinct states of probe mobility, notably fluorescent tracer particles in agarose and actin gels (8). Both distinct states and a continuous spectrum of diffusivities can result in non-Gaussian behavior in the single-trajectory displacement distribution (53, 59).

The non-Gaussian dynamics and broad spectrum of diffusivities may be a general feature of crowded macromolecular systems, with similar results to ours recently reported for the diffusion of membrane receptors in Xenopus embryo muscle cells (64). Another example is a colloidal fluid near its glass transition, which exhibits a broad spectrum of particle dynamics resulting in a stretched-exponential displacement distribution (11) and positive values of the NGP (12). Recent articles simulating the effects of crowding on the lateral motion of proteins in cell membranes show subdiffusive and non-Gaussian displacement behavior as well (65, 66). Previous experiments and simulations show that a high degree of macromolecular crowding is sufficient to result in viscoelastic subdiffusive behavior (67, 68).

Another aspect to consider is the active, nonequilibrium dynamics of the cytoskeleton that would be relevant for the S. cerevisiae cytoplasm. A recent article constructed a model for active dynamics driven by cytoskeletal rearrangement as a set of moving harmonic potentials undergoing nonequilibrium rearrangement that results in a distribution with exponential tails (17). It would be interesting to see if versions of this model can account for other effects seen in the S. cerevisiae cytoplasm, such as the ergodic, subdiffusive MSD and the characteristic timescale-free negative peak of the velocity autocorrelation function due to the medium viscoelasticity.

In the majority of cases analyzed in this work, each RNA-protein particle track is measured in the cytoplasm of a different cell. Due to the small size of E. coli and S. cerevisiae cells, it is difficult to resolve and measure multiple particles within the same cell. An open question remains as to whether the heterogeneity between different particle trajectories is due to heterogeneity of the cytoplasm of a single cell (of which only a portion is sampled) or is due to differences in the cytoplasmic properties between different cells. In theory, performing particle tracking measurements in a high enough number of cells should enable probing of the full range of heterogeneous behavior, assuming that such a distribution of cellular cytoplasm states can be approximated by a distribution with finite moments. Performing such measurements and analysis is enabled by the growing power of high-throughput technologies for single cell analysis (69).

Previous studies describe the bacterial cytoplasm as glassy (15) and the eukaryotic cytoplasm as an active gel (17, 70). However, in this study we see that the RNA-protein particles exhibit very similar behavior in both E. coli and S. cerevisiae cells. Perhaps the simplest reason for this might be that the dynamics can be dependent on the probe size (15). The size of the RNA-protein particle is between the size of individual proteins, which exhibit nearly diffusive behavior (71), and submicron colloidal beads, which are large enough that they appear trapped in local, dynamic cages formed by the cytoskeletal network (70). There may be a contribution to the trajectory heterogeneity from the internal dynamics of the RNA-protein particle itself as opposed to purely probing the physics of the cytoplasmic medium. We note that similar non-Gaussian behavior is seen for a different probe system (specifically, fluorescent protein aggregates) in the E. coli and S. cerevisiae cytoplasm (15, 16).

This work reveals that in vivo diffusive transport exhibits characteristics of subdiffusive motion (attributed to viscoelasticity) and heterogeneity (both spatial and temporal) in the environmental diffusivity. These effects are obscured when analyzing the average displacement alone (i.e., MSD), because the ensemble average merely averages the diffusivity over its distribution. Thus, the analyses presented in this work provide a wealth of information on cellular transport and a procedure for deconvolving the physical mechanism for transport from the considerable variability inherent from cell-to-cell and within a single cell. Our study complements well other work that uses several different statistics to analyze anomalous transport behaviors (58, 64, 72). Cellular transport is involved in virtually all biological processes. This work provides clear evidence for the mechanism of transport within a cell and the impact of cellular variability on the observed motion.

Author Contributions

S.S. generated the reported experimental data; T.J.L., S.S., M.P.B., P.A.W., and A.J.S. analyzed the experimental data; T.J.L. performed the simulations and analyzed simulation results; and T.J.L. and A.J.S. wrote the article.

Editor: Tamar Schlick.