Abstract
We investigated the impact of bound calmodulin (CaM)-target compound structure on the affinity of calcium (Ca2+) by integrating coarse-grained models and all-atomistic simulations with nonequilibrium physics. We focused on binding between CaM and two specific targets, Ca2+/CaM-dependent protein kinase II (CaMKII) and neurogranin (Ng), as they both regulate CaM-dependent Ca2+ signaling pathways in neurons. It was shown experimentally that Ca2+/CaM (holoCaM) binds to the CaMKII peptide with overwhelmingly higher affinity than Ca2+-free CaM (apoCaM); the binding of CaMKII peptide to CaM in return increases the Ca2+ affinity for CaM. However, this reciprocal relation was not observed in the Ng peptide (Ng13–49), which binds to apoCaM or holoCaM with binding affinities of the same order of magnitude. Unlike the holoCaM-CaMKII peptide, whose structure can be determined by crystallography, the structural description of the apoCaM-Ng13–49 is unknown due to low binding affinity, therefore we computationally generated an ensemble of apoCaM-Ng13–49 structures by matching the changes in the chemical shifts of CaM upon Ng13–49 binding from nuclear magnetic resonance experiments. Next, we computed the changes in Ca2+ affinity for CaM with and without binding targets in atomistic models using Jarzynski’s equality. We discovered the molecular underpinnings of lowered affinity of Ca2+ for CaM in the presence of Ng13–49 by showing that the N-terminal acidic region of Ng peptide pries open the β-sheet structure between the Ca2+ binding loops particularly at C-domain of CaM, enabling Ca2+ release. In contrast, CaMKII peptide increases Ca2+ affinity for the C-domain of CaM by stabilizing the two Ca2+ binding loops. We speculate that the distinctive structural difference in the bound complexes of apoCaM-Ng13–49 and holoCaM-CaMKII delineates the importance of CaM’s progressive mechanism of target binding on its Ca2+ binding affinities.
Introduction
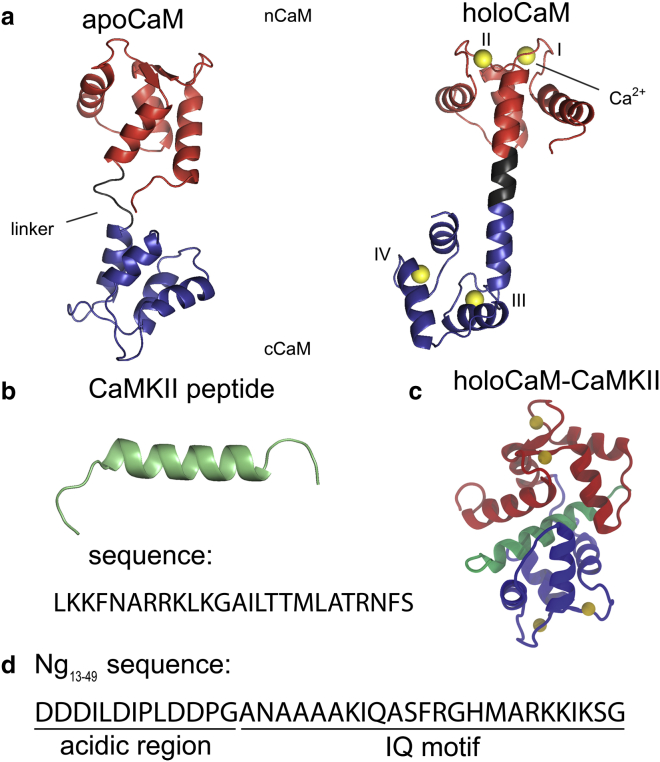
Calcium (Ca2+) is exquisitely used by a cell for transducing external stimuli through its gradient of extracellular (∼1000 μM) and intracellular (∼0.1 μM) concentration (1). A broad spectrum of Ca2+ signals are encoded by protein calmodulin (CaM) (2) (the structure is shown in Fig. 1 a) through specific binding with various targets regulating CaM-dependent Ca2+ signaling pathways in neurons (3). The targets enhance CaM’s affinity for Ca2+ by up to 30 times or accelerate dissociation of Ca2+ from CaM (4). Therefore, this mechanism tunes CaM’s capacity of encoding global Ca2+ signals by its differential binding affinity for Ca2+. Among those targets, Ca2+/CaM-dependent protein kinase II (CaMKII) (5, 6, 7) (the structure and sequence of the CaM-binding domain are shown in Fig. 1 b) and neurogranin (Ng) (8) (the sequence of the Ng13–49 peptide is shown in Fig. 1 c) play an essential role in synaptic plasticity (9), which is critical to learning and memory formation shown by early behavior experiments on Ng-mutated or Ng-knocked-out mice (10, 11). We summarized several experimental observations (3, 7) in Fig. S1 on how CaM sensitizes downstream CaM-binding enzymes to Ca2+ regulating synaptic plasticity in memory formation: CaM activates CaMKII at high Ca2+ levels (6) while the availability of CaM is controlled by a group of postsynaptic proteins including Ng at a lower Ca2+ level (8, 12).
Figure 1.
Illustration of structures of CaM and sequences of the target peptides. (a) Solution structure of Ca2+-free CaM (apoCaM) (PDB: 1CFD) and crystal structure of Ca2+/CaM (holoCaM) (PDB: 1CLL). CaM is colored as follows, red → nCaM (residue 1–76), gray → central linker (residue 77–82), blue → cCaM (residue 83–148), and the Ca2+ ions are colored in green; Ca2+ binding sites are labeled from I to IV. (b) Structure of Ca2+/CaM-dependent kinase II (CaMKII) peptide from the holoCaM-CaMKII crystal structure (PDB: 1CDM) and the sequence of the peptide. (c) X-ray structure of holoCaM-CaMKII (PDB: 1CDM). CaM and the Ca2+ ions are colored as in (a) and the CaMKII peptide is colored in green. (d) Sequence of the neurogranin peptide (Ng13–49). The two minimum compositions of the Ng13–49 peptide are marked as “acidic region” and “IQ motif.” To see this figure in color, go online.
Waxham et al. (13, 14) used fluorescence experiments to show that the CaMKII kinase increases the affinity of Ca2+ for CaM while Ng significantly decreases the affinity of Ca2+ for Ca2+-binding loop III and IV (Fig. 1 a) in C-domain of CaM (cCaM) by up to 60-fold. These experiments raised questions about the dependence of CaM’s affinity for Ca2+ ions on structural models of CaM (13, 15). Recent studies by Le Novère et al. (16, 17) demonstrated the alteration of Ca2+ affinity for CaM by plotting the binding affinity curves with elaborated allosteric models and fitted rates. They investigated the effect of competing targets on CaM by showing the enhancement of binding affinity in the presence of some targets (such as CaMKII), as well as the diminishment in the presence of other targets (such as Ng). Dieckmann et al. (18) used steady-state fluorescence and nuclear magnetic resonance (NMR) experiments and found that the binding of endothelial nitric oxide synthase (eNOS) to CaM enhances CaM’s affinity for Ca2+ while phosphorylated eNOS does not due to electrostatic repulsion. They speculated that the phosphorylation on eNOS diminished its helical propensity, possibly affecting CaM’s affinity for Ca2+. On the other hand, the structural basis of the regulation of Ca2+ affinity for CaM by Ng and CaMKII remains elusive.
CaM has two domains separated by a flexible central linker. Each domain consists of two helix-linker-helix motifs (marked as I–IV in Fig. 1 a), which can bind a Ca2+ ion. The flexible central linker allows adjustable CaM conformations, thus accommodates the binding of distinct CaM binding targets (CaMBTs) (19, 20, 21, 22, 23). In a canonical complex of Ca2+/CaM (holoCaM) and CaMKII peptide, the two domains of holoCaM wrap around the CaMKII peptide, which forms a helical structure (24). In our previous work, by using a combined approach of coarse-grained molecular simulations and experiments, we have established the binding mechanism of holoCaM and CaMKII peptide (25, 26) that follows “conformational and mutually induced fit” (27). Both holoCaM and CaMKII undergoes large conformational changes in the two-step binding mechanism.
Unlike the CaMKII peptide in complex with holoCaM, which was solved by X-ray crystallography decades ago (24), the weak binding between Ng and Ca2+-free CaM (apoCaM) makes the determination of its three-dimensional complex structure challenging (28). Ng belongs to the IQ motif family. In this family, the CaMBTs share a common motif (IQXXXRGXXXR), where X stands for any amino acid. Recently, Kumar et al. (29) determined the crystal structure of apoCaM and IQ motif of Ng (NgIQ), however, NgIQ was artificially covalently linked with cCaM in the bound structure. Furthermore, a previous experimental study (30) revealed that the IQ motif alone cannot represent the biophysical characteristics of the intact Ng protein. Inclusion of the acidic region in the N-terminal before the IQ motif (or Ng13–49), which are largely composed of Asp or Glu residues, reproduced the Ng-mediated affinity of Ca2+ to apoCaM, as well as the intermolecular interactions between the intact Ng and apoCaM. However, the main obstacle to investigate apoCaM-Ng13–49 binding is a lack of experimentally solved structures because of their weak binding affinity (approximately micromolar) (30). To determine the apoCaM-Ng13–49 complex structures, we modeled the interaction between intrinsically disordered Ng13–49 and apoCaM by introducing statistical dihedral angle potentials of Ng13–49 (31). After obtaining the appropriate coarse-grained models of apoCaM-Ng13–49, we reconstructed them into all-atomistic structures (32). We noted that in comparison to the canonical complex of CaM and CaMBT that includes the two domains of CaM wrapping around a helical CaMBT, the conformation of CaM in the complexes of apoCaM-Ng13–49 remains extended instead. The conformations of Ng in the bound complexes are not entirely helical.
The reconstructed atomistic models of the holoCaM-Ng13–49 complex and the crystal structure of holoCaM-CaMKII complex (Protein Data Bank (PDB): 1CDM) allow us to develop a hypothesis that the conformation of the Ca2+ binding loops from cCaM in a holoCaM-CaMBT complex dictates cCaM’s affinity for Ca2+. To validate this hypothesis, we computationally applied all-atomistic steered molecular dynamics (MD) simulations of holoCaM-CaMBT (33) and used Jarzynski’s equality (JE) (34) to calculate the change in Ca2+ binding free energy. As a reference, the same simulations were performed on a conformation of holoCaM without a CaMBT (PDB: 1CLL).
One of the challenges is the modeling of the bivalent Ca2+ ions. It has been shown that the charge on Ca2+ is < +2e due to charge transfer and polarization effects in the solution and especially in the Ca2+-bound state (35, 36, 37). Moreover, Jungwirth et al. (36, 38) suggested that both the size and the charge require adjustment to account for the polarization effects. Following our previous work (39), we computed the charges of calcium ions according to the protonation states of CaM by employing a semiempirical quantum chemistry program MOPAC (40). Thereby we revealed a mechanism that the presence of Ng peptide destabilizes the Ca2+ binding to cCaM, whereas the CaMKII peptide stabilizes the Ca2+ binding to cCaM. We speculate that CaM’s progressive mechanism of target binding, which yields distinctive complexes of apoCaM-Ng13–49 and holoCaM-CaMKII, modulates Ca2+ affinities for CaM.
Materials and Methods
Coarse-grained protein or peptide models
We performed coarse-grained molecular simulations of the intact Ng protein as well as the binding between apoCaM and Ng13–49 peptide. Sample preparation of the intact Ng or the Ng13–49 peptide is provided in Section I of the Supporting Material. The Hamiltonian of the coarse-grained protein models including Ng protein and the apoCaM-Ng13–49 complex is described in Section II of the Supporting Material. Ca2+ ions are absent from the coarse-grained models. The details about the coarse-grained molecular simulations are included in Section III of the Supporting Material.
Free energy calculation using JE
Preparation of the structures
The preparation of the coordinates as initial conditions for the JE calculation is highly nontrivial for the computation of Ca2+ binding free energy ΔG. For both systems, we determined the accurate protonation states by using H++ server (41) according to the protein conformation, pH, and the ionic strength of the solution. We then assigned the partial charges based on the geometry of the proteins by using a semiempirical quantum chemistry program MOPAC (40). We applied those protonated protein structures and partial charges for minimization and further procedures to carry out all-atomistic calculations of the Ca2+ binding free energy (find the details in Section IV of the Supporting Material). For holoCaM and holoCaM-CaMKII, which have experimentally determined structures, we fixed the heavy atoms during the preparation; for holoCaM-Ng, we constrained the atoms with harmonic potentials for the preparation of the structures (holoCaM: calcium-bound calmodulin).
holoCaM-CaMKII and holoCaM. We fixed the positions of Ca2+ atoms and backbone heavy atoms from holoCaM (PDB: 1CLL) or holoCaM-CaMKII (PDB: 1CDM) during the minimization, solvation, ionization, and the equilibration procedures (see Section IV of the Supporting Material for details).
holoCaM-Ng13–49. Since there is no experimentally determined structure, we reconstructed the all-atomistic structures from the selected coarse-grained side-chain-Cα models of apoCaM-Ng13–49 using SCAAL method (32) (see Section IV.1 of the Supporting Material for the criteria of selecting apoCaM-Ng13–49 models). We estimated the position of each Ca2+ ion as the center of mass of the side chains of the corresponding Ca2+-coordinating residues from the four Ca2+ binding loops. We inserted the Ca2+ ions into these positions as an initial condition for the next minimization process with the all-atomistic AMBER99SB-ILDN force field to define their final positions. During the minimization, only the backbone heavy atoms (excluding Ca2+) of the holoCaM-Ng13–49 were constrained. It was then followed by solvation of TIP3P water molecules and ionization of Na+/Cl− ions, which required another round of energy minimization and equilibration. The backbone heavy atoms and the Ca2+ ions were constrained (but not fixed) for the holoCaM-Ng13–49 complexes. After preparation, the positions of the Ca2+ ions were robust and did not drift away because 1) there were ∼5–7 oxygen atoms from the side chains in the loop within 4 Å of each Ca2+ ion; 2) our calculation showed that the average stability of the Ca2+ ions at binding site III and IV is ΔG = −16.0 and −12.8 kcal/mol, respectively.
Pulling simulations and computation of the free energy differences
We performed all-atomistic steered molecular dynamics (MD) simulations (see Sections IV.3 and IV.4 in the Supporting Material for the procedures and details of the steered MD simulations) to calculate the Ca2+ binding free energy (ΔG) using JE (34). JE relates ΔG and the irreversible work along an ensemble of non-equilibrium trajectories pulling the Ca2+ from the bound state to the unbound state (Eq.uation S10). The nonequilibrium trajectories (number M = 100∼150) were generated by steered MD simulations with all-atomistic models. The difference in the Ca2+ binding free energy ΔG between holoCaM-CaMBT (CaMBT: calmodulin binding targets) and CaM is defined as ΔΔG = ΔGholoCaM-CaMBT − ΔGholoCaM. ΔΔG allows us to evaluate the influence of different CaMBTs on Ca2+ binding to CaM, where ΔGholoCaM-CaMBT and ΔGholoCaM were estimated from independent simulations of pulling Ca2+ from the holoCaM-CaMBT and the holoCaM, respectively.
Analyses: calculation of “apparent chemical shifts”
In the NMR experimental work by Hoffman et al. (30), a semiquantitative comparison of amide chemical shifts were presented for residues in apoCaM (calmodulin without calcium ions) that are affected by binding of Ng13–49. In the NMR spectroscopy, the chemical shift is the relative resonant frequency in the local induced magnetic field and is diagnostic of the molecular structure. A threshold was applied to generate a set of Boolean numbers, with “1” representing a significant change in the chemical shifts and “0” indicating no change. We refer to the Boolean series as “apparent chemical shifts” throughout this study. Berjanskii and Wishart (42) showed that the inverse absolute chemical shifts roughly correlates with root mean square fluctuations (RMSF), which reflects the flexibility of the structure. Therefore, to compare with the change of chemical shifts from unbound to bound apoCaM in the experiment, we approximated the amide chemical shifts by the inverse of RMSF of Cα beads and defined “apparent chemical shifts” as Δ = (RMSFunbound/RMSFbound − τ). τ = 50% was used. Δ measures the change of local flexibility of the apoCaM: larger values of Δ indicate stabilization of the corresponding residue upon binding with Ng13–49.
Results
Building weakly bound apoCaM-Ng13–49 complexes in coarse-grained models
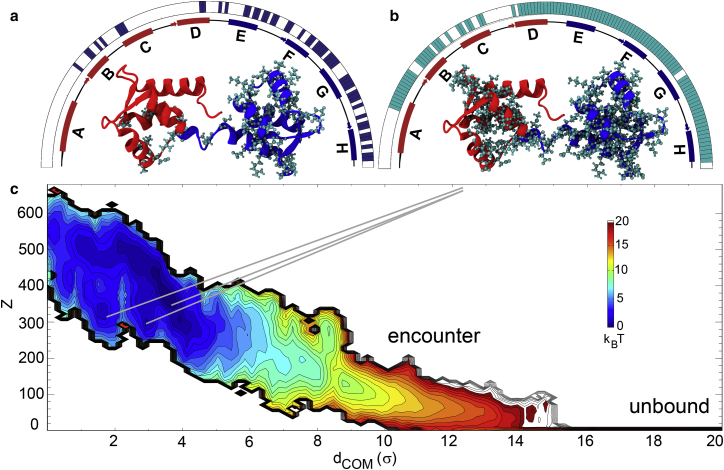
Because of the lack of experimentally determined apoCaM-Ng13–49 complex structures, we used low-resolution information on the bound complex of apoCaM-Ng13–49 from NMR measurements (30) for building plausible models from coarse-grained molecular simulations. The NMR experiments showed the change in the backbone chemical shifts of apoCaM upon Ng13–49 binding (Fig. 2 a). It revealed the residual information on the structural changes of apoCaM upon binding with Ng13–49 (30), but did not guarantee a direct contact between apoCaM and Ng13–49. The experiment showed that the major structural changes occur in cCaM as well as Helices B and C in nCaM, as in Fig. 2 a.
Figure 2.
Reweighted PMF of apoCaM-Ng13–49 binding and changes in chemical shifts for apoCaM upon Ng13–49 binding. (a and b) The residues that experienced significant changes in chemical shifts are projected on the apoCaM structure (PDB: 1CFD) as a ball-and-stick representation from experimental measurement in (a) (30) and from our calculations according to the coarse-grained molecular simulations in (b). (c) The PMF from the coarse-grained molecular simulations is plotted against the center of mass distance between apoCaM and Ng13–49 (dCOM) and the number of intermolecular contacts (Z). The coarse-grained molecular simulations were performed at pH = 6.3 and ionic strength = 0.1 M according to the conditions of the nuclear magnetic resonance experiments (30). We used a reduced unit of length σ = 3.8Å. The color is scaled in kBT, T = 1.1 ε/kB, where ε is reduced unit of energy and kB is Boltzmann constant. For visual guidance, we provided bars above the schematic representation of secondary structures in red and blue segments of apoCaM on the half circles in (a and b). To see this figure in color, go online.
One of the prominent reasons that we used coarse-grained simulations is to achieve efficient sampling of the conformational space (see Sections I–III in the Supporting Material for details about the coarse-grained simulations). We implemented the statistical potentials into the structural Hamiltonian of the Ng13–49, as well as the intermolecular interaction between apoCaM and Ng13–49. For the modeling of apoCaM, we kept limited structural information that favors an extended conformation and matches the structural description of the experimental measurements (25, 43). We found that apoCaM-Ng13–49 complex samples an ensemble of varying conformations through nonspecific intermolecular interactions, indicated by the broad distribution of the bound complex in the potential of mean force (PMF) (see Fig. 2 c).
Once we generated the ensemble of bound complexes, we strategically selected the most probable complex structures of apoCaM-Ng13–49 with the previously mentioned NMR measurement as a guide (Fig. 2 a) by following the procedures: 1) we reweighed the ensemble of apoCaM-Ng13–49 structures from the umbrella sampling simulations (44) using Weighted Histogram Analysis Method (45, 46), and employed an importance sampling method (32) (see Section V.4 in the Supporting Material) to select a subset of 23,722 structures from five million independently sampled conformations. The surprisal value between the sample distribution Psample(dCOM) and the original unbiased distribution Pori(dCOM) = 0.14 to show that the sample distribution represents the original distribution well. 2) We performed a clustering analysis on the sampled structures (see Section V.5 in the Supporting Material for the clustering method); 3) we computed the “apparent chemical shifts” (see Analyses: calculation of “apparent chemical shifts” for the definition, Fig. 2 b) from the major clusters. The population of the major four clusters (comprising 86%, Table S2) and the correlation coefficients between computationally obtained “apparent chemical shifts” from the four clusters and the experimental NMR data are shown in Table S2. We identified the cluster (the dominant cluster) of complex structures, which best matched the experiment (30), with a correlation coefficient of 0.36. From the dominant cluster (i.e., cluster 1 in Table S2), cCaM is mostly stabilized by binding with Ng13–49 and helices B and C are partially stabilized (Fig. 2 c).
We next analyzed the structures of the weakly bound apoCaM-Ng13–49 by comparing the probability of contact formation from the unbound state (defined by dCOM ≈ 20 σ in Fig. 2 c) in Fig. S3. In the selected cluster (cluster 1) of the apoCaM-Ng13–49 complexes, contacts within apoCaM (triangles in solid lines in Fig. S3 c) became less probable upon Ng13–49 binding. In addition, the probability of interdomain contacts between Helix A from nCaM and inter-domain linker, helices G and H from cCaM (the solid rectangles in Fig. S3 c) decreased to allow interaction with Ng13–49 (the solid rectangles in Fig. S3 a). In contrast, after binding with apoCaM, Ng13–49 diminished interactions between IQ motif and the acidic region (Fig. S3 b, the rectangle in dotted lines); subsequently, probability of forming α-helix structure in the IQ motif increases (Fig. S3 b, the rectangle in solid line). Provided that there was no bias to the formation of α-helix structure in Ng13–49, our model predicted formation of secondary structures in the IQ motif after binding with apoCaM.
For the intermolecular interaction of the weakly bound complex from the main cluster, IQ motif of Ng13–49 interacted with Helix A, B/C Helix linker, and Helix D from nCaM, and interdomain linker, Helix E and Helix H, and the F/G Helix linker from cCaM (Fig. S3 a, ellipse in dotted lines). These regions from CaM (either apoCaM or holoCaM) also participate in canonical binding of holoCaM with CaMKI or CaMKII (25). Although the IQ motif of Ng13–49 formed a helical structure and interacts with cCaM of high probability, the acidic region of Ng13–49 remains unstructured (Fig. S3 b, no change in contact formation along diagonal for the acidic region). It is highly probable for the acidic region to interact with both nCaM and cCaM, especially with F/G helix linker and the central linker (Fig. S3 a, ellipse in solid lines). We further calculated the correlation among these pairwise contacts in Section V.6 of the Supporting Material, and found that the interaction between acidic region of Ng13–49 and Ca2+ binding loops from apoCaM anticorrelated with those within cCaM (shown in magenta ellipse in Fig. S4).
Molecular mechanism of apoCaM-Ng13–49 binding
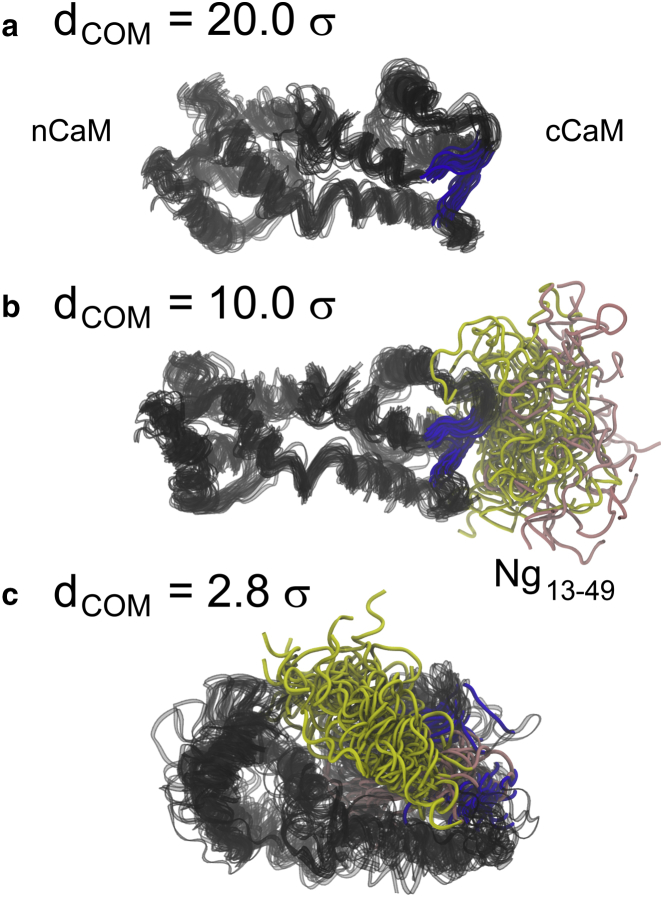
We next investigated the conformational changes of apoCaM-Ng13–49 during the association process along their center-of-mass separation (dCOM) for better understanding of the molecular mechanism of binding. The unbound structure was taken from dCOM = 20.0 σ, where the interaction between the two proteins is negligible; the encounter state structure (25) was taken from dCOM = 10.0 σ, where the two proteins began to make contact; the bound state structure was take from dCOM = 2.8 σ, where the PMF(dCOM) reached the minimum (see the magenta curve Fig. S2 for the PMF). Superposed structures of apoCaM-Ng13–49 complex at dCOM = 20.0, 10.0, and 2.8 σ are shown, representing unbound, encounter, and bound states, respectively (Fig. 3). There was no apparent structural change in apoCaM from the unbound state (Fig. 3 a) to the encounter complex (Fig. 3 b) that the conformation of apoCaM remains extended. The onset of binding in Fig. 3 b shows that the IQ motif of the Ng13–49 mainly interacted with cCaM, which was not involved in a global conformational change of apoCaM. From the encounter complex (Fig. 3 b) to the bound state (Fig. 3 c), Ng13–49 remained partially structured and mainly gained interactions with nCaM and local conformational change of apoCaM was observed. In particular, the EF-hand β-scaffold (47), which stabilizes the two helix-loop-helix motifs (EF-hand) in cCaM (see Fig. S5 for illustration of the EF-hand β-scaffold), is broken by insertion of the acidic region of Ng13–49.
Figure 3.
Illustration of the structural changes in unbound, encounter, and bound ensemble of CaM-Ng13–49 complexes. Structures of CaM in (a) was taken from the unbound state when CaM and Ng13–49 are well separated at dCOM = 20.0 σ. σ = 3.8 Å. (b) Structures from the encounter of binding when apoCaM and Ng is separated at dCOM = 10.0 σ. (c) Structures from the bound state at dCOM = 2.8 σ. For visual guidance, we superposed 20 sets of structures in each panel. The CaM is colored in black; the residues (residues 99∼101 in Ca2+ binding loop III and residues 135∼137 in Ca2+ binding loop IV), which form EF-hand β-scaffold in cCaM are colored in blue; the acidic region and IQ motif of Ng13–49 are colored in pink and yellow, respectively. To see this figure in color, go online.
To understand their binding at the residual level, we plotted the probability of contact formation at dCOM = 20.0, 10.0, and 2.8 σ in Fig. S6. At dCOM = 20.0 σ, or the unbound state, there was no contact formed between apoCaM and Ng13–49 (in Fig. S6 a). The contacts within Ng13–49 were ubiquitous and of low probability, corresponding to the transient nature of conformations of an intrinsically disordered protein/peptide (IDP). Upon initial binding with apoCaM at dCOM = 10.0 σ, only IQ motif from the Ng13–49 gained contacts with Helix F and Ca2+ binding loop IV from cCaM. This indicates a crucial role of the IQ motif in the recognition by apoCaM. Those contacts were kept when dCOM became 2.8 σ, which suggests that the IQ motif also facilitated the stabilization of the apoCaM-Ng13–49 complex. At this stage, the contacts between the acidic region of Ng13–49 and both of nCaM and cCaM formed broadly but with low probability. For apoCaM, from unbound to bound states, most of the contact formation within apoCaM remained the same (of high probability), except when dCOM = 2.8 σ, the side chain-side chain contacts between Helix E and Helix H, between Helix F and Ca2+ binding site IV, and the β-sheet contacts between Ca2+ binding sites III and IV (encircled in Fig. S6). In particular, the probability of the contacts that form the EF-hand β-scaffold (encircled) became less when the acidic region of Ng13–49 formed contacts with cCaM. Ng became partially helical in the bound form. We will relate this finding to its importance of specific functions under Discussion.
Binding of the CaMBTs to CaM modulates the Ca2+ binding affinity validated by atomistic pulling simulations
We found that interactions between the acidic region of Ng13–49 and the Ca2+ binding loops from cCaM-apoCaM competed with those within apoCaM. We hypothesized that, due to this competition, the EF-hand β-scaffold, which is shown to control the opening and closing of the EF-hands (47, 48), become less stable, thus facilitating the release of Ca2+ from CaM. To test this hypothesis, we strategically selected apoCaM-Ng13–49 complex structures from the most dominant cluster (i.e., cluster 1 in Table S2) in the coarse-grained molecular simulations for the calculation of Ca2+ binding free energy. The selection was based on the characteristics of apoCaM binding with either Ng protein or Ng peptides according to the results from several experimental studies: 1) EF-hands in cCaM are open and EF-hands in nCaM are closed from X-ray crystallography and NMR experiments (29, 49); 2) Ng13–49 has more interactions with cCaM as suggested from NMR studies, (30). Zn (Zc) is the number of intermolecular contacts between Ng and nCaM (cCaM). (See Section V in the Supporting Material for the definition of Z.) This was further shown by the EF-hand angles in CaM in forms of Ca2+-absent, Ca2+-loaded, apoCaM-NgIQ, and holoCaM-CaMKII in Table S3. As a result, four coarse-grained structures were selected from the major cluster (cluster 1) for further reconstruction of all-atomistic protein models with four Ca2+ ions included (see (50) for the protocol of reconstructing the all-atomistic model from a side-chain-Cα model).
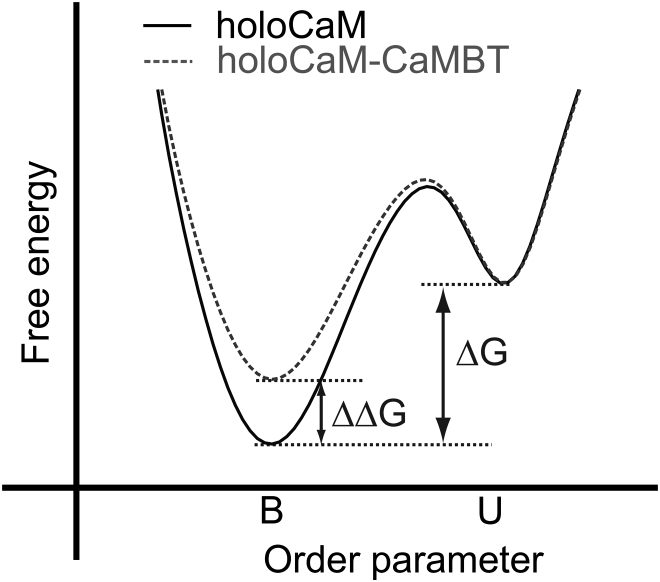
We evaluated the free energy difference between Ca2+-unbound and Ca2+-bound state (ΔG = GB − GU, see Fig. 4 for illustration) using JE (34, 51) by pulling the two Ca2+ ions independently from the Ca2+ binding sites III and IV of the cCaM (see simulations details in IV.5 from the Supporting Material). We further computed the free energy changes in the absence or the presence of a target (ΔΔG = ΔGholoCaM-CaMBT − ΔGholoCaM, see Fig. 4 for illustration). ΔΔG allows us to evaluate the influence of CaMBT on Ca2+ binding to CaM. If ΔΔG >0, it means that the CaMBT destabilizes the bound state and thus decreases the Ca2+ affinity, as illustrated in Fig. 4. If ΔΔG <0, CaMBT enhances Ca2+ affinity for CaM.
Figure 4.
Illustration of the definitions of the binding free energy ΔG and ΔΔG. ΔG = GB − GU. ΔΔG = ΔGholoCaM-CaMBT − ΔGholoCaM. B and U stand for bound and unbound states of the Ca2+, respectively. ΔΔG >0 means that the CaMBT destabilizes the bound state and thus decreases the Ca2+ affinity.
We found that the distribution of work values does not follow Gaussian distribution (Fig. S14). The estimation of free energy difference ΔG could be very inaccurate by directly applying JE or its second-order cumulants approximation (51) (we reported the direct estimation from JE in Table S6). As shown in Fig. S13, the binding free energy ΔG was estimated for Ca2+ at binding site III or site IV of holoCaM and holoCaM-CaMKII using a running JE estimate or a block-average method (BA, i.e., using subsets of all available work data using Jarzynski’s equality). ΔG converged to values, which deviate from experimental values (∼ −5 to −4 kcal/mol). To improve the efficiency of the free energy estimation, we implemented the cumulative integral (CI) extrapolation method developed by Ytreberg and Zuckerman (51). CI uses an integral for more accurate estimations than the linear extrapolation method by extrapolating to 1/n → 0, where n is total number of work values. It was shown that CI extrapolation could reduce the required data by 5- to 40-fold (51, 52). Therefore, we adopted the CI extrapolation method to estimate the free energy difference.
We summarized the binding free energies of Ca2+ estimated by the CI extrapolation in Table 1 for a total of six conformations: four holoCaM-Ng13−49 (showing averaged values), one holoCaM and one holoCaM-CaMKII. For all of the four conformations of holoCaM-Ng13−49, the binding of Ng13−49 to CaM destabilized the Ca2+ in site III and site IV, respectively, by showing an averaged positive ΔΔG (Table 1). In comparison, we examined the importance of the canonical bound structure for the release of Ca2+ from the complex structure of holoCaM-CaMKII (PDB: 1CDM) where the CaM wraps around and binds with a well-formed helical structure of CaMKII peptide at an antiparallel position. From CI extrapolation, each site presented a negative ΔΔG, implying that the presence of CaMKII stabilizes the Ca2+ in both site III and site IV from CaM.
Table 1.
Difference in Binding Free Energy of Ca2+ Calculated from Nonequilibrium Molecular Simulations and from the Experiments at pH = 7.4.
| holoCaM-Ng13–49 | holoCaM-CaMKII | ||
|---|---|---|---|
| ΔΔGCI (kcal/mol) | Site III | 9.2 ± 2.2 | −2.5 |
| Site IV | 22.4 ± 0.9 | −1.7 | |
| ΔΔGexp (kcal/mol) | Site III/IV | 2.5 | −3.3 |
The CI extrapolation was used in the calculation of binding free energy of Ca2+ ΔΔGCI from the simulations. The averaged value of ΔΔG statistical errors from the four conformations of the holoCaM-Ng13–49 complex are provided. The experimental binding free energy ΔΔGexp for holoCaM-Ng13–49 was from literature (30) and the experimental values of the holoCaM-CaMKII were from (14).
Conformation of bound CaM-CaMBT complex dictates Ca2+ release
HoloCaM-CaMKII forms a canonical bound complex, while apoCaM-Ng13−49 does not. In the following, we unveiled the molecular mechanism that governs varying Ca2+ binding affinity for cCaM in complexes of CaM and distinct CaMBTs. We examined one holoCaM-Ng13−49 model reconstructed from the coarse-grained structure that led to a maximal increase of Ca2+ binding free energy, as well as the crystal structure of holoCaM-CaMKII (PDB: 1CLL).
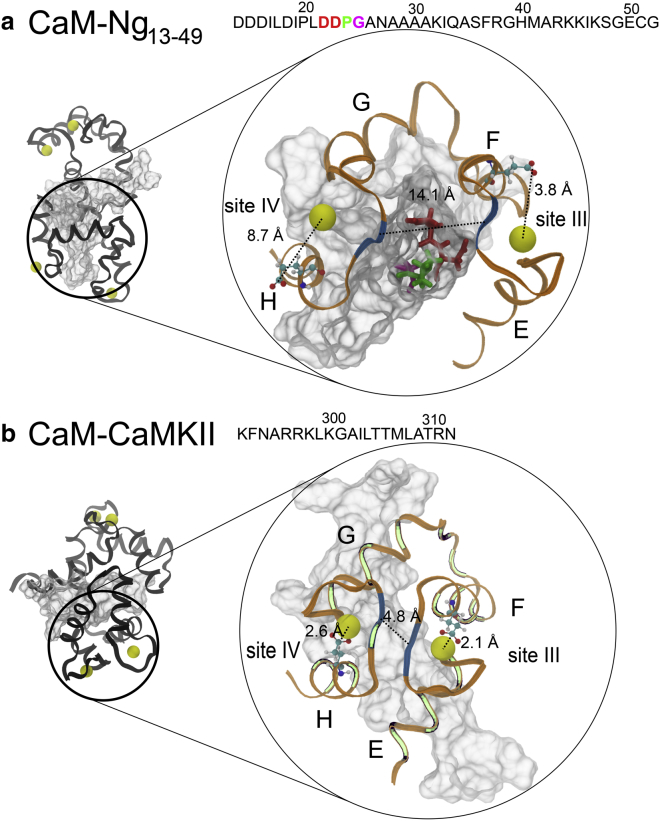
In Fig. 5 a, Ng13–49 is bent from the middle between residues P24 and G25 from the acidic regions (in green and in gray on the amino acid sequence). On the one hand, the IQ motif interacts with Helix F, Helix G, and F/G helix linker from cCaM to stabilize the holoCaM-Ng13−49 complex. On the other hand, the acidic N-term interacts with both nCaM and cCaM. Surprisingly, the four residues D22-D23-P24-G25 (DDPG) (in ball-and-stick representation) before the IQ motif on Ng13−49 stick out and insert into the middle of the EF-hand β-scaffold (colored in blue segments) between Ca2+ binding loops III and IV from cCaM, disrupting the stability of EF-hand β-scaffold. As a result, the distance between the two β-strands becomes 7.9 ± 1.2 Å (average over the four conformations) comparing to ∼5.0 Å in the intact holoCaM (PDB: 1CLL). In contrast, the distance decreases slightly to 4.8 Å in holoCaM-CaMKII (PDB: 1CDM).
Figure 5.
Differential intermolecular interactions in holoCaM-Ng13–49 and holoCaM-CaMKII complex structure tune Ca2+ binding affinity for cCaM. (a) The atomistic structure of holoCaM-Ng13–49 complex was reconstructed from the coarse-grained simulations that led to the largest decrease in Ca2+ affinity for site III and site IV. (b) The structure of holoCaM-CaMKII complex, showing a wrap-around binding pattern, is from the X-ray crystallography (PDB: 1CDM). The complete structures of the complexes are on the left, CaM is in black, Ca2+ ions are represented by yellow beads, and the CaMBTs are in white. The sequences of the CaMBTs are provided above the figures. For visual guidance, the cCaM and the CaMBTs are enlarged and recolored on the right. The cCaM is in ribbon representation and colored in orange. The residues forming EF-hand β-scaffold in the crystal structure, i.e., residues Y99, I100 from site III, and residues Q135, V136 from site IV, are colored in blue. The invariant Glu residue in the 12th position of each Ca2+-binding loop contributes two oxygen atoms to the coordination of the Ca2+ ion and is shown in ball-and-stick representation. The dotted lines show the distance between Ca2+ and the two oxygen atoms from Glu12 and the distance between the two β-strands in cCaM. The four residues that stick out from Ng13–49 are D22 (red) D23 (red) P24 (green) G25 (magenta) in (a).The residues from CaM, which form contacts with CaMKII peptides, are colored in light green in (b). To see this figure in color, go online.
Moreover, the average distance between the Ca2+ and the Ca2+ coordinating oxygen atoms from the 12th residue (Glu-12), or Glu-Ca, in site III and IV from cCaM is 4.5 ± 0.7 and 3.7 ± 0.5 Å, respectively (Fig. 5 a). As a reference, for Ca2+ in site III and site IV of the crystal structure of holoCaM without a target (PDB: 1CLL), Glu-Ca = 2.3 and 2.5 Å, respectively. The 12th residue in the Ca2+ binding loop, or Glu-12, plays a crucial role in stabilizing Ca2+ in the binding loop (1, 47). However, the presence of the acidic region from Ng13−49 increases Glu-Ca in the holoCaM-Ng13–49 complex (Fig. 5 a), especially for site IV, which is slightly closer to the center of mass of the DDPG motif than site III. The motif DDPG from the acidic region of Ng13−49 pries open the EF-hand β-scaffold and facilitates the release of the Ca2+ from cCaM. In comparison, we examined the importance of the canonical bound structure for the release of Ca2+ from the crystal structure of holoCaM-CaMKII (PDB: 1CDM) in Fig. 5 b. In contrast, Glu-Ca for sites III and IV (Fig. 5 b) are similar to those in the crystal structure of holoCaM without a target (PDB: 1CLL).
To understand the evolutionary role of the acidic region of Ng13−49 and its biological significance in modulating Ca2+ binding affinity of CaM, we performed sequence alignment of Ng from different species available in the protein knowledgebase (UniProtKB, http://www.uniprot.org/uniprot/) (Table S14). Sequence alignment results of Ng revealed that the amino acids in the acidic region are either conserved across the species or found as amino acids with similar physicochemical properties (see Fig. S15). In particular, we noted that the cluster of residues “DIPLDDP” from the acidic region of Ng that show anti-correlation with the binding loops III and IV of CaM based on the pairwise contacts (see Fig. S4; Table S8) are conserved across all the species (see Fig. S15). Moreover, the “DDPG” motif from the acidic region of Ng is conserved (see Fig. S15) across the higher vertebrate species (from rodent to human; see Table S14). Interestingly, in the lower vertebrate species the Gly (G) residue of this motif is found as Asp (D) (in reptiles and birds) or Glu (E) (in fish) or Ala (A) (in zebrafish), whereas the rest of the residues (DDP) are conserved across all the vertebrates (see Fig. S15). We also found that the DDPG motif, which maintains close proximity to the middle part of both the Ca2+ binding loops III and IV in the holoCaM-Ng13–49 complex (see Fig. S16) plays an important role in disrupting the EF-hand β-scaffold in CaM as we mentioned before. We speculate that the acidic region of Ng and especially the DDPG motif is evolutionarily important for their biological role in suppressing and/or fine-tuning the Ca2+ binding affinity of CaM.
Discussion
The energy landscape of apoCaM-Ng13–49 binding is rugged
The weakly bound complexes are commonly observed in protein-protein associations involving intrinsic disordered proteins (IDPs) in both experiments (53, 54) and computer simulations (55, 56, 57, 58, 59, 60). Long-range electrostatic interactions enhance the rate of association of several weakly bound complexes (61). Generally, the nonspecific interactions, including hydrophobic and electrostatic interactions, are known to be a major contributor to the weakly bound complexes involving IDPs. Sugase et al. (54) showed from NMR experiments that the weakly bound transient complexes of the phosphorylated kinase inducible domain (pKID) of transcription factor CREB and the kinase-induced domain of the CREB-binding protein were predominantly stabilized by nonspecific hydrophobic contacts instead of electrostatic interactions. The importance of nonspecific intermolecular interactions was further addressed by computer simulations on phosphorylated kinase inducible domain and kinase-induced domain by Turjanski et al. (55), as well as on nuclear-receptor coactivator binding domain of CREB-binding protein and the p160 steroid receptor coactivator ACTR by Chen et al. (57). In both cases structure- or topology- based models (62) were used for the intermolecular interactions that define a specific bound structure.
Determination of the structure of the apoCaM-Ng13–49 complex experimentally is challenging due to its low stability (28). To overcome this problem, we incorporated statistical nonbonded interactions and electrostatic interactions, which do not rely on a specific complex structure, in our protein model. In addition, to model the disordered Ng13–49, we implemented a sequence-based statistical dihedral angle potential (31) in the Hamiltonian. Our study reveals a rugged free energy landscape of apoCaM-Ng13–49 binding (Fig. 2 c). The conformations of apoCaM-Ng13–49 thermally fluctuate between shallow basins separated by 1∼2 kBT (T = 1.1 ε/kB, where ε is reduced unit of energy and kB is Boltzmann constant.).
The weakly bound complexes comprises “fuzzy” structures, in which either one of the binding partners or both stay dynamic (63). According to our simulations of the apoCaM-Ng13–49 complex, Ng13–49 remains partially structured as shown in the low probability of contact formation within Ng13–49 (Fig. S3 b and S6 c). Our model of the CaM model (25) samples a wide range of states by incorporating non-native interactions between residues. This idea of modeling beyond a simple structure-based model meets the experimental exploration of CaM with single-molecule experiments that its energy landscape is rather rugged and complex with plenty of intermediates (19). Our approach differs from the approaches adopted by those studies that the conformational changes of the target were ignored. For example, in the investigation of the interactions between the transcriptional activation domain of an oncoprotein and its target by Chan et al. (64), the target protein was modeled as a sphere of distributed charges on the surface.
To generalize, the structural flexibility and nonspecific interactions, corresponding to entropic and enthalpic effects, respectively, result in the rugged energy landscape of apoCaM-Ng13–49 that presents multiple weakly bound complexes without a global minimum.
IQ motif of Ng13–49 is crucial for the initial binding of apoCaM
It was postulated that the residual structure of an IDP is necessary for molecular recognition in CaM-CaMBT complex formation (65). We found that the residual structure in Ng is crucial for recognition and binding with CaM. We found that the IQ motif started to interact with cCaM at a distance of dCOM = 10 σ and remained during the binding process, indicating its key role in binding with apoCaM. Creamer et al. (66) using CaM-CaMBT systems as well as Clarke et al. (67) using the BH3 motif of the largely disordered protein p53 upregulated modulator of apoptosis (PUMA) and a folded protein induced myeloid leukemia cell differentiation protein (MCL-1), however, postulated that the residual structure of the IDP did not affect binding kinetics, but weakened the binding affinity upon helix-breaking mutation. It is important to note that in Creamer’s study, most of the CaMBTs bind CaM in a canonical form where CaM undergoes large global conformational changes. In such scenarios, the “conformational and mutually induced fit” mechanism (25) is needed for the recognition and binding (see The binding mechanism of CaM-CaMBT might be key to regulating Ca2+ binding affinity on the binding mechanism of CaM-CaMBT). However, Ng predominantly interacts with cCaM and does not form a full helical structure, therefore the binding does not require global conformational changes of CaM.
The acidic region is key to Ng13–49 for tuning CaM’s affinity for Ca2+ comparing to other IQ-motif peptides
Our computation of the change in free energy of Ca2+ binding to cCaM from nonequilibrium atomistic pulling simulations reveals that the target peptides Ng13–49 and CaMKII have opposing effects on Ca2+ binding affinity to cCaM. It is important to note that the CaMKII peptide binds to CaM in a canonical form in which the two domains of CaM wrap around a helical CaMKII peptide (24), whereas Ng13–49 forms weakly bound complexes with a rather extended CaM. Such a difference results in distinct conformations of the EF-hand motifs and the Ca2+ binding loops in CaM.
The binding and dissociation of Ca2+ to/from cCaM essentially depend on the two EF-hand motifs, which are connected by the F/G helix linker and are rigid in holoCaM (Fig. S5). This construct of EF-hand motif pair is often referred as the “EF-hand β-scaffold” (47) proposed by Grabarek (47). The EF-hand β-scaffold immobilizes the Ca2+ ion during its initial binding to the Ca2+ binding site. Our findings with regard to target binding that modulate CaM’s calcium affinity is supported by experimental observations (1). An enhanced structural stability of an EF-hand β-scaffold through target binding in a canonical CaM-CaMBT form increases CaM’s calcium affinity, which is discussed in the detailed review by Gifford et al. (1). In those experiments, a severe disruption in the Ca2+ binding loops due to the repacking of cCaM causes the Ca2+ coordinating oxygen atoms from the Glu-12 of the Ca2+ binding loop to move away from their Ca2+ binding positions and the release of the Ca2+ (68). In addition, several experiments showed that when CaMBT peptides bind to CaM canonically, the Ca2+ affinity for cCaM increases (69): ΔΔG varies from −1.5 kcal/mol for phosphorylase kinase, −3.3 kcal/mol for CaMKII (70) to −4.8 kcal/mol for β-calcineurin (71).
We found from this work that during the binding process, on one hand, IQ motif of Ng13–49 carries the function of recognition and stabilization. On the other hand, the role of the acidic region of Ng13–49 might relate to the biological functions of the protein because of its influence on the stability of EF-hand β-scaffold (Fig. S6 c) regulating Ca2+ binding to CaM. Ng belongs to the IQ motif CaMBTs family. IQ-motif CaMBTs such as the sodium channel (NaV1.2), the calcium channel (CaV1.1 and CaV1.2), PEP-19, and Ng present distinct effects on CaM’s affinity for Ca2+.
The presence of the acidic region rather than the IQ motif determines whether the interactions between CaM and the IQ-motif CaMBT are disruptive or constructive. For NaV1.2 and PEP-19 (Purkinje cell protein 4; PCP 4) that contain an IQ motif and a previous acid region, both of them bind to cCaM. Binding of them lowers the Ca2+ binding affinity for cCaM: binding of the NaV1.2 causes an increase in ΔΔG of about +2 kcal/mol (72) and PEP-19 an increase of about +0.2 kcal/mol (49). However, for CaV1.1 and CaV1.2, which contain an IQ motif but no such previous acidic region, they behave like a canonical binding motif, where the CaMBT forms a helical structure wrapped by the compact CaM, and stabilize the Ca2+ binding by ΔΔG = −1 and −2.6 kcal/mol, respectively (73). The results support the active role of the acidic region, but do not imply the molecular mechanism of how it regulates Ca2+ binding to CaM. By carrying out multiscale molecular simulations, we identified the key residues DDPG in the acidic region of Ng13–49 that “pry” open the β-sheet structure between the two Ca2+ binding loops.
The binding mechanism of CaM-CaMBT might be key to regulating Ca2+ binding affinity
A number of recent advancements have been made in experimental and computational approaches to examine protein-protein interactions involving IDPs (74, 75, 76, 77, 78). A key emerging concept is the idea of “specificity on demand” where protein interactions are dictated by concerted interactions between both binding partners. From this view, the process of binding cannot be inferred even if the structures of the initial reactants and final complex are known. The importance of structural flexibility motivated the development of theories for binding mechanisms (79, 80, 81, 82, 83), such as fly casting (61, 84), folding upon binding (58, 85), “dock-and-coalesce” (74, 86), and conformational selection (87, 88). These multiple steps mechanisms underlie possible kinetic bottlenecks due to subsequent conformational changes in a post-collision event (74, 86). Despite differences in these theories, past efforts that focus on IDPs binding to known structures have not dealt with the complexities of the conformational variability inherent in the binding process that can ultimately lead to different final products involving potentially large changes in both partners. This view is highlighted by our efforts that revealed that CaM binding to its targets is mediated by a conformational and mutually induced fit model (25).
In our previous study (25), we discovered that the binding between CaM and CaMBTs that forms a canonical bound complex, such as the CaMKII peptide, require a “conformational and mutually induced fit” mechanism. In this mechanism, the binding of the CaMKII peptide and CaM presents a two-stage process: at the onset of binding (as in an early stage), the binding is driven by diffusion and electrostatic steering effect that both CaM and CaMKII do not undergo large conformational changes. At the late stage, both experience large conformational changes that the two domains of CaM wrap around the emerging rod-like CaMKII peptide. The latter event of binding dictates a small, but significant, difference in the association rates of CaM with various CaMBTs. However, this is not the case for apoCaM-Ng13–49 binding. After the onset of binding where, the IQ motif of Ng13–49 binds to cCaM, there is no subsequent large conformational change of CaM.
The difference in the bound complexes of CaMBT-CaM along its progressive binding mechanism delineates their effects on Ca2+ binding affinity. The Ca2+ affinity is increased by binding of CaMKII peptide. The EF-hand motifs of CaM wrap around the rod-like CaMKII peptide; hence, they enhances the stability of the “EF-hand β-scaffold” that retains Ca2+ in Ca2+ binding loops. In contrast, the Ca2+ affinity is decreased by binding of Ng peptide because of lack of such wrap-and-enhance pattern of CaM. In addition, insertion of the DDPG motif into the “EF-hand β-scaffold” further destabilizes the Ca2+ binding loops. Therefore, we speculate that the benefit of a progressive binding mechanism of CaM that can be modulated by CaMBTs underlies their distinct effects on CaM’s Ca2+ binding affinities.
Force fields affect the magnitude of free energy estimation
From Table 1, the signs of ΔΔG from our computed values agreed with the experimental measurements. For holoCaM-CaMKII, they were in the same order of magnitude, while for the holoCaM-Ng13–49 complexes, the computed values were about one order of magnitude larger than the experimental measured ones. Majorly the force field contributed to the accuracy in the calculation of ΔΔG. We break the reasoning down into three categories relating to force fields:
Initial structures might matter
We found that the current all-atomistic force fields, including AMBER99SB-ILDN and CHARMM27, alter the initial structures after minimization and equilibration if the positions of the heavy atoms were not strictly fixed in space. This is true for coordinates from the crystal structures of holoCaM and holoCaM-CaMKII, as well as the all-atomistic structures of holoCaM-Ng13–49 reconstructed from coarse-grained models. The shifts in the positions are especially prominent for the Ca2+ ions. According to the study by Shukla et al. (89) on the same structure of holoCaM (PDB: 1CLL) using the AMBER99SB-ILDN force field, the root mean-square deviation of the equilibrated structure from the crystal structure was around 1 Å. This is in agreement with our simulations using the same force field that after minimization and equilibration without fixing the heavy atoms, the displacement between the Ca2+ atom and the center of mass of the corresponding Ca2+ binding loop (dCa) changed by δdCa ∼0.5 Å for holoCaM, δdCa ∼1.0 Å for holoCaM-CaMKII, and δdCa ∼1.0–2.1 Å for holoCaM-Ng13–49. This shift in dCa affected the free energy of any Ca2+ bound state. For a crude estimation of the free energy differences due to a shift in dCa, suppose the average force is 500 kJ/mol/nm, an underestimation of ΔGholoCaM would be by 6 kcal/mol if δdCa = 0.5 Å. Likewise, an underestimate of ΔGholoCaM-CaMKII would be by 12 kcal/mol if δdCa = 1 Å. Such deficiency would cause a net underestimation of ΔΔGholoCaM-CaMKII by 6 kcal/mol.
Therefore, we adopted the following strategy in our estimation of ΔΔG: for a system that has experimentally determined structure, such as holoCaM or holoCaM-CaMKII, we fixed the positions of the Ca2+ atoms and the backbone heavy atoms during the energy minimization and equilibration simulations; otherwise, for holoCaM-Ng13–49 which has no experimentally determined structure, we reconstructed the all-atomistic coordinates from coarse-grained models of apoCaM-Ng13–49 and constrained the positions of the Ca2+ ions and the backbone heavy atoms.
We determined the initial positions of the Ca2+ ions carefully. We estimated the position of each Ca2+ ion as the center of mass of the side chains of the corresponding Ca2+ coordinating residues and minimized the potential energy with the all-atomistic AMBER99SB-ILDN force field for optimization. During the energy minimization, only the backbone heavy atoms (excluding Ca2+) of holoCaM-Ng13–49 were constrained. Afterward, 1) there were ∼5–7 oxygen atoms in the loop within 4 Å of each Ca2+ ion; 2) later calculation showed that the Ca2+ ions at binding site III and IV had average ΔG = −16.0 and −12.8 kcal/mol, respectively. In summary, the final positions of the Ca2+ ions of holoCaM-Ng13–49 in the initial structures were robustly determined. Our results with respect to the sign of the differences in the free energy calculation whether targets are present or not were not affected.
The protonation states of the proteins might matter
ApoCaM is a highly charged protein with a net charge of −24e, where e is the elementary charge. The IDP target peptide Ng13–49 contains 12 charged residues. Therefore, accurate determination of the partial charges according to the protonation states particularly at the Ca2+-binding loops impacts the estimation of the binding free energy of Ca2+ for CaM. The standard procedure of assigning protonation states according to a neural pH and its pKa eludes the correct prediction of the actual protonation states for Glu and Asp amino-acids in the Ca2+-binding loops of CaM. Therefore, it requires a careful treatment on the protonation states. We employed the H++ program (41) to predict the protonation states based on pH and electrostatic energies that vary with the protein conformation and ionic strength of the solution.
After determining the protonation states of the proteins (complexes) at pH = 7.4 and ionic strength of = 0.15 M using H++ server (41), we found that there was a significant change in the net charges in comparison with the outcome from the standard protonation protocol of the MD package GROMACS (90). In the standard protocol, the Asp and the Glu amino acids in the Ca2+-binding are deprotonated at neutral pH and they carry negative charges. However, from the predictions by H++, they are protonated instead. For holoCaM, the newly protonated residues by H++ included D20, D56, E67, D93, and D129 from the Ca2+ binding loops I–IV. For holoCaM-CaMKII, the newly protonated residues by H++ included D20, D56, E67, D93, D133, and E140. For holoCaM-Ng13–49, the results depended on the conformations: most of the protonated residues by H++ included D22, E67, and D93. Because the acetyl groups (-COO−) from the Ca2+ binding loops stabilize the Ca2+-bound state, the numerical estimate of free energies was way off from the experimental values. Once the side chains of these residues in the Ca2+ binding loop were adequately protonated, the order of magnitude in Ca2+ binding free energy from computer simulations became comparable to the experimentally measured ones (shown in Table 1).
As a comparative study, we explored the robustness of our results by changing the pH from 7.4 to 6.8. According to H++, the protonation states of holoCaM remained the same at the range of pH ∈ [6.9–7.8]. However, at pH ∈ [6.5–6.8], E104 at Ca2+ binding loop III was additionally protonated. This changed the net charge of the loop III as well as the charge of the corresponding Ca2+ ion. We found that the Ca2+ binding free energy of loop III (ΔG) at pH = 6.8 increased by 3.15 kcal/mol comparing to that at pH = 7.4. ΔG for holoCaM-CaMKII remains the same at pH = 6.8 as the protonation states did not change. Therefore, ΔΔG for holoCaM-CaMKII still kept the same negative sign at pH = 6.8 as at pH = 7.4. For holoCaM-Ng13−49, depending on different structures, the gain of additional protonated residues at pH = 6.8 varied: residues D58, D11 (from Ng) for the first structure, H107 for the second structure, E84 for the third structure, and D95, H107 for the fourth structure. We found that ΔΔG for holoCaM-Ng13−49 remained the same positive sign at pH = 6.8 as at pH = 7.4. Our results remain robust and can be further tested by experiments.
We provided the calculated ΔΔG values of Ca2+ binding site III for both holoCaM-CaMKII and holoCaM-Ng13−49 in Table S7. When the pH was lowered to 6.8, the ΔΔG values decreased for holoCaM-CaMKII (favoring retaining of the Ca2+) and increased for holoCaM-Ng13−49, (favoring release of Ca2+) as illustrated in Fig. S17. The range of pH we explored here is typical for CaM to carry its specific function in a cell. We concluded that our finding is consistently robust with regard to how CaM encodes calcium incidents by binding to distinctive targets.
The charges of the Ca2+ ions depend on the environment
It has been shown that the charge on Ca2+ can be < +2e due to charge transfer and polarization in the solution and especially in the Ca2+-bound state (35, 36, 37). We computed the charges of calcium ions according to the protonation states of CaM by employing a semiempirical quantum chemistry program MOPAC (40). Similar to our previous work (39), we found that the charges on Ca2+ ions in holoCaM were approximately in the range of +1.2e to +1.6e. However, we did not rescale the size of the calcium ions in this study, which can be critical to the development of proper effective polarizable force fields for Ca2+ according to Jungwirth et al. (36, 38).
Despite those issues, our calculated free energy successfully matched the signs of the experimental values, whereas they differed by an order of magnitude for the holoCaM-Ng13−49 complexes. By using classical MD simulations, we were able to capture that Ng13−49 greatly reduces affinity of Ca2+ for cCaM whereas CaMKII peptide increases the affinity. More importantly, we provided a molecular mechanism of how the CaMBTs tune CaM’s capacity of sensing Ca2+.
The systematic error from the parameters used in steered MD simulations was minimized for the estimation of free energy changes
Computationally, free energy difference can be estimated from equilibrium ensemble using methods including umbrella sampling (44), free energy perturbation (91), and thermodynamic integration (92), as well as from nonequilibrium ensemble by using JE based on nonequilibrium work (51). We employed the nonequilibrium work method by carrying out many steered MD simulations for its simplicity and a particular reaction coordinate is not required. The drawback of this method is that the accuracy is highly dependent on sufficient sampling of the small work (34). Although theoretically JE does not depend on the pathways of pulling when removing Ca2+ from its binding site, in practice, pulling along some relevant pathways leads to small work and small variance of the work distribution; while pulling along irrelevant pathways usually yields larger work and larger variance (51). In the latter case, significantly more trajectories are required for ample sampling. Therefore, in several studies, the pulling was only along one or more predetermined pathways repeatedly (52, 93, 94, 95). However, for complex systems, it becomes even more difficult to find the relevant pathways. To solve this problem, we first searched the pathways leading to small work by pulling the Ca2+ from each binding site for ∼100 times along randomly generated directions. Second, we increased the number of simulations by pulling along those specific pathways that generate smallest work until the differences in the free energy converges between the direct JE estimation and the CI extrapolation estimation. We minimized the systematic error from sampling by running the simulations until the extrapolation from CI as well as JE converges. The signs of ΔΔG for both systems we studied agreed with the experimental measured ones.
There are other computational studies on the mechanisms of Ca2+ releasing/binding in CaM (96, 97) arguing that the deformation of protein structures attributes the discrepancies in the free energy calculation by allowing backbones to sample wide conformations in the pulling simulations (97). Even though the protein conformation can deform during pulling, we argue that this part of the work associated with protein deformation from the course of pulling Ca2+ should be part of the free energy calculation according to the concept of the JE: only the initial state and the final state determine the free energy difference.
Conclusions
CaM coordinates the activation of a family of Ca2+-regulated proteins that are crucial for synaptic plasticity at the molecular and cellular level associated with learning and memory in neurons (3). Ng is a neural-specific postsynaptic IDP, for which Ca2+ decreases binding to CaM (12). Due to the low binding affinity of apoCaM-Ng13−49 interactions, experimentally it is challenging to determine the bound structures. Our coarse-grained molecular simulations of apoCaM-Ng13−49 binding guided by experimental measurements demonstrated the importance of conformational flexibility of both the binding partners in various states of the bound complex. Our study revealed that the acidic region of Ng13−49 (the DDPG residues right before the IQ motif; refer to Fig. 1 for the sequence of Ng13−49) sticks out into the middle and “pries open” the EF-hand β-scaffold of cCaM. We speculate that this feature of destabilizing Ca2+/CaM at low Ca2+ concentration could possibly explain CaM in apo-form in the resting cell. CaMKII on the other hand plays a pivotal role in learning and memory formation for both long-term potentiation and mechanisms for the modulation of synaptic efficacy (98). Our study demonstrated that in an apoCaM-Ng13−49 complex, CaM dominantly remains in an extended conformation. This is in contrast to a canonical bound complex where the two domains of CaM wrap around a rod-like CaMKII peptide that essentially stabilizes the Ca2+ binding loops of CaM. The embedded CaMKII peptide by two domains increases the binding affinity of Ca2+ to CaM. This proposed mechanism leads to a broader understanding of the reciprocal relation between Ca2+/CaM binding and CaM/CaMBT binding (30) that involves major conformational changes in both partners. To the best of our knowledge, this is the first computational study providing a detailed description at atomistic level about how binding of CaM with two distinct targets (Ng and CaMKII) influences the release of Ca2+ from cCaM as a molecular underpinning of CaM-dependent Ca2+ signaling in neurons, which has been investigated for decades (27, 30, 99, 100). Molecular basis for learning and memory formation has aroused attention of the neuroscience community dating back to 1980s (101). We believe this study allows opportunities to connecting the molecular regulations in atomistic detail to the understanding of cellular process cascade of learning and memory formation.
Author Contributions
M.S.C. and P.Z. designed the research; P.Z., S.T., and H.T. performed the research; P.Z., S.T., and H.T. analyzed data; M.S.C., P.Z., and S.T. wrote the article.
Acknowledgments
The authors thank Dr. Neal Waxham and Dr. Dirar Homouz for stimulating discussion and Dr. John Putkey for sharing the chemical shifts data of apoCaM. P.Z. thanks Dr. Edward P. O’Brien for sharing the table of KB dihedral angle potential. All authors acknowledge the Center for Advanced Computing and Data System and the Research Computing Center at the University of Houston for providing high performance computing resources and support.
This research was funded by the National Institute of Health (1R01GM097553), the National Science Foundation (ACI: 1531814), the Center for Advanced Computing and Data Systems at UH, and the Extreme Science and Engineering Discovery Environment (XSEDE, MCB070068). S.T. was supported by Cancer Prevention and Research Institute of Texas (RP140113). M.S.C. acknowledges support from National Science Foundation (PHY-1427654).
Editor: Michael Feig.
Footnotes
Supporting Material, seventeen figures, and fourteen tables are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(17)30116-9.
Supporting Citations
References (102, 103, 104, 105, 106, 107, 108, 109, 110, 111, 112, 113, 114, 115, 116, 117, 118, 119, 120, 121, 122, 123, 124) appear in the Supporting Material.
Supporting Material
References
- 1.Gifford J.L., Walsh M.P., Vogel H.J. Structures and metal-ion-binding properties of the Ca2+-binding helix-loop-helix EF-hand motifs. Biochem. J. 2007;405:199–221. doi: 10.1042/BJ20070255. [DOI] [PubMed] [Google Scholar]
- 2.Yamniuk A.P., Vogel H.J. Calmodulin’s flexibility allows for promiscuity in its interactions with target proteins and peptides. Mol. Biotechnol. 2004;27:33–57. doi: 10.1385/MB:27:1:33. [DOI] [PubMed] [Google Scholar]
- 3.Xia Z., Storm D.R. The role of calmodulin as a signal integrator for synaptic plasticity. Nat. Rev. Neurosci. 2005;6:267–276. doi: 10.1038/nrn1647. [DOI] [PubMed] [Google Scholar]
- 4.Saucerman J.J., Bers D.M. Calmodulin binding proteins provide domains of local Ca2+ signaling in cardiac myocytes. J. Mol. Cell. Cardiol. 2012;52:312–316. doi: 10.1016/j.yjmcc.2011.06.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Yamauchi T. Neuronal Ca2+/calmodulin-dependent protein kinase II--discovery, progress in a quarter of a century, and perspective: implication for learning and memory. Biol. Pharm. Bull. 2005;28:1342–1354. doi: 10.1248/bpb.28.1342. [DOI] [PubMed] [Google Scholar]
- 6.Lisman J., Schulman H., Cline H. The molecular basis of CaMKII function in synaptic and behavioural memory. Nat. Rev. Neurosci. 2002;3:175–190. doi: 10.1038/nrn753. [DOI] [PubMed] [Google Scholar]
- 7.Colbran R.J., Brown A.M. Calcium/calmodulin-dependent protein kinase II and synaptic plasticity. Curr. Opin. Neurobiol. 2004;14:318–327. doi: 10.1016/j.conb.2004.05.008. [DOI] [PubMed] [Google Scholar]
- 8.Díez-Guerra F.J. Neurogranin, a link between calcium/calmodulin and protein kinase C signaling in synaptic plasticity. IUBMB Life. 2010;62:597–606. doi: 10.1002/iub.357. [DOI] [PubMed] [Google Scholar]
- 9.Segal M. Dendritic spines and long-term plasticity. Nat. Rev. Neurosci. 2005;6:277–284. doi: 10.1038/nrn1649. [DOI] [PubMed] [Google Scholar]
- 10.Pak J.H., Huang F.L., Huang K.P. Involvement of neurogranin in the modulation of calcium/calmodulin-dependent protein kinase II, synaptic plasticity, and spatial learning: a study with knockout mice. Proc. Natl. Acad. Sci. USA. 2000;97:11232–11237. doi: 10.1073/pnas.210184697. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Silva A.J., Paylor R., Tonegawa S. Impaired spatial learning in alpha-calcium-calmodulin kinase II mutant mice. Science. 1992;257:206–211. doi: 10.1126/science.1321493. [DOI] [PubMed] [Google Scholar]
- 12.Gerendasy D.D., Herron S.R., Sutcliffe J.G. Mutational and biophysical studies suggest RC3/neurogranin regulates calmodulin availability. J. Biol. Chem. 1994;269:22420–22426. [PubMed] [Google Scholar]
- 13.Kubota Y., Putkey J.A., Waxham M.N. IQ-motif proteins influence intracellular free Ca2+ in hippocampal neurons through their interactions with calmodulin. J. Neurophysiol. 2008;99:264–276. doi: 10.1152/jn.00876.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Gaertner T.R., Putkey J.A., Waxham M.N. RC3/Neurogranin and Ca2+/calmodulin-dependent protein kinase II produce opposing effects on the affinity of calmodulin for calcium. J. Biol. Chem. 2004;279:39374–39382. doi: 10.1074/jbc.M405352200. [DOI] [PubMed] [Google Scholar]
- 15.Kubota Y., Putkey J.A., Waxham M.N. Neurogranin controls the spatiotemporal pattern of postsynaptic Ca2+/CaM signaling. Biophys. J. 2007;93:3848–3859. doi: 10.1529/biophysj.107.106849. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Stefan M.I., Edelstein S.J., Le Novère N. An allosteric model of calmodulin explains differential activation of PP2B and CaMKII. Proc. Natl. Acad. Sci. USA. 2008;105:10768–10773. doi: 10.1073/pnas.0804672105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Lai M., Brun D., Le Novère N. Modulation of calmodulin lobes by different targets: an allosteric model with hemiconcerted conformational transitions. PLoS Comput. Biol. 2015;11:e1004063. doi: 10.1371/journal.pcbi.1004063. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Piazza M., Taiakina V., Dieckmann T. Solution structure of calmodulin bound to the target peptide of endothelial nitric oxide synthase phosphorylated at Thr495. Biochemistry. 2014;53:1241–1249. doi: 10.1021/bi401466s. [DOI] [PubMed] [Google Scholar]
- 19.Stigler J., Ziegler F., Rief M. The complex folding network of single calmodulin molecules. Science. 2011;334:512–516. doi: 10.1126/science.1207598. [DOI] [PubMed] [Google Scholar]
- 20.Tidow H., Nissen P. Structural diversity of calmodulin binding to its target sites. FEBS J. 2013;280:5551–5565. doi: 10.1111/febs.12296. [DOI] [PubMed] [Google Scholar]
- 21.Slaughter B.D., Bieber-Urbauer R.J., Johnson C.K. Single-molecule tracking of sub-millisecond domain motion in calmodulin. J. Phys. Chem. B. 2005;109:12658–12662. doi: 10.1021/jp051666o. [DOI] [PubMed] [Google Scholar]
- 22.Zhang M., Tanaka T., Ikura M. Calcium-induced conformational transition revealed by the solution structure of apo calmodulin. Nat. Struct. Biol. 1995;2:758–767. doi: 10.1038/nsb0995-758. [DOI] [PubMed] [Google Scholar]
- 23.Yang C., Jas G.S., Kuczera K. Structure, dynamics and interaction with kinase targets: computer simulations of calmodulin. Biochim. Biophys. Acta. 2004;1697:289–300. doi: 10.1016/j.bbapap.2003.11.032. [DOI] [PubMed] [Google Scholar]
- 24.Meador W.E., Means A.R., Quiocho F.A. Modulation of calmodulin plasticity in molecular recognition on the basis of x-ray structures. Science. 1993;262:1718–1721. doi: 10.1126/science.8259515. [DOI] [PubMed] [Google Scholar]
- 25.Wang Q., Zhang P., Cheung M.S. Protein recognition and selection through conformational and mutually induced fit. Proc. Natl. Acad. Sci. USA. 2013;110:20545–20550. doi: 10.1073/pnas.1312788110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Tripathi S., Wang Q., Cheung M.S. Conformational frustration in calmodulin-target recognition. J. Mol. Recognit. 2015;28:74–86. doi: 10.1002/jmr.2413. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Waxham M.N., Tsai A.L., Putkey J.A. A mechanism for calmodulin (CaM) trapping by CaM-kinase II defined by a family of CaM-binding peptides. J. Biol. Chem. 1998;273:17579–17584. doi: 10.1074/jbc.273.28.17579. [DOI] [PubMed] [Google Scholar]
- 28.Ran X., Miao H.H., Yang D. Structural and dynamic characterization of a neuron-specific protein kinase C substrate, neurogranin. Biochemistry. 2003;42:5143–5150. doi: 10.1021/bi0271751. [DOI] [PubMed] [Google Scholar]
- 29.Kumar V., Chichili V.P., Sivaraman J. Structural basis for the interaction of unstructured neuron specific substrates neuromodulin and neurogranin with Calmodulin. Sci. Rep. 2013;3:1392. doi: 10.1038/srep01392. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Hoffman L., Chandrasekar A., Waxham M.N. Neurogranin alters the structure and calcium binding properties of calmodulin. J. Biol. Chem. 2014;289:14644–14655. doi: 10.1074/jbc.M114.560656. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Karanicolas J., Brooks C.L., 3rd The origins of asymmetry in the folding transition states of protein L and protein G. Protein Sci. 2002;11:2351–2361. doi: 10.1110/ps.0205402. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Samiotakis A., Homouz D., Cheung M.S. Multiscale investigation of chemical interference in proteins. J. Chem. Phys. 2010;132:175101. doi: 10.1063/1.3404401. [DOI] [PubMed] [Google Scholar]
- 33.Hendrix D.A., Jarzynski C. A “fast growth” method of computing free energy differences. J. Chem. Phys. 2001;114:5974–5981. [Google Scholar]
- 34.Jarzynski C. Nonequilibrium equality for free energy differences. Phys. Rev. Lett. 1997;78:2690–2693. [Google Scholar]
- 35.Dudev T., Lim C. Principles governing Mg, Ca, and Zn binding and selectivity in proteins. Chem. Rev. 2003;103:773–788. doi: 10.1021/cr020467n. [DOI] [PubMed] [Google Scholar]
- 36.Kohagen M., Mason P.E., Jungwirth P. Accurate description of calcium solvation in concentrated aqueous solutions. J. Phys. Chem. B. 2014;118:7902–7909. doi: 10.1021/jp5005693. [DOI] [PubMed] [Google Scholar]
- 37.Mamatkulov S., Fyta M., Netz R.R. Force fields for divalent cations based on single-ion and ion-pair properties. J. Chem. Phys. 2013;138:024505. doi: 10.1063/1.4772808. [DOI] [PubMed] [Google Scholar]
- 38.Kohagen M., Lepšík M., Jungwirth P. Calcium binding to calmodulin by molecular dynamics with effective polarization. J. Phys. Chem. Lett. 2014;5:3964–3969. doi: 10.1021/jz502099g. [DOI] [PubMed] [Google Scholar]
- 39.Wang Q., Liang K.C., Cheung M.S. The effect of macromolecular crowding, ionic strength and calcium binding on calmodulin dynamics. PLoS Comput. Biol. 2011;7:e1002114. doi: 10.1371/journal.pcbi.1002114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Stewart J.J. Optimization of parameters for semiempirical methods V: modification of NDDO approximations and application to 70 elements. J. Mol. Model. 2007;13:1173–1213. doi: 10.1007/s00894-007-0233-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Anandakrishnan R., Aguilar B., Onufriev A.V. H++ 3.0: automating pK prediction and the preparation of biomolecular structures for atomistic molecular modeling and simulations. Nucleic Acids Res. 2012;40:W537–W541. doi: 10.1093/nar/gks375. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Berjanskii M., Wishart D.S. NMR: prediction of protein flexibility. Nat. Protoc. 2006;1:683–688. doi: 10.1038/nprot.2006.108. [DOI] [PubMed] [Google Scholar]
- 43.Anthis N.J., Doucleff M., Clore G.M. Transient, sparsely populated compact states of apo and calcium-loaded calmodulin probed by paramagnetic relaxation enhancement: interplay of conformational selection and induced fit. J. Am. Chem. Soc. 2011;133:18966–18974. doi: 10.1021/ja2082813. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Roux B. The calculation of the potential of mean force using computer-simulations. Comput. Phys. Commun. 1995;91:275–282. [Google Scholar]
- 45.Grossfield, A. 2013. WHAM: an implementation of the weighted histogram analysis method. Version 2.0.4. http://membrane.urmc.rochester.edu/content/wham.
- 46.Kumar S., Bouzida D., Rosenberg J.M. The weighted histogram analysis method for free-energy calculations on biomolecules. 1. The method. J. Comput. Chem. 1992;13:1011–1021. [Google Scholar]
- 47.Grabarek Z. Structural basis for diversity of the EF-hand calcium-binding proteins. J. Mol. Biol. 2006;359:509–525. doi: 10.1016/j.jmb.2006.03.066. [DOI] [PubMed] [Google Scholar]
- 48.Dupuis L., Mousseau N. Understanding the EF-hand closing pathway using non-biased interatomic potentials. J. Chem. Phys. 2012;136:035101. doi: 10.1063/1.3671986. [DOI] [PubMed] [Google Scholar]
- 49.Wang X., Xiong L.W., Putkey J.A. The calmodulin regulator protein, PEP-19, sensitizes ATP-induced Ca2+ release. J. Biol. Chem. 2013;288:2040–2048. doi: 10.1074/jbc.M112.411314. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Homouz D., Perham M., Wittung-Stafshede P. Crowded, cell-like environment induces shape changes in aspherical protein. Proc. Natl. Acad. Sci. USA. 2008;105:11754–11759. doi: 10.1073/pnas.0803672105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Ytreberg F.M., Zuckerman D.M. Efficient use of nonequilibrium measurement to estimate free energy differences for molecular systems. J. Comput. Chem. 2004;25:1749–1759. doi: 10.1002/jcc.20103. [DOI] [PubMed] [Google Scholar]
- 52.Zhang D., Gullingsrud J., McCammon J.A. Potentials of mean force for acetylcholine unbinding from the alpha7 nicotinic acetylcholine receptor ligand-binding domain. J. Am. Chem. Soc. 2006;128:3019–3026. doi: 10.1021/ja057292u. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Tang C., Iwahara J., Clore G.M. Visualization of transient encounter complexes in protein-protein association. Nature. 2006;444:383–386. doi: 10.1038/nature05201. [DOI] [PubMed] [Google Scholar]
- 54.Sugase K., Dyson H.J., Wright P.E. Mechanism of coupled folding and binding of an intrinsically disordered protein. Nature. 2007;447:1021–1025. doi: 10.1038/nature05858. [DOI] [PubMed] [Google Scholar]
- 55.Turjanski A.G., Gutkind J.S., Hummer G. Binding-induced folding of a natively unstructured transcription factor. PLoS Comput. Biol. 2008;4:e1000060. doi: 10.1371/journal.pcbi.1000060. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Higo J., Nishimura Y., Nakamura H. A free-energy landscape for coupled folding and binding of an intrinsically disordered protein in explicit solvent from detailed all-atom computations. J. Am. Chem. Soc. 2011;133:10448–10458. doi: 10.1021/ja110338e. [DOI] [PubMed] [Google Scholar]
- 57.Ganguly D., Zhang W., Chen J. Synergistic folding of two intrinsically disordered proteins: searching for conformational selection. Mol. Biosyst. 2012;8:198–209. doi: 10.1039/c1mb05156c. [DOI] [PubMed] [Google Scholar]
- 58.Levy Y., Wolynes P.G., Onuchic J.N. Protein topology determines binding mechanism. Proc. Natl. Acad. Sci. USA. 2004;101:511–516. doi: 10.1073/pnas.2534828100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Alsallaq R., Zhou H.X. Energy landscape and transition state of protein-protein association. Biophys. J. 2007;92:1486–1502. doi: 10.1529/biophysj.106.096024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Kim Y.C., Tang C., Hummer G. Replica exchange simulations of transient encounter complexes in protein-protein association. Proc. Natl. Acad. Sci. USA. 2008;105:12855–12860. doi: 10.1073/pnas.0802460105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Shoemaker B.A., Portman J.J., Wolynes P.G. Speeding molecular recognition by using the folding funnel: the fly-casting mechanism. Proc. Natl. Acad. Sci. USA. 2000;97:8868–8873. doi: 10.1073/pnas.160259697. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Clementi C. Coarse-grained models of protein folding: toy models or predictive tools? Curr. Opin. Struct. Biol. 2008;18:10–15. doi: 10.1016/j.sbi.2007.10.005. [DOI] [PubMed] [Google Scholar]
- 63.Tompa P., Fuxreiter M. Fuzzy complexes: polymorphism and structural disorder in protein-protein interactions. Trends Biochem. Sci. 2008;33:2–8. doi: 10.1016/j.tibs.2007.10.003. [DOI] [PubMed] [Google Scholar]
- 64.Song J., Ng S.C., Chan H.S. Polycation-π interactions are a driving force for molecular recognition by an intrinsically disordered oncoprotein family. PLoS Comput. Biol. 2013;9:e1003239. doi: 10.1371/journal.pcbi.1003239. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Oldfield C.J., Cheng Y., Dunker A.K. Coupled folding and binding with alpha-helix-forming molecular recognition elements. Biochemistry. 2005;44:12454–12470. doi: 10.1021/bi050736e. [DOI] [PubMed] [Google Scholar]
- 66.Dunlap T.B., Kirk J.M., Creamer T.P. Thermodynamics of binding by calmodulin correlates with target peptide α-helical propensity. Proteins. 2013;81:607–612. doi: 10.1002/prot.24215. [DOI] [PubMed] [Google Scholar]
- 67.Rogers J.M., Wong C.T., Clarke J. Coupled folding and binding of the disordered protein PUMA does not require particular residual structure. J. Am. Chem. Soc. 2014;136:5197–5200. doi: 10.1021/ja4125065. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Schumacher M.A., Rivard A.F., Adelman J.P. Structure of the gating domain of a Ca2+-activated K+ channel complexed with Ca2+/calmodulin. Nature. 2001;410:1120–1124. doi: 10.1038/35074145. [DOI] [PubMed] [Google Scholar]
- 69.Olwin B.B., Edelman A.M., Storm D.R. Quantitation of energy coupling between Ca2+, calmodulin, skeletal muscle myosin light chain kinase, and kinase substrates. J. Biol. Chem. 1984;259:10949–10955. [PubMed] [Google Scholar]
- 70.Peersen O.B., Madsen T.S., Falke J.J. Intermolecular tuning of calmodulin by target peptides and proteins: differential effects on Ca2+ binding and implications for kinase activation. Protein Sci. 1997;6:794–807. doi: 10.1002/pro.5560060406. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.O’Donnell S.E., Yu L., Shea M.A. Recognition of β-calcineurin by the domains of calmodulin: thermodynamic and structural evidence for distinct roles. Proteins. 2011;79:765–786. doi: 10.1002/prot.22917. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Theoharis N.T., Sorensen B.R., Shea M.A. The neuronal voltage-dependent sodium channel type II IQ motif lowers the calcium affinity of the C-domain of calmodulin. Biochemistry. 2008;47:112–123. doi: 10.1021/bi7013129. [DOI] [PubMed] [Google Scholar]
- 73.Halling D.B., Georgiou D.K., Hamilton S.L. Determinants in CaV1 channels that regulate the Ca2+ sensitivity of bound calmodulin. J. Biol. Chem. 2009;284:20041–20051. doi: 10.1074/jbc.M109.013326. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Qin S., Pang X., Zhou H.-X. Automated prediction of protein association rate constants. Structure. 2011;19:1744–1751. doi: 10.1016/j.str.2011.10.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Zheng W., Schafer N.P., Wolynes P.G. Predictive energy landscapes for protein-protein association. Proc. Natl. Acad. Sci. USA. 2012;109:19244–19249. doi: 10.1073/pnas.1216215109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76.Khait R., Schreiber G. FRETex: a FRET-based, high-throughput technique to analyze protein-protein interactions. Protein Eng. Des. Sel. 2012;25:681–687. doi: 10.1093/protein/gzs067. [DOI] [PubMed] [Google Scholar]
- 77.Rogers J.M., Steward A., Clarke J. Folding and binding of an intrinsically disordered protein: fast, but not ‘diffusion-limited’. J. Am. Chem. Soc. 2013;135:1415–1422. doi: 10.1021/ja309527h. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78.Schreiber G., Haran G., Zhou H.X. Fundamental aspects of protein-protein association kinetics. Chem. Rev. 2009;109:839–860. doi: 10.1021/cr800373w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.Uversky V.N. Natively unfolded proteins: a point where biology waits for physics. Protein Sci. 2002;11:739–756. doi: 10.1110/ps.4210102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 80.Wright P.E., Dyson H.J. Intrinsically unstructured proteins: re-assessing the protein structure-function paradigm. J. Mol. Biol. 1999;293:321–331. doi: 10.1006/jmbi.1999.3110. [DOI] [PubMed] [Google Scholar]
- 81.Papoian G.A., Wolynes P.G. The physics and bioinformatics of binding and folding-an energy landscape perspective. Biopolymers. 2003;68:333–349. doi: 10.1002/bip.10286. [DOI] [PubMed] [Google Scholar]
- 82.Sickmeier M., Hamilton J.A., Dunker A.K. DisProt: the database of disordered proteins. Nucleic Acids Res. 2007;35:D786–D793. doi: 10.1093/nar/gkl893. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 83.Chu X., Gan L., Wang J. Quantifying the topography of the intrinsic energy landscape of flexible biomolecular recognition. Proc. Natl. Acad. Sci. USA. 2013;110:E2342–E2351. doi: 10.1073/pnas.1220699110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 84.Chen J. Intrinsically disordered p53 extreme C-terminus binds to S100Bββ through “fly-casting”. J. Am. Chem. Soc. 2009;131:2088–2089. doi: 10.1021/ja809547p. [DOI] [PubMed] [Google Scholar]
- 85.Ganguly D., Chen J. Atomistic details of the disordered states of KID and pKID. Implications in coupled binding and folding. J. Am. Chem. Soc. 2009;131:5214–5223. doi: 10.1021/ja808999m. [DOI] [PubMed] [Google Scholar]
- 86.Zhou H.X., Pang X., Lu C. Rate constants and mechanisms of intrinsically disordered proteins binding to structured targets. Phys. Chem. Chem. Phys. 2012;14:10466–10476. doi: 10.1039/c2cp41196b. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 87.Tsai C.J., Kumar S., Nussinov R. Folding funnels, binding funnels, and protein function. Protein Sci. 1999;8:1181–1190. doi: 10.1110/ps.8.6.1181. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 88.Boehr D.D., Nussinov R., Wright P.E. The role of dynamic conformational ensembles in biomolecular recognition. Nat. Chem. Biol. 2009;5:789–796. doi: 10.1038/nchembio.232. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 89.Shukla D., Peck A., Pande V.S. Conformational heterogeneity of the calmodulin binding interface. Nat. Commun. 2016;7:10910. doi: 10.1038/ncomms10910. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 90.Pall S., Abraham M.J., Lindahl E. Tackling exascale software challenges in molecular dynamics simulations with GROMACS. Lect. Notes Comput. Sci. 2015;8759:3–27. [Google Scholar]
- 91.Zwanzig R.W. High-temperature equation of state by a perturbation method. I. Nonpolar gases. J. Chem. Phys. 1954;22:1420–1426. [Google Scholar]
- 92.Kirkwood J.G. Statistical mechanics of fluid mixtures. J. Chem. Phys. 1935;3:300–313. [Google Scholar]
- 93.Park S., Schulten K. Calculating potentials of mean force from steered molecular dynamics simulations. J. Chem. Phys. 2004;120:5946–5961. doi: 10.1063/1.1651473. [DOI] [PubMed] [Google Scholar]
- 94.Park S., Khalili-Araghi F., Schulten K. Free energy calculation from steered molecular dynamics simulations using Jarzynski’s equality. J. Chem. Phys. 2003;119:3559–3566. [Google Scholar]
- 95.Chen P.C., Kuyucak S. Mechanism and energetics of charybdotoxin unbinding from a potassium channel from molecular dynamics simulations. Biophys. J. 2009;96:2577–2588. doi: 10.1016/j.bpj.2008.12.3952. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 96.Zhang Y., Tan H., Chen G. Ca2+ dissociation from the C-terminal EF-hand pair in calmodulin: a steered molecular dynamics study. FEBS Lett. 2008;582:1355–1361. doi: 10.1016/j.febslet.2008.03.010. [DOI] [PubMed] [Google Scholar]
- 97.Lepsík M., Field M.J. Binding of calcium and other metal ions to the EF-hand loops of calmodulin studied by quantum chemical calculations and molecular dynamics simulations. J. Phys. Chem. B. 2007;111:10012–10022. doi: 10.1021/jp0716583. [DOI] [PubMed] [Google Scholar]
- 98.Miller S.G., Kennedy M.B. Regulation of brain type II Ca2+/calmodulin-dependent protein kinase by autophosphorylation: a Ca2+-triggered molecular switch. Cell. 1986;44:861–870. doi: 10.1016/0092-8674(86)90008-5. [DOI] [PubMed] [Google Scholar]
- 99.Putkey J.A., Waxham M.N. A peptide model for calmodulin trapping by calcium/calmodulin-dependent protein kinase II. J. Biol. Chem. 1996;271:29619–29623. doi: 10.1074/jbc.271.47.29619. [DOI] [PubMed] [Google Scholar]
- 100.Putkey J.A., Waxham M.N., Kleerekoper Q.K. Acidic/IQ motif regulator of calmodulin. J. Biol. Chem. 2008;283:1401–1410. doi: 10.1074/jbc.M703831200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 101.Crick F. Memory and molecular turnover. Nature. 1984;312:101. doi: 10.1038/312101a0. [DOI] [PubMed] [Google Scholar]
- 102.Jurado L.A., Chockalingam P.S., Jarrett H.W. Apocalmodulin. Physiol. Rev. 1999;79:661–682. doi: 10.1152/physrev.1999.79.3.661. [DOI] [PubMed] [Google Scholar]
- 103.Waterhouse A.M., Procter J.B., Barton G.J. Jalview version 2--a multiple sequence alignment editor and analysis workbench. Bioinformatics. 2009;25:1189–1191. doi: 10.1093/bioinformatics/btp033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 104.Bähler M., Rhoads A. Calmodulin signaling via the IQ motif. FEBS Lett. 2002;513:107–113. doi: 10.1016/s0014-5793(01)03239-2. [DOI] [PubMed] [Google Scholar]
- 105.Sugita Y., Okamoto Y. Replica-exchange molecular dynamics method for protein folding. Chem. Phys. Lett. 1999;314:141–151. [Google Scholar]
- 106.Sanbonmatsu K.Y., García A.E. Structure of Met-enkephalin in explicit aqueous solution using replica exchange molecular dynamics. Proteins. 2002;46:225–234. doi: 10.1002/prot.1167. [DOI] [PubMed] [Google Scholar]
- 107.Cheung M.S., Finke J.M., Onuchic J.N. Exploring the interplay between topology and secondary structural formation in the protein folding problem. J. Phys. Chem. B. 2003;107:11193–11200. [Google Scholar]
- 108.Yang Y., Faraggi E., Zhou Y. Improving protein fold recognition and template-based modeling by employing probabilistic-based matching between predicted one-dimensional structural properties of query and corresponding native properties of templates. Bioinformatics. 2011;27:2076–2082. doi: 10.1093/bioinformatics/btr350. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 109.Debye P., Hückel E. The theory of electrolytes. I. Lowering of freezing point and related phenomena. Phys. Z. 1923;24:185–206. [Google Scholar]
- 110.Betancourt M.R., Thirumalai D. Pair potentials for protein folding: choice of reference states and sensitivity of predicted native states to variations in the interaction schemes. Protein Sci. 1999;8:361–369. doi: 10.1110/ps.8.2.361. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 111.Andreasen T.J., Luetje C.W., Storm D.R. Purification of a novel calmodulin binding protein from bovine cerebral cortex membranes. Biochemistry. 1983;22:4615–4618. doi: 10.1021/bi00289a001. [DOI] [PubMed] [Google Scholar]
- 112.Dima R.I., Thirumalai D. Asymmetry in the shapes of folded and denatured states of proteins. J. Phys. Chem. B. 2004;108:6564–6570. [Google Scholar]
- 113.Camacho C.J., Thirumalai D. Kinetics and thermodynamics of folding in model proteins. Proc. Natl. Acad. Sci. USA. 1993;90:6369–6372. doi: 10.1073/pnas.90.13.6369. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 114.Lindorff-Larsen K., Piana S., Shaw D.E. Improved side-chain torsion potentials for the Amber ff99SB protein force field. Proteins. 2010;78:1950–1958. doi: 10.1002/prot.22711. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 115.Jorgensen W.L., Chandrasekhar J., Klein M.L. Comparison of simple potential functions for simulating liquid water. J. Chem. Phys. 1983;79:926–935. [Google Scholar]
- 116.Darden T., York D., Pedersen L. Particle mesh Ewald - an N.Log(N) method for Ewald sums in large systems. J. Chem. Phys. 1993;98:10089–10092. [Google Scholar]
- 117.Parrinello M., Rahman A. Polymorphic transitions in single-crystals - a new molecular-dynamics method. J. Appl. Phys. 1981;52:7182–7190. [Google Scholar]
- 118.Hess B., Bekker H., Fraaije J.G.E.M. LINCS: a linear constraint solver for molecular simulations. J. Comput. Chem. 1997;18:1463–1472. [Google Scholar]
- 119.Lipari G., Szabo A. Model-free approach to the interpretation of nuclear magnetic-resonance relaxation in macromolecules. 1. Theory and range of validity. J. Am. Chem. Soc. 1982;104:4546–4559. [Google Scholar]
- 120.Kudlay A., Cheung M.S., Thirumalai D. Crowding effects on the structural transitions in a flexible helical homopolymer. Phys. Rev. Lett. 2009;102:118101. doi: 10.1103/PhysRevLett.102.118101. [DOI] [PubMed] [Google Scholar]
- 121.Weinkam P., Pletneva E.V., Wolynes P.G. Electrostatic effects on funneled landscapes and structural diversity in denatured protein ensembles. Proc. Natl. Acad. Sci. USA. 2009;106:1796–1801. doi: 10.1073/pnas.0813120106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 122.Carpenter G.A., Grossberg S. ART 2: self-organization of stable category recognition codes for analog input patterns. Appl. Opt. 1987;26:4919–4930. doi: 10.1364/AO.26.004919. [DOI] [PubMed] [Google Scholar]
- 123.Cheung M.S., Thirumalai D. Effects of crowding and confinement on the structures of the transition state ensemble in proteins. J. Phys. Chem. B. 2007;111:8250–8257. doi: 10.1021/jp068201y. [DOI] [PubMed] [Google Scholar]
- 124.Guo Z., Thirumalai D. The nucleation-collapse mechanism in protein folding: evidence for the non-uniqueness of the folding nucleus. Fold. Des. 1997;2:377–391. doi: 10.1016/S1359-0278(97)00052-7. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.