Abstract
Many tools have been developed for haplotype assembly—the reconstruction of individual haplotypes using reads mapped to a reference genome sequence. Due to increasing interest in obtaining haplotype-resolved human genomes, a range of new sequencing protocols and technologies have been developed to enable the reconstruction of whole-genome haplotypes. However, existing computational methods designed to handle specific technologies do not scale well on data from different protocols. We describe a new algorithm, HapCUT2, that extends our previous method (HapCUT) to handle multiple sequencing technologies. Using simulations and whole-genome sequencing (WGS) data from multiple different data types—dilution pool sequencing, linked-read sequencing, single molecule real-time (SMRT) sequencing, and proximity ligation (Hi-C) sequencing—we show that HapCUT2 rapidly assembles haplotypes with best-in-class accuracy for all data types. In particular, HapCUT2 scales well for high sequencing coverage and rapidly assembled haplotypes for two long-read WGS data sets on which other methods struggled. Further, HapCUT2 directly models Hi-C specific error modalities, resulting in significant improvements in error rates compared to HapCUT, the only other method that could assemble haplotypes from Hi-C data. Using HapCUT2, haplotype assembly from a 90× coverage whole-genome Hi-C data set yielded high-resolution haplotypes (78.6% of variants phased in a single block) with high pairwise phasing accuracy (∼98% across chromosomes). Our results demonstrate that HapCUT2 is a robust tool for haplotype assembly applicable to data from diverse sequencing technologies.
Humans are diploid organisms with two copies of each chromosome (except the sex chromosomes). The two haplotypes (described by the combination of alleles at variant sites on a single chromosome) represent the complete information on DNA variation in an individual. Reconstructing individual haplotypes has important implications for understanding human genetic variation, interpretation of variants in disease, and reconstructing human population history (Tewhey et al. 2011; Glusman et al. 2014; Schiffels and Durbin 2014; Snyder et al. 2015). A number of methods, computational and experimental, have been developed for haplotyping human genomes. Statistical methods for haplotype phasing using population genotype data have proven successful for phasing common variants and for genotype imputation but are limited in their ability to phase rare variants and phase long stretches of the genome that cross recombination hot-spots (Browning and Browning 2011; Tewhey et al. 2011).
Haplotypes for an individual genome at known heterozygous variants can be directly reconstructed from reference-aligned sequence reads derived from whole-genome sequencing (WGS). Sequence reads that are long enough to cover multiple heterozygous variants provide partial haplotype information. Using overlaps between such haplotype-informative reads, long haplotypes can be assembled. This haplotype assembly approach does not rely on information from other individuals (such as parents) and can phase even individual-specific variants. Levy et al. (2007) demonstrated the feasibility of this approach using sequence data derived from paired Sanger sequencing of long insert DNA fragment libraries to computationally assemble long haplotype blocks (N50 of 350 kb) for the first individual human genome.
Since then, advancements in massively parallel sequencing technologies have reduced the cost of human WGS drastically, leading to the sequencing of thousands of human genomes. However, the short read lengths generated by technologies such as Illumina (100–250 bases) and the use of short fragment lengths in WGS protocols makes it infeasible to link distant variants into haplotypes. To overcome this limitation, a number of innovative methods that attempt to preserve haplotype information from long DNA fragments (tens to hundreds of kilobases) in short sequence reads have been developed.
The underlying principle for these methods involves generating multiple pools of high-molecular-weight DNA fragments such that each pool contains only a small fraction of the DNA from a single genome. As a result, there are very few overlapping DNA fragments in each pool, and high-throughput sequencing of the DNA in each pool can be used to reconstruct the fragments by alignment to a reference genome (Kitzman et al. 2011; Suk et al. 2011). Therefore, each pool provides haplotype information from long DNA fragments, and long haplotypes can be assembled using information from a sufficiently large number of independent pools (Snyder et al. 2015). A number of methods based on this approach have been developed to phase human genomes (Kitzman et al. 2011; Suk et al. 2011; Peters et al. 2012; Kaper et al. 2013; Amini et al. 2014). Recently, 10X Genomics described a novel microfluidics-based library preparation approach that generates long linked reads that can be assembled into long haplotypes (Zheng et al. 2016). Third-generation sequencing technologies such as Pacific Biosciences (PacBio) generate long sequence reads (2–20 kb in length) that can directly enable genome-wide haplotyping. Pendleton and colleagues demonstrated the feasibility of assembling haplotypes from SMRT reads using variants identified from short read Illumina sequencing (Pendleton et al. 2015).
Haplotype assembly is also feasible with paired-end sequencing, i.e., pairs of short reads derived from the ends of long DNA fragments, but requires long and variable insert lengths to assemble long haplotypes (Tewhey et al. 2011). Selvaraj et al. (2013) used sequence data from a proximity ligation method (Hi-C) to assemble accurate haplotypes for mouse and human genomes. Using mouse data, they demonstrated that the vast majority of intrachromosomal Hi-C read pairs correspond to ‘cis’ interactions (between fragments on the same chromosome) and therefore contain haplotype information equivalent to paired-end reads with long and variable insert lengths. Subsequently, 17× whole-genome Hi-C data was used to assemble chromosome-spanning haplotypes for a human genome, albeit with low resolution (<22% of variants phased).
In summary, multiple different sequencing technologies and protocols have the capability to generate sequence reads with haplotype information but require computational tools to assemble the reads into long haplotypes. A number of combinatorial algorithms have been developed for haplotype assembly (Bansal and Bafna 2008; Duitama et al. 2010; He et al. 2010; Aguiar and Istrail 2012). Among these, HapCUT (Bansal and Bafna 2008) was developed for phasing Sanger WGS data for the first individual genome (Levy et al. 2007). HapCUT utilizes max-cuts in read-haplotype graphs, an approach that is equally adept at handling data with local haplotype information and data with long-range haplotype information such as that from long insert paired-end reads. As a result, it has been successfully utilized to assemble haplotypes from different types of high-throughput sequence data sets, including fosmid pool sequencing (Kitzman et al. 2011), Hi-C data (Selvaraj et al. 2013), and single molecule long reads (Pendleton et al. 2015) with appropriate modifications. However, HapCUT only models simple sequencing errors and does not scale well for long read data. More recently, several algorithms have been designed specifically to enable accurate haplotype assembly from long reads (Duitama et al. 2010; Kuleshov 2014).
The diverse characteristics and specific error modalities of data generated by different haplotype-enabling protocols and technologies continue to pose challenges for haplotype assembly algorithms. Some protocols, such as clone-based sequencing, can generate very long fragments (BAC clones of length 140 kb have been used to assemble haplotypes [Lo et al. 2013]) but may have low fragment coverage. Other protocols, such as PacBio SMRT, generate fragments with shorter mean lengths than clone-based approaches but can be scaled to higher read coverage more easily. 10X Genomics linked reads are long (longest molecules > 100 kb) but have gaps resulting in high clone coverage for each variant. Proximity ligation approaches, such as Hi-C, generate paired-end read data with very short read lengths but with a larger genomic span. Hi-C reads can span from a few kilobases to tens of megabases in physical distance. While an algorithm that leverages characteristics of a specific type of data is likely to perform well on that particular type of data, it may not perform well or not work at all on other types of data. For example, dynamic programming algorithms such as ProbHap (Kuleshov 2014) that were developed for low-depth long read sequence data are unlikely to scale well for data sets with high sequence coverage or for other types of data such as Hi-C. Even if a haplotype assembly algorithm has broad support for data qualities, there remains the challenge that different sequencing protocols each have systematic error modalities. For instance, fragment data from the sequencing of multiple haploid subsets of a human genome (Kitzman et al. 2011; Suk et al. 2011) generate long haplotype fragments, but some of these fragments are chimeric due to overlapping DNA molecules that originate from different chromosomes. Similarly, noise in Hi-C data due to ligated fragments from opposite homologous chromosomes increases with increasing distance between the variants. The accuracy of haplotypes assembled from each sequencing protocol depends on both the haplotype assembly algorithm's ability to effectively utilize the sequence data and its ability to model protocol-specific errors.
Results
To address the challenge of haplotype assembly for diverse types of sequence data sets, we developed HapCUT2, an algorithm that generalizes the HapCUT approach in several ways. Compared to a discrete score optimized by HapCUT, HapCUT2 uses a likelihood-based model, which allows for the modeling and estimation of technology-specific errors such as ‘h-trans errors’ in Hi-C data. To improve memory performance for long read data, HapCUT2 does not explicitly construct the complete read-haplotype graph. Further, it implements a number of optimizations to enable fast runtimes on diverse types of sequence data sets. To demonstrate the accuracy and robustness of HapCUT2, we compared its performance with existing methods for haplotype assembly using simulated and real WGS data sets. Previous publications (Duitama et al. 2012; Kuleshov 2014) have compared different methods for haplotype assembly and concluded that RefHap (Duitama et al. 2010), ProbHap (Kuleshov 2014), FastHare (Panconesi and Sozio 2004), and HapCUT (Bansal and Bafna 2008) are among the best performing methods. Other methods such as DGS (Levy et al. 2007), MixSIH (Matsumoto and Kiryu 2013), and HapTree (Berger et al. 2014) did not perform as well on the data sets evaluated in this study. Therefore, we compared the performance of HapCUT2 with four other methods: RefHap, ProbHap, FastHare, and HapCUT (Table 1).
Table 1.
Comparison of the approach, time complexity, and applicability of five algorithms for haplotype assembly: HapCUT2, HapCUT, RefHap, ProbHap, and FastHare

Overview of HapCUT2 algorithm
The input to HapCUT2 consists of haplotype fragments (sequence of alleles at heterozygous variant sites identified from aligned sequence reads) and a list of heterozygous variants (identified from WGS data). HapCUT2 aims to assemble a pair of haplotypes that are maximally consistent with the input set of haplotype fragments. This consistency is measured using a likelihood function that captures sequencing errors and technology-specific errors such as h-trans errors in proximity ligation data. HapCUT2 is an iterative procedure that starts with a candidate haplotype pair. Given the current pair of haplotypes, HapCUT2 searches for a subset of variants (using max-cut computations in the read-haplotype graph) such that changing the phase of these variants relative to the remaining set of variants results in a new pair of haplotypes with greater likelihood. This procedure is repeated iteratively until no further improvements can be made to the likelihood (see Methods for details).
Comparison of runtimes on simulated data
We used simulations to compare the runtime of HapCUT2 with existing methods for haplotype assembly across different types of sequence data sets. A fair comparison of the performance of different methods is not completely straightforward. Different methods chose to optimize different technology parameters and highlighted performance using those parameters. We considered the following parameters: number of variants per read (V), coverage per variant (d), and the number of paired-end reads spanning a variant (d′). The parameter V is a natural outcome of read length; for example, PacBio provides higher values of V compared to Illumina sequencing. The parameter d is similar to read coverage but only considers haplotype informative reads—higher values result in better accuracy but also increased running time. Finally, many sequencing technologies (such as Hi-C) generate paired-end sequencing with long inserts and d′ can potentially be much greater than d. Some haplotype assembly methods implicitly analyze all paired-end reads spanning a specific position, and their runtime depends upon d′ rather than d.
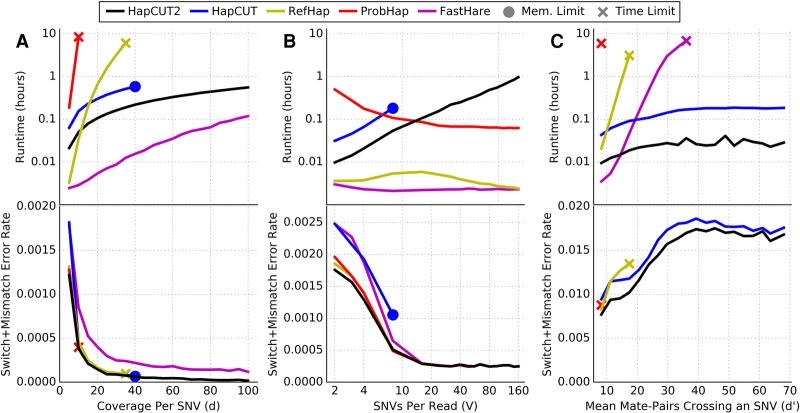
In order to make a fair comparison of runtimes and allow users to determine the most efficient method for any technology, we summarized the computational complexity of each method as a function of these parameters (Table 1) and used simulations to verify the dependence of runtime and accuracy on each parameter (Fig. 1). We simulated reads using a single chromosome of length ∼250 Mb (approximately equal to the length of human Chromosome 1) with a heterozygous variant density of 0.08% and a uniform rate of sequencing errors (2%), performing 10 replicates for each simulation. Standard deviations of runtimes and error rates between replicates were small (Supplemental Fig. S1). A method was cut off if it exceeded 10 CPU-h of runtime or 8 GB of memory on a single CPU, since most methods required significantly less resources than these limits. We note that the runtimes in Table 1 refer to complexity as implemented, with parameters referring to maximum values (e.g., maximum coverage per variant), while in simulations, the parameters refer to mean values (e.g., mean coverage per variant).
Figure 1.
Comparison of runtime (top panel) and switch + mismatch error rate (bottom panel) for HapCUT2 with four methods for haplotype assembly (HapCUT, RefHap, ProbHap, and FastHare) on simulated read data as a function of (A) mean coverage per variant (variants per read fixed at four); (B) mean variants per read (mean coverage per variant fixed at five); and (C) mean number of paired-end reads crossing a variant (mean coverage per variant fixed at five, read length 150 bp, random insert size up to a variable maximum value). Lines represent the mean of 10 replicate simulations. FastHare is not visible on C (bottom) due to significantly higher error rates.
To assess the dependence of runtime on d, we generated reads with a mean of four variants per read (V) and varied the mean read coverage per variant (d) from five to 100. The error rates of HapCUT2, HapCUT, ProbHap, and RefHap were similar and decreased with increasing coverage before reaching saturation. FastHare was significantly faster than other methods but had error rates that were several times greater. As predicted by the computational complexity of the different methods (Table 1), HapCUT2 is significantly faster than HapCUT, RefHap, and ProbHap, once the coverage exceeds 10× (Fig. 1A). For example, RefHap required 10 CPU-h to phase reads at a coverage of 38×, while HapCUT2 took only 34 CPU-min to phase reads with 100× coverage per variant. ProbHap reached the 10-CPU-h limit at a coverage of only 8×. HapCUT shows a similar trend to HapCUT2 but is significantly slower and requires more than 8 GB of memory at coverages of 40× or greater. RefHap constructs a graph with the sequence reads as nodes and performs a max-cut operation that scales quadratically with number of reads. Therefore, its runtime is expected to increase as the square of read-coverage. ProbHap's runtime is exponential in the maximum read-depth (Kuleshov 2014) and exceeds the maximum allotted time for modest values of d. FastHare greedily builds a maximally consistent haplotype from left to right in a single pass, resulting in a low runtime but also lower accuracy. While HapCUT2 has the same asymptotic behavior as HapCUT, it improves upon the memory usage and runtime significantly in practice. It does this by only adding edges that link adjacent variants on each read to the read-haplotype graph, as well as using convergence heuristics that reduce the number of iterations performed (see Methods for details).
Next, we varied the number of variants per read (V) and kept the coverage per variant (d) fixed at 5×. The error rates for each method decrease monotonically (Fig. 1B). HapCUT2, RefHap, and ProbHap have similarly low error rates, while FastHare and HapCUT have error rates higher than the other methods. The runtimes of RefHap and FastHare are consistently very low, although the runtime of RefHap peaks very slightly around V = 15. The runtime of ProbHap decreases monotonically as V increases. This is consistent with the fact that the runtime of these methods has a linear dependence on the read length because for a fixed sequence coverage, the number of reads decreases as the read length increases. In comparison, HapCUT2's runtime is observed to increase linearly with V. This is consistent with the complexity of HapCUT2 being proportional to the square of the number of variants per read (see Table 1). Although HapCUT2's runtime increases, it remains practical across all tested values and is <50 CPU-min for mean read lengths consistent with very long sequences (160 variants per read or 200 kb). The space requirements for HapCUT have a quadratic dependence on the number of variants per read, and therefore, exceeded the memory limit after only eight variants per read.
Finally, we compared runtimes as a function of the average number of paired-end reads crossing a variant (d′). For single-end reads, this parameter is identical to d. Proximity ligation data, on the other hand, consists of pairs of short reads each with a single large gap (insert) between them. The large and highly variable insert sizes result in a large number of reads crossing each variant position. This property is important for linking distant variants, because the extremely long insert size spans of proximity ligation methods are capable of spanning long variant-free regions. For this reason, we simulated paired-end short read data with random insert sizes up to a parametrized maximum value, to represent a generalized proximity ligation experiment. We varied d′ by increasing the maximum insert size value from 6.25 kb (∼5 single-nucleotide variants [SNVs]) to 125 kb (∼100 SNVs) while keeping d and V constant at 5× and 150 base pairs (bp) (0.1195 SNVs), respectively. ProbHap and RefHap exceeded the time limit at d′ = 10 and d′ = 17, respectively. FastHare exceeded the time limit at d′ = 36 but had extremely high error rates (10×–18× higher than HapCUT2). ProbHap's dynamic programming algorithm needs to consider the haplotype of origin for each read crossing a variant; therefore, the complexity scales exponentially in d′. In the case of RefHap and FastHare, the failure to scale with increasing d′ appears to be a result of representing fragments as continuous arrays with length equal to the number of variants spanned by each read. Thus, as implemented, the runtimes for RefHap and FastHare scale with d′ rather than d. In contrast, both HapCUT and HapCUT2 were able to phase data with arbitrarily long insert lengths, reaching d′ = 100 (Fig. 1C). The runtime of HapCUT2 was independent of d′ and 8×–10× faster than that for HapCUT.
Overall, the results on simulated data demonstrate that the complexity of HapCUT2 is linear in the number of reads and quadratic in the number of variants per read. HapCUT2 is fast in practice and effective for both long reads and paired-end reads with long insert lengths, with scalability unmatched by the four other tools we evaluated. Additionally, HapCUT2 and HapCUT were the only tools tested that can reasonably phase paired-end data with long insert lengths that result from proximity ligation (Hi-C) sequencing.
Comparison of methods on diverse WGS data sets for a single individual
We next assessed the accuracy of HapCUT2 using data from four different sequencing data types for a single individual (NA12878): fosmid-based dilution pool sequencing, 10X Genomics linked-read sequencing, single molecule real-time (SMRT) sequencing, and proximity ligation sequencing. Haplotype assembly methods require a set of heterozygous variants as input. Therefore, a set of heterozygous variants for NA12878 identified from WGS Illumina data were used as input to assemble haplotypes for each data type (see Methods for description). The accuracy of the haplotypes was assessed by comparing the assembled haplotypes to gold-standard trio-phased haplotypes and using the switch error rate and mismatch error rate metrics (see Methods).
Fosmid-based dilution pool data
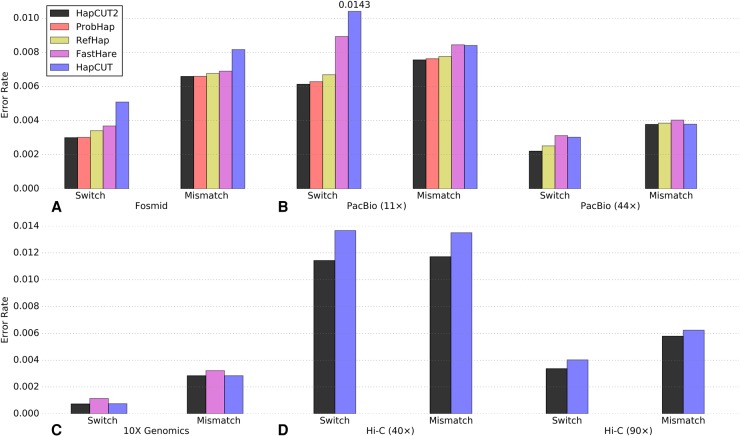
To assess HapCUT2 on long read sequencing data, we used whole-genome fosmid-based dilution pool sequence data for a human individual, NA12878 (Duitama et al. 2012). This data was generated from 1.44 million fosmids (33–38 kb and 38–45 kb in length) that were partitioned into 32 pools such that each pool contains DNA from a small fraction of the genome (∼5%). Subsequently, each pool was sequenced using the ABI SOLiD sequencer and haplotype fragments were identified using read depth analysis (Duitama et al. 2012). Although this data set has low sequence coverage (d ≈ 3×), the processed fragment data (needed as input for haplotype assembly) is publicly available and has been used to assess the performance of haplotype assembly methods in several papers (Duitama et al. 2012; Kuleshov 2014). On this data, the switch error and the mismatch error rates for HapCUT2 were virtually identical or slightly better than ProbHap, the second best performing method, across all chromosomes (Supplemental Fig. S2). However, ProbHap pruned ∼1.2% of the variants from the assembled haplotypes, in comparison to HapCUT2, which only pruned 0.6% of the variants. The switch error rates for RefHap and FastHare were also similar to HapCUT2 and ProbHap (Supplemental Fig. S2). To enable a head-to-head comparison of the switch error rate across different methods, we also calculated the switch and mismatch error rates on a subset of variants that were phased by all tools (not pruned). On this subset of variants, the switch and mismatch error rates for HapCUT2 were similar to but slightly lower than ProbHap (Fig. 2A). In terms of running time, RefHap and FastHare were the fastest methods on this data set, while HapCUT2 took a total of 1:09 CPU-h to phase all chromosomes (Table 2). In summary, HapCUT2 had similar (but slightly better) accuracy to ProbHap, RefHap, and FastHare on this data set and was more accurate than HapCUT.
Figure 2.
Accuracy of HapCUT2 compared to four other methods for haplotype assembly on diverse whole-genome sequence data sets for NA12878. (A) Fosmid dilution pool data (Duitama et al. 2012). (B) PacBio SMRT data (11× and 44× coverage). (C) 10X Genomics linked reads. (D) Whole-genome Hi-C data (40× and 90× coverage, created with MboI enzyme). Switch and mismatch error rates were calculated across all chromosomes using the subset of variants that were phased by all methods. For each data set, only methods that produced results within 20 CPU-h per chromosome are shown.
Table 2.
Comparison of total runtime (h:min, summed across all chromosomes) for different haplotype assembly methods on various sequence data sets for NA12878

10X Genomics linked-read data
We also used HapCUT2 to assemble haplotypes from 10X Genomics linked-read data (Zheng et al. 2016), which is based on a similar idea as the fosmid-based dilution pool approach. 10X Genomics technology labels short DNA fragments originating from a single long DNA fragment with barcodes inside hundreds of thousands of separate nano-scale droplets (Zheng et al. 2016). The linked reads produced can be extremely long (>100 kb). This data set has a short read coverage of 34×, with a linked-read coverage per variant of 12× (Zook et al. 2016). For haplotype assembly, we used the same set of variant calls as for the fosmid data set and extracted haplotype fragments from the 10X aligned reads (see Methods, “Long read data sets”). On this data set, neither RefHap nor ProbHap finished haplotype assembly within the time limit. HapCUT2 was the fastest method and analyzed all chromosomes in 1:55 CPU-h (Table 2). When compared on the subset of variants that were phased by all tools, HapCUT2 had an accuracy slightly better than the next best approach (HapCUT), which took 16:50 CPU-h (Fig. 2C).
PacBio SMRT data
SMRT sequencing on the Pacific Biosciences platform generates long (2–20 kb) but error-prone (>10% indel error rate) reads. We used HapCUT2 to assemble haplotypes from 44× coverage PacBio reads (Pendleton et al. 2015). We extracted haplotype fragments from the PacBio reads that were aligned to the human reference genome (hg19), using the same set of variant calls as for the previous two data sets. On the full data set, HapCUT2 was not only the most accurate but was also significantly faster than RefHap and HapCUT (see Supplemental Fig. S3 for detailed comparisons of error rates and runtimes). We calculated the switch error and mismatch error rates on the subset of variants that were phased by all methods. HapCUT2 had a 12.4% lower switch error and a 2% lower mismatch rate than RefHap. RefHap took 215:53 CPU-h to phase the data set. By comparison, HapCUT2 took only 4:05 CPU-h in total. Because ProbHap was unable to complete within the time limit on the full data set, we also compared the performance of the haplotype assembly tools on a lower, 11× coverage subsample of this data set. On the subsample, HapCUT2 had the lowest switch error and mismatch error rates of the five methods (Fig. 2B). FastHare was the fastest method on this data set and ProbHap was the slowest method, taking 52:32 CPU-h (Table 2).
HapCUT2 implements likelihood-based strategies for pruning low-confidence variants to reduce mismatch errors and splitting blocks at poor linkages to reduce switch errors (see Methods). These post-processing steps allow a user to improve accuracy of the haplotypes at the cost of reducing completeness and contiguity. ProbHap's “transition, posterior, and emission” confidence scores are designed for the same purpose (Kuleshov 2014). Post-processing strategies are of particular interest for haplotype assembly with PacBio SMRT reads because the individual reads have a high error rate. Therefore, we compared HapCUT2's pruning strategies to ProbHap's confidence scores on Chromosome 1 of the 11× coverage PacBio data. For single variant pruning, we found that HapCUT2's confidence scores provided a better trade-off between reducing the mismatch error rate and pruning variants compared to ProbHap's emission scores (Supplemental Fig. S4A). By pruning 3.1% of covered variants, HapCUT2 achieved a 55.1% reduction in mismatch error rate. In comparison, ProbHap mismatch error rate was reduced by <15% when 3.1% of variants were pruned. Similarly, HapCUT2's block splitting strategy resulted in a lower switch error rate compared to ProbHap at a fixed value of the AN50 for the haplotype assembly except at very small AN50's (Supplemental Fig. S4B).
Hi-C data
The Hi-C method was developed to comprehensively detect chromatin interactions in the cell nucleus using proximity ligation and shotgun sequencing of the ligation products (Belton et al. 2012). Selvaraj et al. (2013) demonstrated that the long-range information contained in Hi-C reads can be used to determine the phase between distant variants and assemble chromosome-spanning haplotypes from ∼17× coverage. They collaborated with some of the authors of the current study in customizing HapCUT to assemble haplotypes from Hi-C data. Hi-C reads suffer from a source of error that was referred to as “h-trans interactions.” An h-trans interaction (or h-trans error) occurs when a piece of DNA interacts with a DNA fragment from the homologous chromosome rather than the same chromosome (a “cis” interaction). The probability of h-trans error depends on the insert size and can be estimated if the true haplotypes are known. We use the function τ(I) to refer to the probability of an h-trans error for a read with insert size I. Selvaraj et al. (2013) estimated τ using Hi-C data from a mouse genome and used these estimates to lower the base quality values of reads before running HapCUT. In developing HapCUT2, we were motivated in part by the need to develop a method that could estimate τ directly from the data and use these estimates to improve the accuracy of the haplotypes.
To assess different haplotype assembly tools, we used a high coverage Hi-C data set with ∼395× coverage on NA12878 generated using the MboI enzyme (Rao et al. 2014) and subsampled reads from this data set to generate 40× and 90× coverage. As expected from the simulations using paired-end reads with variable span, only HapCUT and HapCUT2 were able to generate haplotypes from Hi-C data within the 20 CPU-h per chromosome time limit. The error rates were significantly lower for the 90× sample, and HapCUT2 had lower error rates compared to HapCUT at both coverage levels (Fig. 2D). In terms of runtime, HapCUT2 was 4×–5× slower than HapCUT on Hi-C data since it performs the haplotype assembly procedure multiple times in order to estimate τ. We note that if HapCUT2 does account for h-trans errors, it is several times faster than HapCUT (Supplemental Table S1).
At 40× coverage, HapCUT2 achieved a 16.3% lower switch error rate and 13.2% lower mismatch rate compared to HapCUT on variants phased by both methods. Similarly, at 90× coverage, HapCUT2 achieved a 16.4% lower switch error rate and 7.2% lower mismatch rate compared to HapCUT. The lower error rates for HapCUT2 are primarily due to the modeling and estimation of h-trans errors in Hi-C data. HapCUT2 directly models h-trans errors as probabilities in the likelihood formulation and estimates τ directly from the data using an iterative approach (see Methods, “Estimation of h-trans error probabilities in Hi-C data”), eliminating the need for a model data set with known haplotypes. The h-trans function was estimated separately for each chromosome since we observed significant variation in the h-trans error rates across chromosomes (estimated using known haplotypes for NA12878). The per-chromosome h-trans error rates estimated by HapCUT2 were very similar to those obtained using known trio-phased haplotypes for NA12878 (see Supplemental Fig. S5), demonstrating the accuracy of the estimation procedure.
Overall, results on a variety of sequence data sets reaffirm what we observed on simulated reads, i.e., HapCUT2 is the only tool that works across all sequencing paradigms. In particular, haplotype assembly tools that were developed to phase low-coverage long read data, such as ProbHap and RefHap, do not work on Hi-C data. Even on long read data (PacBio SMRT sequencing and 10X Genomics linked reads), HapCUT2 scales better in running time with increasing coverage (Table 2). Moreover, it assembles haplotypes that are more accurate than all other methods that we evaluated in this paper. This was somewhat surprising because ProbHap implements an exact likelihood optimization approach. However, to reduce runtime, ProbHap also uses an initial heuristic to merge reads that convey similar information, and this could reduce the accuracy.
Comparison of haplotypes assembled using Hi-C and SMRT sequencing
Sequencing technologies such as SMRT generate long reads that contain multiple variants per read. Although most of the reads contain haplotype information, the read length limits the ability to phase heterozygous variants that are separated by long runs of homozygosity. In contrast, paired-end reads derived from Hi-C contain very few variants per read pair (most read pairs do not cover any variant or cover only a single variant). However, read pairs that cover a variant at each end have the potential to link distant variants because the insert size of Hi-C reads varies from a few hundred bases to tens of millions of bases. Therefore, haplotypes assembled using these two approaches differ significantly in both contiguity and accuracy. We utilized the PacBio SMRT sequencing and MboI enzyme Hi-C data sets to compare the haplotypes assembled using HapCUT2 for these two technologies.
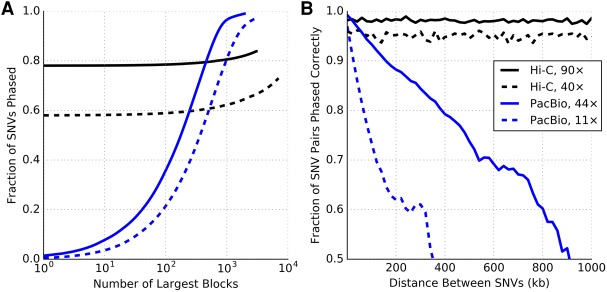
The haplotypes assembled from the 44× coverage SMRT sequence data had an AN50 length of 218 kb, with the largest block being 1.66 Mb in length. Also, 99% of the heterozygous variants could be phased as part of some block. In contrast, the haplotypes assembled from the 90× coverage Hi-C data (for each autosomal chromosome) comprised a large chromosome-spanning block that contains 72%–87% of the variants in addition to numerous small blocks with a median block size of two variants. This effect can be observed in Figure 3A, which shows the cumulative number of variants covered by the haplotype blocks (sorted in descending order) for Chromosome 1. One limitation of Hi-C data is that some of the variants that are far away from restriction enzyme cut-sites cannot be phased due to a lack of reads covering such variants. Chromosome X, which has a lower variant density than autosomes, was more difficult to phase than autosomal chromosomes, with only 55% of SNVs in the largest block and 32% of variants unphased (Supplemental Fig. S6).
Figure 3.
Haplotype completeness and accuracy compared between Hi-C (MboI enzyme, 90× and 40× coverage) and PacBio SMRT (44× and 11× coverage). (A) Cumulative measure of the fraction of variants phased within a given number of the largest haplotype blocks. (B) Fraction of correctly phased variant pairs as a function of distance.
In terms of accuracy measured using switch error rates, both technologies achieve comparable error rates (0.002–0.003) at sufficiently high coverage (Fig. 2). Further, the switch error rates for haplotypes assembled using these two technologies decrease rapidly as coverage is increased initially and saturate quickly after that (Supplemental Fig. S7). Although the switch and mismatch error rates are similar between high-coverage Hi-C data and high-coverage PacBio data, we found that these statistics do not adequately distinguish between short stretches of erroneous phased variants (masquerading as two switch errors) and “point” switches that effectively divide the resulting haplotype into two pieces. Long read data, because of its linear structure, has a tendency for this type of error. In comparison, Hi-C data is more web-like in structure and therefore has essentially no incidence of point switches once there is sufficient coverage. To observe the effect of point switches on accuracy for long reads compared to Hi-C, we plotted the fraction of correctly phased variant pairs separated by a given genomic distance (Fig. 3B). Point switch errors accumulate linearly to diminish the probability of correct phasing with distance for PacBio, but not for Hi-C. For example, two variants separated by 200 kb and phased with the 11× PacBio data have a 62% chance of being phased correctly. On the other hand, MboI Hi-C data maintains a high and constant rate of pairwise phasing accuracy across the entire chromosome: ∼0.96 at 40× and ∼0.98 at 90×. This implies that, not only do Hi-C haplotypes span the entire chromosome, but the overall haplotype structure is also highly accurate.
Considerations when haplotyping with Hi-C
For Hi-C-based haplotyping, the choice of restriction enzyme (RE) and depth of sequence coverage can impact the completeness and accuracy of the haplotypes. Selvaraj et al. (2013) were able to assemble chromosome-spanning haplotypes for NA12878 using Hi-C data generated using the HindIII RE. Despite assembling blocks that spanned the genomic distance of each chromosome, the “resolution” of the largest block was rather low (only 18%–22% of the variants on each chromosome could be linked into haplotypes). The low resolution could potentially be due to the modest sequence depth (∼17×). However, we observe that even at 200× coverage, Hi-C data obtained using the HindIII RE from the Rao et al. (2014) study has <40% of variants phased in the largest block, with 71% of variants phased in total. In contrast, 80% of the heterozygous variants on Chromosome 1 can be successfully phased in a single block using only 90× Hi-C data obtained using the MboI RE. The trend is similar across autosomal chromosomes, with the largest block of each chromosome containing 72%–87% of the heterozygous variants (Supplemental Fig. S6). This indicates that the choice of RE has an important effect on the number of variants that can be phased.
A key step in the Hi-C protocol is the digestion of cross-linked DNA by an RE that cleaves DNA at specific recognition sites. In comparison to the HindIII RE, which recognizes a 6-bp DNA sequence (A^AGCTT), the MboI RE has a 4-bp recognition site that occurs with much greater frequency in the genome (^GATC). The significantly greater completeness of the haplotypes assembled using Hi-C data generated using the MboI RE is primarily due to this reason. Even with an RE with a 4-bp recognition sequence, some fraction of variants are expected to be far away from a cut-site and therefore cannot be captured in Hi-C ligated fragments. Indeed, the fraction of SNVs phased using the MboI Hi-C data saturates with increasing coverage, and 7.3% of SNVs on Chromosome 1 cannot be phased into the largest block even at 395× coverage. The fraction of variants phased can potentially be increased by integrating Hi-C data from different REs or by using imputation-based approaches.
At low sequence coverage (<25×), the largest haplotype block assembled using MboI-derived Hi-C data contains <40% of the variants (Fig. 4A) and has a high error rate (Fig. 4B). With increasing sequence coverage, the fraction of the variants in the largest component increases rapidly and the error rate of the largest haplotype block (measured as the sum of the switch and mismatch error rates) decreases rapidly. The improvements in both these aspects of Hi-C-based haplotype assembly saturate around 80–100× coverage. These results demonstrate that highly accurate, high-resolution, chromosome-spanning haplotypes can be assembled from 80–100× whole-genome Hi-C data for a human genome generated using a single restriction enzyme with a 4-bp recognition sequence.
Figure 4.
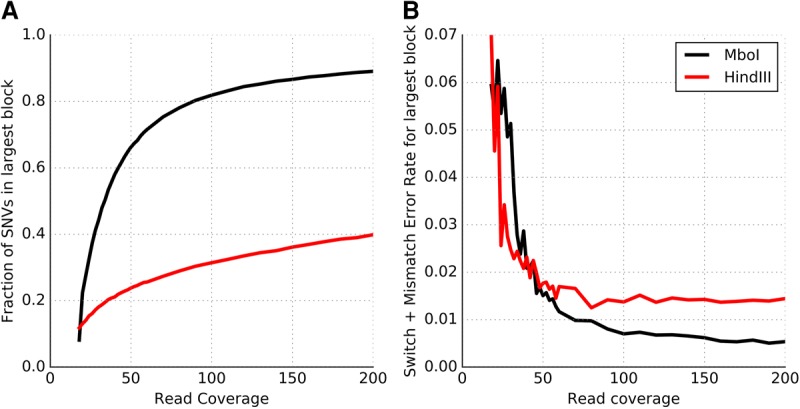
Improvements in the (A) completeness and (B) accuracy (switch + mismatch error rates) of the largest haplotype block with increasing Hi-C sequencing coverage for two different restriction enzymes: MboI and HindIII. Results are presented using data for Chromosome 1 with coverage ranging from 18× to 200×.
Some applications of haplotyping may benefit from combining sequence data derived from different library preparation methods. Fortunately, HapCUT2's flexibility enables haplotype assembly using different sources of data. To demonstrate this, we combined 40× coverage Hi-C data with 10X Genomics linked-read data (34× short read coverage) to assemble haplotypes with 98.9% of variants contained in the largest block for each chromosome (Supplemental Fig. S8). The haplotypes were highly accurate, with a switch error rate of 0.0008 and a mismatch rate of 0.003.
Discussion
We introduced HapCUT2, a maximum likelihood-based algorithm for the haplotype assembly problem that extends the original HapCUT method to model technology-specific errors and can handle sequence data from diverse technologies efficiently. Using simulated and real WGS data, we demonstrated that HapCUT2 can assemble haplotypes for a diverse array of data modalities while other tools are specialized for certain subsets of data modalities. One of the new features of HapCUT2 is its support for long reads such as those generated by dilution-pool sequencing-based methods and long read sequencing technologies such as Pacific Biosciences. Using multiple long read WGS data sets, we demonstrate that HapCUT2 obtains higher accuracy than all leading methods, while offering significantly higher speed and scalability. Apart from PacBio, Oxford Nanopore sequencers are also capable of producing long reads, albeit with lower throughput than PacBio sequencers (Goodwin et al. 2015). As current technologies improve and new long read data types continue to emerge, having a fast and flexible tool like HapCUT2 that can efficiently and accurately assemble haplotypes from any type of data is important.
Using simulated data as well as whole-genome Hi-C data, we observed that HapCUT2 and HapCUT were the only computational methods for haplotype assembly that are reasonably capable of phasing paired-end reads with large insert sizes. We demonstrated that high coverage Hi-C data (e.g., ∼80–100× with a four-cutter restriction enzyme) can be used to phase >75%–80% of the variants per chromosome with high accuracy. While it was known that Hi-C can be used to link distant variants, our results demonstrate that high-resolution whole-chromosome haplotypes can be assembled directly from the sequence reads. In addition, the low rate of pairwise variant error at long genomic distances is a unique feature of the assembled haplotypes and could be useful for applications that require accurate long-range phasing. Although generating Hi-C data requires intact cells, Putnam et al. (2016) recently described a proximity ligation method using in vitro reconstituted chromatin from high-molecular-weight DNA.
HapCUT2 implements an iterative approach for modeling and estimating h-trans error probabilities de novo that reduces errors in assembled Hi-C haplotypes compared to HapCUT. We expect that a similar approach could be utilized to improve the accuracy of haplotypes assembled using data from other technologies that exhibit systemic patterns of error, e.g., chimeric fragments present in dilution pool sequencing and reference allele bias in PacBio reads due to alignment ambiguity. In general, the flexibility of the HapCUT2 likelihood model lends itself well to modeling sources of error that result from experimental protocol and design but are not adequately represented by read quality scores. Another advantage of the HapCUT2 likelihood model and its implementation is the ability to integrate sequence data from diverse methods to generate highly accurate and comprehensive haplotypes for reference human genomes, e.g., NA12878 and other genomes that have been sequenced by the GIAB consortium (Zook et al. 2016). We demonstrated this by assembling accurate and complete chromosome-spanning haplotypes for NA12878 by combining Hi-C data with linked-read data.
Similar to the original HapCUT method, HapCUT2 is a heuristic algorithm that iteratively searches for better haplotypes with increasing likelihood using graph-cuts in a greedy manner. Although it provides no performance guarantees on the optimality of the final haplotype assembly, its performance on multiple sequence data sets demonstrates its high accuracy and suggests that it is able to find haplotypes that are close to the optimum. Further, previous work on exact algorithms for haplotype assembly (He et al. 2010) has shown that the haplotypes assembled using HapCUT are very close to the optimal solution.
Even at high sequencing depth, not all variants on a chromosome can be assembled into a single haplotype block. Using Hi-C data, ∼20% of the variants that are at a large distance from cut-sites for a 4-bp restriction enzyme remain unphased. In comparison, long read technologies can phase the vast majority (>95%) of variants into multiple haplotype blocks for each chromosome (N50 lengths ranging from few hundred kilobases to several megabases). In the absence of additional sequence data, information from population haplotype data can be used to link unphased variants to the chromosome spanning haplotype block in the case of Hi-C (Selvaraj et al. 2013) and to determine the phase between disjoint haplotype blocks assembled from long read data sets (Kuleshov et al. 2014). Recently, a population phasing method, SHAPEIT2, has been extended to incorporate information from haplotype-informative sequence reads in the statistical model for phasing using population haplotypes (Delaneau et al. 2013). Analogous to this, it should be feasible to incorporate information from population haplotypes while assembling haplotypes from sequence reads for an individual in the likelihood-based framework of HapCUT2.
Another important consideration for sequencing-based haplotype assembly is the source of the variant calls. Most haplotype assembly methods, including HapCUT2, require a set of reliably called variants as input. Illumina short read sequencing at ∼30–40× is considered the de facto standard approach to obtain reliable heterozygous calls (Sims et al. 2014). Therefore, the simplest approach would be to perform short read WGS in addition to the sequencing protocol for phasing variants. However, in some cases (e.g., 10X Genomics linked-read data) (Zheng et al. 2016), variants can be called directly from the sequence data used for haplotyping, eliminating the need to generate additional sequence data. In principle, it should also be possible to call variants directly from high-coverage Hi-C data before haplotyping. For PacBio sequence data, variant calling is more challenging due to high error rates, but an integrated variant calling and haplotyping approach could potentially work because haplotype information can be used to distinguish true heterozygous variants from errors.
Finally, all analysis and comparisons of different methods in this paper were performed using SNVs only. Short insertions and deletions (indels) represent the second most frequent form of variation in the human genome and are frequently associated with diseases. Therefore, reconstructing haplotypes that include not only SNVs but also small and large indels is important for obtaining a complete picture of genetic variation in an individual genome. However, the detection and analysis of indels is more challenging compared to SNVs. In principle, HapCUT2 can phase indels along with SNVs. However, it may not be feasible to phase short indels using PacBio reads that have a high rate of indel errors. Recently, Patel et al. (2016) developed a machine learning method to phase large deletions using Hi-C data. Assessing the capability of different sequencing technologies and protocols for haplotyping all forms of genetic variation is an important topic of future work.
Methods
The input to the haplotype assembly problem consists of fragments or “reads” from an individual genome that have been aligned to a reference genome with information about alleles (encoded as 0 and 1 for bi-allelic variants) at each heterozygous variant. The heterozygous variants are assumed to have been identified separately from WGS data for the same individual. Haplotype assembly algorithms for diploid genomes aim to either (1) partition the fragments into two disjoint sets such that fragments in each set originate from the same homologous chromosome, or (2) reconstruct a pair of haplotypes such that the fragments are maximally consistent with the assembled haplotypes. HapCUT belongs to the second type and aims to optimize the minimum error correction (MEC) objective function: the number of allele calls in the fragment matrix that need to be changed for each fragment to be perfectly consistent with one of the two haplotypes (Lippert et al. 2002).
Several algorithms use a probabilistic model for haplotype assembly and attempt to maximize a likelihood function that relates the observed reads to potential haplotypes (Li et al. 2004; Bansal et al. 2008). ProbHap (Kuleshov 2014) aims to optimize a likelihood function that generalizes the MEC criteria. Rather than the MEC criterion, HapCUT2 uses a haplotype likelihood model for sequence reads (Bansal et al. 2008).
Haplotype likelihood for sequence reads
Let H = (H1,H2) represent the unordered pair of haplotypes where H1 is a binary string of length n. H2 is also a binary string of length n. H2 is the bitwise complement of H1 if all sites are heterozygous. Consider a collection of reads R, where each read (fragment) Ri is denoted by a string of length n over the alphabet {0,1,-} where - corresponds to heterozygous loci not covered by the read. Given a haplotype h and a fragment Ri, define the delta function δ(Ri[j],h[j]) = 1 if Ri[j] = h[j] and 0 otherwise. Given qi[j], the probability that the allele call at variant j in read Ri is incorrect, the likelihood of observing read Ri is
| (1) |
Extending this to a haplotype pair H = (H1,H2), we can define
| (2) |
assuming equal probability of sampling the read from either haplotype. Then, P(R|q,H), the data likelihood given a pair of haplotypes H, can be computed as a product over fragments (assuming independence of fragments) as
The read likelihood function assumes a simple copying model where the read Ri is copied from either H1 or H2 with zero or more sequencing errors. It can be modified to account for additional types of errors in reads. For example, Hi-C reads can be ‘cis’ or ‘trans’ (switch error) and the probability of a read being trans depends on the distance between the two interacting loci captured in a Hi-C fragment. Given a set S of variants, H(S) is defined as the haplotype pair formed by flipping the alleles between the haplotype pair at the variants in the set S. If τ(I) is the probability that a read is trans, the likelihood of a Hi-C fragment with insert length I is the sum of two terms:
| (3) |
where S is the set of variants covered by one end of the Hi-C fragment.
Likelihood-based HapCUT2 algorithm
The original HapCUT algorithm is an iterative method that attempts to find better haplotypes using a max-cut heuristic that operates on the read-haplotype graph. This graph is constructed using the fragments and the current haplotype. The nodes of this graph correspond to variants and edges correspond to pairs of variants that are connected by a fragment. Similar to HapCUT, HapCUT2 also uses a greedy method to find a max-cut in the read-haplotype graph such that the variants on one side of the cut can be flipped to improve the current haplotype. However, it utilizes the likelihood function instead of the MEC score, allowing it to account for read quality scores as well as model technology-specific errors such as trans errors in Hi-C data.
To describe the new likelihood-based max-cut procedure used in HapCUT2, we define a partial likelihood function that represents the likelihood of the fragments restricted to a subset of variants S as follows:
| (4) |
where
| (5) |
The objective of the greedy algorithm for finding the maximum likelihood cut is to find a subset of variants or vertices S such that the haplotype H(S) has better likelihood than the current haplotype H. It starts by initializing the two shores (S1 and S2) of the cut using a pair of vertices in the graph and at each step adds a vertex or node to one of the two shores of the cut. Adding a vertex v to S1 results in a new haplotype H(S1 ∪ v) while adding the vertex to S2 does not change the current haplotype H(S1). This vertex v is chosen such that it maximizes the absolute difference between two log likelihoods:
| (6) |
where S = {S1 ∪ S2 ∪ v}.
In other words, we select the vertex v for which adding it to one side of the cut is significantly better than adding it to the other side of the cut. This process is repeated until all variants have been added to one side of the cut. The Maximum-Likelihood-Cut routine (full description available in Supplemental Methods) considers many possible cuts by initializing each cut using a different edge in the graph and selects the cut that gives the maximum improvement in the likelihood of the haplotypes defined by the cut. This maximum-likelihood-cut heuristic is the core of the HapCUT2-Assemble algorithm outlined below:
Initialization: H = H0
Iteration: until p(R|q,H) stops changing:
1. S* = Maximum-Likelihood-Cut (H,R)
2. if p(R|q, H(S*)) > p(R|q, H): H = H(S*)
Return: H
Complexity of HapCUT2
The HapCUT2-Assemble routine is run for T iterations (default value = 10,000) on each connected component of the read-haplotype graph. To speed up the convergence, we utilize a convergence criterion wherein components for which there has been no improvement in the likelihood for C iterations (default value = 5) are not analyzed further. A similar convergence criterion is also used for the maximum-likelihood-cut heuristic. In practice, this simple convergence criterion results in considerable improvement in running time compared to HapCUT.
HapCUT2 does not store an edge for each pair of nodes covered by a read because this leads to prohibitive storage requirements for long reads (proportional to V2 where V is the maximum number of variants per read). Instead, it only stores an edge for adjacent vertices covered by each read. However, it still has to consider all pairs of edges per fragment in order to calculate and update the partial likelihoods. Therefore, the computational complexity of HapCUT2 scales as V2. The runtime of one iteration of the maximum-likelihood-cut routine is O(N log (N) + N · d · V2) , where N is the number of variants, d is the average coverage per variant, and V is the maximum number of variants per read. Therefore, the overall runtime of HapCUT2 is O(T · M · (N log N + N · d · V2)) , where T and M are the maximum number of iterations for the HapCUT2-Assemble and maximum-likelihood-cut routines, respectively.
Estimation of h-trans error probabilities in Hi-C data
In order to properly model h-trans error, we must know the probability that a read pair with insert size I is h-trans, i.e., the two ends of the paired-end read originate from different homologous chromosomes. We assume that the h-trans error probability, represented as τ(I), is the same for all reads with the same insert length I. If the true haplotypes are known, τ(I) can be estimated by comparison of all reads with insert length I to the haplotypes and calculating the fraction of reads that are inconsistent with the haplotypes. Because the true haplotypes are unknown, we use an iterative expectation-maximization-like approach to directly estimate τ from the data. Initially, the HapCUT2-Assemble routine is used to phase all reads with τ(I) = 0 for all I. The assembled haplotypes H are used to calculate a maximum-likelihood estimate of τ(I) for each insert size I. Subsequently, the HapCUT2 routine is used to assemble a new set of haplotypes using τ and the Hi-C version of the read likelihood function. This is repeated until the likelihood of the haplotypes does not improve (see Supplemental Methods for more details).
Post-processing of haplotypes
HapCUT2 assumes that the heterozygous sites are known in advance. However, some of the heterozygous sites in the input may actually be homozygous, e.g., due to errors during variant calling or read alignment. In addition, some variants cannot be phased reliably due to low read coverage or errors. Therefore, the accuracy of the final assembled haplotypes can be improved by removing variants with low confidence phasing. HapCUT2 implements a likelihood-based pruning scheme that considers the possible phasings for each variant individually and calculates a Bayesian posterior probability for each of the four possible configurations (00,11,10,01). If the maximum posterior probability is less than a user-defined threshold (0.8 by default), then the variant is pruned from the output haplotypes (see Supplemental Methods for details). For long read data sets, we also consider the possibility of a switch error between each pair of adjacent variants in a haplotype block, and if the posterior probability of the final haplotype configuration is less than a threshold, the block is split at that position. This can reduce switch errors at the cost of reducing the length of haplotype blocks.
Accuracy and completeness of haplotype assemblies
The AN50 metric summarizes the contiguity of assembled haplotypes (Lo et al. 2011). It represents the span (in base pairs) of a block such that half of all phased variants are in a block of that span or larger. To adjust for unphased variants, the base-pair span of a block is multiplied by the fraction of variants spanned by the block that are phased. For Hi-C data, we assessed the completeness of the haplotypes on a chromosome-wide scale by using the fraction of variants in the largest (also called most-variants-phased or MVP) block (Selvaraj et al. 2013). The accuracy of a haplotype assembly is typically assessed by comparing the assembled haplotypes to ‘truth’ haplotypes and calculating the switch error rate (Duitama et al. 2010; Kuleshov 2014). A “switch error” (also known as long switch) occurs when the phase between two adjacent variants in the assembled haplotypes is discordant relative to the truth haplotypes. Two consecutive switch errors correspond to the flipping of the phase of a single variant and were counted as “mismatch” (also known as short switch) errors instead of two switch errors.
For many applications of haplotyping, the ability to determine the phase between a pair of heterozygous variants is important. To assess the pairwise accuracy of the haplotypes, we utilized a pairwise phasing accuracy metric where all pairs of phased variants in a block were classified as concordant (1) or discordant (0) (by comparison to the gold-standard haplotypes), and the accuracy was defined as the fraction of discordant pairs among all pairs with the same genomic distance (Snyder et al. 2015).
Long read data sets and haplotype assembly tools
Haplotype fragment files corresponding to the whole-genome fosmid sequence data (32 pools) for NA12878 (Duitama et al. 2012) were downloaded from http://owww.molgen.mpg.de/~genetic-variation/SIH/data/. Aligned PacBio SMRT whole-genome read data for NA12878 (Zook et al. 2016) was obtained from the GIAB ftp site: ftp://ftp-trace.ncbi.nlm.nih.gov/giab/ftp/data/NA12878/NA12878_PacBio_MtSinai. Haplotype fragments for phasing were extracted from the sorted BAM files using the extractHAIRS tool (see Supplemental Methods). Aligned 10X Genomics data for NA12878 (Zook et al. 2016) was also obtained from the GIAB ftp site: ftp://ftp-trace.ncbi.nlm.nih.gov/giab/ftp/data/NA12878/10XGenomics. Molecule boundaries were called when the distance between two consecutive reads with the same barcode exceeded 20 kb, and haplotype fragments were generated for each molecule using the extractHAIRS tool (see Supplemental Methods). The software tools RefHap and ProbHap were downloaded from the authors’ websites. For FastHare, we used the implementation of Duitama et al. (2012). Default parameters were used for each tool except for HapCUT, which was run with memory reduction heuristics to enable it to generate results for comparison.
Variant calls and haplotypes for NA12878
The NA12878 trio haplotypes from the 1000 Genomes Project (Duitama et al. 2012) were used as truth haplotypes for assessing the accuracy of all haplotype assemblies. Only single nucleotide variants (SNVs) were considered for phasing. The variants from this data set (aligned to hg18) were used for phasing the fosmid data set. For usage with the PacBio, 10X Genomics, and Rao Hi-C data, the hg18 NA12878 VCF file was carried over to hg19 with CrossMap (Zhao et al. 2014).
Alignment and processing of Hi-C data
Two sets of Hi-C read data sets for NA12878 from Rao et al. (2014) were used: one containing all primary and replicate experiments using the restriction enzyme MboI (total of ∼395× coverage) and another containing all experiments performed with the restriction enzyme HindIII (total of ∼366× coverage). The paired-end reads were mapped as single reads to the reference human genome (hg19) using BWA-MEM (Li 2013). To handle reads that contain the ligation junction for the Hi-C fragments, we developed a post-processing pipeline (see Supplemental Methods) to generate sorted BAM files that were used for haplotyping. Read pair information from intrachromosomal read pairs with an insert size >40 Mb was not used to avoid linkages with excessively high h-trans error rates. To subsample data sets to lower coverage, fragments were randomly sampled from the aggregate data set with the appropriate frequency.
Read simulations
Haplotypes were simulated by randomly introducing heterozygous SNVs at a uniform rate of 0.0008 in a genome of length 250 megabases. Each heterozygous SNV is assigned a random allele ∈{0,1} for haplotype H1, with H2 assigned to the complement. Reads of a given length were generated by selecting the start position randomly, and the corresponding haplotype fragment was obtained by appending all overlapping alleles from one of the two haplotypes. Base miscalls were introduced in the reads with probability 0.02, resulting in an allele flip with probability 1/3 or an uncalled SNV otherwise (to represent miscalls to nonreference, nonalternate calls). Hi-C-like reads of length 150 bp were simulated in pairs. The insert length of each read pair was sampled from the uniform distribution (minimum value of zero and maximum value equal to the maximum insert length).
Software availability
HapCUT2 source code can be found in the Supplemental Material and it is also available for download at https://github.com/vibansal/HapCUT2.
Competing interest statement
V. Bafna is a cofounder, has an equity interest, and receives income from Digital Proteomics, LLC. The terms of this arrangement have been reviewed and approved by the University of California, San Diego in accordance with its conflict-of-interest policies. DP was not involved in the research presented here.
Supplementary Material
Acknowledgments
V. Bansal was supported in part by a grant from the National Institutes of Health (HG007430). V. Bafna and P.E. were supported in part by grants from the National Institutes of Health (HG007836 and GM114362) and the National Science Foundation (DBI-1458557, IIS-1318386).
Footnotes
[Supplemental material is available for this article.]
Article published online before print. Article, supplemental material, and publication date are at http://www.genome.org/cgi/doi/10.1101/gr.213462.116.
References
- Aguiar D, Istrail S. 2012. HapCompass: a fast cycle basis algorithm for accurate haplotype assembly of sequence data. J Comput Biol 19: 577–590. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Amini S, Pushkarev D, Christiansen L, Kostem E, Royce T, Turk C, Pignatelli N, Adey A, Kitzman JO, Vijayan K, et al. 2014. Haplotype-resolved whole-genome sequencing by contiguity-preserving transposition and combinatorial indexing. Nat Genet 46: 1343–1349. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bansal V, Bafna V. 2008. HapCUT: an efficient and accurate algorithm for the haplotype assembly problem. Bioinformatics 24: i153–i159. [DOI] [PubMed] [Google Scholar]
- Bansal V, Halpern AL, Axelrod N, Bafna V. 2008. An MCMC algorithm for haplotype assembly from whole-genome sequence data. Genome Res 18: 1336–1346. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Belton JM, McCord RP, Gibcus JH, Naumova N, Zhan Y, Dekker J. 2012. Hi-C: a comprehensive technique to capture the conformation of genomes. Methods 58: 268–276. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Berger E, Yorukoglu D, Peng J, Berger B. 2014. HapTree: a novel Bayesian framework for single individual polyplotyping using NGS data. PLoS Comput Biol 10: e1003502. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Browning SR, Browning BL. 2011. Haplotype phasing: existing methods and new developments. Nat Rev Genet 12: 703–714. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Delaneau O, Zagury JF, Marchini J. 2013. Improved whole-chromosome phasing for disease and population genetic studies. Nat Methods 10: 5–6. [DOI] [PubMed] [Google Scholar]
- Duitama J, Huebsch T, McEwen G, Suk EK, Hoehe MR. 2010. Refhap: a reliable and fast algorithm for single individual haplotyping. In Proceedings of the first ACM international conference on bioinformatics and computational biology, BCB ’10, pp. 160–169. ACM, New York. [Google Scholar]
- Duitama J, McEwen GK, Huebsch T, Palczewski S, Schulz S, Verstrepen K, Suk EK, Hoehe MR. 2012. Fosmid-based whole genome haplotyping of a HapMap trio child: evaluation of single individual haplotyping techniques. Nucleic Acids Res 40: 2041–2053. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Glusman G, Cox HC, Roach JC. 2014. Whole-genome haplotyping approaches and genomic medicine. Genome Med 6: 73. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goodwin S, Gurtowski J, Ethe-Sayers S, Deshpande P, Schatz MC, McCombie WR. 2015. Oxford Nanopore sequencing, hybrid error correction, and de novo assembly of a eukaryotic genome. Genome Res 25: 1750–1756. [DOI] [PMC free article] [PubMed] [Google Scholar]
- He D, Choi A, Pipatsrisawat K, Darwiche A, Eskin E. 2010. Optimal algorithms for haplotype assembly from whole-genome sequence data. Bioinformatics 26: i183–i190. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kaper F, Swamy S, Klotzle B, Munchel S, Cottrell J, Bibikova M, Chuang HY, Kruglyak S, Ronaghi M, Eberle MA, et al. 2013. Whole-genome haplotyping by dilution, amplification, and sequencing. Proc Natl Acad Sci 110: 5552–5557. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kitzman JO, Mackenzie AP, Adey A, Hiatt JB, Patwardhan RP, Sudmant PH, Ng SB, Alkan C, Qiu R, Eichler EE, et al. 2011. Haplotype-resolved genome sequencing of a Gujarati Indian individual. Nat Biotechnol 29: 59–63. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kuleshov V. 2014. Probabilistic single-individual haplotyping. Bioinformatics 30: i379–i385. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kuleshov V, Xie D, Chen R, Pushkarev D, Ma Z, Blauwkamp T, Kertesz M, Snyder M. 2014. Whole-genome haplotyping using long reads and statistical methods. Nat Biotechnol 32: 261–266. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Levy S, Sutton G, Ng P, Feuk L, Halpern A, Walenz B, Axelrod N, Huang J, Kirkness E, Denisov G, et al. 2007. The diploid genome sequence of an individual human. PLoS Biol 5: e254. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li H. 2013. Aligning sequence reads, clone sequences and assembly contigs with BWA-MEM. arXiv: 1303.3997.
- Li LM, Kim JH, Waterman MS. 2004. Haplotype reconstruction from SNP alignment. J Comput Biol 11: 505–516. [DOI] [PubMed] [Google Scholar]
- Lippert R, Schwartz R, Lancia G, Istrail S. 2002. Algorithmic strategies for the single nucleotide polymorphism haplotype assembly problem. Brief Bioinform 3: 23–31. [DOI] [PubMed] [Google Scholar]
- Lo C, Bashir A, Bansal V, Bafna V. 2011. Strobe sequence design for haplotype assembly. BMC Bioinformatics 12: S24. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lo C, Liu R, Lee J, Robasky K, Byrne S, Lucchesi C, Aach J, Church G, Bafna V, Zhang K. 2013. On the design of clone-based haplotyping. Genome Biol 14: R100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Matsumoto H, Kiryu H. 2013. MixSIH: a mixture model for single individual haplotyping. BMC Genomics 14: S5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Panconesi A, Sozio M. 2004. Fast hare: a fast heuristic for single individual SNP haplotype reconstruction. In International workshop on algorithms in bioinformatics, pp. 266–277. Springer, New York. [Google Scholar]
- Patel A, Edge P, Selvaraj S, Bansal V, Bafna V. 2016. InPhaDel: integrative shotgun and proximity-ligation sequencing to phase deletions with single nucleotide polymorphisms. Nucleic Acids Res 44: e111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pendleton M, Sebra R, Pang AW, Ummat A, Franzen O, Rausch T, Stutz AM, Stedman W, Anantharaman T, Hastie A, et al. 2015. Assembly and diploid architecture of an individual human genome via single-molecule technologies. Nat Methods 12: 780–786. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Peters BA, Kermani BG, Sparks AB, Alferov O, Hong P, Alexeev A, Jiang Y, Dahl F, Tang YT, Haas J, et al. 2012. Accurate whole-genome sequencing and haplotyping from 10 to 20 human cells. Nature 487: 190–195. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Putnam NH, O'Connell BL, Stites JC, Rice BJ, Blanchette M, Calef R, Troll CJ, Fields A, Hartley PD, Sugnet CW, et al. 2016. Chromosome-scale shotgun assembly using an in vitro method for long-range linkage. Genome Res 26: 342–350. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rao SS, Huntley MH, Durand NC, Stamenova EK, Bochkov ID, Robinson JT, Sanborn AL, Machol I, Omer AD, Lander ES, et al. 2014. A 3D map of the human genome at kilobase resolution reveals principles of chromatin looping. Cell 159: 1665–1680. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schiffels S, Durbin R. 2014. Inferring human population size and separation history from multiple genome sequences. Nat Genet 46: 919–925. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Selvaraj S, R Dixon J, Bansal V, Ren B. 2013. Whole-genome haplotype reconstruction using proximity-ligation and shotgun sequencing. Nat Biotechnol 31: 1111–1118. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sims D, Sudbery I, Ilott NE, Heger A, Ponting CP. 2014. Sequencing depth and coverage: key considerations in genomic analyses. Nat Rev Genet 15: 121–132. [DOI] [PubMed] [Google Scholar]
- Snyder MW, Adey A, Kitzman JO, Shendure J. 2015. Haplotype-resolved genome sequencing: experimental methods and applications. Nat Rev Genet 16: 344–358. [DOI] [PubMed] [Google Scholar]
- Suk EK, McEwen GK, Duitama J, Nowick K, Schulz S, Palczewski S, Schreiber S, Holloway DT, McLaughlin S, Peckham H, et al. 2011. A comprehensively molecular haplotype-resolved genome of a European individual. Genome Res 21: 1672–1685. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tewhey R, Bansal V, Torkamani A, Topol EJ, Schork NJ. 2011. The importance of phase information for human genomics. Nat Rev Genet 12: 215–223. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhao H, Sun Z, Wang J, Huang H, Kocher JP, Wang L. 2014. CrossMap: a versatile tool for coordinate conversion between genome assemblies. Bioinformatics 30: 1006–1007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zheng GX, Lau BT, Schnall-Levin M, Jarosz M, Bell JM, Hindson CM, Kyriazopoulou-Panagiotopoulou S, Masquelier DA, Merrill L, Terry JM, et al. 2016. Haplotyping germline and cancer genomes with high-throughput linked-read sequencing. Nat Biotechnol 34: 303–311. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zook JM, Catoe D, McDaniel J, Vang L, Spies N, Sidow A, Weng Z, Liu Y, Mason CE, Alexander N, et al. 2016. Extensive sequencing of seven human genomes to characterize benchmark reference materials. Sci Data 3: 160025. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.