Actin Filament Strain Promotes Severing and Cofilin Dissociation

Abstract

Computational and structural studies have been indispensable in investigating the molecular origins of actin filament mechanical properties and modulation by the regulatory severing protein cofilin. All-atom molecular dynamics simulations of cofilactin filament structures determined by electron cryomicroscopy reveal how cofilin enhances the bending and twisting compliance of actin filaments. Continuum mechanics models suggest that buckled cofilactin filaments localize elastic energy at boundaries between bare and cofilin-decorated segments because of their nonuniform elasticity, thereby accelerating filament severing. Here, we develop mesoscopic length-scale (cofil)actin filament models and evaluate the effects of compressive and twisting loads on strain energy distribution at specific interprotein interfaces. The models reliably capture the filament bending and torsional rigidities and intersubunit torsional flexibility measured experimentally with purified protein components. Buckling is predicted to enhance cofilactin filament severing with minimal effects on cofilin occupancy, whereas filament twisting enhances cofilin dissociation without compromising filament integrity. Preferential severing at actin-cofilactin boundaries of buckled filaments is more prominent than predicted by continuum models because of the enhanced spatial resolution. The models developed here will be valuable for evaluating the effects of filament shape deformations on filament stability and interactions with regulatory proteins, and analysis of single filament manipulation assays.

Introduction

Actin is an essential and abundant eukaryotic protein that plays central roles in cell division, motility, adhesion, and maintenance of cell shape (1, 2). Regulatory actin binding proteins spatially and temporally modulate filament and network assembly dynamics and architecture (2). Severing proteins accelerate filament network remodeling by increasing the concentration of ends where subunits add and dissociate.

The actin regulatory protein cofilin (3) binds filaments cooperatively (4, 5, 6, 7, 8), increases filament bending (9) and twisting (10) dynamics, and promotes spontaneous, thermally driven filament fragmentation preferentially at boundaries between bare and cofilin-decorated segments (7, 11, 12, 13, 14, 15, 16). Active filament shape deformations (e.g., buckling under compressive loads) induced by contractile myosin proteins also promote filament fragmentation (17, 18, 19, 20, 21) and may enhance the filament severing activity of cofilin (5, 22). Filament softening associated with cofilin binding lowers the buckling force, and can potentially introduce an instability to actin bundles and networks (9), which accelerates actin turnover in some cells (18).

Quantitative knowledge of strained filament structure and thermodynamics is necessary for defining the molecular basis of actin filament elasticity and fragmentation mechanism(s). Computational studies spanning a wide range of length- and timescales have proven valuable to providing a molecular account of filament structural dynamics and energetics (23, 24, 25, 26, 27, 28, 29, 30, 31). All-atom molecular dynamics (MD) simulations have revealed key structural elements that influence actin filament bending and twisting stiffness (23), and the mechanism by which cofilin enhances filament compliance (24, 32), but analysis is limited to short filament lengths (<75 nm) and timescales (<100 ns) of thermally driven shape fluctuations. Steered-MD simulations capture behaviors under applied loads (25), but are also restricted to short length scales and, because of the short analysis times, are associated with nanonewton forces that far exceed those exerted by biological motor proteins (33). Continuum mechanics modeling permits analysis of long (>1 μm) filaments under strain with minimal computational cost, but fails to capture pertinent structural information, including that of interprotein interfaces, and thus is inadequate for determining detailed molecular mechanism(s) of fragmentation (22). Accordingly, modeling approaches that bridge the length and timescales of these methods is needed (26).

Here we develop a mesoscopic length-scale, computational (cofil)actin filament model to evaluate the effects of bending and twisting strain on filament fragmentation and cofilin binding. The model incorporates filament topology (e.g., helicity) and changes linked to cofilin occupancy. They also consider protein-protein interface areas, stiffness, and energetics, thus mapping filament strain energy to specific interfaces (e.g., lateral or longitudinal filament contacts). Results from our new model filament simulations indicate that buckling strains longitudinal actin contacts with minimal perturbation of cofilin-actin contacts, and that twisting strongly compromises cofilin-actin interactions, which is predicted to accelerate cofilin dissociation from filaments.

Materials and Methods

Filament modeling

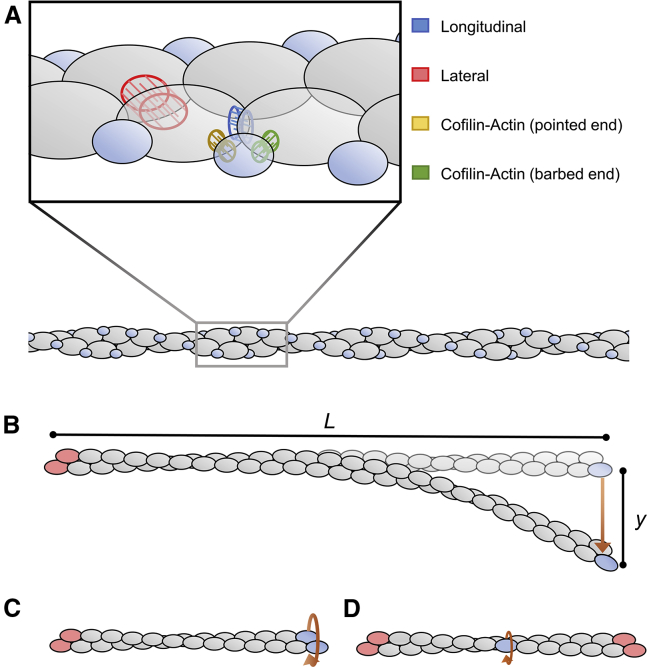
Modeling and simulations were carried out using the software MATLAB 2016b (The MathWorks, Natick, MA (26)). Proteins are modeled as rigid ellipsoids. Actin and cofilin dimensions and filament helicity were calculated from PDB: 2ZWH (actin (34)) and 3J0S (cofilactin (35)). Protein contact interfaces (i.e., actin-actin and cofilin-actin) are defined by a series of elastic bonds (Fig. 1 A), which resist compression/extension, but bend and rotate freely.

Figure 1.

Cofilactin filament model and load-induced deformations. (A) Actin (gray) and cofilin (blue) are modeled as rigid ellipsoids with interface types distinguished by color. (B) Given here is a schematic of cantilever bending used to measure bending rigidity (L_B). (C) Given here is a schematic of filament end twisting used to measure C_fil. (D) Here is single subunit twisting used to measure C_sub. Subunits held in their initial, resting positions and orientations are colored red. The external force (direction depicted by orange arrows) is applied to proteins colored blue. To see this figure in color, go online.

These elastic bonds have a constant resting length and stiffness values obtained from MD model parameters (Table 1), as follows. Periodic structures of ADP actin and cofilactin (cofilin-decorated actin) were constructed and simulated as described in Fan et al. (24), using the molecular dynamics code NAMD (36). After allowing the systems to relax to stable structures for 75 ns (actin) or 175 ns (cofilactin), the next 50 ns of data (collected every 50 ps) were used to generate elastic network models. In this case, each actin and cofilin monomer was mapped to its center of mass, and bonds connected each actin subunit to its four adjacent actin subunits and (for cofilactin) two adjacent cofilin subunits. The spring constants of these bonds were then adjusted iteratively, such that the fluctuations in the bead-spring model maximally reproduce what is seen in the atomistic MD simulations (37).

Table 1.

Model Filament Parameters

Actin Filament	Value
Filament period	71.2 nma
Number of actin subunits in one period	26b
Rise per actin subunit (same strand)	5.52 nmb
Actin filament interaction radius	1.8 nmb
Rotation per subunit	166.1°b
Actin subunit dimensions	5.4 × 5.4 × 3.8 nmc
Stiffness, actin-actin, longitudinal	582.361 kBT/nm2c
Stiffness, actin-actin, lateral	392.007 kBT/nm2c
A-A longitudinal interface area	12.6 nm2d
A-A lateral interface area	4.7 nm2d
Cofilactin Filament	Value
Filament period	55.2 nmb
Number of actin subunits in one period	20.1b
Rise per actin subunit (same strand)	5.49 nmb
Actin filament interaction radius	1.7 nmb
Rotation per subunit	162.1°c
Cofilin filament radius	3.7 nme
Cofilin subunit dimensions	3.1 × 3.3 × 1.3 nme
Stiffness, actin-actin, longitudinal	169.14 nm2e
Stiffness, actin-actin, lateral	429.005 nm2e
A-A longitudinal interface area	4.1 nm2d,e
A-A lateral interface area	7.3 nm2d,e
Stiffness, cofilin-actin, toward pointed end	157.251 kBT/nm2e
Stiffness, cofilin-actin, toward barbed end	204.047 kBT/nm2e
A-C interface area, toward pointed end	13.9 nm2d,e
A-C interface area, toward barbed end	8.9 nm2d,e

^aHoward (43).

^bFan et al. (24).

^cMeasured from PDB: 3J0S (34).

^dNIH Supercomputing Resource, http://helixweb.nih.gov/structbio/basic.html.

^eMeasured from PDB: 3J8I (35).

Electron microscopy reconstructions suggest that multiple actin filament structures exist (38), and the MD simulation captures one of these states. The simulation is run until the root mean squared deviation of the backbone atom positions of the structure (compared to the starting structure) does not change significantly. This corresponds to the relaxation of the experimental structure in accordance with the particular MD force field used. Simulations of these structures have been repeated, and the measured persistence length of the filaments varies little between simulations (e.g., (29, 30, 39, 40)).

The elastic bonds were incorporated into the mesoscale model by placing bonds randomly, with a uniform density, over an area defined by the buried solvent-accessible surface area (calculated by using a calc-surface program accessed from the National Institutes of Health Scientific Supercomputing Resource at http://helixweb.nih.gov/structbio/basic.html for all atoms but water, using a 1.4 Å probe size).

Protein components are defined by their 3D position (G^(k)) and its local frame (a^(k)₁, a^(k)₂, and a^(k)₃); designated by R(ψ^(k)), the rotation that maps the fixed frame (e₁, e₂, and e₃) to (a^(k)₁, a^(k)₂, and a^(k)₃) (Fig. S1 A). The coordinates of any elastic bond attachment point (M^(k)) on the surface of protein k are defined by the mass center (G^(k)) and a vector (X^(k)), which connects the mass center to M^(k) and thus yields the position coordinates in the local reference frame denoted (a^(k)₁, a^(k)₂, and a^(k)₃) (Fig. S1 A). The position of M^(k) on protein k is given by De La Cruz et al. (26) as the following:

$$\mathit{M}=\mathit{G}+R\left(\mathit{\psi }\right)\mathrm{\cdot }\mathit{X}.$$ (1)

Global filament deformations are applied by relative displacements and/or rotations of a subset of the constituent proteins. Filaments, either resting or deformed with imposed external forces, represent a static equilibrium. Inertial and damping forces are neglected in the model, as these are negligible in comparison to elastic forces at this length scale.

Each elastic bond linking two proteins (Fig. S1 B) at an interface is described by a harmonic potential with energy E with a magnitude that depends on the stiffness (S), resting length $\left({\lambda }^{\left(k_1,k_2,j\right)}\right)$, and the distance $\left(\left|{\mathit{M}}^{\left(k_1,j\right)}-{\mathit{M}}^{\left(k_2,j\right)}\right|\right)$ between the attachment points of bond j between proteins k₁ and k₂ according to the following:

$$E^{\left(k_{1,}{k}_2,j\right)}=S/2{\left(\left|{\mathit{M}}^{\left(k_1,j\right)}-{\mathit{M}}^{\left(k_2,j\right)}\right|-{\lambda }^{\left(k_1,k_2,j\right)}\right)}^2.$$ (2)

The elastic energy associated with each interface is given by the sum of all bond energies connecting two proteins at this interface:

$$E^{\left(k_{1,}{k}_2\right)}=\sum _j{E}^{\left(k_{1,}{k}_2,j\right)}.$$ (3)

The total elastic energy is given by the sum of all interface energies throughout the filament:

$$E=\sum _{k_{1,}{k}_2}{E}^{\left(k_{1,}{k}_2\right)}.$$ (4)

We emphasize that E represents an elastic strain energy, and E = 0 for filaments in their resting positions (i.e., $\left|{\mathit{M}}^{\left(k_1,j\right)}-{\mathit{M}}^{\left(k_2,j\right)}\right|$ = ${\lambda }^{\left(k_1,k_2,j\right)}$ for all bonds).

Application of external load

Simulations of filament shape deformation were carried out as described in detail in De La Cruz et al. (26). Briefly, the external, applied force (F_ext) or torque (T_ext) is coded via 3 × N vectors, where N is the number of proteins with an imposed force or torque. The internal forces and torques (F_int and T_int) are computed by summing the elementary forces and torques of all elastic bonds adjoining protein components. Forces are balanced such that at equilibrium, the internal forces and torques are equal to the applied external load (F_int + F_ext = 0 and T_int + T_ext = 0).

Filaments (500 or 100 nm, with or without cofilin clusters sizes predicted to exist over a range of cofilin occupancies (5, 41)) were deformed with external compressive or torsional loads in a series of small steps to maintain force balance equilibrium throughout the simulation. Buckling was imposed by compressing until the end-to-end length reached 70% of the contour length. The filament curvature under these buckling conditions compares to the radius of the curvature required for severing (11), and this specific condition was chosen to match deformations evaluated previously with the continuum mechanics model (22). Filament end orientations were constrained to prevent rotation. Twisting loads were applied for a given number of rotations in either direction (e.g., overtwisting or undertwisting) while constraining the filament end-to-end distance.

The contribution of elastic strain energy to filament severing was calculated relative to the spontaneous (i.e., thermally driven) severing rate constant k_sev according to Dudko et al. (42):

$$\frac{k_{\text{sev}}\left(\text{strained}\right)}{k_{\text{sev}}}={\left(1-\frac{2}{3}\frac{\Delta G_{\text{elastic}}^{°\prime }}{\Delta G^{‡\prime }}\right)}^3\text{exp}(\Delta G_{\text{elastic}}^{°\prime }(1-{\left(1-\frac{2}{3}\frac{\Delta G_{\text{elastic}}^{°\prime }}{\Delta G^{‡\prime }}\right)}^{3/2})),$$ (5)

where ΔG^°′_elastic is the sum of elastic strain energies of the interfaces whose rupture is associated with filament fragmentation (e.g., two longitudinal and one lateral interface for bare actin, plus two additional cofilin-actin interfaces for cofilactin severing), and ΔG^‡′ is the transition state energy barrier to filament severing that governs the value of k_sev (Table 2). The effect of strain on cofilin dissociation was calculated in a similar manner with corresponding rate constants and activation free energies.

Table 2.

Filament Severing and Cofilin Dissociation Rate Constants and Transition State Energies

Filament Severing Site	ksev (s−1)	ΔG‡ (kBT)
Actin-actina,b	1 × 10−6	43.3
Cofilactin-cofilactina,b	1 × 10−6	43.3
Actin-cofilactin boundarya,c	8.3 × 10−6	41.2
Cofilin Binding Mode	kdiss (s−1)	ΔG‡ (kBT)
Isolateda,d (kdiss= k−)	0.18	31.2
Singly contiguousa,d (kdiss= k−ω−)	0.11	31.7
Doubly contiguousa,d (kdiss= k−ω−2)	0.07	32.2

^aSevering and dissociation rates are converted to free energies of severing/rupture via the Eyring equation: k_diss or $k_{\text{sev}}=k_{\text{B}}T/h{e}^{-\Delta {\mathit{G}}^{‡}/k_{\text{B}}T}$.

^bFrom McCullough et al. (11). We note that a range exists in the literature (e.g., a site-specific value of ∼10⁻⁷ s⁻¹ can be estimated from the data in (7, 51)), but the relative enhancements vary much less.

^cKang et al. (12).

^dk₋ is the native dissociation rate of an isolated cofilin from actin filaments. ω₋ is the cooperativity of cofilin dissociation with adjacent cofilin proteins bound (14).

Determination of model filament mechanical properties

The bending persistence lengths (L_B) were calculated from the perpendicular force (F_p) needed to deflect the free end of a tethered filament by distance y, according to (i.e., a cantilever deformation, Fig. 1 B (43)):

$$L_B=\frac{F_p}{y\ast k_{\text{B}}T}\left(\frac{L^3}{3}\right),$$ (6)

where L is the filament contour length, k_B is Boltzmann’s constant, and T is absolute temperature. The filament torsional rigidity, (C_fil) was calculated from the resulting torque (τ) after applying a defined twist (θ, in radians) to a filament end (Fig. 1 C) using Howard (43):

$$C_{\text{fil}}=\frac{\tau \ast L}{\theta }.$$ (7)

The filament (long-axis) intersubunit torsional rigidity (C_sub) was measured by applying a torque to a single subunit (Fig. 1 D) and calculated in a similar manner using the actin subunit rise (r = 5.5 nm):

$$C_{\text{sub}}=\frac{\tau \ast r}{\theta }.$$ (8)

Results

Filament bending and torsional rigidity

The filament models developed here capture the actin and cofilactin filament bending and torsional rigidities measured with purified protein components (Table 3). The bending persistence lengths (L_B) of model actin and cofilactin filaments compare within a factor of 2 of values measured from thermally driven filament shape fluctuations (9). Similarly, the intersubunit torsional rigidities (C_sub) of model actin and cofilactin filaments are within a factor of 3 of time-resolved phosphorescence anisotropy measurements (10). The model actin filament torsional rigidity (C_fil) is also comparable to one (44) but not a second (45) value measured for individual filaments, which vary by approximately a factor of 3, possibly because of the assays employed.

Table 3.

Mechanical Properties of Model Filaments

Deformation	Actin		Cofilactin
	Wet-Lab	Model	Wet-Lab	Model
Bending	LB = 9.8 ± 0.14 μma	LB = 7.0 ± 0.11 μm	LB = 2.2 ± 0.026 μma	LB = 1.3 ± 0.02 μm
	κ = 39 ± 2.0 × 10−27 N m2a	κ = 29 ± 0.45 × 10−27 N m2	κ = 9.4 ± 2.9 × 10−27 N m2a	κ = 5.3 ± 0.08 × 10−27 N m2
Overtwist, filament subunit	LT,sub = 0.56 ± 0.24 μmb	LT,sub = 0.20 ± 0.01 μm	LT,sub = 0.03 ± 0.01 μmb	LT,sub = 0.03 ± 0.02 μm
	Csub = 2.3 ± 1.0 × 10−27 N m2 rad−1b	Csub = 0.84 ± 0.06 × 10−27 N m2 rad−1	Csub = 0.13 ± 0.06 × 10−27 N m2 rad−1b	Csub = 0.13 ± 0.07 × 10−27 N m2 rad−1
Undertwist, filament subunit	LT,sub = 0.56 ± 0.24 μmb	LT,sub = 0.20 ± 0.01 μm	LT,sub = 0.03 ± 0.01 μmb	LT,sub = 0.03 ± 0.02 μm
	Csub = 2.3 ± 1.0 × 10−27 N m2 rad−1b	Csub = 0.82 ± 0.04 × 10−27 N m2 rad−1	Csub = 0.13 ± 0.06 × 10−27 N m2 rad−1b	Csub = 0.12 ± 0.08 × 10−27 N m2 rad−1
Overtwist, filament end	LT,fil = 6.8 ± 0.7 μmc	LT,fil = 3.2 ± 0.1 μm	NDd	LT,fil = 3.2 ± 0.1 μm
	Cfil = 28 ± 3 × 10−27 N m2 rad−1c	Cfil = 13 ± 0.25 × 10−27 N m2 rad−1		Cfil = 13 ± 0.31 × 10−27 N m2 rad−1
Undertwist, filament end	LT,fil = 6.8 ± 0.7 μmc	LT,fil = 1.2 ± 0.1 μm	NDd	LT,fil = 2.2 ± 0.1 μm
	Cfil = 28 ± 3 × 10−27 N m2 rad−1c	Cfil = 4.9 ± 0.28 × 10−27 N m2 rad−1		Cfil = 8.9 ± 0.30 × 10−27 N m2 rad−1

Bending and torsional persistence length (L_B and L_T) and rigidity (κ and C) values are converted using the following formulas: L_B = κ/k_BT, L_T = C/k_BT. Uncertainties in model measurements represent the standard deviation, N = 5.

^aMcCullough et al. (9).

^bProchniewicz et al. (10).

^cYasuda et al. (44).

^dNot determined.

The value of C_fil depends on the direction of applied twist (Table 3). Actin filaments are twofold more compliant in undertwisting than overtwisting. Cofilactin filaments also undertwist more easily than overtwist, but the asymmetry is less pronounced. The intersubunit torsional rigidity (C_sub) is symmetrical in both actin and cofilactin filaments (Table 3).

Strain energy of buckled filaments

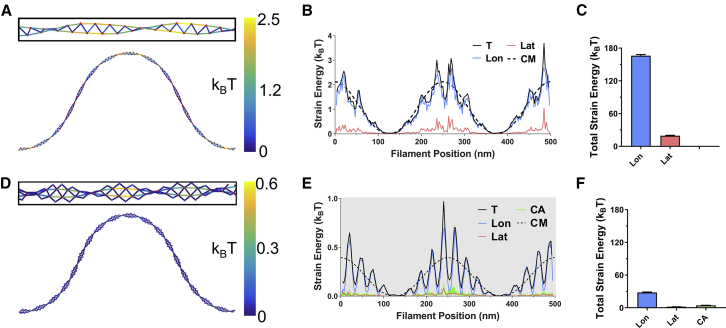
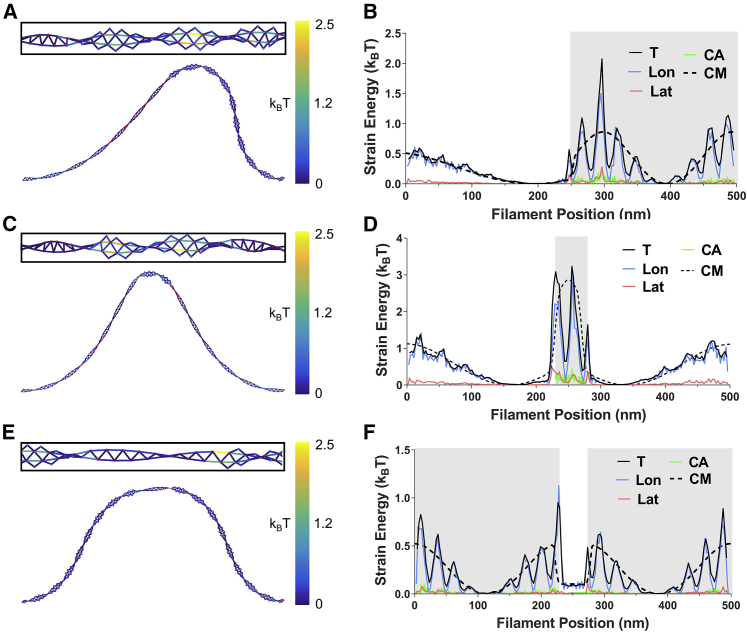
Compressive loads buckle model filaments (Fig. 2). The strain energy along buckled filaments displays three global maxima, corresponding to regions of highest curvature (Fig. 2, A and D). Cofilactin filaments are more compliant than bare actin, so the force required for buckling is lower, as is the total work needed to deform them to a similar end-to-end length. Thus, the total strain energy stored under identical conformations is lower for cofilactin than bare actin (Fig. 2, B and E).

Figure 2.

Shape and strain energy of buckled actin and cofilactin filaments. (A and D) Shown here is a skeletonized representation of single (A) actin and (D) cofilactin filaments (length = 500 nm) buckled to a 350-nm end-to-end length with constrained end orientations. Elastic strain energies of protein interfaces are colored according to the scale at the right. Actin and cofilin nodes (i.e., centers of mass) are indicated with red and blue dots, respectively. (B and E) Shown here is distribution of (B) actin and (E) cofilactin filament interface strain energy along the contour length. Insets are rotated 90°. Shading shows where cofilin is present and individual protein interface types are distinguished by color. The dashed line corresponds to the elastic energy distribution predicted by continuum models (22). (C and F) Shown here is the total elastic strain energy of each interface type. Uncertainty bars represent the standard deviation, N = 5. (T, total (longitudinal plus lateral); Lon, longitudinal; Lat, lateral; CA, cofilin-actin; CM, continuum mechanics total energy.) To see this figure in color, go online.

The overall strain energy profile of model filaments parallels that of continuum mechanics models (22) over long (>100 nm) length scales (Fig. 2 B). However, over shorter length scales, the local strain energy profiles display a periodicity not captured by continuum models (Fig. 2 B). These differences in submicron length-scale energy distribution correspond to the filament helical pitch, where both strands lie in the plane perpendicular to bending (Fig. 2 A). Most of the strain energy (>85% of the total, Fig. 2 C) localizes in longitudinal bonds, and lateral interfaces are minimally strained by bending.

Cofilin changes the (average) filament twist (Fig. 2 D) (4, 34, 35) and introduces a corresponding change in the periodicity of strain energy (Fig. 2 E). Cofilactin filaments are also wider, and thus locally more anisotropic (i.e., more ribbonlike), than bare filaments (4, 9), which enhances the difference between amplitudes of local strain energy maxima and minima. Each cofilactin longitudinal interface is paralleled by two cofilin-actin interfaces. This geometry confers each cofilin-actin interface with more freedom for movement than longitudinal interfaces, thereby straining individual interface bonds less. Because of this, and the tendency for the filament to buckle where filaments are flat relative to the bending plane, bending and buckling minimally strain the cofilin-actin interfaces.

Strain energy of twisted filaments

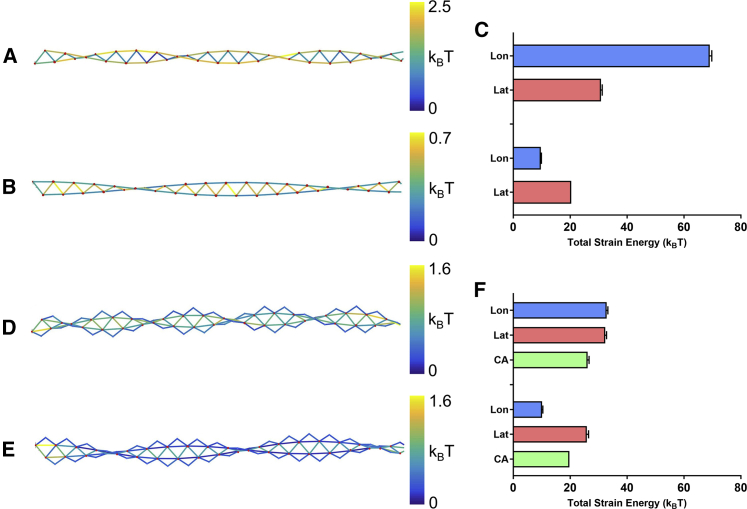
Twisting filament ends in either direction (i.e., over- or undertwist) introduces uniform strain along filaments (Fig. 3, B and D). Overtwisting strains actin longitudinal interfaces more than lateral interfaces. The opposite occurs for undertwisting—lateral contacts are strained more than longitudinal ones. Cofilactin filaments behave similarly, but overtwisting strains longitudinal and lateral contacts equally.

Figure 3.

Shape and strain energy of twisted actin and cofilactin filaments. Shown here is a skeletonized representation of single actin (A and B) or cofilactin (D and E) filaments (length 100 nm) that have been overtwisted (A and D) or undertwisted (B and E) by one half-rotation (i.e., five turns per μm) at their ends with end-to-end lengths constrained. Elastic strain energies of protein interfaces are colored according to the scale at the right. Actin and cofilin nodes (i.e., centers of mass) are indicated with red and blue dots, respectively. (C and F) Shown here is the total elastic strain energy of each interface type in (C) actin and (F) cofilactin filaments. Uncertainty bars represent the standard deviation, N = 5. Lon, longitudinal; Lat, lateral; CA, cofilin-actin interfaces. To see this figure in color, go online.

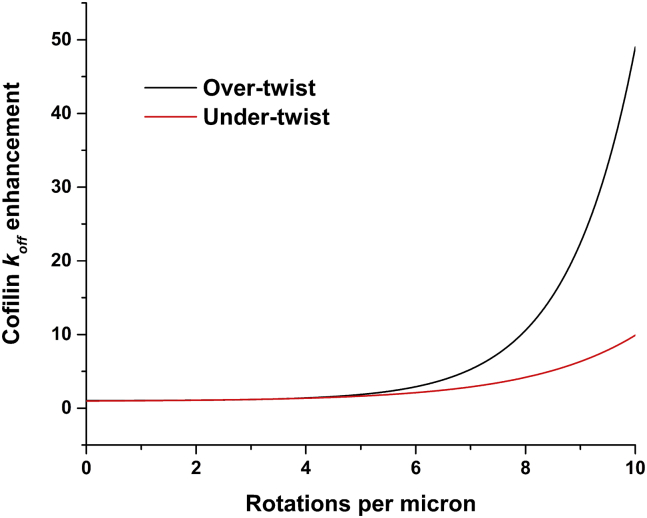
Twisting filament ends also strains cofilin-actin interfaces and significantly accelerates cofilin dissociation (Fig. 4). Overtwisting is predicted to have a greater effect than undertwisting. The enhancement is nonlinear, and the twisting density exponentially accelerates dissociation.

Figure 4.

Filament twisting accelerates cofilin dissociation. The fold-enhancement varies little for all cofilin binding modes, despite the different rate constants (Table 2). Overtwisting (black) has a more pronounced effect on cofilin dissociation than undertwisting (red). We note that in this frame of reference, the x axis is shifted for bare actin because it is undertwisted by 2.5 rotations per μm relative to cofilactin. To see this figure in color, go online.

Strain energy of partially decorated filaments

Filaments partially decorated with cofilin have a nonuniform elasticity. Cofilactin segments are more compliant in bending than bare actin, introducing a mechanical gradient at boundaries between bare and decorated segments (12). The variable stiffness of these filaments causes partially decorated filaments to deform differently from pure actin or cofilactin filaments with uniform elasticity (22).

Half-decorated filaments with centered boundaries buckle asymmetrically under compressive loads (Fig. 5 A). The softer, cofilactin segment deforms more than the stiff bare actin segment (Fig. 5 B). As seen with previous continuum models (22), the strain energy peaks at regions of highest curvature within the cofilactin segment, at sites distal from the boundary.

Figure 5.

Shape and strain energy of partially decorated filaments. Shown here is a skeletonized representation of single filaments (length 500 nm) buckled to a 350-nm end-to-end length with constrained end orientations. Filaments are either (A) half-decorated with a single boundary at the center, or contain a small (10% of filament length) (C) cofilactin or (E) bare segment. Insets are rotated 90°. Elastic strain energies of protein interfaces are colored according to the scale at the right. Actin and cofilin nodes (i.e., centers of mass) are indicated with red and blue dots, respectively. Distribution of filament interface strain energy along the contour length is shown to the right (B, D, and F). Gray shading shows where cofilin is present and individual protein interface types are distinguished by color. The dashed line corresponds to the elastic energy distribution predicted by continuum models (22). T, total (longitudinal plus lateral); Lon, longitudinal; Lat, lateral; CA, cofilin-actin; CM, continuum mechanics total energy. To see this figure in color, go online.

Filaments with a small cofilin cluster (∼10% of filament length) positioned at the center deform symmetrically (Fig. 5 C). Strain energy localizes within the cofilactin segment, in accordance with continuum models (Fig. 5 D) (22). However, the local strain energy peaks immediately adjacent to the boundary. This distribution is not captured by continuum mechanics models, which predict a strain energy peak at the center of the segment (22). Cofilactin filaments with a centered bare segment display similar behaviors (Fig. 5, E and F).

The actin and cofilactin filament torsional rigidities (C_fil) are comparable (Table 3). Accordingly, filaments twisted at their ends deform uniformly (Fig. 3), and do not display an uneven distribution of strain along actin and cofilactin segments as observed with buckling (Fig. 2).

Fragmentation of buckled filaments

The effects of strain on filament fragmentation are interpreted according to a model in which elastic energy destabilizes (i.e., increases G) protein interfaces, thereby promoting rupture. We treat filament severing as a two-state (i.e., intact or fragmented) process (22). This simplified mechanism assumes that the elastic strain energy is stored uniformly throughout the filament cross section and that fragmentation occurs as a single kinetic transition. Here we consider only the “forward” (22) severing rate constants, because reannealing under load is complicated by filament end repositioning shortly after fragmentation.

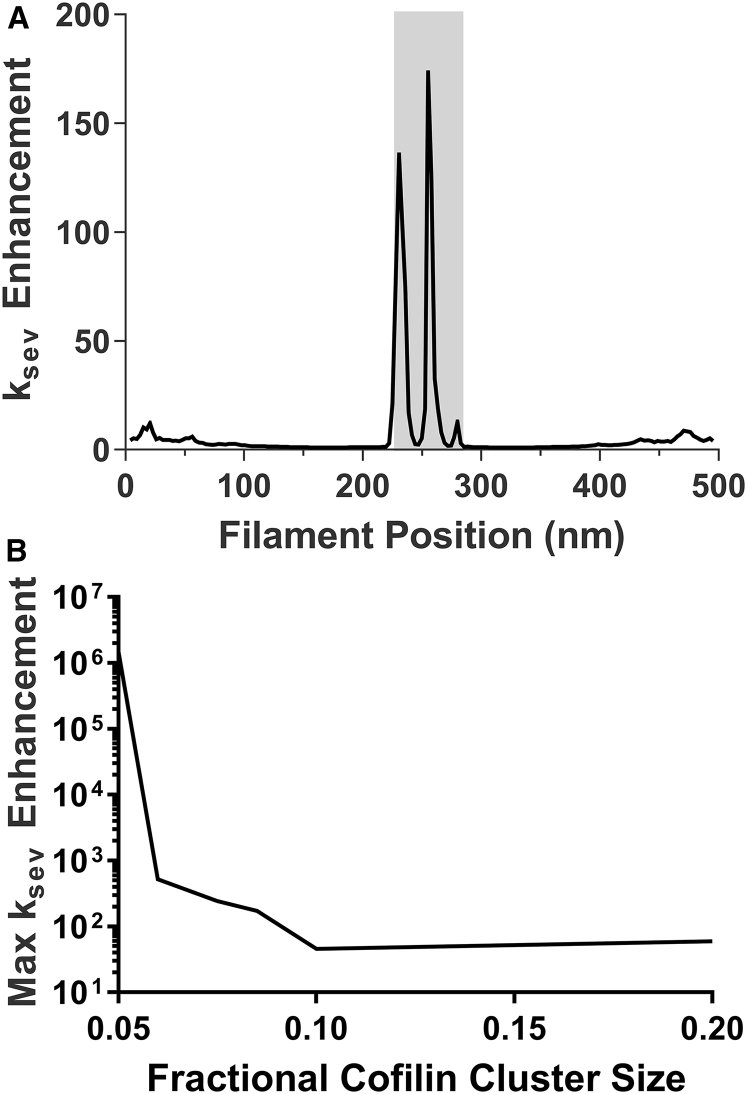
Continuum models predict buckled, partially decorated cofilactin filaments preferentially sever within cofilin clusters because the elastic strain energy distributes preferentially within compliant, cofilactin segments (22). The filament models developed here demonstrate that elastic energy peaks adjacent to boundaries, rather than distributing throughout the cofilin-bound segment (Fig. 6 A). Consequently, the models predict distinct effects of buckling on filament severing than anticipated from continuum analyses. Not only does severing occur preferentially at boundaries, but it is accelerated by at least an order-of-magnitude more (Fig. 6 B). The helically based strain localization captured in this model (Fig. 2) suggests that the maximum strain energy (and therefore maximum severing rate enhancement) will, in most cases, be greater than in the continuum model. However, the average strain energies along the filament are comparable with both models at length scales longer than the filament helical pitch.

Figure 6.

Compressive loads and buckling accelerate filament severing. (A) Given here is a severing rate across a 500-nm filament buckled to a 350-nm end-to-end length with a small (10% of total sites) cofilin cluster at the center (shaded). (B) Given here are maximum filament severing rate constants across different cluster sizes as predicted by the model.

Discussion

The mesoscopic length-scale models developed here capture the mechanical (e.g., bending and twisting rigidities) and structural (e.g., topology and protein-protein interfaces) features of (cofil)actin (cofilactin and bare actin) filaments, although maintaining the computational simplicity to investigate physiologically relevant filament shape deformations. The spatial elastic energy distribution within filaments maps local elastic strain to specific protein-protein interfaces, and thus identifies constituent contacts destabilized by filament shape changes. The effects of strain on filament severing and cofilin occupancy are interpreted with a thermodynamic, protein interface rupture model.

Filament severing mechanisms

Compressive forces driven by contractile motor proteins buckle and fragment actin filaments (16, 18, 19, 46). Because cofilin renders filaments more compliant in bending (9), occupancy could facilitate myosin-induced buckling (i.e., introduce mechanical instability) and subsequent remodeling of actin networks and bundles (18). Buckling primarily strains longitudinal actin-actin contacts of actin and cofilactin filaments (Fig. 3). Hence, these interfaces are likely to be most susceptible to rupture under compressive deformations. Filament interfaces need not be completely ruptured by applied loads. Simply compromising a subset of the severing interfaces may be adequate to accelerate spontaneous (e.g., thermally driven) fragmentation.

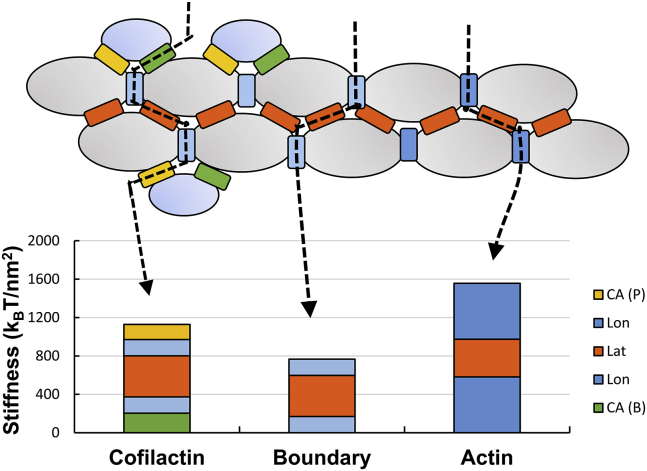
Filaments partially decorated with cofilin (which contain boundaries) can sever via at least three distinct pathways (Fig. 7), depending on the classes of protein interfaces ruptured with severing. Fragmentation can occur within an actin or cofilactin segment, or at a boundary between them. The overall stiffness of these three distinct fragmentation interfaces varies. The boundary interface is least stiff, so an applied compressive force will deform (i.e., strain) boundaries more than cofilactin segments or bare actin (22). This response applies not only for bending driven by externally applied loads, but also for those that are thermally driven. This low boundary stiffness may contribute to the observed hinging at boundaries within partially decorated filaments (11).

Figure 7.

Multiple severing pathways at cofilactin-actin boundaries in partially decorated filaments. Each column represents a sum of the stiffness values of the interfaces required to sever a filament at the shown location. CA (P), cofilin-actin pointed end; Lon, longitudinal; Lat, lateral; CA (B), cofilin-actin barbed end. To see this figure in color, go online.

Influence of filament shape deformations on cofilin binding

Myosin and formin proteins twist and can also bend and buckle actin filaments (16, 20, 47). Compressive loads and buckling weakly affect cofilin binding, but twisting strains cofilin-actin contacts and is predicted to significantly enhance dissociation (Figs. 3 and 4). This response to applied external load predicts that buckling enhances filament severing without compromising cofilin occupancy, and that twisting accelerates cofilin dissociation while preserving filament integrity. Such a mechanism also predicts that elongating formin-capped filaments anchored at their ends, which would undertwist according to the filament helical pitch (∼14 rotations per micron for actin (47)). This may weaken overall cofilin binding and subsequent severing of formin-nucleated filaments. Torsional stresses induced by myosin motors can have similar effects, although these may be more local in nature.

Limitations of the model and analysis

Simulations do not consider thermal motion, so entropic contributions from filament shape fluctuations are not captured by our model. However, entropic contributions to the interface stiffness values are considered in the all-atom MD simulations, and are included in the thermodynamic free energy-based expression, Eq. 5. A severed filament is expected to have more degrees of filament than an intact one, which will favor fragmentation. Therefore, the fragmentation probability predicted by our model, which does not consider configurational entropy, represents a lower estimate (i.e., severing will be faster than predicted for a given strain).

Solution salts (180 mM KCl) are explicitly accounted for in the all-atom MD simulations used to define filament interface stiffness parameters, but are not explicitly incorporated into the filament models developed here. Salts bind and stiffen actin filaments (12, 30, 48), so the mechanical gradient between bare and cofilin-decorated segments is likely salt dependent. We only explore a single solution condition and neglect potential contributions from filament-associated ion dissociation, as our filaments are nonplastic and the protein interaction strength does not change throughout the simulation.

An advantage of the mesoscopic filament models presented here is that elastic strain energy is discretely mapped within protein interfaces along filaments. This spatial dispersal of elastic energy facilitates a thermodynamic link among stored elastic free energy, interface destabilization, and rupture probability, namely filament severing and cofilin dissociation. An assumption in this analysis of severing and dissociation enhancement is that the strain energy at each protein interface is distributed uniformly. However, some regions of the interface may experience variable strain, depending on their interface position. Therefore, some regions of a given protein-protein interface are more susceptible to rupture than others. Future modeling efforts will require extending the mesoscopic models to account for interface remodeling and integrating with all-atom MD simulations to evaluate if severing is best determined by such a multistate pathway with progressive interface rupture, analogous to crack propagation in protein (49) and nonprotein materials (50).

Author Contributions

A.C.S., J.-L.M., and E.M.D.L.C. conceived the project. A.C.S., J.-L.M., and E.M.D.L.C. designed the simulations. A.C.S. performed model simulations. G.M.H. performed MD simulations and analysis. A.C.S., G.M.H., G.A.V., L.B., J.-L.M., and E.M.D.L.C. contributed analytical tools. A.C.S., J.-L.M., and E.M.D.L.C. analyzed data. A.C.S. and E.M.D.L.C. wrote the article. G.M.H., G.A.V., L.B., and J.-L.M. edited the article.

Editor: E. Ostap.