The predictive power of zero intelligence in financial markets

Abstract

Standard models in economics stress the role of intelligent agents who maximize utility. However, there may be situations where constraints imposed by market institutions dominate strategic agent behavior. We use data from the London Stock Exchange to test a simple model in which minimally intelligent agents place orders to trade at random. The model treats the statistical mechanics of order placement, price formation, and the accumulation of revealed supply and demand within the context of the continuous double auction and yields simple laws relating order-arrival rates to statistical properties of the market. We test the validity of these laws in explaining cross-sectional variation for 11 stocks. The model explains 96% of the variance of the gap between the best buying and selling prices (the spread) and 76% of the variance of the price diffusion rate, with only one free parameter. We also study the market impact function, describing the response of quoted prices to the arrival of new orders. The nondimensional coordinates dictated by the model approximately collapse data from different stocks onto a single curve. This work is important from a practical point of view, because it demonstrates the existence of simple laws relating prices to order flows and, in a broader context, suggests there are circumstances where the strategic behavior of agents may be dominated by other considerations.

The traditional paradigm in economics is one of rational utility maximizing agents. Recognizing limitations in human cognition, economists have increasingly explored models in which agents have bounded rationality. We take this direction even further here by testing a model of trading in financial markets that drops agent rationality almost altogether. These results are particularly striking because the model predicts simple quantitative laws relating different properties of markets that are borne out well when tested against data.

Although no one would dispute that agents in financial markets behave strategically, and that for some purposes taking this into account is essential, we show in this paper that there are some problems where other factors may be more important. Previous work along these lines includes that of Becker (1), who showed that random agent behavior and budget constraint are sufficient to guarantee the proper slope of supply and demand curves, and Gode and Sunder (2), who demonstrated that if one replaces the students in a standard classroom economics experiment by zero-intelligence agents with a budget constraint, they perform surprisingly well. More specifically, the model we test here builds on earlier work on the double auction in financial economics (3–6) and physics (7–11). [See also interesting subsequent work (12, 13).] The model makes the simple assumption that agents place orders to buy or sell at random (14, 15), subject to constraints imposed by current prices. Although one might argue that tracking prices requires at least some intelligence, this is the minimal intelligence consistent with the assumptions of the model, which we will loosely refer to as “zero intelligence.” We show here that, for certain problems, such an approach can make surprisingly good quantitative predictions.

Another unusual aspect of the work presented here is the nature of the predictions we test, which take the form of simple quantitative laws. These laws relate one set of market properties to another, placing restrictions on the allowed values of variables that are comparable to the ideal gas law of physics. They make quantitative predictions about magnitude and functional form, which are testable with only minimal auxiliary assumptions. This is in contrast to papers testing standard models based on rationality, which are typically forced to add strong auxiliary assumptions not contained in the original theoretical model, making the final results essentially qualitative.

A literature review, details of the analysis, and further comments are given in Supporting Text, Tables 1 and 2, and Figs. 5–11, which are published as supporting information on the PNAS web site.

The Model

Continuous Double Auction. The continuous double auction is the most widely used method of price formation in modern financial markets. The auction is called “double,” because traders can submit orders to both buy and sell, and “continuous,” because they can do so at any time. Under the terminology we use here, an order that does not cross the opposite best price and so does not result in an immediate transaction is called a limit order. An example is a sell order with a higher price than any existing buy order. An order that does cross the opposite best price and thus causes an immediate transaction is called a market order. Real markets use a host of different order types, which vary from market to market. However, by making appropriate decompositions (sometimes involving splitting an order into two pieces), it is always possible to break down the order flow into components that are effectively either market orders or limit orders. Buy and sell limit orders accumulate in their respective queues, whereas buy and sell market orders cause transactions that remove limit orders. A limit order can also be removed from its queue by being canceled, which can occur at any time. The lowest selling price offered at any point in time is called the best ask, a(t), and the highest buying price, the best bid, b(t). The bid–ask spread s(t) ≡ a(t) - b(t) measures the gap between them. The best prices may change as new orders arrive or old orders are canceled.

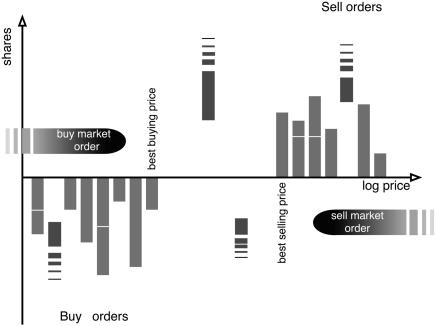
Description of the Model. The model we test here (14, 15) was constructed to be the simplest possible sensible model of agent behavior in a continuous double auction. It assumes that two types of agents place orders randomly according to independent Poisson processes, as shown in Fig. 1. Impatient agents place market orders randomly with a Poisson rate of μ shares per unit time. Patient agents, in contrast, place limit orders randomly in both price and time. Buy limit orders are placed uniformly anywhere in the semiinfinite interval -∞ < p < a(t), where p is the logarithm of the price, and similarly sell limit orders are placed uniformly anywhere in b(t) < p < ∞. Both buying and selling limit orders arrive with the same Poisson rate density α, which is measured in shares per unit price per unit time. The log-price p is continuous and independent of arrival time. Both limit and market orders are of constant size σ (measured in shares). Queued limit orders are canceled according to a Poisson process, analogous to radioactive decay, with a fixed-rate δ per unit time. To keep the model as simple as possible, there are equal rates for buying and selling, and all of these processes are independent except for indirect coupling through the boundary conditions, as explained below.

Fig. 1.

A random process model of the continuous double auction. Stored limit orders are shown stacked along the price axis, with sell orders (supply) stacked above the axis at higher prices and buy orders (demand) stacked below the axis at lower prices. New sell limit orders are visualized as randomly falling down, and new buy orders are visualized as randomly “falling up.” New sell orders can be placed anywhere above the best buying price, and new buy orders can be placed anywhere below the best selling price. Limit orders can be removed spontaneously (e.g., because the agent changes her mind or the order expires), or they can be removed by market orders of the opposite type. This can result in changes in the best prices, which in turn alter the boundaries of the order placement process.

As new orders arrive, they may alter the best prices a(t) and b(t), which in turn change the boundary conditions for subsequent limit order placement. For example, the arrival of a buy limit order inside the spread will alter the best bid b(t), which immediately alters the boundary condition for placing the next sell limit order. It is this feedback between order placement and price diffusion that makes this model interesting and, despite its apparent simplicity, very difficult to understand analytically. This model has been studied by using simulation and with approximate analytic treatments based on mean field theory (14, 15).

Some readers may be puzzled by the use of a constant density over an infinite interval, which gives an infinite total arrival rate. The key is that the normalization is chosen to make the arrival rate in any given price interval finite. This is analogous to a model of snow falling and evaporating on an infinite plane: although the total amount of snow arriving is infinite, the amount of snow falling in any given square during any given time is perfectly well behaved. The situation here is much more complicated, due to the fact that market orders define a point removal process, and there are two kinds of “snow” falling on overlapping and interacting intervals. Nonetheless, the basic trick of normalizing the density rather than the total is the same.

Predictions of the Model. The rather radical assumption of a uniform limit order price density is made because it simplifies analysis, allowing the derivation of simple scaling laws relating the parameters to fundamental properties such as the average bid–ask spread. (For an empirical investigation of the density of limit order placement, see refs. 12 and 16.) The mean value of the spread predicted based on a mean field theory analysis of the model (14, 15) is

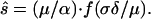[1]

The nondimensional ratio ε ≡ σδ/μ can be thought of as the ratio of removal by cancellation to removal by market orders and plays an important role. f(ε) is a slowly varying monotonically increasing function that can be approximated (15) as f(ε) = 0.28 + 1.86 ε^3/4. The scaling law above is reasonable in that it predicts that the spread increases when there are more market orders or cancellations (which remove stored limit orders) and decreases with more limit orders (which fill in the spread more quickly). The dependence on μ/α can be derived from dimensional analysis, under certain assumptions detailed in Dimensional Analysis in Supporting Text. However, the functional form of f(ε) is not obvious. One of the predictions of the model, which to our knowledge has not been hypothesized elsewhere in the literature, is that the order size σ is an important determinant of the spread.

Another prediction of the model concerns the price diffusion rate, which drives the volatility of prices and is the primary determinant of financial risk. If we assume that prices make a random walk, then the diffusion rate measures the size and frequency of its increments. The variance V of a random walk grows as V(t) = Dt, where D is the diffusion rate and t is time. This is the main free parameter in the Bachelier model of prices (17). Although its value is essential for risk estimation and derivative pricing, there is very little fundamental understanding of what actually determines it. In standard models, it is often assumed to depend on “information arrival” (18), which has the disadvantage that it is impossible to measure directly. For our idealized model, numerical experiments indicate that the shortterm price diffusion rate is to a very good approximation given by the simple formula (14, 15)

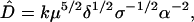[2]

where k is a constant. This formula is reasonable in that it predicts that volatility increases with limit order removal (by either market orders or cancellations) and decreases with limit order placement. The dependence on order size and the values of the scaling exponents are not so obvious. It has so far not been possible to derive this formula from theoretical considerations (although dimensional analysis was essential for guessing this functional form).

We would like to emphasize that the construction of the model and all the predictions derived from it were made before looking at the data. The model was constructed to be simple enough to be analytically tractable and makes many strong assumptions. The assumption of random order placement leads to consequences that might be economically unreasonable in a rational setting, such as the existence of profit-making opportunities. However, this is self-consistent with the assumption that the only intelligence the agents possess is the ability to mechanically adjust the prices of limit orders based on current best prices. Furthermore, simulations suggest that the arbitrage opportunities in this model are not risk-free, yielding only finite risky profits (J.D.F., J. Girard, and J. Rutt, unpublished observations).

A useful concept is that of liquidity, which in this context can be defined as the availability of standing limit orders that allow trading to take place. The impatient market order traders are liquidity demanders, and the limit order traders are liquidity providers. The use of a zero-intelligence agent model makes it possible to study the flow of liquidity in and out of the market and to study its interaction with price formation. This has not been properly addressed by models that attempt to fully treat agent rationality. Abandoning the assumption of rationality gives the ability to focus the modeling effort on other problems, such as those addressed here.

Testing the Scaling Laws

Data. We test this model with data from the electronic open limit order book of the London Stock Exchange, which includes about half of the total trading volume. We used data from 11 stocks in the period from August 1, 1998 to April 30, 2000, which includes 434 trading days and a total of roughly six million events. For all these stocks, the number of total events exceeds 300,000 and was never less than 80 on any given day (where an event corresponds to an order placement or cancellation). Orders placed during the opening auction are removed to accommodate the fact that the model applies only to the continuous auction. See The London Stock Exchange Data Set in Supporting Text for more details.

Testing Procedure. We test the model cross-sectionally over 11 stocks. For each stock, we measure its average order flow rates and calculate the predicted average spread 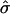and diffusion rate D̂ for that stock by using Eqs. 1 and 2. We then compare these predicted values to the actual values of the spread 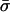and diffusion rate D̄, which we again measure from the data. The comparison is done via linear regressions of the predicted values against the actual measured values. For a discussion, see Measurement of Model Parameters and Estimating the Errors for the Regressions in Supporting Text. Measurement of the parameters μ and σ is straightforward: to measure μ, for example, we simply compute the total number of shares of market orders and divide by time or, alternatively, we compute μ_t for each day and average; we get similar results in either case. However, a problem occurs in measuring the parameters α and δ due to the simplifying assumption of a uniform distribution of prices for limit order placement and a uniform cancellation rate. In the real data, limit order placement and cancellation are concentrated near the best prices (12, 16). To cope with this, we make an auxiliary assumption that order placement is uniform inside a price window around the best prices and zero outside this window. We choose this price window W to correspond to ≈60% of limit orders away from the midprice and compute α by dividing the number of shares of limit orders placed inside this price window per unit time by W. We do this for each day and compute the average value of α for each stock. We similarly compute δ as the inverse of the average lifetime of orders canceled inside the same price window W.

The laws we describe here do not make temporal predictions but rather are restrictions of state variables. The ideal gas law, PV = RT, provides a good analogy. It predicts that pressure P, volume V, and temperature T are constrained; any two of them determine the third. The gas constant R is the only free parameter. In very much the same way, we are testing two relations between properties of order flows and properties of prices. We are not attempting to predict the temporal behavior of the order flows; we are only trying to see whether the restrictions between order flows and prices predicted by the model are valid. It is important to emphasize that, whereas μ, α, δ, and σ can be viewed as free parameters of the model, they are not free parameters in the test of the model. Rather they are now variables, like P, V, and T in the ideal gas law. The only free parameter is the price window W. We chose W = 0.6 as a prior; it turns out it is also roughly the value that maximizes the goodness of fit; however, varying W does not change the goodness of fit substantially.

Spread. To test Eq. 1, we measure the average spread s̄ across the full time period for each stock and compare it with the predicted average spread ŝ based on order flows. Spread is measured as the average of log b(t) - log a(t) (recall that, in the model, p represents the log price). The spread is measured after each event, with each event given equal weight. The opening auction is excluded.

To test our hypothesis that the predicted and actual values coincide, we perform a regression of the form log s̄ = A log ŝ + B. We took logarithms to do the regression, because the spread is positive and the log of the spread is approximately normally distributed. An alternative would have been to take logarithms of each event and average the logarithms. We instead regard this as a test of the cross-sectional averages and take logarithms of the cross-sectional values. We use A and B for hypothesis testing. Based on the model, we predict the comparison should yield a straight line with A = 1 and B = 0. However, because of the degree of freedom in choosing the price interval W as described above, the value of B is somewhat arbitrary; varying W through reasonable values changes B significantly, with much less effect on A.

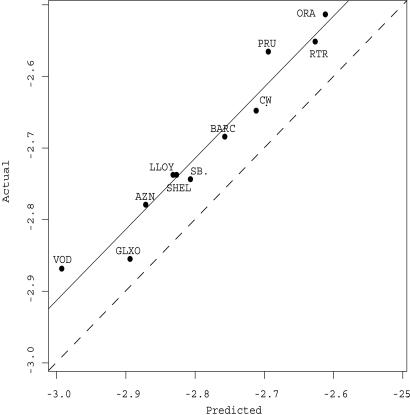
The least-squares regression, shown together with the data comparing the predictions to the actual values in Fig. 2, gives A = 0.99 ± 0.10 and B = 0.06 ± 0.29. Therefore, we strongly reject the null hypothesis that A = 0, indicating the predictions are far better than random. More importantly, we are unable to reject the null hypothesis that A = 1. The regression has R² = 0.96, so the model explains most of the variance. Note that, because of long-memory effects and crosscorrelations between stocks, the errors in the regression are larger than they would be for independent identically distributed data.

Fig. 2.

Regressions of predicted values based on order flow using Eq. 1 vs. actual values for the log spread. The dots show the average predicted and actual value for each stock averaged over the full 21-mo time period. The solid line is a regression; the dashed line is the diagonal representing the model's prediction, with A = 1 and B = 0.

Price Diffusion Rate. As for the spread, we compare the predicted price diffusion rate based on order flows with the actual price diffusion rate D̄ for each stock averaged over the 21-mo period, and regress the logarithm of the predicted vs. actual values, as shown in Fig. 3.

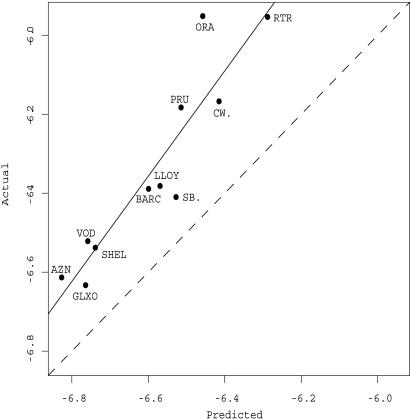
Fig. 3.

Regressions of predicted values based on order flow using Eq. 2 vs. actual values for the logarithm of the price diffusion rate. The dots show the average predicted and actual values for each stock averaged over the full 21-mo time period. The solid line is a regression; the dashed line is the diagonal, with A = 1 and B = 0.

The regression gives A = 1.33 ± 0.25 and B = 2.43 ± 1.75. Thus, we again strongly reject the null hypothesis that A = 0. We are still unable to reject the null hypothesis that A = 1 with 95% confidence, although there is some suggestion that the real values increase faster than the predicted values. In any case, the predictions are at least a good approximation. Although the results are not as good as for the spread, the model still explains most of the variance with R² = 0.76.

Average Market Impact

Market impact is practically important, because it is the dominant source of transaction costs for large trades, and conceptually important, because it provides a convenient probe of the revealed supply and demand functions in the limit order book (see Market Impact in Supporting Text). When a market order of size ω arrives, if it removes all limit orders at the best bid or ask, it will immediately change the midpoint price m ≡ (a + b)/2. We define the average market impact function ϕ in terms of the instantaneous logarithmic midpoint price shift Δp conditioned on order size, ϕ(ω) = E[Δp | ω]. Δp is the difference between the price just before and just after a market order arrives (before any other events).

A longstanding mystery about market impact is that it is a highly concave function of ω (12, 19–25). This is unexpected, because simple arguments would suggest that because of the multiplicative nature of returns, market impact should grow at least linearly (15). We know of no model that explains this. The model we are testing here predicts a concave average market impact function, with the concavity becoming more pronounced for small values of ε = σδ/μ. Intuitively, the concavity is because limit orders near the best price are removed by transactions more rapidly than those far from the best price. As a result, the average density of stored limit orders in the book increases moving away from the midpoint. An increase in density of limit orders implies a decreased price response to a market order of a given size, resulting in a concave market impact function.

Although the predictions of the model are qualitatively correct, from a quantitative point of view, the model predicts a larger variation with ε than we actually observe. Nonetheless, the model is still quantitatively useful for understanding market impact, as described below.

A surprising regularity of the average market impact function is uncovered by simply plotting the data in the nondimensional coordinates dictated by the model, as shown in Fig. 4. If we view market impact in standard dimensional units, such as British pounds or shares, there is large variability from stock to stock; the story becomes much simpler in nondimensional units.

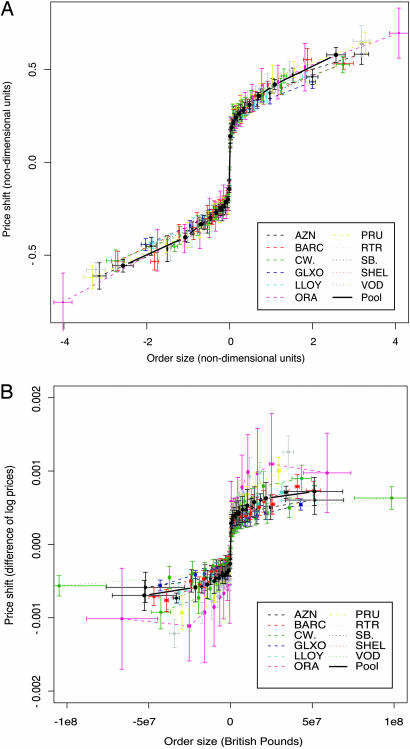
Fig. 4.

The average market impact as a function of the mean order size. In A, the price differences and order sizes for each transaction are normalized by the nondimensional coordinates dictated by the model, computed on a daily basis. Most of the stocks collapse onto a single curve; there are a few that deviate, but the deviations are sufficiently small that, given the long-memory nature of the data and the crosscorrelations among stocks, it is difficult to determine whether these deviations are statistically significant. This means that we understand the behavior of the market impact as it varies from stock to stock by a simple transformation of coordinates. In B, for comparison, we plot the order size in units of British pounds against the average logarithmic price shift.

When we plot the average market impact in standard dimensional coordinates, the behavior is highly variable from stock to stock. For example, in Fig. 4B, we plot the average market impact ϕ(ω) = E[Δp|ω] as a function of order size ω in units of British pounds. We do this by binning together events with similar ω and plotting this versus the corresponding mean price impact Δp for each bin. The result varies widely from stock to stock. We have explored a variety of other ways for renormalizing the order size (see Market Impact in Supporting Text), but they all give similar results.

Plotting the data in nondimensional units tells a simpler story. To do this, we normalize the price shift and order size by appropriate dimensional scale factors based on daily order flow rates. This transforms the standard coordinates to nondimensional coordinates as Δp → Δp·α_t/μ_t and ω → ω·δ_t/μ_t, where α_t, μ_t, and δ_t are the average parameters for day t. Notice that Δp has units of price, but

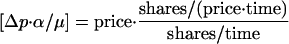[3]

is without dimensions, i.e., the units cancel out. The data collapse onto roughly a single curve, as shown in Fig. 4A. Variations from stock to stock are quite small; on average, the corresponding bins for each stock deviate from each other by ≈8%, roughly the size of the statistical sampling error. We do not find this variation is statistically significant, although we should also say that such tests are complicated by the long-memory property of these time series and crosscorrelations between stocks, so that we do not consider the results fully reliable. In contrast, by using standard dimensional coordinates, the differences are easily shown to be highly statistically significant. This collapse illustrates that the nondimensional coordinates dictated by the model provide substantial explanatory power: we can understand how the average market impact varies from stock to stock by a simple transformation of coordinates. Plotting in double-logarithmic scale shows that the curve of the collapse is roughly a power law of the form ω^0.25. This provides a more fundamental explanation for the empirically constructed collapse of average market impact for the New York Stock Exchange found earlier (24).

Conclusion

We have shown that the model presented here does a good job of predicting the average spread and a decent job of predicting the price diffusion rate. Also, by simply plotting the data in nondimensional coordinates, we get a better understanding of the regularities of market impact. These results are remarkable, because the underlying model largely drops agent rationality, instead focusing all its attention on the problem of understanding the constraints imposed by the continuous double auction.

It is worth comparing our results to those of previous empirical work. For example, Hasbrouck and Saar (26) find a positive correlation between volatility and the ratio of market orders to limit orders. They perform regressions of this ratio against volatility and several other dependent variables, and obtain goodness of fits similar to ours (except that, in their case, volatility was one of several independent variables, whereas in our case it was the dependent variable). They then discuss the results in terms of their consistency with three effects that one would expect from agent rationality. For example, one such effect is called “market order certainty”: When prices are more volatile, market orders become more attractive to a risk-averse rational agent, and so the fraction of market orders should increase. The observed positive correlations are consistent with this idea.

The model we tested here offers an alternative explanation that does not depend on strategic choice. We also predict a positive correlation between volatility and the fraction of market orders (see Eq. 2) but for a different reason: An increase in the rate of market order submission reduces liquidity and thus increases price volatility. We certainly believe that agents respond in important ways to changing market conditions such as volatility, and indeed we have demonstrated this in previous work (16). Nonetheless, we argue that it is also necessary to understand the impact of agents' actions on market conditions. By carefully treating the feedback in both directions between price formation and limit order pricing under minimal assumptions of rationality, this model provides a null hypothesis against which claims of rational behavior can be measured.

An important feature of our model is its parsimony and falsifiability. Our model makes simultaneous quantitative predictions about volatility, spread, and market impact. We postulate specific functional forms for the relation between order flows and spread and volatility; although there are multiple variables involved, there is only one free parameter. Rationality-based theories, in contrast, rarely make predictions about magnitude or functional form, and as a result their predictions are harder to test. Such tests generally require stronger auxiliary assumptions, such as imposed functional forms with multiple free parameters. Empirical studies that test such models often test only the sign of such effects, which often have a variety of alternative explanations. Our model makes sharper predictions, and is consequently more testable (27).

The approach taken here succeeds in part because it is less ambitious than a standard rationality-based model. This can be viewed as a divide-and-conquer strategy. Rather than attempting to explain the properties of the market from fundamental assumptions about utility maximization by individual agents, we divide the problem into two parts. The first (easier) problem, addressed here, is that of understanding the characteristics of the market given the order flows. The second (harder) problem, which remains to be investigated, is that of explaining why order flow varies as it does. Explaining variations in order flow involves behavioral and/or strategic issues that are likely to be much more difficult to understand. It is always desirable to solve easier problems first.

The model succeeds in part by reducing the problem to the measurement of the right variables. By measuring the rate of market order placement versus limit order placement and the rate of order cancellation, we are able to measure how patient or impatient traders are. The model makes quantitative predictions about how this affects other market properties. The agreement with the model indicates that patience is an important determinant of market behavior. Variations in patience might be explained by a rationality-based explanation in terms of information arrival or a behavioral-based explanation driven by emotional response, but in either case they suggest that patience is a key factor.

These results have several practical implications. For market practitioners, understanding the spread and market impact function is very useful for estimating transaction costs and for developing algorithms that minimize their effect. For regulators, they suggest it may be possible to make prices less volatile and lower transaction costs, if desired, by creating incentives for limit orders and disincentives for market orders. These scaling laws might also be used to detect anomalies, e.g., a higher-than-expected spread might be due to improper market-maker behavior.

This is part of a broader research program that might be somewhat humorously characterized as the “low-intelligence” approach: we begin with minimally intelligent agents to get a good benchmark of the effect of market institutions and, once this benchmark is well understood, add more intelligence, moving toward market efficiency. We thus start from almost zero rationality and work our way up, in contrast to the canonical approach of starting from perfect rationality and working down (see ref. 16).

The model we test here was constructed before looking at the data (14, 15) and was designed to be as simple as possible for analytic analysis. A more realistic (but necessarily more complicated) model would more closely mimic the properties of real order flows, which are price-dependent and strongly correlated both in time and across price levels, or might incorporate elements of the strategic interactions of agents. An improved model would hopefully be able to capture more features of the data than those we have studied here. We know there are ways in which the current model is inappropriate, e.g., it allows arbitrage opportunities that do not exist in the real market. Nonetheless, as we have shown above, this extremely simple model does a good job of explaining some important properties of markets. For further discussion, see Extending the Model in Supporting Text.

How is it conceivable to successfully model a situation in which we know that agents engage in clever strategic behavior in terms of a model that completely neglects this? Perhaps a telephone exchange provides a good analogy: even though each customer has a perfectly good reason for picking up the phone, communications engineers design exchanges by assuming they do so at random. Similarly, there are situations in markets where rational behavior can be treated in aggregate as though it were noise. The question is whether rational effects are more important or less important than stochastic effects. Rational effects are clearly important in determining overall price levels, but they may be dominated by random fluctuations in determining volatility. We do not mean to claim that market participants are unintelligent; indeed, one of the virtues of this model is that it provides a benchmark to separate properties driven by the statistical mechanics of the market institution from those driven by the strategic behavior of agents. It suggests that institutions strongly shape our behavior, so that some of the properties of markets may depend more on the structure of institutions than on the rationality of individuals.