Estimating parent-specific QTL effects through cumulating linked identity-by-state SNP effects in multiparental populations

Abstract

The emergence of multiparental mapping populations enabled plant geneticists to gain deeper insights into the genetic architecture of major agronomic traits and to map quantitative trait loci (QTLs) controlling the expression of these traits. Although the investigated mapping populations are similar, one open question is whether genotype data should be modelled as identical by state (IBS) or identical by descent (IBD). Whereas IBS simply makes use of raw genotype scores to distinguish alleles, IBD data are derived from parental offspring information. We report on comparing IBS and IBD by applying two multiple regression models on four traits studied in the barley nested association mapping (NAM) population HEB-25. We observed that modelling parent-specific IBD genotypes produced a lower number of significant QTLs with increased prediction abilities compared with modelling IBS genotypes. However, at lower trait heritabilities the IBS model produced higher prediction abilities. We developed a method to estimate multiallelic QTL effects in multiparental populations from simple biallelic IBS data. This method is based on cumulating IBS-derived single-nucleotide polymorphism (SNP) effect estimates in a defined genetic region surrounding a QTL. Comparing the resulting parent-specific QTL effects with those obtained from IBD approaches revealed high accordance that could be confirmed through simulations. The method turned out to be also applicable to a barley multiparent advanced generation inter-cross (MAGIC) population. The ‘cumulation method’ represents a universal approach to differentiate parent-specific QTL effects in multiparental populations, even if no IBD information is available. In future, the method could further benefit from the availability of much denser SNP maps.

Introduction

During the past decade, several multiparental mapping populations have been established in different plant species to dissect the genetic architecture of important agronomic traits. Especially nested association mapping (NAM) and multiparent advanced generation inter-cross (MAGIC) populations found their way as useful tools to dissect various trait complexes in different crop species like maize (Yu et al., 2008; Bauer et al., 2013; Dell’Acqua et al., 2015), wheat (Huang et al., 2012; Mackay et al., 2014; Milner et al., 2015; Thépot et al., 2015), rice (Bandillo et al., 2013), barley (Maurer et al., 2015; Sannemann et al., 2015; Nice et al., 2016) and sorghum (Jordan et al., 2011). Because of sophisticated mating designs, these populations often represent a mixture of classical linkage mapping and association mapping populations. So far, there is no general method of how to analyse these populations in genome-wide association studies (GWAS). One open question is whether genotype data are modelled as identical by state (IBS) or identical by descent (IBD). Whereas IBS simply makes use of biallelic single-nucleotide polymorphism (SNP) genotype scores to distinguish alleles, IBD also considers their inheritance and therefore enables modelling of parent-specific marker effects. The interpretation of the term IBD is not uniform. Classically, it describes the probability that two homologous alleles are descending from a common ancestor. However, it is not clear how far a common ancestor has to be traced back. Therefore, the probability that two alleles are IBD has to be defined with respect to a specific base (Powell et al., 2010). In a NAM population we know the pedigree and hence the individuals at the top of the pedigree (the parental lines) represent the possible ancestors of an allele. Therefore, in a first step the probability that two alleles are IBD can be determined in relation to the recurrent parent, that is, we can distinguish whether the allele is inherited from the recurrent parent or a wild donor across the whole NAM population. However, one could also assume a common ancestor for the parental lines that could, for instance, be modelled by definition of haplotypes. There are several methods described of how to define these haplotypes in programs like, for instance, clusthaplo (Leroux et al., 2014) or R/mpMap (Huang and George, 2011). However, defining haplotypes is not trivial and requires careful consideration (Ding et al., 2005). There is a multitude of adjusting parameters that have to be defined a priori.

In a classical biparental population, IBS and IBD would be equal, as usually only polymorphic markers are considered. However, if multiparent populations are used, there are SNPs that segregate only in a subset of parents. If we look at the resulting progeny of multiparent crosses, this SNP allele state is not different from a specific reference parent. Nevertheless, this SNP could have been inherited from another parent sharing the same IBS allele state as the reference parent. In this case they would show different IBD states, although they share the same IBS allele.

Here, we derive IBD from IBS genotype data in a wild barley NAM population. Subsequently, we test whether parent-specific IBD calling of SNPs is superior over classical biallelic IBS calling in GWAS. For this, we apply GWAS to four agronomic traits of increasing complexity (grain colour, grain threshability, flowering time and thousand grain weight). Subsequently, we develop a novel approach to model parent-specific quantitative trait locus (QTL) effects in the wild barley NAM population HEB-25 (Maurer et al., 2015) without the need of IBD information or modelling haplotypes a priori. To test the method’s accuracy we perform extensive simulation studies with varying trait complexities. We then show that this approach is also suitable to model parent-specific QTL effects in a barley MAGIC population (Sannemann et al., 2015).

Materials and methods

Plant material

The NAM population HEB-25 (Maurer et al., 2015), consisting of 1420 individual BC1S3 lines in 25 wild barley-derived families, was used in this study. HEB-25 is the result of initial crosses between the spring barley cultivar Barke (Hordeum vulgare ssp. vulgare) and 25 highly divergent exotic wild barley accessions (H. vulgare ssp. spontaneum and H. vulgare ssp. agriocrithon), hereafter referred to as donors. F1 plants of the initial crosses were backcrossed with Barke. For detailed information about the population design, see Maurer et al. (2015).

The barley MAGIC population consists of 533 doubled haploid lines, created through intermating eight founder genotypes of barley breeding in Germany. For more details about this population, see Sannemann et al. (2015).

Phenotype data

Four major agronomic traits were investigated in this study. Phenotype data were collected in field trials in Halle, Germany (51°29′46.47′N; 11°59′41.81′E) during the seasons 2011–2014. Briefly, the complete population was grown in double rows following a randomised complete block design in two replications. For details on the experimental setup, see Maurer et al. (2016). Flowering time (heading (HEA)) and thousand grain weight (TGW) data were taken from Maurer et al. (2016). Grain threshability (THR) was manually scored on a scale from 1 (difficult to thresh) to 9 (easy to thresh), after threshing mature spikes using a home-made rotating threshing drum. In addition, data on grain colour (GrCol), manually scored as 1 (light) or 9 (dark) after visual assessment, were scored. These traits were selected because we assumed that they are controlled by few (GrCol, THR) or many (HEA, TGW) genes.

Genotype data

All 1420 BC1S3 lines and their corresponding parents were genotyped with the barley Infinium iSelect 9K chip (Illumina Inc., San Diego, CA, USA) (Maurer et al., 2015), consisting of 7864 SNP markers as reported in Comadran et al. (2012). SNP markers that did not meet the quality criteria (polymorphic in at least one HEB family, <10% failure rate, <12.5% heterozygous calls) were removed from the data set. A total of 305 markers were removed as they revealed the exact segregation among all HEB lines as a twin marker, indicating that they were in complete linkage disequilibrium (LD). Only one of the twin markers was kept, resulting in a total set of 5398 remaining markers. Out of these markers, 4861 segregated in less than 25 families, and 448 thereof segregated only in a single family.

Defining IBS and IBD matrices

Polymorphic SNP alleles originating from Barke or the wild barley donors of the NAM population HEB-25 are easily distinguishable by state. Based on the Barke reference genotype, the wild barley allele can be specified in each segregating family. To set up the IBS matrix the state of the homozygous Barke allele was coded as 0, whereas HEB lines that showed a homozygous wild barley genotype were assigned a value of 2. Consequently, heterozygous HEB lines were assigned a value of 1. If a SNP was monomorphic in one HEB family but polymorphic in a second family, lines of the first HEB family were assigned a genotype value of 0, as their state is not different from the Barke allele. Gaps resulting from missing genotypes (0.6% of all data points) were filled with the mean of polymorphic flanking markers, based on the map of Maurer et al. (2015). This way a complete genotype data set (IBS) was retained that is required to carry out the following multiple regression GWAS.

To convert the IBS matrix into an IBD matrix, we first replaced each marker value that was monomorphic in a HEB family by an empty value. Then, the resulting gaps (44.9% of all data points) were filled with the mean of the next polymorphic flanking markers of this gap. This way we can distinguish whether the allele is inherited from the recurrent parent Barke or a wild donor across the whole NAM population. The newly assigned IBD value reflects the marker’s probability of being inherited from the wild barley donor.

Both matrices are available as Supplementary Figure S1 and Additional File S1.

Models used for genome-wide association mapping

We used two different multiple linear regression models to conduct genome-wide association mapping on best linear unbiased estimates of each HEB line trait performance. The best linear unbiased estimates were obtained from a linear mixed model with effects for genotype, environment and interaction of genotype and environment.

Model ‘IBS-M’ corresponds to Model-A of Liu et al. (2011), where SNP markers are included as main effects using the quantitative IBS genotype matrix scores.

This model showed the highest predictive power and detected the highest number of QTLs when compared with other joint linkage association mapping models (Würschum et al., 2012). Model ‘IBD-M × F’ models the SNP markers as interaction effect with the HEB family. This model is based on the quantitative IBD genotype matrix scores.

The analyses were carried out with SAS 9.4 Software (SAS Institute Inc., Cary, NC, USA) using Proc GLMSELECT. This procedure selects the best model out of a set of predefined possible factors. In our case, all SNPs were initially defined as possible factors. Significant SNPs were then determined by stepwise forward–backward regression. SNPs were allowed to enter or leave the model at each step until the Schwarz Bayesian criterion (Schwarz, 1978) could not be reduced further. SNPs included in the final model are hereafter referred to as significant SNPs. The total number of significant SNPs included in the final model was recorded. A SNP effect estimate can be interpreted as the allele substitution effect (α) and represents the regression coefficient of the respective SNP in the final model. Note that all significant SNP effect estimates are modelled at the same time in the final model.

Cross-validation

A fivefold cross-validation was run 20 times to increase the robustness of the results. For this, 100 subsets were extracted out of the total phenotypic data. Each subset consisted of 80% randomly chosen HEB lines per family. This set was used as the training set to define significant markers and to estimate their effects, whereas the remaining 20% of lines were used as the validation set. The phenotypes of the validation set lines were predicted based on marker effects estimated in the training set. Prediction ability (R²val) was then calculated as the squared Pearson product–moment correlation between the observed and predicted phenotypes of the validation set, whereas R²train represents the model fit of the training set.

To define QTL regions, we calculated a SNP marker’s detection rate as the number of times, out of 100, it was included in the final model. Robust major QTLs were defined if they were detected more than 20 times in IBD-M × F.

Cumulating SNPs to estimate parent-specific QTL effects

To estimate a parent-specific QTL effect from model ‘IBS-M’ we cumulated significant SNP marker effects. First, a peak marker for each expected parent-specific QTL was selected from model ‘IBD-M × F’ where the number of model inclusions across all 100 cross-validation runs was maximised. Each peak marker was placed central in a 26 cM interval (that resembles the mean introgression size in HEB-25) to look for significant SNPs in this region. Then, ‘IBS-M’ SNP effect estimates of all markers within this interval were cumulated for each of the 25 donors, following 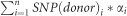, where i iterates through all significant SNPs (n) in the respective QTL interval. SNP (donor)_i represents the quantitative IBS donor genotype (that is, 0 vs 2) of the i-th significant SNP and α_i denotes the SNP effect estimate of this SNP obtained from model ‘IBS-M’. As SNPs show different IBS segregation patterns across the donors of HEB families (Supplementary Table S1), a different cumulated effect was obtained for each donor. This procedure was conducted within each of the 100 cross-validation runs and the mean of them was taken as the final parent-specific QTL effect estimate. For an illustration of the workflow and an example see Supplementary Figure S2.

Finally, we determined cumulation precision that is the correlation of the cumulated parent-specific effects with the effects obtained from model ‘IBD-M × F’. We chose this comparison to check our hypothesis of whether multiple SNPs clustering in specific regions are able to represent parent-specific effects.

To test its general transferability to other multiparental populations, we applied the same approach to a barley MAGIC population comprising 533 doubled haploid lines (Sannemann et al., 2015). We used the above described model ‘IBS-M’ to derive parent-specific QTL effects for flowering time from 4550 biallelic SNP markers. Peak markers were chosen based on minimum P-values and a window of 20 cM was used to cumulate QTL effects on flowering time. We chose this window size, as here LD fell below the population-specific critical value of 0.021 (Breseghello and Sorrells, 2006; Sannemann et al., 2015). We then compared the estimated parent-specific QTL effects with haplotype-based QTL estimates obtained from modelling parental haplotypes with R/mpMap, as presented in Sannemann et al. (2015).

Simulation studies

We performed simulation studies to further check the suitability of the investigated models and the ‘cumulation method’. For this purpose we used our existing real genotype matrices and simulated different QTLs for an artificial trait. We created scenarios that differed in the number of estimated QTLs (1, 3 and 8) and the amount of noise added to the phenotypes to decrease heritability. QTL positions were defined by picking single random SNPs from the IBD genotype matrix throughout the genome. The SNP that was selected for the one QTL scenario was also one of the three SNPs in the three QTL scenario and these three QTLs were part of the eight SNP scenario. The SNP genotypes of the eight simulated QTLs were removed from both genotype matrices and not used in the further analyses. The trait mean was set to 50. Parent-specific allele substitution (α) effects could take defined values (−5, −3, 0, 1 and 2) and were randomly assigned to families (Supplementary Table S2). To add noise to the phenotype data an error term was added that was defined as a normally distributed value (μ=0, σ=1), multiplied by 0 (no noise), 3 (medium noise: noise moderate compared with simulated effect sizes) or 6 (high noise: noise may be bigger than simulated effect sizes). The same training and test sets as described above have been used to scan for significant associations and to estimate prediction abilities. The obtained QTL positions and parent-specific effect estimates were compared with the truly simulated data and the rate of false positives (that is, significant SNPs that did not match the respective QTL interval) and the power to detect QTL precisely (that is, at least one significant marker in a 5 cM interval surrounding the QTL) have been defined for each of the 100 cross-validation runs. In addition, different window sizes (2–40 cM) to cumulate SNP effects in model IBS-M were tested to determine the optimum window for SNP effects to be cumulated. For this purpose, cumulation precision (that is, correlation of cumulated and true parent-specific QTL effects) and the mean difference from the true effect (that is, absolute difference of the cumulated effect and the true parent-specific QTL effect, averaged across parents) have been determined.

Results

QTL detection

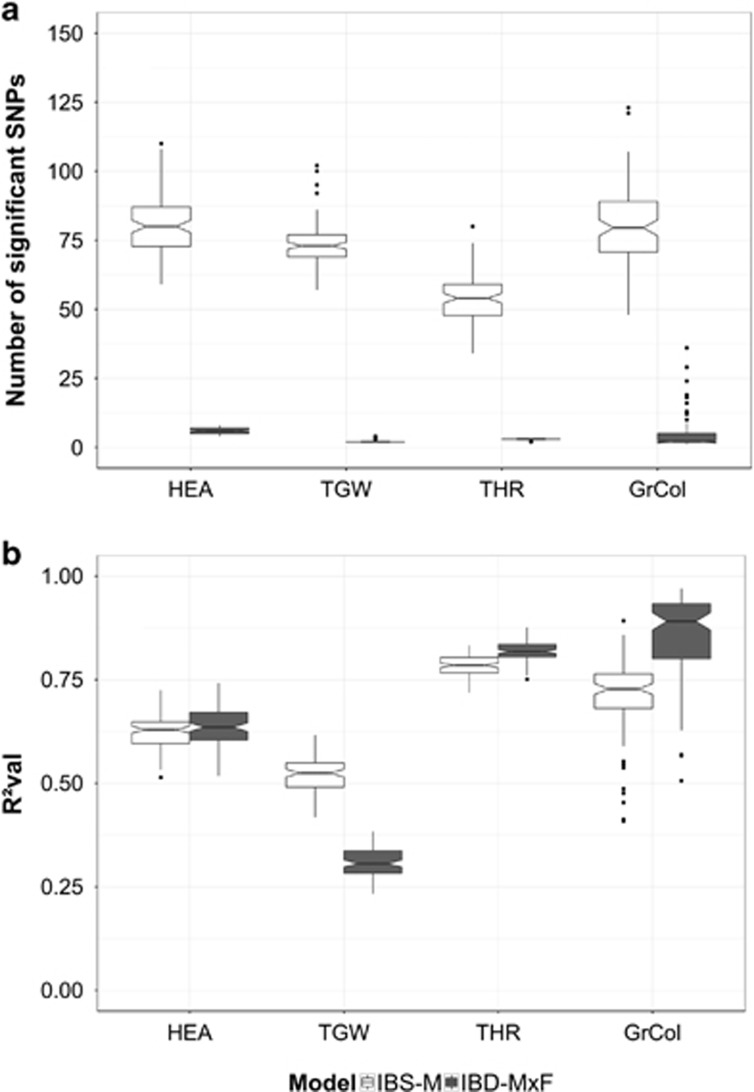
In general, a considerably lower number of significant markers was detected by ‘IBD-M × F’ than by ‘IBS-M’, irrespective of the trait. For instance, on average 80 and 6 significant markers for HEA were detected by model ‘IBS-M’ and model ‘IBD-M × F’, respectively (Figure 1a and Table 1). All significant markers detected by model ‘IBD-M × F’ were also detected by model ‘IBS-M’, irrespective of the trait (Figure 2).

Figure 1.

Variation of number of significant SNPs (a) and variation of prediction ability (R²val) (b) in the barley NAM population. Box plots indicate the distribution across 100 cross-validation runs. Empty and filled boxes represent models ‘IBS-M’ and ‘IBD-M × F’, respectively. Traits are separated by columns.

Table 1. Comparison of mean R ² and mean number of significant SNPs across 100 cross-validation runs, calculated for two models and four traits.

Trait	R2val		R2train		Number of significant SNPs
	'IBS-M'	'IBD-M × F'	'IBS-M'	'IBD-M × F'	'IBS-M'	'IBD-M × F'
HEA	0.62	0.63	0.85	0.76	80	6
TGW	0.52	0.31	0.77	0.40	74	2
THR	0.78	0.82	0.89	0.86	54	3
GrCol	0.71	0.85	0.93	0.95	80	5
Mean	0.66	0.65	0.86	0.74	72	4

Abbreviations: GrCol, grain colour; HEA, heading; IBD, identical by descent; IBS, identical by state; R²train, model fit of the training set; R²val, prediction ability; SNP, single-nucleotide polymorphism; TGW, thousand grain weight; THR, threshability.

Traits studied: HEA, TGW, THR and GrCo; Models applied: only marker main effects based on IBS (‘IBS-M’) and only marker-by-family effects based on IBD genotypes (‘IBD-M × F’). The last row indicates the mean across traits.

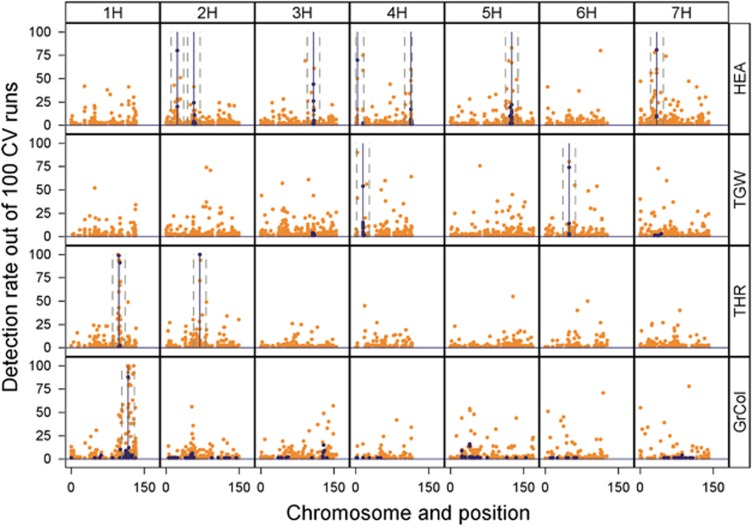
Figure 2.

Comparison of detection rates of significant markers across the genome between models ‘IBS-M’ and ‘IBD-M × F’ in the barley NAM population. Each of the four rows represents a different trait. The height of the peaks indicates the number of significant effects detected per SNP marker out of 100 cross-validation runs, ordered by genetic position according to the map of Maurer et al. (2015). Orange dots represent IBS-M, and blue dots IBD-M × F. Major QTLs detected by IBD-M × F are indicated by vertical lines. Dashed vertical lines indicate the 26 cM window used for cumulation.

Prediction ability

The prediction ability estimates (R²val) of ‘IBS-M’ and ‘IBD-M × F’ were on comparable levels for the traits HEA and THR. Model ‘IBD-M × F’ showed the highest predction abilites for the assumed mono-/oligogenic traits GrCol and THR. However, for TGW, ‘IBS-M’ predicted phenotypes better than ‘IBD-M × F’ (Figure 1b and Table 1). All comparisons of ‘IBS-M’ and ‘IBD-M × F’ were significant at P<0.001 after applying one-way analysis of variance, except for HEA (Supplementary Table S3).

Cumulating SNPs to estimate parent-specific QTL effects

As already mentioned above, model ‘IBS-M’ detected much more significantly associated SNPs than model ‘IBD-M × F’ (Figure 1a and Table 1). In Figure 2, the contrast in detection rate of QTL regions is visualised. The comparison indicates that model ‘IBD-M × F’ detects major QTLs as single associations, whereas numerous significant markers from model ‘IBS-M’ cluster in these major QTL regions. Based on the observed differences, we wondered whether these SNP clusters from model ‘IBS-M’ were able to reflect parent-specific effects obtained from model ‘IBD-M × F’. Therefore, we cumulated SNP effect estimates (taken from model ‘IBS-M’) surrounding the 12 clear QTL peaks obtained from model ‘IBD-M × F’ within a window of 26 cM, representing the mean introgression size in HEB-25 (Supplementary Figure S3).

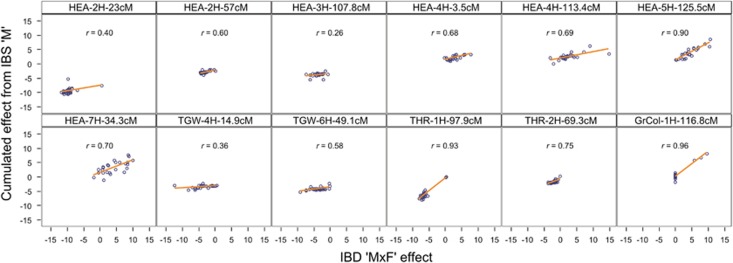
To estimate the cumulation precision as a measure of appropriateness of the method we correlated the averaged cumulated QTL effects with the average IBD-M × F effect estimate for each QTL. Cumulation precision ranged from 0.26 (HEA, 3H-107.8 cM) to 0.96 (GrCol, 1H-116.8 cM) with a mean of 0.65 (Table 2 and Figure 3). In addition, the mean number of significant SNPs per QTL interval was recorded. The mean number ranged from 2.6 (HEA, 3H-107.8 cM) to 24.1 (GrCol, 1H-116.8 cM) and was positively correlated (r=0.69) with the above-mentioned cumulation precision (Table 2).

Table 2. Cumulation precision (r) of major QTLs located in barley NAM and MAGIC populations.

Populationa	Trait	QTL	Cumulation precision (r)b	No. of cumulated SNPsc	CVd
NAM	HEA	2H-23 cM	0.40	4.8	0.25
	HEA	2H-57 cM	0.60	3.2	0.40
	HEA	3H-107.8 cM	0.26	2.6	0.45
	HEA	4H-3.5 cM	0.68	2.7	0.71
	HEA	4H-113.4 cM	0.69	3.9	1.41
	HEA	5H-125.5 cM	0.90	7.7	0.66
	HEA	7H-34.3 cM	0.70	8.1	0.87
	TGW	4H-14.9 cM	0.36	2.8	0.75
	TGW	6H-49.1 cM	0.58	3.6	0.61
	THR	1H-97.9 cM	0.93	10.8	0.32
	THR	2H-69.3 cM	0.75	5.3	0.43
	GrCol	1H-116.8 cM	0.96	24.1	2.85
	Correlation with cumulation precisione			0.69	0.44
MAGIC	FT	QFT.MAGIC.HA-2H.a	0.81	2	6.35
	FT	QFT.MAGIC.HA-3H.a	0.26	1	6.14
	FT	QFT.MAGIC.HA-3H.b	0.51	2	6.51
	FT	QFT.MAGIC.HA-4H.a	0.37	3	3.11
	FT	QFT.MAGIC.HA-5H.a	0.42	2	2.99
	FT	QFT.MAGIC.HA-5H.b	0.89	1	6.82
	FT	QFT.MAGIC.HA-7H.a	0.98	4	6.38
	Correlation with cumulation precision			0.32	0.53

Abbreviations: CV, coefficient of variation; FT, flowering time; GrCol, grain colour; HEA, heading; MAGIC, multiparent advanced generation inter-cross; NAM, nested association mapping; QTL, quantitative trait locus; SNP, single-nucleotide polymorphism; TGW, thousand grain weight; THR, threshability.

^aNAM: barley population HEB-25 (Maurer et al., 2015); MAGIC of barley (Sannemann et al., 2015).

^bCorrelation coefficient of QTL effect, obtained from ‘IBD-M × F’ (NAM) and parental allelic means, obtained from the haplotype approach (MAGIC), respectively, versus QTL effect, estimated by cumulating nearby SNP effects from ‘IBS-M’. Means: 0.67 (NAM); 0.60 (MAGIC).

^cNumber of significant SNPs that were cumulated in an interval surrounding the QTL (NAM: 26 cM, MAGIC: 20 cM). For NAM, the mean across 100 cross-validation runs is shown.

^dCV of all parent-specific QTL effects obtained from model ‘IBD-M × F’ (NAM) and the haplotype approach (MAGIC), respectively.

^ePearson’s correlation coefficient (r) between cumulation precision for NAM and MAGIC population, respectively.

Figure 3.

Scatter plots of the cumulated SNP effects from model ‘IBS-M’ against the M × F effects obtained from model ‘IBD-M × F’ for 12 major QTLs in the barley NAM population. Each dot represents the estimated QTL effect of one exotic HEB donor. A linear regression line (in orange) and Pearson’s correlation coefficients (r), indicating the cumulation precision, are given for each QTL. Axis values represent the absolute difference between exotic and cultivated (that is, Barke) QTL alleles.

When applying the method to a barley MAGIC population to estimate parent-specific QTL effects for flowering time and comparing them with the haplotype-specific QTL effects presented in Sannemann et al. (2015), we observed a mean cumulation precision of 0.60, ranging from 0.26 (QFT.MAGIC.HA-3H.a) to 0.98 (QFT.MAGIC.HA-7H.a, Table 2).

Simulation studies

In a designed simulation study we modelled specific scenarios of possible trait architectures in our NAM population to check the performance of model IBS-M and IBD-M × F and the general suitability of the cumulation method. These scenarios differed for the number of QTLs, the size of QTL effects and the background noise of modelled phenotype values.

Generally, both models detected simulated QTLs with high precision, that is, a significant marker was detected in a 5 cM interval surrounding the true QTL position (Table 3). However, with increasing noise added to the phenotype values, QTL detection was decreased. In particular, model IBD-M × F was not able to detect any QTL if eight QTLs with high background noise were modelled. In contrast, model ‘IBS-M’ could detect all modelled QTL with high precision even at higher background noise. The aforementioned clustering of significant SNPs surrounding the QTLs in model IBS-M was also observed in the simulations (Supplementary Figure S4). The rate of false positive associations that were not part of the respective QTL interval was low for model IBD-M × F, ranging from 0.00 to 0.31, whereas for model IBS-M, rates from 0.46 to 0.83 were obtained (Table 3). Prediction abilities exceeded 0.5 in all scenarios when no noise was added to the phenotypes and decreased with increasing number of simulated QTLs and noise (Table 3). Prediction abilities of model IBD-M × F were higher than those of IBS-M, except when IBD-M × F failed to detect any QTL.

Table 3. Quality parameters of IBS-M and IBD-M × F in different simulation scenarios.

			No noise	Medium noise	High noise
IBS-M	QTL detection powera	1 QTL	1.00	0.48	0.01
		3 QTLs	0.99	0.78	0.37
		8 QTLs	0.91	0.74	0.45
		Mean	0.94	0.72	0.39
	False positivesb	1 QTL	0.63	0.75	0.83
		3 QTLs	0.54	0.57	0.73
		8 QTLs	0.46	0.48	0.55
		Mean	0.55	0.60	0.70
	Prediction abilityc	1 QTL	0.65	0.13	0.03
		3 QTLs	0.64	0.26	0.08
		8 QTLs	0.55	0.28	0.08
		Mean	0.61	0.22	0.07
IBD-M × F	QTL detection power	1 QTL	1.00	1.00	0.07
		3 QTLs	1.00	1.00	0.34
		8 QTLs	1.00	0.96	0.00
		Mean	1.00	0.98	0.09
	False positives	1 QTL	0.31	0.00	0.00
		3 QTLs	0.22	0.00	0.00
		8 QTLs	0.07	0.00	n/a
		Mean	0.20	0.00	0.00
	Prediction ability	1 QTL	0.97	0.35	0.00
		3 QTLs	0.96	0.54	0.13
		8 QTLs	0.95	0.68	0.00
		Mean	0.96	0.52	0.04

Abbreviations: IBD-M × F, identical-by-descent marker-by-family effects; IBS-M, identical-by-state marker main effects; QTL, quantitative trait locus.

All values are averaged across 100 simulated cross-validation runs.

^aQTL detection power is defined as the model’s ability to precisely detect the simulated QTL within a 5 cM window surrounding the true position.

^bFalse positive associations are all detected significant associations that were outside the interval of cumulated single-nucleotide polymorphisms (SNPs; 26 cM) surrounding a QTL.

^cPrediction ability represents the correlation coefficient of predicted phenotypes (based on SNP effects obtained in the training set) and observed phenotypes in the test set.

Applying the cumulation method to estimate parent-specific effects from IBS-M revealed high accordance with the truly estimated effects. Cumulation precision increased with increasing window size of included SNP effects and reached a plateau at ∼22 cM (Supplementary Figure S5). At this position a cumulation precision of 0.94 was obtained if one QTL was simulated and no noise was added. In case of eight simulated QTLs with high noise, a cumulation precision of 0.54 was obtained. The mean difference of cumulated effects and the truly simulated effects decreased with increasing window size. At a window size of 26 cM, a mean difference of 0.6 was obtained if one QTL was simulated and no noise was added.

Discussion

QTL detection

In general, both models reliably detected simulated QTLs with high precision (Table 3 and Supplementary Figure S4). Expectedly, with increasing number of simulated QTLs and increasing noise, QTL detection power was decreased, especially when model IBD-M × F was used. The number of significant markers was higher for ‘IBS-M’ (Table 1, 72 on average in the real data set) than for ‘IBD-M × F’ (4). One reason to explain the higher number of significant SNPs in ‘IBS-M’ is clustering of SNPs in major QTL regions. However, if we look at Figure 2 and Figure S4, we see that additional genomic regions of significant SNPs are present in ‘IBS-M’. On one side, a substantial part of them might be false positive associations, a fact that has also been pointed out in our simulation studies. According to the results obtained therein, up to 83% of associated SNPs were false positives. This is a known issue if the number of available markers exceeds the number of phenotypes to explain, leading to overfitting of the model. However, this problem in defining true associations can be overcome by cross-validation of the results and counting the number of significances across several runs (Valdar et al., 2009; Würschum et al., 2012). If we look at the detection rates across 100 runs, we clearly observe the highest peaks at the positions of true QTLs, both in the real data set (Figure 2) and the simulation studies (Supplementary Figure S4). Besides false positive associations, however, some regions in the real data set might correspond to known QTLs as, for example, the known flowering time gene HvELF3 at 128 cM on 1H (Figure 2). For this locus the weakest effect out of eight major HEA QTLs was observed in Maurer et al. (2015). Most likely, ‘IBD-M × F’ is not able to detect it as smaller subgroups are used for the scan of marker trait associations when only interaction effects are modelled. Similar observations were made by Ogut et al. (2015) in the maize NAM population. The authors observed that for small effect QTL, a joint-family model was able to detect them more reliably than a single-family model. Therefore, model ‘IBD-M × F’ seems to be able to detect predominantly QTLs with strong effects. This makes it suitable to separate useful and valuable major QTLs, explaining a high amount of variance, from minor low-impact QTLs. This finding might be of particular interest for plant breeders.

Prediction abilities

Comparing prediction abilities of the different models enabled us to gain insight into the reliability of estimated QTL effects. We used QTL effects of the training population, which consisted of 80% of randomly chosen lines per family, to predict the phenotypes of the remaining 20% and repeated this procedure 100 times to make it more robust.

It appears that models ‘IBS-M’ and ‘IBD-M × F’ possess a similar power to predict phenotypes of HEA and THR, however there were substantial differences for TGW and GrCol (Table 1). Prediction abilities of polygenic traits like HEA and TGW showed no increase if a parent-specific effect was modelled. Most likely, the reason for this observation is that wild donor-specific QTL effects for HEA are predominantly pointing to the same direction compared with the elite allele of the reference parent Barke (Supplementary Table S4), as a consequence of domestication (Cockram et al., 2011). In particular, it was shown that in the HEB-25 population at the Ppd-H1 gene, which revealed a major impact on HEA by explaining 36% of genotypic variance, 24 out of 25 wild donors carry alleles with almost identical effects (Maurer et al., 2015). Therefore, modelling M × F effects might not be able to substantially improve the model fit. For TGW, we observed a clearly reduced R²val for ‘IBD-M × F’. This might illustrate that with increasing trait complexity and, thus, decreasing heritability, the modelling of parent-specific marker effects impedes detection of relevant QTLs and diminishes reliable effect estimation. This is confirmed by our simulation study where QTL detection power and prediction ability decreased in scenarios with higher trait complexity, represented by more simulated QTLs and higher amount of noise. In contrast, oligo- or monogenic traits like THR and GrCol benefitted from modelling of parent-specific marker effects. This was most prominent for the trait GrCol, a trait that is only segregating in three families (F-06, F-16, F-24) and no more than 46 lines in total are showing the dark-grained phenotype. Under this circumstance, model ‘IBS-M’ was able to reach a prediction ability of 0.71, whereas model ‘IBD-M × F’ reached a prediction ability of 0.85. This outlines the potential to increase prediction ability when parent-specific effects are modelled. Interestingly, although ‘IBS-M’ only assumes marker main effects and no causative SNP for grain colour is available in our marker set, a remarkable prediction ability of 0.71 was observed. This led to the hypothesis that multiple IBS markers can account for parent-specific effects.

Cumulation method enables realistic modelling of parent-specific effects

To check whether linked SNP markers are suited to reflect parent-specific QTL effects, we cumulated SNP effects surrounding the peak marker of each QTL. Thereby, we focussed on strong QTLs that were detected by ‘IBD-M × F’ and compared the estimated M × F effects with the parent-specific effects derived by cumulation of ‘IBS-M’ estimates. We used a window of 26 cM, with the peak marker in its centre, to scan for significant IBS markers. This window size turned out to be reasonable to capture enough SNPs to maximise the prediction ability of parent-specific QTL effects in simulation studies (Supplementary Figure S5). This window size also reflects the mean introgression size in the HEB-25 population. Thus, markers in this window are often inherited together. The idea behind cumulating their effects is that they are estimated at the same time in the final model and each of the corresponding IBS markers segregates in different families. Therefore, if a marker is not segregating in a particular family (that is, genotype score=0=Barke), its effect does not contribute to the cumulated effect (that is, 0 × SNP effect=0), whereas others do (that is, 2 × SNP effect ≠ 0). Consequently, by combining all markers surrounding a QTL, a specific effect for each parent is estimable, based on the combination of differently segregating significant SNPs. This way, we estimated the parent-specific effects for 12 major QTLs.

Giraud et al. (2014) followed a similar approach when comparing QTL effects derived from models assuming ancestral haplotypes with QTL effects gathered from cumulating closely linked single-marker effects. In their case the cumulated effects of two markers already reflected the effect of the respective haplotypes at two different QTLs with high precision.

To estimate how reliable the cumulation of ‘IBS-M’-derived SNP effects is able to predict the parent-specific QTL effect, we correlated the cumulated estimates with the M × F effect obtained from model ‘IBD-M × F’. We chose this comparison as these M × F effect estimates are very robust and presumably give the best insight into the true parent effect. We observed high positive correlation coefficients for most of the QTLs, ranging from 0.26 (HEA, 3H-107.8 cM) to 0.96 (GrCol, 1H-116.8 cM) with a mean of 0.65 (Figure 3). This shows that cumulating SNP main effects within a QTL region is suitable to estimate a parent-specific effect. Especially for oligo- or monogenic traits (THR, GrCol), we observed extremely high cumulation precision, indicating that the method is of special appropriateness if background noise from other QTLs is low.

The presence of parent-specific QTL effects in HEB-25 was first indicated in Maurer et al. (2015), where resequencing of Ppd-H1 clearly revealed the presence of different haplotypes and consequential parent-specific effects. This resulted in one specific haplotype, originating from HEB family F-24, that showed no difference in HEA as compared with the Barke haplotype. In our study, this could also be observed when looking at the ‘IBD-M × F’ estimate of this QTL for F-24. However, the method of cumulating SNP effect estimates from model ‘IBS-M’ failed to detect this fact. We raised the question of why in this obvious case the method seems to fail. One reason could be that in this QTL region there are no F-24-specific SNPs available that could account for the allelic effect. However, in close proximity to the Ppd-H1 gene (BK_12-BK_16, 23.0 cM), there are three tightly linked SNPs available that solely segregate in F-24 (BOPA1_5880_2547 at 23.2 cM, SCRI_RS_182270 at 24.9 cM and SCRI_RS_115892 at 25.4 cM). When checking their linkage in more detail we recognised that there is recombination between them and Ppd-H1 in seven cases, whereas only in four cases they are inherited together (Additional File S1). Estimating a compensating effect for one of these SNPs that could fine-tune the Ppd-H1 effect will therefore not work. Thus, the GWAS procedure is not able to take any of the F-24-specific SNPs into account to optimise the model. We ran ‘IBS-M’ again on the whole data set and excluded those seven lines that showed recombination. As expected, BOPA1_5880_2547 now became significant and, consequently, the cumulation method allowed obtaining a more realistic parent-specific effect estimate (Supplementary Table S5).

In addition, for other flowering QTLs, which were described in HEB-25, we could corroborate the presence of parent-specific effects. For instance, the three vernalisation genes Vrn-H1, Vrn-H2 and Vrn-H3 were supposed to show a parent-specific effect pattern (Maurer et al., 2015, 2016). In this study, we were also able to estimate the parent-specific effects of these QTLs by cumulating SNP effects. We could show that there is plenty of diversification for these vernalisation loci available, depending on the origin of the respective donor. For instance, we observed extremely different parent-specific HEA effects of +8.5 days in F-09 and +1.3 days in family F-19 at Vrn-H1 locus (Supplementary Table S4).

As we do not know the true QTL effects in our real data set, the correlation of the cumulated effects with the IBD-M × F effects might not really represent an adequate measure of appropriateness of the method. Therefore, we also applied the cumulation method to the simulated data set, where we determined exact parent-specific effects. As a result we obtained a high cumulation precision of 0.94 for the case where one QTL was simulated and no noise was modelled (Supplementary Figure S5). Even for eight simulated QTLs with high noise, a cumulation precision of 0.54 was obtained. At the same time, the mean difference of the cumulated effect and the truly simulated parent-specific effects was low (0.6), indicating the appropriateness of the method. This is in particular remarkable as the simulated parent-specific QTL effects were randomly assigned to donors, that is, closely related donors could have opposing effects and vice versa.

Applying the cumulation method to a barley MAGIC population

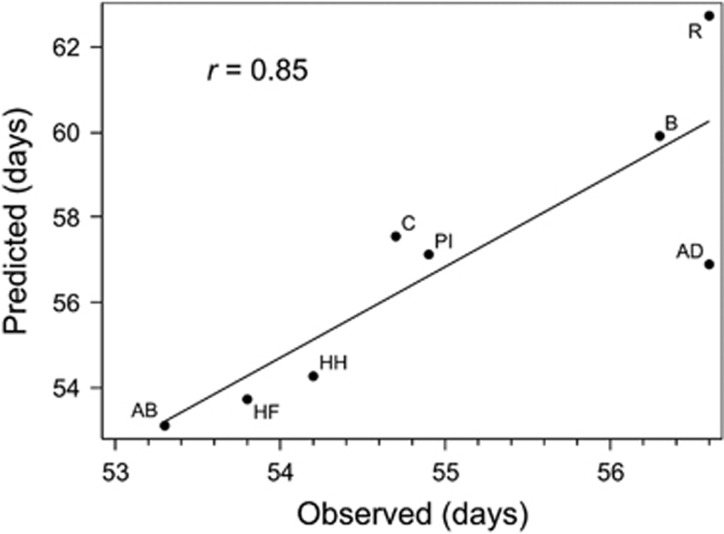
Besides the general suitability of the cumulation method in a NAM population, we checked whether this also works for MAGIC populations. Therefore, we took raw data on flowering time from an eight-way barley MAGIC population (Sannemann et al., 2015) and applied model ‘IBS-M’. Compared with both GWAS approaches presented in Sannemann et al. (2015), model ‘IBS-M’ detected more QTLs, while keeping all QTLs detected before (Supplementary Table S6). Furthermore, total R² increased to 74.8%. When using the effect estimates of all significant SNPs to predict the phenotypes of the eight parents, we obtained high accordance (r=0.85, Figure 4 and Supplementary Table S6), indicating the model’s general suitability. Then, we applied the cumulation method and compared our estimates with the estimates obtained from the haplotype approach, published in Sannemann et al. (2015), that is based on founder haplotype probabilities calculated with R/mpMap (Huang and George, 2011). On average, we observed a correlation of 0.60 between our estimates and those obtained from the haplotype approach (Table 2). For QFT.MAGIC.HA-7H.a, which explains 28.5% of the variance for heading in the MAGIC population, we reached a correlation of 0.98. By using our method it was also possible to estimate a QTL effect for the MAGIC parent ‘Pflugs Intensiv’/‘Criewener 403’, where the haplotype approach used in Sannemann et al. (2015) failed. The given results demonstrate the potential of applying our cumulation method to MAGIC populations to estimate parent-specific QTL effects without the need of haplotype or IBD information.

Figure 4.

Correlation of observed and predicted flowering time of the eight MAGIC founders. Observed phenotypes are presented in Sannemann et al. (2015), and predicted phenotypes are based on the effect estimates of all significant SNPs obtained in model ‘IBS-M’. Founder lines are abbreviated: AB, Ack. Bavaria; AD, Ack. Danubia; B, Barke; C, Criewener 403; HF, Heils Franken; HH, Heines Hanna; PI, Pflugs Intensiv; R, Ragusa.

Prerequisites and characteristics of the cumulation method

The method’s success depends on two major prerequisites. First, map positions of all investigated markers must be known. The more accurate the map is, the higher is the chance to differentiate effects reliably. Second, there must be LD present in the population. The fact that SNPs are inherited together because of genetic linkage enables merging these SNP effects to define a parent-specific effect. LD in a multiparental population can be seen as a function of the LD that is present among the parents and the specific population design. In the NAM population HEB-25, there is low LD present among the parents (Maurer et al., 2015) and F1 plants were backcrossed to the recurrent parent Barke. Because of reduced recombination after backcrossing, the introgressed wild barley segments are relatively large, allowing many SNPs to be included in a QTL-surrounding window. However, with an increasing number of differentially segregating SNPs we expect that a smaller window may be sufficient for cumulation of QTL effects.

Using model ‘IBS-M’ and deriving the parent-specific effect estimate out of it instead of modelling IBD or haplotype effects has several benefits that should be highlighted. (1) More QTLs are detectable compared with a model containing only M × F effects modelled as IBD. This is easily visible in Figure 2 and Supplementary Figure S4, where we see multiple additional SNP peaks for model ‘IBS-M’ compared with model ‘IBD-M × F’. This is most likely because of the fact that in ‘IBD-M × F’ smaller subgroups are used for the scan of marker trait associations that impede detection of minor QTLs. (2) The grouping of SNP effects is not restricted to 25 families as in models assuming a M × F effect in a NAM population. Because of the different segregation patterns of SNPs, much more information can be gathered by specific combinations of these SNPs. This results in the definition of phenotypic clusters rather than parent-specific haplotypes. Especially, if IBD cannot clearly be derived from pedigree information, as it is for instance the case in MAGIC populations, this method represents an excellent way to model allelic effects originating from different parents independent of IBD information. (3) Haplotypes are not defined a priori based on SNP profiles of parental lines like, for example, in clusthaplo (Leroux et al., 2014) or R/mpMap (Huang and George, 2011). Instead, our method represents a more functional approach that is not solely based on ancestral relationships. This enables to track down beneficial genetic variation in a more practical manner.

Besides the above-mentioned beneficial aspects, there are also some limitations that one has to take into account when applying the cumulation method. First, the method is not able to separate effects from tightly linked QTLs, at least not within the selected genetic interval of SNPs being cumulated. Another fact is that the method’s success seems to decrease with increasing trait complexity. Strong QTLs with ample allelic variation are still reliably represented by the cumulation method, but one has to be cautious in interpreting parent-specific effects defined for minor QTLs. Furthermore, the effects estimated by the cumulation method are in general less extreme and show lower variation across parents than IBD-based methods do. Another critical point is the high number of false positive associations detected by the model. Probably, they cause the low prediction ability of IBS-M when background noise increased. However, the parent-specific effects obtained via the cumulation method nevertheless turned out to be clearly correlated to the true QTL effects in the simulations. Therefore, we strongly recommend running several cross-validation runs to identify the most reliable QTL positions before cumulation.

To sum up, the comparison of a family-based method (IBD-M × F) with a method assuming general SNP effects (IBS-M) revealed a slight advantage in prediction ability of IBD-M × F, especially for highly heritable traits. However, IBS-M turned out to be superior for traits with lower heritabilities. The idea of cumulating genetically linked SNP effects from model ‘IBS-M’ provided a novel approach to reconstruct parent-specific QTL effects. This method proved to be applicable to NAM and MAGIC types of multiparental populations even if no IBD information is available. At present, there seems to be the tendency that both haplotype-based linkage models and single-marker association models should be used in a complementary way for QTL detection in multiparental populations (Lorenz et al., 2010; Kump et al., 2011; Tian et al., 2011; Bardol et al., 2013). Our method represents an intermediate path, combining a high QTL detection rate with the possibility to predict parental QTL effects under a reduced computational load. In future, we assume that the cumulation method will benefit from a massive increase in available SNP genotype data that can enhance the precision of this method, for instance by utilising SNP information from exome capture sequencing (Mascher et al., 2013) or increased sizes of SNP chips.

Data archiving

All relevant data are available as supplementary files at Heredity’s website or are taken from published articles (Maurer et al., 2015; Sannemann et al., 2015). Additional files containing genotype and phenotype data used as input as well as the obtained GWAS results are available from the Dryad Digital Repository http://dx.doi.org/10.5061/dryad.36rm1.