Evidence of Disorder in Biological Molecules from Single Molecule Pulling Experiments

Abstract

Heterogeneity in biological molecules, resulting in molecule-to-molecule variations in their dynamics and function, is an emerging theme. To elucidate the consequences of heterogeneous behavior at the single molecule level, we propose an exactly solvable model in which the unfolding rate due to mechanical force depends parametrically on an auxiliary variable representing an entropy barrier arising from fluctuations in internal dynamics. When the rate of fluctuations—a measure of dynamical disorder—is comparable to or smaller than the rate of force-induced unbinding, we show that there are two experimentally observable consequences: nonexponential survival probability at constant force, and a heavy-tailed rupture force distribution at constant loading rate. By fitting our analytical expressions to data from single molecule pulling experiments on proteins and DNA, we quantify the extent of disorder. We show that only by analyzing data over a wide range of forces and loading rates can the role of disorder due to internal dynamics be quantitatively assessed.

Complex systems, characterized by processes that occur over a wide spectrum of time and length scales, often exhibit heterogeneous behavior. Spin glasses with quenched randomness [1] and structural glasses in which randomness is self-generated [2,3] are two classic examples where heterogeneity is indicated by the violation of the law of large numbers [4]. These systems exhibit sub-sample to sub-sample variations in measurable quantities. For biological systems, it is increasingly becoming appreciated that there are cell-to-cell variations (on length scales ∼μm) [5–7] as well as molecule-to-molecule variations (∼nm scales). Manifestation of heterogeneous behavior on the μm length scale is easier to fathom than on the molecular scale. In a pioneering study, evidence for disorder in enzymes was presented using single molecule experiments [8]. Two recent studies [9,10] have further established that on the nm scale biological molecules display heterogeneity and broken ergodicity just as found in cells [11] and glasses [12]. Time traces generated using single molecule fluorescence energy transfer experiments on the Holliday junction, a mobile junction of four DNA strands involved in exchange of genetic information, showed that the conformational space is partitioned into disjoint basins of attraction [9]. Interconversions between the basins do not occur on long time scales unless the system is annealed by first reducing the concentration of Mg²⁺ ions for a period of time, and then increasing Mg²⁺. More recently, it has been demonstrated that the speed of the DNA unwinding motor RecBCD varies from one molecule to another. Persistent heterogeneity in speed can be “reset” by an annealing protocol, which involves depleting and then reintroducing Mg²⁺-ATP to the enzyme [10]. Both these experiments on unrelated systems show that there must be intrinsic disorder between chemically identical molecules.

If the dynamical variations from molecule to molecule in the Holliday junction and RecBCD helicase are due to disorder, then it should be possible to discern the consequences in single molecule pulling experiments, which probe the response of proteins and nucleic acids to mechanical force. Previously, such experiments have been particularly useful in directly measuring some features of the folding landscape [13–16] of biological molecules that are difficult to access by other methods. Here, we show two signatures of molecular disorder: deviations from exponential kinetics in force-induced unfolding of proteins [15,16], and the presence of fat tails in the distribution of rupture forces, P(f), characterizing the unzipping of DNA [17]. These features cannot be explained using standard theories, which involve crossing a one-dimensional free energy barrier in the presence of force. Instead, we propose a generic mechanism, based on a model coupling molecular disorder and function. As an illustration, consider the unbinding (or binding) kinetics of a ligand from a receptor molecule, where the dynamics depends on the time-varying conformation of the receptor (open or closed) [18]. The ligand is more tightly bound in the closed than in the open conformation. Depending on the gating rate λ (the frequency of transitions between the conformations) the ligand is expected to exhibit very different unbinding kinetics. If k is the mean rate of unbinding, and k/λ ≫ 1 or k/λ ≪ 1, the environment appears static to the ligand [18,19]. The ligand experiences either quenched disorder (k/λ ≫ 1), unbinding via parallel paths over a spectrum of multiple barriers, or annealed disorder (k/λ ≪ 1), unbinding via a single path over a rapidly averaging barrier. If $k/\lambda \sim \mathcal{O}(1)$, the gating produces a fluctuating environment along the dynamic pathway of the ligand and affects the unbinding process in a nontrivial fashion. This regime is often termed dynamic disorder [18,19]. The gating mechanism has been extensively studied in both experiments and theories in the context of oxygen binding to myoglobin [18,20,21]. The presence of dynamical disorder in the oxygen-myoglobin system results in a power-law decay of unreacted oxygen and a fractional order dependence of binding rate constant on solvent viscosity [20]. To account for the origin of this phenomenon, Zwanzig proposed a fluctuating bottleneck (FB) model [18], which considers a rate process controlled by passage through a bottleneck whose cross-sectional area, responsible for the reactivity, undergoes stochastic fluctuations.

While the frequency λ governing the internal dynamics, which is intrinsic to a molecule, can, in principle, be varied to a certain extent by changing viscosity [20], the unbinding rate k can be more easily altered by changing force f or the corresponding most probable force f^* under the constant loading rate condition in single-molecule pulling experiments, thus providing a way to infer dynamic disorder. Here, we adopt Zwanzig’s FB concept as a general mechanism for probing the internal disorder in biological molecules, with explicit experimental consequences. By fitting our analytical expressions to single-molecule force data, we extract a measure of dynamic disorder in proteins and DNA.

To model the effect of mechanical force on the dynamics of crossing a free energy barrier in the presence of molecular gating, we modified Zwanzig’s FB model [18] using an effective potential U_eff(x; r) = U (x; r) − fx that depends parametrically on r, the auxiliary variable characterizing the internal dynamics, and explicitly on the molecular extension x conjugate to the applied force, f [22]. The FB model is governed by two Langevin equations of motion:

$$\zeta {\partial }_{t}x=-{\partial }_x{U}_{\mathrm{eff}}(x;r)+F_x(t),{\partial }_{t}r=-\lambda r+F_r(t),$$ (1)

where ζ is the friction coefficient along x. The precise functional form of U (x; r) is arbitrary except it should have a local minimum corresponding to a bound (folded) state at x = x_b, separated by a free energy barrier at x = x_ts > x_b from the unbound (unfolded) ensemble at large x. The variable r is the dimensionless bottleneck radius, imposed with a reflecting boundary condition at r = 0 to satisfy r ≥ 0 [18]. Both the noise-related random force F_x(t) along x and F_r(t), the stochastic fluctuation of r, satisfy the fluctuation-dissipation theorem: 〈F_x(t) F_x(t^′)〉⁼ 2ζk_BTδ(t − t^′) and 〈F_r(t) F_r(t^′)〉⁼ 2λθδ (t − t^′), with k_BT being the thermal energy and 〈r²〉 ≡ θ. Forced unbinding occurs on first passage from x_b to x_ts, with a rate K (f, r) that in general varies with both f and r. In traditional models of barrier crossing, there is no coupling between reaction dynamics in x and other degrees of freedom, so K only depends on f. For example, in the Bell approximation $K(f)\propto e^{f\mathrm{\Delta }{x}^{‡}/k_{B}T}$, where Δx^‡ = x_ts − x_b. In the FB model, the coupling to r is incorporated by making the reaction sink proportional to the area of the bottleneck, K(f, r) ≡ k(f)r². The form of K (f, r) is physical for the applications here because the rate of unfolding of proteins or unzipping of DNA should increase as the solvent accessible area (∝ r²) increases. For simplicity, we assume the force dependence is described by the Bell approximation, $K(f)=k_0{e}^{f\mathrm{\Delta }{x}^{‡}/k_{B}T}$, though the calculations below can be generalized to more complicated models where k(f) reflects movement of the transition state under force [22,23]. The Langevin equations in Eq. (1) can be translated into the following Smoluchowski equation (see Supplemental Material [24] for details):

$${\partial }_t\overline{C}(r,t)=[{ℒ}_r(r)-k(f)r^2]\overline{C}(r,t),$$ (2)

where $\overline{C}(r,t)$ is the mean probability of finding the system still bound (x < x_ts) with bottleneck value r at time t, and ${ℒ}_r(r)=\lambda \theta {\partial }_r({\partial }_r+r/\theta )$ [18,22]. Depending on whether f is constant or is a linearly varying quantity with time, i.e., f(t) = γt, our problem is classified into unbinding under force-clamp or force-ramp conditions, respectively.

Force clamp

For a constant f, Eq. (2) for $\overline{C}(r,t)$ solved analytically with a reflecting boundary condition at r = 0, and an initial condition $\overline{C}(r,0)=\sqrt{(2/\pi \theta )}{e}^{-r^2/2\theta }$ with r ≥ 0. The resulting survival probability ${\displaystyle {\sum }_{\lambda }^f(t)={\displaystyle {\int }_0^{\infty }dr\overline{C}}(r,t)}$ is an extension of the result by Zwanzig [18] in the presence of force, f [22]:

$${{\displaystyle {\sum }_{\lambda }^f(t)=e^{-(\lambda /2)(s(f)-1)t}\left[\frac{{(S(f)+1)}^2-{(S(f)-1)}^{2}E}{4S(f)}\right]}}^{-1/2},$$ (3)

where S(f) ≡ (1 + (4k(f)θ/λ))^1/2 and E ≡ e^−2λS(f)^t. In two asymptotic limits of λ, the expression for ${\displaystyle {\sum }_{\lambda }^f(t)}$ becomes simple. (i) For4k(f)θ/λ ≪ 1,wehaveS ≈ 1 and the survival probability decays exponentially, ${\displaystyle {\sum }_{\lambda }^f(t)}=\exp [-k(f)\theta t]$, with k(f)θ acting as an effective rate constant. (ii) For 4k(f)θ/λ ≫ 1, we get S ≫ 1 and the survival probability exhibits a power-law decay, ${\displaystyle {\sum }_{\lambda }^f(t)}={[1+2k(f)\theta t]}^{-1/2}$ at short times t ≪ [k(f)θλ]^−1/2, changing over into an exponential decay with rate k(f)θ at long times t ≫ [k(f)θλ]^−1/2. In the limit of quenched disorder, as λ → 0, the power-law decay extends to all times.

Using the Bell force dependence for k(f) in Eq. (3), we find S = (1 + e^Λ(f))^1/2, where Λ(f) = (Δx^‡/k_BT) ×(f − f_cr) with f_cr = (k_BT/Δx^‡) log (λ/4k₀θ). Two limiting conditions arise: (i) For λ ≫ 4k₀θ, Λ(f) changes sign from negative to positive at f = f_cr. Therefore, as f is increased, a crossover occurs from an exponential kinetics with S ≈ 1 (f < f_cr) to a power-law kinetics with S ≫ 1 (f > f_cr). (ii) For λ ≪ 4k₀θ, Λ(f) ≫ 1 and S ≫ 1; hence, the power-law behavior persists at all f.

Force ramp

In constant loading rate experiments, where the external force f = γt is ramped at a fixed rate γ, k(f) in Eq. (2) is time dependent, i.e., $k(f)=k[f(t)]=k_0{e}^{\stackrel{\sim }{\gamma }t}$, where $\stackrel{\sim }{\gamma }=\gamma \mathrm{\Delta }{x}^{‡}/k_{B}T$. Thus, $\overline{C}(r,t)$ satisfies a Smoluchowski equation with a time-dependent sink, $\mathcal{S}(r,t)=k_0{r}^2{e}^{\stackrel{\sim }{\gamma }t}$, with an initial condition $\overline{C}(r,0)=\sqrt{2/\pi \theta }{e}^{-r^2/2\theta }$, and a reflecting boundary condition ${\partial }_r\overline{C}(0,t)=0$. The survival probability at time t in this case can be analytically computed (see the Supplemental Material [24] for details of derivation), leading to the result

$${{\displaystyle {\sum }_{\lambda }^{\gamma }(t)=\sqrt{2}{e}^{\frac{\lambda t}{2}}\left[\frac{ℐ(\rho )}{ℐ({\rho }_0)}\right]}}^{-1/2}{\left[1+\kappa (t)\frac{{ℐ}^{\prime }(\rho )}{ℐ(\rho )}\right]}^{-1/2},$$ (4)

where ρ ≡ βκ(t), $\beta \equiv 2\lambda /\stackrel{\sim }{\gamma }$, $\kappa (t)\equiv \sqrt{(4k_0\theta /\lambda }{e}^{t\stackrel{\sim }{\gamma }/2}$, ρ₀ ≡ ρ(0), and $ℐ(\rho )\equiv ({ℐ}_{\beta }^{\prime }({\rho }_0){\mathcal{Q}}_{\beta }(\rho )-{\mathcal{Q}}_{\beta }^{\prime }({\rho }_0){ℐ}_{\beta }(\rho ))-{[\kappa (0)]}^{-1}[I_{\beta }({\rho }_0){\mathcal{Q}}_{\beta }(\rho )-{\mathcal{Q}}_{\beta }({\rho }_0)I_{\beta }(\rho )]$. Here, I_β(ρ) is a modified Bessel function of the first kind, ${\mathcal{Q}}_{\beta }(\rho )=I_{-\beta }(\rho )$ when β is not an integer, and ${\mathcal{Q}}_{\beta }(\rho )=K_{\beta }(\rho )$, when β is an integer, where K_β(ρ) is a modified Bessel function of the second kind. An analytical, but rather complicated expression for the rupture force distribution $P_{\lambda }^{\gamma }(f)$ is obtained from $P_{\lambda }^{\gamma }(f)=-{\gamma }^{-1}d{\displaystyle {\sum }_{\lambda }^{\gamma }(t)/dt}$ (see [24]). As will be discussed below, the distributions $P_{\lambda }^{\gamma }(f)$ for finite λ exhibit fat tails at large f, a consequence of disorder. By fitting the theoretical expression for $P_{\lambda }^{\gamma }(f)$ (Eq. S19 in [24]) to measured force distribution data, one should be able to quantify the extent of disorder in terms of λ.

In the two limits of λ → ∞ and 0, one can obtain explicit expressions for the most probable rupture force f* as a function of $\stackrel{\sim }{\gamma }$: for λ → ∞, $f^{\ast }=(k_{B}T/\mathrm{\Delta }{x}^{‡})\log [\stackrel{\sim }{\gamma }/k_0\theta ]$, while for λ → 0, $f^{\ast }=(k_{B}T/\mathrm{\Delta }{x}^{‡})\log \{(\stackrel{\sim }{\gamma }/k_0\theta )\times (1-2k_0\theta /\stackrel{\sim }{\gamma })\}$ (see [24]). The latter equation is valid when $\stackrel{\sim }{\gamma }\ge 3k_0\theta$. For λ → 0 and $0<\stackrel{\sim }{\gamma }<3k_0\theta$, $P_{\lambda }^{\gamma }(f)$ is peaked at f = 0. The presence of finite probability at f = 0 is due to unfolding through spontaneous transitions [25]. The difference in f* between the two asymptotic limits of λ is maximized when $\stackrel{\sim }{\gamma }=3k_0\theta$ (illustrated in Fig. S1E using synthetic data), but disappears for sufficiently high loading rates, $\stackrel{\sim }{\gamma }\gg 2k_0\theta$. In conventional dynamic force spectroscopy (DFS) theory, f* is linear in log γ. However, a positive curvature often develops when the force response of the molecule is ductile and, hence, the transition state location moves towards the bound state [22,26,27]. We predict that if a system has disorder, negative curvature should be discernible at low loading rates in the f* versus log γ plot especially for f* ≈ 0 when disorder is quenched, i.e., λ → 0 (see Fig. S1E [24]). Besides fitting $P_{\lambda }^{\gamma }(f)$ to force distribution data, a careful investigation of f* vs log γ plots at small γ could be useful to capture the fingerprints of dynamical disorder.

We use our theory, derived from a single model, to analyze two representative sets of force data, one from a force-clamp and one from a force-ramp experiment.

Polyubiquitin stretching

The first is polyubiqutin stretched at constant f in AFM, where the survival probabilities Σ^f(t), obtained from dwell time analysis, exhibited nonexponential decay [15,16]. The experimental data were further interpreted using a Gaussian distribution for free energy barriers and transition state locations separating the folded and unfolded states of ubiquitin [16]. We find that the physics of the measured nonexponential decay can be quanitatively explained using our theory [Eq. (3)] based on the FB model. The almost exact fit of the theory to experiment for ${\displaystyle {\sum }_{\lambda }^f(t)}$ at f = 110 pN in Fig. 1(a) shows the presence of dynamical disorder.

FIG. 1.

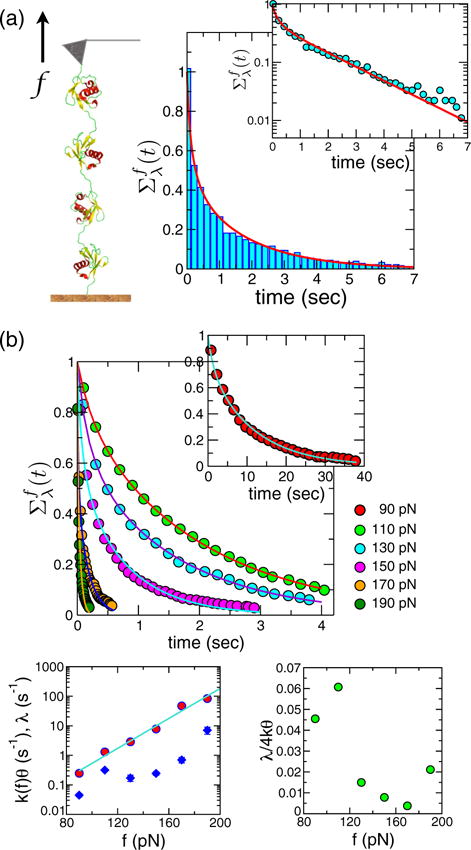
(color online). Interpretation of polyubiquitin data at constant force using the FB model. (a) Survival probability constructed from dwell time analysis of polyubiquitin data in a force clamp at f = 110 pN (digitized from Fig. 1 in Ref. [16]). The line is the fit using Eq. (3). The inset shows Σ^f(t) using a logarithmic scale. (b) (top) Solid lines show our theoretical fits to the survival probability data (colored circles obtained by digitizing the results in Fig. 2 in Ref. [16]) at different values of the force f = 90–190 pN. The extracted parameters k(f)θ (red circles), λ (blue diamonds), and their ratio λ/4k₀θ are plotted against f on the two panels at the bottom.

For polyproteins (used in AFM experiments) there are two possible origins for disorder: (i) couplings between neighboring modules and (ii) disorder inherent to each module. Because a simple statistical relationship such as binomial factorization associated with the kinetics of individual modules [28] is expected to break down for the scenario (i), experiments that change the number of modules can discriminate between the two scenarios. Regardless of the origin of heterogeneity, our theory can be used to extract the parameters characterizing disorder effects.

If the bottleneck represents molecular gating or breathing dynamics in a multimodular construct of polyubiquitin, λ should, in principle, be an increasing function of f. As the applied tension increases, the amplitude of transverse fluctuations decreases, hence, increasing the corresponding frequency. Even in the Bell model, the extracted parameters Δx^‡ and k₀ should be interpreted as capturing the geometry of the landscape, which changes with f [22,26]. From the fits of Σ(t) at different values of force we extracted k(f)θ and λ at each f [bottom of Fig. 1(b)]. The effective rate constant k(f)θ changes exponentially with f, in accord with the Bell model. By using log k(f)θ = log k₀θ + (Δx^‡/k_BT)f we obtain Δx^‡ = 0.24 nm and k₀θ = 0.13 s⁻¹. The value of Δx^‡ is in excellent agreement with experimental measurements [16]. Interestingly, we also find a rough exponentially increasing trend in λ with f. The increase of λ implies that the rate of change of the accessible surface increases as f increases, supporting our physical intuition about the influence of f on the internal dynamics. A nonexponential Σ^f(t) in the force-clamp condition corresponds to a heavy tailed P(f) in the force-ramp condition. The parameters determined for polyubiquitin satisfy λ/4k₀θ ≪ 1 for all f values [Fig. 1 (b)]. Therefore, a heavy tailed P(f) will manifest itself over the entire range of $r_f(=(k_0\theta k_{B}T/\mathrm{\Delta }{x}^{‡})e^{f^{\ast }\mathrm{\Delta }{x}^{‡}/k_{B}T})\approx 230-2.4\times {10}^5$ that gives rise to the most probable forces f* = 80 – 200 pN.

Unbinding of DNA duplexes

The effects of disorder manifest themselves dramatically in unzipping experiments on DNA duplexes between 5′–GGCTCCCTTCTACCACTGACATCGCAACGG–3′ and 3′ – TAGCGTTGCC – 5′, where underlined sequences are complimentary to each other [17]. The measured rupture force distributions have heavy tails at high f, though the physical reasons for the tails were not discussed in the original paper. Figure 2 shows the unzipping force distribution at two pulling speeds, 8 nm/s and 1600 nm/s, and fits using our model, compared to two other models commonly employed in analyzing DFS experiments. It is clear that our theory for $P_{\lambda }^{\gamma }(f)$ using the FB model most accurately fits the force data. Two other models, based on the Bell model [29] and a cubic potential [23], fail to capture the tail part of the data because they incorporate no disorder, only unbinding through a one-dimensional free energy profile. For 8 nm/s, the gating frequencies are almost zero (λ ≈ 2.8 × 10⁻⁵ s⁻¹). However, λ increases by nearly 4 orders of magnitude to λ = 0.48 s⁻¹ at v = 1600 nm/s. Given that the bubble dynamics of a DNA duplex occur with a characteristic time scale of ~50 μs [30], our extracted λ values are too small for the breathing motion of base pairs to be a source of disorder. It is more reasonable to surmise that each duplex is pulled from starkly different and very slowly interconverting conformations, similar to that found in Holliday junctions and RecBCD. The origin of this disorder is likely to be in the heterogeneity of base pairings, although the experiment was intended to probe the unbinding dynamics from a homogeneous sample made of two DNA strands with perfect complimentarity. The large increase in λ as v increases suggests that tension facilitates interconversion between states, which accords well with the expectation that force lowers barriers between distinct bound states.

FIG. 2.

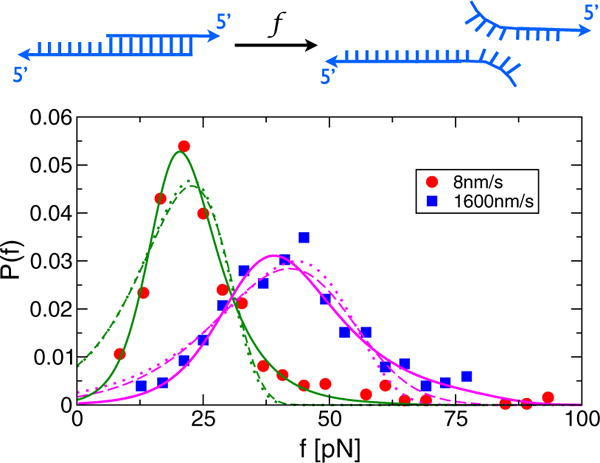
(color online). Analysis of rupture force distributions from a DNA unzipping force spectroscopy experiment (the AFM cantilever spring constant ≈2 pN/nm) [17] using three different models. The fits using $P_{\lambda }^{\gamma }(f)$ (solid lines), based on our FB model, yield (Δx^‡[nm], k₀θ[s⁻¹],λ[s⁻¹]) = (1.1;0.017;2.8×10⁻⁵) for v = 8 nm/s and (0.66, 0.99, 0.48) for v = 1600 nm/s. The fits using P_cubic [ε(f)] = (k(ε)/γ) exp [(k₀/γΔ x^‡) × (1 − (k(ε)/k₀)ε⁻¹⁼²)] (dashed lines) with $k(\epsilon )=k_0{\epsilon }^{1/2}{e}^{\mathrm{\Delta }{G}^{‡(1-{\epsilon }^{3/2})}}$ and ε(f) = 1–2f Δx^‡/3ΔG^‡ [23] yield (Δ x^‡[nm]; k₀[s⁻¹]; ΔG^‡[pN·nm]) = (0.12;0.12;31.9) for v = 8 nm/s and (0.09,7.16,19.0) for v = 1600 nm/s. The fits using $P_{\text{Bell}}(f)={\gamma }^{-1}{k}_0{e}^{f\mathrm{\Delta }{x}^{‡}/k_{B}T}\times \exp (-{\gamma }^{-1}{k}_0{k}_{B}T/\mathrm{\Delta }{x}^{‡}\times (e^{f\mathrm{\Delta }{x}^{‡}/k_{B}T}-1))$ (dotted lines) yield (Δx^‡ [nm]; k₀[s⁻¹]) = (0.49; 0.13) for v = 8 nm=s and (0.32, 8.19) for v = 1600 nm=s. Note that P_λ(f) describes the heavy tails of the distributions better than P_cubic(f) or P_Bell(f), implying that unbinding of these DNA duplexes by force cannot be accounted for using one-dimensional models.

Applications of our theory reveal that by analyzing data from single-molecule pulling experiments over a range of forces, loading rates, and temperatures [31] one can infer the role that dynamical disorder, intrinsic to the molecule, plays in unfolding or unbinding kinetics. The observed nonexponential kinetics in survival probability or fat tails in the unfolding force distributions cannot be captured by theories based on one-dimensional free energy profiles. Our work shows that by using an auxiliary coordinate in addition to extension [32] we can quantitatively predict the consequences of disorder in the dynamics of biological molecules. The theory provides a conceptual framework for analyzing future single molecule pulling experiments on complexes involving proteins, DNA, and RNA in which heterogeneity is sure to play a prominent role.