Inositol trisphosphate receptor and ion channel models based on single-channel data

Abstract

The inositol trisphosphate receptor (IPR) plays an important role in controlling the dynamics of intracellular ${\text{Ca}}^{2+}$. Single-channel patch-clamp recordings are a typical way to study these receptors as well as other ion channels. Methods for analyzing and using this type of data have been developed to fit Markov models of the receptor. The usual method of parameter fitting is based on maximum-likelihood techniques. However, Bayesian inference and Markov chain Monte Carlo techniques are becoming more popular. We describe the application of the Bayesian methods to real experimental single-channel data in three ion channels: the ryanodine receptor, the ${\text{K}}^{+}$ channel, and the IPR. One of the main aims of all three studies was that of model selection with different approaches taken. We also discuss the modeling implications for single-channel data that display different levels of channel activity within one recording.

In this review we focus on an intracellular ${\text{Ca}}^{2+}$ channel, the inositol trisphosphate receptor (IPR), and describe the use of single-channel data in constructing a Markov model of the receptor. We discuss parameter fitting from the point of view of Bayesian inference and Markov chain Monte Carlo (MCMC) techniques and discuss a simple Markov model for the IPR fitted using these techniques. We also discuss models of two other ion channels: the ryanodine receptor (RyR) and a ${\text{K}}^{+}$ channel. Model selection is an important issue and the three ion channels discussed take different approaches to addressing this problem. We also look at the modeling aspects for modal gating behavior.

I. INTRODUCTION

The modulation of free ${\text{Ca}}^{2+}$ concentration is a regulator of numerous physiological processes, including muscle contraction and cell division. However, prolonged periods of elevated ${\text{Ca}}^{2+}$ levels are toxic to cells, and so $\left[{\text{Ca}}^{2+}\right]$ oscillations are used to maintain an average elevated $\left[{\text{Ca}}^{2+}\right]$. The modulation of the ${\text{Ca}}^{2+}$ concentration involves interaction between the mechanisms controlling ${\text{Ca}}^{2+}$ flux across the plasma membrane and across internal cell compartment membranes such as the endoplasmic reticulum (ER).

In many cell types ${\text{Ca}}^{2+}$ release from the ER is via the IPR, which is regulated by ${\text{Ca}}^{2+}$ and ${\text{IP}}_3$ and other ligands.¹ The release of ${\text{Ca}}^{2+}$ from the ER can further modulate the open probability of the channel with the result that complex ${\text{Ca}}^{2+}$ oscillations and waves are formed. It is clear that an understanding of the IPR dynamics is central to a detailed understanding of ${\text{Ca}}^{2+}$ oscillations and waves.

Early binding models took into account the bell-shaped open probability of the receptor as well as adaptive responses. Studies of channel gating have been done under steady-state concentrations of ${\text{IP}}_3$ and ${\text{Ca}}^{2+}$,^2–4 and a major finding is that the steady-state open probability of the IPR is a bell-shaped function of the ${\text{Ca}}^{2+}$ concentration. Furthermore, in response to a step increase in ${\text{Ca}}^{2+}$, the IPR responds in an adaptive manner, first activating and inactivating. This can be interpreted by assuming that ${\text{Ca}}^{2+}$ activates the IPR quickly and inactivates it slowly. The first models to use the ideas of different time scales were those of De Young and Keizer,⁵ Atri et al.,⁶ and Bezprozvanny.⁷ De Young and Keizer⁵ assumed that the IPR consisted of three identical subunits, of which all must be in a conducting state before ${\text{Ca}}^{2+}$ flux could occur. Each subunit had an ${\text{IP}}_3$ binding site, an activating ${\text{Ca}}^{2+}$ binding site, and an inactivating ${\text{Ca}}^{2+}$ binding site. Simplifying assumptions were made that reduced the number of rate constants from 24 to 10 and then these parameters were chosen to give agreement with the steady-state data of Bezprozvanny et al.² This bell-shaped property of the open probability has been a central feature in many models of the IPR.^5,7–11

Steady-state functions can also be used to model the open probability of the channel. From their steady-state measurements in type-I and type-III receptors, Mak and Foskett⁸ and Mak et al.^9–11 used a model-independent biphasic Hill equation to quantify the open probability $P_o$ as a function of $\left[{\text{Ca}}^{2+}\right]$.

The open probability of the channels is both increased and decreased by ${\text{Ca}}^{2+}$. Atri et al.⁶ also modeled the steady-state open probability as a biphasic function made up of three terms where two of the terms give the activation of the receptor by ${\text{IP}}_3$ and ${\text{Ca}}^{2+}$, and the third term describes the inactivation of the receptor.

Time courses of ${\text{Ca}}^{2+}$ release from the channel can also be measured to study the kinetic properties of the receptor. Labeled flux experiments on hepatocytes have shown that after a step increase in ${\text{Ca}}^{2+}$ concentration, the IPR flux first increases and then decreases.^12–15 These methods allow the rates of unidirectional ${\text{Ca}}^{2+}$ flux to be measured during rapid superfusion. Their experiments suggested ideas of sequential binding of ${\text{IP}}_3$ and activating ${\text{Ca}}^{2+}$ (Ref. 16) and ${\text{Ca}}^{2+}$ modulation of the receptor. Another method that can be used to measure the kinetic response is by photoreleasing ${\text{IP}}_3$. Flash photolysis of caged ${\text{IP}}_3$ was used by Parker et al.¹⁷ to gain information about the ${\text{Ca}}^{2+}$ release. Time-dependent data obtained from labeled flux experiments were fitted by Sneyd and Dufour.¹⁸ Their model incorporated the ideas suggested by experiments, those of sequential binding of ${\text{IP}}_3$ and activating ${\text{Ca}}^{2+}$,¹⁶ modulation of ${\text{IP}}_3$ binding by ${\text{Ca}}^{2+}$, time-dependent inactivation on ${\text{IP}}_3$ binding, and saturating binding rates of ${\text{Ca}}^{2+}$.

However, as found recently by Mak et al.,¹⁹ there is no requirement for sequential ${\text{IP}}_3$ and ${\text{Ca}}^{2+}$ binding for channel activation or deactivation, invalidating many models.²⁰ They investigated the response of the channel to step increases in ${\text{Ca}}^{2+}$ and ${\text{IP}}_3$ concentrations and simultaneous jumps in the ligands (these experiments are discussed further below). Their data have yet to be utilized in modeling work, but when used will allow for the construction of more realistic models and thus facilitate a better understanding of ${\text{Ca}}^{2+}$ signaling.

More details on different IPR models can be found in the review by Sneyd and Falcke.²⁰ The models proposed for the IPR have generally included ligand-binding steps that cause the channel to open directly. Many IPR models have been based on the model of Ref. 5, which had the requirement that ${\text{Ca}}^{2+}$ binding was needed for the channel to open. However, such a simple approach ignores the concepts of affinity and efficacy. In 1957, del Castillo and Katz²¹ proposed a model which explicitly separated the agonist-binding step from the gating step. In their model, the binding of an agonist places the receptor in a state that is not open but allows transition to an open state. The agonist-binding step is controlled by the affinity of the receptor to the agonist and the gating is determined by the efficacy of the agonist. Reviews of these concepts, in which the rate of opening saturates, can be found in Colquhoun.^22,23

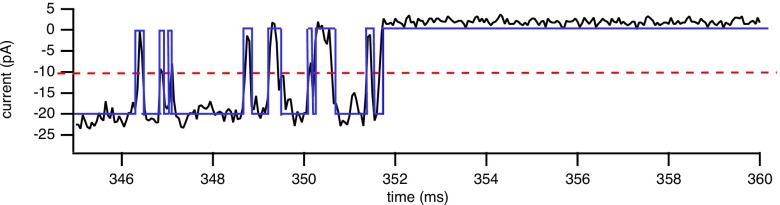
Experimentally, single-channel patch-clamp recordings are a typical way to study ion channels.²⁴ An example of a single-channel recording from the IPR is shown in Fig. 1 (experimental details of this record are given in Sec III C).

FIG. 1.

Whole-cell patch-clamp recordings of the IPR single-channel activity for various $\left[{\text{Ca}}^{2+}\right]$ obtained at a saturating $\left[{\text{IP}}_3\right]$ of $100\mu \text{M}$. Experimental techniques used to obtain these data are given in Sec. III C.

Because of the intracellular location of the IPR, traditional patch-clamp techniques cannot be used and early single-channel measurements were performed in lipid bilayers.^2,25 This approach suffers from the disadvantage that the IPR is not in its natural environment and raises uncertainty about whether the observed channel properties accurately reflect the channel when in its native membrane environment. However, two recent approaches have been developed that allow the receptor to be studied in its native environment. One approach exploits the fact that the ER is continuous with the outer membrane of the nuclear membrane.^26,27 This approach has been used successfully to record the activity in a variety of cells such as Xenopus oocytes, CHO, DT40, and rat parotid acinar cells.¹ In another approach, it has recently been reported that the receptors have been found in the plasma membrane of DT40 cells.²⁸ The advantage of this is that the receptor is orientated such that a normal orientation in the cytoplasm is retained and thus the receptor might expect to be regulated in a normal manner. The plasma membrane lipid environment is also likely to be similar to the ER lipid membrane, although there are reports that phospholipids and cholesterol may be higher in the plasma membrane by Lange et al.²⁹ The IPR is unusual because the same protein is expressed in the ER and plasma membrane and functions in both as an ${\text{IP}}_3$-gated channel. The low occurrence of receptors in the plasma membrane means that a whole-cell configuration can be used to study the properties of the IPR.

Methods such as labeled flux experiments cannot give kinetic information about single channels. To study the response of only a single channel, Mak et al.¹⁹ utilized the fact that the ER is continuous with the outer membrane of the nuclear membrane^26,27 to investigate the kinetic responses of the IPR to rapid ligand concentration changes. Single-channel patch-clamp studies of the channel were done in its native environment using isolated nuclei from cultured insect Ispodoptera frugiperda (Sf9) cells. They collected data on the activation and deactivation latency times. The latency time is defined to be the duration from the solution switch to the first observed opening. The kinetic responses of the channel were measured during rapid changes in $\left[{\text{IP}}_3\right]$ during constant $\left[{\text{Ca}}^{2+}\right]$ and deactivation latencies were also measured during $\left[{\text{IP}}_3\right]$ drops. They also investigated responses to changes in $\left[{\text{Ca}}^{2+}\right]$ for constant $\left[{\text{IP}}_3\right]$ and simultaneous changes in $\left[{\text{Ca}}^{2+}\right]$ and $\left[{\text{IP}}_3\right]$. Among their findings, they discovered that ${\text{IP}}_3$-bound channels respond rapidly to changes in $\left[{\text{Ca}}^{2+}\right]$, a property suited for ${\text{Ca}}^{2+}$-induced ${\text{Ca}}^{2+}$-release, which is important for integrating the IPR with whole-cell ${\text{Ca}}^{2+}$ signaling.³⁰ They also found that there is no requirement for sequential ${\text{IP}}_3$ and ${\text{Ca}}^{2+}$ binding for channel activation or deactivation. As many models use the assumption that ${\text{Ca}}^{2+}$ can only bind to ${\text{IP}}_3$-bound channels, this suggests an overhaul of the models. This wealth of information has yet to be fully used in modeling.

Many models for the IPR have been constructed and this raises the question, which model best describes the gating characteristics of the IPR? Comparison of models has been done by Mak et al.³¹ to determine which fit their steady-state data best. In their experiments, they observed spontaneous ${\text{IP}}_3$-independent activity of the IPR. However, many models assume that only the ${\text{IP}}_3$-bound state of the receptor is active.^5,14,32 Therefore, Mak et al.³¹ examined a series of allosteric models with increasing complexity in order to identify the simplest model that could account for their findings. They found that the simplest model that could describe the observed regulation by ${\text{Ca}}^{2+}$ and ${\text{IP}}_3$ was a Monod–Wyman–Changeux-based “four-plus-two” conformation model (this model is described in more details in Sec. III C). Sneyd et al.³³ did a similar comparison of three models using the data set of Dufour et al.³⁴ Their goal was to determine which model described the time-dependent responses of the IPR rather than the steady-state properties. The models they chose to fit were the De Young–Keizer model,⁵ the Sneyd–Dufour model,¹⁸ and the Dawson–Lea–Irvine model.³⁵ Each of these three models was constructed with different aims. The De Young–Keizer model parameters were chosen to fit steady-state data, the Dawson–Lea–Irvine model to study adaptation. Only the Sneyd–Dufour model was constructed to fit the dynamic responses. To do this, they used Bayesian inference and MCMC techniques to determine the set of rate constants for each of the models and then compared the maximum likelihoods. They also examined the convergence of the rate constants and the ability of the model to reproduce the data. The Sneyd–Dufour model was found to have the highest likelihood, an unsurprising result given it was constructed to model nonsteady-state data. However, it must be kept in mind that the models all have different aims. We will review other approaches to determine the “best” model fitted from steady-state single-channel data and also discuss how kinetic responses can be used to distinguish between different IPR models.

We briefly describe the fitting algorithms that can be used to fit the data. However, the aim of this review is not to present these algorithms in detail, as many excellent expositions already exist, but to discuss the models fitted with these methods using real data. Much theory has been developed for fitting single-channel data and we will review three applications of these methods to experimental data. We first discuss the work of Rosales et al.,³⁶ who apply Bayesian inference and MCMC techniques to single-channel data from the RyR, and de Gunst and Schouten,³⁷ who investigate the gating mechanism of the potassium channel in barley leaf. Gin et al.³⁸ apply this method to experimental IPR single-channel data after first doing an extensive study using simulated data.³⁹

II. CONSTRUCTING A SINGLE-CHANNEL MODEL

A. Fitting techniques

Because of the stochastic nature of the channel, the use of Markov models is a natural modeling approach. Channel transitions between the states of the Markov model can be described by a Markov process. Single-channel recordings allow the observation of the times at which the channel is open or closed, but not the open or closed state in which it resides. The experimental recording is an aggregation of the states into open and closed sets and thus the configuration of the Markov model cannot be observed from the experimental record. This raises issues of model identifiability and the degree to which the structure of the model can be determined, including the number of closed and open states, the transitions between these states, and whether all transitions can be estimated. In addition, the recording is corrupted by noise and subject to the limitations of the experimental resolution making the inverse problem difficult. In model fitting, there are two main steps to consider. In the first step, the data should be used to postulate a Markov model along with considerations such as ligand binding. (However, as described later, the model can also be part of the parameter search.) The second step is then to use the data to determine the parameters, for example, the rate constants governing the transitions between states of the Markov model by some means.

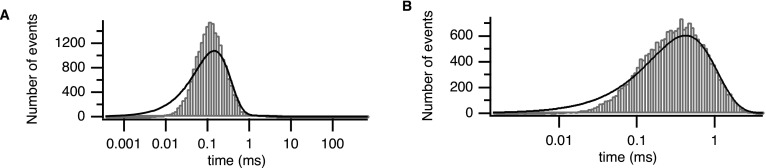
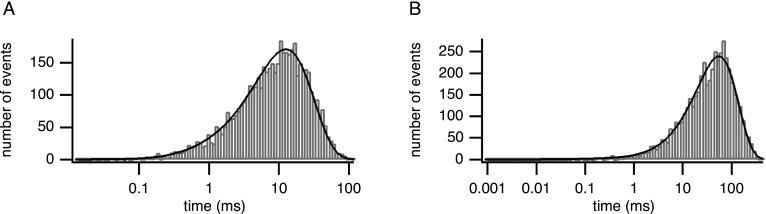
Traditionally, the data extracted and analyzed from single-channel recordings are the durations and sequence of the channel open times and closed times. To extract the sequence of open times and closed times (dwell times) from the single-channel record a threshold algorithm is used. A threshold is set at 50% of the mean open current and everything below the threshold is considered closed, while everything above the threshold is considered open. This is shown in Fig. 2. The closed-time and open-time durations can then be plotted in a histogram to give a distribution of the times. Examples are shown in Figs. 3(a) and 3(b); given the wide range of time scales, it is usually more convenient to look at the logarithm of the time.⁴⁰ However, detection of events also relies on the time resolution of the recording. Very short events, depending on the resolution of the recording, will not have time to cross the threshold and will not be detected. One way to circumvent this is to set the filter to produce an acceptable false event rate given a 50% threshold.⁴¹ Let the threshold be denoted by $\varphi$ and the standard deviation of the baseline noise ${\sigma }_n$ (the noise around the closed-current level). The false event rate is the number of false event rates per second ${\lambda }_f$ given approximately by

$${\lambda }_f=f_c\text{exp}\left(-{\varphi }^2/2{\sigma }_n^2\right),$$

where $f_c$ is the frequency of the recording system.⁴² The false event rate depends on the filter setting and on the ratio of $\varphi /{\sigma }_n$. For example, filtering at 1 kHz, a ratio $\varphi /{\sigma }_n$ of 3 will give 11 false events per second on average. For $\varphi /{\sigma }_n=4$, 0.33 false events per second are detected, and for $\varphi /{\sigma }_n=5$ one false event is detected every 270 s. In Colquhoun,⁴¹ the 50% threshold for their single-channel data $\varphi$ was 1.9 pA. The data were then filtered at 1, 1.5, 2, 3, and 4 kHz and then the standard deviations $\left({\sigma }_n\right)$ of the baseline noise were calculated (0.10, 0.14, 0.19, 0.27, and 0.33 pA, respectively). For the least filtered record (4 kHz), $\varphi /{\sigma }_n=1.9/0.33=5.8$. For a filter setting $f_c$ of 4000 Hz, ${\lambda }_f$ is $0.00025{\text{s}}^{-1}$, which is approximately one false event every 66 min. Therefore, this would be a suitable filter setting. However, as can be seen, this filter setting is imposed after threshold analysis.

FIG. 2.

An experimental IPR single-channel record is shown. The dashed line indicates the 50% threshold and the square-wave form is an idealization of the noisy record obtained using the threshold algorithm.

FIG. 3.

(a) Closed-time distribution. (b) Open-time distribution. Theoretical probability density functions are overlaid.

The theoretical distributions of the open and closed times can then be approximated by sums of decaying exponentials, which are not model specific, but given a particular Markov model, it is a relatively simple matter to calculate the theoretical distributions of the open and closed times^43,44 from its transition matrix. The parameters of the Markov model are determined by fitting to these experimentally determined open time and closed time probability distribution functions (PDFs).

We briefly describe why the distributions can be described by exponentials. The question we want to ask is how long a channel stays in a particular state before switching (the waiting time problem). Consider the following two-state model with one closed state ${\text{C}}_1$ and one open state ${\text{O}}_2$:

$${\text{C}}_1\underset{q_{21}}{\overset{q_{12}}{\rightleftarrows }}{\text{O}}_2.$$

Let $T_i$ be the random time that the channel switches from state ${\text{C}}_1$ to state ${\text{O}}_2$ for the $i\text{th}$ time. Let $P_1\left(t\right)=P\left[T_1\le t\right]$, where $P_1\left(t\right)$ is the probability that the channel has switched state by time $t$. Therefore, the probability that the switch has occurred by time $t+dt$ is the probability that the change has occurred by time $t$ plus the probability that it has not occurred by time $t$ but does occur in the time interval between $t$ and $t+dt$. This gives

$$P_1\left(t+dt\right)=P_1\left(t\right)+(1-P_1\left(t\right))q_{12}dt.$$

Taking the limit $dt\to 0$ gives the differential equation for the waiting time probability

$$\frac{d{P}_1\left(t\right)}{dt}=q_{12}(1-P_1\left(t\right)),$$

and solving gives $P_1\left(t\right)=1-\text{exp}\left(-q_{12}t\right)$. This is the cumulative PDF and the probability density function (in which we are interested) is found by differentiating the cumulative PDF $P_1\left(t\right)$ to give $q_{12}\text{exp}\left(-q_{12}t\right)$. More details can be found in Colquhoun and Hawkes.^43,44

The number of open states and closed states can be estimated from the distribution histograms. Each peak corresponds to an exponential component, and thus to a state, giving a starting point for the model that should be considered first. However, this is provided that there are no states with similar transition rates. This though, could not be identified by the fitting process, making an extra state redundant. The transitions between the states also need to be considered. This could include cycles in the model.

The next step is to use the data to determine the rate constants of the transitions between the states. The most common and straightforward approach to the parameter estimation problem is the maximum likelihood approach.^45–47 In this approach, a likelihood function is constructed, which is the probability of observing the data given the rate constants $p\left(x\mid q\right)$, where $p\left(\cdot \mid \cdot \right)$ denotes a conditional probability, $x$ is the data, and $q$ is the parameter to be determined. This likelihood is then maximized by methods such as the simplex algorithm or steepest descent to obtain the parameter values that give the maximum probability.

More recently though, Bayesian inference and MCMC (Ref. 48) methods have gained popularity. In the Bayesian approach, the parameters are assumed to be random variables that follow a particular distribution. Inferences are made based on the posterior distribution of the parameters given the data. Prior information about the parameters is also taken into account. The MCMC method provides a means of generating a sample from the posterior distributions of the parameters given the data. A new realization from the posterior distributions is obtained by sampling a candidate value of the parameter from the proposal distribution. This candidate value is accepted or rejected by comparison of the current parameter value with the candidate value by calculating the ratio of the density at the current and candidate points. One such algorithm is the Metropolis–Hastings algorithm,^49,50 which generates a Markov chain with equilibrium distribution from the posterior. Full details on constructing the posterior distribution from the data as well as the Bayesian and MCMC algorithm can be found in Gin et al.³⁹ and Ball et al.⁵¹

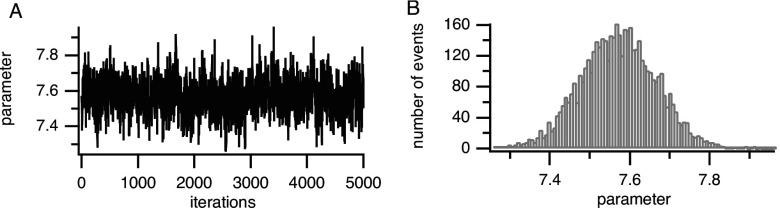
To completely determine a Markov model, it is required that all parameters converge. In order to test the convergence of the parameters, one should examine the plot of the random variable versus the number of iterations; an example is shown in Fig. 4. The iterations represent the sequence of the Markov chain. After an initial burn-in period, the parameter should settle to a steady-state value. The MCMC approach yields statistical information such as the mean value of the parameter and its variance, and thus can indicate how much the parameter may vary without compromising the fit. The parameter distributions also contain more information than can be obtained just from the mean and variance. For example, the distributions can be biased to one side or another or have multiple peaks. Therefore, in order to determine how well the parameter is determined from the data it is important always to examine the parameter distributions and not only the mean and variance.

FIG. 4.

Example of rate constant convergence. Burn-in period is not shown. (a) Convergence plot. (b) Marginal histogram.

B. Fitting the noisy single-channel record, not the open times and closed times

It is clear that the accuracy of the fits relies heavily on the accuracy of the reconstructed sequence of open and closed times. However the single-channel record is always corrupted by noise. To avoid this problem, approaches have been developed that are based on fitting directly to the noisy single-channel record and not the open times and closed times. By fitting directly to the raw record, not only are the rate constants determined, but the sequence of open and closed times can also be restored, reconstructing the single-channel record. Therefore, the open times and closed times are not fixed for the entire fitting procedure, eliminating any inherent error in first obtaining the times. These such methods have been developed by Fredkin and Rice,⁵² Ball et al.,⁵¹ Hodgson,⁵³ and Rosales et al.⁵⁴ Fredkin and Rice⁵² do this in a maximum likelihood framework while Ball et al.,⁵¹ Hodgson,⁵³ and Rosales et al.⁵⁴ use Bayesian inference and MCMC techniques.

C. Correcting for missed events

Due to the limitations of the experimental sampling resolution, very fast openings and closings are undetected. There are a number of ways in which to correct for missed events.^55–57 Hawkes et al.⁵⁷ derive the exact distributions for the approximate open-time and closed-time distributions. However, approximations can also be made.

The method of Blatz and Magleby⁵⁵ assumes that any event that is missed does not contain transitions within states in a certain class, e.g., within the set of closed states or within the set of open states. Missed events only occur for transitions from open to closed and closed to open. A correction is applied to the fitted rate constants and is accurate as long as the rate constants of the Markov model are not too large. Gin et al.³⁹ investigated correcting for missed events using simulated data. They applied the Blatz and Magleby⁵⁵ method and found the corrected rates to be closer to the real values and the distribution calculated from the corrected rates to be also much closer to the true distribution than the one using the fitted rate constants.

The method of Crouzy and Sigworth⁵⁶ introduces “virtual” states into their scheme. The transitions into and out of these states correspond to transitions which are not observed experimentally. This idea was suggested by Blatz and Magleby.⁵⁵ Crouzy and Sigworth⁵⁶ first considered a model consisting of one closed and one open state. Missed closing events will cause the open times to be overestimated and missed opening events will extend the closed times. Taking, for example, the problem of computing the extended closed time distribution (e-closed time distribution), they introduced an additional open state. They compute the exponential probability distributions for the missed times and from there they assign the rate constants for the virtual scheme.

Baran⁵⁸ also dealt with the problem of missed events in their fitting of single-channel data from the IPR. They calculated the error introduced by missed events by estimating the changes in the open probability and the open and closed times caused by successions of up to four undetected events. They imposed a time detection limit and any event with duration lower than this limit was assumed to have equal probability of occurring over the recording. They then approximated the new mean open time and closed time using the uncorrected time constants and the original number of detected events and the reduced number of detected events. From these, the corrected open probability was then calculated. The reliability of this approach was tested using stochastic simulations and they found that averaged values from ten different simulations were in agreement with the theoretical ones for the quantities of interest.

Fitting the noisy single-channel record and estimating the open times and closed times during the parameter search also provide a way to correct for missed events.³⁹ When fitting the noisy record, the duration of the open times and closed times is not fixed but allowed to change, as the transition times are determined by the fitting procedure. Therefore, every time the rate constants are updated, the resulting distribution will be changed slightly. The fitting procedure thus attempts to force the open-time and closed-time distributions to take the inherent shape of an exponential function, which, when plotted on a logarithmic scale, is skewed to the left. In this way, the open and closed times are changed such that they “fill out” the histogram, and it will be short events (the missed events in the experimental record) which will be added in order to fill the histogram, giving a partial correction for the events missed due to limited time resolution.

Another method that can be used in certain cases described by Gin et al.³⁹ fits not to the open and closed times, but the probability of observing an open or closed event at specified times. The specified times are the sampling times of the experimental recording. The fitting of events does not make the assumption that the channel is open the entire time between two sampling points but can move between open and closed states. However, it must be in the open state at the specified times, for example. A comparison between the Blatz and Magleby⁵⁵ method and fitting events was done by Gin et al.³⁹ using simulated data. The rates found were in fact much closer to the real rates than those found from applying the Blatz and Magleby⁵⁵ correction. In fact, the method of fitting to the events gave much more accurate rate constant values than from fitting to the raw single-channel record. However, the method of fitting events was developed for a model with only one open state, so is not yet generally applicable to other models. Full details are given in Gin et al.³⁹

In Sec. III, we review the applications of Bayesian inference and MCMC methods to experimental data from the RyR, ${\text{K}}^{+}$ channel, and IPR.

III. MODEL FITTING AND MODEL SELECTION

A. Fitting the RyR

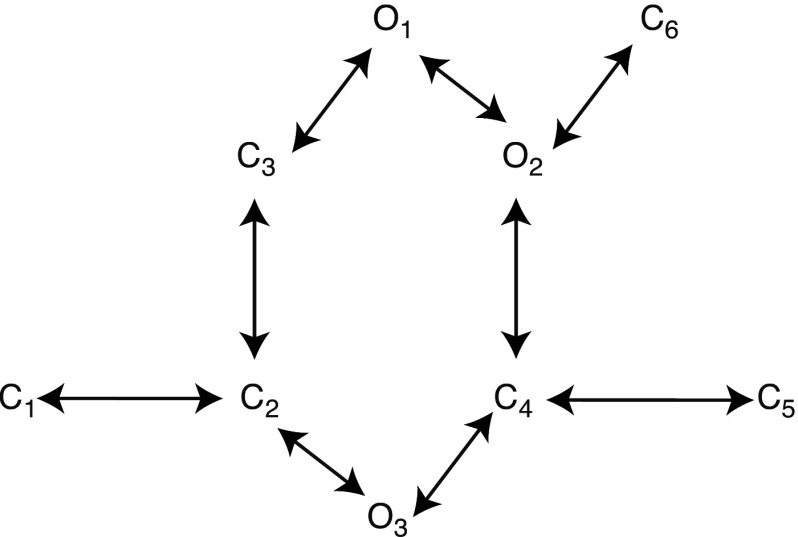
The RyR is an intracellular ${\text{Ca}}^{2+}$ channel. Rosales et al.³⁶ do an extensive model comparison for the type-II RyR. They obtained data from canine ventricular cardiac muscle RyR, reconstituted in planar lipid bilayers. They compared 16 gating models by analyzing three data sets of steady-state activity at three ${\text{Ca}}^{2+}$ concentrations: 1, 10, and $100\mu \text{M}$. Their models included cycles as well as linear models. They include one open state to three open states and two closed states to seven closed states. The aim was to infer the properties of a single RyR directly from the data by imposing only a minimum number of constraints on the Markov model. They addressed three aspects: idealization of the signal, parameter estimation and model selection. The first two aspects were done using Bayesian methods and MCMC. Determining which Markov model more accurately describes the data is commonly done by applying penalized ratio tests such as the Bayes information criterion (BIC) (Ref. 59) or the Akaike information criterion (AIC).⁶⁰ Both criteria are independent of the prior and the BIC penalizes the free parameters more strongly than the AIC. Rosales et al.³⁶ used the BIC to rank the 16 models. From their analysis, they were able to infer six properties of the gating model. They found that models with three open states were favored over those with two open states, which were preferred over one open state and which was consistent with experimental data. They also found that gating schemes with two communicating open states were preferred and those with a hexagonal cycle of states had higher BIC values. Schemes with more than two consecutive closed states not connected to an open state were penalized. Their best-ranked model $M_3$ is reproduced in Fig. 5.

FIG. 5.

Model $M_3$ of Rosales et al. (Ref. 36). Closed states: ${\text{C}}_1\text{-}{\text{C}}_6$, open states: ${\text{O}}_1\text{-}{\text{O}}_3$.

In terms of rate constant convergence, they found that rates leaving short-lived states with only a small occupancy had more variance than rates leaving long-lived states with higher occupancies. Multiple maxima were found for the rates leaving states with low occupancies. Therefore, unique parameter values could not be found.

In order to test the model reliability, they simulated data from the $M_3$ model at $1\mu \text{M}$ $\left[{\text{Ca}}^{2+}\right]$ and data from model $M_{10}$ at $10\mu \text{M}$ $\left[{\text{Ca}}^{2+}\right]$, including noise that mimicked the experimental data. They then fitted their synthetic data to the other models that they had previously trialled, as well as models $M_3$ and $M_{10}$. The rate constants were estimated and then the models were ranked. They found that at both ${\text{Ca}}^{2+}$ concentrations, the model from which the data were simulated was chosen as the best ranked and the estimated rate constants were similar to the original rate constants.

They also compared the rate constants for three Markov models using two data sets at $100\mu \text{M}$ $\left[{\text{Ca}}^{2+}\right]$. Comparing the rates determined for each of the data sets, they found variation due to natural variability between channels. However, they found the relative magnitudes to be consistent between the channels.

While Rosales et al.³⁶ do not correct for missed events, they do illustrate how filtering and thresholding can result in different dwell-time distributions. The data they fitted were filtered down to 10 kHz with a Gaussian filter; for their investigation, it was filtered to 2 kHz. A half-amplitude threshold was used to obtain the open and closed times. Significant differences were found at $1\mu \text{M}$ $\left[{\text{Ca}}^{2+}\right]$ with the fast events in both the open and closed times disappearing almost completely at 2 kHz, with the consequence that both distributions were shifted to the right.

B. Fitting the ${\text{K}}^{+}$ channel

Bayesian inference and MCMC techniques have been used by de Gunst and Schouten³⁷ to fit the experimental data from the ${\text{K}}^{+}$ outward rectifier in barley leaf. Eight recordings from inside-out patch configurations were used. They apply the methods they developed in earlier papers^61,62 and tested on simulated data on the experimental data. Filtering, colored, state-independent noise and white, state-dependent noise were incorporated in their hidden Markov models; they found that omission of any one of these three features results in unreliable results for their data.⁶¹

The main aim of their paper was model selection. They take a different approach to model selection than Rosales et al.³⁶ Instead of using penalized ratio tests, the model is included as an additional parameter to be determined in the Bayesian search. The methods for including the model in the search have been developed by Hodgson and Green⁶³ and de Gunst and Schouten.⁶² In this setup, the model indicator is included as an additional parameter. A set of candidate models is introduced and the MCMC sampler then requires the use of reversible jump sampling techniques.⁶⁴ They set noninformative priors for their model indicator; in other words, each model had an equal prior probability. Three sets A, B, and C of models were considered. Sets A and B were used to analyze the number of closed states required to model the closures. Each set contained two models, all with only one open state. In set A, they compared a two-state model (one closed state, one open state) to a three-state model (two closed states, one open state). In set B, the three-state model in set A was compared to a four-state model (three closed states, one open state). For model set A, they found that the three-state model was preferred to the two-state model and in fact, none of the proposals from the three-state model to the two-state model was ever accepted. In set B, the four-state model was preferred to the three-state model. However, they found that the estimated values for two of the rate constants $q_5$ and $q_6$ in the four-state model were large and physically unrealistic. As well as this, when the sampling was stopped, the generated values had not yet converged and were still increasing. This outcome was found for the other data sets. From these results, they concluded that there are two different types of closed states, one accounting for the long closed times and the other to short closed times. De Gunst and Schouten³⁷ concluded from these results that if the number of states in the model was too large, extra freedom in the model is introduced so that some of the rates determined were physically implausible and had not reached convergence when the sampling was stopped. This was also found to be the case by Gin et al.^38,39 for the IPR model fitting (discussed in Sec. III C).

Set C contained models to determine the number of identical, independent states $L$ that could account for the observed long closed times. Their preliminary analyses indicated that $L$ could range from one to five or six closed states. Analyses also showed that it was sufficient to consider only one closed state accounting for the short closed times. They did not find clear evidence that more than four closed states were needed to describe the long closed times so they selected a model with four slow closed states.

One of their future directions includes identification of the ${\text{Ca}}^{2+}$-dependency of the rate constants. In Sec. III C, we show how this has been done for the IPR by Gin et al.³⁸ In particular, their results show that the rate constants are not simple functions of $\left[{\text{Ca}}^{2+}\right]$.

C. Fitting the IPR

Using Bayesian inference and MCMC methods, Gin et al.³⁸ constructed a model based on single-channel IPR data. They first did an extensive investigation using simulated data on the fitting techniques that can be used to correct for missed events.³⁹ As described earlier, they compared the Blatz and Magleby⁵⁵ method and fitting to the probability of observing an open or closed event at specified times using simulated data. Fitting the probability of events at specified times gave rate constants much closer to the original values used to simulate the data. However, as the method of fitting events was developed for a model with only one open state, Gin et al.³⁸ fitted to the open and closed times and then applied the missing event correction of Blatz and Magleby.⁵⁵ Fitting the noisy record and reconstructing the open times and closed times were not done by Gin et al.³⁸ because the long single-channel records and the number of records meant the computation time required would be prohibitive.

The data used were from experiments performed in chicken DT40-3KO cells engineered to stably express rat $\text{S}1\text{-}/\text{S}2+\text{IPR-}1$. These refer to the major splice variants of the type 1 receptor. The S1-splice site is in the N terminus of the receptor and the $\text{S}2+$ variant is the form found predominately in the brain. Because endogenous IPRs have been genetically deleted in the DT4-3KO cell type, a stable expression of the expressed mammalian IPR allows its study in unambiguous isolation. All experiments were performed using the whole-cell configuration of the patch-clamp technique which allows the measurement of single channel activity from IPR present in the plasma membrane as previously described.^28,65 Data were obtained at ten ${\text{Ca}}^{2+}$ concentrations; some examples are shown in Fig. 1. At ${\text{Ca}}^{2+}$ concentrations of 10, 30, and $100\mu \text{M}$, no activity was evident during the recordings. For each concentration, single-channel data were obtained for five or six cells in each condition, representing between 8 and 29 min of experimental recordings for each case. Using these data, the aim of Gin et al.³⁸ was to fit the most complex model for which the rate constants could be determined and then to determine the ${\text{Ca}}^{2+}$-dependencies of the rate constants. By examining the open-time and closed-time distributions, they identified three closed-time time constants and one open-time time constants. From preliminary work on simulated data,³⁹ for which only three closed states and one open state could be identified, the maximum number of transitions that could be determined from the steady-state data was six. An upper bound on the maximum number of reactions that can be identified is $N_c{N}_o$, where $N_c$ is the number of closed states and $N_o$ is the number of open states.⁶⁶ For the four-state model, the upper bound on the number of reactions is three (giving six transitions). Cycles were included, but the rate constants for these extra connections could not be determined from the available data. Only ratios of rate constants could be identified rather than the individual rates themselves. The data in Gin et al.³⁸ showed three closed states and one open state and using the results of Gin et al.,³⁹ it was decided not to include cycles. It should be noted that longer steady-state recordings or more recordings would not necessarily increase the complexity of the models. More data would only result in smoother histograms for the open and closed distributions giving less ambiguity in the fitting of the rate constants. Gin et al.³⁹ also tested the models with additional states and transitions, but this resulted in nonconvergence of the rate constants. Although ratios of rate constants converged, individual rate constants could not be determined. Therefore, adding additional states when the data cannot support them leads to ambiguity in the rate constants.

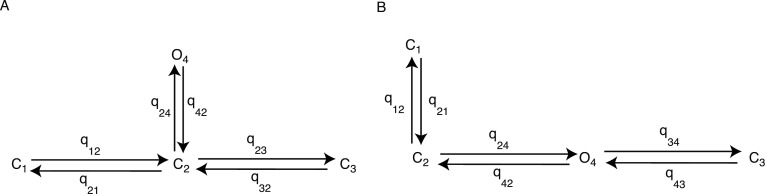
They studied two different configurations of three closed states and one open state, as shown in Fig. 6. An important feature of their four-state models is that they are much simpler than most other current models of the IPR. The construction of the model did not take into account any considerations, such as ligand binding or multiple subunits, as the aim was to fit the most complex model that could be determined by the available data. Previous work using simulated data³⁹ showed that for more complex models, only ratios of rate constants could be determined and not the individual rate constants themselves. Therefore, no constraints were imposed on the model structure and they fitted only the most complex model that could be determined from the available data. As the transitions between the states of the models were found to have complex dependencies on the agonist concentration, they implicitly assume that each of the “states” does not correspond to a physically identifiable single state of the IPR, and that the transitions between states do not correspond to simple binding events. Instead, each of the model states is assumed to be a conglomeration of multiple physical states. Condensing models can be done theoretically by using techniques such as quasisteady-state approximations. In this case, the rate constants are rational functions of the relevant concentrations. The theory and many examples can be found in Refs. 67 and 68. The reduction in a complex Markov model to a simpler model in which the transitions are complex functions of the original rate constants is possible. However, it is not possible to work backward, i.e., given a simple model, the exact complex model from which the simple model was obtained cannot be determined.

FIG. 6.

Four-state Markov models fitted by Gin et al. (Ref. 38). Closed states are ${\text{C}}_1$, ${\text{C}}_2$, and ${\text{C}}_3$. Open state is ${\text{O}}_4$. Left: model 1, right: model 2. Rate constants given by $q_{ij}$ denoting the transition from state $i$ to state $j$.

Gin et al.³⁹ found that when trying to fit a more complex model, the rate constants could not be determined by the steady-state data alone. They simulated the data from a five-state model with four closed states and one open state. If such a model is to be fully determined, then the closed-time distribution should display four distinct peaks. However, when inspecting the closed-time distribution, there were only three peaks. Fitting the five-state model using the simulated data, they found that the rate constants could not all be determined. They then simulated nonsteady-state data, and fitting this data, along with the steady-state data, the five-state model was able to be determined with all rate constants converging.

Additionally, Gin et al.³⁸ were able to determine the $\left[{\text{Ca}}^{2+}\right]$-dependency of the rate constants. Biphasic $\left[{\text{Ca}}^{2+}\right]$-dependencies were found in some of the rate constants, and these were fitted by Hill functions. The prediction from both models is that the main effect of $\left[{\text{Ca}}^{2+}\right]$ is to modulate the probability that the receptor is in a state that is able to open, rather than to modulate the transition rate to the open state. For model 1, the only rate constants found to be ${\text{Ca}}^{2+}$-dependent are $q_{23}$ and $q_{32}$. These rate constants were fitted by biphasic functions. The main contributing factor to an increased open probability was the decrease in the number of long closed-time events (events in state ${\text{C}}_3$), rather than any great increase in the rate $q_{24}$. The mean open time given by $1/q_{42}$ also does not change significantly over the $\left[{\text{Ca}}^{2+}\right]$ range, and therefore is not an important factor in affecting the open probability.

For model 2, two pairs of rate constants were found to have ${\text{Ca}}^{2+}$ dependencies. As for model 1, the transitions into and out of the long closed state (${\text{C}}_1$ in model 2, ${\text{C}}_3$ in model 1) are $\left[{\text{Ca}}^{2+}\right]$-dependent. The rate constants between ${\text{C}}_2$ and ${\text{O}}_4$, $q_{24}$ and $q_{42}$ were also found to be $\left[{\text{Ca}}^{2+}\right]$-dependent. This suggests that ${\text{Ca}}^{2+}$ is directly affecting the transition to opening, whereas for model 1, this was not the case. However, further investigation showed that ${\text{Ca}}^{2+}$ affects the pathway to the main route between closing and opening. In model 1, this is the ${\text{C}}_3\text{-}{\text{C}}_2$ $\left(\text{-}{\text{O}}_4\right)$, and in model 2, the pathway ${\text{C}}_1\text{-}{\text{C}}_2\text{-}{\text{O}}_4$. Once the receptor is in the closed state with the shortest mean time (${\text{C}}_2$ for the first model and ${\text{C}}_3$ for the second model) and the state from which the receptor can open, there is no ${\text{Ca}}^{2+}$-dependency. From fitting the two models, different conclusions about the ${\text{Ca}}^{2+}$-dependency were obtained for the different models, but closer inspection showed that essentially the same mechanism is in effect. Note that we have followed the labeling of Gin et al.,³⁸ but that given the symmetry of model 1, states ${\text{C}}_1$ and ${\text{C}}_2$ can be interchanged.

Heuristic increasing or decreasing functions were used to model the rate constants for both models; clearly values at more concentrations are required to fully characterize the dependencies. No biophysical derivation of these rates is given, but, as mentioned, the construction of the specific complex model from which the current simple model is derived is not possible. The heuristic rate functions fitted were all rational functions of the $\left[{\text{Ca}}^{2+}\right]$ concentrations, and these are consistent with either a pseudosteady-state derivation or an equilibrium approximation. The choice of polynomial function used had no effect on the data, and so, using different functions will have no effect on the conclusions about the effects of the $\left[{\text{Ca}}^{2+}\right]$ concentration changes.

Both models were found to fit the steady-state data equally well. It turns out that with only one open state, all topologies are equivalent and will fit steady-state data equally well.⁶⁹ In order to distinguish between the models, additional data would need to be used in the fitting process. Gin et al.³⁸ fitted their model using only steady-state data, but by simulating non-steady-state data from the fitted model, they were able to make a comparison with experimental data. Experimental non-steady-state data had been obtained by Mak et al.,¹⁹ who investigated the kinetic responses of the IPR to rapid ligand concentration changes. Single-channel patch-clamp studies of the channel were done in its native environment using isolated nuclei from cultured insect Ispodoptera frugiperda (Sf9) cells. They collected data on the activation and deactivation latency times. The latency time is defined to be the duration from the solution switch to the first observed opening. For example, the kinetic responses of the channel were measured during rapid changes in $\left[{\text{Ca}}^{2+}\right]$ from $<10\text{nM}$ to $10\mu \text{M}$ and $2\mu \text{M}$ during constant $\left[{\text{IP}}_3\right]$ of $10\mu \text{M}$ and deactivation latencies were measured during $\left[{\text{Ca}}^{2+}\right]$ drops from 300 to $2\mu \text{M}$. Gin et al.³⁸ simulated this type of data from their two four-state models using the corresponding mean fitted rate constants and then compared to the experimental data of Mak et al.¹⁹ Gin et al.³⁸ simulated the activation latency data from step changes in $\left[{\text{Ca}}^{2+}\right]$ from 50 to $200\text{nM}$ at constant $\left[{\text{IP}}_3\right]$ of $100\mu \text{M}$. The simulated activation times for models 1 and 2 are shown in Fig. 7. Mak et al.¹⁹ found an activation time of 40 ms after a jump from $<10\text{nM}$ to $2\mu \text{M}$ $\left[{\text{Ca}}^{2+}\right]$ at a constant $\left[{\text{IP}}_3\right]$ of $10\mu \text{M}$. Gin et al.³⁸ found that model 2 gives a much closer activation time of 55 ms to their experimental result than model 1, which had a latency time of $\sim 12\text{ms}$, suggesting that model 2 more accurately describes the data. However, they did not take into account the time duration between the solution switches. Mak et al.¹⁹ found that typical solution switches have durations of between 4 and 15 ms by monitoring the change in the closed-channel baseline current level during solution changes. In this way, they were able to control the possible differences in the time courses of various solution switches. In the simulations of Gin et al.,³⁸ the switch time is instantaneous. Therefore, taking into account the experimental time lapse (4–15 ms) between solution switches, it may be that model 1 is a more accurate description of the data.

FIG. 7.

Simulated distributions of times to first opening after a step up from 50 $\left[{\text{Ca}}^{2+}\right]$ to $200\text{nM}$ $\left[{\text{Ca}}^{2+}\right]$ for the IPR model fitted by Gin et al. (Ref. 38). (a) Model 1. (b) Model 2. Theoretical distributions are overlaid.

Gin et al.³⁸ also compared their models to the allosteric model of Mak et al.³¹ Their model consisted of two open states, $A^{\ast }$ and $C^{\ast }$, and four closed states, $A^{\prime }$, $C^{\prime }$, $B$, and $D$. $\left[{\text{Ca}}^{2+}\right]$ and $\left[{\text{IP}}_3\right]$ do not regulate the transitions between rapid closings and openings, $A^{\prime }\text{-}{A}^{\ast }$ and $C^{\prime }\text{-}{C}^{\ast }$ (our ${\text{C}}_3\text{-}{\text{O}}_4$ transition in model 2). The brief closing and opening events are ligand independent, just as Gin et al.³⁸ found. However, $\left[{\text{Ca}}^{2+}\right]$ affects the transition between $A^{\ast }\text{-}B$ and $C^{\ast }\text{-}D$, thus modulating the propensity of the receptor to be in a state capable of opening. In model 2, this corresponds to the ${\text{C}}_2\text{-}{\text{O}}_4$ transition. Model 1 has only one pathway to the open state and therefore this transition cannot be both ligand independent and ligand dependent. Therefore, model 2 is essentially a simplification of the Mak et al.³¹ model. From the latency times simulated and the comparison with the model proposed in Mak et al.,³¹ it can be seen that different types of data are required to resolve the issue of which model more accurately describes the channel.

D. Modeling mode switching

Examination of long records of single-channel activity has revealed that the gating behavior may not be uniform over the entire record. Instead, the channel can display different modes or different levels of channel activity. These modal gating kinetics have been observed in many different ion channels such as the ${\text{Cl}}^{-}$ channel⁵⁵ and the ${\text{K}}^{+}$ channel.⁷⁰ It has also been found in the two major intracellular ${\text{Ca}}^{2+}$ release channels, the RyR (Ref. 36) and the IPR.^38,71 Modal gating in the RyR has been proposed to contribute to the adaptation behavior of the channel in response to jumps in the ${\text{Ca}}^{2+}$ concentration.^36,72 However, as shown by Mak et al.,¹⁹ the IPR does not display adaptation after jumps in both ${\text{Ca}}^{2+}$ and ${\text{IP}}_3$ concentration. Ionescu et al.⁷¹ demonstrated that modal gating plays an important role in ligand regulation of the channel. They found that longer time scales in the IPR channel gating kinetics are likely to be relevant for the kinetics of the ${\text{IP}}_3$-mediated intracellular ${\text{Ca}}^{2+}$ dynamics.

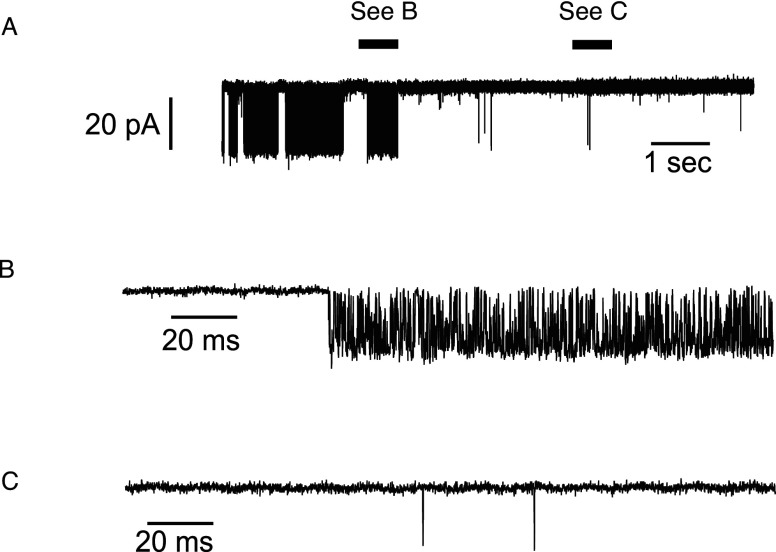
An example is shown in Fig. 8. This is found in the IPR data fitted by Gin et al.³⁸ Two records at $1\mu \text{M}$ $\left[{\text{Ca}}^{2+}\right]$ clearly showed different levels of activity within the single recording. Parts of the single-channel record in panel (a) have been enlarged and are shown in panels (b) and (c). In order to model such data, two different Markov models, each with a different set of rate constants, are needed for the two sections. The two models would then be connected by a pair of rate constants that govern switching between the two models. However, in order to fully characterize the statistics of the switching process, a large number of observations of a switch are required. No such data are available, as a switch was observed only a small number of times. In addition, to account for two levels of activity, two open states are required,⁷¹ but on plotting the open time histograms, Gin et al.³⁸ only found evidence for one open state. The majority of the IPR data used by Ref. 38 showed only one mode throughout the recording and therefore they were not able to make any inference as to which mode the channel is in at each $\left[{\text{Ca}}^{2+}\right]$.

FIG. 8.

Single-channel activity at $1000\text{nM}$ $\left[{\text{Ca}}^{2+}\right]$ and $100\mu \text{M}$ $\left[{\text{IP}}_3\right]$. Panels (a) and (c) show expanded portions from panel (b). Panel (a) shows much higher activity than panel (c).

Ionescu et al.⁷¹ developed an algorithm to identify different modes. Using their algorithm, they found three modes in their IPR data. They developed an algorithm that uses the durations of channel bursts and burst-terminating gaps and in this way, they can determine the gating mode with high accuracy and high temporal resolution. Conventional techniques examined either the open probability of the open times and closed times to determine the modes by averaging over either short segments of the record or by averaging long segments.^55,70 In the former, the value of the averaged parameter could vary widely due to the abrupt changes in modes. In the latter, using long segments failed to capture the abrupt transitions between modes.

A simple model, as fitted by Gin et al.,³⁸ can reproduce the averaged statistics of the different modes but cannot reproduce abrupt changes between different activity levels. In order to model the modes, one can fit a Markov model for each of the modes, determining the rate constants within the modes, and then fit the transition rates between the modes. While this is feasible in theory, in practice it will be more difficult. The main difficulty is obtaining enough data exhibiting multiple modes so that the transitions between modes can be unambiguously determined. Also, if one part of the record shows a very little activity, and thus very few open times and closed times to fit, then the rate constants will not be well determined.

A simple model has been proposed as a starting point by Ionescu et al.⁷¹ who identified three modes within their data: high, intermediate, and low open probabilities. Each mode is described by a two-state model (closed-open) and the three models are interconnected via the closed states. Ionescu et al.⁷¹ found that the open probability within each mode was similar over a wide range of $\left[{\text{Ca}}^{2+}\right]$ and $\left[{\text{IP}}_3\right]$ and therefore, the biphasic $\left[{\text{Ca}}^{2+}\right]$ dependency was a result of the $\left[{\text{Ca}}^{2+}\right]$ regulation of the propensity of each mode with the channel kinetics unaffected by $\left[{\text{Ca}}^{2+}\right]$.

Rosales et al.³⁶ also found the existence of modes at a single $\left[{\text{Ca}}^{2+}\right]$. At both 1 and $10\mu \text{M}$ $\left[{\text{Ca}}^{2+}\right]$, they found that both their open and closed time distributions slowed two clearly defined maxima. At $1\mu \text{M}$ $\left[{\text{Ca}}^{2+}\right]$, their single channel records show at least three gating modes (Fig. 5 in Rosales et al.³⁶). The first $G_o$ consists of long openings interspersed with brief closures; the second $G_z$ consists of brief openings followed by brief closures. The third mode $G_o$ shows brief openings followed by long closed times. They summarized these in their model $M_3$, which is reproduced in Fig. 5. By examining the occupation probabilities in each of the states, they found that the gating mode frequencies are $G_l$, $G_z$, and $G_o$. They also compared how the gating modes changed with different ${\text{Ca}}^{2+}$ concentrations. At 10 and $100\mu \text{M}$ $\left[{\text{Ca}}^{2+}\right]$, the gating modes change. At $10\mu \text{M}$, only two modes are identified: brief openings followed by intermediate-length closures and intermediate openings followed by short closures. Their model showed that the ${\text{Ca}}^{2+}$ dependence of modal gating is highest at a relatively low $\left[{\text{Ca}}^{2+}\right]$ of $\sim 1\mu \text{M}$. This concentration corresponds to the ${\text{Ca}}^{2+}$ concentration range over which adaptation is experimentally observed.⁷²

E. Response to step increases in ligand concentration

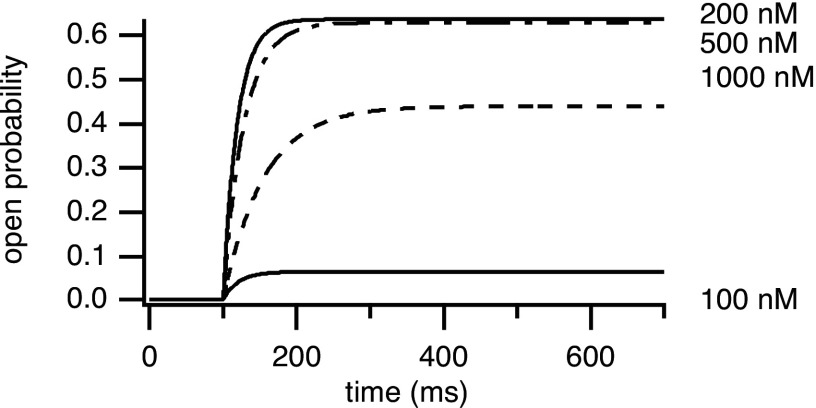
Adaptation behavior has been observed in the RyR.⁷² However, Mak et al.¹⁹ found that the time course of the open probability of the IPR increased monotonically after jumps in $\left[{\text{Ca}}^{2+}\right]$ and $\left[{\text{IP}}_3\right]$. Gin et al.³⁸ used their IPR model to simulate the open probability of the channel after step increases in the ${\text{Ca}}^{2+}$ concentration for their model 1. The $\left[{\text{Ca}}^{2+}\right]$ was held fixed at a low steady-state concentration $\left(\left[{\text{Ca}}^{2+}\right]=50\text{nM}\right)$ and at this concentration, the IPR is mostly in state ${\text{C}}_3$ (because of the symmetry of the model, ${\text{C}}_3$ is equivalent to ${\text{C}}_1$). Therefore, the initial state probabilities were set accordingly. The $\left[{\text{Ca}}^{2+}\right]$ was then increased to 100, 200, and 500 nM and held fixed at a new concentration. The open probability of the IPR increased monotonically to its new value. The responses from model 1 are shown in Fig. 9. Both topologies gave the same responses to step $\left[{\text{Ca}}^{2+}\right]$ increases. Their model predictions agree qualitatively with the experimental observation of Mak et al.¹⁹ However, this model result appears to be in direct disagreement with data from labeled flux experiments,^12,14 where, in response to a step increase in $\left[{\text{Ca}}^{2+}\right]$, the IPR flux first increases then decreases. Possible reason for the difference is the ${\text{IP}}_3$ concentration used. The simulations of Gin et al.³⁸ were done at a saturating concentration of ${\text{IP}}_3$ and thus, data at different concentrations need to be obtained to test whether all give a monotonic increase. However, another possible explanation for this discrepancy is the difference in experimental method, which might cause significant differences in IPR environment and behavior.

FIG. 9.

IPR open probability response to step increases in $\left[{\text{Ca}}^{2+}\right]$ for model 1.

For the RyR, adaptation has been observed experimentally.^73,74 Rosales et al.³⁶ computed the responses to step increases in the $\left[{\text{Ca}}^{2+}\right]$ from their model. Using their best-ranked model $M_3$ reproduced in Fig. 5, they investigated responses to sudden steps in the $\left[{\text{Ca}}^{2+}\right]$. They computed steps from 0 to 1, 10, and $100\mu \text{M}$ $\left[{\text{Ca}}^{2+}\right]$. Their model gave a rapid rise to a peak in the open probability which then relaxed slowly down to an equilibrium, a result that had been experimentally observed. However, they simulated the response using different sets of initial occupancy probabilities in each of the states. For some of these initial state probabilities, only a monotonic increase to an increased open probability was observed. Therefore, the kinetic response of the open probability is strongly dependent on the initial conditions of the state probabilities.

IV. CONCLUSIONS AND FUTURE WORK

While many models of the IPR have been constructed based on a single type of data, it still remains to utilize the different types of data, steady-state and nonsteady-state single-channel data and ${\text{Ca}}^{2+}$ flux data, together to construct a model. The use of multiple types of data could be used to extend the complexity of models for which all the parameters can be fully determined. The degree to which a Markov model can be fully determined is also limited by the experimental data available. As shown by Gin et al.,³⁸ only a four-state model could be fully determined by the steady-state data. De Gunst and Schouten³⁷ also found that trying to fit the models with increasing number of states resulted in rate constants that were not plausible. Therefore, to increase the complexity of the model, different types of data need to be fitted simultaneously.

One study which used different types of data was done by Baran,⁷⁵ who analyzed the data on the properties of IPR binding and also single-channel data. Baran⁷⁵ found that the data can be described by a gating mechanism consisting of triple allosteric interactions between ${\text{Ca}}^{2+}$, ${\text{IP}}_3$, and adenosine triphosphate (ATP). The aim was to find model parameters for each of the different sets of data as close as possible to each other. The model was an extension of the one proposed by Baran,⁵⁸ which was a minimal model to describe the dependence of the open probability, open times, and closed times on ${\text{Ca}}^{2+}$ at saturating levels of $\left[{\text{IP}}_3\right]$ $\left(10\text{mM}\right)$. The model was extended to include dependence of the open probability, open times, and closed times on ${\text{Ca}}^{2+}$, ${\text{IP}}_3$, and ATP as well as describing more data. The model defined consists of three four-state modules controlling gates responsible for activation, inhibition, and inactivation of the channel. Their finding was that essentially the same gating mechanisms are present in the stationary activity of the receptor in studies done in native and artificial environments as well as properties of ${\text{IP}}_3$ binding. Their study was done using only equilibrium data, although they combined binding data and single-channel data.

Another interesting modeling problem yet to be fully investigated is that of fitting modes. Fitting single-channel records that display different modes within a recording and even abrupt changes between these modes require more complex models with more states and extra transitions. But to fully determine these models enough data must be obtained first for the different modes at one ligand concentration and then also enough switches between the modes. In theory, the modeling aspect should not be difficult for the methods already in use, but the data must be obtained.

The theory for fitting single-channel data has been developed and sophisticated methods such as the Bayesian and MCMC approach have been developed for practical fitting applications. This approach can be used to yield statistical information about the fit of the parameters. Methods to deal with the limitations of the experimental techniques, such as the limited sampling resolution, are also available. These have been used in actual fitting of both simulated and experimental ion-channel data. The challenge for future modeling work is to apply these methods to different types of experimental data simultaneously. Advances in experimental techniques have provided more insight into the gating of the IPR and the modeling techniques have been applied successfully to these data. The growing wealth of experimental data will ensure more accurate models of the gating dynamics of the IPR and other ion channels.