Divergence in DNA Specificity among Paralogous Transcription Factors Contributes to Their Differential In Vivo Binding

SUMMARY

Paralogous transcription factors (TFs) are oftentimes reported to have identical DNA-binding motifs, despite the fact that they perform distinct regulatory functions. Differential genomic targeting by paralogous TFs is generally assumed to be due to interactions with protein co-factors or the chromatin environment. Using a computational-experimental framework called iMADS (integrative modeling and analysis of differential specificity), we show that, contrary to previous assumptions, paralogous TFs bind differently to genomic target sites even in vitro. We used iMADS to quantify, model, and analyze specificity differences between 11 TFs from 4 protein families. We found that paralogous TFs have diverged mainly at mediumand low-affinity sites, which are poorly captured by current motif models. We identify sequence and shape features differentially preferred by paralogous TFs, and we show that the intrinsic differences in specificity among paralogous TFs contribute to their differential in vivo binding. Thus, our study represents a step forward in deciphering the molecular mechanisms of differential specificity in TF families.

Graphical abstract

In Brief: This study introduces iMADS, a general framework to quantify, model, and analyze the DNA-binding preferences of paralogous transcription factors. Contrary to the expectation that paralogs bind to identical DNA motifs, iMADS demonstrates that they prefer different DNA-sequence and DNAshape features. This divergence in specificity contributes to differential in vivo binding, and it is most pronounced at mediumand low-affinity sites, which are not captured by standard DNA-motif models.

INTRODUCTION

Transcription factors (TFs) interact with DNA in a sequence-specific manner, and these interactions represent a key mechanism in the regulation of gene expression. In eukaryotes, most TFcoding genes have undergone gene duplication and divergence during evolution (Chen and Rajewsky, 2007; Hsia and McGinnis, 2003; Lynch and Conery, 2000; Taylor and Raes, 2004), resulting in many TFs having highly similar DNA-binding domains (DBDs) and recognizing similar DNA sequence motifs. TFs with such properties that also belong to the same species are called paralogous TFs. Some paralogous TFs have partly (or completely) redundant functions. Most mammalian TFs, however, have evolved regulatory functions that are distinct from their paralogs in the cell (Chen and Rajewsky, 2007; Hsia and McGinnis, 2003; Vaquerizas et al., 2009). In general, paralogous TFs accomplish a wide variety of independent or complementary molecular functions to regulate cellular phenotypes.

Many methods have been developed to learn TF-DNA binding specificity models from high-throughput in vivo and in vitro experimental data, ranging from simple position weight matrices (PWMs) to state-of-the-art deep learning models (Weirauch et al., 2013; Jolma et al., 2013; Alipanahi et al., 2015; Wang et al., 2013; Agius et al., 2010). According to such models, paralogous TFs, especially the ones with high amino acid identity in their DBDs, tend to have indistinguishable DNA-binding specificities (Weirauch et al., 2014). As an important consequence, this restricts the inference of TF-DNA interactions to familywide predictions, rather than predictions for individual family members.

Since paralogous TFs are often co-expressed in the same cells but they perform different, sometimes even opposite, biological functions, being able to identify genomic binding sites of individual TF family members is critical. For example, while c-Myc is a well-known oncoprotein that promotes transcriptional amplification, its co-expressed paralog Mad is a tumor suppressor and represses gene expression (Meyer and Penn, 2008; Dang, 2012). Currently, little is known about the mechanisms that explain the differential genomic targets of paralogous TFs. Furthermore, when analyzing in vivo TF-DNA-binding data, such as data from chromatin immunoprecipitation sequencing (ChIP-seq) assays (Johnson et al., 2007), many genomic studies do not even take into account the presence of paralogous TFs, or the fact that TF family members present in a cell are likely to influence each other’s binding to the genome. Overall, given that most mammalian TFs are part of large protein families with multiple paralogs expressed at the same time, it is surprising how little we know about how paralogous TFs achieve their unique specificities in the cell.

Here, we show that despite having similar DBDs, paralogous TFs have different intrinsic DNA-binding preferences and this contributes to their differential in vivo binding and functional specificity. We focus on closely related TFs reported to have indistinguishable DNA-binding motifs, but distinct sets of targets in vivo. We design custom DNA libraries containing putative TF binding sites in their native genomic sequence context, and we use in vitro genomic-context protein-binding microarray (gcPBM) assays (Gordan et al., 2013) to quantitatively measure binding of each TF to the genomic sequences in our custom library. The quantitative, high-throughput gcPBM measurements revealed extensive differences in binding specificity between paralogous TFs. Most differences are concentrated in the mediumand low-affinity ranges, which explains why they were missed by previous DNA-binding data and models. To quantify the differences in specificity between TF paralogs, we developed a new modeling approach that combines binding data for paralogous TFs with data from replicate experiments to derive weighted least-square regression (WLSR) models of differential specificity. We integrate our high-throughput data and computational models into a general framework called iMADS (integrative modeling and analysis of differential specificity), which we provide as a publicly available web tool (http://imads.genome. duke.edu). Using iMADS data and models, we show that genomic sites differentially preferred by TF paralogs have different sequence features and DNA shape profiles. This divergence in intrinsic specificity contributes to differential in vivo binding and has important implications for the analysis of TF binding changes due to non-coding genetic variants.

RESULTS

Closely Related Paralogous TFs Bind Differently to Their Genomic Target Sites In Vitro

Paralogous TFs have similar DBDs. However, their DBDs are not identical, and the amino acid sequences outside the DBD region are quite different. We hypothesized that these differences in protein sequence could lead to differences in DNA-binding specificity. To test this hypothesis, we focused on 11 closely related human TFs from 4 distinct structural families: basic-helixloop-helix (bHLH), E26 transformation-specific (ETS), E2 factor (E2F), and Runt-related transcription factors (RUNX). The factors were chosen based on: (1) availability of high-quality ChIP-seq data showing both overlapping and unique in vivo genomic targets for the paralogous TFs (Wang et al., 2013; Encode Project Consortium, 2012), and (2) previous reports that the paralogous TFs have identical binding specificities (Weirauch et al., 2014; Wei et al., 2010; Jolma et al., 2013; Matys et al., 2006). Focusing on putative genomic target sites in their native DNA sequence context, we asked whether paralogous TFs have identical DNA-binding preferences, as expected from their indistinguishable PWM models trained on either in vitro (Figure 1A) or in vivo (Figure S1) data. In vitro PWMs for human TFs are typically derived from high-resolution binding data for a large set of artificial or randomized DNA sequences (e.g., universal PBM [Berger et al., 2006] or systematic evolution of ligands by exponential enrichment sequencing [Jolma et al., 2010] data), while in vivo PWMs are derived from low-resolution data on binding to genomic DNA (e.g., ChIP-seq [Johnson et al., 2007] data). Our experimental approach, using gcPBM assays, is different from previous approaches in that we measure TF binding to genomic DNA sequences, i.e., sequences that the TFs also encounter in the cell, but at high resolution and in a controlled environment. Thus, we take advantage of critical aspects of both in vitro and in vivo approaches.

Figure 1. Paralogous TFs with Indistinguishable PWMs Show Distinct In Vitro Specificities.

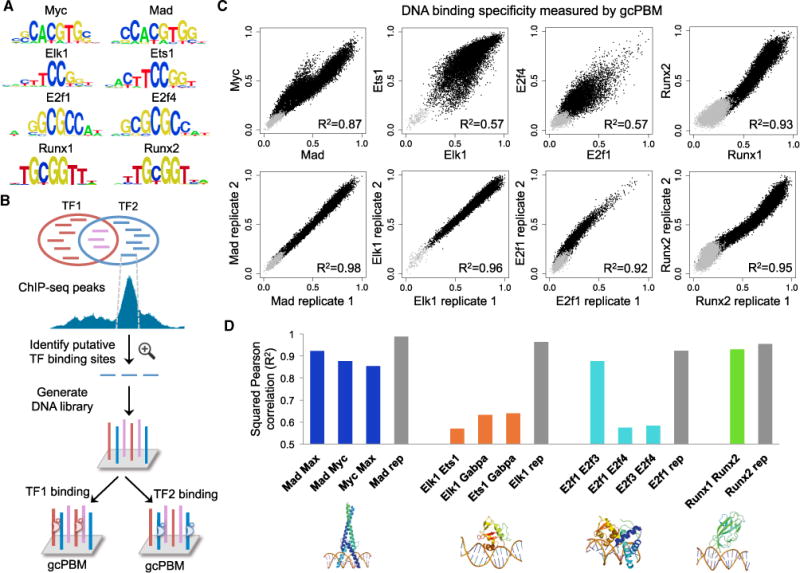
(A) Examples of paralogous TF pairs with indistinguishable PWMs: Myc versus Mad (bHLH family), Elk1 versus Ets1 (ETS family), E2f1 versus E2f4 (E2F family), and Runx1 versus Runx2 (RUNX family). Similar PWMs derived from in vivo data are shown in Figure S1.

(B) Design of a gcPBM library containing putative binding sites for paralogous TFs, selected from unique (red and blue) and overlapping (purple) in vivo genomic targets, as identified by ChIP-seq. We used the gcPBM assay to quantitatively measure in vitro binding of TF1 and TF2 to all selected genomic sites. Figure S2 provides a more detailed description of gcPBM assays.

(C) Direct comparisons of the binding specificities of paralogous TFs for genomic sites (top panels), in contrast to comparisons between replicate gcPBM datasets (bottom panels). Each point in the scatterplot corresponds to a 36-bp genomic region tested by gcPBM. Black points correspond to genomic sequences centered on putative TF binding sites. Gray points correspond to negative control regions, i.e., sequences without binding sites.

(D) Squared Pearson correlation coefficient (R²) for all pairs of paralogous TFs in our study (colored bars) and for representative replicate experiments (gray bars). The lower panels show example 3D structures for one TF in each family, as reported in the PDB (Rose et al., 2015). From left to right: Mad:Max (PDB: 1NLW), Ets1 (PDB: 2STT), E2F4:DP2 (PDB: 1CF7), and Runx1 (PDB: 1HJC). See Figure S3 for a comparison of the similarity in DNA binding specificity versus the amino acid identity in the DNA binding domains of paralogous TFs.

The gcPBM assay measures the level of binding of a TF to tens of thousands of genomic regions simultaneously. In brief, double-stranded DNA molecules attached to a glass slide (microarray) are incubated with an epitope-tagged TF. To detect the amount of TF bound to each DNA spot, the microarray is labeled with a fluorophore-conjugated antibody specific to the epitope tag, and scanned using a standard microarray scanner. The gcPBM protocol is similar to the universal PBM protocol of Berger and Bulyk (2009). The critical difference between the widely used universal PBMs (Berger et al., 2006; Badis et al., 2009; Wei et al., 2010; Weirauch et al., 2013, 2014) and the gcPBM assays in our study is in the design of the DNA library synthesized on the array. Universal PBMs use artificial sequences that cover all possible 10-bp DNA sites. Thus, they provide a comprehensive view of TF-binding specificity for short sequences, but miss important information about the influence of flanking regions, which can significantly affect genomic binding (Gordan et al., 2013). In addition, universal PBMs suffer from significant spatial and location bias, due to the position of a probe on the microarray and the position of a TF binding site on the probe, respectively (Berger et al., 2006; Annala et al., 2011). In comparison, gcPBM libraries contain 30,000 genomic sequences, 36-bp long, centered on putative binding sites for particular TFs or TF families (Figure S2A). Each sequence is represented six times in DNA spots randomly distributed across the array, and we use median values over replicate spots as TF-binding specificity measurements. Our gcPBM libraries are carefully designed to: (1) capture the influence of flanking regions on TF-DNA binding by centering probes on the putative TF binding sites; (2) minimize spatial bias by using median values over replicates spots; and (3) eliminate positional bias in the data by fixing the position of TF binding sites within probes. These critical characteristics of the experimental design lead to TF binding measurements that are highly reproducible, cover a wide range of binding affinities, and are in great agreement with independent binding affinity data (Figures S2B and S2C). In addition, as shown in our proof-of-concept study (Gordan et al., 2013), gcPBM measurements are sensitive enough to capture differences in specificity among related TFs.

To directly compare the binding specificities of TFs within each family, we designed family-specific DNA libraries containing putative binding sites in their native genomic context, and we used gcPBM assays to test in vitro binding of each family member to the selected genomic sites (Figure 1B). The 11 TFs tested in our study are: c-Myc (henceforth referred to as Myc), Max, and Mxd1 (or Mad1, henceforth referred to as Mad) from the bHLH family; Ets1, Elk1, and Gabpa from the ETS family; E2f1, E2f3, and E2f4 from the E2F family; and Runx1 and Runx2 from the RUNX family. For all 11 TFs, the gcPBM assays provided quantitative measurements of in vitro specificity for tens of thousands of genomic sites. The vast majority of these sites were bound with affinities higher than negative controls, indicating that the selected genomic targets are specifically bound.

We analyzed the gcPBM data and, for most pairs of paralogous TFs, we found extensive differences in their in vitro binding specificity for genomic sites, more than expected due to experimental noise (Figures 1C and 1D). In addition, considering all 11 pairs of paralogous TFs in our study, we did not see a correlation between DBD amino acid identity and the similarity in DNA-binding specificity (R² = 0.01; Figure S3), indicating that amino acid identity might not be predictive for whether paralogous TFs prefer similar DNA target sites. The way in which paralogous TFs differ is different for each family (Figure 1C, top panels). bHLH proteins Mad and Myc bind similarly to many of their putative genomic targets, but there is a subset of sites bound with higher affinity by Myc than by Mad. ETS proteins Elk1 and Ets1 bind similarly to their high-affinity genomic sites, but they diverge in specificity for mediumand low-affinity sites. E2F proteins E2f1 an E2f4 show differences across the entire affinity range, but mostly in the medium-affinity sites. We note that although single gcPBM assays do not directly provide affinity measurements, the DNA-binding intensities measured by gcPBM do correlate very well with independently measured affinities (Figure S2C). The paralogous TFs most similar to each other are Runx1 versus Runx2 (rightmost panels in Figures 1C and 1D), which act in different tissue types and are not typically co-expressed under normal cellular conditions (Komori, 2008; Elagib et al., 2003; Lacaud et al., 2002; Hyde et al., 2015; Komori, 2011; Liu and Lee, 2013).

Overall, our gcPBM data show that most TF pairs converge in their specificity for high-affinity sites, but bind differently to lowand medium-affinity sites. This explains why many previous studies reported indistinguishable PWMs for these paralogous TFs (Jolma et al., 2013; Weirauch et al., 2014): PWMs are best at capturing high-affinity sites (Siggers and Gordan, 2014), which are indeed bound the same way by the paralogous factors. However, mediumand low-affinity TF binding sites, which can play important regulatory roles in the cell (Siggers and Gordan, 2014; Scardigli et al., 2003; Gaudet and Mango, 2002; Jaeger et al., 2010; Tanay, 2006), are oftentimes bound differently by TF family members, and may contribute to the differential genomic binding and functional specificity of closely related TFs.

Generalizing TF-Binding Specificities beyond the gcPBM Measurements

In a single gcPBM experiment we can test up to 30,000 genomic sites. However, a library of this size is still not sufficient to cover all putative genomic targets of human TFs. To generalize our TF-DNA binding measurements beyond the genomic sites tested on gcPBMs, we used ε-support vector regression (Drucker et al., 1997) to train positional k-mer regression models for all 11 TFs in our study. We used binary features to encode the identities of mononucleotides (1-mers), dinucleotides (2-mers), and trinucleotides (3-mers) at each position in the TF binding sites and their flanking regions (Figure S4), similar to our previous work (Gordan et al., 2013; Zhou et al., 2015; Mordelet et al., 2013; Yang et al., 2014). For increased accuracy, here we build “core-stratified” SVR models, i.e., a separate SVR model is trained and tested for each “core motif” of a TF (Figure 2A). Core motifs are defined based on gcPBM data and, if available, based on prior structural knowledge about the interactions between DNA and TFs from each family (STAR Methods). Core motifs are short (4–6 bp) and capture the region within TF binding sites that has little degeneracy, likely because of direct interactions with residues in the DBD of the TF (Figures 2B and 2C). For example, for the bHLH TF Mad, the core-stratified SVR model is based on five E-box or E-box-like cores (Figure 2D).

Figure 2. Core-Stratified SVR Approach to Model TF-DNA Binding Specificity.

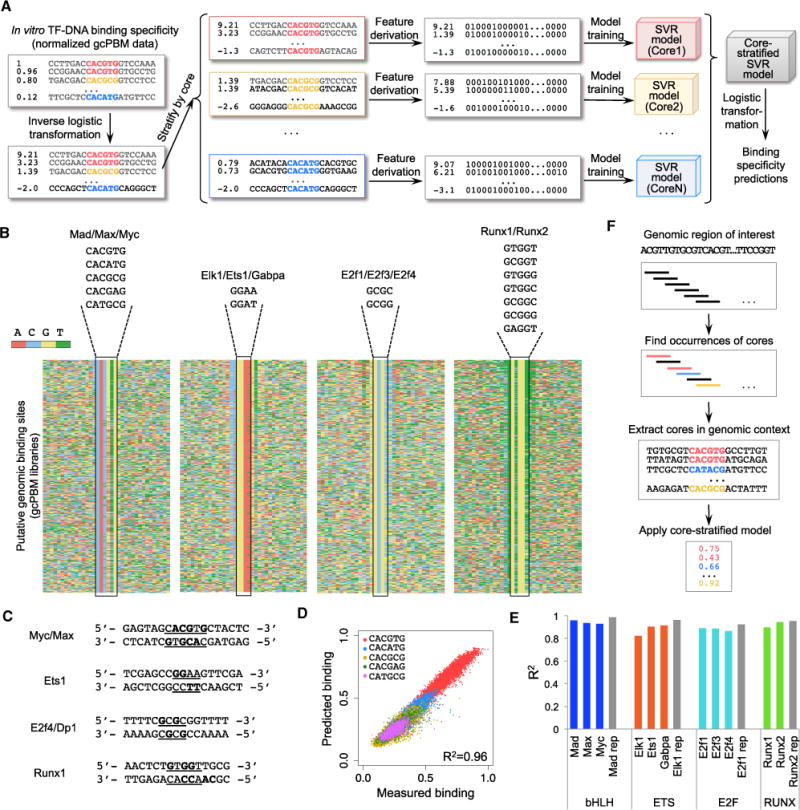
(A) To build core-stratified SVR models of TF specificity, we start with normalized gcPBM data, apply an inverse logistic transformation, separate the gcPBM probes by their core motifs, derive features (Figure S4), and train one SVR model for each core. The predictions made by the SVR models are mapped back to a 0–1 range by applying the logistic transformation (see STAR Methods).

(B) The core motif sequences for each group/family of TFs are shown. Heatmaps show the DNA sequences for all gcPBM probes with binding intensity above the negative control range.

(C) DNA bases that have direct interactions with TF residues, according to available X-ray crystal structures (PDB: 1NKP for Myc/Max; PDB: 2STT for Ets1; PDB: 1CF7 for E2f4/Dp2; and PDB: 1HJC for Runx1). DNA sequences tested in the crystal structure are shown. Core motifs are underlined, and bases that have direct interactions with protein residues are highlighted in bold.

(D) Comparison of measured versus predicted DNA-binding specificity for Tad (from nested 5-fold cross-validation test; STAR Methods). The cores used in the core-stratified SVR model are shown. Figure S5 shows similar plots for all other TFs.

(E) Prediction accuracy of core-stratified SVR models, assessed as the squared Pearson correlation coefficient (R²) between measured and predicted DNA-binding specificity (from nested 5-fold cross-validation test; STAR Methods). Gray bars show the correlation (R²) between replicate experiments. Figure S6 shows comparison with nearest-neighbor models.

(F) Core-stratified SVR models (motivated by the results shown in Figure S7) can be used to make binding specificity predictions for any genomic region.

For all 11 TFs in our study, the core-stratified SVR models achieved high prediction accuracy (R² = 0.82–0.96) on independent, held-out data, indicating that the models accurately capture TF-DNA binding specificity (Figures 2E and S5; Table S1). All validations were performed using nested 5-fold cross-validation tests (STAR Methods). As baseline, we applied a nearestneighbor approach to the same folds as the core-stratified SVR, using Hamming distance as the similarity metric. The nearest-neighbor models had significantly lower accuracy (Figure S6), showing that sequence similarity alone is not sufficient for accurate predictions. Given the high accuracy of our corestratified SVR models, we can confidently use these models to predict TF binding to DNA sites not included in our gcPBM libraries. We note that the core-stratified SVR models have a prediction accuracy close to replicate experiments. Thus, while more complex models of specificity can be derived from our high-quality gcPBM data, we do not expect such models to show large improvements in prediction accuracy compared with the core-stratified SVR models. Our simple, core-stratified approach is motivated by our observation that, for different core motifs, the sequences flanking the core contribute differently to the binding affinity (Figures S7A and S7B). Training a separate SVR model for each core allows us to take into account the dependencies between the core motif and the flanking regions without resorting to complex computational models.

Modeling the Differential DNA-Binding Specificity of Paralogous TFs

Our gcPBM data revealed clear differences in the binding preferences of paralogous TFs for putative genomic target sites (Figure 1). As with all high-throughput technologies that do not measure DNA-binding affinities directly, the binding measurements obtained by gcPBM are not directly comparable between TFs (one reason being that samples used in the experiments may have different concentrations of active TF protein). To address this limitation and perform a robust comparison between paralogous TFs, we developed a weighted regression approach (Figure 3). As described below, this approach allows us to quantify specificity differences and to identify genomic sites differentially preferred by paralogous TFs.

Figure 3. Modeling Differential DNA-Binding Specificity.

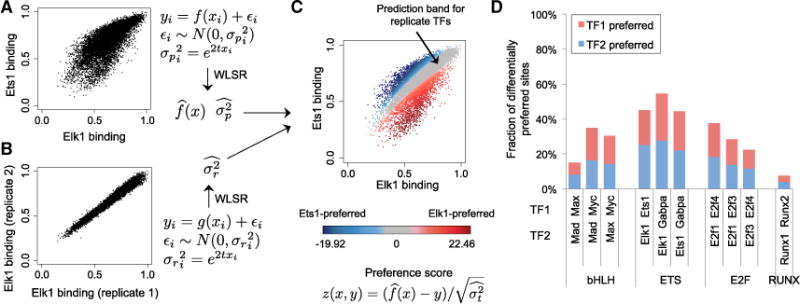
(A) Weighted least-square regression (WLSR) is used to fit the gcPBM data of two paralogous TFs (here, Elk1 versus Ets1), and learn a linear or quadratic function $\widehat{f}$, as well as the variance ${\sigma }_{pi}^2$ at every data point (i.e., genomic site) i.

(B) WLSR is used to learn the variance structure for replicate gcPBM datasets.

(C) By combining the variance learned from replicate data with the WLSR model for paralogous TFs, we compute a “99% prediction band for replicate TFs” (gray), which contains genomic sites bound similarly by the two TFs. Genomic sites outside the prediction band are preferred by one of the two paralogous TFs (red, Elk1; blue, Ets1). The color intensity reflects the quantitative preference score computed according to the WLSR model. Similar plots for all paralogous TFs pairs are shown in Figure S8.

(D) Fraction of genomic sites, among the sites tested by gcPBM, which are differentially preferred by the paralogous TFs in our study.

In brief, we apply WLSR to fit the gcPBM data for two paralogous TFs (Figure 3A), as well as replicate gcPBM datasets (Figure 3B). Next, we integrate information about the variance learned from replicate datasets into the weighted regression model for the paralogous TFs, in order to calculate a “99% prediction band” that comprises all genomic sites bound similarly by the two factors, i.e., sites for which the difference in binding specificity between TF1 and TF2 is within the noise expected for replicate experiments. Intuitively, one can interpret the 99% prediction band as follows: if TF1 and TF2 were replicates, then we would expect 99% of their target sites to fall within the prediction band. We consider the sites outside the prediction band as differentially preferred by TF1 versus TF2, and for each such site we compute a quantitative “preference score” (Figure 3C; STAR Methods). We used the WLSR-based approach to compare all pairs of paralogous TFs in our study (Figure S8). For all TF pairs except Runx1 versus Runx2, we found that between 15% and 55% of the genomic sites tested by gcPBM were differentially preferred (Figure 3D; Table S2). Thus, our WLSR approach allows us to identify genomic sites differentially preferred by paralogous TFs, i.e., sites for which the difference in binding between TFs is larger than the variability observed in replicate experiments.

To facilitate the use of our WLSR models of differential specificity between paralogous TFs, as well as our core-stratified SVR models of binding specificity for individual TFs, we developed the iMADS web server: http://imads.genome.duke. edu. The web server allows users to apply our models for each TF or TF pair to make predictions on any genomic or custom DNA sequence.

Sequence and Structural Characteristics of Genomic Sites Differentially Preferred by Paralogous TFs

We analyzed the differentially bound genomic sites to determine sequence and structural features preferred by each TF. We found that the observed specificity differences between paralogous TFs are due both to the core binding site and the flanking regions, demonstrating the importance of including genomic flanks when measuring and comparing in vitro binding of these TFs. To identify significant differences in core and flanking preferences between TF1 and TF2, we applied the MannWhitney U test to determine, for each core sequence and each 1-mer, 2-mer, and 3-mer feature in the flanking regions, whether the sequence feature is enriched in the set of TF1or TF2preferred genomic sites (Table S3).

Core motifs play critical roles in TF-DNA recognition through direct interactions, mostly hydrogen bonds, between the proteins and DNA. This direct readout mechanism is a major contributor to the binding specificity of TFs. In particular, direct readout in the core binding region is known to be different for different TF families (Rohs et al., 2010). Our results show that even within TF families, the core binding region can contribute to differences in binding specificity between factors (Figures 4A, S9A, and S9B). For example, within the ETS family, the GGAT core is strongly preferred by Ets1 compared with both Elk1 (p = 3.5 × 10⁻⁹⁹; Figure 4A) and Gabpa (p = 1.8 × 10⁻²⁰²; Table S3). Focusing on sequence features in the flanking regions, we identified numerous 1-mer, 2-mer, and 3-mer features differentially preferred by paralogous TFs (Figures 4B, S9A, and S9B; Table S3), which highlights the important role of genomic sequence context in establishing differential DNA binding between TF family members.

Figure 4. DNA Sequence and Shape Preferences Contribute to the Differential Specificity of Paralogous TFs.

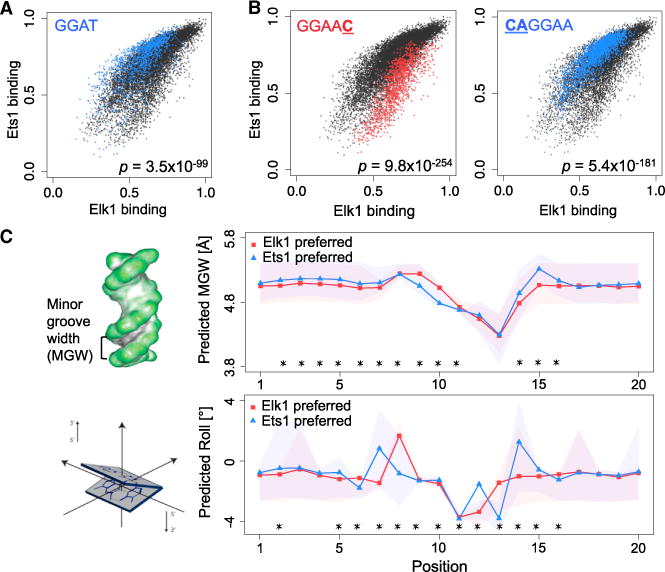
(A) Core motif GGAT shows significant specificity preference for Ets1 versus Elk1. The p value shows the enrichment of the core in Ets1-preferred sites (Mann-Whitney U test).

(B) 1-mer and 2-mer sequences most differentially preferred by Elk1 or Ets1, among sites with the GGAA core. The p values were computed using the Mann-Whitney U test.

(C) Left: schematic of the minor groove width (MGW) and roll structural features. Right: MGW and roll profiles for genomic sites preferred by Elk1 versus Ets1. Asterisks (*) mark the positions within the binding sites (core or flanking region) that are significantly different between the two profiles (p < 10⁻⁵; Mann-Whitney U test). Shaded regions show the 25th–75th percentile ranges at each position. See Figure S9 for comparisons of additional paralogous TF pairs.

Flanking regions are likely contributing to TF-DNA binding specificity through indirect (i.e., shape) readout mechanisms. Using DNAshape (Zhou et al., 2013) predictions of minor groove width, roll, propeller twist, and helix twist, we found that paralogous TFs differ significantly in their preference for certain DNA shape features, especially for minor groove width and roll (Figures 4C, S9C, and S9D; Table S4). These findings are in agreement with previous hypotheses that DNA shape readout is often exploited to distinguish between TF family members (Rohs et al., 2010). Our data and models provide a way to comprehensively study the differences in DNA shape profiles preferred by paralogous TFs.

Differential In Vitro Specificity Contributes to Differential In Vivo Binding of Paralogous TFs

The analyses above demonstrate that, despite their amino acid sequence similarities, paralogous TFs do have distinct intrinsic DNA-binding preferences. The next obvious question is whether these preferences are exploited in vivo to produce differential, TF-specific patterns of genomic binding. Answering this question requires a comparison between our in vitro gcPBM data and data produced in vivo using an orthogonal method. Here, we focus on in vivo data obtained using ChIP-seq, as this is the predominant assay for addressing questions of TF-DNA binding in the cell.

To test whether the differences in intrinsic binding specificity between paralogous TFs, as observed in our gcPBM data, are relevant for differential in vivo binding, we applied iMADS models to make predictions of individual specificity and differential specificity on ChIP-seq peaks for Mad and Myc from H1SC cells, Elk1 and Ets1 from K562 cells, and E2f1 and E2f4 in K562 cells (Encode Project Consortium, 2012). We selected these datasets because they were not included in the gcPBM design, and thus are independent of our training data. For each TF pair, we processed the ChIP-seq data to identify peaks for each TF, we merged the two lists of peaks, and for each peak we computed the natural logarithm of the ratio between TF1 and TF2 ChIP-seq signals (STAR Methods). We then scanned the peak regions and used iMADS models to predict differential binding of TF1 versus TF2 (e.g., Figure 5A).

Figure 5. In Vitro Binding Preferences of Paralogous TFs Partly Explain Their Differential In Vivo Binding.

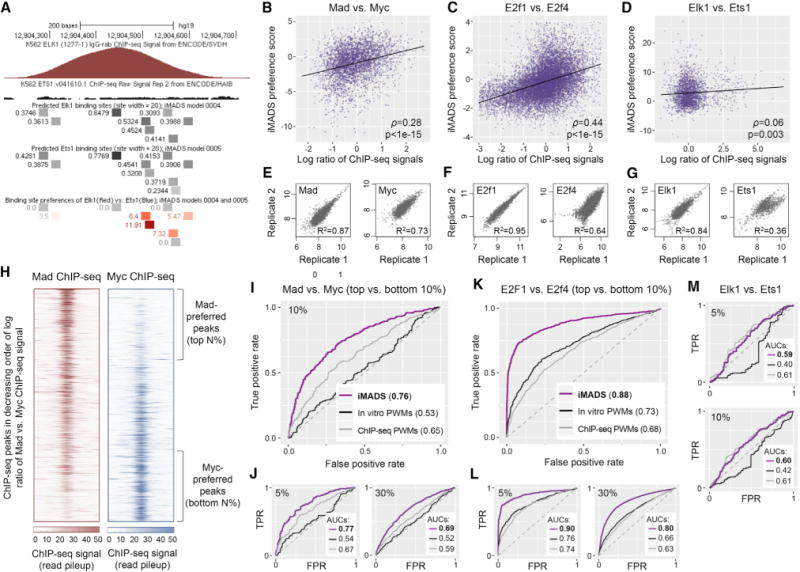
(A) Genomic region bound in vivo by Elk1, but not Ets1 (according to ChIP-seq data [Ayer et al., 1993]) contains binding sites with high preference for Elk1.

(B–D) TF1 versus TF2 in vitro binding preferences, as predicted using our iMADS preference models, have a significant correlation with in vivo binding preferences, as reflected by the log ratios of TF1 versus TF2 ChIP-seq pileup signal (STAR Methods). The Spearman correlation coefficient (ρ) and its statistical significance (p value computed using the asymptotic t approximation [Best and Roberts, 1975]) is shown for each pair of TFs. Due to outlier data points, the scatterplot for E2F factors is limited to peaks with log ratios in the [–3,2.5] interval, and iMADS preference scores in the [–4,4] interval. The full set of peaks, with log ratios in the [–7.79,5.41] interval and iMADS scores in the [–5.89,6.97] interval, are available in Table S5. The full datasets (3,726 peaks for bHLH proteins, 13,004 peaks for E2F proteins, and 2,208 peaks for ETS proteins) were used to assess the correlations and to compute the best fit lines (shown in black).

(E–G) Pearson correlation coefficients between the ChIP-seq pileup signals computed from replicate ChIP-seq datasets. All datasets used in this analysis show good correlation, except for the Ets1 ChIP-seq data. Additional analyses of ChIP-seq data quality are shown in Figure S10.

(H) ChIP-seq data for Mad and Myc, with peaks sorted in decreasing order of the log ratio of Mad versus Myc signal. Regions of 1,000 bp centered at the peak summits are shown. The data can be used to identify “Mad-preferred” and “Myc-preferred” peaks, selected as the top and bottom N% of peaks, respectively. For different values of N, we tested how well iMADS models can distinguish between the peaks preferred by each TF. (I and J) Receiver operating characteristic (ROC) curves showing the performance of iMADS models of differential specificity, as well as PWM models trained on in vitro or in vivo data, in distinguishing Madfrom Myc-preferred peaks. In vitro PWMs were derived from the same gcPBM data used to train iMADS preference models. In vivo PWMs were trained on the ChIP-seq datasets used for testing (STAR Methods). The area under the ROC curve (AUC) is shown for each model. AUC values vary between 0 and 1, with 0.5 corresponding to a random model. Results are shown for N = 5, 10, and 30. (L and K) Similar to (I and J), but for E2F proteins E2f1 versus E2f4.

(M) Similar to (I–K), but for ETS factors Elk1 and Ets1, and showing the results for N = 5 and 10. Additional results are available in Table S6. Additional analyses are shown in Figures S11 and S12.

We first analyzed the data in their entirety, by performing a direct comparison between iMADS preference scores and differential ChIP-seq signal, computed for all peaks. The overall correlation between iMADS preference scores and differential ChIP-seq signal is significant (p < 10⁻¹⁵ for Mad versus Myc and E2f1 versus E2f4, p = 0.003 for Elk1 versus Ets1), although moderate (Spearman correlation ρ = 0.28 for Mad versus Myc, 0.44 for E2f1 versus E2f4, and 0.06 for Elk1 versus Ets1). For comparison, this correlation is similar to or better than the correlation obtained for individual TFs by comparing their ChIPseq data versus individual in vitro binding specificity models (ρ = 0.14 for Mad, 0.22 for Myc, 0.2 for E2f1, 0.26 for E2f4, 0.4 for Elk1, and 0.05 for Ets1; see STAR Methods). As expected based on the low quality of the Ets1 ChIP-seq data (Figures 5G and S10), we found a lower correlation for ETS compared with bHLH and E2F proteins (Figures 5B–5D).

Interpreting these results, however, is challenging because it is unclear what degree of correspondence between gcPBM and ChIP-seq data should be expected in principle. We note that there are at least three reasons for this. First, differences may accurately reflect the influence of biological factors present in the cellular environment but missing in our in vitro system. Second, the resolution of the two methods is inherently different. In gcPBM assays we test TF binding to 36-bp genomic regions containing individual binding sites, and this resolution is independent of the TF measured and the experimental conditions. By contrast, ChIP-seq data have a resolution of 100–500 bp, dependent on both the exact experimental conditions (e.g., antibody used, sonication conditions, etc.) and the methods used for data analysis (e.g., peak calling). Third, ChIP-seq data contain numerous technical biases (Kidder et al., 2011), including formaldehyde crosslinking bias (Solomon and Varshavsky, 1985; Lu et al., 2010; Gavrilov et al., 2015), antibody specificity and variability problems (Parseghian, 2013; Schonbrunn, 2014; Wardle and Tan, 2015) (Figure S15), technical artifacts due to highly expressed regions of the genome (which are not corrected by regular input controls) (Teytelman et al., 2013; Park et al., 2013; Jain et al., 2015), bias due to genome fragmentation and PCR amplification (Bardet et al., 2011; Poptsova et al., 2014), etc. These biases can lead to false-positive and false-negative peaks, and they also significantly affect any quantitative estimates of in vivo TF binding levels derived from ChIP-seq data, in ways that we do not understand well enough to correct (Gavrilov et al., 2015). In contrast, gcPBM measurements are quantitative and they directly reflect the in vitro TF binding level to each tested genomic region.

In an effort to overcome the limitations discussed above, we performed receiver operating characteristic (ROC) curve analyses, an approach that is widely used to evaluate the predictive power of DNA-binding models with respect to in vivo ChIP-seq data (Kulakovskiy et al., 2016; Orenstein and Shamir, 2014; Weirauch et al., 2013; Alipanahi et al., 2015; Mariani et al., 2017; Gordan et al., 2009; Arvey et al., 2012; Isakova et al., 2017). In brief, this approach allowed us to evaluate how well our iMADS models of differential specificity can distinguish between TF1and TF2-preferred ChIP-seq peaks, defined as the top N% and bottom N% of peaks, respectively, sorted according to log ratio of ChIP signals (Figure 5H). For example, for bHLH proteins Mad versus Myc, the iMADS model achieved areas under the ROC curve of 0.69–0.77, depending on the fraction of peaks chosen for the classification test (top and bottom 5%–30% of peaks; Figures 5I and 5J).

To gauge the performance of iMADS models in the ROC analyses, we provide two comparisons. First, we trained in vitro PWMs on the same gcPBM data as the iMADS models, and then tested them on the ChIP-seq data. By this comparison, the performance of iMADS models was superior, as they predicted TF1and TF2-preferred ChIP-seq peaks with higher accuracy than PWMs (Figures 5I–5M). Second, we collected in vivo-derived PWMs trained on the same ChIP-seq datasets used for testing. Despite the important advantage this gives to in vivo PWMs (see STAR Methods), our iMADS models of differential specificity performed best (Figures 5I–5M). Even in the case of ETS proteins, which have poorer quality ChIP-seq data, the performance of our iMADS models (trained on independent data) was comparable with the performance of in vivo motifs (trained on the ChIP-seq data itself), especially when focusing only on the top versus bottom 5%–10% of the peaks (Figure 5M). Taken together, these results suggest that the in vitro binding specificity captured by our iMADS models contribute, to a significant extent, to the differential in vivo binding of paralogous TFs.

Accordingly, when we focused on the genomic sequences in gcPBM data that are differentially preferred by paralogous TFs and we compared the biological functions of genes in the neighborhood of these genomic binding sites, we successfully recovered different gene ontology terms that are enriched for genes associated with differentially preferred sites (Figure S12). In these analyses, many of the terms we recovered had been reported previously in independent studies for the individual ETS factors (Alberstein et al., 2007; Boros et al., 2009; Bories et al., 1995; Teruyama et al., 2001; Soldatenkov et al., 2002).

To facilitate analysis of differential in vivo binding and functional specificity of paralogous TFs, our iMADS web server provides easy access to genome-wide predictions of TF binding specificity (from core-stratified SVR models; Figures S13A and S13B) and differential specificity (from WLSR models; Figure S13C). In addition, users can focus on specific regions around genes, specify custom lists of genes or genomic coordinates to analyze, view predictions in the web server or in the UCSC genome browser, and make predictions of TF binding specificity and differential specificity for any DNA sequence of interest.

Disease-Related Genetic Variants Have Differential Effects on the Specificity of Paralogous TFs

Current studies of the effects of non-coding variants on TF-DNA binding focus on predicting changes in the DNA-binding specificity of individual TFs, assessed using simple PWMs (Andersen et al., 2008; Thomas-Chollier et al., 2011; Ward and Kellis, 2016; McVicker et al., 2013) or complex models (Zhou and Troyanskaya, 2015; Alipanahi et al., 2015; Lee et al., 2015), but ignoring the fact that multiple paralogous factors are co-expressed in the cell and can influence each other’s binding to the genome. The iMADS models allow us to test whether non-coding variants/mutations have differential effects on the binding specificity of paralogous TFs.

To illustrate the use of our iMADS models and web server to analyze non-coding variants, we focused on somatic mutation rs786205688, associated with malignant prostate cancer (Yadav et al., 2015). The mutation resides in the POLK gene region, which is important for DNA damage repair, and it creates a binding site for the ETS family of TFs. According to current models, the newly created binding site has similar specificities for Ets1 and Elk1. However, according to the iMADS model of Elk1 versus Ets1 binding preference, the new site is highly preferred by Elk1, and bound only non-specifically by Ets1, indicating that the functional effect of this mutation could be due to increased Elk1 binding (Figure 6A). This hypothesis is consistent with the fact that upregulation and activation of Elk1 has been reported to associate with malignancy of prostate cancer, and inhibition of Elk1 has been proven effective on inhibiting growth of prostate cancer cells (Patki et al., 2013). In Figure S14 we present the simple steps that users can follow to analyze non-coding variants, such as rs786205688, for their effect on binding of paralogous TFs. We note that the goal of such an analysis is not to conclusively identify a causal relationship between the variant and the phenotype, but to generate mechanistic hypotheses for follow-up analyses.

Figure 6. Analyzing Non-coding Somatic Mutations Using iMADS Models of Specificity and Differential Specificity.

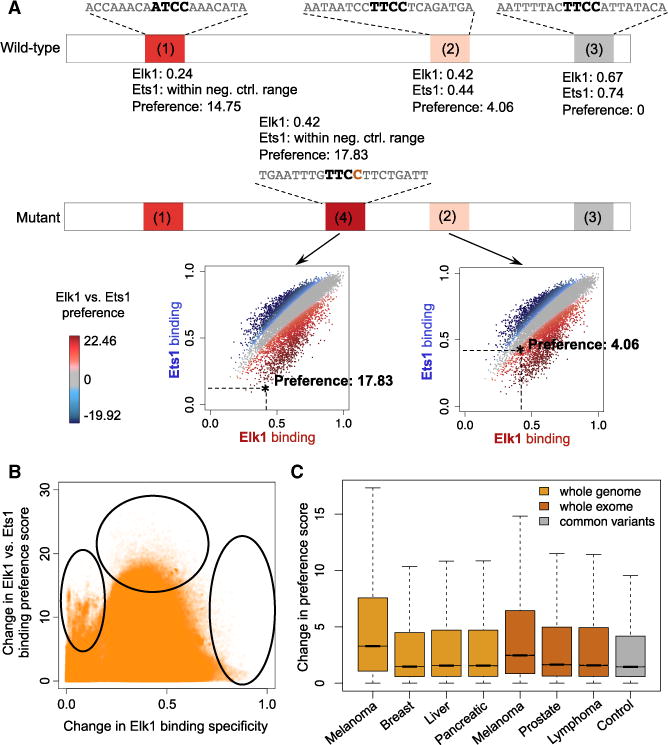
(A) Example of iMADS predictions for variant rs786205688. Plots show predicted ETS sites in a 300-bp genomic region centered on the variant (chr5:74893909). Binding sites (1), (2), and (3) are present both in the wild-type (reference) and the mutant (tumor) sequences. Binding site (4) is created in the tumor by the somatic mutation. The color of the binding sites reflects the Elk1 versus Ets1 preferences, as computed by iMADS. Scatterplots show the binding specificities and preferences of sites (4) and (2) (marked by stars) compared with the genomic sites tested by gcPBM in our study. See Figure S14 for the precise steps users can follow to reproduce the predictions shown here for rs786205688.

(B) Scatterplot of the absolute change in Elk1 binding score compared with the absolute change in preference score of Elk1 versus Ets1, for noncoding somatic mutations identified in melanoma cancer patients (ICGC dataset SKCA-BR). Ovals highlight sets of mutations discussed in the main text.

(C) Boxplot showing the changes in preference score for non-coding somatic mutations identified in different types of tumors, compared with a control set of non-coding variants from the 1000 Genomes Project. The somatic variants were identified from either whole-genome (light orange bars) or whole-exome (dark orange bars) sequencing data from ICGC (STAR Methods). The control variants (gray bar) were randomly selected among common variants with minor allele frequency >0.01 (Zhou and Troyanskaya, 2015). For each dataset, the box shows the median change in preference score and the 25th and 75th percentiles. Whiskers extend to the most extreme data points that are no more than 1.5 times the interquartile range from the box. For all tumor types, preferences changes are significantly larger for somatic mutations than for common variants: one-sided Mann-Whitney U test p value < 2.2 × 10⁻¹⁶.

The case of Elk1 versus Ets1 illustrates how disease-related mutations may affect TF specificity versus preference independently. We analyzed iMADS predictions for somatic mutations from melanoma whole-genome sequencing data (International Cancer Genome Consortium et al., 2010) and found a subset of mutations (Figure 6B, left oval) that have almost no change in Elk1 binding specificity, but large changes in Elk1 versus Ets1 preference. In addition, mutations with the largest change in Elk1 specificity tend to have small changes in preference score (Figure 6B, right oval). This was expected, as large changes in binding specificity will correspond to high-affinity sites (in either wild-type or mutant sequences), which are bound similarly by the two TFs. Finally, we also found that mutations that maximize the change in Elk1 versus Ets1 preference (Figure 6B, top oval) are not the ones that maximize the change in Elk1 binding specificity. Thus, in order to study the effects of such sites on Elk1 binding in vivo, one needs to consider the competitive binding of Elk1 versus Ets1, and potentially other ETS family members.

Next, we extended our analysis of non-coding somatic mutations to several tumor types with publicly available wholegenome or whole-exome sequencing data from the International Cancer Genome Consortium (International Cancer Genome Consortium et al., 2010). (We note that non-coding mutations in close proximity to coding regions can be identified from exome sequencing data.) We analyzed non-coding mutations from melanoma, breast cancer, liver cancer, pancreatic cancer, prostate cancer, and lymphoma, as well as a control set of common non-coding variants (STAR Methods). We found that cancer mutations lead to significantly larger changes in Elk1-Ets1 preferences scores (Figure 6C), suggesting that changes in the relative preferences of paralogous TFs could have important phenotypic effects. Thus, our iMADS models of differential specificity allow us to study the effects of non-coding somatic mutations on the genomic binding of individual TF family members, taking into account the fact that a particular TF can be affected either directly (by mutations that change its specificity) or indirectly (by mutations that change the specificity of competing TF family members).

DISCUSSION

DNA-binding specificity is a fundamental characteristic of TFs. Nevertheless, the contribution of intrinsic sequence specificity to the differential in vivo binding of paralogous TFs is a largely unexplored area of research. Focusing on 11 paralogous TFs across 4 distinct protein families, we show that differences in intrinsic specificity, not captured by current DNA motif models, can be critical for TF family members to distinguish between their genomic targets and achieve functional specificity in the cell. The integrated computational-experimental approach described in our study (Figure 7) is general and can be applied to any pair of paralogous TFs.

Figure 7. The iMADS Framework for Integrative Modeling and Analysis of Differential DNA-Binding Specificity between Paralogous TFs.

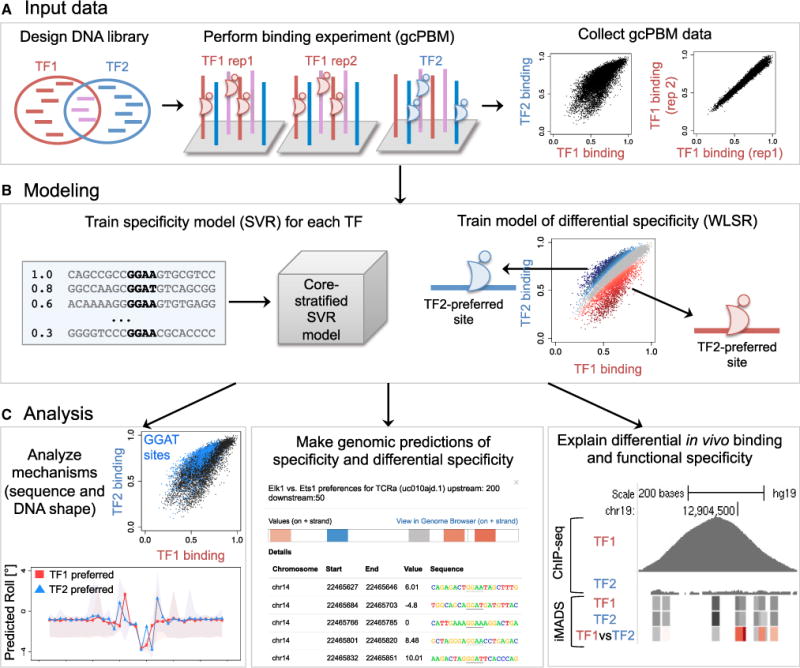
(A) iMADS uses as input gcPBM data for the paralogous TFs, based on a DNA library that contains genomic sites bound by either TF in the cell.

(B) iMADS models are trained using support vector regression (to describe the DNA-binding specificity of individual TFs) and weighted least-square regression (to describe the differential specificity between two TFs).

(C) gcPBM data and iMADS models can be used to analyze sequence and shape preferences of paralogous TFs (left), to make genomic predictions of binding specificity and differential specificity (middle), and to analyze the contribution of differential in vitro specificity to differential in vivo binding (right).

Our observation of differential binding specificity between closely related TFs has implications for interpreting the effects of non-coding genetic variants and mutations. Some diseasecausing mutations could significantly affect binding of a TF by changing its preference relative to other family members expressed in the same cells. To our knowledge, no previous studies of non-coding genetic variations takes into account the potential influence of competing TF family members. Our analysis of somatic non-coding mutations shows that mutations that maximize the change in preference between paralogous TFs are not those that maximize change in specificity for either TF. This suggests that focusing only on changes in binding specificity for individual TFs, as in previous studies, has limited power in understanding the effects of non-coding mutations on TF binding.

Given that most mammalian TFs are part of large protein families with multiple TF paralogs expressed at the same time, it is surprising how little we know about how paralogous TFs achieve their unique specificities in the cell. The in vivo binding of a TF is a result of many factors, including not only the intrinsic DNA-binding specificity of that TF and its paralogs, but also the concentrations of the paralogous TFs, the presence and concentrations of co-factor proteins (Siggers et al., 2011; Slattery et al., 2011; Mann et al., 2009), the chromatin environment, etc. Our study takes an important step in deciphering the molecular mechanisms of differential specificity in TF families, by identifying differences in intrinsic preferences between paralogous TFs and showing that these in vitro differences contribute to differential in vivo binding. We envision that more quantitative highthroughput technologies and computational models will be developed to gain an even deeper understanding of the differential genomic binding and function of paralogous TFs.

STAR★METHODS

Detailed methods are provided in the online version of this paper and include the following:

KEY RESOURCE TABLE

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Antibodies
Alexa488-conjugated anti-His	Qiagen	Cat# 35310
Alexa488-conjugated anti-GST	Invitrogen	Cat# A-11131; RRID: AB_2534137
Bacterial Strains
BL21-CodonPlus (DE3)-RIL	Agilent	Cat# 230245
Deposited Data
Protein-DNA binding data	This study	GEO: GSE97794
Software and Algorithms
Perl	The Perl Foundation	https://www.perl.org/
Python	Python Software Foundation	www.python.org
R 3.2.4	R Development Core Team	https://www.R-project.org
Universal Protein Binding Microarray (PBM) Analysis Suite	Martha Bulyk’s laboratory	http://the_brain.bwh.harvard.edu/software.html
LIBSVM	GitHub	https://github.com/cjlin1/libsvm

CONTACT FOR REAGENT AND RESOURCE SHARING

Further information and requests for resources and reagents should be directed to and will be fulfilled by the Lead Contact, Raluca Gordan (raluca.gordan@duke.edu).

METHOD DETAILS

Protein Expression and Purification

The Life Technologies Gateway cloning system (Liang et al., 2013) was used to insert full length human E2f1, E2f3, and E2f4 genes into the pET-60 destination vector with a C-terminal GST tag. Cells (BL21CodonPlus (DE3)-RIL, Agilent 230245) were grown in LB culture to an OD₆₀₀ of 0.4, then protein expression was induced with 1mM IPTG at 30°C for 2hrs (E2f1), or 20°C overnight (E2f4). Pelleted cells were frozen, then thawed cells were lysed in PBS lysis buffer for two hours at 4°C while gently rocking. The lysate was centrifuged, and the protein was recovered from the soluble lysate using a GE GSTrap FF GST tag affinity column according to manufacturer’s instructions.

Gateway-compatible clones containing the full-length genes for Ets1, Elk1, Gabpa, Runx1, and Runx2 were purchased from GeneCopoeia and the genes were transferred into pDEST15 using the LR Clonase reaction (Life Technologies). This vector enables the production of N-terminally GST-tagged proteins. Cells were grown in LB broth to an OD₆₀₀ of 0.4 to 0.6 and then expression was induced with IPTG at 30° to 37° C. Pelleted cells were frozen, stored at −20 C, and thawed cells were lysed with lysozyme. GSTtagged protein was purified from the soluble portion of the lysate using GST resin (GE Healthcare) according to manufacturer’s instructions.

Full length Myc, Max, and Mad proteins with C-terminal 6xHis tags, as well full-length untagged Max protein were generously provide by Peter Rahl and Richard Young (Whitehead Institute and MIT). The proteins were expressed in bacteria and purified as described by Lin et al. (Lin et al., 2012). As Myc requires heterodimerization with Max to bind DNA efficiently, all Myc universal PBM and gcPBM experiments were performed using both Myc and Max on the same microarray. As in our previous work (Munteanu and Gordân, 2013; Mordelet et al., 2013), we used a 10 times higher concentration of Myc compared with Max to ensure that mostly Myc:Max heterodimers, and not Max:Max homodimers, are formed. Similarly, all Mad universal PBM and gcPBM experiments were performed using both Mad and Max on the same microarray, with a 10 times higher concentration of Mad.

Design of DNA Libraries for gcPBM Assays

The DNA libraries used in gcPBM assays were designed based on genomic data from ChIP-seq assays combined with comprehensive, unbiased, 8-mer E-score data from universal PBM assays. Selected genomic probe sequences were aligned so that the putative TF binding sites were located in the center of the 36-bp probes.

Specifically, to design the gcPBM DNA library for each TF family, we focused on genomic regions bound by the paralogous TFs in vivo, according to available ChIP-seq data. Alternatively, DNase-seq data can be used to design gcPBM libraries; however, we focused on ChIP-seq peaks because these genomic regions are most likely to contain functional TF binding sites. All gcPBM probes designed in this study are 60-bp long, and they contain a 36-bp variable genomic region followed by a constant 24-bp sequence (GTCTTGATTCGCTTGACGCTGCTG) that is complementary to the primer used for DNA double-stranding. The 36-bp genomic regions were selected to contain either: 1) putative TF binding sites in their native genomic sequence context, selected according to ChIP-seq data; or 2) negative control sequences, i.e. genomic sequences without potential binding sites, selected from accessible genomic regions (i.e. DNase-seq peaks) that do not overlap any ChIP-seq peaks. All gcPBM designs contain 6 replicate DNA spots for each genomic probe, randomly distributed across the array surface. The microarrays were synthesized de novo by Agilent. Using the 4×180k Agilent array format (4 chambers that can be used for 4 different tests, with 180k spots per chamber) we were able to test at most 30,000 distinct genomic sites in each gcPBM assay.

Probes Containing Putative Binding Sites

For each ChIP-seq dataset, we scanned the peaks to identify putative TF binding sites using as prior information 8-mer enrichment scores (E-scores) derived from universal PBM data, similar to our previous studies (Gordan et al., 2013; Mordelet et al., 2013; Boyd et al., 2015). The E-score quantifies the relative binding preference of a TF for each 8-mer. The score is a modified form of the Wilcoxon-Mann-Whitney statistic and ranges from −0.5 (least favored sequence) to +0.5 (most favored sequence), with values above 0.35 corresponding, in general, to sequence-specific DNA binding of the tested TF (Berger et al., 2006). Thus, for each TF in our study we performed a universal PBM experiment before designing the gcPBM library. Notably, we note that the experimental protocols for universal PBM and gcPBM assays are very similar, the only difference being the design of the DNA library. Thus, performing universal PBM assays for the TFs in our study was an easy, fast, and cost-effective preliminary step. In addition, the use of 8-mer E-score data to select putative binding sites for the gcPBM design, as opposed to using DNA motifs reported in the literature, ensured that our selection of putative sites was not biased by existing binding models.

Negative Control Probes

Control probes were randomly selected from accessible genomic regions not bound by paralogous TFs (i.e. DNase-seq peaks not overlapping ChIP-seq peaks) and not containing any putative TF binding sites (i.e. with all 8-mers having E-score < 0.2 or 0.3 according to universal PBM data). The specific design for each TF family is described below. Using a stringent cutoff for negative control probes is important to ensure that these probes do not contain any sites bound specifically by the paralogous TFs. As recommended by the microarray manufacturer (Agilent), probe sequences that contained 5 consecutive Cs or 5 consecutive Gs were filtered out in order to eliminate potential technical difficulties during DNA synthesis. In addition, probe sequences with potential binding sites in the flanks were filtered out to ensure that the TF of interest would bind only in the center of the probe, and thus the gcPBM measurements reflect individual TF-DNA binding events. We note that filtering out some the genomic sites is not a problem for our study, as the gcPBM libraries are not meant to be comprehensive. Instead, in designing these libraries we aimed to cover a large and diverse set of TF binding sites in their native genomic context. Computational modeling can be used to generate reliable TF binding predictions for any new DNA sequence (Figure 2).

bHLH Family

We used ENCODE ChIP-seq data for c-Myc (Myc), Max, and Mxi1 (Mad) in HelaS3 and K562 cell lines. We scanned each peak with 8-mer E-score data for Myc, Max, and Mad, and selected regions that contain at least two consecutive 8-mers with E-score R 0.4. Next, we used Myc, Max, and Mad PWMs to align the selected genomic binding sites to each other. The PWMs were derived from the universal PBM data generated in our lab, as described previously (Berger et al., 2006; Berger and Bulyk, 2009), and trimmed to the most informative w=10 positions. To properly align each putative genomic binding site, we expanded the selected genomic sequence (i.e. the sequence will all 8-mer E-scores R 0.4) upstream and downstream by (w-8) base-pairs, we calculated PWM scores for all w-mers in this region, and then we expanded the selected genomic sequence to 36-bp by centering it on the w-mer site with the highest PWM score. Notably, PWMs were not used to select TF binding sites, but only to align them to each other such that the resulting 36-bp probes were all centered on the binding sites. To design negative control probes for the bHLH family, for each protein we randomly selected, from open chromatin regions as identified by DNase-seq (in HelaS3 and K562 cell lines), 300 probes with E-scores < 0.2. 757 negative control probes were selected having E-scores < 0.2 for all three bHLH TFs.

ETS Family

We used ENCODE ChIP-seq data for Ets1, Elk1, and Gabpa in the Gm12878 cell line. Similarly to bHLH proteins, we selected putative binding sites as regions with at least two consecutive 8-mers with E-scores R 0.4 for any of the three TFs. 187 negative control probes were selected at an E-score cutoff of 0.3.

E2F Family

We scanned ChIP-seq peaks for E2f1 in HelaS3 and MCF7 cell lines (for E2f1 and HA-tagged E2f1), E2f4 in Gm12878, HelaS3, and K562 cell lines, and also E2f6 from HelaS3 cell line (to supplement the set of E2F sites). From all the putative binding sites selected, we randomly picked 16,808 probe sequences to use for the gcPBM library. 1000 negative control probes were selected at an E-score cutoff of 0.3.

RUNX Family

We focused on genomic regions bound by Runx1 in primary human HSPC cells and Runx2 in induced osteoblast cells, defined as 300-bp genomic regions surrounding the summits of ChIP-seq peaks called at a MACS2 q-value cutoff of 0.001. To identify putative binding sites from the 300-bp genomic regions, we scanned the peaks for sequences that contain two consecutive 8-mers with E-score R 0.4 for at least one of the paralogous TFs. 6757 negative control probes were selected at an E-score cutoff of 0.3.

Universal and Genomic-Context PBM Assays

Universal PBM and gcPBM experiments were carried out following the standard PBM protocol (Berger and Bulyk, 2009; Berger et al., 2006). Briefly, we first performed primer extension to obtain double-stranded DNA oligonucleotides on the microarray. Next, each microarray chamber was incubated with a 2% milk blocking solution for 1 h, followed by incubations with a PBS-based protein binding mixture (Berger and Bulyk, 2009) for 1 h and with Alexa488-conjugated anti-His antibody (1:20 dilution, Qiagen 35310) or anti-GST antibody (1:40 dilution, Invitrogen A-11131) for 1 h. The array was gently washed as previously described (Berger and Bulyk, 2009) and then scanned using a GenePix 4400A scanner (Molecular Devices) at 2.5-mm resolution. Data were normalized with standard analysis scripts(Berger and Bulyk, 2009; Berger et al., 2006). For gcPBM assays, the normalized data were further processed to compute median values over replicate spots containing identical DNA sequences.

For each TF we performed PBM experiments at different concentrations of the TF, in order to select a concentration that resulted in a wide range of fluorescent intensity values according to the microarray scans. Concentrations that resulted in very dim signal, as well as concentrations that resulted in saturated DNA spots at low scanner intensity settings, were avoided. For bHLH TFs we used 100nM total dimer concentration of His-tagged Myc:Max, Max:Max, and Mad:Max, for both universal PBM and gcPBM assays. For ETS factors, concentrations of 50-100nM were used. For E2F TFs, concentrations of 200nM for both E2f1 and E2f4 were used in universal PBMs, and 200nM and 250nM for E2f1, 250nM for E2f3, and 500nM and 800nM for E2f4 were used in gcPBM. For RUNX family TFs, concentrations of 200nM for both Runx1 and Runx2 were used in universal PBMs, and10nM and 50nM for both Runx1 and Runx2 were used in gcPBM. We note that the concentrations above reflect the total protein in each sample, and not the amount of active protein, which is difficult to measure. The precise concentration of active protein can vary between biological replicates, and thus concentrations reported for different biological replicates are not necessarily comparable.

QUANTIFICATION AND STATISTICAL ANALYSIS

ChIP-Seq and DNase-Seq Data

The ChIP-seq (Johnson et al., 2007) data for transcription factors c-Myc, Mad1(Mxi1), Max, E2f1, E2f4, Ets1, Elk1, and Gabpa were retrieved from ENCODE (Encode Project Consortium, 2012). We used ChIP-seq experiments generated in Gm12878, HelaS3, H1hesc, K562, and MCF7 cell lines. ChIP-seq data for Runx1 and Runx2 were retrieved from the NCBI Gene Expression Omnibus database (Edgar et al., 2002), with accession number GSE45144 for Runx1 in human hematopoietic stem and progenitor cells (HSPCs) (Beck et al., 2013), and GSE49585 for Runx2 in cultured human osteoblasts (Hakelien et al., 2014).

All ChIP-seq data sets were downloaded as bam files, and we applied two peak calling methods: 1) MACS2 (Zhang et al., 2008) peak caller with q-value cutoff = 0.001, using as input merged bam files from replicate ChIP-seq experiments, and 2) IDR (Li et al., 2011) pipeline, with cutoff of false discovery rate = 0.05, as recommended by the authors. The peaks called by MACS2 were used to design DNA libraries for gcPBM experiments (Figures 1B and S2A), while the more stringent IDR peaks were used for the in vivo analyses in this study (Figures 5, S10–S12, and S15).

For each set of peaks, we ran the motif finding tool MEME-ChIP (Machanick and Bailey, 2011) to verify that the most enriched motif corresponds to the TF tested in the ChIP experiment. In only one set of peaks, corresponding to Ets1 replicate 1 ChIP-seq data in Gm12878 cells, the motif was not correct, i.e. MEME-ChIP could not recover the known GGAA motif. Thus, we only used peaks called by MACS2 from replicate 2 ChIP-seq data for Ets1 in Gm12878 cells.

DNase-seq (Song and Crawford, 2010) data were used in the gcPBM design to generate negative control probes, i.e. probes not bound by the TFs of interest. All DNase-seq data were downloaded as peak files from the ENCODE database (Encode Project Consortium, 2012).

gcPBM Data Processing. Identifying Cores

The raw gcPBM data for each TF was processed using standard PBM software (Berger and Bulyk, 2009), then log-transformed using the natural logarithm. Next, we computed median log fluorescent intensities over replicate DNA spots (i.e. DNA spots containing identical sequences), and we performed two filtering steps to remove probes with putative binding sites in the flanking regions. First, for TFs that bind as homodimers, we filtered out probes with large differences in fluorescent intensity between probe orientations (relative to the glass slide). Such differences are likely caused by secondary binding sites in one of the flanking regions, different from the main binding site located in the center of the probe. The cutoff used for this filtering step was the 95^th percentile of the difference in log intensity between the two orientations, as observed for negative control probes. Second, we filtered out probes for which the central 12-bp regions did not contain at least two consecutive 8-mers with E-score > 0.4 (i.e. for which the putative TF binding site was likely to be shifted relative to the center of the probe, due to the PWM alignment step described in section 2 above), as well as probes for which the flanking regions outside the central 10-bp contain one or more 8-mers with E-score >0.35. These filtering steps were applied to ensure that each probe contained a single putative TF binding site, located in the center of the probe. The total number of probes with putative binding sites is available in Figure S7C. For each final gcPBM data set, the log-transformed binding intensities were normalized to values between 0 and 1 in order to facilitate the interpretation of our binding data and predictions.

For each TF family, we used the DNA motifs of the TFs (as generated from our universal PBM data), as well as motif information and TF-DNA co-crystal structures available from literature (Werner et al., 1997; Nair and Burley, 2003; Ferré-D’Amaré et al., 1993; Tahirov et al., 2001; Zheng et al., 1999) to determine the length of the core motif. We used a length of 6-bp for bHLH factors, 4-bp for ETS factors, 4-bp for E2F factors, and 5-bp for RUNX factors (Figure 2). Next, we analyze the gcPBM data for each TF family to determine which cores are bound specifically (i.e. with signal above the 95^th percentile of negative controls) by at least one family member. The list of cores for each family is available in Figure 2B.

Core-Stratified SVR Models of TF-DNA Binding

To build core-stratified support vector regression (SVR) models that accurately reflect TF-DNA binding specificity, we applied the following procedure for each TF:

1. Starting with gcPBM data for the TF, obtained and processed as described above, we first trimmed each 36-bp probe to the center 20 base pairs. We performed this step for two reasons. First, we noticed that including nucleotides outside the central 20-bp region results in insignificant improvements in predictions accuracy. Second, using shorter regions reduces the computational time required to train the models, as well as the prediction time for new DNA sequences. For most sequences in our DNA libraries, there is a one-to-one mapping between the original 36-bp sequences and the trimmed, 20-bp sequences. For cases where two or more 36-bp probes contain the same central 20-mer, the median binding intensity over the 36-mer probes was taken to represent the binding intensity for the 20-mer.

2. We applied an inverse logistic transformation to the normalized gcPBM data. We performed this step because our normalized gcPBM data contains binding scores ranging from 0 to 1, and regression models based on this data can run into extrapolation problems, i.e. predict values smaller than 0 or greater than 1. In order to overcome this problem and improve the stability of our models, we applied the inverse logistic transformation to the (0,1)-normalized gcPBM data, and we used the transformed values during the model-training step.

3. We split the set of 20-mer sequences based on their core motifs, with the cores defined for each TF family as described in section 5 above, and in Figure 2.

4. We generated the feature vector for each 20-mer sequence. The feature vector consists of binary values reflecting the presence (1) or absence (0) of each possible nucleotide (1-mer), dinucleotide (2-mer), or trinucleotide (3-mer) at each position in 20-mer sequence (Figure S4) (Mordelet et al., 2013; Zhou et al., 2015). We note that using feature vectors consisting of only 1-mer features would be equivalent to training position weight matrix (PWM) model. Using 2-mer and 3-mer features allows us to capture dependencies between neighboring positions within TF binding sites and their flanking regions, which can significantly improve the accuracy of binding specificity models (Zhou et al., 2015).

5. We then split the gcPBM data matrix into several data matrices, each corresponding to one core motif (Figure 3A). Using the data matrix for each core, we built an epsilon support vector regression (ε-SVR) model using 1-mer, 2-mer, and 3-mer sequence features. We tested linear and radial basis function (rbf) kernels, and for each TF we used the kernel that performed best in a cross-validation test. For each linear SVR model, we applied nested 5-fold cross-validation to determine the best values for the hyperparameters C (cost) and ε. We tested the following parameter values: C ∈ {0.001, 0.01, 0.05, 0.1, 0.5, 1, 10}, and ε ∈ {0.001, 0.01, 0.05, 0.1, 0.2, 0.3, 0.4, 0.5, 0.75, 1}. For each rbf-kernel SVR model, we applied nested 5-fold cross validation with C ∈ {0.01, 0.05, 0.1, 0.5, 1, 5, 10}, ε ∈ {0.0001, 0.0005, 0.001, 0.005, 0.01, 0.05, 0.1, 0.5, 1}, and g ∈ {0.0001, 0.0005, 0.001, 0.005, 0.01, 0.1, 1, 10}. To perform the nested 5-fold cross validation, we split each data set into 5 folds (Table S1). Using each fold for testing, we trained a model on the remaining 4 folds, and on these 4 folds we used 5-fold cross-validation to learn the values of the hyper-parameters. Thus, we ensure that the test data points are completely independent of the training process. For the genome-wide predictions and the models released through iMADS, we trained a “final” model for eachTF, for each core, by 5-fold cross-validation. Our models and predictions can be downloaded from https://imads.genome.duke.edu/datasources .

Modeling Differential Specificity with WLSR

To identify sites preferred by TF1 or TF2, we used a weighted regression approach that incorporates data from replicate gcPBM experiments. gcPBM data is highly reproducible (Figures 1C and S2B). However, binding measurements vary slightly between replicate experiments, and for some TFs the variance in binding intensity is not constant across the intensity range. In addition, replicate gcPBM experiments are not always done at the same concentration of active TF, because determining this concentration is not trivial. Instead, the protein concentration specified in our binding assays is the total protein concentration in the sample. When different concentrations of active TF are used in replicate experiments, the binding measurements still correlate very well, but the correlation may not be linear (see, for example, the E2f1 replicates in Figure 1C). In order to capture the characteristics of replicate gcPBM datasets, we build the following weighted regression model:

$$y_i=f(x_i)+{\epsilon }_i$$

$${\epsilon }_i~N(0,{\sigma }_i^2)$$

where f() is a linear or quadratic function, in order to capture potentially non-linear correlations resulting from different concentrations of active TF. We note that the SD is not constant, but depends on each data point x_i. For all the replicate data generated in this project, we observed that the variance either increased or decreased with the binding intensity. Therefore, we model the variance structure using an exponential function with a tuning parameter t:

$${\sigma }_i^2=e^{2t{x}_i}$$

After parameterizing the function f(), we can estimate the parameters by maximizing the likelihood function, thus obtaining a weighted least square solution.

A similar WLSR approach can be applied when comparing two paralogous TFs TF1 and TF2, in order to capture those genomic sites bound with similar specificity by the two factors. For paralogous TFs, the variance may be larger and the variance structure may be different than what we observe for replicate datasets. We use $\widehat{f}$ to denote the regression function estimated for paralogous TFs, $\widehat{{\sigma }_p^2}$ to denote the variance estimated for paralogous TFs, and $\widehat{{\sigma }_r^2}$ to denote the variance estimated for replicate datasets. Next, for each data point (x_s, y_s), where x_s is the TF1 binding intensity for site b s, and y_s is the TF2 binding intensity for site s, we want to ask whether the two binding intensities are ‘different’ given the uncertainty in our estimated function $\widehat{f}$ and the variance observed between replicate experiments. To answer this question we adapted the variance structure estimated from replicate data to the paralogous TFs regression function. Let N be the number of observations (i.e. sequences) in the gcPBM data b for paralogous TFs, and x₁,…,x_N be the binding measurements for TF1. For any site s whose TF1 binding intensity is x_s, the total variance is predicted by:

$$\widehat{{\sigma }_t^2}=\widehat{{\sigma }_r^2}+\left(\frac{1}{N}+\frac{{(x_s-\overline{x})}^2}{{\displaystyle {\sum }_{i=1}^N{(x_i-\overline{x})}^2}}\right)\widehat{{\sigma }_p^2}$$

Given the large sample size N, we can approximate $\widehat{{\sigma }_t^2}\approx \widehat{{\sigma }_r^2}$ and thus substantially reduce the time required to compute the total variance.

The total variance term allows us to derive a 99% ‘prediction band’ that reflects the variation we would expect if TF1 and TF2 were replicate TFs (Figure 3C, gray band). Using this 99% prediction band for replicate variation, we can next define differentially preferred sites as the sites outside the band. In addition, for each differentially preferred site s we can calculate a ‘preference score’ z defined as the normalized difference between the real and the predicted data:

$$z(X_s,Y_s)=\frac{\widehat{f}(X_s)-Y_s}{\sqrt{\widehat{{\sigma }_t^2}}}$$

Positive values for z correspond to TF1-preferred sites, while negative values for z correspond to TF2-preferred sites (Figure 3C). Preference scores are not limited to the sites tested by gcPBM, but can be computed for any DNA site s by using core-stratified SVR models to predict x_s and y_s.

Finally, we note that gcPBM experiments are typically done on 4-chamber arrays, i.e. 4 PBM experiments are performed simultaneously but in different chambers of the same microarray slide. In general, the results of replicate gcPBM assays done on the same array (‘within-array replicates’) agree better than those of replicates done on different arrays (‘between-array replicates’). Thus, in our WLSR approach, when we compare TFs tested on the same array we use within-array replicate data, and when we compare TFs tested on different arrays we use between-array replicates.

The iMADS Framework

iMADS is an integrative approach that combines quantitative high-throughput experiments and computational modeling to study the differential DNA-binding properties of closely related TFs (Figure 7). For two paralogous TFs of interest, TF1 and TF2, iMADS takes as input high-throughput quantitative binding data for the two proteins. Here, we generate such data using gcPBM assays (see Sections 4 and 5 above), which are carefully designed to provide binding measurements that are highly reproducible, cover a wide range of affinities, are in great agreement with independent binding affinity data, and are sensitive enough to capture differences in specificity among closely-related TFs (Gordan et al., 2013) (Figure 1C). iMADS uses as input gcPBM data for individual TFs as well as biological replicates (Figure 7A).

iMADS contains two main modeling components (Figure 7B): 1) building quantitative DNA-binding specificity models for individual TFs using support vector regression (SVR)(Drucker et al., 1997), and 2) building models of differential specificity between paralogous TFs using weighted least squares regression (WLSR). The WLSR approach allows us to identify genomic sites differentially preferred by paralogous TFs, i.e. sites for which the difference in binding between TFs is larger than the variability observed in replicate experiments. iMADS models are publicly available through our web server (http://imads.genome.duke.edu), and can be used to make predictions for any DNA sequence.

In the sections below we illustrate the use of iMADS data and models to: 1) explore the DNA sequence and structural features that contribute to differential specificity of paralogous TFs; 2) make quantitative predictions of TF binding and TF preference across the genome, as well as predictions of the effect of DNA mutations; and 3) determine the role of differential DNA binding specificity in the in vivo genomic targeting and functional specificity of paralogous TFs (Figure 7C).

Enrichment Analysis for Sequence Features

The enrichment of specific sequence features in the set of genomic regions preferred by TF1 or by TF2 was calculated using a one-sided Mann-Whitney U test. For testing a core motif X, the null hypothesis is that the preference scores of sequences containing core X are from the same distribution as for the background sets of sequences, where the background is defined as the union of all differentially preferred sites; the alternative hypothesis is that the preference scores of sequences containing core X are either larger or smaller than the scores of background sequences. For testing a flanking sequence feature X, a similar approach was used, with the background set of sequences defined as the union of differentially preferred sites that also contain a common core motif. All p-values were adjusted using the Benjamini-Hochberg procedure.

DNA Shape Analysis

The DNA shape profiles of differentially preferred sequences were predicted using the DNAshape tool (Zhou et al., 2013). For each pair of TFs, we report the median of each DNA shape feature at each position, and the p-value reflecting the significance of the differential DNA shape profiles between TF1and TF2-preferred sites (Table S3).

Differential In Vivo Binding Analysis

We ran MACS2 for each replicate ChIP-seq data for paralogous TFs (p-value cutoff of 0.01). Then we used the bedgraph file generated by MACS2 to calculate the total normalized read counts (i.e. the pileup score) in the stringent peak regions identified using IDR-2.0.2, with an IDR cutoff of 0.05 (see section 1 above). We used the sets of reproducible peaks to test the correlation between our in vitro preference predictions and the in vivo ChIP-seq data.

To calculate preference scores from the ChIP-seq data, we focused on fixed-size genomic regions around the ChIP-seq peaks summits for the TFs of interest. We used 300-bp regions for bHLH proteins Mad and Myc, and E2F proteins E2f1 and E2f4, and 180bp regions for ETS proteins Elk1 and Ets1 (we chose smaller regions for ETS factors due to the higher resolution of the ChIP data and the higher frequency of putative binding sites in genomic regions). For each pair of paralogous TFs, we first normalized the pileup scores using the DEseq2 tool (Love et al., 2014), and then we computed the natural logarithm of the ratio of pileup scores for each fixed-sized peak. The log ratio of pileup scores reflects the in vivo DNA-binding preference of TF1 versus TF2.

To compute the in vitro binding preferences, for each ChIP-seq peak we used iMADS models to make binding predictions in the peak region (Figure 5A). Briefly, we scanned the region to identify putative TF binding sites, defined as 20-bp sequences centered at a core motif for the TF family of interest. (20-mers that do not meet this criterion are unlikely to be bound specifically by TFs in this family, and thus are not considered.) Next, each 20-mer centered at a core motif was scored using the SVR models for that core, for the TFs of interest (TF1 and TF2). The predicted binding specificity scores for TF1 and TF2 were then used in the WLSR model of TF1 vs. TF2 binding preference. For peak regions containing multiple putative binding sites, we averaged the TF1-vs-TF2 preference scores over all sites in the same peak region. We applied this procedure to analyze ChIP-seq peaks for Mad vs. Myc in H1SC cells (3,726 peaks), E2f1 vs. E2f4 in K562 cells (13,004 peaks), and Elk1 vs. Ets1 in K562 cells (2,208 peaks). We selected these three data sets, among all ChIP-seq data available for the TFs in our study, because they were not included in the gcPBM designs, and thus are completely independent of our training data. For analyses of individual TFs, we used the natural logarithm of the ChIPseq read pileup at each peak. For analyses of pairs of paralogous TFs, we used the log ratio of the read pileups for the two proteins.

We compared the preference scores computed from ChIP-seq data and iMADS predictions and we computed the Spearman correlation coefficients and their significance (Figures 5B–5D, left panels). In this analysis we used Spearman correlation coefficients, as opposed to Pearson correlation coefficients, because we expect the ranks in the two data sets to correlate, but not necessarily the values. We also performed analyses on binned ChIP-seq data. Specifically, peaks with similar ChIP-seq preference scores were grouped into 10 fixed-size bins. Next, we compared the distributions of iMADS scores in different bins (Figures 5B–5D, right panels) and found statistically significant differences between bins, with higher iMADS preference scores corresponding, in general, to bins with higher ChIP-seq differential signal. We use Mann Whitney U-tests to compare the iMADS distributions between bins.

We evaluated the in vivo predictive power of our iMADS models using receiver operating characteristic (ROC) curve analyses of the ChIP-seq data. For these analyses, we sorted the ChIP-seq peaks in decreasing order of the differential ChIP signal, as shown in Figure 5H (the heatmaps were generated using deepTools (Ramirez et al., 2014)). We used to top N% of peaks as TF1-preferred (or positives) and the bottom N% of peaks as TF2-preferred (or negatives), for different values of N (5, 10, 15, 20, 25, 30, 35, 40, 45, and 50). Next, we used the iMADS scores of differential specificity to compute ROC curves showing how well the iMADS scores can distinguish TF1-preferred from TF2-preferred peaks. We found that iMADS models perform remarkably well: the areas under the ROC curves (AUCs) were 0.69-0.76 for Mad vs. Myc (for N=5-30), 0.8-0.9 for E2f1 vs. E2f4 (for N=5-30) and 0.59-0.6 for Elk1 vs. Ets1 (for N=5-10; larger values of N lead to insignificant AUCs, which is not surprising given the poor quality of available Ets1 ChIPseq data).

We also compared the performance of iMADS models of differential specificity against the performance of PWMs derived from in vitro and in vivo data. Specifically, we used TF1 and TF2 PWMs to compute differential binding scores by taking the natural logarithm of the ratio between the best TF1 PWM score and the best TF2 PWM score in each peak. As ‘in vitro PWMs’ we used motifs derived from our gcPBM data, as they allow a direct comparison to the iMADS preference scores. As ‘in vivo PWMs’ we chose motifs derived from the same ChIP-seq data sets used for testing. These motifs are expected to have the best performance among PWMs, as they were derived from the test data. For TF Myc we used the top motif reported by ENCODE in the Factorbook database (Wang et al., 2013) (for the H1-hESC ENCSR000EBY data set). For Mad we used the third motif reported by ENCODE in Factorbook (for the H1-hESC ENCSR000EBR data set), because the first motif did not pass the Factorbook quality criteria, and the second reported motif was a wide motif not resembling typical bHLH motifs and present only in a small fraction of peaks. For Elk1, Ets1, and E2f1, the motifs reported in Factorbook did not pass their quality criteria. For this reason, we used HOCOMOCO (Kulakovskiy et al., 2016) motifs derived from the ENCODE ChIP-seq data (motifs IDs: Elk1: ELK1_HUMAN.H11MO.0.B, ETS1_HUMAN.H11MO.0.A, E2F1_HUMAN.H11MO.0.A, E2F4_HUMAN.H11MO.0.A). We also tested several motifs from Jaspar (Mathelier et al., 2016) (IDs MA0470.1, MA0024.1, MA0024.2, MA0024.3, MA0028.2, MA0098.3) but their performance was poor so we decided to focus on the gcPBM-derived motifs and the Factorbook/HOCOMOCO motifs. For the motifs downloaded from Factorbook and HOCOMOCO we added 0.000001 or 0.0000000001 pseudocounts (respectively) for each nucleotide at each position, in order to avoid values of 0 in the probability matrices. The pseudocount values were chosen based on the precision of the motifs in each database. We only considered motif matches with scores > 0 (according to the log ratio of PWM probability versus uniform background probability), as they are more likely to be generated from the motif models rather than from the background model.

For the Elk1 vs. Ets1 analysis presented in Figure S11, ChIP-seq peaks that are differential for Elk1 versus Ets1 were identified using the DEseq2 tool (Love et al., 2014). DEseq2 was applied to estimate the dispersion, and an adjusted p-value cutoff of 0.05 and a fold-change cutoff of 2 were applied to call differential peaks. We refer to differential peaks that have significantly higher ChIP-seq signal for TF1 as ‘TF1-unique’ peaks, and to differential peaks that have significantly higher ChIP-seq signal for TF2 as ‘TF2-unique’ peaks. We note that TF1-unique and TF2-unique peaks can be also be identified by first generating a set of peaks for each TF, and then considering only the peaks that do not overlap between the two sets. However, such an approach is highly sensitive to the cutoffs used to call peaks for each TF, and we noticed that ‘unique’ peaks called according to this method were oftentimes barely above the cutoff for one TF and barely below the cutoff for the other TF. To overcome this problem, we used the DEseq2-based approach described above.

Focusing on Elk1 vs. Ets1, we asked whether differential specificities between TF family members account, at least in part, for their differential in vivo targets. For each TF1-unique and TF2-unique peak with at least one occurrences of a core motif, we identified the 20-mer with the highest TF1 preference. Next, we asked whether the distribution of these TF1 preferences is higher for TF1-unique compared to TF2-unique peaks (Figure S11, left plot). Similarly, focusing on TF2-preferred sites (i.e. sites with a negative preferences score according to the TF1 vs. TF2 preference model), we identified the most TF2-preferred site in each TF1and TF2-unique peak, and we asked whether TF2-unique peaks have higher TF2 preference scores (in absolute value, since TF2 preferences are negative) (Figure S11, right plot). We used Mann-Whitney U tests to assess significance.

Functional Analysis

We used GREAT (McLean et al., 2010) to perform functional analysis of differentially preferred sites. From all ETS sites tested in the gcPBM assay, we first selected the sequences differentially preferred by Elk1 and Ets1, as defined by our WLSR approach using Elk1 vs. Ets1 binding specificities (with the 99% prediction interval defined based on Elk1 replicates). Next, we identified the genomic coordinates of ChIP-seq peaks mapped by differentially preferred sites, and used the selected regions as input for the GREAT tool. We identified 278 and 464 genomic regions mapped for Elk1 and Ets1 preferred sites respectively, and ran the GREAT tool with default parameters to identify enriched GO categories.

Analysis of Non-Coding Genetic Variants

Genomic coordinates of non-coding somatic mutations identified in different tumor types were downloaded from the ICGC project (International Cancer GenomeConsortium et al., 2010) data portal. The data sets used in our study are ICGC_BRCA_EU, ICGC_LIRI-JP, ICGC_MALY-DE, ICGC_PACA-AU, ICGC_PRAD-UK, ICGC_SKCA-BR, and ICGC_SKCM-US. These data sets are either not under embargo, or, for the data sets released within the last two years, we have acquired approval from the data owners. From each data set we used all mutations with the mutation type ‘single base substitution’, and annotated as ‘intergenic_region’, ‘intragenic_variant’, ‘upstream_gene_variant’, ‘downstream_gene_variant’, ‘3_prime_UTR_variant’, ‘5_prime_UTR_variant’, and ‘intron_variant’.

From each genomic coordinate, we fetched the 39-bp genomic sequence centered at the mutated base pair. Each 1-bp mutation affects 20 overlapping 20-mers, over a region of 39 base pairs. Thus, for each mutation we fetched the 39-bp genomic sequence centered at the mutated site. Given that we want to focus on mutations that can affect binding of ETS factors, we filtered out all mutations for which neither the wild-type (WT) nor the mutated (MT) 39-bp regions contained any 20-mers centered at one of the ETS core motifs (GGAA or GGAT). For the remaining mutations, we applied iMADS to make predictions of Elk1 binding, Ets1 binding, and Elk1 vs Ets1 preference for both the WT and MT sequences. To assess the change in binding or preference between WT and MT, we calculate the maximum absolute change in binding score or preference score, over the 20-mers in each 39-bp sequence centered at a mutation. A total of 1,266,609 somatic mutations in melanoma cancer patients with whole genome sequencing were selected and used for the analyses presented in Figures 6B and 6C. The number of somatic mutations selected for other tumor types are: 1,033,656 for breast cancer, 804,713 for liver cancer, 333,992 for pancreatic cancer, 65,482 for the melanoma whole-exome dataset, 36,554 for the prostate cancer whole-exome dataset, and 89,180 for malignant lymphoma whole-exome dataset.

To generate the control dataset of genetic variants, we used 456,285 common (minor allele frequency > 1%) variants from the 1000 Genomes project (1000 Genomes Project Consortium et al., 2012), as reported and used as controls in (Zhou and Troyanskaya, 2015). The common variants were processed similarly to the somatic mutations.

DATA AND SOFTWARE AVAILABILITY

iMADS Web Application and Prediction Server

To allow convenient querying, visualization, and generation of binding scores (for individual TFs) and preference scores (for TF1 vs. TF2), we created the iMADS web application and prediction server. The application was implemented in the Python and JavaScript programming languages, using the Flask (http://flask.pocoo.org) and React (https://facebook.github.io/react/) frameworks, respectively. Users can query TF predictions by genomic regions, as determined by UCSC gene lists (hgdownload.cse.ucsc.edu), or by user-provided custom gene lists or genomic coordinate ranges. Genome-wide predictions are available as genome annotation tracks at http://trackhub.genome.duke.edu/gordanlab. These predictions were combined and stored in a de-normalized PostgreSQL database.

The prediction engine was implemented in Python using libSVM (Chang and Lin, 2011) and Biopython (Cock et al., 2009). Preference scores were generated in R using the nlme (Pinheiro et al., 2018) package. To generate predictions for custom DNA sequences provided by the user, iMADS uses a computational workflow defined in the Common Workflow Language (http://www.commonwl. org; https://dx.doi.org/10.6084/m9.figshare.3115156.v2), an emerging standard for reproducible and reusable computational workflows, and a reproducible software environment in the form of a Docker container to run the prediction engine.

PBM Data Availability

All the raw and processed gcPBM data generated and used in this study are available in GEO: GSE97794. The 36-mer gcPBM probes (both putative binding sites and negative controls) and their genomic coordinates are available in Table S7. The numbers of 36-mer probes and 20-mer genomic sequences used in our analyses are available in Table S8.

An archived version of release 1.0.0 of iMADS is availble at Zenodo: https://zenodo.org/record/1205525. All the source code is available on Github.

• Website: github.com/Duke-GCB/iMADS

• Worker for prediction server: github.com/Duke-GCB/iMADS-worker

• Binding predictions for individual TFs: github.com/Duke-GCB/Predict-TF-Binding

• Preference predictions for TF1 vs. TF2: github.com/Duke-GCB/Predict-TF-Preference

Highlights.

• Paralogous TFs with similar DNA motifs bind differently to genomic DNA, even in vitro

• The divergence in specificity is most pronounced at mediumand low-affinity sites

• Differences in intrinsic specificity contribute to differential in vivo binding

• Non-coding genetic variants may differentially affect binding of paralogous TFs