Abstract
Motivation
Most gene prioritization methods model each disease or phenotype individually, but this fails to capture patterns common to several diseases or phenotypes. To overcome this limitation, we formulate the gene prioritization task as the factorization of a sparsely filled gene-phenotype matrix, where the objective is to predict the unknown matrix entries. To deliver more accurate gene-phenotype matrix completion, we extend classical Bayesian matrix factorization to work with multiple side information sources. The availability of side information allows us to make non-trivial predictions for genes for which no previous disease association is known.
Results
Our gene prioritization method can innovatively not only integrate data sources describing genes, but also data sources describing Human Phenotype Ontology terms. Experimental results on our benchmarks show that our proposed model can effectively improve accuracy over the well-established gene prioritization method, Endeavour. In particular, our proposed method offers promising results on diseases of the nervous system; diseases of the eye and adnexa; endocrine, nutritional and metabolic diseases; and congenital malformations, deformations and chromosomal abnormalities, when compared to Endeavour.
Availability and implementation
The Bayesian data fusion method is implemented as a Python/C++ package: https://github.com/jaak-s/macau. It is also available as a Julia package: https://github.com/jaak-s/BayesianDataFusion.jl. All data and benchmarks generated or analyzed during this study can be downloaded at https://owncloud.esat.kuleuven.be/index.php/s/UGb89WfkZwMYoTn.
Supplementary information
Supplementary data are available at Bioinformatics online.
1 Introduction
The boom in high-throughput genomics results in the acceleration of the identification of candidate genes in genotype-phenotype association studies. Often, thousands of candidate genes are identified that are potentially related to a phenotype (In human genetics, there are many definitions for phenotypes, depending on the different importance given to genetic and environmental factors that determine an organism’s physical appearance and behavior. In this study, we use technically ‘disease phenotypes’ for HPO terms). This creates the need for costly and time-consuming wet lab experiments to validate those candidates. Gene prioritization addresses the need of selecting the most biologically relevant genes, among a large list of candidate genes, for further investigation. For example, hunting disease-associated genes is a demanding process and plays a crucial role in understanding the relationship between a disease phenotype and genes. It has various applications ranging from functional genomics to drug design studies in both pharmacogenomics and personalized medicine.
In the last decade, gene prioritization has received growing attention and has established its credibility in genetic research. Various approaches have been proposed for gene prioritization, based on different genomic data sources and machine learning strategies (Aerts et al., 2006; Britto et al., 2012; Chen et al., 2009; De Bie et al., 2007; Deo et al., 2014; ElShal et al., 2016; Gefen et al., 2010; Hutz et al., 2008; Jiang et al., 2016; Kale et al., 2015; Moreau and Tranchevent, 2012; Tranchevent et al., 2016; Zakeri et al., 2015; Zitnik et al., 2015). Most of these strategies exploit the ‘guilt-by-association’ principle. They assume that causative genes for a disease are indeed the ones similar to those already known to be associated with that disease. As a result, most strategies based on ‘guilt-by-association’ need a set of seed genes to train a model. Then, they rank a set of candidate disease genes for the biological process, phenotype or disease under investigation using the learned models (Aerts et al., 2006). However, these models have the drawback that they fail to handle diseases for which very few genes are known or for which disease-causing genes are yet to be extensively characterized.
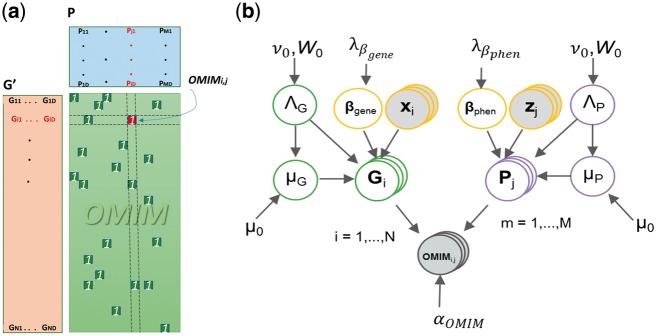
Moreover, the typical approaches for hunting causal disease genes often model each disease separately, which fails to detect patterns in the data common to several diseases or phenotypes. Therefore, instead of modeling each disease individually, we design a gene prioritization model through a multi-task approach that enables us to capture the common patterns in the data. This leads us to formulate the gene prioritization task as the factorization of an incompletely filled gene-phenotype matrix where the objective is to predict the unknown values. By way of illustration, human genome disease association databases, such as the Online Mendelian Inheritance in Man (OMIM; Amberger et al., 2011), can be seen as an incomplete, partially observed matrix where each row corresponds to a gene and each column corresponds to a disease (Fig. 1).
Fig. 1.
The graphical representation of our proposed model. The left panel illustrates the OMIM data base as a partially observed matrix where each row is a gene and each column is a disease phenotype. The goal of our proposed model is to express the OMIM matrix as the product of two matrices GT and P. The right panel shows a graphical representation of our proposed model for Bayesian matrix factorization with side information on both genes and phenotypes
Matrix factorization is a strategy to fill partially observed matrices. Matrix factorization methods aim at approximating an N × M matrix as the product of two thinner factor matrices: an N × D row factor and an M × D column factor, where D denotes the dimension of the latent variables and is smaller than the minimum of N and M. Then the objective is to provide a good approximation for the matrix with the ability to generalize by evaluating its performance on unseen data. Probabilistic Matrix Factorization (PMF; Salakhutdinov and Mnih, 2007) and Bayesian PMF (BPMF; Salakhutdinov and Mnih, 2008) are among the most successful approaches to handle matrix factorization for partially observed data. However, because of the extreme sparsity of the OMIM matrix (the sparsity of about 0.006%), these approaches fail to provide an accurate matrix completion. To deliver more accurate gene-disease matrix completion, we propose an extended BPMF that integrates multiple side information sources, such as biological annotation-based data sources and literature-based data sources extracted from PubMed. In particular, our approach allows us to rank a gene with no known disease association in the gene-disease matrix, among a large list of genes suspected of causing a disease under study. In our proposed model, we combine information about genes and phenotypes at the same time, whereas most of earlier approaches for gene prioritization are limited to only integrating data sources about genes (Aerts et al., 2006; Britto et al., 2012; Chen et al., 2009; De Bie et al., 2007; Deo et al., 2014; ElShal et al., 2016; Gefen et al., 2010; Hutz et al., 2008; Jiang et al., 2016; Kale et al., 2015; Tranchevent et al., 2016; Zakeri et al., 2015; Zitnik et al., 2015) (Gene prioritization methods that only integrate data sources about genes also implicitly use knowledge on diseases because some data sources like GO partially carries such information. But most of gene prioritization methods do not integrate data sources about diseases systematically and directly).
Furthermore, we address the limitation of the user of the Area Under the Curve (AUC) score in evaluating the performance of gene prioritization methods. To emphasize early discovery, we use the Boltzmann-Enhanced Discrimination of ROC (BEDROC) score (Truchon and Bayly, 2007) to assess our gene prioritization model. It is recognized as a proper and robust evaluation measure for early discovery. Accordingly, the advantages of the BEDROC score in early enrichment are discussed in more details later in the paper.
We develop a benchmark based on OMIM associations (Amberger et al., 2011). Experimental results on our benchmarks demonstrate that our proposed model can effectively improve accuracy over a state-of-the-art gene prioritization method. Our proposed model succeeds in ranking highly most of the disease-causing genes in a majority of diseases. For 36 diseases of our benchmark of 65 diseases, at least half of the known disease gene rank in the top 1% of prioritized genes, out of about 15 000 human genes considered in this study.
2 Approach
Standard approaches for gene prioritization often model each disease or each phenotype individually, but this fails to capture patterns common to several diseases or phenotypes. This motivates us to formulate the prediction of gene-disease associations using Human Phenotype Ontology (HPO) terms as a factorization of an incompletely filled gene-disease-matrix (or gene-phenotype-matrix) where the objective is to predict unknown values. For example, we can consider the disease-specific association databases such as OMIM (Amberger et al., 2011) as an incomplete matrix. OMIM focuses on the relationship between human genotype and associated diseases (In fact, diseases in OMIM can be defined by HPO terms, where each disease is associated with several terms). It can be considered as a partially observed matrix where each row is a gene and each column is a disease or phenotype (Fig. 1). We also randomly diffuse five times more 0’s than the known disease-gene relations (1’s) into the incomplete OMIM matrix [Since in the gene prioritization task we only have positive data (1’s in the OMIM matrix) we randomly select negative data (0’s in the OMIM matrix) from unlabled data to train our model]. Then, OMIM matrix is defined in the following way:
Now, we also defined as the set of OMIM matrix row and column indices whose value has been observed. Matrix factorization is an elegant strategy to fill partially observed matrices. Matrix factorization methods aim is to stage, for example, matrix as the product of two matrices and , where denotes the dimension of latent variable. Then the goal is to find a rough approximation for the OMIM matrix with the ability to generalize by evaluating its performance on unseen data. This leads to predicting the relationship between gene i and disease j as the dot product of and Pj (Fig. 1), which is expressed
| (1) |
PMF (Salakhutdinov and Mnih, 2007) is among the most successful approaches to handle matrix factorization for partially observed data. The main notion behind the PMF is to find a factorization that minimizes the mean square error on the observed data, and maintain good performance on those observed data considered for the test set, with the assumption of Gaussian noise in the data (for more details see Supplementary Material).
3 Materials and methods
The generalization ability of PMF will decrease when the sparsity of the matrix increases. To overcome this issue, BPMF (Salakhutdinov and Mnih, 2008) suggests a fully Bayesian treatment of the PMF approach by introducing common multi-variate Gaussian priors for latent variables; one for rows (genes G) and one for columns (phenotypes P). Then, BPMF places the Normal-Wishart priors over the row and column hyperparameters: ΘG and ΘP. and are defined as the row and column hyperparameters, where μG and ΛG (μP and ΛP) are the mean and precision matrices of the Gaussian prior for genes (phenotypes). The BPMF model is then expressed as
| (2) |
| (3) |
where and denote the normal and Normal-Wishart distributions respectively, and θ0 are the fixed hyperparameters of the Normal-Wishart prior. Like PMF, BPMF also uses a linear model with Gaussian observation noise.
| (4) |
where is the precision parameter. In BPMF, is assumed to be known.
3.1 Proposed model
It has been shown that, in general, BPMF outperforms PMF, particularly on sparse and imbalanced datasets (Salakhutdinov and Mnih, 2008). However, BPMF also fails where the data matrix under study is extremely sparse. For example, the sparsity of OMIM benchmark used in this study is approximately 0.006%. To deliver more accurate OMIM matrix completion, we extend BPMF by incorporating extra information available about genes and phenotypes; which is referred to as side information in this article. This leads to having more accurate factorization, especially for genes that have not yet been investigated or characterized. Moreover, our proposed model lets us integrate the corresponding phenotype data, whereas typical gene prioritization models often utilize only genomic data sources as the main feature to achieve their goal.
Similarly to BPMF, we suggest that OMIM matrix has a Gaussian noise model with precision , as expressed in Equation (4). To incorporate the available heterogeneous text mining-based and omics data (genes features ) and corresponding phenotype data (the phenotypes features ), we integrate a term () into Gaussian mean μG (μP). Then, we can rewrite the Equations (3) and (4), used in BPMF, as
| (5) |
| (6) |
where and is the link matrix for the gene (or phenotype) features and () is the dimension of the gene (or phenotype) features. Equations (5) and (6) offer the linear model for latent vectors. Technically, our proposed model learns the link matrices and to predict latent variables Gi and Pj from xi and zj, respectively. This leads to an effective and consistent improvement. For example, for those genes with no observation in the OMIM matrix, their distribution of their latent variables is fully determined by Equation (5). In contrast, for those genes with many observations in the OMIM matrix, their features have only a small effect.
The idea of incorporating side information in the Bayesian-based matrix factorization approaches was first addressed by Porteous and colleagues (2010), and later by Rai and colleagues (2015) and Rao and colleagues (2015). However, their approaches seem to be intractable for our application because of the high-dimensional nature of the genomic and phenotypic feature spaces. Moreover, (Rao et al., 2015) proposed a more scalable method in dealing with side information. They incorporate side information via graph as a regularization term into matrix factorization process. The graph encodes pairwise relationship between rows (columns). (Rao et al., 2015) used k-nearest neighbor (k-NN) to construct such a graph. Their methods offered promising results on investigated benchmarks with low-dimensional feature vectors (about 20). Accordingly, they employ a 10-NN approach using Euclidean distance metric to construct graph information. However, their approach is not suitable for our application because of the high dimensionality of our side information. In fact, it is indeed well known that k-NN suffers from the curse of dimensionality and its predictive performance can be severely reduced by the presence of noisy or irrelevant features, which is a typical situation in biological data.
Indeed, Equations (5) and (6) are at the heart of all Bayesian-based matrix factorization. As described in Salakhutdinov and Mnih (2008), from these equations, it is straightforward to derive a block Gibbs sampler for each latent vector Gi and Pi. This allows us to generate multiple samples of Gi and Pi latent matrices, and then get a better prediction out of it.
3.2 Sampling the link matrix
We can simply extend this block Gibbs sampler to include genomic or phenotypic side information by placing a prior distribution on and (Supplementary Material); for instance, Rai and colleagues (2015) puts a zero mean Gaussian on the link matrix. Then, the Gibbs sampler iteratively samples each model variable from its conditional distribution while keeping others fixed. For example, the latent variable Gi (Pj) is sampled while keeping the latent variable P (G), the link matrix (), the OMIM matrix, and the gene features x (and in the case of phenotype z), fixed. In the similar way, the () is sampled using Gi (Pj) and x (z).
But, the typical methods to sample from multi-variate Gaussian distribution quickly become expensive and demanding as the feature dimension becomes large. In fact, the main issue of proposed sampling-based Bayesian approaches for matrix factorization with side information is that they first need to explicitly compute the covariance matrix of size () (Porteous et al., 2010; Rai et al., 2015). This requires a computational cost of the order . For example, even for the average dimension of 10 000 for genomic data (), the size of the precision matrix is 108, which is computationally intensive. Moreover, they need to employ the Cholesky decomposition to sample the link vector . On the contrary, to sample from our model we design a block sampler which scales well with respect to the number of genes and phenotypes features.
To have a full Bayesian treatment for (), we also consider a zero mean multi-variate normal as its prior. However, our proposed prior on () scales with the precision of latent variables.
| (7) |
where ⊗ denotes the Kronecker product, and denotes the vectorization of , and is the diagonal element of the precision matrix, and ΛG is the precision matrix of the latent variable for genes, which has a key role in the development of an efficient computational noise injection sampler discussed next.
In fact, this prior is natural as the scale of G is not predetermined. Accordingly, we place a gamma distribution hyperprior on because the choice of is problem dependent (Supplementary Material). The same full Bayesian treatment is developed for . Then, as illustrated in Figure 1, our suggested model jointly learns G, P, and through the block Gibbs sampler.
The outline of Gibbs sampling procedure for our proposed model is presented in the Supplementary Material. For the all variables except and , our proposed block Gibbs sampler utilizes the straightforward strategy as used in BPMF. As demonstrated in the Supplementary Material, while in BPMF the Gaussian priors model the latent variables Gi (Pj), in our proposed work the Gaussian priors model the residual (), instead; this being the key difference in comparison with BPMF. Rather, to sample from our model, exclusively for and , we design a noise injection sampler which uses the fact that strength of its prior is dependent on the scale of the latent variables.
The main intuition behind our proposed noise injection sampler is to first form a particular structured linear system whose solution is equivalent to drawing a sample from conditional posterior of (). Alternatively, a sample of can be generated by solving the following linear system.
| (8) |
where X represents and , and each row of matrices and is sampled from . When X is sparse, we can speed up the process of solving this linear system by using an iterative method, such as conjugate gradient (Supplementary Material).
Note that the sample of can be generated by solving the linear system with exactly the same form.
3.3 Benchmark
We developed a benchmark based on OMIM associations (Amberger et al., 2011). OMIM connects genes and diseases for Mendelian inheritance schemes (Amberger et al., 2011). It provides a list of disease-gene annotations based on experimental evidence. We used the 2013 version of OMIM, which released 6733 experimental-based disease-gene associations. The annotation list is one long combination of disease-gene entries that contains both confirmed and non-confirmed entries, as well as different mapping evidence codes. Furthermore, many OMIM entries refer to the same disease concept. We refine this list as we discussed by Elshal and colleagues (2016). To refine the OMIM experimental-based disease-gene associations, we follow the same procedure as it was used in Elshal and colleagues (2016) and Zakeri and colleagues (2015). This leads to 314 disease entries that have at least three genes annotated. This results in about 2600 disease-gene annotations reported in OMIM 2013 (1’s in the incomplete OMIM Matrix), giving a sparsity of about 0.006% for the OMIM matrix (for more details about the benchmark see Supplementary Material).
3.4 Genomic and phenotypic data sources
Many successful gene prioritization methods use multiple genomic data sources to deliver more accurate rankings (Aerts et al., 2006; Chen et al., 2009; De Bie et al., 2007; Hutz et al., 2008; Tranchevent et al., 2016; Zakeri et al., 2015; Zitnik et al., 2015). Finding an efficient technique for integrating heterogeneous biological data sources has received growing attention. Indeed, while a single data source might not be sufficiently effective, fusing several complementary genomic data sources deliver more accurate predictions.
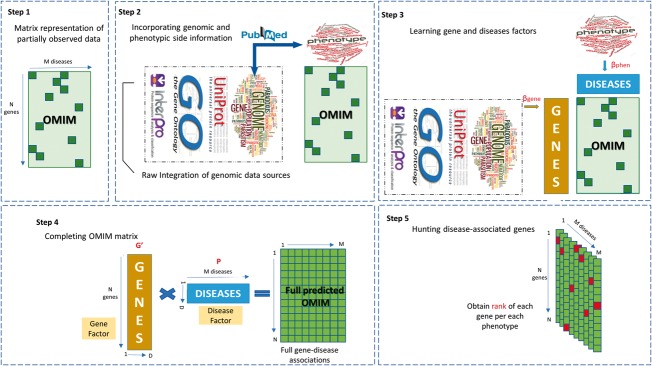
In this study, we consider several genomic data sources including annotation-based data sources, such as Interpret domains (Mitchell et al., 2015), Gene Ontology (GO) (The Gene Ontology Consortium, 2015) and Swiss Prot (SW; Braconi Quintaje and Orchad, 2008) annotation, as well as literature-based data sources extracted from PubMed (), just as in (Aerts et al., 2006; De Bie et al., 2007; ElShal et al., 2016; Tranchevent et al., 2016; Zakeri et al., 2015). We also incorporate the literature-based phenotypic () information on each disease as it was prepared by Elshal and colleagues (2016). To combine genomic data sources, we use full (raw) integration strategy which is a fast and easy approach to combine multiple data sources. To do that, we first normalize all data matrices to have the same Forbenius norm. The architecture of our Bayesian data fusion model for gene prioritization is shown in Figure 2.
Fig. 2.
Concept of gene prioirtization using matrix factorization. In the first step, a gene-disease asscociation database (OMIM in our case) is represented as a paritally observeed matrix. In the second step, extra information available about genes and phenotypes are prepared to be incorporated into the matrix factorization procedure. Both literature-based phenotypic () and literature-based genomic information are extracted from PubMed. A raw fusion approach is employed to integrate multiple genomic data sources. In the third step, our Bayesian data fusion model jointly learns two thin matrices (Gene and Disease factors) and two link matrix (namely, and ). In fact, this step illustrates the architecture of our matrix factorization approach model(GeneHound) for gene prioritization. In the fourth step, we complete the OMIM matrix using the learned gene and disease factors. Finally, in the fifth step, (GeneHound) ranks all genes in each phenotype column of fully predicted OMIM matrix, separately. For each diseases, genes with the highest predicted value are colored in red
3.5 Hunting disease-associated genes strategy
As shown in Figure 2, after incorporating information about the genes and diseases as side information, we factorize the incomplete OMIM matrix using our proposed Bayesian data fusion (GeneHound). Then, we are able to complete the OMIM matrix using the gene factor and the disease factor. Afterwards, we sort and rank all genes in each phenotype column of OMIM matrix separately. Finally, we determine the rank of test genes in each column to assess our model.
A separate issue is the effect of the number of latent dimensions on the performance of our model. In fact, different latent dimensions result in different predictions. Nevertheless, we have observed that our model is robust to overfitting even with large latent dimensions. We use 25 (), 30 () and 40 () latent dimensions as we observed that they are adequate for accurate predictions. To deliver more accurate prediction, our proposed Bayesian data fusion is developed by fusing the prediction results of three models with different latent variables (). We design a final model by first taking the geometric mean of gene ranks produced by each model, and then sorting the results in decreasing order. From the perspective of biological data, we assume that the presence of at least one good ranking suggests that the gene is plausibly relevant, even if the other data sources do not agree. The idea is that a true association can be seen through some data source, while being invisible in the other data sources. In that sense, we expect that taking the minimum rank is better than taking the arithmetic mean of the ranks. However, the minimum rank focuses on a single source and does not allow to discriminate clearly, among genes with several good ranks. The geometric mean allows taking all rankings into account, while providing a solution that is fairly similar to that of the minimum rank (Dwork et al., 2003).
4 Results
4.1 Assessment strategy
We, first, randomly diffuse five times disease-relations 0 (just for training) into the incomplete OMIM matrix. These zeros relations are only used for training the model. Then, among disease-gene annotations in OMIM matrix (when gene i associated with disease j), six random splits into 90% training and 10% test data are prepared (OMIM1 benchmark). The test sets in average contains 138 diseases.
We also investigate the performance of our model on 65 diseases that have at least 10 genes in the OMIM database. Then, the performance of our models is assessed using 5-fold cross validation on 65 diseases-genes annotations (OMIM2 benchmark). The 65 diseases that we tested in our study are listed in the Supplementary Table S1.
4.1.1 Evaluation method
Receiver Operating Characteristic (ROC) curve is often used to evaluate the performance of gene prioritization methods (Aerts et al., 2006; Chen et al., 2009; De Bie et al., 2007; Moreau and Tranchevent, 2012). A ROC curve for a specific disease is a plot of the recall versus false-positive rates for all genes. In early discovery, there is often the need to summarize the ROC curve into a single number without losing its information. For this purpose, the area under the ROC curve (AUC) has been widely used (Aerts et al., 2006; Chen et al., 2009; De Bie et al., 2007; Moreau and Tranchevent, 2012). It can be interpreted as the probability of a disease-associated gene randomly selected being ranked earlier than a not-disease-associated gene selected at random by a uniform distribution.
As demonstrated by Truchon and Bayly (2007), we can show that when the ratio of disease-associated genes (n) to total number of disease-associated genes and unknown genes (N) () becomes too small, which is a typical situation in gene prioritization tasks, AUC score equals to the area under the accumulation curve (AUAC). If TP(x) represents the probability of a disease-associated genes will be ranked earlier than a gene randomly selected from an uniform distribution (in other words, the sensitivity), then AUAC is given by . As shown by Truchon and Bayly (2007), for n disease-associated genes ranked and then normalized , AUAC can be obtained by . Another interesting relationship between these two metrics is that it has been shown that, in general, AUC score is just a Min-Max normalization of AUAC scores (Truchon and Bayly, 2007).
As a result, to estimate the AUC value of a prioritization model, for each disease, we can simply use the normalized rank of disease-associated genes considered for the test set and obtain the AUAC score. Then, the average of all AUAC scores is used to evaluate the performance of a gene prioritization model for all diseases under investigation. However, both AUAC and AUC scores often lead to a misinterpretation of the model performance in early discovery of disease-associated genes. For instance, late recognition has a strong influence on AUAC and AUC scores. Truchon and Bayly (2007), and later on Zhao et al. (2009), have addressed the limitation of AUC score in early discovery and have investigated various early discovery performance measurements.
To emphasize early discovery, we need to provide the probability of a disease-associated gene being ranked before a gene randomly selected from a distribution that top-ranked genes have a higher chance to be chosen. As a result, Truchon and Bayly (2007) have discussed the weighted version of AUAC by introducing the decreasing exponential function as the weight function w(x) in the integral of calculating AUAC. Then, Truchon and Bayly (2007) have exploited the idea of linear transformation of AUAC scores to AUC score, and have proposed the BEDROC as a proper and robust evaluation measurement for early discovery. In fact, BEDROC score is just a Min-Max normalized version of weighted AUAC scores. For n disease-associated genes ranked among N genes (n<<N), the BEDROC score is estimated as follows:
| (9) |
where the parameter α tunes the importance given to early recognition. For example, when α equals 228.5, 80% of the BEDROC score is being accounted for in the top 100 of the ranked genes in our study. BEDROC values can be interpreted as the probability that a disease-associated gene being ranked better than a gene selected at random from an exponential probability distribution function of parameter α.
In this study, we consider values of α equal and , which correspond to 80% of the BEDROC being assigned to the top 30%, 10%, 5%, 1% and top 100 prioritized genes, respectively.
To compare the results of our proposed methods on our benchmarks with gene prioritization tools, already proven to be successful, we develop the BEDROC Score Variation (BSV) curve which is a plot of average BEDROC scores versus the increasing value of alpha in the BEDROC Equation (9). In the BSV curve, the greater alpha, the heavier the weight for early discovery.
4.2 OMIM matrix completion results
4.2.1 Advantage of fusing side information through GeneHound
The performance of incorporating various genomic data and phenotypic data as side information on both genes and phenotypes, on our first benchmark (OMIM1) described before, are illustrated in Supplementary Figure S1. As we can see, restricting our model to use no gene side information is not effective at all to hunt disease-associated genes. However, incorporating the text mining-based data on the genes side () can effectively improve the performance of our model. In fact, BPMF fails to provide an accurate prediction [compared to our simplest proposed model ()]. This is because the sparsity of the OMIM matrix is very high.
Next, to see the advantage of fusing heterogeneous data sources for gene prioritization through our proposed Bayesian data fusion setup, we add more genomic data sources on the gene side. As shown in Supplementary Figure S1, integrating the four genomic data sources [] considered in this study leads to improved predictions of early gene discovery at the top 100, and 30% ranked genes. To this end, we investigate the effect of incorporating phenotypic side information and genomic side information simultaneously. This leads to the best average BEDROC scores of 0.82, 0.69, 0.59, 0.36 and 0.31 at and , respectively. This compares to 0.82, 0.67, 0.57 0.35 and 0.3 when no side information on disease side is used (). It is observed that offers the best average BEDROC scores at the top 100, 1%, 5%, 10% and 30% discovery focuses.
4.2.2 GeneHound versus Endeavour
To compare the results of our proposed methods on our benchmark with gene prioritization tools, already proven to be successful, we run the updated version of Endeavour (Aerts et al., 2006; Tranchevent et al., 2016, 2008). Endeavour is trained using the four genomic data sources mentioned earlier, except the phenotypic side information. Five-folds cross validation are carried on the proposed known disease-related genes benchmark (OMIM2). The same training and testing gene sets are used to evaluate Endeavour.
Table 1 provides the performance of and Endeavour on our benchmark (OMIM2). As listed in Table 1, compared with Endeavour, our proposed geometric-based aggregation approach () results in the best average 1-AUC error of 0.048, which is significantly better than that proposed by Endeavour (0.068).
Table 1.
Comparison of the averaged 1–AUC error for GeneHound and Endeavour
| Methods | Averaged 1-AUC error |
|---|---|
| Endeavour | |
| P-value | 0.00096 |
Notes: The 95% confidence intervals are reported over folds. The lower 1-AUC error is better.
The minimum Averaged 1-AUC error is in bold.
Although we observe that our proposed model offers better average 1-AUC error on OMIM2 benchmark, we explore the performance of GeneHound models and Endeavour in terms of early enrichment using the BEDROC scores at five pre-defined α values. In addition, to investigate the effect of latent dimensions, we suggest three models with different latent dimensions. We use 25, 30 and 40 latent dimensions. To assess this, in Table 2, we summarize the BEDROC scores for GeneHound with different latent dimensions, and this for our proposed data fusion model () and Endeavour. As shown in Figure 3 and Table 2, both and results in a competitive average BEDROC score of 0.70 at . This compares to 0.69 when using 25 latent dimensions. While GeneHound with 40 latent dimensions reaches the best average BEDROC scores of 0.61, 0.42 and 0.38 at and respectively, GeneHound with 30 latent dimensions offers a higher average BEDROC score of 0.83 at which corresponds to the top 30% discovery focus. Moreover, both and results are more robust given different folds compared to .
Table 2.
Comparison of the average BEDROC scores calculated with various α, for GeneHouds and Endeavour
| Methods | Averaged BEDROC score | ||||
|---|---|---|---|---|---|
| α | |||||
| Early enrichment focus | TOP 100 | TOP 1% | TOP 5% | TOP 10% | TOP 30% |
| 0.358 ± 0.057 | 0.396 ± 0.06 | 0.595 ± 0.056 | 0.686 ± 0.045 | 0.818 ± 0.023 | |
| 0.36 ± 0.016 | 0.40 ± 0.017 | 0.608 ± 0.028 | 0.70 ± 0.029 | 0.829 ± 0.019 | |
| 0.383 ± 0.023 | 0.421 ± 0.024 | 0.614 ± 0.027 | 0.699 ± 0.026 | 0.824 ± 0.017 | |
| 0.418 ± 0.031 | 0.458 ± 0.031 | 0.651 ± 0.031 | 0.733 ± 0.029 | 0.85 ± 0.018 | |
| Endeavour | 0.387 ± 0.031 | 0.422 ± 0.030 | 0.609 ± 0.029 | 0.694 ± 0.029 | 0.817 ± 0.021 |
Notes: The confidence intervals are reported over folds. α tunes the early enrichment. For example, in our study when , 80% of BEDROC score is given to the top 100 ranked genes. The best performance for each α is shown in boldface. All models are benchmarked on OMIM2.
The maximum BEDROC scores at different early enrichment focuses are highlighted in bold.
Fig. 3.
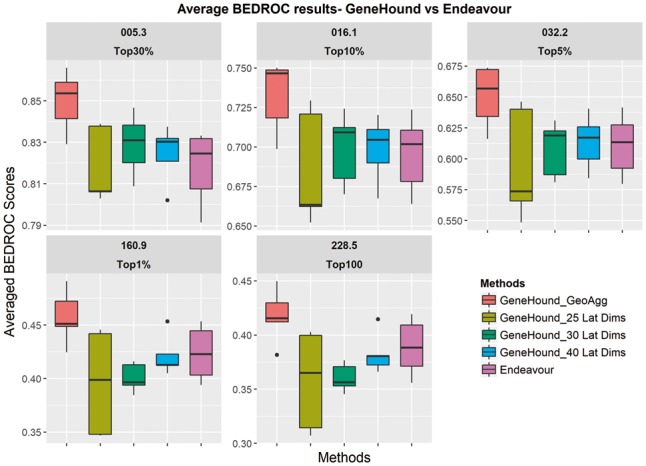
BEDROC scores result: GeneHound versus Endeavour.The performance of GeneHound with various latent dimensions, our final model(), and Endeavour are evaluated on our OMIM2 benchmark. The label of each panel corresponds to the value of α used to evaluate the model. Note that we highlight the black solid lines in the box plots correspond to the median value
As we discussed earlier, our proposed is developed by aggregating the prediction results of theses three models through taking the geometric mean of gene rank results produced by these models. As illustrated in Table 1, offers the best average BEDROC results in this setting, which correspond to an average BEDROC scores of 0.85, 0.73, 0.65, 0.46 and 0.42 at and , respectively. This indicates that fusing the results of three GeneHound models with different latent dimensions through our geometric-based aggregation approach can improve the performance of hunting disease-associated genes according to our benchmark (OMIM2). We also observe that results in robust 5-fold predictions. Moreover, It has been observed that the improvement is more significant in early discovery.
Moreover, according to Figure 3, BEDROC scores of GeneHound with the size of 40 latent dimensions are slightly higher than Endeavor at the top 30%, 10% and 5% enrichment focuses. Nonetheless, both and Endeavour yield competitive results at early discovery focuses. As shown in Figure 3, we observe that the results of is consistently outperforming Endeavour at all pre-defined α’s. Furthermore, the BSV curves are plotted to compare the performance of and Endeavour (Fig. 4). Figure 4 illustrates that achieves a higher average BEDROC scores at all α values. This demonstrates that is more sensitive and specific in hunting known disease-associated genes for all early enrichment focuses.
Fig. 4.
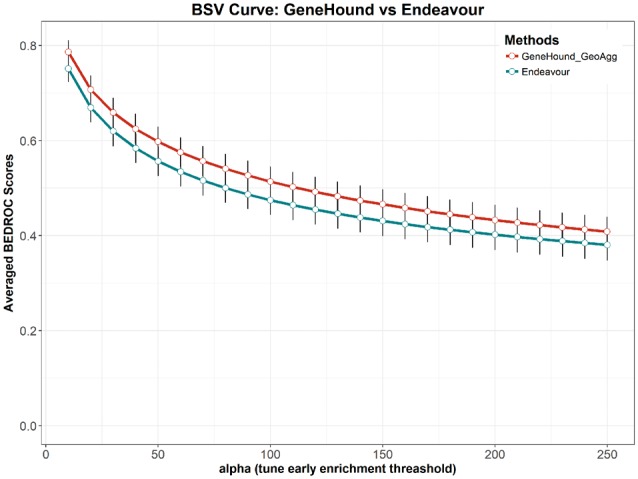
Comparison of the BSV curve for our proposed models and Endeavour. BSV curve is a plot of average BEDROC scores versus the increasing value of alpha in BEDROC Equation (9). In the BSV curve, the greater α, uses the heavier the weight for early discovery. The performance of and Endeavour are evaluated on OMIM2 benchmark
Moreover, Supplementary Figure S2 illustrates the average BEDROC scores over diseases grouped based on number of known/training genes at top 1% and 10% enrichment focuses. Most of investigated diseases in this study (44 out of 65) have less than 20 known genes. Supplementary Figure S2 shows that while both GeneHound and Endeavour obtain competitive results at the 1% and 10% enrichment focus for diseases with less than 20 and more than 12 known genes, GeneHound offers better results than Endeavour at top 1% and 10% enrichment focuses for other disease groups. For example, according to Supplementary Figure S2, GeneHound improves the predictive performance at top 1% enrichment focus by almost 10% on diseases with 10, 11 and 12 known genes. This show the effectiveness of our method, particularly in handling gene prioritization for diseases with very few known genes. Moreover, when we compare the performances of GeneHound and Endeavour, we see that GeneHound can enhance the predictive performance of gene prioritization task by exploiting the multi-task approach.
Lastly, we investigate the results of on OMIM2 benchmark in more details. The OMIM diseases investigated in this study are grouped based on the 10th version of the International Statistical Classification of Diseases and Related Health Problems (International Classification of Diseases (ICD), 2015–10), which is a medical classification list introduced by the World Health Organization (WHO). This leads to 14 ICD-10-based disease groups that for them we have at least one disease in OMIM2 benchmark. Each of the 65 diseases belongs to exactly one chapter of ICD-10, except mitochondrial complex deficiency, which is not classified in ICD-10, and Alzheimer, Parkinson and cataract diseases, which are classified in two chapters of ICD-10. To assess the results of and Endeavour on individual diseases, we report the BEDROC scores at and over all cross-validated genes for each disease. For example, Supplementary Figures S8 and S9 show the results of diseases in OMIM2 benchmark belongs to the diseases of the nervous system and diseases of the eye and adnexa (H). succeeds to offer BEDROC scores of more than 0.5 for 25 diseases of our benchmark (out of 65 diseases) at the top 1% enrichment focus. The results of other disease groups are shown in the Supplementary Figures S3–S17. Moreover, to see the advantage of using GeneHound in more details, we set up a challenge between and Endeavour in terms of early discovery improvements (Supplementary Table S2). It is observed that GeneHound boosts the BEDROC score at for Endeavour by more than 50% for 12 diseases. This compares to three diseases by more than 50% BEDROC score improvement using Endeavour. Furthermore, GeneHound offers more than 100% BEDROC score improvement for three diseases as compared to Endeavour. However, Endeavour does not improve any diseases BEDROC scores provided by GenHound by more than 100%.
Among these fourteen ICD-10-based disease groups, there are nine groups for which them we have at least three diseases in the OMIM2 benchmark. These nine groups include certain infectious and parasitic diseases (A), neoplasms (C), diseases of the blood and blood-forming organs and certain disorders involving the immune mechanism (D), endocrine, nutritional and metabolic diseases (E), mental and behavioural disorders (F), diseases of the nervous system (G), diseases of the eye and adnexa (H), diseases of the circulatory system (I) and congenital malformations, deformations and chromosomal abnormalities (Q). As illustrated in Figure 5, both GeneHound and Endeavour achieve the competitive results at the 10% enrichment focus for A, E and I disease groups in ICD-10. According to Figure 5, while Endeavour offers slightly better results for diseases in group D, achieves a higher average BEDROC score at for diseases in group C. In addition, the performance of our proposed model for diseases in groups F, G, H and Q is considerably higher than that of Endeavour. For example, yields an average BEDROC score of 0.87 at the top 10% enrichment focus on diseases of the eye and adnexa (H), which is significantly higher than a BEDROC score of 0.76 using Endeavour. In summary, we observed that improves an average BEDROC score at for diseases in groups F, G, H and Q by 17%, 8%, 14%, 11% respectively, as compared to Endeavour.
Fig. 5.
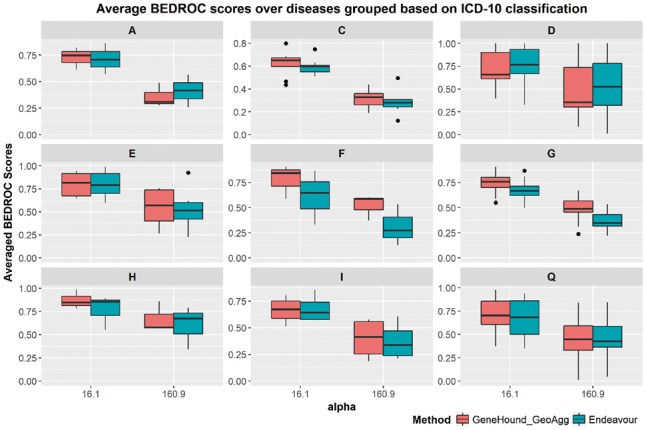
The average BEDROC scores of ICD-10-based disease groups: versus Endeavour.The average BEDROC scores of nine ICD-10-based disease groups with at least three diseases in OMIM2 benchmark. The α are set to 16.1 and 160.9
Figure 5 also shows the average BEDROC score at , which corresponds to the 1% enrichment focus. Both and Endeavour exhibit a similar performance for diseases in the group Q. For diseases in groups C, E and I, does slightly outperform Endeavour in terms of the 1% discovery focus. Rather, for diseases in group A and D, Endeavour achieves a bit higher BEDROC scores. Moreover, does significantly outperform Endeavour on diseases in groups F, G and H, achieving an average BEDROC score of 0.52, 0.48 and 0.66, respectively. This compares to 0.31 and 0.37 and 0.6 using Endeavour. Both methods show their worst performance for group C. This demonstrates the inherent complexity of neoplasms. Nevertheless, performance on neoplasms diseases is still better than that of Endeavour; 0.52 versus 0.48 at . Together, all theses assessments verify the effectiveness of our proposed approach in comparison with the well-established gene prioritization method Endeavour (Aerts et al., 2006; Tranchevent et al., 2008, 2016).
5 Discussion
In modern biology, there is often the need to select the most promising genes for further investigation among a large list of candidate genes. While a single genomic data source might not be sufficiently informative, the integration of several complementary genomic data sources delivers more accurate predictions. We present an innovative multi-task method to address the gene prioritization task, which combines genomic data and phenotypic data sources using matrix factorization. Accordingly, we propose an extended Bayesian matrix factorization with the ability to work with multiple side information sources. Because of the extreme sparsity of gene-disease matrices, BPMF fails to provide accurate predictions. However, our method delivers the largest advantage when the gene-phenotype association matrix is sparsely observed. Our methods provide a BEDROC score of more than 0.5 for 25 diseases of our benchmark (out of 65 diseases) at the top 1% enrichment focus. This confirms the effectiveness of our proposed approach to hunt disease-associated genes.
Moreover, whereas the state-of-the-art gene prioritization methods, such as Endeavour(Aerts et al., 2006; Tranchevent et al., 2016) and ToppGene (Chen et al., 2009), are restricted to only integrate genomic data sources, in our proposed model, we can not only integrate data sources describing genes, but also data sources describing phenotypes, simultaneously. In a recent work, (Zitnik et al., 2015) proposed a data fusion approach that combines several heterogeneous datasets to prioritize gene in an unsupervised fashion. In contrast, our proposed method formulates the gene prioritization task as the factorization of a partially observed matrix with side information in a supervised learning setting. Experimental results on 65 rare diseases investigated in this study show that our proposed method, , results in an average 1-AUC error of 0.048, which is significantly better than that proposed by the state-of-the-art gene prioritization method Endeavour (0.068). ’s effectiveness on early discovery is evaluated using the BEDROC score. Experimental results demonstrate that consistently outperforms the last version of Endeavour, the best established and successful gene prioritization method hitherto published, at all early enrichment focuses.
Furthermore, in contrast with the fact that most of gene prioritization methods deal with each disease separately, we design a gene prioritization model through a multi-task approach in which it is possible to detect patterns in the data common to several diseases or phenotypes. The advantage of multi-task approach for gene prioritization through kernel methods was also discussed by Mordelet and Vert (2011). This particularly appealing aspect of our method, alongside with combining the phenotypic similarity of diseases, enables us to tackle diseases with few or no known genes and genes that have not yet been extensively characterized. For example, our method offers an average BEDROC score of 0.48 at the top 1% enrichment focus (and the average true positive rate of 0.61 at top 1%) on diseases with less than 13 known genes. This compares to 0.44 (and 0.58) using Endeavour.
Besides, , like the state-of-the-art gene prioritizations methods, suffers from relying upon exploiting the ‘guilt-by-association’ principle. In fact, developing a gene priotization model solely based on this assumption might not be enough to understand complex diseases, such as neoplasms. Nevertheless, our proposed methods, by detecting patterns in the data common to several diseases through our multi-task setting, could be less sensitive to a known genetic profile of diseases and consequently delivers less biased results and more accurate hints for researchers. For example, whereas, both Endeavour and fail to offer a good performance to hunt disease-associated genes for neoplastic diseases, still deliver significantly better results on those diseases than that of Endeavour. Our proposed approach also offers promising results on diseases of the nervous system, mental and behavioral disorder, diseases of the eye and adnexa, endocrine, nutritional and metabolic diseases, congenital malformations, deformations and chromosomal abnormalities, and diseases of the blood and blood-forming organs and certain disorders involving the immune mechanism, as compared to Endeavour.
An important limitation of our approach is that, like other gene prioritization methods, it only uses biological annotation-based sources and literature-based data sources extracted from PubMed. These data sources themselves suffer from missing information, false positive annotations, bias studies of human genome and leakage of information across multiple sources, which in case of unreliable information could considerably diminish the advantage of data fusion.
It is also pertinent to mention that some researchers expect that it might be possible to perform perfectly the prioritization task for a biological problem under investigation using a versatile gene prioritization method. However, this view regarding gene prioritization seems too optimistic. In a more realistic interpretation, gene prioritization based on the available incomplete and inconsistent data sources, which themselves incorporate multiple biases, just offers relevant hypotheses to researchers to further investigate.
As future work, it is also worth drawing attention to the fact that one of ’s assets is its flexibility to support multiple gene disease databases at the same time. We have recently developed our Bayesian matrix factorization model (Arany et al., 2015; Simm et al., 2017), which manages the factorization of a wide range of data models, such as tensor relations and multiple relations. As a result, several relations (matrices) with their side information can be factorized together (for example gene-disease and gene-phenotype association matrices). In the future, this will enable us to develop an integrative-based gene prioritization model by combining multiple gene disease databases, such as OMIM (Amberger et al., 2011), Genetic Association Database (GAD) (Becker et al., 2004), DisGenNET (Pinero et al., 2015) and the literature-derived human gene-disease network (Bauer-Mehren et al., 2011).
6 Conclusions
Our work presents an innovative approach to gene prioritization by combining genotype and phenotype data sources using matrix factorization. Here, we reformulate the problem of gene prioritization as the task of factorizing of a very sparsely filled gene-disease-matrix with the goal of predicting the missing values of the matrix. To address this task, we propose a generalization of BPMF that makes it possible to work with multiple side information sources (which is impossible in BPMF). Our gene prioritization method can for the first time not only integrate data sources describing genes, but also data sources describing phenotypes and in this way improve over the state of the art. Moreover, we discuss the advantages of using the BEDROC score in evaluating the performance of gene prioritization algorithms, as opposed to the more classical AUC Score. Finally, experimental results on our benchmarks show that our proposed model can effectively improve accuracy over the state-of-the-art gene prioritization method, Endeavour.
Supplementary Material
Acknowledgements
KU Leuven Internal Funds: CELSA/17/032, KUL CoE PFV/10/016 SymBioSys. Imec ICON GAP, and strategic funding. Flemish Government: IWT 150865 (Exaptation); FWO 06260 (Iterative and multi-level methods for Bayesian multi-relational factorization with features). VIB: ELIXIR Flanders Bioinformatics Infrastructure for Sustainable Agriculture and better Health for Society.
Conflict of Interest: none declared.
References
- Aerts S. et al. (2006) Gene prioritization through genomic data fusion. Nat. Biotech., 24, 537–544. [DOI] [PubMed] [Google Scholar]
- Amberger J. et al. (2011) A new face and new challenges for Online Mendelian Inheritance in Man (OMIM). Hum. Mutat., 32, 564–567. [DOI] [PubMed] [Google Scholar]
- Arany A. et al. (2015) Highly scalable tensor factorization for prediction of drug-protein interaction type. MLCB/MLSB NIPS Workshop. Canada; arXiv: 1512.00315.
- Bauer-Mehren A. et al. (2011) Gene-disease network analysis reveals functional modules in Mendelian, complex and environmental diseases. PLOS One, 6, e20284. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Becker K. et al. (2004) The genetic association database. Nat. Genet., 36, 431–432. [DOI] [PubMed] [Google Scholar]
- Britto R. et al. (2012) GPSy: a cross-species gene prioritization system for conserved biological processes: application in male gamete development. Nucleic Acids Res., 40, W458–W465. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Braconi Quintaje S., Orchard S. (2008) The annotation of both human and mouse kinomes in UniProtKB/Swiss-Prot: one small step in manual annotation, one giant leap for full comprehension of genomes. Mol. Cell Proteomics, 7, 1409–1419. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen J. et al. (2009) ToppGene Suite for gene list enrichment analysis and candidate gene prioritization. Nucleic Acids Res., 37, W305–W311. [DOI] [PMC free article] [PubMed] [Google Scholar]
- De Bie T. et al. (2007) Kernel-based data fusion for gene prioritization. Bioinformatics, 23, i125–i132. [DOI] [PubMed] [Google Scholar]
- Deo R.C. et al. (2014) Prioritizing causal disease genes using unbiased genomic features. Genome Biol., 15, 534. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dwork C. et al. (2003) Rank aggregation revisited. https://www.researchgate.net/publication/2869423.
- ElShal S. et al. (2016) Beegle: from literature mining to disease-gene discovery. Nucleic Acids Res., 44, e18. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gefen A. et al. (2010) Syndrome to gene (S2G): in-silico identification of candidate genes for human diseases. Hum. Mutat., 31, 229–236. [DOI] [PubMed] [Google Scholar]
- Hutz J.E. et al. (2008) CANDID: a flexible method for prioritizing candidate genes for complex human traits. Genet. Epidemiol., 32, 779–790. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jiang J. et al. (2016) A novel prioritization method in identifying recurrent venous thromboembolism-related genes. PLoS One, 11, e0153006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kale S.M. et al. (2015) Prioritization of candidate genes in ‘QTL-hotspot’ region for drought tolerance in chickpea (Cicer arietinum L.). Sci. Rep., 5, 15296. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mitchell A. et al. (2015) The InterPro protein families database: the classification resource after 15 years. Nucleic Acids Res., 43, D213–D221. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mordelet F., Vert J.P. (2011) ProDiGe: prioritization Of Disease Genes with multitask machine learning from positive and unlabeled examples. BMC Bioinformatics, 12, 389.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moreau Y., Tranchevent L.C. (2012) Computational tools for prioritizing candidate genes: boosting disease gene discovery. Nat. Rev. Genet., 13, 523–536. [DOI] [PubMed] [Google Scholar]
- Pinero J. et al. (2015) DisGeNET: a discovery platform for the dynamical exploration of human diseases and their genes. Database, 2015, bav028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Porteous I. et al. (2010) Bayesian matrix factorization with side information and dirichlet process mixtures. In: Proceedings of the Twenty-Fourth AAAI Conference on Artificial Intelligence (AAAI'10), Atlanta, AAAI Press, pp. 563–568. [Google Scholar]
- Rai P. et al. (2015) Leveraging features and networks for probabilistic tensor decomposition In: Proceedings of the Twenty-Ninth AAAI Conference on Artificial Intelligence (AAAI'15), Austin Texas, AAAI Press, pp. 2942–2948. [Google Scholar]
- Rao N. et al. (2015) Collaborative filtering with graph information: consistency and scalable methods. In: Advances in Neural Information Processing Systems 28 (NIPS 2015), Montreal, Curran Associates, Inc., pp. 2107–2115. [Google Scholar]
- Salakhutdinov R., Mnih A. (2007) Probabilistic matrix factorization. In: Advances in Neural Information Processing Systems 20 (NIPS 2007), Vancouver, Curran Associates, Inc., pp.1257–1264. [Google Scholar]
- Salakhutdinov R., Mnih A. (2008) Bayesian probabilistic matrix factorization using Markov chain Monte Carlo In: Proceedings of the 25th International Conference on Machine Learning, Helsinki, Finland, ACM, pp. 880–887. [Google Scholar]
- Simm J. et al. (2017) Macau: scalable Bayesian factorization with high-dimensional side information using MCMC. In: 2017 IEEE 27th International Workshop on Machine Learning for Signal Processing (MLSP). Tokyo, IEEE, pp. 1–6.
- Tranchevent L.C. et al. (2008) Endeavour update: a web resource for gene prioritization in multiple species. Nucleic Acids Res., 36, W377–W384. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tranchevent L.C. et al. (2016) Candidate gene prioritization with Endeavour. Nucleic Acids Res., 44, W117–W121. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Truchon J.F., Bayly C.I. (2007) Evaluating virtual screening methods: good and bad metrics for the ‘early recognition’ problem. J. Chem. Inf. Model., 47, 488–508. [DOI] [PubMed] [Google Scholar]
- Zakeri P. et al. (2015) Gene prioritization through geometric-inspired kernel data fusion. In: 2015 IEEE International Conference on Bioinformatics and Biomedicine (BIBM). Washington, DC, pp. 1559–1565.
- Zhao W. et al. (2009) A statistical framework to evaluate virtual screening. BMC Bioinformatics, 10, 225. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zitnik M. et al. (2015) Gene prioritization by compressive data fusion and chaining. PLoS Comput. Biol., 11, e1004552. [DOI] [PMC free article] [PubMed] [Google Scholar]
- The Gene Ontology Consortium. (2015) Gene ontology consortium: going forward. Nucleic Acids Res., 43, D1049–D1056. [DOI] [PMC free article] [PubMed] [Google Scholar]
- International Classification of Diseases. (2015) Tenth Revision, Clinical Modification. https://www.cdc.gov, (September 2016, date last accessed).
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.