MetaDCN: meta-analysis framework for differential co-expression network detection with an application in breast cancer

Abstract

Motivation

Gene co-expression network analysis from transcriptomic studies can elucidate gene–gene interactions and regulatory mechanisms. Differential co-expression analysis helps further detect alterations of regulatory activities in case/control comparison. Co-expression networks estimated from single transcriptomic study is often unstable and not generalizable due to cohort bias and limited sample size. With the rapid accumulation of publicly available transcriptomic studies, co-expression analysis combining multiple transcriptomic studies can provide more accurate and robust results.

Results

In this paper, we propose a meta-analytic framework for detecting differentially co-expressed networks (MetaDCN). Differentially co-expressed seed modules are first detected by optimizing an energy function via simulated annealing. Basic modules sharing common pathways are merged into pathway-centric supermodules and a Cytoscape plug-in (MetaDCNExplorer) is developed to visualize and explore the findings. We applied MetaDCN to two breast cancer applications: ER+/ER- comparison using five training and three testing studies, and ILC/IDC comparison with two training and two testing studies. We identified 20 and 4 supermodules for ER+/ER- and ILC/IDC comparisons, respectively. Ranking atop are ‘immune response pathway’ and ‘complement cascades pathway’ for ER comparison, and ‘extracellular matrix pathway’ for ILC/IDC comparison. Without the need for prior information, the results from MetaDCN confirm existing as well as discover novel disease mechanisms in a systems manner.

Availability and Implementation

R package ‘MetaDCN’ and Cytoscape App ‘MetaDCNExplorer’ are available at http://tsenglab.biostat.pitt.edu/software.htm.

Supplementary information

Supplementary data are available at Bioinformatics online.

1 Introduction

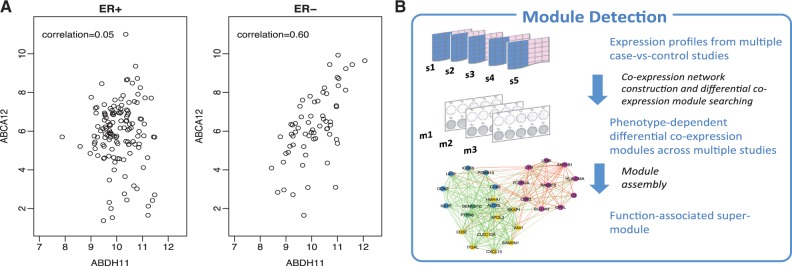
Differential co-expression (DC) refers to the change in gene–gene correlations between two conditions (e.g. cases and controls). Changes in gene–gene correlation may occur in the absence of differential expression, meaning that a gene may undergo radical changes in regulatory pattern that would be undetected by traditional differential expression (DE) analyses (see Fig. 1A). A specific phenotype could be contributed by differential co-expression without altering the expression levels of genes. This phenomenon has been found in aging (Southworth et al., 2009) as well as other biological conditions (Gaiteri et al., 2014). Disease-associated alterations in the regulatory systems that create co-expression changes may be revealed through comparing gene–gene correlations that are computed separately from control and disease populations. Therefore, DC analysis can provide complementary information to standard differential expression (DE) analyses. Differential co-expression in two conditions could shed light on novel biological mechanism. For example, a group of genes may be regulated by a common transcription factor or epigenetic modification, which is active in one condition but disrupted in the other.

Fig. 1.

(A) An example of differential co-expression between ER+ and ER- breast cancers. Each dot represents one sample. Strong co-expression between ABCA12 and ABHD11 can be observed in ER- tumors (right) but not in ER+ tumors (left). Samples are from GSE7390. (B) Diagram of procedures for basic module detection by energy function optimization and supermodule assembly via pathway enrichment criterion (Color version of this figure is available at Bioinformatics online.)

In the literature, Lai et al. (2004) has proposed an expected conditional F-statistics to identify differential co-expressed gene pairs, while Amar et al. (2013) and Bhattacharyya and Bandyopadhyay (2013) developed methods for direct identification of DC gene modules. Choi and Kendziorski (2009) detected differential co-expression using predefined gene sets such as Gene Ontology (GO) categories. Although this approach incorporates prior biological information, it lacks the ability to detect novel DC modules. Another class of methods detected differential modules with genes highly co-expressed in one reference condition but with little or no correlation in the other condition. These types of methods rely on applying clustering methods to one reference condition, causing case-control asymmetry in the analysis (Ihmels et al., 2005; Watson, 2006). To circumvent this problem, Zhang and Horvath (2005) identified co-expressed modules in the entire (cases and controls combined) cohort through clustering and then evaluate their differential co-expression across conditions. Similarly, Tesson et al. (2010) extended this framework to detect differential co-expression modules by introducing the correlation changes between conditions into dissimilarity matrix for clustering (DiffCoEx).

All methods described above for DC network detection focused on single transcriptomic study analysis. The differential correlation relationship could arise from meaningful biological sources as well as uncorrected technical biases (see Figure 1 in Gaiteri et al., 2014). Any mechanism that synchronously regulates transcription of multiple genes, unwanted batch effect, or mixture of tissues could potentially contribute to co-expression relationships. Therefore, instead of looking for DC networks between two conditions in a single study, differential co-expression may be confirmed across multiple datasets via meta-analyses to increase the detection power and stability. DC networks that are significant in one dataset may become more convincing if the DC patterns are preserved across multiple datasets. DC between conditions can be assessed by different choices of measures; for example, differential modules with a predominant measure such as density (Li et al., 2011) or other sophisticated network measures (Kugler et al., 2011; Langfelder et al., 2011).

So far, few studies attempted to detect DC networks across multiple studies. Mehan et al. (2009) proposed a simulated-annealing-based method to detect DC modules of which the network density changes were associated with phenotype. However, their method embedded pathway enrichment in the optimization of objective function; that is, the optimization phase heavily depended on the prior knowledge and also the output module sizes from the method were generally small. In this paper, we have developed a new meta-analytic framework, namely MetaDCN, to search for initial DC modules without prior information. Our method included additional network properties in the energy function to detect biologically meaningful ‘basic DC modules’ and false discovery rate (FDR) was controlled by permutation analysis. We then further combined basic DC modules that share common pathway annotation into more interpretable DC supermodules. We evaluated the method on simulated data and breast cancer studies to search for DCN between ER +  versus ER- and invasive lobular carcinoma (ILC) versus invasive ductal carcinoma (IDC). The identified DCNs were further validated in independent breast cancer studies. The result identified pathways such as ER-mediated immune functions and extracellular matrix heterogeneity between ILC and IDC that help elucidate the underlying disease mechanisms.

2 Methods

MetaDCN combines multiple case-control transcriptomic studies to detect disease-associated modules such that genes in the modules are highly correlated in control samples but the correlations are disrupted in cases or vice versa. An energy function is introduced to detect modules of DC networks across studies. Since direct optimization for large modules is computationally challenging and unstable, we will first aim for detecting a sequence of small ‘basic DC modules’ of sizes between 3 and 30. Basic DC modules are then combined into DC supermodules via a module assembly algorithm based on pathway enrichment information (see Fig. 1B). Such pathway-centric assembly improves functional annotation of detected supermodules that can advance disease understanding and guide further hypothesis generation.

2.1 Basic DC module detection

The algorithm to detect basic DC modules is outlined below. Details of energy function, optimization procedure and false discovery rate control are described.

2.1.1 Energy function

Consider N transcriptomic studies, each containing case and control samples. Gene co-expression networks are first constructed among cases and among controls for each of the N studies, thus generating 2N co-expression networks. In this paper, we demonstrate our method based on unweighted networks but the method can be extended to weighted networks. To build unweighted networks and normalize them across different studies, we first calculated pair-wise gene–gene Spearman’s correlations for robust comparisons. In contrast to Pearson correlation, Spearman’s correlation can capture both linear and non-linear association. Considering the large number of possible edges and computation complexity, we then select the correlation cut-off for edge connections so that only the top 0.4% of possible connections in each network were kept (Lee et al., 2003). This procedure provides robustness because different studies usually have different sample sizes and are conducted using different experimental platforms, which could result in distinct correlation distributions. Our proposed algorithm is developed for the more popular unweighted network but it can be modified for weighted network if desired.

We propose to minimize the following energy function (target function) for detection of gene modules with differential co-expression:

$$E_{\text{tot}}=w_1{E}_{\text{diff}\_\text{mean}}+w_2{E}_{\text{size}}+w_3{E}_{\text{diff}\_\text{var}}$$

The proposed target function comprises the following three components: I) $E_{\text{diff}\_\text{mean}}$ for mean network density difference between two phenotypes across N studies, II) $E_{\text{size}}$ for size of module and III) $E_{\text{diff}\_\text{var}}$ for the consistency of the density difference between the two phenotypes across N studies. Gene modules minimizing $E_{\text{tot}}$ have consistently large correlation difference between cases and controls across multiple studies, as well as reasonable large size. The search direction is bidirectional, meaning that we will identify modules with significantly higher connections in case networks than in control networks and then repeat reversely.

Each component in the target function is described by an exponential decay function. The first component is defined as $E_{\text{diff}\_\text{mean}}=\text{exp}\hspace{0.17em}\left\{-{\alpha }_1\left(\frac{{\sum }_{i=1}^N({\delta }_{i,\text{cases}}-{\delta }_{i,\text{controls}})}{N}\right)\right\}$, where ${\delta }_{i,\text{cases}}$ and ${\delta }_{i,\text{controls}}$ are the densities of case network and control network respectively in study i. The exponential decay function favors larger mean density differences between cases and controls and is the major target of our algorithm. The second component $E_{\text{size}}=\text{exp}\hspace{0.17em}\{-{\alpha }_2(|x|/\gamma )\}$ (where x denotes the genes in the module, $\left|x\right|$ is the module size) is related to the size of the modules which favors larger modules and penalizes smaller modules. We restricted the module size no larger than 30 due to large searching space. We set γ = 30 to rescale the ratio ranging from 0 to 1 to make the three decay parameters (α₁, α₂ and α₃) comparable in later parameter selection. Without $E_{\text{size}}$, dimers or triplets with density 1 or 0 could easily dominate the output by random chance and increase false positives. The third component $E_{\text{diff}\_\text{var}}=\text{exp}\hspace{0.17em}\left\{-{\alpha }_3\left(1-\sqrt{\frac{\sum _i{({\delta }_{i,\text{cases}}-{\delta }_{i,\text{controls}})}^2}{N}}\right)\right\}$ quantifies the variance of the paired difference of network densities between cases and controls across studies to favor consistent differential co-expression among studies. In all three components, the parameters (α₁, α₂ and α₃) control the decay rate in the exponential function. In our implementation, we set ${\alpha }_2=10$ for $E_{\text{size}}$ and ${\alpha }_1={\alpha }_3=5$ for $E_{\text{diff}\_\text{mean}}$ and $E_{\text{diff}\_\text{var}}$. The higher α₂ was used for $E_{\text{size}}$ to avoid extremely small modules as previously mentioned.

To tune the parameters w₁, w₂ and w₃ in the target function, we first constrain the sum of the three parameters to be 1000, i.e. $w_1+w_2+w_3=1000$. We assigned equal importance to $E_{\text{diff}\_\text{mean}}$ and $E_{\text{diff}\_\text{var}}$ by setting w₁ = w₃, and searched for optimal w₂ from 100 to 700 with 100 increments that could output the largest number of basic DC modules under FDR 0.3 (see below for detection of basic DC modules and FDR control).

2.1.2 Optimization by simulated annealing

Due to the non-convex nature of $E_{\text{tot}}$, we applied simulated annealing, a stochastic algorithm for non-convex optimization (Kirkpatrick et al., 1983). In each Monte Carlo (MC) step with simulated annealing, a new state is proposed and denoted as $X_{\text{new}}$, which is either adding a node (gene) from trial set to selected set or removing a node (gene) from selected set to trial set. At the beginning, the trial set is determined as the set of genes that have at least one edge connected to the seed module genes (initial selected set) in any of the N case co-expression networks. If the resulting energy is smaller, the state is accepted. If not, the state is accepted with an acceptance probability as $P_{\text{acc}}=\min \left(1,\frac{\pi (x_{\text{new}})p(x_{\text{new}\to \text{old}})}{\pi (x_{\text{old}})p(x_{\text{old}\to \text{new}})}\right)$, where $P_{\text{acc}}$ is the acceptance probability and $p(x_{\text{old}\to \text{new}})$ is the transition probability from old state to the new state. If a genes is added from trial set to selected set, $p(x_{\text{old}\to \text{new}})/p(x_{\text{new}\to \text{old}})=\left|\text{trialset}\right|/\left|\text{selectedset}\right|$; if a genes is removed from selected set to trial set, $p(x_{\text{old}\to \text{new}})/p(x_{\text{new}\to \text{old}})=\left|\text{selectedset}\right|/\left|\text{trialset}\right|$, where $\left|x\right|$ denotes the size of set x. $\pi (x_{\text{new}})$ is the Boltzmann distribution of the energy function to be minimized: $\pi (x_{\text{new}})=\text{exp}\hspace{0.17em}\{-E_{\text{tot}}(x_{\text{new}})/T\}$, where T is a temperature parameter. When temperature is high, new trial moves will be accepted easily and thus more freely jump out of the local minimum. When temperature gets lower, it tends to converge to a local minimum. We apply the temperature schedule $T_{(k+1)}=0.95·T_k$ and stop the annealing run if the acceptance ratio is smaller than 2%, where the acceptance ratio is calculated as the ratio of steps accepted in every 400 MC steps. Due to large searching space, we bounded the module size between 3 and 30. If current module size is 3, only addition of new node is allowed for a new state while if module size is 30, only node removal is allowed.

Although simulated annealing helps improve local minimum trapping, a good starting point, which is called seed module here, is critical for optimization in high dimensional space. Instead of randomly selecting a subset of genes from the genome to be the seed modules, an edge-study matrix of Spearman correlations was constructed where rows represent all possible edges and columns represent all studies in two conditions of size 2N (Walley et al., 2012). For each edge on the rows, a simple paired t-test is applied to the Spearman correlations to assess candidate differential co-expression edges (require paired t-test P-value < 0.1 and absolute mean difference of Spearman correlation > 0.1). Based on these candidate differential co-expression edges, an initial network is constructed and multiple (denoted as K) connected graphs in the network are identified. If the size of a connected graph is larger than 30, we randomly sample 10 genes from it as the initial seed module for optimization starting points; if the size is smaller than 3, we discard it. Otherwise, the optimization starts from the connected graphs as the seed module directly. In our evaluation for simulations and application, such an algorithm to generate seed modules has performed well. But it is possible to apply other community detection algorithms for this purpose (Fortunato, 2010).

Although simulated annealing helps improve local optimum problem, optimization instability still exists. We will repeat the optimization by starting from K initial seed modules and repeat R times of simulated annealing repeats. For two repeats with Jaccard index greater than 0.8, we will select the one with smaller $E_{\text{tot}}$. This will generate ${\sum }_{k=1}^K{R}_k$ basic differential co-expression (DC) modules for supermodule assembly, where R_k is the number of basic modules from the kth seed modules with pairwise jaccard index smaller than 0.8.

2.1.3 Control of false discovery rate

To avoid detection of spurious modules by chance, false discovery rate is assessed for detected ${\sum }_{k=1}^K{R}_k$ basic DC modules as described below. Denote by E_kj the optimized energy value for detected basic DC module u_kj from the k-th seed module and j-th simulated annealing repeat, where $1\le k\le K$ and $1\le j\le R_k$. We first permute the case-control class labels for samples in each study and then reconstruct the case and control co-expression network as described previously. Simulated annealing optimization is similarly applied to detect ${\sum }_{k=1}^{K}R{\prime }_k$ ‘null’ basic DC modules, where $R{\prime }_k$ is the number of basic modules dected from permuted network with pairwise Jaccard index smaller than 0.8. Suppose the permutation is repeated for B times and the resulting energy values are denoted as $E_{k,j}^{(b)}$ where $1\le b\le B,\hspace{0.17em}1\le k\le K^{(b)},\hspace{0.17em}1\le j\le R_k^{\prime (b)}$. Under null hypothesis, the resulting case and control co-expression networks from permutation have no difference and $E_{k,j}^{(b)}$ will form a null distribution to assess P-values of E_kj. The P-values of basic DC modules u_kj are estimated as $p(u_{kj})=\frac{{\sum }_{b=1}^B{\sum }_{k=1}^{K^{(b)}}{\sum }_{j=1}^{R_k^{\prime (b)}}I\{E_{kj}^{(b)}\le E_{kj}\}+1}{{\sum }_{b=1}^B{\sum }_{k=1}^{K^{(b)}}{R}_k^{\prime (b)}+1}$. Pseudo count 1 is added to both the denominator and the numerator to avoid zero P-values (Phipson and Smyth, 2010). FDR is controlled by Benjamini-Hochberg correction to account for multiple comparisons.

2.2 Supermodule assembly, summarization and visualization

2.2.1 DC supermodule assembly

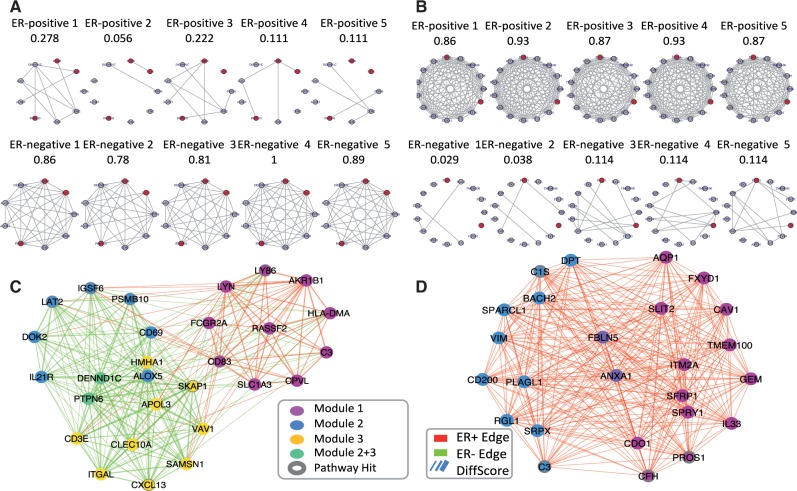
Since the current approach limits the size of the basic DC modules between 3 and 30, small modules often do not yield significant pathway enrichment annotation to inspire further hypothesis generation. Therefore, in order to obtain larger DC modules, we proposed to use statistical significance of pathway enrichment to guide module assembly. Firstly, we applied pathway enrichment analysis using Fisher’s exact test on detected basic DC modules (here we choose FDR $\le$ 0.3) against 2,379 pathways downloaded from MSigDB (http://www.broadinstitute.org/gsea/msigdb/), which contained Biocarta, KEGG, Reactome and Gene Ontology databases (excluding large pathways with more than 250 genes). For each given pathway, we applied Fisher’s meta-analysis method to combine P-values across basic DC modules and selected the top 150 pathways with the most significant meta-analyzed P-values. The restriction is not necessary, but will reduce the computation cost, without changing the results much. For each of the 150 candidate pathways, we searched among combinations of up to three basic DC modules (including both over-connected and under-connected DC modules of case-control comparison) and identify the assembled supermodule such that its pathway enrichment P-value is minimized. Take the immune response pathway in Figure 2C as an example, the pathway enrichment P-values for modules H9, L1 and L2 (H stands for modules with higher density in ER+ patients; L stands for modules with lower density in ER+ patients) are 0.018, $7\times {10}^{-4}$ and 0.02 with module sizes 10, 10 and 11, respectively. The supermodule combining these three basic DC modules contains 28 genes with Fisher’s exact test P-value =  $1.33\times {10}^{-6}$. Assembly of multiple basic DC modules can yield larger supermodules with more genes involved in a specific pathway, which provides better biological interpretation and hypothesis generation. Additionally, if the assembled supermodule contains both over-connected and under-connected basic DC modules (see red and green edges in Fig. 2C), it may suggest an interesting alternative activation mechanism in the pathway related to disease development.

Fig. 2.

(A) Example module (L1) more densely connected in ER- group with red nodes indicate genes belonging to the immune response pathway. (B) Example module (H7) more densely connected in ER+ group with red nodes indicate genes belonging to the complement cascade pathway. Nodes represent genes and links between them represents co-expression relationship. Each column corresponds to one independent study. (C) Visualization of immune response pathway supermodule. (D) Visualization of complement cascades pathway supermodules. The edge color represents the direction of differential gene co-expression, in which positive values (red color) represent ER-positive-favored co-expression and negative values (green color) show ER-negative-favored co-expression. Node color represents its origin of sub-modules, and the genes annotated in the immune response pathway are highlighted with dark circles. Edge width represents edge weight (Z score of differential co-expression) (Color version of this figure is available at Bioinformatics online.)

2.2.2 Summarization and visualization of DC supermodules

Visualization of basic DC modules across N studies can be easily done by displaying the 2N co-expression networks as shown in Figure 2(A, B). For DC supermodules, however, smarter design of visualization is needed. Figure 2(C, D) shows our proposed visualization display for DC supermodules. On the left plot, three basic DC modules (gene nodes displayed by red, blue and yellow) are combined to form the DC supermodule. The edge widths between any pair of gene nodes i and j are controlled proportionally by a standardized score Z_ij to represent the degree of differential co-expression. Denote by $u_{ij}^{(s)}$ and $v_{ij}^{(s)}$ the Spearman correlation between gene i and j in study s in case and control samples, respectively. Let $d_{ij}^s=u_{ij}^{(s)}-v_{ij}^{(s)}$ and let ${\overline{d}}_{ij}$ be the mean of paired correlation differences of all studies, σ_ij be the standard deviation of paired correlation differences and σ₀ be the fudge parameter estimated by the median of all standard deviations σ_ij’s. The the edge widths are proportionally to the standardized score $Z_{ij}=\frac{{\overline{d}}_{ij}}{({\sigma }_{ij}+{\sigma }_0)}$. The fudge parameter σ₀ is to avoid accidentally large Z_ij due to small σ_ij (Tusher et al., 2001). As a result, the DC supermodule can be represented as a weighted undirectional network. P-values of the Z scores were calculated by permuting case and control subjects in each study and randomly subsample the same number of genes to calculate the null permutated Z scores and comparing with them. Only edges with significant P-values passing certain P-value threshold are displayed in the network plot.

We further developed a Cytoscape plug-in application, called ‘MetaDCNExplorer’, which utilizes the power of Cytoscape Java API in visualizing complex networks and integrating topology with attributes. The interface allows users to load the input supermodule attributes and generate interactive network visualization with additional context annotations. First, the user selects a DC supermodule of interest to visualize from the list of biological pathways ranked by the significance of enrichment. The attributes of that supermodule will be loaded. The absolute values of the standardized Z scores for each gene pairs will be interpreted as edge widths, and the initial network view will be generated using edge-weighted force directed layout algorithm provided from prefuse toolkit (see supplement material for more details). In the network view, the edge width represents the edge weight. Nodes with their neighbors connected by high-weight edges will be automatically clustered together, so that the modular organization will be revealed. The edge color represents the direction of differential co-expression interpreted from edge Z scores, in which positive values (red color) indicate over-connected edges and negative values represent under-connected edges in case-control comparison. Node color represents the original basic DC modules where the gene belongs, and the genes annotated under the selected biological pathway are highlighted with outer black circles. To account for the fact that different diseases might have different range of differential co-expression signals, we thus introduced additional factors that control the repelling and attracting force between and within the modules. These factors, together with the edge P-value cut-off threshold, are made adjustable in a control panel so that users can update the network view in real time. In summary, this application is designed to reveal the modular organization of DC supermodules and to suggest alternatively activated sub-pathways that allow biologists to further explore and generate biological hypotheses on potential disease mechanisms.

2.3 Datasets

In this paper, we applied MetaDCN to two breast cancer applications. In the first application, DC supermodules are detected for ER+ versus ER- comparison in five training studies and validated in three independent testing studies. The second application examines invasive lobular carcinoma (ILC) and invasive ductal carcinoma (IDC) comparison in two training studies (with both ILC and IDC samples) and partially validate in two testing studies, where only ILC subjects are available. Details of data description and data preprocessing are available in Supplement Material.

3 Results

3.1 Simulation

We first applied MetaDCN to a simulated dataset including 5 studies. Each study contained case and control groups, with number of subjects in each group drawn from Poisson(50). We generated 1000 artificial genes named 1 to 1000 and a subset of them belonged to 5 gene modules (non-overlapping), each of which containing the number of genes $g_m\sim Poisson(20)$ ($1\le m\le 5$). Let $x_c^{(s)(m)}$ denote the vector of expression intensities of the g_m genes in the m-th module in group c in study s. We generated $x_c^{(s)(m)}\sim N(0,{\Sigma }_c^{(s)(m)})$, where ${\Sigma }_c^{(s)(m)}\sim \text{Inverse}-\text{Wishart}(60,(1-{\rho }_c^m)I+{\rho }_c^{m}J),\hspace{0.17em}{I}_{g_m\times g_m}$ is the identity matrix, $J_{g_m\times g_m}$ is a matrix with all entries as 1, c = 1 for controls, c = 2 for cases, s = 1, 2, …, 5, and m = 1, 2, …, 5. We set different $({\rho }_{c=1}^m,\hspace{0.17em}{\rho }_{c=2}^m)$ pairs for five modules to include both strong and weak signals. They were set to be (0.3, 0.1), (0.1, 0.3), (0.5, 0.1), (0.1, 0.5) and (0.7, 0.1) for 5 modules respectively. Therefore, the first and second modules have smaller signals, while the fifth module has the strongest signal. For genes outside the module, the expressions were i.i.d. drawn from N(0, 1).

With this simulated dataset, we constructed the edge-study matrix based on Spearman correlation. The module search was performed using simulated annealing algorithm with maximum iterations as 500. R = 3 trials with different initial seed modules were repeated, and P-value was calculated using B = 10 permutations. In the end, the best module among 3 repeats was selected based on optimal P-value and energy. For simplicity, here we only evaluate performance of basic DC modules without module assembly. If the Jaccard index (ratio of the intersection set divided by the union set) of the identified basic DC module to the underlying truth is greater than 0.5, we denote this searching as a successful hit.

We generated 50 datasets and compared the performance of MetaDCN with an existing method DiffCoEx (Tesson et al., 2010). The implementation of DiffCoEx used the R code directly from the original paper with the default setting. The soft threshold, as the most sensitive tuning parameter, was chosen based on scale free topology fit (Zhang and Horvath, 2005). The hierarchical tree was cut using dynamicTreeCut R package (Langfelder et al., 2008).

Table 1 shows the lower and upper quartile of number of detected modules and the percentage of successful hit for each of the five modules under different FDR cut-offs for permutation test in the 50 repeated simulations. The result shows that DiffCoEx tends to detect many false positives while still miss the underlying true DC netowkrs.

Table 1.

Percentage of successful hit (Jaccard index >0.5) in simulation study (50 repeats)

Method	FDR	Upper and lower quartile	M1 (%)	M2 (%)	M3 (%)	M4 (%)	M5 (%)
MetaDCN	0.1	(3, 5)	56	58	96	96	100
	0.2	(4, 5)	72	74	100	100	100
	0.3	(5, 5)	78	82	100	100	100
DiffCoEx	–	(3, 39)	8	8	30	26	37

3.2 Breast cancer studies (ER+ versus ER-)

We next applied our method to identify differentially co-expressed modules between networks from ER+ patients and networks from ER- patients. Estrogen receptor, indicating the cancer cell response to hormone estrogen, is an important marker in breast cancer cases for treatment selection. Detecting differential co-expression network between ER+ and ER- patients can help us better understand the difference of disease mechanism, thus designing specific therapies for ER+/ER- patients. In the analysis of training data, five pairs of gene co-expression networks were constructed for ER+ patients and ER- patients across the five studies. Edge-study matrices were calculated and connected components were obtained as initial seed modules for simulated annealing algorithm. FDR was calculated for each of the modules with B = 10 permutations. The best weights were selected based on the results from first 3 repeats with different initial modules. With the optimal weights and R = 10 repeats, at FDR $\le$ 0.3, 12 basic DC modules were detected as over-connected in ER+ networks while another 12 basic DC modules were detected as over-connected in ER- networks. Two example modules, one densely connected in ER+ networks and one densely connected in ER- networks, are illustrated in Figure 2(A, B). Both modules achieved FDR 0.02.

We tested varying number of repeats (R) in each seed module and the results of pathway-centric assembly are quite consistent. We identified 20 supermodules engaged in 40 pathways, sharing at least 3 overlapping genes with the enriched pathway. The top pathways associated with the assembled modules were listed in Table 2(A) (see full list in Supplementary Table S4). Among the list of summarized DC supermodules, ‘complement cascade pathway’ was with highest significance followed by ‘immune response pathway’. Figure 2(C, D) showed the network view for these two DC supermodules.

Table 2.

Top pathway-centric supermodules with at least 3 pathway overlapping genes (with 10 repeats with different initial modules)

(A) Pathway name (ER+ versus ER-)	Pathway size	Module size	# pathway genes	q-value	P-value	Module
REACTOME_COMPLEMENT_CASCADE	32	25	4	2.14E-05	1.93E-07	H7,H8
GO_IMMUNE_RESPONSE	235	28	7	5.63E-05	1.33E-06	H9,L1,L2
REACTOME_REGULATION_OF_COMPLEMENT_CASCADE	14	25	3	5.63E-05	2.47E-06	H7,H8
GO_ORGAN_MORPHOGENESIS	144	35	6	5.63E-05	2.80E-06	H3,H5,L9
BIOCARTA_TCYTOTOXIC_PATHWAY	14	23	3	5.63E-05	2.85E-06	H3,L5

(B) Pathway name (ILC versus IDC)	Pathway size	Module size	# pathway genes	q-value	P-value	Module
GO_PROTEASE_INHIBITOR_ACTIVITY	41	27	3	0.003	6.13E-05	L2,L4,L8
GO_PROTEINACEOUS_EXTRACELLULAR_MATRIX	98	15	3	0.003	0.00085	L5,L7
GO_EXTRACELLULAR_MATRIX	100	15	3	0.003	0.00085	L5,L7

Module starts with H indicates it is more densely connected in ER+ or ILC network, while module starts with L indicates it is more densely connected in ER- or IDC network.

In the literature, studies have shown that estrogen receptors can regulate innate immune cells (Kovats, 2015). Cunningham and Gilkeson (2011) found ERs have prominent effects on immune function in both the innate and adaptive immune responses. ERα expression is associated with outcome in patients with autoimmune diseases such as lupus. Possible alternative activations of immune and complement pathway between ER+ and ER- breast cancer patients have also been revealed in several research studies. Teschendorff et al. (2007) found that the heterogeneity in clinical outcome of ER- breast cancer patients are related with complement and immune pathway, while this association is not observed in ER+ patients.

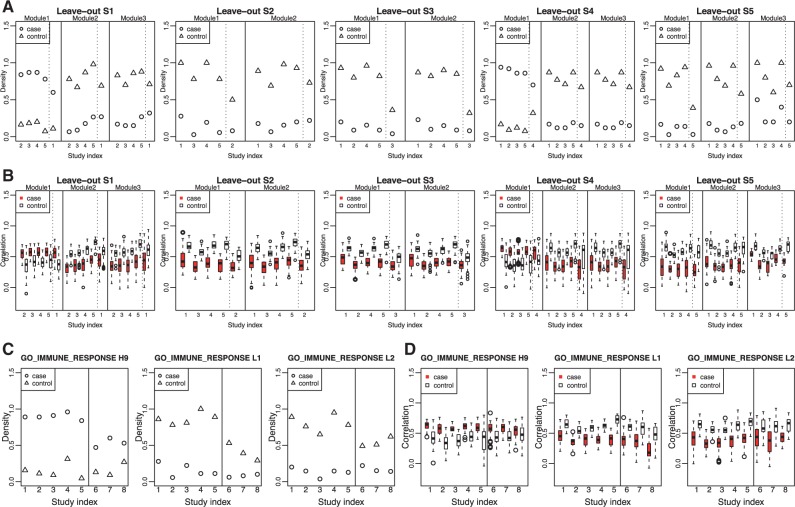
We next validated those two supermodules in leave-one-out cross-validation (LOOCV). Each time, we left one study out as testing set and used the remaining four studies as training set to perform module searching and module ensemble. In each LOOCV, 2 or 3 basic DC modules were merged into a DC supermodule in each pathway. We calculated network averaged densities in each basic DC module in the four training studies (on the left of dashed line) as well as the testing study (on the right of dashed line) in Figure 3(A) and Supplementary Figure S1(A). Similarly, box-plots of Spearman correlation distributions are plotted in Figure 3(B) and Supplementary Figure S1(B). The result consistently shows good validation of the finding.

Fig. 3.

(A) Densities and (B) correlations of the basic modules assembled into immune response pathway supermodules in leave-one-out cross-validation. Solid lines separate modules, and dashed lines separate training set and testing set. (C) Module density and (D) correlations of genes in the basic modules enriched in immune response supermodule in independent validation studies. Solid lines separate training sets and testing sets (Color version of this figure is available at Bioinformatics online.)

Finally, we used the top two pathways and the DC supermodules obtained from five training studies and tested in the three independent validation studies. Same set of genes was used for constructing co-expression network. If genes were not available in a study with different platform, the overlapped gene set was used. Following Figure 3 (A, B) and Supplementary Figure S1(A, B) for LOOCV, we plotted the average network densities and box-plots of Spearman correlation distribution in Figure 3(C, D) and Supplementary Figure S1(C, D) for the basic DC modules of the supermodules enriched in those two pathways. The result provides consistent validation of the differential co-expression pattern of gene modules enriched in these pathways.

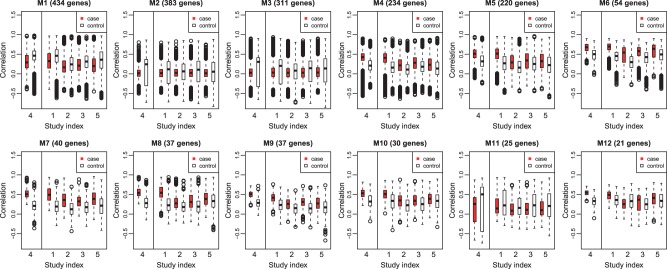
As a comparison, we also applied DiffCoEx (Tesson et al., 2010) to our datasets. Since DiffCoEx is only applicable to a single study, we applied it to the largest study METABRIC using the same procedure as described in the simulation section and evaluated the validation in other studies. By selecting soft threshold based on free topology fit (Zhang and Horvath, 2005) and cutting hierarchical tree using dynamicTreeCut R package (Langfelder et al., 2008), 12 modules were detected in METABRIC by DiffCoEx. The gene–gene pairwise correlation distributions were calculated for METABRIC as well as the other four studies and the boxplots are shown in Figure 4. Most detected modules only showed moderate degree of validation.

Fig. 4.

Gene-gene pairwise correlation distribution of 12 modules detected by applying DiffCoEx on METABRIC. Solid lines separate training sets (S4) and testing sets (S1, S2, S3, S5) (Color version of this figure is available at Bioinformatics online.)

3.3 Breast cancer studies (ILC versus IDC)

We finally applied our method to search for DCN between two breast cancer histological subtypes: ILC (invasive lobular carcinoma) and IDC (invasive ductal carcinoma). IDC and ILC are the two most common subtypes of breast cancers, representing 60-75% and 5-15% of all breast cancer cases, respectively (Guiu et al., 2014). Several studies have shown that they are two biological distinct diseases by comparing their genomic profiles, but the biological process driving for different subtypes are still largely unknown (Michaut et al., 2016). Identifying differential co-expression network between ILC and IDC can potentially unveil different biological mechanism and provide targets for precise treatment for ILC. Using similar parameter settings, with the optimal weights and R = 10 repeats, at FDR $\le$ 0.3, 11 basic DC modules were detected as over-connected in IDC, and no modules were detected as over-connected in ILC. Pathway-enrichment-guided module assembly was performed for varying number of repeats with different initial seed modules. The results were quite consistent. We identified 4 supermodules engaged in 5 pathways, sharing at least 3 overlapping genes with enriched pathway. The top pathways associated with the assembled modules from 10 repeats were listed in Table 2(B) (see full list in Supplementary Table S3). Supplementary Figure S2 (A, B) shows the visualizations of two supermodules enriched in protease inhibitor activity and proteinaceous extracellular matrix pathways. We also validated the densities and correlations of the basic modules ensembled in those two pathways in the validation sets (see Supplementary Fig. S2).

In the literature, alteration of extracellular matrix in tumor stroma has been shown relevant to metastatic potential (Oskarsson, 2013). Previous imaging analysis has further demonstrated different evolution of fibrillary collagen changes in ILC versus IDC throughout tumor progression (Burke et al., 2013).

4 Conclusion

In this study, we proposed a method, MetaDCN, to detect consensus differential co-expression (DC) networks across multiple studies with respect to certain phenotype of interest (e.g. case versus control or ER+ versus ER-). The method optimizes a target function to detect biologically meaningful DC modules. Since global optimization is computationally infeasible and unstable, we developed a simulated annealing algorithm to detect small (size 3–30) basic DC modules and assessed their false discovery rate. Through a pathway-guided module assembly algorithm, basic DC modules passing FDR threshold were merged into DC supermodules that were enriched in certain pathways to allow biological interpretation and hypothesis generation. The module assembly approach also allowed over- and under-connected basic DC modules to be simultaneously merged in a DC supermodule, representing possible alternative sub-pathway activation under different phenotypic conditions. Simulations and two real applications in breast cancer studies (ER+  versus ER- and ILC versus IDC) demonstrated superior performance of MetaDCN to elucidate novel disease-related differential co-expression mechanisms. DC supermodules identified by training breast cancer studies were further validated in independent studies. A Cytoscape plug-in software, MetaDCNExplorer, was developed to visualize and interactively explore the identified DC networks.

Given limited sample size and potentially biased patient cohort or experimental platform in a single transcriptomic study, detection of DC modules from one study is deemed unstable and often difficult to validate. With the rapid accumulation of transcriptomic studies in the public domain, a meta-analytic approach to combine multiple transcriptomic studies is promising to identify biological meaningful and verifiable DC modules. MetaDCN meets the urgent need for this purpose and is expected to elucidate novel mechanisms in many disease investigations.

Funding

National Institutes of Health [R01CA190766 to L.Z., Z.H. and G.C.T.]; L.W. was supported by China Scholarship Council [201508110051] and National Nature Science Foundation of China [11526146]; C.Y.C. was supported to visit G.C.T.’s lab by Ministry of Science and Technology in Taiwan (103-2917-I-002-020); S.O. is a Susan G Komen Scholar, and supported by BCRF.

Conflict of Interest: none declared.