Sequential feature selection and inference using multi-variate random forests

Abstract

Motivation

Random forest (RF) has become a widely popular prediction generating mechanism. Its strength lies in its flexibility, interpretability and ability to handle large number of features, typically larger than the sample size. However, this methodology is of limited use if one wishes to identify statistically significant features. Several ranking schemes are available that provide information on the relative importance of the features, but there is a paucity of general inferential mechanism, particularly in a multi-variate set up. We use the conditional inference tree framework to generate a RF where features are deleted sequentially based on explicit hypothesis testing. The resulting sequential algorithm offers an inferentially justifiable, but model-free, variable selection procedure. Significant features are then used to generate predictive RF. An added advantage of our methodology is that both variable selection and prediction are based on conditional inference framework and hence are coherent.

Results

We illustrate the performance of our Sequential Multi-Response Feature Selection approach through simulation studies and finally apply this methodology on Genomics of Drug Sensitivity for Cancer dataset to identify genetic characteristics that significantly impact drug sensitivities. Significant set of predictors obtained from our method are further validated from biological perspective.

Availability and implementation

https://github.com/jomayer/SMuRF

Supplementary information

Supplementary data are available at Bioinformatics online.

1 Introduction

The general goal in systems medicine is to develop predictive models that can accurately predict sensitivity of an individual tumor to a drug or drug combination. Several predictive models have been developed for drug sensitivity prediction based on genetic characterizations (Haider et al., 2015; Mitsos et al., 2009; Sos et al., 2009; Walther and Sklar, 2011). In a recent community-based effort organized by Dialogue on Reverse Engineering Assessment and Methods (DREAM) project (Costello et al., 2014) and National Cancer Institute that explored multiple different drug sensitivity prediction algorithms applied to a common dataset, a Random Forest (RF)-based predictive methodology turned out to be a top performer (Wan and Pal, 2013).

RF refers to an ensemble of decision trees generated from bootstrap samples of the training data (Breiman, 2001). It relies on recursive partitioning of the feature space, where a randomly selected subset of features is considered at each node of each tree and an optimal node-splitting feature (belonging to this subset) and an optimum splitting rule is obtained via optimization of a specified cost function. Although several methods are available to draw the foregoing subset of features (Amit and Geman, 1997; Geurts et al., 2006; Ye et al., 2013), simple random sampling remains the most popular sampling method. Random sampling strategy decreases the correlation among trees and thus, the average response of multiple decision trees is expected to have lower variance than individual trees. Experimental results from several disciplines demonstrate the ability of RFs in generating accurate predictions (Banfield et al., 2007; Dietterich, 2000; Rahman and Pal, 2016; Rodriguez-Galiano et al., 2012; Schwarz et al., 2010). Furthermore, random sampling of features to generate trees can structurally handle large number of predictors, typically larger than the sample size. Consequently, RF has become a widely popular predictive mechanism, particularly suitable for handling high dimensional feature space. Given its popularity and superior performance in the foregoing DREAM project, we focus exclusively on RF methodology as the predictive tool and develop a strategy that can use RF framework for performing variable selection too.

Note that, in targeted drug therapy, besides prediction, it is also important to identify the genetic features that explain the drug action. In this situation, the most relevant features are the drug targets along with proteins that are closely connected to the drug targets. Information available on the features that are not biologically related to the drug action mechanism is essentially redundant. Typically, the size of this redundant set of features is overwhelmingly large as compared to the size of the relevant features (Hopkins and Groom, 2002; Imming et al., 2006). In such a situation, a random sampling mechanism will produce considerable number of trees that do not contain any relevant features. For instance, consider a complete set of M features out of which $m(\ll M)$ are relevant to the response and the rest M–m are not informative. Then the probability that a randomly chosen set of q (1 < q ≪ M) features at a particular node of a tree will contain at least one relevant feature is $1-\left(\begin{array}{c}M-m\\ q\end{array}\right)/\left(\begin{array}{c}M\\ q\end{array}\right)$. For instance, if M = 5000, m = 10 and q = 5, $1-\left(\begin{array}{c}M-m\\ q\end{array}\right)/\left(\begin{array}{c}M\\ q\end{array}\right)=0.01$. Then for a tree with d splitting nodes, with independent randomized draws of size q_j at each node, the probability that at least one random subset will contain at least one informative features is given by $1-{\prod }_{j=1}^d\left(\begin{array}{c}M-m\\ q_j\end{array}\right)/\left(\begin{array}{c}M\\ q_j\end{array}\right)$. Clearly, one need to grow trees of sufficient depth in order to pick relevant features otherwise the prediction generated from the particular tree would not be useful.

Problem arises because the set m is typically not known, or only partially known, a-priori. Instead, it is customary to use some dimension reduction techniques, as a pre-processing step, to reduce the candidate feature set to a reasonable size and then proceed to use more sophisticated mechanism to generate predictions or obtain the best feature set (Dudoit and Fridlyand, 2003; Hua et al., 2009; Svetnik et al., 2004).

RELIEFF is a widely popular filter feature selection method and its relevance evaluation criterion was shown to provide superior performance in many situations (Robnik-Šikonja and Kononenko, 2003). However, it operates on univariate input and univariate output and produces a ranking of features. It does not explicitly perform variable selection. LASSO (Tibshirani, 1996), on the other hand, is arguably the most popular model based variable selection algorithm. It systematically forces the coefficients associated with the features to be small or to be exact zero while minimizing the fitting errors. Features with coefficients that are close to zero are then eliminated. To handle multi-variate responses, (Obozinski et al., 2010) devised multi-task LASSO (MLASSO) that utilized an ℓ₁/ℓ₂ norm to find the common subspace of features among responses. However, both basic and MLASSO eliminate correlated features (Zou and Hastie, 2005), which may not be a desired property in biological studies (Toloşi and Lengauer, 2011). To alleviate this problem, the multi-task elastic net (MEnet) (Chen et al., 2012) was proposed, which employs an additional ℓ₂ penalty to the coefficients in the MLASSO.

Regardless of the pre-screening methodology, we need to ascertain that the filter step has the ability to accurately select the candidate set of features which will contain the best feature set. What should be the size of candidate set? If it is too small, the follow-up computation would be fast, but we may leave out some important feature (elements of m) and hence the variable importance score that are generated subsequently are not reliable. If it is too large, we can expect to have included the important features but then it will also include large number of spurious features, particularly, if m∕(M–m) is small, and the subsequent prediction from RF will suffer from the aforementioned problem of having too many weak learners–which in turn will affect the prediction performance. What we are alluding to is the fact that a methodology to obtain an objective guideline on how many features need to be selected from the pre-processing stage has not been investigated extensively. For most of the filter-based approaches, the choice of the initial set of candidate features is mostly subjective and fairly arbitrary (Costello et al., 2014). Furthermore, we shall demonstrate via simulation studies (Section 3.1) that the standard RELIEFF approach to obtain the candidate set of features perform poorly, even under simple data generation model, when m/(M–m) is small. For more advanced regularization-based approaches, one cannot easily attach a statement about statistical significance with the selected features.

Besides these standard filter-based approached and regularizations, Dudoit and Fridlyand (2003) and Svetnik et al. (2004) proposed a data-driven methodology to obtain a best model dimension, say r, first and then select the set of r most important features. However, this approach may lead to non-interpretable models where the selected features may not be biologically meaningful (Diaz-Uriarte and Alvarez de Andres, 2006). Regardless of the methodology, determining a best model dimension completely empirically may be too restrictive in a biological setup. Often, a strong penalty on model complexity is imposed purely for estimation purpose. For instance, standard LASSO penalty forces the number of non-trivial parameters to be less than the sample size. Quite obviously, such penalty may lead to non-detection of features even though they may be statistically significant. We shall demonstrate in Section 3 that a harsh LASSO-type penalty induces unnecessary sparsity while a relaxed ridge-type penalty leads to overwhelming false detection.

Our emphasis on interpretability of the model is due to an important aspect in targeted drug therapy where selection of specific features is as important as the identity of those features to find additional targets for increasing the precision of drugs or designing effective drug combinations. Thus, the selected feature set should not only produce accurate prediction but should also be biologically meaningful to be of any practical use. In other words, besides prediction accuracy, we need to identify all the genomic characteristics that significantly impact drug sensitivities. Ideally, we would like to have an inferential mechanism available to us akin to standard linear regression models, where the P–value of each regression coefficient indicates the relative importance of the predictors, the value of the coefficients can be used for prediction and goodness-of-fit measures (AIC or BIC) can be used to objectively identify model complexity. In our case, we have multi-variate responses with number of features overwhelmingly large as compared to sample size and the model complexity is determined both biologically and empirically. So, we would like to perform the following tasks:

1. Variable selection from a very high dimensional feature space explicitly taking into account multi-variate nature of the responses,

2. guarantee that the selected set of features will be both statistically significant and biologically relevant,

3. generate predictions from the features selected in (a) using RF mechanism with the added advantage of eliminating weak learners.

Although several methods are available that can handle individual aspects of the above lists of tasks, for instance, several forms of multi-task feature selection methodologies (Chen et al., 2012; Liu et al., 2009; Nie et al., 2010; Obozinski et al., 2010) can be used to handle the multi-variate nature of responses while performing variable selection, but the significance of the features cannot be tested owing to the bias incurred due to regularization. None of the foregoing methodologies, in their original form, can incorporate biological information associated with the features. Multi-variate group-LASSO (Li et al., 2015) is an attractive alternative that can induce sparsity and include biological information during the variable selection, but this methodology is model dependent and requires precise knowledge of group-structure a-priori. Despite their state-of-art nature, these methodologies would not be able to fulfill task (b).

Instead of selecting variables via regularization, one can use several permutation based importance measures which explicitly perform tests to provide information about statistical significance of the features (Strobl et al., 2007). In particular, the conditional inference framework (Hothorn et al., 2006) provides an algorithm for recursive binary partitioning that actually separates variable selection and splitting procedure at each node of the decision tree. In the variable selection phase, a global null hypothesis of independence between a set of features and the response is tested and the one that shows strongest association with the response is selected as the splitting feature. Unbiasedness in selection procedure is achieved via computation of P–values associated with the conditional distribution of the test statistic. Thus, the feature that has minimum (multiple testing) adjusted P–value which is also below a nominal threshold of α is selected for splitting. Once the splitting variable is selected, any desirable node cost function can be used to determine the actual split. Tree building stops when the global null hypothesis of independence cannot be rejected at level α. Note that, in this approach unbiased variable selection is performed simultaneously with tree generation and the P–values associated with each feature could be used as a variable importance measure in each node.

We can use the conditional inference framework, suitably adapted for multi-variate responses, to generate conditional random forest (CRF). We can then take the union of the set of statistically significant features produced by each tree to create the global pool of statistically significant features. In this article, we exploit this attractive statistical property of CRF and develop an iterative selection mechanism that can handle high dimensional feature space. Such iterative selection mechanism was used by Diaz-Uriarte and Alvarez de Andres (2006) for classification problem and by Hapfelmeier and Ulm (2013) for regression problem. However, none of the above studies have been extended to multi-variate responses. In fact, the permutation based importance measures, recommended by Hapfelmeier and Ulm (2013), cannot be used for multi-variate responses. In this article, we develop a multi-variate extension of the foregoing studies. We describe an easily interpretable variable importance measure to identify strongly informative features from relatively weak ones. We demonstrate the empirical convergence of our selection algorithm with synthetic data. We apply our methodology on drug sensitivity data, obtained on drug pairs that have common targets and hence expected to generate correlated sensitivities. We also describe an intuitive approach that allows our methodology to incorporate biological information in the variable selection stage. We reiterate that the prediction mechanism throughout this article is multi-variate random forest (MRF), we only compare the accuracy of our proposed variable selection methodology with several extant methodologies.

We discuss the details of our methodology in Section 2, provide simulation examples and follow it up with analyses of GDSC data in Section 3. We discuss the implications of our methodology and further research directions in the final section.

2 Materials and methods: sequential multi-response feature selection

The key to the proposed methodology is an iterative selection mechanism that first identifies a sparse set of significant features, ${\mathcal{F}}_w$ and then proceeds to identify a sparser set of strongly informative features, ${\mathcal{F}}_s$, with ${\mathcal{F}}_s\subset {\mathcal{F}}_w$. ${\mathcal{F}}_w$ provides information about adequate model dimension, while ${\mathcal{F}}_s$ is the (empirically justifiable) sparsest feature set that has sufficient explanatory power. We can then use these features in either ${\mathcal{F}}_w$ or ${\mathcal{F}}_s$ to develop a full blown MRF (De’ath, 2002; Rahman et al., 2017) to generate predictions. Below we describe the screening and prediction methodologies.

The basic theoretical idea of screening is repeated use of conditional inference framework of (Hothorn et al., 2006). We offer a brief description of the algorithm used to identify significant features below (A more detailed discussion on conditional inference in decision trees and RFs along with practical guidelines to choose α can be found in Hothorn et al., 2006):

Let the conditional distribution of the multi-variate response variable $\mathit{Y}$ given M features $\mathit{X}=(x_1,x_2,\dots ,x_M)$ be denoted by $D\left(\mathit{Y}\right|\mathit{X})$. Then at each node of a conditional inference tree, involving q features, we need to assess whether these features have sufficient explanatory power. Hothorn et al. (2006) suggested to test the partial null hypothesis $H_0^j:D\left(\mathit{Y}\right|x_j)=D(\mathit{Y})$ individually to assess the global null $H_0:{\cap }_{j=1}^q{H}_0^j$. If H₀ cannot be rejected, at a pre-specified level of significance (α), all q features are declared insignificant. If the H₀ is rejected, then the level of association between $\mathit{Y}$ and x_j is measured by the P–value associated with $H_0^j,j=1,2,\dots ,q$. Under the assumption of independent samples, they derived a linear statistic of the form

$${\mathit{T}}_j=vec\left(\sum _{i=1}^n{w}_i{g}_j\left(x_{ji}\right)h{({\mathit{Y}}_i,({\mathit{Y}}_1,\dots ,{\mathit{Y}}_n\left)\right)}^T\right)$$ (1)

where w_i is the case weight associated with the ith sample with w_i = 1 indicating that the ith sample is observed at the corresponding node of a particular tree and w_i = 0 indicate the absence of the said sample, $g_j(.)$ is a non-random transformation of x_j and $h(.)$ is the influence function that depends on $({\mathbf{Y}}_1,\dots ,{\mathbf{Y}}_n)$ in permutation symmetric way. The null distribution of ${\mathit{T}}_j$ in (1) can be obtained by fixing x_j and permuting the responses. Strasser and Weber (1999) obtained the closed form expression of the conditional mean (${\mathit{\mu }}_j$) and covariance matrix (${\mathbf{\Sigma }}_j$) of ${\mathit{T}}_j$ under H₀ given all permutations. Using this conditional mean, and the Moore-Penrose inverse ${\mathbf{\Sigma }}_j^{+}$ of ${\mathbf{\Sigma }}_j$, Hothorn et al. (2006) obtained a simplified univariate test statistic of the form $({\mathit{T}}_j-{\mathbf{\mu }}_{\mathbf{j}}){\Sigma }_j^{+}{({\mathit{T}}_j-{\mathbf{\mu }}_{\mathbf{j}})}^T$ which has an asymptotic ${\chi }^2$ distribution with degrees of freedom given by the rank of ${\mathbf{\Sigma }}_j$. Given this asymptotic null distribution of the univariate test statistic we can compute the P–value associated with $H_0^j$. To test the global H₀, we use Bonferonni-adjusted P–values obtained from each partial nulls and reject H₀ when the minimum of these individual P–values is less than the nominal threshold of α.

When H₀ is rejected, the feature that produces the minimum adjusted P–value is chosen as the splitting feature and the standard node cost function of multi-variate regression trees (De’ath, 2002) is used to determine the splits. Note that, several features can be declared significant at each node but the splitting feature is conceived as the one that has the strongest association with the response variable.

Based on this conditional inference framework to identify significant features, we propose our Sequential Multi-Response Feature Selection (SMuRFS) algorithm

1. Partition the training data into secondary training and secondary test sets. Specify the nominal level of significance α, number of features $q\ll M$ to be used in each conditional inference tree, and size of a post-hoc dataset, n_test.

2. For a particular tree, draw a random sample of q features from M features. Fit a conditional inference tree on bootstrapped samples. Let Q₁ be the set of features declared to be significant in that tree. Let $Q_2=q-Q_1$ be the set of insignificant features.

3. Assess the significance of the features in Q₂ on the post-hoc dataset, of size n_test, using the conditional inference framework. Let $Q_3\subseteq Q_2$ be the set of features that remain insignificant in both Step 2 and Step 3. Remove the set Q₃ from further consideration.

4. Obtain another bootstrap replicate of the observed samples. Draw a random sample of q features from $M-Q_3$ features and repeat Steps 2 and 3.

5. Stop when both the following conditions are satisfied (a) each of the M features is either declared significant or is deleted and (b) $Q_3=\left\{\right\}$ for the particular tree.

6. Using only the out-of-bag samples in Step 2 will lead to mismatch in power of the tests determining deletion from iteration to iteration. To achieve more balance in power, we augment the out-of-bag samples with randomly selected training samples to obtain the post-hoc dataset whose size, n_test, remains same in all iteration.

7. Perform cross validation to remove potential bias in variable selection.

8. Once the algorithm has converged, the set of features that survives the last iteration, in that particular fold, is declared the set of significant features, ${\mathcal{F}}_w$.

9. Grow a standard multi-variate CRF on the secondary test set using features in ${\mathcal{F}}_w$ and collect the splitting features. This set of features, ${\mathcal{F}}_s$, has the highest evidence against the orthogonality between the response and features. Elements of ${\mathcal{F}}_s$ are termed as strongly informative features.

Evidently, we can attach statements about statistical significance to the screened set of features. Qualitative labels, indicating variable importance, are automatic, i.e. features in ${\mathcal{F}}_s$ are strongly informative while those in ${\mathcal{F}}_w-{\mathcal{F}}_s$ are weakly informative. Finally, the second stage multi-variate CRF, generated with the features in ${\mathcal{F}}_w$, becomes the predictive apparatus (A pseudocode of this algorithm can be found the Supplementary Material. An R code implementing this algorithm can be downloaded from https://github.com/jomayer/SMuRF/). We can also generate another multi-variate CRF on the secondary test data using features in ${\mathcal{F}}_s$ which we call strong-SMuRFS. We demonstrate improved biological relevance of strong-SMuRFS in Section 3.

2.1 Incorporating biological information

Our focal application in this article is targeted drug therapy which contains precise information about drug targets and proteins that are closely connected with those targets. The SMuRFS algorithm described above does not include that additional information while performing variable selection. We offer an intuitive approach to accommodate drug target specific information within the SMuRFS framework.

Observe that, conditional inference framework first partitions the feature space and then estimates partition-based regression relationships. When we have information about drug targets, and features closely connected to those targets, we have a natural dichotomous partition of the feature space. Let, ${\mathit{X}}_A$ be the set containing biologically relevant features (associated with a given drug) and its complementary set, ${\mathit{X}}_A^c$, contains biologically unrelated features and those features whose association with the elements in ${\mathit{X}}_A$ are biologically ambiguous.

We propose an unbalanced penalization rule where features belonging to ${\mathit{X}}_A^c$ need to satisfy stricter inclusion criterion as compared to features belonging to ${\mathit{X}}_A$. As SMuRFS requires that each feature must survive multiple testings before being included in ${\mathcal{F}}_w$, we can subject all the features in ${\mathit{X}}_A^c$ to this standard SMuRFS inclusion rule. In contrast, if the features in ${\mathit{X}}_A$ turn out to be significant in any one of the iterations of SMuRFS algorithm, they are directly included in ${\mathcal{F}}_w$.

3 Results

3.1 Simulation

We compare the variable selection accuracy of our proposed SMuRFS and strong-SMuRFS with that of MLASSO, MEnet and standard RELIEFF methodologies. In particular, we observe how the foregoing two versions of SMuRFS react to (a) a high dimensional feature space, (b) highly correlated predictors and (c) $>2-$dimensional response space [It is to be noted that MLASSO or its elastic net counterpart are not based on hypothesis testing principle and, therefore, do not make binary decisions on whether to retain a feature or discard it. Instead, they produce weights reflecting relative importance of each feature. However, under model misspecification such weights are not reliable (Supplementary Material). Regardless of the incompatibility between SMuRFS and MLASSO/MEnet, the latter are the only methodologies, we know of, that allow simultaneous feature selection for multi-variate responses in a single coherent setup].

First, for the ith sample, we simulate 1000 features, ${\mathit{X}}_i=(X_{1i},\dots ,X_{1000i})$ from a multi-variate normal distribution with zero mean and block diagonal covariance matrix Σ given by $\Sigma =\text{bdiag}(\Omega ,\Omega ,\Omega ,\Omega ,I)$, where ${\Omega }^{25\times 25}$ is given by ${\Omega }_{bb}=1$ and ${\Omega }_{bb\prime }=0.7$ for $b\ne b\prime$, and $I^{900\times 900}$ denotes identity matrix. Next, we simulate the coefficient matrix ${\mathit{\beta }}^{1000\times 4}=[{\mathit{\beta }}_1,{\mathit{\beta }}_2,{\mathit{\beta }}_3,{\mathit{\beta }}_4]$ with ${\mathit{\beta }}_j$ is given by $[{\mathit{\beta }}_{j,s}^{100\times 1},0^{900\times 1}],\hspace{0.17em}j=1,\dots ,4$. Each component of ${\mathit{\beta }}_{j,s}$ is generated independently from a Uniform(1, 3) distribution, for $j=1,\dots ,4$. Then the mean of the ith response corresponding to the jth dimension is generated as

$${\mu }_{ij}={\mathit{X}}_i{\mathit{\beta }}_j+20{\left(1+\text{exp}\hspace{0.17em}({\mathit{X}}_i{\mathit{\beta }}_j)\right)}^{-1}$$ (2)

Finally, we simulate the marginal response Y_ij from a $N({\mu }_{ij},1)$ distribution, $j=1,\dots ,4$. The dependence in the response vector, ${\mathit{Y}}_i=[Y_{i1},Y_{i2},Y_{i3},Y_{i4}]$ is induced via Gaussian copula with correlation coefficient $\rho =0.5$. We simulate n = 500 samples, noting that the first 100 features are actually used to generate the mean. These features are termed as signal features and the remaining 900 are labeled spurious features.

For each competing algorithm, we perform 5-fold cross validation. In each fold, we use 20% of the data as primary test set and the remaining 80% data are randomly split into two equal parts, the training set and the secondary test set. All variable selection algorithms are run on the training set. Performances of the competitors are measured by the number of signal and spurious features that each of them has screened in each fold. Once the features are selected, we train a multi-variate CRF, now on the secondary test set, in each fold using the features selected (by different algorithms) in the previous step. This multi-variate CRF is used to predict the responses in the primary test set. We compare the prediction performances of the competing algorithms using normalized mean squared prediction error (NMSPE) and normalized mean absolute prediction error given by

$$\begin{array}{c}\text{NMSPE}=\frac{{(\mathit{Y}-\widehat{\mathit{Y}})}^T(\mathit{Y}-\widehat{\mathit{Y}})}{{(\mathit{Y}-\overline{Y}·1)}^T(\mathit{Y}-\overline{Y}·1)}\\ \text{NMAPE}=\frac{|\mathit{Y}-\widehat{\mathit{Y}}{|}^{T}1}{\sqrt{{(\mathit{Y}-\overline{Y}·1)}^T(Y-\overline{Y}·1)}},\end{array}$$

where $\mathit{Y}$ and $\widehat{\mathit{Y}}$ denote the vector of actual observations and their corresponding predicted values, respectively. $\overline{Y}$ denote the sample mean of $\mathit{Y}$ and $1$ is the usual unit vector. Computation is performed in R platform using the partykit package (Hothorn and Zeileis, 2015).

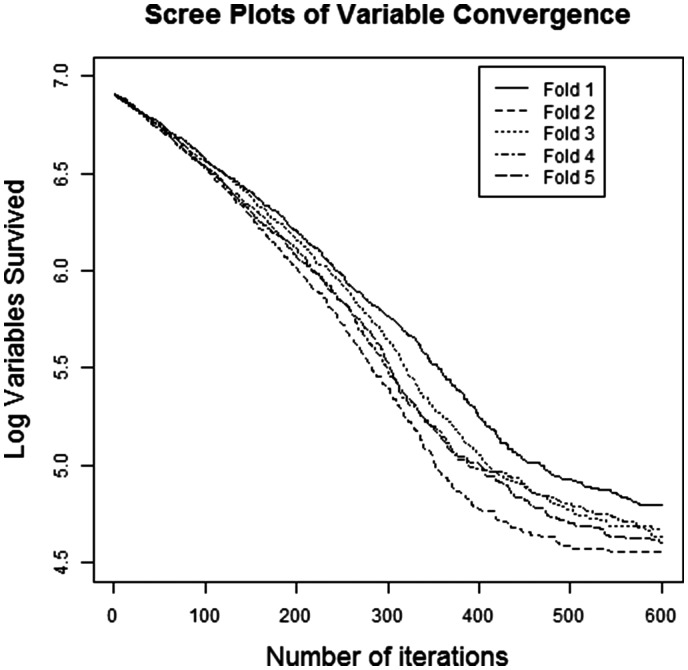
For SMuRFS, we fix q = 5, $\alpha =0.05$ and n_test = 127. We run the SMuRFS algorithm on each fold with the same values of $q,\alpha$ and n_test. The screen plot in Figure 1 summarizes the performance of SMuRFS algorithm. The figure suggests that the number of variables selected in each fold appears to be converging empirically. For MLASSO algorithm, we use the 5-fold cross validated minimum λ and select the features whose corresponding coefficients are non-zero. For MEnet, we use $\alpha =0.8$ and the 5-fold cross validated minimum λ and select the features whose corresponding regression coefficients are non-zero. For both MLASSO and MEnet, we use the glmnet package in R (Friedman et al., 2010; Simon et al., 2011). As RELIEFF works only on univariate response, we apply RELIEFF on $Y_1,\dots ,Y_4$, individually, using CORElearn package in R (Robnik-Sikonja and with contributions from John Adeyanju Alao, 2016) and take the union of top 100 features obtained from this univariate RELIEFF deployment. Table 1 shows the performance of the competing models in identifying the true signals.

Fig. 1.

Empirical convergence of sequential feature selection algorithm for 100 signals

Table 1.

Table showing the selection accuracy of competing algorithms for $m=0.1M$

Method	Fold	Number of	Number of	Number of spurious
		true signal	signals identified	features selected
SMuRFS	Fold 1	100	97	9
	Fold 2	100	93	4
	Fold 3	100	93	8
	Fold 4	100	92	17
	Fold 5	100	100	7
MLASSO	Fold 1	100	46	53
	Fold 2	100	50	37
	Fold 3	100	48	10
	Fold 4	100	41	31
	Fold 5	100	44	10
MEnet	Fold 1	100	99	281
	Fold 2	100	100	323
	Fold 3	100	98	373
	Fold 4	100	93	289
	Fold 5	100	100	186
RELIEFF	Fold 1	100	54	274
	Fold 2	100	59	267
	Fold 3	100	49	267
	Fold 4	100	47	268
	Fold 5	100	59	270

On an average, MEnet picks out 98 signals out of 100, followed by SMuRFS (95), RELIEFF (54) and MLASSO (46). Conversely, on an average, MLASSO selects the sparsest set of features (74), followed by SMuRFS (104), RELIEFF (323) and MEnet (388). Sparsity of MLASSO is due to the sparse nature of the problem and presence of correlated features (Tibshirani, 1996). MEnet consistently selects highest number of signals in each fold, but at the cost of selecting a large number of spurious features. RELIEFF does not perform well in terms of identifying signals nor does it induce sufficient parsimony. The fact that all multi-variate procedures outperform RELIEFF indicates that a univariate selection scheme, i.e. RELIEFF is not appropriate when dealing with multi-variate responses. Although one can argue that sparsity can be induced in RELIEFF if one uses only a few features in each response dimension, but that strategy, in our experience, results in even more non-detection of signals.

Observe that SMuRFS is overwhelmingly superior in terms of the picking up signals and rejecting spurious features in every fold. The average correct detection to false detection ratio (Column 4/Column 5 of Table 1) for SMuRFS is 13.7, followed by MLASSO (2.55), MEnet (0.36) and RELIEFF (0.2). As mentioned before, the splitting features observed in multi-variate CRF trained on the secondary test set identifies the strongly informative features, ${\mathcal{F}}_s$. In this synthetic data, ${\mathcal{F}}_s$ consists of 90 signals and 1 spurious feature across all 5-folds. This demonstrates that strong-SMuRFS can reliably identify true features from spurious ones.

Turning to prediction performances, we report the NMSPE and NMAPE, averaged over the 5-folds, for each competing algorithm in Table 2. To demonstrate the deleterious effect of spurious features, we fit a conditional MRF without any feature selection and report the NMSPE and NMAPE for this baseline model too.

Table 2.

Prediction performance on the test set for simulation

Method	Variable	NMSPE	NMAPE
No reduction	Y1	0.5523	0.6001
	Y2	0.5520	0.5999
	Y3	0.5520	0.5998
	Y4	0.5523	0.6000
SMuRFS	Y1	0.4224	0.5224
	Y2	0.4220	0.5218
	Y3	0.4221	0.5220
	Y4	0.4223	0.5221
strong–SMuRFS	Y1	0.4381	0.5280
	Y2	0.4378	0.5280
	Y3	0.4384	0.5282
	Y4	0.4387	0.5282
MLASSO	Y1	0.4584	0.5425
	Y2	0.4579	0.5419
	Y3	0.4580	0.5422
	Y4	0.4582	0.5421
MEnet	Y1	0.4861	0.5596
	Y2	0.4858	0.5590
	Y3	0.4221	0.5220
	Y4	0.4223	0.5221
RELIEFF	Y1	0.5370	0.5902
	Y2	0.5365	0.5897
	Y3	0.5365	0.5899
	Y4	0.5368	0.5901

Bold entries indicate best results.

The ability of SMuRFS to pick up the signals and remove spurious features enables it to outperform MLASSO and MEnet in terms of predictive accuracy too (Table 2). Note that, we can also train a predictive model using only the strongly informative features belonging to ${\mathcal{F}}_s$. Hence, we also report the prediction performance of strong-SMuRFS in Table 2. Although, its performance is inferior to SMuRFS, but it outperforms MLASSO. Its predictive ability is similar to that of MEnet, but strong-SMuRFS is overwhelmingly parsimonious as compared to MEnet, and hence is preferable. As expected, the performance of the baseline model is worst among all competing models.

Given the evidences from the simulation, we conjecture that inclusion of a large number of spurious features, under extreme sparsity, is perhaps more detrimental than developing a parsimonious model that penalizes complex model more severely. Our sequential approach structurally puts higher weightage on Type I error rate and the resulting test procedure explicitly encourages parsimony without having to resort to difficult-to-interpret tuning parameters.

3.2 Application on GDSC dataset

We apply our feature selection methodology on GDSC gene expression and drug sensitivity dataset (version 5) downloaded from Cancerrxgene.org (Yang, 2013). It includes genomic characterization of numerous cell lines and different drug responses for each cell line. For the current analysis, we consider gene expression data as the genomic characterization information and Area under the Curve as the representation of drug responses. The dataset has 789 cell lines with gene expression data and 714 cell lines with drug response data. We consider only those cell lines for which both drug response and gene expression data are available. Each cell line has 22 277 probe-sets for gene expression, yielding a high dimensional feature space. We consider three sets of drug pairs with each pair having common target pathway, but the target pathways are different for different pairs. The first set $S_{C1}$ consisting of AZD-0530 and Erlotinib target signaling pathway Erbb (Wishart et al., 2006). The second set $S_{C2}$ is AZD6244 and PD-0325901 target ERK MAPK signaling pathway with MEK being the common target for both the drugs (Ciuffreda et al., 2009; Falchook et al., 2012). The third set $S_{C3}$ is Nutlin-3a and PD-0332991 that target the common signaling pathway P53 (Vassilev et al., 2004). The drug sets $S_{C1},\hspace{0.17em}{S}_{C2}$ and $S_{C3}$ have complete record for 308, 645 and 645 cell lines, respectively.

For the competing MLASSO and MEnet, we use $\alpha =0.8$ and the cross validated minimum λ. Once again, we perform 5-fold cross validation, and within each fold, we utilize 20% as the primary test set and the remaining 80% is randomly split in half into a training set and secondary test set. Within each fold, we select features on the training set, train a predictive bivariate CRF utilizing the selected features on the secondary test set and test the predictive performance on the primary test set. Using q = 5 and $\alpha =0.05$, our bivariate SMuRFS identifies 791, 1825 and 837 significant features (elements of ${\mathcal{F}}_w$) for $S_{C1},\hspace{0.17em}{S}_{C2}$ and $S_{C3}$, respectively, across all 5-folds. Subsequent CRF in the secondary test set yield 235, 214 and 222 features as strong features (elements of ${\mathcal{F}}_s$) for $S_{C1},\hspace{0.17em}{S}_{C2}$ and $S_{C3}$, respectively across all 5-folds. In comparison, MLASSO yields 171 222 431 features and MEnet yields 172 227 439 features for $S_{C1},\hspace{0.17em}{S}_{C2}$ and $S_{C3}$, respectively across all 5-folds. Given the incompatibility of RELIEFF in multi-variate set up, as observed in our simulation study, we do not deploy it in this application.

Recall that, one of our tasks was to guarantee that the selected features are both statistically significant and biologically relevant. Although SMuRFS guarantees statistical significance, we now examine the biological relevance of the features, selected by different methods, in human cell targets. As the common signaling pathway of the drug pairs are known, we can retrieve the genes associated with that pathway using Kyoto Encyclopedia of Genes and Genomes (KEGG) (Kanehisa and Goto, 2000) database and compare the number of such genes selected by the different methods. In all the three drug pairs, we observe that strong-SMuRFS (with comparable size of selected features) identifies more genes of the pathway as compared to its regularization-based counterparts (last row of Table 3).

Table 3.

Enrichment analysis for SMuRFS, strong-SMuRFS, MLASSO and MEnet methods for whole genome statistical background with 0.4 confidence interval for $S_{C3}$ drug pair, with common signaling pathway P53, from GDSC dataset

Method	SMuRFS	strong-SMuRFS	MLASSO	MEnet
	Nutlin-3a and PD-0332991
Feature size	837	222	431	439
Number of nodes	657	176	374	381
Number of edges	2287	265	512	539
Average node degree	6.96	3.01	2.74	2.83
Average local clustering coeff	0.35	0.362	0.337	0.332
Expected number of edges	1733	160	426	451
PPI enrichment P-value	0	2.29e–14	3.8e–5	2.9e–5
Ratio of observed to expected edges	1.32	1.65	1.2	1.2
Pathway gene count	14	11	8	8

Bold entries indicate best results.

Apart from this, we have evaluated the statistical over-representation of gene ontology (GO) (Ashburner et al., 2000) categories for the set of features using the Biological Network Gene Ontology tool (Maere et al., 2005) which is a Cytoscape (Shannon et al., 2003) plugin. This tool performs a hypergeometric test with a Benjamini and Hochberg false-discovery rate multiple testing correction against each of the ontologies: biological process, molecular function and cellular component (Maere et al., 2005). Among the GO terms selected at a significance level of 0.05 from the feature set of SMuRFS/strong-SMuRFS for drug set $S_{C3}$, 5 GO terms belong to the P53 signaling pathway which is the common signaling pathway for this drug pair (Buil et al., 2007; Yin et al., 2016). On the other hand, the feature set selected by MLASSO for this drug pair has no GO terms belonging to P53 signaling pathway.

There are a number of other platforms such as STRING (Szklarczyk et al., 2015), GeneMANIA etc., that can evaluate observed number of protein-protein interactions (PPI) among selected features. These interactions are determined based on different prior knowledge and interaction sources such as text-mining, experiments, databases, co-expression, neighborhood, gene fusion and co-occurrences. Using Affymetrix HG-U133PLUS2 for mapping the features or probe-sets into proteins, we arrive at different number of proteins or nodes for different methods that are listed in Table 3 for drug set $S_{C3}$. We use these proteins as inputs in the string-db database (http://string-db.org/) for generating the known PPIs network which is also reported in Table 3. We observe that the network generated using SMuRFS is more enriched in connectivity than any other methods, for all the three drug sets. PPI enrichment P–values and ratio of observed to expected number of edges illustrate that SMuRFS selected proteins are more connected among themselves as compared to MLASSO and MEnet. High ratio of observed to expected number of edges indicates enriched PPI, which is probably because of the functional collaborations between the products of these genes (Taguchi, 2017). As a visual illustration, we include PPI network for top proteins of strong-SMuRFS for drug set $S_{C3}$ in Figure 2. Biological analyses of drug sets $S_{C1}$ and $S_{C2}$ are available in the Supplementary Material (A referee correctly points out that since we resort to PPI analyses to figure out biologically relevant features, we could have included such information in the variable selection stage. However, we only have KEGG for validation of pathway information of selected features and using that information in the selection will certainly bias the results of biological significance. Furthermore, we cannot easily utilize the biological information for standard MLASSO and MEnet. So, to maintain uniformity we prefer to demonstrate that a pure statistical investigation can also lead to biologically valid selection).

Fig. 2.

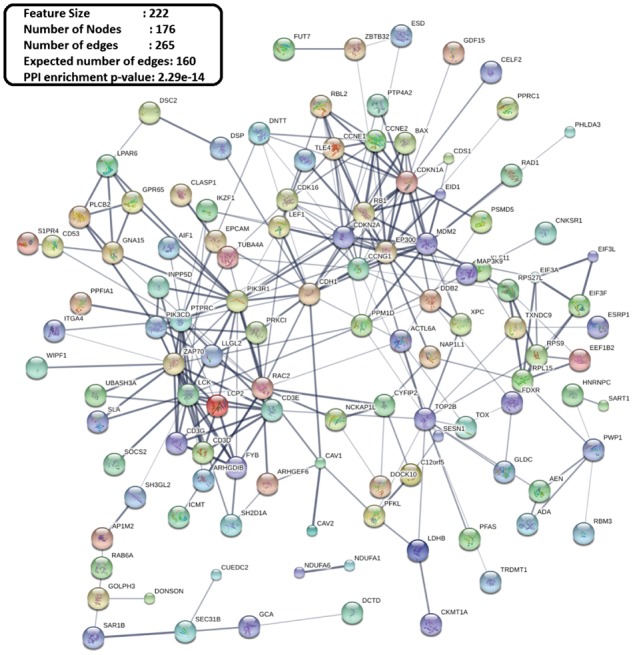
PPI networks for top proteins of Nutlin-3a and PD-0332991 for strong-SMuRFS

We now use the features selected by the competing variable selection algorithms to train a multi-variate CRF on the secondary test set. We compute the predictive performance on the test set using NMSPE and NMAPE. The results of these metrics, for each fold, for drug pair $S_{C3}$, are reported in Table 4. Prediction performances for drug pairs $S_{C1},\hspace{0.17em}{S}_{C2}$ are available in Supplementary Material.

Table 4.

Prediction performances of competing methods for drug set $S_{C3}$

Drug name	Fold	Feature selection	Number of	NMSPE	NMAPE
		Algorithm	Features
Nutlin-3a	1	strong-SMuRFS	149	0.7536	0.5827
		SMuRFS	563	0.7903	0.5958
		MLASSO	185	0.8245	0.6184
		MEnet	185	0.8245	0.6184
	2	strong-SMuRFS	50	0.7209	0.6495
		SMuRFS	210	0.7161	0.6586
		MLASSO	59	0.7638	0.6646
		MEnet	68	0.7552	0.609
	3	strong-SMuRFS	39	0.6795	0.5696
		SMuRFS	100	0.6778	0.5732
		MLASSO	183	0.7824	0.6309
		MEnet	184	0.7795	0.6352
	4	strong-SMuRFS	82	0.6175	0.5850
		SMuRFS	192	0.6346	0.5959
		MLASSO	30	0.6983	0.6238
		MEnet	30	0.6954	0.6209
	5	strong-SMuRFS	34	0.5714	0.5631
		SMuRFS	65	0.5788	0.5648
		MLASSO	49	0.6730	0.6258
		MEnet	49	0.6722	0.6230
PD-0332991	1	strong-SMuRFS	149	0.8508	0.7825
		SMuRFS	563	0.8763	0.7987
		MLASSO	185	0.8998	0.8039
		MEnet	185	0.8998	0.8039
	2	strong-SMuRFS	50	0.8689	0.7392
		SMuRFS	210	0.8571	0.7388
		MLASSO	59	0.8766	0.7452
		MEnet	185	0.8871	0.7507
	3	strong-SMuRFS	39	0.8394	0.7806
		SMuRFS	100	0.8529	0.7961
		MLASSO	183	0.8765	0.8022
		MEnet	185	0.8770	0.7994
	4	strong-SMuRFS	82	0.8452	0.7770
		SMuRFS	100	0.8529	0.7874
		MLASSO	30	0.7769	0.7384
		MEnet	185	0.7799	0.7410
	5	strong-SMuRFS	34	0.8794	0.7756
		SMuRFS	65	0.8853	0.7803
		MLASSO	49	0.9126	0.7942
		MEnet	185	0.9161	0.7926

Bold entries indicate best results.

We observe that either the standard SMuRFS (using all features in ${\mathcal{F}}_w$) or the strong-SMuRFS provides best out-of-sample predictive performance in terms of NMSPE and NMAPE for all three drug pairs in almost all the folds (competing models outperform our approach in at least 1 of the metrics in 5 out of a total of 30-folds). Our results demonstrate that an explanatory model that can identify true signals can provide superior predictive performance as compared to model-based regularization techniques that explicitly minimize in-sample error sum-of-squares.

5 Discussion

In this article, we presented a sequential multi-task feature selection methodology (SMuRFS) that can identify statistically significant features in addition to generating sparse set of features without resorting to regularization techniques or any other modeling assumptions. We utilized, theoretically sound, multi-variate conditional inference methodology to incorporate correlated drug sensitivities in designing a variable selection procedure. Conditional inference methodology allowed us to identify significant features and the subsequent deletion technique allowed us to jettison spurious features–all within a multi-variate framework. We also devised a strategy of labeling the selected features as strongly informative or weakly informative thereby providing us with a qualitative variable importance measure in multi-variate framework- a tool that is not available in extant variable selection approaches. We have also outlined a strategy by which biological information can be included in the variable selection phase.

Utilizing synthetic and biological data, we showed that the proposed sequential approach actually increases the prediction accuracy as compared to the popular regularization-based techniques. The proposed methodology provides a novel technique to identify statistically significant targets in designing multi-drug therapy regimes.

The presented research has strong potential for extension. One such direction will involve increasing the dimension of the responses so that an entire drug-screen, typically consisting of tens of drugs, can be modeled simultaneously. Another direction will be explicitly including biological information in the feature selection strategy itself where pre-identified groups of biologically related features will be tested as blocks, at each node of conditional inference trees, providing us with an analog of multi-variate grouped-LASSO with the added advantage of performing explicit inference on the relevance of the features without making any modeling assumptions.

Funding

Research reported in this article was supported by the The National Institute of General Medical Sciences of the National Institute of Health under award number R01GM122084. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health.

Conflict of Interest: none declared.