Abstract
Atomic force microscopy (AFM) is used to study mechanical properties of biological materials at submicron length scales. However, such samples are often structurally heterogeneous even at the local level, with different regions having distinct mechanical properties. Physical or chemical disruption can isolate individual structural elements but may alter the properties being measured. Therefore, to determine the micromechanical properties of intact heterogeneous multilayered samples indented by AFM, we propose the Hybrid Eshelby Decomposition (HED) analysis, which combines a modified homogenization theory and finite element modeling to extract layer-specific elastic moduli of composite structures from single indentations, utilizing knowledge of the component distribution to achieve solution uniqueness. Using finite element model-simulated indentation of layered samples with micron-scale thickness dimensions, biologically relevant elastic properties for incompressible soft tissues, and layer-specific heterogeneity of an order of magnitude or less, HED analysis recovered the prescribed modulus values typically within 10% error. Experimental validation using bilayer spin-coated polydimethylsiloxane samples also yielded self-consistent layer-specific modulus values whether arranged as stiff layer on soft substrate or soft layer on stiff substrate. We further examined a biophysical application by characterizing layer-specific microelastic properties of full-thickness mouse aortic wall tissue, demonstrating that the HED-extracted modulus of the tunica media was more than fivefold stiffer than the intima and not significantly different from direct indentation of exposed media tissue. Our results show that the elastic properties of surface and subsurface layers of microscale synthetic and biological samples can be simultaneously extracted from the composite material response to AFM indentation. HED analysis offers a robust approach to studying regional micromechanics of heterogeneous multilayered samples without destructively separating individual components before testing.
Introduction
Nanoindentation with atomic force microscopy (AFM) is widely used to evaluate micromechanical properties of soft biological samples. Traditional AFM data analysis applies Hertz contact theory (1), which assumes an infinitely thick sample with homogenous, isotropic, linear elastic material properties. However, these assumptions are unsuitable for most biological samples. To improve AFM analysis for biological applications, various approaches have considered finite sample thickness (2, 3), nonlinear elasticity (4, 5), and nonideal tip geometry (2, 6), but the local material heterogeneity of biological samples remains a challenge. Our published pointwise modulus approach (2) uses a point-by-point analysis of the AFM indentation response to detect depth-dependent changes in apparent elastic properties and identify the mechanical effects of sample heterogeneity. As an AFM tip indents deeper into a sample, it encounters underlying or embedded structures that contribute to the resulting pointwise modulus. Methods built upon homogenization theory can determine the effective elastic modulus of a composite material based on the mechanical properties of the individual substrate and inclusion constituents and are applicable to micromechanical studies including AFM (7). However, the inverse problem of extracting component-specific properties from the composite sample response has remained a challenge that we aim to solve through a combination of theoretical and computational approaches.
Finite element modeling (FEM) provides a powerful computational tool to simulate AFM indentation. FEM has been used to relate measured mechanical properties to structural variations of biological samples (8, 9, 10, 11, 12, 13). Such models can mimic the heterogeneity of a sample and simulate force responses of the AFM tip (12). FEM models have also been combined with AFM experiments on live cells in which biochemical agents were used to isolate specific populations of cytoskeletal fibers and study their mechanical properties (10). In these studies, a double-layered model consisting of cytoskeleton protein fibers and an inner nucleus was applied to determine the elastic moduli of each layer. A stiff cell cortex layer was simulated to explain the consistently stiffer measurement of cell elasticity using a sharp tip compared to a spherical tip (14). In another study, elastic properties of the glycocalyx and cell body of human umbilical vein endothelial cells were determined using a two-layer thin-film method (15) that was originally developed based on FEM for compliant layers on stiffer substrates (16). Indeed, a number of investigators have examined the decoupling of layer-specific mechanical properties with micro- or nanoindentation of various multilayered polymer films having submicron dimensions and modulus ratios up to 10,000-fold (17, 18, 19). A more relevant brush model was reported for multilayered cell structures composed of a penetrable molecular brush surrounding an elastic cell body (20, 21). However, the fully penetrable brush-like superficial layer is not suitable for polymer samples or biological tissues that behave like multilayered elastic continua. Therefore, indentation analysis of more general elastic heterogeneity patterns relevant to mesoscale biological tissues, with micronscale dimensions and layer-specific modulus values that differ by an order of magnitude or less, deserves further development.
The mammalian artery wall is a representative heterogeneous biological tissue often described as a three-layered structure composed of the intima, media, and adventitia. Each layer has specific mechanical properties (22, 23) reflecting distinct cellular and extracellular matrix compositions. Traditionally, mechanical tensile testing has been applied to obtain bulk stress-strain relationships of human (23, 24) and murine (25, 26) arteries. To date, studying the transmural mechanical heterogeneity of individual layers of arteries has required physical separation (23) or pharmacological intervention (26) to dissociate the layers. These perturbations have the potential to disturb or damage key structures, thereby altering the intrinsic tissue properties of interest. Recently, micropipette aspiration has been used to measure layer-specific properties of porcine aortic valves, in which each layer has a dimension of 100–500 μm (27). By comparison, mouse aortas are smaller (20–60 μm thick) (28), which poses a technical challenge for measuring arterial wall biomechanics by conventional methods.
AFM provides a unique tool to map localized micromechanical properties of soft tissues (29, 30, 31, 32), including heterogeneity of mouse aorta (33) and micromechanics of porcine arterial endothelium (34), media (35), and adventitia (35, 36). However, these studies focused on an exposed surface layer without considering the underlying layer, or measured multiple moduli by physically separating individual layers before testing. A more recent AFM indentation study showed age-dependent variations of mechanical properties of intact bilayered Drosophila myocardium composed of a top muscle layer and bottom cardiomyocyte layer (37); however, their bidomain linearized Hertz method of analysis did not include computational validation.
Therefore, the objective of this study was to develop a Hybrid Eshelby Decomposition (HED) method, which to our knowledge is new, for analyzing AFM indentation of soft heterogeneous layered samples with micron-scale dimensions that can be measured independently and with a 2- to 10-fold disparity in layer-specific elastic properties. We validate this method computationally using FEM simulations and experimentally by measuring the dehomogenized, layer-specific properties of spin-coated elastomer samples as well as intact mouse aorta wall tissue, utilizing knowledge of the constituent layer thickness to achieve solution uniqueness. This analysis method for AFM indentation provides a specialized approach for investigating the elastic properties of structurally heterogeneous layered synthetic and natural samples, such as cells embedded in gels, human tissue biopsies, and tissues from small animal models of development and disease, that are impractically tiny for mechanical testing by traditional methods.
Methods
Conceptual approach for deconstructing heterogeneous mechanical properties
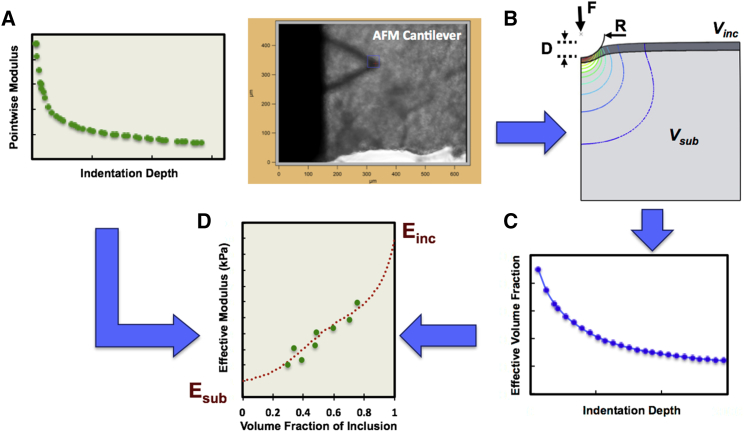
First, four key steps in the HED approach are summarized using AFM indentation of a flattened aortic tissue section to exemplify a multilayer biological sample. AFM indentation is applied to obtain the depth-dependent pointwise moduli of the sample (Fig. 1 A). The layer thicknesses are then obtained using histological staining or fluorescent microscopy of a slice perpendicular to the layers and used to create an FEM to simulate indentation with an appropriate geometry (Fig. 1 B). The resulting apparent modulus versus depth is combined with modified Eshelby homogenization theory to determine the effective volume fraction of the inclusion as a function of indentation depth (Fig. 1 C), which can be represented by a “master curve” for a given indenter and sample geometry. Lastly, the experimental pointwise moduli in Fig. 1 A and the inclusion volume fraction data in Fig. 1 C are combined at each indentation depth by plotting pointwise modulus (Epw) versus the effective volume fraction (feff) and fitting by least squares using the modified Eshelby model (see Eq. 10 below) to extract the individual component moduli (Esub and Einc), as shown in Fig. 1 D. The mathematical and experimental aspects of HED analysis will be further explained in the following sections.
Figure 1.
Hybrid Eshelby Decomposition (HED) method. Starting with experimental AFM indentation data on a layered sample, (A) depth-dependent pointwise moduli confirming a mechanically heterogeneous sample were calculated. (B) An FEM model (e.g., using Abaqus) simulated an AFM indentation response for the given layered sample geometry and AFM probe tip dimensions using arbitrary elastic properties of the simulated sample. (C) The effective volume fraction of the layered inclusion versus indentation depth (i.e., master curve) was estimated for the given sample geometry based on modified Eshelby homogenization theory applied to FEM results. (D) The results of steps (A) and (C) were combined to plot pointwise modulus versus effective volume fraction at matched depths, and least-squares minimization (e.g., in MATLAB) was used to fit this data using modified Eshelby model for finite inclusions; assigning a Poisson ratio (ν = 0.49), the fitting procedure yields values of elastic modulus for the substrate and layered inclusion (Esub and Einc, respectively). To see this figure in color, go online.
FEM
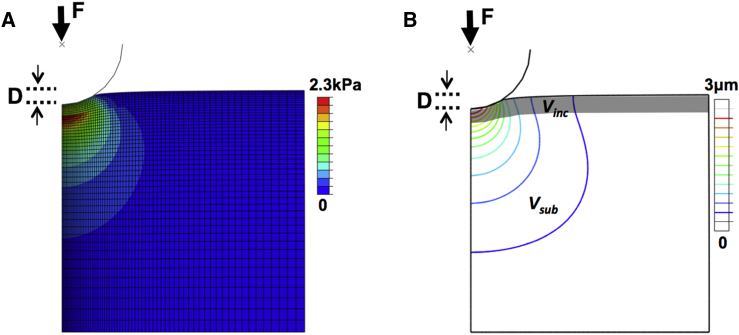
To simulate the AFM indentation problem, Abaqus FEM software (version 6; Dassault Systèmes Simulia, Johnston, RI) was used to model an axisymmetric rigid indenter and a linear elastic substrate material with 50 μm thickness and 50 μm radius (Fig. 2) using four-node linear axisymmetric elements (CAX4). Arbitrary Lagrangian-Eulerian mesh adaptivity with a frequency ranging from 1 to 30 increments and two to five remeshing sweeps was used to avoid excessive mesh distortion and to ensure accuracy and convergence of the solution. Depending on the model geometry, either the structured or the free technique of mesh seeding with proximal meshing bias of 5–10 was applied, yielding a mesh with ∼1800 elements (Fig. 2 A). Furthermore, the bottom surface of the substrate was constrained in rotation (UR3) and axial direction (U2); the centerline of the substrate was constrained in rotation and radial direction (U1). An analytical rigid spherical indenter 10, 15, or 25 μm in diameter underwent a prescribed 3 μm axial displacement (i.e., indentation depth) with frictionless surface-to-surface contact conditions on the substrate and was constrained along the indentation axis. Indentation depth was prescribed as a time-dependent step with 100 increments. The total reaction force (F) and axial displacement (D) on the indenter were recorded to simulate force-depth responses of AFM indentation (Fig. 2 B). Abaqus simulations were performed on a Mac Pro workstation with dual Intel Xeon E5520 2.27 GHz and 2.39 GHz processors (Apple Computer, Cupertino, CA) with 16 GB memory. A single indentation simulation typically ran 2–5 min, depending on the geometry and settings for adaptive meshing.
Figure 2.
Cross section of FEM-simulated indentation of an axisymmetric layer model. The spherical AFM probe moves to a depth, D, in contact with the sample and reports the reaction force, F, at the center of the indenter. (A) The corresponding von Mises stress field shows high stress at the interface of top and bottom layers. (B) The corresponding indentation field, approximated by the range of nonzero axial displacement at a prescribed indentation depth, illustrates the inclusion and substrate volumes (Vinc and Vsub, respectively) within the indentation field demarcated by the outermost displacement contour. To see this figure in color, go online.
Rather than attempt to accurately represent any specific biological material, this idealized model was developed to simulate key aspects of AFM indentation of general layered samples. The spherical indenters of 10, 15, or 25 μm diameter are commonly used in AFM indentation studies of biological tissues (29, 31, 38). For the sample, we used a heterogeneous layered configuration consisting of a top inclusion (3 μm thick and 50-μm radius) and a bottom substrate (47 μm height, 50 μm radius); both soft and stiff inclusion layers were examined with the elastic modulus range of 1–200 kPa in relation to a fixed 10-kPa substrate, simulating cases of stiff-inclusion-to-substrate ratios of 2:1–10:1 and soft-inclusion-to-substrate ratios from 1:10 to 1:2. An incompressibility constraint was imposed (Poisson ratio, ν = 0.49) on all materials. This covers a range of elastic moduli reported for various constituents of living cells and soft tissues in physiological and pathological conditions (39, 40, 41), with different stiffness combinations yielding a diversity of AFM indentation force-depth responses. Postprocessing of the simulated indentation curves followed our established pointwise modulus analysis to determine the depth-dependent apparent elastic properties (2).
Pointwise apparent modulus
Various techniques have been proposed to improve the standard Hertz contact analysis of AFM indentation data, especially for applications on soft samples like cells and tissues. Biological samples are often nonlinear, anisotropic, and heterogeneous. Prior studies have considered the nonlinearity, viscoelasticity, and heterogeneity of biological samples as well as nonideal AFM tip geometry and finite sample thickness (2, 3, 6, 37, 42, 43). Accurate identification of the contact point is also an important challenge with AFM indentation on soft biological samples (3). Our preferred strategy involves fitting the force curve using a bidomain model that assumes a linear precontact region and a polynomial postcontact region, with the actual contact point being a fitted model parameter that ensures C0 continuity of the two regions, as detailed elsewhere (44). Once the contact point is identified, the pointwise modulus analysis method is used to objectively reveal deviations from Hertz contact theory without a priori assumptions about sample material properties; material nonlinearity and heterogeneity lead to characteristic depth-dependent variations in the pointwise elastic modulus (2). Briefly, rather than fitting the entire force-depth response to extract an equivalent Young’s modulus, the pointwise approach evaluates each postcontact indentation force-depth data point and calculates the corresponding apparent elastic modulus. For a spherical indenter tip with radius R, the pointwise modulus equation is
| (1) |
where is the pointwise apparent elastic modulus, and Fi and δi are the matched indentation force and depth for data point i. Note that for a homogeneous linear elastic material, is related to the Young’s modulus, EY, and Poisson’s ratio, ν, as follows:
| (2) |
Modified homogenization theory
Eshelby homogenization theory estimates effective bulk (Keff) and shear moduli (μeff) for sparse, uniformly distributed inclusions, Ω, in an infinite, homogeneous, isotropic elastic substrate medium, M, based on the respective bulk moduli (KM and KΩ) and shear moduli (μM and μΩ), the substrate Poisson’s ratio (υM), and the volume fraction of inclusion (fΩ) (45). As illustrated in Fig. S1 A, a modified Eshelby model extends homogenization theory from a maximal fΩ of ∼0.15 to the full range of inclusion volume fraction (0 ≤ fΩ ≤ 1) using modified Eshelby tensor terms, s1 and s2, derived by Li et al. for inclusions with a circular cross-section in a finite domain (46):
| (3) |
| (4) |
These components can be incorporated into the isotropic elasticity tensor to yield Keff and μeff in terms of fΩ and mechanical properties of the substrate and inclusion (7), as follows:
| (5) |
| (6) |
As with an isotropic linear elastic material, an effective Young’s modulus (Eeff) can then be determined from the effective bulk and shear moduli:
| (7) |
Finally, the pointwise elastic modulus described previously (2, 47) can be related to the effective mechanical properties defined above:
| (8) |
or
| (9) |
To adapt the modified Eshelby homogenization theory to our HED approach, we assumed the spherical inclusion terms, s1 and s2, would also be applicable for a layered inclusion geometry within a finite domain. Note that the Eeff vs. fΩ relationship described by Eq. 7 falls within the upper and lower limits derived by Hashin and Shtrikman for arbitrary inclusion geometries (48) (Fig. S1 B).
To adapt the theory for uniform inclusions to a discrete layered sample, the inclusion volume fraction fΩ, which is constant for a given homogeneous composite sample, was replaced with an effective inclusion volume fraction, feff, that depends on the sample configuration, the indenter geometry, and the indentation depth. As the AFM tip indents a heterogeneous material composed of a fixed substrate and discrete inclusion, the effective volume fraction of the inclusion can vary as the indentation field interrogated by the indenter tip expands. Therefore, we considered feff as the amount of inclusion within the instantaneous indentation field (Vinc) relative to the total volume of the indentation field (Vinc + Vsub), as illustrated in Fig. 2 B; Vsub is the amount of substrate within the indentation field. This representation helps to explain the concept of an effective inclusion volume fraction and how it could vary with indentation depth, but the actual depth-dependent function of feff vs. D is determined as described in the next section.
Finally, the bulk and shear moduli (K and μ) of an isotropic elastic material can be expressed in terms of the Poisson’s ratio (υ) and Young’s modulus (E) as follows: and . Therefore, by substituting these expressions for KM, KΩ, μM, and μΩ in Eqs. 5 and 6, the effective elastic modulus in Eq. 7 can be represented as a function of feff, the Young’s moduli of substrate (Esub) and inclusion (Einc), and the Poisson’s ratio of the substrate (υsub) and inclusion (υinc):
| (10) |
For the specific case of nearly incompressible materials (such as many elastomers and hydrated soft tissues), with υsub = υinc = 0.49, this function takes the following form:
| (11) |
Note that in Eq. 11, the substitutions f = feff, E1 = Esub, and E2 = Einc were made for brevity. A typical modified Eshelby curve for a stiff layer inclusion is illustrated in Fig. 1 D, showing increasing effective modulus as inclusion volume fraction rises (a soft layer inclusion would show a decreasing curve). The substrate modulus is on the left end of the curve (feff = 0), and the layer inclusion modulus is on the right end of the curve (feff = 1).
Determination of effective volume fraction
Determination of effective volume fraction for known substrate and inclusion moduli in an FEM simulation of AFM indention is achieved using theoretical Eshelby curves. For example, a heterogeneous material with 100 kPa inclusion in 10 kPa substrate material has a unique relationship for effective modulus versus volume fraction. Simulated AFM indentations yield the force-depth relationship based on their specific configurations and give rise to distinct depth-dependent pointwise moduli. Accordingly, by combining the theoretical Eeff vs. fΩ Eshelby relationship (Eqs. 5, 6, 7) with the pointwise Eeff vs. D from the FEM (Eqs. 1 and 9), the effective volume fraction at each indentation depth (feff vs. D) is readily obtained at matched values of Eeff, as illustrated in Fig. 1 C and further described in Fig. S2.
Reconstruction of experimental modified Eshelby curves
AFM indentation is simulated using incompressible linear elastic materials in Abaqus. Therefore, by prescribing υ = 0.49 for both substrate and inclusion, the resulting Eeff (Eq. 10) is a function of the variable feff along with two constant coefficients representing the substrate and inclusion elastic moduli (Esub and Einc, respectively) (Fig. 1 D). The average simulated feff vs. depth relationship and the corresponding pointwise moduli versus depth from experimental indentation tests on heterogeneous multilayered samples were combined, and the resulting Eeff vs. feff relationship was fitted with the Eshelby model using least-squares curve-fitting procedures in MATLAB (The MathWorks, Natick, MA), yielding the two parameters of interest, Esub and Einc. Custom software has been developed to extract the substrate and inclusion moduli from AFM indentation data; the entire procedure constitutes our HED analysis.
PDMS fabrication
To experimentally validate the HED approach, synthetic samples of bilayered polydimethylsiloxane (PDMS) were fabricated from silicone elastomer (Sylgard 184) and Xiameter silicone fluid (PMX-200 100CS), both from Dow Corning (Midland, MI), with varying composition of base-polymer:curing agent (weight %Xiameter) to tune the elasticity of PDMS. Two PDMS formulations—stiffer PDMS-A, 20:1 (20%) and softer PDMS-B, 30:1 (100%)—were spun onto 25 × 25 mm glass coverslips using a Laurell spin processor (WS-400E-6NPP; Laurell Technologies, North Wales, PA) at different speeds to fabricate bilayered samples with desired thickness. Materials were cured at 65°C on a hot plate after each spin; the bottom substrate and top inclusion layer were cured for 15 and 10 min, respectively. Two configurations of bilayered PDMS were created (n = 6–8 each), with layer thickness (verified using a Wyko NT1100 optical profiler (Veeco Instruments, Plainview, NY)) and spinning speeds as follows: 1) STIFF inclusion (top PDMS-A: 4.6 ± 0.8 μm, 6000 rpm; bottom PDMS-B: 39.1 ± 8.4 μm, 500 rpm) and 2) SOFT inclusion (top PDMS-B: 4.9 ± 0.54 μm, 5000 rpm; bottom PDMS-A: 37.1 ± 1.3 μm, 1000 rpm). Homogenous control samples of PDMS-A and B were spun twice to mimic the geometry and curing process of the heterogeneous bilayer samples. PDMS samples were stored in deionized (DI) water to prevent further exposure to air before AFM testing.
Mouse aorta isolation
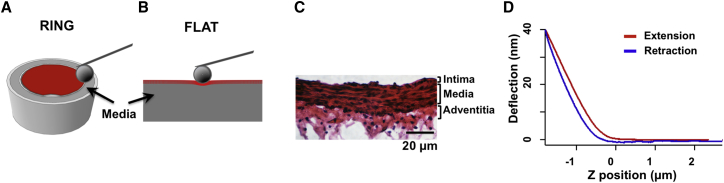
All animals received humane care and treatment compliant with the National Research Council’s Guide for the Care and Use of Laboratory Animals, following experimental protocols approved by the Institutional Animal Care and Use Committee at the Mount Sinai Medical Center. Healthy, three-month-old male wild-type mice (n = 4) were anesthetized by isofluorane (Baxter Healthcare, Deerfield, IL), sacrificed by cervical dislocation, and injected with 100 μL of heparin (Sagent Pharmaceuticals, Schaumburg, IL) to minimize blood clots. The aortic tree was dissected from the root to the diaphragm and cleaned with forceps to remove surrounding soft tissue. Live aortas were kept in culture media, containing Dulbecco’s modified Eagle’s medium (Mediatech, Manassas, VA), 1% penicillin-streptomycin solution (Mediatech), and 10% fetal bovine serum (Atlanta Biologicals, Norcross, GA), as described elsewhere (49). For experimental testing, the abdominal aorta was dissected and sliced into two adjacent ring sections. One was mounted intact with the annular surface facing up (RING configuration, Fig. 3 A) on a 50 mm petri dish using medical-grade double-stick tape (Nearly Me Technologies, Waco, TX); the other was cut axially and mounted flat to expose the lumen side of the vessel (FLAT configuration, Fig. 3 B). Samples were maintained in culture media at 37°C for up to 3 h before AFM testing.
Figure 3.
AFM indentation was performed in the (A) RING and (B) FLAT (the bottom media in gray and top intima in red) configurations for determining the elastic modulus of the medial layer of the vessel wall. (C) The thickness of the aortic intima and media were obtained by histological staining for building a tissue-specific FEM model for HED analysis. (D) A representative AFM indentation response of a FLAT section of mouse aorta shows the probe deflection versus z-sensor position relationship (i.e., force curve); the AFM probe approaches the sample from right to left on the z-position axis, makes contact with the sample, and indents the sample (red extension curve). The probe then withdraws from the sample (blue retraction curve). To see this figure in color, go online.
Histological analysis
Abdominal aorta sections immediately adjacent to those used for AFM testing were fixed in 4% paraformaldehyde (Electron Microscopy Sciences, Hatfield, PA), switched to 15% sucrose solution in phosphate-buffered saline (Sigma-Aldrich, St. Louis, MO), cryosectioned into 10-μm-thick sections, and then stained with hematoxylin and eosin to visualize the tissue geometry and structure. Images were taken from nine aortic sections under 40× magnification; five to six measurements per tissue were quantified for layer-specific dimensions using image processing with ImageJ software (Fig. 3 C). The intima layer thickness was measured from the endothelial surface to internal elastic lamina, the media layer was measured from internal elastic lamina to external elastic lamina, and the adventitia layer was measured from external elastic lamina to the outer vessel wall. Thickness values for the intima, media, and adventitia layers were 3.3 ± 0.5, 22.7 ± 3.0, and 13.1 ± 2.9 μm, respectively.
AFM
Mechanical measurements of bilayered PDMS and live aorta samples were performed using a biological AFM (MFP-3D-BIO; Asylum Research, Santa Barbara, CA) with the control and data acquisition platform running in the Igor Pro (Wavemetrics, Portland, OR) software environment. PDMS samples were pretreated with 2% bovine serum albumin (Sigma-Aldrich) in DI water for 30 min to minimize the adhesion force between the samples and the AFM probe (37) and indented in DI water with a 10-μm-diameter polystyrene spherical probe mounted on a silicon cantilever (spring constant, k = 40 N/m). RING and FLAT aorta sections were indented with a silicon cantilever probe (k = 8.9 N/m) with a 15 μm borosilicate glass spherical probe in culture medium at 37°C. All probes were purchased from Novascan Technologies (Ames, IA). The bilayered PDMS and FLAT aorta samples were indented with a trigger force of 1.6–4.8 μN at a rate of 4 μm/s and 0.45–1.5 μN at a rate of 2 μm/s, respectively, to achieve an indentation depth of at least 3 μm for extracting individual layer properties. AFM indentation of aorta RING sections targeted the middle media layer with an indentation force of 0.3–0.5 μN at a rate of 2 μm/s. AFM indentations were performed at multiple locations using three to five force maps per sample; each force map (array size; scan area) was prescribed based on the available testing area of the samples as follows: PDMS (6 × 6 array; 80 × 80 μm), FLAT aorta samples (4 × 4 array; 20 × 20 μm), and RING aorta samples (4 × 4 array; 10 × 10 μm).
Raw AFM force curves (probe deflection versus z-sensor position) consist of extension and retraction motions of the AFM probe as it approaches and withdraws from the sample (Fig. 3 D). The pointwise elastic modulus was determined as described previously (2) using the extension portion of the force curves. Approximating the measured thickness of bilayered PDMS and FLAT samples, the PDMS FEM had a 5 μm inclusion layer on top of a 50 μm substrate; the FLAT aorta FEM had a 3 μm inclusion layer (intima) on top of a 35 μm substrate layer (media), which subsumed all underlying structures other than the intima (Fig. 3 C). The HED analysis was used to extract layer-specific elastic moduli from AFM indentation tests on the PDMS and FLAT aorta samples.
Statistical analysis
To examine the robustness of the HED algorithm, Monte Carlo simulation was used to analyze the influence of random noise and the volume fraction data range on the extracted elastic properties of substrate and inclusion. A synthetic set of effective modulus versus volume fraction data was generated from a theoretical Eshelby curve for a hypothetical sample with a 10 kPa substrate modulus and a 100 kPa top-layer inclusion. Uniformly distributed random noise was simulated as 10% of the maximal volume fraction (X axis) and effective modulus (Y axis) of the substrate-inclusion combination.
Unless otherwise specified, all results were summarized as mean ± SD. Tissue data were compared using a Student’s t-test. A p-value of <0.05 was considered statistically significant.
Results
FEM indentation response of layered heterogeneous samples: pointwise modulus and effective volume fraction
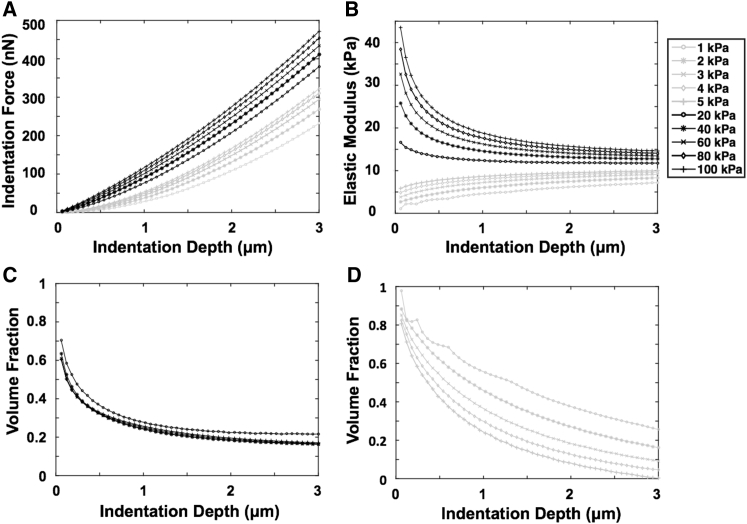
FEMs were constructed with three elements: 1) a 50-μm-thick 10 kPa substrate, 2) 3 μm top-layer inclusions ranging from 1 to 100 kPa to simulate inclusion/substrate modulus ratios for both stiff inclusions (modulus ratio >1) and soft inclusions (modulus ratio <1), and 3) a rigid 25 μm diameter spherical indenter tip. As the tip indented the inhomogeneous sample, the softer material deformed more than the stiffer material, and stresses at the layer interface accumulated toward the stiffer material. Indentation force increased with indentation depth, and the force increased more rapidly on stiff than soft inclusions (Fig. 4 A). Pointwise moduli (Epw) logarithmically decayed or increased with indentation depth in stiff or soft inclusion cases, respectively (Fig. 4 B), mimicking the heterogeneity pattern of the composite material; at low indentation depths, the force response was dominated by the inclusion properties but asymptotically approached the substrate elastic modulus as the indentation field expanded at deeper indentation depths. As expected, a higher inclusion modulus yielded a higher asymptotic value of effective elastic modulus for the composite material. Also, a bigger disparity between the inclusion and substrate properties required a larger indentation depth to reach a plateau. Indeed, we introduced the HED approach to analyze heterogeneities with a 2- to 10-fold difference between the inclusion and substrate moduli. Lower heterogeneity cases with less than a twofold difference exhibit a nearly flat pointwise modulus versus depth curve, and in practice may be less critical to distinguish from their homogenized equivalent.
Figure 4.
Representative FEM results for the layer indentation model with top stiff (black, 20–100 kPa) and soft (gray, 1–5 kPa) inclusions on a 10 kPa bottom substrate. (A) Indentation force versus depth is shown. (B) Corresponding pointwise elastic modulus versus depth is shown; the stiff inclusion curves start high and decrease with indentation depth, whereas soft inclusion curves start low and increase with depth. The effective volume fraction versus depth for (C) stiff inclusion and (D) soft inclusion show distinct characteristics, but each family of curves behaves similarly.
The effective volume fraction decreases as indentation depth increases, with proportionally less inclusion and more substrate being probed by the indenter (Fig. 4, C and D). The volume fraction for stiff and soft inclusions started at similar levels of 0.7–0.9 but propagated with different patterns as two families of curves. The stiff inclusion curves were remarkably insensitive to Einc; the soft inclusion curves had a different characteristic shape that decreased more gradually with indentation depth, and the final value of feff (at the maximal indention depth of 3 μm) increased as Einc decreased.
Master curve approximation
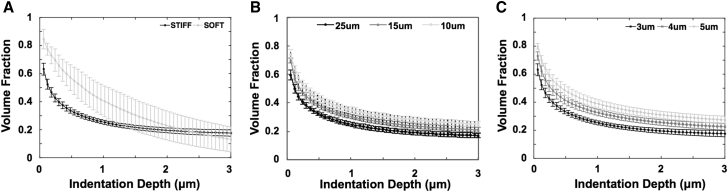
The finding that each inclusion configuration (i.e., stiff versus soft layer) coalesced into two distinct families of curves indicated that feff depends primarily on the geometrical configuration of the layers with relative insensitivity to the specific mechanical properties. Therefore, the two distinct families of curves were averaged to obtain two “master curves,” referred to as STIFF inclusion and SOFT inclusion, to represent the layered geometry without regard to the individual mechanical properties (Fig. 5 A). Each master curve represents the depth-dependent effective inclusion volume fraction for the specific sample configuration.
Figure 5.
Representative master curves for (A) STIFF or SOFT inclusion of a 3 μm top layer indented with a 25 μm spherical indenter; (B) STIFF inclusion of a 3 μm top layer using a 10, 15, or 25 μm spherical indenter; and (C) STIFF inclusion of a 3, 4, or 5 μm top layer using a 25 μm spherical indenter.
In addition to the top-layer configuration (STIFF versus SOFT), the feff vs. D master curves also depended on the AFM indenter size and the thickness of the top inclusion layer. The effect of indenter size (10, 15, or 25 μm diameter) on the master curve for a 3 μm STIFF top layer is shown in Fig. 5 B. A 3 μm maximal indentation depth was prescribed in all the models; therefore, a larger indenter had a larger contact surface and a correspondingly extended indentation field with a relatively smaller contribution from the inclusion layer. Consequently, feff decreased as indenter size increased (f10 μm > f15 μm > f25 μm) at matched indentation depths, and the master curve shifted downward from the 10 to the 25 μm indenter. To evaluate the effect of inclusion geometry, FEM models with varying top-layer thickness (3, 4, or 5 μm) were indented with a 25 μm sphere. A thinner top layer yielded a lower effective volume fraction at a specific indentation depth (f3 μm < f4 μm < f5 μm) such that the master curve shifted downward from the 5 μm to the 3 μm inclusion thickness (Fig. 5 C). In summary, the effective volume fraction of the inclusion varied at different indentation depths and depended on the top inclusion thickness, the diameter of the indenter, and the SOFT or STIFF inclusion configuration. But as noted above, the master curve was relatively insensitive to the specific modulus values for the inclusion and substrate materials.
Extracted substrate and inclusion moduli
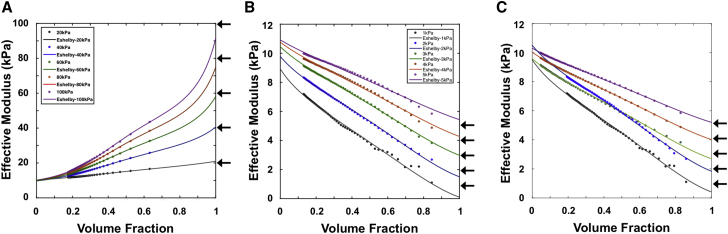
Examples of reconstructed Eshelby curves (modulus versus volume fraction) using Eq. 11 are shown in Fig. 6 for a range of layer inclusion models with a 10 kPa substrate modulus using either the STIFF or SOFT master curves in Fig. 5 A. For the stiff inclusion models, the estimated value of Esub at the feff = 0 end of the curves converged at the prescribed value of 10 kPa with an error less than 4%, and the estimated inclusion moduli (Einc) approached the specified values of 20, 40, 60, 80, and 100 kPa to within 10% error for all cases (Fig. 6 A). Similarly, the soft inclusion models yielded <15% error in the extracted value of Esub and < 10% error in the extracted values of Einc for the cases of 3, 4, and 5 kPa, but the error in Einc increased to 23% for the 2 kPa inclusion and 90% error for the 1 kPa layer (Fig. 6 B). This increased error likely reflected the larger variability in the SOFT master curve (Fig. 5 A). Therefore, a two-step iterative estimation process was implemented to improve the accuracy of deconstructed elastic moduli. Based on the initial estimates of Esub and Einc, a refined master curve was generated that better represents the effective volume fraction versus depth relationship for the particular heterogeneous sample. When applied to the above soft inclusion models, errors in the extracted values of Einc reduced to 10 and 22% for the inclusion cases of 2 and 1 kPa, respectively, and the associated errors in Esub were <5.5% (Fig. 6 C).
Figure 6.
Reconstruction of Eshelby curves of a layer model with a 10 kPa substrate and (A) stiff inclusions ranging from 20 to 100 kPa, (B) soft inclusions ranging from 1 to 5 kPa, and (C) the same soft inclusions using refined master curves. The arrows indicate the actual inclusion elastic modulus values for each case. The refined master curves in (C) yield better estimations of the five soft inclusions and the 10 kPa substrate compared to the primary master curve approximations in (B). To see this figure in color, go online.
Another potential source of error in the estimation of Esub and Einc is related to variability in the top inclusion layer thickness, as occurs with many biological samples. To examine this issue, HED analysis was performed using intentionally inaccurate inclusion layer thickness values to determine the effects on the reconstructed layer-specific elastic moduli. We used simulation results for a 25-μm-diameter sphere indenting a 3-kPa, 4-μm-thick top inclusion layer on a 10 kPa bottom substrate, with data spanning ∼40% of the full volume fraction range, and performed HED analysis using master curves corresponding to 3-, 4-, 5-, 6-, and 7-μm-thick top layers, introducing errors due to under- and overestimation of the top-layer thickness. The reconstructed values of Einc ranged from 2.4 to 3.9 kPa for the 3 and 7 μm cases, whereas the corresponding estimates of Esub ranged from 9.5 to 11.2 kPa. Thus, for top-layer thickness errors ranging from −25 to +75%, the errors in Einc ranged from roughly −20 to +30%, whereas the errors in Esub remained within ∼10% of the true value (Fig. S3). This analysis suggests that uncertainties in top-layer thickness have a greater effect on the estimated values of the top-layer modulus, whereas the substrate modulus appears less sensitive to thickness errors.
Sensitivity analysis
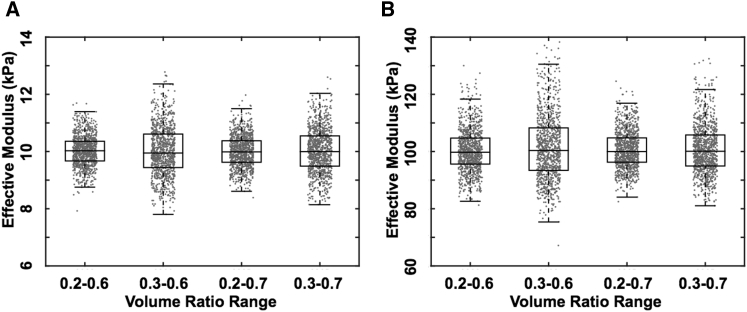
Monte Carlo simulation was used to study the influence of random noise and a restricted volume fraction data range on the extracted values of Esub and Einc from a synthetic set of Eeff vs. feff data for a 100 kPa top-layer inclusion and a 10 kPa substrate. Because a typical AFM indentation experiment will not interrogate all possible volume fractions from 0 to 1, the available data tend to fall into the middle range of feff (see Fig. 1 D). Therefore, restricted subranges representing 30, 40, or 50% of the full feff data range (specifically, 0.2–0.6, 0.3–0.6, 0.2–0.7, or 0.3–0.7) were culled from the synthetic data set. Reconstructed values of Esub and Einc showed robustness to random noise with the distributions of estimated moduli centered on the prescribed values of 10 and 100 kPa, respectively. However, the extracted substrate and inclusion moduli were sensitive to a restricted feff data subrange (Fig. S4). A higher starting value and a lower ending value of feff resulted in more outliers. In particular, the low end of the feff subrange had a strong influence on the accuracy of estimated values of Esub as well as Einc. A subrange width of at least 30% volume fraction coverage without including data at the extreme ends of the range was generally sufficient to reconstruct Esub and Einc with an error in the 50% interquartile range within 10% of the prescribed values, even in the presence of random noise, as summarized in Fig. 7.
Figure 7.
Robustness of the HED algorithm based on synthetic data from the theoretical Eshelby curve for Esub = 10 kPa and Einc = 100 kPa, subject to 10% random noise and a restricted feff data range, as indicated. Eshelby reconstructions were repeated for 1000 runs of each condition using boxplots to compare variation of estimated (A) substrate and (B) inclusion moduli.
PDMS indentation
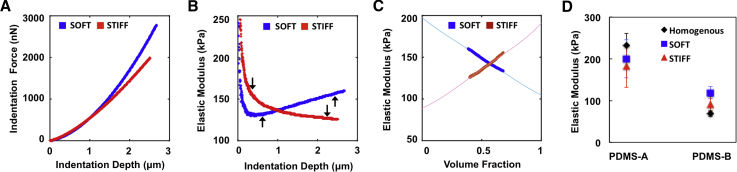
To experimentally validate the HED approach, we used thin synthetic samples of SOFT (soft layer on stiff substrate) and STIFF (stiff layer on soft substrate) bilayered samples made from silicone-based PDMS-A and B elastomers with known layer geometries. At low indentation depths, the force response reflected the top inclusion properties; STIFF inclusion showed a slightly higher force than SOFT inclusion (Fig. 8 A). As the probe indented deeper, the indentation reflected the substrate property; thus, the force increased more rapidly in the SOFT sample, which had a stiffer substrate than that of the STIFF sample (Fig. 8 A). The pointwise modulus showed depth-dependent distributions for the SOFT or STIFF inclusion cases that rose and decreased, respectively, as the indentation depth increased in the data-fitting regions, indicated by the arrows in Fig. 8 B. Using an FEM-generated “master curve” for the effective inclusion volume fraction versus depth relationship using the known geometric parameters (5 μm top layer, 50 μm substrate, and 10 μm spherical indenter), the experimental relationship between effective modulus and volume fraction (Eeff vs. feff) was then generated and fitted with the modified Eshelby model given in Eq. 11, as shown in Fig. 8 C. The volume fraction of 0.4–0.7 was selected for the SOFT and STIFF inclusions, which correlated to the indentation depths of 0.72–2.5 μm (up arrows) and 0.3–2.2 μm (down arrows), respectively (Fig. 8 B). The deconstructed elastic moduli of PDMS-A (EA) and PDMS-B (EB) from the heterogeneous bilayered samples were compared between the two configurations and also with homogeneous samples of PDMS-A and PDMS-B. The resulting elastic moduli of PDMS-A and B extracted using the HED algorithm showed self-consistency between SOFT (EA: 200.0 ± 47.8 kPa; EB: 119.0 ± 15.6 kPa) and STIFF (EA: 182.8 ± 54.1 kPa; EB: 91.2 ± 18.9 kPa) inclusion configurations (Fig. 8 D), confirming that EA was stiffer than EB, as designed. Although these moduli were also comparable to the values of EA (232.0 ± 29.9 kPa) and EB (69.2 ± 7.0 kPa) measured from the homogenous PDMS samples, the results could suggest a tendency for the HED method to underestimate stiff and overestimate soft layer moduli in composite materials. However, the experimental errors are larger than expected based on the above finite element analyses (e.g., Fig. 6), and as discussed below and in the Supporting Materials and Methods related to Fig. S5, the discrepancies appear to primarily reflect the influence of surface films inadvertently created during the PDMS curing process.
Figure 8.
Experimental AFM indentation responses on heterogeneous PDMS samples with SOFT (PDMS-B layered on PDMS-A) and STIFF (PDMS-A layered on PDMS-B) bilayer configurations. (A) Representative indentation force versus depth and (B) the resulting pointwise elastic modulus versus depth curves are shown. (C) Corresponding elastic modulus versus effective inclusion volume fraction is reconstructed using the FEM-generated master curve for each sample configuration. Solid lines represent the best-fit Eshelby curve for each data set, yielding Esub at feff = 0 and Einc at feff = 1. (D) Mean (± SD, n = 6–8) elastic properties of PDMS-A and PDMS-B obtained by HED analysis of AFM indentation of SOFT (squares) and STIFF (triangles) heterogeneous bilayer samples are shown as well as homogeneous samples of PDMS-A and PDMS-B (diamonds). Note: the data ranges of elastic moduli corresponding to the selected volume fraction were indicated by up arrows (SOFT) and down arrows (STIFF). To see this figure in color, go online.
Mouse aorta indentation
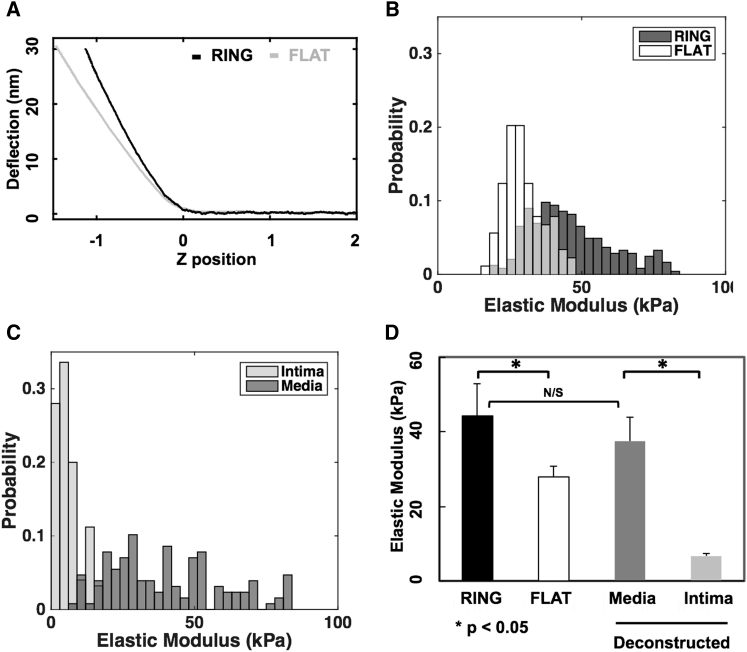
The HED method was applied to measure the layer-specific elastic properties of mouse aortic tissue using AFM indentation. Because of the minuscule size of the mouse abdominal aorta (∼40-μm thick), we were unable to reliably indent just the intimal layer of the aorta in the RING configuration. Furthermore, in both the FLAT and RING configurations, the loose, fibrous structure of the adventitial layer interfered with proper contact between the probe and sample, yielding highly variable and nonreproducible indentation results. Thus, the only comparison of layer-specific mechanical properties between RING and FLAT conditions that could be made with confidence was for the medial layer; in particular, aortic RING samples directly yielded elastic properties of the medial layer (Ering), and FLAT samples yielded apparent pointwise moduli (Eflat) for the composite aortic wall tissue, with HED analysis of Eflat used to extract modulus values for the intimal (Eint) and medial (Emed) layers. Raw force curves from the RING indentation had a steeper postcontact region than from the FLAT configuration (Fig. 9 A), indicating an effectively stiffer material when directly indenting the tunica media versus the composite layered aortic wall. This is confirmed by the histograms in Fig. 9 B, which show that the distribution of moduli for Ering tended to be stiffer than for Eflat. The Ering measurements exhibited a unimodal distribution (Fig. 9 B), suggesting that the selected 15 μm spherical probe tip was large enough for the indentation field to encompass a combination of structures in the media rather than detecting distinct cellular and matrix constituents. The distribution of Eflat was also unimodal (Fig. 9 B), suggesting in-plane mechanical uniformity despite the depth-dependent heterogeneity of the FLAT configuration. The resulting mean value of Ering was 44.3 ± 8.5 kPa, which was significantly stiffer (p < 0.03) than Eflat of 27.9 ± 3.0 kPa (Fig. 9 D, black and white bars, respectively).
Figure 9.
(A) Representative AFM indentation response of mouse aorta showed that indentation of the RING configuration yielded a stiffer measurement than that of the FLAT sample. Distributions show apparent elastic properties from arrays of individual AFM indentations of (B) RING and FLAT sections and (C) the deconstructed intima and media properties extracted from the composite FLAT sections using HED analysis. (D) Mouse aorta elastic properties obtained from AFM indention on RING and FLAT configurations are shown along with the layer-specific elastic moduli of the intima and media obtained by HED analysis of Eflat. Of note, the deconstructed medial layer, Emed, was not significantly different from the directly measured Ering value.
Using the full depth-dependent data for Eflat, HED analysis was used to reconstruct the elastic modulus of the top intima layer and the underlying media substrate. Whereas Eint showed a very narrow distribution, Emed had a broader distribution and was shifted to the right (Fig. 9 C). The resulting mean value of Eint (6.6 ± 0.8 kPa) was significantly softer than Emed (37.5 ± 6.3 kPa, p < 0.001), as shown in Fig. 9 D (gray bars). In these FLAT aorta tests, the effective inclusion volume fraction typically ranged from ∼0.3 or 0.4 up to ∼0.8 (see Figs. S4 and S6), spanning a range that exceeded the 30% minimal coverage for accurate modulus reconstruction determined by the above FEM sensitivity analysis. Notably, the HED-derived Emed was not significantly different from the directly measured Ering (p = 0.34). This demonstrated the ability of HED analysis to separate the mechanics of the intima and the underlying media layer with a single nondestructive test, yielding modulus values that were consistent with direct indentation of the media layer.
Discussion
Herein, we propose the HED approach to analyze AFM indentation data when studying the micromechanical properties of soft samples that have a heterogeneous layered structure. This may be particularly well suited for small biological samples, such as mouse blood vessels or embryologic heart tissues (37), in which the different layers are anatomically interconnected. For example, transgenic mouse models of Marfan syndrome exhibit severe local elastic network disruption in the tunica media of the aorta (50), but the associated changes in layer-specific biophysical properties of the arterial wall are difficult to measure without first dissociating the tissue layers. Also, for developmentally immature or pathologically compromised animal models, the tissues of interest may be small and fragile, requiring gentle mechanical testing with microscale resolution.
AFM indentation is a well-developed experimental technique for testing micromechanical properties of soft samples, but standard data analysis methods utilize the idealized Hertz contact theory, which is based on simplifying assumptions that are fundamentally inappropriate for most biological samples (2). Nix and co-workers have attempted to decouple the mechanical properties of indented multilayered polymer samples (17, 18); the investigators extracted the top layer properties at the nanometer scale but did not extract the modulus of the bottom substrate, which was of equal interest in our study. The transition from a polymer brush layer to elastic indentation of a nanoscale multilayer system has been analyzed by Tsukruk and colleagues using a theoretical model and an experimental layered polymer (18); however, the layer thicknesses were submicron, and the modulus values varied by over 10,000-fold from a compliant polymer (15 MPa) to a silicon substrate (160,000 MPa); such conditions do not apply for many biological samples. Alternatively, a recent study published by Sarrazin and colleagues described an approach called the Coated Half-Space Indentation Model of Elastic Response (CHIMER) to extract the thickness of the upper layer in a bilayer sample based on the apparent Young’s modulus and a numerically derived “weight function” for different modulus mismatches from 10-fold to 10,000-fold (19). However, they only considered top layers with stiffnesses at least 10-fold greater than the bulk (i.e., not applicable for soft top layer on stiffer substrate), with the thickest layer studied being only ∼150 nm. The application of these polymer-film models to biological systems, in which the thickness is on the order of microns and the stiffness ratio is typically not more than ∼10-fold, has not been validated to our knowledge. Sokolov and co-workers sought to improve the estimation of cellular mechanics by accounting for a surface layer of glycoproteins and membrane protrusions treated as a superficial brush structure (20, 21). Penetration of the soft brush layer is assumed at higher indentation depths, where the associated steric repulsion force becomes dominated by the elastic response of the underlying cell material. However, the biophysics of this model is fundamentally different than our case of a soft elastic layer on a stiffer elastic layer (or vice versa), in which penetration of the top layer does not occur. Other modified Hertzian approaches have been developed for analyzing the indentation of a soft layer on a stiffer substrate (16, 37), but computational validation has been limited. As demonstrated in Fig. S7, using this approach to analyze FEM-simulated indentation data can distinguish soft-on-stiff from stiff-on-soft bilayer samples; but in both cases, the extracted modulus values do not accurately recover the prescribed moduli, whereas the HED analysis yields markedly improved estimates of the layer-specific elastic moduli. Ultimately, users will need to decide how to balance the ease of use with the need for accuracy in choosing a data analysis method for specific applications.
The physical interpretation of the effective inclusion volume fraction, feff, in a layered PDMS sample or a flattened full-thickness section of mouse aorta wall can be descried as the relative contribution from the top layer to the total interrogated region of the sample within the indentation field. In an aorta microindentation test, an feff value of 1 indicates that only the thin top intima layer of the vessel is being probed; this might occur immediately after contact if the indentation field does not extend beyond the intima layer. Likewise, an feff value of 0 would mean the underlying media layer is the only contributor to the indentation response, which is not achievable when indenting a flattened aorta sample with the intima and media layers intact. In practice, the indentation field includes contributions from both the intima and media layers, so the limiting feff values of 0 and 1 are not observed experimentally. The same is true for the thin bilayered PDMS samples fabricated for this study. Indeed, the analysis of the effects of restricted data subranges was motivated by experience with AFM indentation on bilayered samples; when the AFM probe initially makes contact with the sample, the pointwise modulus can be noisy or dominated by surface interaction forces, interfering with data in the limit of feff approaching 1.0; similarly, the zero inclusion volume fraction limit is difficult to achieve because with a top layer configuration, there is always some amount of inclusion encompassed within the indentation field. According to our sensitivity analysis, a minimal coverage of 30% of the feff data subrange, biased toward the smaller values of feff achieved during deeper indentations, yielded robust estimates of Esub and Einc; accuracy increased as the subrange width increased. A representative HED analysis of abdominal aorta indentation was examined with a volume fraction range of 0.3–0.6 using the minimal 30% coverage, and this yielded consistent estimates of medial and intimal properties (Fig. S6). Thus, our approach appears to provide an improved analysis to evaluate the mechanical properties of an embedded layer in an intact sample with preserved structural integrity, even when the data range is restricted by some practical limitations of AFM indentation experiments.
Previous FEM analyses of the AFM indentation problem have demonstrated an increase in reaction forces related to boundary and tip-sample interaction conditions (2, 12). To correct for such effects, modifications of the standard AFM indentation analysis have previously been developed to account for finite sample dimensions (3, 5), particularly when the indentation depth exceeds 10% of the sample thickness. Such approaches can improve estimation of the elastic properties of thin soft samples on an underlying rigid substrate, but this does not address through-thickness heterogeneity of the intrinsic sample properties. One approach to mechanical characterization of a thin layer on a deformable substrate (e.g., the glycocalyx on a living cell) has been to simply limit the sample indentation to shallow depths (51), but it is questionable to assume that an underlying layer will not influence measurement of top-layer properties. A new equation was proposed and validated by FEM for determining the nanomechanics of a compliant layer on a stiffer substrate for the application to high-modulus chemical films such as silicon dioxide on silicon (16). Recently, the mechanical properties of the endothelial glycocalyx were reported based on this method (15). However, the applicability for mesoscale soft materials has not been validated, which may involve adapting the equation coefficients derived for stiff polymers to soft samples, extending the range of overlayer thickness, and correcting for substrate effects with indentation depths exceeding one-tenth of the sample thickness (3, 5). Therefore, our HED method was developed and validated specifically for soft samples with at least a twofold disparity in constituent moduli and with layer dimensions on a scale of microns comparable to the indenter diameter and indentation depth. This technique made it possible to simultaneously measure the mechanical properties of the aortic intima and media from individual AFM indentation tests on the composite vessel wall.
PDMS elastomer was readily used to create multilayer thin films with defined thickness by multiple spin coating steps. However, interface characteristics such as adhesion forces, surface charges, and hydrophobicity of PDMS caused significant snap-on events during AFM indentation testing (52, 53). Therefore, PDMS samples were pretreated with bovine serum albumin solution to minimize adhesive interaction between the tip and sample (37). Additionally, the pointwise modulus analysis consistently revealed an initially high apparent stiffness that abruptly decreased with indentation depth in all the tested PDMS configurations (Fig. S5 A), suggesting a very thin and stiff surface film possibly caused by the PDMS curing process. Such a phenomenon has been reported in a previous AFM indentation study of PDMS, which ruled out artifacts due to adhesion force, viscoelastic effects, and mismatched contact point as the underlying cause (54). To explore this phenomenon, a four-layer FEM was created with a very stiff film on top of the bilayer and an interface film between the layers; analysis of the simulated data showed depth-dependent Epw similar to the AFM experiments, which was distinct from a corresponding bilayer model without stiff films (Fig. S5 B). Another study by Kovalev et al. in multilayered polymer thin films documented distinct, step-like transitions in depth-dependent elastic modulus from computational models as well as experimental AFM indentation on synthetic layered materials (18). However, unlike the Kovalev study, our pointwise modulus analysis did not reveal step-like changes with indentation depth, possibly because of the much larger indenter radius and layer thicknesses and substantially smaller heterogeneity in layer-specific modulus values in our samples. Nevertheless, scanning electron microscopy images of a cross section of our bilayered PDMS sample confirmed the presence of a thin interface layer that formed during the PDMS curing process (Fig. S5 C). Because of this surface artifact, AFM indentation of the PDMS samples was more complicated than a simple assumption of one stiff material (PDMS-A) and one soft material (PDMS-B). The surface thin film seems to be the primary reason for the discrepancy in the estimation of soft and stiff material properties when comparing the elastic moduli from homogenous and heterogeneous PDMS samples (Fig. 8 D). However, the purpose of the PDMS indentation was to demonstrate the applicability of the HED analysis to well-controlled heterogeneously layered samples. Therefore, self-consistency of the deconstructed values of EA and EB from both the SOFT and STIFF PDMS layer inclusion configurations was considered a highly relevant experimental validation of the HED method.
AFM indentation of the flattened aorta sample evaluated the apparent elastic properties of the unloaded vessel wall. Assuming a two-layer configuration, the HED-extracted mechanical properties of arterial layers reflected their structural composition: the soft tunica intima consists of endothelial cells and basement membrane, whereas the stiffer tunica media includes vascular smooth muscle cells and sheets of elastic laminae. Our findings support the predictions of Huang et al. (55), who used a heterogeneous fiber matrix theory to model the effects of hydraulic pressure on tissue transport properties, reflecting a more sparse and permeable tissue matrix in the intima compared to the media. By contrast, an experimental study of harvested human coronary arteries with nonatherosclerotic intimal hyperplasia showed that the intima was stiffer than the media based on direct tensile testing of physically dissociated layers of the vessel wall (22). Although the potential impact of dissection artifacts is difficult to assess, these studies suggest that the layer-specific properties of the vessel wall could be altered by pathophysiological adaptive processes compared to healthy arteries. The elastic modulus measured by AFM in our study was comparable to the reported macroscopic modulus of rat abdominal aorta under uniaxial testing in the circumferential direction (66 kPa) but lower than the corresponding longitudinal modulus (590 kPa) (49, 56). Similarly, inflation testing of the mouse abdominal aorta yielded an elastic modulus of ∼50 kPa in the circumferential direction but higher in the longitudinal direction (57). Such macroscopic anisotropy reflects the microstructural organization and preferred alignment of cell and matrix components of the vessel wall and is exacerbated by the material nonlinearity and recruitment of collagen fibers at higher strains (58). We have not considered material anisotropy and nonlinearity in our HED analysis. Identification of such material properties by AFM may require more complex testing capabilities, such as indentation combined with in-plane stretching (2). Also, generation of the master curve requires estimation of the top-layer thickness, which is generally achievable after, if not before, performing the indentation tests. However, if not measured in fresh samples, then tissue layer dimensions obtained from fixed samples should be corrected for potential distortion during processing. Although the 10% shrinkage generally attributed to paraformaldehyde fixation of biological samples is predicted to have minimal impact on the modulus values extracted by HED decomposition, thickness uncertainty impacts the estimated inclusion and substrate moduli, particularly for the surface layer (see Fig. S3). We validated our HED method with multilayered PDMS and mouse aorta samples with a surface layer of 3–5 μm and an elastic modulus heterogeneity of less than 10-fold. The HED method has not been validated for very thin surface layers less than 1 μm thick nor for samples with layer-specific elastic modulus ratios in the 10× to 10,000× range or different Poisson ratios, mainly because these conditions were not immediately relevant for the samples of primary interest. However, the underlying theory can readily generalize to such conditions, and additional targeted validation should be performed in future studies that seek to utilize the HED method for such applications.
AFM indentation involves primarily compressive loading with a finite strain field that is highly localized in an otherwise unloaded sample configuration. Thus, it is encouraging that the modulus values obtained by AFM indentation are on the same scale as some measurements obtained by macroscopic stretching of the composite vessel wall. More importantly, our reconstructed modulus of tunica media extracted from AFM indentation of the composite FLAT tissue configuration agreed remarkably well with direct indentation measurements of aortic media in the RING tissue configuration, further validating the HED analysis method and suggesting that AFM indentation may be less sensitive to tissue anisotropy than macroscopic stretching. In summary, we demonstrated that the HED analysis is able to assess the effective elastic properties of the surface tunica intima and underlying tunica media of mouse aorta in an unloaded but intact condition. Such measurement capabilities could expand our understanding of tissue-specific vascular biomechanics in transgenic animal models of disease, as we have recently shown (59). Extension to other tissue types and disease states should be straightforward.
As we have demonstrated, the accuracy of reconstructed elastic properties using the HED algorithm depends on the available range of inclusion volume fraction data. Thus, the concept of the “master curve” describing volume fraction versus indentation depth can provide a practical tool to aid the design of AFM experiments; knowing the geometry of the subcomponents of a sample of interest, the master curve allows rational selection of the size of the AFM probe tip, the maximal indentation depth required to assess the individual components in layered soft samples, and a cantilever spring constant sufficient to achieve the necessary indentations. In the case of a thick top layer, the range of inclusion volume fraction may be too limited to achieve accurate estimation of individual properties of a bilayer sample. For example, we tried the FLAT aorta configuration with the adventitia layer facing up, but the reconstruction was not successful partly because of the limited volume fraction subrange (<30%) due to the average thickness of the adventitia being ∼10 μm. According to our mathematical validation, a criterion of >30% data range in the deconstructing procedures is essential for successful HED analysis. In cases in which this minimal subrange could be achieved, our results in the PDMS and aorta experiments showed agreement and consistency between our test and control measurements. This confirmed that the HED approach could deconstruct individual properties of a bilayered sample even with a restricted data range, which is a typical limitation of biological experiments compared to a well-defined synthetic system. Lastly, once FEMs are used to generate master curves for different geometric configurations, they will not require substantial access or expertise with Abaqus or similar computer modeling software to utilize the HED method compared to FEM-based inverse modeling approaches (60). So we anticipate that the HED analysis can be readily used by investigators to improve AFM indentation analysis of heterogeneous layered soft samples composed of two nearly incompressible elastic materials.
Conclusions
We validated the HED technique to extract layer-specific elastic moduli of mechanically heterogeneous two-layered samples measured by AFM indentation, with the indenter radius selected to achieve an effective inclusion volume fraction (feff) in the range of 0.3–0.6 or greater for a given top-layer thickness. With particular interest in applications for soft biological samples, we specifically examined nearly incompressible materials having a stiffer or softer top (inclusion) layer with a 2- to 10-fold disparity in elastic properties and a top-layer thickness that could be measured independently as an input for the HED analysis. The method was effective using data simulated by FEM and was robust to random noise and restricted data ranges covering as little as 30% of the central subrange of effective volume fraction values. The mechanical properties of two distinct PDMS formulations (materials A and B) were recovered from AFM indentation experiments on synthetic two-layer elastomer samples. Furthermore, layer-specific mechanical properties of the intima and media of intact mouse aortic wall were obtained by simply indenting the luminal surface of the flattened tissue sample with the AFM. Overall, the study provides an approach to measure the heterogeneous properties of synthetic or biological soft samples that are too small or fragile to be assessed by conventional mechanical testing methods without requiring a priori physical or chemical disruption of the composite structure, opening new opportunities for studying micromechanical properties of biophysically relevant samples using AFM indentation.
Author Contributions
J.-J.L., S.R., E.U.A., and K.D.C. designed the research. J.-J.L., S.R., G.K., and E.U.A. performed the research. J.-J.L. and G.K. contributed analytic tools. J.-J.L. and G.K. analyzed the data. J.-J.L. and K.D.C. wrote the article. G.K. and E.U.A. edited the article.
Acknowledgments
The authors gratefully acknowledge Drs. Chaoqin Xie and Dongtak Jeong for assistance with the animal studies and Drs. Sihong Wang and Ioana Voiculescu for assistance with microfabrication studies.
Funding was provided by a graduate fellowship from the Grove School of Engineering, The City College of New York (J.-J.L.), a fellowship from the Stony Wold-Herbert Fund (J.-J.L.), a Career Development Award from the American Society of Nephrology (E.U.A.), and a shared instrument grant from the National Institutes of Health/National Center for Research Resources S10RR027609 (K.D.C.).
Editor: Celeste Nelson.
Footnotes
Supporting Materials and Methods and seven figures are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(18)30530-7.
Supporting Citations
Reference (61) appears in the Supporting Material.
Supporting Material
References
- 1.Radmacher M. Measuring the elastic properties of living cells by the atomic force microscope. Methods Cell Biol. 2002;68:67–90. doi: 10.1016/s0091-679x(02)68005-7. [DOI] [PubMed] [Google Scholar]
- 2.Costa K.D., Yin F.C. Analysis of indentation: implications for measuring mechanical properties with atomic force microscopy. J. Biomech. Eng. 1999;121:462–471. doi: 10.1115/1.2835074. [DOI] [PubMed] [Google Scholar]
- 3.Dimitriadis E.K., Horkay F., Chadwick R.S. Determination of elastic moduli of thin layers of soft material using the atomic force microscope. Biophys. J. 2002;82:2798–2810. doi: 10.1016/S0006-3495(02)75620-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Lin D.C., Shreiber D.I., Horkay F. Spherical indentation of soft matter beyond the Hertzian regime: numerical and experimental validation of hyperelastic models. Biomech. Model. Mechanobiol. 2009;8:345–358. doi: 10.1007/s10237-008-0139-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Long R., Hall M.S., Hui C.Y. Effects of gel thickness on microscopic indentation measurements of gel modulus. Biophys. J. 2011;101:643–650. doi: 10.1016/j.bpj.2011.06.049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Briscoe B.J., Sebastian K.S., Adams M.J. The effect of indenter geometry on the elastic response to indentation. J. Phys. D Appl. Phys. 1994;27:1156–1162. [Google Scholar]
- 7.Li S., Wang G. World Scientific; Singapore: 2008. Introduction to Micromechanics and Nanomechanics. [Google Scholar]
- 8.Ohashi T., Ishii Y., Sato M. Experimental and numerical analyses of local mechanical properties measured by atomic force microscopy for sheared endothelial cells. Biomed. Mater. Eng. 2002;12:319–327. [PubMed] [Google Scholar]
- 9.Kasas S., Wang X., Catsicas S. Superficial and deep changes of cellular mechanical properties following cytoskeleton disassembly. Cell Motil. Cytoskeleton. 2005;62:124–132. doi: 10.1002/cm.20086. [DOI] [PubMed] [Google Scholar]
- 10.Kim Y., Kim M., Kim J. Characterization of cellular elastic modulus using structure based double layer model. Med. Biol. Eng. Comput. 2011;49:453–462. doi: 10.1007/s11517-010-0730-y. [DOI] [PubMed] [Google Scholar]
- 11.Bernick K.B., Prevost T.P., Socrate S. Biomechanics of single cortical neurons. Acta Biomater. 2011;7:1210–1219. doi: 10.1016/j.actbio.2010.10.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Vaziri A., Lee H., Mofrad M.R.K. Deformation of the cell nucleus under indentation: mechanics and mechanisms. J. Mater. Res. 2006;21:2126–2135. [Google Scholar]
- 13.Charras G.T., Horton M.A. Determination of cellular strains by combined atomic force microscopy and finite element modeling. Biophys. J. 2002;83:858–879. doi: 10.1016/S0006-3495(02)75214-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Vargas-Pinto R., Gong H., Johnson M. The effect of the endothelial cell cortex on atomic force microscopy measurements. Biophys. J. 2013;105:300–309. doi: 10.1016/j.bpj.2013.05.034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Marsh G., Waugh R.E. Quantifying the mechanical properties of the endothelial glycocalyx with atomic force microscopy. J. Vis. Exp. 2013;72:e50163. doi: 10.3791/50163. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Clifford C.A., Seah M.P. Nanoindentation measurement of Young’s modulus for compliant layers on stiffer substrates including the effect of Poisson’s ratios. Nanotechnology. 2009;20:145708. doi: 10.1088/0957-4484/20/14/145708. [DOI] [PubMed] [Google Scholar]
- 17.Saha R., Nix W.D. Effects of the substrate on the determination of thin film mechanical properties by nanoindentation. Acta Mater. 2002;50:23–38. [Google Scholar]
- 18.Kovalev A., Shulha H., Tsukruk V.V. Nanomechanical probing of layered nanoscale polymer films with atomic force microscopy. J. Mater. Res. 2004;19:716–728. [Google Scholar]
- 19.Sarrazin B., Brossard R., Malloggi F. Investigation of PDMS based bi-layer elasticity via interpretation of apparent Young’s modulus. Soft Matter. 2016;12:2200–2207. doi: 10.1039/c5sm02133b. [DOI] [PubMed] [Google Scholar]
- 20.Dokukin M.E., Guz N.V., Sokolov I. Quantitative study of the elastic modulus of loosely attached cells in AFM indentation experiments. Biophys. J. 2013;104:2123–2131. doi: 10.1016/j.bpj.2013.04.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Guz N., Dokukin M., Sokolov I. If cell mechanics can be described by elastic modulus: study of different models and probes used in indentation experiments. Biophys. J. 2014;107:564–575. doi: 10.1016/j.bpj.2014.06.033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Holzapfel G.A., Sommer G., Regitnig P. Determination of layer-specific mechanical properties of human coronary arteries with nonatherosclerotic intimal thickening and related constitutive modeling. Am. J. Physiol. Heart Circ. Physiol. 2005;289:H2048–H2058. doi: 10.1152/ajpheart.00934.2004. [DOI] [PubMed] [Google Scholar]
- 23.Sokolis D.P., Kritharis E.P., Iliopoulos D.C. Effect of layer heterogeneity on the biomechanical properties of ascending thoracic aortic aneurysms. Med. Biol. Eng. Comput. 2012;50:1227–1237. doi: 10.1007/s11517-012-0949-x. [DOI] [PubMed] [Google Scholar]
- 24.Okamoto R.J., Wagenseil J.E., Sundt T.M., III Mechanical properties of dilated human ascending aorta. Ann. Biomed. Eng. 2002;30:624–635. doi: 10.1114/1.1484220. [DOI] [PubMed] [Google Scholar]
- 25.Ferruzzi J., Collins M.J., Humphrey J.D. Mechanical assessment of elastin integrity in fibrillin-1-deficient carotid arteries: implications for Marfan syndrome. Cardiovasc. Res. 2011;92:287–295. doi: 10.1093/cvr195. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Eberth J.F., Taucer A.I., Humphrey J.D. Mechanics of carotid arteries in a mouse model of Marfan syndrome. Ann. Biomed. Eng. 2009;37:1093–1104. doi: 10.1007/s10439-009-9686-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Zhao R., Sider K.L., Simmons C.A. Measurement of layer-specific mechanical properties in multilayered biomaterials by micropipette aspiration. Acta Biomater. 2011;7:1220–1227. doi: 10.1016/j.actbio.2010.11.004. [DOI] [PubMed] [Google Scholar]
- 28.Huang Y., Guo X., Kassab G.S. Axial nonuniformity of geometric and mechanical properties of mouse aorta is increased during postnatal growth. Am. J. Physiol. Heart Circ. Physiol. 2006;290:H657–H664. doi: 10.1152/ajpheart.00803.2005. [DOI] [PubMed] [Google Scholar]
- 29.Elkin B.S., Azeloglu E.U., Morrison B., III Mechanical heterogeneity of the rat hippocampus measured by atomic force microscope indentation. J. Neurotrauma. 2007;24:812–822. doi: 10.1089/neu.2006.0169. [DOI] [PubMed] [Google Scholar]
- 30.Park S., Costa K.D., Ateshian G.A. Microscale frictional response of bovine articular cartilage from atomic force microscopy. J. Biomech. 2004;37:1679–1687. doi: 10.1016/j.jbiomech.2004.02.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Engler A.J., Rehfeldt F., Discher D.E. Microtissue elasticity: measurements by atomic force microscopy and its influence on cell differentiation. Methods Cell Biol. 2007;83:521–545. doi: 10.1016/S0091-679X(07)83022-6. [DOI] [PubMed] [Google Scholar]
- 32.Plodinec M., Loparic M., Schoenenberger C.A. The nanomechanical signature of breast cancer. Nat. Nanotechnol. 2012;7:757–765. doi: 10.1038/nnano.2012.167. [DOI] [PubMed] [Google Scholar]
- 33.Hayenga H.N., Trache A., Humphrey J.D. Regional atherosclerotic plaque properties in ApoE-/- mice quantified by atomic force, immunofluorescence, and light microscopy. J. Vasc. Res. 2011;48:495–504. doi: 10.1159/000329586. [DOI] [PubMed] [Google Scholar]
- 34.Peloquin J., Huynh J., Reinhart-King C.A. Indentation measurements of the subendothelial matrix in bovine carotid arteries. J. Biomech. 2011;44:815–821. doi: 10.1016/j.jbiomech.2010.12.018. [DOI] [PubMed] [Google Scholar]
- 35.Beenakker J.W., Ashcroft B.A., Oosterkamp T.H. Mechanical properties of the extracellular matrix of the aorta studied by enzymatic treatments. Biophys. J. 2012;102:1731–1737. doi: 10.1016/j.bpj.2012.03.041. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Lindeman J.H., Ashcroft B.A., Oosterkamp T.H. Distinct defects in collagen microarchitecture underlie vessel-wall failure in advanced abdominal aneurysms and aneurysms in Marfan syndrome. Proc. Natl. Acad. Sci. USA. 2010;107:862–865. doi: 10.1073/pnas.0910312107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Kaushik G., Fuhrmann A., Engler A.J. In situ mechanical analysis of myofibrillar perturbation and aging on soft, bilayered Drosophila myocardium. Biophys. J. 2011;101:2629–2637. doi: 10.1016/j.bpj.2011.10.042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Loparic M., Wirz D., Stolz M. Micro- and nanomechanical analysis of articular cartilage by indentation-type atomic force microscopy: validation with a gel-microfiber composite. Biophys. J. 2010;98:2731–2740. doi: 10.1016/j.bpj.2010.02.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Hofmann U.G., Rotsch C., Radmacher M. Investigating the cytoskeleton of chicken cardiocytes with the atomic force microscope. J. Struct. Biol. 1997;119:84–91. doi: 10.1006/jsbi.1997.3868. [DOI] [PubMed] [Google Scholar]
- 40.Azeloglu E.U., Costa K.D. Cross-bridge cycling gives rise to spatiotemporal heterogeneity of dynamic subcellular mechanics in cardiac myocytes probed with atomic force microscopy. Am. J. Physiol. Heart Circ. Physiol. 2010;298:H853–H860. doi: 10.1152/ajpheart.00427.2009. [DOI] [PubMed] [Google Scholar]
- 41.Kuznetsova T.G., Starodubtseva M.N., Zhdanov R.I. Atomic force microscopy probing of cell elasticity. Micron. 2007;38:824–833. doi: 10.1016/j.micron.2007.06.011. [DOI] [PubMed] [Google Scholar]
- 42.Darling E.M., Zauscher S., Guilak F. Viscoelastic properties of zonal articular chondrocytes measured by atomic force microscopy. Osteoarthritis Cartilage. 2006;14:571–579. doi: 10.1016/j.joca.2005.12.003. [DOI] [PubMed] [Google Scholar]
- 43.Guo S., Akhremitchev B.B. Packing density and structural heterogeneity of insulin amyloid fibrils measured by AFM nanoindentation. Biomacromolecules. 2006;7:1630–1636. doi: 10.1021/bm0600724. [DOI] [PubMed] [Google Scholar]
- 44.Costa K.D. Imaging and probing cell mechanical properties with the atomic force microscope. Methods Mol. Biol. 2006;319:331–361. doi: 10.1007/978-1-59259-993-6_17. [DOI] [PubMed] [Google Scholar]
- 45.Eshelby J.D. The determination of the elastic field of an ellipsoidal inclusion, and related problems. Proc. R. Soc. Lond. A Math. Phys. Sci. 1957;241:376–396. [Google Scholar]
- 46.Li S., Sauer R., Wang G. A circular inclusion in a finite domain I. The Dirichlet-Eshelby problem. Acta Mech. 2005;179:67–90. [Google Scholar]
- 47.Azeloglu E.U., Kaushik G., Costa K.D. Developing a hybrid computational model of AFM indentation for analysis of mechanically heterogeneous samples. Conf. Proc. IEEE Eng. Med. Biol. Soc. 2009;2009:4273–4276. doi: 10.1109/IEMBS.2009.5334043. [DOI] [PubMed] [Google Scholar]
- 48.Hashin Z., Shtrikman S. A variational approach to the theory of the elastic behaviour of multiphase materials. J. Mech. Phys. Solids. 1963;11:127–140. [Google Scholar]
- 49.Gleason R.L., Wilson E., Humphrey J.D. Biaxial biomechanical adaptations of mouse carotid arteries cultured at altered axial extension. J. Biomech. 2007;40:766–776. doi: 10.1016/j.jbiomech.2006.03.018. [DOI] [PubMed] [Google Scholar]
- 50.Bunton T.E., Biery N.J., Dietz H.C. Phenotypic alteration of vascular smooth muscle cells precedes elastolysis in a mouse model of Marfan syndrome. Circ. Res. 2001;88:37–43. doi: 10.1161/01.res.88.1.37. [DOI] [PubMed] [Google Scholar]
- 51.Wiesinger A., Peters W., Kümpers P. Nanomechanics of the endothelial glycocalyx in experimental sepsis. PLoS One. 2013;8:e80905. doi: 10.1371/journal.pone.0080905. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Gupta S., Carrillo F., Puttlitz C. Adhesive forces significantly affect elastic modulus determination of soft polymeric materials in nanoindentation. Mater. Lett. 2007;61:448–451. [Google Scholar]
- 53.Sun Y., Akhremitchev B., Walker G.C. Using the adhesive interaction between atomic force microscopy tips and polymer surfaces to measure the elastic modulus of compliant samples. Langmuir. 2004;20:5837–5845. doi: 10.1021/la036461q. [DOI] [PubMed] [Google Scholar]
- 54.Xu W., Chahine N., Sulchek T. Extreme hardening of PDMS thin films due to high compressive strain and confined thickness. Langmuir. 2011;27:8470–8477. doi: 10.1021/la201122e. [DOI] [PubMed] [Google Scholar]
- 55.Huang Y., Rumschitzki D., Weinbaum S. A fiber matrix model for the filtration through fenestral pores in a compressible arterial intima. Am. J. Physiol. 1997;272:H2023–H2039. doi: 10.1152/ajpheart.1997.272.4.H2023. [DOI] [PubMed] [Google Scholar]
- 56.Assoul N., Flaud P., Bataille I. Mechanical properties of rat thoracic and abdominal aortas. J. Biomech. 2008;41:2227–2236. doi: 10.1016/j.jbiomech.2008.04.017. [DOI] [PubMed] [Google Scholar]
- 57.Guo X., Kassab G.S. Variation of mechanical properties along the length of the aorta in C57bl/6 mice. Am. J. Physiol. Heart Circ. Physiol. 2003;285:H2614–H2622. doi: 10.1152/ajpheart.00567.2003. [DOI] [PubMed] [Google Scholar]
- 58.Groenink M., Langerak S.E., Spaan J.A. The influence of aging and aortic stiffness on permanent dilation and breaking stress of the thoracic descending aorta. Cardiovasc. Res. 1999;43:471–480. doi: 10.1016/s0008-6363(99)00095-4. [DOI] [PubMed] [Google Scholar]
- 59.Lee J.J., Galatioto J., Costa K.D. Losartan attenuates degradation of aorta and lung tissue micromechanics in a mouse model of severe marfan syndrome. Ann. Biomed. Eng. 2016;44:2994–3006. doi: 10.1007/s10439-016-1616-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Roy R., Desai J.P. Determination of mechanical properties of spatially heterogeneous breast tissue specimens using contact mode atomic force microscopy (AFM) Ann. Biomed. Eng. 2014;42:1806–1822. doi: 10.1007/s10439-014-1057-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Rotsch C., Jacobson K., Radmacher M. Dimensional and mechanical dynamics of active and stable edges in motile fibroblasts investigated by using atomic force microscopy. Proc. Natl. Acad. Sci. USA. 1999;96:921–926. doi: 10.1073/pnas.96.3.921. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.