Abstract
Actin filaments continually assemble and disassemble within a cell. Assembled filaments “age” as a bound nucleotide ATP within each actin subunit quickly hydrolyzes followed by a slower release of the phosphate Pi, leaving behind a bound ADP. This subtle change in nucleotide state of actin subunits affects filament rigidity as well as its interactions with binding partners. We present here a systematic multiscale ultra-coarse-graining approach that provides a computationally efficient way to simulate a long actin filament undergoing ATP hydrolysis and phosphate-release reactions while systematically taking into account available atomistic details. The slower conformational changes and their dependence on the chemical reactions are simulated with the ultra-coarse-graining model by assigning internal states to the coarse-grained sites. Each state is represented by a unique potential surface of a local heterogeneous elastic network. Internal states undergo stochastic transitions that are coupled to conformations of the underlying molecular system. The model reproduces mechanical properties of the filament and allows us to study whether conformational fluctuations in actin subunits produce cooperative filament aging. We find that the nucleotide states of neighboring subunits modulate the reaction kinetics, implying cooperativity in ATP hydrolysis and Pi release. We further systematically coarse grain the system into a Markov state model that incorporates assembly and disassembly, facilitating a direct comparison with previously published models. We find that cooperativity in ATP hydrolysis and Pi release significantly affects the filament growth dynamics only near the critical G-actin concentration, whereas far from it, both cooperative and random mechanisms show similar growth dynamics. In contrast, filament composition in terms of the bound nucleotide distribution varies significantly at all monomer concentrations studied. These results provide new insights, to our knowledge, into the cooperative nature of ATP hydrolysis and Pi release and the implications it has for actin filament properties, providing novel predictions for future experimental studies.
Introduction
Actin is a major component of the eukaryotic cytoskeleton and has important functions in cell motility and division. The monomeric form, globular actin (G-actin), polymerizes into filamentous actin (F-actin) and associates with filament-binding proteins to form dynamic filaments of various architectures that are meticulously regulated to perform these functions. Actin monomers are large single-domain proteins made of 375 amino acids, and they contain a bound nucleotide at their center. The nonpolymerized G-actin in the cell is predominantly found in an ATP-bound state (1). Polymerization of actin is followed by actin-catalyzed hydrolysis of the bound nucleotide ATP, and the hydrolysis in F-actin subunits has been estimated to be >40,000 times faster than in G-actin owing to the structural changes that G-actin undergoes as it transforms into an F-actin upon polymerization, during which it becomes more planar (2, 3, 4, 5, 6).
An actin monomer is not symmetric, and the actin filaments are polar in nature. New actin monomers predominantly add at the “barbed” end of the filament and have a faster rate of depolymerization at the “pointed” end (7). Depending upon the G-actin concentration in the local environment, a filament can either grow from both ends (high concentration), shrink at both ends (low concentration), or grow at the barbed end while shrinking at the pointed end. At a particular concentration, these two rates are balanced and filaments undergo treadmilling, whereby a constant filament length is maintained on average. Experimental evidence suggests that incorporation of a new actin monomer into the filament does not immediately induce ATP hydrolysis, nor does hydrolysis have to occur for subsequent monomers to be added (8). It is also believed that the rate of exchange of nucleotides in a filament with those in solution is negligible (9, 10). Instead, ATP is predominantly incorporated into the filament through polymerization of ATP-bound G-actin. The interplay of polymerization and hydrolysis results in a time lag associated with the hydrolysis in the filament with respect to polymerization and hence results in an ATP-bound cap in filaments at high G-actin concentration (11, 12). In F-actin, the hydrolysis of ATP to form ADP is not direct (11) but proceeds as a fast conversion to ADP with a protein-bound inorganic phosphate (ADP-Pi), followed by a slow release of the inorganic phosphate to the solution (13, 14, 15, 16). ATP hydrolysis occurs on a timescale of seconds, whereas Pi release takes place over minutes (2, 7, 13, 14, 17).
There are multiple cation-binding sites in actin with varying affinities that modulate the mechanical properties of the filament (12, 18, 19, 20, 21). Additionally, the state of the bound nucleotide also strongly influences its mechanical properties. The persistence length of actin filaments decreases as the bound nucleotide changes from ATP to ADP, as shown from experimental measurements (22). Recent simulation work also predicts that the bound nucleotide state affects the response of G-actin to various applied stresses (23).
Simplified mechanistic models parameterized using a top-down approach, in which model parameters are tuned to obtain certain target filament properties, have been successfully used to study actin filaments and their mechanical properties (24, 25). Such models reduce large-scale complex processes into simpler phenomenology but typically have somewhat limited predictive power and can potentially lack a rigorous justification for the choice of parameters involved. On the other hand, bottom-up coarse-grained (CG) models of actin filaments that are parameterized into a heteroelastic network (26) by using reference all-atom simulations have been found to be adequate in capturing actin filament mechanical properties as a function of the state of the nucleotides even at a highly coarse resolution of four CG sites per actin subunit (27, 28). A CG model with twelve CG sites per actin subunit has been shown to capture several other important structural aspects of actin (29). Such models that use a particle representation with an associated pairwise effective interaction potential are, however, often limited in their ability to represent certain molecular changes, including chemical or structural changes, that cannot be represented at the resolution of the CG sites, even if such changes ultimately affect the system behavior at the resolution of the CG model. Moreover, the underlying atomistic simulations further limit the configurations that such CG models can explore, as only configurations sampled by the atomistic model inform the effective potential, “locking” the CG model to, e.g., a given nucleotide composition. An example of such configurational changes is the state of the nucleotide bound to actin subunits in a filament. Although the CG particle representation has been shown to capture many essential conformational changes in actin subunits conditional on the state of bound nucleotide, these CG models do not offer insight about the hydrolysis dynamics involved, primarily because neither ATP hydrolysis nor Pi release are realized in all-atom simulations because of the timescales involved.
In contrast to the CG particle representation, a bottom-up model can be constructed using a discrete state representation, characterized by instantaneous transitions between different configurational states; these models are termed Markov state models (MSMs) (30, 31, 32, 33). Generally, the rates governing the behavior of MSMs are obtained through statistics derived from fine-grained all-atom simulations. Bottom-up MSMs are traditionally only able to study systems for which statistics have been directly obtained (32, 34, 35); including other states or rates in the model requires the computational scientist to use additional knowledge to determine the modified rate coefficients.
In this work, we first utilized the emerging concept of the ultra-coarse-grained (UCG) model, which combines both the particle and discrete state representations in a systematic way by defining an internal state associated with the CG particles (36, 37, 38, 39). The internal states of the CG particles can in principle account for any reactions or conformational changes within the CG particles, making the UCG model ideal for actin filaments to study ATP hydrolysis and Pi release reactions. The UCG model was then used to systematically parametrize an MSM, which was analyzed to make conclusions about the spatial cooperativity present in an actin filament.
The macroscopic rates of the polymerization, depolymerization, ATP hydrolysis, and Pi release reactions have been measured indirectly from experiments using fluorescence labeling, radioactive labeling, etc., by assuming an underlying kinetic model (9, 10, 11, 13, 17, 40, 41). In experiments involving a conserved system, in which the total mass of actin (G-actin + F-actin) in the system remains constant throughout the experiment, a characteristic sigmoidal-shaped curve is obtained for time evolution of filament growth and ATP hydrolysis, showing that hydrolysis lags behind the polymerization at high initial G-actin concentrations (13, 42). Since it was established that ATP hydrolysis is decoupled from polymerization, there have been two major classes of hydrolysis models in the literature: the random model and the cooperative model. The random hydrolysis model (11, 34), first proposed before the intermediate ADP-Pi was discovered, assumes that ATP bound to any F-actin subunit throughout the filament hydrolyzes at the same rate. Indirectly, this implies that the conformation of the neighboring subunits does not significantly affect the rate of hydrolysis, as the neighboring nucleotide state modulates the local conformational sampling of each monomer. Alternatively, the nucleotide state of neighboring subunits could modulate the rate constant, as is assumed in the cooperative hydrolysis models. Among the cooperative models, the vectorial model is the most distinct from the random hydrolysis model because it assumes that ATP hydrolysis can occur predominantly in those subunits in the filament that have an adjoining ADP subunit and hence are at an ATP/ADP (or ATP/ADP-Pi) interface. In the strictest version of the vectorial model (35, 43), at the most two interfaces (exactly two if the filament is growing from both its ends) can exist in a filament because hydrolysis is assumed to occur exclusively at the ATP/ADP interface and the interface simply moves toward the growing end of the filament as time progresses. The more realistic version of the vectorial model (cooperative model) assigns a relatively small nonzero hydrolysis rate for ATP subunits that are not present at the interface (8, 44).
There have been a number of studies attempting to perform a systematic comparison between the two classes of models (8, 35, 42, 45, 46, 47). However, common experimentally measured quantities such as rate of filament elongation, fluctuations in filament length, and size of unhydrolyzed ATP cap near the filament end are found to be insensitive to the mechanism of hydrolysis over a wide range of G-actin concentration, with small quantitative difference very close to the critical concentration (35, 47). A mixture of ATP-bound G-actin and ADP-bound G-actin can be used to introduce a different number of ATP-ADP interfaces in the filament by varying the composition of the mixture, thereby providing a way of enhancing the effective rate of hydrolysis within the context of the vectorial model (42). Fitting the predictions of a cooperative model to the time course of polymerization and ATP hydrolysis measured in these experiments eliminates the possibility of the strict vectorial model being accurate in all cases and suggests that the rate of hydrolysis at the ATP-ADP interface must be less than 100 times faster than the rate of hydrolysis away from the interface, although the predictions of a random hydrolysis mechanism were also shown to be able to explain the observed experimental data (42, 46). By using the nearest-neighbor cooperativity in such a model as a parameter to fit experimentally measured Pi release profiles, it was shown that the possibility of a high degree of cooperativity in Pi release could not be completely excluded, however, with some ambiguity in the data analysis involved (41, 44, 48, 49). The random and vectorial models are based on two simple microscopic physical hypotheses that are able to accurately explain the experimental observations. An intermediate model could be constructed by assuming a more complex cooperativity that goes beyond the two-body binary cooperativity (two possible hydrolysis rates, one at the interface and one away from the interface) previously used in the vectorial and cooperative models. However, lack of any direct experimental evidence differentiating these hypotheses makes empirically justifying and parameterizing such a complex cooperative model difficult. The central contribution of this manuscript is the prediction of the nature and extent of such complex cooperativity present in both ATP hydrolysis and Pi release reactions using a systematic CG modeling framework. As described below, this prediction was obtained through a multiscale CG approach that involved making careful assumptions, and it was constructed with all-atom molecular dynamics simulations at its foundation. Hence, the UCG model was essentially limited by the accuracy of the atomistic force field and the assumptions made.
Our UCG model, derived from all-atom (AA) molecular dynamics simulations, is able to provide a complex but detailed physical picture of the ATP hydrolysis and Pi release processes based on the behavior produced by a general atomistic force field (CHARMM27 + CMAP (50)). We constructed a UCG model that serves as a good representation of an actin filament at a low resolution and also, for the first time to our knowledge, takes into account the nucleotide state of each actin subunit explicitly. The UCG filament model and conformational coupling between subunits was derived via a systematic procedure from AA molecular dynamics simulations, whereas the instantaneous conformation-dependent rates of state transitions were approximated based on physical principles and implemented via a stochastic-state hopping procedure with resulting macroscopic rates tied to experimental observations. After ensuring that the UCG model provided reasonable predictions for the mechanical properties of the filament, an MSM was constructed at the coarse resolution of traditional biological models. In the MSM, only the nucleotide composition along the position of subunits in the filament was retained, whereas conformational fluctuations were integrated out. The model did not explicitly impose any cooperativity with respect to the nucleotide composition of neighboring subunits but was instead able to predict the spatial dependence of ATP hydrolysis and Pi release in actin filaments, allowing us to directly compare results with established hydrolysis models in the literature. Finally, the MSM was extended using experimental knowledge to explore the effects of concurrent hydrolysis and polymerization and used to compare the implications of the predicted cooperativity by modifying two representative models proposed in (34, 47).
Methods
CG model
Our modeling approach is fundamentally based on using AA molecular dynamics simulations as the primary basis for constructing lower resolution CG models. The configurational behavior of the CG model of the filament conditional on nucleotide composition was parameterized in two steps: 1) using a systematic map to reduce the AA structure to fewer CG sites or “beads” (see Fig. 1), and 2) using mapped system distributions to construct a CG effective force field that governs the conformations of those CG beads in such a way that the AA behavior is faithfully reproduced. An essential feature of the UCG model in the current context is then the assignment of additional discrete internal states to the CG beads, with a different CG force field associated with each state. In actin, for example, we used this additional model flexibility to represent the states of the bound nucleotide. The CG F-actin filament dynamics were then modeled using continuous-time Langevin dynamics simulations of the CG beads using appropriate force fields based on the instantaneous set of internal states of the neighboring CG beads, in addition to allowing discrete jumps between the various internal states. In other words, kinetics of ATP hydrolysis or Pi release in a subunit is controlled by the rates governing the switching between these states, which inherently must also take into account the conformational changes that the subunit undergoes upon hydrolysis or Pi release and additionally take into account the interdependence on the nucleotide states of its neighboring subunits. It is important to note that the latter significantly increases the complexity of the problem, and to make progress, we must invoke certain assumptions. Firstly, we restricted the CG force field to pairwise interactions and imposed a degree of locality on these interactions. As described in (36), without the locality approximation, there is an exponentially large number of possible states to consider, making the UCG approach infeasible. The local nature of the interactions is somewhat based on biological intuition. Second, we constructed the CG force field from AA simulations only for actin filaments consisting of subunits with identical nucleotides and used a simple mixing rule to construct the CG force field otherwise. A justification for the mixing rule is provided in the Supporting Materials and Methods. The details of the AA simulations are also described in the Supporting Materials and Methods. Briefly, a periodic 13-subunit actin filament was constructed using the Oda structure for each state of the bound nucleotide (29, 50, 51, 52, 53, 54, 55, 56). Three AA simulation trajectories were obtained, one for a pure ATP-bound actin filament, one for a pure ADP-Pi-bound actin filament, and one for a pure ADP-bound actin filament. Each of these AA trajectories was used to obtain CG models for the filaments with corresponding states of the bound nucleotide. The UCG force field and the UCG discrete state-switching algorithm are described below.
Figure 1.
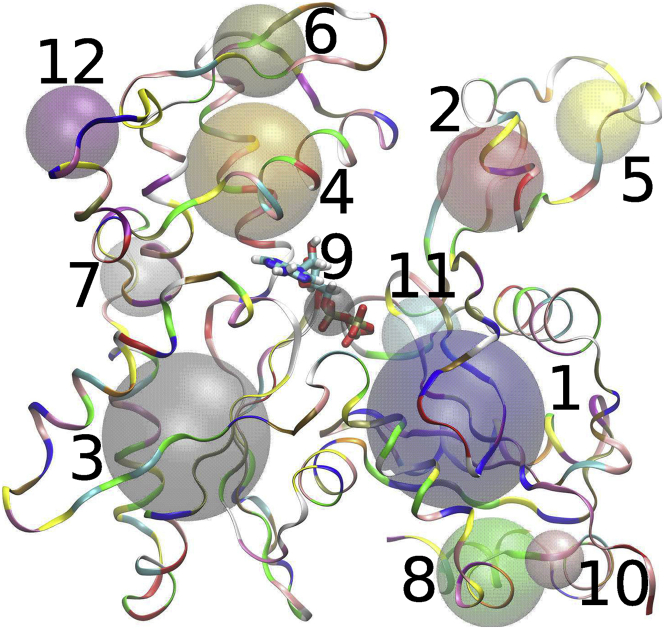
Schematic showing the CG mapping used in our study. The atomistic structure of ADP-Pi bound actin subunit is shown as ribbons, with the corresponding CG sites shown as beads. CG bead indices 1–12 are marked next to each CG site. Our final model has five major beads corresponding to CG sites with indices 1–5. To see this figure in color, go online.
UCG force field
Each of the ATP-, ADP-Pi-, and ADP-bound states of actin filament were independently coarse grained using a 12-site mapping (29, 57) (Fig. 1) and a hybrid force field. The hybrid force field consisted of an intrasubunit heterogeneous elastic network model (hENM (27)) and an intersubunit pairwise interaction modeled with an inverted Gaussian potential, which will allow for future studies to include (de)polymerization at the UCG resolution. The details of these potentials are provided in the Supporting Materials and Methods. First, AA simulation trajectories of an actin filament with 13 subunits (bound exclusively with either ATP, ADP-Pi, or ADP) were used to generate a force field for a filament in a pure nucleotide state. To build the hybrid model, we started by connecting all pairs of intrasubunit beads by springs. We then connected intersubunit beads with springs, but to simplify the conversion of intersubunit interactions to be dissociable, we chose to only include springs between a subset of CG sites that we call “major beads” and restricted these intersubunit springs to bead pairs that are less than three actin subunits apart to help enforce the locality of UCG interactions discussed earlier. Finally, we used the hENM procedure to assign spring constants that maximally match the fluctuations in the AA trajectory. To choose which CG sites to use for intersubunit interactions, we tested varying numbers of major beads, adding them in increasing order of their CG index as labeled in Fig. 1. A model including the first five beads as major beads was chosen based on physical considerations (important domains in actin that mediate intersubunit interactions) and because it gave the best agreement in persistence length (22, 27, 28, 58, 59, 60, 61, 62, 63) (see Supporting Materials and Methods for details). The five major beads in an actin subunit correspond to the four major subdomains in actin and the D-loop region (Fig. 1). The D-loop region inserts into actin’s barbed end “target binding cleft” and is an important mediator of longitudinal interactions in the filament (20, 56, 59, 64, 65, 66, 67).
After the hENM procedure, the intersubunit springs between actin monomers in the filament were converted into soft potentials. This was done by converting each intersubunit elastic spring potential into an inverted Gaussian potential by least-square fitting to the elastic-spring-potential well in the region corresponding to a well depth of 3 kcal/mol. The well depth was set to be strong enough to prevent adjacent subunits in a filament from leaving the filament but weak enough to prevent any large jumps in energy of the system that would lead to large numerical integration errors.
The intersubunit inverted Gaussian potential for a pair of CG beads with distinct states (e.g., ATP:ADP-Pi) of the bound nucleotide was obtained using a simple mixing rule that involved averaging parameters of the potential for each of the individual pure states (ATP:ATP and ADP-Pi:ADP-Pi), as described in the Supporting Materials and Methods. All UCG simulations were performed in the Large-scale Atomic/Molecular Massively Parallel Simulator Molecular Dynamics software (68).
UCG state switching
Each of the actin subunits was assigned an internal state depending on its bound nucleotide. The ATP hydrolysis and Pi release reactions were then represented as switching of these internal states (37). The simulation methodology consisted of evolving continuous variables (positions, velocities of CG beads) using Langevin dynamics along with discrete state transitions. Physically, these discrete transitions correspond to either hydrolysis or phosphate release, with the instantaneous rate an expression of how the barrier of the reaction changes depending on the instantaneous configuration of the filament. The nature of this dependence indirectly produces all hydrolysis and phosphate release cooperativity observed in the current study.
However, full rigorous parametrization of this dependence, either through experimental data or reactive atomistic simulation, is infeasible. Experimental data cannot achieve the required resolution, and a reactive atomistic simulation is computationally prohibitive when considering the dependence of a complex reaction on a multitude of protein environments. Instead, simple arguments on the transition state stability as a function of the reactants or product stability were used. Fundamentally, the approach is similar to kinetic implications of the Hammond postulate: the free energy of the transition state has approximately the same dependence on configuration as either the products or reactants, depending on which of the products or reactants is closer in free energy to the transition state (see Supporting Materials and Methods for an additional discussion) (69, 70, 71, 72). Additional dependence of the transition state free energy on the local configuration, such as the dihedral angle of the monomeric unit, was introduced through terms k(ϕ) in the equations below. This approach resulted in the following instantaneous rate expressions. For a given subunit initially in the state i, the instantaneous rate of switching to state j is given by the following equation based on the Metropolis-Hastings-like criterion
| (1) |
where
| (2) |
Here, Uj − Ui is the energy difference between states j and i, ϕ − ϕ0 is the difference between the instantaneous dihedral angle between CG beads 2-1-3-4 of the subunit and its average value in state i, and η is the parameter that controls the explicit dihedral angle dependence, whereas and are model parameters. Computationally, the prefactor ki → j(ϕ) can be seen as specifying the rate of attempting a state transition, and pi → j gives the probability of accepting the transition. As the transition describes a chemical reaction in an equilibrium system, detailed balance implies that the rate for the reverse reaction, in which a subunit initially in state j switches to state i, is given by
| (3) |
where
| (4) |
The explicit dihedral angle dependence was modeled as a smooth step function such that it resulted into an increase in ki → j(ϕ) for the forward reaction and decrease in kj → i(ϕ)for the reverse reaction as the dihedral angle ϕ increases. The explicit dihedral angle dependence was based on our previous work (4, 5, 6), which attributes the increase in rate of hydrolysis to the flattening of the actin subunit. We set ϕ0 = −10° and used η = 0.125 for the ATP hydrolysis reaction but turned off the explicit dihedral angle dependence for the Pi release reaction by setting η = 0 (73). Additional discussion of the physical meaning of these parameters can be found in the Supporting Materials and Methods.
Parameter estimation
The parameters , , and are the UCG model parameters that need to be estimated. These were optimized using the following three conditions. The instantaneous forward and reverse reaction rates, on average, must match the known macroscopic reaction rates. This provides two conditions, one for the forward reaction and one for the reverse reaction. These two conditions were specified by the system being simulated. The third condition has more freedom in its choice, and we selected this condition such that the average acceptance probability for the forward reaction had a desired value. The motivation behind this choice was that it provides a handle to control the sensitivity of state transitions to the energy difference (Ui − Uj) between the two states. The details of parameter estimation are provided in the Supporting Materials and Methods (5, 6, 74, 75). In the final model, we set the average acceptance probability to 0.01 for both ATP hydrolysis and Pi release reactions.
Markov state model
The UCG simulations performed were analyzed through their behavior at the resolution of an MSM. The MSM resolution was based on the kinetic models used in the literature (34, 47). In this MSM description, an actin filament contains no configurational behavior; we only considered the length of actin filaments and their composition in terms of the nucleotide state. In other words, the actin filament system was represented by a state vector, with positions of elements of the vector corresponding to positions of actin subunits in a filament and the value of each element (ATP, ADP-Pi, or ADP) corresponding to the state of the nucleotide bound to the respective subunit. Mean first passage times were estimated using the mapped statistics observed in the UCG simulations and were used to parameterize the MSM. This procedure is described in more detail in the next section.
The MSM model was further extended to include polymerization and depolymerization of actin subunits. Note that we ignored any modified hydrolysis or phosphate release behavior at the ends of the filament in our MSM for simplicity. For example, the Pi release rate in the terminal subunits at the filament ends has been predicted to be different than that in the interior of the filament (40, 41), which we did not express in our model. We additionally ignored any multibody cooperative effects on the rates of polymerization and depolymerization at the two ends of the filament. As the addition of ATP-bound actin to the filament introduces energy into the local system represented by the MSM, the constraint of detailed balance was not imposed when considering the transitions related to the addition or removal of actin units. As a result, when considering polymerization, the length of the state vector at a given instant was equal to the length of the filament at that instant, and the two terminal positions of the state vector corresponded to the barbed and pointed ends of the filament. Polymerization (depolymerization) at the ends resulted in expansion (shrinking) of the state vector, whereas ATP hydrolysis and Pi release of a particular subunit resulted in a change in the value of the corresponding element of the state vector. To further understand the importance of the cooperativity in the filament, the rate parameters via the results of the UCG model were uniformly scaled to probe the effect of increased or decreased cooperativity. The model was sampled using a Monte Carlo algorithm (see Supporting Materials and Methods for details).
Results and Discussion
Multibody effects in kinetics of ATP hydrolysis and Pi release
The UCG model was used to study multibody effects in ATP hydrolysis and Pi release at the resolution of the MSM model. The hydrolysis of each actin subunit can be affected by several neighboring subunits. Ideally, one needs to consider all possible combinations of the nucleotide states of several neighboring units to study their effect on the rate of hydrolysis. To keep the number of such combinations tractable, we limited the study to a fairly small number of neighboring subunits by invoking the local nature of interactions between CG beads. The longest pairwise interactions in our model were between CG beads belonging to actin subunits that are two monomers apart in the filament. Hence, we limited our study of multibody effects to three neighboring subunits on each of the two sides of a given subunit, as described below.
For ATP hydrolysis, we designed a long UCG filament model consisting of 18,265 actin subunits (an integer number of copies of 13 subunits) as follows: we capped the barbed end of the filament with 26 ATP-bound subunits and the pointed end with 39 ATP-bound subunits to avoid any possible end effects. The remaining 18,200 subunits in the “bulk” of the filament were divided into sets of seven-subunit-long sections. The fourth subunit (marked subunit) in each section was an ATP-bound subunit, whereas three of its nearest neighbors toward the pointed end (1–3) and toward the barbed end (5–7) were randomly chosen to be either ATP-bound or ADP-Pi-bound subunits. In practice, the nucleotide states of the six neighbors of a marked subunit in each of the 2600 sections were randomly chosen from all 26 = 64 possible combinations such that there were at least 40 copies of each combination in a single filament at random locations along its length. Only marked subunits were allowed to hydrolyze, whereas all the neighbors simply underwent Langevin dynamics and were constrained to remain in their initial nucleotide state. UCG simulations were run until all marked subunits hydrolyzed. These simulations were repeated 640 times, each with a unique filament design, and the conditional mean first passage time (MFPT) for each combination of neighboring states was calculated. The inverse of the MFPT for all the hydrolysis events provides the rate for that reaction in the UCG parametrized MSM when considering reactions at the full granularity of neighbors (76). At coarser resolutions, we refer to the corresponding effective rate as the average rate, given by .
In the following, a unique six-digit “key” is used to denote a section with a particular combination of neighboring subunits. An unhydrolyzed ATP-bound subunit is represented as 0, and a hydrolyzed ADP-Pi-bound subunit is represented as 1. The key is simply the word formed by concatenating these representations, starting with the third nearest neighbor toward the pointed end and going through each consecutive neighbor up to the third nearest neighbor toward the barbed end.
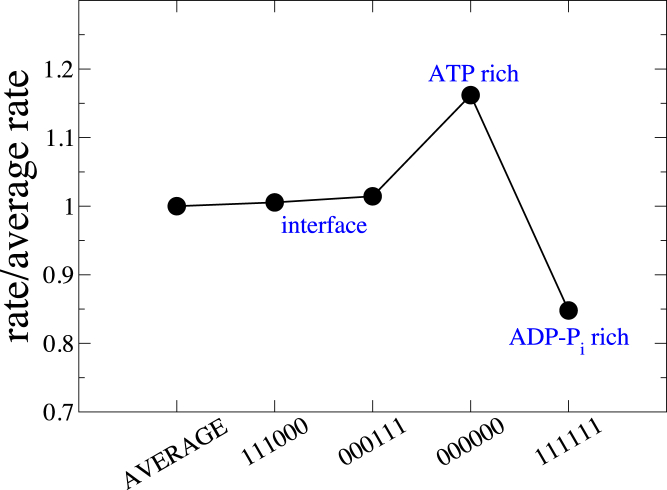
Fig. 2 and Fig. S5 a show the variation in rate of ATP hydrolysis relative to the average rate as a function of certain representative combinations of states of neighboring subunits. The explicit dihedral angle dependence in Eqs. 2 and 4 was used, with η = 0.125. The ATP hydrolysis rate of a given subunit was found to vary by a maximum of about ±20% relative to its average rate depending on whether it was in an ATP-rich or an ADP-Pi-rich environment. The reaction rate was enhanced when all six neighboring subunits were in the unhydrolyzed ATP-bound state, whereas it was suppressed when all these neighbors were in the ADP-Pi-bound state. Similar variation in hydrolysis rate was observed even when ignoring the dependence of the two farthest neighbors (data corresponding to keys X0000X and X1111X in Fig. S5 a), supporting our assumption of the local nature of interactions. The observed variation was found to be insensitive to the explicit dihedral dependence (Fig. S5 b).
Figure 2.
Multibody effect in ATP hydrolysis plotted as a ratio of the conditional rate with the average rate for specific combinations of nucleotide states of neighboring subunits. Combinations of neighboring subunit states are indicated using a key on the x axis that denotes the state (0 = unhydrolyzed, 1 = hydrolyzed) of each of the neighboring subunits, starting from the third neighbor toward the pointed end to the third neighbor toward the barbed end. Error bars indicate the standard error for each data point and are smaller than the symbol size for most of the data. To see this figure in color, go online. See Fig. S5b for data corresponding to all 64 possible combinations.
For Pi release, we designed long actin filaments similar to those used in the above simulations, and the barbed and pointed ends of the filaments were capped with ADP-Pi-bound subunits. The “bulk” of the filament was divided into seven-subunit-long sections, and each section was randomly chosen such that the fourth subunit was initially ADP-Pi bound and was allowed to release its Pi, whereas the rest of its six neighboring subunits mimicked all 64 possible combinations of states (either ADP-Pi or ADP bound) and were forced to remain in their initial state.
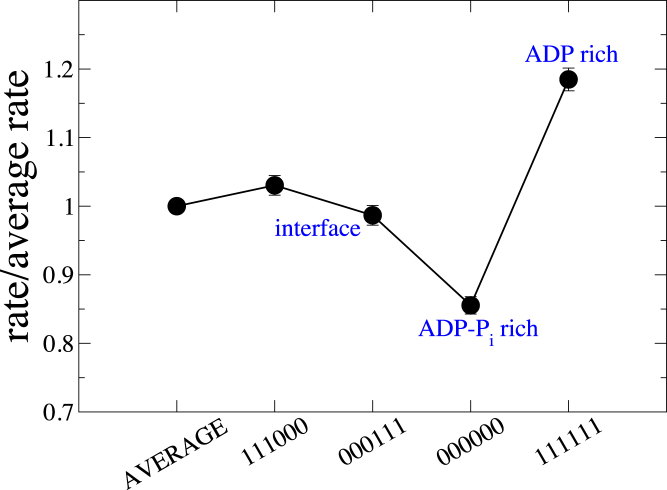
The Pi release reaction rate was also affected by the state of neighboring subunits by a maximum of about ±20% over its average rate, as seen from Fig. 3 (also see Figs. S6 and S7). Note that the explicit dihedral angle dependence in Eqs. 2 and 4 was switched off in the Pi release reaction by setting η = 0. In contrast to ATP hydrolysis, the Pi release rate of a given subunit was enhanced when all of its neighbors were free of Pi. The rate was suppressed when all of its neighboring subunits were ADP-Pi bound. At the interface, where all three neighbors along the pointed end side of the marked subunit were ADP bound and those along the barbed end side of the marked subunit were ADP-Pi bound (corresponding to key 111000), the rate of reaction was only marginally higher relative to its average value. The observed variation was found to persist within a range of the chosen value for average acceptance probability (see Fig. S6).
Figure 3.
Multibody effect in Pi release plotted as a ratio of the conditional rate to the average rate for specific combinations of nucleotide states of neighboring subunits. The key on the x axis is similar to that described in Fig. 2 (except for the new definitions 0 = ADP-Pi, 1 = ADP). Error bars indicate the standard error for each data point. To see this figure in color, go online. See Fig. S7 for data corresponding to all 64 possible combinations.
Filament growth and role of multibody effects
The role of ATP hydrolysis and Pi release on filament growth has been previously studied using kinetic models that include polymerization and depolymerization of subunits at the ends of the filament, along with ATP hydrolysis in subunits belonging to the filament (34, 35, 47). These models have been shown to agree well with experimental data in terms of the average filament growth rate, independent of whether the vectorial (35) or stochastic (34) mechanism of hydrolysis and/or Pi release is assumed. In these models, multibody effects were ignored to keep the models tractable and possibly because of lack of any evidence suggesting such effects. On the other hand, our UCG model predicted a strong multibody effect, manifested through a significant variation in both the ATP hydrolysis and the Pi release kinetics depending on the state of neighboring subunits.
In the following, we tested the implications of the cooperativity predicted by our UCG model. This was performed by extending the previous MSM characterizing only hydrolysis via the addition of states and transitions representing polymerization and depolymerization. As described below, the primary distinguishing feature of our MSM with respect to existing kinetic models was the explicit dependence of rates of ATP hydrolysis and Pi release on the nucleotide states of neighboring subunits, based on the predictions of our UCG model (Figs. S5 b and S7).
We chose to study the implication of this cooperativity by modifying two representative models reported in (34, 47) as follows: 1) in (34), the filament growth kinetics at a constant free actin concentration was studied by assuming a random mechanism of ATP hydrolysis and Pi release, and the resulting constant average filament growth rate was reported. For direct comparison, we modified their model to include the cooperativity in ATP hydrolysis and Pi release while keeping the rest of the model unmodified. 2) Filament growth kinetics in a conserved system was studied in (47), in which the total mass of actin was assumed to be constant such that at steady state, the average filament length remained constant. ATP and ADP-Pi were made indistinguishable in their model by assuming fast ATP hydrolysis. To enable a direct comparison, we only modified their model at places involving random Pi release to include our predicted cooperativity in Pi release while keeping the rest of the model unmodified.
The filament was initialized with n0 subunits and was assumed to be in a solution of free monomeric subunits at a specified concentration. Addition of a free ATP-bound subunit at the barbed end of the filament increased the filament length, whereas dissociation of the terminal subunit (ATP or ADP-Pi or ADP bound) at the barbed or pointed ends decreased its length. The rest of the subunits belonging to the filament underwent ATP hydrolysis and/or Pi release as in the original models in (34, 47). The macroscopic rate constants for these reactions are given in Table 1 and were chosen to be same as in the original models with which we compared our predictions.
Table 1.
Macroscopic Rate Constants Used in the Kinetic Models
| Model reference | Kpol. (μM−1s−1) |
Kdis., barbed (s−1) |
Kdis., pointed (s−1) |
Khyd. (s−1) | Krel. (s−1) | ||||
|---|---|---|---|---|---|---|---|---|---|
| barbed | pointed | ATP | ADP-Pi | ADP | ATP | ADP | |||
| (34) | 11.6 | – | 1.4 | 1.1 | 7.2 | – | – | 0.3 (34) | 0.004 |
| (47) | 11.6 | – | 1.4 | – | 7.2 | 0.8 | 0.27 | – | 0.003 |
Kpol. is the polymerization rate constant, Kdis., barbed is the depolymerization rate constant at the barbed end, and Kdis., pointed is that at the pointed end. Khyd. and Krel. are rate constants of ATP hydrolysis and Pi release, respectively.
The model was sampled using a Monte Carlo (MC) algorithm to study evolution of the filament, keeping track of the location of all the actin subunits in the filament. For each set of parameters, 1000 statistically independent simulations were run. Details of the MC algorithm are provided in the Supporting Materials and Methods.
Filament dynamics at constant free actin concentration
In (34), the total free actin concentration was assumed to be constant. This mimics experimental conditions in which, for example, a solution of G-actin at constant concentration is flowing through the system using microfluidic devices. Because the total concentration of free actin does not change with time, the resulting filament either grows with time if the free actin concentration is above the critical concentration or shrinks with time if the concentration is lower than the critical concentration.
The filament growth rates at different free actin concentrations obtained in experiments have been shown to be in agreement with either the vectorial or stochastic mechanisms of hydrolysis (34, 35, 47). We modified our MSM based on the kinetic model in (34) by using corresponding parameters from the first row of Table 1. For direct comparison with (34), we included all three possible bound nucleotide states of subunits in our model: ATP, ADP-Pi, and ADP. Additionally, we assumed that no polymerization or dissociation took place at the pointed end, similar to the original model in (34). Thus, the model consisted of polymerization and dissociation at the barbed end, with ATP hydrolysis and Pi release throughout the filament, and hence was identical to the model in (34). We then modified the model to incorporate the multibody effects observed in our UCG simulations by modulating the ATP hydrolysis and Pi release rates using the data in Figs. 2 and 3 (and Figs. S5 b and S7) as follows. Our MC algorithm was designed to keep track of the states of all actin subunits in the filament. This allowed us to use all of the data in Figs. S5 b and S7 because we knew the instantaneous nucleotide state of neighbors of each actin subunit.
We introduced a parameter X in the model, as discussed below, to have the ability to interpolate between a purely stochastic mechanism (X = 0) and the UCG predictions (X = 1). Because the multibody effects predicted by our UCG model were sensitive to the UCG parameters (although similar in trends; see Figs. S5 a and S6), the parameter X also allowed us to extrapolate beyond the UCG model predictions specific to the choice of UCG parameters in our final model. Given a state of neighboring subunits with a corresponding key, the net rate of ATP hydrolysis is defined as
| (5) |
where
| (6) |
Here, the first term on the right-hand side of Eq. 6 is the ratio of conditional rate of ATP hydrolysis K for a combination of states of neighboring subunits specified with key, to the average rate of ATP hydrolysis Khyd. for all such possible combinations (same quantity as the y axis in Figs. 2 and S5 b). For example, the ratio K/Khyd. (key = 000000) ≈ 1.16 for a subunit surrounded by all ATP-bound neighbors. The rate of ATP hydrolysis for each ATP-bound subunit was similarly modulated by using in Eq. 6 the ratio K/Krel. from Fig. S5 b corresponding to its instantaneous key at each MC step. When an ATP-bound subunit hydrolyzed during an MC step with an ATP hydrolysis rate governed by the instantaneous nucleotide state of its neighbors, the keys of all its neighboring subunits were updated at the end of the step, which in turn modulated the ATP hydrolysis rates of its neighboring ATP-bound subunits in all future MC steps.
The multibody rate of Pi release, , was similarly defined as follows to take into account the variation with state of neighbors:
| (7) |
where
| (8) |
The first term of the right-hand side of Eq. 8 is the ratio of conditional rate of Pi release K for a combination of states of neighboring subunits specified with the key, to the average rate of Pi release Krel. for all such possible combinations (same quantity as the y axis in Figs. 3 and S7). For example, the ratio K/Krel. (key = 111111) ≈ 1.18 for a subunit surrounded by all ADP-bound neighbors, as observed from Fig. 3. The rate of Pi release for each ADP-Pi-bound subunit was similarly modulated by using in Eq. 8 the ratio K/Krel. from Fig. S7 corresponding to its instantaneous key at each MC step. When a ADP-Pi-bound subunit released its Pi during an MC step with a Pi release rate governed by the instantaneous nucleotide state of its neighbors, the keys of all its neighboring subunits were updated at the end of the step, which in turn modulated the Pi release rates of its neighboring ADP-Pi-bound subunits in all future MC steps.
The free actin subunits were implicitly present at a constant concentration c. The filament initially consisted of n0 subunits, with a two-third fraction of the filament near the pointed end being ADP bound and the reminder tip near the barbed end made of ATP-bound subunits.
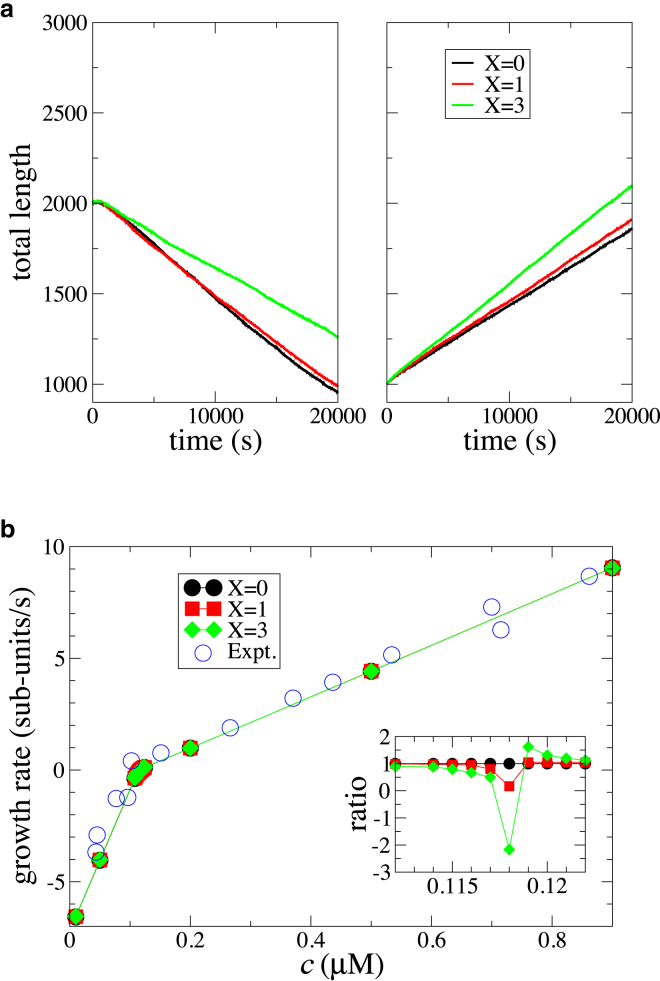
Fig. 4 a shows the mean total filament length (number of subunits) obtained from 1000 statistical runs for two different free actin concentrations. The left panel corresponds to a free actin concentration below the critical concentration. The filament, initially made of n0 = 2000 subunits, shrunk at a constant rate as subunits dissociated. The right panel corresponds to a free actin concentration above the critical concentration. The filament, initially made of n0 = 1000 subunits, grew at a constant rate. For both concentrations, the filament growth followed a different trajectory depending on the strength of multibody effects incorporated into the model.
Figure 4.
(a) Filament length dynamics for different strengths of multibody effect shown in different colors at concentrations below (left panel, c = 0.116 μM) and above (right panel, c = 0.120 μM) the critical concentration. (b) Filament growth rate (filled symbols) as a function of concentration of free actin is shown. Different colors represent different strengths of multibody effects. Open circles are experimental data taken from (34), originally extracted from experiments in (47). The inset shows the ratio of growth rate at a given strength of multibody effects compared to the growth rate at X = 0. To see this figure in color, go online.
The slope of the filament length curves, ignoring the initial transient (see Fig. S9), gives the growth rate of the filament. Fig. 4 b shows the growth rate of the filament as a function of the free actin concentration. It is evident that the filament growth rate is not dramatically affected by absence (X = 0) or presence of the multibody effects. Note that small differences in the growth rate can affect the filament length trajectories significantly, especially at longer times. Near the critical concentration, at which the growth rate is zero, the strength of multibody effects incorporated in the model affected the growth rate significantly, as the inset of Fig. 4 b shows. However, the absolute growth rate near the critical concentration was too low to make these variations significant.
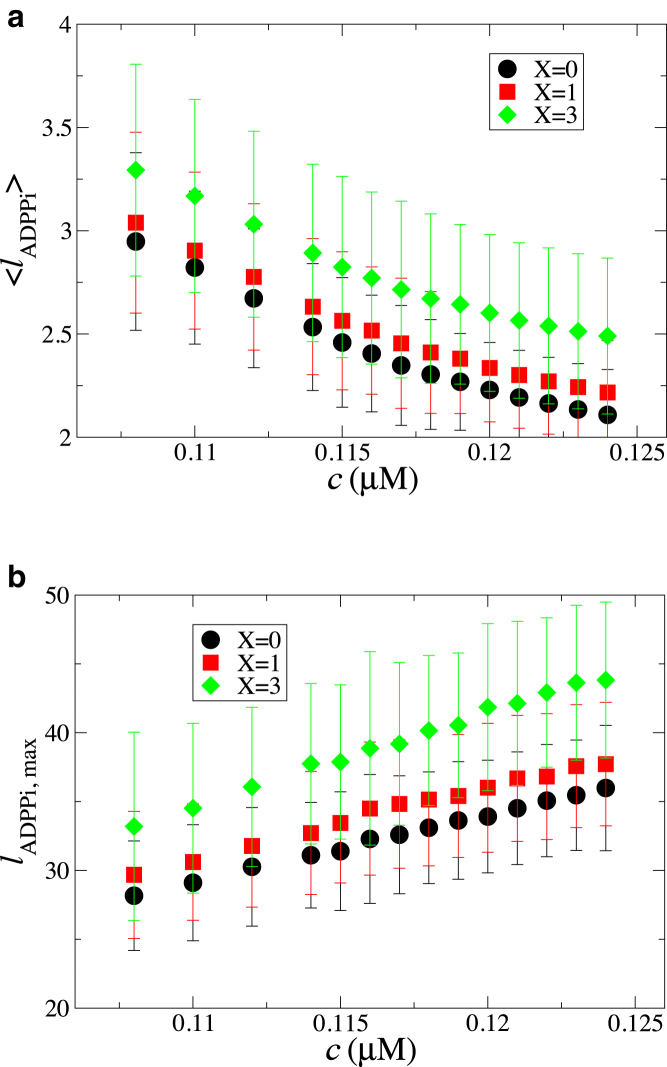
Although the filament growth kinetics were not affected significantly by the mechanism of hydrolysis and Pi release, the composition of the filaments changed significantly as multibody effects were made stronger in the model. As the filament grew at a constant rate above the critical concentration, more and more ATP subunits were added to its barbed end. These subunits then underwent hydrolysis and Pi release. As the model ignored any dissociation at the pointed end, the number of ADP subunits also grew with time. On the other hand, the number of ADP-Pi subunits remained nearly constant after an initial transient. Fig. 5 a shows the average length of a contiguous ADP-Pi section for a range of free actin concentrations obtained as a mean over the nearly constant regime and over 1000 simulation runs. At a given free actin concentration, the average length increased with increasing strength of multibody effects. This trend was also reflected in the mean value of maximal length of a contiguous ADP-Pi section shown in Fig. 5 b.
Figure 5.
Variation in filament composition due to incorporation of multibody effects in ATP hydrolysis and Pi release shown in terms of (a) the average length of a contiguous ADP-Pi section along the filament and (b) maximal length of a contiguous ADP-Pi section along the filament. Different symbols indicate varying strengths of multibody effects, as indicated in the legend. To see this figure in color, go online.
When the free actin concentration is kept constant, the filament is either growing or shrinking at a constant rate with time except at the critical concentration, for which the growth rate is zero. Because there is no steady state with constant filament length in this system (except at critical concentration), we listed 90 unique compositions for an arbitrarily chosen filament length of 325 subunits based on MC runs of the system at c0 = 0.120 μM (just above the critical concentration; see Fig. 4 b) to calculate the persistence length. The average persistence length for a filament length of 325 subunits for the random mechanism corresponding to X = 0 cooperativity was found to be 14.2 (± 0.2) μm, whereas that for X = 3 cooperativity was found to be 14.4 (± 0.2) μm.
Filament dynamics in a conserved system
A conserved system (in which the total number of subunits in the system, including free monomers and polymerized subunits, remains constant in time) was proposed in (47) to study the effect of vectorial versus stochastic hydrolysis on the transient part (see Fig. 6) of filament growth. For the conserved system, starting with an initial filament of a certain length and an initial free monomer concentration c0 that is above the critical concentration at which the net filament growth rate is positive, the free monomer concentration keeps on dropping as the filament grows, thereby reducing the polymerization rate. This continues until the concentration is just enough to balance the net polymerization and dissociation rates, resulting in a nearly steady filament length at larger times. It was predicted that although the vectorial and random mechanisms would result in a similar steady filament length, the transient from the initial filament to the steady filament would show significant variation depending on the mechanism of hydrolysis and Pi release. For a direct comparison with (47), we further modified our model such that the phenomenology between the two models was exactly the same. Firstly, ATP hydrolysis was assumed to be fast relative to Pi release, identical to the model in (47). Hence, ATP and ADP-Pi were made indistinguishable in the model, as done in (47). Further, the filament was allowed to polymerize only at the barbed end. The resulting model consisted of only two states of the nucleotide bound to actin subunits in the filament: ATP and ADP. Note that we used the notation ATP to be consistent with (47), although it equivalently corresponds to the bound nucleotide state ADP-Pi and undergoes Pi release reaction, resulting in the nucleotide state ADP. The rate constants in the second row of Table 1 corresponding to (47) were used.
Figure 6.
The total number of subunits (dotted lines) and the number of hydrolyzed subunits (solid lines) in the filament as a function of simulation time. Different colors correspond to varying strengths of multibody effects incorporated in the model, with X = 0 corresponding to a purely stochastic hydrolysis. The left panel corresponds to c0 = 0.3 μM, and the right panel corresponds to c0 = 0.7 μM. To see this figure in color, go online.
To incorporate the multibody effects as revealed in the UCG simulations into the model, an additional modification was made. The multibody rate of Pi release, , was defined using Eq. 7 to take into account the variation with state of neighbors. Similar to the preceding section, the rate of Pi release for each ATP (= ADP-Pi)-bound subunit was modulated by using in Eq. 8 the ratio K/Krel. from Fig. S7 corresponding to its instantaneous key at each MC step. When an ATP-bound subunit released its Pi during an MC step with a Pi release rate governed by the instantaneous nucleotide state of its neighbors, the keys of all its neighboring subunits were updated at the end of the step, which in turn modulated the Pi release rates of its neighboring ATP-bound subunits in all future MC steps. As mentioned earlier, the parameter X was used to vary the strength of multibody effects in the model. The specific values implied by the UCG parameters chosen in this work corresponded to X = 1. However, acknowledging the possibility of other choices for the UCG parameters, we allowed X to vary up to X = 5 (because for X = 6 and beyond).
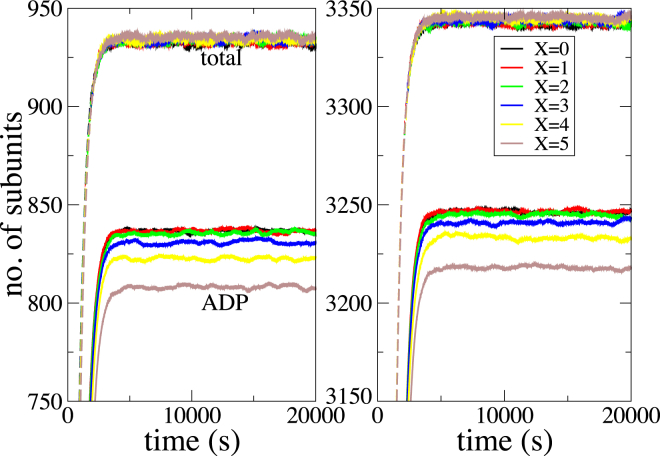
Fig. 6 shows the multibody effect on mean filament dynamics observed across 1000 simulation runs for two values of initial concentration c0. The number of hydrolyzed subunits, initially set to four, underwent a transient, beyond which it remained nearly constant. Although the qualitative features were similar across all strengths of multibody effects studied, there was an increasing delay in hydrolysis relative to the filament growth dynamics as this strength increased. Moreover, the asymptotic value of hydrolyzed subunits systematically decreased. The total number of subunits and hence the filament length remained nearly constant after undergoing a transient from its initial value of six. However, both the transient and the asymptotic value of the filament length were not found to be sensitive to the strength of multibody effects.
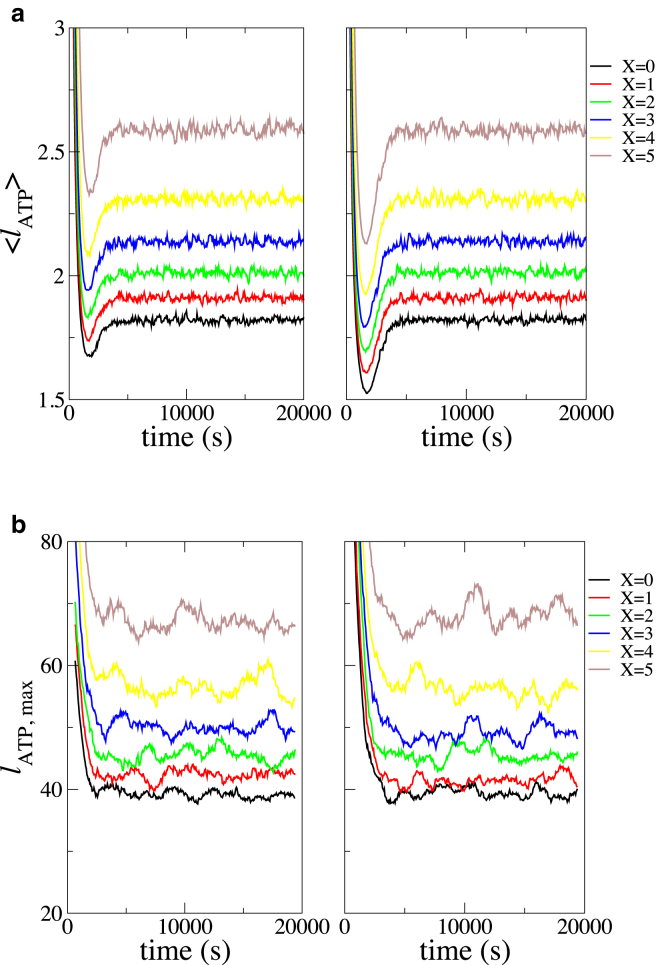
On the other hand, the filament composition showed a stronger dependence on the mechanism of Pi release. A contiguous ATP section, throughout which all the consecutive subunits were ATP bound, could easily be identified in our simulations. At every instant, we identified the number and length of these sections in the filament and calculated their mean values across all 1000 simulation runs. Fig. 7 a shows the average length of a contiguous ATP section as a function of time. In comparison to a purely random Pi release, the multibody cooperative effects predicted much longer contiguous ATP sections. The same trend was also observed in the mean of the maximal length of these sections across each simulation run, as shown in Fig. 7 b.
Figure 7.
Variation in filament composition due to incorporation of multibody effects in Pi release reaction shown as (a) average length of a contiguous ATP section along the filament and (b) maximal length of a contiguous ATP section along the filament. Different colors indicate varying strengths of multibody effects, as indicated in the legend. The left panel corresponds to c0 = 0.3 μM, and the right panel corresponds to c0 = 0.7 μM. To see this figure in color, go online.
For systematic comparison of persistence length with the previous section, we chose an initial actin concentration c0 = 0.2 μM that gave a filament of average length 325 subunits. We listed ∼90 unique compositions that the filament of length 325 subunits exhibited and calculated the average persistence length based on these compositions. The average persistence length of the filament under these conditions was found to be 13.5 (± 0.2) μm for the random mechanism corresponding to X = 0 cooperativity, 13.6 (± 0.2) μm for X = 3 cooperativity, and 13.9 (± 0.2) μm for X = 5 cooperativity.
Conclusions
Two classes of kinetic models have been proposed for actin filaments based on the mechanism of hydrolysis of ATP and the subsequent release of Pi. The random hydrolysis mechanism (2, 34, 42, 46) assumes an equal probability of ATP hydrolysis and Pi release at every position in the filament. On the other extreme, the vectorial model (8, 35, 43, 45) assumes that hydrolysis can take place only at the boundary between the unhydrolyzed and hydrolyzed parts of the filament. Although the two models fundamentally differ in terms of hydrolysis, the difference seems to be insignificant for filament dynamics, especially in terms of the filament growth rate that is typically measured in experiments.
The random hydrolysis mechanism assumes no cooperativity in hydrolysis, so that subunits at any position along the filament hydrolyze at the same rate at all times. The vectorial mechanism assumes maximal cooperativity in hydrolysis such that only those subunits that are at the interface between unhydrolyzed and hydrolyzed units undergo hydrolysis at a nonzero rate and all other subunits throughout the filament effectively have a zero rate of hydrolysis. Our UCG and kinetic models allowed us to explore the possibility of intermediate levels of cooperativity, in which the nearby neighbors affect the rate of hydrolysis of a given subunit in a filament.
More specifically, the UCG model predicted a substantial variation in the rates of hydrolysis and Pi release. The rate of ATP hydrolysis was enhanced by ∼20% when an ATP actin subunit was in an ATP-rich environment and decreases by ∼20% when in an ADP-Pi-rich environment. In the scenario of a growing actin filament, such a variation implies that the filament would be more fragmented in ATP in comparison to random hydrolysis because subunits in the ATP-rich region will hydrolyze faster to form ADP-Pi, which then slows down the hydrolysis of nearby neighbors to a certain extent. Data from our kinetic model reflected this in terms of the average and maximal lengths of ATP sections (data not shown). In contrast, the rate of Pi release from an ADP-Pi subunit was suppressed when it was in an ADP-Pi-rich environment and enhanced by about ∼20% when in an ADP-rich environment. This implies that in a growing filament, the filament would be less fragmented in ADP-Pi in comparison to random hydrolysis because subunits in the ADP-Pi-rich region of the filament will release their Pi slower to form ADP, which will then accelerate the Pi release of neighboring subunits to a certain extent. This is exactly what we observed in our kinetic model, as shown by the data in Fig. 5.
Our predictions imply that there is substantial cooperativity in ATP hydrolysis and Pi release reactions, characterized by a variation of about ±20% in the rates of these reactions relative to the corresponding average rates, and hence provide evidence for a significant deviation from a random mechanism in each of these reactions. Further, we observe that the cooperativity extends beyond the nearest neighbors. On the other hand, the rate of ATP hydrolysis at the ATP/ADP-Pi interface is not different from the average rate of ATP hydrolysis in the filament, characterized by a variation within ±1.5% relative to the average rate (Fig. 2). The same is true for the Pi release reaction (Fig. 3), in which the rate of Pi release at the interface is approximately the same as the average rate of Pi release in the filament, characterized by a variation within ±3% relative to the average rate. This is in contrast with the prediction of a strong cooperativity and the resulting implication of an enhancement in rate of Pi release at the interface by a factor of 106–108 relative to the average rate made in (44), although their analysis ignored any multibody effects beyond a simpler nearest-neighbor cooperativity (44, 48, 49). Clearly, the nature of our predicted cooperativity does not show any signs in support of a purely vectorial ATP hydrolysis or Pi release. A detailed comparison of our model with available experimental data is beyond the scope of this work and is left to be studied in the future.
An important point to consider is that the hydrolysis reaction is faster than the Pi release reaction by about two orders of magnitude (Table 1). Although the relative variation in rates of hydrolysis and Pi release are of the same extent in Figs. 2 and 3, the variation in absolute rate of the faster hydrolysis reaction is expected to play an insignificant role in filament dynamics and composition. The slower Pi release reaction is the rate-determining step and hence should have the strongest effect on filament dynamics and composition.
Although the filament composition changes significantly with the cooperativity in ATP hydrolysis and Pi release, long-length-scale filament properties such as the persistence length do not reflect this change to a measurable extent. As seen from Fig. 6, in a conserved system, a steady state characterized by a filament length that fluctuates around a constant average value was reached as the actin monomer concentration approached the treadmilling concentration. The average persistence length of the filament under these conditions was found to be approximately identical between random and cooperative mechanisms. When the free actin concentration was kept constant, the persistence length for 90 representative compositions of identical filament lengths was also found to exhibit a weak dependence on the mechanism of hydrolysis. The changes in persistence length corresponding to the changes in composition were expected to be small, given the narrow range between persistence lengths for a pure ATP filament, a pure ADP-Pi filament, and a pure ADP filament (Fig. S1).
In conclusion, our bottom-up CG strategy enabled us to probe the cooperative nature of ATP hydrolysis and Pi release in F-actin in detail. We found that the mechanism of these reactions is not fully random but does depend on the state of neighboring subunits. Although the vectorial model is a reasonable attempt made at simplifying a more accurate but complicated cooperativity such as the one we observe in this work, we did not find any evidence supporting the extent of variation in rates as is suggested by a purely vectorial model.
Our UCG model provides a framework to investigate many important problems related to ATP hydrolysis in actin. Several actin binding proteins (e.g., cofilin (77)) have affinities that depend on the state of the bound nucleotide. In recent work (60), a bottom-up mesoscale modeling approach based on atomistic simulations was used to simulate different modes of applying strain in actin filaments and to study the resulting effect on the binding and activity of the actin binding protein cofilin. Our model can be used to further investigate the implications of applying strain in actin filaments on the hydrolysis of the bound nucleotide and the resulting combined effect of strain and nucleotide state on binding of actin-binding proteins.
Author Contributions
H.H.K., A.D., and G.M.H. contributed to simulation design and analysis. H.H.K. and A.D. designed simulation code. H.H.K., A.E.P.D., and A.D. designed parameter optimization algorithms. G.A.V. designed research. A.C.S. and E.M.D.L.C. provided crucial biological insights. H.H.K., A.E.P.D., and G.M.H. drafted the manuscript.
Acknowledgments
This research was supported in part by the National Science Foundation (NSF) through NSF grant CHE-1465248 and in part by the Department of Defense Army Research Office through Multidisciplinary University Research Initiative grant W911NF1410403. The computations in this work used the Extreme Science and Engineering Discovery Environment, which is supported by NSF grant number ACI-1548562. Additional computational resources were provided by the Research Computing Center at The University of Chicago. G.M.H. was supported by a Ruth L. Kirschstein National Research Service Award (National Institute of General Medical Sciences, F32 GM11345-01). A.E.P.D. acknowledges support by the Department of Defense through the National Defense Science & Engineering Graduate Fellowship Program. E.M.D.L.C. and A.C.S. were supported by the National Institutes of Health through grant R01-GM097348.
Editor: David Sept.
Footnotes
Supporting Materials and Methods and nine figures are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(18)31011-7.
Supporting Material
References
- 1.Kabsch W., Mannherz H.G., Holmes K.C. Atomic structure of the actin:DNase I complex. Nature. 1990;347:37–44. doi: 10.1038/347037a0. [DOI] [PubMed] [Google Scholar]
- 2.Blanchoin L., Pollard T.D. Hydrolysis of ATP by polymerized actin depends on the bound divalent cation but not profilin. Biochemistry. 2002;41:597–602. doi: 10.1021/bi011214b. [DOI] [PubMed] [Google Scholar]
- 3.Rould M.A., Wan Q., Trybus K.M. Crystal structures of expressed non-polymerizable monomeric actin in the ADP and ATP states. J. Biol. Chem. 2006;281:31909–31919. doi: 10.1074/jbc.M601973200. [DOI] [PubMed] [Google Scholar]
- 4.Saunders M.G., Voth G.A. Water molecules in the nucleotide binding cleft of actin: effects on subunit conformation and implications for ATP hydrolysis. J. Mol. Biol. 2011;413:279–291. doi: 10.1016/j.jmb.2011.07.068. [DOI] [PubMed] [Google Scholar]
- 5.McCullagh M., Saunders M.G., Voth G.A. Unraveling the mystery of ATP hydrolysis in actin filaments. J. Am. Chem. Soc. 2014;136:13053–13058. doi: 10.1021/ja507169f. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Sun R., Sode O., Voth G.A. Simulating protein mediated hydrolysis of ATP and other nucleoside triphosphates by combining QM/MM molecular dynamics with advances in metadynamics. J. Chem. Theory Comput. 2017;13:2332–2341. doi: 10.1021/acs.jctc.7b00077. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Pollard T.D. Rate constants for the reactions of ATP- and ADP-actin with the ends of actin filaments. J. Cell Biol. 1986;103:2747–2754. doi: 10.1083/jcb.103.6.2747. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Carlier M.F., Pantaloni D., Korn E.D. The mechanisms of ATP hydrolysis accompanying the polymerization of Mg-actin and Ca-actin. J. Biol. Chem. 1987;262:3052–3059. [PubMed] [Google Scholar]
- 9.Wegner A. The mechanism of ATP hydrolysis by polymer actin. Biophys. Chem. 1977;7:51–58. doi: 10.1016/0301-4622(77)87014-2. [DOI] [PubMed] [Google Scholar]
- 10.Brenner S.L., Korn E.D. Evidence that F-actin can hydrolyze ATP independent of monomer-polymer end interactions. J. Biol. Chem. 1984;259:1441–1446. [PubMed] [Google Scholar]
- 11.Pollard T.D., Weeds A.G. The rate constant for ATP hydrolysis by polymerized actin. FEBS Lett. 1984;170:94–98. doi: 10.1016/0014-5793(84)81376-9. [DOI] [PubMed] [Google Scholar]
- 12.Carlier M., Pantaloni D., Korn E. The effects of Mg2+ at the high-affinity and low-affinity sites on the polymerization of actin and associated ATP hydrolysis. J. Biol. Chem. 1986;261:785–792. [PubMed] [Google Scholar]
- 13.Carlier M.F., Pantaloni D. Direct evidence for ADP-Pi-F-actin as the major intermediate in ATP-actin polymerization. Rate of dissociation of Pi from actin filaments. Biochemistry. 1986;25:7789–7792. doi: 10.1021/bi00372a001. [DOI] [PubMed] [Google Scholar]
- 14.Carlier M.F. Measurement of Pi dissociation from actin filaments following ATP hydrolysis using a linked enzyme assay. Biochem. Biophys. Res. Commun. 1987;143:1069–1075. doi: 10.1016/0006-291x(87)90361-5. [DOI] [PubMed] [Google Scholar]
- 15.Carlier M.F., Pantaloni D., Webb M.R. The hydrolysis of ATP that accompanies actin polymerization is essentially irreversible. FEBS Lett. 1988;235:211–214. doi: 10.1016/0014-5793(88)81264-x. [DOI] [PubMed] [Google Scholar]
- 16.Carlier M.F., Pantaloni D. Binding of phosphate to F-ADP-actin and role of F-ADP-Pi-actin in ATP-actin polymerization. J. Biol. Chem. 1988;263:817–825. [PubMed] [Google Scholar]
- 17.Melki R., Fievez S., Carlier M.F. Continuous monitoring of Pi release following nucleotide hydrolysis in actin or tubulin assembly using 2-amino-6-mercapto-7-methylpurine ribonucleoside and purine-nucleoside phosphorylase as an enzyme-linked assay. Biochemistry. 1996;35:12038–12045. doi: 10.1021/bi961325o. [DOI] [PubMed] [Google Scholar]
- 18.Orlova A., Egelman E.H. Structural basis for the destabilization of F-actin by phosphate release following ATP hydrolysis. J. Mol. Biol. 1992;227:1043–1053. doi: 10.1016/0022-2836(92)90520-t. [DOI] [PubMed] [Google Scholar]
- 19.Kang H., Bradley M.J., De La Cruz E.M. Identification of cation-binding sites on actin that drive polymerization and modulate bending stiffness. Proc. Natl. Acad. Sci. USA. 2012;109:16923–16927. doi: 10.1073/pnas.1211078109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Kang H., Bradley M.J., De La Cruz E.M. Regulation of actin by ion-linked equilibria. Biophys. J. 2013;105:2621–2628. doi: 10.1016/j.bpj.2013.10.032. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Hocky G.M., Baker J.L., Voth G.A. Cations stiffen actin filaments by adhering a key structural element to adjacent subunits. J. Phys. Chem. B. 2016;120:4558–4567. doi: 10.1021/acs.jpcb.6b02741. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Isambert H., Venier P., Carlier M.F. Flexibility of actin filaments derived from thermal fluctuations. Effect of bound nucleotide, phalloidin, and muscle regulatory proteins. J. Biol. Chem. 1995;270:11437–11444. doi: 10.1074/jbc.270.19.11437. [DOI] [PubMed] [Google Scholar]
- 23.Mehrafrooz B., Shamloo A. Mechanical differences between ATP and ADP actin states: a molecular dynamics study. J. Theor. Biol. 2018;448:94–103. doi: 10.1016/j.jtbi.2018.04.010. [DOI] [PubMed] [Google Scholar]
- 24.Yogurtcu O.N., Kim J.S., Sun S.X. A mechanochemical model of actin filaments. Biophys. J. 2012;103:719–727. doi: 10.1016/j.bpj.2012.07.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Bidone T.C., Kim T., Kamm R.D. Multiscale impact of nucleotides and cations on the conformational equilibrium, elasticity and rheology of actin filaments and crosslinked networks. Biomech. Model. Mechanobiol. 2015;14:1143–1155. doi: 10.1007/s10237-015-0660-6. [DOI] [PubMed] [Google Scholar]
- 26.Lyman E., Pfaendtner J., Voth G.A. Systematic multiscale parameterization of heterogeneous elastic network models of proteins. Biophys. J. 2008;95:4183–4192. doi: 10.1529/biophysj.108.139733. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Chu J.W., Voth G.A. Coarse-grained modeling of the actin filament derived from atomistic-scale simulations. Biophys. J. 2006;90:1572–1582. doi: 10.1529/biophysj.105.073924. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Fan J., Saunders M.G., Voth G.A. Coarse-graining provides insights on the essential nature of heterogeneity in actin filaments. Biophys. J. 2012;103:1334–1342. doi: 10.1016/j.bpj.2012.08.029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Saunders M.G., Voth G.A. Comparison between actin filament models: coarse-graining reveals essential differences. Structure. 2012;20:641–653. doi: 10.1016/j.str.2012.02.008. [DOI] [PubMed] [Google Scholar]
- 30.Prinz J.H., Wu H., Noé F. Markov models of molecular kinetics: generation and validation. J. Chem. Phys. 2011;134:174105. doi: 10.1063/1.3565032. [DOI] [PubMed] [Google Scholar]
- 31.Bowman G.R., Pande V., Noe F. Springer; Dordrecht, The Netherlands: 2014. An Introduction to Markov State Models and Their Application to Long Timescale Molecular Simulation. [Google Scholar]
- 32.Chodera J.D., Noé F. Markov state models of biomolecular conformational dynamics. Curr. Opin. Struct. Biol. 2014;25:135–144. doi: 10.1016/j.sbi.2014.04.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Nuske F., Wu H., Noe F. Markov state models from short non-equilibrium simulations-analysis and correction of estimation bias. J. Chem. Phys. 2017;146:094104. [Google Scholar]
- 34.Vavylonis D., Yang Q., O’Shaughnessy B. Actin polymerization kinetics, cap structure, and fluctuations. Proc. Natl. Acad. Sci. USA. 2005;102:8543–8548. doi: 10.1073/pnas.0501435102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Stukalin E.B., Kolomeisky A.B. ATP hydrolysis stimulates large length fluctuations in single actin filaments. Biophys. J. 2006;90:2673–2685. doi: 10.1529/biophysj.105.074211. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Dama J.F., Sinitskiy A.V., Voth G.A. The theory of ultra-coarse-graining. 1. General principles. J. Chem. Theory Comput. 2013;9:2466–2480. doi: 10.1021/ct4000444. [DOI] [PubMed] [Google Scholar]
- 37.Davtyan A., Dama J.F., Voth G.A. The theory of ultra-coarse-graining. 2. Numerical implementation. J. Chem. Theory Comput. 2014;10:5265–5275. doi: 10.1021/ct500834t. [DOI] [PubMed] [Google Scholar]
- 38.Dama J.F., Jin J., Voth G.A. The theory of ultra-coarse-graining. 3. Coarse-grained sites with rapid local equilibrium of internal states. J. Chem. Theory Comput. 2017;13:1010–1022. doi: 10.1021/acs.jctc.6b01081. [DOI] [PubMed] [Google Scholar]
- 39.Jin J., Voth G.A. Ultra-coarse-grained models allow for an accurate and transferable treatment of interfacial systems. J. Chem. Theory Comput. 2018;14:2180–2197. doi: 10.1021/acs.jctc.7b01173. [DOI] [PubMed] [Google Scholar]
- 40.Fujiwara I., Vavylonis D., Pollard T.D. Polymerization kinetics of ADP- and ADP-Pi-actin determined by fluorescence microscopy. Proc. Natl. Acad. Sci. USA. 2007;104:8827–8832. doi: 10.1073/pnas.0702510104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Jégou A., Niedermayer T., Romet-Lemonne G. Individual actin filaments in a microfluidic flow reveal the mechanism of ATP hydrolysis and give insight into the properties of profilin. PLoS Biol. 2011;9:e1001161. doi: 10.1371/journal.pbio.1001161. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Pieper U., Wegner A. The end of a polymerizing actin filament contains numerous ATP-subunit segments that are disconnected by ADP-subunits resulting from ATP hydrolysis. Biochemistry. 1996;35:4396–4402. doi: 10.1021/bi9527045. [DOI] [PubMed] [Google Scholar]
- 43.Pantaloni D., Hill T.L., Korn E.D. A model for actin polymerization and the kinetic effects of ATP hydrolysis. Proc. Natl. Acad. Sci. USA. 1985;82:7207–7211. doi: 10.1073/pnas.82.21.7207. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Burnett M.M., Carlsson A.E. Quantitative analysis of approaches to measure cooperative phosphate release in polymerized actin. Biophys. J. 2012;103:2369–2378. doi: 10.1016/j.bpj.2012.10.032. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Korn E.D., Carlier M.F., Pantaloni D. Actin polymerization and ATP hydrolysis. Science. 1987;238:638–644. doi: 10.1126/science.3672117. [DOI] [PubMed] [Google Scholar]
- 46.Ohm T., Wegner A. Mechanism of ATP hydrolysis by polymeric actin. Biochim. Biophys. Acta. 1994;1208:8–14. doi: 10.1016/0167-4838(94)90153-8. [DOI] [PubMed] [Google Scholar]
- 47.Ranjith P., Mallick K., Lacoste D. Role of ATP-hydrolysis in the dynamics of a single actin filament. Biophys. J. 2010;98:1418–1427. doi: 10.1016/j.bpj.2009.12.4306. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Jégou A., Niedermayer T., Romet-Lemonne G. On phosphate release in actin filaments. Biophys. J. 2013;104:2778–2779. doi: 10.1016/j.bpj.2013.05.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Burnett M.M., Carlsson A.E. Response to “on phosphate release in actin filaments”. Biophys. J. 2013;104:2780. doi: 10.1016/j.bpj.2013.05.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Mackerell A.D., Jr., Feig M., Brooks C.L., III Extending the treatment of backbone energetics in protein force fields: limitations of gas-phase quantum mechanics in reproducing protein conformational distributions in molecular dynamics simulations. J. Comput. Chem. 2004;25:1400–1415. doi: 10.1002/jcc.20065. [DOI] [PubMed] [Google Scholar]
- 51.Humphrey W., Dalke A., Schulten K. VMD: visual molecular dynamics. J. Mol. Graph. 1996;14:33–38. doi: 10.1016/0263-7855(96)00018-5. 27–28. [DOI] [PubMed] [Google Scholar]
- 52.Phillips J.C., Braun R., Schulten K. Scalable molecular dynamics with NAMD. J. Comput. Chem. 2005;26:1781–1802. doi: 10.1002/jcc.20289. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Van Der Spoel D., Lindahl E., Berendsen H.J. GROMACS: fast, flexible, and free. J. Comput. Chem. 2005;26:1701–1718. doi: 10.1002/jcc.20291. [DOI] [PubMed] [Google Scholar]
- 54.Bussi G., Donadio D., Parrinello M. Canonical sampling through velocity rescaling. J. Chem. Phys. 2007;126:014101. doi: 10.1063/1.2408420. [DOI] [PubMed] [Google Scholar]
- 55.Oda T., Iwasa M., Narita A. The nature of the globular- to fibrous-actin transition. Nature. 2009;457:441–445. doi: 10.1038/nature07685. [DOI] [PubMed] [Google Scholar]
- 56.Pfaendtner J., Branduardi D., Voth G.A. Nucleotide-dependent conformational states of actin. Proc. Natl. Acad. Sci. USA. 2009;106:12723–12728. doi: 10.1073/pnas.0902092106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Saunders M.G., Tempkin J., Voth G.A. Nucleotide regulation of the structure and dynamics of G-actin. Biophys. J. 2014;106:1710–1720. doi: 10.1016/j.bpj.2014.03.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.McCullough B.R., Blanchoin L., De la Cruz E.M. Cofilin increases the bending flexibility of actin filaments: implications for severing and cell mechanics. J. Mol. Biol. 2008;381:550–558. doi: 10.1016/j.jmb.2008.05.055. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Pfaendtner J., Lyman E., Voth G.A. Structure and dynamics of the actin filament. J. Mol. Biol. 2010;396:252–263. doi: 10.1016/j.jmb.2009.11.034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Schramm A.C., Hocky G.M., De La Cruz E.M. Actin filament strain promotes severing and cofilin dissociation. Biophys. J. 2017;112:2624–2633. doi: 10.1016/j.bpj.2017.05.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.De La Cruz E.M., Roland J., Martiel J.L. Origin of twist-bend coupling in actin filaments. Biophys. J. 2010;99:1852–1860. doi: 10.1016/j.bpj.2010.07.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.De La Cruz E.M., Gardel M.L. Actin mechanics and fragmentation. J. Biol. Chem. 2015;290:17137–17144. doi: 10.1074/jbc.R115.636472. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.De La Cruz E.M., Martiel J.L., Blanchoin L. Mechanical heterogeneity favors fragmentation of strained actin filaments. Biophys. J. 2015;108:2270–2281. doi: 10.1016/j.bpj.2015.03.058. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Otterbein L.R., Graceffa P., Dominguez R. The crystal structure of uncomplexed actin in the ADP state. Science. 2001;293:708–711. doi: 10.1126/science.1059700. [DOI] [PubMed] [Google Scholar]
- 65.Graceffa P., Dominguez R. Crystal structure of monomeric actin in the ATP state. Structural basis of nucleotide-dependent actin dynamics. J. Biol. Chem. 2003;278:34172–34180. doi: 10.1074/jbc.M303689200. [DOI] [PubMed] [Google Scholar]
- 66.Chu J.W., Voth G.A. Allostery of actin filaments: molecular dynamics simulations and coarse-grained analysis. Proc. Natl. Acad. Sci. USA. 2005;102:13111–13116. doi: 10.1073/pnas.0503732102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Fan J., Saunders M.G., Voth G.A. Molecular origins of cofilin-linked changes in actin filament mechanics. J. Mol. Biol. 2013;425:1225–1240. doi: 10.1016/j.jmb.2013.01.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Plimpton S. Fast parallel algorithms for short-range molecular-dynamics. J. Comput. Phys. 1995;117:1–19. [Google Scholar]
- 69.Hammond G.S. A correlation of reaction rates. J. Am. Chem. Soc. 1955;77:334–338. [Google Scholar]
- 70.Dinner A.R., Karplus M. Is protein unfolding the reverse of protein folding? A lattice simulation analysis. J. Mol. Biol. 1999;292:403–419. doi: 10.1006/jmbi.1999.3051. [DOI] [PubMed] [Google Scholar]
- 71.Alemany A., Rey-Serra B., Ritort F. Mechanical folding and unfolding of protein barnase at the single-molecule level. Biophys. J. 2016;110:63–74. doi: 10.1016/j.bpj.2015.11.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Alemany A., Ritort F. Force-dependent folding and unfolding kinetics in DNA hairpins reveals transition-state displacements along a single pathway. J. Phys. Chem. Lett. 2017;8:895–900. doi: 10.1021/acs.jpclett.6b02687. [DOI] [PubMed] [Google Scholar]
- 73.Chou S.Z., Pollard T.D. Mechanism of actin polymerization revealed by cryo-em structures of actin filaments with three different bound nucleotides. bioRxiv. 2018 doi: 10.1073/pnas.1807028115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Tran Q.H., Unden G. Changes in the proton potential and the cellular energetics of Escherichia coli during growth by aerobic and anaerobic respiration or by fermentation. Eur. J. Biochem. 1998;251:538–543. doi: 10.1046/j.1432-1327.1998.2510538.x. [DOI] [PubMed] [Google Scholar]
- 75.Wackerhage H., Hoffmann U., Zange J. Recovery of free ADP, Pi, and free energy of ATP hydrolysis in human skeletal muscle. J. Appl. Physiol. 1998;85:2140–2145. doi: 10.1152/jappl.1998.85.6.2140. [DOI] [PubMed] [Google Scholar]
- 76.Buchete N.V., Hummer G. Coarse master equations for peptide folding dynamics. J. Phys. Chem. B. 2008;112:6057–6069. doi: 10.1021/jp0761665. [DOI] [PubMed] [Google Scholar]
- 77.Suarez C., Roland J., Blanchoin L. Cofilin tunes the nucleotide state of actin filaments and severs at bare and decorated segment boundaries. Curr. Biol. 2011;21:862–868. doi: 10.1016/j.cub.2011.03.064. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.