Selection of Effects in Cox Frailty Models by Regularization Methods

Summary.

In all sorts of regression problems, it has become more and more important to deal with high-dimensional data with lots of potentially influential covariates. A possible solution is to apply estimation methods that aim at the detection of the relevant effect structure by using penalization methods. In this article, the effect structure in the Cox frailty model, which is the most widely used model that accounts for heterogeneity in survival data, is investigated. Since in survival models one has to account for possible variation of the effect strength over time the selection of the relevant features has to distinguish between several cases, covariates can have time-varying effects, time-constant effects, or be irrelevant. A penalization approach is proposed that is able to distinguish between these types of effects to obtain a sparse representation that includes the relevant effects in a proper form. It is shown in simulations that the method works well. The method is applied to model the time until pregnancy, illustrating that the complexity of the influence structure can be strongly reduced by using the proposed penalty approach.

1. Introduction

Proportional hazards (PH) models, and in particular the semi-parametric Cox model (Cox, 1972) play a major role in the modeling of continuous event times. The Cox model assumes the semi-parametric hazard

$$\lambda (t\mid x_i)={\lambda }_0(t)\exp ({\mathit{x}}_i^T\beta ),$$

where λ(t|x_i) is the hazard for observation i at time t, conditionally on the covariates x_i^T = (x_i1, … , x_ip). λ₀(t) is the shared baseline hazard, and β the fixed effects vector. Note that for continuous time the hazard rate λ(t|x_i) is defined as

$$\lambda (t\mid {\mathit{x}}_i)=\underset{\Delta t\to 0}{lim}P(t\le T<t+\Delta t\mid T\ge t,{\mathit{x}}_i)∕\Delta t,$$

representing the instantaneous risk of a transition at time t. Inference is usually based on maximization of the corresponding partial likelihood. This approach allows estimation of β while ignoring λ₀(t) and performs well in classical problems with more observations than predictors. As a solution to the p > n problem, Tibshirani (1997) proposed the use of the so-called least absolute shrinkage and selection operator (LASSO) penalty in the Cox model. Since then, several extensions have been proposed. In order to fit the penalized model, Gui and Li (2005) provided an algorithm using Newton–Raphson approximations and the adjusted LARS solution. Park and Hastie (2007) applied the elastic net penalty to the Cox model and proposed an efficient solution algorithm, which exploits the near piecewise linearity of the paths of coefficients to approximate the solution with different constraints. They numerically maximize the likelihood for each constraint via a Newton iteration. Also, Goeman (2010) addressed this problem and developed an alternative algorithm based on a combination of gradient ascent optimization with the Newton–Raphson algorithm. Another fast algorithm to fit the Cox model with elastic net penalties was presented by Simon et al. (2011), employing cyclical coordinate descent.

Frailty models aim at modeling the heterogeneity in the population. They can be used to account for the influence of unobserved covariates. They are especially useful if observations come in clusters, for example, if one models survival of family members or has repeated events for the same individual as in unemployment studies. The extreme case occurs if each individual forms its own cluster. For a careful investigation of identifiability issues see Van den Berg (2001). Parameter estimation in frailty models is more challenging than in the Cox model since the corresponding profile likelihood has no closed form solution. In the Cox PH frailty model, also known as mixed PH model, the hazard rate of subject j belonging to cluster i, conditionally on the covariates x_ij and the shared frailty b_i, is given by

$${\lambda }_{\mathit{ij}}(t\mid {\mathit{x}}_{\mathit{ij}},b_i)=b_i{\lambda }_0(t)\exp ({\mathit{x}}_{\mathit{ij}}^T\beta ),i=1,\dots ,n,j=1,\dots ,N_i,$$

where the frailties b_i are frequently assumed to follow a gamma distribution because of its mathematical convenience. The R package frailtypack (Rondeau et al., 2012) allows to fit such a Cox frailty model, covering four different types of frailty models (shared, nested, joint, and additive frailties). In the R package survival (Therneau, 2013) a simple random effects term can be specified, following a gamma, Gaussian, or t-distribution. A different fitting approach based on hierarchical likelihoods allowing for log-normal and gamma frailty distributions is implemented in the R package frailtyHL, see Do Ha et al. (2012). A first approach to variable selection for gamma frailty models was proposed by Fan and Li (2002). They used an iterative, Newton–Raphson-based procedure to find the penalized maximum likelihood estimator and considered three types of penalties, namely the LASSO, the hard thresholding, and the smoothly clipped absolute deviation (SCAD) penalty. However, no software implementation is available yet. The penalized gamma frailty model methodology of Fan and Li (2002) was extended to other frailty distributions, in particular to inverse Gaussian frailties by Androulakis et al. (2012). They imposed the penalty on a generalized form of the full likelihood function designed for clustered data, which allows direct use of different distributions for the frailty term and which includes the Cox and gamma frailty model as special cases. For the gamma frailty case, they modified the likelihood presented by Fan and Li (2002). However, again, no corresponding software package is available yet.

While some multiplicative frailty distributions, such as, the gamma and the inverse Gaussian, have already been extensively studied (compare Androulakis et al., 2012) and closed form representations of the log-likelihoods are available, in some situations the log-normal distribution is more intuitive and allows for more flexible and complex predictor structures though the corresponding model is computationally more demanding. The conditional hazard function of cluster i and observation j with multiplicative frailties following a multivariate log-normal distribution has the general form

$$\lambda (t\mid {\mathit{x}}_{\mathit{ij}},{\mathit{u}}_{\mathit{ij}},{\mathit{b}}_i)={\lambda }_0(t)\exp ({\mathit{x}}_{\mathit{ij}}^T\beta +{\mathit{u}}_{\mathit{ij}}^T{\mathit{b}}_i),$$

where u_ij^T = (u_ij1, …, u_ijq) is the covariate vector associated with random effects b_i, which follow a multivariate Gaussian distribution, that is, b_i ~ N(0, Q(θ)), with mean vector 0 and covariance matrix Q(θ), which is depending on a vector of unknown parameters θ. Ripatti and Palmgren (2000) show how a penalized quasi-likelihood (PQL) approach based on the Laplace approximation can be used for estimation. The method follows the fitting approach proposed by Breslow and Clayton (1993) for the generalized linear mixed model (GLMM). If, additionally, penalization techniques are incorporated into the procedure, it becomes especially important to provide effective estimation algorithms, as standard procedures for the choice of tuning parameters such as cross-validation are usually very time-consuming. A preliminary version of this work is available as technical report (Groll et al., 2016).

2. Cox Frailty Model with Time-Varying Coefficients

While for Cox frailty models with the simple predictor structure ${\eta }_{\mathit{ij}}={\mathit{x}}_{\mathit{ij}}^T\beta +{\mathit{u}}_{\mathit{ij}}^T{\mathit{b}}_i$ in the hazard function some solutions have already been given (Fan and Li, 2002, and Androulakis et al., 2012), often more complex structures of the linear predictor need to be taken into account. In particular, the effects of certain covariates may vary over time yielding time-varying effects γ_k(t). A standard way to estimate the time-varying effects γ_k(t) is to expand them in equally spaced B-splines yielding ${\gamma }_k(t)={\sum }_{m=1}^M{\alpha }_{k,m}{B}_m(t;d)$ where α_k,m, m = 1, …, M, denote unknown spline coefficients that need to be estimated, and B_m(t; d) denotes the m-th B-spline basis function of degree d. For a detailed description of B-splines, see, for example, Wood (2006) and Ruppert et al. (2003).

At this point, we address the specification of the baseline hazard λ₀(t). In general, for the cumulative baseline hazard Λ₀(·) often the “least informative” non-parametric modeling is considered. More precisely, with $t_1^0<\dots <t_N^0$ denoting the observed event times, the least informative non-parametric cumulative baseline hazard Λ₀(t) has a possible jump h_j at every observed event time $t_j^0$, that is, ${\Lambda }_0(t)={\sum }_{j=1}^N{h}_{j}I(t_j^0\le t)$. The estimation procedure may be stabilized, if, similar to the time-varying effects, a semi-parametric baseline hazard is considered, which can be flexibly estimated within the B-spline framework. Hence, in the following we use the transformation γ₀(t) : = log(λ₀(t)) and expand γ₀(t) in B-splines.

Let now z_ij^T = (1, z_ij1, …, z_ijr) denote the covariate vector associated with both baseline hazard and time-varying effects and let ${\alpha }_k^T=({\alpha }_{\mathit{k},1},\dots ,{\alpha }_{k,M})$, k = 0, …, r, collect the spline coefficients corresponding to baseline hazard or k-th time-varying effect γ_k(t), respectively. Further, let B^T(t) := (B₁(t; d), …, B_M(t; d)) represent the vector-valued evaluations of the M basis functions in time t. Then, with ν_ijk := z_ijk · B(t), one can specify the hazard rate

$$\lambda (t\mid {\mathit{x}}_{\mathit{ij}},{\mathit{z}}_{\mathit{ij}},{\mathit{u}}_{\mathit{ij}},{\mathit{b}}_i)=\exp ({\eta }_{\mathit{ij}}(t)),\text{with}{\eta }_{\mathit{ij}}(t)≔{\mathit{x}}_{\mathit{ij}}^T\beta +\sum _{k=o}^r{\mathit{v}}_{\mathit{ijk}}^T{\alpha }_k+{\mathit{u}}_{\mathit{ij}}^T{\mathit{b}}_i.$$ (1)

In general, the estimation of parameters in the predictor (1) can be based on Cox’s well-known full log-likelihood, which is given by

$$l(\beta ,\alpha ,\mathit{b})=\sum _{i=1}^n\sum _{j=1}^{N_i}{d}_{\mathit{ij}}{\eta }_{\mathit{ij}}(t_{\mathit{ij}})-{\int }_0^{t_{\mathit{ij}}}\exp ({\eta }_{\mathit{ij}}(s))\mathit{ds},$$ (2)

where n denotes the number of clusters, N_i the cluster sizes, and the survival times t_ij are complete if d_ij = 1 and right censored if d_ij = 0.

As mentioned in the introduction, a possible strategy to maximize the full log-likelihood (2) is based on the PQL approach, which was originally suggested for GLMMs by Breslow and Clayton (1993). Typically, the covariance matrix Q(θ) of the random effects b_i depends on an unknown parameter vector θ. Hence, the joint likelihood-function can be specified by the parameter vector of the covariance structure θ and parameter vector δ^T := (β^T, α^T, b^T). The corresponding marginal log-likelihood has the form

$$l^{\mathit{mar}}(\delta ,\theta )=\sum _{i=1}^n\log \left(\int L_i(\beta ,\alpha ,{\mathit{b}}_i)p({\mathit{b}}_i\mid \theta )d{\mathit{b}}_i\right),$$

where p(b_i|θ) denotes the density function of the random effects and the quantities $L_i(\beta ,\alpha ,{\mathit{b}}_i≔\underset{j=1}{\overset{N_i}{\Pi }}\exp ({\eta }_{\mathit{ij}}(t_{\mathit{ij}}){)}^{d_{\mathit{ij}}}\exp (-{\int }_0^{t_{\mathit{ij}}}\exp ({\eta }_{\mathit{ij}}(s))\mathit{ds})$ represent the likelihood contributions of single clusters i, i = 1, …, n. Approximation along the lines of Breslow and Clayton (1993) yields

$$\begin{array}{cc}\hfill l^{\mathit{app}}(\delta ,\theta )=& \sum _{i=1}^n\log L_i(\beta ,\alpha ,{\mathit{b}}_i)-\frac{1}{2}{\mathit{b}}^T\mathit{Q}(\theta )\mathit{b}\hfill \\ \hfill =& \sum _{i=1}^n\sum _{j=1}^{N_i}\left(d_{\mathit{ij}}{\eta }_{\mathit{ij}}(t_{\mathit{ij}})-{\int }_0^{t_{\mathit{ij}}}\exp ({\eta }_{\mathit{ij}}(s))\mathit{ds}\right)-\frac{1}{2}{\mathit{b}}^T\mathit{Q}(\theta )\mathit{b}.\hfill \end{array}$$ (3)

The penalty term b^TQ(θ)b results from Laplace approximation. The PQL approach usually works within the profile likelihood concept. It is distinguished between estimation of δ, given the plug-in estimate $\widehat{\theta }$ and resulting in the profile likelihood l^app (δ, $\widehat{\theta }$), and estimation of θ.

3. Penalization

In general, the roughness or “wiggliness” of the estimated smooth functions can be controlled by applying a difference penalty directly on the spline coefficients, see, for example, Eilers (1995) and Eilers and Marx (1996). However, with potentially varying coefficients in the predictor, model selection becomes more difficult. In particular, one has to determine which covariates should be included in the model, and, which of those included have a constant or time-varying effect. So far, in the context of varying coefficient models in the literature only parts of these issues have been addressed. For example, Wang et al. (2008) and Wang and Xia (2009) used procedures that simultaneously select significant variables with (time-)varying effects and produce smooth estimates for the non-zero coefficient functions, while Meier et al. (2009) proposed a sparsity-smoothness penalization for high-dimensional generalized additive models. More recently, Xiao et al. (2016) proposed a method that is able to identify the structure of covariate effects in a time-varying coefficient Cox model. They use a penalization approach that combines the ideas of local polynomial smoothing and a group non-negative garrote. It is implemented in the statistical program R and the corresponding code is available on one of the authors’ webpages. Also for functional regression models several approaches to variable selection have been proposed, see, for example, Matsui and Konishi (2011), Matsui (2014) and Gertheiss et al. (2013). Leng (2009), for example, presented a penalty approach that automatically distinguishes between varying and constant coefficients. The objective here is to develop a penalization approach to obtain variable selection in Cox frailty models with time-varying coefficients such that single varying effects are either included, are included in the form of a constant effect or are totally excluded. The choice between this hierarchy of effect types can be achieved by using a specifically tailored penalty. We propose to use

$$\xi \cdot J_{\zeta }(\alpha =\xi \left(\zeta \sum _{k=1}^r\psi {\omega }_{\Delta ,k}{\parallel {\Delta }_M{\alpha }_k\parallel }_2+(1-\zeta )\sum _{k=1}^r\varphi {\omega }_k{\parallel {\alpha }_k\parallel }_2\right),$$ (4)

where ∥ · ∥₂ denotes the L₂-norm, ξ ≥ 0 and ζ ∈ (0, 1) are tuning parameters and Δ_M denotes the ((M − 1) × M)-dimensional difference operator matrix of degree one, defined as

$${\Delta }_M=\left(\begin{array}{cccc}\hfill -1\hfill & \hfill 1\hfill & \hfill \hfill & \hfill \hfill \\ \hfill \hfill & \hfill \ddots \hfill & \hfill \ddots \hfill & \hfill \hfill \\ \hfill \hfill & \hfill \hfill & \hfill -1\hfill & \hfill 1\hfill \end{array}\right).$$ (5)

The first term of the penalty controls the smoothness of the time-varying covariate effects, whereby for values of ξ and ζ large enough, all differences α_k,l − α_k,l−1, l = 2, …, M, are removed from the model, resulting in constant covariate effects. As the B-splines of each variable with varying coefficients sum up to one, a constant effect is obtained if all spline coefficients are set equal. Hence, the first penalty term does not affect the spline’s global level. The second term penalizes all spline coefficients belonging to a single time-varying effect in the way of a group LASSO and, hence, controls the selection of covariates. Both tuning parameters ξ and ζ should be chosen by an appropriate technique, such as, for example, K-fold cross-validation (CV). The terms $\psi ≔\sqrt{M-1}$ and $\varphi ≔\sqrt{M}$ represent weights that assign different amounts of penalization to different parameter groups, relative to the respective group size. In addition, we use the adaptive weights $w_{\Delta ,k}≔1∕\parallel {\Delta }_M{\widehat{\alpha }}_k^{(\mathit{ML})}{\parallel }_2$ and $w_k≔1∕\parallel {\widehat{\alpha }}_k^{(\mathit{ML})}{\parallel }_2$, where ${\widehat{\alpha }}^{(\mathit{ML})}$ denotes the corresponding (slightly ridge-penalized) maximum likelihood estimator. Within the estimation procedure, that is, the corresponding Newton–Raphson algorithm, local quadratic approximations of the penalty terms are used following Oelker and Tutz (2015). Note that the penalty from above may be easily extended by including a conventional LASSO penalty for time-constant fixed effects β_k, k = 1, …, p.

Since the baseline hazard in the predictor (1) is assumed to be semi-parametric, another penalty term should be included controlling its roughness. If the smooth log-baseline hazard γ₀(t) = log(λ₀(t)) is twice differentiable, one can, for example, penalize its second order derivatives, similar to Yuan and Lin (2006). Alternatively, if γ₀(t) is expanded in B-spline basis functions, that is, ${\gamma }_0(t)={\sum }_{m=1}^M{\alpha }_{0,\mathit{m}}{B}_m(t;d)$, simply second order differences of adjacent spline weights α_0,m, m = 1, …, M, can be penalized. Hence, in addition to ξ · J_ζ(α) the penalty

$${\xi }_0\cdot J_0({\alpha }_0)={\xi }_0{\parallel {\Delta }_M^2{\alpha }_0\parallel }_2^2$$ (6)

has to be included. Although this adds another tuning parameter ξ₀, it turns out that in general it is not worthwhile to also select ξ₀ on a grid of possible values. Similar findings with regard to penalization of the baseline hazard have been obtained for discrete frailty survival models, see Groll and Tutz (2016). While some care should be taken to select ξ and ζ, which determine the performance of the selection procedure, the estimation procedure is already stabilized in comparison to the usage of the “least informative” non-parametric cumulative baseline hazard ${\Lambda }_0(t)={\sum }_{j=1}^N{h}_{j}I(t_j^0\le t)$ for a moderate choice of ξ₀.

4. Estimation

Estimation is based on maximizing the penalized log-likelihood, obtained by expanding the approximate log-likelihood l^app(δ,θ) from (3) by the penalty terms ξ₀ · J₀(α₀) and ξ · J_ζ(α), that is,

$$l^{\mathit{pen}}(\delta ,\theta )=l^{\mathit{app}}(\delta ,\theta )-{\xi }_0\cdot J_0(\alpha {)}_0-\xi \cdot J_{\zeta }(\alpha ).$$ (7)

The estimation procedure is based on a conventional Newton–Raphson algorithm, while local quadratic approximations of the penalty terms are used, following Fan and Li (2001).

The presented algorithm is implemented in the pencoxfrail function of the corresponding R-package (Groll, 2016; publicly available via CRAN, see http://www.r-project.org).

4.1. Fitting Algorithm

In the following, an algorithm is presented for the maximization of the penalized log-likelihood l^pen(δ, θ) from equation (7). For notational convenience, we omit the argument θ in the following description of the algorithm and write l^pen(δ) instead of l^pen(δ, θ). For fixed penalty parameters ξ₀, ξ and ζ, the following algorithm can be used to fit the model:

Algorightm PenCoxFrail

(1)

Initialization Choose starting values ${\widehat{\beta }}^{(0)}$, ${\widehat{\alpha }}^{(0)}$, ${\widehat{\mathit{b}}}^{(0)}$, ${\widehat{\theta }}^{(0)}$ (see Section (A.3) of supplementary materials).

(2)

Iteration  For l = 1, 2,… until convergence:  (a) Computation of parameters for given ${\widehat{\theta }}^{(l-1)}$     Based on the penalized score function spen(δ) = ∂lpen/∂δ and the penalized information matrix Fpen(δ) (see Section (A.1) of supplementary materials) the general form of a single Newton-Raphson step is given by $${\widehat{\delta }}^{(\mathrm{l})}={\widehat{\delta }}^{(l-1)}+({\mathit{F}}^{\mathit{pen}}({\widehat{\delta }}^{(l-1)}){)}^{-1}{\mathit{s}}^{\mathit{pen}}({\widehat{\delta }}^{(l-1)}).$$     As the fit is within an iterative procedure it is sufficient to use just one single step.  (b) Computation of variance-covariance components     Estimates ${\widehat{\mathit{Q}}}^{(\mathrm{l})}$ are obtained as approximate EM-type estimates (see Section (A.2) of supplementary materials), yielding the update ${\widehat{\theta }}^{(\mathrm{l})}$.

The PenCoxFrail algorithm stops if there is no substantial change in the estimated regression parameters collected in the parameter vector δ^T = (β^T, α^T, b^T). More mathematically, for a given small number ε the algorithm is stopped, if

$$\parallel {\delta }^{(l+1)}-{\delta }^{(l)}{\parallel }_2∕\parallel {\delta }^{(l)}{\parallel }_2\le \epsilon .$$ (8)

4.2. Computational Details of PenCoxFrail

In the following, we give a more detailed description of the single steps of the PenCoxFrail algorithm. In Web Appendix A of the supplementary materials, we describe the derivation of score function and information matrix. Then, an estimation technique for the variance-covariance components is given. Finally, we give details for computation of starting values.

As already mentioned in Section 3, the tuning parameter ξ₀ controlling smoothness of the log-baseline hazard γ₀(t) = log(λ₀(t)) needs not to be selected carefully. A possible strategy is to specify for both ζ and ξ suitable grids of possible values and then use K-fold CV to select optimal values. From our experience for the second tuning parameter ζ, which controls the apportionment between smoothness and shrinkage, a rough grid is sufficient, whereas a fine grid is needed for ξ. A CV error measure on the test data is the model’s log-likelihood evaluated on the test data, that is,

$$\mathit{cve}({\widehat{\delta }}^{\text{train}})=\sum _{i=1}^{n^{\text{test}}}\sum _{j=1}^{N_i^{\text{test}}}{d}_{\mathit{ij}}{\widehat{\eta }}_{\mathit{ij}}(t_{\mathit{ij}})-{\int }_0^{t_{\mathit{ij}}}\exp ({\widehat{\eta }}_{\mathit{ij}}(s))\mathit{ds},$$

where n^test denotes the number of clusters in the test data and $N_i^{\text{test}}$ the corresponding cluster sizes. The estimator ${\widehat{\delta }}^{\text{train}}$ is obtained by fitting the model to the training data, resulting in the linear predictors ${\widehat{\eta }}_{\mathit{ij}}(t)$. As K-fold CV can generally be time-consuming, it is again advisable to successively decrease the penalty parameter ξ and use the previous parameter estimates as starting values for each new fit of the algorithm while fixing the other penalty parameters ξ₀ and ζ. This strategy can considerably save computational time.

5. Simulation Studies

The underlying models are random intercept models with balanced design

$${\lambda }_{\mathit{ij}}(t\mid {\mathit{z}}_{\mathit{ij}},u_i)=\exp ({\eta }_{\mathit{ij}}(t)),i=1,\dots ,n,j=1,\dots ,N_i,{\eta }_{\mathit{ij}}(t)={\gamma }_0(t)+\sum _{k=1}^r{z}_{\mathit{ijk}}{\gamma }_k(t)+b_i,$$

with different selections of (partly time-varying) effects γ_k (t), k ⊂ {1, …, r}, and random intercepts $b_i~N(0,{\sigma }_b^2)$, σ_b ∈ {0, 0.5, 1}. We consider three different simulation scenarios, and the performance of estimators is evaluated separately for the structural components and the random effects variance. A detailed description of the simulation study design is found in Web Appendix B. In order to show that the penalty (4), which combines smoothness of the coefficient effects up to constant effects together with variable selection, indeed improves the fit in comparison to conventional penalization approaches, we compare the results of the PenCoxFrail algorithm with the results obtained by three alternative penalization approaches. The first approach, denoted by Ridge, is based on a penalty similar to the first term of the penalty (4), but with a ridge-type penalty on the spline coefficients, that is, $\xi \cdot \tilde{J}(\alpha )=\xi ({\sum }_{k=1}^r\parallel {\Delta }_M^2{\alpha }_k{\parallel }_2^2)$. Hence, smooth coefficient effects are obtained, though neither constant effect estimates are available nor variable selection is performed. The alternative competing approaches, denoted by Linear and Select, are obtained as extreme cases of the PenCoxFrail algorithm, by choosing a penalty parameter ζ equal to 1 or 0, respectively. The former choice yields a penalty that can choose between smooth time-varying and constant effects, while the latter one yields a penalty that simultaneously selects significant variables with time-varying effects and produces smooth estimates for the non-zero coefficient functions.

In addition, we compare the results of the PenCoxFrail algorithm with the results obtained by using the R functions gam (Wood, 2011) and coxph (Therneau, 2013), which are available from the mgcv and survival library, respectively. However, it should be noted that although both functions can in principle be used to fit Cox frailty models with time-varying effects, the use of these packages is not straightforward. Even though the gam function has recently been extended to include the Cox PH model, the estimation is based on penalized partial likelihood maximization and, hence, no time-varying effects can be included in the linear predictor. However, Holford (1980) and Laird and Olivier (1981) have shown that the maximum likelihood estimates of a piece-wise PH model and of a suitable Poisson regression model (including an appropriate offset) are equivalent. In the piece-wise PH model time is subdivided into reasonably small intervals and the baseline hazard is assumed to be constant in each interval. Therefore, after construction of an appropriate design matrix by “splitting” the data one can use the gam function to fit a Poisson regression model with time-varying coefficients and obtains estimates of the corresponding piece-wise PH model. In the gam function, an extra penalty can be added to each smooth term so that it can be penalized to be zero. This means that the smoothing parameter estimation that is part of the fitting procedure can completely remove terms from the model. Though the equivalence of piece-wise PH model and the offset Poisson model is generally well-known, to the best of our knowledge, the concept of combining it with the flexible basis function approach implemented in the gam function, including time-varying effects, has not been exploited before.

In order to fit a time-varying effects model with coxph, we first constructed the corresponding B-spline design matrices. Next, we reparametrized them following Fahrmeir et al. (2004), such that the spline coefficients are decomposed into an unpenalized and a penalized part, and then incorporated the transformed B-spline matrices into the design matrix. Finally, to obtain smooth estimates for the time-varying effects, we put a small ridge penalty on the penalized part of the corresponding coefficients. However, for this fitting approach no additional selection technique for the smooth terms, in our case the time-varying coefficients, is available. The fit can be considerably improved if the data set is again enlarged by using a similar time-splitting procedure as for the gam function.

Averaging across 50 data sets, we consider mean squared errors for baseline hazard (mse₀), smooth coefficient effects (mse_γ) and σ_b (mse_σb), defined in Web Appendix B. In addition, we investigate proportions of correctly identified null, constant and time-varying effects as well as of the correctly identified exact true model structure. Finally, all methods are also compared with regard to computational time and proportions of non-convergent simulation runs.

Simulation Study I (n = 100, N_i = 5)

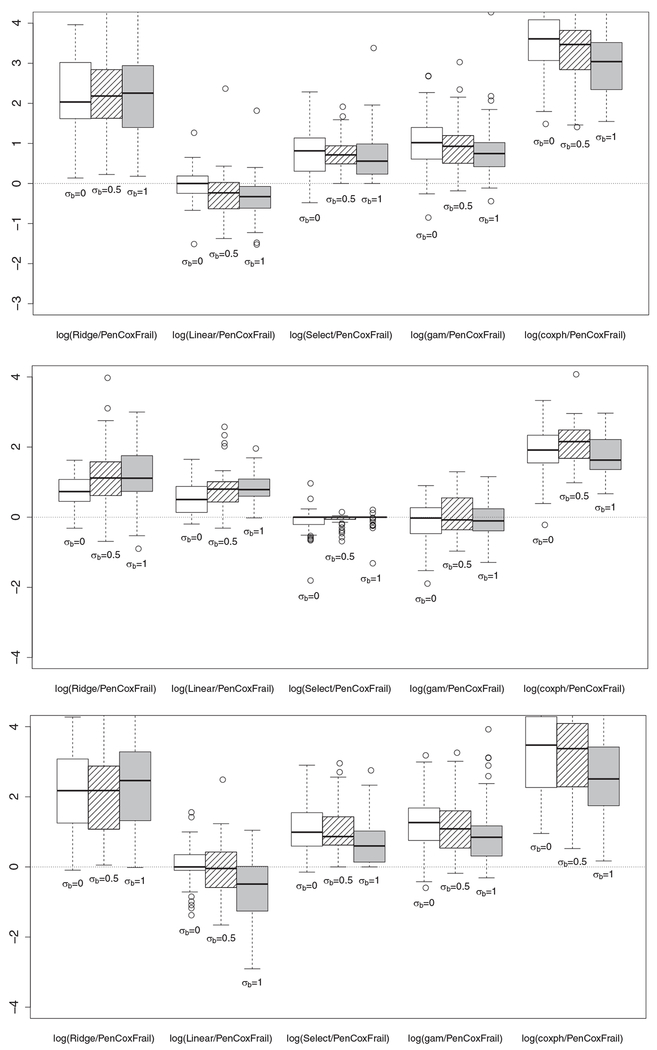
Table 1 and Web Tables S1 and S2 show the three different mean squared errors (B.1) for the Ridge, Linear, Select, gam, coxph, and the PenCoxFrail method for the three different simulation Scenarios A, B, and C. In Figure 1, the performance of the methods is compared to PenCoxFrail.

Table 1.

Results for mse_γ (standard errors in brackets)

Scenario	σb	Ridge	Linear	Select	PenCoxFrail	gam	coxph
	0	3283 (3772)	337 (427)	562 (210)	305 (276)	760 (524)	10709 (7403)
A	.5	17270 (84558)	307 (247)	769 (265)	406 (221)	992 (489)	11737 (6958)
	1	9894 (20740)	429 (583)	1044 (1064)	529 (375)	1234 (1212)	10411 (6027)
	0	1401 (958)	1196 (918)	775 (1885)	734 (878)	549 (331)	4731 (3396)
B	.5	6333 (22140)	1925 (1369)	744 (346)	835 (483)	944 (750)	7020 (3989)
	1	27218 (153493)	2798 (1609)	1140 (680)	1205 (648)	1123 (699)	7293 (4382)
	0	1474 (1820)	217 (286)	361 (210)	177 (217)	478 (323)	5248 (4937)
C	.5	1558 (1767)	200 (502)	438 (230)	204 (224)	500 (323)	4414 (2897)
	1	5024 (8620)	179 (212)	516 (236)	316 (256)	773 (735)	4057 (3336)

Figure 1.

Simulation study I: boxplots of log(mse_γ(·)/mse_γ(PenCoxFrail)) for Scenario A (top), B (middle), and C (bottom).

First of all, it is obvious that the Ridge and coxph method are clearly outperformed by the other methods in terms of mse₀ and mse_γ. It turns out that in terms of mse₀, the Select and PenCoxFrail procedures always perform very well, while the best performer in terms of mse_γ is changing over the scenarios: in Scenario A and C, where mostly time-constant or only slightly time-varying effects are present, the Linear procedure performs very well, while in Scenario B, where several strongly time-varying effects are present, the Select and gam procedures perform best. Altogether, here, the flexibility of the combined penalty (4) becomes obvious: regardless of how the underlying set of effects is composed of, the PenCoxFrail procedure is consistently among the best performers and yields estimates that are close to the estimates of the respective “optimal type of penalization.” As this optimal type of penalization can change from setting to setting and is usually not known in advance, its automatic selection provides a substantial benefit in the considered class of survival models. With respect to the estimation of the random effects variance ${\sigma }_b^2$ all approaches yield satisfactory results, with slight advantages for the Select, gam, and PenCoxFrail methods.

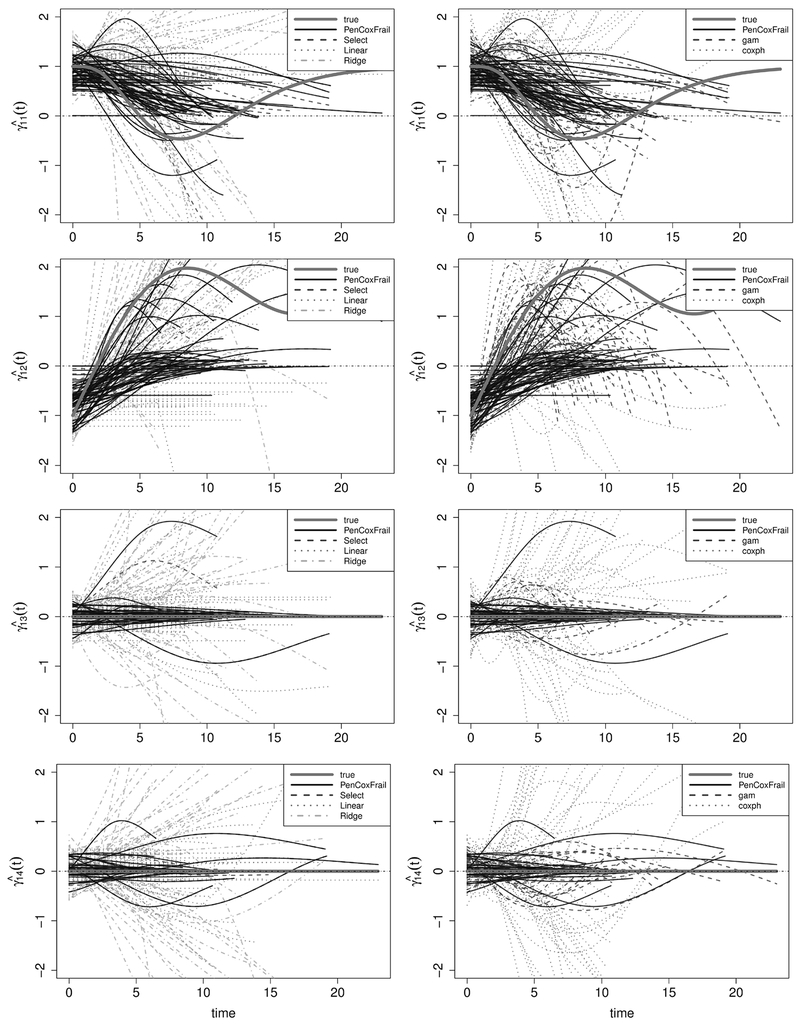
Next, we investigate the performance of the four different procedures focussing on the time-varying coefficient functions. Exemplarily, Figure 2 and Web Figures S1 and S2 show the estimated effects of the coefficient functions obtained by all six methods in Scenario B with σ_b = 1. Though generally capturing some features of the coefficient functions, the Ridge and coxph methods do not yield satisfying results, in particular with respect to coefficient functions that are zero (compare $\widehat{{\gamma }_{13}}(t)$ and $\widehat{{\gamma }_{14}}(t)$ in Figure 2). In the chosen scenario, the Select, gam, and PenCoxFrail procedures do a very good job in shrinking coefficients of noise variables down to zero, see again $\widehat{{\gamma }_{13}}(t)$ and $\widehat{{\gamma }_{14}}(t)$, as well as in capturing the features of the strongly time-varying coefficient functions γ₉(t) to γ₁₂(t). With respect to these effects, the three procedures clearly outperform the other approaches. For the time-constant coefficient functions, γ₅(t) and γ₆(t), the Linear method yields the best estimates. In general, note that though the Select and the PenCoxFrail method capture the features of the coefficient functions quite well, there is a substantial amount of shrinkage noticeable in the non-zero coefficient estimates, $\widehat{{\gamma }_5}(t)$, $\widehat{{\gamma }_6}(t)$, and $\widehat{{\gamma }_9}(t)$ to $\widehat{{\gamma }_{12}}(t)$. The resulting bias is a typical feature of LASSO-type estimates and is tolerated in return for the obtained variance reduction.

Figure 2.

Estimated (partly time-varying) effects $\widehat{{\gamma }_{11}}(t)$ to $\widehat{{\gamma }_{14}}(t)$, exemplarily for Scenario B and σ_b = 1; left: Ridge (dashed-dotted light gray), Linear (dotted gray), Select (dashed dark gray) and PenCoxFrail (black); right: gam (dashed dark gray), coxph (dotted gray) and PenCoxFrail (black); true effect in thick gray.

The Linear and Select approaches only yield good results either with respect to distinction between constant and time-varying effects or with respect to variable selection, whereas the PenCoxFrail method performs well in terms of both criteria. Also gam yields good results regarding the distinction between zero and time-varying effects, however, it fails to correctly identify constant effects. While in Scenarios A and B not a single approach is able to correctly identify the exact true model structure, in Scenario C at least the PenCoxFrail succeeds in about one fifth of the simulation runs in the three σ_b settings (compare Web Table S5).

In terms of computational time, the coxph method is by far the fastest approach, followed by the three methods ridge, linear, and select, which all depend on a single tuning parameter. Together with gam, the PenCoxFrail approach is the most demanding method because it uses two tuning parameters (compare Web Table S3). In addition, we considered the proportions of non-convergent simulation runs. The methods are considered to have converged, if criterion (8) was reached within 100 iterations. Although the ridge, linear, select, and PenCoxFrail methods did not converge in some scenarios, their performance with respect to the three mean squared errors (B.1), including the non-convergent simulation runs, is nevertheless satisfactory, particularly for PenCoxFrail (compare Web Table S4). Two additional simulation studies are presented in the supplementary materials, see Web Appendix B.

6. Application

In the following, we will illustrate the proposed method on a real data set that is based on Germany’s current panel analysis of intimate relationships and family dynamics (pairfam), release 4.0 (Nauck et al., 2013). The panel was started in 2008 and contains about 12,000 randomly chosen respondents from the birth cohorts 1971–73, 1981–83, and 1991–93. Pairfam follows the cohort approach, that is, the main focus is on an anchor person of a certain birth cohort, who provides detailed information, orientations and attitudes (mainly with regard to their family plans) of both partners in interviews that are conducted yearly. A detailed description of the study can be found in Huinink et al. (2011).

The present data set was constructed similar to Groll and Abedieh (2016). For a subsample of 2501 women retention time (in days) until birth of the first child is considered as dependent variable, starting at their 14th birthdays. To ensure that the (partly time-varying) covariates are temporally preceding the events, duration until conception (and not birth) is considered, that is, the event time is determined by subtracting 7.5 months from the date of birth, which is when women usually notice pregnancy. For each woman, the employment status is given as a time-varying covariate with six categories. Note that due to gaps in the women’s employment histories, the category “no info” is introduced. As in the preceding studies, for women remaining in this category longer than 24 months it is set to “unemployed.” Besides, several other time-varying and time-constant control variables are included. Web Tables S9 and S10 give an overview of all considered variables together with their sample proportions and Table 2 shows an extraction of the data set.

Table 2.

Structure of the data

Id	Start	Stop	Child	Job	Rel.status	Religion	Siblings	…	Federal state
1	0	365	0	School	Single	Christian	1	…	Niedersachsen
1	365	730	0	No info	Single	Christian	1	…	Niedersachsen
1	730	2499	0	Unempl./job-seeking/housewife	single	Christian	1	…	Niedersachsen
1	2499	3261	0	Full-time/self-employed	Single	Christian	1	…	Niedersachsen
1	3261	3309	1	Full-time/self-employed	Partner	Christian	1	…	Niedersachsen
2	0	365	0	School	Single	None	0	…	Thüringen
2	365	730	0	No info	Single	None	0	…	Thüringen
⋮	⋮	⋮	⋮	⋮	⋮	⋮	⋮	⋮	⋮

Note that due to the incorporated time-varying covariates, the 2501 observations have to be split whenever a time-varying covariate changes. This results in a new data set containing 20,550 lines. In order to account for regional fertility differences, we incorporate a random intercept for the German federal state where the women were born. Though this model could generally be fit with the gam function by construction of an appropriate design matrix, further splitting the data and then fitting a Poisson regression model with time-varying coefficients, in the present application this strategy would create an extremely large data set, which is not manageable. For this reason, we abstain from using the gam function. Moreover, as already pointed out in Section 5, in order to fit a time-varying effects model with coxph, again the data would have to be manually enlarged by using a similar time-splitting procedure. So, we restrict our analysis to a conventional Cox model with time-constant effects, which we use for comparison with our PenCoxFrail approach.

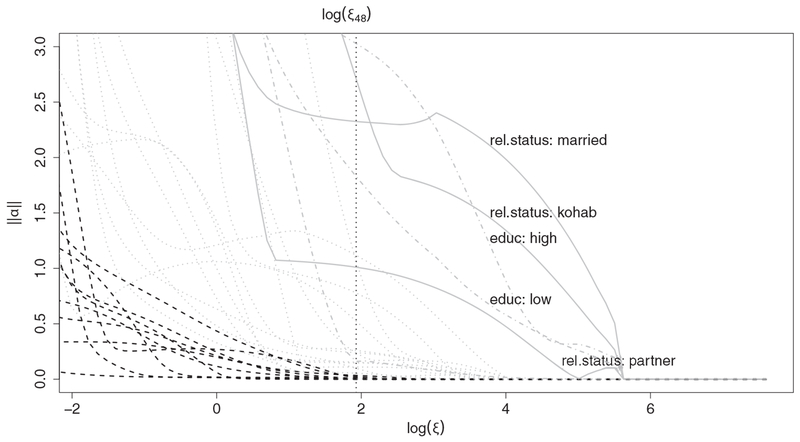
When fitting the data with PenCoxFrail, because of the quite large sample size cross-validation as the standard procedure for the choice of the tuning parameters turned out to be extremely time-consuming. Hence, we use an alternative ad hoc strategy to determine the optimal tuning parameter ξ proposed in Liu et al. (2007) and Chouldechova and Hastie (2015). In addition to considering the original variables in the data set, we generate 10 noise variables and include them in the analysis. We simply fix the second tuning parameter to ζ = 0.5 and fit PenCoxFrail using 5 basis functions for all 16 covariates. Figure 3 shows the regularization plots, which display ∥α∥₂ along the sequence of ξ values. It turns out that there are two strong predictors that enter well before the “bulk,” namely the “relationship status” (solid) and “education level” (dashed-dotted).

Figure 3.

Coefficient built-ups for the pairfam data along a transformation of the tuning parameter, namely log(ξ). The gray solid, dashed-dotted and dotted lines correspond to the original six variables, black dashed lines to the simulated noise variables; the horizontal dotted line represents the chosen tuning parameter log(ξ₄₈) = log(6.09).

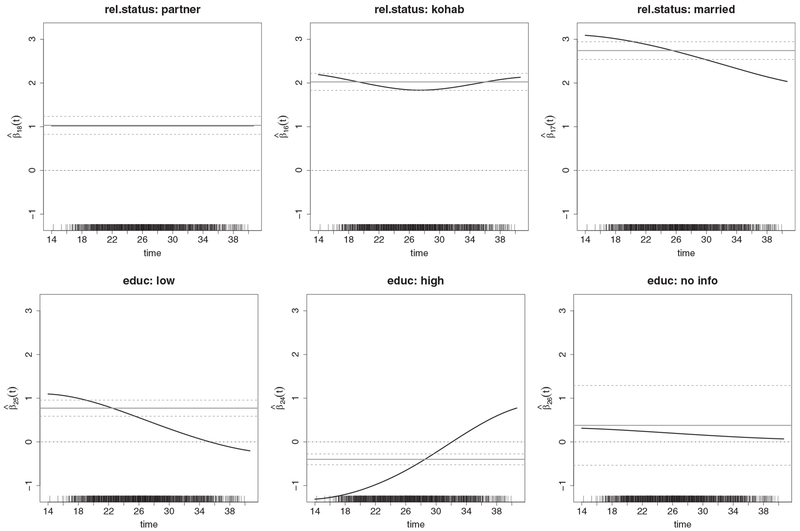
Figure 4 shows the estimated time-varying effects of the two strongest predictors, the “relationship status” and the “education level” right before the noise variables enter (that is, their corresponding spline coefficients excess the threshold ∥α∥₂ > 0.05), which corresponds to a tuning parameter choice ξ₄₈ = 6.09.

Figure 4.

Pairfam data: estimated time-varying effects for the categorical covariates “relationship status” and “education level” versus time (women’s age in years) at the chosen tuning parameter ξ₄₈ = 6.09; for comparison, time-constant effects of a conventional Cox model are shown (gray solid line) together with 95% confidence intervals.

The baseline hazard exhibits a bell shape, which is in accordance with the typical female fertility curve: it is increasing from early adolescence with a maximum in the early thirties, before it decreases when the female menopause approaches (compare Web Figure S4). For the conventional Cox model with simple time-constant effects (red dashed line) the bell shape is more pronounced in comparison to our time-varying effects approach (black solid line), where covariates are allowed to have more complex effects over time. As expected, compared to the reference single there is a positive effect on the transition rate into motherhood if women have a partner in the sense that the closer the relationship the stronger the effect. The strongest positive effect is observed for married women, though this effect clearly declines when women get older and approach menopause. Besides, it turns out that a low (high) education level of women clearly increases (decreases) the transition rate into motherhood compared to the reference medium education. Again, it is remarkable that these effects on the fertility are clearly vanishing when women approach menopause. For the remaining covariates we obtained the following results: no level of the employment status seems to have an effect on the transition into motherhood, except for the category school for which the probability of a transition into motherhood is clearly reduced as woman are usually quite young when attending school. Furthermore, we found a clear positive, time-constant effect of women having three or more siblings (reference category: no siblings), a slightly positive effect of the women’s parents educational level belonging to the category no info (reference: medium education) and a negative effect of the women’s parents being highly educated, which is diminishing over time. Moreover, negative effects of the categories other religion and Christian (reference: no religion) were observed, which both decline when women approach menopause. Finally, a certain amount of heterogeneity is detected between German federal states with an estimated standard deviation ${\widehat{\sigma }}_b=0.179$.

7. Concluding Remarks

It turns out that combining the proposed penalization approach for model selection in Cox frailty models with time-varying coefficients with the promising class of multivariate log-normal frailties results in very flexible and sparse hazard rate models for modeling survival data. The conducted simulations illustrate the flexibility of the proposed combined penalty: regardless of the underlying set of true effects, the PenCoxFrail procedure can automatically adopt to it and yields estimates close to the “optimal type of penalization.” As this optimal type of penalization can change from setting to setting and is usually unknown in advance, its automatic selection provides a substantial benefit in the considered class of survival models.

PenCoxFrail uses the Laplace approximation, which yields a log-likelihood (3) that already contains a quadratic penalty term. By appending structured penalty terms that enforce the selection of effects one obtains a penalized log-likelihood that contains all the penalties. An alternative strategy would be the indirect maximization of the log-likelihood by considering the random effects as unobservable variables. Then an EM algorithm could be derived, in which the penalization for effect selection is incorporated in the M-step. For the GLMM, the EM strategy has the advantage that one can use maximization tools from the generalized linear models framework, however, this simplification may not work for the Cox model.